Oscillatory stimuli differentiate adapting circuit topologies

Abstract

Adapting pathways consist of negative feedback loops (NFLs) or incoherent feedforward loops (IFFLs), which we show can be differentiated using oscillatory stimulation: NFLs but not IFFLs generically show ‘refractory period stabilization’ or ‘period skipping’. Using these signatures and genetic rewiring we identified the circuit dominating cell cycle timing in yeast. In C. elegans AWA neurons we uncovered a Ca2+-NFL, diffcult to find by other means, especially in wild-type, intact animals. (70 words)

Introduction

A complementary approach to the gene-by-gene approach of molecular biology is to test for response signatures (i.e., characteristic input-output features) that are associated with specific circuit motifs. A confirmed signature establishes the outlines of a biological network before the components are known. The requirements for measuring response signatures are minimal: an experimentally controlled stimulus and a measurable output; biochemical or genetic manipulations are not inherently necessary. This makes the approach attractive for many biological systems that are difficult to manipulate or have many possible genes to pursue. For example, bistability, hysteresis, or irreversibility are signatures of positive feedback loops and their detection has supported specific mechanisms(1–3).

Adaptation is a dynamic feature of biological systems, in which the output returns to (near) baseline after stimulation onset. For circuit motifs capable of adaptation, generic response signatures are currently unknown, even though adaptation is ubiquitous and serves important biological functions(4).

Only two basic types of circuits can exhibit adaptation: incoherent feedforward loops (IFFLs) and negative feedback loops (NFLs)(5–7) (Fig. 1A–D). In adapting pathways, the stimulus S (e.g., an odor) causes the temporary build-up of the response element R (e.g., intracellular Ca2+), and the subsequent decrease in R, which is the hallmark of adaptation, is either independent of R/direct (IFFL) or dependent on R/indirect (NFL): In IFFLs, S also generates an inhibitor I independently of R, and I interrupts the build-up of R or depletes R (Fig. 1A). Alternatively, a factor X, which contributes to the build-up of R, is depleted independently of R (Fig. 1B). In an NFL, the generation of the inhibitor I (or depletion of X) depends on the response R itself, i.e., I (or X) is downstream of R (Fig. 1C, D). (The output O of the pathway can be R itself or downstream of R (Fig. 1A–D).) These 2×2 fundamental options for adaptation (inhibition by I or depletion of X; dependence on R (NFL) or independence (IFFL)) are logically exhaustive, which is supported by computational exploration(6) and rigorous mathematical proofs(7). (Ours and previous definitions(6,7) of IFFLs and NFLs agree.) Thus, all models describing individual adaptation mechanisms, including integral control(5,8) and state-dependent inactivation(9,10) models, can be subsumed in these two categories; rewriting the models in mathematically equivalent forms can help expose their topologies, see Results and Supplementary Notes. (In real pathways, we expect and find that different circuits with different topologies dominate at different timescales.)

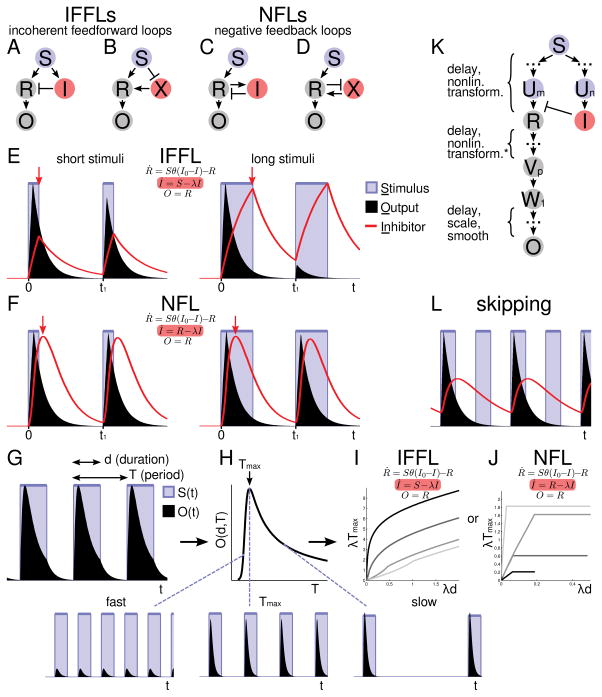
Figure 1. Discriminating IFFLs and NFLs.

A–D: Four fundamental wiring diagrams for adaptation. Here, arrows can represent multiple intermediate nodes. E, F: Stimuli always turn on at the same times 0 and t1. Red arrows indicate when the inhibitor I begins to decay. E: An IFFL system (same model as in panel I) receives two consecutive stimulus pulses of different widths but with the same onset times. F: Same as E except NFL instead of IFFL (same model as in panel J). G: Periodic stimulus pulses of duration d and period T produce output O(t)=O(t, d, T). H: The time average of O(t) is denoted by O(d, T). O(d, T) has a maximum at T_max(d). Periodic solutions shown for stimuli that are faster, exactly at, or slower than T_max (left to right). I, J: θ(x) is the step function which is 0 for x < 0 and 1 otherwise. I: IFFL model as in panel A (IFFL 1 in Fig. S2 with n→∞). Model parameters: λI₀ = 0.01, 0.1, 0.5, 0.75 (dark → light). J: NFL model as in panel C (NFL 1 in Fig. S2 with n→∞). NFL parameters: (λ, λI₀) = (0.1,0.3), (0.1,0.1), (0.4,0.1), (0.1,0.01) (dark → light). T_max(d) plot is terminated when the pulse duration d exceeds the absolute refractory time, above which the circuit would be activated twice for each stimulus pulse. K: Schematic showing equivalent classes of circuits with the same T_max(d). The asterisk denotes the specific nature of the nonlinear transformations analyzed (see Supplementary Notes). L: Period skipping in an NFL circuit (mathematical model in panels F, J).

Response signatures for IFFLs and NFLs would help elucidate a wide spectrum of poorly understood biological systems; for example, such measurements ought to resolve contrasting mechanisms which have been proposed for the same systems, e.g., the gonadotropin-releasing hormone pathway(11,12). The distinction between IFFLs and NFLs is itself biologically important because each can lead to different system behavior, e.g., steady state or oscillations.(13)

Dynamical stimuli have been used to explore biological pathways(14) and to uncover interesting new biology(15–18). Specifically, step-like and ramp-like inputs were applied to distinguish specific models(8,19–23). In an attempt to explore the general applicability of these approaches, we simulated simple adapting models and found various counterexamples, which show that it is at least unclear how previous discriminants can be used generally (Fig. S1 A–H). Also, varying stimulus strengths, e.g., ramps, can be problematic: many inducible promoters are all-or-nothing and thus threshold the stimuli; furthermore, at different concentrations or strengths, stimuli may activate different subnetworks(24), confounding the analysis.

Results

We found that a single on-off stimulus pulse does not suffice for discriminating adapting circuit types since IFFL and NFL models fit the same experimental adaptation time course equally well (Fig. S1 I, J).

Refractory period stabilization

The next more complicated on-off stimulation pattern consists of two or more pulses. Considering two simple representations of IFFLs and NFLs (Fig. 1E, F, also see Fig. S1 K, L), we noticed a fundamental difference in their responses to a second stimulus pulse: In an IFFL, the inhibitor I grows (activator X decreases) independently of the response (up to saturation) (Fig. 1A, B), and, therefore, the response to a second stimulus pulse should be smaller, the longer the first stimulus pulse was (Fig. 1E). Considering NFLs (Fig. 1F), on the other hand, we see that if the first stimulus was long enough for adaptation to ‘kick in,’ the entire circuit can be effectively shut off and the inhibition mechanism (I or X) can begin to reset; lengthening the first stimulus pulse further matters little for the second response (Fig. 1F). So, the recovery time or the “refractory period” should always be increasing with the stimulus duration in IFFLs, and should be stabilized (robust) in NFLs.

We needed a general, rigorous definition for the refractory period, and thus considered repeated on-off stimuli of duration d and period T; we defined the refractory period T_max(d) as the period at which the time-averaged output <O(t, d, T)> =: O(d, T) is maximal for fixed d (Fig. 1G, H). At the refractory period, the stimuli produce maximal output. This generalizes the common understanding of the refractory period, where for T below T_max, stimulus pulses are too fast for the system to recover due to adaptation (O(d, T) decreases with decreasing T<T_max), and above T_max, the responses recover but their time average decreases (O(d, T)~1/T for T≫T_max).

For the IFFL and NFL models in Fig. 1E, F, we calculated T_max(d) analytically and found that the slope of T_max(d) is >1 everywhere for the IFFL model while the NFL model’s T_max(d) is flat (slope=0) for intermediate d (Fig. 1I, J), which describes refractory period stabilization in Fig. 1E, F quantitatively. To check more complicated models numerically, we set 1/2 as a practical threshold for the slope ∂T_max/∂d, in-between the minimum slopes in Fig. 1I, J. We consider the refractory period ‘stabilized,’ if its slope is below 1/2 in an appropriate range of pulse durations d (to be determined by numerical exploration, see below).

There are a number of inherent advantages to defining the refractory period by way of periodic stimuli and the maximum of the time-averaged output (see Supplementary Notes), including for the mathematical analysis and for the experimental data analysis. Crucially, this paradigm allows us to only explicitly analyze the refractory periods of small circuits; the same results hold (T_max(d) is invariant) for an infinite number of additions to these circuits (Fig. 1K and Supplementary Notes).

Period skipping

Another response signature can be deduced by considering that when an NFL adapts to a stimulus, the entire circuit can be shut off from the stimulus until the inhibition resets and the system recovers (Fig. 1L). Any stimuli administered while the circuit is insulated ought to have little effect. This would result in responses ‘skipping’ stimulus pulses (a simple response pattern being 0-1-0-1-0-… (Fig. 1L), although more complicated patterns are possible (Fig. S1 M, N)).

IFFLs cannot exhibit such dynamics because of the following properties (mathematical proofs in Supplementary Notes): (1) Period skipping cannot occur in purely feedforward systems (such as the IFFLs modeled in this work including Fig. 1E, I) because these systems entrain to the stimulus period T. (2) Adding positive feedback loops (PFLs) to a (purely feedforward) IFFL does not produce period skipping because a PFL system of two species cannot show period skipping, and (3) general PFL systems cannot access period skipping solutions with on-off stimuli. These results rule out period skipping in biologically realistic IFFL circuits, leaving that possibility generically to NFLs.

Generality and uniqueness of discriminants

To explore how generic or unique these response signatures are (uniqueness of period skipping in NFLs is guaranteed), we systematically analyzed nonlinear IFFL and NFL models numerically. (Linear systems entrain and their O(d, T) are monotonic.)

First, we ruled out that the observed differences between IFFLs and NFLs were particular to the abrupt nature of the inhibition function or to the output functions in Fig. 1I, J. So, we replaced the step function θ(I₀-I) by Michaelis-Menten terms with Hill coefficients ≥1 and varied parameters and output functions (see Table S1). None of the IFFL models showed refractory period stabilization or period skipping, while 71% of the NFL models, which showed sufficient adaptation (see Methods), did. Thus, the two NFL signatures were robust to such variations.

For a more comprehensive exploration of model space, we generated >6*10⁵ implementations of IFFLs and NFLs with 86 differing wiring diagrams, interaction types, and numbers of nodes. Specifically, we analyzed systems with i) inhibitors I or activators X (Fig. 1A–D), ii) inhibitors that block the increase of a target or degrade the target, iii) nonzero baseline activities, iv) saturation due to Michaelis-Menten kinetics, v) nonlinearities due to cooperativity, and vi) additional dynamical nodes (Fig. S2). We varied parameters in an unbiased manner (0.1,1,10 for most parameters). We focused particularly on finding false positives (IFFL loops showing refractory period buffering) rather than minimizing false negatives (NFL loops failing to show signatures), which underestimates the generality of period skipping in NFLs (see Methods). For this reason also, we limited ourselves to 4 subtypes of NFLs with 3+1 nodes (+1 for output node) but covered all 82 possible IFFLs with 3+1 or 4+1 nodes. As expected, none of the IFFL circuits exhibited period skipping. A small number of IFFL circuits showed refractory period stabilization when the stimulus duration d was small, where our previous argument based on intermediate pulse durations d (Fig. 1E, F) does not apply. Requiring that refractory period stabilization occurs when d is large enough (1.5× adaptation time, i.e., time to peak when a step stimulus is turned on), left few false positives, and the likelihood of assigning an NFL circuit correctly would be 150:1 (Table 1). (See Fig. S3 for examples of T_max(d) plots.)

Table 1.

circuit type	total # tested	# adapting	# skipping + # refrac. period stabilization
NFL	315549	22188	9712 (44%)
IFFL	307584	16502	48 (0.29%)
Ratio:			150:1

Period skipping and refractory period stabilization are generic in NFLs but not in IFFLs. These results are based on a computational analysis of the set of circuit models in Fig. S2. (For details, see Methods.)

Surprisingly, both signatures occurred with or without cooperativity. Also, refractory period stabilization was detected about as often as period skipping in our computational searches (0.8:1 in the data underlying Table 1, see Methods), suggesting that neither is rare.

Published models

We also analyzed two classes of models from the literature that are thought to describe a wide spectrum of different biological systems (see Supplementary Notes for details): 1) The state-dependent inactivation model(9,10) is essentially an IFFL and neither showed period skipping nor refractory period stabilization, as expected. 2) Fold-change detection models(25) can be either IFFLs or NFLs. Using the models in ref.(26), we detected period skipping in the NFLs, but neither NFL signature in the IFFLs, as expected.

Application to experimental systems

Experimentally, we began with trial runs to establish the pulse widths and periods that were appropriate for the biological system at hand. We chose the smallest and the largest appropriate pulse durations to find T_max at those pulse durations. (By the mean value theorem, it suffices to determine the slope of a straight line through two data points to infer the slope of any smooth interpolation at a point in-between, which suffices to show refractory period stabilization.) In that process, we also detected period skipping around the smallest pulse periods we applied, which an analysis of the simple NFL models in Fig. 1F, J suggested (Fig. S4).

Circuits dominating cell cycle timing in S. cerevisae

The cell cycle control system in budding yeast involves dozens of interacting genes and consists at its core of at least the CDK-APC/C oscillator(27) (Fig. 2A, subcircuits in B–F) and a proposed ‘global transcriptional oscillator’ (GTO)(28–31), a cyclical chain of transcription factors (Fig. 2G). Given the many different subsystems, it is unclear which one(s) predominantly set(s) cell cycle dynamics, i.e., timing and robustness, if any.

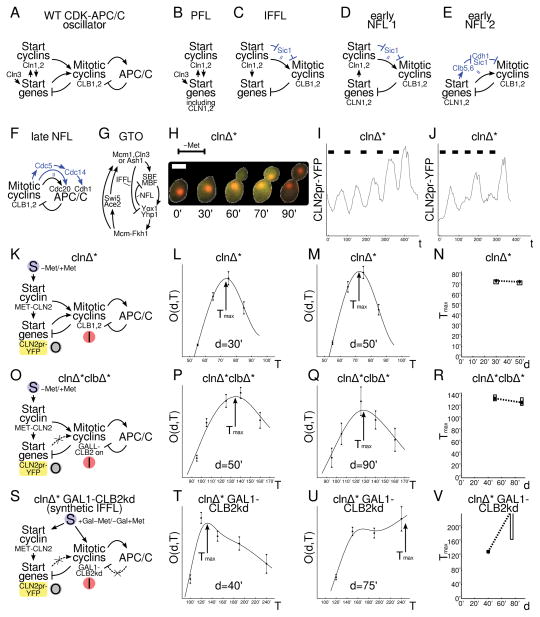
Figure 2. Signatures identify dynamically important NFLs in yeast cell cycle control mutants and can be abolished by an artificial IFFL.

All cells have the same CLN2pr-YFP construct by crossing. Abbreviations: clnΔ*=cln1–3Δ MET-CLN2, clbΔ*=clb1–6Δ GALL-CLB2, −Met/+Met = absence/presence of methionine in the media, Gal = galactose. A: Schematic of the wild-type CDK-APC/C cell cycle control system. B–F: Subcircuits from panel A with blue arrows indicating the intermediate steps which the black arrows summarize. G: Schematic of global transcriptional oscillator (GTO) model adapted from ref.(30,31). H: A clnΔ* cell undergoes one cell cycle after MET-CLN2 is induced from 0′ to 30′ in −Met medium. Nuclei marked by Htb2-mCherry. Scale bar (white): 5 μm. I: Sample time course of CLN2pr-YFP in a clnΔ* cell subjected to five −Met pulses of duration d=30′ and period T=85′ (black bars) inducing five complete cell cycles. J: A clnΔ* cell showing period skipping (−Met pulses d=30′, T=65′ (black bars)). The cell cycle starts (and completes) only in response to pulses 1, 3, 5, as determined by budding, nuclear division, and cytokinesis. K, O, S: Schematic of CDK-APC/C cell cycle control system in indicated strains, with stimulus (S), inhibitor (I), and output (O) indicated. Crossed-out, dashed arrows indicate the circuits and interactions that have been eliminated or crippled. L,M,P,Q,T,U: Output (fluorescence from fraction of consistently responding (non-skipping) cells) mean +/− SEM vs. stimulus period T for fixed pulse duration d, shown together with smooth spline fit used for estimating the peaks. Number of cells (about 100–200) underlying each data point specified in Methods. N,R,V: Best fit T_max(d) (diamond), central 90% confidence interval (box), and linear interpolation (dashed line).

By deleting CLN1–3 cyclins and introducing a MET-CLN2 construct (Start cyclin CLN2 expressed during methionine withdrawal (−Met)), we eliminated the PFL and the early NFL 1 (Fig. 2B, D) and placed cell cycle Start under exogenous control in clnΔ*(=cln1–3Δ MET-CLN2) cells(32) (Fig. 2H–K). With a long MET-CLN2 pulse which stops short of initiating a second cell cycle, transcription of cell-cycle periodic genes rises and falls once(32), demonstrating that the system adapts to Cln2, which rules out the simplest version of the GTO lacking IFFLs or NFLs. We also introduced a CLN2pr-YFP construct to report Start (SBF) cluster gene activity, which turns on roughly with budding (Fig. 2H).

We administered five −Met (Cln2 on) pulses of varying durations d and periods T (Fig. 2I, J). For long periods, cells responded to all five pulses (≈60% (n=102) at d=50′, T=65′) (Fig. 2I). In contrast, with short periods, cells commonly skipped stimulus pulses (14% (n=126) performed 5 cell cycles with d=50′, T=55′) (Fig. 2J). Given our mathematical results, we concluded that the overall dynamic was governed by NFLs, e.g., the early (2), late, or GTO NFLs (Fig. 2E–G); the IFFLs (Fig. 2C, G) played a minor role, if any. (For skipping in a related context, see ref.(33))

In this system, the refractory period describes the time it takes for the cell cycle to reset, potentially correlated with cell cycle completion. Which subcircuits, if any, make this timing robust is unknown. We defined the output O(d, T) as the fraction of consistently responding (non-skipping) cells, multiplied by their CLN2pr-YFP signal (see Methods and Fig. S5). The peak in O(d, T), defining the refractory period, was due to fast pulses lowering the fraction of cells that responded to MET-CLN2 pulses and large periods decreasing the time-averaged CLN2pr-YFP signal. T_max was remarkably stable (73′-74′, ≈cell cycle period for mother cells in SC glucose) as we changed d (=30′,50′) (Fig. 2L–N, slope T_max(d) <1/2 with >99.9% confidence). So, in addition to period skipping, refractory period stabilization also indicated that cell cycle dynamics was set by NFLs (e.g., early (2), late, or GTO), not the IFFLs.

We wondered whether refractory period robustness was a consequence of the interlocking NFLs in the system (Fig. 2A, K). So, we deleted CLB1–6 cyclins and induced mitotic cyclin CLB2 constitutively in clnΔ*clbΔ*(=clnΔ*clb1–6Δ GALL-CLB2) cells in galactose, which eliminated the early NFL 2 (Fig. 2E) as well as any transcriptional control of mitotic cyclins (Fig. 2O). Again, the refractory period turned out to be well-stabilized (128′-135′, ≈cell cycle period in SC galactose) when d (=50′,90′) changed (Fig. 2P–R, slope T_max(d) < 1/2 with >98% confidence). Thus, the early NFL 2, in addition to the early NFL 1 and the IFFLs, was unnecessary for normal overall timing and robustness in the cell cycle control system.

To investigate whether the late NFL (Fig. 2F) between B-type cyclins and APC was responsible for refractory period stabilization, we constructed a clnΔ* GAL1-CLB2kd strain, in which a pulse of galactose/-Met simultaneously induced cell cycle entry, Start transcription, and a pulse of undegradable Clb2kd, which blocks mitotic exit (plausibly ultimately overcome by autonomous Cdc14 pulses)(34,35). This system constituted an artificial IFFL (Fig. 2S). Now, T_max(d) changed markedly between 132′ at d=40′ and >167′ at d=75′ (Fig. 2T–V, slope T_max(d)>1/2 with > 99.9% confidence). This was due to longer Clb2kd induction blocking Start transcription for longer periods, as expected for an IFFL (Fig. 1E). So, this artificial IFFL revealed the predicted T_max(d) signature for IFFLs; thus, our procedure was effective at detecting IFFLs, if they existed. Furthermore, breaking or overriding all three CDK-APC/C NFLs, including the late Clb1,2-CDK-APC/C loop, finally eliminated refractory period stabilization; the late Clb1,2-CDK-APC/C NFL dominated the dynamics; the other circuits, including the GTO adaptation loops, played a minor role in the overall cell cycle dynamics.

Circuit for adaptation in C. elegans AWA neurons

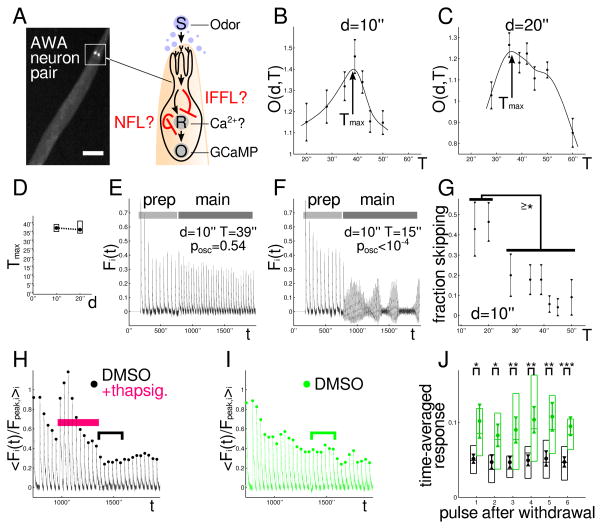
Response adaptation is a core feature of most neurons and plays a key role in behavior.(4) We turned to sensory neurons in C. elegans, several of which, e.g., AWA, ADL, and ASH, show a spike and subsequent adaptation in intracellular Ca2+ upon step-like odor stimulation. Ca2+ adaptation, specifically, is thought to play a key role in C. elegans behavior(24,36). We focused on the AWA neuron pair, which is one of two main chemoattractive olfactory sensory neuron pairs in C. elegans(37). Although many genes involved in C. elegans sensory processing have been discovered, a molecular circuit-level understanding of adaptation, a key neuronal computation, is currently lacking.

We analyzed odor-evoked Ca2+ responses in intact, wild-type animals (Fig. 3A). We stimulated worms expressing an AWA-specific Ca2+ sensor (GCaMP)(24,38), with periodic on-off pulses of diacetyl, a known AWA odor(38) (Fig. S6 A–G and Methods for details). We measured total AWA Ca2+ output for seven different pulse periods T at two pulse durations d (=10″,20″) (Fig. 3B–D, see E for a sample trace). (We first administered a series of 10 preparatory odor pulses allowing responses to stabilize(24,38) and for calibration across recordings (Methods).) The output peaked at refractory period T_max=37″-38″ at both pulse durations (Fig. 3B–D); thus, the slope of T_max(d) was close to zero in-between (<1/2 with confidence 0.96) and was therefore stabilized, indicating an NFL.

Figure 3. A Ca2+-NFL leads to adaptation in C. elegans AWA neurons.

A: C. elegans worms expressing GCaMP in the AWA olfactory sensory neurons pulsed with diacetyl. ‘?’ indicates that the detailed molecular mechanism of Ca2+ adaptation, including circuit type and the adapting node R, were unknown. Scale bar: 100 μm. B, C: Output mean +/− SEM vs. stimulus period T for fixed pulse duration d, shown together with smooth spline fit used for estimating the peaks. Number of worms underlying each data point: 28,15,28,28,35,24,11 (B), 29,49,62,37,31,27,11 (C) (left to right). Experiments repeated to ensure sufficiently small SEM/mean ratio. D: Mean T_max(d) (circle), central 90% confidence interval (box), and linear interpolation (dashed line). For d=10″: mean=38″, interval=36″-40″; for d=20″: mean=37″, interval=35″-42″. E, F: Recordings without (E) or with (F) detectable period skipping at relatively low or high stimulus frequencies, respectively. The first ten preparatory pulses have the same period and duration across all trials. G: Fraction of worms +/− SEM showing significant period skipping (p_osc<0.05) at d=10″. (≥*): Differences between fractions are at least significant with respect to p=0.05 threshold -- or lower. H, I: Pulses under brackets compared in panel J. H: Ca2+ levels before, during, and after thapsigargin application (magenta bar). The last preparatory pulse is the first pulse shown. Beginning with the second pulse shown, the pulse duration and period were switched to d=20″, T=39″. Normalization by the average of the last two prep response pulse peak heights. (Normalization by mean of the last two prep response pulses yields similar results.) Media contain 0.3% DMSO throughout. Mean over 25 worms. I: Same as H except DMSO-only control. Mean over 13 worms. J: Time-average of the response pulses after removal of thapsigargin in H (black), compared to control in I (green), showing continued depression of the responses. Circle: mean, triangles: mean +/− SEM, box: 1st, 2nd, and 3rd quartiles. (Analyzed pulses indicated by black or green bracket in H and I, respectively.) *: p<0.05, **: p<0.01, ***: p<0.001. All p value tests one-sided.

Also, with fast odor pulses (T=15″ or 20″), many of the worms showed clearly noticeable period skipping (Fig. 3F). We devised a statistical test (p_osc) for detecting low-frequency modulations(32) (Methods) and observed a significant jump in the number of worms with low-frequency response modulations in our T=15″ or T=20″ recordings compared to other periods (Fig. 3G). According to our mathematical analysis, this was another indicator of an NFL.

We wondered whether Ca2+ forms an NFL onto itself. In the absence of our measurements, we had no particular reason to pursue this hypothesis given that previous results, if anything, suggested an IFFL(39,40). We tested for a Ca2+-NFL in AWA by dynamically manipulating Ca2+ levels using thapsigargin, a widely-used inhibitor of SERCA Ca2+-pumps, which remove Ca2+ from the cytosol(41). We added thapsigargin to the media for ten odor pulses (Fig. 3H). The odor-induced Ca2+ responses surged initially, as expected for thapsigargin; however, the responses adapted again within 5–7 odor pulses, consistent with Ca2+ boosting its own inhibition mechanism. Removal of thapsigargin caused a depression of Ca2+ levels (hyper-adaptation) compared to the no-drug control (Fig. 3I, J), which is consistent with the inhibition mechanism decaying slowly, reflecting a memory of elevated Ca2+ levels. (In contrast, elevated Ca2+ would not increase inhibition in an IFFL, and after thapsigargin removal, odor responses would be at normal levels.) Subsequent recovery showed that over-adaptation was not due to (permanent) damage. Furthermore, longer thapsigargin treatment excluded Ca2+ depletion or non-specific cell exhaustion for causing adaptation (Fig. S6 H). Thapsigargin itself did not act noticeably as an odor itself (Fig. S6 I). Since the changes in Ca2+ were at biologically relevant time scales and magnitudes, these results provide evidence for a physiological Ca2+-NFL causing adaptation in AWA neurons in intact C. elegans worms.

Discussion

The refractory period is a natural way of characterizing adapting systems, in part, because it involves quantities with intuitive units (d, T_max: time, ∂T_max/∂d: unitless). It is also germane to biology and not derived from other fields of science or engineering.

Our approach has inherent limitations: not all IFFLs and NFLs can be distinguished by dynamical measurements(42), and the detection of circuit motifs does not, for example, specify biochemical species. However, our response signatures were reliable and useful in practice, and the same limitations apply to bistability, hysteresis, and irreversibility, which do not identify all PFLs(43), but have proven their usefulness nevertheless.

A stabilized refractory period implies that NFLs have robust timing, which may be an advantageous feature, e.g., rendering cell cycle timing robust to noise. We speculate that this leads to NFLs predominating in nature, which may also be why the dependence of the refractory period on stimulus duration has been overlooked. Skipping in NFLs represents a strong high-frequency filter, which ignores fast pulses. For the cell cycle, this may be advantageous but for other systems, the failure to track inputs might represent a trade-off in exchange for other NFL properties, e.g., a stable refractory period.

Online Methods

1 Computational exploration of model circuits

The following algorithm was implemented in Matlab R2010b (code available upon request):

1. Ordinary differential equations (ODEs) with parameters and interactions described in Fig. S2 or Table S1 were generated.

2. Steady-state levels were calculated for the dynamic variables at S=0 and S=1 (only S=0 for NFLs) by plugging the model parameters into formulas for the steady-state solutions, which had been derived for each model by hand. If the steady-state levels were not defined (i.e., =±∞), the model was not analyzed further.

3. To quantify how well the model adapted, the ODEs were solved numerically for a step stimulus (S=0 to S=1). Nine output nonlinearities (O=R, O=R², O=R³, …) corresponding to the output functions in Fig. S2 and Table S1 were tested. Only those models and output functions were pursued further, in which adaptation was sufficiently strong (after a transient peak, the output declined by more than 80%).

4. The ODEs were then solved with repeated on (S=1) and off (S=0) stimuli of duration d and period T using Matlab’s ode45 function. We employed various means to speed up the calculations, such as interpolating initial conditions based on neighboring solutions and extrapolating exponential convergence. The computations were stopped if the solution vector x(t) converged ||x(t_i)−x(t_i−T)||/||x(t_i)||<10⁻¹², where t_i is the time point right after the i’th S=1 stimulus, before 20000/T repetitions. If the solutions did not converge, a test for period skipping was performed and, if positive, the model was counted toward the number of adapting models in Tables 1 and S1, but otherwise not analyzed further. For period skipping, the solutions to the last n={1,…,5} stimulus pulses were simply checked for convergence to the n prior solutions (fractional error < 10⁻¹²). We focused particularly on finding false positives (IFFL loops showing refractory period buffering) rather than minimizing false negatives (NFL loops failing to show signatures) by gearing our computer code primarily to calculating T_max(d) and detecting period skipping only if it occurs in that process. Since the search algorithm stopped when period skipping was detected, the number of models with period skipping includes models which may also stabilize refractory periods, see main text.

5. Initially, a fixed set of pulse durations d={0.05,0.15,…,0.55,0.75,…,2.15,2.65} and a set of periods T ranging from d+0.005 to 10 or 30 (depending on d) were studied. If O(d, T) was increasing for the largest values of T in this set, T was increased incrementally (up to a maximum value of 1000) until O(d, T) decreased. If O(d, T) had a maximum as a function of T, the intervals around the maximum were bisected to identify the maximum more accurately. If O(d, T) had multiple maxima as a function of T, the largest period corresponding to a maximum was taken for T_max(d). Only those models were pursued further, in which O(d, T) showed a maximum for T>d, i.e., where T_max>d, for some d in the initial set. The number of these models was added to the number of adapting models from step 4., and the sums are indicated in Tables 1 and S1. (Thus, we counted as the number of adapting models those that adapted sufficiently to a step function and showed either a nontrivial T_max refractory period or period skipping.)

6. If O(d, T) had a maximum for T>d for any of the initial d values (5.), d was increased and T_max(d) calculated until the slope of T_max(d) (∂T_max(d)/∂d) approached 1 or until T_max exceeded the maximum allowed T. Then, T_max(d) was smoothed everywhere by calculating additional T_max(d) points on a denser set of d where the slope of T_max(d) changed rapidly.

2 Strains

2.1 S. cerevisae strains

Standard methods were used throughout. All strains were W303-congenic. Strains SJR14a4d and SJR12a5a were used previously(32). The CLB2kd mutation and the GAL1-CLB2kd construct have been used in ref.(34) and ref.(35), respectively.

Genotypes:

• SJR14a4d: cln1Δ cln2Δ:CLN2pr-Venus:TRP1 cln3Δ:LEU2 trp1Δ:TRP1:MET3-CLN2 HTB2-mCherry:HIS5

• SJR12a5a: SJR14a4d background, clb1Δ-clb6Δ:KanMX clb2Δ:GALL-CLB2:URA3-clb5Δ:KanMX clb3Δ:TRP1 clb4Δ:his3:KanMX

• SJR82c10b: SJR14a4d background, ura3Δ:GAL1-CLB2kd:URA3

2.2 C. elegans strains

We used the N2-based CX14887 strain with integrated gpa-6::GCaMP2.2b which has been described in ref.(24). Animals were raised at 20C on nematode growth medium (NGM) plates, seeded with Escherichia coli OP50 bacteria as a food source. All experiments were performed with young adults, age-synchronized by picking L4 stage animals to fresh food plates 12–24 h before the experiment.

3 Experimental set-up

3.1 S. cerevisae experiments

Cells were grown overnight and diluted to OD≈0.02 about 6 hrs before the experiment to ensure return to log-phase. Fluorescence microscopy was performed on cells trapped in a microfluidic device (CellASIC) while the media were changed. Initially, cells were synchronized by arresting in off (S=0) medium for 120′. Then, the media were switched periodically between on (S=1) and off (S=0) pulse media.

SJR14a4d: Overnight medium: D-Met; On (S=1) pulse medium: D-Met; Off (S=0) pulse medium: D+Met

SJR12a5a: Overnight medium: G-Met; On (S=1) pulse medium: G-Met; Off (S=0) pulse medium: G+Met

SJR82c10b: Overnight medium: R-Met; On (S=1) pulse medium: RG-Met; Off (S=0) pulse medium: R+Met

Abbreviations: D=Glucose, G=galactose, R=raffinose, −Met=absence of methionine, +Met=presence of methionine. The sugars complemented synthetic complete medium.

Images were taken every 5′.

3.2 C. elegans experiments

The experimental set-up was basically as described in ref.(38) for paralyzed worms. In all pulsing experiments, we switched between S basal medium with 1 mM (−)-tetrasimole hydrochloride (Sigma-Aldrich) with (odor on) or without (odor off) 1.15 μM diacetyl (Sigma-Aldrich).

The time interval between images was 0.1″. In every experiment, 10 preparatory odor pulses were administered (10″ duration, 60″ period) before switching to the main measurement pulses of duration d and period T. (The 11′th pulse followed 60″ after the beginning of the 10′th pulse.)

For the thapsigargin experiments, we dissolved the drug (Santa Cruz Biotech) at 10 mg/ml in DMSO and then dissolved the solution at 0.3% by volume in S basal. The final concentration of thapsigargin was about 46 μM. We spun the thapsigargin-S basal solution down in Eppendorf tubes at 13200 rpm for 1 min and saw no precipitation. For the DMSO-only controls, we added DMSO at 0.3% by volume to S basal.

4 Image and data analysis

4.1 S. cerevisae experiments

Automated image segmentation and fluorescence quantification of yeast grown under time-lapse conditions were performed as previously described.(3)

To find T_max(d) for each yeast mutant, we needed to measure the time-averaged output O(d, T) for fixed pulse duration d as the pulse period T was varied. In brief (details below), we defined the system output O(d, T) as the fraction of cells p(d, T) that underwent normal cell cycles at least until some time point t, multiplied by their time-averaged CLN2pr-YFP fluorescence y(d, T) just before t. We estimated T_max(d) by fitting a spline through the means of the O(d, T) data points, and calculated the uncertainty based on the standard errors in O(d, T). (All times are relative to the onset of the first stimulus pulse at 0′.)

In all experiments, we applied 5 on-off pulses, which allowed us to follow and quantify about 100–200 cells for each d and T. (More than 5 pulses generally led to overgrowth in the imaging arena since each stimulus pulse about doubled the number of cells.) The exact number of cells analyzed for each data point were (left to right): Fig. 2 L: 201, 136, 194, 125; M: 126, 102, 100, 70; P: 130, 150, 123, 174, 67; Q: 110, 123, 97, 162, 62; T: 69, 273, 287, 129, 61; U: 389, 346, 212, 95. The number of cells was determined by the noise in each data point: additional cell colonies were analyzed when the SEM was too large compared to the mean to allow a reasonable comparison with other data points.

To define and compare the output O(d, T) for different T, we needed a specific, fixed time point t in our recordings, which was late so that sufficiently many pulses had been administered but which also occurred in all of the recordings with the same strain. (With the number of pulses fixed, the experiments with shorter periods are overall shorter.) We chose the onset of the last stimulus pulse t = 4 T₂ of the second-shortest stimulus period T₂ for each strain (T₂=65′ for clnΔ*, T₂=105′ for clnΔ*clbΔ*, T₂=120′ for clnΔ* GAL1-CLB2kd) because it was a late time point, contained in all related recordings, and allowed the following quantification: We counted the number of cells n(d, T) that replicated in response to every stimulus pulse prior to t and at least budded in response to the first stimulus pulse starting after t, if any. (These cells skipped no stimulus pulses at least until t and the following stimulus pulse.) For example, cells pulsed with period T had to undergo four normal, on-time cell cycles and at least bud a fifth time to be counted. Cells pulsed with period 2T had to undergo two normal, on-time cell cycles and at least bud in response to the third stimulus pulse. The ratio of these cells compared to the initial number of cells N(d, t) defined p(d, T)=n(d, T)/N(d, T), and the standard error was Δp=(P(1−P)/N)^1/2, where P=(n + 2)/(N + 4) takes into account the Agresti-Coull correction. (We suppress the dependence on d and T, i.e., P=P(d, T), when the notation becomes too cumbersome otherwise.)

The CLN2pr-YFP fluorescence time courses of these (non-skipping) cells (F_i(t)) were averaged (<F_i(t)>_i) and the height of the first peak in <F_i(t)>_i was computed (=F_norm) to normalize each recording. (F_norm was obviously independent of T). The running average of F_i(t)/F_norm was computed over a time window of size T (average from t-T/2 to t+T/2 assigned to t). The running average was again averaged from 3T₂ to 3.5T₂ for the clnΔ* and clnΔ*clbΔ* experiments and from 2T₂ to 3T₂ for the clnΔ* GAL1-CLB2kd experiment to yield y_i. (Using these running averages ensured that mostly only fluorescence measurements from before t were taken into consideration, which ensures that these cells are not skipping and performing on-time and normal cell cycles.) The mean (y) and standard error (Δy) of the y_i’s were computed.

The mean of the output was defined as O(d, T)=p(d, T)y(d, T) with standard error ΔO(d, T)=[Δp(d, T)²y(d, T)² + p(d, T)²Δy(d, T)²]^1/2, where we neglected the small Δp(d, T)²Δy(d, t)² term. We approximated the distribution of O(d, T)’s by a Gaussian with standard deviation ΔO(d, T) and generated 10⁴ random configurations of different outputs at each T. Using matlab, we fit smoothing splines through each one of the configurations. The maximum of the spline was taken as the T_max for each sampled configuration. The whole distributions of T_max(d) generated for the two pulse durations d for each strain were compared to each other. The confidence values that we report are the fraction of T_max slopes smaller than 0.5. (We varied the smoothing parameter for the smoothing spline over a wide range (0.001, 0.01, 0.1, 0.3) but the confidences for the slope of T_max(d) hardly changed.) For the plots, we used smoothing parameters 0.1, 0.01, 0.001 for clnΔ*, clnΔ*clbΔ*, clnΔ* GAL1-CLB2kd, respectively, reflecting the different distances between data points in T.

4.2 C. elegans experiments

4.2.1 Tracking AWA neurons

The images were processed basically as described in ref.(38). Occasionally, the worms moved despite general paralysis due to tetramisole in the media. To determine the coordinates of the AWA neurons in time, we tracked GCaMP fluorescence in each frame computationally (residual fluorescence, sufficient to identify AWA, was detectable even when the odor was off); the previously described NeuroTracker software suite ref.(38) was used (see Fig. S6 A for a sample frame). We tried to track the AWA neurons of every worm in the arena, for which, in some instances, repeated manual readjustments of the brightness threshold to identify the AWA neurons were necessary. We gave up tracking individual worms if the AWA detection could not be stabilized despite repeated manual interventions. This was the case for about 1 in 15 worms in each experiment, where, usually, another close-by worm interfered with and diverted the tracker.

4.2.2 Background and baseline subtraction

For each worm i, the average raw intensity F_R,i(t) was read out of a 13×13 pixel square window (4 μm/pixel) centered on the tracked AWA neurons’ coordinates (Fig. S6 A). In order to correct for background, the median intensity F_BG,i(t) in a ring around worm i’s AWA neurons (ring inner radius: 10 pixels, outer radius: 19 pixels) was also read out and subtracted to yield F_noBG,i(t)=F_R,i(t)-F_BG,i(t) (Fig. S6 B).

Next, we corrected for baseline fluorescence, which can drift during the course of the recordings; so, we constructed a time-dependent baseline function (Fig. S6 C). Here and elsewhere, we used a 5″ time window from −7.5″ to −2.5″ before odor pulses reached the microfluidic chamber to define the baseline fluorescence preceding each odor pulse and we defined the center of the window (at −5″) as the beginning of each output pulse. We calculated the average of F_noBG,i(t) over each such time window preceding each odor pulse. A piecewise linear function F_BL,i(t) was fit through these baseline averages, which were assigned to the beginning of each odor pulse. Between these points, F_BL,i(t) interpolated linearly. Thus, F_BL,i(t) reflected shifts in the baseline fluorescence in time. Using this time-dependent baseline function, we normalized the signal, F_i(t) = (F_noBG,i(t)−F_BL,i(t))/F_BL,i(t) (Fig. S6 D).

4.2.3 Exclusion of poorly responding worms

We tried to record and compute the responses of every worm in our experiments but we excluded 10% of the worms from further analysis because their responses were obviously problematic. To filter worms in an objective fashion, we set up quantitative criteria. We applied these tests to F_noBG,i(t), that is, after background correction but before baseline correction (Fig. S6 B). The first 10 preparatory odor pulses (of 10″ duration and 60″ period), which preceded the main measurement pulses in every experiment, allowed the worms to be evaluated before and independently of their responses to the main odor pulses and in a consistent manner across all experiments. The responses to prep pulses 9 and 10 were especially important because we used them to calibrate the rest of the responses, as explained in section 4.2.4.

We filtered out worms whose output pulses 9 and 10 varied too much from one another; we eliminated 8 (of 463 total) worms because the baseline F_BL,i(t) changed by more than 6% before and after pulse 9 (or before and after pulse 10) with respect to the average of F_BL,i(t) before and after pulse 9 (or 10). (Exclusion if |F_BL,i(t_j)−F_BL,i(t_j+1)|/(F_BL,i(t_j)/2+F_BL,i(t_j+1)/2)>0.06 where t_j is the start of pulse j, and j is either 9 or 10.) One such trace is plotted in red in Fig. S6 B.

Of the remaining, we filtered out 40 worms because the signal-to-noise ratio was too low; we defined the signal-to-noise ratio as the height of pulse 9 or 10 divided by the standard deviation of the baseline (F_noBG,i(t) over the preceding 5″ time window) before or after pulses 9 or 10. (Exclusion if σ(F_noBG,i(t))_{t={tj−2.5″,…,tj+2.5″}}/(F_noBG,i(t_k)−F_BL,i(t_j))>0.11 for at least two of the four possible combinations where t_j is the start of pulse 9, 10, or 11 and t_k is the time of the peak of the closest output pulse 9 or 10.) One such trace is plotted in orange in Fig. S6 B.

These thresholds are, of course, ultimately arbitrary, however, i) since they were used in a consistent manner across all experiments, ii) since we applied them to preparatory pulses before and independently of the responses to the main odor pulses, iii) since we only excluded the ‘worst’ 10% of all of the worms in our experiments, iv) since we included all of the worms that we could track initially, e.g., despite weak AWA responses, and v) since all of the response traces that were discarded were visibly problematic and unusual, we believe that these criteria were reasonable.

4.2.4 Calculation of average responses

For the worms that passed the two filters, we calculated F_norm,i, the average of F_i(t) over the responses to pulses 9 and 10, i.e., over a time window starting at the beginning of odor pulse 9 and extending to the start of odor pulse 11. F_norm,i serves to normalize the AWA responses for each worm (Fig. S6 E). (Again, odor pulses 9 and 10 are the last prep pulses; beginning with pulse 11, we switched to odor pulse duration d and period T.) Next, we computed the running average of F_i(t) from pulse 11 onward over a time window of size T (Fig. S6 E). We normalized the running average of each worm by F_norm,i (Fig. S6 F). We fit a linear least-squares regression through the normalized running average, starting 100″ after the start of odor pulse 11 and ending 700″ thereafter (Fig. S6 F). (For T=39″ pulses, about three full odor pulses had been administered (2 × 39″+10″ or 2 × 39″+20″) before the start of the linear fit. The span of 700″ is fairly long (about 18 × 39″ period pulses, for example) and it allowed us to include all of our recordings, including some experiments that aborted early.) For each worm, we took as the output O_i(d, T) the estimated response at 100″ by calculating the value of the linear fit at 100″ (Fig. S6 G). The mean and the SEM over O_i(d, T) are shown in Figs. 3 and S6 G. Taking points later than 100″ from the same linear fit as the output O_i(d, T) yielded similar results: The confidence that the slope of T_max between d=10″ and d=20″ is less than 0.5 is 0.96 at 100″, 0.96 at 200″, 0.94 at 300″, 0.87 at 400′. The gradual loss of confidence at later times can be due to experimental artifacts, accumulation of random noise with time, loss of correlation to the prep pulses, or, potentially and more interestingly, the activation of pathways with slower time scales, etc. (As shown in Fig. S5 A, it is important to compare the output at a specific time after the onset of stimulation.) Given the high confidence of our results up to about 300″ after the onset of the main odor pulses, we did not investigate these issues further.

4.2.5 Calculation of T_max, slopes, and confidence intervals

Based on the mean and SEM of the output O_i(d, T) over all worms i for each T for any fixed d, we approximated the distribution by a Gaussian and generated 10⁴ random configurations of different outputs at each T. Using matlab, we fit a smoothing spline with smoothing parameter 0.1 through each one of the configurations. With noticeably smoother (smoothing parameter: 0.01, resulting confidence: 0.94) or more flexible (smoothing parameter 0.3, resulting confidence: 0.96) splines, we arrived at essentially the same results (confidences in the slope of T_max). The maximum of the spline was taken as the T_max for each configuration. The whole distribution of T_max thus generated for pulse duration d=10″ was compared to the distribution of T_max for pulse duration d=20″. The confidence values that we report are the fraction of T_max slopes smaller than 0.5.

4.2.6 Statistical test for period skipping

The test for period skipping used here was developed from a related statistical oscillation test in ref.(32). The basic idea is to 1) find the best fit of an enveloping sinusoidal function of period T′>T for each recording, and 2) compare the goodness of the fit to best fits for random reshufflings of the same recording. The fraction of random reshufflings that produce better fits than the original recording defines the p value p_osc. Specifically, for each recording, we calculated Fourier-type coefficients c_i(T′)=Σ′_t F_i(t) e^i2πt/T′, where the Σ′t only includes time points t beginning with the first odor pulse at least 100″ after the beginning of odor pulse 11. (As before (4.2.4), ignoring the first 100″ of the main odor responses served as a rough way to allow some of the initial transients to dissipate.) c(T′) was calculated for skipping periods T′ ranging from 0″ to 600″ by 1″ increments. The largest possible skipping period 600″ was chosen so as to allow at least two full skipping periods to fit into most of our recordings. As the best fit, we chose the largest |c(T′)|² peak after the peak at T′=T. Then, we created 10³ reshufflings of the original recording by cutting up each recording in intervals of length T beginning with the first odor pulse after 100″ after the beginning of pulse 11 and permuting them. For each reshuffled recording we computed the largest |c(T′)|², as before. We finally ranked the largest |c(T′)|² for the original recording against the reshuffled data to obtain p_osc.

Note that because there is no noise in the numerical analysis of circuit models and because we were willing to accept false negatives (missing period skipping in some NFLs) for faster computations, the periodicity test that we applied in our computational search of model space was much simpler.

5 Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.