Sensitivity and specificity considerations for fMRI encoding, decoding, and mapping of auditory cortex at ultra-high field

Abstract

Following rapid technological advances, ultra-high field functional MRI (fMRI) enables exploring correlates of neuronal population activity at an increasing spatial resolution. However, as the fMRI blood-oxygenation-level-dependent (BOLD) contrast is a vascular signal, the spatial specificity of fMRI data is ultimately determined by the characteristics of the underlying vasculature. At 7 Tesla, fMRI measurement parameters determine the relative contribution of the macro- and microvasculature to the acquired signal. Here we investigate how these parameters affect relevant high-end fMRI analyses such as encoding, decoding, and submillimeter mapping of voxel preferences in the human auditory cortex. Specifically, we compare a T₂* weighted fMRI dataset, obtained with 2D gradient echo (GE) EPI, to a predominantly T₂ weighted dataset obtained with 3D GRASE. We first investigated the decoding accuracy based on two encoding models that represented different hypotheses about auditory cortical processing. This encoding/decoding analysis profited from the large spatial coverage and sensitivity of the T₂* weighted acquisitions, as evidenced by a significantly higher prediction accuracy in the GE-EPI dataset compared to the 3D GRASE dataset for both encoding models. The main disadvantage of the T₂* weighted GE-EPI dataset for encoding/decoding analyses was that the prediction accuracy exhibited cortical depth dependent vascular biases. However, we propose that the comparison of prediction accuracy across the different encoding models may be used as a post processing technique to salvage the spatial interpretability of the GE-EPI cortical depth-dependent prediction accuracy. Second, we explored the mapping of voxel preferences. Large-scale maps of frequency preference (i.e., tonotopy) were similar across datasets, yet the GE-EPI dataset was preferable due to its larger spatial coverage and sensitivity. However, submillimeter tonotopy maps revealed biases in assigned frequency preference and selectivity for the GE-EPI dataset, but not for the 3D GRASE dataset. Thus, a T₂ weighted acquisition is recommended if high specificity in tonotopic maps is required. In conclusion, different fMRI acquisitions were better suited for different analyses. It is therefore critical that any sequence parameter optimization considers the eventual intended fMRI analyses and the nature of the neuroscience questions being asked.

Graphical abstract

1. Introduction

At ultra-high magnetic fields, functional MRI (fMRI) benefits from increased blood-oxygenation-level-dependent (BOLD)-based susceptibility contrast (Ogawa et al., 1992; Yacoub et al., 2001) and a higher signal-to-noise ratio (SNR; Vaughan et al., 2001), allowing the acquisition of images at an increased spatial resolution. 3T fMRI experiments are typically run with 2–3 mm isotropic resolutions, whereas at 7T millimeter to submillimeter spatial resolutions are not uncommon. This has attracted substantial interest from the neuroscientific community, as the higher spatial resolution allows exploring the human brain non-invasively at an unprecedented spatial scale. Specifically, a submillimeter isotropic resolution could allow investigations of functional processing separately in deep, middle, and superficial cortical depths. As different cortical depths have characteristic patterns of anatomical connectivity and unique functional roles (Douglas and Martin, 2004; Larkum, 2013), the possibility of obtaining non-invasive laminar functional data is intriguing (Kok et al., 2016; Muckli et al., 2015; Olman et al., 2012). Moreover, the cortical depth-dependent exploration of functional responses to stimulus features (e.g., visual orientation, or sound frequency) enables examining the stability of feature preference throughout cortical depth (Zimmermann et al., 2011; De Martino et al., 2015; Nasr et al., 2016). This may provide information regarding the existence and functional role of columnar feature organizations, a neuroscientific topic that has been debated and unresolved to date (Horton and Adams, 2005; Rakic, 2008).

Simply acquiring higher resolution fMRI images does not guarantee a corresponding increase in the specificity of the measured functional processes, as the BOLD signal reflects the hemodynamic response to neural activity. The spatial specificity of the BOLD signal is therefore constrained by the underlying vasculature. Importantly, fMRI data can be acquired in various ways at ultra-high fields, impacting the overall sensitivity of the signals to different components of the vasculature. The most common approach is to use gradient-echo echo-planar imaging (GE-EPI), a T₂* weighted sequence. The acquired GE-EPI signal contains contributions both from macro- and microvasculature (Uğurbil et al., 2003; Uludağ et al., 2009; Yacoub et al., 2005). The macrovasculature includes large diving veins penetrating the gray matter (GM) and the large pial veins situated on top of the GM (Duvernoy et al., 1981). These large draining vessels produce a strong BOLD effect (i.e., a high sensitivity), while also decreasing the spatial specificity as they generate responses away from the actual site of neuronal activity (e.g., higher signal towards the GM surface; Goense et al., 2007; Harel et al., 2006; Kok et al., 2016; Koopmans et al., 2011, 2010; Polimeni et al., 2010; Ress et al., 2007; Siero et al., 2011; Zhao et al., 2004). Several approaches have previously been used in order to minimize the contribution of large and unspecific veins to GE-EPI data. The first approach involves excluding the voxels closest to veins from the analysis. The superficial cortical layers may be excluded altogether, or venous voxels may be identified and excluded (Koopmans et al., 2010; Lu et al., 2010; Shmuel et al., 2007). As a second approach, post processing techniques have been used to suppress the BOLD signal of large veins after acquisition. For example, the complex fMRI signal (both magnitude and phase) can be used to estimate and remove the part of the signal that originated from the macrovasculature (Menon, 2002; Vu and Gallant, 2015). A third approach can be used if a priori information about the representation of the stimulus on the cortex is available. Such a priori information may be used to identify voxels with spatially non-specific responses. These voxels can then be excluded from the analysis, and the remainder of the GE-EPI dataset can be used to map high resolution organizations (Muckli et al., 2015; Yacoub et al., 2007).

Alternatively, at high fields it is also possible to collect submillimeter T₂ weighted functional images (for example using a spin echo (SE) sequence). Such a T₂ weighted sequence suppresses the contribution of large vessels (Yacoub et al., 2003), and thus the acquisitions have relatively more signal from smaller veins. This results in signals with high spatial specificity (De Martino et al., 2013b; Duong et al., 2003; Goense et al., 2007; Harel et al., 2006; Uludağ et al., 2009; Zhao et al., 2004), which are ideal for laminar and columnar investigations of the human cortex. Indeed, in a direct comparison, SE was shown to be more specific than GE in identifying ocular dominance columns in human primary visual cortex (V1; Yacoub et al., 2007).

While T₂ weighted SE sequences are superior in terms of spatial specificity, they also suffer from several drawbacks. Their acquisition time is longer, measured BOLD contrast is lower (lower sensitivity), and specific absorption rate (SAR) is higher compared to T₂* weighted sequences. As such, to make submillimeter T₂ weighted acquisitions a realistic option for high field fMRI applications, significant tradeoffs are made in the imaging field of view (FOV) and the volume coverage (i.e., data can be collected from only a small region of the brain). For 2D SE-EPI this has led to acquisitions with a single thick slice and a small in plane FOV (Yacoub et al., 2008, 2007). More recently, to overcome some of the limitations of SE-EPI, such as relatively low functional contrast to noise (CNR) and the anisotropic voxel resolution, 3D inner volume gradient and spin echo (3D GRASE) was proposed as an alternative (Feinberg et al., 2008; Oshio and Feinberg, 1991). Using a train of refocusing pulses to encode a 3D slab, combined with inner volume selection, 3D GRASE provides a predominantly T₂ weighted signal (Kemper et al., 2015a). However, in order to keep the acquired signal predominantly T₂ weighted and reduce the spatial blurring along the phase encode directions (partition and in-plane phase encode), the field of view (FOV) is still limited (Kemper et al., 2015b). Further, while the measured BOLD CNR with 3D GRASE is higher than with a SE-EPI sequence (Kemper et al., 2015a), it is still substantially smaller than the BOLD contrast measured with GE-EPI (De Martino et al., 2013b). In spite of these constraints, the imaging advantages of the 3D GRASE approach permitted the first columnar mapping study in humans outside of V1 (Zimmermann et al., 2011), and the first human columnar mapping study outside of visual cortex (De Martino et al., 2015).

Given the advantages and disadvantages of both T₂* and T₂ weighted acquisitions, currently there is no generic answer as to the optimal strategy for exploring laminar and columnar processing in the human cortex at high magnetic fields. Here, we directly compared a T₂* weighted sequence (multislice GE-EPI) to a predominantly T₂ weighted sequence (3D GRASE), both acquired at 0.8 mm isotropic, in a study of the human auditory cortex of six volunteers at 7T. We conducted two investigations of cortical depth-dependent functional processing. First, we compared the performance of the two datasets following a decoding analysis. fMRI decoding assesses the information present in a brain region or subset of voxels, and can thus also be used to quantify the information present as a function of cortical depth (Muckli et al., 2015). We based sound decoding on two different computational encoding models which reflect different hypotheses about auditory cortical processing (Moerel et al., 2012; Santoro et al., 2014). Second, we compared the two datasets with respect to sound feature mapping (i.e., estimation of the voxels’ tonotopic frequency preference and selectivity). We interpret results in light of the voxels’ proximity to large veins.

Our results suggest that different fMRI acquisitions are well suited for different analyses. Compared to the 3D GRASE dataset, the GE-EPI dataset had the advantage of higher prediction accuracy in the encoding/decoding analyses. While prediction accuracy in the GE-EPI dataset increased towards the pial surface, we propose that the difference between the encoding models’ performances can be used as a post processing technique that salvages the interpretability of the GE-EPI cortical depth-dependent prediction accuracy. While large-scale maps of frequency preference (i.e., tonotopy) showed no observable bias, cortical depth-dependent tonotopic maps displayed a bias in the assigned best frequency preference and selectivity in the GE-EPI dataset only. Thus, the mapping of cortical feature preference organized at this fine spatial scale benefitted from the high specificity of the 3D GRASE dataset. In conclusion, at ultra-high fields, where a choice between signals with high CNR dominated by large draining veins or signals with lower CNR dominated by the microvasculature is possible, it is essential that the choice of imaging sequence considers the intended subsequent fMRI analyses.

2. Material and methods

2.1 Ethics statement

The experimental procedures were approved by the Institutional Review Board (IRB) for human subject research at the University of Minnesota. Informed consent was obtained from each participant before commencement of the measurements.

2.2 Subjects

Six healthy volunteers participated in this study (mean age [SD] = 28.5 [7.8]; two males and four females). The subjects had no history of hearing disorder or neurological disease.

2.3 Experimental design and stimuli

The study involved three experimental sessions, in which all subjects participated. The first session served to collect high resolution anatomical data for the purpose of segmentation, cortical layer sampling (Zimmermann et al., 2011), and vessel segmentation. In the second and third session, high resolution GE-EPI and 3D GRASE data were collected, respectively, while subjects listened to natural sounds. One subject participated in a fourth session, during which a Time of Flight (TOF) dataset and susceptibility-weighted images (SWI) were acquired. The TOF and SWI images served to create an angiogram and venogram respectively, used for validating the vessel segmentation procedure.

The natural sounds included recordings of the following sound categories: speech, voices, animal cries, music, tools, and nature scenes (144 sounds in total; 24 sounds per category). Sounds were sampled at 16 kHz and their duration was 1000 ms. Sound onset and offset were ramped with a 10 ms linear slope, and their energy (RMS) levels were equalized. Sounds were presented to the subjects in the MRI scanner using the MRI-compatible S14 model earbuds of Sensimetrics Corporation (www.sens.com) with a linear frequency transfer up to 8 kHz.

The natural sounds were divided into 4 non-overlapping sets of 36 sounds each. These sets were created randomly under the constraint that all semantic categories should be equally represented in each set. Sessions 2 and 3 consisted of 12 and 16 fMRI data collection runs, respectively. We presented one stimulus set (36 distinct sounds) per run, and each set was presented three or four times across the full session (i.e., 3 or 4 runs per sound set for sessions 2 and 3, respectively). Stimuli were presented at a jittered inter-stimulus interval of 2, 3, or 4 TRs. Sounds were played, with additional random jitter, in silent gaps between functional volume acquisitions. Trials where no sound was presented were added (8% of the trials). Subjects were instructed to attend to the sounds and perform a one-back task. That is, they indicated with a button press if the exact same sound was played on consecutive trials (occurring on 6% of the trials; repeat trials were not considered in the training and testing of encoding models).

2.4 MRI acquisition

All measurements were performed on a 90 cm bore 7 Tesla whole body magnet (Magnex Scientific, Abingdon, UK) driven by a Siemens console (Siemens Medical Systems, Erlangen) using a custom whole head 32 channel loop transceiver and a high performance head gradient insert. In the first session, T₁, proton density [PD], and T₂* weighted data with full brain coverage were collected at a voxel size of 0.6 mm isotropic. Two T₁ weighted scans were acquired using a modified magnetization-prepared rapid gradient-echo (MPRAGE) sequence. PD datasets were acquired with the same MPRAGE as the T₁ weighted image but without the inversion recovery module. See Table 1 for the acquisition parameters.

Table 1.

Acquisition parameters

	TR (ms)	TI (ms)	Gap (ms)	TE (ms)	echo spacing (ms)	flip angle (°)	GRAPPA
T1	3100	1500	na	3.5	na	4	3
PD	2160	na	na	3.5	na	4	3
T2*	3700	na	na	16	na	4	3
GE-EPI	2400	na	1200	22.8	0.7	90	3
3D GRASE	2000	na	310	29.2	0.7	90; 180	na
TOF	25	na	na	3.3	na	22	2
SWI	28	na	na	14.4	na	15	2
	MB	Matrix size	slices	Voxel resolution	averages	TA (min)
T1	na	384 × 384	256	0.6 mm	2	14
PD	na	384 × 384	256	0.6 mm	1	5
T2*	na	384 × 384	256	0.6 mm	1	8
GE-EPI	2	232 × 256	36	0.8 mm	na	5 per run
3D GRASE	na	28 × 250	16	0.8 mm	na	4 per run
TOF	na	452 × 576	80	0.4 mm	1	6
SWI	na	432 × 576	80	0.4 mm	2	12

Acquisition parameters for all acquired datasets. TR = repetition time; TI = inversion time; gap = silence between acquisitions during which sound is presented, computed as TR – acquisition time of one volume; TE = echo time; GRAPPA = generalized autocalibrating partially parallel acquisition; MB = multiband; TA = acquisition time of the dataset. Voxel resolution was isotropic for all datasets.

In the second session, GE-EPI images were acquired (see Table 1 for the acquisition parameters). Slice placement included the bilateral auditory cortex. This session consisted of 12 runs, each ~5 minutes in duration. In session two and three, a T₁ weighted scan was acquired for the purpose of realignment across sessions and slice placement.

The third session served to collect high-resolution 3D GRASE images (see Table 1). Due to the limited FOV of the 3D GRASE settings, slice placement included Heschl’s gyrus (HG) and regions at its anterior and posterior adjacency. In 3/6 subjects these regions were covered bilaterally, and in the other subjects only the left hemisphere was covered. This session consisted of 16 runs, each ~4 minutes in duration.

TOF and SWI data was collected from an oblique slab oriented along the lateral sulcus, which covered the auditory cortex bilaterally. Parameters of the TOF and SWI datasets are listed in Table 1.

2.5 Anatomical data analysis

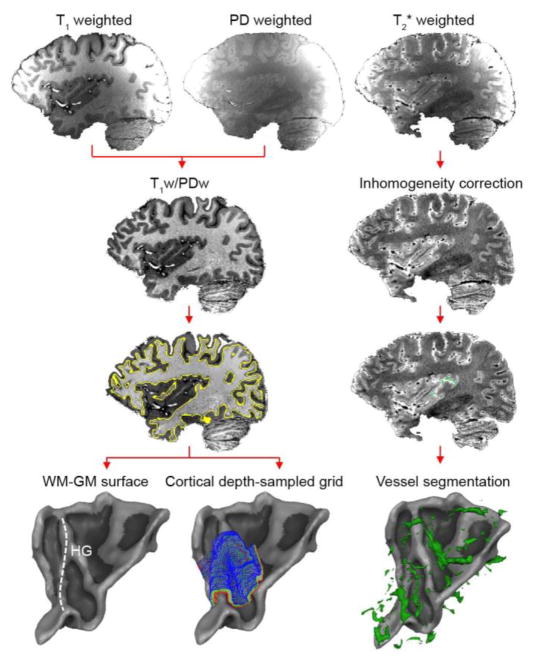
PD images were used to minimize receive coil inhomogeneities in T₁ weighted images (Van de Moortele et al., 2009; left column of Fig. 1). The resulting T₁/PD datasets were further corrected for residual inhomogeneities, and down-sampled to 0.8 mm isotropic resolution matching the resolution of the functional data. Automatic tools of BrainVoyager QX were used to detect the white matter (WM)-GM, and GM-cerebrospinal fluid (CSF) boundaries. Both boundaries were manually edited to ensure a correct definition of the regions of interest (HG and regions at its anterior and posterior adjacency).

Figure 1. Anatomical data analysis.

For each subject, the 0.6 mm isotropic T₁w, PDw, and T₂*w data are collected. Left column: the T₁w/PDw image is segmented, and used for the creation of WM-GM surfaces and cortical depth-dependent grids. Right column: the T₂*w image is used to identify vessels.

Next, cortical thickness was measured as implemented in BrainVoyager QX 2.8 (Brain Innovation, Maastricht, Netherlands), which uses a procedure based on the Laplace equation (De Martino et al., 2013b; Jones et al., 2000; Zimmermann et al., 2011). In brief, this procedure defines the intensity values at the inner and outer gray matter boundary (i.e., the WM-GM and GM-CSF boundary, respectively), and smooths the intensity values of voxels between these boundaries. The solution of Laplace’s equation creates a smooth field that allows calculating a gradient at each voxel. Integrating gradients across voxels results in ‘streamlines’ that define the maximum change (i.e., the shortest path) between the WM-GM and GM-CSF boundaries. Based on this cortical thickness computation, cortical depth-dependent grids are defined. Note that the Laplace equation is only used to the compute cortical thickness. Instead, the cortical depth-dependent grids are spaced equidistantly across cortical depth, rather than as being defined by the Laplace solution. That is, the first regularly spaced grid is created orthogonal to, and halfway through, the streamlines (cortical thickness = 0.5). Additional grids (closer to the WM, or to the CSF) are created by moving up or down along the streamlines to get corresponding grid points at other cortical depths (left column of Fig. 1). For each subject and hemisphere, we created a grid containing nine (ranging from 0.1 [close to WM] to 0.9 [close to CSF] cortical thickness) cortical depths. The WM-GM and GM-CSF boundaries as defined on the anatomical data are not included in these grids.

Vessels were identified by selecting the darkest voxels in the T₂* and SWI datasets, and the brightest voxels in the TOF dataset, followed by manual corrections (right column of Fig. 1). Separately for each dataset (i.e., separately for the T₂*, SWI, and TOF data), the Euclidean distance between each gridpoint and all voxels identified as vessels was computed. Each gridpoint’s distance to a vessel was assigned as the minimum distance (in mm; i.e., the distance to the closest vessel). Correspondence between the T₂*, SWI, and TOF-based vessel segmentation was assessed with a correlation analysis.

2.6 Functional data analysis

The functional data were analyzed with BrainVoyager QX and custom MATLAB (The MATHWORKS Inc., Natick, MA, USA) code. Preprocessing consisted of slice scan-time correction (with sinc interpolation), 3-dimensional motion correction, temporal high pass filtering (removing drifts of 2 cycles and less per run), and temporal smoothing of the time series (2 data points). Functional data were co-registered to the anatomical data, the result of which was reviewed in each subject and adjusted where needed. Next, the data were brought to ACPC space (i.e., rotation to bring the line between the anterior and posterior commissure horizontal). Overall percent signal change (PSC) maps were computed based on the responses to natural sounds and sampled at different cortical depths (using the grids described in ‘section 2.5 Anatomical data analysis’). The relation between PSC and distance to veins was assessed by grouping gridpoints per cortical depth according to their distance to a vein (4 groups, 25% of gridpoints per group for each cortical depth), and computing PSC separately for each group. We tested for a significant correlation between PSC and distance to veins using a non-parametric analysis, implemented in order to correctly deal with the fact that 6 out of 9 data points came from the same three subjects. That is, we performed 2^{NumberOfSubjects} permutations of the sign of the data to generate a null distribution, where the data coming from the same subject was kept together across permutations. The p-value was assigned as the number of permutations that resulted in a correlation further away from zero than the original data divided by the total number of permutations.

2.7 Comparison of computational model performance across datasets

After exploring the cortical depth-dependent PSC and its relation to veins in the GE-EPI and 3D GRASE dataset, we next tested how these cortical depth-dependent patterns affected the performance of decoding based on two different encoding models in the two datasets. We chose to test two encoding models, as we were not only interested in overall decoding performance but also wished to explore how cortical depth-dependent variations in PSC would interact with the performance across encoding models. The following two encoding models were tested (for details, see Moerel et al., 2012; Santoro et al., 2014): a simple frequency model, and a model that defined voxel responses in terms of their frequency-specific modulation tuning (i.e., tuning to temporal modulation rates and spectral modulation scales). The representation of the sounds in the frequency model space was obtained as the output of the first (early) stage of a biologically inspired model of auditory processing (Chi et al., 2005; NSL Tools package, available at http://www.isr.umd.edu/Labs/NSL/Software.htm). This model mimics the spectral transformation of sounds passing through the cochlea to the midbrain, and includes a bank of 128 overlapping bandpass filters equally spaced along a logarithmic frequency axis (180–7040 Hz; range of 5.3 octaves). To represent sounds by the frequency model, the spectrograms resulting as the output of this model were averaged over time resulting in 128 model parameters to estimate.

For the modulation model, the output of the first stage of the NSL model was passed to a second model stage. This stage mimics cortical auditory processing by extracting the modulation content from the sounds’ spectrograms using a set of modulation filters (temporal modulation frequencies of ω = [1, 3 9, 27] Hz; spectral modulation frequencies Ω of = [0.5, 1, 2, 4] cycles/octave). The filter output was computed at each frequency bin, and then averaged over time. To limit the number of (correlated) features, we divided the frequency axis in 8 bins with equal bandwidth in octaves, and averaged the modulation energy within each frequency bin. This resulted in 128 model parameters (8 frequencies × 4 temporal modulation rates × 4 spectral modulation scales) to estimate. In summary, each computational model represents the sounds in an [S × F] feature matrix W, where S is the number of natural sounds and F is the number of features to estimate.

The model parameters were estimated in 4-fold cross-validation, where each cross-validation consisted of 108 training sounds S_train and 36 testing sounds S_test. Per cross-validation, we computed the response to training sounds for each voxel i, Y_train,i [S_train × 1] as follows. The data were first denoised (Kay et al., 2013; http://kendrickkay.net/GLMdenoise/) and then a voxel-wise hemodynamic response function (HRF) common to all sounds was estimated (Kay et al., 2008a). This HRF was used to compute a beta weight for each sound (see Moerel et al., 2015, 2012 for details). The response for each voxel i to testing sounds, Y_test,i [S_test × 1], was computed following the same procedure but used the HRF as estimated on the training sounds.

The response to the sounds in voxel i was modeled as a linear transformation of the feature matrix W:

$$Y_{\mathit{train},i}={\mathbf{W}}_{\mathbf{train}}{R}_i$$ (1)

where W_train [S_train × F] is the representation of the training sounds in the model space, and R_i is an [F×1] vector of model parameters whose elements R_ij quantify the contribution of feature j to the overall response of voxel i. Equation 1 was solved using ridge regression (Hoerl and Kennard, 1970a). The regularization parameter λ was determined independently for each voxel by automatically inspecting the stability of the ridge trace (Hoerl and Kennard, 1970b; Santoro et al., 2014). We assessed model performance as its accuracy in predicting responses to novel testing sounds (“sound identification analysis”; Kay et al., 2008b; Moerel et al., 2013; Santoro et al., 2014). Namely, we used the estimated feature preference of each voxel i to predict the response Ŷ_test,i as:

$${\widehat{Y}}_{\mathit{test},i}={\mathbf{W}}_{\mathbf{test}}{R}_i$$ (2)

where W_test [S_test × F] is the representation of the testing sounds in the model space.

We evaluated model prediction by computing a sound identification score. This score expresses to what extent a model could accurately predict a specific testing sound from the pool of all testing sounds. The sound identification score is computed as follows. For each sound k we horizontally concatenated the predicted response Ŷ_test,k [1 × V] across cross-validations, and computed its correlation to the measured fMRI responses to all testing sounds Y_test [S_test × V] horizontally concatenated across cross-validations. Rank r_k of the correlation between predicted and observed responses to sound k measures the models ability to correctly match predicted response Ŷ_test,k [1 × V] with measured response Y_test,k [1 × V]. Thus, a rank of 1 indicates perfect prediction, while a rank of S_test/2 represents chance, and S_test (where the number of testing sounds = 36) represents the worst outcome. The rank was normalized between 0 and 1. Prediction accuracy P_k of each sound was defined as 1 - the normalized rank:

$$P_k=1-\frac{r_k-1}{S_{\mathit{test}}-1}$$ (3)

Values of P_k range between 0 and 1, with perfect prediction = 1 and chance = 0.5. The overall accuracy of the model was obtained as the mean prediction accuracy across all testing sounds. Models and datasets were statistically compared by performing a two-way repeated measures ANOVA after Fisher transformation of the prediction accuracy values.

Cortical depth-dependent model performance was assessed by sampling matrices Y and R at 9 cortical depths (using the grids described in ‘Anatomical data analysis’), and repeating the analysis procedure per cortical depth. Statistical significance was assessed for deep, middle, and superficial cortical depths (0.2, 0.5, and 0.8 cortical depth, respectively). Separately for GE EPI and 3D GRASE, a two-way repeated measures Analysis of Variance (ANOVA) with factors ‘Computational Model’ and ‘Cortical Depth’ after Fisher transformation of the prediction accuracy values was performed.

The relationship between computational model performance and distance to veins was assessed by grouping gridpoints per cortical depth according to their distance to a vein (4 groups, 25% of gridpoints per group for each cortical depth), and computing the models’ prediction accuracy separately for each group.

2.8 Comparison of estimated voxel preferences

Next, we evaluated the mapping of the voxels’ frequency preference (i.e., tonotopy) in detail. Large-scale tonotopy maps were created by color-coding each voxel according to the frequency with the highest weight in the trained modulation model (the voxel’s best frequency [BF]). A red-yellow-green-blue color scale was used, where preference for low and high frequencies was assigned to red and blue colors, respectively. GE-EPI and 3D GRASE tonotopy maps were smoothed with a Gaussian kernel (FWHM = 4 voxels; map smoothing applied on this volume-based analysis only; all cortical depth dependent analyses were performed on unsmoothed maps), and correlated to each other. Significance of observed correlations between the tonotopic maps as defined by the two datasets was assigned based on permutation testing (N = 200; null-distribution consists of the correlation between maps after imposing the same map smoothness on randomized 3D GRASE maps).

For the left hemisphere only, we computed group tonotopy maps by bringing the anatomical and functional data to Talairach space and performing a cortex-based alignment (CBA; Goebel et al., 2006) on the anatomical WM-GM surfaces. Functional maps were sampled on these CBA surfaces. Group maps display the mean preferred frequency for those vertices that were included in the map of at least 3 subjects.

We compared the specificity of cortical depth dependent tonotopic maps as computed on the GE-EPI and 3D GRASE datasets. To this end, the weights of the trained modulation model were sampled at different cortical depths. As for the large-scale tonotopy maps, each gridpoint’s BF was assigned as the frequency with the highest weight in the trained modulation model. The relationship between BF and cortical depth was assessed by plotting the BF histogram separately for each cortical depth. Following the computation of tuning width in animal electrophysiology (Q-value; Cheung et al., 2001; Imaizumi et al., 2004) and previous fMRI studies (De Martino et al., 2013a; Moerel et al., 2012), the tuning width (TW; i.e., the selectivity of the gridpoint’s frequency preference) of each gridpoint g was computed by fitting a Gaussian curve (with its mean constrained to the gridpoint’s BF) to the voxel’s frequency weights, computing TW_g = BF_g/FWHM_g (where FWHM_g = full width at half maximum of the best fitting Gaussian curve). Note that high and low values of TW indicate narrow and broad frequency tuning, respectively. In deep, middle and superficial cortical depths, the difference in TW across datasets was tested for significance with a non-parametric analysis. Specifically, 2^{NumberOfSubjects} permutations of the data labels (‘GE EPI’ or ‘3D GRASE’) were performed to generate a null distribution. In these permutations, the data coming from the same subject was kept together. The p-value was assigned as the number of permutations that resulted in a larger difference in TW than the original data, divided by the total number of permutations.

Finally, we assessed the relationship between the correspondence in tonotopy maps across datasets and distance to veins. For each gridpoint, we computed the difference in BF (in octaves) as assigned by the GE-EPI and 3D GRASE dataset. Per cortical depth, the gridpoints were grouped according to their distance to a vein (10 groups, 10% of gridpoints per group for each cortical depth). In deep, middle and superficial cortical depths, the average difference in BF across datasets was compared between the group closest and furthest from veins with a non-parametric analysis. Specifically, 2^{NumberOfSubjects} permutations of the data labels (‘close to veins’ or ‘far from veins’) were performed to generate a null distribution. In these permutations, the data coming from the same subject was kept together. The p-value was assigned as the number of permutations that resulted in a larger difference between locations close to and far from veins than the original data, divided by the total number of permutations.

3. Results

3.1 Cortical depth-dependent responses to the natural sounds

We observed significant responses to the sounds on HG, Heschl’s sulcus, and parts of planum polare (PP), planum temporale (PT) and the superior temporal gyrus (STG) in both the GE-EPI and 3D GRASE dataset (q [FDR] < 0.05; see Supplementary Figure 1). Due to limitations in the 3D GRASE coverage, bilateral auditory cortex was only covered in 3/6 subjects. In the remaining subjects, only the left auditory cortex was included. For both datasets, results are reported for 9 hemispheres (6 left hemispheres and 3 right hemispheres).

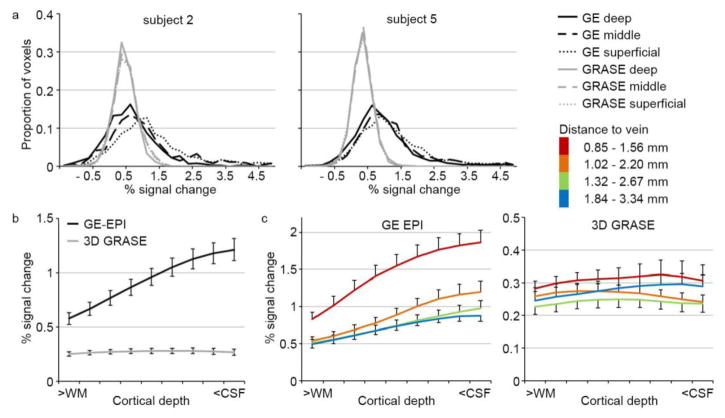
We examined the percent signal change (PSC) across cortical depths by sampling the data on the cortical depth-dependent grids. Note that due to the grid sampling, the same subset of voxels was analyzed across datasets. Overall, PSC was lower for 3D GRASE than for GE-EPI. This magnitude was to be expected as the BOLD signal in auditory cortex is much lower than in visual cortex, and the 3D GRASE percent signal change can be expected to be less than 50% of that of the GE-EPI (De Martino et al., 2013b). In spite of the low PSC, the observation of significant responses to the sounds (see Supplementary Figure 1) indicates that the lower responses in GRASE are accompanied by a relatively low variability. While PSC was constant across cortical depths for the 3D GRASE dataset, PSC increased towards the surface for the GE-EPI dataset. This pattern was present at the level of individual subjects (Fig. 2a), and was preserved when averaging across 9 hemispheres (Fig. 2b).

Figure 2. Cortical depth-dependent percent signal change.

(a) Cortical depth-dependent percent signal change (PSC) for subject 2 (left) and subject 5 (right) in the GE-EPI and 3D GRASE dataset (in black and gray, respectively). (b) Average PSC across 9 hemispheres, separate for GE-EPI and 3D GRASE in black and gray, respectively. Error bars indicate the standard error across hemispheres. (c) Average PSC across 9 hemispheres for GE-EPI (left) and 3D GRASE (right), separate for gridpoints with varying distance to a vein. Error bars indicate the standard error across hemispheres. The legend provides the distance to veins (in mm) in superficial and deep cortical depths for each group. WM = white matter; CSF = cerebrospinal fluid.

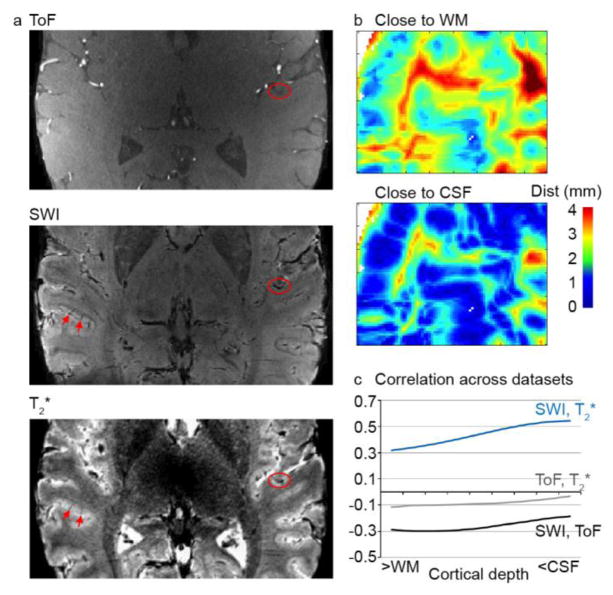
Next, we analyzed the relationship between a gridpoint’s PSC and its distance to a vein. As a first step, we validated our T2*-based vessel segmentation procedure against standard methods of angiogram or venogram creation (i.e., vessel segmentation on a SWI and TOF dataset, respectively). Figure 3a shows matched slices from the TOF, SWI, and T₂* datasets. As expected, low intensity voxels in the SWI dataset (reflecting veins) corresponded to low intensity voxels in the T₂* dataset. Both surface veins located on top of the GM and diving veins could be observed (Fig. 3a, red circles and arrows, respectively). This correspondence between the datasets was confirmed quantitatively. Gridpoint distances to a vessel (in mm; Fig. 3b) were negatively correlated when defined on the SWI and TOF datasets (average Fisher’s transformed correlation across cortical depth [SE] r = −0.26 [0.016]), confirming that these datasets identify different vessels (veins and arteries, respectively; Fig. 3c). Distances to vessels defined by the SWI and T₂* datasets were positively correlated (average Fisher’s transformed correlation across cortical depth [SE] r = 0.44 [0.037]), confirming that they both identified veins (Fig. 3c).

Figure 3. Validation of vessel segmentation.

(a) Matched slice for a TOF, SWI, and T₂* dataset. Arteries are identified as bright voxels in the TOF images. Veins are identified as dark voxels in the SWI dataset, and match the T₂* images (red circles and arrows). (b) Minimum distance to a vessel (in mm), for GM locations close to the WM (top) and close to the CSF (bottom). (c) Correlation in minimum distance to a vessel across datasets. SWI and TOF distances are negatively correlated (black line), confirming that they identify different vessels. SWI and T₂* are positively correlated (blue line), confirming that they both identify veins. GM = gray matter; WM = white matter; CSF = cerebrospinal fluid.

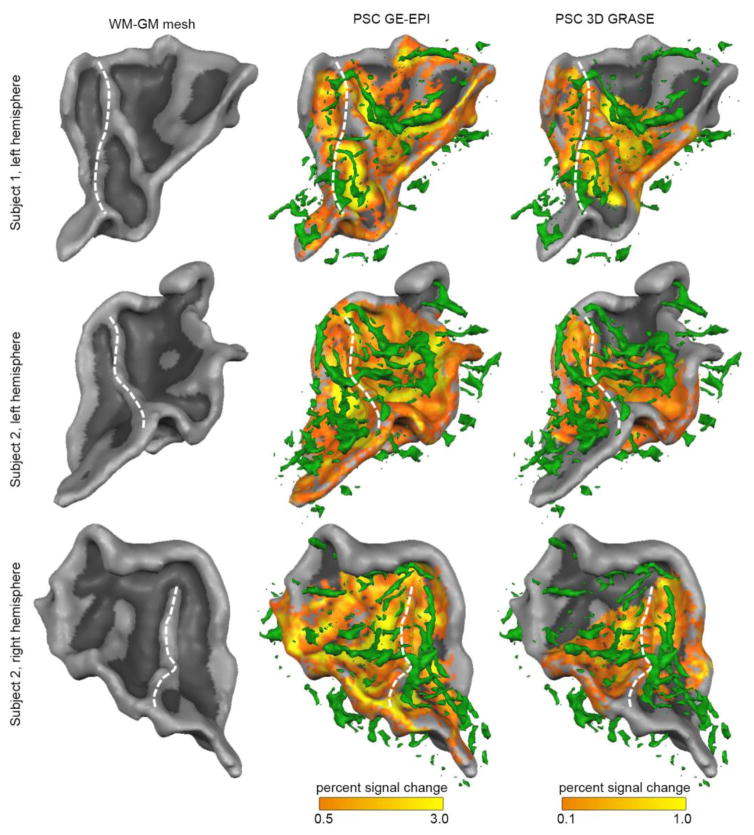
When overlaying the T₂*-based venogram with the maps of PSC, a visual correspondence between vein locations and highest PSC was evident (Fig. 4). This correspondence was most noticeable in the GE-EPI dataset. Quantification of the correspondence between distance to a vein (in mm) and PSC showed a significant negative correlation for GE-EPI (average Fisher’s transformed correlation [SE] r = −0.34 [0.030]; non-parametric permutation analysis; p = 0.016), confirming that locations with a lower distance (i.e., closer) to veins had a higher PSC. No significant correlation was present in the 3D GRASE dataset (average Fisher’s transformed correlation [SE] r = −0.01 [0.052]. We further explored the cortical depth dependency of PSC by dividing the gridpoints in four groups according to their distance to veins (see Supplementary Figure 2). For GE-EPI, the cortical depth dependency of PSC was stronger for gridpoints closest to veins (red line in Fig. 2c; increase from 0.83 PSC close to the WM to 1.87 PSC close to the CSF) than for gridpoints furthest from veins (blue line in Fig. 2c; increase from 0.49 PSC close to the WM to 0.88 PSC close to the CSF). However, even for gridpoints furthest from veins (blue line in Fig. 2c), an increase of PSC towards the GM-CSF surface could still be observed. Moreover, the proximity to veins changed PSC also in deep GM (0.1–0.3 cortical depth).

Figure 4. Overlay of percent signal change and vein proximity.

The overlay between the T2*-based vein segmentation (green; second and third column) and the percent signal change (PSC) in response to the natural sounds is shown for three hemispheres. The second and third column show PSC in the GE-EPI and 3D GRASE dataset, respectively. The white dotted line indicated the location of HG.

3.2 Encoding and decoding performance

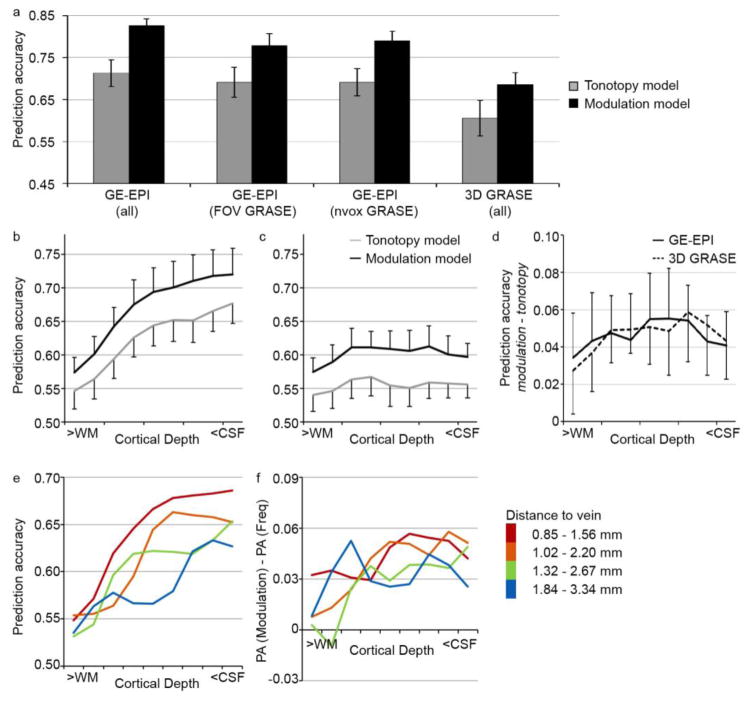
As a next step, we analyzed the GE-EPI and 3D GRASE datasets using on a model-based decoding analysis. For both the tonotopy and the modulation model, we examined prediction accuracy throughout the superior temporal plane, irrespective of cortical depth (including all voxels that responded significantly to sounds [p < 0.05 uncorrected]; voxels selected per dataset). The modulation model significantly outperformed the simpler tonotopy model across datasets (two-way repeated measures ANOVA on Fisher transformed values, on ‘Model’ [tonotopy, modulation] and ‘Method’ [GE-EPI (all), 3D GRASE (all)]; no significant interaction; main effect of ‘Model’; F[1,5] = 52.43; p = 0.0008). Overall prediction accuracy was significantly higher in the GE-EPI than 3D GRASE dataset (Fig. 5a: compare ‘GE-EPI (all)’ to ‘3D GRASE (all)’; main effect of ‘Method’; F[1,5] = 22.54; p = 0.0051). To further explore the origin of the prediction accuracy difference between the GE-EPI and 3D GRASE dataset, we repeated the analysis of the GE-EPI dataset while limiting the number of voxels in two ways. First, when selecting only those voxels within the FOV of the 3D GRASE dataset, overall prediction accuracy for GE-EPI decreased (Fig. 5a: compare ‘GE-EPI (all)’ to ‘GE-EPI (FOV GRASE)’), but was significantly higher than that of the 3D GRASE dataset (two-way repeated measures ANOVA on Fisher transformed values; no significant interaction; main effect of ‘Model’; F[1,5] = 17.07; p = 0.0091; main effect of ‘Method’; F[1,5] = 8.74; p = 0.032). Second, we computed the prediction accuracy on the GE-EPI dataset using the same number of voxels as selected in the 3D GRASE dataset (within the FOV of the 3D GRASE dataset; Fig. 5a: ‘GE-EPI (nvox GRASE)’). Overall prediction accuracy for GE-EPI was still significantly higher than that of the 3D GRASE dataset (two-way repeated measures ANOVA on Fisher transformed values; no significant interaction; main effect of ‘Model’; F[1,5] = 19.50; p = 0.0069; main effect of ‘Method’; F[1,5] = 12.58; p = 0.016).

Figure 5. Performance of computational models.

(a) Model performance, expressed as prediction accuracy, on the GE-EPI dataset (bilateral auditory cortex), on the GE-EPI dataset including only the FOV for which 3D GRASE data was collected, on the GE-EPI dataset while including the same number of voxels as included in the 3D GRASE data, and on the 3D GRASE dataset. Voxels are included that responded significantly to the natural sounds (p < 0.05 uncorrected, selected per dataset). Error bars indicate the standard error across subjects. (b–d) Cortical depth-dependent model performance for the tonotopy and modulation model in the GE-EPI (b) and 3D GRASE (c) dataset, and the difference in prediction accuracy between the two encoding models (d). Error bars indicate the standard error across hemispheres. (e–f) Performance of the modulation model (left) and the experimental effect (difference in performance between the computational models; right), separate for gridpoints with varying distance to a vein. The legend provides the distance to veins (in mm) in superficial and deep cortical depths for each group.

We next analyzed prediction accuracy per cortical depth (Fig. 5b–c). For the GE-EPI dataset (Fig. 5b), prediction accuracy increased towards the CSF for both models (two-way repeated measures ANOVA on Fisher transformed values, on ‘Model’ [tonotopy, modulation] and ‘Cortical depth’ [deep, middle, superficial]; no significant interaction; significant main effect of ‘Model’; F[1,5] = 12.55; p = 0.017, and main effect of ‘Cortical depth’; F[2,10] = 10.63; p = 0.0033). While the modulation model outperformed the tonotopy model across cortical depths in the 3D GRASE data, the prediction accuracy was instead stable across cortical depths, irrespective of the model (Fig. 5c; two-way repeated measures ANOVA on Fisher transformed values; no significant interaction; no significant main effect of ‘Cortical depth’; significant main effect of ‘Model’; F[1,5] = 8.02; p = 0.037). Thus, while only the GE-EPI dataset showed a significant increase in prediction accuracy with cortical depth, the difference in the model performance was the same across datasets (Fig. 5d). In the GE-EPI dataset only, the voxels closest to veins (with the highest PSC) had the highest prediction accuracy (Fig. 5e). The experimental effect (i.e., the difference in computational model performance), however, was not related to vein distance (Fig. 5f).

3.3 Specificity of cortical depth-dependent tonotopic maps

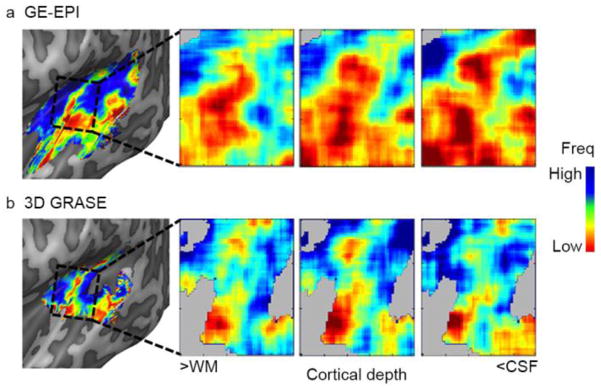
We compared the mapping of frequency preference (i.e., tonotopy) based on the trained modulation model across datasets. While small differences between tonotopic maps across datasets were observed, on a large spatial scale these maps were significantly similar across datasets in 5 out of 6 subjects (average correlation across subjects [Fisher’s transformation] r = 0.35; p < 0.005 in 5 subjects based on permutation testing). Their large-scale pattern was in accordance with previously reported tonotopy maps. That is, maps contained a low frequency cluster on HG, bordered postero-medially and antero-laterally by preference for high frequencies (first column of Fig. 6 shows tonotopic maps in an individual, and Supplementary Figure 3 shows tonotopy group maps; Da Costa et al., 2011; Formisano et al., 2003; Moerel et al., 2012; Saenz and Langers, 2014).

Figure 6. Large-scale and cortical depth-dependent tonotopy maps.

The first column shows the large-scale tonotopy map in the left hemisphere of subject 2, as extracted by GE-EPI (a) and 3D GRASE (b). The remainder of the figure shows the cortical depth-dependent tonotopy in deep, middle, and superficial auditory cortex. While an overrepresentation of low frequency voxels in superficial depths of the GE-EPI dataset can be seen, the preferred frequency content across cortical depths was stable in the 3D GRASE dataset.

Next, we explored tonotopy maps separately for deep, middle, and superficial cortical depths. Figure 6 shows cortical depth-dependent tonotopy maps for a representative subject. While the BF across the cortex was stable throughout deep, middle, and superficial cortical depths in the 3D GRASE dataset, the overall BF in this particular subject decreased towards superficial cortical depths (i.e., maps became more red) in the GE-EPI dataset. For other subjects/hemispheres, both increases and decreases in overall BF were observed. This suggests the presence of a bias in BF in the GE-EPI dataset.

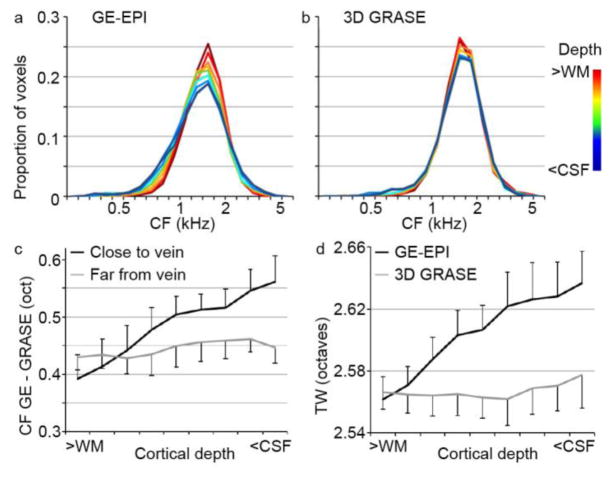
Three analyses support the presence of a bias in the estimated frequency tuning in the GE data. First, across hemispheres, the histogram of the gridpoints’ BF broadens toward the CSF in GE-EPI, indicating a shift in frequency preference (Fig. 7a–b). Second, to test if biases in frequency preference were related to a gridpoint’s distance to large veins, the difference between the GE-EPI and 3D GRASE tonotopy maps (in octaves) was computed separately for voxels close to and far from veins. The difference between the GE-EPI and 3D GRASE tonotopy maps (in octaves) was significantly higher in gridpoints close to veins than far from veins (Fig. 7c). This effect was marginally significant in middle cortical depths (non-parametric permutation analysis, p = 0.078), and significant in superficial cortical depths (non-parametric permutation analysis, p = 0.016). Finally, we tested if frequency selectivity (i.e., gridpoint’s tuning width) was biased in the GE-EPI and 3D GRASE dataset. The tuning width (TW) of voxels increased toward the cortical surface in the GE-EPI dataset only (Fig. 7d). TW was significantly higher in GE-EPI than 3D GRASE for both middle and superficial cortical depths (non-parametric permutation analysis, p = 0.047 and p = 0.031 for middle and superficial cortical depths, respectively).

Figure 7. Cortical depth-dependent bias in voxel frequency preferences.

(a–b) Histograms of frequency preference (BF) across cortical depths, in the GE-EPI and 3D GRASE dataset respectively. For GE-EPI only (a), a widening of preferred frequencies can be observed in cortical depths closer to the CSF. (c) The gridpoint-wise difference (in octaves) in frequency preference between the GE-EPI and 3D GRASE dataset was significantly larger in gridpoints close to veins than in gridpoints far from veins. This effect emerged in cortical depths closer to the CSF. In (c–d), error bars indicate the standard error across hemispheres. (d) Cortical depth-dependent tuning width increased (i.e., frequency selectivity decreased) in cortical depths closer to the CSF for GE-EPI but not for 3D GRASE.

4. Discussion

At ultra-high fields, because of the high functional CNR, there are several options as to how fMRI data can be acquired. Based on the data and analyses presented here, we argue that the optimal choice in sequence and acquisition parameters depends on the nature of the neuroscience question being asked and on the subsequent planned analyses.

4.1 Cortical depth-dependent sound responses and their spatial relation to large vessels

We explored the difference in cortical depth-dependent responses across the GE-EPI and 3D GRASE dataset by investigating their dependence on proximity to veins. Given the spatial resolution of the anatomical data, resulting venograms were likely sensitive to large pial veins (typically 1–4 mm in diameter; Duvernoy et al., 1981) and surely missed a large number of smaller (e.g., diving) veins. In the GE-EPI dataset, locations closer to large veins identified by the venograms displayed higher BOLD responses. This relationship between vein distance and GE-EPI PSC was strongest at the GM surface, where we observed more than a twofold increase in response strength when comparing locations close to and far from veins. The correspondence between vein distance and response strength diminished towards the WM. Interestingly, though, while the dependence between PSC and distance to veins decreased it did not disappear in deep GM. That is, even in deep GM (i.e., close to WM), functional responses were substantially larger in locations close to veins than in locations further from veins (1.7 fold increase). Even in the 25% of gridpoints furthest from veins, response strength increased towards the GM surface (1.8 fold increase).

As a large number of veins could not be identified with the spatial resolution of our measurements, our results likely underestimated the effect of veins on PSC, prediction accuracy, and map specificity. It would be of interest to extend this work at higher spatial resolution (possibly in animal models; Yu et al., 2016) to more completely estimate the effect of veins. Importantly, even while underestimating the effect of veins, our results show that while the dependence between PSC and distance to superficial veins decreased it did not disappear in deep GM. Thus, while “large vein” effects can be reduced using post-processing techniques that remove voxels in close proximity to vessels (Ahveninen et al., 2011; Menon, 2002; Polimeni et al., 2010; Yacoub et al., 2001), our results demonstrate that large vein contaminations affect every cortical depth in a GE-EPI dataset.

4.2 Coverage and PSC beneficial for encoding and decoding analyses

How does the large vein contribution to the GE-EPI dataset affect the results of the fMRI analysis? Across datasets, the modulation model significantly outperformed the simpler tonotopy model. This is in accordance with our previous work (Santoro et al., 2014), and confirms that auditory cortical processing can be well described by the frequency-specific tuning of auditory cortical neuronal populations to joint temporal and spectral modulations. While the datasets give the same ‘neuroscientific’ answer, we furthermore observed that prediction accuracy was higher for GE-EPI than for 3D GRASE. Part of this difference in performance between GE-EPI and 3D GRASE was due to the difference in spatial coverage, shown by a reduction in GE-EPI prediction accuracy when coverage was equalized across datasets. The remaining difference in performance between GE-EPI and 3D GRASE may be driven by the higher CNR of GE-EPI compared to 3D GRASE.

The difference in prediction accuracy between the datasets could also be observed in the cortical depth-dependent decoding analysis. The consistently higher prediction accuracy in GE-EPI confirms that the measured GE-EPI responses to sounds, while driven by large veins, were stable. Moreover, it shows that the GE-EPI responses preserve information on the auditory neuronal population functional preferences. Compared to decoding throughout the volume, cortical depth-dependent explorations suffer from lower power due to a decreased number of data points (i.e., voxels). For such analyses, the gain in prediction accuracy due to the higher PSC of GE-EPI may therefore prove critical. That is, while a 3D GRASE dataset may not perform above chance when computing prediction accuracy per cortical depth because of an insufficient number of voxels or CNR, a GE-EPI dataset may have sufficient power to detect cortical depth-dependent differences in information content (Muckli et al., 2015).

Throughout analyses, stronger responses to the sounds coincided with higher prediction accuracy. One exception can be seen when further exploring the PSC and prediction accuracy across different distances to veins (compare Fig. 2c to Fig. 5e). That is, the difference in PSC between the 25% of gridpoints closest to large veins compared to the rest of the grid (compare the red line in Fig. 2c to the other lines) is relatively larger than the corresponding difference in prediction accuracy (Fig. 5e). This may hint at the presence of a trade-off between higher PSC in the GE-EPI dataset, and lower noise and possibly higher spatial specificity in the 3D GRASE dataset.

4.3 The effect of unspecific signals on decoding

While the higher prediction accuracy provided by GE-EPI is valuable, GE-EPI datasets suffer from a large drawback. GE-EPI decoding is based on stable, but spatially unspecific signals (Yacoub et al., 2007). Thus, if the goal is to link the observed decoding effect to a cortical location or depth, these spatially unspecific signals will hamper the interpretation. That is, unspecific signals may change the real spatial variation of decoding. A large vein may carry information outside of its original cortical location (Formisano and Kriegeskorte, 2012; Kriegeskorte et al., 2010; Vu and Gallant, 2015; Yacoub et al., 2007). In the current study, large veins induced higher PSC at the GM surface, and GE-EPI prediction accuracies correspondingly displayed a bias (i.e., increase) towards the GM surface. The increased performance of a model towards the GM-CSF boundary could thus not be interpreted.

Leveraging the higher CNR of GE-EPI could be beneficial if the contribution of large and unspecific veins could be disregarded. There is no straightforward solution to this problem. Previous studies have taken various approaches to ameliorate the influence of unspecific veins on a GE-EPI dataset. A first approach is to exclude those voxels that are closest to large veins. The superficial cortical layers may be excluded altogether, or venous voxels may be identified and excluded (Koopmans et al., 2010; Lu et al., 2010). Our results show that this approach does not solve the problem, as voxels throughout cortical depth (and outside venous voxels) are biased by their proximity to large veins. In fact, removing such voxels may create a problem, as it will produce gaps in the dataset (possibly decreasing the ability to interpret spatial patterns throughout cortical depth). Second, techniques can be used to suppress the BOLD signal of large veins after acquisition. Based on the complex fMRI signal, both magnitude and phase, these methods estimate and remove the part of the signal that originated from macrovasculature (Menon, 2002; Vu and Gallant, 2015). It would be of interest to explore the extent to which these techniques can remove the cortical depth-dependent increase of PSC in submillimeter GE-EPI datasets, and if their employment would improve the specificity of GE-EPI datasets (i.e., improve correspondence between cortical depth-dependent maps as measured by GE-EPI and 3D GRASE). Third, if information regarding the stimulus and the expected response patterns is available, such a priori information may be used to identify voxels with spatially non-specific responses (Muckli et al., 2015). However, as a priori information on the spatial organization of the cortical stimulus representation is often not available, this technique is not applicable in the general case.

Here, we propose an alternative post-processing technique. That is, our results suggest that while cortical depth-dependent performance of a single condition cannot be interpreted, the difference in cortical depth-dependent prediction accuracy between models is unbiased (see Fig. 5d). Caution must be taken in this approach, as not any differential effect is safe (Polimeni et al., 2010; Vu and Gallant, 2015). The comparison between conditions must be very tight, ensuring that the conditions are affected in the same manner by the macrovasculature. Model comparison is uniquely suited for dealing with unspecific GE-EPI signals by differential analysis, as both models use the same GE-EPI data as input. This ensures that both conditions (i.e., models) are equally affected by differences in the presence of, and distance to, large veins. Our results confirm this, as the difference between model performances was unbiased, interpretable, and in complete accordance with results from the 3D GRASE dataset.

4.4 Spatial specificity is crucial for cortical depth-dependent feature maps

Throughout the auditory pathway, neuronal populations can be characterized by the sound frequency to which they respond best (their best frequency [BF]). At each processing stage of the auditory hierarchy, neuronal populations are spatially ordered according to their BF resulting in one or multiple tonotopic maps. At the level of the auditory cortex, tonotopic maps are organized on a relatively large spatial scale. Consequently, tonotopic maps can be delineated with sufficient accuracy also at 3 Tesla (Moerel et al., 2012; Saenz and Langers, 2014). Beyond this large-scale tonotopic organization, invasive animal studies suggest that additional topographic organizations may be in place at a finer spatial scale. For example, invasive studies throughout species showed that frequency preference is constant perpendicular to the cortical surface resulting in ‘frequency columns’ (Abeles and Goldstein Jr., 1970; Shamma et al., 1993; Shen et al., 1999; Sugimoto et al., 1997). To explore the stability of frequency preference throughout the cortical depth non-invasively, as was recently achieved using T₂ weighted fMRI (3D GRASE; De Martino et al., 2015), an unbiased high specificity feature tuning estimate per cortical depth was necessary.

We evaluated mapping frequency preference across datasets both in a less challenging setting (averaged across cortical depths) and in a situation demanding high specificity (cortical depth-dependent tonotopic maps). The large-scale tonotopic distribution was similar across datasets, and the small differences in tonotopic maps that existed did not hamper the detection of the major tonotopic gradient. Given its larger spatial coverage and sensitivity, GE-EPI dataset is preferable in studies that aim to delineate the large-scale tonotopic map in human auditory cortex. Instead, consistent with results from visual cortex (De Martino et al., 2013b; Yacoub et al., 2007), GE-EPI cortical depth-dependent tonotopic maps were biased both in the assigned preferred frequency of a location, and in the selectivity of their frequency preference. Preference biases were observed in middle and superficial (but not deep) cortical depths, in accordance with reports of higher GE-EPI specificity close to the WM (De Martino et al., 2013b; Muckli et al., 2015; Nasr et al., 2016; Polimeni et al., 2010).

The vascular contamination in GE-EPI cortical depth-dependent topographic maps reported here and previously (De Martino et al., 2013b; Nasr et al., 2016; Yacoub et al., 2007) may be detrimental to the planned analysis. For example, Yacoub et al. (2007) showed that cortical columns as estimated by T2 and T2* weighted acquisitions were in accordance with each other only in parts of the visual cortex. Further, recent work by Nasr et al. (2016) acknowledged that the surface contamination may have even artificially “enhanced” the columnar organization in their data. Our data corroborate these findings, showing that the large vein effect in GE-EPI data penetrates to the deepest layers. Therefore, mapping columnar organizations or assigning voxel feature preference using GE-EPI data is compromised irrespective of cortical depth location.

To summarize, when the goal of a study is to observe cortical feature preference organized at a fine spatial scale, deep WM GE-EPI data is preferable over GE-EPI data at more superficial cortical depths. Studies that aim to evaluate the stability and variability of feature preference throughout cortical depth (e.g., to evaluate the presence of a columnar organization, or transformations of stimulus representations throughout the cortical depth) cannot exclude middle and superficial GM from the analysis and, consequently, the acquisition of a T₂ weighted datasets or multiple experimental conditions to remove the large vein bias effect is preferable if the continuity and integrity of the maps is to be preserved.

5. Conclusions

At ultra-high field, the choice of sequence and acquisition parameters should depend on the planned analyses and/or the nature of the neuroscience question being asked. While encoding and decoding profit from the large coverage and high signal in GE-BOLD acquisitions, cortical depth dependent investigations using T₂* weighted images must be based on differential comparisons between conditions that are equally influenced by the macrovasculature. Such differential analysis has the potential to suppress the cortical depth dependent bias present in resulting prediction accuracies. For assigning feature preference on the submillimeter scale, a T₂ weighted acquisition is preferable.

Highlights.

• At ultra-high fields tradeoffs between sensitivity, specificity, and coverage exist

• We compared a T₂*w (GE-EPI) to a T₂w (3D GRASE) fMRI dataset across analyses

• Encoding and decoding analyses profited from the coverage and sensitivity of GE-EPI

• Comparisons across encoding models may salvage the GE-EPI laminar interpretability

• The 3D GRASE dataset achieved higher specificity in topographic maps