Abstract
Seasonal influenza is a serious public health and societal problem due to its consequences resulting from absenteeism, hospitalizations, and deaths. The overall burden of influenza is captured by the Centers for Disease Control and Prevention’s influenza-like illness network, which provides invaluable information about the current incidence. This information is used to provide decision support regarding prevention and response efforts. Despite the relatively rich surveillance data and the recurrent nature of seasonal influenza, forecasting the timing and intensity of seasonal influenza in the U.S. remains challenging because the form of the disease transmission process is uncertain, the disease dynamics are only partially observed, and the public health observations are noisy. Fitting a probabilistic state-space model motivated by a deterministic mathematical model [a susceptible-infectious-recovered (SIR) model] is a promising approach for forecasting seasonal influenza while simultaneously accounting for multiple sources of uncertainty. A significant finding of this work is the importance of thoughtfully specifying the prior, as results critically depend on its specification. Our conditionally specified prior allows us to exploit known relationships between latent SIR initial conditions and parameters and functions of surveillance data. We demonstrate advantages of our approach relative to alternatives via a forecasting comparison using several forecast accuracy metrics.
Keywords: Bayesian modeling, state-space modeling, SIR model, forecasting, influenza, time-series
1. Introduction
Between 1976 and 2006, estimates of annual influenza-related deaths in the United States range from 3000 to 49,000 people [Centers for Disease Control and Prevention (2014b)]. Intervention strategies such as targeted vaccination campaigns [Harris, Maurer and Kellermann (2010)] and public education efforts [Centers for Disease Control and Prevention (2014a)] help mitigate and counteract the potentially severe effects of seasonal influenza. Despite these successful efforts, seasonal influenza persists and poses a serious risk to both national security and public health [Germann et al. (2006)].
Disease surveillance systems play an integral role in public health preparedness against seasonal influenza. The Centers for Disease Control and Prevention’s (CDC) Outpatient Influenza-like Illness Surveillance Network (ILINet) monitors influenza-like illness (ILI) levels in the United States, with more than 2900 outpatient healthcare providers from all 50 states, Puerto Rico, the District of Columbia, and the U.S. Virgin Islands participating [Centers for Disease Control and Prevention (2015)]. ILINet is considered the gold standard for ILI surveillance [Nsoesie, Mararthe and Brownstein (2013)].
Compartmental models have been used to describe infectious disease transmission since the early 1900s [Ross (1911)]. When coupled with disease surveillance data, compartmental models are invaluable tools for analyzing historical disease transmission dynamics [e.g., Mills, Robins and Lipsitch (2004)], systematically discriminating between the transmission properties of various pathogens [e.g., Yang, Lipsitch and Shaman (2015)], and estimating meaningful functions of model parameters [e.g., Heffernan, Smith and Wahl (2005)].
Recently, attention has turned from characterizing historical influenza outbreaks to forecasting them. Reliable forecasts with actionable lead times of meaningful outbreak metrics, such as the peak intensity (PI) and timing of the peak intensity (PT), would be valuable to public policy makers. Accurate forecasts of the anticipated overall impact of an outbreak would provide public health practitioners additional information when making decisions about resource allocation, intervention strategy implementation, and timely communications to the public [Chretien et al. (2014), Nsoesie et al. (2014)]. Location-specific flu forecasts with lead times of multiple weeks or months would also benefit the staffing decisions and last push vaccination efforts of hospitals and clinics. Though accurate forecasting multiple weeks or months out is currently not a capability of flu forecasting, it is the goal.
Nsoesie et al. (2014) and Chretien et al. (2014) independently reviewed the influenza forecasting literature and noted a variety of forecasting and modeling approaches, including statistical approaches (e.g., time series models, generalized linear models, classification models) and compartmental modeling approaches [e.g., the susceptible-infectious-recovered (SIR) model, the susceptible-exposed-infectious-recovered (SEIR) model, the susceptible-infectious-recovered-susceptible (SIRS) model].
Probabilistic, state-space modeling approaches that mimic compartmental models, on average, have recently been proposed in the literature. We refer to these probabilistic state-space models as being motivated by a compartmental model. Shaman and Karspeck (2012) considered a humidity-driven state-space model motivated by a SIRS compartmental model, while the ensemble adjustment Kalman filter [Anderson (2001)] was used for fitting. They showed the potential near real-time value of a state-space modeling approach by forecasting the influenza season given only a few weeks of ILI data. Shaman and Karspeck (2012) made a normality assumption for the likelihood, assumed no process error, and used external plug-in estimates for the observational noise. Dukic, Lopes and Polson (2012) considered a state-space model motivated by an SEIR model to track seasonal influenza. Dukic, Lopes and Polson (2012) provided model flexibility and hedged against model misspecification by allowing for an estimating process and measurement error. Furthermore, Dukic, Lopes and Polson (2012) worked with the growth rate of the infectious population rather than the ILI data directly, justifying their normality assumptions. Both Shaman and Karspeck (2012) and Dukic, Lopes and Polson (2012) adopted a simulation-based or Bayesian approach to estimation. They specified a joint prior on the parameter vector by specifying prior distributions to the components of the parameter vector marginally.
In this work, we consider a state-space model motivated by a compartmental model, and take a Bayesian approach to inference and forecasting, similar to Shaman and Karspeck (2012) and Dukic, Lopes and Polson (2012). Like Dukic, Lopes and Polson (2012), our approach allows for both process and measurement error. However, unlike Dukic, Lopes and Polson (2012), our primary interest lies in influenza forecasting, not tracking. Unlike the work of both Shaman and Karspeck (2012) and Dukic, Lopes and Polson (2012), we make distributional choices that account for various modes of uncertainty and circumvent the need to either transform out of the original scale [Dukic, Lopes and Polson (2012)] or implement ad hoc approaches to deal with support boundaries [Shaman and Karspeck (2012)].
We consider a state-space model motivated by the parsimonious SIR model rather than an SEIR or SIRS model. The SIR model choice was made for multiple pragmatic reasons: (1) The SIR model has known analytical relationships between the initial conditions (ICs) and parameters of the SIR model and functions of surveillance data not available to either the SIRS or SEIR models. These known relationships can subsequently be leveraged in an informative prior specification. (2) As noted by Capaldi et al. (2012), the deterministic SIR model is effectively unidentifiable when only incidence data is available [the situation we share with Dukic, Lopes and Polson (2012) and Shaman and Karspeck (2012)]. Model unidentifiability can make estimation and sampling challenging. As the SIRS and SEIR models can be viewed as adding complexity to the SIR model, sampling and estimation problems are likely exacerbated. (3) Deterministic SIRS and SEIR models are more flexible than the deterministic SIR model, possibly making them more attractive choices. At no point, however, are we fitting a deterministic SIR model. Rather, we are fitting a state-space model motivated by the SIR model. The stochastic state-space modeling framework makes our modeling approach quite flexible.
A major contribution of our work is the conditional rather than marginal specification of the prior. The conditional prior specification is facilitated by relating the deterministic SIR model to the stochastic state-space model and expanding the parameter vector by carefully chosen latent quantities.
In Section 2, we describe the data. Section 3 provides a general overview of the SIR model, while Section 4 describes our SIR motivated state-space model. In Section 5, we discuss posterior simulation. Section 6 describes our prior specification procedure. Section 7 presents forecasting results. We finish with a discussion of future work with Section 8.
2. Data description
The CDC collects, organizes, and analyzes flu activity information year round. They accomplish these tasks via a collaborative effort with state, local, and territorial health departments, public health and clinical laboratories, and emergency departments [Centers for Disease Control and Prevention (2015)]. One such collaborative effort is ILINet. ILINet consists of more than 2900 outpatient healthcare providers within the United States. Each week, approximately 2000 outpatient healthcare providers around the country report data to the CDC on the total number of patients seen for any reason and the number of those patients with ILI, where ILI is defined as a temperature of 100 degrees Fahrenheit or higher and a cough and/or sore throat without a known cause other than influenza [Centers for Disease Control and Prevention (2015)]. Estimates of ILI are updated weekly and are available nationally and regionally, where regions correspond to Health and Human Service (HHS) regions [U.S. Department of Health and Human Services (2017)].
By virtue of its construction, ILI data will include patients with respiratory viruses other than influenza. To better approximate the proportion of ILINet patients with influenza, we couple ILINet data with virologic surveillance data for influenza from the National Respiratory and Enteric Virus Surveillance System (NREVSS) and US-based World Health Organization (WHO) Collaborating Laboratories. Data from these approximately 350 clinical laboratories include the weekly total number of specimens tested, number of positive influenza tests, and percent positive by influenza type.
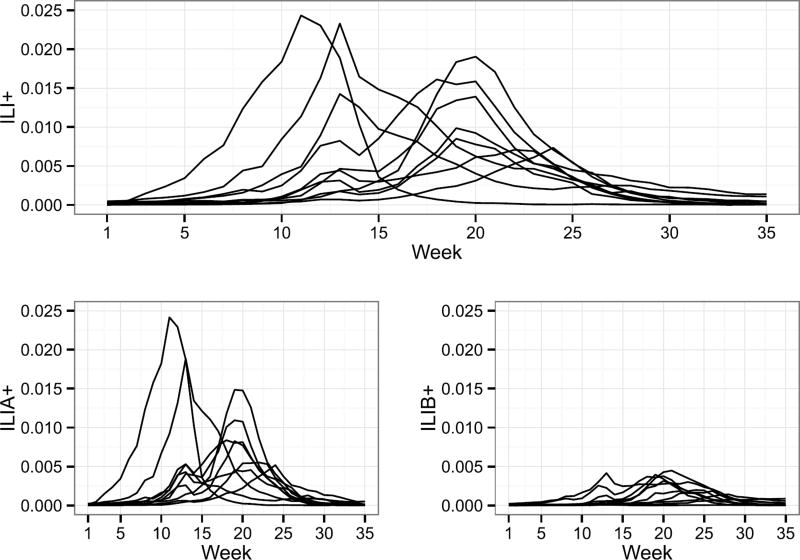
There are two main types of influenza viruses, A and B. Both types cause flu outbreaks and co-circulate every year. Influenza A, however, is typically more prevalent than B (Figure 1 for reference). Type A flu virus is constantly mutating and is generally responsible for the large epidemics. Type B flu virus does not mutate as frequently as A and is typically milder. Stratifying the different types of influenza is important for monitoring the temporal and geographic differences in the infectious population.
Fig. 1.
ILI+ (top), ILIA+, and ILIB+ (bottom) for influenza seasons 2002–2007 and 2010–2013. Weeks 1 and 35 roughly correspond to the beginning of October and the end of May, respectively.
Following the approach of Shaman et al. (2013), we multiply ILI data by the proportion of ILI samples that tested positive for influenza based on virologic surveillance data, and refer to this metric as ILI+, where ILI+ is a proportion. Furthermore, we compute ILIA+ and ILIB+ analogously to ILI+ for influenza types A and B, respectively. In what follows, we work only with ILI+, ILIA+, and ILIB+. For more details on the ILI adjustment, the reader is directed to the methods section of Shaman et al. (2013). For more information about the influenza testing procedure performed by the NREVSS and WHO Collaborating Laboratories, the reader is directed to the Centers for Disease Control and Prevention (2015).
We consider ten influenza seasons, 2002–2007 and 2010–2013 where, for example, influenza season 2002 means 2002–2003. We omit the H1N1 dominant influenza seasons of 2008 and 2009 because they correspond to a pandemic, and we chose to focus only on forecasting seasonal influenza. Seasonal and pandemic flu transmission dynamics are very different. People tend to have residual immunity to seasonal influenza strains, but little to no immunity to pandemic strains. Furthermore, seasonal flu outbreaks follow somewhat predictable patterns and occur every year. Pandemics are comparatively unpredictable and rare, with only three pandemics occurring in the 20th century: 1918, 1957, and 1968 [CDC.gov (2017)].
In what follows, epidemiology week 40 is referred to as week 1 (t = 1). This date roughly corresponds to the first week of October, a common choice for the start of the influenza season [e.g., Nsoesie, Mararthe and Brownstein (2013)]. We define the duration of the influenza season to be 35 weeks, roughly corresponding to the end of May. Both national and regional data are analyzed in this paper. We compute ILI+, ILIA+, and ILIB+ regionally in the same manner as described earlier in this section. For illustrative and simplifying purposes, we discuss our modeling approach with respect to nationwide ILI+. Modeling comments, however, extend to regional levels and other flu types. For reference, nationwide ILI+, ILIA+, and ILIB+ for 2002–2007 and 2010–2013 are shown in Figure 1.
3. Susceptible-infectious-recovered model
We first present a basic transmission model for a directly transmitted infectious disease, the SIR model [Kermack and McKendrick (1927)]. Our presentation of the SIR model is meant to introduce the reader to the motivating model for the state-space model presented in Section 4.
Consider a closed population of individuals, partitioned into three compartments: susceptible (S), infectious (I), and recovered (R). At any time t = 0, 1, …, T, every individual is a member of exactly one of these three compartments. We denote the proportion of the population in the susceptible, infectious, and recovered compartments by St, It, and Rt, respectively, such that St + It + Rt = 1 for all t.
The SIR model is described by the following set of nonlinear, ordinary differential equations:
| (3.1) |
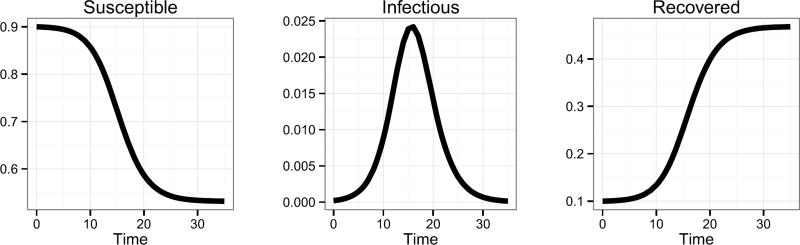
where β > 0 is the disease transmission rate and γ > 0 is the recovery rate. Conceptually, susceptible individuals become infectious (i.e., move from the susceptible compartment to the infectious compartment), and then ultimately recover from the infection (i.e., move from the infectious compartment to the recovered compartment). The rates at which they move from one compartment to another depend on the proportion of the population in each of these compartments, as well as the transmission and recovery rates associated with the disease. For illustration, a simulated SIR curve is shown in Figure 2 with ICs S0 = 0.9, I0 = 0.0002, R0 = 0.0998, and parameters β = 2 and γ = 1.4. We note that, in this paper, R0 represents the proportion of the population in the recovered compartment at time t = 0 for the SIR model and does not represent the “basic reproductive number” (i.e., the average number of secondary infections produced by a typical case of an infection in a completely susceptible population). Note that an SIR curve is comprised of three trajectories—one for each compartment. ILI+ provides an estimate of the infectious trajectory. To the best of our knowledge, data related to the susceptible or recovered trajectories are either not publicly available or do not exist. Not having data for the susceptible and recovered trajectories restricts model validation to only the infectious trajectory. Estimated susceptible and recovered trajectories should thus be viewed as plausible but not validated.
Fig. 2.
Simulated SIR curve with S0 = 0.9, I0 = 0.0002, R0 = 0.0998, β = 2, and γ = 1.4.
Weiss (2013) presents a useful property of the SIR model, the Epidemic Threshold Theorem (ETT). For SIR models defined as in equation (3.1), if S0 ≤ γ/β, then It decreases monotonically to zero as t → ∞ (designated as nonepidemic). If S0 > γ/β, then It starts increasing, reaches its maximum, and then decreases to zero as t → ∞ (designated an epidemic). The data presented in Figure 1 exhibit the characteristics of an epidemic. We will return to this epidemic/nonepidemic distinction in the prior specification of Section 6.
4. Dirichlet-Beta state-space model
Consider two generic random variables X and Y. We adopt the notation where brackets around a random variable X, [X], represent shorthand notation for the probability density function of X. Similarly, [X|Y] corresponds to the probability density function of X given Y. In what follows, we denote time-indexed latent states as θt, and denote model parameters by non-θ Greek letters, generically referred to as ϕ.
We introduce a probabilistic state-space model motivated by the deterministic SIR model of Section 3 (i.e., a state-space model that, on average, mimics the dynamics of the deterministic SIR model). Additionally, we desire a model that obeys both the sum to unity constraint of the latent state vector and the support of the ILI+ data without the need to transform out of the original scale. The devised probabilistic state-space model is more flexible than the deterministic SIR model, as it accounts for uncertainty in the parameters, in the form of the disease transmission mechanism (i.e., process error) and in the ILI+ data (i.e., measurement error) simultaneously. The state-space model we propose, henceforth referred to as the Dirichlet-Beta state-space model (DBSSM), is defined as
| (4.1a) |
| (4.1b) |
where yt is ILI+ at time t = 1, 2, …, T, represents the true but unobservable susceptible, infectious, and recovered proportions of the population, respectively, ϕ = {θ0, γ, β, κ, λ} where γ > 0 is the recovery rate, β > 0 is the disease transmission rate, κ > 0 controls the variance of equation (4.1b), λ > 0 controls the variance of equation (4.1a), and f (θt−1, β, γ) ∈ ℝ3 is defined in detail in the following paragraph. Furthermore, and for all t. The DBSSM assumes θ0:T = (θ0, θ1, …, θT) is a first-order Markov chain (i.e., [θt|θ0:(t−1)] = [θt|θt−1] for all t) and for all t ≠ s, yt is independent of ys, given θt.
We define f(·) as the solution to equation (4.2),
| (4.2) |
starting the ODE at θt−1. The solution to equation (4.2) is not known explicitly, and thus f(·) is replaced with a numerical approximation. We set f(·) equal to the fourth order Runge–Kutta (RK4) approximation known to be numerically stable for a wide range of nonlinear systems. Other choices for approximations to f(·) are possible, however (e.g., Euler’s method). The details of the RK4 approximation to f(·) are described in the Supplementary Material [Osthus et al. (2017)]. We emphasize that f(·) plays the role of propogating the latent state θt forward in time one step.
We model the yt|θt, ϕ with a beta distribution, a natural modeling choice for data restricted to the [0, 1] interval. The parameterization in equation (4.1a) was chosen such that
| (4.3a) |
| (4.3b) |
The conditional expectation of yt is unbiased for the true but unobservable infectious proportion of the population, . The conditional variance of yt is a function of and λ. The parameter λ plays a role in controlling the conditional variance, but does not play a role in the conditional expectation. As λ tends toward infinity, the conditional variance (i.e., the measurement error) of yt tends toward zero.
We model θt|θt−1, ϕ with a Dirichlet distribution, a natural modeling choice for vector-valued data subject to the constraint that all elements of the vector are non-negative and sum to unity. The parameterization in equation (4.1b) was chosen such that
| (4.4a) |
| (4.4b) |
where “○” is the Hadamard product and 1 is a 3 × 1 vector of ones. The conditional mean structure of the latent state process (i.e., the conditional expectation of θt) is unbiased for the one-step-ahead solution to equation (4.2) starting at θt−1. The conditional variance of θt is a function of f(θt−1, β, γ) and κ. The parameter κ plays a role in controlling the conditional variance, but does not play a role in the conditional expectation. As κ tends toward infinity, the conditional variance (i.e., the process error) of yt tends toward zero.
We note that other, possibly more conventional approaches to modeling a stochastic SIR model exist, such as the stochastic differential equation version of the SIR model (SDE-SIR) or the continuous time Markov chain version of the SIR model (CTMC-SIR) [e.g., Brauer, van den Driessche and Wu (2008)]. We, however, elected not to use either of these approaches for various reasons. The Gaussian error term of the SDE-SIR model does not ensure compartmental support boundaries are respected, resulting in potentially impossible (e.g., negative) forecasted numbers of infections. On the other hand, the Dirichlet and beta distributions of the DBSSM were chosen primarily to respect the supports of the latent states and observations, ensuring all forecasted latent states and observations are plausible. The CTMC-SIR is most commonly used for modeling emerging epidemics rather than seasonal epidemics because its ability to capture the stochastic nature of the timing of epidemic onset. Furthermore, the CTMC-SIR model treats the latent state variable as discrete, requiring step sizes small enough such that the “infinitesimal transition probabilities” are applicable. Nationally, flu incidence counts from week to week can be in the hundreds of thousands, requiring an exceedingly small step size to apply the CTMC-SIR method, resulting in increased computation time. The DBSSM, however, working with proportions rather than discrete counts and using the RK4 method, requires step sizes of only one week, keeping computational cost relatively low. For more information on the CTMC-SIR model and the SDE-SIR model, we direct the reader to Brauer, van den Driessche and Wu (2008).
5. Posterior simulation and forecasting
We take a Bayesian approach to inference and forecasting within the state-space modeling framework. For t′ ∈ 1, 2, …, T, our interest lies in estimating the joint posterior density of all latent states and parameters given the observed data,
| (5.1) |
where [ϕ] is the prior density for ϕ. The equality of equation (5.1) holds because of the DBSSM’s conditional independence assumptions.
The posterior density of equation (5.1) is unavailable in closed form. Thus, simulation-based methods are used to approximate (5.1). We use Markov chain Monte Carlo (MCMC) methods, specifically Gibbs sampling [Geman and Geman (1984)], to simulate from the posterior distribution. Gibbs sampling requires sampling iteratively from the full conditional distributions of each latent state and each parameter, conditioned on the most recent draws of all other latent states, parameters, and the observed data. To execute the sampling, we used the rjags package [Plummer (2014)] within the R programming language [R Core Team (2015)], which calls the software “Just Another Gibbs Sampler,” or JAGS [Plummer et al. (2003)]. JAGS queries a library of internal samplers ranging from efficient but specialized samplers to highly generic, but possibly inefficient base samplers (e.g., the slice sampler).
Forecasts for the future observations, y(t′+1):T, are based on the posterior predictive distribution, whose density is given by
| (5.2) |
To sample from all T posterior (predictive) distributions, we adopt a parallelized off-line or batch sampling approach. This is a computationally viable sampling strategy because offline posterior inference for each t′ is trivially parallelizable.
6. Prior specification of ϕ
For the purposes of forecasting seasonal influenza, prior specification is challenging because the parameters of the DBSSM have a nonlinear relationship to the data, forecasting is necessarily done with incomplete data, and the forecasts are sensitive to the prior specification. Furthermore, combinations of parameters of the DBSSM that agree with ILI+ early in the influenza season will not necessarily result in reasonable forecasts when propogated forward in time. For example, consider the task of forecasting weeks 10 through 35 of the 2010 influenza season, after observing weeks one through nine. The left of Figure 3 plots the mean of the process defined by equation (4.1b) corresponding to two combinations of parameters over the first nine weeks. Both mean processes are consistent with these ILI+ observations. However, when these mean processes are propagated forward in time, they take divergent trajectories. The forecasted trajectory in the top right of Figure 3 appears reasonable, in that it is consistent with historically observed ILI+ for weeks 10 through 35. The forecasted trajectory in the bottom right of Figure 3, however, is unreasonable, as it departs dramatically from historically observed ILI+.
Fig. 3.
The mean process defined by equation (4.1b) for two sets of parameters are displayed. The parameters corresponding to the dashed trajectory (top) are , , , β = 2.22, γ = 1.7017, and κ = 20,000. The parameters corresponding to the dotted trajectory (bottom) are , , , β = 0.3912, γ = 0.077, and κ = 20,000. Points are 2010 ILI+ observations for weeks one through nine. Grey lines are the ILI+ trajectories for years 2002–2007 and 2011–2013 for weeks 10 through 35.
Figure 3 illustrates that forecasts are sensitive to parameter choices, and thus forecasts will in general be sensitive to the prior specification, stressing the importance of specifying a prior thoughtfully and defensibly. Thus, the goal of this section is to specify a joint prior distribution on ϕ such that the prior predictive distribution is consistent with historically observed ILI+, where the density of the prior predictive distribution is
| (6.1) |
To accomplish our prior predictive specification goal, we expand the parameter vector ϕ by the latent quantity z = (PI,PT). The latent quantity PI represents the peak/maximum infectious proportion during the influenza season, and the latent quantity PT represents the week on which PI occurs. We expand ϕ with z to facilitate an informative prior specification with desired forecast properties.
The joint prior distribution of (ϕ, z) is conditionally specified where [ϕ, z] is factorized into the product of conditional distributions via the product rule. Specifically, we factorize [ϕ, z] as follows:
| (6.2) |
where ρ = γ/β. Furthermore, we assume
| (6.3) |
What remains is the specification of [κ] and the conditional prior distributions of (6.3).
We illustrate prior specification using historical nationwide ILI+ for years 2002–2007 and 2010–2013 to derive hyperparameters. The resulting prior would subsequently be used for fitting and forecasting the 2014 nationwide influenza season. We emphasize, however, that we are outlining a prior specification procedure. All hyperparameters derived from historical data are specific to this 2014 nationwide flu illustration. To avoid using the data twice, the historical data used to determine hyperparameters should not contain the data the prior will subsequently be used to model.
6.1. Specification of [κ] and [λ]
The parameter κ governs the magnitude of process error in equation (4.1b). The parameter λ governs the magnitude of measurement error in equation (4.1a). Relatively flat prior distributions with relatively large expected values were assigned to κ and λ, reflecting little prior information about these two parameters. Specifically,
| (6.4) |
| (6.5) |
with E(κ) = 2 × 104 and Var(κ) = 2 × 108.
6.2. Specification of [θ0]
We follow the precedent of Dukic, Lopes and Polson (2012) and Nsoesie, Mararthe and Brownstein (2013) and treat as fixed. In what follows, we assume 90% of the population is initially susceptible to seasonal influenza, and assign the following degenerate distribution to :
| (6.6) |
where δ() is a Dirac delta function (i.e., is a point mass prior at 0.9).
We assign a beta distribution to , which we assume is equal to the distribution of . The hyperparameters are determined by fitting a beta distribution to historical ILI+ for t = 0. For the purposes of forecasting the 2014 influenza season, we define the prior on as
| (6.7) |
where and .
Recall the latent state constraint for all t = 0, 1, …, T. The prior distribution for is specified to preserve latent state balance, namely,
| (6.8) |
Putting together equations (6.6)–(6.8), the joint prior specification for θ0 is
| (6.9) |
6.3. Specification of [z|θ0]
Specifying a prior on the latent quantity z = (PI,PT) allows us to more easily encode complex dependencies on the joint prior of ϕ than specifying a joint prior on ϕ directly. Figure 4 plots the bivariate distribution of historically observed peak intensities vs. peak timings for ILI+ (black points). Influenza seasons with early peaks correspond to more intense peaks, while seasons with later peaks are often less intense. Explanations for this relationship have been posited in the literature [e.g.,Towers et al. (2013)].
Fig. 4.
The peak intensity (PI) on the y-axis vs. the timing of peak intensity (PT) on the x-axis for years 2002–2007 and 2010–2013 (black points). 10,000 samples were drawn from the truncated normal distribution of equation (6.10) with and plotted in grey.
A truncated, bivariate normal distribution was fit to the data (black points) in Figure 4. The bounds of the truncated normal distribution respect support constraints and enforce prior beliefs. We enforce our prior belief that an epidemic will occur by setting the lower bound on PI to . PI is a proportion, and thus the upper bound was set to 1. The lower and upper bound for PT was set to 1 and 35, respectively, aligning with the support of the influenza forecasting season. The full specification for [z|θ0] is
| (6.10) |
where T N(µ, Σ, lower, upper) stands for “truncated normal” distribution with mean µ, covariance matrix Σ, lower bound “lower,” and upper bound “upper.” 10,000 draws from the distribution of equation (6.10) are displayed in Figure 4.
6.4. Specification of [ρ|z, θ0]
Expanding the parameter vector ϕ by the latent quantity z in the prior specification allows us to leverage relationships between the ICs and parameters of the SIR model in equation (3.1) and functions of observable ILI+. As κ tends toward infinity in equation (4.1b), the mean process of equation (4.1b) tends toward the deterministic SIR model [assuming (S0, I0, R0, β, γ) in equation (3.1) equals ( , , , β, γ) in equation (4.1b)]. For suitably large κ, we expect the mean process of equation (4.1b) to be close (in some sense) to the deterministic SIR model. Furthermore, in this large κ regime, we expect the known analytical relationships between the ICs and parameters of the SIR model and functions of ILI+ to provide relevant guidance for constraining the parameter space of (ϕ, z).
One such analytical relationship between PI and the ICs and parameters of the SIR model of equation (3.1) is noted in Section 2.2.7 of Weiss (2013):
| (6.11) |
where ρ = γ/β. That is, for the SIR model, the quantity PI is a known deterministic function of S0, I0, and ρ. If we consider S0 and I0 known in equation (6.11), then PI = g(ρ|S0, I0) is a function only of ρ. For ρ ∈ [0, S0) (i.e., epidemics by the ETT), ρ = g−1 (PI, S0, I0) exists and is single valued because g is a monotone transformation over this range. For κ suitably large, we expect the relationship in equation (6.11) to hold for the mean process of equation (4.1b) with and . Thus, for the DBSSM, we specify [ρ|z, θ0] as
| (6.12) |
6.5. Specification of [β|ρ, z, θ0]
We do not know PT to correspond to a known analytical function of ϕ, thus one must be estimated. To estimate this relationship, we simulated SIR curves and recorded the PT of each curve for the full factorial design of 10 evenly spaced values of ρ between 0.6 and 0.89, 35 evenly spaced values of β between 0.75 and 4.5, and 15 evenly spaced values of I0 between 0.00001 and 0.001, for a total of 5250 simulated SIR curves. For all simulated SIR curves, S0 = 0.9. We then regressed log(β) on a subset of a fourth degree polynomial interaction model using log(PT), log(I0), and log(ρ) as covariates. The estimated parameters, τ̂, can be found in the Supplementary Material [Osthus et al. (2017)].
As in Section 6.4, we expect the relationships between PT and the ICs and parameters of the deterministic SIR model to carry over to the mean process of the DBSSM for suitably large κ. We specified the degenerate distribution for β|ρ, z, θ0 as the mean of a log-normal distribution and chose to ignore the variability in the estimates of τ because of the high estimated R2 (0.99) and correspondingly small estimated mean squared error (0.04212). Specifically,
| (6.13) |
where X is a 1 × 17 design matrix with columns corresponding to the rows of Table 1 (replacing I0 with ) in the Supplementary Material [Osthus et al. (2017)], τ̂ is the vector of corresponding parameter estimates found in Table 1 of the Supplementary Material [Osthus et al. (2017)], and σ̂2 = 0.04212.
Table 1.
Percentage of scenarios model was deemed best, by metric. Bold numbers indicate the largest percentage for each metric
| Model | M1 | M2 | M3 |
|---|---|---|---|
| DBSSM | 60.3 | 38.8 | 54.8 |
| SM1 | 5.5 | 0.0 | 6.1 |
| SM2 | 34.2 | 61.2 | 39.1 |
6.6. Prior predictive distribution for y1:T
With [ϕ, z] in equation (6.2) specified, we can sample from [y1:T] of equation (6.1). The prescription to do so is outlined in the Supplementary Material [Osthus et al. (2017)].
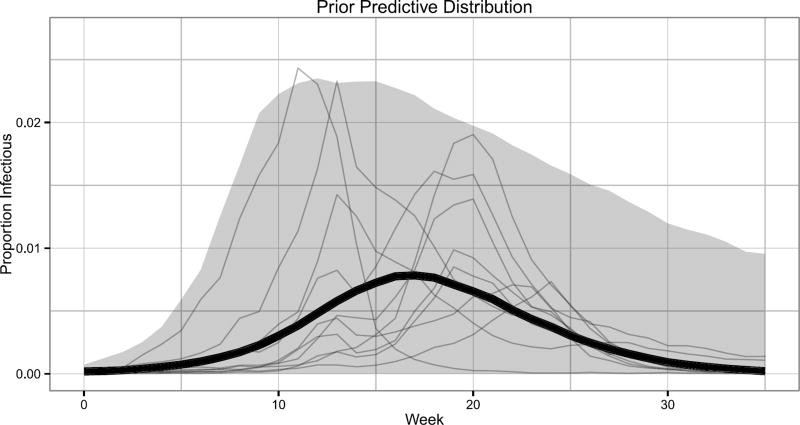
For illustration, M = 5000 samples were drawn from the prior predictive distribution. For each t = 1, 2, …, T = 35, we plotted the median (black line) and 95% prediction intervals (grey bands), and overlaid historical ILI+ in Figure 5. The prior predictive distribution is visually consistent with historically observed ILI+, as desired.
Fig. 5.
The median (thick black line) and 95% prediction intervals (grey band) based on M = 5000 draws from the prior predictive distribution. Historical ILI+ observations are displayed for reference (thin grey lines).
7. Forecasting results
7.1. Forecasting illustration
For the illustration in this section and for each t′ ∈ 1, 2, …, T, we simulated 62,500 draws from the posterior density, [θ1:t′, ϕ|y1:t′], discarding the first 12,500 as burn-in and thinning the remaining 50,000 every tenth iteration for each of four chains. Posterior summaries are thus based on M = 20,000 draws. For the full analysis presented in Section 7.2, summaries are based on M = 5000 draws, as we ran only one chain. Given M draws from the posterior distribution, the prescription for simulating from the posterior predictive density, [y(t′+1):T|y1:t′], is outlined in the Supplementary Material [Osthus et al. (2017)].
Gibbs sampling can have difficulties sampling from compartmental models due to highly correlated posterior structures. The DBSSM is not a compartmental model, but shares some of these difficulties. Gibbs sampling proved tractable due to our informative prior specification and choice to work with ρ = γ/β [equation (6.12)] and β [equation (6.13)] rather than γ and β directly. The informative prior specification placed little to no prior weight on low probability regions of the posterior parameter space, helping focus the Gibbs sampler. The parameter transformation facilitated the sampling of two relatively uncorrelated parameters (ρ and β) instead of two highly correlated parameters (γ and β). Chain mixing and stationarity for various estimands of interest were assessed with the Gelman–Rubin diagnostic [Gelman and Rubin (1992)] and effective sample sizes. For more details on both posterior correlation structure and MCMC diagnostics, the reader is directed to the Supplementary Material [Osthus et al. (2017)].
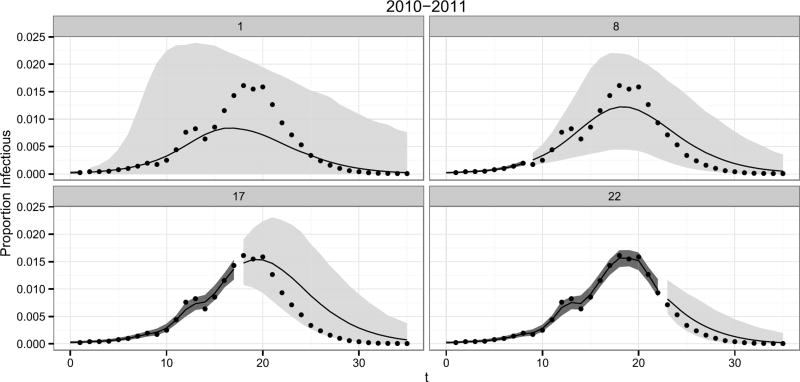
Percentiles of the posterior density for the latent infectious states, , and the posterior predictive density, [y(t′+1):T|y1:t′], for the 2010 nationwide influenza season are shown in Figure 6. For t′ = 1 (upper left of Figure 6), the 95% prediction intervals capture the unknown future observations. The forecast has much uncertainty, as expected with only a single observation for the 2010 influenza season. As more data are observed and incorporated into the analysis, plausible forecast trajectories become constrained, resulting in tighter prediction intervals. We note that the deterministic SIR model cannot capture the two peaks exhibited by 2010 nationwide ILI+, as the infectious curve of the SIR model can have at most one peak. However, the DBSSM is able to capture the two peaks exhibited by the 2010 influenza season because the DBSSM explicitly accounts for process error.
Fig. 6.
95% posterior predictive intervals for [y(t′+1):T|y1:t′] (light grey bands) and 95% credible intervals for (dark grey bands). Posterior medians (black lines) and ILI+ observations (points) are also displayed for the 2010 nationwide, influenza seasons. The number at the top of each panel is t′. All plots are based on 5000 simulations.
7.2. Forecasting comparison
It is our desire to compare the forecast accuracy of the DBSSM with competing models. Accurately reproducing these competing models for the purposes of comparison, however, is challenging due to the varied and, often times incomplete, available model descriptions. Even comparing reported forecast accuracy metrics with competing models can be challenging, as forecasting methods, forecasting outcomes, and reported validation metrics vary widely in the literature [Chretien et al. (2014)]. For these reasons, we leave the comparison of the DBSSM’s forecasting accuracy with competing models to future work.
Some degree of comparison of forecast accuracy is needed, however. To judge the forecasting quality and justify the complexity of the DBSSM, we compare the DBSSM’s ability to forecast quantities related to PT and PI marginally, as well as jointly, to two readily available models. The first model (SM1) is the prior predictive distribution of the DBSSM. The second model (SM2) is the model presented in Hickmann et al. (2015). For all historic influenza seasons not forecasted, SM2 computes the mean and standard deviation of ILI+ for each time point. A draw from SM2 is a time series, where each point of the time series is independently drawn from a normal distribution with a time point specific mean and standard deviation. Comparing the DBSSM forecasts to the forecasts of SM1 allows us to directly investigate whether updating the DBSSM when new data become available is beneficial to forecasting, relative to our prior. Comparing the DBSSM forecasts to the forecasts of SM2 allows us to directly investigate whether fitting the DBSSM is worth the effort. Note that neither SM1 nor SM2 incorporate observations into the analysis within a flu season, while the DBSSM does. We refer to the incorporation of observations into the model fitting within a flu season as “assimilating data.” The forecasts for SM1 and SM2 are produced on the basis of historical influenza seasons, not the current season.
For t′ = 1, 2, …, 34 and m = 1, 2, …, M, let
| (7.1) |
| (7.2) |
| (7.3) |
| (7.4) |
| (7.5) |
| (7.6) |
where qa(x) returns the sample quantile of x for probability a ∈ [0, 1]. We consider three metrics (M1, M2, and M3) to assess a model’s ability to forecast PI and PT both marginally (M1 and M2) and jointly (M3). Each metric can be viewed as a score, where M1, M2, and M3 ∈ [0, 1] and 1 is a perfect score. The score itself is a weighted combination of accuracy (coverage) and confidence (prediction interval width). M1, M2, and M3 are respectively defined as follows:
where T* = min(PT + 4, T − 1). The quantity T* represents an early cutoff for the influenza season determined by the week the peak occurs. For example, in the nationwide 2010 influenza season used for illustration in Section 7.1, PT = 18 so that T* = min(18 + 4, 35 − 1) = 22. The metrics M1, M2, and M3 are evaluated over the time period [1, T*] rather than [1, T] since shortly after the PI and PT are observed, the DBSSM is able to accurately identify them. Therefore, comparing DBSSM to SM1 and SM2 over [1, T] would give an unfair advantage to the DBSSM, as neither SM1 nor SM2 assimilate data. Also, by restricting M1, M2, and M3 to [1, T*], we can focus on a model’s ability to forecast the PI and PT prior to observing the PI and PT.
We consider 330 scenarios comprised of all year-region-type combinations of ten years (2002–2007 and 2010–2013), eleven geographic regions (ten HHS regions and nationwide), and three strains of influenza (ILI+, ILIA+, and ILIB+). For each scenario, we compute M1, M2, and M3 for the DBSSM, SM1, and SM2. For each scenario and metric, we determine the best model, where best means the model with the corresponding metric closest to 1. The results are summarized in Table 1.
The DBSSM is the preferred model for forecasting PI marginally and jointly with PT, as it was the best model in the highest percentage of scenarios for M1 and M3, respectively. SM2, however, is the preferred model with respect to forecasting PT marginally, as it was the best model in the highest percentage of scenarios for M2. SM1 is the least preferred model with respect to all considered metrics. Thus, based on the results of Table 1, there is strong evidence to support the claim that assimilating data is beneficial relative to the prior of the DBSSM.
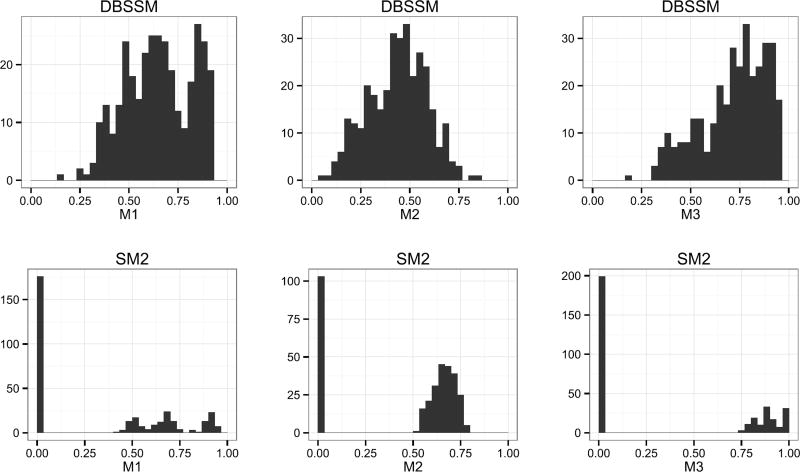
It would appear the DBSSM and SM2 are competitive with each other but with different strengths. Examination of the distribution of M1, M2, and M3 scores, however, provide more insight into the differences between the DBSSM and SM2 models. The distribution of scores across all scenarios are displayed in Figure 7.
Fig. 7.
Distribution of M1, M2, and M3 scores for the DBSSM (top) and SM2 (bottom).
For SM2, we see a spike at zero and a clustering of scores generally above 0.5 for all metrics. Because SM2 does not assimilate data, the forecast made for every t′ is identical. The forecast for each scenario is either accurate or inaccurate, with inaccurate forecasts assigned a score of zero. The spike at zero in Figure 7 for SM2 is thus the marking of a nondata assimilating model.
The relatively high volume of zeros coupled with relatively high scores, however, is the marking of a nondata assimilative model which is overconfident in its predictions. Small prediction interval widths (i.e., confident forecasts) have the potential to yield high scores, but carry an increased likelihood of inaccuracy (i.e., scores of zero). For SM2, roughly 50%, 30%, and 60% percent of all scenarios were inaccurate for metrics M1, M2, and M3, respectively.
Assimilating data hedges against the dichotomy of accuracy and inaccuracy. As can be seen, the DBSSM seldom has a score near zero, but also seldom has a score near one.
Finally, for each model, scenario, and t′, it is of interest to know if the worst of the influenza season has occurred. Knowing this has implications for resource allocation and communication approaches with the public. We estimate the probability the peak intensity has not yet been observed, P(PT > t′|y1:t′), by
| (7.7) |
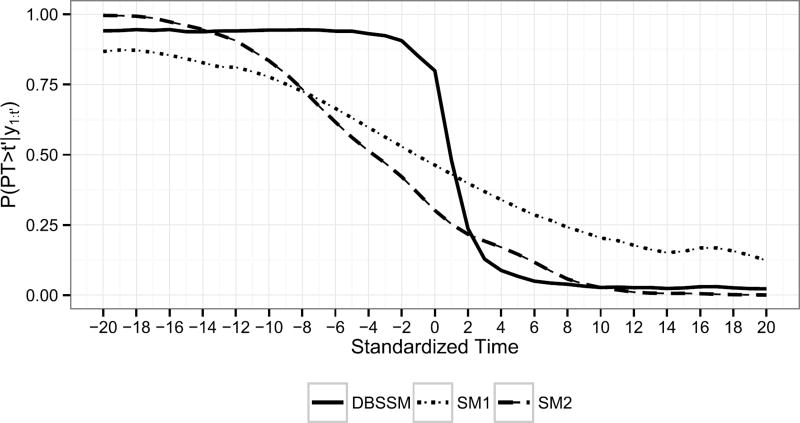
For each model, Figure 8 displays P̂(PT > t′|y1:t′) averaged over all scenarios versus standardized time, where standardized time is t′ − PT.
Fig. 8.
P̂(PT > t′|y1:t′) averaged over all scenarios versus standardized time.
Figure 8 shows the superiority of the DBSSM over both SM1 and SM2 with respect to estimating P(PT > t′|y1:t′). The DBSSM can correctly and confidently predict that the peak intensity has not yet been observed prior to observing it. The same cannot be said for either SM1 or SM2. The DBSSM has difficulty recognizing the peak intensity has been observed on the week the peak intensity is observed. However, the DBSSM is able to quickly recognize the PI has been observed one to two weeks after observing it. By three weeks after observing the peak intensity, the DBSSM is able to correctly and confidently predict the peak intensity has occurred. Knowing that the worst of the influenza season has been observed shortly after observing it has practical value and is a strength of the DBSSM.
8. Discussion
In this paper, we present the DBSSM, a probabilistic statespace model motivated by the deterministic SIR model. The beta and Dirichlet distributions of equations (4.1a) and (4.1b), respectively, naturally obey support constraints without the need for transforming the data. Parallel sampling with JAGS [Plummer (2014), Plummer et al. (2003)] proved computationally feasible, even for the forecasting analysis with 330 scenarios.
A major contribution of this work was the prior specification of Section 6. By expanding ϕ by the latent quantity z and conditionally specifying the prior, we were able to exploit both known and estimated relationships between the ICs and parameters of the SIR model and functions of ILI+. Incorporating prior information into the prior specification is a crucial component to forecasting seasonal influenza. Forecasts are most desired and valuable when data for the current influenza season are scarce. The prior distribution is the mechanism by which to incorporate information from historical influenza seasons. We stress that results depend critically on the prior specification, emphasizing the importance of its thoughtful and careful specification.
Fitting flu seasons sequentially to obtain a prior via a Bayesian updating procedure is a plausible alternative modeling approach. We, however, chose not to pursue a sequential updating approach for a couple reasons. By specifying the prior conditionally rather than adopting a sequential approach, we were able to leverage known analytical relationships for the SIR model and, in a sense, open up the “black box” that is the prior distribution. Furthermore, a sequential approach to prior specification works well when the underlying data-generating mechanism remains relatively constant. For seasonal influenza, this is not the case. We know influenza changes from year to year based on factors such as weather, vaccine efficacy, and mutating flu strains. Flu transmission dynamics one year are not necessarily predictive of flu transmission dynamics the following year.
Arguably, a more natural Bayesian modeling approach than our approach would be a hierarchical model. This approach would model all flu seasons jointly and could avoid much of the prior specification details presented in Section 6. We speculate the main drawbacks to such an approach would be increased computation time (fitting all available flu seasons rather than one) and a diminished ability for forecasts to quickly adjust to newly observed data (as our approach can, as displayed in Figure 8).
Alternative disease surveillance systems to ILINet include variants of the recently defunct Google Flu Trends [e.g.,Ginsberg et al. (2009)]. One such variant is Wikipedia [e.g.,Generous et al. (2014),Hickmann et al. (2015)]. Rather than select one disease surveillance system for influenza forecasting, multiple disease surveillance systems could be incorporated into a principled, probabilistic, data-assimilating model. This multiple data stream modeling approach has the potential to leverage the accuracy of traditional surveillance systems (i.e., ILINet) and the timeliness and geographic resolution of alternative surveillance systems (e.g., Wikipedia).
As more forecasting models are developed, the need for standard and meaningful forecasting metrics along with approaches to compare competing models will increase. Nsoesie et al. (2014) and Chretien et al. (2014) note the importance for studies to clearly define the predicted event and corresponding accuracy measures and the need to report head-to-head comparisons between competing forecasting approaches. We agree with these general conclusions and recommendations. When comparing forecasting models, the determination of the “best” model will necessarily be relative to a forecasting metric or multiple forecasting metrics. Figure 7 suggests comparisons between forecasting methods should be broadly demonstrated, not narrowly illustrated. Undesirable features of a forecasting approach (e.g., overconfidence) will not be apparent when applied to a single or even a few scenarios.
Supplementary Material
Acknowledgments
The authors thank Brian Weaver for his computational assistance, along with the constructive and helpful comments of the associate editor and two anonymous reviewers. LANL is operated by Los Alamos National Security, LLC for the Department of Energy under contract DE-AC52-06NA25396. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Approved for public release: LA-UR- 15-26537.
Footnotes
Supported in part by NIH/NIGMS/MIDAS under grant U01-GM097658-01.
References
- Anderson JL. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 2001;129:2884–2903. [Google Scholar]
- Brauer F, van den Driessche P, Wu J, editors. Mathematical Epidemiology. Lecture Notes in Math. Vol. 1945. Berlin: Springer; 2008. MR2452129. [Google Scholar]
- Capaldi A, Behrend S, Berman B, Smith J, Wright J, Lloyd AL. Parameter estimation and uncertainty quantification for an epidemic model. Math. Biosci. Eng. 2012;9:553–576. doi: 10.3934/mbe.2012.9.553. MR2957535. [DOI] [PubMed] [Google Scholar]
- CDC.gov. [Accessed: 02-06-2017];Influenza (Flu) Past Pandemics. 2017 Available at http://www.cdc.gov/flu/pandemic-resources/basics/past-pandemics.html.
- Centers for Disease Control and Prevention. [Accessed: 05-5-2015];Free resources. 2014a Available at http://www.cdc.gov/flu/freeresources/
- Centers for Disease Control and Prevention. [Accessed: 02-06-2017];Estimating Seasonal Influenza-Associated Deaths in the United States. 2014b Available at http://www.cdc.gov/flu/about/disease/us_flu-related_deaths.htm.
- Centers for Disease Control and Prevention. [Accessed: 04-30-2015];In Overview of influenza surveillance in the United States. 2015 Available at http://www.cdc.gov/flu/weekly/overview.htm.
- Chretien J-P, George D, Shaman J, Chitale RA, Mckenzie FE. Influenza forecasting in human populations: A scoping review. PLoS ONE. 2014;9:e94130. doi: 10.1371/journal.pone.0094130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dukic V, Lopes HF, Polson NG. Tracking epidemics with Google Flu Trends data and a state-space SEIR model. J. Amer. Statist. Assoc. 2012;107:1410–1426. doi: 10.1080/01621459.2012.713876. MR3036404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statist. Sci. 1992;7:457–472. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Generous N, Fairchild G, Deshpande A, Valle SYD, Priedhorsky R. Global disease monitoring and forecasting with Wikipedia. PLoS Comput. Biol. 2014;10:e1003892. doi: 10.1371/journal.pcbi.1003892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Germann TC, Kadau K, Longini IM, Macken CA. Mitigation strategies for pandemic influenza in the United States. Proc. Natl. Acad. Sci. USA. 2006;103:5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ginsberg J, Mohebbi MH, Patel RS, Brammer L, Smolinski MS, Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457:1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- Harris KM, Maurer J, Kellermann AL. Influenza vaccine. N. Engl. J. Med. 2010;363:2183–2185. doi: 10.1056/NEJMp1012333. [DOI] [PubMed] [Google Scholar]
- Heffernan J, Smith R, Wahl L. Perspectives on the basic reproductive ratio. J. Roy. Soc. Interface. 2005;2:281–293. doi: 10.1098/rsif.2005.0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickmann KS, Fairchild G, Priedhorsky R, Generous N, Hyman JM, Deshpande A, Valle SYD. Forecasting the 2013–2014 influenza season using Wikipedia. PLoS Comput. Biol. 2015;11:e1004239. doi: 10.1371/journal.pcbi.1004239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack WO, McKendrick AG. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. Vol. 115. The Royal Society; 1927. A contribution to the mathematical theory of epidemics; pp. 700–721. [Google Scholar]
- Mills CE, Robins JM, Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature. 2004;432:904–906. doi: 10.1038/nature03063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nsoesie E, Mararthe M, Brownstein J. Forecasting peaks of seasonal influenza epidemics. PLoS Curr. 2013;5 doi: 10.1371/currents.outbreaks.bb1e879a23137022ea79a8c508b030bc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nsoesie EO, Brownstein JS, Ramakrishnan N, Marathe MV. A systematic review of studies on forecasting the dynamics of influenza outbreaks. Influenza and other Respiratory Viruses. 2014;8:309–316. doi: 10.1111/irv.12226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osthus D, Hickmann KS, Caragea PC, Higdon D, Del Valle SY. Supplement to “Forecasting seasonal influenza with a state-space SIR model.“. 2017 doi: 10.1214/16-AOAS1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plummer M. rjags: Bayesian graphical models using MCMC. R package version. 2014. pp. 3–14. [Google Scholar]
- Plummer M, et al. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd International Workshop on Distributed Statistical Computing; Vienna: 2003. p. 125. [Google Scholar]
- Ross R. Some quantitative studies in epidemiology. Nature. 1911;87:466–467. [Google Scholar]
- Shaman J, Karspeck A. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. USA. 2012;109:20425–20430. doi: 10.1073/pnas.1208772109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaman J, Karspeck A, Yang W, Tamerius J, Lipsitch M. Real-time influenza forecasts during the 2012–2013 season. Nat. Commun. 2013;4:2837. doi: 10.1038/ncomms3837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. [Google Scholar]
- Towers S, Chowell G, Hameed R, Jastrebski M, Khan M, Meeks J, Mubayi A, Harris G. Climate change and influenza: The likelihood of early and severe influenza seasons following warmer than average winters. PLoS Curr. 2013;5 doi: 10.1371/currents.flu.3679b56a3a5313dc7c043fb944c6f138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- U.S. Department of Health and Human Services. [Accessed: 02-06-2017];Regional Offices. 2017 Available at http://www.hhs.gov/about/agencies/regional-offices/
- Weiss HH. Materials Matemàtics. 2013. The SIR model and the foundations of public health. 0001–17. [Google Scholar]
- Yang W, Lipsitch M, Shaman J. Inference of seasonal and pandemic influenza transmission dynamics. Proc. Natl. Acad. Sci. USA. 2015;112:2723–2728. doi: 10.1073/pnas.1415012112. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.