Competing species leave many potential niches unfilled

Abstract

A cornerstone of biology is that coexisting species evolve to occupy separate ecological niches. Classical theory predicts that interspecific competition should lead to all potential niches being occupied, yet observational data suggest that many niches are unfilled. Here we show that theory can be reconciled with observational data by reconceptualising competition in the Hutchinsonian niche space to distinguish between substitutable and non-substitutable resources. When resources are substitutable (e.g. seeds of different size), the components of competition along the niche axes combine multiplicatively, leading to a densely packed niche space. However, when resources are non-substitutable (e.g. seeds and nest sites), we show that the components of competition combine additively. Disruptive selection therefore limits niche overlap between non-substitutable niche axes, leaving most potential niches unfilled. A key corollary is that increasing the number of niche axes may greatly increase the number of potential niches but does not necessarily increase diversity. We discuss observational data that are consistent with our model and consider implications for systems with invasive species. Our work reinforces the power of competition to drive major ecological patterns: while niche space informs on species that might exist, only a small and potentially arbitrary subset will coexist in sympatry.

One of the fundamental goals in ecology and evolutionary biology is to understand the spatial and temporal distribution of species. Early on, this led to the concept of an ecological niche, and the Hutchinsonian niche space, to describe a community of interacting organisms¹. Niche space can be conceptualised as a multidimensional space encapsulating all environmental factors that impact species survival (e.g. temperature, pH, food source, nest sites, and predators). While the notion of niche space can be interpreted and used in many ways, the key use in ecological theory has been to understand how ecological competition affects the coexistence of species^1–7. This is typically done by studying niches axes that correspond to variation in the characteristics of one or more depletable resources (e.g. food or nest sites), or more generally, regulating factors (e.g. predators)^2,3,6–9. A particular niche is then equivalent to a certain region (or hypervolume) of this space that characterises the subset of regulating factors that affect the associated species. Niche theory assumes that competition between two species occurs when their niches overlap: the greater the overlap, the greater the strength of competition. This has led to a large body of ecological research that aims to understand the mapping between species, their traits, and niche space^1–11. Specifically, to what extent does niche overlap affect species coexistence?

Theory predicts that when populations compete in 1-dimensional niche space, disruptive selection drives species to self-organise in a manner that maintains a characteristic distance between occupied niches. This phenomenon is often referred to as “species packing”^6,8,12. However, a regulating factor such as food source may vary in more than one characteristic (e.g. size, colour, and shape), and real populations are regulated by many factors (e.g. food source, nest sites, parasites, and predators), which raises the question of how species diversify in multidimensional niche space. Existing theory of multidimensional niche space is based on a direct extension of the species-packing principle from a single dimension: separation by a characteristic distance along any dimension is sufficient to facilitate coexistence and as a result niche space is predicted to be densely packed^2,3,7. However, it is not clear if this principle should apply when niche space consists of different types of regulating factors. Empirically there is little evidence to support the notion of densely packed niche space, with most observational data suggesting that it is in fact largely unfilled^13,14. The failure of competition-based theory to explain the sparsity of niche space has increased focus on alternative mechanisms that predict unoccupied niches, including phylogenetic constraints or environmental fluctuations^15,16.

Here we re-examine the underlying assumptions of competition in multidimensional niche space. We argue that the current conceptualisation of resource utilisation and competition only applies when niche space contains substitutable regulating factors (e.g. different food sources), but does not apply when regulating factors are not substitutable (e.g. food source and nest sites). This allows us to reconcile the theory of ecological competition with observations of sparsely packed niche space. We show that species must reduce niche overlap across every non-substitutable regulating factor, as disruptive selection is independent on each one. The result is that most potential niches (i.e. possible resource combinations) are left unfilled.

Model overview

We want to understand how ecological competition affects the ability of species with different characteristics to coexist in niche space. We follow the original Hutchinsonian definition of a multidimensional niche space, which combines all the biotic and abiotic environmental variables that allow a species to survive¹. We define a “potential niche” to be a unique combination of resources or regulating factors. In order to investigate the effects of competition, one must focus on those variables – and niche axes – over which one species may compete with another^{1–8,10–12,17}. That is, we study the subspace of Hutchinsonian niche space that captures variation in regulating factors such as predation, parasitism, and depletable resources (e.g. food and territory), as opposed to non-depletable environmental variables such as pH, temperature, or preferred oxygen content. Species do not directly compete over these latter variables. However, species may compete for territories that are defined by certain environmental conditions and, if limiting, territory may be a regulating factor. We assume competition between individuals proceeds according to the well-known Lotka-Volterra equations (see Methods), which are commonly used to understand the effects of competition in ecology and evolution^2,3,6–8,12. We follow the classical literature in focusing on the ‘resource utilisation’ of each species⁸, but the concept can be generalised for any regulating factor, such as parasites or predators⁹.

Clearly the form of the utilisation function is key for determining the strength of competition. We consider two scenarios: first, where niche space corresponds to a continuum of substitutable resources (e.g. different food sources, Fig. 1a), and second, where niche space consists of different resource types (or other regulating factors) that are not substitutable (e.g. food source and nest sites, Fig. 1b). Note that the axes of our niche space represent variation in the characteristics of the resources (e.g. size, colour, height), rather than in the quantity of the resources. The utilisation functions are normalised for each resource type rather than across all resource types, so that species consume the same overall quantities of a particular type of resource (e.g. food, nest sites), but may differ in the characteristics of the resources that they consume (e.g. seed size, nest height). Our model therefore differs to the seminal work by Tilman (1982)¹⁸, which showed that two species may coexist on two essential resources if there is a trade-off in consumption such that species A is a better competitor for resource 1 and a worse competitor for resource 2 than species B. Here, we assume there is no such trade-off.

Figure 1.

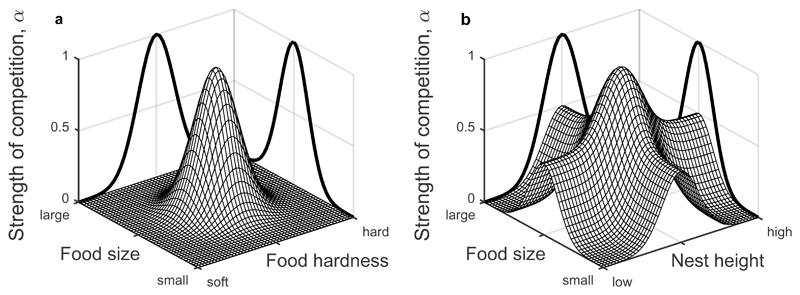
Competition (A) within and (B) across resource types based on the overlap of resource utilisation functions (equations (3) and (6)). Panels show how the strength of competition (α) varies for a species whose resource utilisation function peaks at the centre of the x-y plane. The black curves show the (unscaled) components of competition on each axis. (A) Resource utilisation functions combine multiplicatively within each resource type (here: food size and food hardness, more generally, for substitutable regulating factors) and so the competition kernel is a multivariate Gaussian. (B) Resource utilisation functions combine additively across different resource types (here: food size and nest height, more generally, for non-substitutable regulating factors) as they are independent of each other; hence differentiation within a single resource type has no impact on competition among other resource types. Note that the components of competition on each axis are rescaled when combined so that 0≤α_ij≤1.

Results

Multidimensional niche space with substitutable resources

We begin by considering a scenario where individuals compete over a single type of substitutable resource varying in multiple characteristics (e.g. seeds of varying size and colour). Conceptually, this means that each point in the corresponding n-dimensional niche space represents a unique niche variable. That is, each point in niche space corresponds to a unique resource and the n dimensions correspond to variation in the resource’s characteristics. For example, if the resource type in question is food then each dimension could correspond to an attribute such as size, colour, or fat content, so that a particular point in niche space corresponds to a preference for a certain type of food.

Given a single type of resource, what is a reasonable form for the utilisation function, U_i(z)? The assumption in classical studies^2,3 is that the U_i(z) are multivariate Gaussian functions only differing in the position of their peaks, with the correlation of each distribution equal (or close to) 0 (in the case where sizable correlations between certain attributes exist, one could reduce the dimensionality of the system through principal component analysis). The utilisation functions are therefore given by³:

$$U_i\left(\mathit{z}\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^n{\displaystyle {\prod }_{k=1}^n{\sigma }_k^2}}}\text{exp}\left\{-\frac{1}{2}{\displaystyle \sum _{k=1}^n{\left(\frac{z_k-{\widehat{z}}_k\left(i\right)}{{\sigma }_k}\right)}^2}\right\}$$ (1)

where ${\widehat{z}}_k\left(i\right)$ and ${\sigma }_k^2$ denote the mean position and variance of the distribution along the kth dimension and z_k is the kth component of z. From equation (8) (see Methods) we see that the competition coefficient is:

$${\alpha }_{ij}=\frac{{\displaystyle \int \text{exp}\left\{-\frac{1}{2}{{\displaystyle {\sum }_{k=1}^n\left(\frac{z_k-{\widehat{z}}_k\left(i\right)}{{\sigma }_k}\right)}}^2\right\}\text{exp}\left\{-\frac{\text{1}}{\text{2}}{\displaystyle {\sum }_{k=1}^n{\left(\frac{z_k-{\widehat{z}}_k\left(j\right)}{{\sigma }_k}\right)}^2}\right\}d\mathit{z}}}{{\displaystyle \int \text{exp}{\left\{-\frac{1}{2}{{\displaystyle {\sum }_{k=1}^n\left(\frac{z_k-{\widehat{z}}_k\left(i\right)}{{\sigma }_k}\right)}}^2\right\}}^{2}d\mathit{z}}}$$ (2)

which reduces to³

$$\begin{array}{l}{\alpha }_{ij}={\displaystyle \prod _{k=1}^n\text{exp}\left\{-\frac{1}{2}{\left(\frac{{\widehat{z}}_k\left(i\right)-{\widehat{z}}_k\left(j\right)}{{\sigma }_k}\right)}^2\right\}}\hfill \\ ={\displaystyle \prod _{k=1}^n{\alpha }_{ij}^k}\hfill \end{array}$$ (3)

where ${\alpha }_{ij}^k$ is the component of competition along the kth dimension. Thus, the components of competition in each dimension combine multiplicatively to give the overall competition coefficient, α_ij, which means that the competition kernel peaks for individuals that utilise the same resource, and falls away equally in all directions as niches diverge. Hence displacement by a given amount in any direction reduces competition by the same amount (assuming the carrying capacity function does not contain irregular shapes that support an uneven species trait distribution). As a result, the classical assumption of a multivariate Gaussian utilisation function, or more generally the assumption that competition in each dimension of niche space combines multiplicatively, necessarily leads to a saturated niche space with coexisting species packed at a characteristic distance from one another⁸ (Fig. 2a). In summary, niche space is saturated, as species only need to differ along one dimension to coexist.

Figure 2.

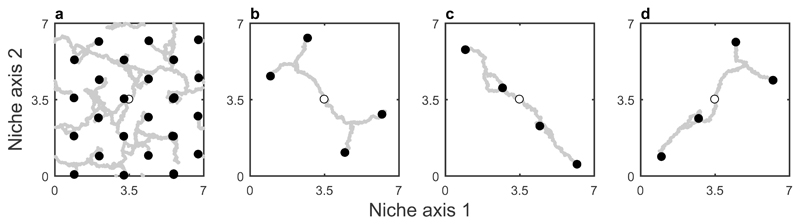
Evolutionary trajectories of species in 2-dimensional niche space consisting of (A) substitutable resources (e.g. different food sources), and (B-D) non-substitutable resources (e.g. food source and nest sites). Open and closed circles show initial and final occupied niches, respectively, and grey lines correspond to evolutionary trajectories. Niche space is toroidal to remove boundary effects. When niche space consists of substitutable resources the components of competition along both dimensions combine multiplicatively, leading to a densely packed niche space (A). However, when niche space consists of non-substitutable resources the components of competition combine additively, leading to separation on both axes (competition is independent for each resource and so selection proceeds diagonally), resulting in a sparsely packed niche space and potentially arbitrary associations between traits. Parameters: K_i=1, r_i=1, ε₁=0.1, ε₂=0.05, σ_k=1.

Multidimensional niche space with non-substitutable resources

In the previous section we assumed that an n-dimensional niche space described variation in characteristics of a single type of resource (or regulating factor), such that each point in the space corresponds to a unique niche variable. Under the assumption that the utilisation functions are multivariate Gaussian with zero correlation, disruptive selection on any dimension (or combination of dimensions) is sufficient to remove competition on all others, leading to the saturation of niche space (Fig. 2a). However, one cannot combine the utilisation functions of different types of resources (e.g. food and nest sites) in this way. This is because each point in the niche space now corresponds to a unique set of niche variables (e.g. small seeds and high nest sites) rather than a unique niche variable (e.g. small black seeds). Classical niche theory does not make this crucial distinction^2,3,7. But combining the competition terms for non-substitutable resources multiplicatively would imply that differentiating on food source can remove competition for nest sites, or vice versa (Fig. 1b). Hence there is a clear need to better understand how competition and species relationships unfold when niche space consists of non-substitutable resources.

How does one combine the utilisation functions for non-substitutable resources (more generally, regulating factors)? Let us assume that there are m non-substitutable resource types, each consisting of n_p attributes (p = 1, … , m). Hence, each resource type is characterised by an n_p-dimensional subspace of the overall M-dimensional niche space, with $M={\displaystyle {\sum }_{p=1}^m{n}_p.}$ Following equations (1)-(3), the utilisation function for the pth resource type is:

$$U_i^p\left({\mathit{z}}_{\mathit{p}}\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^{n_p}{\displaystyle {\prod }_{k=1}^{n_p}{\left({\sigma }_k^p\right)}^2}}}\text{exp}\left\{-\frac{1}{2}{\displaystyle \sum _{k=1}^{n_p}{\left(\frac{z_k^p-{\widehat{z}}_k^p\left(i\right)}{{\sigma }_k^p}\right)}^2}\right\}$$ (4)

and the strength of competition between species i and j for this resource type is therefore:

$$\begin{array}{l}{\alpha }_{ij}\left(p\right)={\displaystyle \prod _{k=1}^{n_p}\text{exp}\left\{-\frac{1}{2}{\left(\frac{{\widehat{z}}_k^p\left(i\right)-{\widehat{z}}_k^p\left(j\right)}{{\sigma }_k^p}\right)}^2\right\}}\\ ={\displaystyle \prod _{k=1}^{n_p}{\alpha }_{ij}^k\left(p\right)}\end{array}$$ (5)

As each resource type is independent of all others, there is no overlap between the utilisation functions for different resource types. Thus the overall strength of competition between species i and j is simply the sum of the α_ij(p) over all resource types, weighted by the relative importance of each resource type, W_p ≥ 0, with ${\displaystyle {\sum }_{\text{p}=1}^{\text{m}}{\text{w}}_{\text{p}}=1:}$

$${\alpha }_{ij}={\displaystyle \sum _{p=1}^m{w}_p{\alpha }_{ij}\left(p\right)}$$ (6)

Competition for certain resource types (e.g. food) may be more intense than competition for others (e.g. nest sites); the parameter w_p captures this variation (hereafter we set w_p = 1/m for simplicity).

Competition across non-substitutable resources clearly differs from competition over substitutable ones in a fundamental way; the components of competition for the latter combine multiplicatively (equation (3)), but combine additively for non-substitutable resources (equation (6)). Consequently, disruptive selection can completely remove competition within a resource type, but it has no impact on other types of resource. For example, if w₁ = w₂ = 1/2 in the food source-nest site scenario, then differentiation on food source alone cannot reduce α_ij below 1/2 (Fig. 1b). We will now show that this subtle change in the nature of competition strongly affects the coexistence of multiple species.

Consider the selection gradient in n-dimensional niche space given constant r_i and K_i. Suppose species x₁ is at the origin and let us introduce a species, x₂, at a Euclidean distance d > 0 from x₁. If the niche space corresponds to a single resource type then ${\alpha }_{12}=e^{-\frac{1}{2}{d}^2}$ wherever x₂ is placed along the arc centred at the origin with radius d. Thus, the selection gradient is the same in every direction; diverging by d on one axis has precisely the same impact as diverging by d_k ≥ 0 on each axis when $d^2={\Sigma }_{k=1}^n{d}_k^2.$ If instead each axis corresponds to a different resource type then ${\alpha }_{12}=\frac{1}{n}\Sigma e^{-\frac{1}{2}{d}_k^2};$ the selection gradient is therefore greatest when $d_k=d/\sqrt{n}$ on each axis. Hence, species x₂ tends to diverge diagonally away from the origin. The implication of this simple result is that selection will favour species that diverge across all non-substitutable resources or other regulating factors.

These predictions were borne out in our simulations; while species that overlap on non-substitutable resources may coexist over ecological timescales, disruptive selection causes species to diverge across all non-substitutable resources over evolutionary timescales, leaving many potential niches unfilled. The system eventually reaches a quasi-equilibrium where further mutations do not qualitatively change the pattern of species dispersal. All else being equal, which niches are filled and which are left unfilled is potentially arbitrary and largely determined by founder effects, leading to alternative patterns in different radiations (Fig. 2b-d). We refer to these gaps in niche space as unfilled “potential niches”, because they can be filled in other simulations, which represent different incarnations of the evolutionary radiation in the ecosystem. However, the unfilled niches are not vacant in the traditional sense, which is generally taken to imply that the niches can be filled in future but are currently empty due to non-equilibrium dynamics¹⁹. Here, no more niches can be filled once the system reaches a quasi-equilibrium. These patterns are in stark contrast to the typical view of species packing, where niche space is fully saturated and there is a characteristic distance between any two neighbouring species^2,3,7; in our model these patterns only emerge among niche axes that correspond to substitutable regulating factors (e.g. a single food source; Fig. 2a).

In summary, our model agrees with classical niche theory in that species may separate on as little as one dimension when resources, or regulating factors, can be substituted for one another. Here, increasing the dimensionality of niche space can drive an exponential increase in species diversity due to the associated increase in resource diversity. This means that while only three species can coexist in a discrete niche space consisting of small, medium, and large seeds, nine species can coexist if a second axis is added to the niche space corresponding to black, brown, and green seeds because there are now nine distinct resources to choose from (e.g. species A: small black seeds; species B: small brown seeds, and so on).

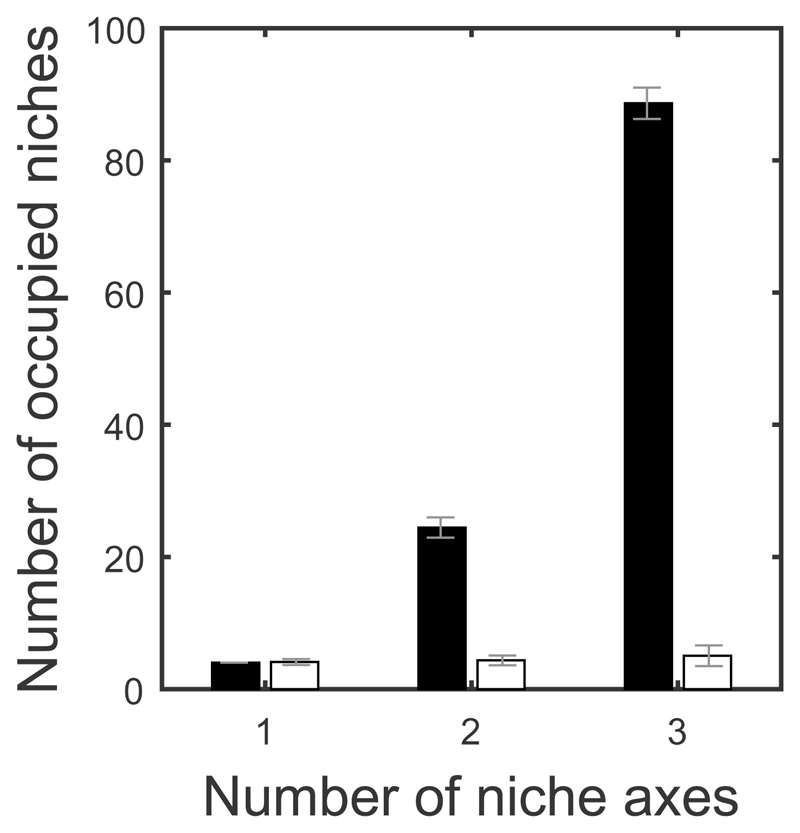
In contrast, species must diverge across all non-substitutable regulating factors leaving many potential niches unfilled. For example, if we replace the second axis in the example above with a non-substitutable resource such as nest sites (e.g. high, intermediate, or low), then each species requires one resource of each type and so the niche space can only be partitioned with no overlap by three species, not nine (e.g. species A: small black seeds and high nests; species B: medium brown seeds and intermediate nests; species C: large green seeds and low nests). Therefore while the number of potential niches has increased from three to nine (all possible combinations), only three niches are filled because each species requires two of the six available resources. While numerical analysis indicates that it is possible for more species to coexist over ecological timescales (and hence temporarily overlap on non-substitutable resources), such cases are unlikely to persist because disruptive selection drives species to diverge on both resource types. Hence, increasing the number of niche axes does not increase long-term species richness within each community (Fig. 3, Supplementary Fig. 1), although different potential niches may be filled in other communities (Fig. 2b-d). This is because increasing the dimensionality of niche space opens up a new avenue of competition, rather than providing species with alternative resources.

Figure 3.

Number of occupied niches at equilibrium. Mean number of occupied niches (± sd) when niche space consists of substitutable (black) or non-substitutable (white) resources (20 simulations). Note that the two models are equivalent in the single axis scenario. The number of coexisting species increases exponentially with dimensionality when niche space contains substitutable resources, but remains constant when not substitutable. Here, the demographic parameters are held constant for all species, but the results are broadly similar when demographic parameters vary (Supplementary Fig. 1). Parameters as in Fig. 2 (the results are qualitatively similar for different parameters).

Discussion

The idea that species occupying different positions in niche space can coexist is a fundamental tenet of ecology and evolution^1–11. We have explored how the distinction between substitutable and non-substitutable resources (in general: regulating factors) – overlooked in classical niche theory – affects patterns of species coexistence. Critically, competition acts differently in Hutchinsonian niche space depending on whether the resources on one axis can be substituted for resources on another. For non-substitutable resources, disruptive selection occurs across all axes leading to a sparsely packed niche space with many potential niches left unfilled. Our model makes three important predictions: (i) much of niche space remains unfilled; (ii) associations between different components of a species’ niche may be arbitrary; and (iii) increasing the dimensionality of niche space in terms of non-substitutable regulating factors does not increase species diversity.

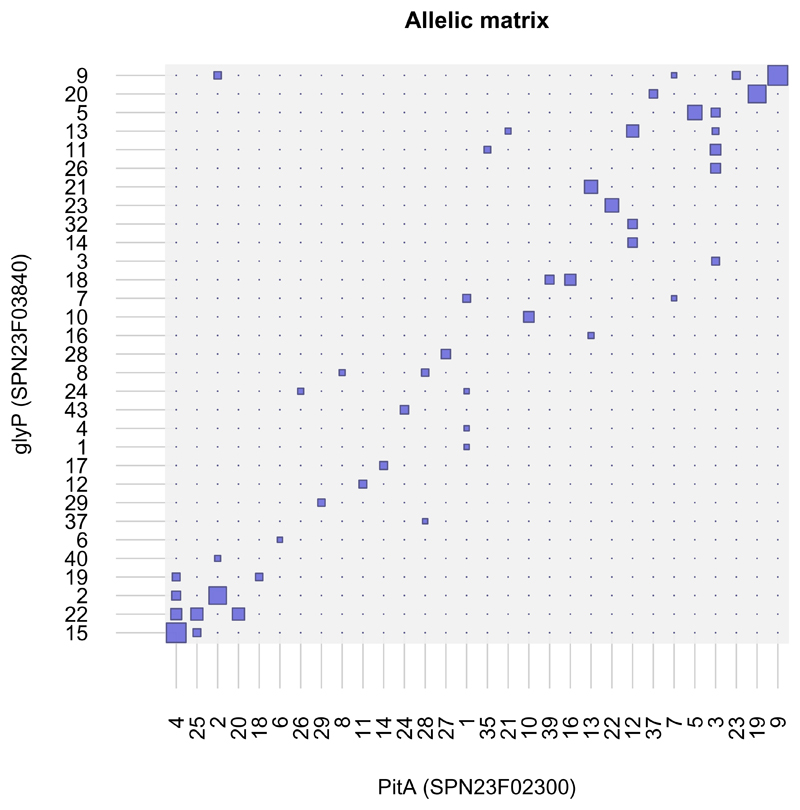
The prediction of potentially arbitrary non-overlapping trait combinations has a precedent in infectious diseases where co-circulating pathogen strains have been shown to have unique repertoires of antigenic variants, despite high levels of recombination: here, immunological competition drives the pathogen population to self-organize into non-overlapping combinations of allelic variants at relevant antigenic loci^20–22. It has also recently been proposed that the metabolic loci of several pathogenic bacterial species may be organised into discrete metabolic types²³. These metabolic types are thought to approximate niches associated with the utilisation of different resource types (i.e. non-substitutable regulating factors). If so, our model predicts that the bacterial strains will have to differ across multiple metabolic loci in order to coexist. Consistent with this prediction, different metabolic loci across 616 whole genomes of the human pathogen Streptococcus pneumoniae²⁴ are more often in linkage disequilibrium with each other than non-metabolic loci²³ and particular combinations of metabolic genes serve as good predictors of capsular serotype²⁵. The potential strength of such effects is illustrated in Fig. 4, which contrasts allelic variants at two metabolic loci: the gene PitA encoding for an iron ATP-binding cassette transporter, and glyP which is involved in sodium uptake. Functional or regulatory epistasis could also drive such association of alleles. However, the loci are predicted to target different resources (iron versus sodium). Accordingly, no tight functional interaction is expected that would strongly favour particular allelic combinations.

Figure 4.

Illustration of nonoverlapping allelic associations in 616 isolates of Streptococcus pneumoniae collected in Massachusetts, USA between 2001-2007²⁴. Allelic associations between the genes PitA, one of two genes within the pit operon encoding for an ABC transporter involved in iron uptake, and glyP, encoding a sodium symporter. Allele numbers were generated by the Genome Comparator tool (www.pubmlst.org) and labelled arbitrarily (see Methods of ²³).

Further evidence that niche space is sparsely packed is provided by studies of phenotypic diversity. This includes a recent study of bird morphology, which concluded that the number of species is, at best, weakly correlated with the volume of niche space²⁶. Niche theory does not perfectly capture data based upon morphological traits rather than resource axes, as species do not compete over morphological traits per se. Nevertheless, a weak relationship between the niche space volume and species number is consistent with our predictions for loose species packing.

In addition to understanding character displacement over evolutionary timescales, our model has interesting implications for systems with invasive species. For example, Inoue and Yokohama (2010)²⁷ suggest that the native bumblebee species Bombus hypocrita sapporoensis and B. diversus tersatus are under threat from the invasive B. terrestris. B. hypocrita sapporoensis and B. terrestris have a high degree of niche overlap as they compete for the same flower species (first niche axis) and nest sites (second niche axis), but B. diversus tersatus only competes with B. terrestris for nest sites²⁷. Although B. terrestris and B. diversus tersatus differ on flower species they do not differ on another, non-substitutable regulating factor (nest sites); accordingly, the data suggest that B. terrestris is able to exclude B. diversus tersatus²⁷. Interestingly, a third native species, B. pseudobaicalensis, shares the same flower species as B. terrestris, but differs on nest site. This species does not currently appear to be under threat from B. terrestris, as flower resources do not appear to be as limiting as nest sites (i.e. competition along this niche dimension is relatively weak). However, competition can intensify when flower resources are limiting^28,29, which suggests that a reduction in flower abundance or diversity could lead to competitive exclusion of B. pseudobaicalensis.

Our study directly extends a large body of theoretical work on niche space, which asks how resource competition affects species coexistence^1–8,10. In this body of theory, as in our work, niche axes describe depletable resources such as food or nest sites, or more generally, regulating factors such as parasites and predators⁹. In other areas of ecology, niche axes have been used to represent environmental properties such as pH and temperature, often because these are usefully mapped to species distributions³⁰. For such axes, there is no clear barrier to filling niche space as each coordinate can, in principle, represent a novel environment where a particular specialist species can dominate. Our model then emphasises the importance of distinguishing between different types of niche axes³⁰. Nevertheless, the two types of axes can be combined in one representation of multidimensional niche space¹ and, so long as there are non-substitutable regulating factors, niche space is again expected to remain unfilled.

The study of diversity is central to biology and it is clear that many factors contribute to species form and function. This includes the roles of phylogeny, where the recent ancestry of a species can strongly predict its characteristics³¹, potentially irrespective of the potential for ecological competition. In addition, even when ecological competition is important, it is possible for highly similar species to coexist for long periods as they will be subject to largely neutral dynamics¹², although the robustness of the coexistence is predicted to be low⁹. While phylogenetic and neutral processes are undoubtedly important, however, the concept of niche remains central to explanations of diversity and the role of competition in many systems is well supported. Here we have shown that species characters will separate themselves across all non-substitutable regulating factors. The evolution of these distinct characteristics may either occur in sympatry by character displacement³² or in allopatry where successful immigration to the focal environment is linked to a lack of niche overlap with resident species³³. While simple, the prediction that species separate on multiple axes has significant implications for our understanding of biological diversity. Crucially, it suggests that niche space will be sparsely rather than densely packed, with many potential niches unfilled. Even though many potential niches are unfilled, the concept of niche space retains its value by showing all of the potential species that might exist. In practice, however, only a few of these species will coexist, and those that do may differ between radiations.

Methods

The equations for competition among S species are given by:

$$\frac{d{N}_i}{dt}=r_i{N}_i\left(1-{\displaystyle \sum _{j=1}^s\frac{{\alpha }_{ij}{N}_j}{K_i}}\right)$$ (7)

where N_i is the abundance of species i, which has a maximum per capita growth rate of r_i and carrying capacity K_i, and α_ij is the strength of competition with species j. The strength of competition between two individuals depends on the degree to which their niches overlap and hence the similarity of their regulating factors. Competition between species i and j is given by:

$${\alpha }_{ij}=\frac{{\displaystyle \int U_i\left(\mathit{z}\right)U_j\left(\mathit{z}\right)d\mathit{z}}}{{\displaystyle \int U_i{\left(\mathit{z}\right)}^{2}d\mathit{z}}}$$ (8)

where z is a vector describing a position in niche space and U_i(z) is the resource utilisation function for species i. This function measures the strength of interspecific competition relative to intraspecific competiton, such that α_ij ∈ [0,1] and α_ii = 1.

We use simulations to explore the evolutionary dynamics resulting from competition in multidimensional niche space with substitutable and non-substitutable resources. We are interested in the long-term evolution of species distributions rather than ecologically stable coexistence, which may be transient due to evolutionary dynamics. The simulations are analogous to adaptive dynamics (evolutionary invasion analysis³⁴). Starting with a single 'resident' species at its carrying capacity, we introduce a 'mutant' species that randomly differs from the resident by up to ε₁ > 0 on each niche dimension (we restrict the size of each niche dimension to prevent an infinite number of species emerging and remove boundary effects by making niche space toroidal). We allow the population dynamics to approach equilibrium again and remove a species if it has fallen below a threshold abundance of ε₂ > 0. If one species has excluded the other, then it becomes the new resident. If the two species are able to coexist, then they are both classed as residents. We repeat the process by introducing a 'mutant' for each resident that has survived the previous iteration, allowing population dynamics to reach equilibrium again, removing species that fall below the extinction threshold. We allow the system to reach a quasi-stable state (i.e. the relative positions of species in niche space are approximately constant) and count the number of distinct niches that are occupied.

Data Availability

The dataset analysed during the current study was generated by Croucher et al²⁴ and transformed into Whole Genome MLST by Watkins et al²³.