Quantitative Investigation of MDA-MB-231 Breast Cancer Cell Motility: Dependence on Epidermal Growth Factor Concentration and Its Gradient

Abstract

Enhanced cell motility is one of the primary features of cancer. Accumulated evidence demonstrates that Epidermal Growth Factor Receptor (EGFR) mediated pathways play an important role in breast cancer cell proliferation and migration. We have quantified the MDA-MB-231 breast cancer cell migration in response to the stimulation of EGFR pathways with its ligand EGF to determine how cell motility of MDA-MB-231 cells depend on the ligand concentration and its gradient. Analysis at the single cell level combined with mathematical modeling and the ability to vary the ligand concentration and gradients locally using microfluidic devices allowed us to separate the unique contributions of ligand concentration and ligand gradients to cell motility. We tracked the motility of 6,600 cells individually using time lapse imaging under varying EGF stimulation conditions. Trajectory analysis of the tracked cells using non-linear multivariate regression models showed that: i) Cell migration of MDA-MB-231 breast cancer cells depends on ligand gradient but not on the ligand concentration. This observation was valid for both the total (direction independent) and directed (along gradient direction) cell velocities. Although the dependence of the directed motility on ligand gradient is to be expected, dependence of the total velocity solely on ligand gradient was an unexpected novel observation. ii) Enhancement of motilities of individual cells in a population upon exposure to ligand was highly heterogeneous, and only a very small percentage of cells responded strongly to the external stimuli. Separating out the non-responding cells using quantitative analysis of individual cell motilities enabled us to establish that enhanced motility of the responding cells indeed increases monotonically with increasing EGF gradient. iii) A large proportion of cells in a population were unresponsive to ligand stimulation, and their presence introduced considerable random intrinsic variability to the observations. This indicated that studying cell motilities at individual cell level is necessary to better capture the biological reality and that population averaging methods should be avoided. Studying motilities at individual cell level is particularly important to understand the biological processes which are possibly driven by the action of a small portion of cells in a population, such as metastasis. We discuss the implications of our results on the total and chemotactic movement of cancer cells in the tumor microenvironment.

INTRODUCTION

Phenotypic responses of tumor cells depend on their microenvironment, which define their interactions with the other residing cell types (such as immune and stromal cells) and scaffold structures^1–7. This can lead to individual tumor cells exhibiting distinct morphological and phenotypical behavior⁸. Therefore, improved understanding of how phenotypic responses of individual tumor cells are impacted by the composition and condition of their microenvironment can be extremely useful in cancer studies. A good example to altered phenotypic response in tumors is the increased motility, which is a contributing factor to metastasis. It is well established that cell migration has a highly heterogeneous nature and that a multitude of biological and physiological factors regulate cancer cell migration and metastasis^{2, 5, 9, 10}. However, it is still unclear if mere availability of growth factors and hormones in the microenvironment, or if their spatial distribution (i.e, gradients) is more important in increasing the cell motility. Therefore, there is a need for developing new approaches that can quantitatively characterize how cell motility depends on the factors in the tumor microenvironment, while accounting for the spatial heterogeneity and cell-to-cell variations.

A case that nicely exemplifies the important role of the microenvironment in tumor cell motility is the hypothesized paracrine signaling between macrophages and tumor epithelial cells. Epidermal Growth Factor (EGF) secreted by macrophages works as chemo-attractant for tumor cells to increase their motility^11–13. It has been proposed that this interaction contributes to metastasis^{14, 15} because the binding of EGF to its receptor (EGF receptor, EGFR) stimulates the cell proliferation and motility processes in epithelial cells^16–18. Previous studies have identified the signaling pathways that regulate cell motility upon stimulation through EGFR activation^19–22, and it has been shown that cancer cell lines which overexpress EGFR are more metastatic^23–29. Although the enhancement of cell motility by EGF and other growth factors is rather well established, detailed quantitative characterization of how cells respond to ligand stimulation is still lacking. For example, it is not known whether the availability of growth factors, or their spatial distribution creating gradients in the microenvironment is more critical in stimulating cell motility. Cellular production and uptake of growth factors or other small messenger molecules will induce heterogeneity in their spatio-temporal distribution causing regions with gradients in their distribution. Thus, there is an inevitable strong coupling between substrate availability and its gradient formation. Therefore, it is not trivial to distinguish if the impact of stimulants on cell motility is merely due to their availability or due to their heterogeneous distribution which creates gradients. Similarly, if there are certain threshold limits for ligand concentration and gradient for enhanced cell motility is not well known, either. Additionally, the motility of a cell can be characterized by both the total cell movement (direction information is not considered, as in consideration of random motions) and movement along the direction of the gradients that the cell is exposed to (i.e., directed motion or chemotaxis). Effects of the availability or gradients of growth factors can be different for these motility categories.

Earlier cell migration studies typically utilized chamber-based chemotaxis assays (e.g., Boyden chamber, Dunn chambers, Zigmond chambers) and micropipette based assays to study cell motility in response to stimulants^{30, 31}. These methods utilize cell populations exposed to gradients, and they are semi-quantitative at best when measuring the cell migration rates. Recently, use of microfluidic devices became popular in cell motility studies because they offer the ability to monitor cellular movement in a spatio-temporally resolved manner³². Microchip-based motility assays have additional advantages such as good control of stimulant concentration and gradient formation, manipulation and observation of individual cells, and better mimicking of in vivo microenvironments at miniaturized scales^33–46. For example, microfluidic devices were used to show that uniform EGF stimulation induces chemo-kinesis or enhanced random motility and that EGF gradient induces chemotaxis or enhanced directed motility in EGFR expressing cancer cell lines^47–50. However, these studies were based on selective growth factor doses and did not consider separating the above discussed interlinked effects of stimulant concentration and its gradient. Our study extended these earlier studies in both the environmental exposure continuum and the individual cell behavior dimensions by sampling a very large number (> 6,000) of model breast cancer epithelial cells individually when cells were exposed to a continuum of ligand dose and gradients. Measured cell motilities were analyzed using multivariate regression models to quantify and separate the unique contributions of determinant environmental factors to cell motilities.

We measured the motilities of individual cells using two types of microdevices under carefully designed measurement conditions to distinguish the unique contributions of EGF concentration and its gradient to the motility of MDA-MB-231 breast cancer epithelial cells. Our integrative approach combined optical microscopy experiments with transport modeling and simulations to relate the motility of a cell to its local environmental conditions at the individual cell level. Obtained quantitative data was analyzed to determine the statistical distributions of total (direction independent) and directed (along the gradient direction) velocities of cells as a function of ligand concentration ([L]) and its gradient (∇L). Multivariate, non-linear regression analysis of the observed cell motilities established that: i) Only ∇L plays a vital role in total cell motility where the impact of [L] is insignificant, and that directed cell motility and persistent motion are also dependent only on ∇L. Our results for the impact of ∇L on total and directed cell motilities agreed with the earlier results. Observation that ligand concentration [L] is an insignificant factor in the enhanced motility of MDA-MB-231 cells were unexpected, and this novel finding can help to better understand the cell motility response in tumor microenvironments. ii) Enhancement of motilities of individual cells in a population was highly heterogeneous, and only a small percentage of cells responded strongly to the external stimuli. We separated out the non-responding cells in a population by analyzing individual cell motilities. This quantitative analysis allowed us to establish that enhanced motility of the responding cells indeed increase monotonically with increasing EGF gradient. iii) Since a large percentage of cells are non-responsive to ligand stimulation, their presence introduces considerable random intrinsic variability to the observations at the population scale. Therefore, when sampled appropriately, studying cell motilities at individual cell level captures the biological reality much better than population averaging methods and it should be the preferred approach. Studying motilities at individual cell level is particularly important to understand the biological processes which are possibly driven by the action of a small portion of cells in a population, such as metastasis.

Most importantly, our study has developed an integrated approach in which the image data is analyzed in combination with simulation results, to uniquely identify the relative contributions of different system variables to cell motilities. This new integrated approach to analyze cell motions at the individual cell level allowed us to uniquely factor out the contributions of EGF dose and its gradient to cell motility. Our novel multivariate approach can easily be extended to motility studies that uses multiple ligand types, to co-culture studies with multiple cell lines, and to other microdevices which can deliver the ligands in a different manner.

MATERIALS and METHODS

Cell lines, reagents, and antibodies

MDA-MB-231 adenocarcinoma cells are EGFR+ and ER−/PR−/HER2− (i.e., triple negative) breast cancer epithelial cells and they were obtained from American Type Culture Collection (ATCC catalog name: HTB-26). MDA-MB-231 cells were labeled with GFP for efficient tracking during analysis of the collected time lapse images. MDA-MB-231 cells were maintained in Leibovitz’s L-15 media supplemented with 10% fetal bovine serum (FBS) and 1% penicillin-streptomycin. For cell starvation, L-15 media with 1% penicillin-streptomycin and no FBS was used. Cells were stimulated with EGF (Pepro Tech, catalog no: AF-100-15).

Microfluidic devices and their pretreatment

Cell motilities were measured using two types of microdevices which were purchased from the Ibidi company: 2D chemotaxis µ-slide (catalog no: 80306) and 3-in-1 µ-slide (catalog no: 80316). These devices were prepared for the migration experiments by coating the cell attachment surfaces in the interior channels with collagen type-I. Solution containing collagen type-I (300 µg/ml) was injected into the devices, and after 2 hours of incubation at room temperature, the device was washed thoroughly with ultrapure water. The slides were then dried overnight before use in the experiments.

Cell motility experiments

Because of their shape and the way we utilized them in this study, we refer to the 2D chemotaxis and 3-in-1 µ-slides as “double chamber” and “y-channel” devices, respectively, in the remainder of the article. As further explained below, use of different devices has allowed us to vary the EGF concentration and gradient in different ways: In double chamber device, there is a constant EGF gradient in the central channel while different regions of the y-channel device have differing EGF concentrations and gradients thus allowing for a multiplexed approach. Cell motility experiments using these microdevices were run as follows:

1. Double chamber device: MDA-MB-231 cells were loaded to the central channel of the device and allowed to attach for 4 hours. The media inside the central channel was then replaced with the starvation media (L-15 media with no FBS and 1% penicillin-streptomycin) and cells were starved for 5–6 hours. To initiate the motility experiments, media in the central channel region as well as the side chambers were replaced with the stimulation media (L-15 media supplemented with 1% FBS and 1% penicillin-streptomycin), and 30 ng/ml EGF was added to one of the side chambers. Gradient in the central channel region was allowed to form for 30 minutes after EGF addition to establish a steady state spatial distribution of the stimulant in the device. Cellular positions were imaged for 120 minutes at 5 minute intervals. Motility experiments with the double chamber device were run in triplicate when EGF was added to the side chamber at a concentration of 30 ng/ml and also when no EGF was added (i.e., control experiments with [EGF]=0 ng/ml). For each experiment, motion of about 200 cells were tracked for individual cell analysis.

2. Y-channel device: This device has three inlets leading to one central channel. Only two end (upper and lower) inlets were used and middle inlet was kept sealed in our experiments. As in the double chamber case, MDA-MB-231 cells were first loaded into the device, allowed to attach to the bottom surface, and then starved for 5–6 hours before ligand stimulation. In the motility experiments, syringe pumps were used to inject L-15 media with 1% FBS and 1% penicillin-streptomycin through the inlets at a 0.5 µl/min flow rate. Injected solution for one of the inlets contained no EGF and EGF was added to the solution for the other inlet at a fixed concentration. Experiments were performed for 0, 5, 15, 35 ng/ml EGF input concentrations in duplicate. Time lapse imaging was done for 120 minutes at 10 minute intervals. Cellular motions were captured at four different regions along the flow channel, and motions of around 200 cells were tracked in each experiment.

As it may have an effect, we insured that cell seeding was the same and uniform inside both devices. Seeding density corresponded to ~65–70% confluency in both devices. This level was achieved by using 60 µl of 8.5×10⁵ cells/ml suspension in the y-channel device experiments and 6 µl of 2.5×10⁶ cells/ml cell suspension in the double chamber device experiments. Time lapse imaging experiments were run with a Zeiss Axio Vert.1 inverted microscope with AxioCam MRm camera using the Zen software. Collected images were analyzed using the Volocity image analysis software for cell tracking and in house Matlab codes for additional quantification and statistical analysis.

Cell trajectory analysis

Goal of our study was to investigate cellular motilities at the individual cell level to determine whether stimulant dose or its gradient is the main regulator of the motility. Time lapse images collected at N time points with time interval ∆t provides the cellular positions at snapshot times. We characterized the motilities of the cells by computing (Fig. 1) i) average total instantaneous velocity of the cells v_tot, which is the velocity independent of movement direction, ii) average instantaneous velocity component along the ligand gradient direction v_d, which corresponds to directed (chemotactic) velocity, and iii) average instantaneous velocity along the direction perpendicular (normal) to gradient direction, v_p.

Figure 1.

Schematic diagram for cell velocity components: i) average total instantaneous velocity of the cells v_tot, ii) average instantaneous velocity component along the EGF gradient direction v_d, and iii) average instantaneous velocity along the normal to gradient direction, v_p.

Average total instantaneous velocity v_tot of a cell is computed from its measured locations as ${\mathrm{v}}_{\text{tot}}=\frac{1}{\mathrm{N}-1}{\sum }_{\mathrm{k}=2}^{\mathrm{N}}|{\overrightarrow{r}}_k-{\overrightarrow{r}}_{k-1}|/\mathrm{\Delta }\mathrm{t}$ where k is the frame index of the image time-series data. This average instantaneous velocity is equal to the ratio of the total trajectory length of a cell to the total elapsed time. Note that v_tot is a scalar quantity and does not have direction dependence.

Average instantaneous velocity component along the EGF gradient direction v_d was computed similar to v_tot except that v_d is directional and corresponds to a vector quantity. If the gradient is along the y-direction, then ${\mathrm{v}}_{\mathrm{d}}=\frac{1}{\mathrm{N}-1}{\sum }_{\mathrm{k}=2}^{\mathrm{N}}(y_k-y_{k-1})/\mathrm{\Delta }\mathrm{t}$ where y_k is the y-position of the cell in the k^th frame of the time-series image data.

Lastly the average instantaneous velocity component perpendicular (orthogonal) to the gradient direction v_p was also computed. If the gradient is along y-axis, v_p would be the average instantaneous velocity along the x-direction. As the directed motility along this perpendicular direction is expected to be random, the v_p calculations were used as the negative control to check for the biases in the experiments.

As an additional measure of the directed motion, we analyzed the cell trajectories by computing the directed persistence of cells as well⁹. Directed persistence (P_d) of a cell is defined as the ratio of cell’s net movement along the gradient direction to the total trajectory length over the course of time. If the gradient is along the y-direction, then ${\mathrm{P}}_{\mathrm{d}}=(y_N-y_1)/{\sum }_{\mathrm{k}=2}^{\mathrm{N}}|{\overrightarrow{r}}_k-{\overrightarrow{r}}_{k-1}|$. Directed persistence ranges from −1 (cell persistently moves opposite to the gradient direction) to 1 (cell persistently moves along the gradient direction). Small absolute P_d values correspond to mostly random cell movement.

The focus of our analysis was to characterize the velocity of a cell as a function of the local EGF concentration and its gradient at cell’s location. This uniquely integrated approach enabled us to separate the contributions of these interlinked system variables. We achieved this by experimentally measuring the cell velocities and computing the local EGF distribution in microchip devices in fluid dynamics simulations using the COMSOL Multiphysics software version 5.1. This allowed us to relate the velocities of cells to local EGF concentration and its gradient at the individual cell level. Collected individual cell data was then analyzed using multivariate non-linear regression method to establish the dependence of cell velocities to EGF concentration and EGF gradient. Pursued analysis consisted of the following steps:

1. Identify the cells in time-lapse image frames and obtain their position: We used the commercial Volocity image analysis software for automated cell tracking. An image sequence was created from the time lapse images (czi format). The “Find Object” task was used to select the cells in the image sequence by selecting an appropriate intensity limit. We then used the “Track” task to follow the motion of selected objects. Settings for the tracking were: a) ignore new objects, b) ignore static object, and c) automatically join broken tracks. Maximum cell to cell distance for tracking was 19 µm. This setup was appropriate to track cells correctly throughout the whole imaging duration. Quality of tracking was further validated visually. Using GFP expressing cells made cell tracking process easier. We note that several groups have used manual tracking for analyzing the cell motility, which can be highly susceptible to errors. For example, Huth et al. showed that manual cell tracking can lead to miscalculation of migration rates by up to 410%⁵¹. Using an automated tracking system enabled us to avoid such errors.

2. Compute the EGF concentration [L] and gradient (∇L) distribution within microdevices and determine the ([L], ∇L) values at individual cell locations: Time-dependent distribution of chemoattractant was computed using the COMSOL program. Because the used growth media was mostly water based, properties of the bulk media in the devices were considered equivalent to water. Diffusion constant of EGF was chosen as 134 µm²/s⁵². Two types of microdevices which were used to collect the motility data differed in terms of the presence of flow. Therefore, their computational analysis was slightly different.

   Double chamber device: EGF applied to one of the side chambers is distributed through the narrow channel to the whole device by diffusion (Fig. 2). As there was no fluid flow, there was no EGF transport through convection. Therefore, EGF distribution was computed using the Fick’s equation for diffusion

   $$\frac{{\mathit{\text{dc}}}_i}{\mathit{\text{dt}}}=D_i{\mathit{\nabla }}^2{c}_i$$

   where c_i is the concentration of dissolved species (EGF) and D_i is its diffusion constant. As in the experiments, 30 ng/ml EGF was added to one of the side chambers and the other chamber had no EGF. Simulation of ligand distribution in the device revealed that EGF concentration varied in the 4–24 ng/ml range across the narrow channel after 30 minutes of initial stabilization period and ligand distribution resulted in an almost linear gradient across the narrow central channel. This linear gradient remained stable and varied only in a very narrow range of ~20–24 ng/ml/mm over the study period (Fig. 2C). From the experimental trajectory files cell positions were identified and corresponding EGF concentration and EGF gradients were interpolated from COMSOL simulation results with the help of a MATLAB program.
   Y-channel device: Experimental conditions for the y-channel device (Fig. 3) included flow through the device. Mass transport of dissolved species can occur through two mechanisms in these devices: Diffusional transport due to concentration gradient and convectional transfer due to the bulk fluid flow. Therefore, diffusional transport of diluted species is coupled to laminar flow. This was accounted for by coupling the Fick’s diffusion equation with the convection mass transfer equation to compute the spatio-temporal distribution of EGF in the y-channel device

   $$N_i=-D_i\mathit{\nabla }{c}_i+c_{i}u$$

   $$\frac{{\mathit{\text{dc}}}_i}{\mathit{\text{dt}}}=-\mathit{\nabla }{N}_i$$

   where u is the fluid velocity and N_i is the local flux. Because of the continuous pumping, laminar flow was at steady state in our system. At this limit, streamlines along velocity field do not cross each other and this prohibits convectional mass transfer to adjacent fluid layers. Therefore, only the diffusional mass transfer contributes to the formation of EGF gradient in the y-channel device.

Figure 2.

(A) Schematic diagram of the double chamber device, top and side views. (B) EGF distribution across the cross section of the device after 300 min as computed in the simulations. The color bar at the right shows the EGF concentration in ng/ml. (C) EGF concentration across the narrow mixing channel at different time points during the course of time-series experiments as computed in the simulations. Results shown in parts (B) and (C) were computed using the COMSOL program with the conditions detailed in the text. Size of the imaged area was approximately 1 mm by 1 mm. Because it is the region with the most linear gradient, imaged area was centered at the middle of the channel (i.e., around the 0.5 mm point in the graph).

Figure 3.

(A) Schematic diagram of the y-channel device. Middle inlet was sealed and not used and ligand was injected through the lower inlet. (B) Steady-state EGF distribution within the device when the input EGF concentration was 15 ng/ml. Cellular motilities were imaged at the center axis at four different downstream positions along the device after the y-junction. Size of the imaged area was approximately 1 mm by 1 mm. Dashed lines indicate the imaged positions: blue (5 mm), green (10 mm), red (15 mm), and cyan (20 mm) where the numbers in the paranthesis refer to the distance from the y-junction. (C) EGF concentration along the direction perpendicular to flow at the imaged positions which are marked with dashed lines in part (B). Imaged area was centered at the middle of the channel (i.e., around the 1.5 mm point in the graph (C)). As can be seen, formed gradient at the imaged areas are almost linear and vary along the length of the device. Results shown in parts (B) and (C) were computed using the COMSOL program with the conditions detailed in the text.

To minimize the shear stress on the cells due to fluid flow, a low flow rate of 0.5 µl/min through each of two inlets of the y-channel device was utilized (Fig. 3). At this flow rate, computed shear stress on cells was 0.0022 dyne/cm². Note that this value is about 10 times lower than the values typically used in literature³⁸. To cover a wide EGF concentration and gradient ranges, experiments were performed with several different EGF concentrations through one of the inlets (cf., cell motility experiments section above). Overall, pursued y-channel device based experiments covered a range of 0–35 ng/ml for EGF concentration and 0–37 ng/ml/mm for its gradient. It should be noted that these stimulation ranges overlap with the ranges that were used with the double chamber device.

• iii)Using the computed EGF distribution in the devices (cf., step ii), we determined the ([L],∇L) values at individual cell locations which were determined in the first step. A MATLAB program developed in house was used for this step. The [L] and ∇L exposure values for each cell were calculated using the mean position of the cell over its trajectory during the imaging period. Since cells typically moved only short distances during monitoring time (typically less than 50 µm over 200 minutes), choice of mean cell position as the coordinate for ([L],∇L) estimation was reasonable. To test whether this choice biased our conclusions, analysis was repeated by estimating the ([L],∇L) values the cell is exposed to by using the starting coordinates of a cell at the beginning of the imaging time (results not shown). The conclusions of analyses with different coordinate choices agreed with each other.
• iv)
  Perform multivariate non-linear regression analysis to determine the dependence of cell velocities on EGF concentration [L] and its gradient ∇L: As described above (Fig. 1), we computed multiple velocity properties (v_tot, v_d, v_p, persistence) to characterize the cell motion. For each of these properties, we fitted the results for all individual cells to regression models. Four models were considered:

  $$\text{Model }1:\mathrm{v}=C+C_{\mathit{\text{conc}}}{[\mathrm{L}]}^{n_{\mathit{\text{conc}}}}+C_{\mathit{\text{grad}}}\nabla {\mathrm{L}}^{n_{\mathit{\text{grad}}}}+C_{\mathit{\text{cross}}}{[\mathrm{L}]}^{n_{c,c}}\nabla {\mathrm{L}}^{n_{g,c}}$$ (Eq. 1)

  $$\text{Model }2:\mathrm{v}=C+C_{\mathit{\text{conc}}}{[\mathrm{L}]}^{n_{\mathit{\text{conc}}}}+C_{\mathit{\text{grad}}}\nabla {\mathrm{L}}^{n_{\mathit{\text{grad}}}}$$ (Eq. 2)

  $$\text{Model }3\mathrm{C}:\mathrm{v}=C+C_{\mathit{\text{conc}}}{[\mathrm{L}]}^{n_{\mathit{\text{conc}}}}$$ (Eq. 3a)

  $$\text{Model }3\mathrm{G}:\mathrm{v}=C+C_{\mathit{\text{grad}}}\nabla {\mathrm{L}}^{n_{\mathit{\text{grad}}}}$$ (Eq. 3b)

  These non-linear models varied in complexity and inclusion of [L] and ∇L as independent system variables. These models consist of constant term C (corresponding to [L] or ∇L independent response), EGF concentration dependent term (C_conc[L]^n_conc), EGF gradient dependent term (C_grad∇L^n_grad), and a cross-term that depends on both EGF concentration and gradient (C_cross[L]^n_c,c∇L^n_g,c). These terms have the power form, allowing for accommodating possible non-linear dependencies. Optimal values of the regression model parameters were obtained using MATLAB curve fitting toolbox where root mean square error (RMSE) was the optimization criteria. Fitted regression models were further examined by ensuring that the residual (i.e., model prediction − experimental data) values for individual cells had a random distribution with no obvious systemic trends.

It should be noted that, since the concentration must be finite to be able to create a gradient, a complete coverage of the ligand concentration and gradient space is not feasible technically. However, our experiments were performed for conditions that made it possible to cover a large portion of the mentioned space. As can be seen in Figure 4, coverage of the variable space was substantial, which increased the confidence of our conclusions.

Figure 4.

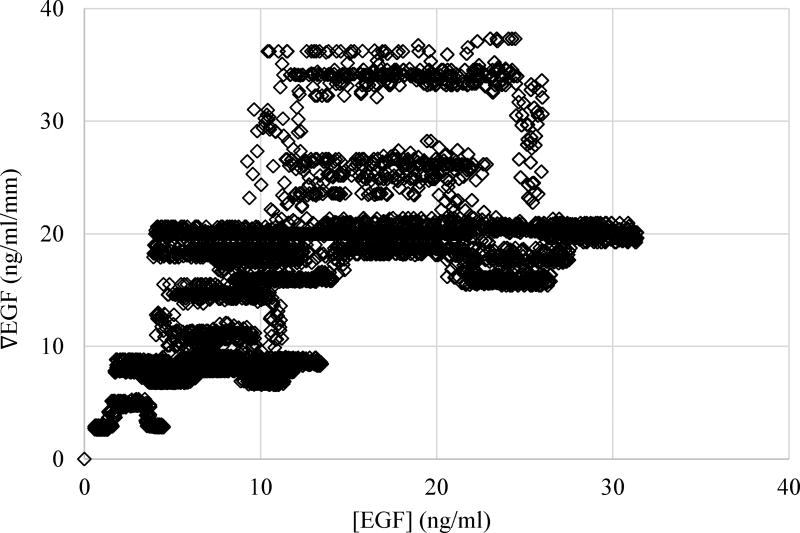
Coverage of the EGF concentration, [EGF], and EGF gradient, ∇EGF, space in our motility experiments. Each point in the figure corresponds to a cell and reports the EGF concentration and gradient that the cell was exposed to during the experiment. Exposure of the cells to EGF concentration and gradient covered a wide range of the parameter space, which made our study unique and enabled us to investigate the effect of EGF concentration and gradient changes independently.

RESULTS AND DISCUSSIONS

Studies to investigate the effect of EGF gradients on the motility of MDA-MB-231 cells typically use somewhat randomly chosen discrete EGF gradient values and/or concentrations^{38, 53}. Utilized concentrations may also be much higher than the physiological concentrations^{38, 53}. To overcome these issues, our experiments were designed such that individual cells in a population were exposed to a range of [EGF] and ∇EGF values. Particularly the use of y-channel device (Fig. 3) has allowed us to locally vary the EGF stimulation conditions for the cells in a continuous manner. Integrating these experiments with computations enabled us to measure the motilities of individual MDA-MB-231 breast cancer cells when they were exposed to a continuum of EGF doses and gradients instead of a limited selection of doses and/or gradients. When combined, collected experimental data equaled exposing the MDA-MB-231 cells to EGF concentration [L] in the 0 to 32 ng/ml range and to EGF gradients in the ∇L = 0 to 37 ng/ml/mm range. We note that lower end of the EGF concentration range mimics physiological EGF concentrations. Higher end of the [L] and ∇L ranges provide the information about how the simultaneous changes in both EGF concentration and concentration gradients effect cell motility.

Total Instantaneous Velocity

As described in the Methods section, average total instantaneous velocity v_tot of each cell was calculated as total distance travelled per unit time. Because of the heterogeneity in the cell behavior among a population of cells, it is expected that there would be large variations in the dependence of v_tot on EGF stimulation.

Supplementary Figure 1 shows how the measured v_tot of cells depend on [EGF] and ∇[EGF]. The main goal of this study was to investigate whether the cellular motilities depend on both EGF concentration and its gradient, and determine which of these two factors is more dominant in impacting cell velocities. To separate out the unique contributions of [EGF] and ∇[EGF], we pursued a multivariate non-linear regression analysis of the collected data (cf., Methods section). Utilized dataset consisted of data for 6,600 individual cells. Data obtained using the double chamber (1,100 cells) and y-channel (5,500 cells) devices were combined in this analysis. Results obtained with these two devices overlapped very well (Supplementary Figure 1). Utilized regression models (Equations 1–3) varied in complexity to include all the possible parameter dependencies. We started with the most complex model (Model 1) and then eliminated certain terms in a stepwise manner to construct simpler models (Models 2 and 3). This systematic approach enabled us to establish the importance of the cross-term between [L] and ∇L (compare Model 1 to Model 2), as well as the importance of the [L] and ∇L terms individually (compare Model 2 to Models 3C and 3G). Parameters of the regression models fitted to the average instantaneous total velocities are reported in Table 1.

Table 1.

Regression models for average instantaneous total cell velocity^*

vtot= C + Cconc[L]nconc + Cgrad∇Lngrad + Ccross[L]nc,c∇Lng,c
Parameter	Model 1	Model 2	Model 3C	Model 3G
RMSE	0.08955	0.08945	0.09080	0.08944
C	0.103	0.103	0.108	0.105
Cconc	7.66E−3	2.34E−3	1.28E−2	N/I
nconc	0.219	1.32E−6	0.588	N/I
Cgrad	3.62E−3	5.22E−3	N/I	5.27E−3
ngrad	0.946	0.878	N/I	0.876
Ccross	4.83E−7	N/I	N/I	N/I
nc,c	1.74E−7	N/I	N/I	N/I
ng,c	2.53E−7	N/I	N/I	N/I

^*N/I: not included. Note that scientific format is used to express some of the values. Units are: velocity, µm/min; ligand concentration, ng/ml; and ligand gradient, ng/ml/mm.

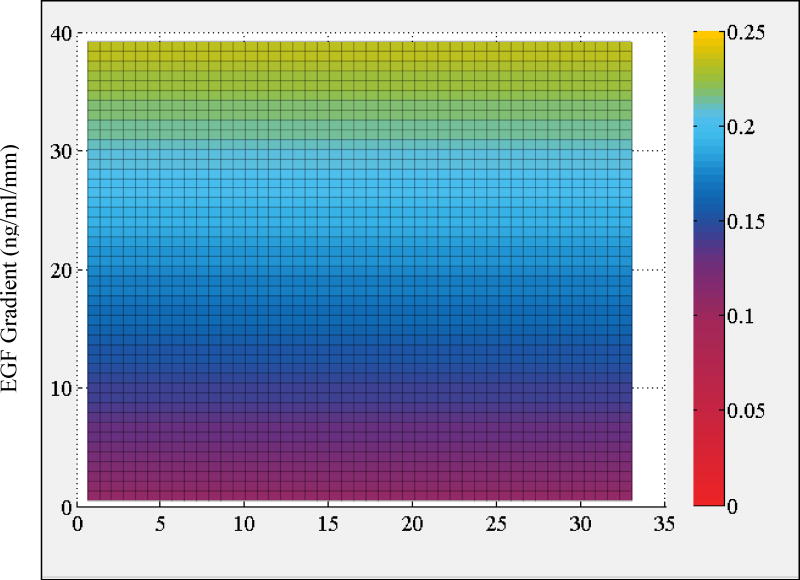
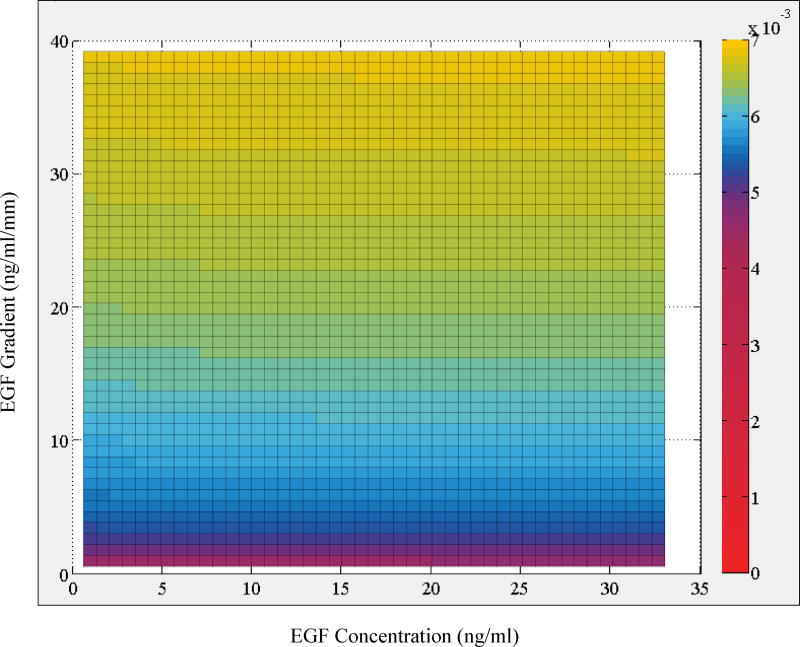
Regression analysis results showed that the cross-term in the most complex model (Model 1) is not supported by the data because the exponents of the variables are nearly 0 and magnitude of its coefficient is much smaller than the other terms. These effectively convert the cross-term to a constant with a very small magnitude. This is further reflected in the results for Model 2, which neglects the cross-term. This reduced model with fewer parameters is as good in explaining the data as Model 1. Analysis with Model 2 indicated that exponent of concentration term n_conc is very small, which indicates a very weak dependence on the concentration term (Fig. 5). This finding was further validated in the analysis that Model 3G which omits the EGF concentration term was equally successful in explaining the data (Table 1). In contrast, model that neglects the EGF gradient term (Model 3C) was much poorer and resulted in a considerably higher root mean square error. Based on the goodness of the fit and parameters of Model 3G and Model 2, we therefore conclude that total instantaneous velocity of MDA-MB-231 cells can be characterized with its dependence on EGF gradient only and that dependence on EGF concentration is non-significant and can be excluded from the analysis.

Figure 5.

Heat map plot of the regression model predictions for average instantaneous total velocity v_tot as a function of local [EGF] and ∇EGF. Color bar on the side shows the magnitude of cell velocity v_tot (µm/min) as computed by Model 2 (cf., main text).

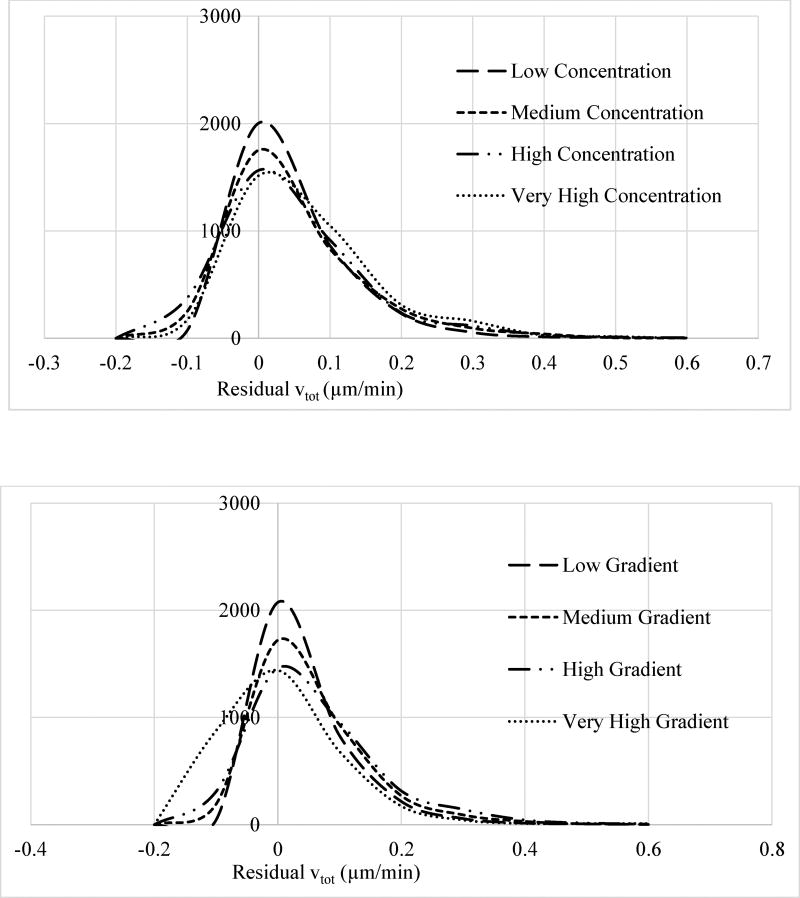
A general concern with model fits to experimental data is the possible biases in the model parameter estimation step. This can stem from preferential weighting of the certain regions of the considered parameter space. To validate that our fits were reasonable, we computed the residuals (model prediction – experimental result) to test whether the residuals have a random distribution regardless of the EGF concentration and gradient ranges as they should in a proper regression analysis (Fig. 6). The residuals should not in principle depend on the exposure levels of the cells to ligand concentration and gradient in an unbiased analysis. This bias analysis was done by grouping the results for individual cells into regions as follows: In addition to the no ligand exposure group, we defined four cell groups based on if they were exposed to low (0–8 ng/ml), medium (8–16 ng/ml), high (16–24 ng/ml), and very high (24–32 ng/ml) levels of EGF concentration, and computed the histogram distributions for v_tot residuals separately for cells in these groups (Fig. 6). In a similar manner, we split cells into four groups per their exposure to EGF gradient ranges in a separate analysis. Groups were defined as low (0–9.5 ng/ml/mm), medium (9.5–19 ng/ml/mm), high (19–28.5 ng/ml/mm), and very high (28.5–38 ng/ml/mm) gradient ranges. Figure 6 compares the residual v_tot histograms for these groups. As can be seen in Figure 6, apart from widening of the residuals at high exposure levels, residual distributions for the groups were found to be very similar with the same peak positions and distribution shapes. This analysis validated that the used model fitting process did not have a bias.

Figure 6.

Histogram of the average total velocity v_tot residual distributions for the four cell groups described in main text) which were defined based on the levels of cells’ exposure to (top) EGF concentration and (bottom) EGF gradient. As discussed in the main text, EGF concentration range (top) for the four groups were: low (0–8 ng/ml), medium (8–16 ng/ml), high (16–24 ng/ml), and very high (24–32 ng/ml). EGF gradient range (bottom) for the four groups were: Low (0–9.5 ng/ml/mm), medium (9.5–19 ng/ml/mm), high (19–28.5 ng/ml/mm), and very high (28.5–38 ng/ml/mm). Histograms were normalized separately for each group and y-axis has arbitrary units. Apart from widening at high ligand concentration or gradient levels, residual distributions for the groups were very similar with the same peak positions and distribution shapes further confirming the unbiased model fit.

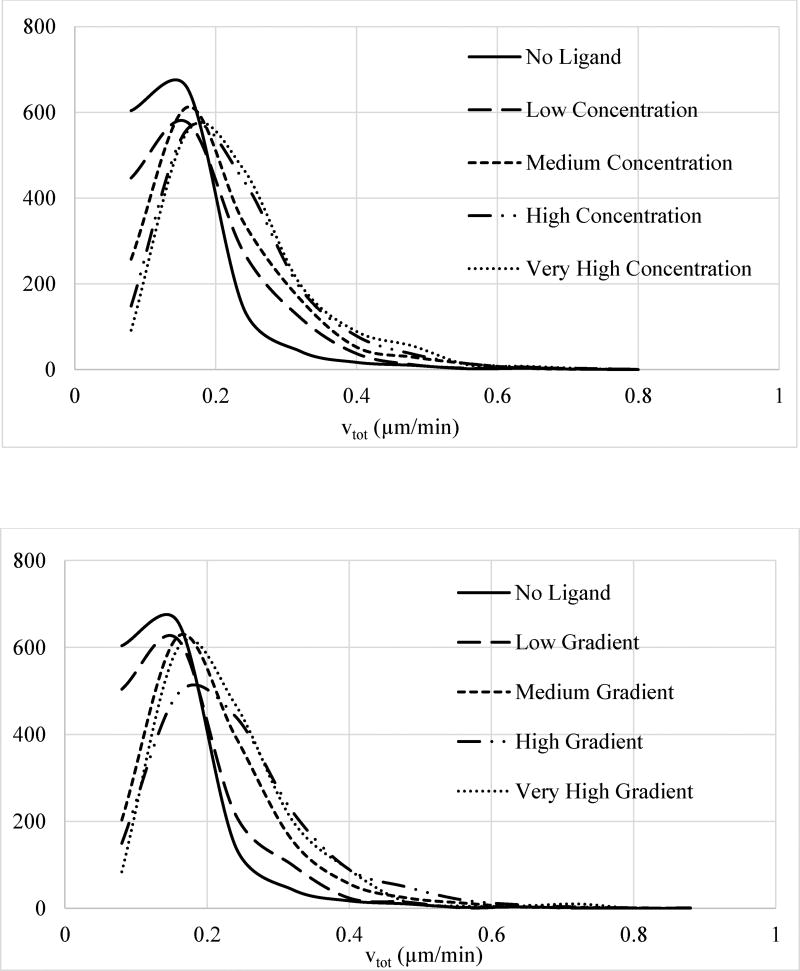
Our multivariate analysis results show that there is a clear increase in the velocity upon ligand gradient exposure. To illustrate this in another way and, most importantly, to highlight the risks of not pursuing multivariate analysis, we repeated the analysis by projecting the multivariate data onto individual parameter axes (Supplementary Figure 1) and looking at the trends in the dependence of v_tot on EGF concentration and gradient separately. We used the cell groupings based on cell’s exposure to EGF concentration or gradient, which was described in the previous paragraph. We computed the distribution of cellular v_tot for each of the defined groups separately (Fig. 7). This comparative analysis indicated that v_tot is enhanced at higher ligand exposure. It however also indicated that v_tot depends on both EGF concentration and gradient, a false misleading conclusion which was contrary to more appropriate result obtained in the multivariate analysis. These results clearly illustrated that “one-dimensional” groupings based on ligand concentration or gradient can be misleading because they ignore the dependence on the other variable. This stems from the inevitable interdependence of the system variables (cf., discussion in the Methods section). This simple analysis established the necessity to incorporate all relevant system variables into analysis and to avoid dimensionality reduction for proper accuracy and reliability.

Figure 7.

Normalized histogram distribution of instantaneous total velocities v_tot for cells exposed to different levels of (top) EGF concentration and (bottom) EGF gradient. Histograms were normalized separately for each group and y-axis has arbitrary units. As discussed in the main text, EGF concentration range (top) for the four groups were: low (0–8 ng/ml), medium (8–16 ng/ml), high (16–24 ng/ml), and very high (24–32 ng/ml). EGF gradient range (bottom) for the four groups were: Low (0–9.5 ng/ml/mm), medium (9.5–19 ng/ml/mm), high (19–28.5 ng/ml/mm), and very high (28.5–38 ng/ml/mm). Distributions for the groups are shown with: No ligand, solid line; low stimulation, long dash line; medium stimulation, dash line; high stimulation, long dash-dot-dot line; and very high stimulation, dot line. Legends for the curves are also reported in the figures.

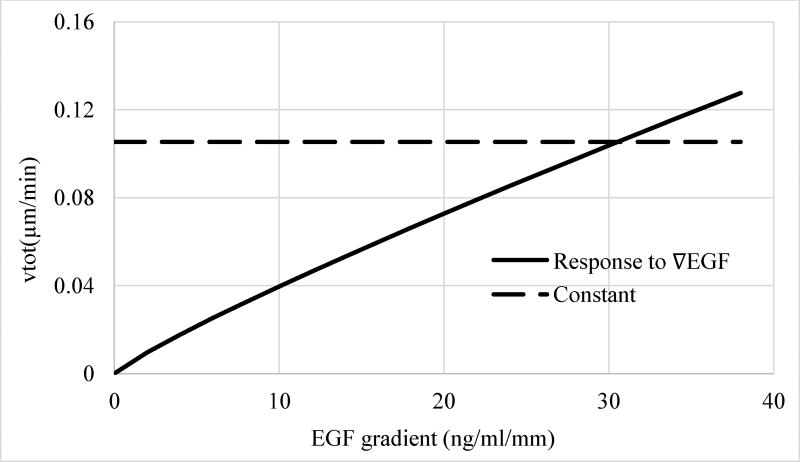
In addition to establishing that instantaneous total cell velocity is only dependent on ∇EGF and not on [EGF], regression analysis also indicated that the power of the gradient n_grad term is close to unity (Table 1), which indicates a linear dependence of v_tot on EGF gradient. Figure 8 compares the contribution of the EGF gradient term to v_tot to the constant term, corresponding to random, average basal velocity of MDA-MB-231 cells, as predicted by Model 3G. The basal motility dominates the instantaneous total cell velocity up to a rather large (~30 ng/ml/mm) EGF gradient values. Therefore, the ligand-induced increase in the non-directed random velocity of the MDA-MB-231 cells can be expected to be relatively insignificant at small gradients formed at low physiological EGF doses, which is ~40 pM, i.e., ~0.25 ng/ml, in serum^54–56.

Figure 8.

Contribution of the different terms of the regression model Model 3G (Table 1) to the instantaneous total velocity v_tot of cells. Dashed line, constant term and solid line, ligand gradient term. The exponent of the ∇EGF term is 0.876, i.e., close to 1, indicating a near linear relationship.

Gating Analysis of Total Instantaneous Velocity

Haessler et al. have used a gating analysis to group individual cells in a population to characterize their motilities⁹. Gating analysis enabled them to distinguish the cells with high directed migration rates from the rest in a heterogeneous cell population. They varied the interstitial flow through microfluidic device and determined the fraction of highly migrating (i.e., responding) cells as a function of the flow rate⁹. We utilized an analogous approach to determine the fraction of cells which had a velocity higher than a defined cutoff (i.e., gating) value. These highly motile cells can be considered as cells that are responding to the ligand stimulation in a heterogeneous population.

To derive a realistic cutoff (gating) value, we took advantage of the statistical information contained in our dataset. First, we grouped the investigated cells based on ligand gradient that they were exposed to. Groups were defined by ranking the cells according to the EGF gradient in their local environment. We formed seven groups with equal number of cells (e.g., the size of the groups was 1/7^th of the total number of cells, ~950 cells) in each group using this rank-ordered list. We then computed the histogram distributions for the average instantaneous total velocities of the cells belonging to these groups. To compare how v_tot changes with stimulation level, we contrasted the histogram distributions for four groups formed from cells which were exposed to: i) the lowest (i.e., cells 1 to N_tot/7 in the sorted order), ii) third lowest (i.e., cells (2N_tot/7+1) to 3N_tot/7), iii) third highest (i.e., cells (4N_tot/7+1) to 5N_tot/7), and iv) the highest (i.e., cells (6N_tot/7+1) to N_tot) EGF gradient (Supplementary Figure 2). Skipping the in-between (i.e., 2^nd, 4^th, and 6^th) groups eliminated the possible biases due to group selection. This comparison of v_tot distributions helped us to select the cutoff value for the gating analysis rationally by finding the v_tot value at which the difference in the histogram distributions was most distinct among the groups. Cutoff value for v_tot was determined as 0.22 µm/min with this statistical variation based selection. Further details of this selection are provided with Supplementary Figure 2.

We then re-analyzed the individual cell trajectories to compute the percentage of time cells’ instantaneous total velocity were higher than the chosen cutoff value, H^%_v,tot. For a time-series image with time internal ∆t between frames, the instantaneous total velocity of a cell between frames k and k−1 is v_tot,inst = |r⃗_k − r⃗_k−1|/Δt. We calculated the instantaneous velocity between the frames and computed H^%_v,tot as the percentage of times when v_tot,inst > v_tot,cutoff with v_tot,cutoff=0.22 µm/min.

We repeated the multivariate non-linear regression analysis using the computed H^%_v,tot values for each cell (Table 2). Ideally, conclusions of the regression analysis for H^%_v,tot should be very similar to the regression analysis results for v_tot. Regression analysis for H^%_v,tot with Model 1 showed that the cross-term exponents are on the order of 10⁻⁶, i.e., the cross-term would actually behave like constant and, therefore, it can be omitted from the model (Table 2). Results for Model 2 without the cross-term indicated that, as in the v_tot case, EGF concentration term may also be omitted because its exponent n_conc is only ~0.02 indicating a very weak dependence on EGF concentration (Table 2 and Figure 9). Results for Model 3G which omits the EGF concentration term resulted in an exponent for the gradient term of n_grad ~0.843, which was very close to the exponent value obtained for the v_tot analysis discussed above. The residual plots (i.e., model prediction – experimental result) indicated that the residuals have a random distribution as they should in a reasonable regression fit (Supplementary Figure 3). Thus, as expected, conclusions of the regression analysis for H^%_v,tot were almost identical to the conclusions of the regression analysis for v_tot. By repeating the regression analysis for different v_tot,_cutoff values (0.22 ± 0.02), we tested whether these reached conclusions depended on the chosen v_tot,cutoff value (results not shown) and did not find any notable dependence on v_tot,_cutoff selection. Thus, regression analysis results for H^%_v,tot were very much in line with the results for v_tot, and this close agreement supported the robustness of our analysis.

Table 2.

Regression models for instantaneous total cell velocity above cut-off^*

H%v,tot = C + Cconc[L]nconc + Cgrad∇Lngrad + Ccross[L]nc,c∇Lng,c
Parameter	Model 1	Model 2	Model 3C	Model 3G
RMSE	0.1732	0.1732	0.1759	0.1731
C	0.060	0.076	0.082	0.078
Cconc	0.0005	0.001	0.031	N/I
nconc	0.019	0.021	0.559	N/I
Cgrad	0.013	0.013	N/I	0.013
ngrad	0.836	0.829	N/I	0.843
Ccross	0.017	N/I	N/I	N/I
nc,c	1.12E−06	N/I	N/I	N/I
ng,c	1.72E−06	N/I	N/I	N/I

^*N/I: not included. Units are: H^%_v,tot, percentage; ligand concentration, ng/ml; and ligand gradient, ng/ml/mm.

Figure 9.

Heat map plot of the regression model predictions for average instantaneous total velocity above cut-off H^%_v,tot as a function of local [EGF] and ∇EGF Color bar on the side shows the magnitude of H^%_v,tot as predicted by Model 2 (cf., main text). The histogram for residual plots (i.e., model prediction – experimental result) indicated that the residuals have a random distribution as they should in a reasonable regression fit (Supplementary Figure 3).

Directed (Chemotactic) Velocity

Directed velocity along the direction of the chemoattractant gradient v_d was calculated as the distance travelled toward higher EGF concentration per unit time for each cell (cf., Methods section). Individual cell data for v_d can be found in Supplementary Figure 4. We performed multivariate non-linear regression analysis to determine how the directed cell motility depended on [EGF] and ∇EGF. Like in the total instantaneous velocity (v_tot) analysis discussed above, we tried different regression models (Equations 1–3) to determine how well they each explained the experimentally measured v_d responses of the cells. Only exception was that, as the directional velocity should be random and unbiased when there is no stimulant, the constant term in the regression models was set to zero, i.e., excluded from the models. The directed velocity and total instantaneous velocity datasets were for the same 6,600 cells.

Parameters of the obtained regression models are tabulated in Table 3. Most general regression model (Model 1) gave very low values for the exponents of [L] and ∇L factors of the cross-term (n_c,c and n_g,c) and amplitude of the cross-term was relatively small as well (Table 3). Therefore, cross-dependence of v_d on [L] and ∇L is insignificant and can be ignored. Results for Model 2 (Table 3; Figure 10) indicated that, relative to the EGF gradient term, the exponent and amplitude of the EGF concentration term are small. Repeating the regression analysis by neglecting the concentration term (Model 3G) showed that the quality of the fit does not deteriorate and the model parameters change only modestly (Table 3). As v_d corresponds to the directional velocity, the constant term in the regression models was set to zero in our analysis. Repeating the regressions by including the constant term C in the models resulted in small values for the constant term (results not shown). Also, the residual plot (i.e., model prediction – experimental result) indicated that the residuals have a random distribution (Supplementary Figure 5). These additional tests further supported the reasonability of our numerical analysis. Therefore, we conclude that directed migration of MDA-MB-231 cells are mainly enhanced by the EGF gradients and not by EGF concentration.

Table 3.

Regression models for average instantaneous directed cell velocity^*

vd = C + Cconc[L]nconc + Cgrad∇Lngrad + Ccross[L]nc,c∇Lng,c
Parameter	Model 1	Model 2	Model 3C	Model 3G
RMSE	0.06168	0.06166	0.06167	0.06166
C	N/I	N/I	N/I	N/I
Cconc	2.22E−07	3.15E−04	5.29E−03	N/I
nconc	1.85E−04	3.26E−14	0.054	N/I
Cgrad	4.47E−03	4.43E−03	N/I	4.76E−03
ngrad	0.104	0.106	N/I	0.099
Ccross	2.91E−04	N/I	N/I	N/I
nc,c	5.55E−05	N/I	N/I	N/I
ng,c	4.20E−06	N/I	N/I	N/I

^*N/I: not included. Units are: velocity, µm/min; ligand concentration, ng/ml; and ligand gradient, ng/ml/mm.

Figure 10.

Heat map plot of the regression model predictions for average instantaneous directed velocity v_d as a function of local [EGF] and ∇EGF. Color bar on the side shows the magnitude of v_d as predicted by Model 2 (cf., main text). The histogram for residual plots (i.e., model prediction – experimental result) indicated that the residuals have a random distribution as they should in a reasonable regression fit (Supplementary Figure 5).

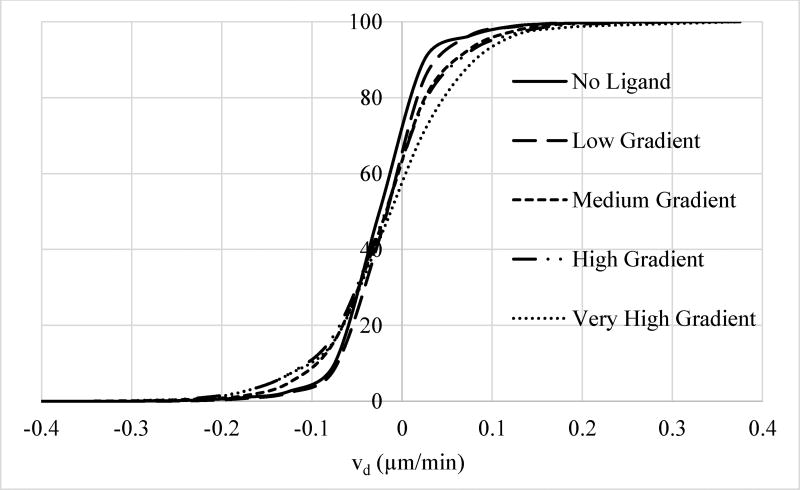
Like the analysis for v_tot reported above, another way to illustrate the impact of ligand gradient on directed cell motility is to compare the distribution of cellular v_d for different gradient ranges. As the cumulative histogram diagrams reported in Figure 11 shows, percentage of the responding cells (i.e., cells with sizable directed velocity) increases with increased exposure to EGF gradient. This can have significant biological implications: For biological processes, such as metastasis, driven by a small percentage of cells, even a small shift in the directed motility can have major impact on biological outcomes by increasing the number of highly motile cells. Our results (Fig. 11) clearly show that, as EGF gradient increases, percentage of cells with strong chemotactic response increases by 4-fold considerably.

Figure 11.

Normalized cumulative histogram distribution (i.e., percentage of cells with velocities smaller or equal than a particular velocity) of directed cell velocities v_d for cells exposed to different levels of EGF gradient. Softening of the steepness in the cumulative histogram distribution with increasing gradient is showing that a larger percentage of cells are chemotactically responding to ligand stimulation at higher gradients. For example, percentage of cells with v_d > 0.12 µm/min is 4.10% for cells exposed to very high gradient compared to 1.25% for no ligand control case, about a 3.3 fold increase. As discussed in the main text, EGF gradient range for the four groups were: Low (0–9.5 ng/ml/mm), medium (9.5–19 ng/ml/mm), high (19–28.5 ng/ml/mm), and very high (28.5–38 ng/ml/mm). Distributions for the groups are shown with: No ligand, solid line; low stimulation, long dash line; medium stimulation, dash line; high stimulation, long dash-dot-dot line; and very high stimulation, dot line. Legend for the curves is also reported in the figure.

Gating Analysis of Directed (Chemotactic) Velocity

We also analyzed the directed cell velocity data using an approach similar to the gating analysis for v_tot mentioned above. We again chose the cut-off value based on the statistical distribution of the velocities (Supplementary Figure 6), which indicated that a cut-off value of 0.12 µm/min would be reasonable for v_d gating analysis. Analysis of the directed velocity data was performed by computing the percentage of times the individual cells had an instantaneous directed velocity higher than the chosen cut-off value, H^%_v,d. We calculated the directed instantaneous velocity of a cell as v_d,inst = (y_k − y_k−1)/Δt where y_k is the y-position (which is the direction along ligand gradient) of the cell in the k^th image frame of the time-series data and Δt is the time difference between image frames. Using the directed instantaneous velocity data for each cells, we computed H^%_v,d as a the percentage of times when v_d,inst > v_d,cutoff with v_d,cutoff = 0.12 µm/min.

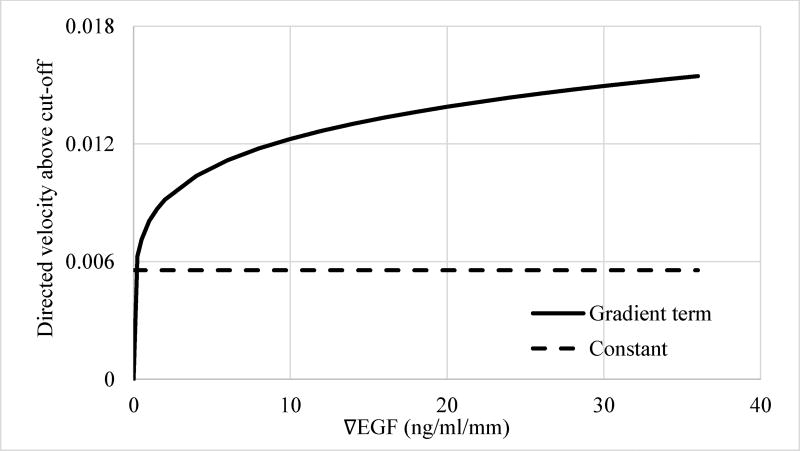
We then repeated the multivariate non-linear regression analysis with the computed H^%_v,d values for individual cells (Table 4). Results and conclusions of this analysis were very similar to those of the analysis for v_d: i) Cross and ligand concentration terms make insignificant contributions and they can be neglected, i.e., EGF gradient is more less the sole determinant of the directed velocity of the MDA-MB-231 cells. ii) Dependence of H^%_v,d on ∇L is non-linear and saturates at small gradient values (Fig. 12). Compared to the v_d regression analysis, H^%_v,d analysis made the dependence on EGF gradient more obvious (compare the n_grad exponents in Tables 3 and 4). This exemplifies the advantage of gating-type analysis because it places more emphasis on the sub-population of cells that are responding more strongly to the EGF stimulation. By concentrating on the range away from the noise, gating-type analysis can better capture the trends in the data.

Table 4.

Regression models for instantaneous directed cell velocity above cut-off^*

H%v,d = C + Cconc[L]nconc + Cgrad∇Lngrad + Ccross[L]nc,c∇Lng,c
Parameter	Model 1	Model 2	Model 3C	Model 3G
RMSE	0.1937	0.1936	0.1936	0.1936
C	0.001	0.001	7.95E−07	0.005
Cconc	0.005	0.005	0.017	N/I
nconc	0.001	4.33E−05	0.037	N/I
Cgrad	0.006	0.006	N/I	0.008
ngrad	0.247	0.247	N/I	0.181
Ccross	9.97E−05	N/I	N/I	N/I
nc,c	0.0001	N/I	N/I	N/I
ng,c	0.0007	N/I	N/I	N/I

^*N/I: not included. Units are: H^%_v,d, percentage; ligand concentration, ng/ml; and ligand gradient, ng/ml/mm.

Figure 12.

Contribution of the different terms of the regression model Model 3G (Table 4) to the instantaneous directed velocity of cells that fall above cut-off, H^%_v,d. Dashed line, constant term and solid line, ligand gradient term. The exponent of the ∇EGF term is 0.181 indicating a nonlinear relationship.

These conclusions were also similar to the conclusions for v_tot with the following differences: i) impact of the EGF gradient on v_d becomes significant at much lower gradient values (compare Figure 12 to Figure 8), and ii) dependence of v_d on ∇L is more non-linear and saturates at rather small gradient values. As we discuss later below, these can have implications on the metastatic responses of the MDA-MB-231 cells.

Velocity Component Perpendicular to EGF Gradient

We also investigated if the cell velocity component in the direction normal to EGF gradient (v_p) is impacted by the ligand stimulation (Fig. 1). Because this velocity component should in principle be random and not depend on EGF gradient, we used this analysis as a negative control for our studies to investigate if there is any bias in our experiments. Values of v_p for individual cells were first computed from the image data and then analyzed using regression models just as in the v_tot and v_d cases discussed above to which identified its dependence on [EGF] and ∇EGF. Data for how v_p of cells depends on EGF concentration and gradient can be seen in Supplementary Figure 7. The regression analysis of the v_p data did not identify any notable dependence on neither [EGF] nor ∇EGF (results not shown). This confirmed its expected outcome, which further supported the good quality of our data.

Directed Persistence Analysis

Another measure of the directed motility of cells is their directed persistence (P_d; cf., Methods section). A P_d value close to 1 indicates highly persistent movement along the gradient direction while small, near 0 values indicates mostly random movement. Using the four regression models (Equations 1–3), we have computed the dependence of the directed persistence of cells on varying [EGF] and ∇EGF conditions. Results and conclusions of the multivariate non-linear regression analysis (Table 5) supported the findings of the v_d and H^%_v,d analyses. Most notable difference in the regression analysis results were that for Pd, the exponent in the EGF concentration term n_conc is comparable to the exponent of the EGF gradient term n_grad. However, the large ratio of the amplitudes of the two terms (cf., Model 2) supported the findings of the v_d and H^%_v,d analyses that directed persistence P_d is mainly a function of EGF gradient only.

Table 5.

Regression models for instantaneous directed cell persistence^*

Pd = C + Cconc[L]nconc + Cgrad∇Lngrad + Ccross[L]nc,c∇Lng,c
Parameter	Model 1	Model 2	Model 3C	Model 3G
RMSE	0.3648	0.3647	0.3647	0.3646
C	N/I	N/I	N/I	N/I
Cconc	0.0025	0.0039	0.0382	N/I
nconc	0.0447	0.0478	0.0577	N/I
Cgrad	0.0342	0.0329	N/I	0.0370
ngrad	0.0702	0.0775	N/I	0.0696
Ccross	0.0004	N/I	N/I	N/I
nc,c	0.0060	N/I	N/I	N/I
ng,c	0.0684	N/I	N/I	N/I

^*N/I: not included. Units are: ligand concentration, ng/ml; and ligand gradient, ng/ml/mm.

To contrast the directed persistence P_d of cells based on their exposure to EGF gradients, we compared the distribution of P_d for the five cell groups that were defined above in the total and directed cell velocity sections. As in v_d results (Fig. 11), P_d distribution shifted to positive values and percentage of the responding cells (i.e., cells with sizable persistence) increased with increasing exposure to EGF gradient (Supplementary Figure 8). This result supported the v_d analysis results.

DISCUSSION and CONCLUSIONS

Most biological malfunctions are triggered by the dysregulated behavior of a small number of cells in a population. Therefore, knowing how selected cells behave instead of population averages is necessary to significantly improve our understanding of the biological inner working of cells. In this study, we have investigated the motility of a model epithelial breast cancer cell line, MDA-MB-231, upon exposure to EGF, a major growth factor involved in cell proliferation and enhanced motility processes. Our quantitative study at the individual cell level established that indeed only a small percentage of the epithelial cells (~4%, Figure 11) attain enhanced motility upon exposure to EGF or its gradients. Our study also established that MDA-MB-231 cells respond to EGF gradients and not to the ligand concentration levels.

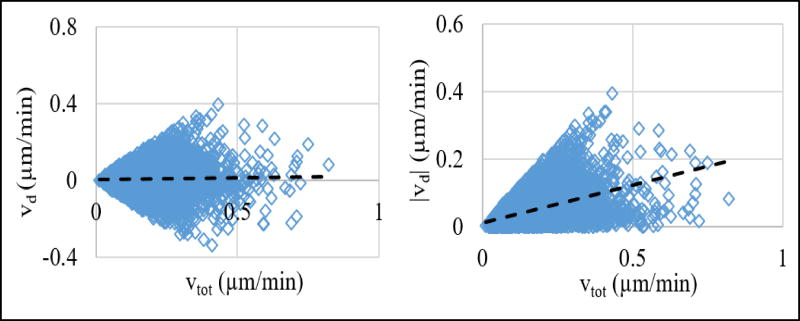
Gradient formation of chemoattractant ligands inevitably requires the availability of ligands in the first place. This makes answering the question of whether mere existence of ligands or their spatiotemporal distributions, which may give rise to gradients, is more important in regulating cellular dynamics. Our combined experimental and computational approach introduced a unique way to answer this question by enabling the separation of the contributions of ligand concentration and its gradient to cellular response. Using our integrated approach, we have investigated whether the motility of MDA-MB-231 breast cancer cells are enhanced by the growth factor, its gradient, or both. We found that both the total (direction independent) and directed (along the chemotactic gradient direction) velocities are mainly a function of EGF gradient, and that level of EGF concentration by itself does not impact the cell motility. Our results showing increasing growth factor gradient induces enhanced directed motility of MDA-MB-231 cells are supported by previous studies³⁸. However, EGF concentration having a minimal, if any, effect on cell motility was somewhat unexpected. This was particularly surprising for the total cell motility case because basal random velocity of cells can be expected to depend on EGF concentration^{38, 50}. Enhancement of both the total and directed velocities only with EGF gradient raised the question of whether the increases in these two velocity types were inter-related (Fig. 13). To answer this question, we computed the correlation coefficient between these velocities: correlation coefficient between v_tot and v_d was 0.03 and correlation coefficient between v_tot and |v_d| was 0.47. These low correlations implied that regression analysis results for v_tot and v_d were not critically affected by each other.

Figure 13.

Comparison of the total (v_tot) and directed (v_d) velocities of individual cells. Each point corresponds to the velocities of a cell. Plots show relationship of (left) v_d vs. v_tot and (right) |v_d| vs. v_tot. Lines show the best linear fit to the reported data. Note that, since v_d is a component of v_tot (Fig. 1), |v_d| is always smaller than v_tot.

Another interesting finding was that the impact of EGF gradient on directed cell motility is imminent at a low gradient range (Fig. 12), while the impact on the total cell velocity is mostly at a very high gradient range (Fig. 8). This implies that the role of growth factor gradients is limited to enhancing the directed motility of the MDA-MB-231 cells under physiological conditions where the ligand concentrations and gradients are expected to be low. This is because most of the growth factors are locally produced by cells but diffusional spread of the secreted growth factors in 3D would not allow for the formation of steep gradients. Therefore, it can be expected that even the heterogeneous production of growth factors would lead to a smoothly varying spatial distribution in tissues and tumors. Thus, created gradients would not be high enough to impact the total velocity of cells. An implication of this prediction would be that growth factors secreted near tumors can contribute to the increased metastasis by creating a ligand gradient near the tumor boundary. An example of this process has actually been observed where EGF secreted by macrophages work as chemo-attractant for tumor cells to increase their motility and contribute to metastasis^{11–13,14, 15}. Interestingly, the majority of the involved macrophages has been found to reside on the periphery of the tumor. This inhomogeneous macrophage distribution could be enhancing the gradient of the growth factors they are secreting at the most optimal location to maximize metastasis. Because the tumor cells which are on the tumor tissue surface (i.e., the cells that could physically separate from the tumor most easily) would have their chemotactic velocity increased the most, this distribution would maximize the potential metastasis from the site. Therefore, in tumor microenvironment, growth factor gradient at the periphery could be the most potential factor that controls the overall tumor migration and metastasis. Our experiments showed that motility of only a small portion of cells in a population are enhanced upon ligand stimulation. However, initiation of certain processes such as metastasis by a small number of cells would be enough for the process to proceed. Therefore, investigation of strongly stimulated cells in a population is needed to obtain useful biological insight into biological processes.

There are earlier studies which investigated the motility of MDA-MB-231 cells using comparable setups. Wu et al. used a gating analysis to study the effect of EGF gradient and the combined effect of EGF and SDF-1α gradient on the motility of MDA-MB-231 cells⁴⁶. The velocity cutoff was arbitrarily chosen as 0.2 µm/min in their gating analysis, and they only analyzed the motion of the cells with motility above this cutoff. Their chosen cutoff was comparable to the value that we have used. Jeon et al. studied the effect of differential EGF gradient profiles on MDA-MB-231 cell migration³⁸. Their study covered the 0–50 ng/ml EGF range, and observed average cell velocity was 0.5 µm/min. Our results for 0–35 ng/ml EGF range gave 0.16 µm/min average velocity. Although the ligand profiles in Jeon et al. and our studies overlapped to some degree, the device geometry, collagen concentration, flow rate were different than ours. Therefore, a direct comparison may be misleading. Haessler et al. used similar flow chambers to characterize cell motility⁹. The average total velocity v_tot reported by them was 0.16 µm/min whereas in our experiments average cell motility rate was 0.11 µm/min. However, again a direct comparison may be misleading because this average cell motility rate in our study corresponds to the population of cells which were exposed to a range of ligand concentration and gradients. Therefore, we can only expect to obtain values in the same order of magnitude of other studies, and our results are comparable to the observations in these earlier studies.

Our evaluation of the validity of different models were largely based on the estimated model parameter values because the RMSE of the obtained models were relatively small. There is no commonly accepted criteria for how the quality of the fit as reflected in RMSE should vary as the number of independent variables change in models. There are several information theory-based metrics that scientists have been using to evaluate and compare models, such as the Akaike information criterion⁵⁷. Such metrics typically have two terms: i) RMSE of how well the fitted data is explained by the model, and ii) a normalization term that accounts for the number of parameter (variable) difference between compared models. However, the relative weight of the normalization term decreases significantly as the number of experimental data increases. Therefore, in our case with results for >6,000 cells, such model comparison criteria become highly questionable. Hence, model comparison based on such metrics were not pursued. We instead evaluated the obtained regression models using a combination of whether the observed change in RMSE was “large” and if the values obtained for the model parameters were sensible. Whether the change in RMSE was large was decided based on the RMSE values obtained in all of our model fits. Although admittedly subjective, this provided a context to evaluate whether the observed change was significant.

Our analysis results also clearly indicated that “one-dimensional” grouping of multi-dimensional data based on only ligand concentration or gradient can be misleading because they ignore the dependence on the other variable. This stems from the inevitable interdependence of the system variables (cf., Methods section) and that the sampling of the parameter space was not uniform (Fig. 4). For example, cells that are exposed to high EGF gradients are also exposed to typically high EGF concentrations (Fig. 4). Therefore, distributions obtained by reducing the system dimension averages out the dependence on the reduced system variable, which can skew the results. Hence, as pursued in this study, analyzing the velocities as a function of both variables simultaneously is the most appropriate method and analysis based on dimensionality reduction should be avoided.

EGF receptors and their ligands are known to undergo endocytosis, which can cause depletion of ligands in the extracellular environment. This possible issue was one of the reasons that the reported experiments mostly utilized the y-channel device where the effect is minimal. Continuous flow of EGF into the y-channel device allows the maintenance of a steady-state EGF distribution and ligand distribution within the device would not be affected from endocytosis. This setup also eliminates the question of whether EGF endocytosis may depend on EGF concentration because the steady ligand inflow replaces the internalized ligand regardless of where cells reside in the device and what the ligand concentration is. To validate that endocytosis did not impact our conclusions, we repeated the regression analysis by excluding the double chamber data set and using the data for the y-channel device only. Conclusions that v_tot and v_d both depend only on EGF gradient but not on EGF concentration were unchanged (results not shown). This comparison indicated that possible role of endocytosis can be safely neglected in our model identification analysis.

Although the used regression models cannot provide mechanistic details of cell motility, they may still provide justification to existing mechanical models. For example, the comparison of the parameters of the models informed us about the fundamentals of the ligand-enhanced cell motility that ligand concentration by itself does not have much impact but the ligand gradient is the main driver of the enhanced motility. This finding in fact supports the earlier mechanistic models which characterized the cell motility as a function of the cell polarization between front and rear ends of the cells due to ligand gradient^58–60. Our study provides clear experimental evidence for such models.