Abstract
Topological methods are emerging as a new set of tools for the analysis of large genomic datasets. They are mathematically grounded methods that extract information from the geometric structure of data. In the last few years, applications to evolutionary biology, cancer genomics, and the analysis of complex diseases have uncovered significant biological results, highlighting their utility for fulfilling some of the current analytic needs of genomics. In this review, the state of the art in the application of topological methods to genomics is summarized, and some of the present limitations and possible future developments are reviewed.
Introduction
Since the advent of next-generation high-throughput sequencing in the past decade [1–3], there has been an explosion of available genomic data, accelerating research in most areas of biology. Simultaneously, the nature and size of these data are posing challenges to traditional computational methods, which are largely based on clustering and combinatorics. In some cases, the nature of existing data is not suited to current approaches (for instance, the continuous nature of cell differentiation is not suited to clustering methods); in others, its size makes the analysis infeasible with current computing resources. New computational approaches are needed in systems biology to address these challenges.
Topological data analysis (TDA) [4–7] has recently emerged as a framework for extracting information from the geometric structure of data. TDA encompasses a number of computationally fast methods particularly tailored to the analysis of continuous data structures. In recent years, TDA has proven useful in several biological contexts, including the study of horizontal evolution [8,9], cancer genomics [10,11], complex diseases [12,13], disease spreading [14], chromatin folding [15], and gene expression [16,17]. In this note, the main rationale behind some of the applications of this emerging field to genomics is reviewed. For a more technical introduction to TDA (not necessarily in the context of genomics), the reader may also consider [4–7].
The notion of phase space
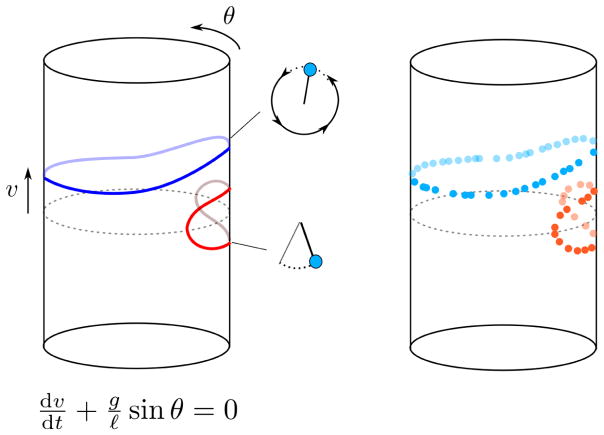
In the last century, the development of modern physics has been partially driven by the incorporation of a few key concepts. A phase space is the spatial representation of all possible states of a dynamical system, where each point uniquely identifies a state. This simple but powerful idea emerged in the second half of the 19th century [18], during the golden era of differential geometry, and it is at the core of modern classical, quantum, and statistical mechanics. The trajectory that a dynamical system describes in the phase space as it evolves with time contains rich information about the system. For instance, by looking at the shape of the trajectories that a pendulum describes in its phase space, we can infer the existence of different dynamical regimes, or the ratio between the length of the pendulum and the acceleration of gravity (Figure 1).
Figure 1. The phase space of a simple pendulum without friction.
The phase space of a simple pendulum is a two-dimensional cylinder, where the periodic coordinate corresponds to the angle (θ) of the pendulum with respect to the vertical, and the longitudinal coordinate to its angular velocity (v). Each point in this space specifies a unique combination of the position and velocity and uniquely determines the subsequent evolution. For small angular velocities, the pendulum oscillates back and forth around the equilibrium point. For large velocities, the pendulum describes a circular motion. These two regimes are represented by qualitatively different trajectories in the phase space which cannot be continuously deformed into each other (in mathematical terms, they are homotopically inequivalent). By just looking at the shape of the trajectories in the phase space, we can extract information about a dynamical system. The dynamics of the simple pendulum is fully described by a differential equation depending on the length of the pendulum (ℓ) and the acceleration of gravity (g). In biological systems the mathematical equations describing trajectories in the phase space are usually unknown, but current technologies allow to reconstruct trajectories from high-throughput measurements.
Physical systems like the pendulum are usually defined in terms of a set of mathematical equations which determine their time evolution. The phase space of the system can be derived from these defining equations with absolute precision. Biological systems, such as living cells or organisms, are in this respect very different from most physical systems. They contain a vast number of interrelated degrees of freedom that behave very differently from each other (consider, for instance, the protein levels of a cell). The behavior of a biological system in general cannot be described in terms of a simple set of equations, and it is often unclear what the “right” variables to characterize the system are. Additionally, biological systems are intrinsically noisy. Thus, the idea of phase space has been traditionally of very limited use in biology.
In the last decade, however, biological sciences have experienced a major technological revolution with the advent of next-generation high-throughput sequencing [1–3]. Determining the DNA sequence of an organism or measuring the mRNA, methylation, or protein levels of a sample are now accessible tasks to most laboratories. Remarkably, the most recent advances permit some of these measurements with single cell resolution [19–21], for thousands of cells simultaneously. The relevance of these high-throughput measurements is two-fold. First, they provide a set of natural variables to partially characterize the state of a cell, tissue, or organism. Second, although a description in terms of a set of mathematical equations is not available, by using these techniques we can effectively sample points from the phase space of the system. If enough points are sampled, we can partially reconstruct the structure of the phase space of the biological system, gaining a rich understanding of the underlying molecular processes (Figure 1). A simple example can be found in transcription phase spaces. Each point in these spaces corresponds to a unique configuration of mRNA levels of a sample, with the distance between two points indicating the degree of similarity between the expression profiles of two samples (for instance, as measured by the correlation of their mRNA levels). Samples could be as diverse as single cells from a cellular differentiation process or disease progression, or tumors from a cross-sectional cancer study. Another example, discussed below, is genetic phase spaces. Each point in these spaces represents the genetic sequence of a sample and distances between points indicate genetic distances. Trajectories in a genetic phase space are the result of evolutionary processes and contain a great deal of information about those processes.
Topology, topological data analysis, and persistent homology
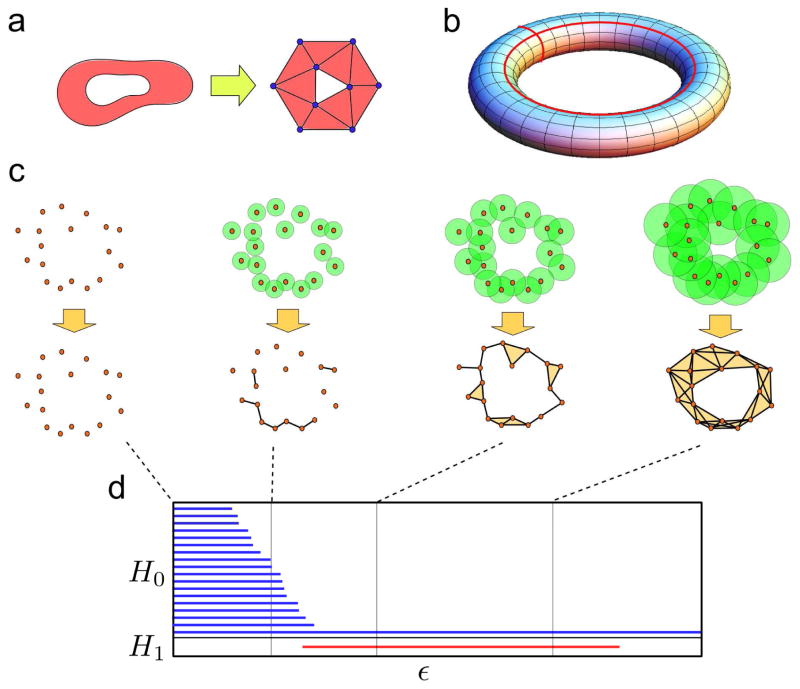
The previous paragraph outlines the importance of understanding the structure of the phase space. Topology [22,23], a mathematical field developed in the last two centuries, provides the necessary tools for that purpose. Topology studies topological features of spaces: namely, properties preserved under continuous deformations of the space, like the number of connected components, loops, or holes. To that end, in algebraic approaches to topology [24] it is a common practice to replace the original space by a simpler one, known as a simplicial complex, containing the same topological features as the original space (Figure 2a). A simplicial complex is a generalization of a network that, apart from nodes and edges, contains triangles, tetrahedrons and higher dimensional polytopes. These shapes are known as simplices. The robust mathematical properties of simplicial complexes allow for the implementation of algebraic operations to identify and classify the topological features of the space. These can be arranged in mathematical structures known as homology groups (Figure 2b). The kth homology group of a space classifies inequivalent (in the sense of being impossible to continuously deform one into another) (k+1)-dimensional voids of the space. Hence, elements of the 0th homology group are connected pieces of the space (clusters), elements of the 1st homology group are loops, elements of the 2nd homology group are 3-dimensional cavities, etc. (Figure 2b).
Figure 2. Topology, persistent homology, and barcodes.
(a) A simplicial complex is a simplified representation of the original space with the same topological features. It is a generalization of a network which, apart from nodes and edges, contains higher dimensional polytopes such as triangles and tetrahedrons. (b) An empty torus consists of one connected component, two independent loops (marked in red), and a two-dimensional void. The dimensions of its 0th, 1st, and 2nd homology groups are respectively 1, 2, and 1. (c) In a Vietoris-Rips filtration a simplicial complex is built from the data at each scale ε by considering the intersection of balls of radii ε centered at the points. Points whose balls intersect are connected in the simplicial complex. Persistent homology groups track how the topological features associated to the simplicial complexes change with the scale ε. (d) Barcodes are a suitable representation of persistent homology groups, where each interval indicates the range of ε for which a given topological feature is associated to the data. In this figure, the 0th and 1st persistent homology groups are represented in the barcode.
Motivated by the recent explosion of available data, topological data analysis [4–7] has emerged in the last few years as a branch of applied topology. It aims to infer the topological features of a space when only a finite set of points (and a notion of distance between them) is given (Figure 2c). Persistent homology [25,26], a tool from TDA, assigns simplicial complexes to these data, from which the topological features of the underlying space can be inferred. As there is an infinite number of topological spaces compatible with a finite set of points, persistent homology structures this spectrum of possibilities by introducing a notion of scale (ε). A Vietoris-Rips filtration is a widely-used construction in persistent homology that produces simplicial complexes by taking balls of radius ε centered on the data points (Figure 2c). If two balls intersect, the points at the center of the balls are connected by an edge in the simplicial complex. If three balls have all pairwise intersections, they are connected by a triangle, etc. In this way, there is a simplicial complex (and a set of topological features) associated to the data at each value ε. Tracking how homology groups change with ε provides a summary of the topological features of the data.
A convenient representation of persistent homology is provided by barcodes [27] (Figure 2d). Barcodes are collections of intervals, where each interval represents the range of ε for which a particular topological feature (for instance, a loop) is compatible with the data. Given a finite set of points sampled from an unknown phase space, we can use persistent homology to infer the topological features of the space and represent them as a barcode.
Topology of evolution
Based on these ideas, applications of persistent homology to evolutionary biology have emerged in the last three years [8,9,28–30]. Consider an organism that evolves exclusively through the acquisition of point mutations (vertical evolution). Assuming homoplasies are infrequent, the genetic distance between samples can only increase with time. In systems like this, trajectories in the genetic phase space cannot form loops. This intuition was formalized in a theorem by Chan et al. in 2013 [8] showing that in vertically evolving systems the first persistent homology group of a sample of genetic sequences vanishes. Thus, the evolutionary relationships in such systems can always be represented as phylogenetic trees.
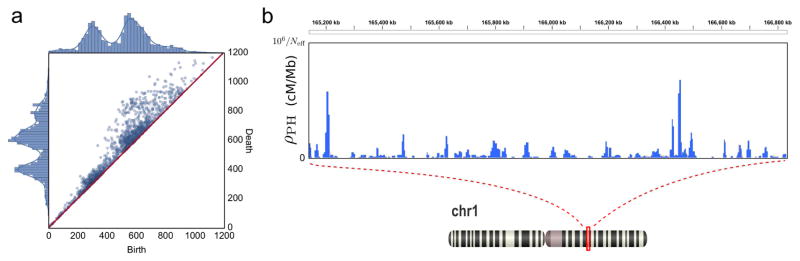
There is a large body of evidence, however, that most organisms also evolve non-vertically through reticulate evolution. Recombination [31], reassortment [32], and lateral gene transfer [33] are examples of pervasive reticulate processes that cannot be captured by tree-like representations. Inferring the frequency and scale of such processes from a sample of genetic sequences has proven to be technically challenging. It follows from the theorem mentioned above that the first persistent homology group gives information about the number and scale of reticulate events required to explain a sample of sequences. That observation was exploited in [8] to identify reassortments in the genome of the avian influenza virus and recurrent cosegregation patterns. Remarkably, they pointed out that multiple reassortments, like the triple reassortment of the H7N9 avian influenza [34], produce higher dimensional voids in the genetic phase space, which can be detected using higher persistent homology groups. An important aspect of the TDA approach, also emphasized in [30], is that it provides information on the genetic scale of the reassortment. For instance, reassortments involving the same hemagglutinin (HA) subtype occur at a smaller scale than reassortments involving multiple HA subtypes, and both are suitably captured by persistent homology (Figure 3a). These are clear examples of topological structure demonstrating different biological processes.
Figure 3. The topology of evolution.
(a) Persistence diagram computed from an avian influenza dataset. The distributions of birth and death times (the positions of the two end points of each interval in the barcode) are shown. Their bimodality indicates two scales of topological structure, corresponding to intra-subtype (involving one HA subtype) and inter-subtype (involving multiple HA subtypes) viral reassortments. Figure adapted from [30] with permission of the authors. (b) Position-dependent recombination rate for a region in human chromosome 1, according to the topological maps of human recombination developed in [9]. Peaks correspond to recombination hotspots. Map based on 89 individuals from the British and Scotland (GBR) population sequenced by 1,000 Genomes Project [47].
These results on viruses suggest that persistent homology can be also used to study other forms of reticulate evolution, such as homologous recombination in eukaryotes. Recently, statistical estimators of the recombination rate were developed using persistent homology [9]. Compared to standard linkage-based estimators, TDA can deal with larger number of SNPs and genomes without incurring excessive computational costs. Application of these estimators to phased genotype data of 647 human individuals has led to high-resolution, genome-wide maps of human recombination (Figure 3b). These maps have uncovered novel associations with human recombination, such as the enrichment for recombination sites at the binding sites of specific transcription factors, and are a promising resource for population studies.
From high to low number of dimensions
We note from the above examples that biological systems generally have an enormous number of degrees of freedom, and therefore the dimensionality of their phase spaces is very large, even when restricted to specific measurements like genetic sequences or mRNA levels. For instance, the dimensionality of a genetic phase space is approximately given by the number of segregating characters (SNPs, indels, etc). The sensitivity of persistent homology to detect topological features rapidly decreases with the sparseness of the data [35] and, therefore, with the dimensionality of the phase space. To keep statistical power under control, suitable algorithms for dimensional reduction are required. Furthermore, apart from the list of topological features and scales provided by persistent homology, information on how those features relate to one another is sometimes also required.
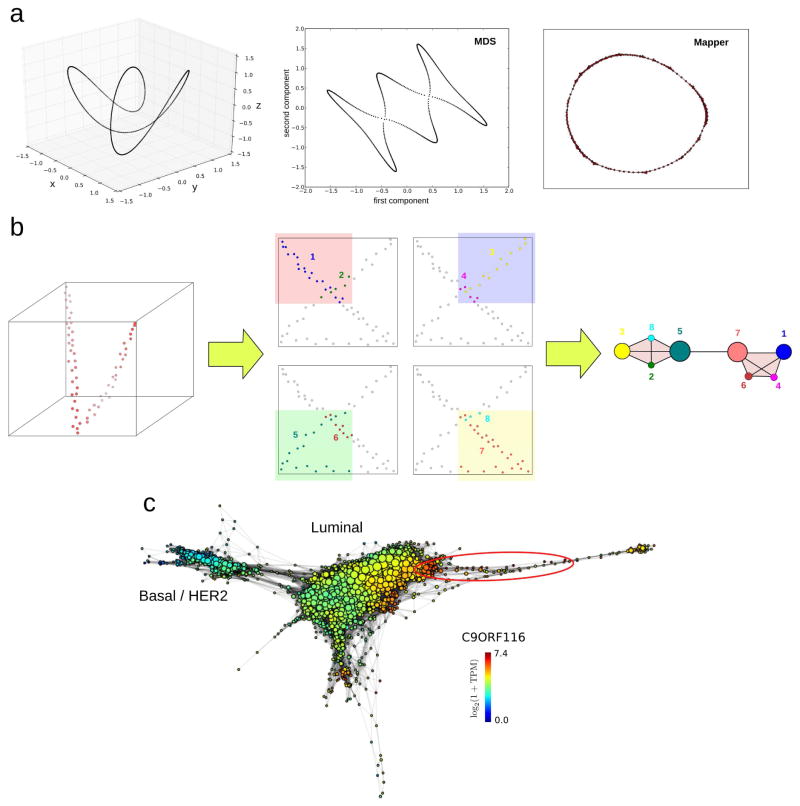
An important consideration when reducing a phase space is that most information resides in its local structure. When a physical or biological system evolves, it moves locally in its phase space. Suitable dimensional reduction algorithms should therefore preserve local relationships. Widely-used algorithms, like principal component analysis, independent component analysis, or multidimensional scaling, fail to do so (Figure 4a). Two points close to each other in a representation obtained by any of these algorithms are not necessarily close in the original space. Hence, although in practice these algorithms often work well, in many situations they can produce severely distorted representations. A more suitable approach is the Mapper algorithm [36]. Mapper builds upon any given dimensional reduction algorithm, and produces a low-dimensional simplicial complex representation of the data which preserves locality. To that end, the projection obtained by a dimensional reduction algorithm is covered with overlapping bins, and clustering of the data within each bin is performed in the original high-dimensional space (Figure 4b). A low-dimensional simplicial complex representation of the data is then constructed by assigning a node to each cluster. Clusters that share one or more points are connected in the simplicial complex. Local relationships in the low-dimensional simplicial complex thus correspond to local relationships in the high-dimensional space, preserving much of the local structure.
Figure 4. Dimensional reduction of phase spaces.
(a) Commonly used algorithms for dimensional reduction produce low-dimensional representations which fail to preserve local relationships of the original space. Points close to each other in these representations are not necessarily close in the original space. In this figure a twisted circular trajectory in three dimensions (left) has been reduced to two dimensions using multidimensional scaling (MDS) (center), and the topological method Mapper (right). MDS leads to additional loops which are not present in the original space. To the contrary, Mapper preserves the topological features of the original space. (b) The Mapper algorithm [36] builds upon any given dimensional reduction algorithm and produces a low-dimensional simplicial complex representation of the data where local relationships of the original space are preserved. In this example a 2-dimensional projection of a twisted linear trajectory in 3-dimensions (left) produces a “loop” that is not present in the original space. The Mapper algorithm builds on top of this projection by covering the plane with overlapping patches and clustering in the original space the points that lie within each patch. The procedure is illustrated here with four patches (center). Points in each cluster are represented with the same color, and clusters are numbered from 1 to 8. In the low-dimensional Mapper representation, a node is assigned to each cluster. Node sizes are proportional to the number of points in the cluster. If two clusters intersect, the corresponding nodes are connected by an edge. The resulting simplicial complex representation (right) has the same topology than the original high-dimensional linear trajectory, with no loops. (c) Mapper representation of the RNA-seq data of 768 breast invasive carcinoma tumors from The Cancer Genome Atlas (TCGA) [48], labelled according to expression levels of C9ORF116. Basal, HER2, and luminal tumor subtypes are indicated. The group of ER+-patients identified in [10], with excellent survival and high expression levels of C9ORF116 and DNALI1, is encircled in red. Representation built using the implementation of Mapper by Ayasdi Inc, based on a two-dimensional nearest-neighbor graph projection and correlation distance between expression profiles.
Topologies of cancer and disease progression
The Mapper algorithm is very useful in cases where an explicit representation of the phase space is needed. Such situations arise often in genomics, for instance, in large cross-sectional cancer studies. To define suitable targeted therapies, patients within a cancer type can be stratified in subtypes based on their expression, methylation, genetic, and other phenotypic profiles [37]. These classification schemes are usually based on clustering patients according to their profiles. In practice, however, boundaries between different subtypes are often diffuse, with many patients presenting characteristics of two or more subtypes. A more comprehensive approach requires taking into account the continuous nature of the phenotypic phase space. To that end, Nicolau and collaborators [10] considered the transcription phase space of breast cancer tumors, using expression data of 295 tumors [38]. They performed a 1-dimensional projection that quantifies the deviation of the expression profile of the tumor from that of the normal tissue, and used Mapper to build a low-dimensional simplicial complex representation of the phase space. Using this representation, they identified a previously unreported group of estrogen receptor positive (ER+) tumors with excellent prognosis and distinctive molecular signatures (Figure 4c). These results show the power of using explicit representations of the phase space in cases where its continuous nature is essential to the problem.
Similar Mapper reductions of transcription phase spaces have also been recently used to track disease progression, in this case exploiting topological features belonging to the first homology group. Using blood mRNA expression data of mice infected with the malaria parasite Plasmodium chabaudi, Torres et al. [39] reconstructed the circular trajectories that mice describe in the transcription phase space when going from a healthy state, to a sick state, and back to a healthy state. Similar trajectories were obtained when considering data from humans infected with malaria. These representations may serve to obtain a better understanding of disease progression, and the effect of stage-specific differences in the subsequent evolution.
Conclusions
TDA is a new and developing field. Its applications shown here demonstrate the value of topological methods in situations where phase space features can be readily interpreted. Its successful application to other biological systems will largely depend on the ability to interpret topological features of phase spaces meaningfully. Future formal developments in TDA may facilitate this process. There is a pressing need for the introduction of statistical tests capable of assessing the significance of a topological feature or comparing multiple topological representations (for instance, across biological replicates, genotypic and phenotypic spaces, etc.). Although some efforts in this direction have been initiated for persistent homology [40–42], there are yet no general results for the representations produced by Mapper. In addition, a general framework for combining different types of genomic information is still missing. This is particularly important in cancer applications, where heterogeneity originates from a combination of genetic and epigenetic factors.
The current TDA repertoire includes other tools apart from persistent homology and Mapper which may potentially be useful in genomic applications. Zigzag [43,44] and multidimensional [45] persistence are, for instance, promising methods for the analysis of temporal genomic data. Recent advances in dimensional reduction leveraging the modularity of topologically stratified spaces [46] will probably result in valuable tools for the analysis of genomic data. In summary, a rich interplay between formal developments and new applications is expected in upcoming years, which may place TDA in the standard toolbox of computational biology.
Acknowledgments
I thank Raúl Rabadán, Arnold Levine, Patrick van Nieuwenhuizen, Richard Wolff, and Udi Rubin for critical reading of early versions of the manuscript. I also thank them, as well as Daniel Rosenbloom, Kevin Emmett, Abbas Rizvi, Tom Maniatis, Elena Kandror, and Thomas Roberts for collaboration in related projects. This work is supported by the NIH grants U54-CA193313-01 (PI: Raúl Rabadán) and R01GM117591 (PI: Raúl Rabadán).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Goodwin S, McPherson JD, McCombie WR. Coming of age: ten years of next-generation sequencing technologies. Nat Rev Genet. 2016;17:333–351. doi: 10.1038/nrg.2016.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Metzker ML. Sequencing technologies - the next generation. Nat Rev Genet. 2010;11:31–46. doi: 10.1038/nrg2626. [DOI] [PubMed] [Google Scholar]
- 3.Buermans HP, den Dunnen JT. Next generation sequencing technology: Advances and applications. Biochim Biophys Acta. 2014;1842:1932–1941. doi: 10.1016/j.bbadis.2014.06.015. [DOI] [PubMed] [Google Scholar]
- 4.Carlsson G. Topology and data. Bulletin of the American Mathematical Society. 2009;46:255–308. [Google Scholar]
- 5.Carlsson G. Topological pattern recognition for point cloud data. Acta Numerica. 2014;23:289–368. [Google Scholar]
- 6.Ghrist R. Elementary applied topology. Createspace; 2014. [Google Scholar]
- 7.Edelsbrunner H, Harer J. Computational topology: an introduction. American Mathematical Soc; 2010. [Google Scholar]
- ••8.Chan JM, Carlsson G, Rabadan R. Topology of viral evolution. Proc Natl Acad Sci U S A. 2013;110:18566–18571. doi: 10.1073/pnas.1313480110. This paper proposes the use of persistent homology of genetic phase spaces to study reticulate evolution, and they apply this idea to viral reassortment and recombination. [DOI] [PMC free article] [PubMed] [Google Scholar]
- •9.Camara PG, Rosenbloom DI, Emmett KJ, Levine AJ, Rabadan R. Topological Data Analysis Generates High-Resolution, Genome-wide Maps of Human Recombination. Cell Syst. 2016;3:83–94. doi: 10.1016/j.cels.2016.05.008. The authors introduce a novel estimator of the recombination rate based on persistent homology and apply it to human genotype data to build high-resolution, genome-wide maps of meiotic human recombination. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ••10.Nicolau M, Levine AJ, Carlsson G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc Natl Acad Sci U S A. 2011;108:7265–7270. doi: 10.1073/pnas.1102826108. Using the Mapper algorithm, the authors build low-dimensional topological representations of the transcription phase space of breast cancer tumors and identify a previously unreported group of patients with excellent prognosis and distinctive molecular signatures. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Arsuaga J, Borrman T, Cavalcante R, Gonzalez G, Park C. Identification of copy number aberrations in breast cancer subtypes using persistence topology. Microarrays. 2015;4:339–369. doi: 10.3390/microarrays4030339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- •12.Li L, Cheng WY, Glicksberg BS, Gottesman O, Tamler R, Chen R, Bottinger EP, Dudley JT. Identification of type 2 diabetes subgroups through topological analysis of patient similarity. Sci Transl Med. 2015;7:311ra174. doi: 10.1126/scitranslmed.aaa9364. The authors explore the phenotypic space of 11,210 type 2 diabetes patients using the Mapper algorithm, and identify 3 previously unreported subgroups of patients with distinct genetic and disease associations. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hinks TS, Brown T, Lau LC, Rupani H, Barber C, Elliott S, Ward JA, Ono J, Ohta S, Izuhara K, et al. Multidimensional endotyping in patients with severe asthma reveals inflammatory heterogeneity in matrix metalloproteinases and chitinase 3-like protein 1. J Allergy Clin Immunol. 2016 doi: 10.1016/j.jaci.2015.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cahoy JD, Emery B, Kaushal A, Foo LC, Zamanian JL, Christopherson KS, Xing Y, Lubischer JL, Krieg PA, Krupenko SA, et al. A transcriptome database for astrocytes, neurons, and oligodendrocytes: a new resource for understanding brain development and function. J Neurosci. 2008;28:264–278. doi: 10.1523/JNEUROSCI.4178-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Emmett K, Schweinhart B, Rabadan R. Multiscale Topology of Chromatin Folding. 2015 arXiv preprint arXiv:1511.01426. [Google Scholar]
- 16.Perea JA, Deckard A, Haase SB, Harer J. SW1PerS: Sliding windows and 1-persistence scoring; discovering periodicity in gene expression time series data. BMC Bioinformatics. 2015;16:257. doi: 10.1186/s12859-015-0645-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dequeant ML, Ahnert S, Edelsbrunner H, Fink TM, Glynn EF, Hattem G, Kudlicki A, Mileyko Y, Morton J, Mushegian AR, et al. Comparison of pattern detection methods in microarray time series of the segmentation clock. PLoS One. 2008;3:e2856. doi: 10.1371/journal.pone.0002856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nolte DD. The tangled tale of phase space. Physics today. 2010 [Google Scholar]
- 19.Gawad C, Koh W, Quake SR. Single-cell genome sequencing: current state of the science. Nat Rev Genet. 2016;17:175–188. doi: 10.1038/nrg.2015.16. [DOI] [PubMed] [Google Scholar]
- 20.Macaulay IC, Voet T. Single cell genomics: advances and future perspectives. PLoS Genet. 2014;10:e1004126. doi: 10.1371/journal.pgen.1004126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clark SJ, Lee HJ, Smallwood SA, Kelsey G, Reik W. Single-cell epigenomics: powerful new methods for understanding gene regulation and cell identity. Genome Biol. 2016;17:72. doi: 10.1186/s13059-016-0944-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lefschetz S. Introduction to topology. Princeton University Press; 2015. [Google Scholar]
- 23.Mendelson B. Introduction to topology. Courier Corporation; 1990. [Google Scholar]
- 24.Hatcher A. Algebraic topology. Cambridge UP; Cambridge: 2002. p. 606. [Google Scholar]
- 25.Zomorodian A, Carlsson G. Computing persistent homology. Discrete & Computational Geometry. 2005;33:249–274. [Google Scholar]
- 26.Edelsbrunner H, Letscher D, Zomorodian A. Topological persistence and simplification. Discrete and Computational Geometry. 2002;28:511–533. [Google Scholar]
- 27.Ghrist R. Barcodes: the persistent topology of data. Bulletin of the American Mathematical Society. 2008;45:61–75. [Google Scholar]
- 28.Emmett KJ, Rabadan R. Characterizing scales of genetic recombination and antibiotic resistance in pathogenic bacteria using topological data analysis. International Conference on Brain Informatics and Health; Springer; 2014. pp. 540–551. [Google Scholar]
- 29.Camara P, Levine A, Rabadan R. Inference of Ancestral Recombination Graphs through Topological Data Analysis. PLoS Comput Biol. 2016;12:e1005071. doi: 10.1371/journal.pcbi.1005071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Emmett K, Rosenbloom D, Camara P, Rabadan R. Parametric inference using persistence diagrams: A case study in population genetics. 2014 arXiv preprint arXiv:1406.4582. [Google Scholar]
- 31.Hunter N. Meiotic Recombination: The Essence of Heredity. Cold Spring Harb Perspect Biol. 2015:7. doi: 10.1101/cshperspect.a016618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.McDonald SM, Nelson MI, Turner PE, Patton JT. Reassortment in segmented RNA viruses: mechanisms and outcomes. Nat Rev Microbiol. 2016;14:448–460. doi: 10.1038/nrmicro.2016.46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ochman H, Lawrence JG, Groisman EA. Lateral gene transfer and the nature of bacterial innovation. Nature. 2000;405:299–304. doi: 10.1038/35012500. [DOI] [PubMed] [Google Scholar]
- 34.Gao R, Cao B, Hu Y, Feng Z, Wang D, Hu W, Chen J, Jie Z, Qiu H, Xu K, et al. Human infection with a novel avian-origin influenza A (H7N9) virus. N Engl J Med. 2013;368:1888–1897. doi: 10.1056/NEJMoa1304459. [DOI] [PubMed] [Google Scholar]
- 35.Weinberger S. The complexity of some topological inference problems. Foundations of Computational Mathematics. 2014;14:1277–1285. [Google Scholar]
- 36.Singh G, Mémoli F, Carlsson GE. SPBG. Citeseer: 2007. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition; pp. 91–100. [Google Scholar]
- 37.Chin L, Andersen JN, Futreal PA. Cancer genomics: from discovery science to personalized medicine. Nat Med. 2011;17:297–303. doi: 10.1038/nm.2323. [DOI] [PubMed] [Google Scholar]
- 38.van de Vijver MJ, He YD, van’t Veer LJ, Dai H, Hart AA, Voskuil DW, Schreiber GJ, Peterse JL, Roberts C, Marton MJ, et al. A gene-expression signature as a predictor of survival in breast cancer. N Engl J Med. 2002;347:1999–2009. doi: 10.1056/NEJMoa021967. [DOI] [PubMed] [Google Scholar]
- •39.Torres BY, Oliveira JH, Thomas Tate A, Rath P, Cumnock K, Schneider DS. Tracking Resilience to Infections by Mapping Disease Space. PLoS Biol. 2016;14:e1002436. doi: 10.1371/journal.pbio.1002436. The authors make use of the Mapper algorithm to reproduce the circular trajectories which mice and humans infected with the malaria parasite describe in the transcription phase space when going from a healthy state, to a sick state, and back to a healthy state. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Blumberg AJ, Gal I, Mandell MA, Pancia M. Robust statistics, hypothesis testing, and confidence intervals for persistent homology on metric measure spaces. Foundations of Computational Mathematics. 2014;14:745–789. [Google Scholar]
- 41.Chazal F, Glisse M, Labruère C, Michel B. Convergence rates for persistence diagram estimation in topological data analysis. Journal of Machine Learning Research. 2015;16:3603–3635. [Google Scholar]
- 42.Balakrishnan S, Fasy B, Lecci F, Rinaldo A, Singh A, Wasserman L. Statistical inference for persistent homology. 2013 [Google Scholar]
- 43.Carlsson G, De Silva V, Morozov D. Zigzag persistent homology and real-valued functions. Proceedings of the twenty-fifth annual symposium on Computational geometry; ACM; 2009. pp. 247–256. [Google Scholar]
- 44.Carlsson G, De Silva V. Zigzag persistence. Foundations of computational mathematics. 2010;10:367–405. [Google Scholar]
- 45.Carlsson G, Zomorodian A. The theory of multidimensional persistence. Discrete & Computational Geometry. 2009;42:71–93. [Google Scholar]
- 46.Bendich P, Gasparovic E, Tralie CJ, Harer J. Scaffoldings and Spines: Organizing High-Dimensional Data Using Cover Trees, Local Principal Component Analysis, and Persistent Homology. 2016 arXiv preprint arXiv:1602.06245. [Google Scholar]
- 47.1000 Genomes Project Consortium. Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, Handsaker RE, Kang HM, Marth GT, McVean GA. An integrated map of genetic variation from 1,092 human genomes. Nature. 2012;491:56–65. doi: 10.1038/nature11632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cancer Genome Atlas N. Comprehensive molecular portraits of human breast tumours. Nature. 2012;490:61–70. doi: 10.1038/nature11412. [DOI] [PMC free article] [PubMed] [Google Scholar]