A Review of Multivariate Distributions for Count Data Derived from the Poisson Distribution

Abstract

The Poisson distribution has been widely studied and used for modeling univariate count-valued data. Multivariate generalizations of the Poisson distribution that permit dependencies, however, have been far less popular. Yet, real-world high-dimensional count-valued data found in word counts, genomics, and crime statistics, for example, exhibit rich dependencies, and motivate the need for multivariate distributions that can appropriately model this data. We review multivariate distributions derived from the univariate Poisson, categorizing these models into three main classes: 1) where the marginal distributions are Poisson, 2) where the joint distribution is a mixture of independent multivariate Poisson distributions, and 3) where the node-conditional distributions are derived from the Poisson. We discuss the development of multiple instances of these classes and compare the models in terms of interpretability and theory. Then, we empirically compare multiple models from each class on three real-world datasets that have varying data characteristics from different domains, namely traffic accident data, biological next generation sequencing data, and text data. These empirical experiments develop intuition about the comparative advantages and disadvantages of each class of multivariate distribution that was derived from the Poisson. Finally, we suggest new research directions as explored in the subsequent discussion section.

Introduction

Multivariate count-valued data has become increasingly prevalent in modern big data settings. Variables in such data are rarely independent and instead exhibit complex positive and negative dependencies. We highlight three examples of multivariate count-valued data that exhibit rich dependencies: text analysis, genomics, and crime statistics. In text analysis, a standard way to represent documents is to merely count the number of occurrences for each word in the vocabulary and create a word-count vector for each document. This representation is often known as the bag-of-words representation, in which the word order and syntax are ignored. The vocabulary size—i.e. the number of variables in the data—is usually much greater than 1000 unique words, and thus a high-dimensional multivariate distribution is required. Also, words are clearly not independent. For example, if the word “Poisson” appears in a document, then the word “probability” is more likely to also appear signifying a positive dependency. Similarly, if the word “art” appears, then the word “probability” is less likely to also appear signifying a negative dependency. In genomics, RNA-sequencing technologies are used to measure gene and isoform expression levels. These technologies yield counts of reads mapped back to DNA locations, that even after normalization, yield non-negative data that is highly skewed with many exact zeros. This genomics data is both high-dimensional, with the number of genes measuring in the tens-of-thousands, and strongly dependent, as genes work together in pathways and complex systems to produce particular phenotypes. In crime analysis, counts of crimes in different counties are clearly multidimensional, with dependencies between crime counts. For example, the counts of crime in adjacent counties are likely to be correlated with one another, indicating a positive dependency. While positive dependencies are probably more prevalent in crime statistics, negative dependencies might be very interesting. For example, a negative dependency between adjacent counties may suggest that a criminal gang has moved from one county to the other.

These examples motivate the need for a high-dimensional count-valued distribution that permits rich dependencies between variables. In general, a good class of probabilistic models is a fundamental building block for many tasks in data analysis. Estimating such models from data could help answer exploratory questions such as: Which genomic pathways are altered in a disease e.g. by analyzing genomic networks? Or, which county seems to have the strongest effect, with respect to crime, on other counties? A probabilistic model could also be used in Bayesian classification to determine questions such as: Does this Twitter post display positive or negative sentiment about a particular product (fitting one model on positive posts and one model on negative posts)?

The classical model for a count-valued random variable is the univariate Poisson distribution, whose probability mass function for x ∈ {0, 1, 2, …} is:

$${\mathrm{\mathbb{P}}}_{\text{Poiss}}(x|\mathrm{\lambda })={\mathrm{\lambda }}^x\exp (-\mathrm{\lambda })/x!,$$ (1)

where λ is the standard mean parameter for the Poisson distribution. A trivial extension of this to a multivariate distribution would be to assume independence between variables, and take the product of node-wise univariate Poisson distributions, but such a model would be ill-suited for many examples of multivariate count-valued data that require rich dependence structures. We review multivariate probability models that are derived from the univariate Poisson distribution and permit non-trivial dependencies between variables. We categorize these models into three main classes based on their primary modeling assumption. The first class assumes that the univariate marginal distributions are derived from the Poisson. The second class is derived as a mixture of independent multivariate Poisson distributions. The third class assumes that the univariate conditional distributions are derived from the Poisson distribution—this last class of models can also be studied in the context of probabilistic graphical models. An illustration of each of these three main model classes can be seen in Fig. 1. While these models might have been classified by primary application area or performance on a particular task, a classification based on modeling assumptions helps emphasize the core abstractions for each model class. In addition, this categorization may help practitioners from different disciplines learn from the models that have worked well in different areas. We discuss multiple instances of these classes in the later sections and highlight the strengths and weaknesses of each class. We then provide a short discussion on the differences between classes in terms of interpretability and theory. Using two different empirical measures, we empirically compare multiple models from each class on three real-world datasets that have varying data characteristics from different domains, namely traffic accident data, biological next generation sequencing data, and text data. These experiments develop intuition about the comparative advantages and disadvantages of the models and suggest new research directions as explored in the subsequent discussion section.

Figure 1.

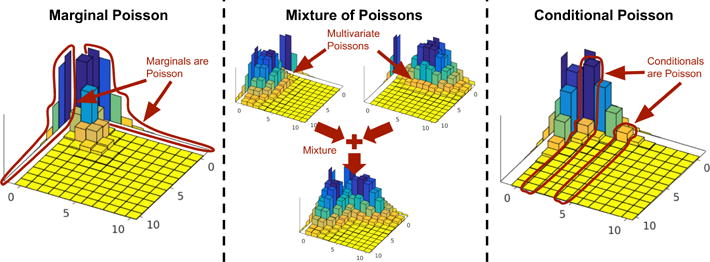
(Left) The first class of Poisson generalizations is based on the assumption that the univariate marginals are derived from the Poisson. (Middle) The second class is based on the idea of mixing independent multivariate Poissons into a joint multivariate distribution. (Right) The third class is based on the assumption that the univariate conditional distributions are derived from the Poisson.

Notation

ℝ denotes the set of real numbers, ℝ₊ denotes the nonnegative real numbers, and ℝ₊₊ denotes the positive real numbers. Similarly, $\mathrm{\mathbb{Z}}$ denotes the set of integers. Matrices are denoted as capital letters (e.g. X, Φ), vectors are denoted as boldface lowercase letters (e.g. x, ϕ) and scalar values are non-bold lowercase letters (e.g. x, ϕ).

Marginal Poisson Generalizations

The models in this section generalize the univariate Poisson to a multivariate distribution with the property that the marginal distributions of each variable are Poisson. This is analogous to the marginal property of the multivariate Gaussian distribution, since the marginal distributions of a multivariate Gaussian are univariate Gaussian, and thus seems like a natural constraint when extending the univariate Poisson to the multivariate case. Several historical attempts at achieving this marginal property have incidentally developed the same class of models, with different derivations^57;12;76;70. This marginal Poisson property can also be achieved via the more general framework of copulas^77;62;59.

Multivariate Poisson Distribution

The formulation of the multivariate Poisson¹ distribution goes back to M’Kendrick⁵⁷ where authors use differential equations to derive the bivariate Poisson process. An equivalent but more readable interpretation to arrive at the bivariate Poisson distribution would be to use the summation of independent Poisson variables, as follows¹²: Let y₁, y₂ and z be univariate Poisson variables with parameters λ₁, λ₂ and λ₀ respectively. Then by setting x₁ = y₁ + z and x₂ = y₂ + z, (x₁, x₂) follows the bivariate Poisson distribution, and its joint probability mass is defined as:

$$\begin{array}{l}{\mathrm{\mathbb{P}}}_{\text{BiPoi}}(x_1,x_2|{\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,{\mathrm{\lambda }}_0)\\ =exp(-{\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2-{\mathrm{\lambda }}_0)\frac{{\mathrm{\lambda }}_1^{x_1}}{x_1!}\frac{{\mathrm{\lambda }}_2^{x_2}}{{ }_2!}{\displaystyle \sum _{z=0}^{min(x_1,x_2)}\left(\begin{array}{c}{x}_1\\ z\end{array}\right)}\left(\begin{array}{c}{x}_2\\ z\end{array}\right)z!{\left(\frac{{\mathrm{\lambda }}_0}{{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2}\right)}^z.\end{array}$$ (2)

Since the sum of independent Poissons is also Poisson (whose parameter is the sum of those of two components), the marginal distribution of x₁ (similarly x₂) is still a Poisson with the rate of λ₁ + λ₀. It can be easily seen that the covariance of x₁ and x₂ is λ₀ and as a result the correlation coefficient is somewhere between 0 and $min\{\frac{\sqrt{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_0}}{\sqrt{{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_0}},\frac{\sqrt{{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_0}}{\sqrt{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_0}}\}$²⁹. Independently, Wicksell⁷⁶ derived the bivariate Poisson as the limit of a bivariate binomial distribution. Campbell¹² show that the models in M’Kendrick⁵⁷ and Wicksell⁷⁶ can identically be derived from the sums of 3 independent Poisson variables.

This approach to directly extend the Poisson distribution can be generalized further to handle the multivariate case $\mathit{x}\in {\mathrm{\mathbb{Z}}}_{+}^d$, in which each variable x_i is the sum of individual Poisson y_i and the common Poisson x₀ as before. The joint probability for a Multivariate Poisson is developed in Teicher⁷⁰ and further considered by other works^20;68;75;42:

$${\mathrm{\mathbb{P}}}_{\text{MulPoi}}(\mathit{x};\mathbf{\lambda })=exp\left(-{\displaystyle \sum _{i=0}^d{\mathrm{\lambda }}_i}\right)\left({\displaystyle \prod _{i=1}^d\frac{{\mathrm{\lambda }}_i^{x_i}}{x_i!}}\right){{\displaystyle \sum _{z=0}^{{min}_i{x}_i}\left({\displaystyle \prod _{i=1}^d\left(\begin{array}{c}{x}_i\\ z\end{array}\right)}\right)z!\left(\frac{{\mathrm{\lambda }}_0}{{\displaystyle {\prod }_{i=1}^d{\mathrm{\lambda }}_i}}\right)}}^z.$$ (3)

Several have shown that this formulation of the multivariate Poisson can also be derived as a limiting distribution of a multivariate binomial distribution when the success probabilities are small and the number of trials is large^46;47;35. As in the bivariate case, the marginal distribution of x_i is Poisson with parameter λ_i + λ₀. Since λ₀ controls the covariance between all variables, an extremely limited set of correlations between variables is permitted.

Mahamunulu⁵⁴ first proposed a more general extension of the multivariate Poisson distribution that permits a full covariance structure. This distribution has been studied further by many^{50;37;35;38;72}. While the form of this general multivariate Poisson distribution is too complicated to spell out for d > 3, its distribution can be specified by a multivariate reduction scheme. Specifically, let y_i for i = 1, …, (2^d − 1) be independently Poisson distributed with parameter λ_i. Now, define A = [A₁, A₂, … A_d] where A_i is a $d\times {(}_i^d)$ matrix consisting of ones and zeros where each column of A_i has exactly i ones with no duplicate columns. Hence, A₁ is the d × d identity matrix and A_d is a column vector of all ones. Then, x = Ay is a d-dimensional multivariate Poisson distributed random vector with a full covariance structure. Note that the simpler multivariate Poisson distribution with constant covariance in Eq. 3 is a special case of this general form where A = [A₁, A_d].

The multivariate Poisson distribution has not been widely used for real data applications. This is likely due to two major limitations of this distribution. First, the multivariate Poisson distribution only permits positive dependencies; this can easily be seen as the distribution arises as the sum of independent Poisson random variables and hence covariances are governed by the positive rate parameters λ_i. The assumption of positive dependencies is likely unrealistic for most real count-valued data examples. Second, computation of probabilities and inference of parameters is especially cumbersome for the multivariate Poisson distribution; these are only computationally tractable for small d and hence not readily applicable in high-dimensional settings. Kano and Kawamura³⁷ proposed multivariate recursion schemes for computing probabilities, but these schemes are only stable and computationally feasible for small d, thus complicating likelihood-based inference procedures. Karlis³⁸ more recently proposed a latent variable based EM algorithm for parameter inference of the general multivariate Poisson distribution. This approach treats every pairwise interaction as a latent variable and conducts inference over both the observed and hidden parameters. While this method is more tractable than recursion schemes, it still requires inference over ${(}_2^d)$ latent variables and is hence not feasible in high-dimensional settings. Overall, the multivariate Poisson distribution introduced above is appealing in that its marginal distributions are Poisson; yet, there are many modeling drawbacks including severe restriction on the types of dependencies permitted (e.g. only positive relationships), a complicated and intractable form in high-dimensions, and challenging inference procedures.

Copula Approaches

A much more general way to construct valid multivariate Poisson distributions with Poisson marginals is by pairing a copula distribution with Poisson marginal distributions. For continuous multivariate distributions, the use of copula distributions is founded on the celebrated Sklar’s theorem: any continuous joint distribution can be decomposed into a copula and the marginal distributions, and conversely, any combination of a copula and marginal distributions gives a valid continuous joint distribution⁶⁶. The key advantage of such models for continuous distributions is that copulas fully specify the dependence structure hence separating the modeling of marginal distributions from the modeling of dependencies. While copula distributions paired with continuous marginal distributions enjoy wide popularity (see for example¹³ in finance applications), copula models paired with discrete marginal distributions, such as the Poisson, are more challenging both for theoretical and computational reasons^22;60;61. However, several simplifications and recent advances have attempted to overcome these challenges^65;60;61.

Copula Definition and Examples

A copula is defined by a joint cumulative distribution function (CDF), C(u): [0, 1]^d → [0, 1] with uniform marginal distributions. As a concrete example, the Gaussian copula (see left subfigure of Fig. 2 for an example) is derived from the multivariate normal distribution and is one of the most popular multivariate copulas because of its flexibility in the multidimensional case; the Gaussian copula is defined simply as:

$$C_R^{\text{Gauss}}(u_1,u_2,\cdots ,u_d)=H_R(H^{-1}(u_1),\cdots ,H^{-1}(u_d)),$$

where H⁻¹(·) denotes the standard normal inverse cumulative distribution function, and H_R(·) denotes the joint cumulative distribution function of a $\mathcal{N}(0,R)$ random vector, where R is a correlation matrix. A similar multivariate copula can be derived from the multivariate Student’s t distribution if extreme values are important to model¹⁸.

Figure 2.

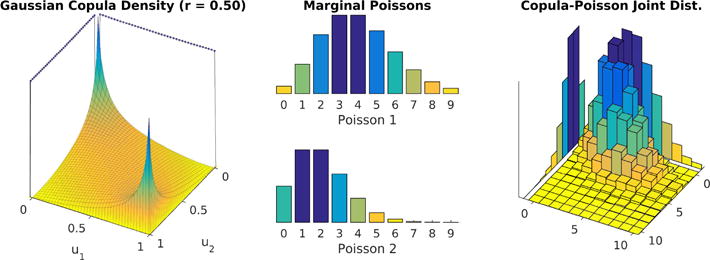
A copula distribution (left)—which is defined over the unit hypercube and has uniform marginal distributions—, paired with univariate Poisson marginal distributions for each variable (middle) defines a valid discrete joint distribution with Poisson marginals (right).

The Archimedean copulas are another family of copulas which have a single parameter that defines the global dependence between all variables⁷¹. One property of Archimedean copulas is that they admit an explicit form unlike the Gaussian copula. Unfortunately, the Archimedean copulas do not directly allow for a rich dependence structure like the Gaussian because they only have one dependence parameter rather than a parameter for each pair of variables.

Pair copula constructions (PCCs)¹ for copulas, or vine copulas, allow combinations of different bivariate copulas to form a joint multivariate copula. PCCs define multivariate copulas that have an expressive dependency structure like the Gaussian copula but may also model asymmetric or tail dependencies available in Archimedean and t copulas. Pair copulas only use univariate CDFs, conditional CDFs, and bivariate copulas to construct a multivariate copula distribution and hence can use combinations of the Archimedean copulas described previously. The multivariate distributions can be factorized in a variety of ways using bivariate copulas to flexibly model dependencies. Vines, or graphical tree-like structures, denote the possible factorizations that are feasible for PCCs⁹.

Copula Models for Discrete Data

As per Sklar’s theorem, any copula distribution can be combined with marginal distribution CDFs ${\{F_i(x_i)\}}_{i=1}^d$ to create a joint distribution:

$$G(x_1,x_2,\cdots ,x_d|\theta ,F_1,\cdots ,F_d)=C_{\theta }(u_1=F_1(x_1),\cdots ,u_d=F_d(x_d)).$$

If sampling from the given copula is possible, this form admits simple direct sampling from the joint distribution (defined by the CDF G(·)) by first sampling from the copula u ∼ Copula(θ) and then transforming u to the target space using the inverse CDFs of the marginal distributions: $\mathit{x}=[F_1^{-1}(u_1),\cdots ,F_d^{-1}(u_d)]$.

A valid multivariate discrete joint distribution can be derived by pairing a copula distribution with Poisson marginal distributions. For example, a valid joint CDF with Poisson marginals is given by

$$G(x_1,x_2,\cdots ,x_d|\theta )=C_{\theta }(F_1(x_1|{\mathrm{\lambda }}_1),\cdots ,F_d(x_d|{\mathrm{\lambda }}_d)),$$

where F_i(x_i | λ_i) is the Poisson cumulative distribution function with mean parameter λ_i, and θ denotes the copula parameters. If we pair a Gaussian copula with Poisson marginal distributions, we create a valid joint distribution that has been widely used for generating samples of multivariate count data^77;78;16—an example of the Gaussian copula paired with Poisson marginals to form a discrete joint distribution can be seen in Fig. 2.

Nikoloulopoulos⁵⁹ present an excellent survey of copulas to be paired with discrete marginals by defining several desired properties of a copula (quoted from⁵⁹):

1. Wide range of dependence, allowing both positive and negative dependence.

2. Flexible dependence, meaning that the number of bivariate marginals is (approximately) equal to the number of dependence parameters.

3. Computationally feasible cumulative distribution function (CDF) for likelihood estimation.

4. Closure property under marginalization, meaning that lower-order marginals belong to the same parametric family.

5. No joint constraints for the dependence parameters, meaning that the use of covariate functions for the dependence parameters is straightforward.

Each copula model satisfies some of these properties but not all of them. For example, Gaussian copulas satisfy properties (1), (2) and (4) but not (3) or (5) because the normal CDF is not known in closed form and the positive definiteness constraint on the correlation matrix. Nikoloulopoulos⁵⁹ recommend Gaussian copulas for general models and vine copulas if modeling dependence in the tails or asymmetry is needed.

Theoretical Properties of Copulas Derived from Discrete Distributions

From a theoretical perspective, a multivariate discrete distribution can be viewed as a continuous copula distribution paired with discrete marginals but the derived copula distributions are not unique and hence, are unidentifiable²². Note that this is in contrast to continuous multivariate distributions where the derived copulas are uniquely defined⁶⁷. Because of this non-uniqueness property, Genest and Nešlehová²² caution against performing inference on and interpreting dependencies of copulas derived from discrete distributions. A further consequence of non-uniqueness is that when copula distributions are paired with discrete marginal distributions, the copulas no longer fully specify the dependence structure as with continuous marginals²². In other words, the dependencies of the joint distribution will depend in part on which marginal distributions are employed. In practice, this often means that the range of dependencies permitted with certain copula and discrete marginal distribution pairs is much more limited than the copula distribution would otherwise model. However, several have suggested that this non-uniqueness property does not have major practical ramifications^59;39.

We discuss a few common approaches used for the estimation of continuous copulas with discrete marginals.

Continuous Extension for Parameter Estimation

For estimation of continuous copulas from data, a two-stage procedure called Inference Function for Marginals (IFM)³⁴ is commonly used in which the marginal distributions are estimated first and then used to map the data onto the unit hypercube using the CDFs of the inferred marginal distributions. While this is straightforward for continuous marginals, this procedure is less obvious for discrete marginal distributions when using a continuous copula. One idea is to use the continuous extension (CE) of integer variables to the continuous domain¹⁹ by forming a new “jitter” continuous random variable $\stackrel{\sim }{x}$:

$$\stackrel{\sim }{x}=x+(u-1),$$

where u is a random variable defined on the unit interval. It is straightforward to see that this new random variable is continuous and $\stackrel{\sim }{x}\le x$. An obvious choice for the distribution of u is the uniform distribution. With this idea, inference can be performed using a surrogate likelihood by randomly projecting each discrete data point into the continuous domain and averaging over the random projections as done in^27;28. Madsen⁵²; Madsen and Fang⁵³ use the CE idea as well but generate multiple jittered samples $\{{\stackrel{\sim }{x}}^{(1)},{\stackrel{\sim }{x}}^{(1)},\dots ,{\stackrel{\sim }{x}}^{(m)}\}$ for each original observation x to estimate the discrete likelihood rather than merely generating one jittered sample $\stackrel{\sim }{x}$ for each original observation x as in^27;28. Nikoloulopoulos⁶⁰ find that CE-based methods significantly underestimate the correlation structure because the CE jitter transform operates independently for each variable instead of considering the correlation structure between the variables.

Distributional Transform for Parameter Estimation

In a somewhat different direction, Rüschendorf⁶⁵ proposed the use of a generalization of the CDF distribution function F (·) for the case with discrete variables, which they term a distributional transform (DT) denoted by $\stackrel{\sim }{F}(\cdot )$:

$$\stackrel{\sim }{F}(x,v)\equiv F(x)+v\mathrm{\mathbb{P}}(x)=\mathrm{\mathbb{P}}(X<x)+v\mathrm{\mathbb{P}}(X=x),$$

where v ∼ Uniform(0, 1). Note that in the continuous case, ℙ(X = x) = 0 and thus this reduces to the standard CDF for continuous distributions. One way of thinking of this modified CDF is that the random variable v adds a random jump when there are discontinuities in the original CDF. If the distribution is discrete (or more generally if there are discontinuities in the original CDF), this transformation enables a simple proof of a theorem akin to Sklar’s theorem for discrete distributions⁶⁵.

Kazianka and Pilz⁴⁴; Kazianka⁴³ propose using the distributional transform (DT) from⁶⁵ to develop a simple and intuitive approximation for the likelihood. Essentially, they simply take the expected jump value of $\mathbb{E}(v)=0.5$ (where v ~ Uniform(0, 1)) and thus transform the discrete data to the continuous domain by the following:

$$u_i\equiv F_i(x_i-1)+0.5\mathrm{\mathbb{P}}(x_i)=0.5(F_i(x_i-1)+F_i(x_i)),$$

which can be seen as simply taking the average of the CDF values at x_i −1 and x_i. Then, they use a continuous copula such as the Gaussian copula. Note that this is much simpler to compute than the simulated likelihood (SL) method in⁶⁰ or the continuous extension (CE) methods in^27;28;52;53, which require averaging over many different random initializations.

Simulated Likelihood for Parameter Estimation

Finally,⁶⁰ propose a method to directly approximate the maximum likelihood estimate by estimating a discretized Gaussian copula. Essentially, unlike the CE and DT methods which attempt to transform discrete variables to continuous variables, the MLE for a Gaussian copula with discrete marginal distributions F₁, F₂, …, F_d can be formulated as estimating multivariate normal rectangular probabilities:

$$\mathrm{\mathbb{P}}(\mathit{x}|\gamma ,R)={\displaystyle {\int }_{{\varphi }^{-1}[F_1(x_1-1|{\gamma }_1)]}^{{\varphi }^{-1}[F_1(x_1|{\gamma }_1)]}\cdots }{\displaystyle {\int }_{{\varphi }^{-1}[F_1(x_d-1|{\gamma }_d)]}^{{\varphi }^{-1}[F_d(x_d|{\gamma }_d)]}{\mathrm{\Phi }}_R(z_1,\dots ,z_d)d{z}_1\dots d{z}_d,}$$ (4)

where γ are the marginal distribution parameters, ϕ⁻¹(·) is the univariate standard normal inverse CDF, and Φ_R(⋯) is the multivariate normal density with correlation matrix R. Nikoloulopoulos 60 propose to approximate the multivariate normal rectangular probabilities via fast simulation algorithms discussed in²³. Because this method directly approximates the MLE via simulated algorithms, this method is called simulated likelihood (SL). Nikoloulopoulos⁶¹ compare the DT and SL methods for small sample sizes and find that the DT method tends to overestimate the correlation structure. However, because of the computational simplicity, Nikoloulopoulos⁶¹ give some heuristics of when the DT method might work well compared to the more accurate but more computationally expensive SL method.

Vine Copulas for Discrete Distributions

Panagiotelis et al.⁶³ provide conditions under which a multivariate discrete distribution can be decomposed as a vine PCC copula paired with discrete marginals. In addition, Panagiotelis et al.⁶³ show that likelihood computation for vine PCCs with discrete marginals is quadratic as opposed to exponential as would be the case for general multivariate copulas such as the Gaussian copula with discrete marginals. However, computation in truly high-dimensional settings remains a challenge as 2d(d − 1) bivariate copula evaluations are required to calculate the PMF or likelihood of a d-variate PCC using the algorithm proposed by Panagiotelis et al.⁶³. These bivariate copula evaluations, however, can be coupled with some of the previously discussed computational techniques such as continuous extensions, distributional transforms, and simulated likelihoods for further computational improvements. Finally, while vine PCCs offer a very flexible modeling approach, this comes with the added challenge of selecting the vine construction and bivariate copulas¹⁷, which has not been well studied for discrete distributions. Overall, Nikoloulopoulos⁵⁹ recommend using vine PCCs for complex modeling of discrete data with tail dependencies and asymmetric dependencies.

Summary of Marginal Poisson Generalizations

We have reviewed the historical development of the multivariate Poisson which has Poisson marginals and then reviewed many of the recent developments of using the much more general copula framework to derive Poisson generalizations with Poisson marginals. The original multivariate Poisson models based on latent Poisson variables are limited to positive dependencies and require computationally expensive algorithms to fit. However, estimation of copula distributions paired with Poisson marginals—while theoretically has some caveats—can be performed efficiently in practice. Simple approximations such as the expectation under the distributional transformation can provide nearly trivial transformations that move the discrete variables to the continuous domain in which all the tools of continuous copulas can be exploited. More complex transformations such as the simulated likelihood method⁶⁰ can be used if the sample size is small or high accuracy is needed.

Poisson Mixture Generalizations

Instead of directly extending univariate Poissons to the multivariate case, a separate line of work proposes to indirectly extend the Poisson based on the mixture of independent Poissons. Mixture models are often considered to provide more flexibility by allowing the parameter to vary according to a mixing distribution. One important property of mixture models is that they can model overdispersion. Overdispersion occurs when the variance of the data is larger than the mean of the data—unlike in a Poisson distribution in which the mean and variance are equal. One way of quantifying dispersion is the dispersion index:

$$\delta =\frac{{\sigma }^2}{\mu }.$$ (5)

If δ > 1, then the distribution is overdispersed whereas if δ < 1, then the distribution is underdispersed. In real world data as will be seen in the experimental section, overdispersion is more common than underdispersion. Mixture models also enable dependencies between the variables as will be described in the following paragraphs.

Suppose that we are modeling univariate random variable x with a density of f(x|θ). Rather than assuming θ is fixed, we let θ itself to be a random variable following some mixing distribution. More formally, a general mixture distribution can be defined as⁴¹:

$$\mathrm{\mathbb{P}}\left(x|g(\cdot )\right)={\displaystyle {\int }_{\mathrm{\Theta }}f\left(x|\theta \right)g\left(\theta \right)d\theta },$$ (6)

where the parameter θ is assumed to come from the mixing distribution g(θ) and Θ is the domain of θ.

For the Poisson case, let $\mathbf{\lambda }\in {\mathrm{ℝ}}_{++}^d$ be a d-dimensional vector whose i-th element λ_i is the parameter of the Poisson distribution for x_i. Now, given some mixing distribution g(λ), the family of Poisson mixture distributions is defined as

$${\mathrm{\mathbb{P}}}_{\text{MixedPoi}}\left(\mathit{x}\right)={\displaystyle {\int }_{{\mathrm{ℝ}}_{++}^d}g\left(\mathbf{\lambda }\right)}{\displaystyle \prod _{i=1}^d{\mathrm{\mathbb{P}}}_{\text{Poiss}}\left(x_i|{\mathrm{\lambda }}_i\right)d\mathbf{\lambda }},$$ (7)

where the domain of the joint distribution is any count-valued assignment (i.e. x_i ∈ ℤ₊, ∀i). While the probability density function (Eq. 7) has the complicated form involving a multidimensional integral (a complex, high-dimensional integral when d is large), the mean and variance are known to be expressed succinctly as

$$\mathbb{E}\left(\mathit{x}\right)=\mathbb{E}\left(\mathbf{\lambda }\right),$$ (8)

$$\text{Var}\left(\mathit{x}\right)=\mathbb{E}\left(\mathbf{\lambda }\right)+\text{Var}\left(\mathbf{\lambda }\right).$$ (9)

Note that Eq. 9 implies that the variance of a mixture is always larger than the variance of a single distribution. The higher order moments of x are also easily represented by those of λ. Besides the moments, other interesting properties (convolutions, identifiability etc.) of Poisson mixture distributions are extensively reviewed and studied in Karlis and Xekalaki⁴¹.

One key benefit of Poisson mixtures is that they permit both positive as well as negative dependencies simply by properly defining g(λ). The intuition behind these dependencies can be more clearly understood when we consider the sample generation process. Suppose that we have the distribution g(λ) in two dimensions (i.e. d = 2) with a strong positive dependency between λ₁ and λ₂. Then, given a sample (λ₁, λ₂) from g(λ), x₁ and x₂ are likely to also be positively correlated.

In an early application of the model, Arbous and Kerrich⁸ constrain the Poisson parameters as the different scales of common gamma variable λ: for i = 1, …, d, the time interval t_i is given and λ_i is set to t_iλ. Hence, g(λ) is a univariate gamma distribution specified by λ ∈ ℝ₊₊—which only allows simple dependency structure. Steyn⁶⁹, as another early attempt, choose the multivariate normal distribution for the mixing distribution g(λ) to provide more flexibility on the correlation structure. However, the normal distribution poses problems because λ must reside in ℝ₊₊ while the the normal distribution is defined on ℝ.

One of the most popular choice for g(λ) is the log-normal distribution thanks to its rich covariance structure and natural positivity constraint²:

$${\mathcal{N}}_{\text{log}}\left(\mathbf{\lambda }|\mathit{\mu },\sum \right)=\frac{1}{{\displaystyle {\prod }_{i=1}^d{\mathrm{\lambda }}_i\sqrt{\left(2\pi \right)d|\sum |}}}\exp \left(-\frac{1}{2}{\left(\log \mathbf{\lambda }-\mathit{\mu }\right)}^{\top }{\sum }^{-1}\left(\log \mathbf{\lambda }-\mathit{\mu }\right)\right).$$ (10)

The log-normal distribution above is parameterized by μ and Σ, which are the mean and the covariance of (log λ₁, log λ₂, ⋯, log λ_d), respectively. Setting the random variable x_i to follow the Poisson distribution with parameter λ_i, we have the multivariate Poisson log-normal distribution³ from Eq. 7:

$${\mathrm{\mathbb{P}}}_{\text{PoiLogN}}\left(\mathit{x}|\mathit{\mu },\sum \right)={\displaystyle {\int }_{{\mathrm{ℝ}}_{+}^d}{\mathcal{N}}_{\text{log}}\left(\mathbf{\lambda }|\mathit{\mu },\sum \right)}{\displaystyle \prod _{i=1}^d{\mathrm{\mathbb{P}}}_{\text{Poiss}}\left(x_i|{\mathrm{\lambda }}_i\right)d\mathbf{\lambda }}.$$ (11)

While the joint distribution (Eq. 11) does not have a closed-form expression and hence as d increases, it becomes computationally cumbersome to work with, its moments are available in closed-form as a special case of Eq. 9:

$$\begin{array}{l}{\alpha }_i\equiv \mathbb{E}\left(x_i\right)=\exp \left({\mu }_i+\frac{1}{2}{\sigma }_{ii}\right),\\ \text{Var}\left(x_i\right)={\alpha }_i+{\alpha }_i^2\left(\exp \left({\sigma }_{ii}\right)-1\right),\\ \text{Cov}\left(x_i,x_j\right)={\alpha }_i{\alpha }_j\left(\exp \left({\sigma }_{ii}\right)-1\right).\end{array}$$ (12)

The correlation and the degree of overdispersion (defined as the variance divided by the mean) of the marginal distributions are strictly coupled by α and σ. Also, the possible Spearman’s ρ correlation values for this distribution are limited if the mean value α_i is small. To briefly explore this phenomena, we simulated a two-dimensional Poisson log-normal model with mean zero and covariance matrix:

$$\sum =2\log \left({\alpha }_i\right)\left[\begin{array}{cc}1& \pm 0.999\\ \pm 0.999& 1\end{array}\right],$$

which corresponds to a mean value of α_i per Eq. 12 and the strongest positive and negative correlation possible between the two variables. We simulated one million samples from this distribution and found that when fixing α_i = 2, the Spearman’s ρ values are between −0.53 and 0.58. When fixing α_i = 10, the Spearman’s ρ values are between −0.73 and 0.81. Thus, for small mean values, the log-normal mixture is limited in modeling strong dependencies but for large mean values the log-normal mixture can model stronger dependencies. Besides the examples provided here, various Poisson mixture models from different mixing distributions are available although limited in the applied statistical literature due to their complexities. See Karlis and Xekalaki⁴¹ and the references therein for more examples of Poisson mixtures. Karlis and Xekalaki⁴¹ also provide the general properties of mixtures as well as the specific ones of Poisson mixtures such as moments, convolutions, and the posterior.

While this review focuses on modeling multivariate count-valued responses without any extra information, the several extensions of multivariate Poisson log-normal models have been proposed to provide more general correlation structures when covariates are available^{14;51;64;21;2;83}. These works formulate the mean parameter of log-normal mixing distribution, log μ_i, as a linear model on given covariates in the Bayesian framework.

In order to alleviate the computational burden of using log-normal distributions as an infinite mixing density as above, Karlis and Meligkotsidou⁴⁰ proposed an EM type estimation for a finite mixture of k > 1 Poisson distributions, which still preserves similar properties such as both positive and negative dependencies, as well as closed form moments. While⁴⁰ consider mixing multivariate Poissons with positive dependencies, the simplified form where the component distributions are independent Poisson distributions is much simpler to implement using an expectation-maximization (EM) algorithm. This simple finite mixture distribution can be viewed as a middle ground between a single Poisson and a non-parametric estimation method where a Poisson is located at every training point—i.e. the number of mixtures is equal to the number of training data points (k = n).

The gamma distribution is another common mixing distribution for the Poisson because it is the conjugate distribution for the Poisson mean parameter λ. For the univariate case, if the mixing distribution is gamma, then the resulting univariate distribution is the well-known negative binomial distribution. The negative binomial distribution can handle overdispersion in count-valued data when the variance is larger than the mean. Unlike the Poisson log-normal mixture, the univariate gamma-Poisson mixture density—i.e. the negative binomial density—is known in closed form:

$$\mathrm{\mathbb{P}}\left(x|r,p\right)=\frac{\mathrm{\Gamma }\left(r+x\right)}{\mathrm{\Gamma }\left(r\right)\mathrm{\Gamma }\left(x+1\right)}{p}^r{\left(1-p\right)}^x.$$

As r → ∞, the negative binomial distribution approaches the Poisson distribution. Thus, this can be seen as a generalization of the Poisson distribution. Note that the variance of this distribution is always larger than the Poisson distribution with the same mean value.

In a similar vein to using the gamma distribution, if instead of putting a prior on the Poisson mean parameter λ, we reparametrize the Poisson distribution by the log Poisson mean parameter θ = log(λ), then the log-gamma distribution is conjugate to parameter θ. Bradley et al.¹¹ recently leveraged the log-gamma conjugacy to the Poisson log-mean parameter θ by introducing the Poisson log-gamma hierarchical mixture distribution. In particular, they discuss the multivariate log-gamma distribution that can have flexible dependency structure similar to the multivariate log-normal distribution and illustrate some modeling advantages over the log-normal mixture model.

Summary of Mixture Model Generalizations

Overall, mixture models are particularly helpful if there is overdispersion in the data—which is often the case for real-world data as seen in the experiments section—while also allowing for variable dependencies to be modeled implicitly through the mixing distribution. If the data exhibits overdispersion, then the log-normal or log-gamma distributions¹¹ give somewhat flexible dependency structures. The principal caveat with complex mixture of Poisson distributions is computational; exact inference of the parameters is typically computationally difficult due to the presence of latent mixing variables. However, simpler models such as the finite mixture using simple expectation maximization (EM) may provide good results in practice (see comparison section).

Conditional Poisson Generalizations

While the multivariate Poisson formulation in Eq. 3 as well as the distribution formed by pairing a copula with Poisson marginals assume that univariate marginal distributions are derived from the Poisson, a different line of work generalizes the univariate Poisson by assuming the univariate node-conditional distributions are derived from the Poisson^{10;79;80;82;31;32}. Like the assumption of Poisson marginals in previous sections, this conditional Poisson assumption seems a different yet natural extension of the univariate Poisson distribution. The multivariate Gaussian can be seen to satisfy such a conditional property since the node-conditional distributions of a multivariate Gaussian are univariate Gaussian. One benefit of these conditional models is that they can be seen as undirected graphical models or Markov Random Fields, and they have a simple parametric form. In addition, estimating these models generally reduces to estimating simple node-wise regressions, and some of these estimators have theoretical guarantees on estimating the global graphical model structure even under high-dimensional sampling regimes, where the number of variables (d) is potentially even larger than the number of samples (n).

Background on Exponential Family Distributions

We briefly describe exponential family distributions and graphical models which form the basis for the conditional Poisson models. Many commonly used distributions fall into this family, including Gaussian, Bernoulli, exponential, gamma, and Poisson, among others. The exponential family is specified by a vector of sufficient statistics denoted by T(x) ≡ [T₁(x), T₂(x), ⋯, T_m(x)], the log base measure B(x) and the domain of the random variable $\mathcal{D}$. With this notation, the generic exponential family is defined as:

$$\begin{array}{l}{\mathrm{\mathbb{P}}}_{\text{ExpFam}}\left(\mathit{x}|\mathit{\eta }\right)=\exp \left({\displaystyle \sum _{i=1}^m{\eta }_i{T}_i\left(\mathit{x}\right)=B\left(\mathit{x}\right)-A\left(\mathit{\eta }\right)}\right)\\ A\left(\mathit{\eta }\right)=\log {\displaystyle {\int }_{\mathcal{D}}\exp \left({\displaystyle \sum _{i=1}^m{\eta }_i{T}_i\left(\mathit{x}\right)+B\left(\mathit{x}\right)}\right)\mathrm{d}\mu \left(\mathit{x}\right)},\end{array}$$

where η are called the natural or canonical parameters of the distribution, μ is the Lebesgue or counting measure depending on whether $\mathcal{D}$ is continuous or discrete respectively, and A(η) is called the log partition function or log normalization constant because it normalizes the distribution over the domain $\mathcal{D}$. Note that the sufficient statistics ${\left\{T_i\right(\mathit{x}\left)\right\}}_{i=1}^m$ can be any arbitrary function of x; for example, T_i(x) = x₁x₂ could be used to model interaction between x₁ and x₂. The log partition function A(η) will be a key quantity when discussing the following models: A(η) must be finite for the distribution to be valid, so that the realizable domain of parameters is given by $\{\mathit{\eta }\in \mathcal{D}\text{:}A\left(\mathit{\eta }\right)<\mathrm{\infty }\}$. Thus, for instance, if the realizable domain only allows positive or negative interaction terms, then the set of allowed dependencies would be severely restricted.

Let us now consider the exponential family form of the univariate Poisson:

$$\begin{array}{l}{\mathrm{\mathbb{P}}}_{\text{Poiss}}\left(x|\mathrm{\lambda }\right)={\mathrm{\lambda }}^x\exp \left(-\mathrm{\lambda }\right)/x!\\ =\exp \left(\log \left({\mathrm{\lambda }}^x\right)-\log \left(x!\right)-\mathrm{\lambda }\right)\\ =\exp (\underset{\eta }{\underbrace{\log \left(\mathrm{\lambda }\right)}}\underset{T\left(x\right)}{\underbrace{x}}+\underset{B\left(x\right)}{\underbrace{\left(-\log \left(x!\right)\right)}}-\mathrm{\lambda }),\text{and therefore}\\ {\mathrm{\mathbb{P}}}_{\text{Poiss}}\left(x|\eta \right)=\exp \left(\eta x-\log \left(x!\right)-\exp \left(\eta \right)\right),\end{array}$$ (13)

where η ≡ log(λ) is the natural parameter of the Poisson, T(x) = x is the Poisson sufficient statistic, − log(x!) is the Poisson log base measure and A(η) = exp(η) is the Poisson log partition function. Note that for the general exponential family distribution, the log partition function may not have a closed form.

Background on Graphical Models

The graphical model over x given some graph $\mathcal{G}$—a set of nodes and edges—is a set of distributions on x that satisfy the Markov independence assumptions with respect to $\mathcal{G}$⁴⁸. In particular, an undirected graphical model gives a compact way to represent conditional independence among random variables—the Markov properties of the graph. Conditional independence relaxes the notion of full independence by defining which variables are independent given that other variables are fixed or known.

More formally, let $\mathcal{G}=\left(\mathcal{V},\mathrm{ℰ}\right)$ be an undirected graph over d nodes in $\mathcal{V}$ corresponding d random variables in x where $\mathrm{ℰ}$ is the set of undirected edges connecting nodes in $\mathcal{V}$. By the Hammersley-Clifford theorem¹⁵, any such distribution has the following form:

$$\mathrm{\mathbb{P}}\left(\mathit{x}|\mathit{\eta }\right)=\exp \left({\displaystyle \sum _{C\in \mathcal{C}}{\eta }_C{T}_C\left({\mathit{x}}_C\right)-A\left(\mathit{\eta }\right)}\right)$$ (14)

where $\mathcal{C}$ is a set of cliques (fully-connected subgraphs) of $\mathcal{G}$ and T_C(x_C) are the clique-wise sufficient statistics. For example, if $C=\left\{1,2,3\right\}\in \mathcal{C}$, then there would be a term η_1,2,3T_1,2,3(x₁, x₂, x₃) which involves the first, second and third random variables in x Hence, a graphical model can be understood as an exponential family distribution with the form given in Eq. 14. An important special case—which will be the focus in this paper—is a pairwise graphical model, where $\mathcal{C}$ consists of merely $\mathcal{V}$ and $\mathrm{ℰ}$—i.e. |C|={1,2}, $\forall C\in \mathcal{C}$, so that we have

$$\mathrm{\mathbb{P}}\left(\mathit{x}|\mathit{\eta }\right)=\exp \left({\displaystyle \sum _{i\in \mathcal{V}}{\eta }_i{T}_i\left(x_i\right)}+{\displaystyle \sum _{\left(i,j\right)\in \mathrm{ℰ}}{\eta }_{ij}{T}_{ij}\left(x_i,x_j\right)-A\left(\mathit{\eta }\right)}\right).$$

Since graphical models provide direct interpretations on the Markov independence assumptions, for the Poisson-based graphical models in this section, we can easily investigate the conditional independence relationships between random variables rather than marginal correlations.

As an example, we will consider the Gaussian graphical model formulation of the standard multivariate normal distribution (for simplicity we will assume the mean vector is zero, i.e. μ = 0):

$$\begin{array}{lll}\mathbf{S}\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{d}\mathbf{a}\mathbf{r}\mathbf{d}\mathbf{F}\mathbf{o}\mathbf{r}\mathbf{m}\hfill & \iff \hfill & \mathbf{G}\mathbf{r}\mathbf{a}\mathbf{p}\mathbf{h}\mathbf{i}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{M}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}\mathbf{F}\mathbf{o}\mathbf{r}\mathbf{m}\hfill \\ \sum =-\frac{1}{2}{\mathrm{\Theta }}^{-1}\hfill & \iff \hfill & \mathrm{\Theta }=-\frac{1}{2}{\sum }^{-1}\hfill \end{array}$$ (15)

$$\begin{array}{lll}\mathrm{\mathbb{P}}\left(\mathit{x}\right|\sum )\propto \exp (-\frac{1}{2}{\mathit{x}}^T{\sum }^{-1}\mathit{x})\hfill & \iff \hfill & \mathrm{\mathbb{P}}\left(\mathit{x}\right|\mathrm{\Theta })\propto \exp ({\mathit{x}}^T\mathrm{\Theta }\mathit{x})\hfill \\ \hfill & \iff \hfill & =\exp \left({\displaystyle \sum _i{\theta }_{ii}{x}_i^2}+{\displaystyle \sum _{i\ne j}{\theta }_{ij}{x}_i{x}_j}\right).\hfill \end{array}$$ (16)

Note how Eq. 16 is related to Eq. 14 by setting η_i = θ_ii, η_ij = θ_ij, $T_i\left(x_i\right)=x_i^2$, T_ij(x_i, x_j) = x_ix_j and $\mathrm{ℰ}=\left\{\left(i,j\right):i\ne j,{\theta }_{ij}\ne 0\right\}$ — i.e. the edges in the graph correspond to the non-zeros in Θ. In addition, this example shows that the marginal moments—i.e. the covariance matrix Σ—are quite different from the graphical model parameters—i.e. the negative of the inverse covariance matrix $\mathrm{\Theta }=-\frac{1}{2}{\sum }^{-1}$. In general, for graphical models such as the Poisson graphical models defined in the next section, the transformation from the covariance to the graphical model parameter (Eq. 15) is not known in closed-form; in fact, this transformation is often very difficult to compute for non-Gaussian models⁷³. For more information about graphical models and exponential families see^45;73.

Poisson Graphical Model

The first to consider multivariate extensions constructed by assuming conditional distributions are univariate exponential family distributions, such as and including the Poisson distribution, was Besag¹⁰. In particular, suppose all node-conditional distributions—the conditional distribution of a node conditioned on the rest of the nodes—are univariate Poisson. Then, there is a unique joint distribution consistent with these node-conditional distributions under some conditions, and moreover this joint distribution is a graphical model distribution that factors according to a graph specified by the node-conditional distributions. In fact, this approach can be uniformly applicable for any exponential family beyond the Poisson distribution, and can be extended to more general graphical model settings^79;82 beyond the pairwise setting in¹⁰. The particular instance with the univariate Poisson as the exponential family underlying the node-conditional distributions is called a Poisson graphical model (PGM).³

Specifically, suppose that for every i ∈ {1, ⋯, d}, the node-conditional distribution is specified by univariate Poisson distribution in exponential family form as specified in Eq. 13:

$$\mathrm{\mathbb{P}}\left(x_i|{\mathit{x}}_{-i}\right)=\exp \left\{\psi \left({\mathit{x}}_{-i}\right)x_i-\log \left(x_i!\right)-\exp \left(\psi \left({\mathit{x}}_{-i}\right)\right)\right\},$$ (17)

where x_−i is the set of all x_j except x_i, and the function ψ(x_−i) is any function that depends on the rest of all random variables except x_i. Further suppose that the corresponding joint distribution on x factors according to the set of cliques $\mathcal{C}$ of a graph $\mathcal{G}$. Yang et al.⁸² then show that such a joint distribution consistent with the above node-conditional distributions exists, and moreover necessarily has the form

$$\mathrm{\mathbb{P}}\left(\mathit{x}|\mathit{\eta }\right)=\exp \left\{{\displaystyle \sum _{C\in \mathcal{C}}{\eta }_C}{\displaystyle \prod _{i\in C}{x}_i}+{\displaystyle \sum _{i=1}^d\log \left(x_i!\right)-A\left(\mathit{\eta }\right)}\right\},$$ (18)

where the function A(η) is the log-partition function on all parameters $\mathit{\eta }={\left\{{\eta }_C\right\}}_{C\in \mathcal{C}}$. The pairwise PGM, as a special case, is defined as follows:

$${\mathrm{\mathbb{P}}}_{\text{PGM}}\left(\mathit{x}|\mathit{\eta }\right)=\exp \left\{{\displaystyle \sum _{i=1}^d{\eta }_i{x}_i}+{\displaystyle \sum _{\left(i,j\right)\in \mathrm{ℰ}}{\eta }_{ij}{x}_i{x}_j}-{\displaystyle \sum _{i=1}^d\log \left(x_i!\right)-A_{\text{PGM}}\left(\mathit{\eta }\right)}\right\},$$ (19)

where $\mathrm{ℰ}$ is the set of edges of the graphical model and $\mathit{\eta }=\left\{{\eta }_1,{\eta }_2,\cdots ,{\eta }_d\right\}\cup \{{\eta }_{ij},\forall \left(i,j\right)\in \mathrm{ℰ}\}$. For notational simplicity and development of extensions to PGM, we will gather the node parameters η_i into a vector θ = [η₁, η₂, ⋯, η_d] ∈ ℝ^d and gather the edge parameters into a ·, symmetric matrix Φ ∈ ℝ^d×d such that ${\varphi }_{ij}={\varphi }_{ji}={\eta }_{ij}/2,\forall \left(i,j\right)\in \mathrm{ℰ}$ and ${\varphi }_{ij}=0,\forall \left(i,j\right)\notin \mathrm{ℰ}$. Note that for PGM, Φ has zeros along the diagonal. With this notation, the pairwise PGM can be equivalently represented in a compact vectorized form as:

$${\mathrm{\mathbb{P}}}_{\text{PGM}}\left(\mathit{x}|\mathit{\theta },\mathrm{\Phi }\right)=\exp \{{\mathit{\theta }}^T\mathit{x}+{\mathit{x}}^T\mathrm{\Phi }\mathit{x}-{\displaystyle {\sum }_{i=1}^d\log \left(x_i!\right)-A_{\text{PGM}}\left(\mathit{\theta },\mathrm{\Phi }\right)}\},$$ (20)

Parameter estimation in a PGM is naturally suggested by its construction: all of the PGM parameters in Eq. 20 can be estimated by considering the node-conditional distributions for each node separately, and solving an ℓ₁-regularized Poisson regression for each variable. In contrast to the previous approaches in the sections above, this parameter estimation approach is not only simple, but is also guaranteed to be consistent even under high dimensional sampling regimes, under some other mild conditions including a sparse graph structural assumption (see Yang et al.^79,82 for more details on the analysis). As in Poisson log-normal models, the parameters of PGM can be made to depend on covariates to allow for more flexible correlations⁸¹.

In spite of its simple parameter estimation method, the major drawback with this vanilla Poisson graphical model distribution is that it only permits negative conditional dependencies between variables:

Proposition 1 (Besag¹⁰)

Consider the Poisson graphical model distribution in Eq. 20. Then, for any parameters θ and Φ, A_PGM(θ, Φ) < +∞ only if the pairwise parameters are non-positive: ${\varphi }_{ij}\le 0,\forall \left(i,j\right)\in \mathrm{ℰ}$.

Intuitively, if any entry in Φ, say Φ_ij, is positive, the term Φ_ijx_ix_j in Eq. 20 would grow quadratically, whereas the log base measure terms −log(x_i!)− −log(x_j!) only decreases as O(x_i log x_i + x_j log x_j), so A(θ, Φ) → ∞ as x_i,x_j → ∞. Thus, even though the Poisson graphical model is a natural extension of the univariate Poisson distribution (from the node-conditional viewpoint), it entails a highly restrictive parameter space, with severely limited applicability. Thus, multiple PGM extensions attempt to relax this negativity restriction to permit positive dependencies as described next.

Extensions of Poisson Graphical Models

To circumvent the severe limitations of the PGM distribution which in particular only permits negative conditional dependencies, several extensions to PGM that permit a richer dependence structure have been proposed.

Truncated PGM

Because the negativity constraint is due in part to the infinite domain of count variable, a natural solution would be to truncate the domain of variables. It was Kaiser and Cressie³⁶ who first introduced an approach to truncate the Poisson distribution in the context of graphical models. Their idea was simply to use a Winsorized Poisson distribution for node-conditional distributions: x is a Winsorized Poisson if $z=\mathbb{I}(z\prime <R)z\prime +\mathbb{I}(z\prime \ge R)R$, where z′ is Poisson, $\mathbb{I}(\cdot )$ is an indicator function, and R is a fixed positive constant denoting the truncation level. However, Yang et al.⁸⁰ showed that Winsorized node-conditional distributions actually does not lead to a consistent joint distribution.

As an alternative way of truncation, Yang et al.⁸⁰ instead keep the same parametric form as PGM (Eq. 20) but merely truncate the domain to non-negative integers less than or equal to R—i.e. ${\mathcal{D}}_{\text{TPGM}}=\left\{0,1,\cdots ,R\right\}$, so that the joint distribution takes the form⁸²:

$${\mathrm{\mathbb{P}}}_{\text{TPGM}}\left(\mathit{x}\right)=\exp \left\{{\mathit{\theta }}^T\mathit{x}+{\mathit{x}}^T\mathrm{\Phi }\mathit{x}-{\displaystyle {\sum }_i\log \left(x_i!\right)-A_{\text{TPGM}}\left(\mathit{\theta },\mathrm{\Phi }\right)}\right\}.$$ (21)

As they show, the node-conditional distributions of this graphical model distribution belong to an exponential family that is Poisson-like, but with the domain bounded by R. Thus, the key difference from the vanilla Poisson graphical model (Eq. 20) is that the domain is finite, and hence the log partition function A_TPGM(·) only involves a finite number of summations. Thus, no restrictions are imposed on the parameters for the normalizability of the distribution.

Yang et al.⁸⁰ discuss several major drawbacks to TPGM. First, the domain needs to be bounded a priori, so that R should ideally be set larger than any unseen observation. Second, the effective range of parameter space for a non-degenerate distribution is still limited: as the truncation value R increases, the effective values of pairwise parameters become increasingly negative or close to zero—otherwise, the distribution can be degenerate placing most of its probability mass at 0 or R.

Quadratic PGM and Sub-Linear PGM

Yang et al.⁸⁰ also investigate the possibility of Poisson graphical models that (a) allows both positive and negative dependencies, as well as (b) allow the domain to range over all non-negative integers. As described previously, a key reason for the negative constraint on the pairwise parameters ϕ_ij in Eq. 20 is that the log base measure ${\displaystyle {\sum }_i\log (x_i!)}$ scales more slowly than the quadratic pairwise term x^T Φx where $\mathit{x}\in {\mathrm{\mathbb{Z}}}_{+}^d$. Yang et al.⁸⁰ thus propose two possible solutions: increase the base measure or decrease the quadratic pairwise term.

First, if we modify the base measure of Poisson distribution with “Gaussian-esque” quadratic functions (note that for the linear sufficient statistics with positive dependencies, the base measures should be quadratic at the very least⁸⁰), then the joint distribution, which they call a quadratic PGM, is normalizable while allowing both positive and negative dependencies⁸⁰:

$${\mathrm{\mathbb{P}}}_{\text{QPGM}}\left(\mathit{x}\right)=\exp \{{\mathit{\theta }}^T\mathit{x}+{\mathit{x}}^T\mathrm{\Phi }\mathit{x}-A_{\text{QPGM}}\left(\mathit{\theta },\mathrm{\Phi }\right)\}.$$ (22)

Essentially, QPGM has the same form as the Gaussian distribution, but where its domain is the set of non-negative integers. The key differences from PGM are that Φ can have negative values along the diagonal, and the Poisson base measure ${\displaystyle {\sum }_i-\log (x_i!)}$ is replaced by the quadratic term ${\displaystyle {\sum }_i{\varphi }_{ii}{x}_i^2}$. Note that a sufficient condition distribution to be normalizable is given by:

$${\mathit{x}}^T\mathrm{\Phi }\mathit{x}<-c{\Vert \mathit{x}\Vert }_2^2\forall \mathit{x}\in {\mathrm{\mathbb{Z}}}_{+}^d,$$ (23)

for some constant c > 0, which in turn can be satisfied if Φ is negative definite. One significant drawback of QPGM is that the tail is Gaussian-esque and thin rather than Poisson-esque and thicker as in PGM.

Another possible modification is to use sub linear sufficient statistics in order to preserve the Poisson base measure and possibly heavier tails. Consider the following univariate distribution over count-valued variables:

$$\mathrm{\mathbb{P}}\left(z\right)\propto \exp \left\{\theta T\left(z;R_0,R\right)-\log z!\right\},$$ (24)

which has the same base measure log z! as the Poisson, but with the following sub-linear sufficient statistics:

$$T\left(z;R_0,R\right)=\{\begin{array}{ll}z\hfill & \text{if }z\le R_0\hfill \\ -\frac{1}{2\left(R-R_0\right)}{z}^2+\frac{R}{R-R_0}x-\frac{R_0^2}{2\left(R-R_0\right)}\hfill & \text{if }{R}_0<z\le R\hfill \\ \frac{R+R_0}{2}\hfill & \text{if }z\ge R.\hfill \end{array}$$ (25)

For values of x up to R₀, T(x) increases linearly, while after R₀ its slope decreases linearly, and finally after R, T(x) becomes constant. The joint graphical model, which they call a sub-linear PGM (SPGM), specified by the node-conditional distributions belonging to the family in Eq. 24, has the following form:

$${\mathrm{\mathbb{P}}}_{\text{SPGM}}\left(\mathit{x}\right)=\exp \left\{{\mathit{\theta }}^{T}T\left(\mathit{x}\right)+T{\left(\mathit{x}\right)}^T\mathrm{\Phi }T\left(\mathit{x}\right)-{\displaystyle {\sum }_i-\log \left(x_i!\right)-A_{\text{SPGM}}\left(\mathit{\theta },\mathrm{\Phi }|R_0,R\right)}\right\},$$ (26)

where

$$A_{\text{SPGM}}\left(\mathit{\theta },\mathrm{\Phi }|R_0,R\right)=\log {\displaystyle \sum _{\mathit{x}\in {\mathrm{\mathbb{Z}}}_{+}}\exp \left\{{\mathit{\theta }}^{T}T\left(\mathit{x}\right)+T{\left(\mathit{x}\right)}^T\mathrm{\Phi }T\left(\mathit{x}\right)-{\displaystyle {\sum }_i\log \left(x_i!\right)}\right\}},$$ (27)

and T(x) is the entry-wise application of the function in Eq. 25. SPGM is always normalizable for ϕ_ij ∈ ℝ∀i ≠ j⁸⁰.

The main difficulty in estimating Poisson graphical model variants above with infinite domain is the lack of closed-form expressions for the log partition function, even just for the node-conditional distributions that are needed for parameter estimation. Yang et al.⁸⁰ propose an approximate estimation procedure that uses the univariate Poisson and Gaussian log partition functions as upper bounds for the node-conditional log-partition functions for the QPGM and SPGM models respectively.

Poisson Square Root Graphical Model

In the similar vein as SPGM in the earlier section, Inouye et al.³² consider the use of exponential families with square-root sufficient statistics. While they consider general graphical model families, their Poisson graphical model variant can be written as:

$${\mathrm{\mathbb{P}}}_{\text{SQR}}\left(\mathit{x}|\theta \right)=\exp \left\{{\mathit{\theta }}^T\sqrt{\mathit{x}}+{\sqrt{\mathit{x}}}^T\mathrm{\Phi }\sqrt{\mathit{x}}-{\displaystyle {\sum }_i\log \left(x_i!\right)-A_{\text{SQR}}\left(\mathit{\theta },\mathrm{\Phi }\right)}\right\},$$ (28)

where ϕ_ii can be non-zero in contrast to the zero diagonal of the parameter matrix in Eq. 20. As with PGM, when there are no edges (i.e. ϕ_ij = 0 ∀i ≠ j) and θ = 0, this reduces to the independent Poisson model. The node conditionals of this distribution have the form:

$$\mathrm{\mathbb{P}}\left(x_i|{\mathit{x}}_{-i}\right)\propto \exp \left\{{\varphi }_{ii}{x}_i+\left({\theta }_i+2{\varphi }_{i,-i}^T\sqrt{\mathit{x}-i}\right)\sqrt{x_i}-\log \left(x_i!\right)\right\},$$ (29)

where ϕ_i,_−i is the i-th column of Φ with the the i-th entry removed. This can be rewritten in the form of a two parameter exponential family:

$$\mathrm{\mathbb{P}}(x_i|{\eta }_1,{\eta }_2)=\exp \left\{{\eta }_1{x}_i+{\eta }_2\sqrt{x_i}-\log \left(x_i!\right)-A\left({\eta }_1,{\eta }_2\right)\right\},$$ (30)

where η₁ = ϕ_ii, ${\eta }_2={\theta }_i+2{\varphi }_{i,-i}^T\sqrt{{\mathit{x}}_{-i}}$ and A(η₁, η₂) is the log partition function. Note that a key difference with the PGM variants in the previous section is that the diagonal of Φ_SQR can be non-zero whereas the diagonal of Φ_PGM must be zero. Because the interaction term ${\sqrt{\mathit{x}}}^T\mathrm{\Phi }\sqrt{\mathit{x}}$ is asymptotically linear rather than quadratic, the Poisson SQR graphical model does not suffer from the degenerate distributions of TPGM as well as the FLPGM discussed in the next section, while still allowing both positive and negative dependencies.

To show that SQR graphical models can easily be normalized, Inouye et al.³² first define radial-conditional distributions. The radial-conditional distribution assumes the unit direction is fixed but the length of the vector is unknown. The difference between the standard 1D node conditional distributions and the 1D radial-conditional distributions is illustrated in Fig. 3. Suppose we condition on the unit direction $\mathbf{v}=\frac{\mathit{x}}{{\Vert \mathit{x}\Vert }_1}$ of the sufficient statistics but the scaling of this unit direction z = ║x║₁ is unknown. With this notation, Inouye et al.³² define the radial-conditional distribution as:

$$\begin{array}{r}\mathrm{\mathbb{P}}\left(\mathit{x}=z\mathbf{v}|\mathbf{v},\mathit{\theta },\mathrm{\Phi }\right)\propto \exp \left\{{\mathit{\theta }}^T\sqrt{z\mathbf{v}}+{\sqrt{z\mathbf{v}}}^T\mathrm{\Phi }\sqrt{z\mathbf{v}}-{\displaystyle {\sum }_i\log \left(\left(z{\upsilon }_i\right)!\right)}\right\}\\ \propto \exp \left\{\left({\mathit{\theta }}^T\mathbf{v}\right)\sqrt{z}+\left({\sqrt{\mathbf{v}}}^T\mathrm{\Phi }\sqrt{\mathbf{v}}\right)z-{\displaystyle {\sum }_i\log \left(\left(z{\upsilon }_i\right)!\right)}\right\}.\end{array}$$

Figure 3.

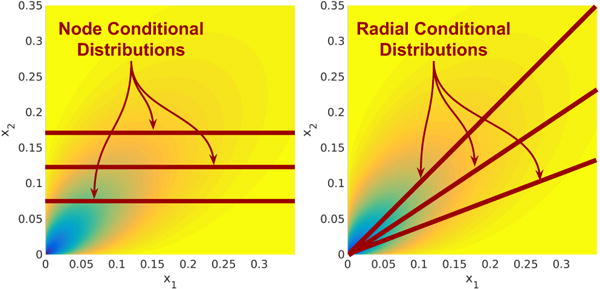
Node-conditional distributions (left) are univariate probability distributions of one variable conditioned on the other variables, while radial-conditional distributions are univariate probability distributions of the vector scaling conditioned on the vector direction. Both conditional distributions are helpful in understanding SQR graphical models. (Illustration from³².)

Similar to the node-conditional distribution, the radial-conditional distribution can be rewritten as a two parameter exponential family:

$$\mathrm{\mathbb{P}}\left(z|\mathbf{v},\mathit{\theta },\mathrm{\Phi }\right)=\exp (\underset{O\left(z\right)}{\underbrace{{\overline{\eta }}_{1}z+{\overline{\eta }}_2\sqrt{z}}}+\underset{O\left(-z\log \left(z\right)\right)}{\underbrace{{\stackrel{\sim }{B}}_{\mathbf{v}}\left(z\right)}}-A_{\text{rad}}\left({\overline{\eta }}_1,{\eta }_2\right)),$$ (31)

where ${\overline{\eta }}_1={\sqrt{\mathbf{v}}}^T\mathrm{\Phi }\sqrt{\mathbf{v}},{\overline{\eta }}_2={\mathit{\theta }}^T\mathbf{v}$, and ${\stackrel{\sim }{B}}_{\mathbf{v}}\left(z\right)=-{\displaystyle {\sum }_{i=1}^d\log \left(\left(z{\upsilon }_i\right)!\right)}$. The only difference between this exponential family and the node-conditional distribution is the different base measure—i.e. $-{\displaystyle {\sum }_{i=1}^d\log \left(\left(z{\upsilon }_i\right)!\right)\ne -\log \left(z!\right)}$. However, note that the log base measure is still O(−z log(z)) and thus, the base measure will overcome the linear term as z → ∞. Therefore, the radial-conditional distribution is normalizable for any ${\overline{\eta }}_1,{\overline{\eta }}_2\in \mathrm{ℝ}$.

With the radial-conditional distributions notation, Inouye et al.³² show that the log partition function for Poisson SQR graphical models is finite by separating the summation into a nested radial direction and scalar summation. Let $\mathcal{V}=\{\mathbf{v}:{\Vert \mathbf{v}\Vert }_1=1,\mathbf{v}\in {\mathrm{ℝ}}^d\}$ be the set of unit vectors in the positive orthant. The SQR log partition function A_SQR(θ, Φ) can be decomposed into nested summation over the unit direction and the one dimensional radial conditional:

$$A_{\text{SQR}}\left(\mathit{\theta },\mathrm{\Phi }\right)=\log {\displaystyle \underset{\mathbf{v}\in \mathcal{V}}{\int }{\displaystyle \sum _{z\in \widehat{\mathrm{\mathbb{Z}}}}\exp \left\{{\overline{\eta }}_1\left(\mathbf{v}|\mathrm{\Phi }\right)z+{\overline{\eta }}_2\left(\mathbf{v}|\mathit{\theta }\right)\sqrt{z}-{\displaystyle {\sum }_i\log \left(z{\upsilon }_i!\right)}\right\}\mathrm{d}\mathbf{v}}},$$ (32)

where ${\overline{\eta }}_1\left(\mathbf{v}|\mathrm{\Phi }\right)$ and ${\overline{\eta }}_2\left(\mathbf{v}|\mathit{\theta }\right)$ are the radial conditional parameters as defined above and $\widehat{\mathrm{\mathbb{Z}}}=\left\{z:z\mathbf{v}\in {\mathrm{\mathbb{Z}}}_{+}^d\right\}$. Note that $\widehat{\mathrm{\mathbb{Z}}}\subset \mathrm{\mathbb{Z}}$, and thus the inner summation can be replaced by the radial-conditional log partition function. Therefore, because $\mathcal{V}$ is a bounded set and the radial-conditional log partition function is finite for any ${\overline{\eta }}_1\left(\mathbf{v}|\mathit{\theta }\right)$ and ${\overline{\eta }}_2\left(\mathbf{v}|\mathrm{\Phi }\right)$, A_SQR < ∞ and the Poisson SQR joint distribution is normalizable.

The main drawback to the Poisson SQR is that for parameter estimation, the log partition function A(η₁, η₂) of the node conditionals in Eq. 30 is not known in closed form in general. Inouye et al.³² provide a closed-form estimate for the exponential SQR but a closed-form solution for the Poisson SQR model seems unlikely to exist. Inouye et al.³² suggest numerically approximating A(η₁, η₂), since it only requires a one dimensional summation.

Local PGM

Inspired by the neighborhood selection technique of Meinshausen and Bühlmann⁵⁵, Allen and Liu^4,5 propose to estimate the network structure of count-valued data by fitting a series of ℓ₁-regularized Poisson regressions to estimate the node-neighborhoods. Such an estimation method may yield interesting network estimates, but as Allen and Liu⁵ note, these estimates do not correspond to a consistent joint density. Instead, the underlying model is defined in terms of a series of local models where each variable is conditionally Poisson given its node-neighbors; this approach is thus termed the local Poisson graphical model (LPGM). Note that LPGM does not impose any restrictions on the parameter space or types of dependencies; if the parameter space of each local model was constrained to be non-positive, then the LPGM reduces to the vanilla Poisson graphical model as previously discussed. Hence, the LPGM is less interesting as a candidate multivariate model for count-valued data, but many may still find its simple and interpretable network estimates appealing. Recently, several have proposed to adopt this estimation strategy for alternative network types^25;26.

Fixed-Length Poisson MRFs

In a somewhat different direction, Inouye et al.³¹ propose a distribution that has the same parametric form as the original PGM, but allows positive dependencies by decomposing the joint distribution into two distributions. The first distribution is the marginal distribution over the length of the vector denoted ℙ(L)—i.e. the distribution of the ℓ₁-norm of the vector or the total sum of counts. The second distribution, the fixed-length Poisson graphical model (FLPGM), is the conditional distribution of PGM given the fact that the vector length L is known or fixed, denoted ℙ_FLPGM(x | ║x║₁ = L). Note that this allows the marginal distribution on length and the distribution given the length to be specified independently.⁴ The restriction to negative dependencies is removed because the second distribution given the vector length ℙ_FLPGM(x | ║x║₁ = L) has a finite domain ${\mathcal{D}}_{\text{FLPGM}}=\left\{\mathit{x}:\mathit{x}\in {\mathrm{\mathbb{Z}}}_{+}^d,{\Vert \mathit{x}\Vert }_1=L\right\}$ and is thus trivially normalizable—similar to the normalizability of the finite-domain TPGM. More formally, Inouye et al.³¹ defined the FLPGM as:

$$\mathrm{\mathbb{P}}\left(\mathit{x}|\mathit{\theta },\mathrm{\Phi },\mathrm{\lambda }\right)=\mathrm{\mathbb{P}}\left(L|\mathrm{\lambda }\right){\mathrm{\mathbb{P}}}_{\text{FLPGM}}(\mathit{x}|{\Vert \mathit{x}\Vert }_1=L,\mathit{\theta },\mathrm{\Phi }),$$ (33)

$${\mathrm{\mathbb{P}}}_{\text{FLPGM}}(\mathit{x}|{\Vert \mathit{x}\Vert }_1=L,\mathit{\theta },\mathrm{\Phi })=\exp \{{\mathit{\theta }}^T\mathit{x}+{\mathit{x}}^T\mathrm{\Phi }\mathit{x}-{\displaystyle {\sum }_i\log \left(x_i!\right)-A_L\left(\mathit{\theta },\mathrm{\Phi }\right)}\},$$ (34)

where λ is the parameter for the marginal length distribution—which could be Poisson, negative binomial or any other distribution on nonnegative integers. In addition, FLPGM could be used as a replacement for the multinomial distribution because it has the same domain as the multinomial and actually reduces to the multinomial if there are no dependencies. Earlier, Altham and Hankin⁷ developed an identical model by generalizing an earlier bivariate generalization of the binomial⁶. However, in^7;6, the model assumed that L was constant over all samples, whereas³¹ allowed for L to vary for each sample according to some distribution ℙ(L).

One significant drawback is that FLPGM is not amenable to the simple node-wise parameter estimation method of the previous PGM models. Nonetheless, in Inouye et al.³¹, the parameters are heuristically estimated with Poisson regressions similar to PGM, though the theoretical properties of this heuristic estimate are unknown. Another drawback is that while FLPGM allows for positive dependencies, the distribution can yet yield a degenerate distribution for large values of L—similar to the problem of TPGM where the mass is concentrated near 0 or R. Thus, Inouye et al.³¹ introduce a decreasing weighting function ω(L) that scales the interaction term:

$$\begin{array}{l}{\mathrm{\mathbb{P}}}_{\text{FLPGM}}(\mathit{x}|{\Vert \mathit{x}\Vert }_1=L,\mathit{\theta },\mathrm{\Phi },\omega (\cdot ))\\ =\exp \left\{{\mathit{\theta }}^T\mathit{x}+\omega \left(L\right){\mathit{x}}^T\mathrm{\Phi }\mathit{x}-{\displaystyle {\sum }_i\log \left(x_i!\right)-A_L\left(\mathit{\theta },\omega \left(L\right)\mathrm{\Phi }\right)}\right\}.\end{array}$$ (35)

While the log-likelihood is not available in tractable form, Inouye et al.³¹ approximate the log likelihood using annealed importance sampling⁵⁸, which might be applicable to the extensions covered previously as well.

Summary of Conditional Poisson Generalizations

The conditional Poisson models benefit from the rich literature in exponential families and undirected graphical models, or Markov Random Fields. In addition, the conditional Poisson models have a simple parametric form. The historical Poisson graphical model—or the auto-Poisson model¹⁰)—only allowed negative dependencies between variables. Multiple extensions have sought to overcome this severe limitation by altering the Poisson graphical model so that the log partition function is finite even with positive dependencies. One major drawback to graphical model approach is that computing the likelihood requires approximation of the joint log partition function A(θ, Φ); a related problem is that the distribution moments and marginals are not known in closed-form. Despite these drawbacks, parameter estimation using composite likelihood methods via ℓ₁-penalized node-wise regressions (in which the joint likelihood is not computed) has solid theoretical properties under certain conditions.

Model Comparison

We compare models by first discussing two structural aspects of the models: (a) interpretability and (b) the relative stringency and ease of verifying theoretical assumptions and guarantees. We then present and discuss an empirical comparison of the models on three real-world datasets.

Comparison of Model Interpretation

Marginal models can be interpreted as weakly decoupling modeling marginal distributions over individual variables, from modeling the dependency structure over the variables. However, in the discrete case, specifically for distributions based on pairing copulas with Poisson marginals, the dependency structure estimation is also dependent on the marginal estimation, unlike for copulas paired with continuous marginals²². Conditional models or graphical models, on the other hand, can be interpreted as specifying generative models for each variable given the variable’s neighborhood (i.e. the conditional distribution). In addition, dependencies in graphical models can be visualized and interpreted via networks. Here, each variable is a node and the weighted edges in the network structure depict the pair-wise conditional dependencies between variables. The simple network depiction for graphical models may enable domain experts to interpret complex dependency structures more easily compared to other models. Overall, marginal models may be preferred if modeling the statistics of the data, particularly the marginal statistics over individual variables, is of primary importance, while conditional models may be preferred if prediction of some variables given others is of primary importance. Mixture models may be more or less difficult to interpret depending on whether there is an application-specific interpretation of the latent mixing variable. For example, a finite mixture of two Poisson distributions may model the crime statistics of a city that contains downtown and suburban areas. On the other hand, a finite mixture of fifty Poisson distributions or a log-normal Poisson mixture when modeling crash severity counts (as seen in the empirical comparison section) seems more difficult to interpret; even the model empirically well fits the data, the hidden mixture variable might not have an obvious application-specific interpretation.

Comparison of Theoretical Considerations

Estimation of marginal models from data has various theoretical problems, as evidenced by the analysis of copulas paired with discrete marginals in²². The extent to which these theoretical problems cause any significant practical issues remains unclear. In particular, the estimators of the marginal distributions themselves typically have easily checked assumptions since the empirical marginal distributions can be inspected directly. On the other hand, the estimation of conditional models is both computationally tractable, and comes with strong theoretical guarantees even under high-dimensional regimes where n < d⁸². However the assumptions under which the guarantees of the estimators hold are difficult to check in practice, and could cause problems if they are violated (e.g. outliers caused by unobserved factors). Estimation of mixture models tend to have limited theoretical guarantees. In particular, finite Poisson mixture models have very weak assumptions on the underlying distribution—eventually becoming a non-parametric distribution if k = O(n)—but the estimation problems are likely NP-hard, with very few theoretical guarantees for practical estimators. Yet, empirically as seen in the next section, estimating a finite mixture model using Expectation-Maximization iterations performs well in practice.

Empirical Comparison

In this section, we seek to empirically compare models from the three classes presented to assess how well they fit real-world count data.

Comparison Experimental Setup

We empirically compare models on selected datasets from three diverse domains which have different data characteristics in terms of their mean count values and dispersion indices (Eq. 5) as can be seen in Table 1. The crash severity dataset is a small accident dataset from⁵⁶ with three different count variables corresponding to crash severity classes: “Property-only”, “Possible Injury”, and “Injury”. The crash severity data exhibits high count values and high overdispersion. We retrieve raw next generation sequencing data for breast cancer (BRCA) using the software TCGA2STAT⁷⁴ and computed a simple log-count transformation of the raw counts: ⌊log(x + 1)⌋, a common preprocessing technique for RNA-Seq data. The BRCA data exhibits medium counts and medium overdispersion. We collect the word count vectors from the Classic3 text corpus which contains abstracts from aerospace engineering, medical and information sciences journals.⁵ The Classic3 dataset exhibits low counts—including many zeros—and medium overdispersion. In the supplementary material, we also give results for a crime statistics dataset and the 20 Newsgroup dataset but they have similar characteristics and perform similarly to the the BRCA and Classic3 datasets respectively; thus, we omit them for simplicity. We select variables (e.g. for d = 10 or d = 100) by sorting the variables by mean count value—or sorting by variance in the case of the BRCA dataset as highly variable genes are of more interest in biology.

Table 1.

Dataset Statistics

Dataset	(Per Variable ⇒)		Means			Dispersion Indices			Spearman’s ρ
	d	n	Min	Med	Max	Min	Med	Max	Min	Med	Max
Crash Severity	3	275	3.4	3.8	9.7	6	9.3	16	0.61	0.73	0.79
BRCA	10	878	3.2	5	7.7	1.5	2.2	3.8	−0.2	0.25	0.95
	100	878	1.1	4	9	0.63	1.7	4.6	−0.5	0.08	0.95
	1000	878	0.51	3.5	11	0.26	1	4.6	−0.64	0.06	0.97
Classic3	10	3893	0.26	0.33	0.51	1.4	3.4	3.8	−0.17	0.12	0.82
	100	3893	0.09	0.14	0.51	1.1	2.1	8.3	−0.17	0.02	0.82
	1000	3893	0.02	0.03	0.51	0.98	1.7	8.5	−0.17	−0	0.82

In order to understand how each model might perform under varying data characteristics, we consider the following two questions: (1) How well does the model (i.e. the joint distribution) fit the underlying data distribution? (2) How well does the model capture the dependency structure between variables? To help answer these questions, we evaluate the empirical fit of models using two metrics, which only require samples from the model. The first metric is based on a statistic called maximum mean discrepancy (MMD)²⁴ which estimates the maximum moment difference over all possible moments. The empirical MMD can be approximated as follows from two sets of samples $X\in {\mathrm{ℝ}}^{n_1\times d}$ and $Y\in {\mathrm{ℝ}}^{n_2\times d}$:

$$\widehat{\text{MMD}}\left(\mathcal{G},X,Y\right)=\underset{f\in \mathcal{G}}{\sup }\frac{1}{n_1}{\displaystyle \sum _{i=1}^{n_1}f\left({\mathit{x}}_i\right)-\frac{1}{n_2}{\displaystyle \sum _{j=1}^{n_2}f({\mathit{y}}_j)}},$$ (36)

where $\mathcal{G}$ is the union of the RKHS spaces based on the Gaussian kernel using twenty one σ values log-spaced between 0.01 and 100. In our experiments, we estimate the MMD between the pairwise marginals of model samples and the pairwise marginals of the original observations:

$$D_{st}^{\text{MMD}}=\{\begin{array}{ll}\widehat{\text{MMD}}(\mathcal{G},[{\mathit{x}}^{\left(s\right)}],[{\widehat{\mathit{x}}}^{\left(s\right)}]),\hfill & s=t\hfill \\ \widehat{\text{MMD}}(\mathcal{G},[{\mathit{x}}^{\left(s\right)},{\mathit{x}}^{\left(t\right)}],[{\widehat{\mathit{x}}}^{\left(s\right)},{\widehat{\mathit{x}}}^{\left(t\right)}]),\hfill & \text{otherwise}\hfill \end{array}.$$ (37)

where x^(s) is the vector of data for the s-th variable of the true data and ${\widehat{\mathit{x}}}^{\left(s\right)}$ is the vector of data for the s-th variable of samples from the estimated model—i.e. x^(s) are observations from the true underlying distribution and ${\widehat{\mathit{x}}}^{\left(s\right)}$ are samples from the estimated model distribution. In our experiments, we use the fast approximation code for MMD from⁸⁴ with 2⁶ number of basis vectors for the FastMMD approximation algorithm. The second metric merely computes the absolute difference between the pairwise Spearman’s ρ values of model samples and the Spearman’s ρ values of the original observations:

$$D_{st}^{\rho }=|\rho ({\mathit{x}}^{\left(s\right)},{\mathit{x}}^{\left(t\right)})-\rho ({\widehat{\mathit{x}}}^{\left(s\right)},{\widehat{\mathit{x}}}^{\left(t\right)})|,\forall s,t.$$ (38)

The MMD metric is of more general interest because it evaluates whether the models actually fit the empirical data distribution while the Spearman metric may be more interesting for practitioners who primarily care about the dependency structure, such as biologists who specifically want to study gene dependencies rather than gene distributions.

We empirically compare the model fits on these real-world data sets for several types of models from the three general classes presented. As a baseline, we estimate an independent Poisson model (“Ind Poisson”). We include Gaussian copulas and vine copulas both paired with Poisson marginals (“Copula Poisson” and “Vine Poisson”) to represent the marginal model class. We estimate the copula-based models via the two-stage Inference Functions for Margins (IFM) method³⁴ via the distributional transform⁶⁵. For the mixture class, we include both a simple finite mixture of independent Poissons (“Mixture Poiss”) and a log-normal mixture of Poissons (“Log-Normal”). The finite mixture was estimated using a simple expectation-maximization (EM) algorithm; the log-normal mixture model was estimated via MCMC sampling using the code from⁸³. For the conditional model class, we estimate the simple Poisson graphical model (“PGM”), which only allows negative dependencies, and three variants that allow for positive dependencies: the truncated Poisson graphical model (“Truncated PGM”), the Fixed-Length Poisson graphical model with a Poisson distribution on the vector length L = ║x║₁ (“FLPGM Poisson”) and the Poisson square root graphical model (“Poisson SQR”). Using composite likelihood methods of penalized ℓ₁ node-wise regressions, we estimate these models via code from^82,30,33 and the XMRF⁶ R package. After parameter estimation, we generate 1,000 samples for each method using different types of sampling for each of the model classes.

To avoid overfitting to the data, we employ 3-fold cross-validation and report the average over the three folds. Because the conditional models (PGM, TPGM, FLPGM, and Poisson SQR) can be significantly different depending on the regularization parameter—i.e. the weight for the ℓ₁ regularization term in the objective function for these models—, we select the regularization parameter of these models by computing the metrics on a tuning split of the training data. For the mixture model, we similarly tune the number of components k by testing k = {10, 20, 30, ⋯, 100}. For the very high dimensional datasets where d = 1000, we use a regularization parameter near the tuning parameters found when d = 100 and fix k = 50 in order to avoid the extra computation of selecting a parameter. More sampling and implementation details for each model are available in the supplementary material.

Empirical Comparison Results

The full results for both the MMD and Spearman’s ρ metrics for the crash severity, breast cancer RNA-Seq and Classic3 text datasets can be seen in Fig. 4, Fig. 5, and Fig. 6 respectively. The low dimensional results (d ≤ 10) give evidence across all the datasets that three models outperform the others in their classes:⁷ The Gaussian copula paired with Poisson marginals model (“Copula Poisson”) for the marginal model class, the mixture of Poissons distribution (“Mixture Poiss”) for the mixture model class, and the Poisson SQR distribution (“Poisson SQR”) for the conditional model class. Thus, we only include these representative models along with an independent Poisson baseline in the high-dimensional experiments when d > 10. We discuss the results for specific data characteristics as represented by each dataset.⁸

Figure 4.

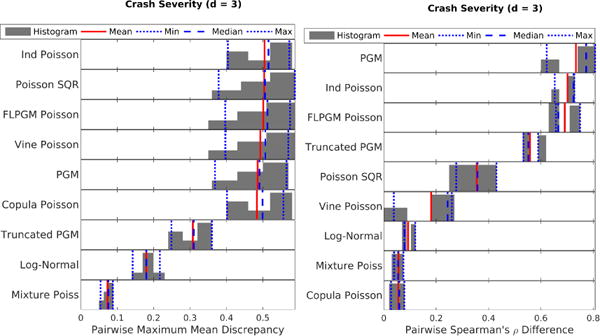
Crash severity dataset (high counts and high overdispersion): MMD (left) and Spearman ρ’s difference (right). As expected, for high overdispersion, mixture models (“Log-Normal” and “Mixture Poiss”) seem to perform the best.

Figure 5.

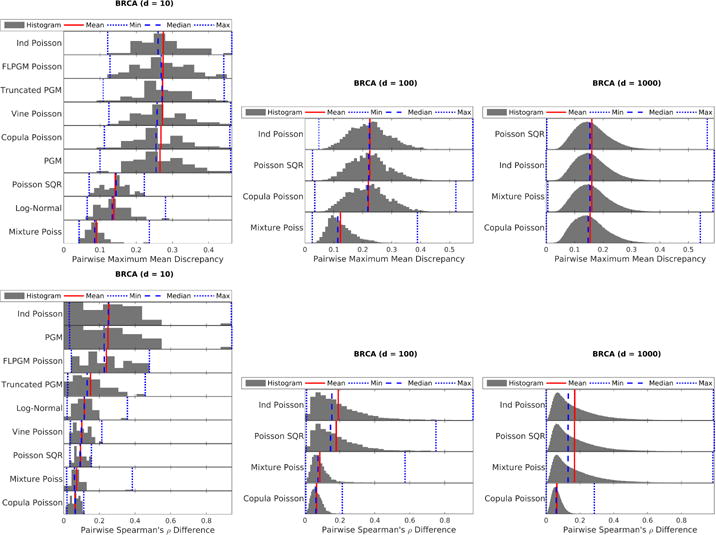
BRCA RNA-Seq dataset (medium counts and medium overdispersion): MMD (top) and Spearman ρ’s difference (bottom) with different number of variables: 10 (left), 100 (middle), 1000 (right). While mixtures (“Log-Normal” and “Mixture Poiss”) perform well in terms of MMD, the Gaussian copula paired with Poisson marginals (“Copula Poisson”) can model dependency structure well as evidenced by the Spearman metric.

Figure 6.

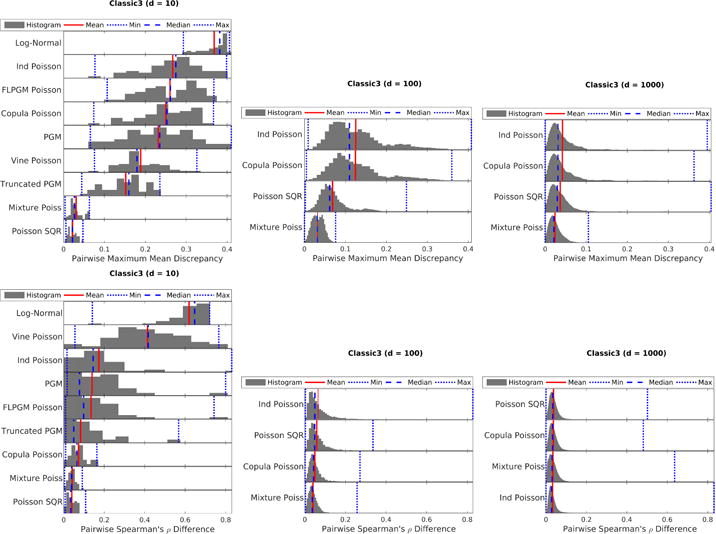
Classic3 text dataset (low counts and medium overdispersion): MMD (top) and Spearman ρ’s difference (bottom) with different number of variables: 10 (left), 100 (middle), 1000 (right). The Poisson SQR model performs better on this low count dataset than in previous settings.

For the crash severity dataset with high counts and high overdispersion (Fig. 4), mixture models (i.e. “Log-Normal” and “Mixture Poiss”) perform the best as expected since they can model overdispersion well. However, if dependency structure is the only object of interest, the Gaussian copula paired with Poisson marginals (“Copula Poisson”) performs well. For the BRCA dataset with medium counts and medium overdispersion (Fig. 5), we note similar trends with two notable exceptions: (1) The Poisson SQR model actually performs reasonably in low dimensions suggesting that it can model moderate overdispersion. (2) The high dimensional (d ≥ 100) Spearman’s ρ difference results show that the Gaussian copula paired with Poisson marginals (“Copula Poisson”) performs significantly better than the mixture model; this result suggests that copulas paired with Poisson marginals are likely better for modeling dependencies than mixture models. Finally, for the Classic3 dataset with low counts and medium overdispersion (Fig. 6), the Poisson SQR model seems to perform well in this low-counts setting especially in low dimensions unlike in previous data settings. While the simple independent mixture of Poisson distributions still performs well, the Poisson log-normal mixture distribution (“Log-Normal”) performs quite poorly in this setting with small counts and many zeros. This poor performance of the Poisson log-normal mixture is somewhat surprising since the dispersion indices are almost all greater than one as seen in Table 1. The differing results between low counts and medium counts with similar overdispersion demonstrate the importance to consider both the overdispersion and the mean count values when characterizing a dataset.

In summary, we note several overall trends. Mixture models are important for overdispersion when counts are medium or high. The Gaussian copula with Poisson marginals joint distribution can estimate dependency structure (per the Spearman metric) for a wide range of data characteristics even when the distribution does not fit the underlying data (per the MMD metric). The Poisson SQR model performs well for low count values with many zeros (i.e. sparse data) and may be able to handle moderate overdispersion.

Discussion

While this review analyzes each model class separately, it would be quite interesting to consider combinations or synergies between the model classes. Because negative binomial distributions can be viewed as a gamma-Poisson mixture model, one simple idea is to consider pairing a copula with negative binomial marginals or developing a negative binomial SQR graphical model. As another example, we could form a finite mixture of copula-based or graphical-model-based models. This might combine the strengths of a mixture in handling multiple modes and overdispersion with the strengths of the copula-based models and graphical models which can explicitly model dependencies.

We may also consider how one type of model informs the other. For example, by the generalized Sklar’s theorem⁶⁵, each conditional Poisson graphical model actually induces a copula—just as the Gaussian graphical model induces the Gaussian copula. Studying the copulas induced by graphical models seems to be a relatively unexplored area. On the other side, it may be useful to consider fitting a Gaussian copula paired with discrete marginals using the theoretically-grounded techniques from graphical models for sparse dependency structure estimation especially for the small sample regimes in which d > n; this has been studied for the case of continuous marginals in⁴⁹. Overall, bringing together and comparing these diverse paradigms for probability models opens up the door for many combinations and synergies.

Conclusion

We have reviewed three main approaches to constructing multivariate distributions derived from the Poisson using three different assumptions: 1) the marginal distributions are derived from the Poisson, 2) the joint distribution is a mixture of independent Poisson distributions, and 3) the node-conditional distributions are derived from the Poisson. The first class based on Poisson marginals, and in particular the general approach of pairing copulas with Poisson marginals, provides an elegant way to partially⁹ decouple the marginals from the dependency structure and gives strong empirical results despite some theoretical issues related to non-uniqueness. While advanced methods to estimate the joint distribution of copulas paired with discrete marginals such as simulated likelihood⁶¹ or vine copula constructions provide more accurate or more flexible copula models respectively, our empirical results suggest that a simple Gaussian copula paired with Poisson marginals with the trivial distributional transform (DT) can perform quite well in practice. The second class based on mixture models can be particularly helpful for handling overdispersion that often occurs in real count data with the log-normal-Poisson mixture and a finite mixture of independent Poisson distributions being prime examples. In addition, mixture models have closed-form moments and in the case of a finite mixture, closed-form likelihood calculations—something not generally true for the other classes. The third class based on Poisson conditionals can be represented as graphical models, thus providing both compact and visually appealing representations of joint distributions. Conditional models benefit from strong theoretical guarantees about model recovery given certain modeling assumptions. However, checking conditional modeling assumptions may be impossible and may not always be satisfied for real-world count data. From our empirical experiments, we found that (1) mixture models are important for overdispersion when counts are medium or high, (2) the Gaussian copula with Poisson marginals joint distribution can estimate dependency structure for a wide range of data characteristics even when the distribution does not fit the underlying data, and (3) Poisson SQR models perform well for low count values with many zeros (i.e. sparse data) and can handle moderate overdispersion. Overall, in practice, we would recommend comparing the three best performing methods from each class: namely the Gaussian copula model paired with Poisson marginals, the finite mixture of independent Poisson distributions, and the Poisson SQR model. This initial comparison will likely highlight some interesting properties of a given dataset and suggest which class to pursue in more detail.

This review has highlighted several key strengths and weaknesses of the main approaches to constructing multivariate Poisson distributions. Yet, there remain many open questions. For example, what are the marginal distributions of the Poisson graphical models which are defined in terms of their conditional distributions? Or conversely, what are the conditional distributions of the copula models which are defined in terms of their marginal distributions? Can novel models be created at the intersection of these model classes that could combine the strengths of different classes as suggested in the discussion section? Could certain model classes be developed in an application area that has been largely dominated by another model class? For example, graphical models are well-known in the machine learning literature while copula models are well-known in the financial modeling literature. Overall, multivariate Poisson models are poised to increase in popularity given the wide potential applications to real-world high-dimensional count-valued data in text analysis, genomics, spatial statistics, economics, and epidemiology.