Computer modeling for pharmacological treatments for dystonia

Abstract

Dystonia is a movement disorder that produces involuntary muscle contractions. Current pharmacological treatments are of limited efficacy. Dystonia, like epilepsy is a disorder involving excessive activty of motor areas including motor cortex and several causal gene mutations have been identified. In order to evaluate potential novel agents for multitarget therapy for dystonia, we have developed a computer model of cortex that includes some of the complex array of molecular interactions that, along with membrane ion channels, control cell excitability.

Introduction

A number of movement disorders, as well as epilepsy are associated with increased activity, and likely with hyperexcitability, in cortex. Dystonia is a movement disorder which produces involuntary muscle contractions. It involves pathology in multiple brain areas including basal ganglia, thalamus, cerebellum, and sensory and motor cortices. Although much of the research in dystonia has looked at the role of the basal ganglia, pharmacological treatment is often provided directly to the muscle through injection of botulinum toxin, anticholinergic agents and benzodiazepines. Motor cortex is another possible target for drug therapy, with manifestations that include augmented beta oscillations. Using a mechanistic multiscale model of primary motor cortex, we have assessed parameter combinations that produce dystonia to suggest potential drug combinations that might interfere with these pathological dynamics.

Schematized and mechanistic models for dystonia

Dystonia is a movement disorder that produces intermittent prolonged involuntary muscle activation that results in twisting, turning or posturing of a limb or other body part and repetitive prolonged movements. As with other movement disorders, the difficulty in modeling dystonia stems from the complexity of the motor system itself: the large set of specialized nuclei in brain and spinal cord that are interacting to produce movement in continuous concert with sensory areas in the sensorimotor loop. These areas include basal ganglia, thalamus, cerebellum, red nucleus, anterior horn, etc. Even when a primary pathology can be localized to a particular area, plastic responses in other motor and sensory areas will alter the expression of the disease in a way that can either ameliorate or exacerbate disability, and treatments may target areas other than the area of primary pathology. For example, although task-specific focal dystonia such as writers cramp is thought to occur due to overlearning in sensory and motor cortical areas, some of the treatments used are targeting basal ganglia.

The large number of areas involved in motor activity would be best served by simulations that encompass all of these areas. Such an approach requires working out plausible input and output signal patterns for each nucleus or area, and then requires working with highly schematized models. Schematized models typically use mean-field approximations, where brain areas are approximated by scalar signals representing overall activity. Some schematized models may include more detailed integrate-and-fire or scalar (perceptron) neural network models (O’Reilly and Munakata, 2000; Eliasmith et al., 2012; Kerr et al., 2013). However, this intermediate modeling level also lacks the cell and molecular details useful for comparison with pharmacological intervention.

Sanger and Merzenich (2000) used a schematized model to identify likely patterns of positive feedback between sensory and motor cortical areas that would lead to runaway excitation. Their cortical control-theory model was able to identify particular dynamical patterns that could potentially be interrupted to prevent the recurrence of these pathological patterns. Interestingly, this provided some suggestion as to the mechanism of self-treatment using “sensory tricks”, where the patient relaxes the dystonia by touching a particular spot – e.g., often on the side of the chin to reduce the head-turning of torticollis. However, the limitation of this model, as for other schematized models, was that it could not suggest drugs or drug targets for treatment.

Mechanistic multiscale modeling is an alternative to schematized models that does afford the opportunity to reach down to the molecular scale of pharmacology and thereby assist in the development of novel treatments. These models will include more levels or scales than are included in the schematized model, and for purposes of drug discovery should include some molecular detail.

A mechanistic model of cortical hyperexcitability

Dystonia is a dynamical disorder that can be defined by its particular patterns of muscle activation. The excessive muscle activity of dystonia is a consequence of dynamical disorder in brain and spinal cord, associated with higher than normal activity patterns. To the extent that the disease is caused by cortical dysfunction, as assumed by control theory models (Sanger and Merzenich, 2000), we identify hyper-activity as a manifestation of hyperexcitability.

The major disorder of cortical hyperexcitability is epilepsy, manifested by seizures. In both epilepsy and dystonia, underlying causes will include changes or anomalies in ion channel and receptor densities, as well as in cortical wiring (Dyhrfjeld-Johnsen et al., 2009), which produce excitation/inhibition imbalances and with excessive cortical firing and excessive synchrony (Dupont et al., 1998; Lytton, 2008; Neymotin et al., 2010; Lytton et al., 2014; Lytton et al., 2014). The intensity, pattern, and spread of hyper-synchrony differs between epilepsy and dystonia. Electroencephalographic signatures of the two disorders also differs, with seizures characterized by powerful discharges that may be time locked to the movement while dystonia shows an increase in beta (12–25 Hz) oscillations (Crowell et al., 2012; Mallet et al., 2008; Jin et al., 2011). In addition to there being various patterns of hyperexcitability in cortex, there are various ways to produce hyperexcitability in silico.

We developed a mechanistic multiscale model of cortex (Fig. 1) in which we could identify patterns of activity for: 1. normal; 2. dystonia; 3. epileptiform (seizure) (Neymotin et al., 2016). Model scales ranged from molecular to network so as to permit us to associate potential pharmacological manipulations with alterations in network dynamics. These models therefore combine the domain of computational systems biology – molecular interactions, with the traditional approach to computational neuroscience – models of cells as electrically interacting units with only ion channels represented at the molecular level.

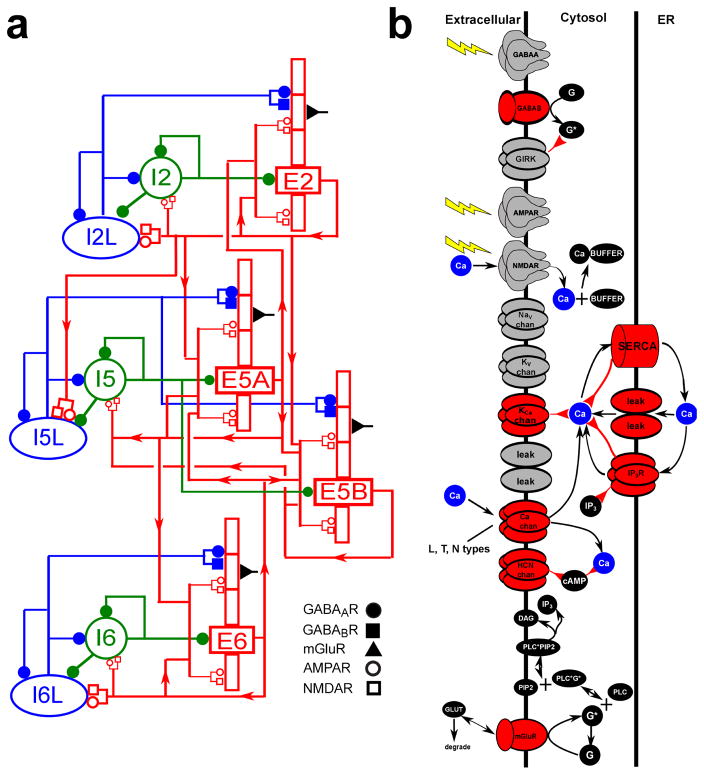
Figure 1. Schematic of cortical model showing (A) neuronal network connectivity; (B) molecular interactions in pyramidal cells.

(A) Red rectangles represent populations of 5-compartment excitatory cells (largest rectangle represents soma, 3 apical-dendrite compartments point upward, basal dendrite compartment points downward; multiple compartments allow more realistic spatial/temporal integration of synaptic inputs); green circles represent fast-spiking interneurons; blue ellipses represent low-threshold firing interneurons. Lines (with arrows) indicate connections between the populations. E cells synapse with AMPAR/NMDARs; I cells synapse with GABA_AR / GABA_BRs. Filled circles represent GABA_AR / GABA_BRs. Open circles and rectangles represent AMPAR/NMDARs. (B) Schematic of chemical signaling in pyramidal cells showing fluxes (black arrows) and second- (and third-etc) messenger modulation (red back-beginning arrows). We distinguish membrane-associated ionotropic and metabotropic receptors and ion channels involved in reaction schemes in red. External events are represented by yellow lightning bolts – there is no extracellular diffusion; the only extracellular reaction is glutamate binding, unbinding and degradation on mGluR1 after an event. Ca²⁺ is shown redundantly in blue – note that there is only one Ca²⁺ pool for extracellular, 1 pool for cytoplasmic, and 1 pool for ER. (PLC: phospholipase C, DAg: diacyl-glycerol, cAMP: cyclic adenosine monophosphate; PIP₂: phosphatidylinositol 4,5-bisphosphate).

Varying the densities of voltage-sensitive ion channels and receptor densities on pyramidal neurons and interneurons within reasonably ranges resulted in families of models that could be classified as having normal, dystonia-like, or epileptiform activity patterns (Fig. 2). Dystonia models were characterized by syn-chronous population discharges at beta frequency (~20 Hz). In each case, there were multiple parameter sets that produced similar dynamics (Golowasch et al., 2002; Prinz and Marder, 2003; Bucher et al., 2005; Prinz et al., 2004). This phenomenon is well known in biology where the combinatorics of multiple alleles for every feature, for every ion channel, enzyme and receptor, means that no two people are entirely alike. Despite not being alike, all people show similar dynamics, a phenomenon referred to as parameter degeneracy (Edelman and Gally, 2001).

Figure 2.

Raster plot showing 1 s patterns of normal activity (left column) compared to dystonia activity (right column) in multiple cortical models. Red, blue, green dots are from excitatory neurons, low-threshold spiking interneurons, and fast-spiking interneurons respectively. Spikes are arranged by cortical layer (Layers 2/3 at top, layer 6 at bottom). (Within each model, channel densities of neurons of a given type are identical.)

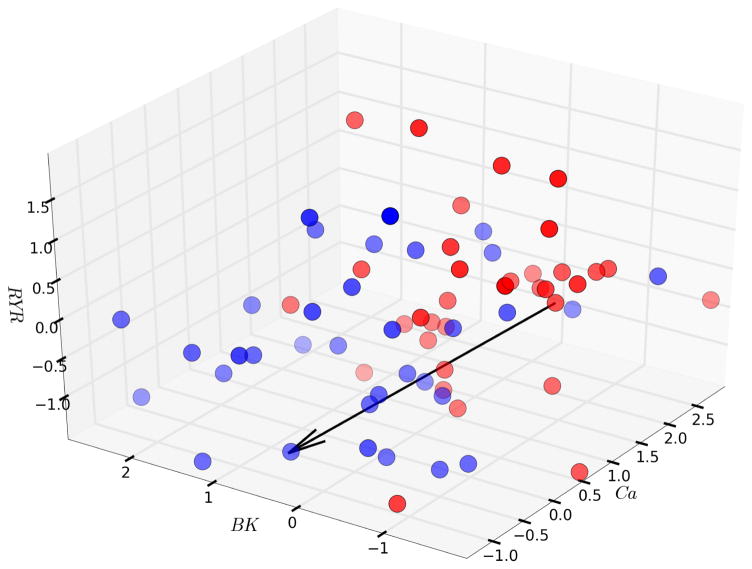
We locate particular models that produce dystonia in high-dimensional parameter space. A three-dimensional slice of the eleven-dimensional parameter space (Fig. 3), shown in a normalized space relative to a baseline value, demonstrated that dystonia cases tend to have higher levels of voltage-gated Ca²⁺ channels (L-, N-, T-types; labeled Ca), lower levels of BK K⁺ channels in the plasma membrane, and higher levels of ryanodine (RYR) channels in endoplasmic reticulum. In a particular case, we can indicate a direction in parameter space (Fig. 3, arrow) going from a dystonia parameter-set to a normal parameter-set. For any dystonic case in our set, we can identify a simple path, involving one or two parameter changes, which leads to a normal set, indicating alterations to be effected in our simulated “patient” that would treat the disorder (personalized medicine); the same manipulation would not work for other cases and would therefore not be expected to provide a universal therapeutic approach (similarly we know of many types of dystonias and different gene mutations that can produce hereditary forms). Furthermore, the normal (blue) and dystonia (red) groups do not form well defined clouds. It is difficult to separate normal from dystonic sets, or to separate out different groups of dystonic patients to be treated in a common way. We therefore could not separate out different groups of dystonic patients who could be treated identically within group – precision medicine – despite different treatments between groups.

Figure 3.

Navigating through three dimensions. Dystonia cases in red and control in blue.

While it is already difficult to navigate among cases and controls in the three dimensional subspace of Fig. 3, it is impossible to visualize higher dimensions to identify separations between groups in 4 or more dimensions. Instead, machine-learning algorithms are used to identify what is where in high-dimensional parameter spaces. In this case, we first tried an entirely unsupervised algorithm, k-means, which attempts to find a certain number k of galaxy-like clusters of points in the space. Consistent with our difficulties identifying such clusters in 3-space (e.g., Fig. 3), the algorithm failed to separate the data into 2 well-separated groups corresponding to normal and dystonic parameters or, to provide multiple group separations when run with higher k.

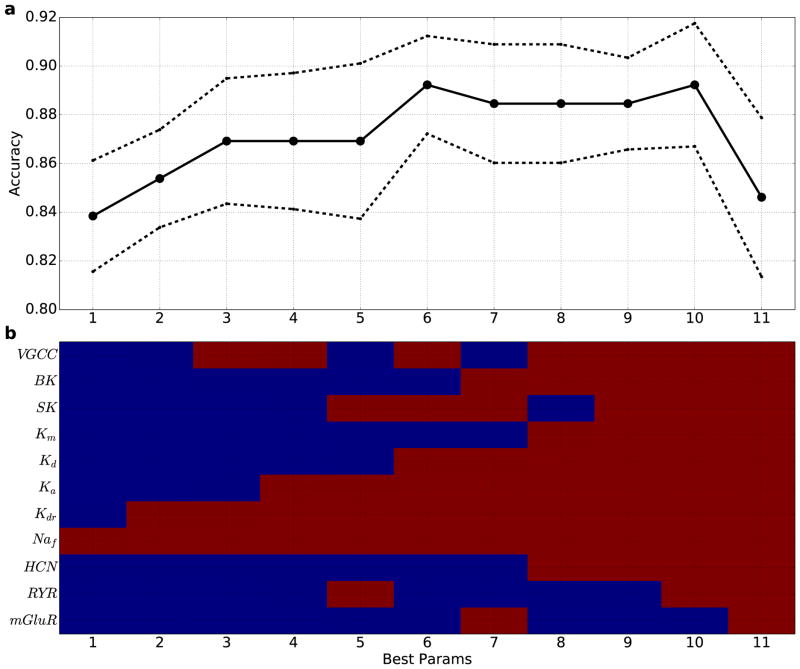
We then turned to support vector machines (SVM), a supervised machine-learning algorithm which separates groups based on user-provided labels - in this case dystonia vs control. SVMs were run for every potential subspace to determine which combination at that dimensionality gives the best separation. SVMs were able to separate out the 2 groups with a gradual increase in the quality of separation at higher dimensions up to 6 dimensions (Fig. 4). From there, plateauing was seen up to 10 dimensions, likely indicating further improvement in distinction masked by the “curse of dimensionality” (using a constant number of data points, the density of points falls off exponentially with increase in dimension making the separation problem correspondingly harder for algorithms to perform, and thereby providing an underestimate of the predictive strength of the optimal separation (Bishop, 2006; Noble, 2006)).

Figure 4. SVM classification accuracy generally increases when using 1–10 parameters, indicating utility of multitarget pharmacy approach to treating dystonia.

(a) Best classification accuracy from all combinations of x parameters (solid line: mean cross-validation accuracy (n = 10); dotted line: standard error). (b) Best parameter combinations (red: parameter used; blue: parameter not used). x-axis in (a),(b) indicates number of parameters used.

The value of these SVM results of Fig. 4 is that they not only suggest the number of parameters that might need to be modified to relieve pathology (6–10), but also identify the individual parameters in order of importance. These parameters at the molecular level are therefore governing, in combination, the ability to define a plane separating two subspaces that best separates pathology from normal physiology. We would then predict that a mathematical “therapy” for our dystonic simulations could be effected by following the direction normal to this separation across that set of parameters. Going from mathematical therapy to patient therapy, these parameter changes would be brought about by using drugs that modulate that particular channel or signaling interaction.

In making the translation from simulation to therapy, we would want to remain mindful that some combinations of parameter alterations may tend to simply shut down the network, suggesting that the corresponding drug treatments might not be tolerated due to these types of side effects that are typically seen with drugs that reduce activity (e.g., benzodiazepines). For example, we can propose a hypothetical 4-drug cocktail using Fig. 4. We would start by addressing the first 2 parameters identified, the fast sodium and delayed rectifier potassium channels. These are of course the channels responsible for fast spiking. We might therefore start with a drug that reduces fast spiking, such as diphenylhydantoin. Noting now that the voltage-gated calcium channel parameter at the top of Fig. 4b is red in the third column, we might then consider the addition of a VGCC blocker, for example verapamil. Similarly, we would look for a drug that would augment K_A and a drug that blocks the ryanodine (RYR) receptor. We note that the mapping from parameter to drug will never be one-to-one. Most drugs have effects at multiple targets – so-called “dirty drugs”. However this is something that we could test directly in the model by modulating the multiple drug targets simultaneously, thereby making this limitation into a positive feature by identifying drugs with a particular molecular spectrum of action that more closely match directions in parameter space that are identified by the model.

Conclusions

Multiscale mechanistic simulations could be used to develop polypharmaceutical drug cocktails or to inform the use of multi-target therapeutic agents (dirty drugs) through parameter space assessments after separation of pathological from physiological activity patterns for dynamic diseases such as dystonia and epilepsy.