EXTENDING MULTIVARIATE DISTANCE MATRIX REGRESSION WITH AN EFFECT SIZE MEASURE AND THE ASYMPTOTIC NULL DISTRIBUTION OF THE TEST STATISTIC

Abstract

Person-centered methods are useful for studying individual differences in terms of (dis)similarities between response profiles on multivariate outcomes. Multivariate distance matrix regression (MDMR) tests the significance of associations of response profile (dis)similarities and a set of predictors using permutation tests. This paper extends MDMR by deriving and empirically validating the asymptotic null distribution of its test statistic, and by proposing an effect size for individual outcome variables, which is shown to recover true associations. These extensions alleviate the computational burden of permutation tests currently used in MDMR and render more informative results, thus making MDMR accessible to new research domains.

1. Introduction

Research in the social sciences often requires the collection and analysis of multivariate (MV) dependent variables. There are two classes of methods for analyzing such data that differ in how they describe structure in the MV outcome: variable-centered methods and person-centered methods. The current paper extends a new person-centered regression method by providing analytic p values as well as a measure of effect size.

Variable-centered methods describe structure in a MV outcome by analyzing the similarities among its variables, which are commonly aggregated in a covariance matrix. Because they are based on covariances, these methods treat subjects as interchangeable and rely on the assumption that all relationships between variables are linear. If these two main assumptions are appropriate, variable-centered methods are well suited to situations in which the goal is to derive substantive meaning from the relationship among the variables. These assumptions, however, are not always reflective of reality. Subjects can belong to different clusters in a population, in which case they are not all interchangeable, and relationships between variables can be non-linear (Cassady & Finch, 2015; Etezadi-Amoli & McDonald, 1983; Kubarych et al., 2010; Lubke & Muthén, 2005; McDonald, 1962;Yalcin & Amemiya, 2001).

Person-centered methods describe structure in a MV outcome by analyzing similarities among all pairs of subjects in the data (Bergman & Magnusson, 1997). These similarities are typically quantified using a measure of distance between each pair of response profiles (i.e., vectors of scores along each outcome variable), which are commonly aggregated in a distance matrix. Person-centered methods are useful tools for research focused on inter-individual differences among response profiles (Muthén & Muthén, 2000). Furthermore, they are viable alternatives to variable-centered methods when MV data are expected to violate the assumptions of linearity or interchangeability (Bauer & Shanahan, 2007; Bernstein et al., 2010; Breslau, Reboussin, Anthony, & Storr, 2005; Osborne & Weiner, 2015). Person-centered methods are more flexible in their treatment of variables because the distance between response profiles can be calculated in many different ways, some of which do not rely on these assumptions (Johnson, 1967; Kruskal, 1964b; McArdle & Anderson, 2001). For example, the COSA algorithm (Friedman & Meulman, 2004) can be used to compute an iteratively optimized distance matrix that requires no a priori specification of variable structure and even accounts for the possibility that variables may differentially characterize subsets of the population.

Both covariance matrices and distance matrices can be subjected to further analyses. Often times, the goal of these analyses is to represent the MV outcome in a lower-dimensional space with minimal information loss in order to further investigate a parsimonious representation of the MV outcome. Principal component analysis (PCA) is a common variable-centered approach to this problem, and multidimensional scaling (MDS) is a conceptually similar person-centered method.

PCA maps a MV outcome’s p × p covariance matrix onto p orthogonal axes, or “principal components.” Each component is a linear combination of the p original variables, and each successive component explains as much variance as possible in the original data, conditional on the previous components. The original covariance matrix can be perfectly reproduced using all p components, but their maximum-variance property typically allows the covariance matrix to be approximated with a small subset of components with minimal loss of information with respect to the variance of the original variables. As such, subjects’ scores along a small subset of components can typically serve as a reasonable representation of the MV outcome in subsequent analyses. PCA can also be conducted on a correlation matrix, but results will differ to the extent that the scales of the original variables in the MV outcome differ from one another.

MDS (Kruskal, 1964a; Torgerson, 1952), sometimes called principal coordinates analysis (Gower, 1966), is computationally similar to conducting PCA on subjects rather than variables. MDS is used to map a n × n distance matrix computed on the MV outcome onto n orthogonal axes in Euclidean space. These axes do not represent linear combinations of variables, but rather each subject’s coordinates in n-dimensional Euclidean space based on distances between their response profiles. These coordinates depend not only on the response profiles themselves, but also on the manner in which distances between response profiles are quantified. Analogous to PCA, the original distance matrix can be perfectly reproduced using all n axes, but most axes usually contribute little to this reproduction, so a small subset can typically approximate the original distance matrix in low-dimensional Euclidean space.

If a researcher is interested in investigating the association between a MV outcome and a set of independent variables, the first few principal components or MDS axes can be regressed onto a set of predictors in lieu of conducting separate regressions for each variable comprising the MV outcome. In some special cases, approaching this problem from a person-centered framework with MDS regression yields the same results as a variable-centered approach using PCA regression (Meulman, 1992). MDS regression has been shown to be a useful person-centered association test more generally as well (Kiers, Vicari, & Vichi, 2005). However, its results depend on the number of axes used, and there is no strong theory to guide this choice (Kiers et al., 2005). As is the case with PCA, there are diminishing returns associated with each additional dimension, but Meulman (1992) noted that m MDS axes always differentiate subjects as well as, or better than, m − 1. As a result, information about the MV outcome is typically lost via the dimension reduction at the core of MDS regression.

Multivariate Distance Matrix Regression (MDMR) is an alternative person-centered regression method that avoids this problem by directly testing the association of a full distance matrix and a set of predictors without the intermediate data reduction step conducted by MDS regression (Anderson, 2001, McArdle & Anderson, 2001). It is conceptually similar to simultaneously regressing all n MDS dimensions in a single test. Prior to the regression, the distance matrix used in MDMR needs to be transformed such that its trace equals the sum of squared distances between each pair of response profiles that defines the distance matrix. This transformation, proposed by Gower (1966), is at the heart of MDS as well, but the two methods utilize the resulting transformed matrix in different ways. Whereas MDS is used to map it onto n orthogonal axes in Euclidean space, MDMR is used to directly partition its trace into a portion due to regression onto a set of predictors and a portion due to error. MDMR is therefore analogous to standard regression with the difference that the MDMR test statistic is used to partition the sum of squared distances between response profiles rather than the sums of squares of the variables comprising those profiles.

Because MDMR uses all information in the distance matrix, it avoids the disadvantages associated with selecting a subset of MDS axes, and MDMR has been shown to have additional desirable properties as well. MDMR can be used with sample sizes that are smaller than the number of outcome variables, and it has been shown to yield high power and well-controlled Type-I error (Zapala & Schork, 2012). Furthermore, the ability to quantify (dis)similarities between response profiles using any distance metric can be leveraged to relax distributional assumptions required when using other regression methods. This property has led to higher power compared to alternative variable-centered methods in case of population heterogeneity (Lubke & McArtor, 2014).

This paper presents two improvements to MDMR that should further motivate its use as a MV regression tool. First, we derive and present the asymptotic null distribution of MDMR’s test statistic. Currently, MDMR significance tests are permutation-based, and the computation time of these tests grows as a function of n², making them impractical for large samples. Furthermore, reliably estimating small permutation p values (≪0.05) requires an increasingly large number of permutations (Efron & Tibshirani, 1994), making these tests impractical when precise small p values are required. Second, we propose a measure of effect size for individual variables comprising the MV outcome used to construct the distance matrix. If a significant predictor is identified, it will usually be of substantive interest to identify which variables in the MV outcome are primarily driving the association, but MDMR cannot currently be used to do so.

The next section explains MDMR in more detail, which is followed by the derivation of the asymptotic null distribution of the test statistic. Next, a univariate effect size is proposed based on a randomization procedure. This statistic quantifies the effect size on a particular variable in a MV outcome by assessing the decrease in MDMR’s existing measure of overall effect size after dissociating that variable from the predictor(s) and recomputing the overall effect. The proposed improvements to MDMR are then evaluated in two simulation studies. The first simulation compares the new theoretical p values to permutation p values, and the second investigates the behavior of the proposed effect size measure and also assesses the power of MDMR relative to multivariate multiple regression. Finally, the utility of MDMR in the context of behavioral research is illustrated with the presentation of an empirical analysis in which MDMR is used to identify predictors that are significantly associated with individual differences in personality profiles.

2. Multivariate Distance Matrix Regression

Let the n × q matrix Y denote centered multivariate outcome data that a researcher aims to regress onto X, a n ×(p +1) matrix of p predictor variables and a column of 1’s, corresponding to the intercept term. The standard linear model and MDMR both test the association of Y and X by partitioning a representation of the sum of squares of the outcome into a portion due to regression onto X and a portion due to error.

In the standard linear model, the sum of squares of each outcome variable y_l (l = 1, …, q) is found on the l^th diagonal element of Y′Y, the inner-product of Y. The trace of this inner product is therefore equal to the total sum of squares of Y. The linear model proceeds by partitioning tr [Y′Y] into two independent quadratic forms corresponding to the sum of squares due to regression and residual. These quadratic forms are based on the symmetric, idempotent “projection matrix,” H = X(X′X)⁻¹X′. The sum of squares due to regression is tr [Y′HY] and the sum of squares due to residual is tr [Y′ (I − H)Y], where I is an n ×n identity matrix, and (I − H) is also symmetric and idempotent. This partitioning leads to the familiar ratio,

$$F^{\ast }=\frac{\text{tr}[{\mathbf{Y}}^{\prime }\mathbf{HY}]/p}{\text{tr}[{\mathbf{Y}}^{\prime }(\mathbf{I}-\mathbf{H})\mathbf{Y}]/(n-p-1)}.$$ (1)

If Y is a univariate normally distributed variable whose relationship with X is linear, then the trace of the quadratic forms in the numerator and the denominator each follows χ² distributions with degrees of freedom corresponding to the rank of the matrices used to construct them (i.e., H and I − H). The quotient of two χ² variables divided by their respective degrees of freedom follows an F distribution, so F^* ~ F(p, n − p − 1) is the omnibus test statistic of multiple regression if Y is univariate. If, on the other hand, Y is multivariate, then neither trace follows a χ² distribution. As a result, the test statistic F^* in Eq. 1 is not F-distributed if q > 1.

MDMR differs from the standard linear model in its representation of the sum of squares of the outcome. The standard linear model can be viewed as a variable-centered approach to regression that is used to partition the sum of squared Euclidean distances between each subject’s vector of scores on Y and the mean vector of Y. MDMR facilitates a person-centered approach that instead partitions the sum of squared distances between all pairs of individuals. Specifically, let D denote a symmetric n × n distance matrix with elements d_ij that each represent a quantification of the dissimilarity between the response profiles of subjects i and j. MDMR is used to decompose

$$\mathit{SSD}=\sum _{i<j}{d}_{ij}^2=\sum _{j<i}{d}_{ij}^2$$ (2)

into a portion attributable to X and a portion due to residual. In the special case that D is computed using Euclidean distances, that is, the distance between subjects i and j is defined as ${\left[{\sum }_{k=1}^q{\left(y_{ik}-y_{jk}\right)}^2\right]}^{1/2}$, then SSD/n is equal to the sums of squares used in standard linear regression. This is not the case, however, for any other distance metrics (Anderson, 2001).

The test statistic of the linear model is used to partition the sum of squares of the outcome using the trace operator, but SSD cannot be analogously partitioned using the trace operator on D because tr [D] = 0 by definition. Gower (1966) showed, however, that D can be transformed into a symmetric n × n matrix G such that the ith diagonal element of G is proportional to the sum of squared distances between subject i and all other subjects, resulting in tr [G] = SSD/n. This transformation allows the construction of a test statistic analogous to Eq. 1 based on person-centered distances rather than variable-centered distances. Gower’s G is computed as

$$\mathbf{G}=\left(\mathbf{I}-\frac{1}{n}\mathbf{J}\right)\mathbf{A}\left(\mathbf{I}-\frac{1}{n}\mathbf{J}\right),$$ (3)

where J is a square n-dimensional matrix of 1’s, and $\mathbf{A}=\left\{a_{ij}\right\}=\left\{-\frac{1}{2}{d}_{ij}^2\right\}$.

The partitioning conducted with the standard linear model test statistic relies on the fact that Y is a matrix of locations (scores) in Euclidean space that can be mapped into orthogonal subspaces indexed by H and I − H. This decomposition cannot be conducted on G directly because its elements do not represent scores in Euclidean space, but rather transformed measures of squared pair-wise distances. However, Gower, (1966) also showed that for any measure of dissimilarity used to construct the distance matrix (Euclidean or otherwise), G can be factored as G = ZZ′, where Z is a n × n matrix whose rows correspond to each subjects’ location mapped into n-dimensional Euclidean space based on the pair-wise distances in D. That is, Z is the matrix of all n axes resulting from conducting MDS on D. Because Z denotes coordinates in Euclidean space, it can be partitioned using H and I − H analogously to Y in the linear model. To find Z, conduct a spectral decomposition on G = UΛU′, in which Λ is the diagonal n × n matrix whose elements λ_k (k = 1, …, n) are the eigenvalues of G, and U is the n × n matrix whose columns u_k are the orthogonal eigenvectors of G corresponding to λ_k. The matrix of MDS axes is computed as Z = UΛ^1/2.

Similar to the linear model, in which the trace of the inner product of Y equals the total sum of squares, the matrix of MDS axes computed from D has the property tr [Z′Z] = tr [ZZ′] = tr [G] = SSD/n. Therefore, replacing Y with Z in Eq. 1 results in a test statistic based on SSD rather than the sum of squares of Y. This statistic is given by

$$\stackrel{\sim }{F}=\frac{\text{tr}[{\mathbf{Z}}^{\prime }\mathbf{HZ}]/p}{\text{tr}[{\mathbf{Z}}^{\prime }(\mathbf{I}-\mathbf{H})\mathbf{Z}]/(n-p-1)}.$$ (4)

Importantly, when non-Euclidean distances are used to quantify the dissimilarity between observations, it is often the case that the resulting G is not positive-semidefinite (PSD), so the diagonal of Λ may contain some negative numbers. When G is not PSD, the columns of Z that correspond to negative eigenvalues will therefore be composed of imaginary numbers. These imaginary axes are not easily interpretable in the context of MDS regression, so they are typically discarded. The information loss resulting from the omission of these imaginary axes, however, artificially inflates SSD (McArdle & Anderson, 2001). It is therefore important to utilize all n MDS axes, both real and imaginary, in the formulation of F̃. In order to do so while also avoiding the inconvenience of working with imaginary numbers, the MDMR test statistic can be expressed in a form that utilizes the information in all n MDS axes (both real and imaginary) without the direct use of the potentially complex matrix Z. Using the fact that H and I − H are idempotent as well as the fact that the matrix trace operator is invariant to cyclic permutations (i.e., tr [ABC] = tr [CAB] = tr [BCA] for any compatible matrices A, B and C), Eq. 4 is written in terms of the real matrix G = ZZ′ rather than the potentially complex matrix Z as

$$\stackrel{\sim }{F}=\frac{\text{tr}[\mathbf{HGH}]/p}{\text{tr}[(\mathbf{I}-\mathbf{H})\mathbf{G}(\mathbf{I}-\mathbf{G})]/(n-p-1)}.$$ (5)

Equation 5 is the omnibus MDMR test statistic as proposed by Anderson (2001) and McArdle and Anderson, (2001). In the special case that D is constructed with Euclidean distances, the outer product of Z (i.e., ZZ′ = G) is equal to the outer product of the data used to construct the distance matrix. That is, G = YY′. As a result, Eqs. 1, 4 and 5 are equivalent if D is Euclidean, so the MDMR test statistic is F-distributed if D is Euclidean and Y is univariate. However, if these conditions do not hold, F̃ is not F-distributed, and permutation tests have typically been used to estimate MDMR p values. Note that, the degrees of freedom p and n − p − 1 are constants that do not influence permutation-based p values, so they are typically omitted from the MDMR test statistic (Anderson, 2001;McArdle & Anderson, 2001). For the sake of consistency with existing literature, they will be subsequently omitted here as well because they are not necessary for the derivation of the null distribution of F̃ presented in the following section.

In the case of multiple predictors, MDMR can be used to test hypotheses about subsets of predictors. Analogous to the standard linear model, this is done in a model comparison framework by creating a design matrix for the reduced model, X₀, that does not contain the predictors of interest. Denoting H₀ as the projection matrix of X₀ and omitting the degrees of freedom, the MDMR test statistic for the conditional effects of a subset of predictors is given by

$${\stackrel{\sim }{F}}_s=\frac{\text{tr}[(\mathbf{H}-{\mathbf{H}}_0)\mathbf{G}(\mathbf{H}-{\mathbf{H}}_0)]}{\text{tr}[(\mathbf{I}-\mathbf{H})\mathbf{G}(\mathbf{I}-\mathbf{H})]}.$$ (6)

Like the omnibus test, the MDMR test statistic for a subset of predictors is equivalent to the standard linear model when q = 1 and D is Euclidean, but Eq. 6 does not follow a standard distribution otherwise. Additional permutation tests are typically used to compute p values for subsets of predictors.

There are many ways to conduct MDMR permutation tests. The most efficient involves using Eq. 5 B times based on B random permutations of the rows of X. Using matrix algebra, Eq. 5 is evaluated in a less interpretable, but more computationally efficient manner by expressing F̃ in terms of the inner product of two n² × 1 vectors (vec [H] and vec [G]). The computational burden of MDMR permutation tests is therefore a function of Bn². Furthermore, the precision of permutation-based p values is a function of B, such that increasingly stringent significance criteria require increasingly large B. These considerations result in MDMR permutation tests that require an infeasible amount of computation time when sample sizes are large and/or when highly precise p values are required.

3. The Null Distribution of the MDMR Test Statistic

This section utilizes ideas at the core of MDS to show that the MDMR test statistic is asymptotically distributed as the quotient of two independent linear combinations of independent chi-square variables.

3.1. Derivation of the Distribution

Recall the spectral decomposition of G = UΛU′ discussed above. Using this equality and omitting the degrees of freedom, Eq. 5 is rewritten as

$$\stackrel{\sim }{F}=\frac{\text{tr}[\mathbf{HU}\mathbf{\Lambda }{\mathbf{U}}^{\prime }\mathbf{H}]}{\text{tr}[(\mathbf{I}-\mathbf{H})\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\prime }(\mathbf{I}-\mathbf{H})]}.$$ (7)

Because H and I − H are symmetric, F̃ can be expressed as

$$\stackrel{\sim }{F}=\frac{\text{tr}\left(\mathbf{HU}\mathbf{\Lambda }{(\mathbf{HU})}^{\prime }\right)}{\text{tr}[(\mathbf{I}-\mathbf{H})\mathbf{U}\mathbf{\Lambda }{((\mathbf{I}-\mathbf{H})\mathbf{U})}^{\prime }]}.$$ (8)

Next, denote Û = HU and R = (I − H)U. The columns of these two matrices contain the fitted values and residuals resulting from regressing each eigenvector of G onto X. Because U is orthogonal, these two matrices can be expressed in terms of the eigenvectors, denoted u_k (k = 1, …, n), as, Û = [Hu₁, …, Hu_n] and R = [(I − H)u₁, …, (I − H)u_n]. This representation makes explicit the fact that the k^th columns of Û and R are the vectors of fitted values and residuals from regressing u_k onto X using standard linear regression. Denote these column vectors as û_k and r_k. Eq. 8 is now be expressed as

$$\stackrel{\sim }{F}=\frac{\text{tr}(\widehat{\mathbf{U}}\mathbf{\Lambda }{\widehat{\mathbf{U}}}^{\prime })}{\text{tr}(\mathbf{R}\mathbf{\Lambda }{\mathbf{R}}^{\prime })}=\frac{\text{tr}(\mathbf{\Lambda }{\widehat{\mathbf{U}}}^{\prime }\widehat{\mathbf{U}})}{\text{tr}(\mathbf{\Lambda }{\mathbf{R}}^{\prime }\mathbf{R})}$$ (9)

or equivalently,

$$\stackrel{\sim }{F}=\frac{{\sum }_{k=1}^n{\lambda }_k\text{tr}\left[{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k\right]}{{\sum }_{k=1}^n{\lambda }_k\text{tr}\left[{\mathbf{r}}_k^{\prime }{\mathbf{r}}_k\right]}=\frac{{\sum }_{k=1}^n{\lambda }_k{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k}{{\sum }_{k=1}^n{\lambda }_k{\mathbf{r}}_k^{\prime }{\mathbf{r}}_k}.$$ (10)

Through Eq. 10, it is clear that MDMR is not only conceptually related to MDS regression, but its test statistic can be exactly reproduced by conducting all n MDS regressions for a given D and X. Recall that MDS maps G onto n orthogonal dimensions in Euclidean space by eigendecomposing G so that the vector of scores in the kth dimension of Euclidean space is ${\mathbf{z}}_k={\lambda }_k^{1/2}{\mathbf{u}}_k$. The kth summands in the numerator and denominator of Eq. 10 are therefore equal to the sum of squares due to regression ( ${\lambda }_k{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k$) and to residual ( ${\lambda }_k{\mathbf{r}}_k^{\prime }{\mathbf{r}}_k$) resulting from the regression of the kth MDS axis onto X. Not only does this equivalence allow the derivation of the null distribution of F̃, but it also facilitates a deeper understanding of MDMR as a simultaneous association test of all n MDS axes with X.

Given the assumption that Y comes from a homogeneous population, the central limit theorem implies that the u_k’s are asymptotically normally distributed because they are linear combinations of the elements of G, which are iid if the rows of Y are iid. In this case, ${\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k$ and ${\mathbf{r}}_k^{\prime }{\mathbf{r}}_k$ are independent and follow χ² distributions with p and (n − p − 1) degrees of freedom, respectively. In addition to the independence of the numerator terms from the denominator terms, the summands in each term are themselves mutually independent because the eigenvectors of G are orthogonal.

The MDMR test statistic F̃ is therefore asymptotically distributed as a weighted sum of n independent χ²(p) variables divided by a weighted sum of n independent χ²(n − p − 1) variables, where both sets of weights are the eigenvalues of G. This distributional form holds for any dimensionality of the Y that is used to construct D. Critically, due to the fact that MDMR is based on coordinates in Euclidean space derived from D regardless of the measure of (dis)similarity used to construct it, this distributional form also holds for any measure of dissimilarity used to construct D (Euclidean or otherwise). These coordinates depend on the selected measure of dissimilarity, but the weights (λ_k) of the composite χ² variables do as well, thus accounting for these differences and resulting in a correct null distribution regardless of the measure of dissimilarity used to compute D.

The same derivation can be applied to the test statistic corresponding to a subset of predictors (F̃_s, Eq. 6) to conclude that it has the same distributional form. For this statistic, the only difference is that the degrees of freedom of the composite χ² distributions are p₀ and n − p − 1, where p₀ denotes the number of parameters being tested.

Recall that unless D is computed using Euclidean distances, some of the eigenvalues of G will be smaller than zero. In this case, some of the weights (λ_k) of the linear combinations that characterize the null distribution of F̃ will be negative. A χ²-distributed variable is bound by zero and infinity, so a linear combination of χ² variables in which some weights are negative will be bound by negative and positive infinity. When G is not PSD, the null distribution of the MDMR test statistic is therefore unbounded, unlike the standard F-distribution that has a lower bound of zero. Note, however, that despite the potentially negatively infinite lower bound of F̃, hypothesis tests based on F̃ are always one-sided, with larger values implying smaller p values. The manner in which these p values can be computed based on the asymptotic null distribution of F̃ is discussed below.

3.2. Computing Theoretical p values

In general, the probability density function of a quotient of linear combinations of independent χ² variables does not have a closed form, but its cumulative density function (CDF) can be approximated with a high degree of accuracy using an algorithm proposed by Davies (1980). This algorithm numerically inverts the known characteristic function of a linear combination of independent χ² variables in to order approximate its CDF, and thus p values, within a user-specified margin of error. Davies’ algorithm is implemented in the CompQuadForm package (Duchesne & Micheaux, 2010) in R (R Core Team, 2015). This implementation is fast, running in a matter of seconds for a wide range of sample sizes and levels of precision.

Given a set of weights (λ_k) and degrees of freedom for each composite χ² variable, the Davies’ algorithm can be used to attain p values for the specified linear combination, but it does not immediately provide a method to calculate p values for quotients of such linear combinations, which are necessary to assess the MDMR test statistic. However, the CDF of a quotient of linear combinations of χ² variables can be expressed in terms of a single linear combination of χ² variables. Specifically, the CDF of F̃ evaluated at f̃ can be written as

$$\begin{gathered} P(\stackrel{\sim }{F}\le \stackrel{\sim }{f})=P\left(\frac{\text{tr}[\mathbf{HGH}]}{\text{tr}[(\mathbf{I}-\mathbf{H})\mathbf{G}(\mathbf{I}-\mathbf{H})]}\le \stackrel{\sim }{f}\right) \\ =P\left(\frac{{\sum }_{k=1}^n{\lambda }_k{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k}{{\sum }_{k=1}^n{\lambda }_k{\mathbf{r}}_k^{\prime }{\mathbf{r}}_k}\le \stackrel{\sim }{f}\right) \\ =P\left(\sum _{k=1}^n{\lambda }_k{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k-\stackrel{\sim }{f}\sum _{k=1}^n{\lambda }_k{\mathbf{r}}_k^{\prime }{\mathbf{r}}_k\le 0\right). \end{gathered}$$ (11)

This final expression has the form of the CDF of a single linear combination of χ² variables evaluated at zero with weights {λ₁, …, λ_n, (− f̃λ₁), …, (− f̃λ_n)} and corresponding degrees of freedom {p, …, p, (n − p − 1), …, (n − p − 1)}. The Davies algorithm can therefore be used to quickly compute theoretical MDMR p values without conducting a permutation test.

An R package titled MDMR is currently available on CRAN that provides functions to conduct MDMR with the analytic p values presented above. This package also provides functions that can be used to compute the univariate effect size on each outcome variable, described below.

4. Univariate Effect Size

The current MDMR framework does not provide a means to identify which variables comprising Y are primarily responsible for the association between D and X. The only available measure of effect size quantifies the effect on the distance matrix as a whole without providing any information about effects on individual variables. The pseudo-R² statistic used in MDMR is conceptually similar to R² in the standard linear model, which quantifies the proportion of the total sum of squares of the outcome that can be explained by the predictor. The pseudo-R² statistic instead measures the proportion of SSD that can be explained by the predictors, and it is computed by dividing the numerator of the MDMR test statistic by the total sum of squared pair-wise distances rather than the portion of SSD attributable to error,

$${\stackrel{\sim }{r}}^2=\frac{\text{tr}[\mathbf{HGH}]}{\text{tr}[\mathbf{G}]}.$$ (12)

Importantly, recall that the numerator of r̃² can be expressed as ${\sum }_{k=1}^n{\lambda }_k{\widehat{\mathbf{u}}}_k^{\prime }{\widehat{\mathbf{u}}}_k$. In the case that G is not PSD, this term can be negative, resulting in r̃² being a negative number because the trace of G is always positive. This only tends to occur in practice, however, when the effect of X on D is trivially small, so negative values of r̃² are interpreted in the same way as values of zero.

Although r̃² does not directly provide information about the effect size on each variable comprising Y, it is a key component in the statistic developed below that can be used to estimate these effects. We propose an effect size measure δ for each individual variable y_k (k = 1, …, q) comprising Y that is defined as the decrease in r̃² resulting from the dissociation of y_k and X. The effect size δ is computed for y_k with the following procedure. First, create Y_(k) by randomly permuting the kth column of Y. Then using the same distance metric used to construct D, compute a distance matrix based on Y_(k), denoted D_(k), and transform it into G_(k) using Eq. 3. Next, compute ${\stackrel{\sim }{r}}_{(k)}^2=\text{tr}\left[\mathbf{H}{\mathbf{G}}_{(k)}\mathbf{H}\right]/\text{tr}\left[{\mathbf{G}}_{(k)}\right]$, the measure of overall effect size on the version of the data with the kth outcome variable randomly permuted. The effect size on y_k is then defined as

$$\delta ={\stackrel{\sim }{r}}^2-{\stackrel{\sim }{r}}_{(k)}^2.$$ (13)

The rationale to consider δ as an effect size measure is as follows. If the predictors have a large effect size on y_k, we would expect that dissociating it from X would notably shrink the overall effect size measure on D, and therefore larger values of δ suggest a larger effect on y_k. On the other hand, if the effect on y_k is small, we would expect that dissociating it from X would not have a large impact on the overall effect size measure, so smaller values of δ indicate a smaller effect size on y_k.

It is important to note that δ is a relative measure of effect size whose scale depends on the dimensionality and covariance matrix of Y as well as the distance metric used to form D. As the number of variables in Y increases and as their covariance increases, dissociating a single outcome variable from X will have a less drastic effect on r̃², so δ cannot be used to compare effect sizes across studies. Rather, it is intended to discriminate effect sizes between variables used to construct a particular distance matrix. It can be used to determine if all variables are relatively equally affected by the predictors, or if a subset is driving the association between X and D more than others.

In this procedure, y_k is permuted (i.e., its elements are randomly shuffled) rather than removed from the data because removing it would change the total sums of squared distances between individuals, and therefore the denominator of r̃². Permuting y_k rather than removing it changes the proportion of the squared distances that can be explained by X (tr [HGH]) while keeping the total sum of squares (tr [G]) constant, and thus facilitates meaningful comparison of r̃² and ${\stackrel{\sim }{r}}_{(k)}^2$. As a consequence of permuting y_k rather than removing it, negative values of δ are possible when the effect size on y_k is small because in this case, a single random permutation may actually serve to increase its association with X by random chance. To avoid this possibility, we recommend computing δ with multiple random permutations of y_k and averaging the results. This practice is particularly valuable with small sample sizes because small n can result in an appreciable risk of spurious associations after a single random permutation. Furthermore, the computational burden of computing δ multiple times will typically be trivial with a small sample. We have found that averaging δ estimates from 10 random permutations is typically sufficient to protect against the possibility of spurious relationships.

Finally, just as MDMR can be used for both omnibus tests and tests of subsets of predictors, δ can be computed based on the entire set of predictors or using a only subset of predictors while conditioning on the rest. Basing δ on the entire set of predictors results in an omnibus effect size that is conceptually similar to R² in the linear model, and basing it on a single predictor measures the effect size of a single predictor on y_k, conditional on all other predictors. This second measure is conceptually similar to a squared standardized regression coefficient. To compute δ based on a subset of predictors, replace the projection matrix in Eq. 10 with (H −H₀) as was done in Eq. 6, where H₀ is the projection matrix of the reduced model.

5. Simulation Study I: Validity of Analytic p values

Research investigating the statistical properties of MDMR demonstrated that permutation tests result in well-controlled Type-I rates (Zapala & Schork 2012). To test the validity of our proposed analytic p values, a simulation study will be conducted that compares them to the established permutation-based p values. Subsection 3.1 notes that the null distribution of the MDMR test statistic relies on the central limit theorem, implying that it is an asymptotic distribution. As a result, it is expected that the validity of the proposed analytic p values will depend on features of the data including, but not necessarily limited to, sample size. The primary goal of this simulation study is to investigate which conditions must hold in order for the analytic null distribution to result in correct p values.

Subsection 5.1 presents an array of conditions that will be used to generate data, and MDMR will be conducted on each generated dataset using both analytic p values and permutation tests. The consistency of the resulting p values will be modeled as a function of the data-generating conditions to achieve the goal of this study. It is important to note that permutation-based p values include random error that preclude the expectation of exactly equal results under any circumstances. A criterion must therefore be established that determines whether or not the two approaches yield consistent p values for a given dataset. This criterion is discussed in Subsect. 5.2 before presenting the results of the study in Subsect. 5.3.

5.1. Data-Generating Conditions

Data are generated under the null hypothesis of no association by generating X and Y independently, each from a multivariate normal distribution in which variables have unit variance. The correlation among all predictors in the population will be set to either ρ_X = 0.0 or 0.3 and the correlation among outcomes will be either ρ_Y = 0.0 or 0.5. It is noted in Subect. 3.1 that the proposed null distribution should hold regardless of the distribution of each variable comprising Y. In order to assess this claim empirically, categorical outcome data are also generated by dichotomizing normally distributed variables at their population mean. This study also considers the impact of sample size, the number of predictors, the number of outcome variables, and distance metric used to quantify the dissimilarity among response profiles. To this end, the sample size (n = 50, 100, 150, 200, 250, 500, 1000), number of predictors (p = 1, 3, 5, 10), number of outcome variables (q = 1, 3, 5, 10, 20, 50), and distance metric used to construct D vary across simulation conditions. We use Euclidean as well as Manhattan distances. Manhattan distances are a robust alternative to Euclidean distances that are defined as the sum of absolute (rather than squared) distances between the variables comprising the response profiles.

The computational burden of permutation tests limits the number of datasets that can be compared in each condition. The consistency of the analytic approach with permutation tests is most important when p values are small (<0.05) because in this case, even small differences between the methods could lead to inconsistent statistical inference. In order to focus our finite computational resources on such cases without limiting our evaluation to a specific range of values for the test statistic (i.e., F̃ resulting in p < 0.05), this study was conducted twice, with each version focusing on one of these two goals. In the first version, we focus on comparing the two approaches using datasets that result in small p values. To do so, datasets are randomly generated in each condition until 100 have been produced that result in analytic p values less than or equal to 0.05. Permutation tests are then conducted on these 100 datasets, and the consistency of the two methods is determined by the method described below. In the second version, 100 datasets are generated under the null hypothesis in each condition in order to compare the consistency of analytic and permutation-based p values across the full spectrum of possible p values.

5.2. A Criterion for p Value Equivalence

Permutation tests rely on an empirical null distribution specific to the dataset being analyzed. When conducting MDMR, this distribution is defined by recomputing the test statistic using the observed distance matrix and every possible permutation of the rows of X. There are n! unique permutations of this kind. More formally, let F̃_m denote the MDMR test statistic computed from the m^th (m = 1, …, n!) permutation of the rows of X, and let F̃_p denote a vector of length n! with entries F̃_m. That is, F̃_p is the permutation-based null distribution of the MDMR test statistic. Using 𝕀 to denote the indicator function, permutation p values are defined as

$$p_p(\stackrel{\sim }{F})=\frac{{\sum }_{m=1}^{n!}\mathbb{I}(\stackrel{\sim }{F}\le {\stackrel{\sim }{F}}_m)}{n!}.$$ (14)

Because it is infeasible to conduct all n! possible permutations unless n is extremely small, F̃_p is usually estimated using B (≪n!) random permutations of the rows of X. This results in an estimated permutation distribution F̃_B, comprising the B test statistics resulting from B random permutations of the rows of X. If F̃_b (b = 1, …, B) are the elements of F̃_B, then the estimated permutation p value is computed as

$${\widehat{p}}_p(\stackrel{\sim }{F})=\frac{{\sum }_{b=1}^B\mathbb{I}(\stackrel{\sim }{F}\le {\stackrel{\sim }{F}}_b)}{B}.$$ (15)

In this study, B = 5000 random permutations will be conducted to estimate p_p.

The necessity of using p̂_p to estimate p_p adds an element of uncertainty to the computation of permutation-based p values that is not shared with standard analytical p values. Rather than a fixed value computed given data and a test statistic, p̂_p is a random variable that varies based on the randomly selected subset of possible permutations used to compute it. Due to the fact that the B permutations are randomly sampled from the n! possible permutations, Efron and Tibshirani (1994) note that Bp̂_p ~ bin(p_p, B). To account for this random variation in p̂_p, the binomial distribution of Bp̂_p can be used to form an exact confidence interval for p_p according to the method described by Clopper (1934).

We define the coverage of an observed theoretical p value as whether or not it falls within its corresponding 99% confidence interval for p_p. This statistic is the focus of the study. To establish conditions that must be met in order for the theoretical p values to be consistent with results from permutation tests, coverage can be modeled as a Bernoulli-distributed variable with a coverage rate (i.e., probability of coverage) that depends on the data-generating conditions. Phrased differently, the goal of this study is to identify the conditions that must hold to result in a high coverage rate, which implies equivalent permutation and analytic p values and therefore the satisfaction of the asymptotic requirements of the analytic null distribution.

5.2.1. Note on Confidence Interval Width

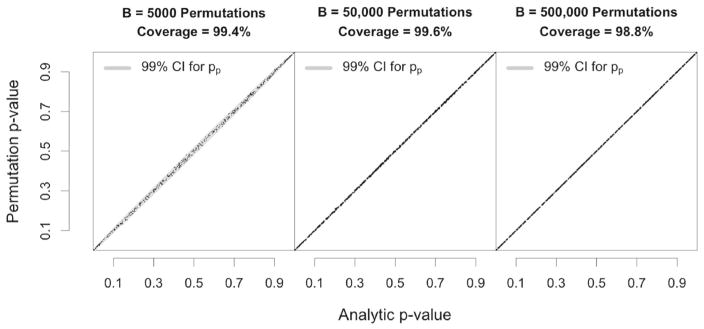
Because the variance of a binomial variable depends on the number of trials and probability of success, the width of the 99%confidence interval around each estimated p̂_p depends on both B and the value of p̂_p. Using B = 5000, the smallest possible 99% Clopper-Pearson interval has a width of 0.0011 (at p̂_p = 0 and p̂_p = 1), and the largest interval has width 0.0366 (at p̂_p = 0.5). Increasing B would serve to narrow these intervals and result in more precise point estimates for p_p, but importantly, the coverage rates of the analytic p values are asymptotically invariant with respect to B. With larger B, the increased precision of p̂_p results in less noise in the estimated permutation-based p values, making them more similar, on average, to the true underlying p_p. The confidence interval for p_p narrows proportionally to this reduction in estimation error, resulting in analytic p value coverage that is asymptotically constant with respect to B. This phenomenon is illustrated empirically in Fig. 1, which shows the analytic p-value coverage over 500 randomly generated datasets when B = 5000, 50000, and 500000. Although the permutation and analytic p values are more highly correlated as B increases, all three conditions result in virtually equal coverage.

Figure 1.

Coverage rates as a function of B. The points in each subfigure illustrate the analytic p values versus the estimated permutation p values for 500 randomly generated datasets. The same 500 datasets were used to create each subfigure, with the only difference between conditions being the number of permutations that were used to estimate p_p. The width of the confidence interval (shaded region) adjusts to keep the coverage rate constant across levels of B, within sampling error.

5.3. Simulation I Results

5.3.1. AsymptoticValidity

The pattern of results was the same for both versions of the simulation study. When considering data generated such that p < 0.05 and when considering data generated under the null hypothesis, the logistic regression model predicting coverage from the simulation conditions (n, p, q, ρ_X, ρ_Y, distance metric, and distribution of Y) indicated a highly complex relationship between these predictors and coverage rates. All main effects except for the effect of ρ_X were highly statistically significant, as were many higher-order terms ranging from two- to six-way interactions. In both versions of the study, the predictive quality of the resulting model was strong, correctly classifying coverage for 91%of the observed analytic p values in both cases. The model’s complexity, however, makes it impractical for providing guidelines to researchers regarding when they should expect the asymptotic null to hold.

A much simpler model can be constructed by recognizing that the effects of q, ρ_Y, the distributional form of Y, and the distance metric used to compute Y can be characterized using statistics computed from the G matrix. Specifically, differences in these data-generating conditions are related to differences in the eigenvalues of G. We found that a single variable based on n, p, and these eigenvalues can be used to model coverage rates in a simple logistic regression model that is interpretable and yields a similar classification accuracy to the more complex model described above (92% when modeling data generated such that p < 0.05, 89% when modeling data generated under H₀). To build this model, we define the “adjusted sample size” as

$$\stackrel{\sim }{n}=(n-p-1)\frac{{\lambda }_1}{{\sum }_{k=1}^n{\lambda }_k}=(n-p-1)\frac{{\lambda }_1}{\text{tr}[\mathbf{G}]},$$ (16)

where λ₁ is the largest eigenvalue of G. This statistic equals the denominator degrees of freedom of the linear model multiplied by the proportion of SSD explained by the first MDS axis. Stated differently, this statistic penalizes n − p − 1 based on the number of independent dimensions that are required to describe the bulk of SSD. As is the case when considering the eigenvalues of a covariance matrix, λ₁ will tend to be small relative to ${\sum }_{k=1}^n{\lambda }_k$ if Y comprises many largely unrelated variables. This results in increasing penalization as the amount of independent information in the columns of Y increases, which is consistent with the common statistical idea that more observations are needed to fit more complex models.

Results from the simple logistic regression models regressing coverage onto ñ indicate that as ñ increases, so does the coverage rate of analytic p values in the corresponding data-generating conditions. When data were generated with uniformly small analytic p values, an adjusted sample size of 33 results in a model-implied coverage rate of 80 %. According to this model, ñ ≥ 74 is required to attain a coverage rate of 99 %, which would be expected if the null distribution is exactly correct based on the use of 99% confidence intervals for the permutation p values. When modeling coverage from datasets generated freely under the null hypothesis, an adjusted sample size of 22 results in model-implied coverage of 80%, and ñ ≥ 95 is required to attain model-implied coverage of 99 %.

Figure 2 illustrates the model-implied coverage rates as a function of ñ based on both versions of the simulation study. The differences between these two models highlight an important result. When focusing exclusively on datasets that result in small p values, coverage rates are more sensitive to ñ than when considering data generated freely under the null hypothesis. That is, the consequences of failing to obtain a sufficiently large adjusted sample size seem to be exaggerated when p < 0.05. It is here, in the tail of the distribution, that p value accuracy is most important because when a p value is near a pre-specified significance criterion, even relatively small biases can lead to incorrect statistical inference.

Figure 2.

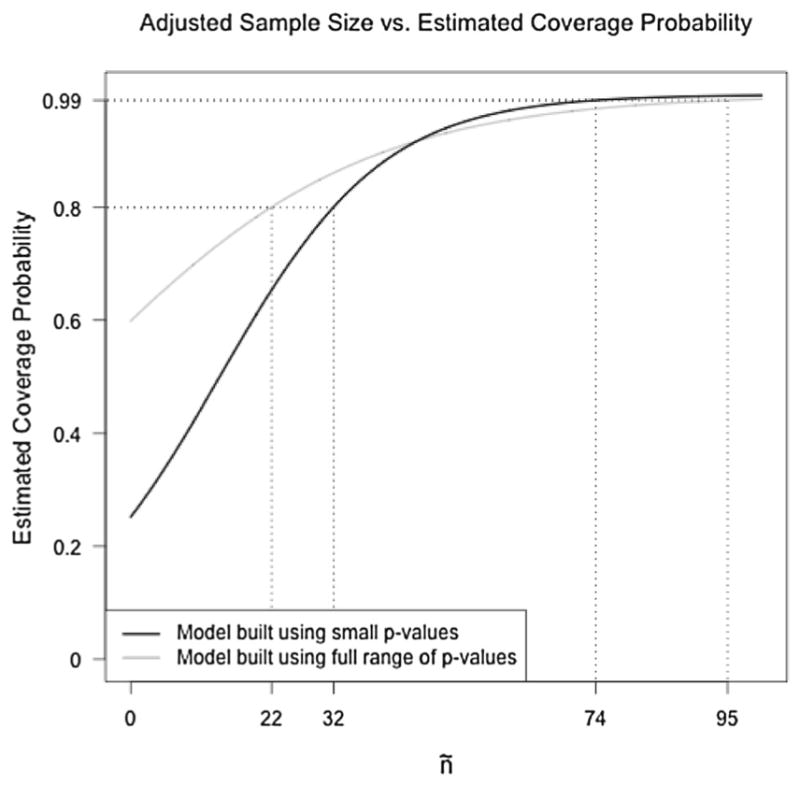
Model-implied coverage probability as a function of ñ, where “coverage probability” refers to the probability that an analytic p value yields consistent results with a permutation test based on a 99%confidence interval for the permutation p value. The darker line corresponds to the model fit to data generated such that p < 0.05, and the lighter line corresponds to the model fit to data generated freely under H₀.

We therefore recommend using the set of results based on small p values as a guideline for choosing between analytic and permutation-based p values in practice. Obtaining an adjusted sample size of at least 74 should be sufficient to satisfy the asymptotic requirements of the null distribution and therefore result in unbiased analytic p values. For smaller values of ñ, the asymptotic requirements of the model are unlikely to hold exactly. In these situations, it is up to the reader to weigh the computational benefits of adopting analytic p values against the likely bias that will result from their use. The type of bias that can be expected when using analytic p values with insufficient ñ is discussed below.

5.3.2. Bias

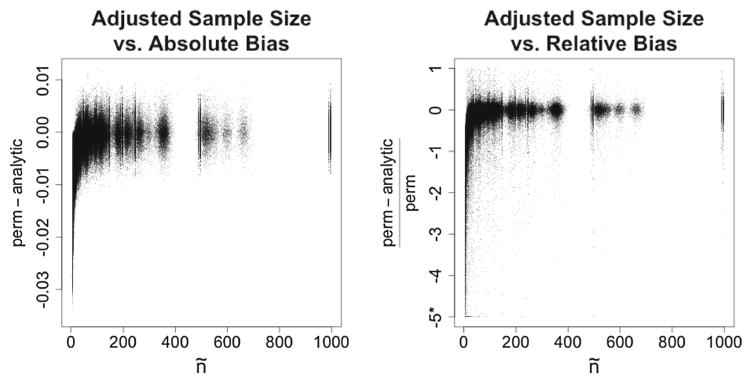
A researcher may want to conduct MDMR in a scenario in which ñ is small, but the sample size is large enough to preclude the use of permutation tests due to computational infeasibility. In cases like these, analytic p values can still be used without inflated Type-I error rates because they are systematically conservative when the adjusted sample size is insufficient to result in analytic p values that are consistent with the results of permutation tests. Using results from the simulations focusing on small p values, Fig. 3 illustrates the bias of the analytic p values as a function of ñ. When ñ is small, analytic p values tend to be larger than their permutation-based counterparts. As ñ increases such that the coverage approaches 99 %, the differences between analytic and permutation-based p values converge to zero, with variability attributable to the random error of permutation tests.

Figure 3.

Difference between permutation-based and analytic p values as a function of ñ. In the right panel, values smaller than −5 were recoded to −5 because a few outlying observations as small as −30 were obfuscating the figure. In both panels, note that as ñ becomes large, all differences are centered around zero, reflecting the high coverage when ñ is large.

6. Simulation Study II: Effect Size and Power

6.1. Study Design

A second Monte Carlo simulation study assesses the behavior of δ as well as the power of MDMR using both Euclidean and COSA distances (Friedman & meulman, 2004) relative to multivariate multiple regression (MMR), a common variable-centric approach to multivariate association tests. Two data-generating models are considered. In the first, data are drawn from a homogeneous population that is ideal for MMR. The second uses a heterogeneous population that should be better suited to MDMR, especially with COSA distances as the outcome because this distance metric accounts for the possibility that different variables can characterize different subsets of the population.

The first set of conditions uses MMR as the data-generating model in order to study the power of MDMR relative to the correctly specified model as well as the behavior of δ relative to the effect size measures of MMR. First, we generate one dichotomous predictor that influences a single dichotomous outcome in order to verify that all three methods perform similarly in the case of a univariate outcome. Second, data are generated such that only one of ten dichotomous outcome variables is affected by the predictor in order to assess the effect of including many noise-variables in the MV outcome, as is common in many high-dimensional research domains. In the third condition, the predictor influences five of ten generated outcome variables, which can occur in reality, for example, if only one subscale of a questionnaire is related to a predictor variable. Finally in the fourth condition, five dichotomous predictors are generated that influence five of ten generated outcome variables differentially in order to investigate the behavior of δ and MDMR in the presence of multiple predictors that jointly influence the same outcome variables. In all conditions, the sample size is fixed at 200, and the dichotomous outcome variables are created by categorizing simulated multivariate normal data with a mean split. The residual covariance of these underlying normal variables is fixed at 0.3 so that the observed outcome variables are related to one another independent of the predictor variables, as is typically the case in real data. Each condition is split into five sub-conditions that use different values for the proportion of variance explained in each affected outcome variable (0.000, 0.025, 0.050, 0.075, 0.100), and data from each of these sub-conditions are randomly generated and analyzed 100 times.

Across all of these conditions, we expect the power of MMR to represent an upper bound for the power of MDMR because it is the correctly specified model. MDMR using Euclidean distances should have similar performance, and the power of COSA-MDMR will likely be lower than the other two methods because COSA distances are designed for data in which different variables characterize different subsets of the population. Regarding δ, in the first three conditions, we compare Euclidean- and COSA-MDMR estimates of δ for each variable to the estimated R² from MMR. In the fourth condition, because we have multiple predictors, we will compare δ computed for each predictor separately to squared estimates of the standardized regression coefficients from the linear model (β̂²) in order to study the behavior of the δ measure based on individual predictors. Across all four conditions, we expect that δ will be linearly related to its MMR counterpart using both distance measures, but we expect that the correspondence will be stronger using Euclidean distances because Euclidean-MDMR is more similar to MMR than is COSA-MDMR.

The second set of conditions mirrors the first, but introduces a heterogeneous regression effect. There are two equal-sized subgroups in the population whose affected variables are mutually exclusive in each condition. Person-centered methods (or hybrid methods combining person- and variable-centered methods) are generally better-suited to handle heterogeneous populations (Lubke & Muthén, 2005; Muthén and Muthén 2000). It is therefore important to assess the behavior of δ and power of MDMR in these circumstances. In light of this type of heterogeneity, MMR is misspecified and should not necessarily outperform MDMR. In particular, COSA-MDMR is well suited to this scenario because the COSA algorithm is designed to compute distances between subjects that come from a heterogeneous population, and it accounts for the fact that different variables can characterize different subsets of the sample. The signal from the affected variables in the affected subset of the population should be amplified with the COSA algorithm, leading to higher power than the other two methods that assume a homogeneous population. With respect to effect sizes, MMR and Euclidean-MDMR should still perform similarly, but estimates of δ resulting from COSA-MDMR should do a better job differentiating affected variables from unaffected variables than MMR, so the relationship will no longer necessarily be linear.

6.2. Results

Recall that when q = 1 and D is computed with Euclidean distances, the MDMR test statistic is equivalent to the linear model test statistic. Furthermore, when COSA distances are computed on a single outcome variable, they are equivalent to Euclidean distances. As a result, the condition in which one predictor variable influences a single outcome variable led to identical test statistics and measures of effect size whether analyzed with linear regression, Euclidean-MDMR, or COSA-MDMR, as expected. Results are therefore presented only for the conditions that differentiated the three methods. We begin by reporting results concerning the statistical power of the three techniques. Then we discuss the relationship between the MDMR randomization-based effect size measure δ and measures of effect size from the linear model, and finally we report the ability of δ to correctly identify associations between predictors and outcomes.

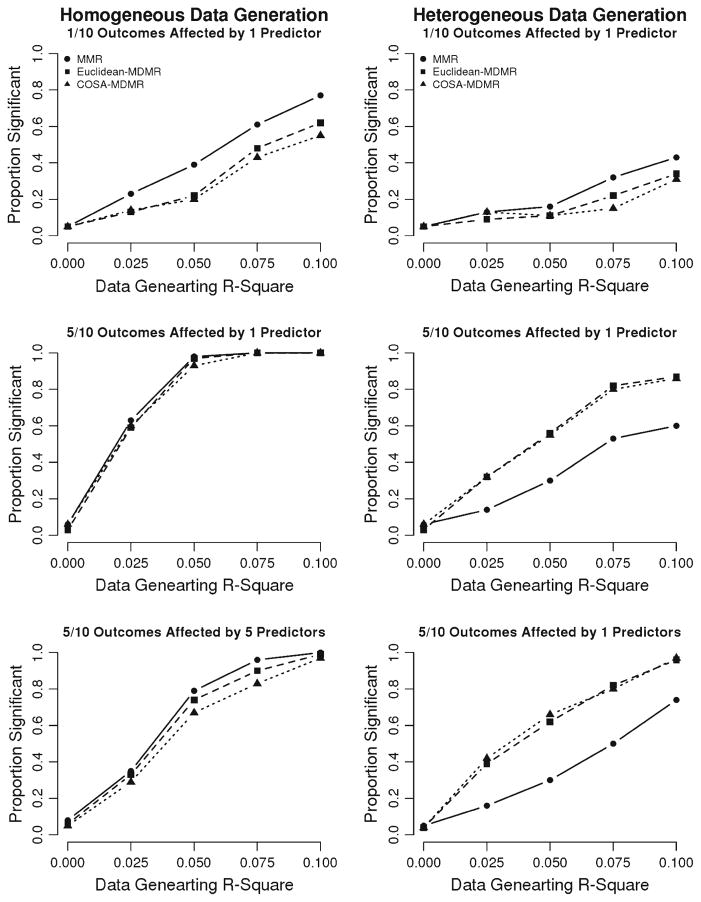
The sub-conditions in which the predictors and outcomes were generated independently demonstrated that all three methods yield well-controlled Type-I error across all data-generating conditions considered. As expected, the power of MMR was slightly greater than or equal to the power of MDMR when data came from a homogeneous population (i.e., when MMR was the true data-generating model). This was also the case given a heterogeneous population in which only one variable was affected in each sub-group by a single predictor variable. When the number of affected variables in a heterogeneous population, however, was increased to five, both Euclidean- and COSA-MDMR resulted in notably higher power than MMR, which requires the assumption of fixed regression coefficients for the entire population. Across all conditions, the power of MDMR was similar using both Euclidean and COSA distances. See Fig. 4 for illustrations of the power of all three techniques in each data-generating condition.

Figure 4.

Power of MMR, Euclidean-MDMR, and COSA-MDMR with dichotomous outcomes. Each row corresponds to a data-generating model. The left column displays results coming from a homogeneous population in which the same outcome variables were affected in the entire population. The right column corresponds to scenarios in which two unobserved subgroups in the population differed in which outcome variables were affected by the predictor(s).

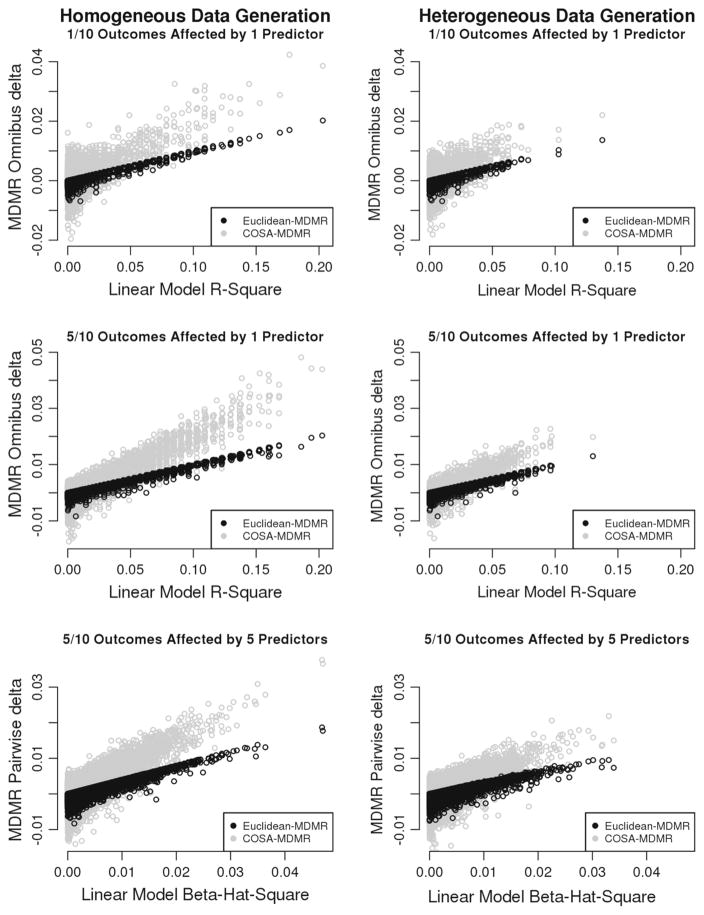
Across all conditions, δ was linearly related to the corresponding effect size measure from the linear model. That is to say, in the conditions that used only one predictor, the overall measure of δ was linearly related to R², and in the conditions that used multiple predictors, the measure of δ computed for each predictor-outcome pair was linearly related to β̂² from the linear model. The Euclidean-based δ, denoted δ_E, had a stronger relationship with the effect sizes of the linear model than did δ based on COSA distances (δ_C), and δ_C grew faster relative to the effect size measures of the linear model than did δ_E. When R² or β̂² was near zero, δ_E varied between roughly 0.00 and −0.01, and δ_C varied between roughly 0.01 and −0.01, with the negative estimates reflecting spurious increases in r̃² resulting from randomly permuting variables that had no true effect. As discussed in Sect. 4, negative estimates of δ can be interpreted in the same way as a zero-estimate, and they are not uncommon when using a single permutation to compute δ, which was done here for the sake of computation time. As expected, all measures of effect size tended to be larger when computed on data arising from a homogeneous population. See Fig. 5 for illustrations of the results comparing δ to corresponding measures of effect size from the linear model.

Figure 5.

Effect size measures of the linear model (horizontal axes) versus MDMR (vertical axes) with dichotomous outcomes. Like Fig. 4, each row corresponds to a data-generating model. The left column displays results coming from a homogeneous population in which the same outcome variables were affected in the entire population. The right column corresponds to scenarios in which two unobserved subgroups in the population differed in which outcome variables were affected by the predictor(s).

Beyond comparing δ to measures of effect size in the linear model, it is important to assess the ability of δ to detect which variables are indeed related to the predictors and which are not. That is, it is important to estimate the probability to correctly detect predictor-outcome associations using δ as well as the probability that δ will incorrectly conclude that unrelated predictors and outcomes are related. Doing so is not straight-forward, however, because δ is not a decision criterion, but rather a continuous measure of effect size. In order to estimate true- and false-positive rates for detecting associated predictors and outcomes, a threshold must be applied to δ such that estimates of δ above the threshold result in the conclusion that a predictor and outcome are related, and estimates below the threshold result in the conclusion that they are not. The true- and false-positive rates will depend on the chosen threshold, with larger thresholds resulting in lower true-positive rates and smaller thresholds resulting in higher false-positive rates. Rather than conducting this procedure for a single threshold, we employ receiver operating characteristic (ROC) curves that estimate δ’s true-positive and false-positive rates across all possible thresholds.

Figure 6 displays the results of these analyses in four plots that correspond to different data-generating effect sizes for the subset of affected variables. In each plot, the ROC curves for δ_E and δ_C are displayed that were computed on both homogeneous and heterogeneous populations. The true-positive rate (TPR) increases much more quickly relative to the false-positive rate (FPR) when considering data arising from a homogeneous population, and higher data-generating R² results in higher TPR relative to FPR. The COSA-based δ_C performs worse than δ_E for most thresholds. However, as the data-generating R² begins to grow, the ROC curves for both δ_E and δ_C begin to approach the top-left corner of the plot, indicating simultaneously high TPR and low FPR, and therefore strong performance in correctly detecting associations between predictors and outcomes. It is likely that the performance of both δ_E and δ_C would be even stronger given a larger sample size and/or if more random permutations of each outcome variable were used to compute δ.

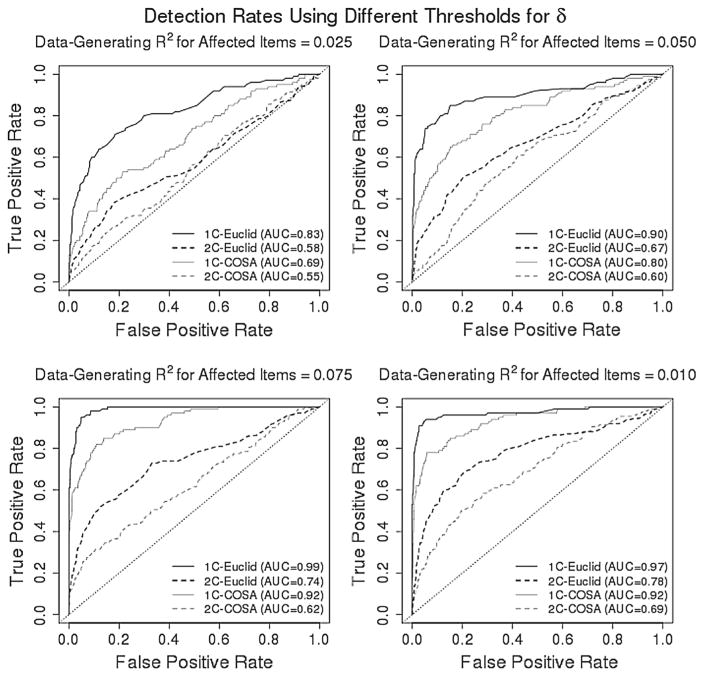
Figure 6.

Receiver operating characteristic (ROC) curves that estimate δ’s true-positive and false-positive rates across all possible decision criteria based on δ. These results correspond to conditions in which one of ten dichotomous outcome variables was affected by a single predictor. The four plots are separated by data-generating R² for the variable that was affected, and within each plot, the ROC curves are given for both Euclidean- and COSA-based δ computed on both homogeneous (1C) and heterogeneous (2C) populations. The dotted diagonal line across each plot indicates performance from random chance, and the closer a ROC curve gets to the top-left corner of the plot (i.e., 100% detection of true effects and a zero false-positive rate), the better the performance of the classifier. This performance is quantified using the area under the curve (AUC), with larger AUC indicating better performance.

Finally, we note that MMR requires the assumption of a normally distributed outcome variable. To compare the methods when this assumption is satisfied, we also conducted these analyses on normally distributed outcomes in all data-generating conditions. The results of this followup mirrored the results described above with respect to the power of Euclidean-MDMR and MMR, as well as the behavior of δ_E. The only substantial change in results associated with the switch to normally distributed outcome data concerned not MDMR, but rather the COSA algorithm. In its attempt to account for the possibility that different variables can characterize different subsets of the population, it tended to amplify the signal of unaffected outcome variables rather than affected variables when the outcomes were normally distributed. As a result, the power of COSA-MDMR relative to Euclidean-MDMR and MMR was lower for normally distributed outcomes than for dichotomous outcomes, and δ_C performed poorly on normally distributed outcomes.

7. Empirical Example: Predicting Personality Profiles

To illustrate the usefulness of MDMR in the context of quantitative behavioral research, we present an empirical example that employs MDMR to identify predictors associated with individual differences in personality profiles. This example illustrates how to conduct MDMR in practice, and it shows that using MDMR can result in the detection of multivariate associations that are not marked as significant by MMR.

7.1. Data Description

A cross-sectional sample of 985 participants in the Notre Dame Study of Health & Well-Being (Bergeman & Deboeck, 2014) provided personality data using the NEO five-factor inventory (Costa & McCrae, 1992). Using these data, scores on 26 personality facets were computed (see the vertical axis of Fig. 7 for a list of the facets). The goal of the analysis was to explain individual differences among these personality profiles using age (18–91 years), sex (58% female), education level, and self-reported health measured by the Health Status Checklist (Belloc, Breslow, & Hochstim, 1971). The effects of interactions between these predictors on personality profiles were also of interest. After removing subjects with any missing data (assumed to be missing at random), our operational sample size was 891.

Figure 7.

Estimates of the omnibus (leftmost column) and conditional (remaining columns) effect size δ on each personality facet (rows). Results are shaded according to the size of the estimated effect, and blank cells correspond to zero (or below zero) estimates.

7.2. Analyses Performed

All outcome variables were scaled to unit variance prior to both analyses so that they each had equal impact on the test statistics. A standard MMR model was fit to the data including the four main effects as well as all possible two-, three-, and four-way interactions between the covariates, resulting in 15 total predictor variables. The same design matrix was used in a Euclidean-MDMR analysis in order to compare results from the two approaches.

Some outcome variables followed non-normal, long-tailed distributions. The extreme scores in these distributions have the potential to be disproportionately influential when modeled by methods like MMR and Euclidean-MDMR that are based on squared differences. For example, “angry hostility” is an ordered four-category variable with a substantial positive skew such that only 2.9% of subjects scored in the highest category. In light of these distributions, MDMR was also conducted on a distance matrix constructed using the more robust Manhattan distance between each pair of personality profiles.

7.3. Results

7.3.1. Identifying Significant Effects

Prior to conducting MDMR, we assessed whether permutation tests or analytic p values should be used by computing ñ = 203.84 for Euclidean distances ñ = 257.20 for Manhattan distances. According to the guidelines discussed in Subsect. 5.3 that are illustrated in Fig. 2, ñ was large enough in both cases to inspire confidence in the validity of the analytic null distribution for this application, so MDMR p values were all computed analytically.

The use of Euclidean-MDMR and MMR both resulted in very small p values for all four main effects (all less than 5 × 10⁻⁸). Both sets of results indicated that the interaction between age and health is also significantly related to the personality facets (p values of 0.006 and 0.028 for Euclidean-MDMR and MMR), as is the interaction between age and education (p = 0.002, 0.005).

The methods resulted in different conclusions, however, regarding the effects of two other predictors. Using MMR to model the sums of squares of the outcome variables resulted in the identification of a significant interaction between age and sex (p = 0.011) that did not meet the standard significance criterion (α = 0.05) using Euclidean-MDMR (p = 0.056). On the other hand, modeling these data from a person-centered approach resulted in the detection of a higher-order effect that was not deemed relevant when using the variable-centered approach. Specifically, Euclidean-MDMR suggested that four-way interaction between all of the covariates was found to be a significant predictor of individual differences among personality profiles (p = 0.020). The variable-centered approach had virtually no power to detect this effect (p = 0.499).

The robust approach to MDMR using Manhattan distances yielded the same inferences as Euclidean-MDMR, though the p values differed slightly. Most notably, the robust approach resulted in less power to detect the age by sex interaction (p = 0.102) and more power to detect the four-way interaction (p = 0.010) than both Euclidean-MDMR and MMR.

These results illustrate that there is not necessarily a single best statistical approach to answering a complex multivariate research question. Rather, researchers should choose a method that reflects their goals and assumptions. Beyond the philosophical distinction between variable- and person-centered methods that differentiates MMR and MDMR in general, the three methods used in this example reflect different practical assumptions as well, which contributes to their differing results. Both MMR and Euclidean-MDMR are appropriate for modeling outcomes with thin-tailed distributions due to the explicit normality assumption required to conduct MMR and the sensitivity to outliers that characterizes Euclidean-MDMR. Manhattan distances are less sensitive to outliers, making Manhattan-MDMR potentially more attractive for researchers interested in conducting a person-centered association test when the outcome variables are characterized by skewed or otherwise heavy-tailed distributions. Importantly, Euclidean and Manhattan distances are only two examples from a pool of diverse distance metrics that can be used to quantify differences between response profiles in many different ways that have been designed to reflect different assumptions about a multivariate outcome. Prior to conducting a person-centered association test with MDMR, researchers should carefully consider their data and their goals in order to select an appropriate quantification for the distance between response profiles.

7.3.2. Interpreting MDMR Effects

To further investigate the nature of the covariate effects on differences among subjects’ personality profiles, δ statistics (Eq. 13) were computed to evaluate the effect size of the omnibus effect on each personality facet. Pairwise δ statistics were also computed to measure the conditional effect sizes of each predictor that was identified as significantly related to differences among personality profiles. Each δ statistic was computed 50 times with different random permutations each time, and Fig. 7 reports the median value of each statistic when computed on Euclidean distances. Manhattan distances resulted in the same pattern of effect sizes.

The omnibus δ statistics suggested that some personality facets (e.g., “angry hostility,” “anxiety,” “trust”) were more highly related to the set of predictors than others (e.g., “assertiveness,” “gregariousness”). All estimated omnibus effect sizes, however, were greater than zero, indicating that all facets contributed to the significant relationship between response profile (dis)similarities and the set of predictors as a whole.

The pairwise δ estimates quantify the different conditional effects of each predictor on each outcome variable. The conditional main effect of self-rated health was found to be highly related to personality facets like “activity” and “positive emotions” but weakly related to facets like “values” and “aesthetics.” Age was found to have a more substantial relationship with “trust” and “vulnerability” than many other facets, and the facet most impacted by the conditional effect of education was “ideas.” The main effects tended to have larger and broader conditional effects than the interactions, which tended to influence a smaller subset of personality facets with comparatively weaker effects.

8. Discussion

Person-centered methods are useful tools for studying differences between response profiles on a MV dependent variable. The two major advantages relative to variable-centered methods are the fact that they do not require the specification of a particular distribution for the variables comprising the MV outcome and that they do not require assumptions regarding the relationships among the outcome variables (Bauer & Shanahan, 2007; Bergman & Magnusson, 1997; Breslau et al., 2005). The current paper has extended multivariate distance matrix regression (MDMR), a person-centered regression technique that tests the association of response profile differences and a set of independent variables (Anderson, 2001; McArdle & Anderson, 2001), by deriving and validating the asymptotic null distribution of its test statistic as well as providing a measure of effect size for each variable comprising the MV outcome.

The availability of theoretical p values makes MDMR a newly viable tool in fields that require large sample sizes and/or precise, small p values. For example, Zapala & Schork (2012) expressed interest in using MDMR in gene-finding studies that seek to find genetic markers associated with multivariate outcome data, but noted that such tests were not computationally feasible using permutation tests because of the stringent multiple testing correction associated with testing hundreds of thousands of genetic markers. Furthermore, online resources such as Amazon Mechanical Turk have made the collection of large, multivariate survey data easier than ever (Buhrmester, Kwang, & Gosling, 2011). The derivation of the asymptotic null distribution of the MDMR test statistic facilitates the use of MDMR on such datasets, and the empirical example presented in Sect. 7 illustrates the potential advantages of doing so.

MDMR can be used to model data characterized by a sample size that is smaller than the number of outcome variables. In these cases, all of the n MDS axes of the resulting distance matrix are likely to be relevant in describing individual differences among the q outcome variables because n < q. This would typically result in a small adjusted sample size (Eq. 16) and therefore a failure to meet the asymptotic requirements to confidently utilize the null distribution. When a dataset is insufficient to result in a valid asymptotic null distribution, permutation tests are recommended if they are computationally feasible. If, however, permutation tests are computationally infeasible despite a sample size small enough that the asymptotic null distribution is inappropriate, then analytic p values can still be utilized without an inflated Type I error rate. Our simulations indicated that they are likely to be conservatively biased in this case, but having the option to conduct an underpowered test is preferable to being unable to conduct the test at all.

The derivation of the asymptotic distribution of the MDMR test statistic also has implications for theoretical developments to multivariate multiple regression (MMR) and MANOVA. When using these methods, significance tests rely on approximate F-statistics which in turn yield approximate p values. There are several approaches to computing such approximations (e.g., Wilks’ Lambda, Pillai’s Trace, Hotelling-Lawley Trace, Roy’s Largest Root) that can yield different results when applied to the same data (Bray & Maxwell, 1985). Due to the computational similarities between the MDMR test statistic and the multivariate generalization of linear model test statistic, we have used an approach similar to the one presented in Sect. 3 to derive what we believe to be the true asymptotic null distribution of the multivariate generalization of the F-statistic. We are validating this distribution empirically in an ongoing study.

Regarding the proposed measure of MDMR effect size, the second simulation study demonstrated that the effect size measure δ can indeed be used to characterize associations between predictors and individual outcome variables, thereby rendering MDMR a more informative statistical tool. Importantly, the simulation results also illustrated the fact that the behavior of δ will differ depending on the measure of dissimilarity used to construct D. We therefore suggest studying its behavior with a brief simulation study prior to using the δ statistic in conjunction with a distance metric not discussed here.

The empirical example, as well as the second simulation study, illustrated that MDMR can result in higher power than MMR in some circumstances. On the other hand, the second simulation study also demonstrated that several of the outcome variables must be associated with the predictors in order for MDMR to perform well. Because distances between individuals are computed using all outcome variables, the signal of a few affected variables is notably diminished by the inclusion of variables unrelated to the predictors, leading to suboptimal power when using MDMR. This is unlikely a problem in practice, however, because multivariate regression techniques including MDMR are typically used with the expectation that the predictors will influence multiple variables in the outcome data.

We expected that the combination of MDMR with a signal-amplification algorithms such as COSA (Friedman & Meulman, 2004) would further increase the odds of detecting effects in potentially heterogeneous populations. However, in the simulations presented here, combining MDMR with COSA distances did not result in notably higher power than using Euclidean distances when outcome data were dichotomous, and COSA-MDMR underperformed its Euclidean counterpart when using normally distributed outcomes. This is likely due to the COSA algorithm being underpowered to differentiate subgroups with a sample size of only 200. With larger sample sizes, COSA-MDMR has been shown to demonstrate high power even with effect sizes smaller than those considered here (Lubke & Mcartor, 2014), so it is likely that COSA-MDMR would gain an advantage over Euclidean-MDMR if these simulations were repeated with a larger sample size.

It is important to note that in fields like ecology and genetics, MDMR is commonly utilized with distance metrics that are quite different than the ones considered here. We have not studied the properties of the proposed null distribution in conjunction with such distance metrics in great detail. The fact that it depends on the properties of each distance matrix that it is used to evaluate inspires confidence that it should be asymptotically correct when using virtually any distance metric. That said, researchers who use MDMR with distance metrics that are highly dissimilar to the ones presented here are advised to assess the behavior of the analytic p values before adopting them.

Since it was first proposed, MDMR has become a popular person-centered method for multivariate association tests that has seen frequent use in the fields of ecology (Anderson & Walsh, 2013; Braeckman, Van Colon, Soetaert, Vincx, & Vanaverbeke, 2011), biology (Carmody et al., 2015), genetics (Kelly et al., 2015, Salem, O’Connor, & Schork 2010), and neuroscience (Satterthwaite et al., 2015; Shehzad et al., 2014), among others. The empirical example presented here illustrates the benefits of with using MDMR in the context of psychological research, and the two proposed developments to the MDMR framework substantially increase the appeal of MDMR as a powerful, informative, person-centered alternative to traditional variable-centered regression.