Distinct structural mechanisms determine substrate affinity and kinase activity of protein kinase Cα

Abstract

Protein kinase Cα (PKCα) belongs to the family of AGC kinases that phosphorylate multiple peptide substrates. Although the consensus sequence motif has been identified and used to explain substrate specificity for PKCα, it does not inform the structural basis of substrate-binding and kinase activity for diverse substrates phosphorylated by this kinase. The transient, dynamic, and unstructured nature of this protein–protein interaction has limited structural mapping of kinase–substrate interfaces. Here, using multiscale MD simulation-based predictions and FRET sensor-based experiments, we investigated the conformational dynamics of the kinase–substrate interface. We found that the binding strength of the kinase–substrate interaction is primarily determined by long-range columbic interactions between basic (Arg/Lys) residues located N-terminally to the phosphorylated Ser/Thr residues in the substrate and by an acidic patch in the kinase catalytic domain. Kinase activity stemmed from conformational flexibility in the region C-terminal to the phosphorylated Ser/Thr residues. Flexibility of the substrate–kinase interaction enabled an Arg/Lys two to three amino acids C-terminal to the phosphorylated Ser/Thr to prime a catalytically active conformation, facilitating phosphoryl transfer to the substrate. The structural mechanisms determining substrate binding and catalytic activity formed the basis of diverse binding affinities and kinase activities of PKCα for 14 substrates with varying degrees of sequence conservation. Our findings provide insight into the dynamic properties of the kinase–substrate interaction that govern substrate binding and turnover. Moreover, this study establishes a modeling and experimental method to elucidate the structural dynamics underlying substrate selectivity among eukaryotic kinases.

Introduction

Substrate selectivity of protein kinases is currently best rationalized by a consensus amino acid sequence flanking the phosphorylated serine or threonine, termed the substrate recognition motif (1). As we have shown recently (3), this rationale does not inform the relative specific activity of kinases for distinct substrates, nor does it address the molecular mechanisms for substrate selectivity in a cellular environment (2). We have recently reported an inverse correlation between specific activity and binding affinity for protein kinase Cα (PKCα) (3). In this study, we build upon this observation to broadly dissect the structural basis of kinase-specific activity for PKCα.

Despite the multitude of high-resolution structures of protein kinases (4), there is limited structural information on the kinase–substrate interface (5) due to major challenges. 1) The inherently transient nature of kinase–substrate interactions, thereby restricting high-resolution structures to high affinity, often autoinhibitory substrates (6). 2) The phosphorylation site is often located in structurally disordered regions of the substrate protein, which may allow for more flexible accommodation in the kinase active site (7, 8). 3) Although the catalytic domains of eukaryotic kinases are structurally conserved (9, 10), the local environment around the substrate-binding pocket of the kinase catalytic domain varies between kinases (11). To overcome these challenges that limit conventional structural methods, we have combined multiscale molecular dynamics (MD)⁴ simulations with novel FRET-based sensors to obtain detailed structural information on the dynamics of the kinase–substrate interaction.

We have previously used FRET sensors to probe the weak (μm) interactions between kinase and peptides derived from substrate proteins (3, 12). These FRET sensors are designed using Systematic Protein Affinity Strength Modulation (SPASM) (13), which has the sensitivity to measure weak protein–protein interactions and is scalable to multiple substrates. Using SPASM measurements on 14 different substrate peptides (shown in supplemental Fig. S1) with PKCα, we showed that above a minimum-required binding affinity to induce kinase activity, the kinase-specific activity is inversely correlated with the substrate-binding affinity (3). This inverse correlation between the binding affinity and kinase activity toward substrates are shown in supplemental Fig. S1. Consequently, substrates with high-affinity but low activity outcompete their low-affinity but high activity counterparts, suggesting a simple biochemical mechanism for selective substrate phosphorylation in cells. However, our FRET sensor measurements lack the structural resolution to dissect the conformational dynamics of the interaction, and identify specific residues that modulate binding affinity and activity. Given that the region of the substrate peptide that binds to PKCα is largely disordered, multiscale MD simulation methods are ideally suited to study the ensemble of conformations that the substrate peptides adopt when they bind to PKCα.

The generalized Newton-Euler inverse mass operator (GNEIMO) internal coordinate molecular dynamics method has several advanced multiresolution features that are essential for the enriched conformational sampling of disordered substrate binding to PKCα (14, 15). The GNEIMO method allows coarsening of the dynamic model of the protein, without using a coarse grain force field that loses the atomistic resolution of the simulations (16–18). In GNEIMO torsional MD, the helices/β-sheets in the catalytic domain are treated as a rigid body, whereas the loops and peptide-binding surfaces in the kinase and the entire substrate peptide are modeled as flexible torsions (see supplemental Fig. S2). Use of such a coarse grain model permits a broader range of conformational sampling of the kinase-substrate conformational ensemble. Here, we have used the GNEIMO coarse grain dynamic model to perform torsional MD simulations of the binding of 14 peptide substrates (shown in supplemental Table S1) to PKCα. The predictions of the residues in the substrate that contribute to binding and kinase activity from the GNEIMO MD model have been tested extensively with SPASM FRET sensors and kinase activity assays to gain insight into the structural dynamics of kinase–substrate interactions. The schematic of the workflow combining the GNEIMO with SPASM FRET methods to probe the dynamics of the kinase peptide substrate interactions is shown in Fig. 1. Details of this workflow are described under “Experimental procedures.”

Figure 1.

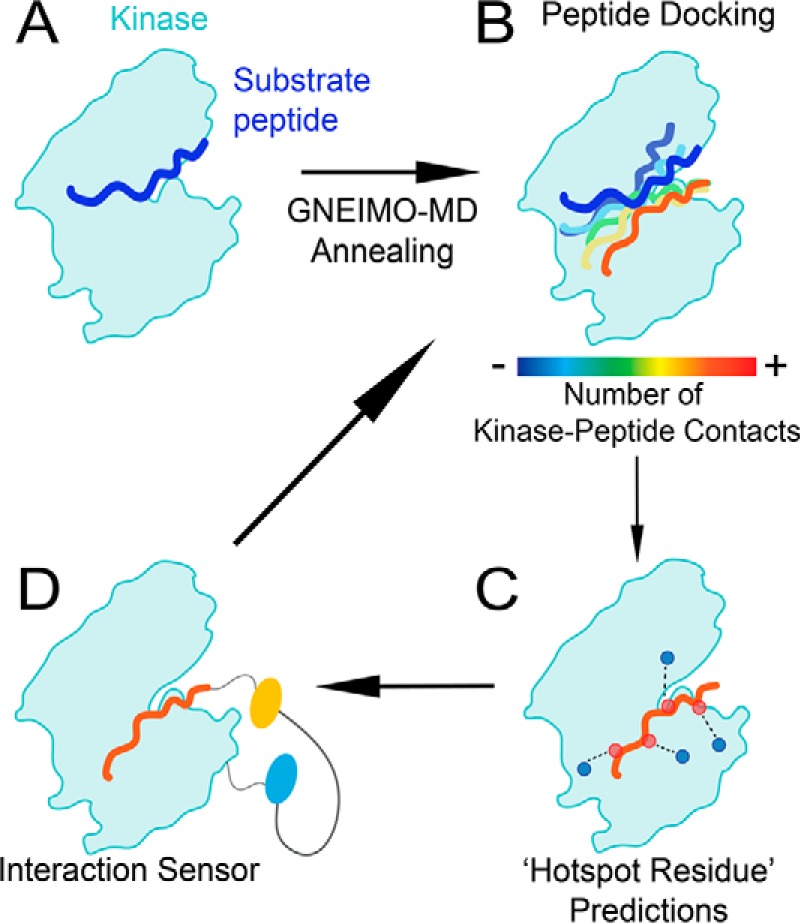
Combining computational and experimental approaches to dissect the kinase–substrate interaction. A, PKC–substrate interaction is homology modeled from the PKCι–Par3 interaction (PDB ID 5HI1). B, GNEIMO torsional MD is used to obtain a kinase–substrate conformational ensemble. C, structural analysis is used to identify hot spot residues and motifs within the kinase and substrate that contribute to binding and catalytic activity. D, SPASM FRET sensors are used to test GNEIMO-MD predictions using site-directed mutagenesis. Experimental results are used to validate GNEIMO-MD predictions and refine computational methods.

Using this combination of computational and experimental methods, we find that the substrate region N-terminal to the phosphorylated serine residue determines the kinase–substrate interaction affinity. In contrast, high kinase activity requires a high degree of conformation flexibility within the substrate region C-terminal to the phosphorylated serine residue. High activity substrates show greater conformational flexibility within the kinase active site compared with their low activity counterparts. An arginine residue located either two or three amino acids C-terminal to the phosphorylated serine residue, optimally positions the phosphorylated serine for catalysis. Taken together, our study reveals two distinct mechanisms that dictate substrate-binding affinity and activity, whereas emphasizing the importance of substrate conformational dynamics in determining the relative activity of a kinase for distinct substrates.

Results

The residues in the N terminus of the peptide substrates contribute to substrate binding in PKCα

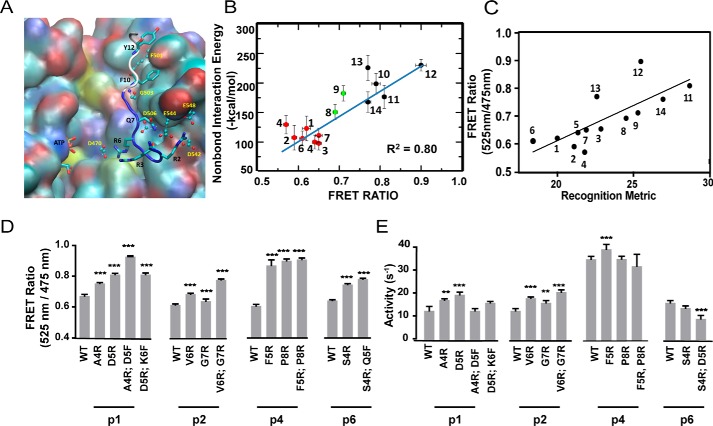
We have studied the dynamics of 14 peptide substrates binding to the catalytic domain of PKCα using GNEIMO coarse grain MD simulations followed by all-atom MD simulations. Fig. 2A shows the binding groove of the tight binding peptide p12 that shows the lowest kinase activity among the 14 peptides (see supplemental Fig. S1 for the relative binding affinities and kinase activity of all 14 substrate peptides). Our MD simulation results indicate that an acidic patch of residues located in the substrate-binding groove of PKCα make strong electrostatic interactions with the basic residues in the N terminus of the peptide substrates (Fig. 2A and supplemental Fig. S3). In contrast, the residues in the kinase that interact with the C terminus of the peptide are hydrophobic, resulting in a deep insertion of the peptide C terminus (Fig. 2A). We analyzed the residues in PKCα that make sustained (present in over 40% of the snapshots from MD simulations) salt bridge, hydrogen bond, or van der Waals contact with residues in the N terminus of the peptides. The acidic patch of residues consisting of Asp³⁸³, Asp⁴⁷⁰, Asp⁵⁰⁶, Glu⁵³³, and Glu⁵⁴⁴, Glu⁵⁴⁸, and Asp⁵⁴² (shown in spheres and sticks in Fig. 2A) make close contact with the N terminus residues of the peptide substrates (see the electrostatic surface shown in supplemental Fig. S3). Many of these acidic residues listed above are conserved across the PKC family as shown in supplemental Fig. S4.

Figure 2.

Electrostatic interactions between residues in the N terminus of the peptide substrate and the kinase catalytic domain are major determinants of binding strength. A, predicted binding site of the tight binding peptide substrate p12 in PKCα. The backbone atoms of the residues before the Ser that gets phosphorylated in the substrate p12 are shown in blue and the residues after Ser are shown in white. The residues in the peptide substrate are shown in sticks. The residues in PKCα that make strong contact with the peptide are shown in ball and sticks. B, calculated average interaction energy of the N terminus of the peptide substrates with PKCα versus FRET intensity ratio. For clarity, the weak, medium, and strong binding peptide substrates are shown in red, green, and black spheres, respectively. The error bars for FRET measurement and the non-bond interaction energy represent the mean ± S.E. and the standard deviation, respectively. C, FRET ratio of SPASM sensors show a linear correlation with a recognition metric derived by Nishikawa et al. (14). D, site-directed mutagenesis of residues in peptides p1, p2, p4, and p6 identified from the MD simulation analysis to improve the binding affinity. Mutagenesis of N-terminal residues to Arg enhances kinase-substrate interaction as measured by FRET ratio. E, kinase activity of mutant peptide substrates shown in D. Mutagenesis of N-terminal residues to Arg marginally increase kinase specific activity compared with wild-type counterparts. The FRET results are expressed as mean ± S.E. of three independent experiments performed in triplicate (n ≥ 9). *, p < 0.05; **, p < 0.005; ***, p < 0.0005; ****, p < 0.0001.

The stronger electrostatic interactions of the peptide N terminus compared with the C terminus suggested that this region contributes substantially to the peptide-binding energy. To test this possibility, we calculated the average interaction energies, averaged across the three all-atom MD trajectories for each peptide substrate and compared them to previous FRET measurements (3). The calculated interaction energies between the N terminus residues of the peptide substrate with the catalytic domain of PKCα correlate linearly with the measured binding affinity of kinase–substrate peptide interaction (3, 13) with a R² = 0.8, as shown in Fig. 2B. However, the calculated interaction energies of the entire peptide substrate with the catalytic domain of PKCα did not show a good correlation (R² = 0.48; supplemental Fig. S5).

The structural ensemble for the peptide–PKC interface interactions were generated using GNEIMO-MD simulations followed by all-atom MD simulations as described under “Experimental procedures.” To test these predicted peptide–kinase interactions, we proposed mutations in the poor binding and high activity peptides such as p1, p2, p4, and p6 to improve their binding affinity to the kinase without affecting the kinase activity toward these peptides. We calculated the average interaction energy of each residue in every peptide substrate with the kinase. Using the residues that contribute weakly to the substrate–kinase interaction, we predicted mutations in these four weak binding peptides and these mutants were expressed as FRET sensors along with the catalytic domain of PKCα (see “Experimental procedures”). Residue numbering on the peptide substrates is from the N to C terminus with the phosphorylated Ser/Thr numbered as position 9 for all peptide substrates (see supplemental Table S1). Each of these mutations showed a significant increase in FRET ratio, suggesting an increase in binding affinity of the peptide for the catalytic domain (Fig. 2D). It is clearly seen that mutation of N terminus residues to a basic residue such as Arg increases affinity for the acidic patch of PKCα and therefore improves their binding.

As seen in Fig. 2E, most of the mutations in the N terminus residues of p1, p2, p4, and p6 showed a small but not significant increase in kinase activity. This suggests that the kinase activity on these 14 peptide substrates may be governed additionally by other mechanisms. Interestingly, the kinase–substrate-binding affinity correlates linearly with a recognition metric derived based on the consensus motif (14) (Fig. 2C). Nishikawa et al. (14) characterized the substrate recognition motif of PKCα using a degenerate peptide library phosphorylated by the kinase. For each location relative to the phosphorylated serine/threonine, they reported the fold-enrichment in substrate phosphorylation with a specific amino acid compared with a degenerate sequence. With the assumption that the reported fold-enrichments are additive, we linearly combined these values for all conserved residues to arrive at a recognition metric. Our finding highlights the role of consensus motif and its correlation to the peptide substrate-binding affinity correlation to the peptide substrate-binding affinity and not to the kinase activity. We examined further the properties of the dynamics of the peptide substrate that would correlate to the kinase activity. The peptide substrates with good kinase activity show an enrichment of catalytic conformations during the dynamics simulations.

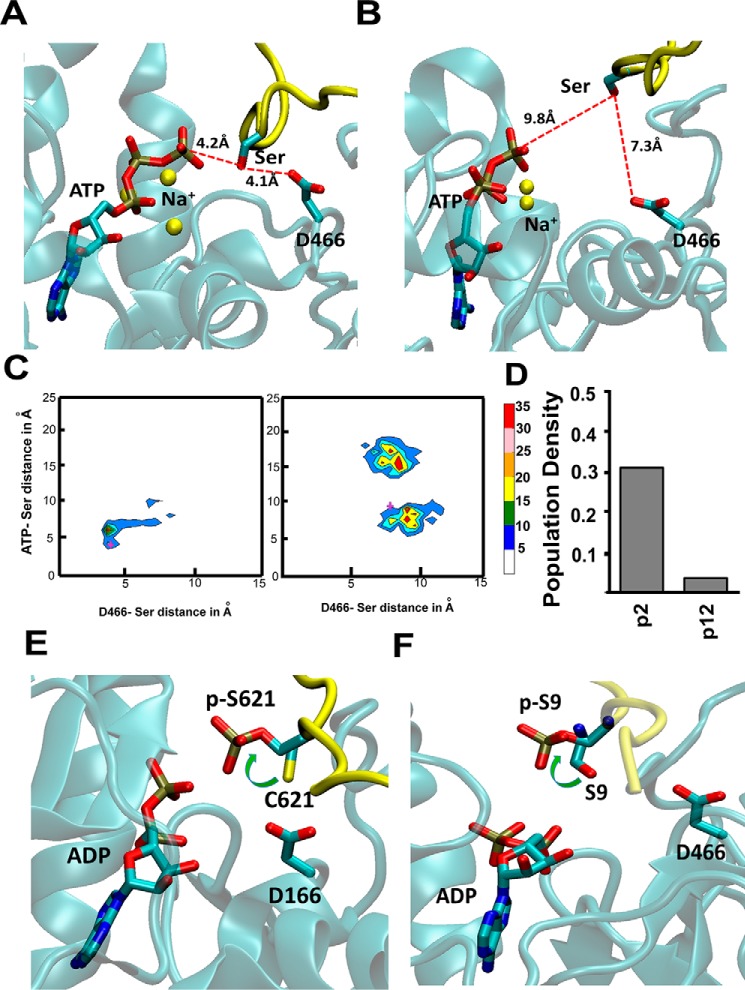
Recently, Gerlits et al. (15) solved crystal structures of PKA that represent different snapshots of the kinase in the catalytic process of transferring the PO₄ group, to show a plausible “catalytic conformation” of PKA. Such a catalytic conformation shows the Ser/Thr that gets phosphorylated in the peptide substrate close to the Asp¹⁶⁶ (residue number as in PKA) as well as the γ-PO₄ group of the ATP. The Asp¹⁶⁶ is involved in abstracting the proton from the hydroxyl group of the pSer that enables the transfer of the PO₄ group from ATP to pSer/Thr in the peptide substrate. We used this definition of the catalytic conformation to analyze the differences in the population of the catalytic conformation in the conformational ensemble derived from MD trajectories for the high activity peptides p1, p2, and p3 compared with the poor activity peptides p10, p11, and p12.

Fig. 3A shows a snapshot from the MD simulation trajectory of high activity peptide p2 that shows the shortest distance between the Ser in p2 and Asp⁴⁶⁶ and the γ-PO₄ group of the ATP. This conformation is representative of a plausible catalytic conformation of PKCα as seen in our dynamics simulations. The oxygen atom of the Ser in the peptide is about 4 Å from both the Asp⁴⁶⁶ of PKCα and the γ-PO₄ group of the ATP. We also observed that the Na⁺ ions used to neutralize charges in the MD simulations cluster around the PO₄ groups of the ATP. The position of these Na⁺ ions is similar to the Ca²⁺ ions in the crystal structure (PDB code 4XW5) of the catalytic conformation of PKA (15). Fig. 3B shows the snapshot with the closest distance of the poor activity peptide p12 to Asp⁴⁶⁶ and γ-PO₄ group of the ATP extracted from the MD simulations. As anticipated, the catalytic distances in this low activity peptide is longer than that of the good activity of p2, thus leading to lower kinase activity of this peptide substrate. We clustered the MD ensemble for peptides p1, p2, p3, p9, p11, and p12 by the two distances of the phosphorylated Ser/Thr to Asp⁴⁶⁶ and the γ-PO₄ group of ATP as shown in Fig. 3C and supplemental Fig. S6. This population distribution shows that the highest population cluster for the good activity peptides p1, p2, and p3 is around shorter distances and is much tighter for high activity peptides compared with their low activity counterparts p9, p11, and p12 (Fig. 3C and supplemental Fig. S6). This suggests that peptides with high kinase activity are more likely to populate catalytic conformations compared with the low activity peptides as shown in Fig. 3D.

Figure 3.

High activity peptides populate catalytically favorable conformations when bound to the kinase. A and B, snapshots from MD trajectories showing the plausible catalytic conformation of the high activity peptide p2 (A) and low activity peptide p12 (B), bound to PKCα. These snapshots were selected based on the shortest distance between the Ser in the substrate to Asp⁴⁶⁶ that abstracts the proton from Ser and also to the γ-PO₄ group of the ATP. C, population distribution of various peptide conformations from three 100-ns all-atom MD trajectories for peptide substrates p2 and p12. The MD ensemble was clustered by two distances. The distance between ATP(γP) and S/T(OG) of the substrate peptide and between D466(OD) and S/T(OG). The cross marks in these two figures are the conformations for which these distances are shown in A and B. D, population density of the catalytic conformations as captured in the MD simulations. We used a cutoff of 4.2 Å in the ATP(γP) and S/T(OG) distance and 4.1 Å in the D466(OD) and S/T(OG) distance to calculate this population density. E, rotamer flip change in the χ₁ angle of the pSer/Thr in peptide substrates as seen from crystal structures before (PDB code 4XW5, PKA) and after (PDB code 4IAK, PKA) the phosphoryl transfer. F, all-atom MD simulations after the PO₄ transfer was done showed a rotamer flip in pSer in the good activity peptide substrate p1 after the PO₄ transfer to the pSer in the peptide. The panel shows the most populated rotamer of Ser/Thr in the simulations of the peptide p1 before and after the PO₄ transfer. The peptide backbone is colored in yellow and the Ser and pSer are shown in sticks.

The crystal structures of PKA (16) show a rotamer flip in the χ₁ angle of the phosphorylated Ser/Thr as shown in Fig. 3E. The side chain rotamer of the Ser/Thr in the peptide substrate flips its rotamer after the PO₄ transfer to the Ser/Thr of the peptide. To verify if we could capture this rotamer flip in the pSer/Thr in the substrate, we performed MD simulations after transferring the PO₄ group from ATP to the pSer/Thr in the substrate. To this end we extracted the best catalytic conformation with the shortest distance of Ser/Thr (OG) to the γ-PO₄ of ATP as well as to Asp⁴⁶⁶ (OD), in the peptide p1 as detailed under ”Experimental procedures.“ We then transferred the PO₄ group to the Ser/Thr of the peptide, leaving ADP in the ATP-binding site. We performed all-atom MD simulations on these two peptides bound to PKCα. We then examined the rotamer conformations of the Ser/Thr residue in the peptide substrate before and after phosphoryl transfer. Fig. 3F shows the rotamer flip of the χ₁ angle of the Ser/Thr in peptide substrates before and after the phosphoryl transfer. The rotamer change leads to moving the side chain of Ser/Thr away from Asp⁴⁶⁶ (Fig. 3F). The repulsion between the PO₄ group in pSer/Thr with Asp⁴⁶⁶ could trigger the rotamer flip in the pSer/Thr, and we speculate that this could be the initiating event for the peptide substrate to move away from the catalytic conformation before it dissociates from the kinase. In summary, our simulations show that high activity peptides show a higher population of the kinase–substrate conformations that are conducive to catalysis, with subsequent phosphoryl transfer leading to an expected change in rotamer of the pSer as seen in the crystal structures. Our dynamics simulations capture the conformational changes that lead to the catalysis of PO₄ transfer.

Basic residues at either two or three positions C-terminal to the phosphorylated serine/threonine in the peptide substrate are required to elicit good kinase activity

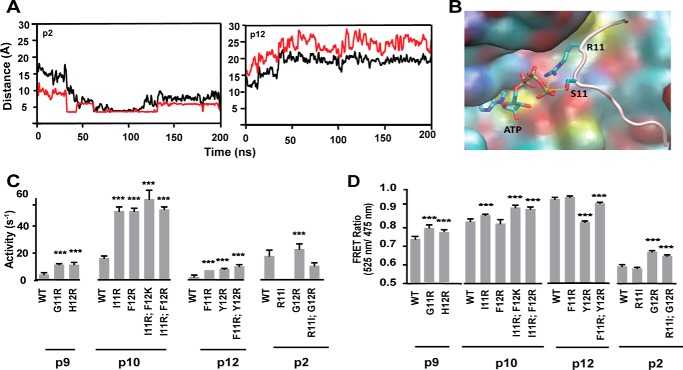
Why do high activity peptides more frequently populate active conformations? Analysis of the MD simulation results showed that long range Coulombic attraction of the Arg/Lys, located two or three residues C-terminal to the phosphorylated residue (positions 11 and 12), to the γ-PO₄ group of the ATP ushers the Ser/Thr that is adjacent to this residue closer to the ATP thereby priming phosphoryl transfer. Fig. 4A shows the plot of distance between the γ-PO₄ group of ATP and the residues at positions (Ser) 9 and 11 in the peptide substrates p2 and p12 with time in nanoseconds. In the high activity peptide p2, the Arg¹¹ in p2 gets close to the γ-PO₄ group of ATP thereby ushering in its neighbor Ser at position 9 in the peptide substrate p2. Such a long range Coulombic attraction between Phe¹¹ in peptide p12 and the γ-PO₄ group of ATP is not possible in the low activity peptide p12. Fig. 4B shows a snapshot from the MD simulations demonstrating the proximity of the γ-PO₄ group of ATP to Ser⁹ and Arg¹¹ of peptide p2. To test this further using our kinase Glo assays, we mutated to Arg/Lys these positions in the low activity peptides p9, p10, and p12 (supplemental Fig. S1). Mutation of residues at positions 11 and 12 in low activity peptides p9, p10, and p12 to Arg or Lys shows improved activity in all the three peptides (Fig. 4C). Interestingly, peptide p2 has only two basic residues, Arg⁴ and Arg¹¹, but exhibits high kinase activity. Mutagenesis of Arg¹¹ to Ile is sufficient to completely abolish the activity of this peptide (Fig. 4C). Likewise, transfer of Arg to position 12 (R11I and G12R) retains partial peptide activity attesting to the importance of the long-range Coulomb interaction mediated by an Arg/Lys residue 2–3 amino acids C-terminal to the phosphorylated Ser/Thr in driving kinase-specific activity. These single point and double mutations to Arg in the peptides p2, p9, p10, and p12 do not change their FRET ratio and therefore their binding affinities, as shown in Fig. 4D.

Figure 4.

Arginine positioned two or three residues C-terminal to the phosphorylated serine in the peptide substrate is necessary and sufficient for high kinase activity. A, plot of the time variation of the distance between the γ-PO₄ group of ATP and the OG atom in Ser in peptide substrates p2 and p12 shown in black lines and the distance between residue at position 11 to the γ-PO₄ group of ATP shown in red lines. B, representative snapshot from the MD simulations showing the close distance between the side chain Arg¹¹ and Ser⁹ of the peptide to the γ-PO₄ group of ATP. C, kinase activity measured for mutants of position 11 in peptide substrates p9, p10, p12, and p2 to show the role of Arg in position 11 of the peptides to improve the activity. Arg at positions 11 or 12 is necessary for high kinase activity. D, FRET ratio of peptide substrates. Results are expressed as mean ± S.E. of three independent experiments performed in triplicate (n ≥ 9). *, p < 0.05; **, p < 0.005; ***, p < 0.0005; ****, p < 0.0001.

High activity peptides exhibit greater conformational flexibility when bound to the kinase catalytic domain

As seen in supplemental Fig. S1, peptide substrates p10 and p13 show similar binding affinities but p13 shows significantly different kinase activity. What are the differences in the dynamics of p10 and p13 that explain the differences in their kinase activities? To examine the dynamics of the peptide substrate when bound to the kinase, we compared the root mean square fluctuation (r.m.s. fluctuation) of p10 and p13. The r.m.s. fluctuation for every residue in the peptide substrate reflects the flexibility of the peptide in the binding groove in PKCα. Supplemental Fig. S7 shows the population density of r.m.s. fluctuation for every residue in p10 and p13 when bound to PKCα during all-atom explicit MD simulations. The r.m.s. fluctuation is calculated with respect to the average structure derived from the MD trajectories as reference. Position 9 in the figure is the position of the Ser/Thr that gets phosphorylated by PKCα. Although residues N-terminal to the phosphorylated Ser/Thr display overlapping distributions of r.m.s. fluctuation, the C-terminal residues of p13 have a considerably broader distribution than p10. We examined the peptide substrates p4, p5, and p13 that exhibit similar kinase activity but substantial differences in binding affinity (supplemental Fig. S1; p4 > p5 > p13). These three peptides show similar flexibility (by r.m.s. fluctuation) for all the residues in the peptides (shown in supplemental Fig. S8). However, the interaction energies of the residues N terminus to pSer/Thr in these substrates correspond to the reported binding strengths of these peptides (shown in supplemental Table S2). Thus, higher flexibility in the region C-terminal to pSer/Thr in the peptide substrates corresponds to the better kinase activity.

Discussion

The goal of this study is to provide mechanistic insights into the structural and dynamic features of the PKCα–peptide interface that contribute to the binding and kinase activity of 14 different peptide substrates. We identify that the basic residues (Arg/Lys) located N-terminal to the pSer/Thr in the peptide substrates contribute significantly to their binding affinity. The acidic residues Asp³⁸³, Asp⁴⁷⁰, Asp⁵⁰⁶, Glu⁵³³, and Glu⁵⁴⁴, Glu⁵⁴⁸, and Asp⁵⁴² in PKCα form a negatively charged patch to embed the Arg/Lys-rich N terminus of the tight binding peptide substrates. This is in agreement with Nishikawa's metric (14) for consensus motif in the peptide sequences. However, the consensus motif metric does not correlate with the kinase activity toward these peptides. We observed that flexibility of the amino acid residues located C-terminal to the pSer/Thr in the peptides regulate the kinase activity. The more flexible the C terminus of the peptide, the better is its activity toward PKCα. The Arg/Lys positioned one or two residues from the pSer/Thr plays an important role in long-range attraction of ATP and threads the Ser/Thr close to the γ-phosphate of ATP and the catalytic residue Asp⁴⁶⁶ in PKCα. These dynamics lead to formation of catalytically competent conformations. As shown in Fig. 5, the peptide substrates that show high structural flexibility when bound to PKCα increase the proportion of conformations that position the serine/threonine residue in proximity of both the γ-PO₄ and the aspartic acid (Asp⁴⁶⁶) that is important for proton abstraction. These findings explain the wide range of kinase-specific activity observed for a range of PKCα peptide substrates.

Figure 5.

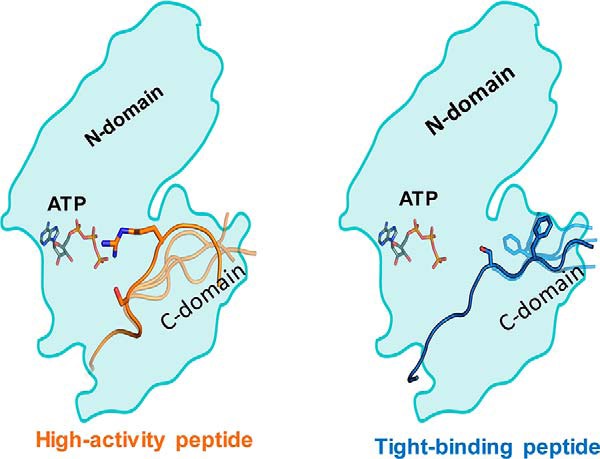
Distinct mechanisms of kinase activity and substrate-binding strengths. Left, high activity peptides display greater conformational flexibility in the domain C-terminal to the phosphorylated Ser/Thr (C-domain). An Arg/Lys residue 2–3 amino acids C-terminal to the phosphorylated Ser/Thr threads the formation of a catalytically active conformation. Right, tight binding peptides have several Arg/Lys residues N-terminal to the phosphorylated Ser/Thr that undergo strong columbic interactions with an acidic patch in the kinase catalytic domain.

The strength of the kinase–substrate interaction as determined by the FRET ratio of our SPASM sensors correlates linearly with the computed interaction energies of the kinase with the N terminus of the substrate ensemble. Interestingly, our binding rather than activity measurements correlate with an average recognition metric derived from the previously reported substrate recognition motif for PKCα. Hence, our study shows that whereas the recognition motif can guide kinase–substrate selectivity, a high degree of conservation does not imply high activity. In fact, we have shown an inverse correlation between kinase activity and binding affinity, suggesting that beyond a threshold, increased conservation of the recognition motif may reduce rather than increase kinase activity. For instance, PTP1B has a much higher specific activity that EGFR despite more residues in the latter matching the consensus motif.

Structural studies of the kinase–substrate interface have been limited by the dynamic, transient nature of this interaction. Our study showcases the synergies between multiscale molecular dynamics and SPASM FRET biosensors to gain insights into the kinase–substrate conformational ensemble. Specifically, both the multiscale MD and FRET sensors are scalable to compare and contrast distinct kinase–substrate pairings and rigorously test those using FRET measurements and kinase assays. Although the current study is focused on PKCα, the conceptual insights and technologies can be readily generalized to other kinase–substrate interactions. One of the caveats to be noted is that the absolute binding energy of the peptide to the kinase would be affected by the full-length substrate protein and not just the peptide that has been modeled in this work. However, we believe that the relative binding energies calculated from MD simulations and binding constants measured with the FRET sensors for various peptides would be proportional to the relative binding constants of the whole protein, although the absolute values of the on and off rates of the peptides may differ from the full protein substrates.

Experimental procedures

Computational methods

Homology modeling of the PKCα kinase structure

The template structure closest to PKCα is that of PKC βII with the ANP bound (PDB ID 3PFQ) (17) and hence this was used for the homology modeling of PKCα with Modeler 9 (18). Of 10 models retained from Modeler we selected the top scoring (by DOPE score in Modeler) homology model of the PKCα. We then modeled the binding of 14 different peptide substrates shown in supplemental Table S1. The starting coordinates for each peptide substrate were obtained from the crystal structure of PKB (PDB ID 1O6L) (19) that has a 10-amino acid bound peptide. We aligned the PKCα homology model to the crystal structure of PKB and then transferred the peptide from PKB by retaining the contact between the phosphorylated serine in the peptide to Asp⁴⁶⁶ in PKCα (which is Asp²⁷⁵ in the PKB crystal structure). We mutated the residues in the peptide transferred from PKB to their appropriate amino acid sequences shown in supplemental Table S1, using the mutation function in Maestro from Schrodinger Inc. Most of the peptides in supplemental Table S1 are longer than the one in the PKB crystal structure. We grew longer peptides by adding the residues in N or C terminus of the peptides using the loopModel.pl script in Modeler. After the entire peptide was grown, we optimized the side chain conformations of residues within 5 Å of each amino acid residue in the peptide taking into account the residues that are common to the neighborhood of one or more residues in the peptide. We used the Prime module in the Maestro program (20) for the side chain repacking, and then the whole complex was minimized in energy with the PRCG (Polak-Ribier conjugate gradient) method using Macromodel. The force field parameters for the initial 14 PKC–substrate complexes with ATP bound for MD simulations were assigned using the CHARMM package (21). All starting complexes were solvated using TIP3P water molecules (22), neutralized to an ionic strength of 0.15 m by adding Na⁺ and Cl⁻ ions. The system was then minimized in energy, and heated from 0 to 310 K using the default settings in the simulated annealing module of GROMACS, and equilibrated by performing 5.2 ns of MD at 310 K using NVT ensemble followed by 55 ns of MD under NPT ensemble with pressure at 1.0 atm. During the first 35 ns of the equilibration we placed position restraints to the atoms in PKCα, the peptide, and ATP, which was gradually decreased from 5 to 0 kcal/mol in steps of 1 kcal/mol. We also placed a hydrogen bond distance restraint from ATP to Lys³⁵⁰, Glu⁴²¹, and Val⁴²³ in its binding site. In addition, we also used a distance restraint from the Ser/Thr of the peptide to Asp⁴⁶⁶ in the C-lobe of PKCα. We removed all the restraints of the last 20 ns of the equilibration simulations. All the equilibration simulations for the 14 peptides bound to PKCα were performed using GROMACS5.1.0 and the CHARMM36 force field (23). A net charge of −2.0 was used for ATP. The final complex structures obtained after equilibration were used for further simulations using GNEIMO torsional MD simulation.

Optimization of peptide-binding conformation using GNEIMO-REMD dynamics simulations

The GNEIMO method is an internal coordinate MD method and when the bond lengths and bond angles are treated as rigid holonomic constraints GNEIMO performs torsional MD simulations (24–27). In this study we used the GNEIMO torsional MD method combined with the replica exchange method (REMD) (28) for enhancing the conformational sampling. We have previously shown that this GNEIMO-REMD is effective in folding small protein structures (29) as well as refinement of homology models of proteins (27, 30, 31). We have recently combined the software GneimoSim (31) with the Rosetta software for combining the advantages of torsional Monte Carlo with torsional MD simulations as well as use the side chain packing algorithms in Rosetta along with torsional MD simulations of GNEIMO for protein structure refinement. We developed the GNEIMO-REMD-ROSETTA protocol for performing annealing torsional MD simulations. This protocol as described below, is efficient in protein structural refinement and for generating an ensemble of the structures for the peptide-bound PKCα.

In this study we developed a multiscale MD protocol to optimize the binding site of the 14 different peptides to PKCα. The workflow of the multiscale MD simulations is shown in supplemental Fig. S9. We used GNEIMO-REMD with Rosetta (32) as a coarse grain dynamic model to anneal and optimize the binding of the 14 peptides in PKCα. One of the advantages of GNEIMO is that we could treat the backbone of secondary structure elements such as helices or β sheets as rigid bodies, whereas sampling the side chain and other loop regions as flexible torsions during the dynamics. Supplemental Fig. S2 shows the dynamic model of PKCα we have used in the GNEIMO-REMD simulations. The backbone torsion angles shown in blue color in supplemental Fig. S2 are treated as rigid bodies, whereas their side chains are flexible torsions. The backbone and side chain torsion angles of residues within 5 Å of ATP and the peptide are all treated as flexible torsions during GNEIMO torsional MD simulations. The details of the GNEIMO-REMD torsion MD simulations with Rosetta are given in the supplemental data.

All atomic MD simulations

We performed all-atom MD simulations in explicit solvent for each of the 14 peptide-bound PKCα. The starting conformations of PKC complex with ATP and peptide substrate for the all atomic MD simulations were obtained as follows. We clustered the conformations from the GNEIMO-REMD simulations by the root mean square deviation (r.m.s. deviation) of the main atoms. From the most populated cluster of conformations, we then chose the conformation that showed the maximum number of favorable peptide–kinase interactions for each of the 14 peptides. To this starting conformation, hydrogens were added, and the structures were solvated in the explicit TIP3P water molecules (22). MD simulations on PKC with periodic boundary conditions were performed using the GROMACS package (33) with CHARMM36 force field (23). The LINCS algorithms (34) were used for the bond and angle for water and all other bonds, allowing 2 fs of time step. For the analysis, the coordinates were saved every 2 ps. A cutoff distance of 12 Å for nonbond interactions was introduced, and the particle mesh Ewald method (35, 36) was used for long-range Van der Waals interactions. We performed MD simulations on 14 systems, each 100 ns long. Each of the 14 systems were heated slowly and equilibrated by performing 5 ns of MD at 310 K using a NVT ensemble followed by the MD under NPT conditions with a pressure of 1 bar, with initial velocities sampled from the Boltzmann distribution and with 5 kcal/mol/Ų harmonic position restraints applied to all non-hydrogen atoms of the protein and peptide substrate and distance restraints applied to crucial residues of peptide substrate and kinase receptor. Detailed information is shown in supplemental Table S1. The position and distance restraints were linearly tapered over the 55 ns of equilibration period. After equilibration to the expected temperature and pressure, a total of three production simulations of up to 200 ns were performed for each initial conformation with different initial velocities using the NPT ensemble. For the trajectory analysis, the last 100 ns of trajectory per each simulation from the MD simulations were considered using tools provided by GROMACS and Python scripts. All detailed simulation procedures are shown in supplemental Fig. S5.

Analysis of the catalytic conformations

To quantify the activity of the PKCα toward several substrates, we analyzed the distances between the phosphorous atom of the γ-PO₄ group of ATP and the side chain oxygen atom of Ser/Thr of the substrate peptide. We also calculated the distance between the side chain oxygen atom of Ser/Thr of the substrate peptide and the oxygen atom of Asp⁴⁶⁶ of the PKCα. The Asp⁴⁶⁶ is known to be involved in catalysis and proton abstraction from the hydroxyl group of the Ser/Thr of the substrate peptide. We clustered the conformations from all-atom MD simulations for each peptide by these two distances to identify which peptide substrates lead to an enrichment of the catalytic conformations. These distances are 4.4 and 2.5 Å, respectively, in the crystal structure of ATP bound with the CP20 peptide in PKA (PDB ID 4XW5) (16). Here the Ser of the SP20 peptide substrate is mutated to Cys. This crystal structure captures the optimal distances required for direct phosphoryl catalysis to happen. We call this conformation as the catalytic conformation.

MD simulations of PKCα after the phosphoryl transfer

We extracted the catalytic conformation nearest to the crystal catalytic conformation from the all-atom MD simulations for each of the 14 substrate-bound PKCα. We used this conformation and transferred the PO₄ group from ATP to the Ser/Thr of each peptide. To understand the PKCα dynamics after the phosphoryl transfer from ATP to the Ser/Thr of the 14 substrate peptides, we did the following: (i) transferred the phosphate group to the Ser/Thr of the substrate peptide and started the MD simulations of PKCα. The all-atom MD simulations were done on PKCα bound to ADP and pSer/Thr peptide substrates. The peptide substrate of amino acid Ser⁹ was converted to phosphorylated Ser⁹. We used the patch SP2 in the CHARMM36 force field to assign force field parameters for pSer and pThr. Using the same MD simulation conditions, we performed all-atom MD simulations, solvated with explicit TIP3 water with periodic boundary conditions using the GROMACS package with CHARMM36 force field. We performed MD simulations for high activity peptide p1 for 100 ns.

Analysis of GNEIMO and all atomic MD trajectories

R.m.s. deviation and fluctuation

To compare the inherent flexibility and dynamics of proteins as generated by GNEIMO simulations, we calculated the r.m.s. fluctuations relative to the average structure for each residue. The r.m.s. deviations and fluctuations were calculated using the gmx rmsf utilities in GROMACS MD package (33).

Binding affinity calculation

To estimate the binding energy of small peptide substrate to kinase receptor, we calculated the interaction energy between the N terminus of the peptide and kinase using the gmx energy in the GROMACS MD package (33). The interaction energy of the PKCα for the peptide substrate is determined by the non-bonded energies, short range Coulomb and Lennard-Jones energies.

R.m.s. deviation clustering

To obtain the representative conformation from the most populated conformational clusters, we used r.m.s. deviation-based clustering to cluster all the conformations within the most populated cluster from the molecular dynamics trajectories. A r.m.s. deviation cut-off of 1.5 Å was used and a representative snapshot was taken from the closest r.m.s. deviation from the average structure from the most populated clusters.

Inter-molecular contact

For inter-molecular hydrogen bond analysis using 3.5 Å and 30° for the cut-off distance and angle, respectively, the gmx_hbond utility of GROMACS was used. Inter-molecular hydrogen bond interactions were derived from the stable hydrogen bond criteria having more than 50% occupancy (population) through all trajectories, which is normalized by setting the most densely populated point to 1. For the inter-molecular hydrophobic (Van der Waals) interactions over the whole trajectories with more than 50% of duration during MD simulations, contactFreq of the Tcl script was used.

Reagents and peptides

Buffer chemicals were purchased from various commercial vendors and used without further purification. Peptides (1, 2, 4, 6, 9, 10, and 12) and the corresponding mutant peptides (Figs. 2 and 4) were custom-synthesized by GenScript and solubilized in PKC buffer (20 mm HEPES (pH 7.5), 5 mm MgCl₂, 0.5 mm EGTA, and 2 mm DTT).

Constructs

Human PKCα catalytic domain, mCerulean (FRET donor), mCitrine (FRET acceptor), 10-nm ER/K single α-helix and Ala-substituted substrate peptides, were PCR amplified and cloned into unique restriction sites in the pBiex1 expression vector (Novagen). Gly-Ser-Gly linkers were inserted between protein domains to allow for rotational freedom. Mutant peptides were introduced into sensors by digestion, followed by phosphorylation and ligation of appropriately phosphorylated oligonucleotides. Sanger sequencing was used to confirm appropriate insertion and mutagenesis.

Insect cell expression and protein purification

Plasmids were transfected into (Sf9) insect cells using a protocol reported previously (3). Briefly, pBiex1 vectors were transiently transfected into Sf9 insect cells cultured in Sf900-II media (ThermoFisher) using Escort IV transfection reagent (Sigma) and Opti-MEM 1 (ThermoFisher). Cells were harvested (250 × g, 5 min at 4 °C) and lysed using lysis buffer (20 mm HEPES (pH 7.5), 200 mm NaCl, 4 mm MgCl₂, 0.5% sucrose, 0.5% IGEPAL, 2 mm DTT, 50 μg/ml of PMSF, 5 μg/ml of aprotinin, and 5 μg/ml of leupeptin). Clarified lysate after ultracentrifugation (13,435 × g, 25 min at 4 °C) was incubated with anti-FLAG M2 affinity resin (Sigma) for 1–2 h and washed with wash buffer (20 mm HEPES (pH 7.5), 150 mm NaCl, 10 mm MgCl₂, 2 mm DTT, 5 μg/ml of PMSF, 5 μg/ml of aprotinin, and 5 μg/ml of leupeptin). The proteins were eluted with FLAG peptide (Sigma, 100 μg/ml) and buffer exchanged to PKC buffer (20 mm HEPES (pH 7.5), 5 mm MgCl₂, 0.5 mm EGTA, and 2 mm DTT) using Zeba Spin Desalting columns (40 kDa, Pierce). Protein concentration for the centrifuged protein was determined from the fluorescent emission of mCit (excitation 490, emission 525 nm) compared with a standard on a FluoroMax-4 fluorimeter (Horiba Scientific) or by fluorophore absorbance on a NanoDrop One (ThermoFisher).

Kinase activity assay

The kinase–substrate interaction was measured by monitoring ATP consumption with the KinaseGlo Max Luminescence Assay Kit (Promega). ATP depletion can be monitored in a highly sensitive manner with Kinase-Glo® Reagent, which uses luciferin, oxygen, and ATP as substrates in a reaction that produces oxyluciferin and light. The luminescent signal is correlated with the amount of ATP present and inversely correlated with the amount of kinase activity. Control experiments in which the substrates were incubated with the assay buffer and then assayed with the luciferase showed the substrate interactions were insignificant under the assay conditions.

Activity assays were performed using the catalytic domain (25–75 nm) and 500 μm peptide in PKC buffer. Reactions were initiated by the addition of 250 μm ATP to a total reaction volume of 80 μl in U-bottom, white 96-well plates. Following 3 min incubation at 22 °C, the reaction was quenched and subsequent steps were performed as per instructions from the kit provider. End point luminescence was measured in a FlexStation 3 plate reader (Molecular Devices). Control experiments with only the kinase or the substrate showed negligible ATP consumption. For each experimental condition, ≥2 independent measurements were performed for ≥3 protein preparations (n ≥ 6).

Steady-state FRET measurements

FRET experiments including our FRET sensor (SPASM) experiments have now been used extensively to study protein–protein interactions including experiments in live cells (13, 12, 37). The FRET sensor experiments that we have used in this work provide a direct measure of the binding constants of the substrate peptides (3, 38). This in turn yields insights into the effect of binding of ATP on the binding affinity of various peptide substrates and its ultimate effect on the turnover. Hence, we do not anticipate any artifacts arising inter-intra molecular interaction influencing FRET readout. Before each experiment, purified sensors were centrifuged (17,645 × g at 4 °C) to remove any insoluble protein. All experiments were performed with 50 nm protein in PKC buffer at 21–22 °C. Samples were prepared in tubes pre-coated with BSA (0.1 mg/ml) to limit protein loss through adsorption to tube walls. FRET measurements were performed using FluoroMax-4 fluorimeter (Horiba Scientific). Sensors were loaded in a quartz cuvette (1-cm path length) and excited at 430 nm with an 8-nm band pass, and emission monitored (4-nm band pass) from 450 to 650 nm. The FRET ratio was calculated from the ratio of the emission for mCitrine (525 nm) to mCerulean (475 nm). For each experimental condition, ≥2 experimental replicates were measured for ≥3 independent protein batches (n ≥ 6).

Author contributions

S. L., T. D., H. D. S., M. S., A. L., R. F. S., A. J., N. V., and S. S. planned, designed the experiments, and contributed equally for this work. S. L., T. D., and H. D. all contributed equally for the experiments and analyzing the results. S. L., T. D., H. D. S., N. V., and S. S. wrote the manuscript.