Causal Genetic Inference Using Haplotypes as Instrumental Variables

Abstract

In genomic studies with both genotypes and gene or protein expression profile available, causal effects of gene or protein on clinical outcomes can be inferred through using genetic variants as instrumental variables (IVs). The goal of introducing IV is to remove the effects of unobserved factors that may confound the relationship between the biomarkers and the outcome. A valid inference under the IV framework requires pairwise associations and pathway exclusivity. Among these assumptions, the IV expression association needs to be strong for the casual effect estimates to be unbiased. However, a small number of single nucleotide polymorphisms (SNPs) often provide limited explanation of the variability in the gene or protein expression and can only serve as weak IVs. In this study, we propose to replace SNPs with haplotypes as IVs to increase the variant-expression association and thus improve the casual effect inference of the expression. In the classical two-stage procedure, we developed a haplotype regression model combined with a model selection procedure to identify optimal instruments. The performance of the new method was evaluated through simulations and compared with the IV approaches using observed multiple SNPs. Our results showed the gain of power to detect a causal effect of gene or protein on the outcome using haplotypes compared with using only observed SNPs, under either complete or missing genotype scenarios. We applied our proposed method to a study of the effect of interleukin-1 beta (IL-1β) protein expression on the 90-day survival following sepsis and found that overly expressed IL-1β is likely to increase mortality.

Introduction

During the past decade, many studies have been conducted to identify differentially expressed genes or proteins related to complex diseases [Dermitzakis, 2008; Emilsson et al., 2008; Hanash, 2003]. However, remarkable heterogeneity exists across study results [Chan et al., 2008; Ein-Dor et al., 2006; Schanstra and Mischak, 2014; Zhang et al., 2008], even after various observed confounders including demographic and clinical variables were controlled for. One possible explanation is that the estimated association between gene or protein expression and complex diseases may be spurious or distorted due to other unobserved or unmeasurable factors [Smith and Ebrahim, 2004]. For example, several proteins including homocysteine and C-reactive protein (CRP) have been reported to be associated with coronary heart diseases (CHD); however, both high blood pressure and smoking can elevate the levels of the above proteins and are also independent risk factors for CHD [Davey Smith et al., 2004]. So it was unclear whether high and CRP levels reflected CHD risk factors such as smoking or blood pressure or whether homocysteine and CRP contributed causally to the development of CHD. In addition, numerous experimental design, lab operations, staff training, microarrays processing batch, environmental factors, and genetic background can affect gene product expression in some systematic way and may also be correlated with disease outcomes due to unpredicted nonrandom procedures [Leek and Storey, 2007]. Ignoring the potential confounding effects tends to produce results that are both biologically less interpretable and less reproducible across independent studies. Originally developed in econometric studies [Hausman, 1978], the instrumental variables (IVs) method is recently introduced and successfully applied in genetic epidemiology to infer the causal association between biomarkers and disease phenotypes, by controlling confounding in differential expression analyses.

The IV method, also called Mendelian randomization, considers a genetic variant as an instrument to estimate the causal effect of a continuous gene or protein expression variable on a binary or continuous trait. The method assumes that genetic variant is randomly assigned at the gamete formation and leads to the diseases through modifying the expression of a gene. It further assumes that the genotype distributes independently from other unobserved confounders and its effect on the outcome is mediated only through the intermediate gene expression [Didelez and Sheehan, 2007; Lawlor et al., 2008a]. A popular example is the use of a functional variant rs1801133 within gene MTHFR (encodes methylenetetrahydrofolate reductase) in understanding the effect of homocysteine, a protein mentioned in the previous example, on CHD. Because rs1801133 is highly predictive of homocysteine level but has no correlation with other confounders such as smoking or blood pressure, the predicted value of homocysteine using rs1801133 is independent of confounder effect and the effect of the predicted homocysteine on CHD can be considered “causal” [Davey Smith et al., 2004]. Conversely, genetic variations in the CRP gene alter CRP protein levels but these CRP genetic variants are not associated with CHD indicating that CRP does not causally contribute to CHD; it is simply an association [Brunner et al., 2008; Hausman, 1978].

Most IV approaches considered one gene expression and one single nucleotide polymorphism (SNP) whose relationship with exposure of interest has been well established. These approaches generally consist of two major stages. In stage 1, the predicted values of the expression variable are obtained through an ordinary regression model with the SNP as a predictor. In stage 2, the outcome is regressed on the expression prediction from stage 1 (rather than original expression variable) to infer causal associations between the gene expression and disease traits. However, using an IV that is only weakly associated with the expression would produce a low and variable correlation between the outcome and predicted expression value, which often implies unreliable casual effect estimate [Murray, 2006]. To improve the strength of IV, multiple SNPs can be used as IVs [Palmer et al., 2012], though there might be a noticeable percentage of subjects with at least one SNP missing. Moreover, when the true causal variants are not genotyped, the surrogate markers that only have weaker associations with the expression may be worse IVs.

As combinations of closely linked alleles along single chromosome, haplotypes harbor the linkage disequilibrium (LD) information between the typed and the casual variants and may increase power to detect a variant underlying a phenotypic trait in association models compared with single SNP association methods. The haplotype disease association method often starts with reconstructing the pair of haplotypes of each individual using population haplotype frequencies. Many early haplotype-based methods used only the most likely haplotypes as the true haplotypes, leading to biased estimation of haplotype effects [Li et al., 2007]. Later models can take haplotype inference uncertainty into account and may increase the accuracy of the effect estimate and further the power of detecting associations [Li et al., 2006; Zaykin et al., 2002]. The power gain from the inferred haplotypes was most remarkable in the presence of polygenetic effect and epistasis [Schaid, 2004]. In addition, haplotype methods can handle missing genotypes directly without an additional imputation step and may provide additional power gain compared with simple linear regression at the presence of missing genotypes. A few IV studies have used haplotypes as IVs to infer causal associations of serum CRP levels with insulin resistance [Brunner et al., 2008] and metabolic syndrome [Timpson et al., 2005]. In these studies, most likely haplotype phases within a three-SNP region were inferred for each subject. Only the haplotype phases with high certainty were included as the predictors for CRP, while ambiguous haplotype phases were believed to cause weak IVs and were excluded [Lawlor et al., 2008a].

Motivated by the aforementioned studies, we proposed a framework to use haplotypes as IVs to infer the causal effect of gene or protein expression on an outcome and hypothesized that using haplotype as IV would provide more accurate inference than using single or even multiple SNPs. Instead of using only common haplotypes and most likely phases for each individual, we took advantage of all haplotypes and possible phases simultaneously to provide stronger instruments. Our method resides within the classic two-stage setup and includes a new prediction model in step 1. The new regression model takes all possible haplotypes into initial account simultaneously and then reduces the number of haplotype classes through a novel model selection procedure. We evaluated the performance of our proposed IV approaches in extensive simulations with various IV strengths, confounding levels, and mechanisms of missing data. The performance of our approach was compared to the approach using multiple SNPs as IVs. Finally, we apply both approaches to a real study to estimate the causal effect of plasma interleukin-1 beta (IL-1β) protein expression on mortality following septic shock.

Methods

Notations and Assumptions

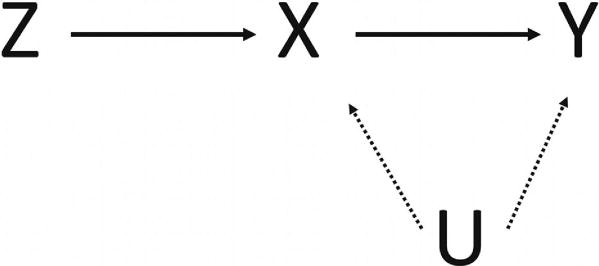
We consider a normally distributed outcome variable Y, a gene or protein expression variable X, and m adjacent SNP genotype variables within a haplotype block summarized in an m-dimensional vector Z, in a study of n subjects. We assume that the true relationship among X, Y, Z, and an unobserved confounder variable U is shown as in Figure 1: the expression X has a direct effect on the outcome Y and indirect effect through the confounder U, and the genotype Z causes Y only through X. Such assumptions imply that (1) the genotype Z is associated with the gene or protein expression X; (2) the genotype Z is independent of the confounder U between X and Y; (3) conditional on X and U, the genotype Z and the outcome Y are independent, i.e., the genotype Z has no direct effect on the outcome Y and can affect the latter only indirectly through the expression X [Didelez et al., 2010].We further denote that there are t possible haplotypes H₁, …, H_t in the population with frequencies π = (π₁, …, π_t) in the haplotype block spanned over the m SNPs. Here, the key question of interest is how big the true (causal) effect of X on Y is without the indirect influence of U.

Figure 1.

Diagram of IV model. Y, clinic outcome; X, exposure of interest such as gene or protein expression; z, instrumental variable; U, unobserved confounding.

Method 1 in Step 1: Choosing Multiple SNPs as IVs

The true effect of X on Y is generally estimated through a two-stage lease squares (2SLS) approach. The first step is to predict X using Z, and the second step is to regress Y on predicted value x̂. As a single SNP often accounts for a small fraction of variability of a gene or protein expression, a single SNP might be a weak IV for inferring the causal effect. If multiple SNPs cumulatively explain more variability in the expression, they can jointly serve as better instruments to improve the prediction of the expression and its causal effect estimate on the outcome in the next step. Using all m SNPs as instruments, we first fit the model:

$$x_i={\beta }_0+z_{1i}{\beta }_1+z_{2i}{\beta }_2+\dots +z_{mi}{\beta }_m+{\epsilon }_i,i=1,2,\dots .,n$$ (1)

where β₀ is the intercept, β₁, …, β_m are the effects of m SNPs on the gene or protein expression x, and ε is a random error, following N(0, σ²). Typically after the model (1) is fitted and parameter estimates β̂₀, β̂₁, …, β̂_m are obtained, the predicted expression value x̂_i for individual i can be determined by x̂_i = β̂₀ + z_1iβ̂₁ + z_2iβ̂₂ +… + z_miβ̂_m. Because some SNPs may not be associated with the expression or but can be associated with the confounders just by chance, including those SNPs in model (1) may introduce spurious association or between X and Y. The more such SNPs or the higher the confounder effect, the higher chances the spurious association can be. To overcome this problem, we used a classic stepwise selection procedure to select most valuable predictors in step 1 [Hocking, 1976]. The stepwise regression started with the full model including all SNPs as predictors. At each iteration, the SNP with poorest incremental prediction and corresponding P-value for β > 0.05 was then removed. All removed SNPs were checked one by one to see whether their additional contribution was resumed to be large (P < 0.05) with the current set of SNPs included in the model. If one SNP meets the criteria, the updated model will reinclude that SNP that was removed previously; if more than one SNP meet the criteria, the one with the largest contribution would be reselected first and others be checked for new contribution iteratively. The above iterations were repeated until all fitted SNPs had P < 0.05. Such model selection procedure can remove the unrelated SNPs in step 1 and avoid inflated type-I errors in step 2. Then, the predicted value x̂_i was determined by the final model.

Method 2 in Step 1: Haplotypes as IV

Here, we introduce a multivariate model using all haplotypes within a block as IVs to improve the inference of casual effect of a particular gene on a disease trait:

$$x_i=\sum _{j=1}^t{\beta }_j[I(h_i^1=H_j)+I(h_i^2=H_j)]p(h_i^1{h}_i^2|Z_i,\pi )+{\epsilon }_i,$$ (2)

where β_j represents the effect of one more copy of the haplotype j on the expression x, $h_i^1{h}_i^2$ is any possible haplotype pairs (so-called diplotype) for individual i, and $p(h_i^1{h}_i^2|Z_i,\pi )$ is the posterior probability of the diplotype given the genotypes of subject i. For the convenience, we call each value $[I(h_i^1=H_j)+I(h_i^2=H_j)]p(h_i^1{h}_i^2|Z_i,\pi )$ “weight” corresponding to each H_j. Under the Hardy-Weinberg equilibrium (HWE), $P(h_i^1=h_i^2=H_k)={\pi }_k^2$, for 1 ≤ k ≤ t; $P(h_i^1=H_k,h_i^2=H_l)=2{\pi }_k{\pi }_l$, for 1 ≤ k ≠ l ≤ t. Haplotype population frequencies (π₁, …, π_t) and $p(h_i^1{h}_i^2|Z_i,\pi )$ of individual i can be estimated based on all unrelated subjects through the EM algorithm [Dempster et al., 1977].

Because each individual is supposed to have two haplotypes (so-called diplotype) at one locus, i.e., $\sum _{j=l}^t[I(h_i^1=H_j)+I(h_i^2=H_j)]p(h_i^1{h}_i^2|Z_i,\pi )=2$, the haplotype full design matrix with an intercept would be a singular matrix. To avoid the singularity, model (2) does include all haplotypes but not the intercept. This model is actually equivalent to the following model (3) that includes intercept β₀ and treats one haplotype as reference:

$$x_i={\beta }_0+\sum _{j=2}^t{\beta }_j[I(h_i^1=H_j)+I(h_i^2=H_j)]p(h_i^1{h}_i^2|Z_i,\pi )+{\epsilon }_i$$ (3)

We used model (2) for the convenience of the following model selection. If we use the same model selection strategy as in model (1), each β̂ represents the expression mean change for one copy of the haplotype compared with the reference group. If a haplotype group with the largest P value is removed, it was equivalent to merge this haplotype to the reference haplotype group. Such merging may lead to the disappearance of multiple haplotypes groups even with large between-group differences if all of them have relatively small effect compared with the reference group. In that circumstance, how to choose the reference actually affects the result of model selection. Ideally, a method should be robust to such choice so we developed an iterative clustering approach. In this approach, clustering at each step is based on haplotypes with most similar effects, similar to the idea of Tabu search method that uses a heuristic neighborhood search for optimization [Glover, 1989]. The goal is to merge one haplotype group into a closest group in each step until the number of haplotype groups included in the model is optimized. To start, we fit the model (2) with all t haplotypes and obtain t corresponding effect estimates β̂₁, β̂₂, …, β̂_t.

We sorted all β_i in an ascending order, denoted as β̂₍₁₎ < β̂₍₂₎ < … < β̂_(t) and also ranked all haplotypes accordingly. Next, we checked the difference in the effects between two adjacent haplotype groups and tested for its significance, and adjacent haplotypes with the smallest difference were merged into one group. At this step, the total number of haplotype clusters in the model would decrease by one and the weight corresponding to the new cluster in the new model would be the summation of the weights corresponding to the previous two groups. If all haplotypes have the same population frequency, the standard error (s.e.) of any pairwise β̂ difference would be the same and the relative order of the P-value for the difference will reflect the order of the magnitude of the difference, similar to the pairwise group difference in a balanced analysis of variance (ANOVA) design. So the magnitude of β̂ difference can be used for merging adjacent clusters. However, with different haplotype frequencies, the order of the P-value for any pairwise difference is also affected by the frequency of the involved haplotypes. The rarer two haplotype groups are, the smaller the P-value for the corresponding β̂ difference is. So we did not use P-value as the merging criteria to avoid the influence of the group frequencies. The fitting and merging procedure was repeated until all differences between two groups with smallest effect difference became significant at a level of 0.05. The predicted expression value x̂_i for individual i was then determined after the final model is fitted and parameter estimates are obtained.

Step 2: Casual Effect Estimate

The predicted value x̂ is obtained for each sample based on the final model, which is one part isolated from x and independent of the confounder U. Thus, the confounding effect is then controlled by regressing y on the predicted value x̂, i.e., fitting model y_i = γx̂_i + ε_i,i = 1, 2,…., n where γ represents the true (or causal) effect of expression on the outcome through the unique genotype expression outcome pathway, not affected by the latent confounder U. We will call the method using multiple SNPs as the “SNP-IV” method and our proposed method using haplotypes as the “haplotype-IV” method.

Binary Outcomes

For binary outcomes, two-stage residual inclusion (2SRI) should be used. Instead of substituting the original x with the predicted value x̂ in the 2SLS approach, 2SRI calculates residuals e = x – x̂ from step 1 and includes the residual e as well as the original x in the logistic model in step 2, i.e., log[Pr(y_i = 1|x_i)/(1 − Pr(y_i = 1|x_i))] = γx_i + ηe_i, i = 1, 2, ...., n, where Pr(y_i = 1|x_i) is the disease probability given x_i for subject i. exp(γ̂) is the estimated causal odds ratio for a given expression value, but the regression coefficient η of the residual term is generally not of interest. Under the null hypothesis, the causal odds ratio of the expression value on the outcome is 1, i.e., γ = 0. The hypothesis testing is often done by the Wald test to obtain the P-value corresponding to γ, as in ordinary logistic regression models. 2SRI is generally recommended to use for better consistency for binary outcomes [Terza et al., 2008].

Simulations

Genotypes

The genotypes of 200 subjects were generated based on an 11-locus haplotype block within gene PDGFC. PDGFC locates at chr 4:156,761–156,971 kb and encodes a member of the platelet-derived growth factor family, which regulates embryonic development and angiogenesis, and has been associated with and contribute to the pathophysiology of hepatocellular carcinoma and associate sepsis [Campbell et al., 2005; Hu, 2013]. The LD structure of this block with Utah residents with ancestry from northern and western Europe (known as CEU population) is summarized in Supplementary Figure S1. Nine of the 11 SNPs are common and there are 11 haplotypes in the population. The averaged D′ and R² across all SNP pairs are 0.89 and 0.28, respectively, a moderate LD among loci within haplotype blocks. Assuming HWE, each subject’s diplotypes were generated based on the CEU population frequencies of the PDGFC haplotypes.

Expression and Continuous Outcome

To allow some variations in the LD between the casual SNP and neighboring markers, we chose two of the 11 SNPs in turn to be the causal SNPs, with their (0, 1, 2) coding denoted as Z₁, Z₂. Then, a common unobserved confounder U that affected both gene expression X and outcome Y was generated from $N(0,{\sigma }_u^2)$. Two random variables ε₁ and ε₂ were generated from $N(0,{\sigma }_{\epsilon }^2)$ independently. The expression X was then generated according to an additive model:

$$X={\beta }_1{Z}_1+{\beta }_2{Z}_2+U+{\epsilon }_1$$ (4)

where β₁ and β₂ are the effects of two causal SNPs on the expression X. The outcome Y was then simulated according to Y = γX + U + ε₂, where γ is the effect of the expression on the outcome.

Parameter Setting

Because the total proportion explained by SNPs reflects the IV strength, we call the setting with three values 5%, 10%, and 20% as weak, medium, and strong IV settings. We varied the values of β₁, β₂, so that the proportion of variability of expression explained by each SNP is the same, i.e., 2.5%, 5%, and 10% of the total variability of the expression. We allowed the ratio of variance in confounder and variance in random noise ${\sigma }_u^2/{\sigma }_{\epsilon }^2$, which specifies the confounding level (so-called endogeneity), to change from ~10% (we call “moderate’) to ~20% (we call “high”). Under the null hypothesis that there is no causal effect of expression X on outcome Y, we let γ equal 0; under alternative hypothesis that there is a causal effect of expression X on outcome Y, we fixed γ at 0.3. We generated 10,000 datasets for type I error and 500 dataset for power at each setup.

As missing genotype is common in genotyping platforms, we investigated the performance of two IV models under two common missing scenarios: (1) all SNPs have random missing of 2% due to experimental conditions such as insufficient DNA quality or small molecular effects and (2) casual SNPs were completely untyped.

Last, we applied both SNP-IV and haplotype-IV models to obtain the causal effect of the expression X on the outcome Y.

Application to Real Data

Septic shock remains a common cause of death in the intensive care unit, with mortality rates as high as 35% [Annane et al., 2003; Kumar et al., 2011]. Multiple inflammatory cytokines have been associated with adverse outcomes in septic shock, though the causal role of those cytokines is unknown [Hausman, 1978]. IL-1β mediates several autoinflammatory conditions and contributes to innate and inflammatory immune responses [Brunner et al., 2008]. Recently, our study has indicated that plasma IL-1β levels might be inversely associated with survival following septic shock in a large clinic trial population [Meyer et al., 2014]. However, the effect of plasma IL-1β levels on septic shock has not been well studied due to several confounder factors such as IL-1β detection, genetic background, and other proteins. In this study, we extracted SNPs around gene IL1B (encodes IL-1β) region, then applied both SNP-IV and haplotype-IV models to examine potential effect of plasma IL-1β levels on 90-day mortality following septic shock.

Plasma IL-1β protein levels drawn within 24 hr of vasopressor-dependent septic shock and genome-wide genotype (Illumina 1M array) were available for 390 subjects from the vasopressin and septic shock trial (VASST), a published clinical trial comparing two vasopressor strategies inmortality following septic shock. The details of the original study were described in Russell et al. [2008], Lawlor et al. [2008b], and Meyer et al. [2014].Genotypes of 82 SNPs were extracted from the region of gene IL1B (chr2:113,303, 808–113,310, 827) and its 100-kb flanking region, according to Human genome built NCBI 36/hg18. None of SNPs showed large derivations from HWE (P < 0.001) or missing genotyping rate greater than 10%. Genetic background of each sample was determined by principle component analyses with integrating with HapMap3 data (http://hapmap.ncbi.nlm.nih.gov/). Because 90-day mortality following septic shock is a binary outcome, the 2SRI method was used in the final step for both IV models adjusted for covariates sex, age, and the first two PCs [Price et al., 2006].

Results

Type 1 Errors

Table 1 shows that the type 1 error rates at the nominal level of 0.05 across all 55 casual SNP pairs for both SNP-IV and haplotype-IV methods. The type I error rates were well reserved under various IV strength and any combination of casual SNPs. Without the model selection procedure, the type I errors were reserved only under strong IV, but inflated up to 7.7% with an average inflation of 1.8% when IV strength was weak and endogeneity was high (~20%) (Supplementary Table S1).

Table 1.

Type I error rates

IV strength	No missing		Missing scenario 1a		Missing scenario 2b
	SNP	Haplotype	SNP	Haplotype	SNP	Haplotype
Endogeneity ~10%
20%	0.051	0.051	0.051	0.051	0.051	0.052
10%	0.051	0.052	0.05	0.052	0.05	0.052
5%	0.05	0.053	0.049	0.053	0.048	0.052
Endogeneity ~20%
20%	0.051	0.053	0.051	0.053	0.051	0.053
10%	0.053	0.057	0.053	0.057	0.053	0.057
5%	0.053	0.061	0.053	0.061	0.051	0.059

^aTwo percent of genotypes is missing for each SNP.

^bTwo causal SNPs are completely not typed.

Power

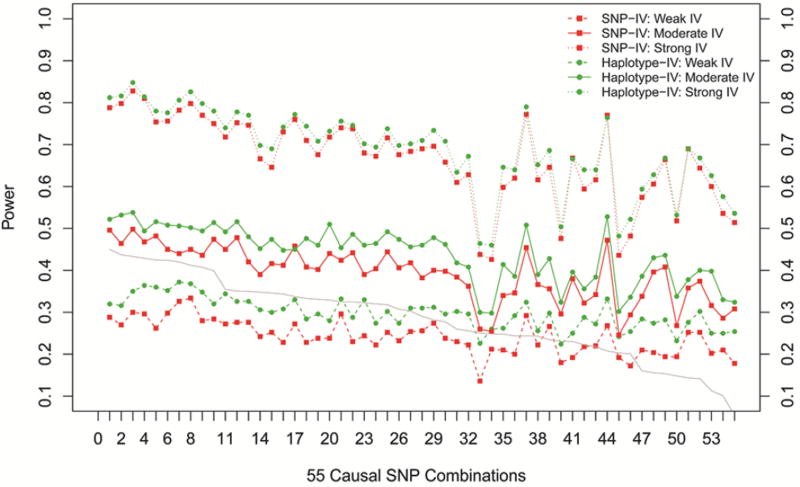
The power for two IV models (SNP-IV and haplotype-IV) under different levels of IV strength was presented in Figure 2, ordered by the average R² between the two causal SNPs and other markers within the haplotype block. The bottom, middle, and top were for IV strength being weak, medium, and strong, respectively. The average R² for each SNP pair, summarizing the LD strength between casual and other typed markers, was shown by the gray line with values matched to the right Y-axis. As the average R² increased, the power of declaring a significant casual effect generally increased in both SNP-IV and haplotype-IV models. However, in a few combinations when the minor allele frequency (MAF) at either causal locus was small (MAF < 0.05), the power in both models dropped compared with the setup with similar average R² between casual and other SNPs. Such trend remained with moderate or even weak IV strength. But the power always increased with increasing R² when IV strength increased. Compared with the SNP-IV model (red solid lines), the haplotype-IV model had consistent power gain ranging from 1% to 12%, with an average of 6.1% gain. Note that such power gain could be more substantial when IVs were weak and power from the SNP-IV models was small. However, when average R² was small (<20%) and the power from the SNP-IV was low, the additional power gain from the haplotype-IV model was minor, especially in the weak IV case. This was because the additional information from small correlated markers was limited.

Figure 2.

Power for different causal SNP combinations. From top to bottom, IV strength varies from strong to weak. X-axis indicates 55 causal SNP combinations ordered along descending average adjacent R². Left Y-axis indicates the power. Green color represents the haplotype-IV model, and red color represents the SNP-IV model. Gray line shows the average adjacent R² of each combination.

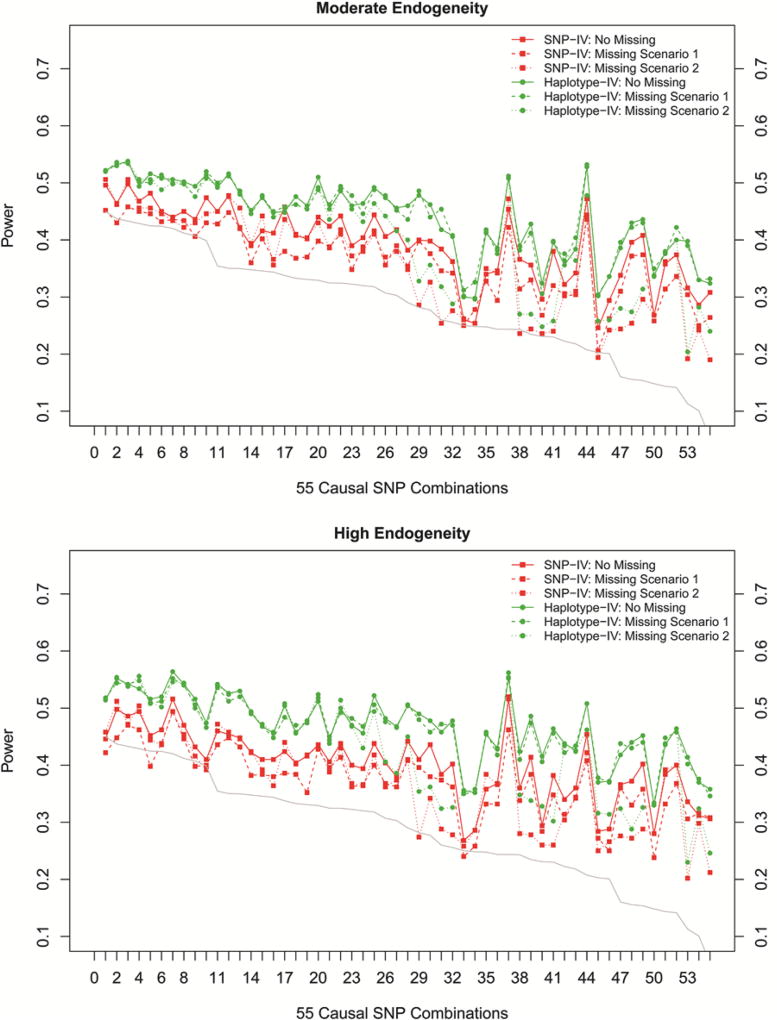
We further evaluated how two IV models perform if some of genotypes were missing or not typed. The power from two missing conditions was presented in dashed and dotted lines in Figure 3a, adjacent averaged R² of 55 SNP pairs were still positively correlated with power in missing scenario 1 (SNPIV vs. haplotype-IV: 0.83 vs. 0.80) and missing scenario 2 (SNP-IV vs. haplotype-IV: 0.83 vs. 0.81). For the SNP-IV model, an average power loss of 3.0% and 3.6% was observed across 55 SNP pairs among missing scenario 1 and missing scenarios 2, respectively. For the haplotype-IV model, power almost remained the same in missing scenario 1 as in no missing scenario, for any causal SNP combination, but this was true only for several scenarios in the missing condition 2 in which causal SNPs were in high LD (adjacent averaged R² > 0.30).

Figure 3.

Power for increased endogeneity and two missing scenarios. (a) Moderate endogeneity is set at ~10%. (b) High endogeneity is set at ~10%.Missing scenario 1:2% of genotype is missing randomly for each SNP. Missing scenario 2: it means only two causal SNPs (true instruments) are not genotyped. X-axis indicates 55 causal SNP combinations ordered along descending average adjacent R². Left Y-axis represents the power for each SNP pair. Green color represents the haplotype-IV model, and red color represents the SNP-IV model. Gray line shows the average adjacent R² of each combination.

As confounding effect is critical issue in IV application, we assessed two IV models with increasing endogeneity. Consistent with previous results, given the same sample size, the haplotype-IV model still demonstrated consistent power gain when endogeneity increase up to 20% (Fig. 3b). The haplotype-IV model achieved mean power 47% across all 55 causal SNP combinations, higher than the mean power 40% observed from the SNP-IV model. When 2% missing rate occurred at each SNP, the power of the haplotype-IV model was almost identical to no missing scenario, but the power of the SNP-IV model dropped by an average of 2.8%. When two causal SNPs were not typed, the power loss (an average of 3.2%) of the SNP-IV model was tiny compared with no missing scenario; the power loss of the haplotype-IV model is even more sparse and only occurred for several causal SNP combinations when those causal SNPs had low LD with other typed SNPs (adjacent averaged R² < 0.30).

Causal Effect Estimates

Table 2 presents the casual effect estimates of the expression X on the outcome Y using two IV models as well as using an ordinary linear regression without applying the IV approach under a random pair of casual SNPs. Under the alternative hypothesis, the true effect of the expression on the outcome was fixed at 0.30. The effects estimated from an ordinary linear regression without any instrument were all much higher than the true effect, and more biased in the high endogeneity (γ_{no iv} = 0.48, SD = 0.07). In the scenario of moderate endogeneity and strong IV strength, causal effects estimated from two IV models were very close to the true effect (γ_SNP = 0.32, SD = 0.10; γ_haplotype = 0.32, SD = 0.10). When IV strength became weak, the causal effect estimates from both models changed little with large variation (γ_SNP = 0.33, SD = 0.23; γ_haplotype = 0.33, SD = 0.21). Although a little bias was observed in an extreme scenario of high endogeneity and weak IV strength (γ_SNP = 0.32, SD = 0.25; γ_haplotype = 0.36, SD = 0.22), the causal effect estimates from IV models were still less biased than estimations from the ordinary regression. Similar results were observed in two missing scenarios. The above results suggest IV estimators using either SNPs or haplotypes are highly sensitive to endogeneity and less sensitive to IV strength and missing schemes.

Table 2.

Mean (SD) of causal effect estimates from two IV models

IV strength	No IV	No missing		Missing scenario 1a		Missing scenario 2b
		SNP	Haplotype	SNP	Haplotype	SNP	Haplotype
Endogeneity ~10%
20%	0.39 (0.06)	0.32 (0.10)	0.32 (0.10)	0.32 (0.11)	0.32 (0.10)	0.32 (0.10)	0.32 (0.10)
10%	0.39 (0.06)	0.31 (0.15)	0.32 (0.15)	0.31 (0.15)	0.32 (0.15)	0.31 (0.15)	0.32 (0.15)
5%	0.41 (0.07)	0.33 (0.23)	0.33 (0.21)	0.33 (0.24)	0.34 (0.21)	0.33 (0.23)	0.33 (0.21)
Endogeneity ~20%
20%	0.44 (0.06)	0.31 (0.10)	0.32 (0.10)	0.31 (0.11)	0.32 (0.10)	0.32 (0.10)	0.32 (0.10)
10%	0.47 (0.06)	0.32 (0.16)	0.33 (0.16)	0.32 (0.17)	0.33 (0.16)	0.34 (0.15)	0.34 (0.15)
5%	0.48 (0.07)	0.32 (0.25)	0.36 (0.22)	0.32 (0.25)	0.36 (0.22)	0.36 (0.20)	0.37 (0.20)

^aTwo percent of genotypes is missing for each SNP.

^bTwo causal SNPs are completely not typed.

Haplotype-IV Analysis in the VASST Population

Plasma IL-1β levels were log-transformed to follow normal distribution. As displayed in Supplementary Figure S2, program Haploview [Barrett, 2009] was used to identify four LD blocks across 82 SNPs within the specified IL1B region based on Gabriel approach [Gabriel et al., 2002]. Then, we applied the ordinary logistic regression and two IV methods to each of the blocks. Without applying any instrument, measured IL-1β level was positively associated with the mortality following septic shock (odds ratio [OR] = 1.25, P = 0.0001); the odds of postshock death increased by 1.25-fold, while IL-1β level increased one unit. SNP-IV models in four different blocks yielded three ORs of IL-1β level on mortality larger than 1 and one smaller than 1, though all ORs had wide confidence intervals and were far from being significant (Table 3).

Table 3.

Causal effect estimates of plasma IL-1β on 90 days mortality following septic shock

Blocks	SNP-IV				Haplotype-IV
	m0a	m1b	OR (95% CI)	P-value	t0a	t1b	OR (95% CI)	P-value
1	50	4	1.69 (0.90–3.19)	0.104	11	3	1.78 (0.93–3.42)	0.081
2	3	2	1.27 (0.53–3.05)	0.598	5	2	1.50 (0.60–3.73)	0.386
3	14	1	1.14 (0.42–3.10)	0.803	8	2	3.21 (1.47–7.01)	0.003
4	15	1	0.90 (0.30–2.75)	0.858	5	2	0.95 (0.33–2.73)	0.922

^am0 and t0 are the total number of SNPs and haplotypes, respectively.

^bm1 and t1 are the total number of SNPs and haplotypes selected in the optimal models, respectively.

In contrast, all first three haplotype-IV models resulted in stronger ORs than those estimated by the SNP-IV model. In addition, the casual OR of IL-1β on mortality using the final haplotype-IV model in block 3 (59th–72th SNP, Supplementary Fig. S2) was significant (OR = 3.21, P = 0.0003) and that one unit increase in IL-1β level increased the odds of postshock death by 3.21-fold. In block 3, seven haplotypes and one rare group (haplotypes with frequencies < 1% were merged) were estimated from the population and added to the initial model. The final IVs were formed between two subgroups with significantly different means in IL-1β levels (P = 0.004): one subgroup contained four haplotypes (CGAACGGGGGGAGA, CGAACGGGGGGGGA, CAGGAGGCGAAAAG, and rare group) and contributed increased IL-1β levels, and the other subgroups contained remaining four haplotypes (CGGGCGGGGGGAGG, CGGGAGGCGAAAAG, CGGACGGGGGGAGA, and GGGGCAAGAGGAGG) and contributed to decreased IL-1β levels. The OR estimate from the model in the last block was very close to 1. The above results suggested that IL-1β levels controlled by LD block 3 in gene IL1B might positively contribute to postshock mortality.

Discussion and Conclusions

Genetic markers (e.g., SNP) have been used as instruments in massive observational epidemiologic studies; however, selection and identification of valid instruments is still a challenging issue. This study proposed a new IV model that applied multilocus haplotypes to serve as instruments to estimate the causal effect of an expression on a clinic outcome. Our simulation showed that the method using haplotype as instruments will improve power compared with that using multiple SNPs directly, specifically in the presence of missing genotypes, weak SNP-expression association, or large confounder effect. In a clinical trial database, we demonstrated one example that applying the haplotype-IV model identified a statistically strong effect of plasma IL-1β levels on mortality of patients with septic shock.

Generally, SNPs with greater than 5% or 10% missing rate are excluded due to bad DNA quality or calling errors. Two percent of missing rate in simulation could cause considerable power loss in the SNP-IV model but not in the haplotype-IV model (Fig. 3). Another common phenomenon in genetic studies is that a large number of variants identified from SNP-phenotype and SNP-expression associations are presumed to be marker SNPs that are in LD with the causal one, because functional evidence is lacking or if the causal SNP is not covered by commercial genotyping array or by reads in next-generation sequencing. Such proxy SNPs might result in false-positive signals or biased estimation. When causal SNPs were not genotyped, results demonstrated that power of two IV models using adjacent markers would drop dramatically if causal SNPs are in low LD (adjacent averaged R² < 0.30), which primarily results from the presence of rare SNPs (MAF < 0.05).Thus, we would prefer to use the haplotypes-IV model if rare SNP appeared in IV studies.

One of the critical issues in application of IV model is to identify valid instrument, which requires that the first assumption of IV model to be satisfied: genotype Z is associated with the gene or protein expression X. Most IV studies employ one instrument to estimate the causal effect of gene product expression on clinical outcome, and it may not improve the inference of causal effect if the single SNP only accounts of a small proportion of variability of expression or if some genotypes are missing. In a few IV studies, multiple instruments are applied but the estimation may be biased due to inclusion of nonvalid instruments. In this study, we use a stepwise regression strategy to select the optimal model with the best prediction of expression in stage 1. Our approach appears very useful to eliminate bias due to introducing nonvalid instruments. Our simulation shows that type 1 errors were slightly inflated in same scenarios without model selection (Supplementary Table S1). Compared with estimations using stepwise regressions, our simulation study shows that the simple multivariate model without model selection strategy can cause biased estimates (Supplementary Table S2). Our explanation is that model selection can eliminate variance in expression introduced by irrelevant SNPs and also unnecessary covariance/redundancies among correlated SNPs, which can help the prediction. As in any model selection algorithm, overfitting might be a concern in step 1. However, its potential influence on the cause effect estimate was reduced in the two-step procedure. Because the predicted expression part due to the overfitting in step 1 generally will not increase the association signal between the gene expression and the outcome and thus will not bias the inference of the causal effect.

As true genetic variants determining IL-1β levels were unclear, four LD blocks across gene IL1B region were all used to infer causal effect of IL-1β levels on postshock mortality. Only the haplotype-IV model identified a significant effect of IL-1β levels using haplotypes on block 3, which was stronger than the effect estimate (OR = 1.25) without applying any instrument. Block 3 was found to be located in the gene body of IL1B, while other blocks were in the flanking regions, so the variants in block 3 are more likely to have functional roles in regulating IL-1β levels. Other LD blocks are away from the IL1B gene body and their effect (if any) may be too weak to identify [Albert and Kruglyak, 2015; Wang et al., 2011]. The causal estimates using two other blocks were not significant but in the same direction as the effect estimate using block 3, suggesting the higher IL-1β value may increase the mortality if all IV assumptions are met. Using any model selection approach with a uniform variable selection, cut-off may be controversial as the true SNPs with small effect may be removed from the model. Thus, we also presented causal effect estimations of IL-1β levels on postshock mortality without model selection (Supplementary Table S3), the directions are consistent for the haplotype-IV method but not for the SNP-IV method. The true correlation between genetic variants and gene or protein expression is often unknown, and the correlation between genetic variants and confounders may be known. When the correlation between the confounders and genetic variants is ignorable, the IV approach with a model selection procedure may obtain similar results compared with no model selection. Additionally, we noticed that the OR estimate of IL-1β on postshock mortality from the IV models was higher than the unadjusted OR estimate without using IV. In the simulations, the effect estimates from the IV models were smaller than the unadjusted estimates because the confounder was positively associated with both the expression and the outcome. Additional simulations were conducted with opposite directions of the confounder effects on the expression and the outcome, and the result was consistent with what was observed in the real study (Supplementary Table S4). In either case, the causal effect estimates were closer to the true value than the unadjusted effect estimates.

There are many stepwise regression approaches to select a subset of most informative SNPs or haplotype. For example, stepwise regression in a SNP-IV model is based on largest P-value criteria and tends to remove SNPs with nonsignificant effect on gene expression. For the haplotype-IV model, the traditional approach will first specify one haplotype (usually common one) as reference for avoiding singularity, and the nonsignificant haplotype will be removed and merged with references in later iterative steps. In our study, we used an alternative approach to merge haplotypes based on the smallest difference criteria, which is intuitive and straightforward to apply. It does not require specifying one haplotype as reference; each time it sorts haplotypes based on their effect and merges two haplotypes with smallest difference into one subgroup. Subgroups in the fitted model are distinct and contribute differently to gene expression.

We also evaluated the performance of two IV models when the clinical outcome is binary with similar setups as for the continuous outcome, in which we apply the 2SRI method with models (1) and (2). The results of simulation are consistent with those for the continuous outcome. Because inclusion of an interaction term can remarkably increase the total number of the predictors in the model, we did not examine epistasis on performance of two IV models, while in theory, the haplotype-based approach in the presence of epistasis is expected to have more power gain over the SNP-based approach. More effort is warranted to improve the haplotype-IV model with allowing inclusion of rare SNPs and epistasis.

As our clinical dataset example is a focused regional and low-dimensional case, our methods have been centered on relatively small numbers of SNPs and haplotypes. When the use of a more complicated region is justified as IVs, the numbers of SNPs and haplotypes can be big compared with the sample size. Then, high-dimensional variable selection strategies such as fused lasso [Tibshirani and Wang, 2008] and 2SR method [Lin et al., 2014] may be considered and the theoretical properties of such methods warrantee further studies.