Atmospheric evidence for a global secular increase in carbon isotopic discrimination of land photosynthesis

Significance

Climate change and rising CO₂ are altering the behavior of land plants in ways that influence how much biomass they produce relative to how much water they need for growth. This study shows that it is possible to detect changes occurring in plants using long-term measurements of the isotopic composition of atmospheric CO₂. These measurements imply that plants have globally increased their water use efficiency at the leaf level in proportion to the rise in atmospheric CO₂ over the past few decades. While the full implications remain to be explored, the results help to quantify the extent to which the biosphere has become less constrained by water stress globally.

Abstract

A decrease in the ¹³C/¹²C ratio of atmospheric CO₂ has been documented by direct observations since 1978 and from ice core measurements since the industrial revolution. This decrease, known as the ¹³C-Suess effect, is driven primarily by the input of fossil fuel-derived CO₂ but is also sensitive to land and ocean carbon cycling and uptake. Using updated records, we show that no plausible combination of sources and sinks of CO₂ from fossil fuel, land, and oceans can explain the observed ¹³C-Suess effect unless an increase has occurred in the ¹³C/¹²C isotopic discrimination of land photosynthesis. A trend toward greater discrimination under higher CO₂ levels is broadly consistent with tree ring studies over the past century, with field and chamber experiments, and with geological records of C₃ plants at times of altered atmospheric CO₂, but increasing discrimination has not previously been included in studies of long-term atmospheric ¹³C/¹²C measurements. We further show that the inferred discrimination increase of 0.014 ± 0.007‰ ppm⁻¹ is largely explained by photorespiratory and mesophyll effects. This result implies that, at the global scale, land plants have regulated their stomatal conductance so as to allow the CO₂ partial pressure within stomatal cavities and their intrinsic water use efficiency to increase in nearly constant proportion to the rise in atmospheric CO₂ concentration.

The accumulation of excess CO₂ in the atmosphere over the past century has been associated with a closely related decrease in the ¹³C/¹²C ratio of the CO_2. This isotopic trend, first reported in 1979 (1), has become known as the “carbon-13 Suess effect” (2), by analogy to the decrease in the radiocarbon (¹⁴C) content of CO₂ discovered in 1955 by Hans Suess (3). Measurements from air trapped in ice cores (4) show that the preindustrial background δ¹³C value was around −6.4‰. As of 2014, the average value was around −8.4‰ (Figs. 1 and 2).

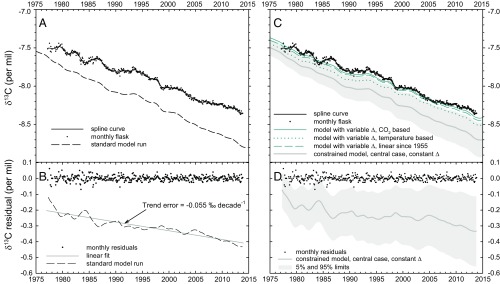
Fig. 1.

Measured and modeled trends in δ¹³C of atmospheric CO₂. Measurements are based on average monthly values at Mauna Loa and South Pole stations, after removing seasonal cycles. (A) Measurements vs. standard model run. (B) Measurements and standard model run as residuals from spline fit. The linear fit through the model residual with slope of −0.055‰ decade⁻¹ quantifies the failure of the standard model to account for the observed δ¹³C trend. This slope error is independent of the overall offset of the model from the data, which depends on the assumed preindustrial model value of −6.4‰. (C and D) Measurements vs. optimized model run, where the optimization is based on radiocarbon and other constraints, also allowing for ocean warming and wind shift effects (SI Appendix). Gray shading reflects 5% and 95% confidence limits on optimized run. Also shown are runs for three scenarios with variable land discrimination Δ, each of which was optimized to also match the rate of change in δ¹³C since 1978. All model runs initiated at a value of δ¹³C = −6.4‰ in year 1765.

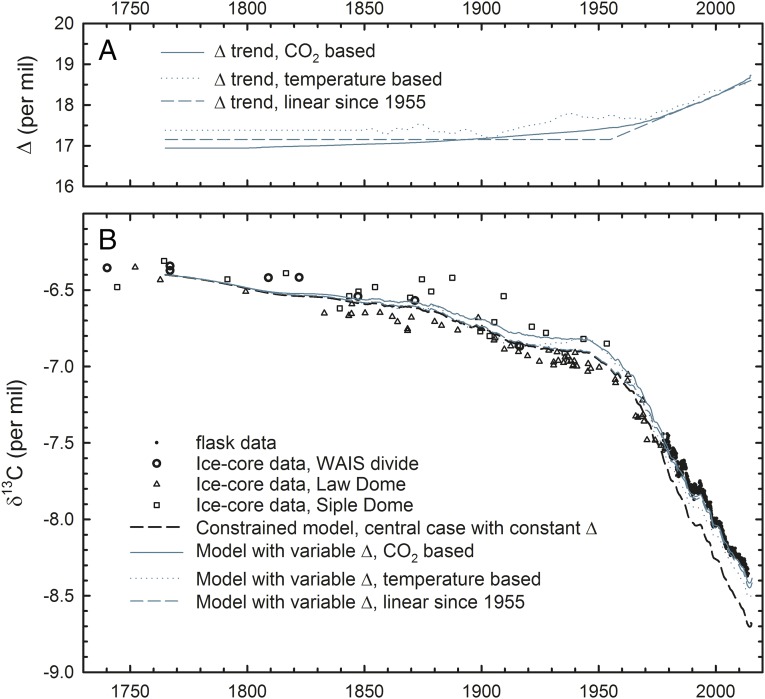
Fig. 2.

(A) Variation in the isotopic discrimination of land photosynthesis for three variable Δ scenarios, each of which was optimized to match the rate of change in δ¹³C since 1978. (B) Measured vs. modeled δ¹³C. Ice core data sources: WAIS divide (4), Law Dome (53), and Siple Station (54). All runs initiated at a value of δ¹³C = −6.4‰ in year 1765. In the model–data comparison, trends are significant but not absolute differences.

The ¹³C-Suess effect, like that for ¹⁴C, is driven primarily by the input of CO₂ from fossil fuels. Fossil fuels are slightly depleted in ¹³C because they were initially formed from photosynthesis, which involves isotopic discrimination, that is, selective uptake of ¹²CO₂ over ¹³CO₂. The emission of fossil fuel CO₂ therefore lowers the atmospheric ¹³C/¹²C ratio. A second important influence on the ¹³C-Suess effect is the natural back-and-forth exchanges of CO₂ with land and ocean carbon reservoirs. These gross exchanges, also known as “disequilibrium fluxes,” scramble carbon atoms between reservoirs, thereby spreading the Suess effect into the land and oceans while reducing the atmospheric signal. A third influence is net gain or loss of carbon by the land biosphere, which is depleted in ¹³C because of photosynthesis, similar to fossil fuels. A sink for excess CO₂ on land therefore offsets the influence of fossil fuel burning, not just on CO₂ amount, but also on its isotopic composition. In contrast, ocean uptake of excess CO₂ has little influence on δ¹³C of atmospheric CO₂ (5).

The ¹³C-Suess effect has been applied to quantify the global land carbon sink and hence the ocean sink by mass balance of total CO₂ (6–8). The method resolves the land sink from the observed δ¹³C trend after correcting for the fossil fuel and disequilibrium flux contributions. The method is not without challenges, however. The isotopic discrimination of photosynthesis can vary, depending on photosynthetic pathway (e.g., C₃ vs. C₄) and the leaf environment (e.g., water stress). Systematic variations in discrimination, in turn, can impart variability in the disequilibrium fluxes, which are hard to quantify. For example, during El Nino events, drought in tropical land masses not only causes a temporary release of CO₂, but also reduces discrimination, causing variations in δ¹³C of CO₂ that are not related to this CO₂ source (9–13) and that are not represented in traditional disequilibrium flux estimates (6, 14–16). A further difficulty is that the global δ¹³C budget does not balance convincingly (11).

Here, we update the longest direct time series for δ¹³C of CO₂, starting in 1978, from the flask program at the Scripps Institution of Oceanography. Rather than resolving carbon sinks, we use data/model comparison to show that there must exist an additional process, previously neglected, that reduces the atmospheric ¹³C-Suess effect. We suggest that the missing process is an ongoing systematic global increase in the isotopic discrimination of land photosynthesis, which has implications for trends in plant water-use efficiency at the global scale.

We derive a global record by combining data from Mauna Loa and South Pole after removing seasonal cycles. We interpret the trend using a model (Materials and Methods and SI Appendix), run from 1765 to 2015, which treats the atmosphere and the ocean mixed layer as well-mixed reservoirs, the land biosphere as consisting of three boxes, and the ocean interior as a 1D diffusive system. The model, which is constrained by radiocarbon measurements, includes a one-box representation of the marine biological pump and allows for ocean warming (17, 18) and the warming-associated impact on CO₂ solubility and air–sea isotopic fractionation. Interannual variations in globally averaged sea surface temperature were also included as were effects of interannually varying winds over the ocean. The model is run as a single deconvolution, that is, the land sink is adjusted to balance the global carbon budget. The trend in atmospheric δ¹³C is diagnosed from the simulated carbon fluxes under different assumptions for land discrimination, and these results are then compared with δ¹³C observations.

Results

The standard model run, which holds land discrimination constant at 18‰ (detailed in SI Appendix, Table S1), is compared with observations in Fig. 1A. This run yields a δ¹³C trend that has an offset from the observations that grows with time. We focus here on the trend in offset, noting the average offset is sensitive to uncertainty in the ice core-based preindustrial δ¹³C value (−6.4‰ in 1765) and laboratory-to-laboratory calibration offsets. The trend in offset reflects the tendency of the model to overpredict the decrease in atmospheric δ¹³C from 1978 to 2014. This overprediction is much larger than the uncertainty in the δ¹³C data and well resolved despite interannual variability in the observations. The model also underrepresents interannual variability in part because no climatic impacts on discrimination are included (9, 11, 12). A linear fit to the model–data difference (Fig. 1B) yields a trend error of −0.055 ± 0.013‰ decade⁻¹ or −0.20 ± 0.05‰ over the whole 36-y-long record, where the uncertainty accounts for measurement imprecision and serial correlation associated with interannual variability in the model–data difference, but not systematic model error (SI Appendix, section 5).

To investigate the robustness of the model and possible sources of model–data trend differences, we carry out multiple runs that span a wide range of model parameters (SI Appendix, Tables S2 and S4). The parameter which most strongly influences the land and ocean CO₂ sinks is the ocean vertical diffusivity, but this parameter only weakly influences the atmospheric δ¹³C trend (SI Appendix, Fig. S3). The parameters with the greatest influence are the coefficients governing air–sea exchange and the turnover of carbon in the land biosphere. The collective impact of these and several other parameters including total fossil fuel emissions and the land photosynthetic fertilization factor (SI Appendix, Table S2, set 1) on modeled ¹³C-Suess effect is quite effectively constrained by requiring the model to also match estimates for the total ¹⁴C produced from nuclear weapons testing and the associated ocean ¹⁴C excess (19, 20) (SI Appendix, Figs. S4 and S5). Applying these ¹⁴C constraints shows that the parameters in the standard model are nearly optimal, while also quantifying uncertainties.

Another important influence is ocean warming, which reduces air–sea equilibrium fractionation and increases the ocean disequilibrium flux. This drives atmospheric δ¹³C upward, reducing the model/data trend mismatch (SI Appendix, Table S2, set 2). Accounting for this warming reduces the overprediction of the trend from −0.055‰ decade⁻¹ to −0.035‰ decade⁻¹. Potentially countering this warming effect, however, are shifts in the surface winds governing air–sea gas exchange. Over recent decades, the surface winds at high latitudes have generally strengthened (21), thereby increasing the gas exchange rate in colder regions, which by itself could cause a cooling trend in the gas exchange-weighted sea surface temperature, thereby countering the overall ocean-warming effect. We quantify this wind shift effect (SI Appendix, Table S2, set 3), using three different global wind speed products and two different assumptions for the dependence of gas exchange on winds (linear vs. quadratic). Overall, the wind shift effect contributes uncertainty to the modeling, while generally increasing the modeled trend error.

We also explore a wide range of additional processes with apparently minor impacts on the δ¹³C trend. We find that inclusion of a steady marine biological pump in the ocean model has very little impact. Allowing for increases in marine pump efficiency with time, as might occur due to warming-induced stratification (22), slightly increases the overprediction error (SI Appendix, Table S2, set 4). The trend error is slightly reduced (−0.052‰ decade⁻¹ instead of −0.055‰ decade⁻¹) by allowing for a secular increase in the isotopic discrimination of marine photosynthesis (23) owing to rising CO₂ (SI Appendix, Table S2, set 5). We also explore the impact of uncertainty in δ¹³C of fossil fuel emissions (SI Appendix, Table S2, set 6) and the uncertainty in the (assumed constant) value of land discrimination (SI Appendix, Table S2, set 7). However, taking these effects into account, including uncertainty in the standard model parameters (as constrained by radiocarbon) and the warming/wind effects, it still does not appear possible to account for the observed trend (P < 0.020) (Fig. 1 C and D, and SI Appendix, Fig. S6).

We identify only one reasonable way to adjust the model to match the atmospheric δ¹³C trend, which is to assume that land discrimination has increased systematically over time. A variant of the central constrained model run, which assumes that discrimination has increased linearly with CO₂ concentration is shown in Fig. 1C. This run was optimized to match the observed δ¹³C trend by adjusting the sensitivity of discrimination to CO₂. For this run, a sensitivity of 0.014‰ ppm⁻¹ was required, although this run, by itself, does not explore the full uncertainties. Using a large ensemble of runs in model parameters and input datasets (SI Appendix, section 5) and imposing constraints based on radiocarbon and other estimated parameter uncertainties, and adjusting the discrimination changes to match the observed trend from 1978 to 2014 to within the uncertainties, we find an optimum sensitivity of 0.014 ± 0.007‰ ppm⁻¹.

It is equally possible to match the observed δ¹³C trend by assuming that discrimination has increased for other reasons, unrelated to the rise in CO₂. We therefore investigated two additional scenario types, either assuming the discrimination changed linearly in proportion to changes in global average surface air temperature since 1850 or second assuming discrimination was constant from 1765 to 1955, after which it increased linearly with time for an unspecified reason. Variants of the standard run which allow for changing discrimination according to these scenarios and which are optimized to match the observed trend are also shown in Fig. 1C. To quantify uncertainties, we explored an ensemble of runs that considered all three discrimination change scenarios (CO₂ based, temperature based, linear; SI Appendix, section 5). We use this ensemble to place constraints on the discrimination changes from 1975 to 2005, which is well constrained by the data because of the several-year lag between discrimination changes and the atmospheric response. Accordingly, we find that a discrimination increase of 0.66 ± 0.34‰ (90% CI from 0.18 to 1.2‰) is required from 1975 to 2005 to match the observed δ¹³C trend to within the uncertainties. Over this period, atmospheric CO₂ increased from 330 to 377 ppm. Dividing the discrimination increase of 0.65 ± 0.33‰ by the 47-ppm CO₂ increase, again supports a sensitivity estimate of 0.014 ± 0.007‰ ppm⁻¹. We find that the runs with changing discrimination that are constrained to match the trend from 1978 to 2014 also agree, to within the larger uncertainties, with the ice core data from 1765 to 1978, as shown in Fig. 2.

Discussion

Increasing land discrimination reduces the atmospheric ¹³C-Suess effect by increasing the accumulation of ¹²C over ¹³C in the land biosphere, thus also yielding an amplified Suess effect in the land biosphere. An effect of this sort is indeed generally corroborated by tree ring δ¹³C sequences, which show decreases in δ¹³C that are stronger than the observed atmospheric trend, depending on location and vegetation type (23–26). The stronger decrease in tree rings is commonly assumed to result from the impact of rising CO₂ on discrimination, and corrections between 0.0 and 0.02‰ ppm⁻¹ are typically applied to tree ring δ¹³C sequences to recover signals related to other phenomena besides rising CO₂ (24, 25). Our global estimate of 0.014‰ ppm⁻¹ falls within this range.

Evidence for increasing discrimination with higher CO₂ has also been found in chamber and field studies on C₃ plants under altered CO₂ conditions as well as from paleo data (26, 27), although exceptions to this pattern have also been found (28). In a compilation of prior work, Schubert and Jahren (26) find a best-fit sensitivity of ∼0.014‰ ppm⁻¹ at 355 ppm, which also matches well with the sensitivity we require to match the atmospheric δ¹³C trend.

The atmospheric δ¹³C data thus provide strong evidence that land discrimination is increasing on a global scale. This shift must largely reflect changes in C₃ plants, which produce 95% of global biomass (29) and therefore control the disequilibrium flux that is tied to changing discrimination on decadal and longer timescales. This shift has implications for understanding leaf-level processes that impact growth and water balance of global ecosystems.

In C₃ plants, discrimination is related to the ratio of the CO₂ concentration within the stomatal cavity (C_i) to the ambient CO₂ concentration (C_a) via the following:

$$\mathrm{\Delta }=a+\left(b-a\right)\left(C_i/C_a\right)-\left(b-a_m\right)\left(A/C_a\right)/{\mathrm{g}}_{\mathrm{i}}-f{\mathrm{\Gamma }}^{\ast }/C_a,$$ [1]

where a = 4.4‰, b = 30‰, a_m = 1.8‰, A is leaf-level gross photosynthesis, g_i is mesophyll conductance, f is the discrimination due to photorespiration, and Γ* is the CO₂ compensation point in the absence of day respiration (30–32). The last two terms in Eq. 1 account for mesophyll and photorespiration effects, which are typically neglected but are relevant for a first-order understanding of how Δ varies with C_a (32). If these terms can be quantified, then changes in Δ can be related to changes in C_i/C_a, which in turn constrains the stomatal conductance influencing both CO₂ gain and water loss. The constraint can be framed in terms of the leaf-level intrinsic water use efficiency, which measures photosynthesis per unit stomatal conductance and is given by the following:

$$\text{iWUE}=A/{\text{g}}_{\text{s}}=C_a\left(1-C_i/C_a\right)/1.6,$$ [2]

where g_s is the stomatal conductance and 1.6 is the ratio of the diffusivities of H₂O and CO₂ in air (33).

The mesophyll and photorespiration terms in Eq. 1 are both negative, but their absolute magnitudes decrease with C_a owing to the presence of C_a in the denominator. These terms therefore both contribute to increasing discrimination with rising CO₂. For a change in C_a from 330 to 377 ppm, the photorespiration term in Eq. 1 increases discrimination by 0.19 ± 0.06‰, contributing to a sensitivity of 0.0041 ± 0.0014‰ ppm⁻¹. This estimate adopts f = 12 ± 4‰ (31) and Γ* ≈ 43 ppm, appropriate for leaves at a typical temperature of 25 °C (34). The mesophyll term is potentially quite variable, as it depends on A and g_i, which vary with leaf environment and plant type (35). Also, A generally increases with C_a, but slower than proportionally (36), thus partly offsetting the impact of C_a in the denominator. Allowing that A has increased linearly with CO₂ at a rate corresponding to a 45 ± 25% increase for a doubling in C_a (36) and taking representative values (32) (A = 9 ± 3 μmol⋅m⁻²⋅s⁻¹; g_i = 0.2 ± 0.05 mol⋅m⁻²⋅s⁻¹), we estimate a globally averaged mesophyll contribution to the sensitivity (centered on ∼355 ppm) of 0.006 ± 0.003‰ ppm⁻¹. Added together, the mesophyll and photorespiration terms thus contribute 0.010 ± 0.004‰ ppm⁻¹ to the overall sensitivity.

This calculation shows that mesophyll and photorespiration terms in Eq. 1 are potentially sufficient to account the full global sensitivity of 0.014 ± 0.007‰ ppm⁻¹ estimated from the ¹³C budget to within the uncertainties. It follows from Eq. 1 that C_i/C_a has remained constant to within the uncertainties, and from Eq. 2 that iWUE has increased in proportion to C_a to within the uncertainties. We estimate a residual sensitivity after correcting for mesophyll and photorespiration effects of 0.004 ± 0.008‰ ppm⁻¹. Assuming this near-zero residual sensitivity holds over the 20th century when C_a increased by 71 ppm (from 296 to 367 ppm), this corresponds to a residual change in Δ of 0.3 ± 0.6‰. From this, we calculate from the second term on the right-hand side of Eq. 1, a change in C_i/C_a of 0.011 ± 0.022 or 1.5 ± 3.3% (relative to a mean value of C_i/C_a ∼0.7 for C₃ photosynthesis). This corresponds to a relative increase in iWUE of 20 ± 9% over the 20th century, driven primarily by the additional factor of C_a that appears in Eq. 2.

Our estimate of the global iWUE change of 20 ± 9% for the 20th century can be compared with results for Europe based on tree ring δ¹³C sequences by Frank et al. (37). However, because Frank et al. (37) neglected the mesophyll and photorespiration terms in Eq. 1, we first add 14 ± 10% to their estimates of relative changes in iWUE for these effects, yielding increase in iWUE of 28 ± 14% for broadleaf and 36 ± 11% for conifer sites. Here, we assessed the mesophyll/photorespiration correction by carrying out calculations with and without these terms in Eq. 1 and also using b = 27‰ for the uncorrected calculation, as assumed by Frank et al. (37). Assuming these European estimates are representative of the global extratropics, the comparison with our global estimate implies that tropical ecosystems, which must exert considerable leverage on the long-term δ¹³C trend, have also potentially seen increases in iWUE. Our results stand in contrast with results from direct water vapor and CO₂ flux measurements of North American forests from the early 1990s through 2010 (38), which appeared to show C_i remaining essentially constant with time, therefore requiring even larger increases in iWUE. The time period covered by direct flux measurements may be too short, however, to resolve systematic trends that are evident globally over the longer time frame of the atmospheric and tree ring δ¹³C measurements.

A possible explanation for near constancy in the ratio C_i/C_a is provided by the optimality hypothesis, which assumes that plants adjust their stomatal conductance to maximize overall carbon gain, considering also the metabolic costs of supplying water for transpiration (39–41). This hypothesis predicts that C_i/C_a will vary in association with plant traits, including sapwood-to-leaf area ratios, as well as on the leaf-to-air vapor pressure deficit and ambient temperature, which influences water viscosity. However, C_i/C_a is otherwise predicted to be largely independent of ambient of C_a and should therefore remain roughly constant as atmospheric CO₂ rises, at least over intermediate ranges (42). Optimal stomatal behavior must break down at sufficiently high C_a because stomatal and cuticle resistance must have upper bounds. In this high limit, C_a– C_i presumably approaches a constant and C_i/C_a approaches unity, consistent with observations at very high CO₂ where Δ ≈ b (43).

Our study also has implications for using δ¹³C data to constrain the land/ocean partitioning of the global CO₂ sinks, highlighting a problem with previous applications that decouple the ocean CO₂ sink from the ocean δ¹³C disequilibrium flux. As mentioned above, the main parameter which influences the sink partitioning is the ocean vertical diffusivity, but this parameter has little impact on the predicted atmospheric δ¹³C trend. This insensitivity was noted in early work (2) but neglected in most subsequent studies (11, 16, 44). The insensitivity arises because of compensation between two terms in the isotopic budget, that is, the ocean disequilibrium and land sink terms (SI Appendix, Fig. S3). The ocean disequilibrium flux depends on ocean diffusivity directly, via the impact of vertical mixing on the uptake of the δ¹³C isotopic signal by the oceans. The land sink and its effect on δ¹³C depend on diffusivity indirectly, via its control of the ocean sink and hence the land sink via global CO₂ mass balance. The two effects tend to cancel in terms of the impact on the atmospheric δ¹³C trend. Because of this compensation, the atmospheric δ¹³C trend does not provide a useful constraint on global land/ocean sink partitioning. Instead, it provides a constraint on the sum of land and ocean sinks which is redundant to the constraint from the atmospheric CO₂ trend. Previous studies have overcome this limitation mainly by relying on measurements of δ¹³C in the ocean (7, 11, 44). This approach, however, neglects the fact that the ocean CO₂ sink and the ocean disequilibrium flux are not mechanistically independent, as they both depend on the rate of vertical mixing or diffusion in the ocean. An additional need would be to show that the ocean sink and disequilibrium fluxes are mutually compatible, given this link.

The 1D ocean model used here has the advantage that it maintains a mechanistic link between total CO₂ and ¹³C in the ocean. On the other hand, this very simple model cannot fully capture complexities in the coupling between total CO₂ and isotopic air–sea exchanges, and further studies with 3D ocean models are clearly warranted. In any case, the land–ocean sink partitioning is now quite well constrained, not just by radiocarbon measurements, but also by measurements of atmospheric O₂ (45) and of additional ocean tracers (46), which all give convergent estimates. These advances allow the ¹³C budgeting to be turned around, from constraining sinks to constraining discrimination effects.

Campbell et al. (47) recently reported a 20th-century increase in land gross primary production (GPP) of 31 ± 5% based on trends in atmospheric carbonyl sulfide (OCS). GPP can related to iWUE according to the following:

$$\text{GPP}=\text{iWUE}\cdot \text{Tr}/\text{VPD},$$ [3]

where Tr is leaf transpiration (in moles of H₂O per year) and VPD is an average measure of leaf-to-air vapor pressure deficit (in pascals). Together, the global trends in GPP (from OCS) and iWUE (from δ¹³C) require that Tr/VPD has increased globally by 11 ± 10% over the 20th century. At the leaf level, Tr/VPD is equivalent to stomatal conductance, which is expected to have decreased under elevated CO₂ (48), but this could be offset globally by increased leaf area and growing season length (37). Eq. 3 provides an alternate framework using iWUE for estimating trends in GPP, once reliable estimates of trends in Tr and VPD are developed.

Despite the low contribution of C₄ photosynthesis to global biomass, a reviewer raised the concern that shifts between C₃ and C₄ photosynthesis might significantly impact the long-term atmospheric δ¹³C trend, especially via the C₄ contribution to soil carbon. In this context, Scholze et al. (10) showed that C₃/C₄ changes have caused global average Δ (NPP-weighted) to decrease by ∼0.5‰ since preindustrial times, dominated by land use via conversion of forest to C₄ pasture before 1960, with only minor C₃/C₄ effects from climate and CO₂ fertilization. To address this effect, we imposed the land use-driven C₃/C₄ discrimination change as an additional time-varying forcing on our model and found that this drives an overall decrease in atmospheric δ¹³C of ∼0.1‰ from 1765 to 1975, with a weak recovery of ∼0.01‰ since 1975. Allowing for this effect decreases the model–data trend error (Fig. 1B) very slightly by ∼0.002‰ decade⁻¹, requiring a very small decrease in the discrimination sensitivity to CO₂ (from 0.014 to 0.013‰ ppm⁻¹) to match the observed trend since 1978. This is likely an upper bound to any C₃/C₄ effect, because it neglects the shorter turnover time of C₄ compared with C₃ carbon, both in plant tissues as well as in soil carbon (49). Earlier studies suggesting larger C₃/C₄ effects appear to have assumed unrealistically long turnover of soil carbon (10, 50). On this basis, the shift in Δ required by the recent atmospheric budget indeed appears to be heavily dominated by C₃ photosynthesis and not by C₃/C₄ shifts.

During review, we also learned of recent study using tree ring isotopic data (51), mainly from Europe, boreal Asia, and western North America, which found no systematic change in Δ through the 20th century, contrary to our atmospheric results and contrary to other tree ring studies (24, 25) which suggest Δ has increased. A direct comparison is difficult, however, because of differences in spatial coverage, with the atmospheric data giving a more truly global constraint over recent decades. The recent tree ring study (51) implies a 20th-century increase in iWUE of 27% compared with our atmospheric estimate of 20% globally, but the comparison is complicated by inconsistent treatment of the photorespiration and mesophyll terms in Eq. 1.

Our analysis yields a balanced global δ¹³C budget (SI Appendix, Table S5) that is backed by radiocarbon measurements in the atmosphere and oceans and consistent with a mechanistic understanding of the controls on terrestrial isotopic discrimination. Recognizing the insensitivity of the δ¹³C trend to the land/ocean sink partitioning and other advances in carbon budgeting, our study involves a change in perspective on the main application of measuring the long-term δ¹³C trend, from resolving sinks to resolving changes in discrimination.

Materials and Methods

Atmospheric samples were collected in 5-L flasks and analyzed at Scripps and Groningen using methods described in Keeling et al. (52) and SI Appendix. Based on short-term variability in monthly mean δ¹³C values at the sampling sites and based on limitations to long-term calibration, we allow an uncertainty in the long-term trend in δ¹³C of ±0.01‰ decade⁻¹ over the ∼36-y time frame of the measurements, not counting the additional error due to serial correlation from interannual variability. Model calculations were carried out using a variant of the box diffusion model as described briefly in the Introduction and detailed in SI Appendix. The model was forced with historical estimates of CO₂ emissions from fossil fuel burning, land use change, changing sea surface temperature, changing wind impact on air–sea gas exchange, including a depiction of the marine biological pump, and allowing for changes in land and ocean photosynthetic discrimination. Three types of scenarios for changing land discrimination were investigated, as described previously. The scenario for changing marine discrimination is based on Young et al. (23). The model was run from year 1765 to 2015. A total of 2,760 runs were carried out to explore the impact of uncertainty in model parameters and input datasets in the context of two questions: (i) What is the probability distribution of the modeled atmospheric δ¹³C trend, considering the full range of uncertainty but keeping land biospheric discrimination constant ? (ii) What is the probability distribution of the long-term trend in land biospheric discrimination that is consistent with the observed δ¹³C trend and other constraints. For both questions, the model runs were weighted according to their ability to account for the estimated total bomb radiocarbon production and ocean radiocarbon excess in year 1994. For the second question, the runs were also weighted according to their ability to account for the observed long-term trend in atmospheric δ¹³C trend from 1978 to 2014 to within the uncertainties.