Evolution of flexibility and rigidity in retaliatory punishment

Significance

Two aims of behavioral science, often pursued separately, are to model the evolutionary dynamics and cognitive mechanisms governing behavior in social conflicts. Combining these approaches, we show that the dynamics of proximate mechanisms such as reward learning can play a pivotal role in determining evolutionary outcomes. We focus on a widespread feature of human social life: People engage in retributive punishment with surprising disregard for its efficacy, yet they respond to punishment with behavioral flexibility finely tuned to costs and benefits. We explain this pattern and offer a general picture of when evolution favors rigid versus flexible social behaviors.

Abstract

Natural selection designs some social behaviors to depend on flexible learning processes, whereas others are relatively rigid or reflexive. What determines the balance between these two approaches? We offer a detailed case study in the context of a two-player game with antisocial behavior and retaliatory punishment. We show that each player in this game—a “thief” and a “victim”—must balance two competing strategic interests. Flexibility is valuable because it allows adaptive differentiation in the face of diverse opponents. However, it is also risky because, in competitive games, it can produce systematically suboptimal behaviors. Using a combination of evolutionary analysis, reinforcement learning simulations, and behavioral experimentation, we show that the resolution to this tension—and the adaptation of social behavior in this game—hinges on the game’s learning dynamics. Our findings clarify punishment’s adaptive basis, offer a case study of the evolution of social preferences, and highlight an important connection between natural selection and learning in the resolution of social conflicts.

Human social behavior is sometimes remarkably rigid, and other times remarkably flexible. A key challenge for evolutionary theory is to understand why. That is, when will natural selection favor “reflexive” social behaviors, and when will it instead favor more flexible processes that guide social decision-making by learning?

We investigate a case study of this problem that illuminates some general principles of the evolution of social cognition. Specifically, we model the dynamic between antisocial behavior and retaliatory punishment in repeated relationships. Our goal is to understand when natural selection will favor flexibility (e.g., “try stealing and see if you can get away with it”) versus rigidity (“punish thieves no matter what”). We approach this question through both a game-theoretic model of punishment and agent-based simulations that allow for the evolution of the rewards that guide learning. We demonstrate that the evolution of punishment depends on the learning dynamics of competing flexible agents, and that this interaction between learning and evolution can produce individuals with innate “social preferences,” such as a taste for revenge (1–4).

The Evolution of Retaliatory Punishment

Individuals often punish those who harm them, even at a cost to themselves (5, 6). The adaptive rationale of this behavior seems clear in repeated or reputational interactions: Punishment promises a long-run gain by deterring social partners from doing future harm. This logic was classically formalized with a simple two-party repeated game (5) (Fig. 1A). On each round, a thief has the option to either steal from a victim (earning $s$ and inflicting a cost $-s$) or do nothing. In response, the victim may either punish (paying a cost $-c$ to inflict a cost $-p$) or do nothing. Formal analysis shows that “punish all theft/stop stealing from victims who punish” is evolutionarily stable. This model, and many others that followed, offered a straightforward explanation for retaliatory punishment in repeated/reputational interactions (7–10). As a consequence, much attention has shifted to the puzzle of “altruistic” punishment in one-shot, anonymous settings (11, 12).

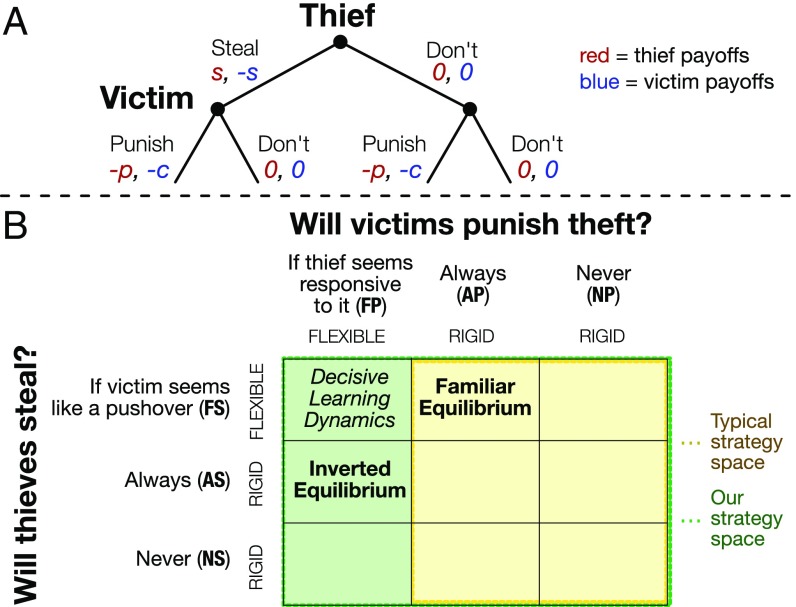
Fig. 1.

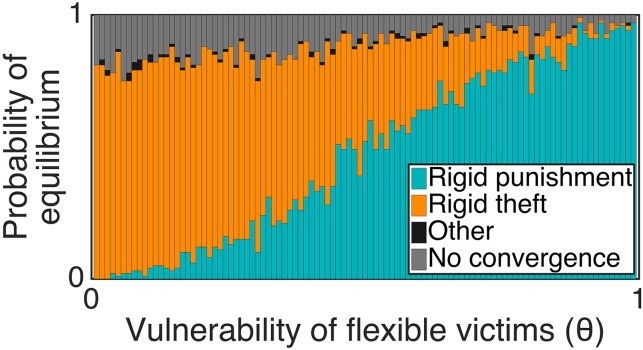
(A) A round of the steal/punish game (5). $s$ is the value of the stolen good, $c$ the cost of punishing, and $p$ the cost of being punished. $s,c>0$ and $p$ > $s$. The game is repeated for $N$ rounds. (B) Pure strategies in the steal/punish game. Typical strategy spaces in models of retaliatory punishment, depicted by the yellow area, produce the familiar equilibrium of rigid punishment and flexible theft. Extending this strategy space to allow flexible victims reveals an inverted equilibrium: rigid theft and flexible punishment. The direction of selection hinges on the outcome of flexible thief against flexible victim: Whichever role tends to “back down” first evolves rigidity to compensate. (See Fig. S1 for payoffs.)

Models of retaliatory punishment embody a peculiar assumption, however: Thieves can flexibly adjust to different victim types, but victims must commit to identical behaviors against all thief types (Fig. 1B). The first element is uncontroversial: A discerning thief will steal from victims who never punish (i.e., pushovers), while respecting the property of those who do. This form of flexibility is sometimes also called “facultative adjustment” (10) or “opportunism” (9). In fact, it is necessary for retaliatory punishment to be adaptive: Punishment only pays when people adjust their behavior in response (5, 7, 10).

Our focus is the second element of this assumption. In contrast to thieves, it is typically assumed that victims are relatively rigid—that is, unable to tailor punishment to different types of opponents. In the classic model (5), whereas thieves can play “steal from pushovers, don’t steal from retaliators,” victims can only pick between two relatively rigid strategies: “always punish theft” or “never punish theft.” Similarly, while many models show that punishment can help maintain cooperation in public goods settings, they typically assume that free-riders can play flexible strategies (like “cooperate with retaliators, defect against pushovers”), while victims of free-riding can only pick between “always punish defection” or “never punish defection” (7–10).

What are the consequences of relaxing this assumption? In theory, victims could profit from playing a flexible strategy. When facing a thief who learns from punishment (i.e., a flexible opponent), the victim would punish theft. Facing a rigid thief who cannot learn, however, the victim would abandon this costly and ineffectual punishment. (The latter possibility is well understood by parents who capitulate to incorrigible toddlers or towns that accede to entrenched organized crime.)

We introduce this possibility by incorporating a symmetric, role-neutral notion of flexibility into an evolutionary model of retaliatory punishment. Using this model, we demonstrate that there are two potential equilibria: the familiar equilibrium (in which victims rigidly punish all theft and thieves flexibly learn who to steal from) and an inverted equilibrium, in which thieves rigidly steal and victims flexibly learn who to punish. In the inverted equilibrium, thieves are incorrigible, and flexible victims cease punishing them when they learn that it is costly and useless.

These two rival equilibria establish a formal framework in which to investigate the adaptive underpinnings of flexible versus rigid social cognition. Prior work has identified numerous benefits of rigid “commitment” to behaviors like punishment (13–15). For instance, when agents can honestly signal a commitment to inflexibly punish in irrational settings (e.g., one-shot games), this motivates opponents to desist from theft (14, 16). Building on this tradition, we identify another strategic benefit of rigidity in competitive repeated games: It can compensate for systematic weaknesses in the learning mechanisms that enable flexibility. Some opponent strategies can bias flexible agents to represent a behavior as suboptimal, when, in fact, it would have been optimal in the long run. For an important class of learning algorithms, we show that flexible victims are more vulnerable to this weakness than flexible thieves. This asymmetry can drive victims to evolve rigid punishment—which, in the reward learning framework, corresponds with an innate “taste” for retaliation (1–3). We conclude by confirming a simple behavioral prediction of the model: People playing the steal/punish game rigidly persist in costly punishment, even when it appears ineffectual.

Model and Evolutionary Analysis

We begin by incorporating a role-neutral notion of flexibility into the steal/punish game and analyzing its evolutionary implications. We define a strategy space that encompasses the two rival equilibria described above (Fig. 1B), and determine the conditions under which each strategy is evolutionarily stable (17) and risk-dominant (18). We then support these static analyses by simulating the evolution of agents in a finite population under a wide range of parameter values. All results point to the same conclusion: Selection between the two equilibria hinges on the outcome of a multiagent learning scenario, flexible thief versus flexible victim. The role with the greater difficulty in learning an optimal strategy will evolve rigidity to compensate.

Strategy Space.

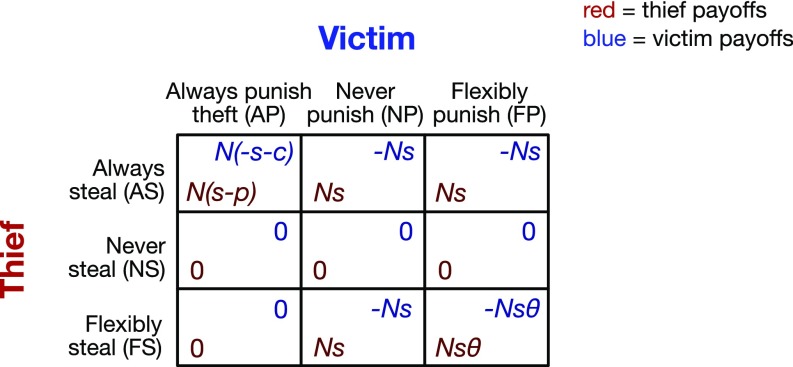
In our model, random pairs of agents in a large, well-mixed population play the steal/punish game for $N$ rounds (Fig. 1). Each agent inherits a strategy specifying its behavior in the game. We consider three pure strategies for each role: always, never, or flexibly steal ($AS$, $NS$, or $FS$, respectively) and always, never, or flexibly punish theft ($AP$, $NP$, or $FP$, respectively). The always/never strategies rigidly persist in their behavior, even when it is suboptimal against the current partner.

In contrast, flexible agents adopt the behavior of whichever inflexible strategy is optimal against the current partner. An agent playing $FS$ never steals (i.e., adopts the inflexible strategy $NS$) when facing an opponent who punishes (i.e., $AP$), and always steals when facing an opponent who doesn’t (i.e., $NP$). An agent playing $FP$ never punishes when facing $AS$, and is indifferent when facing $NS$ (in this case, both options—always or never punish theft—yield zero payoff).

The critical case is when two flexible agents meet ($FS$ versus $FP$). Here, we assume there are two stable outcomes: Either the thief learns to steal and the victim gives up on punishing (i.e., thief adopts $AS$ and victim $NP$), or the victim learns to punish and the thief gives up on stealing (thief adopts $NS$ and victim $AP$). In other words, we assume that the flexible agents will fall into one of the two weak Nash equilibria among the inflexible strategies: $AS$/$NP$ or $NS$/$AP$. We define $\theta$ as the probability of the former (the thief learns to steal), and $1-\theta$ as the probability of the latter (the victim learns to punish theft).

This case captures the vulnerability of flexible strategies. When flexible victims learn not to punish flexible thieves (high $\theta$), they abandon a behavior that would be optimal in the long run and are disadvantaged. In contrast, if flexible thieves learn not to steal from flexible victims (low $\theta$), then the thieves are disadvantaged. $\theta$ thus captures the relative vulnerability of flexible victims/thieves to learning suboptimal behavior. We find that $\theta$ is a critical determinant of the evolutionary outcome.

Population Diversity.

Our aim is to identify the strategic benefits of rigid and flexible strategies. The benefit of flexibility is the ability to adjust to diverse opponents. In the static equilibrium analysis we use here, such diversity between individuals is represented by a single individual playing a mixed strategy [e.g., a population of 75% AS, 25% NS is represented by the strategy “play AS with probability $\frac{3}{4}$ and NS with $\frac{1}{4}$” (19)]. However, in games like ours with asymmetric roles, mixed strategies are always erased by selection (20). (See SI Text for proof.) Thus, the population has no permanent diversity, and there is no stable benefit to flexibility. If flexible strategies cannot be stable, neither can punishment: Punishing is only useful if opponents flexibly modify their behavior in response.

Consequently, past work implicitly assumed that ancestral populations were permanently diverse (5), or analyzed more complex evolutionary dynamics with mutation rates that ensured diversity (9). Our approach is to model diversity explicitly within a simpler, static analytic framework. We define an “epsilon game” (a second-order game parameterized by a constant $ϵ$), where each pure strategy is a probabilistic mixture of the pure strategies in the basic game. Specifically, if $s$ is a pure strategy in the basic game (a “basic” strategy), then the corresponding pure strategy in the epsilon game (an “epsilon” strategy) is $s_{ϵ}$, which plays $s$ with probability $1-ϵ$ and the other two role-specific strategies each with probability $\frac{ϵ}{2}$. For example, a thief playing $F{S}_{ϵ}$ would play $FS$ with probability $1-ϵ$, and $AS$ or $NS$ each with probability $\frac{ϵ}{2}$. By combining these epsilon strategies, agents can play any mixture of the basic strategies $AS$, $NS$, etc., but the probability of a basic strategy being played never falls below $\frac{ϵ}{2}$, where $ϵ>0$. This approach allows us to model the effects of population diversity within a simple static framework, motivating the evolution of flexible strategies.

Evolutionarily Stable Strategy Analysis.

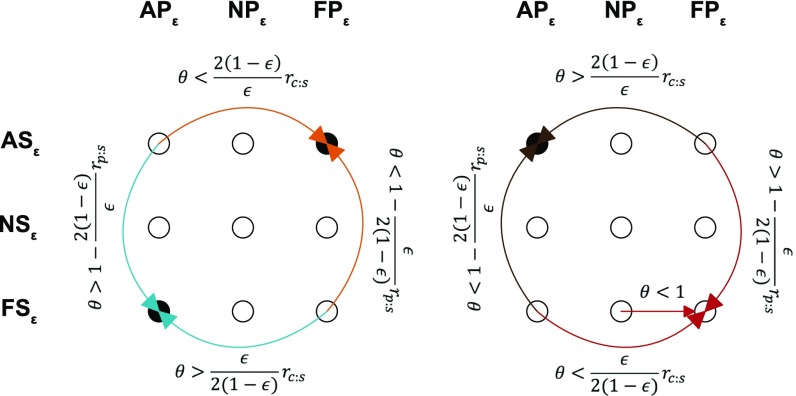
Each agent inherits both a thief and victim epsilon strategy, plays both roles equally throughout its life, and reproduces in proportion to its accumulated payoffs. We write an agent’s strategy as (thief strategy, victim strategy). To explore the outcome of selection, we use the static solution concept of an evolutionarily stable strategy (ESS). Intuitively, a strategy is an ESS if, once it has taken over the population, it cannot be invaded by isolated appearances of other strategies (“mutations”) (17). Using this rule, we derive the conditions of evolutionary stability for the two potential equilibria: rigid punishment/flexible theft and rigid theft/flexible punishment. In the epsilon game, these outcomes are represented by the strategies $(F{S}_{ϵ},A{P}_{ϵ})$ and $(A{S}_{ϵ},F{P}_{ϵ})$ (Fig. S2).

Fig. S2.

The relevant selection pressures in the epsilon steal/punish game. Each arrow shows the direction of selection under the stated condition. A strategy pair is an ESS iff the conditions of all its incoming arrows are fulfilled. When the conditions for both blue arrows are fulfilled, $(F{S}_{ϵ},A{P}_{ϵ})$ is an ESS; likewise for orange/$(A{S}_{ϵ},F{P}_{ϵ})$, red/$(F{S}_{ϵ},F{P}_{ϵ})$, and brown/$(A{S}_{ϵ},A{P}_{ϵ})$.

The conditions involve four parameters: $\theta$ (a flexible victim’s relative vulnerability), $ϵ$ (percent of the population that is permanently diverse), the ratio of $c$ to $s$, and the ratio of $p$ to $s$. We denote $r_{c:s}=\frac{c}{s}$ and $r_{p:s}=\frac{p}{s}-1$ (the −1 is convenient for mathematical reasons). For exposition, assume that $ϵ=0.05$.

The resulting stability conditions are shown in Fig. 2. Roughly, when $\theta$ is high—i.e., flexible victims are relatively more vulnerable—only the familiar ($F{S}_{ϵ}$, $A{P}_{ϵ}$) pair is stable. When $\theta$ is low—flexible thieves are more vulnerable—only the inverted ($A{S}_{ϵ}$, $F{P}_{ϵ}$) pair is stable. [The conditions with arbitrary $ϵ$ are derived in SI Text and conform to the same pattern (Fig. S3).]

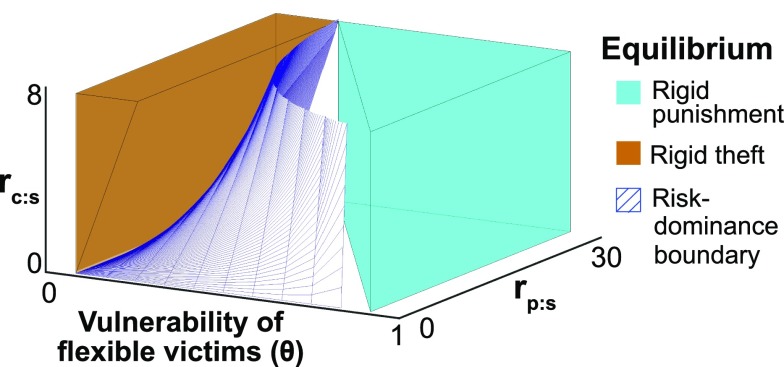
Fig. 2.

Stability conditions in the steal/punish game (assuming $ϵ=0.05$, $r_{p:s},r_{c:s}>\frac{1}{38}$, and $r_{p:s}+r_{c:s}<38$). When $\theta$ is high, only the familiar $(F{S}_{ϵ},A{P}_{ϵ})$ is stable (blue-green region). When $\theta$ is low, only the inverted $(A{S}_{ϵ},F{P}_{ϵ})$ is stable (orange region). In the middle region, both are stable, and risk-dominance is determined by the boundary [$(F{S}_{ϵ},A{P}_{ϵ})$ to the right and $(A{S}_{ϵ},F{P}_{ϵ})$ to the left]. The evolution of rigid punishment depends on the relative vulnerability of flexible strategies in each role (see SI Text).

Fig. S3.

ESS conditions for different values of $ϵ$. In the middle region between the orange and blue sections, both strategies are stable. (Note the changing scale of the axes.)

In other words, rigid punishment/flexible theft is the equilibrium strategy specifically when flexible victims find it difficult to learn to punish flexible thieves. This result holds as long as punishment is not exceedingly strong (with our default parameters, no more than 38 times the value of the stolen good; see SI Text for robustness across parameter settings).

Risk-Dominance Analysis.

When $\theta$ is moderate, both equilibria are stable (middle region in Fig. 2). To analyze this case, we use a standard criterion for selecting between two equilibria: “risk-dominance” (18, 21). Roughly, one equilibrium risk-dominates the other if it has a larger basin of attraction. The condition for risk-dominance here is simple: When both outcomes are stable, rigid punishment is risk-dominant if and only if $\theta >\frac{r_{c:s}}{r_{c:s}+r_{p:s}}$. Otherwise, rigid theft is risk-dominant.

Moran Process Simulations.

Next, we simulate the system’s evolution with a Moran process (22). This tests the robustness of our result to a relaxation of assumptions. The simulated agents live in a small population and use strategies from an extended space that includes all four “reactive” strategies [where a player’s move can be conditioned on her opponent’s last move (23)] and a flexible strategy (Fig. S4). Each generation, all agents play each other, one agent “dies” at random, and its replacement inherits a new strategy with probability proportional to the strategies’ accumulated payoff. The process repeats many times.

Fig. S4.

Payoffs in the expanded strategy space used in the Moran process simulations.

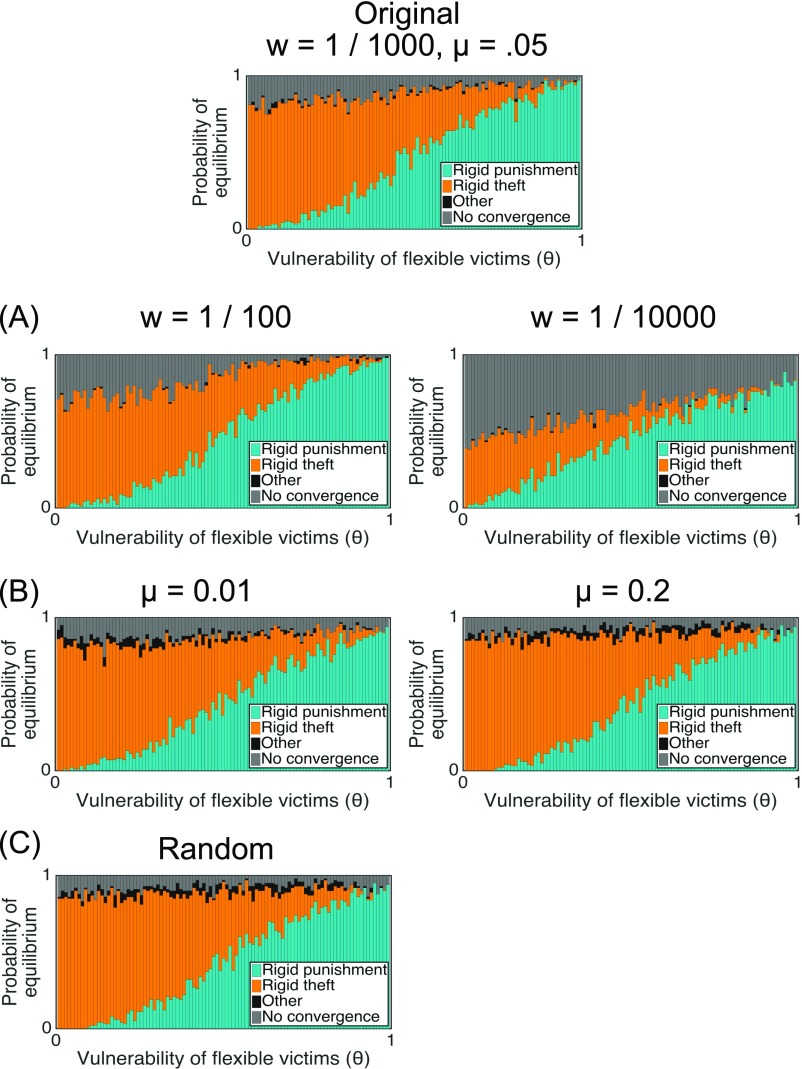
We vary $\theta$ from 0 to 1, sampling the other parameters from a large space (Table S1). As an alternate method of incorporating population diversity, we include stochastic mutation. The result confirms our formal analysis (Fig. 3): As flexible victims become more vulnerable, agents become more likely to evolve to rigidly punish. [This finding holds for a broad range of mutation rates and selection intensities (Fig. S5).]

Table S1.

Default parameters in the Moran process simulations

Parameter	Description	Value
$s$	Value of stolen good	$Uniform(0,10)$
$c$	Cost of punishment	$Uniform(0,10)$
$p$	Damage inflicted by punishment	$Uniform(s,s+20)$
$N$	No. of rounds per game	5,000
$K$	No. of agents in population	100
$w$	Selection intensity	$\frac{1}{1,000}$
$\mu$	Mutation rate	0.05

Fig. 3.

The simulated evolution of strategies in the steal/punish game for different values of $\theta$ (see Materials and Methods). As flexible victims become more vulnerable, the population is more likely to converge to the familiar equilibrium with rigid punishment and flexible theft.

Fig. S5.

(A and B) Moran process simulations, across different selection intensities (A) and mutation rates (B). (C) We randomly sample both parameters for each match, from the ranges $Uniform(\frac{1}{10,000},\frac{1}{100})$ and $Uniform(0,\frac{2}{3})$, respectively.

How Learning Dynamics Determine Relative Vulnerability

Our model suggests that, for a broad parameter space, the evolution of punishment in repeated relationships hinges on the outcome of a multiagent learning scenario: a flexible thief ($FS$) playing against a flexible victim ($FP$). In this competitive setting, flexible strategies have a vulnerability. They may learn to give up on a behavior (i.e., punishment or theft) that would have been optimal in the long run. Whichever role is more vulnerable in this scenario will evolve rigidity. We captured the outcome of this multiagent learning process with a parameter $\theta$. Next, we seek a more principled way to predict the outcome of this process by considering a plausible cognitive model of behavioral flexibility.

Flexible behavioral control in humans is often accomplished via reward learning, including in social contexts (3, 24). To model this, we adopt the reinforcement-learning (RL) framework (25), a formalization of reward learning widely used in computer science, neuroscience, and psychology. In brief, RL agents choose actions by estimating their value: the sum of their expected future rewards. If agents experience rewards equal to the payoffs of the game, then they learn to choose payoff-maximizing actions against diverse opponents (26–28). We focus on a popular class of RL algorithms (“model-free”) that directly estimate the value of actions based on historical returns (Materials and Methods). Using these algorithms, we aim to identify factors influencing the relative vulnerability of flexible strategies in each role. In other words, we ask: What happens when a reward-learning thief meets a reward-learning victim?

Learning Dynamics for RL Agents.

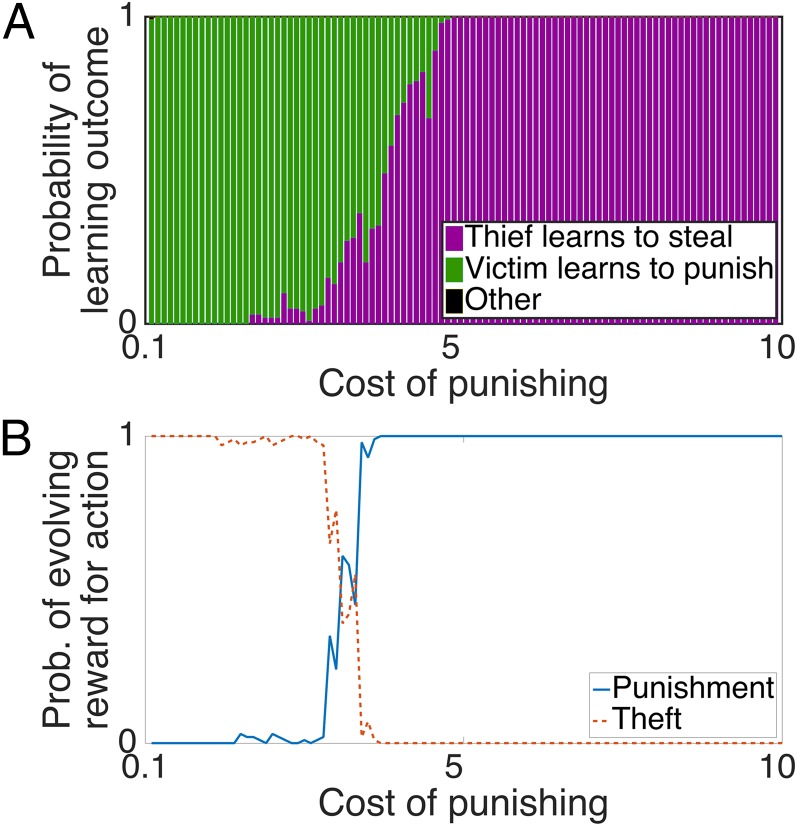
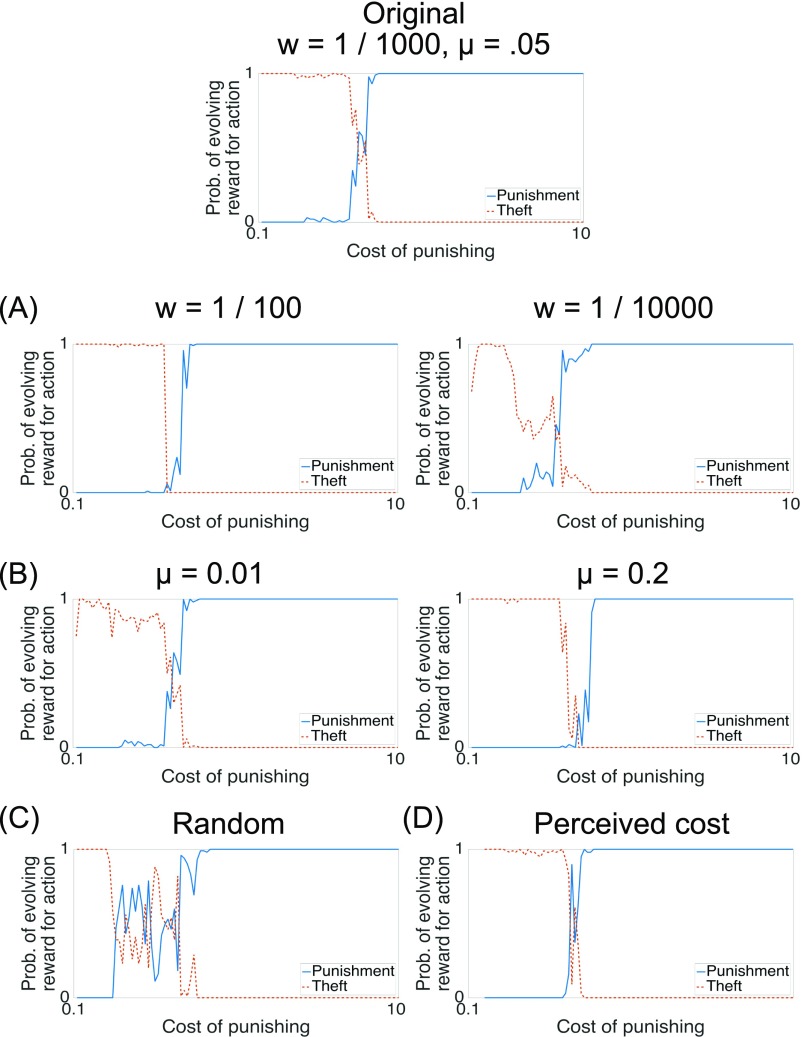
We perform Monte Carlo simulations of two RL agents playing each other in the steal/punish game, with payoffs as the reward function and randomly sampled $s$, $c$, and $p$ (Table S1). [We use the popular algorithm Q-learning (29) with eight internal states. See Materials and Methods for details.] In 72% of games, the thief learns to steal and the victim to not punish; in the remaining 28% of games, the victim learns to punish theft and the thief to stop stealing. In other words, under these conditions, $\theta$ = 0.72.

Why are victims more vulnerable? Across games, variability in three parameters all strongly predict the outcome: As $s$ and $c$ increase, the victim becomes less likely to learn to punish (i.e., becomes more vulnerable), and as $p$ increases, the victim becomes more likely to learn to punish (i.e., the thief becomes more vulnerable; logistic regression, $p$s $<$ 0.001).

To illustrate how these parameters influence the learning dynamics, we highlight the effect of just one: the cost of punishing $c$. Intuitively, it is hard to learn that punishing has long-term value because it carries short-term costs. There is not a comparable obstacle to learning the long-term value of theft: Indeed, the most immediate consequences of theft are positive (you obtain the stolen good). Thus, when a reward-learning victim meets a reward-learning thief, the victim is biased against learning to punish, while the thief is biased toward learning to steal. All else being equal, the most probable outcome of these learning dynamics is persistent theft and no punishment (i.e., high $\theta$).

To demonstrate this effect, we rerun the RL simulations above while varying $c$, and holding the other parameters constant. RL victims are more vulnerable when punishment costs are high, but not when those costs are negligible (Fig. 4A). [This result holds as long as $s$ is low; otherwise, flexible thieves have too strong a learning advantage, and $\theta$ is always high (SI Text).]

Fig. 4.

(A) Outcome of two RL agents in the steal/punish game. As the cost of punishing increases, victims become less likely to learn to punish (i.e., become relatively more vulnerable). (B) We embedded the RL agents in an evolutionary simulation, allowing selection for hedonic biases for or against stealing/punishing. As the cost of punishing increases, selection increasingly favors an intrinsic hedonic bias for punishing (rather than stealing) (see Materials and Methods). Prob., probability.

This clarifies why flexibility bears a strategic risk, beyond its previously identified relation to signaling (14). Although RL algorithms are guaranteed to converge to an optimal policy in stationary environments (25), there is no such blanket guarantee for competitive multiagent settings. In the steal/punish game, each learning agents is in a “race” to discover the policy that establishes their preferred behavioral equilibrium before their opponent does. Punishment’s initial costs can bias learning away from its preferred equilibrium, exposing a systematic strategic risk of flexibility for this role. (See SI Text for details.)

The Evolution of Social Rewards.

In our evolutionary analysis, we show that when flexible victims fail to learn to punish against flexible thieves (i.e., $\theta$ is high), victims evolve rigid punishment to compensate. We also show that when flexibility is accomplished via reward learning, punishment’s short-term cost causes flexible victims to fail to learn to punish against flexible thieves. Combining these results, punishment’s cost should bias selection toward the equilibrium with rigid punishment, which will evolve to compensate for the disadvantage of flexible punishment.

We test this prediction by embedding the RL agents described above in an evolutionary agent-based simulation. To model the flexible strategies ($FS$ and $FP$), we again use Q-learning and set rewards equal to the game’s payoffs.

To model the rigid strategies ($AS$, $AP$, $NS$, and $NP$), we use Q-learning agents with additional rewards conditioned on performing certain actions (30). These agents find stealing or punishing theft intrinsically rewarding or aversive, over and above the objective fitness payoffs. A thief who finds stealing sufficiently intrinsically aversive would never steal; a victim who finds punishing sufficiently intrinsically rewarding would rigidly punish theft; etc. In other words, agents can evolve social rewards—strong intrinsic rewards for social behaviors like retribution that can dominate their other costs. This technique incorporates a notion of rigidity into the RL framework, and affords a natural computational interpretation of economists’ notion of social preferences as tastes for retribution, fairness, and so forth (3).

An agent’s genotype, then, comprised two values subject to mutation: an intrinsic bias for or against theft and an intrinsic bias for or against punishing theft [denoted “(theft bias, punish-theft bias)”]. For example, an agent with genotype $(0,+)$ would play like $(FS,AP)$. We simulate the evolution of these agents with the same Moran process as before, with reproductive success proportional to accumulated payoff and stochastic mutation ensuring permanent population diversity (Materials and Methods). To elucidate the effect of punishment’s cost on selection, we vary $c$ while holding the other payoffs constant.

The results support our analysis (Fig. 4B). When punishment is costly (and thus flexible victims are more vulnerable), agents evolve an intrinsic hedonic bias for punishing theft. However, when the cost is negligible (and thus flexible thieves are more vulnerable), agents evolve an intrinsic bias for stealing, not punishing. Ironically, then, for reward learning agents, selection can favor rigid punishment precisely when it is costly.

Of course, other learning algorithms exist that might perform differently in this game. Because reward learning is a key basis for much human social behavior (3, 24), it is a particularly interesting and important case study.

Rigid Punishment in Humans

Our analyses suggest that, when punishment carries a short-term cost, evolution will favor the familiar equilibrium of rigid punishment and flexible theft. In the context of RL, people will find punishing, but not stealing, intrinsically rewarding. Consistent with these results, people seem to find punishment rewarding (1, 2, 31) and rigidly punish in irrational settings (32, 33). Past work has not, however, explicitly tested for a behavioral asymmetry in the flexibility of punishment and theft. We conclude by demonstrating this asymmetry.

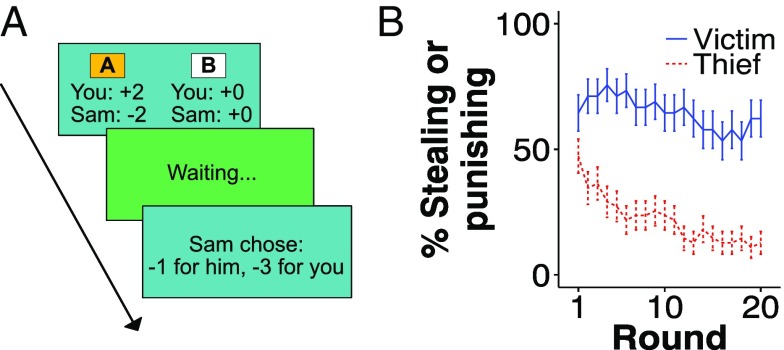
Human participants from Mechanical Turk are endowed with money and play repeated steal/punish games against real opponents (Fig. 5A). Participants are randomly assigned to the thief or victim role. To facilitate the procedure, one player in each game secretly precommits to one of several strategy choices, including two crucial options: rigidly steal and rigidly punish theft. These participants are matched with freely acting participants, who choose their actions sequentially with full knowledge of the opponent’s prior actions. We focus on the behavior of the freely acting participant when facing rigid opponents.

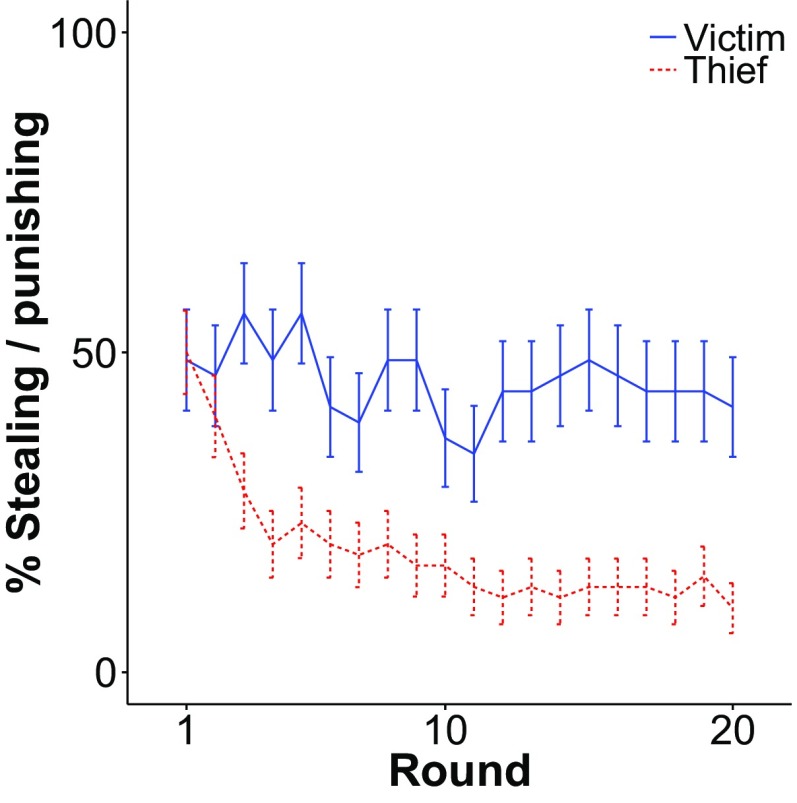
Fig. 5.

(A) Example round of the behavioral experiment. (B) Rate of theft/punishment against rigid opponents. Thieves learn to stop stealing, but victims do not learn to stop punishing theft. (Bars are ± SEM.)

We designed the payoffs such that, absent an asymmetric bias, participants in both roles would show identical learning curves: The thief would learn to stop stealing, and the victim to stop punishing, at similar rates. (See Materials and Methods for details.) Yet people persist much longer in punishing than stealing (Fig. 5B). We fit a mixed-effects model, regressing participant choices on their role, the round number, and the interaction between role and round. The interaction between role and round is significant (likelihood ratio test, ${\chi }^2(1)=24.3$, $P<0.001$; ${\eta }_G^2=0.03$, 95% CI = [0.024, 0.24]). Consistent with our predictions, in repeated games against inflexible opponents, thieves act relatively flexibly and victims act relatively rigidly. [This result holds for a variety of payoff settings (SI Text).]

Although consistent with an asymmetry in the intrinsic reward of punishment versus theft, this result has several alternative explanations. People may have learned different instrumental values for theft/punishment from experience, or different expectations about the pliability of thieves versus victims. To adjudicate between these explanations, future work should investigate the neural and psychological mechanisms that underlie this asymmetry, and test for the asymmetry in children and across cultures.

Discussion

Prior models of punishment assume that only “thieves” (harm-doers or free-riders), and not victims, can flexibly adapt their behavior to different opponent types (5, 7, 10). By relaxing this assumption, we show that there are two potential equilibria: one with rigid punishment/flexible theft and another with rigid theft/flexible punishment. Evolutionary outcomes hinge on the multiagent learning dynamics when two flexible players interact. Modeling this in the RL framework (25), we find that punishment’s initial cost can make flexible victims more vulnerable to suboptimal learning than flexible thieves. This asymmetry favors the evolution of inflexible punishment—in the RL framework, an innate taste for retribution.

Our model makes three significant contributions. First, it helps explain the relatively inflexible nature of human punishment. People clearly exhibit some flexibility in their punishment choices, often tailoring punishment to minimize the risk of retaliation (e.g., they punish a coworker, but not a mob boss). However, people are remarkably insensitive to the contextual potential for effective deterrence (6, 32)—punishing, for instance, in one-shot anonymous settings (33). We find that people also persist in punishment, but not theft, for several rounds of a repeated game against opponents who never learn.

Why do people possess a deterrence mechanism (punishment) that persists in contexts where it is ineffectual? Some prior analyses have posited that inflexibility is strategically beneficial because it signals your commitment to punish even in “irrational” contexts (e.g., one-shot interactions) (13–15).

We identify an additional strategic benefit of inflexibility: By committing to punish in “rational” contexts, it prevents proximate learning mechanisms from converging on suboptimal behavior in repeated games. Moreover, our model explains why evolution would commit people to punishment, but not theft: Punishment’s immediate cost makes flexible victims asymmetrically vulnerable to this weakness. This result extends our understanding of the adaptive underpinnings of social inflexibility. It also complements the prior suggestion that inflexibility can compensate for weakness in planning due to temporal discounting [as opposed to learning, as we investigate here (14)].

Second, our model highlights an ironic (but perhaps common) interaction between learning and evolution: A social role that tends to “lose” in the learning dynamic may consequently “win” in the evolutionary dynamic. For instance, when victims are relatively handicapped in learning the benefits of punishment, they evolve a rigid punishment strategy that ultimately achieves their preferred in-game pattern: no theft. This parallels prior research demonstrating that, in mutualisms between two species, the species which is slower to adapt ends up receiving more benefits in the long run, because it is more committed to its preferred outcome (34). In both cases, relative weakness at a shorter timescale fosters relative strength at a longer timescale (35).

Third, our work is a step toward reconciling proximate and ultimate models of social behaviors like punishment. A wealth of evidence suggests that punishment decisions are guided by systems of value and reward. People often report hedonic satisfaction from punishing (31) (i.e., “revenge is sweet”), and punishing wrongdoers is associated with activation in the striatum (2) and orbitofrontal cortex (1, 36), brain regions central to reward-based decision-making. The same is true for fairness, cooperation, and other social behaviors, suggesting that people have a suite of evolved tastes that guide their social decisions (3, 24).

Evolutionary models, however, typically rely on abstracted versions of these behaviors, and rarely incorporate details about proximate mechanisms (37); they model “eats apples,” not “loves fructose.” By embedding RL agents in an evolutionary model, we attempt to bridge this gap. Our model offers a precise account of how and why evolution would make punishment intrinsically rewarding. This basic approach can be used to predict other social behaviors that people will find rewarding and to explain why.

Our analysis has several limitations. People are relatively rigid when punishing, but they still exhibit some flexibility; our model does not explain when or how this occurs. Our model does not allow agents to abstain from future interactions (38) or to counterpunish (4). Our formal evolutionary analysis uses a static framework, which is only an approximation for more accurate dynamic models. Finally, we interrogate one plausible reward-learning algorithm, but learning comes in many varieties. Future work must fill these gaps.

Despite these limitations, our case study of punishment highlights the utility of evolutionary models defined over plausible psychological mechanisms (37, 39), a research path promising fruitful insight into the origins of social behavior.

Materials and Methods

All code and data can be found at https://github.com/adammmorris/rigid-punishment. See SI Text for ESS and risk-dominance calculations.

Moran Simulations.

To simulate the evolution of this system, we use a Moran process with selection and mutation. A population of $K$ agents evolves over ${10}^3$ generations. Each agent $A_i$ inherits both a thief and victim strategy (see SI Text for the expanded strategy space), plays each other agent as both thief and victim, and receives a fitness score $f_i$ equal to its average payoff. Then, one agent dies at random, and another agent is chosen to reproduce according to a softmax function: $P(A_i)=e^{w{f}_i}/{\sum }_{j=1}^K{e}^{w{f}_j}$, where $w$ controls selection intensity. We also include a mutation rate $\mu$. When an agent reproduces with probability $1-\mu$, it passes on its strategy pair, and with probability $\mu$, it passes on a random different strategy pair. (This models a death–birth process with exponential payoff to fitness mapping.)

We vary $\theta$ from 0 to 1 and run 100 simulations for each value. We classify each simulation as “converging” to a strategy when, averaged across all generations past 1,000, >$1-\mu -0.1$ of the population inherit that strategy. (If no strategy meets that criterion, we classify the simulation as having no equilibrium.) See SI Text for the parameters we use, along with a detailed analysis of how the results vary with different parameter values. Notably, the results are robust to variation in $w$ and $\mu$ (Fig. S5).

RL Simulations.

We adopt the RL framework to model the multiagent learning scenario of flexible thief versus flexible victim. The steal/punish game can be conceptualized as a Markov decision process (MDP), with a set of states $S$ that agents can be in (e.g., “I was punished last turn”), a set of actions $A_s$ each agent can take in each state (e.g., steal or do nothing), a reward function that maps state–action pairs onto payoffs, and a transition function between states. RL algorithms learn to choose the behaviors in a MDP that maximize their total reward and can be used as a model of learning in games like steal/punish (28).

Specifically, we take Q-learning as our model of learning (29). In Q-learning, the agent estimates the long-term expected value of each action $a$ in each state $s$, $Q(s,a)$. When a game starts, these Q-values are initialized to zero. At each time step, the agent selects an action $a$ from state $s$ based on its current Q-value estimates (using a softmax function with parameter $\beta$) and then updates those estimates according to:

$$Q(s,a)\leftarrow Q(s,a)+\alpha (r+\gamma \underset{a\prime \in A_s\prime }{\max }Q(s\prime ,a\prime )-Q(s,a))$$

where $\alpha$ is a learning rate, $\gamma$ is a discount rate, $r$ is the observed reward, and $s\prime$ is the subsequent state.

The learning agent must represent what state of the game it is in. Following prior work (28), our agents keep track of the last two moves. For instance, one state might be, “On the last two moves, I stole and was punished.” A Q-learner reacts to its partner’s type by estimating the value of being in the states following its actions. For example, if a thief is facing a victim who always punishes, then it will learn a negative value for the state following stealing. This allows a Q-learner to mold its behavior to different opponents without building an explicit model of the opponent’s behavior (hence its designation as model-free RL).

First, we simulate 10,000 Q-learning agents playing each other in the steal/punish game, randomly sampling $s$, $c$, and $p$ from the distributions given in Tables S1 and S2. For each simulation, we analyze all turns past 1,000 and categorize it as “punisher exploited” if the thief stole and the victim refrained from punishing on >95% of turns, and as “thief exploited” if the thief refrained from stealing on >95% of turns. Then, we rerun the simulations, varying $c$ from 0.1 to 10 while fixing $s=5$, $p=15$ (Fig. 4A). [We choose these values for s and p because they highlight the illustrative effect that c can have on punishment’s learning dynamics. However, in other ranges, s and p can drown out the effect of c (SI Text).]

Table S2.

Default parameters in the RL simulations

Parameter	Description	Value
$\alpha$	Learning rate	$0.2$
$\beta$	Inverse temperature of softmax function	$20$
$\gamma$	Discount rate	$0.95$

Finally, we embed the RL agents in an evolutionary simulation where agents have a heritable genotype (theft bias, punish-theft bias). As a baseline, the reward an agent receives for a behavior is equal to the behavior’s payoff, equivalent to its fitness consequences. A nonzero bias alters the agent’s reward function: An agent with a steal bias of +2, e.g., would experience an additional 2 units of reward upon stealing. This extra reward only affects the agent’s experience during learning, not its fitness.

There are three possible steal biases and punishing biases (corresponding to the three thief and victim strategies in the evolutionary analysis). The numerical magnitude of each bias is chosen as the smallest integer necessary to guarantee the appropriate behavior (SI Text). We simulate the evolution of these agents with the same Moran process as above. To make the simulations tractable, we first cache the results of each genotype playing each other genotype in 100 full games. Then, in each generation, we sample one of those results for each genotype–genotype match.

We again vary $c$ from 0.1 to 10 (with $s=5$ and $p=15$), run 100 Moran simulations for each value, and record the percentage in which agents evolve an intrinsic reward for stealing or punishing theft (using the convergence criterion described above; Fig. 4B). In SI Text, we describe the assumptions, design, and results of these simulations in more detail. All results are robust to variation in parameters (Fig. S6). We also describe an analysis which suggests that the results are due to the effect of $c$ on the learning dynamics, not the change in the payoffs themselves.

Fig. S6.

(A and B) Combined evolutionary and RL simulations, across different selection intensities (A) and mutation rates (B). (C) We randomly sample the learning parameters for each match, with $\alpha$ from $Uniform(0.05,0.25)$ and $\beta$ from $Uniform(10,100)$. (D) We manipulate the perceived cost of punishing while holding the actual cost constant, to demonstrate that our effect is due to the cost’s influence on the learning dynamics (Isolating the Effect of Learning Dynamics). The x-axis scale is linear for all graphs. Prob., probability.

Behavioral Experiment.

One hundred participants were recruited on Amazon Mechanical Turk. All gave informed consent, and the study was approved by Harvard’s Committee on the Use of Human Subjects. Each participant plays one focal game against an opponent who always steals/punishes (as either thief or victim) and two background games against the other opponent types (one as thief, one as victim). Game order is varied between participants and controlled for in the analysis. The focal game lasts 20 rounds; the background games last a random number of rounds, chosen uniformly between 10 and 20. Participants do not know the game lengths. In each round, participants are presented with a choice of two (neutrally labeled) actions: steal (+2 cents to you and −2 to partner) or do nothing (0 to both) when thief, and punish (−1 cent to you and −3 to partner) or do nothing when victim. They are then informed of their partner’s decision. (When playing as victim, participants are told whether their partner stole before deciding whether to punish.)

The payoffs of $s=2$, $c=1$, $p=3$ present identical pecuniary incentives to thieves and victims: Compared with the alternative of doing nothing, thieves receive a net −1 cent for stealing, and victims −1 cent for punishing (when facing opponents who rigidly punish theft or steal). Thus, without some asymmetric bias, people should show identical learning curves in the two roles. [The result is robust to variation in payoffs (Fig. S7).]

Fig. S7.

Results of the follow-up experiment with randomly varied payoffs for each participant. The graph depicts the percentage of participants who chose to steal/punish against an opponent who always stole/punished, across 20 rounds.

1. Evolutionary Analysis

Our evolutionary analysis has three complementary parts. First, we derive the conditions under which the two proposed equilibria—flexible theft/rigid punishment and rigid theft/flexible punishment—are ESSs in the steal/punish game. Second, when they are both ESSs, we derive the conditions under which one risk-dominates the other. Third, we simulate the evolutionary dynamics in a finite population using a Moran process.

Each analysis requires a subtly different set of assumptions. Thus, we apply each analysis to a subtly different version of the steal/punish game. This is a weakness of our approach, because we do not offer one exact, consistent model of antisocial behavior and retaliatory punishment. However, it is also a strength. The different versions of the game embody the same core concepts, while differing in their technical assumptions. By applying different analyses to different versions of the game, we demonstrate that our qualitative result is robust to variations in those assumptions.

We label the three different versions of the game: the epsilon, 2 × 2, and expanded games. The ESS analysis applies to the epsilon game, risk-dominance to the 2 × 2 game, and Moran simulations to the expanded game.

1.1. Deriving the ESS Conditions.

Basic Game.

All variants of the game stem from the basic game. In the basic game, agents play rounds of the sequential steal/punish game (Fig. 1A) as either the “thief“ or “victim.” The game is characterized by five parameters: $N$, the number of rounds; $s$, the value of the stolen good; $c$, the cost of punishing; $p$, the cost of being punished; and $\theta$, the probability that, when a flexible thief faces a flexible victim, the thief learns to steal (and the victim doesn’t learn to punish). All parameters are strictly positive real numbers ($c$ and $p$ represent the absolute value of their costs), $\theta \in [0,1]$, and $p>s$. (If $p\le s$, punishment is too weak to deter theft and can never evolve.)

An agent’s strategy defines its actions in all possible states of the game. An agent plays as both thief and victim throughout its lifetime, and we assume that the two experiences are independent. Therefore, a complete strategy is characterized by the pair (thief strategy, victim strategy). This approach allows a game with asymmetric roles (thief and victim) to be technically symmetric across agents, which in turn allows us to apply the ESS concept (20). It also cleaves closer to actual ancestral conditions: People likely had the opportunity to both steal and punish throughout their lives.

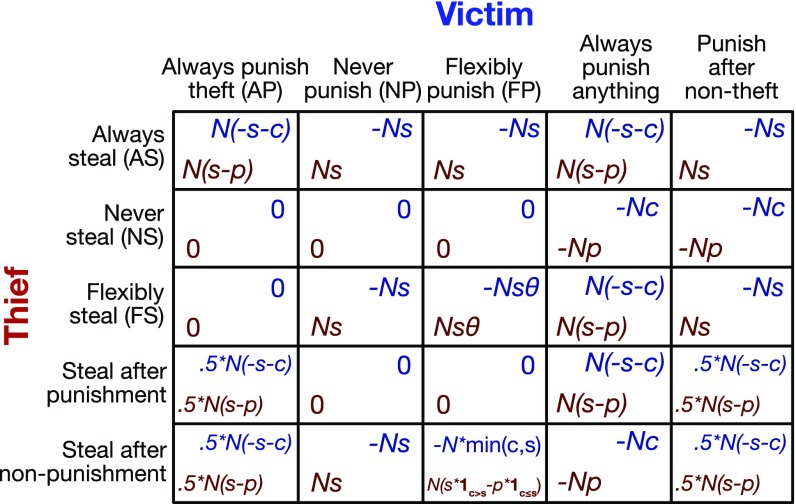
Let $\tau =\{AS,NS,FS\}$ be the set of pure thief strategies, and $\varphi =\{AP,NP,FP\}$ the set of pure victim strategies. Their behavior is described in the main text. When thief strategy $T\in \tau$ faces victim strategy $V\in \varphi$, they receive payoffs ${\pi }_T(V)$ and ${\pi }_V(T)$, respectively (Fig. S1). When an agent with strategy pair $(T_1,V_1)$ faces another agent with strategy pair $(T_2,V_2)$, they receive ${\pi }_{(T_1,V_1)}(T_2,V_2)$ and ${\pi }_{(T_2,V_2)}(T_1,V_1)$, respectively. Technically, a full description of our game would specify payoffs for every strategy pair facing every other strategy pair (a symmetric 9 × 9 matrix). However, since thief and punisher strategies only interact with each other, and an agent’s rounds as a thief are independent of her rounds as a punisher, the payoffs for strategy pairs are simply additive. Thus, ${\pi }_{(T_1,V_1)}(T_2,V_2)={\pi }_{T_1}(V_2)+{\pi }_{V_1}(T_2)$, and we can represent the agent payoffs (symmetric 9 × 9 matrix) with the simpler role payoffs (asymmetric 3 × 3 matrix) in Fig. S1. [For example, when the strategy pair $(AS,NP)$ faces $(NS,FP)$, it receives ${\pi }_{AS}(FP)+{\pi }_{NP}(NS)=Ns+0=Ns$.]

Fig. S1.

Payoffs in the basic game, for each pure thief strategy against each pure victim strategy.

An important note: We assume that the time it takes for a flexible agent to learn which strategy to adopt is negligible compared with the length of the game, and thus omit the learning period from the payoffs of $FS$/$FP$. This omission allows us to focus on the strategic consequences of flexibility.

Mixed Strategies Cannot Be Stable in the Basic Game.

As described in the main text, an essential goal of our analysis is to model the costs/benefits of flexibility for each role, and to understand how this tradeoff influences the evolution of punishment. The benefit of flexible strategies is that they can mold their behavior to fit diverse opponents. In ESS analyses, such diversity in opponents is captured by mixed strategies. However, in games with asymmetric roles, mixed strategies cannot survive in equilibrium (20).

To see this, consider the definition of an ESS. In our basic game, a strategy pair $(T,V)\in \tau \times \varphi$ is an ESS if and only if (iff), for all $(T\prime ,V\prime )\ne (T,V)$,

$${\pi }_{(T,V)}(T,V)>{\pi }_{(T\prime ,V\prime )}(T,V),\text{or}$$ [S1]

$${\pi }_{(T,V)}(T,V)={\pi }_{(T\prime ,V\prime )}(T,V)\hspace{0.17em}\text{and}\hspace{0.17em}{\pi }_{(T,V)}(T\prime ,V\prime )>{\pi }_{(T\prime ,V\prime )}(T\prime ,V\prime )$$

In other words, a strategy is an ESS if it performs better against itself than any alternative strategy does against it; or, if there is an alternative strategy which performs equally well against it, then it performs better against the alternative strategy than the alternative does against itself. These conditions guarantee that, in a large, well-mixed population, an ESS that has taken over the population cannot be invaded by isolated mutations (17). The first condition guarantees that mutants cannot spread; the second condition guarantees that, if a mutant does (neutrally) spread, the ESS will beat it back. [The ESS concept has been successfully applied to explain many features of human and animal social behavior, and is intimately linked to the stability criteria from more detailed modeling of evolutionary dynamics (19).]

Typically, mixed strategies can be evolutionarily stable. However, in games like ours with asymmetric roles, the ESS conditions become more restrictive and preclude this possibility. Here, a strategy pair $(T,V)$ is an ESS iff:

$${\pi }_T(V)>{\pi }_{T\prime }(V)\text{for all}\hspace{0.17em}T\prime \ne T,\text{and}$$ [S2]

$${\pi }_V(T)>{\pi }_{V\prime }(T)\text{for all}\hspace{0.17em}V\prime \ne V$$ [S3]

In other words, for a strategy pair $(T,V)$ to be an ESS in our game, the equilibrium thief strategy $T$ must be a strict best response to $V$, and the equilibrium victim strategy $V$ must be a strict best response to $T$.

To see why this is true, suppose that there exists a strategy pair $(T,V)$ which satisfies the conditions in Eqs. S2 and S3. Because payoffs are additive across roles [i.e., ${\pi }_{(T,V)}(T,V)={\pi }_T(V)+{\pi }_V(T)$ and ${\pi }_{(T\prime ,V\prime )}(T,V)={\pi }_{T\prime }(V)+{\pi }_{V\prime }(T)$], the top condition in Eq. S1 is automatically satisfied, and the strategy pair is an ESS. Hence, the conditions in Eqs. S2 and S3 are sufficient for $(T,V)$ to be an ESS. Moreover, suppose that for a strategy pair $(T,V)$, there exists another thief strategy $T\prime$ such that ${\pi }_T(V)\le {\pi }_{T\prime }(V)$. Then, crucially, $(T,V)$ cannot resist invasion from the mutant strategy $(T\prime ,V)$. (If the mutant thief strategy $T\prime$ is a strictly better response than the current strategy $T$—i.e., ${\pi }_T(V)<{\pi }_{T\prime }(V)$—then ${\pi }_{(T,V)}(T,V)<{\pi }_{(T\prime ,V)}(T,V)$ and both conditions in Eq. S1 fail automatically. If the two earn an equal payoff—i.e., ${\pi }_T(V)={\pi }_{T\prime }(V)$—then ${\pi }_{(T,V)}(T,V)={\pi }_{(T\prime ,V)}(T,V)$, so we must check the bottom condition in 1. In this case, $(T\prime ,V)$ can always neutrally invade, because ${\pi }_{(T,V)}(T\prime ,V)={\pi }_{(T\prime ,V)}(T\prime ,V)$; the bottom condition in Eq. S1 fails.) Hence, a strategy pair which fails the condition in Eq. S2 cannot be an ESS. An identical argument shows that a strategy pair which fails the condition in Eq. S3 cannot be an ESS. Thus, the conditions in Eqs. S2 and S3 are both necessary and sufficient for a strategy pair to be an ESS in our game.

In summary, the fact that a mutant can introduce a novel half of the strategy pair (e.g., introduce $T\prime$) but retain the other half (e.g., retain $V$) makes the conditions in 1 impossible to satisfy—unless both halves of the strategy pair are strict best responses to each other.

Why is this relevant to mixed strategies? A mixed strategy cannot be a strict best response. (For a mixed strategy to be a best response, all its component pure strategies must earn an equal payoff; otherwise, a strategy which puts more weight on the better pure strategies will be a better response. However, this fact precludes the mixed strategy from being a strict best response, because all other mixtures perform equally well.) Hence, in our game, a mixed strategy cannot be an ESS.

The absence of stable mixed strategies is a problem, because without population diversity in equilibrium, flexibility—and thus punishment itself—can never be stable. [In fact, in the basic steal/punish game, there is no ESS—or, if you included some fixed cost of learning, the only ESS would be $(AS,NP)$.] Moreover, actual ancestral populations were probably consistently diverse. We can illuminate the costs and benefits of flexibility, and capture an important feature of ancestral populations, by explicitly modeling this baseline level of population diversity.

Epsilon Game.

To accomplish this, we define a second-order game parameterized by a value $ϵ$, which we denote the epsilon game. In the epsilon game, the set of thief strategies is ${\tau }_{ϵ}=\{A{S}_{ϵ},N{S}_{ϵ},F{S}_{ϵ}\}$, and the set of victim strategies is ${\varphi }_{ϵ}=\{A{P}_{ϵ},N{P}_{ϵ},F{P}_{ϵ}\}$. A pure strategy $s_{ϵ}$ in the epsilon game is equivalent to a mixed strategy in the basic game that plays $s$ with probability $1-ϵ$ and each other strategy with probability $\frac{ϵ}{2}$. Agents can also play mixed strategies in the epsilon game. For example, a mixed strategy in the epsilon game of $\frac{1}{2}{s}_{ϵ}$ and $\frac{1}{2}{r}_{ϵ}$ is equivalent to a mixed strategy in the basic game that plays $s$ and $r$ each with probability $\frac{1}{2}\ast (1-ϵ)+\frac{1}{2}\ast \frac{ϵ}{2}=\frac{1}{2}(1-\frac{ϵ}{2})$, and the other strategy with probability $\frac{ϵ}{2}$.

By playing pure and mixed strategies in the epsilon game, agents can play the equivalent of any mixed strategy in the basic game, with one constraint: The fraction of behavior associated with any basic pure strategy cannot fall below $\frac{ϵ}{2}$. Thus, the epsilon game captures the notion of permanent population diversity. If $ϵ=0$, it reduces to the basic game. We therefore restrict $ϵ>0$. (We also restrict $ϵ<2/3$; if not, the behavior associated with one basic pure strategy can never be more prevalent than the other strategies.)

When two epsilon strategies $T_{ϵ}$ and $V_{ϵ}$ play each other, the payoffs are complex and unwieldy. Fortunately, to determine the ESS conditions, we do not need to work with these payoffs. $(T_{ϵ},V_{ϵ})$ is an ESS when $T_{ϵ}$ outcompetes all other epsilon thief strategies against opponent $V_{ϵ}$ (and mutatis mutandis for the victim). However, $T_{ϵ}$ can only outcompete the other epsilon thief strategies if the basic pure strategy on which it places most of its weight—$T$—outcompetes the other basic pure strategies when facing $V_{ϵ}$. Formally:

$$\forall T\prime \ne T:{\pi }_{T_{ϵ}}(V_{ϵ})>{\pi }_{{T\prime }_{ϵ}}(V_{ϵ})\iff {\pi }_T(V_{ϵ})>{\pi }_{T\prime }(V_{ϵ})$$ [S4]

For simplicity of exposition, we omit the proof of Eq. S4. It is easily shown by writing out the payoffs of the left-hand expression and canceling/rearranging terms.

Using Eq. S4, we compute the conditions under which each epsilon strategy outcompetes each other epsilon strategy, against each opponent. The results are shown in Fig. S2. Each arrow indicates the direction of selection guaranteed by the associated parameter condition. For example, the horizontal orange arrow in the upper left indicates that, when $\theta <\frac{2(1-ϵ)}{ϵ}{r}_{c:s}$, $F{P}_{ϵ}$ always outcompetes $A{P}_{ϵ}$ when facing opponent $A{S}_{ϵ}$. (Note that the $N{S}_{ϵ}$ and $N{P}_{ϵ}$ strategies are irrelevant to the ESS conditions. Because $NS$ and $NP$ are weakly dominated in the basic game, $N{S}_{ϵ}$ and $N{P}_{ϵ}$ cannot be part of ESS pairs, and the $N{S}_{ϵ}$ and $N{P}_{ϵ}$ strategies can never outcompete other strategies, or, if they can, the conditions under which they do so are redundant with other conditions. Thus, we can ignore them in our calculations. The one exception, described later, is the $\theta <1$ condition in the lower right corner of Fig. S2.)

To see how these conditions are derived, consider the horizontal blue arrow in the lower left corner of Fig. S2. Using Eq. S4, $A{P}_{ϵ}$ is guaranteed to outcompete $F{P}_{ϵ}$ against $F{S}_{ϵ}$ when:

$$\begin{array}{c}\hfill {\pi }_{A{P}_{ϵ}}(F{S}_{ϵ})>{\pi }_{F{P}_{ϵ}}(F{S}_{ϵ})\hfill \\ \hfill \iff {\pi }_{AP}(F{S}_{ϵ})>{\pi }_{FP}(F{S}_{ϵ})\hfill \\ \hfill \iff (1-ϵ){\pi }_{AP}(FS)+\frac{ϵ}{2}{\pi }_{AP}(AS)+\frac{ϵ}{2}{\pi }_{AP}(NS)>\hfill \\ \hfill (1-ϵ){\pi }_{FP}(FS)+\frac{ϵ}{2}{\pi }_{FP}(AS)+\frac{ϵ}{2}{\pi }_{FP}(NS)\hfill \\ \hfill \iff (1-ϵ)\ast 0+\frac{ϵ}{2}N(-s-c)+\frac{ϵ}{2}\ast 0>\hfill \\ \hfill (1-ϵ)(-Ns\theta )+\frac{ϵ}{2}(-Ns)+\frac{ϵ}{2}\ast 0\hfill \\ \hfill \iff \frac{ϵ}{2}N(-s-c)>(1-ϵ)(-Ns\theta )+\frac{ϵ}{2}(-Ns)\hfill \\ \hfill \iff -\frac{ϵ}{2}c>-(1-ϵ)s\theta \hfill \\ \hfill \iff \theta >\frac{ϵ}{2(1-ϵ)}{r}_{c:s}\hfill \end{array}$$

The other conditions are derived the same way.

ESS Conditions in the Epsilon Game.

We use the conditions in Fig. S2 to derive the epsilon game’s ESS conditions. As in the basic game, only a pair of pure strategies in the epsilon game can be an ESS. Each pure strategy pair (i.e., each circle in Fig. S2) is an ESS iff the conditions for both its incoming arrows are satisfied. For instance, the familiar strategy pair $(F{S}_{ϵ},A{P}_{ϵ})$—the circle in the lower left corner of Fig. S2—is an ESS iff $\theta >max(\frac{ϵ}{2(1-ϵ)}{r}_{c:s},1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s})$. Similarly, the inverted strategy pair $(A{S}_{ϵ},F{P}_{ϵ})$—the circle in the upper right corner of Fig. S2—is an ESS iff $\theta <min(\frac{2(1-ϵ)}{ϵ}{r}_{c:s},1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s})$. This pattern supports the analysis in the main text: When flexible victims are relatively vulnerable ($\theta$ is high), victims evolve to rigidly punish. However, when flexible thieves are relatively vulnerable ($\theta$ is low), thieves evolve to rigidly steal.

Care must be taken here, however. There are only certain ranges of the non-$\theta$ parameters in which the various $\theta$ conditions in Fig. S2 are possible to satisfy. For instance, if $r_{c:s}>\frac{2(1-ϵ)}{ϵ}$, then $\frac{ϵ}{2(1-ϵ)}{r}_{c:s}>1$, and the condition for the blue horizontal arrow can never be fulfilled. Thus, when the cost of punishing is high enough, the familiar $(F{S}_{ϵ},A{P}_{ϵ})$ cannot be an equilibrium, no matter how vulnerable the victim. These boundaries allow us to explicitly demarcate the ranges of the non-$\theta$ parameters in which our conclusions about the role of $\theta$ apply.

There are six different cases for the non-$\theta$ parameters, each with different ESS results. (We show proofs only for the first case.) Summarizing across all cases, the pattern presented in the main text holds: When it is possible for a role to evolve flexibility or rigidity, the outcome of selection depends on the relative vulnerability of the role’s flexible strategy. Vulnerable roles evolve rigidity; nonvulnerable roles evolve flexibility.

• 1.Suppose $\frac{ϵ}{2(1-ϵ)}<r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}$.

This range is large. For example, if $ϵ=0.05$ and $c=s$, then this captures all punishment magnitudes $p$ that are up to 38 times as strong as the value of the stolen good $s$. For retaliatory punishment in real, long-term repeated relationships, the non-$\theta$ parameters likely fall into this range. This case is therefore the focus of the main text. In this case, when $\theta$ is high, victims evolve rigid punishment; when $\theta$ is low, thieves evolve rigid theft; and when $\theta$ is middling, both are ESSs. (As we will show, similar but subtly different conclusions apply in the other cases.)

Formally, in this case:

• (a)If $\theta >\max \left(\frac{ϵ}{2(1-ϵ)}{r}_{c:s},1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}\right)$ and $\theta >\min (1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s},\frac{2(1-ϵ)}{ϵ}{r}_{c:s})$, then the familiar $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.

Proof.

If $\theta >\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$ and $\theta >1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}$, then the conditions for both incoming arrows to $(F{S}_{ϵ},A{P}_{ϵ})$ in Fig. S2 are satisfied, and $(F{S}_{ϵ},A{P}_{ϵ})$ is an ESS. (Since $r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}\Rightarrow r_{c:s}<\frac{2(1-ϵ)}{ϵ}\Rightarrow \frac{ϵ}{2(1-ϵ)}{r}_{c:s}<1$, the first inequality is possible to satisfy. Since $p>s\Rightarrow r_{p:s}>0\Rightarrow 1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}<1$, the second inequality is also possible to satisfy.) These conditions also guarantee that $(A{S}_{ϵ},A{P}_{ϵ})$ and $(F{S}_{ϵ},F{P}_{ϵ})$ are not ESSs.

Moreover, if either $\theta >1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$ or $\theta >\frac{2(1-ϵ)}{ϵ}{r}_{c:s}$, then one of the conditions for the incoming arrows to $(A{S}_{ϵ},F{P}_{ϵ})$ is not satisfied, and $(A{S}_{ϵ},F{P}_{ϵ})$ cannot be an ESS. (Since $p>s\Rightarrow r_{p:s}>0\Rightarrow 1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}<1$, at least one of the inequalities is always possible to satisfy.)

Finally, for reasons stated above, strategy pairs involving $NS$ or $NP$ can never be ESSs. Thus, $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.

• (b)If $\theta <\max (\frac{ϵ}{2(1-ϵ)}{r}_{c:s},1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s})$ and $\theta <\min (1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s},\frac{2(1-ϵ)}{ϵ}{r}_{c:s})$, then the paradoxical $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.

Proof.

The same as above, with reversed inequalities.

• (c)If $\theta >\max (\frac{ϵ}{2(1-ϵ)}{r}_{c:s},1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s})$ but $\theta <\min (1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s},\frac{2(1-ϵ)}{ϵ}{r}_{c:s})$, then both $(F{S}_{ϵ},A{P}_{ϵ})$ and $(A{S}_{ϵ},F{P}_{ϵ})$ are ESSs.

Proof.

By similar logic as above, these conditions would guarantee that both $(F{S}_{ϵ},A{P}_{ϵ})$ and $(A{S}_{ϵ},F{P}_{ϵ})$ are ESSs, and that no other strategy pairs are stable. All that’s left to show is that the conditions can be simultaneously satisfied. In other words, we must show that all of $\theta$’s upper bounds are higher than all of its lower bounds. There are two upper bounds and two lower bounds, and thus four inequalities to check.

First, we must check that $\frac{2(1-ϵ)}{ϵ}{r}_{c:s}>\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$. This is guaranteed because $ϵ<\frac{2}{3}\Rightarrow \frac{2(1-ϵ)}{ϵ}>\frac{ϵ}{2(1-ϵ)}$. Similar logic shows that $1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}>1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}$.

Then, we must check that $\frac{2(1-ϵ)}{ϵ}{r}_{c:s}>1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}$. After rearranging, this is equivalent to $\frac{ϵ}{2(1-ϵ)}<r_{p:s}+r_{c:s}$, which is assumed in this case.

Finally, we must check that $1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}>\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$. This is equivalent to $r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}$, which is also assumed in this case.

• 2Suppose $r_{p:s}+r_{c:s}<\frac{ϵ}{2(1-ϵ)}$.

Here, $p$ and $c$ are extremely small relative to the value of the stolen good. This case patterns like case 1, except that the two rival strategy pairs can no longer both be stable. Instead, a middling $\theta$ causes both roles to evolve rigidity.

• (a)If $\theta >1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}$, then $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.
• (b)If $\theta <\frac{2(1-ϵ)}{ϵ}{r}_{c:s}$, then $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• (c)If $\frac{2(1-ϵ)}{ϵ}{r}_{c:s}<\theta <1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}$, then $(A{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.
• 3Suppose $\frac{2(1-ϵ)}{ϵ}<r_{p:s}+r_{c:s}$ but $r_{p:s},r_{c:s}<\frac{2(1-ϵ)}{ϵ}$.

Here, $p$ and $c$ are slightly larger than case 1, but still bounded. This case also patterns like case 1, except a middling $\theta$ causes both roles to evolve flexibility.

• (a)If $\theta >\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$, then $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.
• (b)If $\theta <1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$, then $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• (c)If $\frac{ϵ}{2(1-ϵ)}{r}_{c:s}<\theta <1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$, then $(F{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• 4Suppose $\frac{2(1-ϵ)}{ϵ}<r_{p:s}$ but $r_{c:s}<\frac{2(1-ϵ)}{ϵ}$.

Here, $p$ is large and unbounded, but $c$ is still bounded. This is when cases start diverging more from case 1. In this case, rigid theft cannot evolve. (Intuitively, when punishment is very strong, the gains of rigid theft are not worth the inevitable episodes of punishment.) The only question is whether victims evolve flexibility or rigidity, which is determined by $\theta$ in the usual pattern.

• (a)If $\theta >\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$, then $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS.
• (b)If $\theta <\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$, then $(F{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• 5.Suppose $\frac{2(1-ϵ)}{ϵ}<r_{c:s}$ but $r_{p:s}<\frac{2(1-ϵ)}{ϵ}$.

Here, $c$ is large and unbounded, but $p$ is still bounded. In this case, rigid punishment cannot evolve, and $\theta$ determines whether thieves evolve flexibility or rigidity. One hiccup here is that, if $\theta =1$, there is no ESS because $(F{S}_{ϵ},F{P}_{ϵ})$ has identical payoffs to $(F{S}_{ϵ},N{P}_{ϵ})$. This is the one case where the “never” strategies can affect selection.

• (a)If $1>\theta >1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$, then $(F{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• (b)If $\theta <1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$, then $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS.
• (c)If $\theta =1$, there is no ESS.
• 6.Suppose $\frac{2(1-ϵ)}{ϵ}<r_{p:s},r_{c:s}$.

Here, both $p$ and $c$ are large and unbounded. In this case, rigidity cannot evolve, and the only ESS is $(F{S}_{ϵ},F{P}_{ϵ})$.

The Focal Case.

Let’s return to case 1, the focus of our analysis. This is the case in which $\frac{ϵ}{2(1-ϵ)}<r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}$—or, if $ϵ=0.05$, $\frac{1}{38}<r_{p:s}+r_{c:s}<38$. Suppose we simplify further, and assume (without much loss of generality) that $r_{p:s}$ and $r_{c:s}$ (and not just their sum) are both greater than $\frac{ϵ}{2(1-ϵ)}$, e.g., $\frac{1}{38}$.

Then, the ESS conditions become simple. If $\theta >1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$, then the familiar $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS. If $\theta <\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$, then the inverted $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS. If $\theta$ is in between, they are both ESSs.

The proof goes as follows. Since $r_{p:s},r_{c:s}>\frac{ϵ}{2(1-ϵ)}$, $1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s}<0$ and $\frac{2(1-ϵ)}{ϵ}{r}_{c:s}>1$. Hence, the conditions under which $(F{S}_{ϵ},A{P}_{ϵ})$ is the only ESS (from case 1A) reduce to $\theta >\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$ and $\theta >1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$. Moreover, $r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}$ implies that $1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}>\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$. Hence, the conditions reduce further to $\theta >1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s}$—the condition given above. A similar argument proves that the conditions under which $(A{S}_{ϵ},F{P}_{ϵ})$ is the only ESS (from case 1B) reduce to $\theta <\frac{ϵ}{2(1-ϵ)}{r}_{c:s}$.

By fixing $ϵ$ at a particular value, these conditions become linear relationships between $\theta$ and $r_{p:s}$ or $r_{c:s}$. Fig. 2 shows those conditions at $ϵ=0.05$.

Fig. S3 shows the results at $ϵ=0.01$ and $0.2$. The same pattern holds; the bounds of the graph just expand or contract. The main effect of $ϵ$ is that when $ϵ$ is lower, it is more likely that both strategies will be ESSs (because the values of $r_{p:s}$ and $r_{c:s}$ required to reach the blue or orange regions become less plausible). When $ϵ$ is higher, it is more likely that either one strategy or the other will be an ESS.

Risk-Dominance.

In the focal case (case 1), there is a large set of $\theta$ values in which both $(F{S}_{ϵ},A{P}_{ϵ})$ and $(A{S}_{ϵ},F{P}_{ϵ})$ are ESSs. To adjudicate between these equilibria, we turn to the notion of risk-dominance.

Risk-dominance is an equilibrium selection concept with a number of interpretations. On a nonevolutionary view, one equilibrium risk-dominates the other if it follows from a larger swath of players’ beliefs about their opponent (18). More relevant to our purpose, risk-dominant equilibria are the unique outcome of a variety of stochastic evolutionary processes (21). We therefore derive the conditions under which each equilibrium is risk-dominant (within the parameter range of case 1).

Risk-dominance, however, has only been linked to evolutionary processes (and is only generally analytically tractable) in the case of 2 × 2 games (40). We thus reduce the epsilon game used in the ESS analysis to a 2 × 2 game by making two simplifying assumptions. First, we assume that the dominated strategies $N{S}_{ϵ},N{P}_{ϵ}$ will not affect equilibrium selection, and we drop them from the game. Second, we assume the game is genuinely asymmetric: Each agent plays as either thief or victim, not both. [Recall that, although the epsilon games could be conceptualized as an asymmetric game between the thief and victim roles, it is technically symmetric because each agent plays as both thief and victim. This symmetry makes the number of strategies for each player (after excluding $N{S}_{ϵ},N{P}_{ϵ}$) 4, not 2. The second assumption is therefore necessary.] Thus, in the 2 × 2 game, the thief can play either $A{S}_{ϵ}$ or $F{S}_{ϵ}$, and the victim can play either $A{P}_{ϵ}$ or $F{P}_{ϵ}$. The payoffs are derived directly from the epsilon game.

Following case 1, we assume that $\frac{ϵ}{2(1-ϵ)}<r_{p:s}+r_{c:s}<\frac{2(1-ϵ)}{ϵ}$ and $\max (\frac{ϵ}{2(1-ϵ)}{r}_{c:s},1-\frac{2(1-ϵ)}{ϵ}{r}_{p:s})<\theta <\min (1-\frac{ϵ}{2(1-ϵ)}{r}_{p:s},\frac{2(1-ϵ)}{ϵ}{r}_{c:s})$. Thus, $(F{S}_{ϵ},A{P}_{ϵ})$ and $(A{S}_{ϵ},F{P}_{ϵ})$ are both strict Nash equilibria, and one risk-dominates the other when the product of its deviation losses is larger. Formally, $(F{S}_{ϵ},A{P}_{ϵ})$ is risk-dominant in the 2 × 2 game iff (18):

$$({\pi }_{F{S}_{ϵ}}(A{P}_{ϵ})-{\pi }_{A{S}_{ϵ}}(A{P}_{ϵ}))\ast ({\pi }_{A{P}_{ϵ}}(F{S}_{ϵ})-{\pi }_{F{P}_{ϵ}}(F{S}_{ϵ}))>({\pi }_{A{S}_{ϵ}}(F{P}_{ϵ})-{\pi }_{F{S}_{ϵ}}(F{P}_{ϵ}))\ast ({\pi }_{F{P}_{ϵ}}(A{S}_{ϵ})-{\pi }_{A{P}_{ϵ}}(A{S}_{ϵ}))$$

Otherwise, $(A{S}_{ϵ},F{P}_{ϵ})$ is risk-dominant.

When two epsilon strategies meet, the payoffs are complex and unwieldy. Fortunately, as in the ESS derivation, we can reduce this complexity. For any two epsilon thief strategies $T_{ϵ},{T\prime }_{ϵ}$ and any epsilon victim strategy $V_{ϵ}$:

$${\pi }_{T_{ϵ}}(V_{ϵ})-{\pi }_{{T\prime }_{ϵ}}(V_{ϵ})=\left(1-\frac{3}{2}ϵ\right)({\pi }_T(V_{ϵ})-{\pi }_{T\prime }(V_{ϵ}))$$ [S5]

The proof, which we omit here, comes simply from canceling and rearranging terms. Since $ϵ<\frac{2}{3}\Rightarrow 1-\frac{3}{2}ϵ>0$, we can simplify the risk-dominance condition by substituting using Eq. S5 and dividing out the common $1-\frac{3}{2}ϵ$ terms. Thus, the risk-dominance condition becomes:

$$({\pi }_{FS}(A{P}_{ϵ})-{\pi }_{AS}(A{P}_{ϵ}))\ast ({\pi }_{AP}(F{S}_{ϵ})-{\pi }_{FP}(F{S}_{ϵ}))>({\pi }_{AS}(F{P}_{ϵ})-{\pi }_{FS}(F{P}_{ϵ}))\ast ({\pi }_{FP}(A{S}_{ϵ})-{\pi }_{AP}(A{S}_{ϵ}))$$

Substituting the payoffs (derived from the epsilon game), $(F{S}_{ϵ},A{P}_{ϵ})$ is risk-dominant iff:

$$\left(Ns\frac{ϵ}{2}(1+\theta )-Ns+Np(1-ϵ)\right)\ast \left(Ns\left(\theta -ϵ\theta +\frac{ϵ}{2}\right)-N(s+c)\frac{ϵ}{2}\right)>$$

$$\left(Ns-Np\frac{ϵ}{2}-Ns(\theta -ϵ\theta +\frac{ϵ}{2})\right)\ast \left(N(s+c)(1-ϵ)-Ns\left(\frac{ϵ}{2}\theta -ϵ+1\right)\right)\iff \left(s\left(\frac{ϵ}{2}\theta +\frac{ϵ}{2}-1\right)+p(1-ϵ)\right)\ast \left(s\theta (1-ϵ)-c\frac{ϵ}{2}\right)>\left(s\left(\theta ϵ-\theta -\frac{ϵ}{2}+1\right)-p\frac{ϵ}{2}\right)\ast \left(c(1-ϵ)-s\theta \frac{ϵ}{2}\right)$$

After expanding terms, canceling, and rearranging, this becomes:

$$s^2\theta \left(2ϵ-\frac{3}{4}{ϵ}^2-1\right)-sp\theta \left(2ϵ-\frac{3}{4}{ϵ}^2-1\right)-sc(1-\theta )\left(2ϵ-\frac{3}{4}{ϵ}^2-1\right)>0⟺\left(2ϵ-\frac{3}{4}{ϵ}^2-1\right)(\theta (s-p)+(1-\theta )c)>0$$

Since $2ϵ-\frac{3}{4}{ϵ}^2-1=\frac{1}{4}{ϵ}^2-{(1-ϵ)}^2$ and $ϵ<\frac{2}{3}\Rightarrow 1-ϵ>\frac{ϵ}{2}$, $2ϵ-\frac{3}{4}{ϵ}^2-1<0$. Thus, the above expression is equivalent to:

$$\theta (s-p)+(1-\theta )c<0\iff \theta >\frac{c}{c+(p-s)}\iff \theta >\frac{r_{c:s}}{r_{c:s}+r_{p:s}}.$$

This is the risk-dominance condition presented in the main text. Consistent with the pattern in the ESS conditions, agents will converge on flexible theft/rigid punishment when $\theta$ is high, and rigid theft/flexible punishment when $\theta$ is low. Notably, this result is independent of the value of $ϵ$ (as long as $0<ϵ<\frac{2}{3}$).

One wrinkle in this analysis is that risk-dominance has been linked to evolutionary outcomes most clearly in the context of symmetric games (40). In asymmetric games (like our 2 × 2 game), stochastic evolutionary processes have only been shown to select risk-dominant equilibria under extra assumptions, which we do not engage with here (40, 41). We acknowledge this weakness, and supplement the risk-dominance analysis of the 2 × 2 game with the Moran process simulations.

1.3 Moran Process Simulations.

The details of our Moran simulations are described in the main text. Here, we fill in two details: the expanded strategy space, and the parameter values.

Expanded Strategy Space.

The Moran simulations were conducted on a variant of the steal/punish game that differed from the epsilon game in two respects. First, it used the basic strategies ($AS$, $NS$, etc.) and not the epsilon strategies ($A{S}_{ϵ}$, $N{S}_{ϵ}$, etc.). We did this because the Moran process offers a natural alternative implementation of population diversity: a mutation rate $\mu$. We used $\mu$ in place of stipulating epsilon strategies to show that our pattern of results was robust to alternative assumptions.

Second, to show that our results were robust to an expansion of the strategy space, we included two more strategies for each role. For the thief, we added “steal after punishment” and “steal after nonpunishment,” which stole only if the victim (didn’t) punish on the prior round. For the victim, we added “always punish anything,” which punished no matter what action the thief took on the prior round, and “punish after nontheft,” which punished only if the victim didn’t steal on the prior round. This expanded strategy space thus included every reactive inflexible strategy, where agents can condition their move on their opponents’ prior move (23), plus the flexible strategies.

The payoffs for this expanded game are shown in Fig. S4. The matches between strategies which both condition on the opponent’s previous move have ambiguous results: The agents can settle into one of two possible action cycles. To derive payoffs for these matches, we average the payoffs from the two possible cycles. (This approach is compatible with the view that agents have “trembling hands” and thus alternate between the cycles.) Also, when “steal after nonpunishment” faces “flexibly punish” ($FP$), the optimal rigid strategy for $FP$ to adopt depends on the parameter settings. We assume that $FP$ picks the better of the two options.

Parameters.

For the simulation in Fig. 3, we used the parameters in Table S1. We then systematically varied the nonpayoff parameters to ensure that our results were robust and to understand how our result was affected by parameter variation.

We focus on two crucial parameters: the selection intensity $w$ and mutation rate $\mu$. Fig. S5A shows the result of simulations with different selection intensities; Fig. S5B shows the result of simulations with different mutation rates. Fig. S5C shows an additional simulation in which we randomly sampled $w$ and $\mu$ for each match from the ranges $Uniform(\frac{1}{\mathrm{10,000}},\frac{1}{100})$ and $Uniform(0,\frac{2}{3})$, respectively. (To interpret the selection intensity magnitudes, note that fitness scores are on the order of $\sim$10,000.)

In most cases, the results were qualitatively identical. The only difference arises when the selection intensity is low ($w=\frac{1}{\mathrm{10,000}}$). Here, when $\theta$ is low, the population often fails to converge, and instead oscillates between $(AS,FP)$ (the predicted equilibrium) and $(AS,NP)$. This effect occurs because, when $\theta$ is low, $(AS,FP$) earns only a slightly higher payoff than $(AS,NP)$—and the low selection intensity prevents it from consistently outcompeting $(AS,NP)$.

This effect is not predicted by our ESS analysis, but it is relatively inconsequential. $(AS,FP)$ and $(AS,NP)$ lead to extremely similar behavioral patterns: Thieves always steal, and victims either never punish or quickly learn to stop punishing. The general conclusion still holds: The role that is relatively vulnerable when flexible will evolve rigidity to compensate. (A similar effect occurs in the RL simulations; see Effects of Costly Learning Time.)

2. RL Simulations

Our RL simulations are described in the main text. Here, we provide details about the setup and results of the simulations.

2.1 Outcome of Flexible Thief Versus Flexible Victim.

Background.

In Learning Dynamics for RL Agents, we argued that, when a flexible thief faces a flexible victim, the outcome is typically that the thief learns to steal and the victim learns to give up on punishing (i.e., $\theta$ is typically high). This effect, at least in the parameter space we chose, was due to punishment’s costs.

Here, we expand on this argument. Model-free RL agents attempt to estimate the value of stealing/punishing by averaging the total reward received after taking the action in the past. (Recall that, in RL algorithms, the value of an action is the expected sum of future reward conditional on performing the action.) The value estimate thus has two components, one short-term and one long-term. The short-term component is the immediate reward obtained from taking the action. The long-term component is the expected (time-discounted) sum of future rewards, conditional on being in the subsequent state to which the action leads. (In words, estimating the long-term component is akin to answering questions like: Will stealing now allow me to steal in the future? Will punishing now prevent me being stolen from in the future? Or, in MDP terms, what is the value of the state to which I transition after stealing/punishing?). For both the thief and the victim, the long-term component will ultimately come to dominate the value estimates of stealing/punishing.

However, because the long-term component is noisy (it depends on what your opponent does) and takes time to estimate, initial value estimates will be dominated primarily by the short-term component. Since punishment is immediately costly (and theft immediately beneficial), victims will initially dislike punishing, and thieves will initially like stealing. This reflects the influence of the short-term element for each.

In stationary environments, this initial shortsightedness wouldn’t be a problem; a well-designed RL algorithm will eventually estimate the true values associated with actions in the optimal policy. However, in a competitive multiagent environment where both agents are flexible, an agent’s initial estimate influences the behavior of its opponent. The fact that victims initially dislike punishing makes thieves like stealing more, because they experience fewer negative consequences of theft. In turn, the thieves’ increased preference for theft will make victims dislike punishing even more, because it appears less and less useful. And this makes thieves prefer stealing even more, etc. In this way, the victim’s initial preference against punishment (and the thief’s initial preference for theft) initiates a sequence which results in the self-reinforcing equilibrium of theft and no punishment.

All three payoffs influence this process. The thief’s initial preference for theft is determined by a combination of $s$ and $p$. The victim’s initial preference against punishing is determined by $c$. When $s$ is high enough and $p$ is low enough, $c$ doesn’t matter; the thief’s initial preference for theft is strong enough to guarantee convergence to the theft/no punishment equilibrium.

For the sake of exposition, however, we chose a payoff space ($s=5$, $p=15$) in which $c$ determines the outcome. Here, when $c$ is high, the victim’s initial dispreference for punishing sends the pair of agents into a spiral toward the theft/no punishment equilibrium. However, when $c$ is trivial and the victim has no initial preference, the agents instead converge to the inverted equilibrium in which the victim learns to punish theft and the thief learns to desist from stealing.

Why, you might ask, do agents in the low-cost condition consistently converge to the inverted equilibrium? The victim has no initial preference against punishment, but, it seems, the thief still has an initial preference for stealing. By our logic, this preference should be sufficient to tip the scales toward the theft/no punishment equilibrium—even when punishment’s costs are trivial.

The answer is that the thief does not actually always have an initial preference for theft. Suppose that, in the beginning of the game, the RL victim punishes $\sim$50% of the time. (In the low-cost condition, this assumption is approximately accurate.) Then, the thief’s initial estimate of the value of stealing will be $s-\frac{1}{2}p$, or, with our payoffs, $-2.5$. By our logic, then, the outcome of the game should depend on whether the victim’s initial estimate of punishment’s value—determined by $c$—is stronger or weaker than $-2.5$. This is, roughly, what we find (Fig. 4A).

Parameters.

For the simulation in Fig. 4A, we sampled $s,c,p$ from the distributions in Table S1, and used the RL parameters in Table S2. We also ran a version with randomly sampled parameters, with $\alpha$ from $Uniform(0.05,0.25)$, $\beta$ from $Uniform(10,100)$, and $\gamma$ from $Uniform(0.75,0.99)$. The results were qualitatively identical.

2.2 Combined Evolution + RL Simulations.

Modeling Assumptions.

When embedding the RL agents in our evolutionary simulation, we make two common assumptions. First, as a baseline, we set the agents’ reward function equal to the objective payoffs of the game. For example, since $s=5$, an RL thief experiences a reward of 5 for stealing. In this way, RL agents learn to choose payoff-maximizing actions (26–28). (We then allow evolution to modify this reward function by introducing subjective biases, as described in the main text and below.)

Second, we assume that agents’ fitness is proportional to success in the game (i.e., we set the fitness function equal to the payoff function). In this way, evolution produces agents that choose payoff-maximizing actions (17, 19).

Combining these assumptions, the RL agents’ baseline reward function is equal to the fitness function. In other words, the agents possess a proximate learning mechanism that seeks to maximize ultimate outcomes.

Is it plausible to assume that agents directly “perceive” fitness in this way? There are two justifications for this assumption. The first is that evolution has likely already prepared a reward function that closely approximates the fitness consequences of many outcomes. For example, if the thief steals food and eats it, we assume that on average the reward of eating that food is a proportional representation of the food’s contribution to fitness. This is not because the agent perceives fitness, but because natural selection would tend to fine-tuned the rewards of various foods (and other experiences) to approximate their relative fitness consequences.

However, this logic clearly does not apply to all outcomes—for example, the money that participants earn in our experiment. (In other words, we did not evolve to find money rewarding). Here, the justification is as follows. The reason that people value money is because they have learned that money leads to other primary rewards specified by natural selection: food, warmth, social status, and so on. [In the framework of RL, the value of money—and other “secondary” rewards—converges precisely to the expected sum of future rewards conditional on receiving that money (25).] We have already argued that those primary rewards have evolved to be rewarding in lieu of their fitness consequences. If an outcome like winning money is valuable in proportion to the primary rewards it produces, and the primary rewards have evolved to be rewarding in proportion to the fitness consequences they produce, then, by transitivity, money is also rewarding in proportion to its fitness consequences.

This simplifying assumption is consistent with prior investigations of the evolutionary dynamics of RL systems (30). The purpose of our investigation, of course, is to understand when evolution will deviate from this sensible baseline by imposing further “biased” rewards, such as a taste for retribution.

Reward Function Biases.

Each genotype in the combined evolution and learning simulations was defined by a numerical bias that changed the subjective reward the agent received from performing its action (i.e., stealing or punishing theft). The magnitude of the numerical bias was always the smallest integer necessary to guarantee that the appropriate behavior would receive the greatest value estimate.

The three genotypes for the thief had steal biases: +11 (corresponding to AS), −6 (NS), and 0 (FS). Recall that the payoffs for these simulations were set to: $s=5$, $p=15$, and $c$ varies between 0.1 and 10. The value +11 was the lowest integer large enough, with our payoffs, to make the experience of theft worth the cost of being punished ($s-p=-10$, requiring a steal bias of +11 to overcome it), thereby motivating the agent to always steal. The value −6 was the least negative integer necessary to make the experience of theft consistently negative (because $s=5$), thereby instantiating NS. And an agent with 0 would learn to steal iff it wasn’t being consistently punished for theft, instantiating FS.

The three punishment biases were: +11 (corresponding to AP), −52 (NP), and 0 (FP). The value +11 was the lowest integer large enough to make inflicting punishment rewarding (because $c$ could reach as high as 10), and −52 was the least negative integer necessary to make inflicting punishment never worthwhile, even when it would have prevented future theft (because the long-term benefit of preventing indefinite future theft in our MDP is $\frac{s}{1-{\gamma }^2}$—or, with our parameters $s=5$ and $\gamma =.95$, around 51).

Parameters.

For the simulation in Fig. 4B, we used the Moran parameters in Table S1, but with fixed $s=5$ and $p=15$. We used the RL parameters in Table S2.

To ensure that our results were robust, we systematically varied $w$ and $\mu$; the results are shown in Fig. S6 A and B. Fig. S6C shows a version with randomly sampled learning parameters, with $\alpha$ from $Uniform(0.05,0.25)$ and $\beta$ from $Uniform(10,100)$. (We kept $\gamma$ fixed because it is needed to determine the reward function biases.)

Effects of Costly Learning Time.

In all cases, the results were qualitatively similar. When the cost of punishment is high, people evolve an intrinsic reward for punishment; when the cost is high, people evolve an intrinsic reward for theft.

This method of presenting the results is intuitively clear, but it obscures a subtle complication. The equilibrium genotypes are composed of both a theft bias and a punish bias. When the cost of punishment is high, the population converges to the familiar equilibrium: rigid punishment (i.e., intrinsic reward for punishing) and flexible theft (no bias). However, when the cost is low, the population doesn’t always converge to be inverted equilibrium of rigid theft and flexible punishment. Instead, for some parameters, the population oscillates between rigid theft/flexible punishment and rigid theft/no punishment (i.e., an intrinsic bias against punishing).

This was not predicted by our evolutionary analysis. In the evolutionary analysis, flexibly punish always outcompetes never punish because it performs better against flexibly steal (when $\theta$ is low, as it is here)—and equally well against always steal and never steal. This latter result depends on a critical simplifying assumption. As stated above, we assume that the time it takes for a flexible agent to learn which strategy to adopt is negligible compared with the length of the game, and thus omit the learning period from the payoffs of the flexible agent. In other words, the evolutionary analysis assumes that there is no practical cost to being a learning agent. (This omission allowed us to focus on the strategic costs of flexibility.)

However, when simulating actual learning agents, there is such a practical cost. RL agents go through an initial exploration phase before settling into their preferred actions, and this exploration comes at a small, but nonzero, cost. For example, when facing a thief who always steals, it takes longer for a flexible RL victim (no reward bias for/against punishment) to learn to stop punishing than it does for a victim with a strong bias against punishment.

Hence, against always steal and never steal, a victim with a bias against punishing will have some advantage over a flexible victim. This advantage is counterbalanced by the fact that a flexible victim achieves a much higher payoff against the portion of the population that plays flexibly steal. Because of the fluctuating nature of stochastic selection in a finite population, the relative advantage of the two strategies continually shifts, and the strategies oscillate.

Despite this complication, the practical result is similar: When the cost of punishment is low, people evolve an intrinsic bias for theft, and punishment is absent in equilibrium (either because flexible victims learn that it is useless or because victims are born with an intrinsic bias against punishing). Hence, we present the simple version in the main text.

Isolating the Effect of Learning Dynamics.

The simulations demonstrated that, in the payoff range we chose, the cost of punishment is a critical factor in determining the outcome of selection. However, exactly how it influences selection is ambiguous. The cost could, as we suggest, influence selection via its effect on the learning dynamics (altering the crucial outcome of flexible thief vs. flexible victim). However, it could also influence selection simply by being a change in the payoff function.

To demonstrate that punishment’s cost influences selection via the learning dynamics, and not just via a change in the objective payoffs, we ran a follow-up simulation in which we varied the perceived cost of punishing while holding the objective cost fixed. We fixed $c=5$ and systematically simulated agents that perceived from as little as 10% of $c$, up to 200% of $c$. This manipulation affects the learning dynamics without directly altering the fitness structure. The results were qualitatively similar to the previous simulations (Fig. S6D), suggesting that $c$ influences selection via its effect on the learning dynamics.

3. Behavioral Experiment

Variable Payoffs.

To demonstrate that our behavioral results were not an artifact of the specific payoffs we used, we ran a follow-up study that randomly varied the payoffs for each participant. $s$ and $c$ were chosen from $Uniform(1,4)$, and $p$ from $Uniform(s+1,s+4)$.

Thieves were sensitive to $s$, stealing more when the payoff was higher (${\chi }^2(1)=7.93$, $P<0.01$, ${\eta }_G^2=0.02$, 95% CI$=[0,0.10]$). It is unclear whether victims were sensitive to $c$. They punished less when $c$ was higher, but only when facing opponents who always stole, and the trend was nonsignificant (${\chi }^2(1)=3.78$, $p=0.052$, ${\eta }_G^2=0.01$, 95% CI = [0, 0.08]). They were, however, significantly sensitive to $p$, punishing more when it was more effective (only against opponents who always stole; ${\chi }^2(1)=5.6$, $p=0.02$, ${\eta }_G^2=0.03$, 95% CI = [0, 0.11]). This finding supports the notion that people exhibit some flexibility in their punishment choices, but the details are unclear (see Discussion). (Thieves were not sensitive to $c$ or $p$.)

Crucially, however, our main result held (Fig. S7). In the focal match against opponents who always stole/punished theft, thieves quickly learned to stop stealing, while victims were relatively inflexible when punishing. The interaction between role and round was significant (${\chi }^2(1)=25.0$, $P<0.001$, ${\eta }_G^2=0.03$, 95% CI = $[0.011,0.20]$).

Effect Sizes.

To report effect sizes, we ran a simplified version of each analysis. For the predicted interaction of role X match round, we dropped all rounds except the first and last. This gave us a 2 × 2 design (thief vs. victim and first round vs. last round), allowing us to perform an ANOVA and extract the interaction’s generalized eta-squared (a measure of the percentage of variance explained by the effect). Similarly, for the main effects in the random-payoffs experiment reported in Variable Payoffs, we collapsed across trials, obtaining an average choice for each subject. We then performed an ANOVA on this simplified dataset and extracted the main effect’s generalized eta-squared.

For the purposes of determining significance, we still report likelihood ratio tests over the mixed-effects models; but for effect sizes, we report eta-squared. We use the R package MBESS to compute 95% CIs (42).