Significance
The phenomenon of spontaneous nanodroplet formation termed the “Ouzo effect” is the basis for many processes, from preparation of pharmaceutical products, to formulation of cosmetics and insecticides, to liquid–liquid microextraction. This work attempts to disentangle the effects of concentration gradients from the extrinsic mixing dynamics by spatiotemporally following the nanodroplet formation from the Ouzo effect confined in a quasi-2D geometry. We observe striking universal branch structures of the nucleating droplets under the external diffusive field, analogous to the ramification of stream networks in large scale, and the enhanced local mobility of colloidal particles driven by the concentration gradient emerging from the development of the branch patterns. We further demonstrate that these nanodroplets can be exploited for single-step nanoextraction and detection.
Keywords: Ouzo effect, nanodroplet, branch patterns, diffusive growth, diffusiophoresis
Abstract
We report the self-organization of universal branching patterns of oil nanodroplets under the Ouzo effect [Vitale S, Katz J (2003) Langmuir 19:4105–4110]—a phenomenon in which spontaneous droplet formation occurs upon dilution of an organic solution of oil with water. The mixing of the organic and aqueous phases is confined under a quasi-2D geometry. In a manner analogous to the ramification of ground stream networks [Devauchelle O, Petroff AP, Seybold HF, Rothman DH (2012) Proc Natl Acad Sci USA 109: 20832–20836 and Cohen Y, et al. (2015) Proc Natl Acad Sci USA 112:14132–14137] but on a scale 10 orders of magnitude smaller, the angles between the droplet branches are seen to exhibit remarkable universality, with a value around 74° ± 2°, independent of the various control parameters of the process. Numerical simulations reveal that these nanodroplet branching patterns are governed by the interplay between the local concentration gradient, diffusion, and collective interactions. We further demonstrate the ability of the local concentration gradient to drive autonomous motion of colloidal particles in the highly confined space, and the possibility of using the nucleated nanodroplets for nanoextraction of a hydrophobic solute. The understanding obtained from this work provides a basis for quantitatively understanding the complex dynamical aspects associated with the Ouzo effect. We expect that this will facilitate improved control in nanodroplet formation for many applications, spanning from the preparation of pharmaceutical polymeric carriers, to the formulation of cosmetics and insecticides, to the fabrication of nanostructured materials, to the concentration and separation of trace analytes in liquid–liquid microextraction.
The Ouzo effect occurs in a ternary mixture typically consisting of water, oil, and ethanol, when the oil dissolved in the alcohol precipitates out to form tiny droplets upon the addition of water (1). This effect can also be seen, for example, when eucalyptus disinfectants and mosquito repellents are diluted with water, where the oils are miscible with the alcohol but immiscible with water. This spontaneous droplet formation does not require mechanical agitation to disperse the liquid or the addition of surfactants or other stabilizers. As such, it constitutes the basis for the formation of stable emulsion droplets in a broad range of applications such as the formulation of beverages, perfumes, and insecticides (2–4) and the fabrication of hollow nanomaterials (5, 6). In liquid–liquid microextraction, the oil droplets from the Ouzo effect are used to concentrate and separate trace hydrophobic analytes from their aqueous samples before forensic analysis, biomedical diagnosis, or environment/safety monitoring (7–9). Small hydrophobic organic molecules, lipids, or polymers dissolved in a polar organic solvent exhibit similar effects to that of the oil phase, forming submicron particles with narrow size distributions upon dilution with water. In a process referred to as nanoprecipitation, solvent displacement, or solvent shifting (10–12), water-insoluble drugs can be incorporated into biopolymeric nanocarriers with the possibility of tailoring their size distribution in controlled release delivery.
Despite the long history of the Ouzo effect and its relevance to a wide range of applications, a quantitative understanding of its underlying mechanism and the ability to predict the growth and stability of the nanodroplets remains elusive. More specifically, the effect takes place when the compositions of the water, solute, and organic solvent lie within a metastable region between the spinodal and binodal curves in the ternary phase diagram. Homogeneous droplet nucleation, which is a rapid process in response to a sudden increase in the oversaturation as a consequence of the addition of the aqueous phase, requires extremely rapid mixing between the two phases, for example, by coflowing streams in a microfluidic device, impinging jets, or continuous turbulent mixing (13–15). The droplet size and distribution is determined not only by the physicochemical properties and concentrations of the solvents but also by the temporal and spatial characteristics associated with the mixing dynamics (12, 16–20). Complex physical events, such as fast solvent diffusion, interfacial instability, and local concentration gradient-driven mass transport, have been proposed to account for such dynamical aspects in the early stages of droplet formation. Nevertheless, the underlying mechanism responsible for the Ouzo effect can only be elucidated largely through an understanding of the later or final stages in the evolution of the ternary system, due to the extremely short order of microsend time scale and small dimensions of the nucleating nanodroplets. As such, finding an optimal operating window to achieve a desired droplet size still relies, to date, on trial and error, necessitating the screening of a large library of solvent combinations and solvent injection conditions. A better understanding of the fundamental physicochemical mechanisms underlying the Ouzo effect will therefore be extremely useful in guiding the rational design of appropriate solutions and mixing conditions for droplet formation.
In this work, we disentangle the coupled effects between the concentration gradient and extrinsic mixing dynamics in the bulk liquid by confining the Ouzo effect within a quasi-2D fluid geometry such that the process is diffusion-dominated. Given that the aqueous phase is now brought into contact with the organic phase purely by diffusion, it is thus possible to spatially and temporally follow the dynamics of the nanodroplet formation. We observe the formation of universal nanodroplet branch patterns that remarkably resemble the ramification of groundwater streams, albeit at much smaller scales. Our simulations confirm that the nanodroplet branches result from the interplay between the local concentration gradient, diffusion, and collective interactions. The pronounced local concentration gradient emerging from the droplet branches is clearly revealed by the enhancement in the transport of colloidal particles along the branches in this highly confined space. In addition to demonstrating that these droplet branches offer an opportunity as a single-step nanoextraction technique, we also expect that the insight into the dynamical aspects of the Ouzo effect will be valuable for better understanding ways to control the droplet formation in other applications.
Results and Discussion
Confined Ouzo Effect in Quasi-2D Geometry.
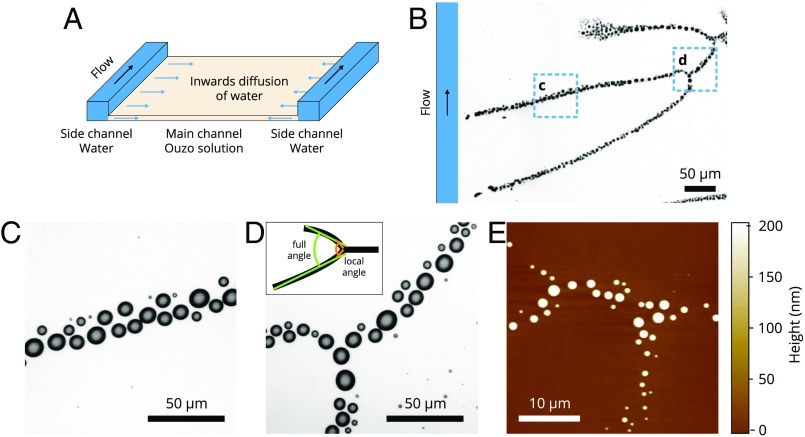
The confined Ouzo effect in our experiments was realized in a horizontal rectangular flow channel as sketched in Fig. 1A. The entire channel was initially filled with the first solution, which is oil dissolved in aqueous ethanol solution (i.e., the Ouzo solution). The poor solvent, water, was injected from one end of the channel, flowing inside the deeper 1.7-mm side channels to the other end. In the direction perpendicular to the primary flow, water diffuses sideways into the quasi-2D main channel, which is 20 m in height, from the inner rim of the side channel.
Fig. 1.
(A) A 3D schematic illustration of the fluid channel setup used for the formation of the nanodroplet branches. The horizontal flow cell consisted of a substrate and a glass window whose main flow channel is flanked by two narrow side channels as indicated by the orange zones in the sketch. The length was 7.65 cm for both the main and side channels, whereas the width was 6 mm and 250 m and the depth was 20 m and 1.7 mm for the main and the side channels, respectively. The flow was in the direction indicated by the black arrow. In this experimental geometry, the side channels were deep enough that water flew almost exclusively along them, as the very thin (Hele–Shaw-like) slot (main channel) filled with Ouzo between the two deep water channels provided a high hydrodynamic resistance. The branches (green) extended into the main channel. (B–D) Optical images and (E) AFM image of representative branch structures; the close-up (C and D) shows the individual droplets along the branches. Inset in D shows the definition of a full angle and a local angle near the merging point. The branch morphological features will be characterized by these two angles.
As the water mixes with the Ouzo solution, we observe the development of striking branch patterns inside the main channel. The high-resolution optical images in Fig. 1 C and D show that these branches consist of discrete nanodroplets, which is further confirmed by the atomic force microscopy images of the polymerized droplets in Fig. 1E. The individual droplets typically grow up to 3 m to 6 m in lateral diameter and 100 nm to 1 m in height (and are therefore simply referred to as nanodroplets). The branches consist of, at most, a few individual droplets in width (Fig. 1 C–E), which is negligible compared with its extent of millimeters.
The top of the droplet branches start from the inner rim of the side channel or from several spots in the main channel. For a given channel, the branch tips always start from the very same locations on the rim of the side channel, at locations containing structural defects of a few microns in size (Movies S1 and S2). To verify the role of these defects in the branch formation, we deliberately indented evenly distributed microstructures along the side-channel rim, subsequent to which we observed the position of the branch tips to also be evenly distributed along the rim (Movie S3). The results thus clearly show that the onset of the droplet branches is determined by local geometrical structures. In the quasi-2D main channel, neighboring branches are observed to tilt toward each other and merge at locations farther away from the side channel. The morphology of an entire branching structure is dendritic, analogous to a tree with the top at the rim of the side channel and with the root extending into the inner area of the 2D main channel.
Universality in the Merging Angle.
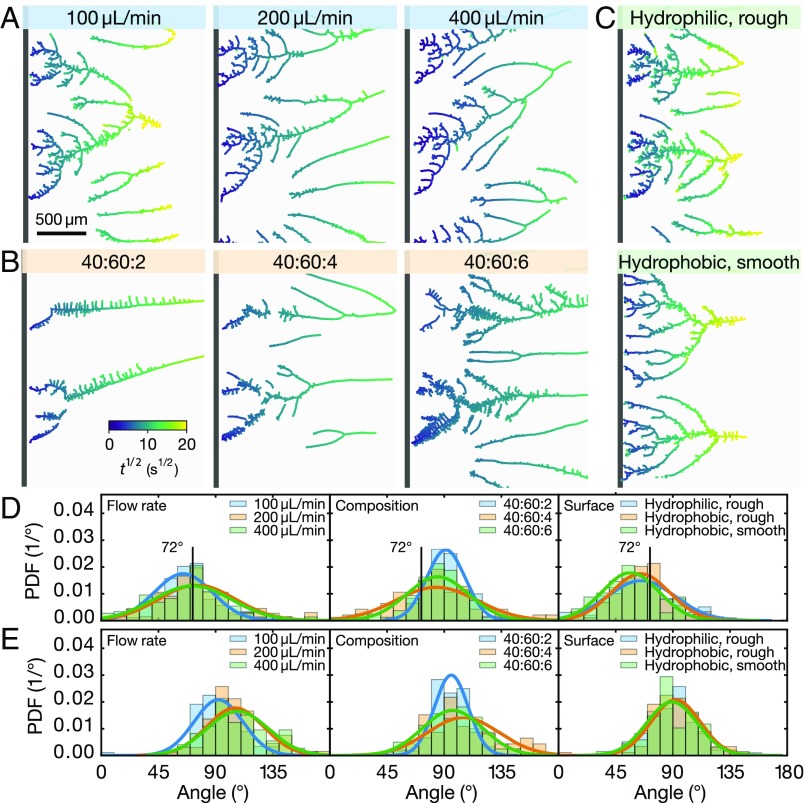
To examine the universality of the branch formation from the confined Ouzo effect, we varied the flow rate of water in the side channel, the composition of the Ouzo solution, and the hydrophobicity of the main-channel wall. As shown in Fig. 2 A–C, the overall morphology of the formed branches was very similar under the wide range of conditions examined.
Fig. 2.
Formation of nanodroplet branches up to 400 s after the start of branch growth. The color at any location indicates the time at which the branch reached a given location. (A–C) Optical images of the branches formed under eight different conditions. (A) The flow rate of water in the side channel was 100 L/min, 200 L/min, and 400 L/min. The composition of the Ouzo solution was the same for all three flow rates (water:ethanol:oil = 50:50:2). (B) The ratio of water, ethanol, and oil in the Ouzo solution was 40:60:2, 40:60:4, and 40:60:6 with a flow rate of water of 100 L/min. (C) The substrates were hydrophilic or hydrophobic, while the rim of the side channel was either rough or smooth. The flow rate of water was 100 L/min, and the composition in the Ouzo solution was 50:50:2. (D and E) Corresponding PDFs of the angles between two merged branches (D) over their full range and (E) from the segments near the merging point. The hydrophobic and rough channel was used for all cases in A and B; 100 L/min in A is presented as “Hydrophobic, rough” in the plots.
To quantify the common features in the branching structure, we measured and analyzed 660 angles, in total, between the merging branches. To allow for the comparison, we determined the full angle in exactly the same way as that carried out in the work on ground stream ramification (21, 22). In all of the eight cases shown in Fig. 2, the corresponding probability distribution functions (PDF) of the merging angle is plotted in Fig. 2D, with no significant differences observed between them. The mean branching angle of all 660 angles was found to be (95% confidence interval).
Although the branch formation process, in general, is universal with respect to morphology, angle distribution, and value of the most probable angle, closer inspection of the eight cases analyzed in Fig. 2 reveals some detailed variations: As the oil concentration increases, the number of branches increases and the main branches become more “hairy” with tiny protrusions arising on both sides. Moreover, a higher flow rate of water in the side channel causes a more pronounced tilt of the entire structure of the branches toward the flow direction.
Diffusion-Dominated Growth Dynamics.
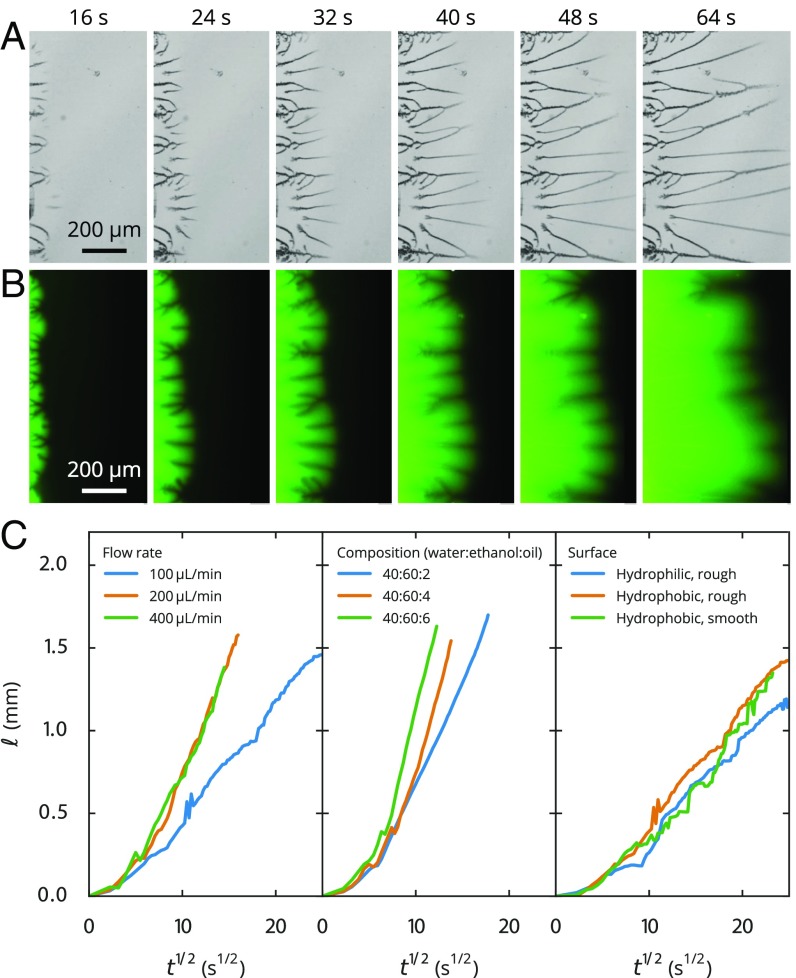
To reveal the mechanism for the development of droplet branches, we followed the droplet growth with bright-field imaging and the transport of dyed water in the 2D channel separately with fluorescent imaging. Movies S1 and S2 show that the branches extended concurrently with the moving front of water into the main quasi-2D channel. The emerging branches at the moving front in the inner area, on the other hand, grew toward a parent branch nearby. In any case, the entire tree of branches was observed to extend toward the “tree root” in the direction of the inner main channel.
To quantify the growth rate, we measured the branch length from the branch top to the water front at different times , plotting the data as a function of in Fig. 3C. After a short initial transient, the branch length is seen to increase roughly as , regardless of the flow rate of water, solution composition, or substrate properties. This behavior in the branch extension evidently suggests that the branch formation is dominated by diffusion; that is, the mixing between two solutions is driven by the transverse diffusion of water. By fitting the data (excluding the transients for ) with the 1D diffusion relationship , we obtained effective diffusion constants in the range of for the smallest oil concentration of the Ouzo solution, which is comparable to the diffusivity of water in ethanol. We note that, for higher oil concentrations of the Ouzo solution, the growth rates and thus the fitted effective diffusion constants of the branches are up to a factor of 10 larger, presumably due to some convective contribution, resulting in a slightly steeper increase than .
Fig. 3.
Growth of droplet branches. (A) Bright-field and (B) fluorescent images of the growing branches. Water was dyed green, and the dark lines in the images are the nanodroplet branches. (C) Plots of the distance from the start of the branch to its growing front as a function of . The nearly linear relationship between and after an initial transient reveals close to diffusive behavior that underpins the branch growth. We note, however, that the diffusiophoresis will also cause some convective effects, as we will see from Fig. 5. The optical images of the formed branches are shown in Fig. 2 A–C.
Mechanism and Simulations for the Branch Formation.
We now propose the mechanism for the confined Ouzo effect and the universal merging angles between two droplet branches. First, the water diffusing from the side channel into the quasi-2D main channel filled with the Ouzo solution leads to a local reduction in the ethanol concentration, so that the oil becomes oversaturated—the Ouzo effect. Irregularities such as microstructures at the edge of the side channel toward the quasi-2D main channel then facilitate droplet nucleation out of the oil-oversaturated solution, thus initiating the branch. In the quasi-2D geometry, the concentration gradient is sharpest at the moving front of water into the oil-rich solution in the main channel. Although the water front [providing a pulse of local oil oversaturation in the Ouzo solution (18)] moves across the entire cross-section of the main channel, new droplets only selectively nucleate behind older ones, showing that uniform and unperturbed diffusion of water into the Ouzo solution is not sufficient to trigger droplet nucleation, but that local distortions are required. These are provided by the older droplets or, in some cases, by irregularities in the main channel, from which new branches emerge. The extension of an old branch may induce an asymmetry in the concentration gradient, which directs the growth of the new side branches toward it, eventually leading to merging of the two branches.
The growth and merging process of the branches resembles the ramification of stream networks incised by underground water, where the characteristic bifurcating angle is found to be about (21, 22), close to the value found here. In similar fashion, the growth of the 1D streams in the network is controlled by 2D diffusion. Such processes are accessible to an analytical treatment of the harmonic field obeying the 2D Laplace equation with the help of the Loewner transformation (23, 24), as very elegantly shown for the formation and ramification of the stream networks in the porous estuary (21). Based on this approach, Löwner and others could analytically calculate the bifurcation angle of the 1D streams in the 2D harmonic field, obtaining , in agreement with their and our experimental results.
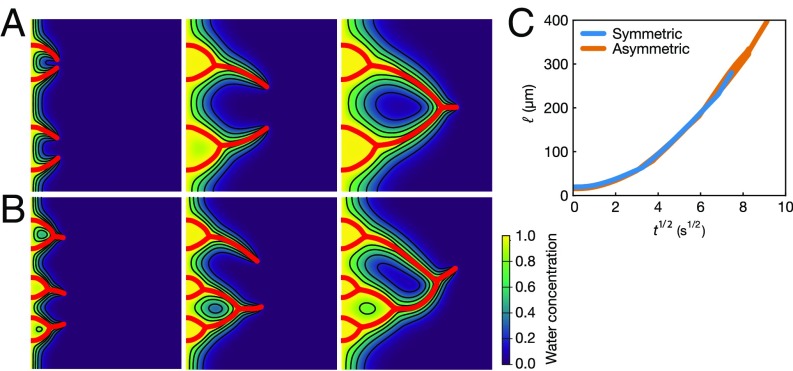
The above qualitative description of the branch growth and merging process is supported by numerical simulations of the 2D diffusion equation, with the growing branches being implemented by the immersed boundary method; see Materials and Methods for details. Fig. 4 A and B shows snapshots of the branch growth process and the corresponding concentration field of water, both resulting from the numerical simulations. The starting points of the branches on the left wall are small perturbations of the (computational) domain, which we put in a symmetric (Fig. 4A) or asymmetric (Fig. 4B) way. On the tip of these roughness perturbations, the concentration gradient is maximized, which drives the branch to grow from there. Once a branch grows, the concentration gradient is maximized on the tip of the branch, which causes the branch to further grow. No matter whether the initial perturbation has been symmetric or asymmetric, the tips of the branches always follow the diffusive scaling law (Fig. 4C), corroborating the experimental observation. Averaging the bifurcating angles occurring in the numerical simulations, we got , in good agreement with the theoretic argument and the experimental observations. These simulations capture the main features of the evolution of the droplet branches, in terms of the overall morphology, the growth rate, and, in particular, the characteristic merging angles. The numerical model, however, is not sophisticated enough to allow for a one-to-one comparison with the experiment. Such quantitative comparison is beyond the scope of the present paper.
Fig. 4.
Results from the numerical simulations in which the red lines show the trajectories of the branches and the contours map the water concentration field. Oil droplets form on the branches, and thus the water concentration in the region near the branches is highest. (A) Symmetric case with four identical initial perturbations at . (B) Asymmetric case with six different initial perturbations at . (C) Regardless of whether the branches are symmetric or not, their tips follow very similar diffusion-dominated behavior, as seen from the linear scaling governing the distance between the tips and the left boundary beyond the initial transient, similar to that observed in Fig. 3C.
Local Competitive Effect of the Growing Droplets.
Detailed inspection of the images in Fig. 2 A–C, in particular, in the local region around the bifurcations, reveals that two merging branches grow slightly outward before they merge. Fig. 2E shows the PDFs of the local angles obtained through the fitting of the two branch segments near the node. The width of the PDFs is similar to those for the globally determined bifurcation angles, and the mean angle is now , much larger than the angle of from fitting the entire branch. These larger angles reflect the competition between neighboring growing droplets for the dissolved oil in oversaturation. A similar competitive effect was observed in the self-organization process of these growing droplets confined on the rim of a microlens from an oil-oversaturated solution (25), which arose as a consequence of the selective growth of the droplets in the direction of the larger concentration, which is the direction where no other droplets grow.
Enhanced Mobility of Colloidal Particles from the Local Concentration Gradient.
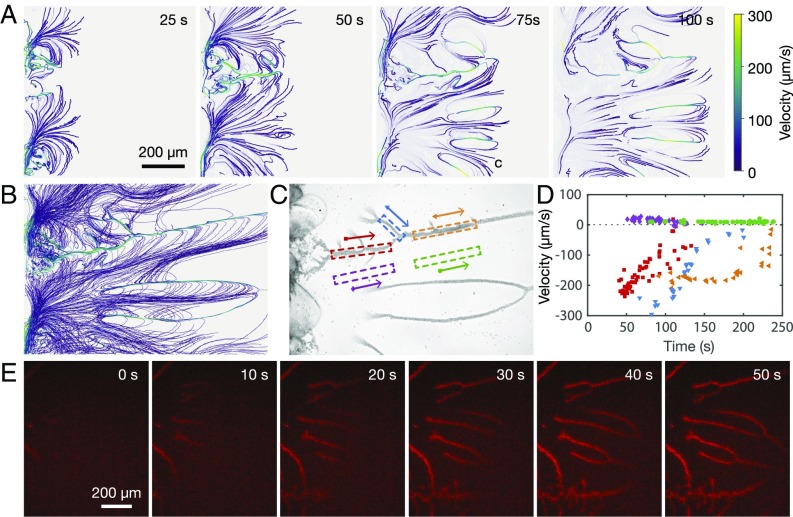
We now reveal the local concentration gradient as the significant consequence of the droplet branches by following the motion of colloidal particles in the confinement of a 2D fluid channel. As the control experiment, we first examined how water enters into the main channel filled with the oil-free ethanol solution. The dyed water with fluorescein at 0.02% concentration was observed to completely fill the side channel along the inner channel before diffusing into the main channel. When tracer microparticles with a diameter of 2 m were added to the water, the fluorescent images revealed that these microparticles remained in the side channel, suggesting that water diffuses into the ethanol solution without incurring sufficient concentration gradient to transport the colloidal particles into the main channel. In other words, the pressure gradient along the water channels did not lead to any flow into the Ouzo solution. Once the droplet branches form as a consequence of the 2D confined Ouzo effect, however, we observe the mobility of the colloidal particles to be significantly enhanced, as shown in Fig. 5 and Movies S4–S6. The microparticles entered into the main channel with the moving front, and were subsequently attracted to the branches. Once there, the particles moved rapidly in the direction opposite to that of the front, although some appeared to recirculate along the side branches of the droplets. Interestingly, we note that the particles usually follow the same path and recirculate over several cycles along the same side branch. Quantitative analysis of their trajectories showed that the velocity of the microparticles far from the branches was approximately 25 m/s, decaying to around 10 m/s after about 100 s. The velocity in the opposite direction along the branches was about times higher, up to 300 m/s at the moving front.
Fig. 5.
Droplet branches for enhanced colloidal particle transport and nanoextraction in the quasi-2D channel. (A) Velocity profile of tracer microparticles in the main channel. The microparticles suspended in water entered into the main channel from the left at s. The ratio of water:ethanol:oil in the Ouzo solution was 25:25:1. (B) Comparison of all particle trajectories up to s, clearly showing the slow motion of particles into the channel in between the branches, followed by their quick return along the branches. (C) Images of the branches and (D) the velocity of the particles as a function of time. The colors/symbols correspond to the velocities of individual particle trajectories as they pass within the box with the same color highlighted in C in the direction of the corresponding arrows. (E) Fluorescent images showing the development of the droplet branches but with water doped by a red dye at an extremely low concentration of 10 nM. The dye can be seen to be extracted from water, accumulating and concentrating within the nucleated oil droplets.
We attribute the significantly enhanced mobility of the colloidal particles to diffusiophoresis, the motion of colloidal particles driven by solutal concentration gradients (26). Here, the concentration gradient is created during the formation of oil droplet branches, as revealed in the contour map in Fig. 4. These findings therefore suggest an approach to enhance colloidal transport in extremely confined space in a ternary liquid system. Such locally enhanced colloidal mobility is complementary to that by diffusiophoresis arising from electrolyte and nonelectrolyte concentration gradients in a bulk solution, a flux of solute emitting from a “beacon” or Marangoni flow in the presence of surface tension gradients (27–32). Moreover, the colloidal mobility here may also be relevant to a range of intriguing phenomena, such as maze solving or self-propelling droplets, enhanced particle transport in the dead end of channels, or autonomous motion of self-powered micropumps in nanoscale and microscale systems (3, 27).
Toward Controlled Quasi-2D Nanoextraction.
We will now briefly demonstrate that the formation of nanodroplet branches can potentially be applied for nanoextraction for concentrating, separating, and analyzing hydrophobic solutes in aqueous solutions. In this proof-of-principle demonstration, water doped with a red dye at a concentration of 10 nM is driven through the side channel, triggering the confined Ouzo effect as seen in Fig. 5B. The red dye in water is extracted and concentrated within the oil droplets on the branches, as reflected by the gradually increasing intensity in the red coloration of the droplets over time.
This nanoextraction technique is applicable to a wide range of hydrophobic compounds in water, similar to the dispersive liquid–liquid microextraction (7–9). The small volume and large surface area of the droplets allow for rapid concentration and separation. However, we envisage even further potential for the nanoextraction process: The solute enrichment into the surface nanodroplets occurs directly from water, without necessitating the dispersive organic solvents typically required in microextraction. As such, higher preconcentration factors are expected for many hydrophobic compounds. Furthermore, the concentration and analysis of the hydrophobic solute are integrated into a single step. The entire process of our proposed approach thus makes it possible to analyze the solute without requiring the extra step of separating the concentrated solute from the mixture of the analyte-enriched oil phase in the dispersion.
Conclusions
In this work, we report the formation of nanodroplets when the Ouzo effect is confined within a quasi-2D channel. Such confinement gives us the unique opportunity to temporally and spatially follow the process of droplet formation, and to disentangle the convolution of multiple physicochemical processes from the mixing dynamics. We observed dendritic branching patterns of oil nanodroplets, exhibiting universal branching angles with a value of , the quantitative analysis of which suggests that the formation of these branches is governed by the external diffusive field. This work further demonstrates that the local oil concentration gradient generated from the droplet branches can drive rapid autonomous motion of colloidal particles, a phenomenon that may be potentially applied to dramatically enhance local colloidal transport in highly confined 2D space. We also used these nanodroplet branches for nanoextraction of a hydrophobic solute in water to dramatically simplify solute concentration and in situ analysis into a single step. The insight gained from this work provides valuable guidance for designing the solvent and mixing conditions to control nanodroplet formation arising from the Ouzo effect, which is useful for a wide range of applications in analytical technology, beverage, pharmaceutics, cosmetics, and advanced materials.
Materials and Methods
Chemicals and Solutions.
A stock solution of polymerizable oil was prepared by mixing 1,6-hexanediol di-acrylate (HDODA; Sigma-Aldrich) and the photoinitiator 2-hydroxy-2-methylpropiophenone (Sigma-Aldrich) at 10:1 vol ratio. The first solution (i.e., the Ouzo solution) was prepared by adding the above mixture to an aqueous ethanol solution. The volumetric ratio of water and ethanol in the solution was 50:50 or 40:60. Similar results were obtained when we tried nonpolymerizable oils, such as vitamin A in liquid form, oleic acid, and dodecane. The second solution comprised oil-saturated water or simply water in the case of the oils with extremely low solubility. Silicon substrates coated with octadecyltrichlorosilane (OTS-Si) were prepared and cleaned using a previously documented procedure (33).
Experimental Setup and Characterization of the Branch Growth.
The flow channel sketched in Fig. 1 was constructed by assembling the OTS-Si substrate between two glass top plates sealed with an O-ring. The distance from the top plate to the substrate surface is approximately 20 m. The channel was filled with the Ouzo solution from the inlet, followed by the injection of water into the channel at a constant flow of 200 L/min with a syringe pump. The water then displaced the Ouzo solution in the deep side channels before transversely diffusing into the much narrower inner channel, resulting in the formation of the droplet branches. Following their formation, the substrate was illuminated with a UV lamp (20 W, 365 nm) through the glass top plate, allowing the polymerization of the droplets using established protocols (34). The polymerized droplets were then characterized with a reflection-mode optical microscope or an atomic force microscope.
To visualize the mixing process, water was doped with fluorescein (0.02%), and a fluorescent microscope was used to observe the formation of branch patterns in the main channel. The branch structures were analyzed by measuring the branch length (main structure) at different times under both bright-field and fluorescence microscopy. Additionally, fluorescent microbeads in dyed water were tracked by fluorescent microscopic imaging. The videos were acquired at 60 frames per second.
Statistical Analysis of Merging Branch Angles.
In our angle measurements, the branch structure was binarized and skeletonized to find the branch points. To facilitate comparison between the branches observed here and those in bifurcating streams, we determined the “full” angle in exactly the same way as that reported in refs. 21 and 22, approximating the branches as linear segments using the reduced major axis. We note that the theoretical prediction in those papers actually looked at the angle in the limit close to the branch points. On the other hand, we characterized the angle near the branch points by adopting the reduced major axis of branch segments in close proximity to the merging points. After filtering the short hairy twigs, which cannot be distinguished from the protruding drops, there were between 47 and 160 angles in each case, with a total of 660 angles. We obtained a mean angle of (95% confidence interval) for all full angles, and a mean angle of for all near angles.
Numerical Simulations.
Given that the branch formation process is governed purely by diffusion, we solved the diffusion equation
| [1] |
with an immersed boundary method to allow for the moving boundary. Here is the concentration field, is the diffusion coefficient, and is the Eulerian source term used to mimic the effects of the immersed body on the concentration field. The immersed boundaries are discretized into a set of Lagrangian points, which represent the branches. The Eulerian and Lagrangian source terms are related to each other through a regularized delta function, given by
| [2] |
where and are the position vectors of the Eulerian and Lagrangian points, respectively, and is the Lagrangian source term.
To enforce the prescribed conditions on the boundary, we define the Lagrangian concentration field, again using the regularized delta function,
| [3] |
where is the Lagrangian concentration field on the boundary.
In the computations, a tentative concentration field is first calculated with the Eulerian source terms from the previous time step. Next, is interpolated to the boundary using Eq. 3 to obtain an updated Lagrangian concentration , from which we compute a new Lagrangian source term using
| [4] |
where is the time step. Subsequently, we populate the in the Eulerian field using Eq. 2. Finally, the diffusion equation is recalculated to finish updating this time step. A second-order implicit finite difference method is used for the discretization.
The regularized delta function used is defined as
| [5] |
Here is in the form of a four-point piecewise delta function proposed in ref. 35,
| [6] |
Experimental conditions were same for the videos shown in Movies S1–S5. The composition of Ouzo solution was 25:25:1 for water:ethanol:oil. Movie S6 was collected when the aqueous ethanol solution was used, instead of the Ouzo solution. The volumetric ratio was 2:3 for water:ethanol. For all videos, the flow rate of water was 100 L/min, and the substrate was hydrophobic. All scale bars are 100 m.
Supplementary Material
Acknowledgments
X.H.Z. acknowledges support from Australian Research Council (FT120100473 and DP140100805). We also acknowledge financial support from Nederlandse Organisatie voor Wetenschappelijk Onderzoek and from Netherlands Center for Multiscale Catalytic Energy Conversion.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. M.P.B. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1704727114/-/DCSupplemental.
References
- 1.Vitale S, Katz J. Liquid droplet dispersions formed by homogeneous liquid-liquid nucleation: “The ouzo effect”. Langmuir. 2003;19:4105–4110. [Google Scholar]
- 2.Aubry J, Ganachaud F, Cohen Addad JP, Cabane B. Nanoprecipitation of polymethylmethacrylate by solvent shifting:1. Boundaries. Langmuir. 2009;25:1970–1979. doi: 10.1021/la803000e. [DOI] [PubMed] [Google Scholar]
- 3.Lach S, Yoon SM, Grzybowski BA. Tactic, reactive, and functional droplets outside of equilibrium. Chem Soc Rev. 2016;45:4766–4796. doi: 10.1039/c6cs00242k. [DOI] [PubMed] [Google Scholar]
- 4.Schubert S, Delaney JT, Jr, Schubert US. Nanoprecipitation and nanoformulation of polymers: From history to powerful possibilities beyond poly(lactic acid) Soft Matter. 2011;7:1581–1588. [Google Scholar]
- 5.Haase MF, Stebe KJ, Lee D. Continuous fabrication of hierarchical and asymmetric bijel microparticles, fibers, and membranes by solvent transfer-induced phase separation (STRIPS) Adv Mater. 2015;27:7065–7071. doi: 10.1002/adma.201503509. [DOI] [PubMed] [Google Scholar]
- 6.Grauzinyte M, Forth J, Rumble KA, Clegg PS. Particle-stabilized water droplets that sprout millimeter-scale tubes. Angew Chem Int Ed Engl. 2015;54:1456–1460. doi: 10.1002/anie.201408365. [DOI] [PubMed] [Google Scholar]
- 7.Rezaee M, et al. Determination of organic compounds in water using dispersive liquid–liquid microextraction. J Chromatogr A. 2006;1116:1–9. doi: 10.1016/j.chroma.2006.03.007. [DOI] [PubMed] [Google Scholar]
- 8.Rezaee M, Yamini Y, Faraji M. Evolution of dispersive liquid-liquid microextraction method. J Chromatogr A. 2010;1217:2342–2357. doi: 10.1016/j.chroma.2009.11.088. [DOI] [PubMed] [Google Scholar]
- 9.Jain A, Verma KK. Recent advances in applications of single-drop microextraction: A review. Anal Chim Acta. 2011;706:37–65. doi: 10.1016/j.aca.2011.08.022. [DOI] [PubMed] [Google Scholar]
- 10.Fessi H, Puisieux F, Devissaguet J, Ammoury N, Benita S. Nanocapsule formation by interfacial polymer deposition following solvent displacement. Int J Pharm. 1989;55:R1–R4. [Google Scholar]
- 11.Mora-Huertas C, Fessi H, Elaissari A. Influence of process and formulation parameters on the formation of submicron particles by solvent displacement and emulsification-diffusion methods: Critical comparison. Adv Colloid Interface Sci. 2011;163:90–122. doi: 10.1016/j.cis.2011.02.005. [DOI] [PubMed] [Google Scholar]
- 12.Lepeltier E, Bourgaux C, Couvreur P. Nanoprecipitation and the “ouzo effect”: Application to drug delivery devices. Adv Drug Deliv Rev. 2014;71:86–97. doi: 10.1016/j.addr.2013.12.009. [DOI] [PubMed] [Google Scholar]
- 13.Johnson BK, Prud’homme RK. Mechanism for rapid self-assembly of block copolymer nanoparticles. Phys Rev Lett. 2003;91:118302. doi: 10.1103/PhysRevLett.91.118302. [DOI] [PubMed] [Google Scholar]
- 14.Karnik R, et al. Microfluidic platform for controlled synthesis of polymeric nanoparticles. Nano Lett. 2008;8:2906–2912. doi: 10.1021/nl801736q. [DOI] [PubMed] [Google Scholar]
- 15.D’Addio SM, Prud’homme RK. Controlling drug nanoparticle formation by rapid precipitation. Adv Drug Deliv Rev. 2011;63:417–426. doi: 10.1016/j.addr.2011.04.005. [DOI] [PubMed] [Google Scholar]
- 16.Stroock AD, et al. Chaotic mixer for microchannels. Science. 2002;295:647–651. doi: 10.1126/science.1066238. [DOI] [PubMed] [Google Scholar]
- 17.Lohse D, Zhang X. Surface nanobubbles and nanodroplets. Rev Mod Phys. 2015;87:981–1035. [Google Scholar]
- 18.Zhang X, et al. Formation of surface nanodroplets under controlled flow conditions. Proc Natl Acad Sci USA. 2015;112:9253–9257. doi: 10.1073/pnas.1506071112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tan H, et al. Evaporation-triggered microdroplet nucleation and the four life phases of an evaporating ouzo drop. Proc Natl Acad Sci USA. 2016;113:8642–8647. doi: 10.1073/pnas.1602260113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zemb TN, et al. How to explain microemulsions formed by solvent mixtures without conventional surfactants. Proc Natl Acad Sci USA. 2016;113:4260–4265. doi: 10.1073/pnas.1515708113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Devauchelle O, Petroff AP, Seybold HF, Rothman DH. Ramification of stream networks. Proc Natl Acad Sci USA. 2012;109:20832–20836. doi: 10.1073/pnas.1215218109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cohen Y, et al. Path selection in the growth of rivers. Proc Natl Acad Sci USA. 2015;112:14132–14137. doi: 10.1073/pnas.1413883112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Löwner K. Untersuchungen über schliche konforme abbildungen des einheitskreises. Math Ann. 1923;89:103–121. [Google Scholar]
- 24.Gruzberg IA, Kadanoff LP. The Loewner equation: Maps and shapes. J Stat Phys. 2004;114:1183–1198. [Google Scholar]
- 25.Peng S, Lohse D, Zhang X. Spontaneous pattern formation of surface nanodroplets from competitive growth. ACS Nano. 2015;9:11916–11923. doi: 10.1021/acsnano.5b04436. [DOI] [PubMed] [Google Scholar]
- 26.Anderson JL, Lowell ME, Prieve DC. Motion of a particle generated by chemical gradients. Part 1. Non-electrolytes. J Fluid Mech. 1982;117:107–121. [Google Scholar]
- 27.Abecassis B, Cottin-Bizonne C, Ybert C, Ajdari A, Bocquet L. Boosting migration of large particles by solute contrasts. Nat Mater. 2008;7:785–789. doi: 10.1038/nmat2254. [DOI] [PubMed] [Google Scholar]
- 28.Kar A, Chiang TY, Ortiz Rivera I, Sen A, Velegol D. Enhanced transport into and out of dead-end pores. ACS Nano. 2015;9:746–753. doi: 10.1021/nn506216b. [DOI] [PubMed] [Google Scholar]
- 29.Velegol D, Garg A, Guha R, Kar A, Kumar M. Origins of concentration gradients for diffusiophoresis. Soft Matter. 2016;12:4686–4703. doi: 10.1039/c6sm00052e. [DOI] [PubMed] [Google Scholar]
- 30.Banerjee A, Williams I, Azevedo RN, Helgeson ME, Squires TM. Soluto-inertial phenomena: Designing long-range, long-lasting, surface-specific interactions in suspensions. Proc Natl Acad Sci USA. 2016;113:8612–8617. doi: 10.1073/pnas.1604743113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Prieve DC. Particle transport: Salt and migrate. Nat Mater. 2008;7:769–770. doi: 10.1038/nmat2283. [DOI] [PubMed] [Google Scholar]
- 32.Shin S, et al. Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc Natl Acad Sci USA. 2016;113:257–261. doi: 10.1073/pnas.1511484112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang M, Liechti KM, Wang Q, White JM. Self-assembled silane monolayers: Fabrication with nanoscale uniformity. Langmuir. 2005;21:1848–1857. doi: 10.1021/la048483y. [DOI] [PubMed] [Google Scholar]
- 34.Zhang XH, et al. From transient nanodroplets to permanent nanolenses. Soft Matter. 2012;8:4314–4317. [Google Scholar]
- 35.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.