Prior expectations induce prestimulus sensory templates

Significance

The way that we perceive the world is partly shaped by what we expect to see at any given moment. However, it is unclear how this process is neurally implemented. Recently, it has been proposed that the brain generates stimulus templates in sensory cortex to preempt expected inputs. Here, we provide evidence that a representation of the expected stimulus is present in the neural signal shortly before it is presented, showing that expectations can indeed induce the preactivation of stimulus templates. Importantly, these expectation signals resembled the neural signal evoked by an actually presented stimulus, suggesting that expectations induce similar patterns of activations in visual cortex as sensory stimuli.

Abstract

Perception can be described as a process of inference, integrating bottom-up sensory inputs and top-down expectations. However, it is unclear how this process is neurally implemented. It has been proposed that expectations lead to prestimulus baseline increases in sensory neurons tuned to the expected stimulus, which in turn, affect the processing of subsequent stimuli. Recent fMRI studies have revealed stimulus-specific patterns of activation in sensory cortex as a result of expectation, but this method lacks the temporal resolution necessary to distinguish pre- from poststimulus processes. Here, we combined human magnetoencephalography (MEG) with multivariate decoding techniques to probe the representational content of neural signals in a time-resolved manner. We observed a representation of expected stimuli in the neural signal shortly before they were presented, showing that expectations indeed induce a preactivation of stimulus templates. The strength of these prestimulus expectation templates correlated with participants’ behavioral improvement when the expected feature was task-relevant. These results suggest a mechanism for how predictive perception can be neurally implemented.

Perception is heavily influenced by prior knowledge (1–3). Accordingly, many theories cast perception as a process of inference, integrating bottom-up sensory inputs and top-down expectations (4–6). However, it is unclear how this integration is neurally implemented. It has been proposed that prior expectations lead to baseline increases in sensory neurons tuned to the expected stimulus (7–9), which in turn, leads to improved neural processing of matching stimuli (10, 11). In other words, expectations may induce stimulus templates in sensory cortex before the actual presentation of the stimulus. Alternatively, top-down influences in sensory cortex may exert their influence only after the bottom-up stimulus has been initially processed, and the integration of the two sources of information may become apparent only during later stages of sensory processing (12).

The evidence necessary to distinguish between these hypotheses has been lacking. fMRI studies have revealed stimulus-specific patterns of activation in sensory cortex as a result of expectation (9, 13), but this method lacks the temporal resolution necessary to distinguish pre- from poststimulus periods. Here, we combined magnetoencephalography (MEG) with multivariate decoding techniques to probe the representational content of neural signals in a time-resolved manner (14–17). The experimental paradigm was virtually identical to the ones used in our previous fMRI studies that studied how expectations modulate stimulus-specific patterns of activity in the primary visual cortex (9, 11). We trained a forward model to decode the orientation of task-irrelevant gratings from the MEG signal (18, 19) and applied this decoder to trials in which participants expected a grating of a particular orientation to be presented. This analysis revealed a neural representation of the expected grating that resembled the neural signal evoked by an actually presented grating. This representation was present already shortly before stimulus presentation, showing that expectations can indeed induce the preactivation of stimulus templates.

Results

Participants (n = 23) were exposed to auditory cues that predicted the likely orientation (45° or 135°) of an upcoming grating stimulus (Fig. 1 A and B). This grating was followed by a second grating that differed slightly from the first in terms of orientation and contrast. In separate runs of the MEG session, participants performed either an orientation or contrast discrimination task on the two gratings (details are in Materials and Methods).

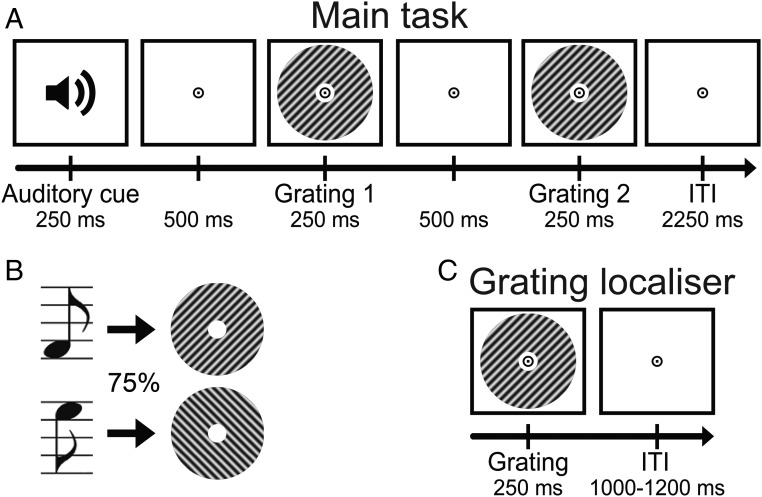
Fig. 1.

Experimental paradigm. (A) Each trial started with an auditory cue that predicted the orientation of the subsequent grating stimulus. This first grating was followed by a second one, which differed slightly from the first in terms of orientation and contrast. In separate runs, participants performed either an orientation or contrast discrimination task on the two gratings. (B) Throughout the experiment, two different tones were used as cues, each one predicting one of the two possible orientations (45° or 135°) with 75% validity. These contingencies were flipped halfway through the experiment. (C) In separate grating localizer runs, participants were exposed to task-irrelevant gratings while they performed a fixation dot dimming task.

Behavioral Results.

Participants were able to discriminate small differences in orientation (3.9° ± 0.5°, accuracy = 74.0 ± 1.6%, mean ± SEM) and contrast (4.6 ± 0.3%, accuracy = 76.6 ± 1.5%) of the cued gratings. There was no significant difference between the two tasks in terms of either accuracy (F_1,22 = 3.38, P = 0.080) or reaction time (RT) (mean RT = 633 vs. 608 ms, F_1,22 = 2.89, P = 0.10). Overall, accuracy and reaction times were not influenced by whether the cued grating had the expected or the unexpected orientation (accuracy: F_1,22 = 0.21, P = 0.65; RT: F_1,22 < 0.01, P = 0.93), and there was no interaction between task and expectation (accuracy: F_1,22 = 0.96, P = 0.34; RT: F_1,22 = 0.09, P = 0.77). Note that these discrimination tasks were orthogonal to the expectation manipulation in the sense that the expectation cue provided no information about the likely correct choice.

During the grating localizer (Fig. 1C; details are in Materials and Methods), participants correctly detected 91.2 ± 1.6% (mean ± SEM) of fixation flickers and incorrectly pressed the button on 0.2 ± 0.1% of trials, suggesting that participants were successfully engaged by the fixation task.

MEG Results—Localizer Orientation Decoding.

As mentioned, participants were exposed to auditory cues that predicted the likely orientation of an upcoming grating stimulus. The question that we wanted to answer was whether the expectations induced by these auditory cues would evoke templates of the visual stimuli before the presentation of the gratings. To be able to uncover such sensory templates, we trained a decoding model to reconstruct the orientation of (task-irrelevant) visual gratings (Fig. 1C) from the MEG signal in a time-resolved manner. We found that this model was highly accurate at reconstructing the orientation of such gratings from the MEG signal (Fig. 2). Grating orientation could be decoded across an extended period (from 40 to 655 ms poststimulus, P < 0.001 and from 685 to 730 ms, P = 0.018), peaking around 120–160 ms poststimulus (Fig. 2C). Furthermore, in the period around 100–330 ms poststimulus, orientation decoding generalized across time, meaning that a decoder trained on the evoked response at, for example, 120 ms poststimulus could reconstruct the grating orientation represented in the evoked response around 300 ms and vice versa (Fig. 2D). In other words, certain aspects of the representation of grating orientation were sustained over time.

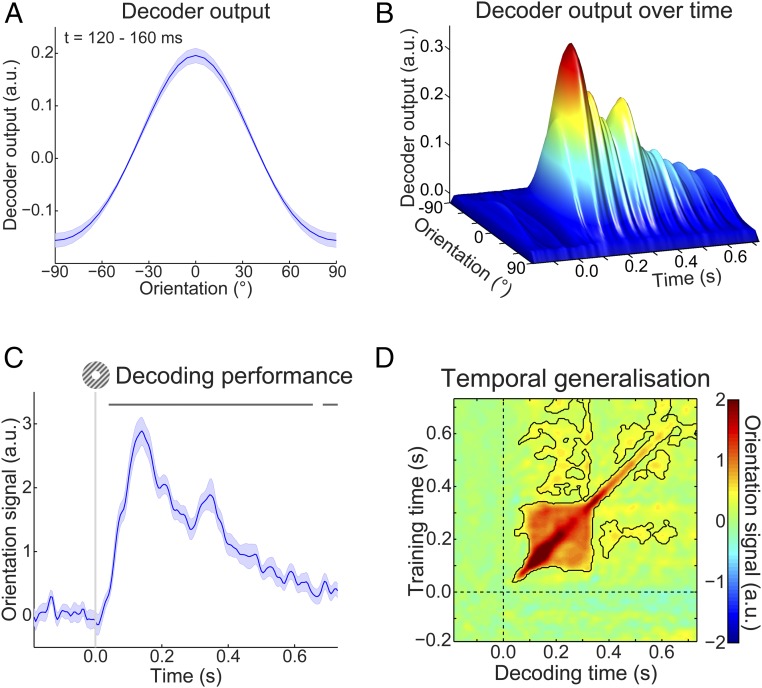
Fig. 2.

Localizer orientation decoding. (A) The output of the decoder consisted of the responses of 32 hypothetical orientation channels; shown here are decoders trained and tested on the MEG signal 120–160 ms poststimulus during the grating localizer (cross-validated). Shaded region represents SEM. (B) Decoder output over time, trained and tested in 5-ms steps (sliding window of 29.2 ms), showing the temporal evolution of the orientation signal. (C) The response of the 32 orientation channels collapsed into a single metric of decoding performance (SI Materials and Methods) over time. Shaded region represents SEM; horizontal lines indicate significant clusters (P < 0.05). (D) Temporal generalization matrix of orientation decoding performance obtained by training decoders on each time point and testing all decoders on all time points (as above, steps of 5 ms and a sliding window of 29.2 ms). This method provides insight into the sustained vs. dynamical nature of orientation representations (15). Solid black lines indicate significant clusters (P < 0.05); dashed lines indicate grating onset (t = 0 s).

MEG Results—Expectation Induces Stimulus Templates.

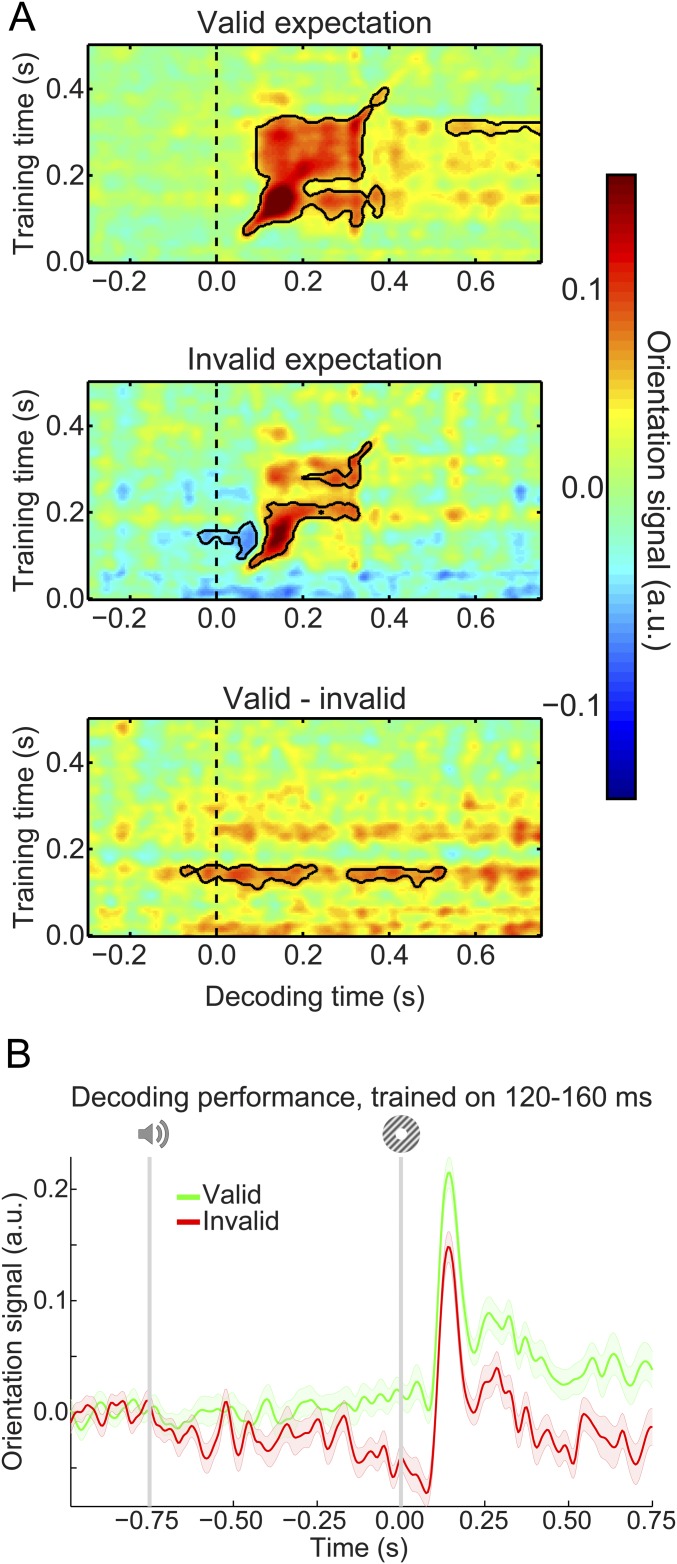
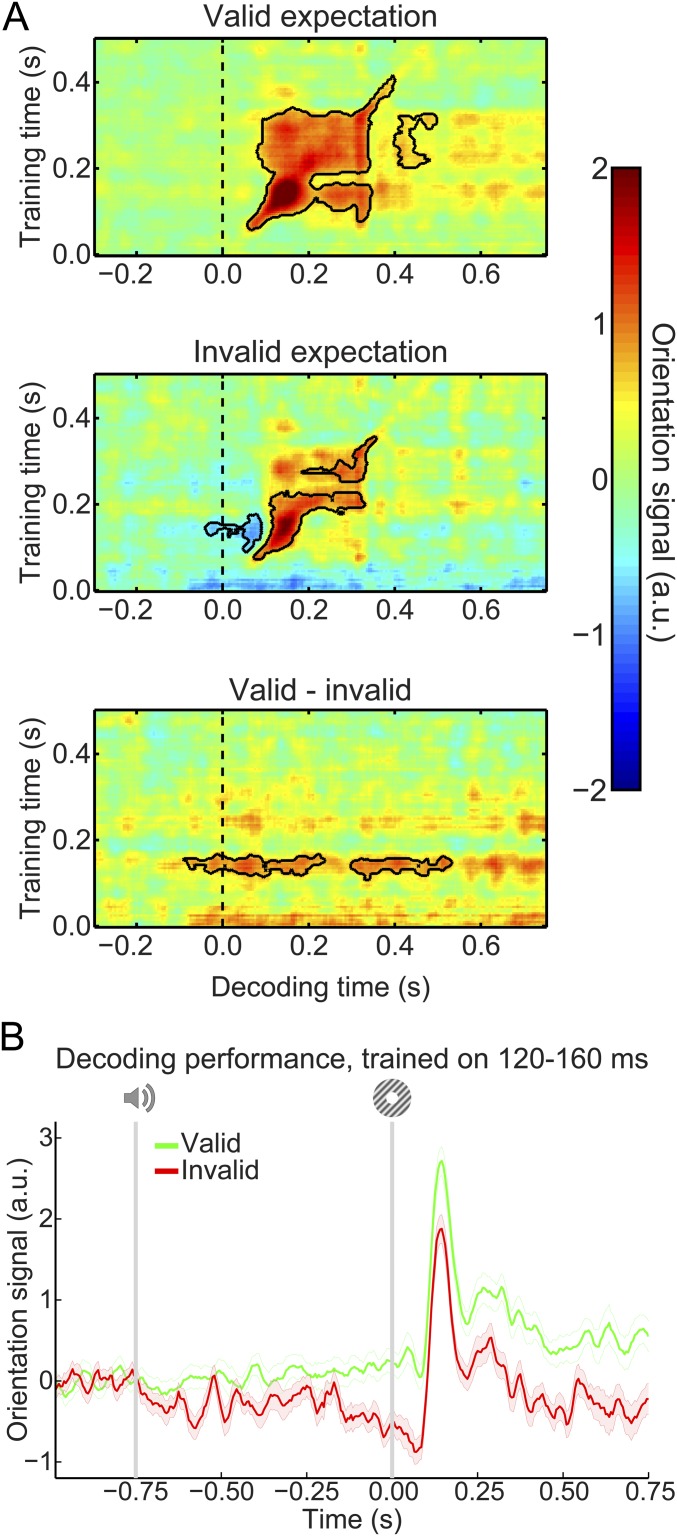
Our main question pertained to the presence of visual grating templates induced by the auditory expectation cues during the main experiment. Therefore, we applied our model trained on task-irrelevant gratings to trials containing gratings that were either validly or invalidly predicted (Fig. 3A). In both conditions, the decoding model trained on task-irrelevant gratings succeeded in accurately reconstructing the orientation of the gratings presented in the main experiment (valid expectation: cluster from training time 60–410 ms and decoding time 60–400 ms, P < 0.001 and from training time 205–325 ms and decoding time 400–495 ms, P = 0.045; invalid expectation: cluster from training time 75–225 ms and decoding time 75–330 ms, P = 0.0012 and from training time 250–360 ms and decoding time 195–355 ms, P = 0.027).

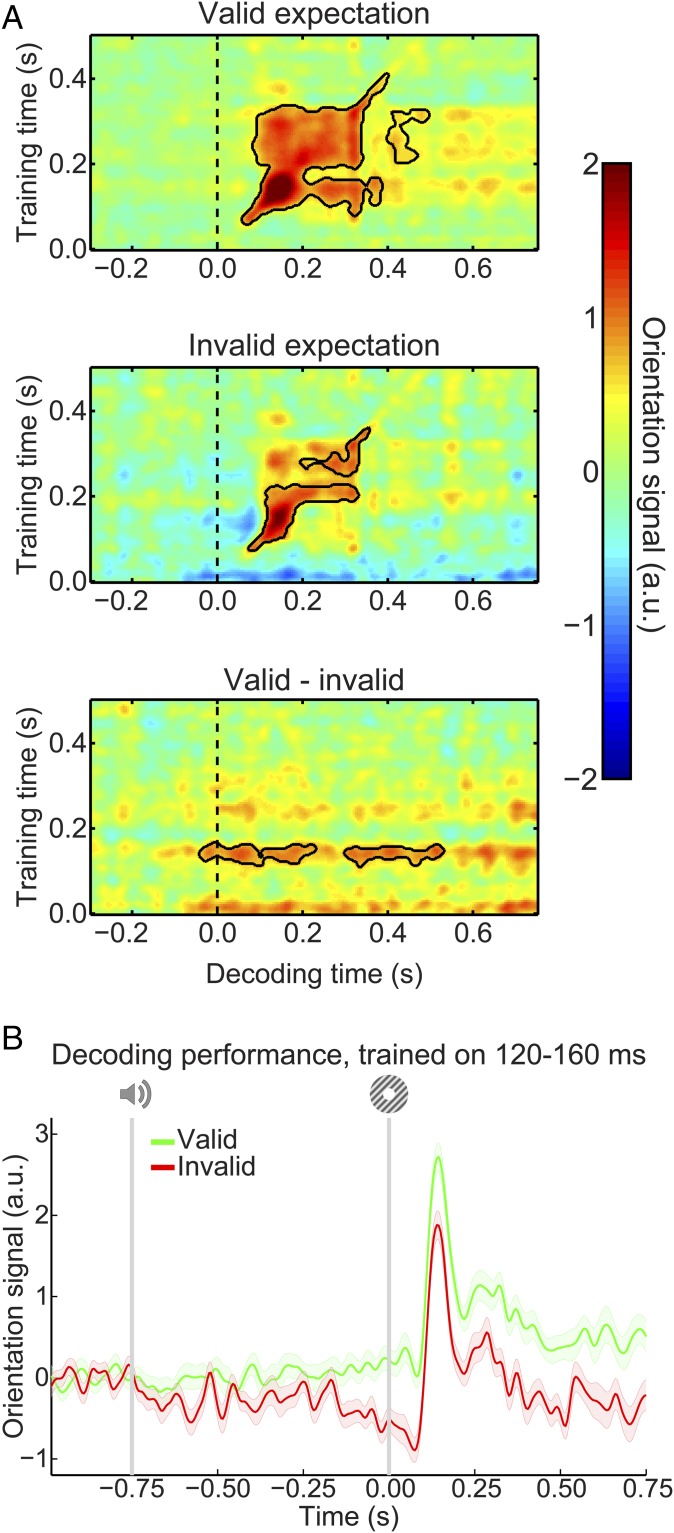
Fig. 3.

Expectation induces stimulus templates. (A) Temporal generalization matrices of orientation decoding during the main experiment. Decoders were trained on the grating localizer (training time on the y axis) and tested on the main experiment (time on the x axis; dashed vertical line indicates t = 0 s, onset of the first grating). Decoding shown separately for gratings preceded by a valid expectation (Top), an invalid expectation (Middle), and the subtraction of the two conditions (i.e., the expectation cue effect; Bottom). Solid black lines indicate significant clusters (P < 0.05). (B) Orientation decoding during the main task averaged over training time 120–160 ms poststimulus during the grating localizer. That is, B shows a horizontal slice through the temporal generalization matrices above at the training time for which we see a significant cluster of expected orientation decoding, for visualization. Shaded regions indicate SEM.

If the cues induced sensory templates of the expected grating, one would expect these to be revealed in the difference in decoding between validly and invalidly predicted gratings (details of the subtraction logic are in Materials and Methods). Indeed, this analysis showed that the auditory expectation cues induce orientation-specific neural signals (Fig. 3A, Bottom). These signals were present already 40 ms before grating presentation and extended into the poststimulus period (from decoding time −40 to 230 ms, P = 0.0092 and from 300 to 530 ms, P = 0.016). Furthermore, these signals were uncovered when the decoder was trained on around 120–160 ms poststimulus during the grating localizer (Fig. 3B), suggesting that these cue-induced signals were similar to those evoked by task-irrelevant gratings. In other words, the auditory expectation cues evoked orientation-specific signals that were similar to sensory signals evoked by the corresponding actual grating stimuli (Fig. S1A).

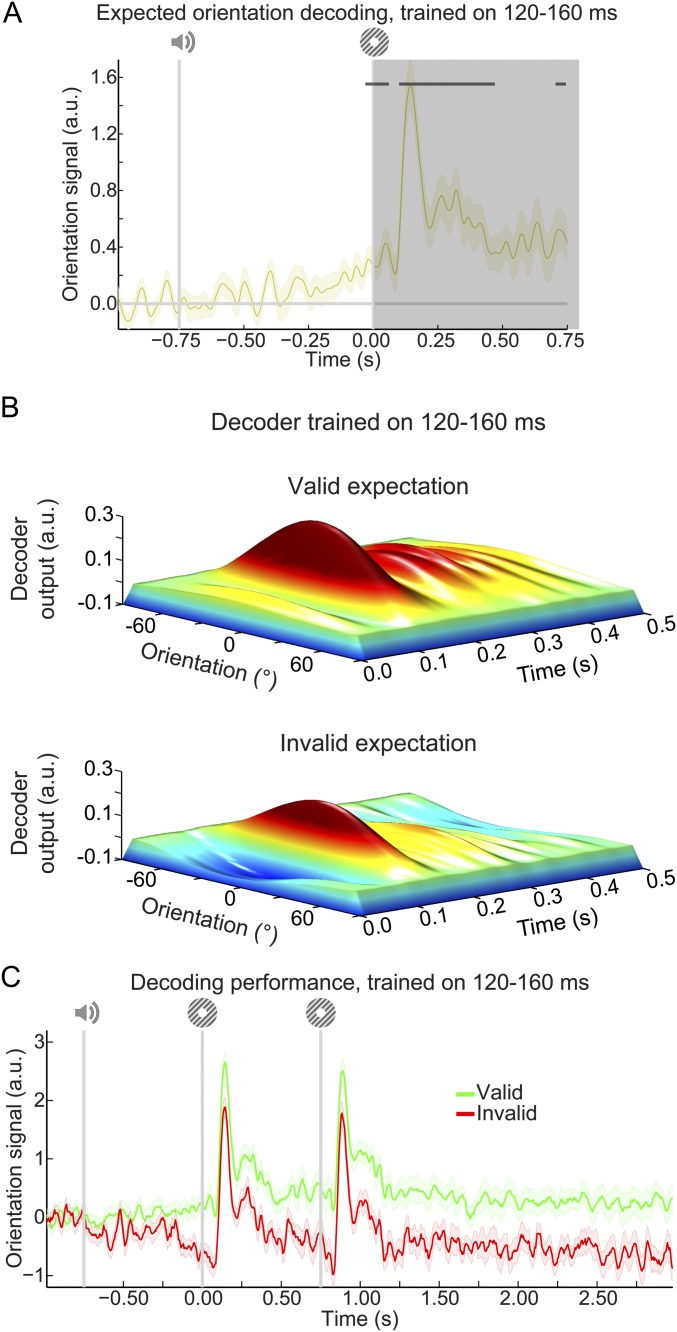
Fig. S1.

Expectation affects orientation decoding throughout the trial. (A) Decoded orientation signals resulting from aligning trials to the expected rather than the presented orientation. Note that poststimulus (t > 0 ms; shaded region) decoding signals cannot be unambiguously assigned to the expectation cue, since on 75% of trials, the presented orientation is the same as the expected orientation. It can be seen that there is already significant decoding of the cued orientation before t = 0 ms. Note that this prestimulus decoding signal is also significant when only time points before t = 0 ms are submitted to the cluster-based permutation test. Horizontal stripes indicate significant clusters. (B) Output of the 32 orientation channels over time during the main task separately for gratings preceded by a valid (Upper) or an invalid (Lower) expectation cue. Here, decoders were trained on 120–160 ms poststimulus during the grating localizer, similar to the data in Fig. 3B. That is, this figure depicts similar results as in Fig. 3B but displays the output of all 32 orientation channels rather than collapsing the channel responses into a decoding performance score (compare with Fig. 2B). (C) Orientation decoding during the main task averaged over training time of 120–160 ms poststimulus during the grating localizer. Same as in Fig. S6B but with an extended x axis to show the sustained nature of the expectation templates. Shaded regions indicate SEM.

In sum, expectations induced prestimulus sensory templates that influenced poststimulus representations as well; invalidly expected gratings had to “overcome” a prestimulus activation of the opposite orientation, while validly expected gratings were facilitated by a compatible prestimulus activation (Fig. S1B). The poststimulus carryover of these expectation signals lasted throughout the trial (Fig. S1C).

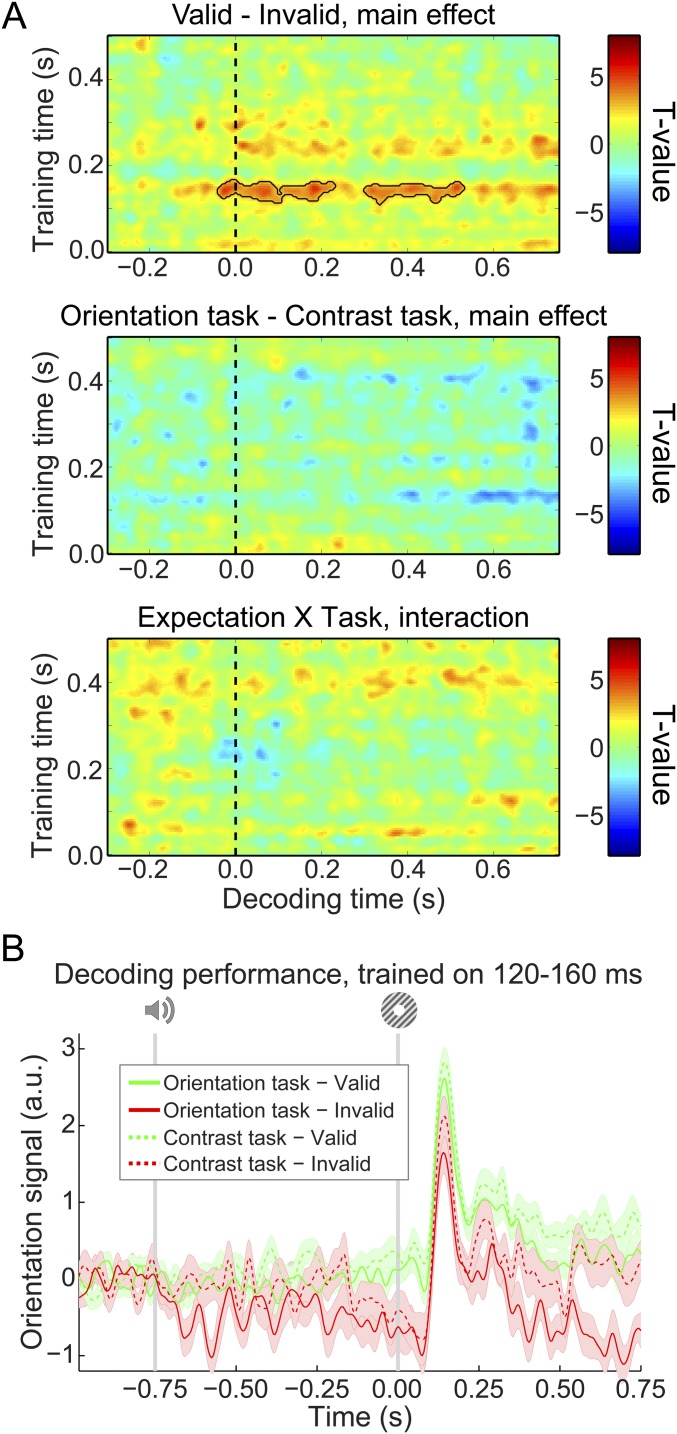
As in previous studies using a similar paradigm (11, 20), there was no interaction between the effects of the expectation cue and the task (orientation vs. contrast discrimination) that participants performed (no clusters with P < 0.05) (Fig. S2A). In other words, expectations evoked prestimulus orientation signals to a similar degree in both tasks (Fig. S2B). This suggests that influences of expectation on neural representations are relatively independent of the task relevance of the expected feature, in line with our previous fMRI study (11). Note, however, that, unlike in that study, there was no significant modulation of the orientation signal by task relevance (no clusters with P < 0.05) (Fig. S2A). The reason for this lack of difference is unclear, although it should be noted that there was a trend toward participants having higher accuracy and faster reaction times (see above) on the contrast task than on the orientation task. This may suggest that the two tasks were not optimally balanced in terms of difficulty, precluding a proper comparison of the effect of task set in this study.

Fig. S2.

Effects of expectation and task relevance on neural orientation signals. (A) Temporal generalization matrices of the effects of expectation (Top), task relevance (Middle), and the interaction between the two factors (Bottom). Note that Top is identical to Fig. 3A, Bottom. Solid black lines indicate significant clusters (P < 0.05). (B) Orientation decoding separately for validly and invalidly cued gratings split up for the two tasks averaged over training time 120–160 ms poststimulus during the grating localizer. Shaded regions indicate SEM.

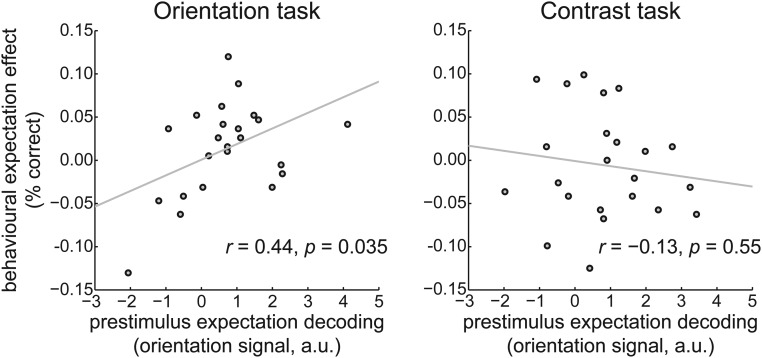
In our previous fMRI study, we found a relationship between the effects of expectation on neural stimulus representations and performance on the orientation discrimination task. Specifically, participants for whom valid expectations led to the largest improvement in neural stimulus representations also showed the strongest benefit of valid expectations on behavioral performance during the orientation discrimination task (11). This relationship was absent for the contrast discrimination task when grating orientation was task-irrelevant. This study allowed us to test for a similar relationship, with an important extension: here, we could test whether neural prestimulus expectation signals are related to behavioral performance improvements. We quantified the decoding of the expected orientation just before grating presentation (−50 to 0 ms, training window 120 to 160 ms) and correlated this with the difference in task accuracy for valid and invalid expectation trials, across participants. This analysis revealed that participants with a stronger prestimulus reflection of the expected orientation in their neural signal also had a greater benefit from valid expectations on performance on the orientation task (r = 0.44, P = 0.035) (Fig. 4, Left). No such relationship was found for the contrast task, where the orientation of the gratings was not task-relevant (r = −0.13, P = 0.55) (Fig. 4, Right). This is exactly the pattern of results that we found in our previous fMRI study but with the important extension that it is the prestimulus expectation effect that is correlated with behavioral performance, whereas the previous study did not have the temporal resolution to distinguish pre- from poststimulus signals.

Fig. 4.

Correlation between neural expectation signals and behavioral improvement by expectation. Neural prestimulus expectation decoding (on the x axis) correlated with behavioral improvement induced by valid expectations (on the y axis) during the orientation discrimination task (Left). This correlation was absent during the contrast discrimination task (Right).

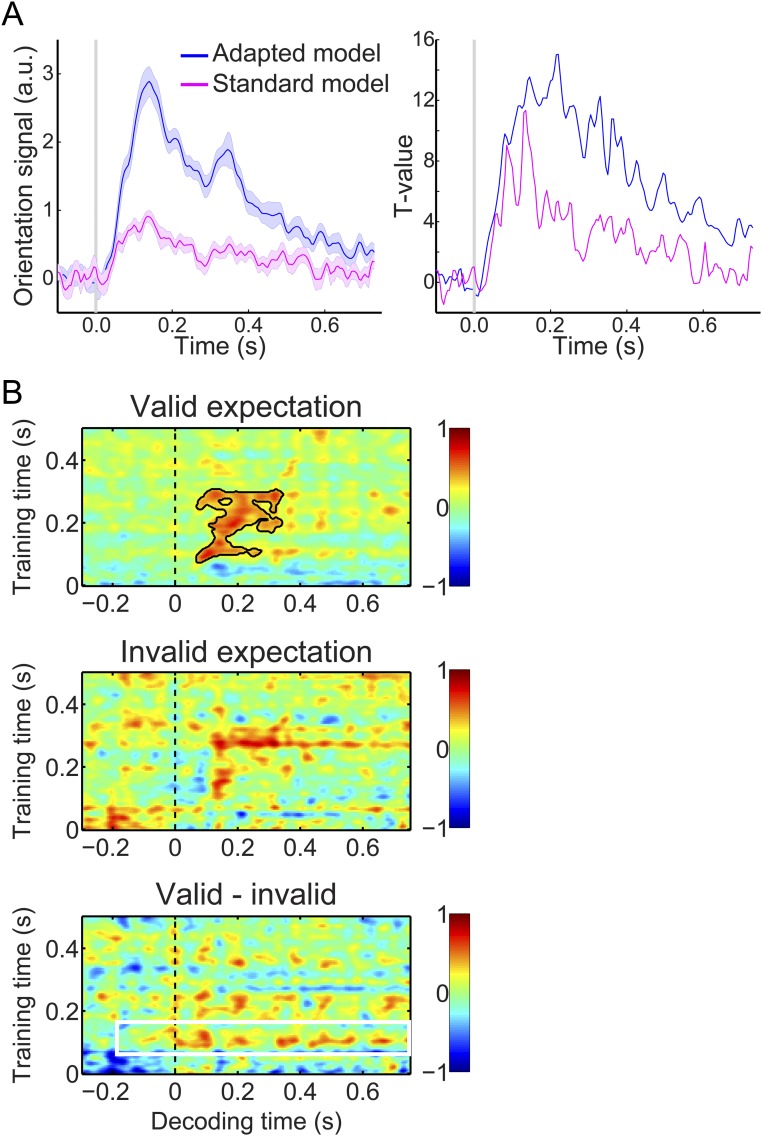
In this study, neural orientation signals were probed by applying a forward model that takes the noise covariance between MEG sensors into account (details are in SI Materials and Methods). This model was superior to a forward model that did not correct for the noise covariance (Fig. S3), suggesting that feature covariance is an important factor to take into account when applying multivariate methods to MEG data. Corroborating this notion, a two-class decoder that corrected for noise covariance (16) was able to reproduce our effects of interest (Fig. S4), showing that the expectation effects do not depend on a specific analysis technique as long as the covariance between MEG sensors is taken into account.

Fig. S3.

Orientation decoding using a standard forward model. Unlike the main analyses, this model does not take the noise covariance between MEG sensors into account (details are in SI Materials and Methods). (A) Orientation decoding within the localizer separately for our adapted forward model (in blue) and a standard forward model (in pink). Left shows mean decoding performance (shaded regions represent SEM), and Right shows T values over participants. (B) Temporal generalization matrices of orientation decoding during the main experiment. Same format as Fig. 3A using a suboptimal standard forward model rather than our adapted forward model. As expected, applying this less sensitive standard model to our main task data results in far less reliable decoding in the main task (note that the unexpected gratings are no longer significantly decoded at all; Middle). Decoding of the expected orientation (Bottom) is numerically still reflected by a horizontal stripe around training time 120–160 ms (indicated by the white box), but this effect is not statistically significant. This is likely because of the fact that the standard model is far less sensitive to neural orientation signals, as illustrated by A. Solid black lines indicate significant clusters (P < 0.05).

Fig. S4.

Expectation effects as revealed by a two-class decoder. Same format as Fig. 3, except that orientation signals were decoded using a two-class decoding method rather than a forward model as in the main analyses (SI Materials and Methods). (A) Temporal generalization matrices of orientation decoding during the main experiment. Solid black lines indicate significant clusters (P < 0.05). (B) Orientation decoding during the main task averaged over training time 120–160 ms poststimulus during the grating localizer. Shaded regions indicate SEM.

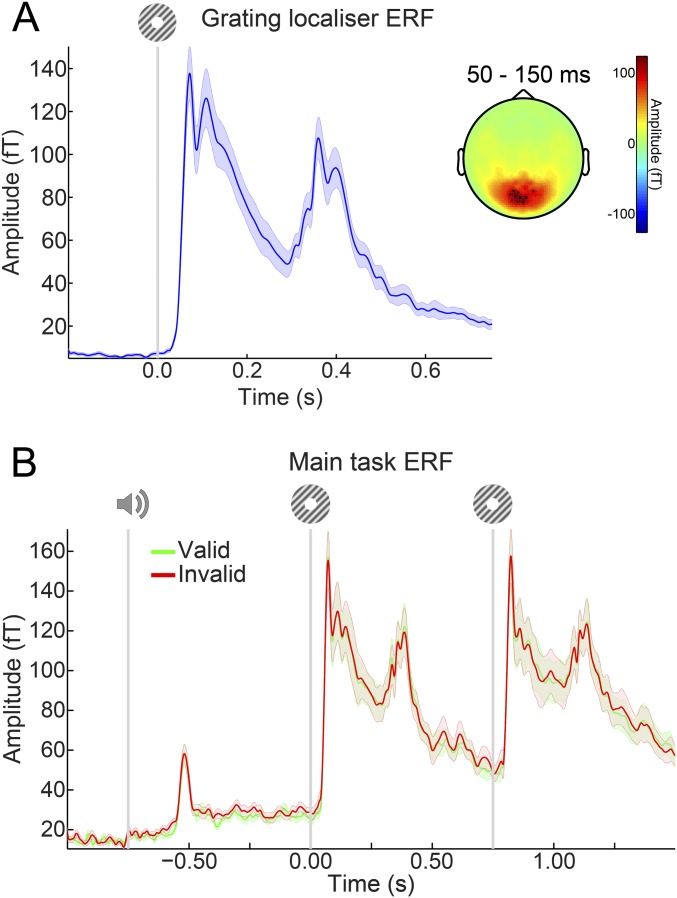
Finally, there was no difference in the overall amplitude of the neural response evoked between validly and invalidly expected gratings (no clusters with P < 0.4) (Fig. S5).

Fig. S5.

ERFs. (A) ERFs during the grating localizer in the 10 channels showing the largest response from 50–150 ms poststimulus. (B) ERFs during the main task in the same 10 channels as in A selected on the basis of the grating localizer response. There were no significant differences between ERFs for validly and invalidly predicted gratings. Shaded regions indicate SEM.

SI Materials and Methods

Participants.

Twenty-three (15 female, age 26 ± 9 y old, mean ± SD) healthy individuals participated in the experiment. All participants were right-handed and had normal or corrected to normal vision. The study was approved by the local ethics committee [Commissie Mensgebonden Onderzoek (CMO) Arnhem-Nijmegen, The Netherlands] under the general ethics approval (Imaging Human Cognition, CMO 2014/288), and the experiment was conducted in accordance with these guidelines. All participants gave written informed consent according to the Declaration of Helsinki.

Stimuli.

Grayscale luminance-defined sinusoidal grating stimuli (spatial frequency: 1.0 cycle per 1°) were generated using MATLAB (MathWorks) in conjunction with the Psychophysics Toolbox (60). Gratings were displayed in an annulus (o.d.: 15° of visual angle, i.d.: 1°) surrounding a black fixation bull’s eye (4 cd/m²) on a gray (580 cd/m²) background. The visual stimuli were presented with an LCD projector (1,024 × 768 resolution, 60-Hz refresh rate) positioned outside the magnetically shielded room and projected on a translucent screen via two front-silvered mirrors. The projector lag was measured at 36 ms, which was corrected for by shifting the time axis of the data accordingly. The auditory cue consisted of a pure tone (500 or 1,000 Hz, 250-ms duration, including 10 ms on- and off-ramp times) presented over MEG-compatible earphones.

Experimental Design.

Each trial consisted of an auditory cue followed by two consecutive grating stimuli (750-ms stimulus-onset asynchrony between auditory and first visual stimulus) (Fig. 1A). The two grating stimuli were presented for 250 ms each separated by a blank screen (500 ms). A central fixation bull’s eye (0.7°) was presented throughout the trial as well as during the ITI (2,250 ms). The auditory cue consisted of either a low- (500 Hz) or high-frequency (1,000 Hz) tone, which predicted the orientation of the first grating stimulus (45° or 135°) with 75% validity (Fig. 1B). In the other 25% of trials, the first grating had the orthogonal orientation. Thus, the first grating had an orientation of either exactly 45° or 135° and a luminance contrast of 80%. The second grating differed slightly from the first in terms of both orientation and contrast (see below) as well as being in antiphase to the first grating (which had a random spatial phase). The contingencies between the auditory cues and grating orientations were flipped halfway through the experiment (i.e., after four runs), and the order was counterbalanced over subjects.

In separate runs (64 trials each, ∼4.5 min), subjects performed either an orientation or a contrast discrimination task on the two gratings. When performing the orientation task, subjects had to judge whether the second grating was rotated clockwise or anticlockwise with respect to the first grating. In the contrast task, a judgment had to be made on whether the second grating had lower or higher contrast than the first one. These tasks were explicitly designed to avoid a direct relationship between the perceptual expectation and the task response. Furthermore, as in a previous fMRI study (11), these two different tasks were designed to manipulate the task relevance of the grating orientations to investigate whether the effects of orientation expectations depend on the task relevance of the expected feature. Subjects indicated their response (response deadline: 750 ms after offset of the second grating) using an MEG-compatible button box. The orientation and contrast differences between the two gratings were determined by an adaptive staircase procedure (61), which was updated after each trial. This was done to yield comparable task difficulty and performance (∼75% correct) for the different tasks. In this study, unlike in our previous fMRI study (11), we did not run separate staircasing for the valid and invalid expectation conditions. In that study, we were concerned that, after the first grating on a trial violated the expectation, this might lead to increased difficulty in comparing this unexpected grating with the second grating. This hypothetical chain of events would be triggered only after the first grating had been processed; however, in an fMRI study, one cannot separate such a relatively late effect from any early expectation effects. In this study, however, we could, since we used MEG. Any prestimulus expectation effects, which were the target of this study, could not possibly be affected by any poststimulus difficulty effects. Therefore, for simplicity, we ran a single staircase for all trials, one per task. Staircase thresholds obtained during one task were used to set the stimulus differences during the other task to make the stimuli as similar as possible in both contexts.

All subjects completed eight runs (four of each task, alternating every two runs, order was counterbalanced over subjects) of the experiment, yielding a total of 512 trials. The staircases were kept running throughout the experiment. Before the first run as well as in between runs 4 and 5, when the contingencies between cue and stimuli were flipped, subjects performed a short practice run containing 32 trials of both tasks (∼4.5 min).

Interleaved with the main task runs, subjects performed eight runs of a grating localizer task (Fig. 1C). Each run (∼2 min) consisted of 80 grating presentations (ITI uniformly jittered between 1,000 and 1,200 ms). The grating annuli were identical to those presented during the main task (80% contrast, 250-ms duration, 1.0 cycle per 1°, random spatial phase). Each grating had one of eight orientations (spanning the 180° space, starting at 0°, in steps of 22.5°), each of which was presented 10 times per run in pseudorandom order. A black fixation bull’s eye (4 cd/m², 0.7° diameter, identical to the one presented during the main task runs) was presented throughout the run. On 10% of trials (counterbalanced across orientations), the black fixation point in the center of the bull’s eye (0.2°, 4 cd/m²) briefly turned gray (324 cd/m²) during the first 50 ms of grating presentation. Participants task was to press a button (response deadline: 500 ms) when they perceived this fixation flicker. This simple task was meant to ensure central fixation, while rendering the gratings task-irrelevant. Trials containing fixation flickers were excluded from additional analyses.

Finally, participants were exposed to a tone localizer (∼1.5 min) presented at the start of, end of, and halfway through the MEG session. These runs consisted of 81 presentations of the two tones used in the main experiment. Data from these runs were not analyzed further.

Before the MEG session (1–3 d), all participants completed a behavioral session. The aim of this session was to familiarize participants with the tasks and to initialize the staircase values for both the orientation and the contrast discrimination task (see above). The behavioral session consisted of written instructions and 32 practice trials of each task followed by four runs (∼4.5 min each) of the main experiment (each task twice, alternating between runs, cue contingencies switching between the second and third runs). Finally, participants were exposed to one run each of the grating and tone localizer to familiarize them with the procedure.

MEG Recording and Preprocessing.

Whole-head neural recordings were obtained using a 275-channel MEG system with axial gradiometers (CTF Systems) located in a magnetically shielded room. Throughout the experiment, head position was monitored online and corrected if necessary using three fiducial coils that were placed on the nasion and on earplugs in both ears (62). If subjects had moved their head more than 5 mm from the starting position, they were repositioned during block breaks. Furthermore, both horizontal and vertical electrooculograms (EOGs) as well as an ECG were recorded to facilitate removal of eye- and heart-related artifacts. The ground electrode was placed at the left mastoid. All signals were sampled at a rate of 1,200 Hz.

The data were preprocessed offline using FieldTrip (63) (www.fieldtriptoolbox.org). To identify artifacts, the variance (collapsed over channels and time) was calculated for each trial. Trials with large variances were subsequently selected for manual inspection and removed if they contained excessive and irregular artifacts. Independent component analysis was subsequently used to remove regular artifacts, such as heartbeats and eye blinks. Specifically, for each subject, the independent components were correlated to both EOGs and the ECG to identify potentially contaminating components, and these were subsequently inspected manually before removal. For the main analyses, data were low-pass filtered using a two-pass Butterworth filter with a filter order of six and a frequency cutoff of 40 Hz. To rule out that the temporal smoothing caused by low-pass filtering may have artificially decreased the onset latency of neural signals, we repeated the decoding analyses (see below) on data that were not low-pass filtered (Fig. S6). Here, only notch filters were applied at 50, 100, and 150 Hz to remove line noise and its harmonics. The absence of any low-pass filtering or smoothing in this analysis precluded the possibility that any prestimulus effects could be caused by backward smoothing of stimulus-driven effects. No detrending was applied for any analysis. Finally, main task data were baseline corrected on the interval of −250 to 0 ms relative to auditory cue onset, and grating localizer data were baseline corrected on the interval of −200 to 0 ms relative to visual grating onset.

Fig. S6.

Expectation effects in the absence of low-pass filtering. (A) Temporal generalization matrices of orientation decoding during the main experiment without low-pass filtering the data. Otherwise, it is identical to Fig. 3A. Solid black lines indicate significant clusters (P < 0.05). (B) Orientation decoding during the main task averaged over training time 120–160 ms poststimulus during the grating localizer. Shaded regions indicate SEM.

Event-Related Field Analysis.

Event-related fields (ERFs) were calculated per participant and subjected to a planar gradient transformation (64) before averaging across participants. The planar transformation simplifies the interpretation of the sensor-level data, because it typically places the maximal signal above the source. To avoid differences in the amount of noise when comparing conditions with different numbers of trials, we matched the trial count by randomly selecting a subsample of trials from the conditions with more trials (i.e., valid expectations).

Orientation Decoding Analysis.

To probe sensory representations in the visual cortex, we used a forward modeling approach to reconstruct the orientation of the grating stimuli from the MEG signal (17–19, 57). This method has been shown to be highly successful at reconstructing circular stimulus features, such as color (18), orientation (17, 19, 57), and motion direction (22), from neural signals. Neural representations in MEG signals have also been successfully investigated using binomial classifiers (58); however, when it comes to a continuous stimulus feature, such as orientation, forward model reconstructions provide a richer decoding signal than binomial classifier accuracy (59). We made certain changes to the forward model proposed by Brouwer and Heeger (18) (most notably, taking the noise covariance into account; see below for details) to optimize it for MEG data given the high correlations between neighboring sensors (based on ref. 16). In sum, this previously published and theoretically motivated decoding model was optimally suited for recovering a continuous feature from MEG data.

The forward modeling approach was twofold. First, a theoretical forward model was postulated that described the measured activity in the MEG sensors given the orientation of the presented grating. Second, this forward model was used to obtain an inverse model that specified the transformation from MEG sensor space to orientation space. The forward and inverse models were estimated on the basis of the grating localizer data. The inverse model was then applied to the data from the main experiment to generalize from sensory signals evoked by task-irrelevant gratings to the gratings and expectation signals evoked in the main task. To test the performance of the model, we also applied it to the localizer data themselves using a cross-validation approach: in each iteration, one trial of each orientation was used at the test set, and the remaining data were used as the training set.

The forward model was based on work by Brouwer and Heeger (18, 19) and involved 32 hypothetical channels, each with an idealized orientation tuning curve. Each channel consisted of a half-wave–rectified sinusoid raised to the fifth power, and the 32 channels were spaced evenly within the 180° orientation space, such that a tuning curve with any possible orientation preference could be expressed exactly as a weighted sum of the channels. Arranging the hypothesized channel activities for each trial along the columns of a matrix C (32 channels × n trials), the observed data could be described by the following linear model:

$$\mathbf{B}=\mathbf{W}\mathbf{C}+\mathbf{N},$$

where B indicates the (m sensors × n trials) MEG data, W is a weight matrix (m sensors × 32 channels) that specifies how channel activity is transformed into sensory activity, and N indicates the residuals (i.e., noise).

To obtain the inverse model, we estimated an array of spatial filters that, when applied to the data, aimed to reconstruct the underlying channel activities as accurately as possible. In doing so, we extended Brouwer and Heeger’s (18) approach in three respects. First, since the MEG signal in (nearby) sensors is correlated, we took into account the correlational structure of the noise. Second, we estimated a spatial filter for each orientation channel independently. As a result, the number of channels used in our model was not constrained, whereas the maximum number of channels would otherwise be dependent on the number of presented orientations. In practice, this resulted in smoothing in orientation space, because the channels were not truly independent. Third, each filter was normalized, such that the magnitude of its output matched the magnitude of the underlying channel activity that it was designed to recover. Before estimating the inverse model, B and C were demeaned, such that their average over trials equaled zero for each sensor and channel, respectively.

As stated above, the inverse model was estimated on the basis of the grating localizer data. On each localizer trial, one of eight orientations was presented (see above), and the hypothetical responses of each of the channels could thus be calculated for each trial, resulting in the response row vector ${\mathbf{c}}_{train,\hspace{0.17em}i}$ of length $n_{train}$ trials for each channel i. The weights on the sensors ${\mathbf{w}}_i$ could now be obtained through least squares estimation for each channel:

$${\mathbf{w}}_i={\mathbf{B}}_{train}{\mathbf{c}}_{train,i}^{\mathrm{T}}{\left({\mathbf{c}}_{train,i}{\mathbf{c}}_{train,\hspace{0.17em}i}^{\mathrm{T}}\right)}^{-1},$$

where ${\mathbf{B}}_{train}$ indicates the (m sensors × $n_{train}$ trials) localizer MEG data. Subsequently, the optimal spatial filter ${\mathbf{v}}_i$ to recover the activity of the ith channel was obtained as follows (16):

$${\mathbf{v}}_i=\frac{{\stackrel{\sim }{\mathrm{\Sigma }}}_i^{-1}{\mathbf{w}}_i}{{\mathbf{w}}_i^{\mathrm{T}}{\stackrel{\sim }{\mathrm{\Sigma }}}_i^{-1}{\mathbf{w}}_i},$$

where ${\stackrel{\sim }{\mathrm{\Sigma }}}_i$ is the regularized covariance matrix for channel i. Incorporating the noise covariance in the filter estimation leads to the suppression of noise that arises from correlations between sensors. The noise covariance was estimated as follows:

$${\widehat{\mathrm{\Sigma }}}_i=\frac{1}{n_{train}-1}{\mathbf{\epsilon }}_i{\mathbf{\epsilon }}_i^{\mathrm{T}}$$

$${\mathbf{\epsilon }}_i={\mathbf{B}}_{train}-{\mathbf{w}}_i{\mathbf{c}}_{train,i},$$

where $n_{train}$ is the number of training trials. For optimal noise suppression, we improved this estimation by means of regularization by shrinkage using the analytically determined optimal shrinkage parameter (details are in ref. 65), yielding the regularized covariance matrix ${\stackrel{\sim }{\mathrm{\Sigma }}}_i$.

Such a spatial filter was estimated for each hypothetical channel, yielding an m sensors × 32 channel filter matrix V. Given that we performed our decoding analysis in a time-resolved manner, V was estimated at each time point of the training data in steps of 5 ms, resulting in array of filter matrices or decoders. To improve the signal-to-noise ratio, the data were first averaged within a window of 29.2 ms centered on the time point of interest. The window length of 29.2 ms was based on an a priori chosen length of 30 ms but minus one sample, such that the window contained an odd number of samples for symmetric centering (16). These filter matrices could now be applied to estimate the orientation channel responses in independent data—in this case, the trials from the main experiment:

$${\mathbf{C}}_{test}={\mathbf{V}}^{\mathrm{T}}{\mathbf{B}}_{test},$$

where ${\mathbf{B}}_{test}$ indicates the (m sensors × $n_{test}$ trials) main experiment data. These channel responses were estimated at each time point of the test data in steps of 5 ms, with the data being averaged within a window of 29.2 ms at each step. This procedure resulted in a 4D (training time × testing time × 32 channel × $n_{test}$) matrix of estimated channel responses for each trial in the main experiment. Each trials’ channel responses were shifted, such that the channel with its hypothetical peak response at the orientation presented on that trial (i.e., 45° or 135°) ended up in the position of the 0° channel before averaging over trials within each condition (i.e., valid vs. invalid expectation). Thus, the presented orientation was defined as 0° by convention. Note that, for 3D surface plots that show the evolution of channel responses over time (e.g., Fig. 2B), the response of the 90° channel (i.e., orthogonal to the presented orientation) was used as a baseline to avoid negative numbers for visualization purposes.

To quantify decoding performance, the channel responses for a given condition were converted into polar form and projected onto a vector with angle 0° (the presented orientation; see above):

$$r=\left|z\right|\cos \left(\arg \left(z\right)\right),\hspace{1em}z=\mathbf{c}\hspace{0.17em}{e}^{2i\mathbf{\phi }},$$

where c is a vector of estimated channel responses, and $\mathbf{\phi }$ is the vector of angles at which the channels peak (multiplied by two to project the 180° orientation space onto the full 360° space). The scalar projection r indicates the strength of the decoder signal for the orientation presented on screen. (Note that this approach is practically identical to subtracting the estimated response of the 90° channel from that of the 0° channel.) This quantification yielded (training time × testing time) temporal generalization matrices of orientation-decoding performance.

To establish the importance of including the noise covariance term in the forward model, we compared decoding performance with a standard forward model that did not take noise covariance into account (Fig. S3). This analysis showed that the adapted forward model was far superior to the standard model. To ensure that our results were not dependent on one specific decoding implementation, we also reproduced our effects of interest using a two-class decoder that takes noise covariance into account, equivalent to a linear discriminant analysis (16). Details and equations underlying this model are in ref. 16. Given that training the decoder only on 45° and 135° gratings would only allow us to use 25% of the localizer trials, we trained the decoder to distinguish right-tilted (22.5°, 45°, and 67.5°) from left-tilted (112.5°, 135°, and 157.5°) using 75% of the localizer trials. This decoder was then applied to the main task, revealing virtually identical expectation effects as our adapted forward model (Fig. S4).

To isolate any orientation-specific neural signals evoked by the expectation cues, we applied the following subtraction logic. On valid expectation trials, the expected and presented orientations are identical, and thus, the orientation signal induced by both the cue and stimulus can be expected to be positive by convention. On invalid expectation trials, however, the expected and presented orientations are orthogonal; thus, the orientation signal induced by the stimulus would be positive, and the signal induced by cue would be expected to be negative. Thus, subtracting the orientation decoding signal on invalid trials from that on valid trials would subtract out the stimulus-evoked signal, while revealing any cue-induced orientation signal. Additionally, we investigated cue-induced orientation signals by simply aligning trials by the expected rather than the presented orientation (Fig. S1A).

Statistical Testing.

Neural signals evoked by the different conditions were statistically tested using nonparametric cluster-based permutation tests (66). For ERF analyses, we averaged over the spatial (sensor) dimension on the basis of independent localization of the 10 sensors that showed the strongest visual-evoked activity during the grating localizer between 50 and 150 ms poststimulus. Therefore, our statistical analysis considered 1D (temporal) clusters. For orientation decoding analyses, the data consisted of 2D (training time × testing time) decoding performance matrices, and the statistical analysis thus considered 2D clusters. For both 1D and 2D data, univariate t statistics were calculated for the entire matrix, and neighboring elements that passed a threshold value corresponding to a P value of 0.01 (two tailed) were collected into separate negative and positive clusters. Elements were considered neighbors if they were directly adjacent, either cardinally or diagonally. Cluster-level test statistics consisted of the sum of t values within each cluster, and these were compared with a null distribution of test statistics created by drawing 10,000 random permutations of the observed data. A cluster was considered significant when its P value was below 0.05 (two tailed).

Discussion

Here, we show that expectations can induce sensory templates of the expected stimulus already before the stimulus appears. These results extend previous fMRI studies showing stimulus-specific patterns of activation in sensory cortex induced by expectations that could not resolve whether these templates indeed reflected prestimulus expectations or instead, stimulus specific error signals induced by the unexpected omission of a stimulus (9, 13). Furthermore, the strength of these prestimulus expectation signals correlated with the behavioral benefit of a valid expectation when the expected feature (i.e., orientation) was task-relevant (11). These results suggest that valid expectations facilitate perception by allowing sensory cortex to prepare for upcoming sensory signals. As in a previous fMRI study using a very similar experimental paradigm (11), the neural effects of orientation expectations reported here were independent of the task relevance of the orientation of the gratings, suggesting that the generation of expectation templates may be an automatic phenomenon.

The fact that expectation signals were revealed by a decoder trained on physically presented (but task-irrelevant) gratings suggests that these expectation signals resemble activity patterns induced by actual stimuli. The expectation signal remained present throughout the trial and extended into the poststimulus period, suggesting the tonic activation of a stimulus template. These results are in line with a recent monkey electrophysiology study (10), which showed that neurons in the face patch of inferior temporal cortex encode the prior expectation of a face appearing both before and after actual stimulus presentation. When the subsequently presented stimulus is noisy or ambiguous, such a prestimulus template could conceivably bias perception toward the expected stimulus (21–24).

What is the source of these cue-induced expectation signals? One candidate region is the hippocampus, which is known to be involved in encoding associations between previously unrelated discontiguous stimuli (25), such as the auditory tones and visual gratings used in this study. Furthermore, fMRI studies have revealed predictive signals in the hippocampus (13, 26, 27), and Reddy et al. (28) reported anticipatory firing to expected stimuli in the medial temporal lobe, including the hippocampus. One intriguing possibility is that predictive signals from the hippocampus are fed back to sensory cortex (13, 29, 30).

Previous studies have suggested, both on theoretical (31) and on empirical (32, 33) grounds, that top-down (prediction) and bottom-up (stimulus-driven or prediction error) signals are subserved by distinct frequency bands. Therefore, one highly interesting direction for future research would be to determine whether the expectation templates revealed here are specifically manifested in certain frequency bands (i.e., the alpha or beta band).

In addition to expectation, several other cognitive phenomena have been shown to induce stimulus templates in sensory cortex, such as preparatory attention (17, 34), mental imagery (35–37), and working memory (38, 39). In fact, explicit task preparation can also induce prestimulus sensory templates that last into the poststimulus period (17). Note that, in this study, the task did not require explicit use of the expectation cues, and the task response was, in fact, orthogonal to the expectation. Furthermore, there was no difference in the expectation signal between runs in which grating orientation was task-relevant (orientation discrimination task) and when it was irrelevant (contrast discrimination task); suggesting expectation may be a relatively automatic phenomenon (11, 40). In fact, neural modulations by expectation have even been observed during states of inattention (41), in sleep (42), and in patients experiencing disorders of consciousness (43). One important question for future research will be to establish whether the same neural mechanism underlies the different cognitive phenomena that are capable of inducing stimulus templates in sensory cortex or whether different top-down mechanisms are at work. Indeed, it has been suggested that expectation and attention, or task preparation, may have different underlying neural mechanisms (20, 44, 45). For instance, predictive coding theories suggest that attention may modulate sensory signals in the superficial layers of sensory cortex, while predictions modulate the response in deep layers (5, 46).

One may wonder why this study does not report a modulation of the overall neural response by expectation, while previous studies have found an increased neural response to unexpected stimuli (40, 47–51), including some using an almost identical paradigm as this study (11, 20). Of course, this study reports a null effect, from which it is hard to draw firm conclusions. However, it is possible that the type of measurement of neural activity plays a role in the absence of the effect. Most previous studies reporting expectation suppression in visual cortex used fMRI, whereas this study used MEG. It is possible that the blood oxygen level-dependent (BOLD) signal, a mass action signal that integrates synaptic and neural activity as well as integrating over time, is sensitive to certain neural effects that MEG, which is predominantly sensitive to synchronized activity in pyramidal neurons oriented perpendicular to the cortical surface, is not. It is even possible that, within MEG, different types of sensors (i.e., magnetometers, planar and axial gradiometers) differ in their sensitivity to expectation suppression (52).

Recent theories of sensory processing state that perception reflects the integration of bottom-up inputs and top-down expectations, but ideas diverge on whether the brain continuously generates stimulus templates in sensory cortex to preempt expected inputs (10, 23, 53, 54) or rather, engages in perceptual inference only after receiving sensory inputs (55, 56). Our results are in line with the brain being proactive and constantly forming predictions about future sensory inputs. These findings bring us closer to uncovering the neural mechanisms by which we integrate prior knowledge with sensory inputs to optimize perception.

Materials and Methods

Participants.

Twenty-three (15 female, age 26 ± 9 y old, mean ± SD) healthy individuals participated in the MEG experiment. All participants were right-handed and had normal or corrected to normal vision. The study was approved by the local ethics committee [Commisie Mensgebonden Onderzoek (CMO) Arnhem-Nijmegen, The Netherlands] under the general ethics approval (Imaging Human Cognition, CMO 2014/288), and the experiment was conducted in accordance with these guidelines. All participants gave written informed consent according to the Declaration of Helsinki.

Experimental Design.

Each trial consisted of an auditory cue followed by two consecutive grating stimuli (750-ms stimulus-onset asynchrony between auditory and first visual stimulus) (Fig. 1A). The two grating stimuli were presented for 250 ms each separated by a blank screen (500 ms). A central fixation bull’s eye (0.7°) was presented throughout the trial as well as during the intertrial interval (ITI; 2,250 ms). The auditory cue consisted of either a low- (500 Hz) or high-frequency (1,000 Hz) tone, which predicted the orientation of the first grating stimulus (45° or 135°) with 75% validity (Fig. 1B). In the other 25% of trials, the first grating had the orthogonal orientation. Thus, the first grating had an orientation of either exactly 45° or 135° and a luminance contrast of 80%. The second grating differed slightly from the first in terms of both orientation and contrast (see below) as well as being in antiphase to the first grating (which had a random spatial phase). The contingencies between the auditory cues and grating orientations were flipped halfway through the experiment (i.e., after four runs), and the order was counterbalanced over subjects.

In separate runs (64 trials each, ∼4.5 min), subjects performed either an orientation or a contrast discrimination task on the two gratings. When performing the orientation task, subjects had to judge whether the second grating was rotated clockwise or anticlockwise with respect to the first grating. In the contrast task, a judgment had to be made on whether the second grating had lower or higher contrast than the first one. These tasks were explicitly designed to avoid a direct relationship between the perceptual expectation and the task response. Furthermore, as in a previous fMRI study (11), these two different tasks were designed to manipulate the task relevance of the grating orientations to investigate whether the effects of orientation expectations depend on the task relevance of the expected feature.

Interleaved with the main task runs, subjects performed eight runs of a grating localizer task (Fig. 1C). Each run (∼2 min) consisted of 80 grating presentations (ITI uniformly jittered between 1,000 and 1,200 ms). The grating annuli were identical to those presented during the main task (80% contrast, 250-ms duration, 1.0 cycle per 1°, random spatial phase). Each grating had one of eight orientations (spanning the 180° space, starting at 0°, in steps of 22.5°), each of which was presented 10 times per run in pseudorandom order. A black fixation bull’s eye (4 cd/m², 0.7° diameter, identical to the one presented during the main task runs) was presented throughout the run. On 10% of trials (counterbalanced across orientations), the black fixation point in the center of the bull’s eye (0.2°, 4 cd/m²) briefly turned gray (324 cd/m²) during the first 50 ms of grating presentation. Participants’ task was to press a button (response deadline: 500 ms) when they perceived this fixation flicker. This simple task was meant to ensure central fixation, while rendering the gratings task-irrelevant. Trials containing fixation flickers were excluded from additional analyses.

Orientation Decoding Analysis.

To probe sensory representations in the visual cortex, we used a forward modeling approach to reconstruct the orientation of the grating stimuli from the MEG signal (17–19, 57). This method has been shown to be highly successful at reconstructing circular stimulus features, such as color (18), orientation (17, 19, 57), and motion direction (22), from neural signals. Neural representations in MEG signals have also been successfully investigated using binomial classifiers (58); however, when it comes to a continuous stimulus feature, such as orientation, forward model reconstructions provide a richer decoding signal than binomial classifier accuracy (59). We made certain changes to the forward model proposed by Brouwer and Heeger (18) (most notably, taking the noise covariance into account; details are in SI Materials and Methods) to optimize it for MEG data, given the high correlations between neighboring sensors, based on ref. 16. In sum, this previously published and theoretically motivated decoding model was optimally suited for recovering a continuous feature from MEG data. For our main analyses, the forward model was trained on the data from the localizer runs, in which the gratings were task-irrelevant, and then applied to the main task data to uncover sensory templates induced by prestimulus expectations (details are in SI Materials and Methods). Our effects of interest (Fig. 3 and Fig. S6) were reproduced using a two-class decoder (Fig. S4).

The full methods can be found in SI Materials and Methods.