Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation

Significance

The cell is divided into compartments where specific biochemical functions are performed. These compartments can be delineated by membranes or through phase separation of proteins or protein and nucleic acids to form membraneless organelles. The latter situation occurs with an intrinsically disordered region of Ddx4, a major constituent of germ granules. The nature of the interior of membraneless organelles is poorly understood. Here, we use NMR to show that the intrinsically disordered Ddx4 region remains disordered and highly dynamic in the phase-separated state, while diffusing as slowly as a particle the size of a bacterial cell. Ddx4 molecules form a network of interactions on phase separation, providing an alternative environment to that found in membrane-encapsulated organelles.

Abstract

Membrane encapsulation is frequently used by the cell to sequester biomolecules and compartmentalize their function. Cells also concentrate molecules into phase-separated protein or protein/nucleic acid “membraneless organelles” that regulate a host of biochemical processes. Here, we use solution NMR spectroscopy to study phase-separated droplets formed from the intrinsically disordered N-terminal 236 residues of the germ-granule protein Ddx4. We show that the protein within the concentrated phase of phase-separated Ddx4, $\text{Ddx}{4}_{\text{cond}}$, diffuses as a particle of 600-nm hydrodynamic radius dissolved in water. However, NMR spectra reveal sharp resonances with chemical shifts showing $\text{Ddx}{4}_{\text{cond}}$ to be intrinsically disordered. Spin relaxation measurements indicate that the backbone amides of $\text{Ddx}{4}_{\text{cond}}$ have significant mobility, explaining why high-resolution spectra are observed, but motion is reduced compared with an equivalently concentrated nonphase-separating control. Observation of a network of interchain interactions, as established by NOE spectroscopy, shows the importance of Phe and Arg interactions in driving the phase separation of Ddx4, while the salt dependence of both low- and high-concentration regions of phase diagrams establishes an important role for electrostatic interactions. The diffusion of a series of small probes and the compact but disordered 4E binding protein 2 (4E-BP2) protein in $\text{Ddx}{4}_{\text{cond}}$ are explained by an excluded volume effect, similar to that found for globular protein solvents. No changes in structural propensities of 4E-BP2 dissolved in $\text{Ddx}{4}_{\text{cond}}$ are observed, while changes to DNA and RNA molecules have been reported, highlighting the diverse roles that proteinaceous solvents play in dictating the properties of dissolved solutes.

Cellular organization is most often thought to involve membrane-delimited organelles, such as the nucleus and mitochondria. Recently, many cellular features that play critical roles in biology have been revealed to be dense proteinaceous bodies, termed membraneless organelles (1–4). These include nucleoli, speckles, and Cajal bodies in the nucleus and stress, germ, and neuronal granules in the cytoplasm (5–9) as well as signaling puncta found beneath activated plasma membrane receptors (10–12). These cellular compartments often contain nucleic acids and are involved in a variety of biochemical functions, including RNA processing and signaling (11, 13, 14).

The interactions driving both the phase separation and the disassembly of these proteinaceous bodies as well as the physical properties underlying their function are currently the focus of intense investigation (15). Their assembly and disassembly are dependent on dynamic changes in the cell and are sensitive to the cell cycle as well as to environmental stressors (15–17). Formation of these bodies is driven by multivalent weak interactions, including by multiple modular binding domain motif interactions or by self-association of intrinsically disordered proteins (IDPs) (11, 15, 16, 18–26). Rosen and coworkers (10, 12) have shown that repeats of disordered proline-rich motifs in NCK bind to multiple SH3 domains of N-WASP, leading to liquid droplet formation. In this case, multivalency of the binding partners is essential; increasing the number of both SH3 domains and proline-rich motifs reduces the protein concentration required for phase separation. Similarly, the nucleolar protein nucleophosmin interacts in a multivalent manner with arginine-rich motifs, promoting phase separation (27). IDP regions of EWS, FUS, and TAF-15 containing repetitive [G/S]Y[G/S] motifs have been shown to self-associate to form liquid droplets or hydrogels in vitro (23, 24). Additionally, the disordered P granule protein Laf-1, which is highly enriched in RGG motifs, undergoes phase separation into dense liquid droplets (18), and phase separation of low-complexity regions of hnRNPA1 and TDP-43 underlies the formation of stress granules (21).

Many of the cell’s proteinaceous bodies have liquid-like properties, including germ granules or nuage, P granules, the nucleolus of Caenorhabditis elegans, and stress granules (9, 18, 21). RNA can promote the liquid-phase separation of RNP granule proteins, including Whi3 in yeast and the RNA binding protein hnRNPA1, tuning the viscoelastic properties of liquid droplets (20, 28). However, there remains much to be learned about the physical properties of the proteins that comprise diverse phase-separated compartments, in particular with regard to their dynamics and the resulting solution hydrodynamics, as well as the atomic-level interactions that drive the phase transition. Additionally, little is known about solute molecules encapsulated within phase-separated protein states, including small molecules, proteins, and nucleic acids.

We recently observed the liquid-phase separation of the germ-granule protein Ddx4 into membraneless organelles in cells and into dense protein bodies in vitro (15). Ddx4 is a germ cell-specific protein that is the major constituent of the nuage/chromatoid body, a membraneless organelle present in the cytoplasm of spermatocytes and spermatids (29). Ddx4 contains an intrinsically disordered N terminus of $\sim$250 residues, a DEAD-box RNA helicase, and a disordered C terminus of $\sim$50 residues. A construct of Ddx4 retaining the disordered regions but substituting the DEAD-box helicase domain for YFP forms liquid membraneless organelles in nuclei when expressed in HeLa cells (15). The dense micrometer-sized spherical bodies in the nucleus are morphologically similar to liquid droplets formed in vitro from the N-terminal disordered region of the protein, Ddx4(1–236). Fluorescence recovery after photobleaching (FRAP) data from Ddx4 bodies in cells and in vitro are very similar, consistent with a 100-fold reduced mobility inside the droplet but retention of liquid dynamics. Phase separation of Ddx4(1–236), referred to as Ddx4 below, can be induced by lowering the temperature or by reducing the salt concentration and is highly reversible. Charge patterning with conserved F residues within positively charged blocks and conserved RG/GR and FG/GF motifs are important for formation of Ddx4 organelles and for in vitro and in-cell phase separation (15). These observations provide considerable insight as have analyses of the dilute concentration region of phase diagrams using Flory–Huggins (15) and random-phase approximation (RPA) (30) theories to obtain measures of entropy and enthalpy contributions to phase separation and to rationalize the dependence of phase separation on the charge pattern along the Ddx4 sequence. Nonetheless, a detailed understanding of Ddx4 phase separation in terms of the specific atomic-level interactions involved as well as the structural and dynamic features of Ddx4 and its solution hydrodynamic properties in the phase-separated state remain to be elucidated. Information on such properties is essential, however, for deciphering the biological functions of the membraneless organelles underpinned by Ddx4 phase separation.

Here, we take several substantive steps toward characterizing the molecular properties of the phase-separated state of Ddx4 by first mapping protein concentrations in both the condensed, $\text{Ddx}{4}_{\text{cond}}$, and dilute, $\text{Ddx}{4}_{\text{dil}}$, phases as a function of temperature and added salt. These data are used to construct full coexistence curves for Ddx4 by fitting to a simple Flory–Huggins model, wherein the salt dependence informs on the role of electrostatic interactions in driving phase separation. Solution NMR spectroscopy is then used to explore structural, hydrodynamic, and motional features of the Ddx4 molecules in $\text{Ddx}{4}_{\text{cond}}$. ¹H-¹⁵N and ¹H-¹³C correlation spectra establish that $\text{Ddx}{4}_{\text{cond}}$ is intrinsically disordered, with extensive mobility at both backbone and sidechain sites; however, nuclear Overhauser experiments measuring intermolecular contacts show an extensive network of interactions. Moreover, Ddx4 molecules in $\text{Ddx}{4}_{\text{cond}}$ diffuse $\sim$100-fold more slowly than for $\text{Ddx}{4}_{\text{dil}}$, and small molecules with hydrodynamic radii varying from 1 to 5 Å, including water, have significantly reduced translational diffusion rates in $\text{Ddx}{4}_{\text{cond}}$, all pointing to a highly viscous environment in membraneless organelles. When the intrinsically disordered but highly compact eukaryotic translation initiation factor 4E binding protein 2 (4E-BP2) is incorporated into $\text{Ddx}{4}_{\text{cond}}$, there is a significant reduction in translational mobility, as observed for small molecules, with little change in compaction or structural propensities. In contrast, a number of RNA and DNA solutes are significantly affected on dissolution into $\text{Ddx}{4}_{\text{cond}}$ (31), suggesting that the concentrated phase-separated milieu can have diverse effects on solutes that play different functional roles.

Results

Constructing a Homogenous NMR Sample of $\text{Ddx}{4}_{\text{cond}}$.

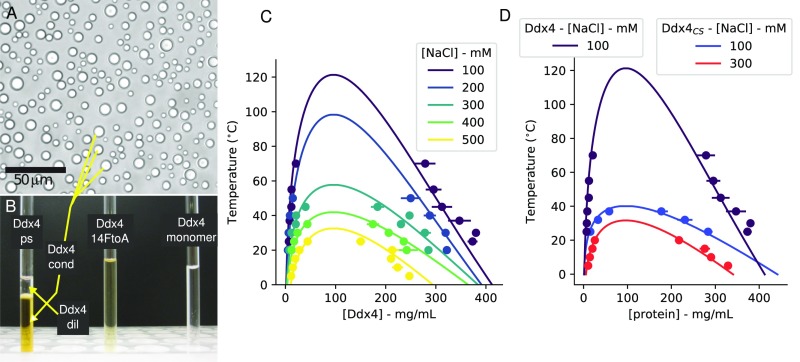
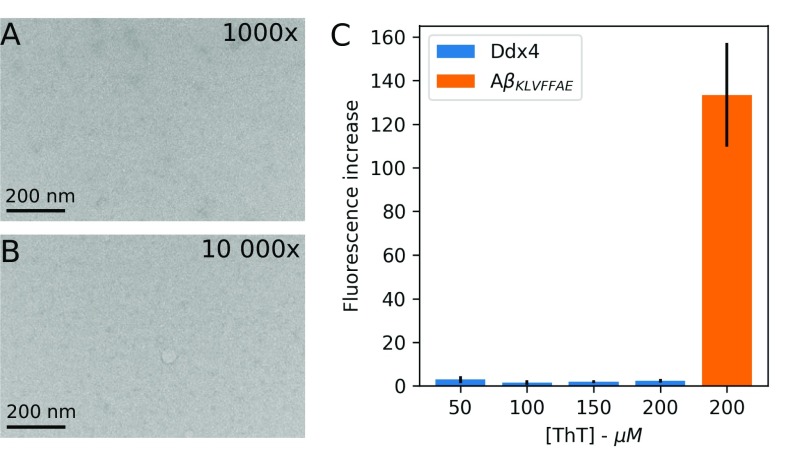
To directly probe residue-specific interactions and local motions within $\text{Ddx}{4}_{\text{cond}}$, we set out to create a homogeneous solution of $\text{Ddx}{4}_{\text{cond}}$ for study by solution NMR. As has been shown previously, Ddx4 droplets are liquid-like and therefore, are able to coalesce together (15). We, therefore, generated a homogeneous NMR sample of Ddx4, in which all droplets are coalesced within the NMR tube (Materials and Methods). Specifically, $\text{Ddx}{4}_{\text{cond}}$ droplets (Fig. 1A) were coalesced at 4 °C to a volume of ∼250–500 $\mu$L, transferred to an NMR tube, and appeared turbid. Samples were then incubated at 30 °C for several hours until transparent, as in Fig. 1B, Left. NMR samples of phase-separated Ddx4 can be visually identified as having two discrete phases (Fig. 1B, Left) and are distinct from samples of either the mutant $\text{Ddx}{4}_{14\text{FtoA}}$ (see below) at 250 $\text{mg}/\text{mL}$ (Fig. 1B, Center) or dilute concentrations of Ddx4 in high salt (2.5 mg/mL), $\text{Ddx}{4}_{\text{monomer}}$ (Fig. 1B, Right), both of which are not phase-separated. Note that, in Fig. 1B, Left, the boundary between phase-separated compartments of Ddx4 is readily apparent; the top component, $\text{Ddx}{4}_{\text{dil}}$, is dilute in protein concentration ($\sim$7 mg/mL; 100 mM NaCl; 30 °C; see below), while the bottom component, $\text{Ddx}{4}_{\text{cond}}$, of interest here is a condensed Ddx4 solution ($\sim$380 mg/mL; see below). NMR experiments (SI Materials and Methods) were performed on Ddx4 samples where the majority of the supernatant containing dilute protein was removed, and care was taken to ensure that only $\text{Ddx}{4}_{\text{cond}}$ was within the volume of the NMR coil. Samples could be incubated for extended periods (at least 1 wk) at 30 °C without noticeable changes in appearance or in NMR spectra. We did not observe irreversible maturation of droplets in the case of Ddx4 (32, 33), and old samples (>3 wk), although sometimes gel-like, could be readily dissolved into buffer containing fresh reducing agent [100 mM NaCl, 20 mM sodium phosphate (NaPi), 10–20 mM DTT, pH 6.5]. Critically, negative stain EM and Thioflavin T fluorescence experiments were carried out on dilutions of the condensed phase after prolonged incubations and did not show evidence for aggregation or amyloid fibril formation (SI Materials and Methods and Fig. S1).

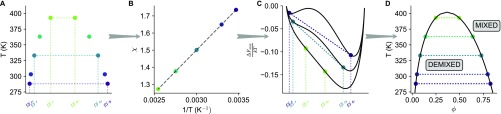
Fig. 1.

A phase-separated Ddx4 sample for NMR analysis. (A) Bright-field microscopy image of $\text{Ddx}{4}_{\text{cond}}$ droplets (200 $\mu$M protein, 200 mM NaCl) at 25 °C. (B) NMR samples of (Left) phase-separated Ddx4, $\text{Ddx}{4}_{\text{ps}}$; (Center) $\text{Ddx}{4}_{14\text{FtoA}}$, 250 mg/mL; and (Right) $\text{Ddx}{4}_{\text{monomer}}$, 2.5 mg/mL. Note the separation of phases in $\text{Ddx}{4}_{\text{ps}}$, with the concentrated phase at the bottom (380 mg/mL) studied here. $\text{Ddx}{4}_{\text{ps}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$ are dissolved in 20 mM NaPi, buffer, and 100 mM NaCl, while the buffer for $\text{Ddx}{4}_{\text{monomer}}$ contains 20 mM NaPi and 400 mM NaCl. (C) Phase diagrams for Ddx4 at NaCl concentrations between 100 and 500 mM. Fits to Flory–Huggins model (binodal) are shown with solid lines (SI Materials and Methods). Liquid–liquid demixing occurs at Ddx4 concentrations within the regions beneath the curves. (D) Phase diagrams for $\text{Ddx}{4}_{\text{CS}}$, 100 or 300 mM NaCl and Ddx4, 100 mM NaCl.

Fig. S1.

Negative stain EM of Ddx4. The 1,000- (A) and 10,000-fold (B) dilutions of Ddx4_cond into 20 mM NaPi, 100 mM NaCl, and 10 mM DTT, pH 6.5. Samples were prepared by staining with uranyl acetate [2% (wt/vol) solution] on Cu/Rh 400 mesh grids, with a fresh continuous carbon layer applied over a nitrocellulose film. Images were taken on a Tecnai F20 microscope (FEI) at a nominal magnification of 25,000×, and defocus ranged from 0.5 to 1.0 μm. Ddx4_cond readily dissolved into buffer on dilution below the concentration at which phase separation occurs. Extensive searching of grids revealed no signs of aggregation or fibril formation. Samples were incubated for 2 d before imaging. (C) Ratio of ThT fluorescence with and without Ddx4 or A$\beta$ fibrils. Error bars represent one SD from at least six replicates. Fluorescence excitation (emission) of ThT was recorded at 450 (482) nm using a SpectraMax i3x Microplate Reader system (Molecular Devices). The Ddx4 sample had been incubated at room temperature for 3 wk before measurement.

Generating a Highly Concentrated Monomeric Ddx4 Control.

We have previously shown through bioinformatics and mutational analysis that conserved RG and FG motifs as well as charge patterning are important for phase separation of Ddx4 (15). Since a mutant in which nine highly conserved Phe residues were mutated to Ala, $\text{Ddx}{4}_{9\text{FtoA}}$, does not phase separate in HeLa cells on overexpression, we intended to use it here as a control sample for comparison with $\text{Ddx}{4}_{\text{cond}}$. Samples were concentrated in an attempt to reach the protein concentration of the phase-separated sample ($\sim$400 mg/mL) but still remain in a mixed state. Ddx4_9FtoA remained a single phase to a concentration of approximately 100 mg/mL in NaPi at pH 6.5 and 100 mM NaCl (30 °C) before phase separation occurred at a protein concentration roughly fourfold more dilute than Ddx4_cond. We next created a construct where all 14 Phe were mutated to Ala, $\text{Ddx}{4}_{14\text{FtoA}}$. This protein remained a single phase through concentrations in excess of 400 mg/mL in 20 mM NaPi, 100 mM NaCl, and 5 mM Tris(2-carboxyethyl)phosphine (TCEP) at pH 6.5 (30 °C) and was, therefore, chosen as an appropriate control. Unlike Ddx4 that spontaneously concentrates itself by $\sim$50-fold under the conditions used here, as described below, high concentrations of $\text{Ddx}{4}_{14\text{FtoA}}$ ($\sim$400 mg/mL) at temperatures in excess of 0 °C are only achievable via extensive centrifugation. It is worth noting, however, that $\text{Ddx}{4}_{14\text{FtoA}}$ is able to phase separate spontaneously by incubating samples on ice; raising the temperature to 5 °C leads to mixing of the two phases. We have also used a second mutant as a control in a number of studies in which all 24 Arg in Ddx4 are replaced by Lys, such that the resulting $\text{Ddx}{4}_{24\text{RtoK}}$ preserves the overall protein charge (−3.4 at pH 6.5). Under identical conditions to $\text{Ddx}{4}_{14\text{FtoA}}$, $\text{Ddx}{4}_{24\text{RtoK}}$ remained as a single phase up to concentrations in excess of 400 mg/mL. Finally, to prevent WT Ddx4 from phase separating, both high salt (400 mM NaCl) and dilute protein concentration (2.5 mg/mL; 30 °C) were required for the $\text{Ddx}{4}_{\text{monomer}}$ state. As described above, it is possible to work with $\text{Ddx}{4}_{\text{dil}}$, in which case NMR samples are prepared with only a very small amount of condensed phase at the bottom of the tube that does not contribute to the signal.

A Phase Diagram for Ddx4.

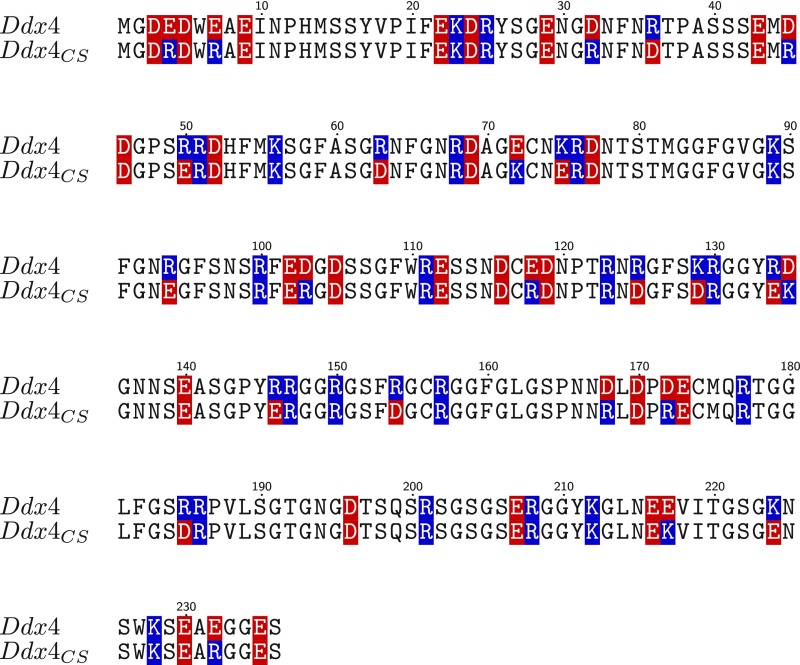
For proteins involved in the formation of membraneless organelles, phase diagrams that map the temperature and salt dependence of not only the dilute phase but also, the condensed phase are currently lacking. As far as Ddx4 is concerned, a preliminary attempt was made (15), but attention was focused exclusively on the dilute side of the coexistence curve. Here, Fig. 1 A–C clearly indicates that Ddx4 can phase separate into condensed and dilute phases, distinct from solutions of $\text{Ddx}{4}_{\text{monomer}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$. Fig. 1C shows coexistence curves for Ddx4 at five salt concentrations ranging from 100 to 500 mM obtained by measuring protein concentrations in both the dilute and condensed phases under equilibrium conditions (Materials and Methods and SI Materials and Methods). The upper critical solution temperatures (UCSTs), corresponding to the temperatures above which the solution is always mixed regardless of protein concentration as estimated by the fitted curves, are strongly dependent on ionic strength and display an approximately 100 °C decrease from 100 to 500 mM NaCl, highlighting the ability of salt to disrupt the interactions driving the phase separation of Ddx4. Consistent with the simple Flory–Huggins theory used to fit the data, the concentration of protein in the condensed phase reduces with increasing temperature. Our experimental data indicate that addition of salt also reduces the concentration of protein in the condensed phase. Notably, as observed previously (15) and rationalized by RPA theory (30), sequence details, such as the distribution of charged blocks, are important determinants of phase behavior. This feature of sequence-dependent phase separation is reinforced by the coexistence curves in Fig. 1D for a charge scrambled version of Ddx4, Ddx4_CS (Fig. S2) [denoted previously as Ddx4^N1CS (15)], showing significant decreases in UCSTs and a lowering of the protein concentration in the condensed phase relative to the WT protein. This sequence sensitivity is consistent with RPA predictions (Discussion).

Fig. S2.

Sequence alignment showing positions of positive (blue) and negative (red) charged residues for WT Ddx4 and Ddx4_CS. A metric, $\kappa$, has been developed to describe the linear distribution of charges in a sequence (75), with $\kappa =\mathrm{\hspace{0.17em}1}$ for complete segregation of charge and $\kappa =\mathrm{\hspace{0.17em}0}$ for no charge asymmetry. Using this metric, $\kappa$ values of 0.272 and 0.069 are obtained for WT Ddx4 (15) and Ddx4_CS, respectively, indicating that Ddx4_CS has a significantly more even distribution of charged residues than Ddx4.

Translational Diffusion of Ddx4.

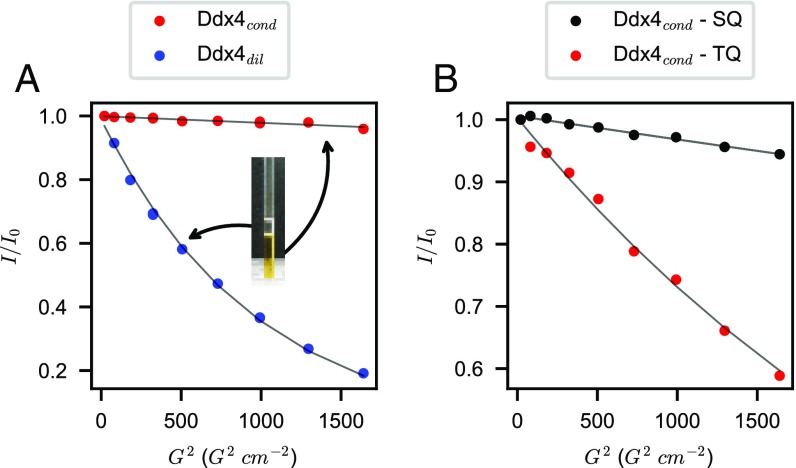
To better understand how hydrodynamic properties couple with phase separation, we next performed pulsed field gradient NMR experiments to measure the diffusion constants, D, of Ddx4_cond and $\text{Ddx}{4}_{\text{dil}}$ at 30 °C (Fig. 2A) using a standard single-quantum longitudinal encode–decode ¹³C-edited diffusion experiment (34). Because signal intensity scales proportionally to exp($-\alpha D$), where $\alpha$ takes into account experimental settings, large intensity losses are associated with faster diffusing molecules. In contrast to the $\text{Ddx}{4}_{\text{dil}}$ trace that decays significantly with encode/decode gradient strength squared (G²), the profile for Ddx4_cond (380 mg/mL) shows only a very slight decrease of signal $(\sim 5\%)$, making reliable estimation of diffusion constants difficult. To surmount this technical obstacle, we have developed a pulse sequence that selects for methyl triple-quantum ¹H magnetization while still retaining close to 75% of the sensitivity of the single-quantum experiment (35), neglecting relaxation effects. Application of encoding/decoding gradients to a triple-quantum state enhances the effective gradient strength by threefold (36, 37), enabling accurate measurement of diffusion constants that are an order of magnitude slower than is possible with traditional single-quantum approaches (Fig. 2B). Accordingly, the diffusion coefficient of $\text{Ddx}{4}_{\text{cond}}$ was measured to be $7.5\pm 0.4\times {10}^{-9}{\text{cm}}^2/\text{s}$, which is comparable with values obtained using FRAP on in vitro droplets of Ddx4, where a value of $4\times {10}^{-9}{\text{cm}}^2/\text{s}$ was reported (15). The NMR-based diffusion coefficient of $\text{Ddx}{4}_{\text{dil}}$ (7 mg/mL) was determined to be $8.8\pm 0.2\times {10}^{-7}{\text{cm}}^2/\text{s}$, a factor of 100 times faster than for $\text{Ddx}{4}_{\text{cond}}$.

Fig. 2.

(A) Translational diffusion as measured by 1D single-quantum (SQ) ¹³C-edited longitudinal encode–decode pulsed field gradient diffusion experiments recorded on $\text{Ddx}{4}_{\text{dil}}$ (blue; 7 mg/mL) and $\text{Ddx}{4}_{\text{cond}}$ (red; 380 mg/mL) with encoding/decoding gradient times of 4 ms and a diffusion interval of 100 ms. (B) Comparative $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL) diffusion profiles obtained from 1D ¹³C-edited SQ (black) vs. triple-quantum (TQ; red) sequences with 4-ms gradient encoding/decoding durations and a diffusion interval of 400 ms. A decay of ∼40% is observed for the TQ sequence, enabling accurate extraction of diffusion constants. In A and B, $I$ is the intensity of integrated 1D spectra measured using encode/decode gradient strengths squared of G², while $I_0$ is the extrapolated value to 0 gradient strength. Experimental points are indicated by circles, and best fitted exponentials are shown in curves.

Ddx4 Is Disordered in the Liquid Droplet Form.

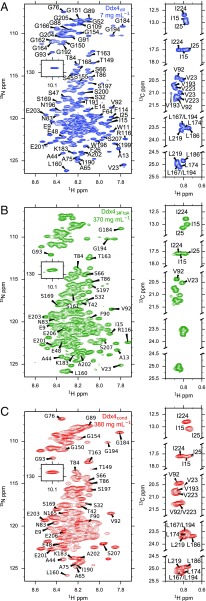
We have previously shown by solution NMR spectroscopy that $\text{Ddx}{4}_{\text{dil}}$ is intrinsically disordered (15). In the case of $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL) (Fig. 3C, red), there is extensive line broadening in the ¹H-¹⁵N heteronuclear single-quantum coherence (HSQC) spectrum, although the amide backbone resonances overlap well with $\text{Ddx}{4}_{\text{dil}}$ (Fig. 3A, blue and Fig. S3A) with only minor chemical shift changes, indicating that Ddx4 molecules in $\text{Ddx}{4}_{\text{cond}}$ are also disordered. ¹H-¹⁵N spectra of $\text{Ddx}{4}_{14\text{FtoA}}$ (370 mg/mL) (Fig. 3B, green) are very similar to those of $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{\text{dil}}$ (Fig. 3 and Fig. S3B), with line broadening that is intermediate between the two. Similar to what was observed in ¹H-¹⁵N spectra, a comparison of the corresponding ¹³C datasets also establishes that $\text{Ddx}{4}_{\text{cond}}$ is intrinsically disordered, with methyl resonances of Ile, Leu, and Val residues showing little deviation from random coil chemical shift values (Fig. 3, Right) (38). Analysis of backbone chemical shift data also revealed little to no propensity for secondary structure formation (Fig. S3C). Interestingly, there is no significant line broadening of resonances in ¹H-¹³C spectra of $\text{Ddx}{4}_{\text{cond}}$ relative to $\text{Ddx}{4}_{\text{dil}}$ and only minor chemical shift changes. Thus, despite the increased effective viscosity of the $\text{Ddx}{4}_{\text{cond}}$ solution, the side chains of the protein remain locally highly dynamic, leading to an efficient averaging of magnetic interactions that would otherwise contribute to resonance broadening.

Fig. 3.

Ddx4 is intrinsically disordered in the condensed phase-separated state. ¹H-¹⁵N HSQC spectra (Left) and selected methyl region of constant time ${}^1\text{H}-^{13}\text{C}$ HSQC spectra (Right) of (A) $\text{Ddx}{4}_{\text{dil}}$ (7 mg/mL), (B) $\text{Ddx}{4}_{14\text{FtoA}}$ (370 mg/mL), and (C) $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL) at 30 °C and 18.8 T. Isoleucine, leucine, and valine (ILV) methyl groups were assigned by mutagenesis in $\text{Ddx}{4}_{\text{dil}}$, and assignments were transferred to spectra of $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$. Amides were partially (40%) assigned using standard triple-resonance experiments.

Fig. S3.

(A and B) Overlays of ¹H-¹⁵N HSQC spectra of Ddx4_cond with Ddx4_dil (A) and Ddx4_cond with Ddx4_14FtoA (B). All spectra were recorded at 18.8 T and 30 °C. (C) $\delta 2\text{D}$ scores (76) as a function of residue based on available backbone assignments for Ddx4 (PPII is polyproline II helix secondary structure propensity). ${}^{13}\text{C}\alpha$, ${}^{13}\text{C}\beta$, and carbonyl shifts were used for each residue. Values close to one indicate a high propensity to form the indicated secondary structural element. The average coil propensity across the sequence was calculated to be 0.92.

The small diffusion constant of Ddx4_cond ($7.5\pm 0.4\times {10}^{-9}$ ${\text{cm}}^2$/s; 30 °C) is predicted from the Stokes–Einstein relation (39) for a protein of hydrodynamic radius ∼550 nm in dilute aqueous solution. The slow tumbling of such a large molecule would normally preclude recording of NMR spectra. Thus, the observation of backbone amide resonances, albeit broadened, and sharp ¹³C side-chain resonances indicates that Ddx4 undergoes rapid local motions in the condensed phase, as discussed further below.

Fast Timescale Dynamics of Ddx4.

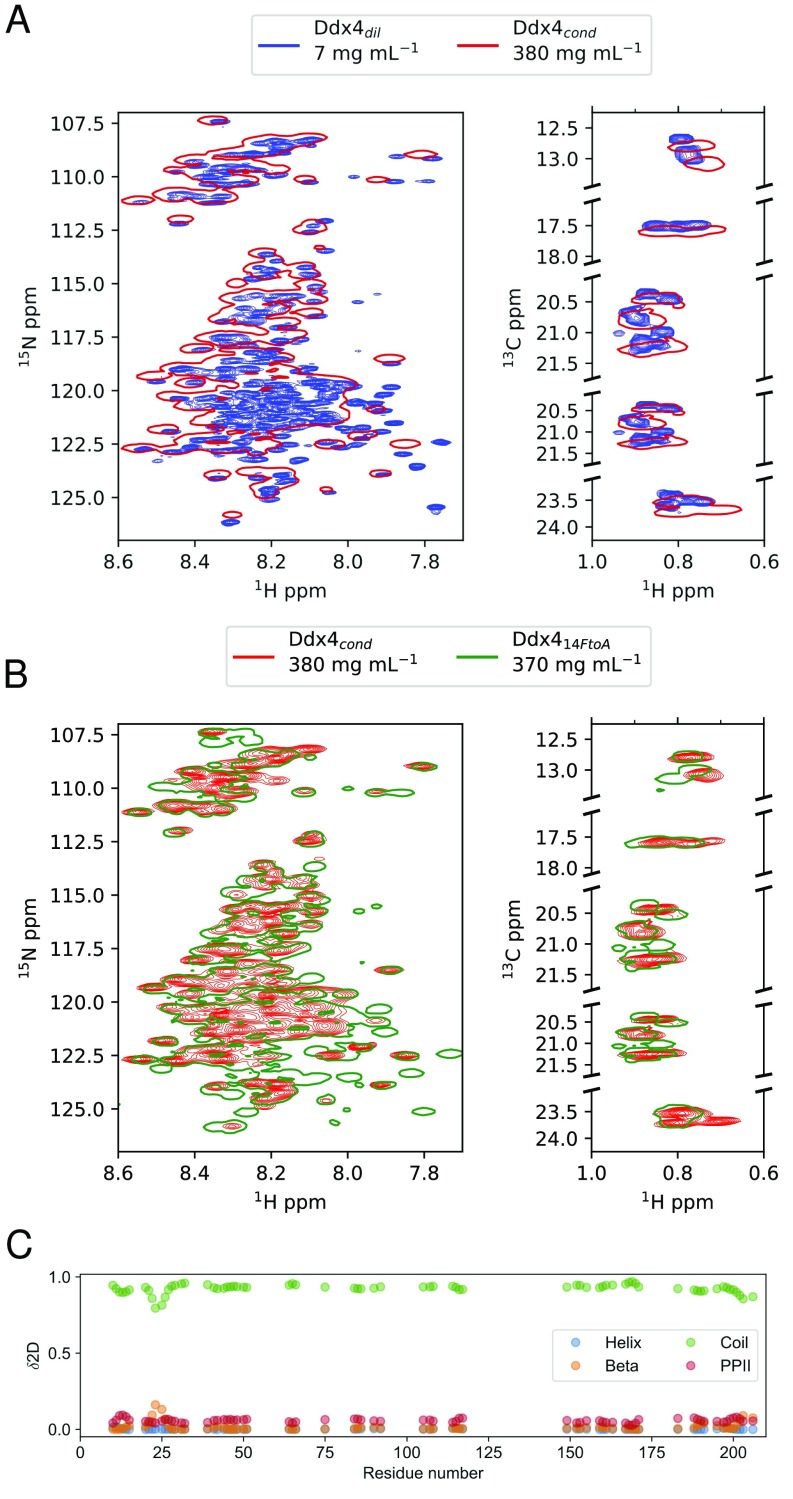
To better understand the reasonably sharp resonances in NMR spectra of $\text{Ddx}{4}_{\text{cond}}$, despite the extremely slow translational diffusion, we recorded ¹⁵N $R_1$, $R_2$ rates and ¹⁵N{${}^1\text{H}$} NOE values (40) of $\text{Ddx}{4}_{\text{dil}}$ ($\sim$7 mg/mL), $\text{Ddx}{4}_{14\text{FtoA}}$ (370 mg/mL), and $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL). The histograms in Fig. 4 A–C and E show $R_2$ and ¹⁵N{¹H} NOE values for residues that are sufficiently well-isolated, such that cross-peak intensities could be quantified; in the case of $\text{Ddx}{4}_{\text{cond}}$, data for 39 resonances could be obtained of 231 non-Pro residues. Of these, 23 resonances were sufficiently isolated that they could be unambiguously paired with the corresponding peaks in $\text{Ddx}{4}_{\text{dil}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$, although a great many more could be correlated in spectra of $\text{Ddx}{4}_{\text{dil}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$.

Fig. 4.

Extensive internal dynamics in $\text{Ddx}{4}_{\text{cond}}$. Histogram plots showing the distribution of $R_2$ rates for $\text{Ddx}{4}_{\text{dil}}$ (A), $\text{Ddx}{4}_{14\text{FtoA}}$ (B), and $\text{Ddx}{4}_{\text{cond}}$ (C). (D) Mean $R_2$ values and distribution (vertical lines) for $\text{Ddx}{4}_{\text{dil}}\text{, Ddx}{4}_{\text{cond}}$, and $\text{Ddx}{4}_{14\text{FtoA}}$ are plotted as a function of protein concentration. (E) ${}^{15}\text{N}\{{}^1\text{H}\}$ NOE values of $\text{Ddx}{4}_{\text{dil}}$ (blue), $\text{Ddx}{4}_{14\text{FtoA}}$ (green), and $\text{Ddx}{4}_{\text{cond}}$ (red). Mean and SDs for each dataset are indicated in A–C and E.

The ¹⁵N $R_2$ relaxation rates for $\text{Ddx}{4}_{\text{dil}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$ measured at a number of concentrations (7, 250, and 370 mg/mL) (Fig. 4D) are consistent with values for an IDP, with rates ranging from 1 to 6 ${\text{s}}^{-1}$ and from 2 to 14 ${\text{s}}^{-1}$, respectively, at 18.8 T and 30 °C. $R_2$ rates for both Ddx4_cond and $\text{Ddx}{4}_{14\text{FtoA}}$ become significantly larger at high concentrations, to some extent reflecting increased sample viscosities (Fig. 4D). Strikingly, at equivalent concentrations, average $R_2$ values for $\text{Ddx}{4}_{\text{cond}}$ are almost twofold larger than for $\text{Ddx}{4}_{14\text{FtoA}}$, with a broader distribution ($16.4\pm 6.1{\text{s}}^{-1}$ for $\text{Ddx}{4}_{\text{cond}}$, 380 mg/mL, vs. $9.8\pm 3.9{\text{s}}^{-1}$ for $\text{Ddx}{4}_{14\text{FtoA}}$, 370 mg/mL). Of interest, relaxation dispersion studies (41) showed small (<1 ${\text{s}}^{-1}$) dispersion profiles for both $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$ that were not quantified in this study. Steady-state ¹⁵N{${}^1\text{H}$} NOE values, sensitive to local motions on the picosecond to nanosecond timescale, range from −0.7 to 0.6 and do not show a significant difference between samples.

To compare picosecond to nanosecond timescale motions between the different Ddx4 samples, we have recast the $R_1$, $R_2$, and ¹⁵N{${}^1\text{H}$} NOEs in terms of the product $S^2{\tau }_C$ (SI Materials and Methods). The parameters $S^2$ and ${\tau }_C$ correspond to the square of the order parameter that describes the amplitude of the amide bond vector motions and the residue-specific tumbling time, respectively (42, 43). Their product provides a measure of the extent of motion at each backbone site in the protein. Values of $S^2{\tau }_C$ were calculated for the resolved resonances that could be quantified in samples of Ddx4_dil (79 residues), $\text{Ddx}{4}_{14\text{FtoA}}$ (78 residues), and $\text{Ddx}{4}_{\text{cond}}$ (37 residues). On average, $S^2{\tau }_C$ values for amides in $\text{Ddx}{4}_{\text{cond}}$ are $8.5\pm 3$ ns, a factor of 6.5 times larger than for $\text{Ddx}{4}_{\text{dil}}$ ($1.3\pm 0.6$ ns) and 1.8 times higher than for Ddx4_14FtoA. This suggests an additional slowing of backbone motions in $\text{Ddx}{4}_{\text{cond}}$, potentially the result of transient intermolecular contacts that mediate phase separation.

Intermolecular Contacts in Ddx4_cond.

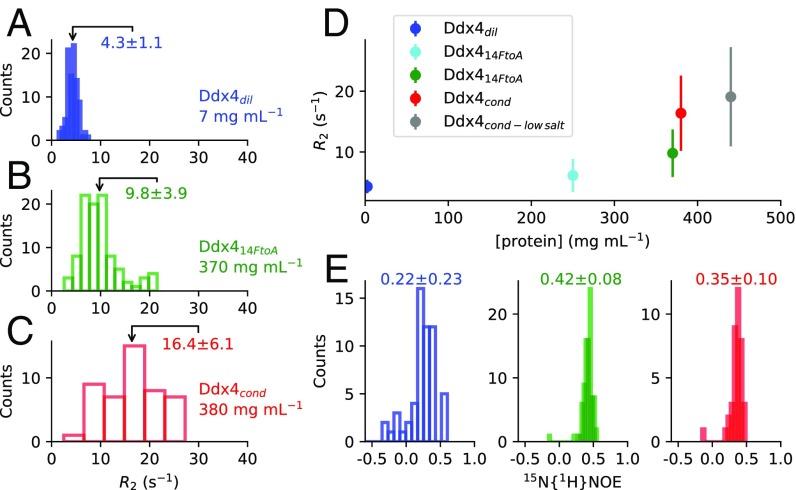
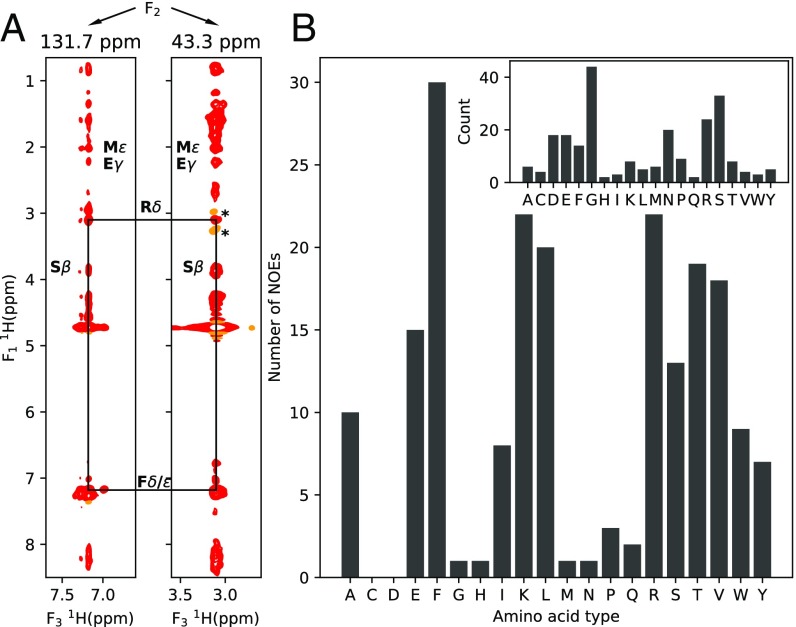
Intermolecular contacts between Ddx4 monomers in $\text{Ddx}{4}_{\text{cond}}$ were probed by recording F₁ ¹³C-filtered, F₂ ¹³C-edited NOESY spectra (44) of samples prepared by mixing 10% ¹³C-labeled Ddx4 with 90% unlabeled Ddx4. In these spectra, the observed NOEs derive from intermolecular contacts between pairs of protons (Fig. S4). Fig. 5A shows strips through 3D datasets extracted at a pair of ¹³C frequencies, highlighting intermolecular contacts between Phe and Arg residues that are thought to be particularly important in establishing both cation–pi and pi–pi interactions that can play significant roles in stabilization of $\text{Ddx}{4}_{\text{cond}}$ (15). Fig. 5B tabulates the number of intermolecular NOEs vs. amino acid type. In this regard, it is noteworthy that there are more intermolecular NOEs involving Phe than any other residue in $\text{Ddx}{4}_{\text{cond}}$, with a large number for Arg as well. In this analysis, NOEs could not be assigned to specific residues but only to residue types, and quantification was only possible in cases where well-resolved cross-peaks that report on a given residue type could be identified. The data are thus biased by these limitations. Nevertheless, a comparison of NOE spectra recorded for $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{\text{FtoA}}$ (Fig. S4) establishes, for example, that there are a large number of NOEs involving Phe, highlighting the importance of Phe interactions. Interestingly, an extensive network of intermolecular NOEs was also observed for $\text{Ddx}{4}_{14\text{FtoA}}$ at an equivalent concentration to $\text{Ddx}{4}_{\text{cond}}$ (Fig. S4). However, the contacts in $\text{Ddx}{4}_{14\text{FtoA}}$ are not sufficient to drive phase separation. Rather, such contacts for the FtoA mutant are a direct result of the high protein concentration used that is only possible through extensive centrifugation (see above).

Fig. S4.

Measurement of intermolecular NOEs in samples of Ddx4_cond (A; 380 mg/mL; red) and Ddx4_14FtoA (B; 370 mg/mL; green) as described in the text at 30 °C, 14. 1 T, and mixing $\text{time}=150$ ms. Samples were prepared by mixing 10% (1 mM) ¹⁵N, ¹³C-labeled Ddx4 with 90% unlabeled Ddx4. As expected, more NOE peaks are present in the aromatic region of the Ddx4_cond spectrum and in the Ala region of the Ddx4_14FtoA spectrum. Ala ${\text{H}}^{\beta }$ region at $1.35\pm 0.30$ ppm and Phe aromatic proton region, $7.0\pm 0.5$ ppm, are highlighted (red outline). It is noteworthy that a comparison of NOE intensities can only be qualitative as differences in dynamics between molecules in Ddx4_cond, and Ddx4_14FtoA (Fig. 4) will affect cross-relaxation efficiencies. As a control, a sample of 100% unlabeled Ddx4 was also prepared (380 mg/mL), from which the spectrum of C (blue) was obtained. For comparison, horizontal traces (D; 3.1 ppm in F₁; marked by dashed lines in A and C) are illustrated. These show a very low level of intramolecular cross-peaks arising from natural abundance ¹³C that, therefore, do not significantly affect our conclusions. Spectra are displayed at the same contour level.

Fig. 5.

An extensive network of intermolecular contacts for $\text{Ddx}{4}_{\text{cond}}$. (A) Selected planes from 3D ${\text{F}}_1$ ¹³C-filtered, ${\text{F}}_2$ ¹³C-edited NOESY experiments (44) (150-ms mixing times) recorded on Ddx4_cond (380 mg/mL) at 30 °C. NOEs between Arg $\text{H}\delta$ and Phe $\text{H}\delta /ϵ$ side-chain protons are highlighted by black lines between strips. Sample was prepared with 90% unlabeled and 10% ¹⁵N,¹³C-labeled protein. Artifacts from imperfect purging in F₁ are labeled with asterisks. (B) Number of NOEs as a function of amino acid type for $\text{Ddx}{4}_{\text{cond}}$. (B, Inset) Number of each amino acid type found in the sequence of Ddx4 (residues 1–236).

Diffusion of Small Molecules and Compact Proteins in $\text{Ddx}{4}_{\text{cond}}$.

In cells, membraneless organelles are often composed of a mixture of multiple proteins, RNA, and small molecules (1, 3). The motion of these molecules depends on the solvent environment of the organelle and is important for regulating the kinetics and thermodynamics of molecular interactions within the droplet (15) and for controlling chemical properties within the organelle, such as enzymatic activity (17, 45, 46). In addition to providing insight into how binding and reactivity might be affected by the phase-separated environment, quantifying rates of motion of molecules inside the droplet also inform on the intrinsic physical nature of the concentrated phase of the protein that provides the matrix of the proteinaceous organelle.

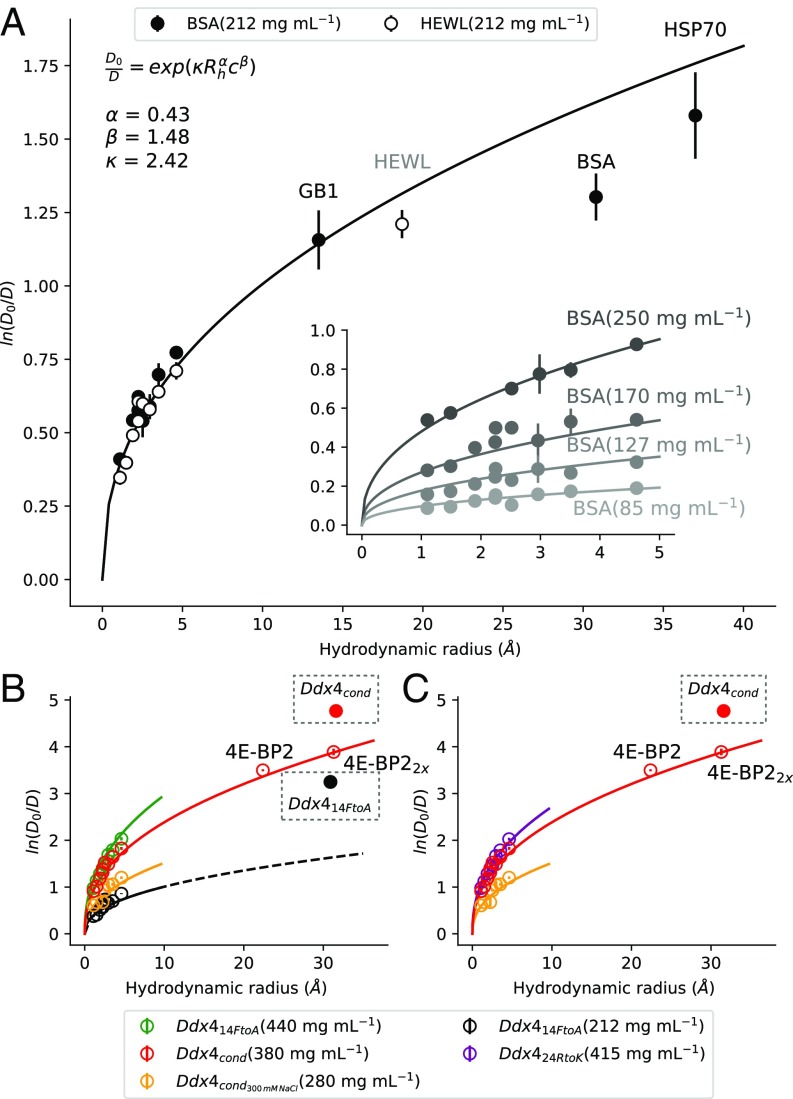
Pulsed field gradient NMR diffusion measurements were performed to obtain $D_o/D$ values for nine small probe molecules varying in hydrodynamic radius, $R_p$, from 1.1 to 4.6 Å and dissolved in $\text{Ddx}{4}_{\text{cond}}$ (Fig. 6), where D and $D_o$ are diffusion constants of the probe within a polymer solution of concentration $C$ and in buffer, respectively. $D_o/D$ values were initially quantified in the presence of two folded proteins, either BSA at concentrations of 85–250 mg/mL in steps of $\sim$50 mg/mL or hen egg white lysozyme (HEWL) at 212 mg/mL (Fig. 6A and SI Materials and Methods). In addition, diffusion measurements for a number of probe proteins have also been included, as indicated in Fig. 6A. The diffusion coefficient ratios increase monotonically with $R_p$, indicating that the diffusion of larger probes is slowed more than in smaller ones. Note that, in this analysis, the probe hydrodynamic radius is assumed to be invariant to the presence of the added proteins (Ddx4, BSA, HEWL).

Fig. 6.

The diffusion of small molecules and the compact disordered protein 4E-BP2 in $\text{Ddx}{4}_{\text{cond}}$ can be explained by an excluded volume model. Logarithm of the diffusion coefficient, $D$, of probe molecules in (A) 212 mg/mL HEWL and 212 mg/mL BSA, (B) $\text{Ddx}{4}_{\text{cond}}$ (280 and 380 mg/mL) and $\text{Ddx}{4}_{14\text{FtoA}}$ (440 and 212 mg/mL), and (C) $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{24\text{RtoK}}$ (415 mg/mL) relative to diffusion in buffer, $D_o$, as a function of probe hydrodynamic radius ($R_h$; units of meters for the Phillies equation) at 30 °C. A, Inset shows similar plots as a function of BSA concentrations ranging from 85 to 250 mg/mL. Probes used in these experiments and their hydrodynamic radii include ${\text{H}}_2\text{O}$ (1.1 Å), methanol (1.49 Å), ethanol (1.9 Å), acetate (2.24 Å), isopropanol (2.25 Å), glycerol (2.5 Å), ribose (2.96 Å), glucose (3.5 Å), sucrose (4.6 Å), 4E-BP2 (22.4 Å; $\text{Ddx}{4}_{\text{cond}}$ only), $4\text{E-BP}{2}_{2\text{x}}$ (31.3 Å; $\text{Ddx}{4}_{\text{cond}}$ only), B1 domain from Ig binding protein G (13.5 Å; 212 mg/mL BSA only), HEWL (19 Å; 212 mg/mL HEWL only), BSA (31 Å; 212 mg/mL BSA only), and heat shock protein 70 (37 Å; 212 mg/mL BSA only). Diffusion data (circles) were fitted to the Phillies equation (36) (solid lines) as described in the text. Fitting parameters $(\kappa ,\alpha ,\beta )$ obtained from the diffusion series in concentrated samples of BSA and HEWL in A are used to generate the solid curves in B and C. The self-diffusion of $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$ (boxed points) is slower than predicted by the Phillies equation with these parameters, consistent with interactions between adjacent molecules.

While it remains a challenge to understand and predict the diffusion of both small and large molecules within a protein system from first principles, there are empirical models based on organic polymers that can be used to obtain insight (47, 48). Many of these models are based on the obstruction effect, whereby the “solvent” polymer chains, in this case protein molecules, are proposed to retard the motion of the “solvated” probe by reducing the free volume available for it to move (47). Here, we have used one such polymer model based on an equation proposed by Phillies (49, 50), $D_0/D=\text{exp}(\kappa R_h^{\alpha }{c}^{\beta })$, where $\kappa$, $\alpha$, and $\beta$ are fitted constants; $R_h$ is the hydrodynamic radius of the probe (meters); and $c$ is the concentration of the polymer (milligrams per milliliter), to quantify the $D_o/D$ vs. $R_h$ profiles that have been obtained using BSA, HEWL, $\text{Ddx}{4}_{14\text{FtoA}}$, and $\text{Ddx}{4}_{\text{cond}}$ as the proteinaceous solvents. We refer to these proteins as solvents while recognizing that they are, in fact, cosolvents with significant hydration present in all cases. Even at a protein concentration of 380 mg/mL, approximately 73% of the volume of the $\text{Ddx}{4}_{\text{cond}}$ droplet is water based on prediction and verified using NMR experiments that quantify water in samples of the concentrated Ddx4 phase (SI Materials and Methods).

Fig. 6A shows that the Phillies equation is able to fit (black curve) the diffusion data (circles) acquired at all BSA and HEWL concentrations quantitatively with extracted values of $\kappa$, $\alpha$, and $\beta$ as indicated. The corresponding fits in Fig. 6B for probes dissolved in $\text{Ddx}{4}_{14\text{FtoA}}$ at 440 (green) and 212 mg/mL (black) or $\text{Ddx}{4}_{\text{cond}}$ at 380 (red) and 280 mg/mL (orange) as well as $\text{Ddx}{4}_{24\text{RtoK}}$ at 415 mg/mL (magenta in Fig. 6C) use the same fitting parameters as optimized for diffusion data recorded with HEWL or BSA polymers. Good fits are obtained despite the fact that Ddx4 is intrinsically disordered, while HEWL and BSA are folded proteins. That the same $\kappa$, $\alpha$, and $\beta$ parameters are relevant for these four different proteinaceous solvents, with essentially identical $D_o/D$ profiles for a constant polymer concentration, is to be expected (i) if the protein obstructs probe motion through an excluded volume effect and (ii) if all protein solvents considered have similar densities, so that equivalent masses of protein would occupy similar volumes. In this regard, it is noteworthy that Ddx4 in the nonphase-separated state is highly compact, with an effective hydrodynamic radius of 30 Å (Table S1) that is much closer to what is predicted for a folded protein of the same number of amino acids (23.3 Å) than for an unfolded protein (50.4 Å) (51). Thus, individual molecules in $\text{Ddx}{4}_{\text{cond}}$ and $\text{Ddx}{4}_{14\text{FtoA}}$ are expected to have similar densities as folded proteins, such as HEWL and BSA. By means of comparison, we have also included $\text{ln}(D_o/D)$ values measured at 30 °C for $\text{Ddx}{4}_{14\text{FtoA}}$ and $\text{Ddx}{4}_{\text{cond}}$ at concentrations of 370 and 380 mg/mL, respectively (boxes in Fig. 6 B and C). Unlike the case for the small molecules with diffusion properties that follow the Phillies equation and thus, behave as “hard spheres” in $\text{Ddx}{4}_{\text{cond}}$, the self-diffusion of Ddx4 molecules in the phase-separated milieu is slower than predicted, consistent with substantial interactions among Ddx4 molecules in the condensed phase.

Table S1.

Rotational and translational diffusion of Ddx4

Protein	Concentration	MW(kDa)	D(cm2/s)*	RH†	$<$${{\mathrm{S}}^2}_{{\tau }_c}$$>$‡ (ns)
Ubiquitin§		8.5	2.0 × 10−6 ($\pm$0.1)	15.7	3.3
${\text{Ddx4}}_{dil}$	7 mg/mL¶	25.8	8.8 × 10−7 ($\pm$0.2)	31.6	1.5($\pm$0.5)
${\text{Ddx4}}_{14FtoA}$	${\text{D}}_0$#	24.8	9.0 × 10−7 ($\pm$0.1)	30.9	‖
${\text{Ddx4}}_{14FtoA}$	250 mg/mL	24.8	3.5 × 10−8 ($\pm$0.1)	**	2.4($\pm$0.8)
${\text{Ddx4}}_{14FtoA}$	370 mg/mL	24.8	9.2 × 10−9 ($\pm$0.9)	**	4.8($\pm$1.5)
${\text{Ddx4}}_{cond}$	380 mg/mL	25.8	7.5 × 10−9 ($\pm$0.4)	**	8.5($\pm$3)
${\text{Ddx4}}_{cond}$††	440 mg/mL	25.8	5.4 × 10−9 ($\pm$0.4)	**	10.4($\pm$4)

D₀, concentration extrapolated to 0; MW, molecular mass.

^*Measured by pulsed field gradient NMR as described in SI Materials and Methods (30 °C).

^†Hydrodynamic radius (RH) calculated from measured diffusion coefficient in buffer along with diffusion of acetate (30 °C) (SI Materials and Methods).

^‡Product of square of order parameter for backbone amide, S², and residue-specific overall tumbling time, τ_C, averaged over residues for which data is available (30 °C).

^§$<{{\mathrm{S}}^2}_{{\tau }_c}>$ data from refs. 57 and 58.

^¶Sample obtained from the dilute phase of phase-separated Ddx4

^#Extrapolated from self-diffusion data as a function of concentration to zero concentration.

^‖Relaxation data not measured.

^**Hydrodynamic radius cannot be accurately extracted from diffusion measurements on concentrated samples because of elevated viscosity. All estimates of R_H make use of dilute Ddx4 samples.

^††A lower NaCl concentration was used (7.5 mM) relative to all other Ddx4 samples to achieve a higher protein concentration in the condensed phase.

Structural Properties of Intrinsically Disordered 4E-BP2 Within $\text{Ddx}{4}_{\text{cond}}$.

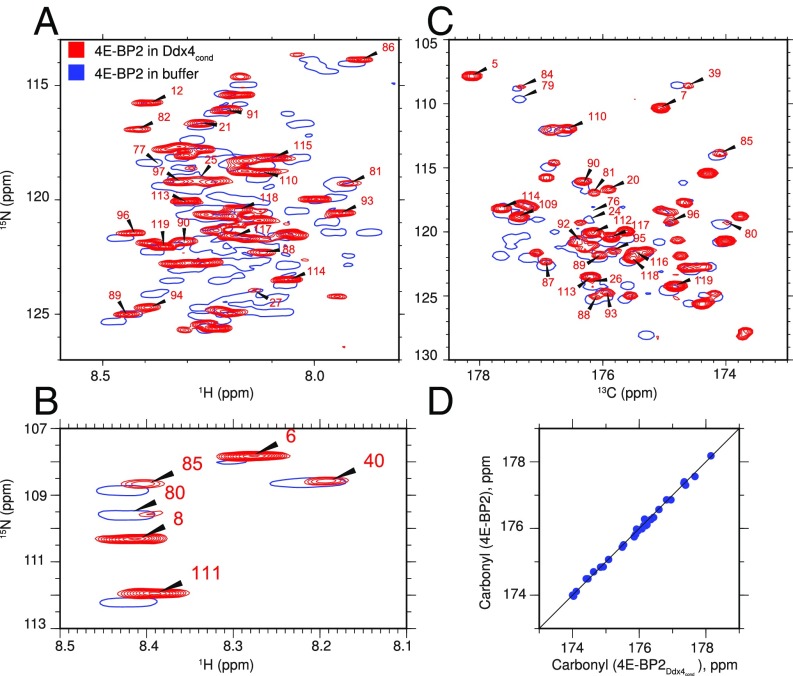
Despite the obvious functional relevance, there is currently very little information on the structural properties of proteins solvated within a membraneless organelle. Proteins, such as GFP and YFP, have been used in photobleaching experiments and as markers for organelles (15, 25), suggesting that they retain photoactive, native-like conformations. Even less is known regarding IDPs solvated within organelles. The eukaryotic translation initiation factor 4E-BP2 is an IDP that plays an important role in the initiation of translation and is found in neuronal RNA granules, membraneless organelles regulating local mRNA translation in brain function (52, 53). We study it here as a model for IDPs that do not phase separate but are found inside membraneless organelles by characterizing the structural properties of 4E-BP2 solvated within $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL; 30 °C). Assignments for $\sim$30% of the backbone resonances of 4E-BP2 dissolved in Ddx4_cond were obtained, corresponding to ∼90% of the observed 4E-BP2 cross-peaks, based primarily on transfer from spectra recorded on 4E-BP2 dissolved in buffer (54). As illustrated in Fig. 7, the ¹H-¹⁵N spectrum of 4E-BP2 solvated in $\text{Ddx}{4}_{\text{cond}}$ shows some amide shift differences relative to a dataset recorded in buffer (Fig. 7 A and B), with few changes in ¹³CO shifts (Fig. 7 C and D). Taken together, the data are consistent with little change in fluctuating secondary structure of 4E-BP2 when solvated in $\text{Ddx}{4}_{\text{cond}}$, although it must be kept in mind that only 30% of the reporters of structure give rise to observable cross-peaks in spectra.

Fig. 7.

NMR spectra of the intrinsically disordered 4E-BP2 protein in Ddx4_cond. (A and B) Overlay of ${}^1\text{H}-^{15}\text{N}$ HSQC spectra of 250 μM ${}^{15}\text{N}$, ${}^{13}\text{C}$-labeled 4E-BP2 in buffer (blue; single contour) and in Ddx4_cond (red; 380 mg/mL) at 30 °C and 14.1 T. (C) Overlay of ${}^{15}\text{N}-^{13}\text{CO}$ projections from HNCO datasets recorded on the same samples. (D) Linear correlation plot of carbonyl shifts of 4E-BP2 dissolved in buffer (y axis) and in $\text{Ddx}{4}_{\text{cond}}$ (x axis).

To further explore the effects of $\text{Ddx}{4}_{\text{cond}}$ on dissolved solutes, samples were doped with small amounts ($\sim$3%) of ¹⁵N,¹³C-labeled 4E-BP2. Although the small amount of label compromises the sensitivity of experiments for measuring intermolecular NOEs, diffusion coefficients for a number of 4E-BP2 constructs could be obtained using an HNCO-based longitudinal encode–decode experiment that we developed (Fig. S5). These include 4E-BP2 (120 residues) and a protein made by joining the N and C termini of a pair of 4E-BP2 molecules ($4\text{E}-\text{BP}{2}_{2\text{x}}$) (Fig. 6 B and C). Interestingly, the diffusion data for these proteins could be well-fit with the corresponding data recorded on the small molecules, suggesting that 4E-BP2 diffusion in $\text{Ddx}{4}_{\text{cond}}$ can be modeled as motion of hard spheres in the same way as that for the small molecules considered above (Fig. 6). Indeed, although 4E-BP2 is an IDP, it is compact, with an NMR diffusion-based measured hydrodynamic radius of 23 Å that is only slightly larger than that predicted for a folded protein (19 Å) using an empirical relation derived by Smith and coworkers (51). It appears from our measurements that $\text{Ddx}{4}_{\text{cond}}$ is no better (or worse) a solvent for 4E-BP2 than water, allowing 4E-BP2 to maintain structural tendencies that are present in buffer.

Fig. S5.

HNCO-based longitudinal encode–decode scheme for measurement of diffusion of ¹⁵N,¹³C-labeled proteins. Although a 3D version of the experiment is illustrated here, all diffusion experiments in this work were performed in “1D” mode, where ${}^{13}\text{C}^{\alpha }$ and ¹⁵N pulses in the center of the t₁ period were eliminated and replaced by a ¹³CO pulse and ${\text{t}}_1={\text{t}}_2=\mathrm{\hspace{0.17em}0}$. Narrow and wide rectangles correspond to 90° and 180° pulses, respectively, applied along the $x$ axis unless otherwise indicated. ¹H decoupling is achieved using a 6-kHz WALTZ-16 decoupling element (77). The ¹H, ¹⁵N, and ¹³C carriers are placed at water, 119 and 176 ppm, respectively for the duration of the experiment. ${}^{13}\text{C}^{\alpha }$ and ¹³CO rectangular pulses are applied with fields of $\zeta$/$\sqrt{3}$ Hz (180°) or $\zeta$/$\sqrt{15}$ Hz (90°), where $\zeta$ is the frequency difference in hertz between the centers of the ${}^{13}\text{C}^{\alpha }$ (58 ppm) and ${}^{13}\text{CO}$ (176 ppm) spectral regions (78). ${}^{13}\text{C}^{\alpha }$ decoupling during t₂ is achieved using an ∼1-kHz SEDUCE element (79). Note that, in 1D mode, this element is not required. Delays are ${\tau }_{\text{a}}=2.3$ ms, ${\tau }_{\text{b}}=2.7$ ms, ${\tau }_{\text{c}}=\mathrm{\hspace{0.17em}12.4}$ ms, ${\tau }_{\text{d}}=\mathrm{\hspace{0.17em}5.5}$ ms, ${\tau }_{\text{e}}=\mathrm{\hspace{0.17em}3.0}$ ms, and $T_{\text{N}}=\mathrm{\hspace{0.17em}12.4}$ ms. The phase cycle is ${\varphi }_1=\hspace{0.17em}4(x),4(-x)$, ${\varphi }_2=2(x)$, 2(−x), ${\varphi }_3=x,-x$, ${\varphi }_4=\mathrm{\hspace{0.17em}8}(\text{x}),8(-\text{x})$, ${\varphi }_5=x$, and $\text{rec}=x,2(-x),x,-x,2(x),-x$. Gradient levels and durations (gauss per centimeter; milliseconds) are g1 = (16; 0.5), g2 = (30; 2.0), g3 = (−10; 0.4), g4 = (24; 0.6), g5 = (40; 0.75), g6 = (24; 0.6), g7 = (10,0.3), g8 = (20; 0.2), gA = diffusion encoding/decoding gradient (arrayed, typically 2 ms), gB = (60; 1.25), and gB′ = (59.2; 0.125). Quadrature in $F_1$ is achieved via States-TPPI (time proportional phase incrementation) (80) of ${\varphi }_2$. Quadrature in $F_2$ is achieved using the gradient enhanced sensitivity method (81, 82), whereby separate datasets are recorded with $({\varphi }_5,\text{gB})$ and $({\varphi }_5+{180}^{\circ },-\text{gB})$. For each t₁ increment, ${\varphi }_2$ and the receiver phase are incremented by 180° (80).

SI Materials and Methods

NMR Spectroscopy.

Experiments were performed on Varian INOVA and Bruker Ascend III (11.7, 14.0, and 18.8 T) spectrometers equipped with triple-resonance gradient probes. NMR spectra were processed using the NMRPipe suite of programs (62) and analyzed using Sparky (63) and CCPN Analysis (64). The program FUDA (www.biochem.ucl.ac.uk/hansen/fuda/) was used to extract peak intensities from all multidimensional datasets.

Translational diffusion measurements.

Translational diffusion coefficients for the small molecule probes in BSA, HEWL, Ddx4_14FtoA, and $\text{Ddx}{4}_{\text{cond}}$ were measured by recording a series of 2D ¹³C-edited spectra at 30 °C using a pulse scheme that is similar to a previously published ¹⁵N-edited experiment with ¹⁵N and ¹³C pulses interchanged (34). The constant delay diffusion period (after initial encoding of magnetization) was set to 100 ms. Diffusion coefficients of BSA (in BSA) and HEWL (in HEWL) were measured using a 1D water-suppressed longitudinal encode–decode (sLED) scheme (65), while diffusion measurements of ¹³C-labeled Ig binding protein G (GB1) and heat shock protein 70 (HSC70; in BSA) were obtained as a series of 1D ¹³C-edited spectra, 30 °C, with a diffusion period of 100 ms and an array of dephasing/rephasing gradients with strengths ranging from 10 to 31 G/cm (1-ms duration). Translational diffusion coefficients of Ddx4 in Ddx4_cond were obtained from measurements on a sample where $\sim$1.5 mM $\text{U}{-}^{15}\text{N}{,}^{13}\text{C}$-labeled protein was mixed with $\sim$13.5 mM unlabeled protein. A series of 1D ¹³C-edited ¹H triple-quantum spectra, 30 °C, was recorded with a diffusion period of 400 ms and an array of bipolar dephasing/rephasing gradients (4-ms duration each) with strengths ranging from 4.5 to 40.5 G/cm (the pulse sequence is available on request). Translational diffusion coefficients of ¹⁵N,¹³C-labeled 4E-BP2 and 4E-BP2_2x were measured using the 1D version of the HNCO longitudinal encode–decode scheme of Fig. S5. The diffusion period was set to 400 ms, and an array of dephasing/rephrasing gradients with strengths ranging from 3.6 to 53.7 G/cm (2- to 2.5-ms duration) was used. Gradient strengths were calibrated by measuring the diffusion coefficient of the residual HDO in a D₂O sample using the known diffusion coefficient of water: 1.9 × 10⁻⁵ cm²/s at 25 °C (66). In this case, a 1D longitudinal encode–decode pulsed field gradient NMR experiment was used (65).

Measurement of fractional water content.

One-dimensional ¹H spectra were recorded on Ddx4_cond samples, and the integrated water signals were compared with the corresponding integrals obtained from a spectrum recorded of buffer (the same buffer composition as used for Ddx4_cond). For phase-separated samples, it was ensured that the entirety of the probe coil was occupied by the condensed phase, thus avoiding contaminating signals from the more hydrated dilute phase. Spectra were recorded using both small flip angle $(\theta <{10}^{\circ })$ and $\theta ={90}^{\text{o}}$ pulses, with very similar results in both cases.

Dynamics measurements.

NMR spin relaxation experiments (40) were performed at 18.8 T and 30 °C on a Bruker spectrometer equipped with a cryogenically cooled triple-resonance probe; ¹⁵N{¹H} NOE values were determined from peak intensities in spectra obtained with/without 6-s proton saturation and a total delay of 14 s between scans (including saturation). ¹⁵N $R_1$ relaxation rates were measured using relaxation delays of (10, 250, 500, 750); (10, 80, 160, 250, 360, 480, 620, 800); and (10, 250, 375, 500, 625, 750) ms for $\text{Ddx}{4}_{\text{dil}}$, $\text{Ddx}{4}_{14\text{FtoA}}$, and $\text{Ddx}{4}_{\text{cond}}$, respectively. ¹⁵N $R_{1\rho }$ relaxation rates were recorded with spin lock (2-kHz) delays of (10, 20, 30, 40, 50, 60, 70, 90, 100, 120); (1, 7, 15, 23, 32, 42, 54, 66, 81, 98); and (10, 50, 100, 150) ms for Ddx4_dil ($\sim$7 mg/mL), Ddx4_14FtoA (370 mg/mL), and Ddx4_cond (380 mg/mL), respectively. More extensive $R_{1\rho }$ datasets were recorded for Ddx4_cond on Varian spectrometers, and the $R_2$ rates obtained were essentially identical. $R_2$ values were calculated from experimental $R_1$ and $R_{1p}$ rates as detailed below.

Assignment of ILV residues.

Each of the 12 Ile, Leu, and Val residues (4 Ile, 3 Leu, and 5 Val) in Ddx4 were substituted with Ala in a series of mutations that included I15A_V193A_L194A, V23A_I25A_L167A, L219A_V223A_I224A, V92A_L174A, and L186A. This led to unambiguous assignment of these residues in Ddx4_dil, and the assignments could then be transferred directly to Ddx4_14FtoA and Ddx4_cond.

NOESY spectra.

F₁ ¹³C-filtered, F₂ ¹³C-edited NOESY spectra (44) were recorded on samples prepared by mixing 10% (1 mM) ¹³C-labeled Ddx4 with 90% unlabeled Ddx4 to probe intermolecular interactions in $\text{Ddx}{4}_{14\text{FtoA}}$ and $\text{Ddx}{4}_{\text{cond}}$. A concentration of 370 mg/mL was used for $\text{Ddx}{4}_{14\text{FtoA}}$, similar to Ddx4_cond (380 mg/mL). The 3D (2D) spectra were recorded at 11.7 T (14.0 T) and 30 °C using a 150-ms mixing time. NOEs were assigned to a particular amino acid type only when there was unambiguous identification based on reported random coil chemical shift values by Wishart et al. (38).

Assignment of 4E-BP2 in Ddx4_cond.

Backbone chemical shifts for 4E-BP2 (500 $\mu$M) dissolved in buffer composed of 20 mM NaPi, 100 mM NaCl, 5 mM TCEP, 1 mM Benzamadine, and 1 mM EDTA, pH 6.5 at 30 °C were obtained using HNCO, HN(CA)CO, CBCA(CO)NH, HNCACB, and HNN/HN(C)N experiments (67, 68). ${}^1\text{H}-^{15}\text{N}$ HSQC and HNCO experiments were collected for 250 μM 4E-BP2 in Ddx4_cond, 20 mM NaPi, 100 mM NaCl, 5 mM TCEP, 1 mM Benzamadine, and 1 mM EDTA, pH 6.5 at 30 °C, and assignments were transferred from 4E-BP2 in buffer to 4E-BP2 in $\text{Ddx}{4}_{\text{cond}}$. Approximately 55% of backbone and ¹³C^$\beta$ shifts could be assigned for 4E-BP2 in buffer (many peaks are weak or absent because of exchange with water), and 30% of the assignments in $\text{Ddx}{4}_{\text{cond}}$ could be obtained by transferring those in buffer.

Extraction of Relaxation Parameters.

$R_2$ values were calculated from experimental $R_1$ and $R_{1\rho }$ rates according to (40)

$$R_2=\frac{R_{1\rho }-R_1{\text{cos}}^2\theta }{{\sin }^2\theta },$$ [S1]

where $\theta ={\text{tan}}^{-1}(v_{\text{sl}}/\mathrm{\Delta }v)$, $\mathrm{\Delta }\nu$ is the offset of the peak from the carrier frequency, and ${\nu }_{sl}$ is the strength of the spin lock field. The $T_1$, $T_2$ relaxation times and ${}^{15}\text{N}\{{}^1\text{H}\}$ NOE values can be expressed as (69)

$$\frac{1}{T_1}=d^2\left[J\left({\omega }_H-{\omega }_N\right)+3J\left({\omega }_N\right)+6J\left({\omega }_H+{\omega }_N\right)\right]+c^{2}J({\omega }_N)$$ [S2]

$$\frac{1}{T_2}=0.5d^2\left[4J\left(0\right)+J\left({\omega }_H-{\omega }_N\right)+3J\left({\omega }_N\right)+6J\left({\omega }_H\right)+6J\left({\omega }_H+{\omega }_N\right)\right]+\frac{1}{6}{c}^2\left[3J\left({\omega }_N\right)+4J\left(0\right)\right]$$ [S3]

$$NOE=1+\left[\left(\frac{{\gamma }_H}{{\gamma }_N}\right)d^2\left\{6J\left({\omega }_H+{\omega }_N\right)-J\left({\omega }_H-{\omega }_N\right)\right\}{T}_1\right],$$ [S4]

where $d^2=0.1{[{\mu }_{0}h{\gamma }_{\text{H}}{\gamma }_{\text{N}}/8{\pi }^2]}^2<\text{r}{\mathrm{NH}}^{-3}{>}^2,c^2=2/15({\omega \text{N}}^2){({\sigma }_{\parallel }-{\sigma }_{⟂})}^2$; ${\mu }_0$ is the permeability of free space; ${\gamma }_{\text{j}}$ and ${\omega }_{\text{j}}$ are the gyromagnetic ratio and nuclear Larmor frequency of spin j, respectively; $h$ is Planck’s constant; ${\text{r}}_{\mathrm{NH}}$ is the length of the amide bond (1.02 Å); and ${\sigma }_{\parallel }$ and ${\sigma }_{⟂}$ are the parallel and perpendicular components of the assumed axially symmetric ${}^{15}\text{N}$ chemical shift tensor [(${\sigma }_{\parallel }$ – ${\sigma }_{⟂}$) = −172 ppm], respectively (70)_. The spectral density, $J(\omega )$, in Eqs. S2–S4 is given by

$$J\left(\omega \right)=\frac{S^2{\tau }_c}{(1+{(\omega {\tau }_c)}^2)}+\frac{\left(1-S^2\right)\tau }{(1+{(\omega \tau )}^2)},$$ [S5]

where ${\tau }^{-1}={\tau }_c^{-1}+$ ${\tau }_e^{-1}$; ${\tau }_c$ and ${\tau }_e$ are residue-specific correlation times describing overall tumbling and rapid motion of the amide bond vector, respectively; and $S^2$ is the square of the order parameter. Values of $S^2$, ${\tau }_c$, and ${\tau }_e$ were extracted by fitting experimental $T_1$, $T_2$, and ¹⁵N{¹H} NOE values using Eqs. S2–S5, and the product $S^2{\tau }_c$, averaged over all residues, is reported in Table S1.

Fitting of Translational Diffusion Measurements.

Signal intensities in translational diffusion experiments are dependent on the gradient strength $(G)$ and the diffusion coefficient $(D)$ of the probe of interest according to the expression

$$\frac{I}{I_0}=\text{exp}(-e{G}^2),$$ [S6]

where $e$ is a constant that depends, among other things, on $D$. Values of the hydrodynamic radii of probe molecules in Fig. 6 (x axis), $R_p$, were measured using samples containing a small amount of acetate as a reference, so that $R_p=e_{acetate,buff}/e_{probe,buff}\cdot R_{p,acetate}$, where$R_{p,acetate}$ = 2.24 Å (71), and the subscript buff emphasizes the fact that the diffusion measurements were made in buffer samples (as opposed to proteinaceous samples). In this manner, $R_p$ values for the small molecule probes used in this study that included ¹³C-labeled methanol, 1-¹³C ethanol, 2-¹³C acetate, 2-¹³C isopropanol, 2-¹³C glycerol, 1-¹³C ribose, ¹³C glucose, and ¹³C sucrose as well as GB1, HEWL, BSA, and HSC70 protein probes, were obtained. The diffusion of small molecules in Ddx4_cond (380 mg/mL), Ddx4_14FtoA (212 mg/mL), and BSA (250 mg/mL) was measured at concentrations of 2 and ∼10 mM. There was no appreciable change between concentrations, indicating no interactions with the protein crowding agent. Diffusion constants of small molecule and protein probes dissolved in HEWL, BSA, $\text{Ddx}{4}_{14\text{FtoA}}$, Ddx4_24RtoK, and $\text{Ddx}{4}_{\text{cond}}$ were obtained from expressions like those in Eq. S6 and subsequently analyzed as described in the text.

Diffusion of Proteins Within Ddx4_cond.

We have measured diffusion coefficients for 4E-BP2 and 4E-BP2_2x in $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL) using the pulse scheme illustrated in Fig. S5. A major complication in measuring spectra of tracer proteins in Ddx4_cond has been residual signal that arises from the very high concentration of Ddx4 in the phase-separated state (10 mM), although it is unlabeled. For example, at typical concentrations of 5% mole fraction-labeled tracer, ∼20% of the signal in a ¹³C-edited dataset originates from Ddx4 that is readily observed in spectra (especially considering that Ddx4 is unfolded). Notably, we can also record very high-quality natural abundance ¹⁵N-edited spectra of Ddx4 that would interfere with any measurements of tracer proteins that use a selection based on ¹⁵N. We have, therefore, chosen to develop an HNCO-based longitudinal encode–decode sequence that makes use of combined ¹⁵N,¹³C filtering to eliminate Ddx4 from spectra. Of particular importance is the coherence transfer selection from ¹⁵N to ¹H at the end of the pulse sequence that was achieved using gradients (B and B′ in Fig. S5), since on our spectrometers (and in our noisy magnetic environment), we were not able to eliminate spurious peaks derived from Ddx4 based on phase cycling alone.

Fits of Phase Diagrams to Simple Flory–Huggins Theory.

The free energy of mixing per unit volume (lattice site) for a solution comprising a polymer chain (protein) and solvent (water), denoted here as $\mathrm{\Delta }{F}_{\text{mix}}$, may be described approximately according to the mean field Flory–Huggins theory by

$$\frac{\mathrm{\Delta }{F}_{mix}}{kT}=\frac{\varphi }{N_1}\ln \varphi +\frac{(1-\varphi )}{N_2}\ln (1-\varphi )+\chi \varphi (1-\varphi ),$$ [S7]

where $\varphi$ and $1-\varphi$ are the volume fractions of protein and water, respectively; $N_1$ and $N_2$ are the numbers of lattice sites occupied by protein (number of amino acids) and water, respectively, with $N_1=241$ (for Ddx4) and $N_2=1$ in the case of interest; and $\chi$ is a temperature-dependent interaction parameter, $\chi =A+B/T$. For simplicity, unlike approaches in more involved treatments (59), here we assume that each lattice site is fully occupied by either a solvent molecule or a protein residue. The logarithmic terms in Eq. S7 describe the purely entropic contributions to the mixing energy. The value of $\varphi$ is calculated according to

$$\varphi =\frac{c}{\rho },$$ [S8]

where $c$ is the protein concentration in milligrams per milliliter, and $\rho$ is the protein density. Following standard treatments (2, 59), if the free energy function $\mathrm{\Delta }{F}_{mix}$ is convex throughout, then the solution will be mixed at all compositions. However, if the landscape contains concave features (Fig. S7), then the system can phase separate. The volume fraction of protein in the dilute and concentrated sides of the phase diagram, $\varphi \prime$ and. ${\varphi }^{″}$, respectively, can be calculated from the following relations (72):

$${\left(\frac{\partial \mathrm{\Delta }{F}_{mix}}{\partial \varphi }\right)}_{\varphi =\varphi \prime }={\left(\frac{\partial \mathrm{\Delta }{F}_{mix}}{\partial \varphi }\right)}_{\varphi ={\varphi }^{″}}$$ [S9.1]

$$\frac{\mathrm{\Delta }{F}_{mix}(\varphi \prime )-\mathrm{\Delta }{F}_{mix}({\varphi }^{″})}{\varphi \prime -{\varphi }^{″}}={\left(\frac{\partial \mathrm{\Delta }{F}_{mix}}{\partial \varphi }\right)}_{\varphi =\varphi \prime or{\varphi }^{″}},$$ [S9.2]

where

$$\left(\frac{\partial \mathrm{\Delta }{F}_{mix}}{\partial \varphi }\right)=kT\left[\frac{\ln \varphi }{N_1}+\frac{1}{N_1}-\frac{\ln (1-\varphi )}{N_2}-\frac{1}{N_2}+\chi (1-2\varphi )\right],$$ [S10]

yielding

$$\chi =A+\frac{B}{T}=\frac{\frac{1}{N_1}\ln \left(\frac{\varphi ″}{\varphi \prime }\right)+\frac{1}{N_2}\ln \left(\frac{1-\varphi \prime }{1-{\varphi }^{″}}\right)}{2({\varphi }^{″}-\varphi \prime )}.$$ [S11]

Thus, if the phase diagram is determined experimentally, $\chi (T)$ is established from the measured $\varphi \prime$ and ${\varphi }^{″}$ values by obtaining the best fit $A$ and $B$ values (Fig. S7 A and B). The fitted phase diagram (solid line in Fig. S7D) is then obtained by calculating the free energy function for each $\chi$ as in Fig. S7C. Values of $\varphi \prime$ and ${\varphi }^{″}$ are obtained from the free energy profile by enforcing Eq. S9 (Fig. S7C). After these are determined, the phase diagram is calculated. In the fits of the salt-dependent $\text{Ddx}{4}_{\text{cond}}$ phase diagrams, each salt series was considered independently, and the density of $\text{Ddx}{4}_{\text{cond}}$ was a fitted parameter ($\rho =1587$ mg/mL) that was optimized to give the best fit over the complete salt range.

Fig. S7.

Schematic illustrating fitting of phase diagrams. (A) Experimental phase diagram. At each temperature, volume fractions of protein from dilute and concentrated regions of demixed solutions are measured to give the curve in A. Values of $\varphi \prime$ and ${\varphi }^{″}$ at each temperature, $T$, are used to calculate the best fit $\chi (T)$ in B using Eq. S11. Values of $\chi (T)$ are then used to generate energy landscapes (C) (Eq. S7), from which a continuous set of [$\varphi \prime (T)$, ${\varphi }^{″}(T)$] pairs is calculated by enforcing Eq. S9 that, in turn, generates the solid curve in D.

Estimating the Effective Attractive Energy Between Ddx4 Chains Using Simple Flory–Huggins Theory.

The Flory–Huggins expression $\mathrm{\Delta }{F}_{\text{mix}}$ in Eq. S7 for the free energy per unit volume implies that $\mathrm{\Delta }{F}_{\text{mix}}/\varphi$ is the free energy per amino acid, because the probability of any volume being occupied by a residue is $\varphi$. It follows that the interaction energy component of $\mathrm{\Delta }{F}_{\text{mix}}/\varphi$ is equal to $kT\chi (1-\varphi )$ and that the configurational entropic component is $kT(\text{ln}\varphi )/N_1+kT[(1-\varphi )/\varphi ]\text{ln}(1-\varphi )$, where we have used $N_2=1$ as stated above. Fitting the simple Flory–Huggins model to the data in Fig. 1 for Ddx4 at [NaCl] = 100, 300 mM and Ddx4_CS at [NaCl] = 100 mM yields a condensed-phase volume fraction $\varphi \approx 0.2$ for all three cases (0.22, 0.17, and 0.16, respectively). At $T=300$ K, the $kT\chi$ values for these three systems are 0.362, 0.352, and 0.350 kcal mol⁻¹, respectively; hence, the corresponding average total interaction energies per residue are $kT\chi (1-\varphi )$ = 0.283, 0.291, and 0.295 kcal mol⁻¹, respectively [i.e., the average interaction energy per residue in phase-separated Ddx4 (and variants) is $\approx$0.3 kcal mol⁻¹]. This is much weaker than the $\approx$1.5 kcal mol⁻¹ per residue for protein folding. The latter follows from an average loss of 1.4 kcal mol⁻¹ per residue in the conformational entropic component of free energy (57) and a decrease of 0.05 to 0.12 kcal mol⁻¹ per residue in overall free energy on folding of globular proteins (58). The mixing entropies per residue of the condensed phase of the three sequences/salt concentrations considered (see above) are given by their corresponding free energies $kT(\text{ln}\varphi )/N_1+kT[(1-\varphi )/\varphi ]\text{ln}(1-\varphi )\approx$−0.88, −0.91, and −0.92 $kT$, respectively. The Flory–Huggins mixing entropy is defined to be relative to the completely demixed scenario ($\varphi =1$), in which each residue gains about $kT\text{ln}e=kT$ = 0.59 kcal mol⁻¹ of free energy from the conformational entropy component relative to an unrestrained conformer (73). Taken together, the free energy contributions per residue from conformational entropy in the Ddx4 condensed phases considered above are only 0.12, 0.09, and 0.08 $kT$ or 0.083, 0.062, and 0.055 kcal mol⁻¹, respectively, higher than for the corresponding unrestrained conformer. The configurational entropy predicted by the simple Flory–Huggins theory is thus reasonable, because a high degree of conformational freedom is expected for a condensed phase with $\varphi \approx 0.2$.

Ddx4_cond Does Not Form Irreversible Aggregates or Fibrils.

Much has been made in the literature of droplet “maturation” and the possibility of the phase-separated state acting as a path toward aggregation or fibrillation (23, 32, 33, 74). To explore these possibilities for Ddx4_cond, we performed Thioflavin T (ThT) fluorescence and negative stain EM experiments on samples that had been incubated for extended periods (up to 3 wk). No evidence was found for irreversible aggregation or amyloid fibril formation. Negative stain EM was performed on samples of Ddx4_cond, which were incubated at 30 °C for 2 d. Since the concentration of protein in Ddx4_cond is orders of magnitude greater than that required for EM, samples were diluted 1,000- and 10,000-fold into buffer containing 20 mM NaPi, 100 mM NaCl, and 10 mM DTT, pH 6.5 for final protein concentrations of $\sim$0.4 and $\sim$0.04 mg/mL, respectively. As has been previously observed (in the text), the condensed protein phase mixed readily on dilution into buffer, forming a single transparent and homogeneous phase, and the resulting electron micrographs (Fig. S1 A and B) showed no evidence of aggregation or fibril formation. Additionally, we measured ThT fluorescence on a sample of Ddx4, which had been incubated at room temperature for >3 wk. Fresh DTT (20 mM) was added to the sample to reduce cysteine side chains (see below). The ratio of ThT fluorescence with and without Ddx4 was recorded at four concentrations of ThT (50, 100, 150, and 200 μM), keeping the amount of Ddx4 constant (Fig. S1C). Fluorescence excitation (emission) of ThT was recorded at 450 (482) nm using a SpectraMax i3x (Molecular Devices) Microplate Reader system. No significant increase in fluorescence was observed for different concentrations of ThT, in contrast to the extent of ThT fluorescence in the presence of amyloid-$\beta$ (A$\beta$) fibrils (KLVFFAE sequence; donation of Simon Sharpe, Hospital for Sick Children, Toronto, ON, Canada). There is thus no evidence for Ddx4 fibril formation. Notably, however, Ddx4_cond does form a gel-like state after an extended period of incubation (3 wk) at room temperature (20 mM NaPi, 100 mM NaCl, 20 mM DTT, pH 6.5). This can be primarily attributed to the oxidation of cysteine side chains, since addition of fresh reducing agent readily liquefied the gel. It should be noted that we have been careful to use TCEP as reducing agent in NMR samples because of its greatly increased stability compared with DTT. We have not observed any evidence for irreversible maturation of Ddx4 droplets, as samples can always be redissolved into low-salt buffer (20 mM NaPi, 100 mM NaCl, 10–20 mM DTT), while phase-separated samples provide high-quality NMR spectra for weeks.

Discussion

The matrix of a membraneless organelle is composed of a dense network of proteins and often nucleic acids, creating a unique environment, in which many important biochemical processes can occur. For example, the half-time to completion of the N-WASP–stimulated actin assembly by the Arp2/3 complex is significantly decreased within a nephrin-NCK-N-WASP droplet (11). It has also been postulated that RNA processing is greatly increased within membraneless organelles (17, 45). Therefore, to ascertain the physical basis of the biological function of these organelles, it is of tremendous interest to understand the dynamic and hydrodynamic properties of phase-separated proteins and to quantify how solutes might move within phase-separated droplets.

As shown above, solution NMR spectroscopy is ideally suited for probing the motions of proteins forming phase-separated organelles as well as for monitoring the dynamics of both small molecules and protein solutes within these bodies. Unlike many other physical methods that require attachment of bulky reporters to the molecule of interest, NMR studies can focus on specific molecules that are enriched with NMR active nuclei, such as ¹⁵N and ¹³C, without structural perturbation. Here, we have used a range of different NMR experiments to explore the structure and dynamics of Ddx4 in a phase-separated environment. Rates of translational diffusion of Ddx4 molecules within this condensed phase are reduced by at least 100-fold relative to protein in the coexisting dilute phase (Table S1). Despite this large reduction in translational mobility, high-resolution NMR spectra could nevertheless be recorded. These findings establish that Ddx4 is intrinsically disordered and flexible in the condensed phase-separated state, as also evidenced by limited spectral dispersion in the amide proton region of ¹H-¹⁵N datasets and in corresponding ¹H-¹³C spectra and by the fact that spectra are very similar to those recorded on the IDP $\text{Ddx}{4}_{\text{dil}}$ or $\text{Ddx}{4}_{\text{monomer}}$ (15) (Fig. 3 and Fig. S3A). The reasonably sharp resonances in the NMR data establish further that both protein backbone and side chains retain considerable local dynamics. Specifically, despite an approximately 100-fold reduction in translational diffusion relative to $\text{Ddx}{4}_{\text{dil}}$, an average value of $S^2{\tau }_C$ of $8.5\pm 3$ ns (380 mg/mL; 30 °C) was calculated from a set of backbone ¹⁵N spin relaxation data that is only a factor of three larger than $<S^2{\tau }_C>$ for the 76-residue protein ubiquitin (Table S1). A similar conclusion regarding significant disorder and flexibility in the condensed phase-separated state of the FUS low-complexity region was made by Fawzi and coworkers (25).

Backbone amide ¹⁵N $R_2$ relaxation rates are $\sim$1.7 times larger for $\text{Ddx}{4}_{\text{cond}}$ relative to an equivalently concentrated mixed state, Ddx4_14FtoA. NOE experiments further establish the presence of intermolecular interactions between neighboring molecules in the phase-separated environment that may contribute to the increased transverse relaxation rates observed for amide probes in $\text{Ddx}{4}_{\text{cond}}$. Assuming relatively compact proteins, the concentration $(C\ast )$ at which the transition between a dilute and semidilute solution occurs, the latter corresponding to the regime where protein molecules are in contact with each other, can be estimated from the relation

$$C^{\ast }=\frac{3MW}{4\pi N_a{R}_H^3},$$

where $MW$ and $R_H$ are the protein molecular weight and hydrodynamic radius, respectively, and $N_a$ is Avogadro’s number (55). For Ddx4, using $R_H=31.6$ Å, $C\ast$ is calculated to be $\sim$325 mg/mL, similar to the Ddx4 protein concentration in $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL; 100 mM NaCl). $\text{Ddx}{4}_{\text{cond}}$ is thus expected to approximate a semidilute protein solution in which Ddx4 molecules partially overlap with one another, leading to transient intermolecular contacts.

Insights into the driving forces for phase separation, summarized in Table S2, can be gained from the salt dependence of the phase diagrams (Fig. 1C). As the salt concentration is increased from 100 to 500 mM, the concentration of Ddx4 in the condensed phase decreases from ∼400 to 250 mg/mL, while the protein concentration in the dilute phase increases. When the data are fit to a simple Flory–Huggins model, the UCST decreases by ∼100 °C as the salt concentration is raised from 100 to 500 mM, underscoring the importance of electrostatic interactions to Ddx4 phase separation. In contrast, the mutant $\text{Ddx}{4}_{14\text{FtoA}}$ is only able to phase separate at 0 °C in the absence of salt (using a buffer of 5 mM NaPi, 2.5 mM TCEP, pH 6.5), while conditions for phase separation of $\text{Ddx}{4}_{24\text{RtoK}}$ have yet to be been found. This points to cation–pi and pi–pi interactions involving Arg–Phe pairs as important determinants in phase separation, consistent with the large numbers of intermolecular contacts involving these amino acid types as quantified in NOE spectra. Note that pi interactions are thought to involve induced quadrupolar electrostatic components that may also be expected to have salt dependence (56). Assuming that the simple Flory–Huggins mixing entropy provides a quantitatively reasonable account of conformational entropy, the Flory–Huggins $\chi$ parameter fitted to the data in Fig. 1 suggests that each amino acid in Ddx4 contributes, on average, about 0.3 kcal ${\text{mol}}^{-1}$ effective energy to phase separation through favorable interactions with other Ddx4 residues. The highly approximate nature of this estimate notwithstanding, it is definitively weaker than the effective energy of $\approx 1.5$ kcal ${\text{mol}}^{-1}$ per residue that favors folding of globular proteins (57, 58) (SI Materials and Methods). This energetic consideration is consistent with the semidilute and dynamic nature of $\text{Ddx}{4}_{\text{cond}}$. Note that, while a simple Flory–Huggins theory is used here to model each coexistence curve with two parameters (Materials and Methods and SI Materials and Methods) and to estimate the average affinity between individual Ddx4 proteins, this fitting procedure does not by itself account physically for how charge blocks, aromatics, and other unique sequence features affect Ddx4 phase separation. Additional physical insights in that regard require more complex theoretical descriptions, such as RPA (30, 59), and explicit-chain simulations (60), the detailed investigation of which is beyond the scope of this work. The situation is best exemplified by the charge scrambled mutant Ddx4_CS (Fig. S2) that phase separates poorly, with an UCST that is $\sim$80 °C lower relative to WT Ddx4 (Fig. 1D). Thus, the ordering of charged amino acids is critical for Ddx4 phase separation, as has been noted (15, 30, 59). Quite reassuringly, the general Ddx4 vs. $\text{Ddx}{4}_{\text{CS}}$ sequence dependence trend of these phase diagrams spanning both low and high Ddx4 concentrations can also be rationalized by RPA, although theoretical improvements are still needed to provide a quantitatively accurate account of the salt dependence (Fig. S6).

Table S2.

Summary of driving forces for phase separation of Ddx4

Parameter	Effect on phase separation	Evidence	Probable cause
Loss of Arg	Decreases propensity	${\text{Ddx4}}_{24\text{RtoK}}$	Loss of potential $\pi$–$\pi$/cation–$\pi$ interactions abrogates ability to phase separate (in the text)
Loss of Phe	Decreases propensity	${\text{Ddx4}}_{14\text{FtoA}}$	Loss of potential $\pi$–$\pi$/cation–$\pi$ interactions abrogates ability to phase separate (in the text)
Charge segregation	Increases propensity	${\text{Ddx4}}_{CS}$	Scrambling of segregated charges reduces propensity to phase separate (Fig. 1)
Salt	Decreases propensity	Phase diagrams	Increasing salt concentration reduces critical temperature at which phase separation occurs
Temperature	Decreases propensity	Phase diagrams	Increasing temperature disfavors phase separation of Ddx4 (UCST)

Fig. S6.

Experimental data (circles) compared with phase diagrams (solid curves) predicted by the $\text{random phase approximation}\left(\text{RPA}\right)+\text{Flory-Huggins}\left(\text{FH}\right)$ theory of Lin et al. (30, 59). To provide a physical account for sequence-dependent phase behavior, only three parameters, namely ${ϵ}_{\text{r}}$ and two parameters for a global $\chi$, are used to describe all coexistence curves (i.e., unlike the simple Flory–Huggins approach used for Fig. 1, different coexistence curves here are not fitted using different $\chi$ parameters). The parameters are optimized by simultaneously fitting to the 100 mM NaCl data of WT Ddx4 and charge-scrambled Ddx4_CS (magenta and blue curves, respectively). Results shown indicate that this set of fitted parameters affords a reasonably accurate prediction for the two sets of 300 mM NaCl data that were not used to determine the fitting parameters. This comparison shows that the $\text{RPA}+\text{FH}$ theory successfully rationalizes the difference between WT and charge-scrambled Ddx4 caused by their different charge patterns. Salt dependence is also considered by the same theory, but the discrepancies with experiment increase with increasing salt concentrations. The fitting procedure used here is similar to that for the simple Flory–Huggins model in the text, except an additional RPA contribution from electrostatic free energy (30, 59) is included in this case. In the notation of refs. 30 and 59, the size of an amino acid residue in this calculation is taken to be $r=\mathrm{\hspace{0.17em}3.72}$ times that of a water molecule, and the fitted parameters are ${ϵ}_{\text{r}}=\mathrm{\hspace{0.17em}61.5}$, ${ϵ}_h=\mathrm{\hspace{0.17em}0.0754}$, and ${ϵ}_s=\mathrm{\hspace{0.17em}0.415}$.

Having shown that $\text{Ddx}{4}_{\text{cond}}$ diffuses slowly but has significant amplitude picosecond to nanosecond timescale dynamics, we proceeded to investigate how small molecules and well-folded proteins would diffuse within the Ddx4 phase-separated environment. We found that the diffusion data for small molecules and the compact IDP 4E-BP2 dissolved in $\text{Ddx}{4}_{14\text{FtoA}}$ and $\text{Ddx}{4}_{\text{cond}}$ could be well-fit to the Phillies model using parameters obtained from the analysis of diffusion data measured in proteinaceous solvents comprising the folded proteins BSA or HEWL. This suggests that the diffusion of small molecules and compact proteins in $\text{Ddx}{4}_{\text{cond}}$ is well-approximated by the hard-sphere approximation in the case of minimal interactions between solute and Ddx4 solvent. Notably, ∼75% of the volume of the $\text{Ddx}{4}_{\text{cond}}$ (380 mg/mL) droplet is predicted to be water, and we have verified this by recording NMR experiments that quantify water in samples of phase-separated Ddx4. The effective relative permittivity ${ϵ}_{\text{r}}$ (dielectric constant) of $\text{Ddx}{4}_{\text{cond}}$ is thus expected to be significantly lower than that of water. It has been estimated to be more like that of DMSO $({ϵ}_{\text{r}}\approx 47)$ (15), and a more recent analytical treatment suggested that ${ϵ}_{\text{r}}$ may be as low as 20 based on a 75% volume fraction of water (59). All in all, the phase-separated state provides a unique solvent environment that is predicted to enhance electrostatic interactions. This effect is expected to impact on the behavior of charged RNA molecules and many disordered proteins found in proteinaceous organelles.

A large number of distinct membraneless organelles and other cellular bodies (5–7, 9, 52) are formed via interactions between phase-separated proteins of low-complexity disordered regions (15, 16, 18–22, 25) or via dynamic multivalent interactions involving modular binding domains and motifs within disordered regions (10–12, 27). This raises the question of how specific the interactions driving phase separation are and what the rules for enabling or prohibiting specific cophase separation might be. Ddx4 disordered regions form membraneless organelles in the nuclei that do not colocalize with nucleoli, speckles, promyelocytic leukemia (PML), or Cajal bodies (15). In contrast, different cytoplasmic RNA processing bodies can have some similarities in protein composition (52), highlighting the diversity of protein cosolubility in defining cellular compartmentalization. FUS and hnRNPA1 phase-separated protein regions selectively recruit various low-complexity disordered proteins to different extents (20), and a recent study shows that proteins can be included or excluded from phase-separated Ddx4 depending on their charge properties, while structured RNA inside droplets is stabilized and DNA melted (31). Taken together with our finding that $\text{Ddx}{4}_{\text{cond}}$ is able to solvate the compact but disordered 4E-BP2 protein with little change to its secondary structural propensities, it is clear that a wide range of interactions is possible between the constituent biomolecules within a phase-separated environment. These results suggest that a detailed description of the interactions underlying phase separation in various cellular bodies will be essential for understanding how the cell organizes itself.

It has been proposed that membraneless organelles are important hubs for reactions to occur (15, 16, 45) and that the high concentration of reactants, such as proteins and nucleic acids, may increase rates of catalysis (45). By contrast, slower translational diffusion would be expected to attenuate reaction rates that are influenced by collision frequencies. In this regard, it is noteworthy that the presence of small molecules and RNA can affect diffusion rates, as evidenced by the fact that the liquidity of Whi3 containing cytoplasmic RNA granules is tuned by RNA (28). Furthermore, formation of phase-separated mRNA processing bodies has been observed in vitro to reduce the catalytic activity of mRNA decapping enzymes (46). Additional experiments are needed to probe the properties of both biomolecules and small molecule solutes in a variety of different phase-separated droplets to better appreciate the unique environment that this milieu provides and how it affects the biochemistry that occurs within it. This study makes it clear that solution NMR spectroscopy is well-poised to contribute to this important goal.

Materials and Methods

Sample Preparation.

Monomeric samples.

Genes for Ddx4, $\text{Ddx}{4}_{14\text{FtoA}}$, $\text{Ddx}{4}_{24\text{RtoK}}$, and $\text{Ddx}{4}_{\text{CS}}$ were synthesized and subcloned into pET Sumo vectors by Genscript. Isotopically labeled Ddx4 was overexpressed in Escherichia coli and purified as described in detail previously (15). Briefly, cell pellets were resuspended in buffer [50 mM Tris, pH 8.0, 6 M guanidinium (Gdm) HCl, 20 mM imidazole, 500 mM NaCl, 1 mM TCEP] and lysed. Proteins were purified by nickel affinity chromatography (His Trap HP 5-mL column; GE Healthcare Life Sciences) and eluted in buffer containing 50 mM Tris, pH 8.0, 400 mM imidazole, 500 mM NaCl, and 1 mM TCEP. The Sumo tag was removed with Ulp1 protease, and the sample was passed over the Ni column again to remove the cleaved tag after dialyzing out the imidazole. The protein was further purified and buffer-exchanged by size-exclusion chromatography into storage buffer (20 mM NaPi, pH 6.5, 500 mM NaCl, 5 mM TCEP). 4E-BP2 and $4\text{E}-\text{BP}{2}_{2\text{x}}$ were overexpressed in E. coli and purified as described previously (54). $\text{Ddx}{4}_{14\text{FtoA}}$ and $\text{Ddx}{4}_{24\text{RtoK}}$ could be concentrated to $\sim$250 mg/mL using a 3-kDa molecular mass cutoff (MWCO) Amicon Ultra 4-mL filters at 4,000 × g at room temperature. To reach concentrations in excess of 250 mg/mL, samples were centrifuged at 10,000 × g at room temperature in Sartorius VivaSpin 500 centrifugal concentrators (3.0-kDa MWCO). Samples were retrieved from 500 $\mu$L concentrators by centrifuging the inverted concentrator in a 1.5-mL tube. Sample concentrations were obtained from absorption measurements at 280 nm using an extinction coefficient of 23, 950 ${\text{M}}^{-1}{\text{cm}}^{-1}$ (Phase Diagram of Ddx4).

Phase-separated NMR samples.

Phase separation was induced by dialysis of a high concentration of Ddx4 in 20 mM NaPi, 1 M NaCl, and 5 mM TCEP, pH 6.5 into a buffer containing 20 mM NaPi, 100 mM NaCl, and 5 mM TCEP, pH 6.5. Phase separation occurs in the dialysis container in the form of small droplets, which then coalesce into a single large drop that can be transferred to either 3-mm tubes (Wilmad) or 5-mm Shigemi tubes to perform NMR measurements. Typically, ∼50 mL of 200 $\mu$M Ddx4 was dialyzed against 4 L NMR buffer to produce one NMR sample. Samples were gently centrifuged in the NMR tube and allowed to equilibrate at 30 °C for a minimum of 24 h.

Small molecule diffusion in viscogen.

BSA and HEWL samples were prepared by dissolving lyophilized protein powder (purchased from Sigma and BioBasic, respectively) in 20 mM NaPi, 100 mM NaCl, and 90% H₂O/10% D²O, pH 6.5 (BSA) or 20 mM ${\text{Na}}_3{\text{C}}_6{\text{H}}_5{\text{O}}_7$ (sodium citrate) and 100 mM NaCl, pH 5 (HEWL). The different buffer systems reflect the poor solubility of HEWL in NaPi buffer. Small molecule probes were added at a concentration of 2–10 mM, and experiments were repeated at a pair of concentrations to ensure that there were no interactions between probes and protein viscogens; ¹³C isotopically labeled small molecules (Fig. 6 shows the list) were generously donated by Cambridge Isotope Laboratories.

Phase Diagram of Ddx4.

Phase diagrams or coexistence curves (temperature vs. concentration) were constructed for Ddx4 and $\text{Ddx}{4}_{\text{CS}}$ over a range of NaCl concentrations. Initially, the two phases of the demixed sample were dispersed by pipetting up and down until a milky dispersion was formed. Equal volumes ($\sim$200 $\mu$L) of sample were then incubated in triplicate at the desired temperature using a PCR thermocycler with a heated lid (90 °C) for at least 1 h before measurement. Subsequently, samples were briefly centrifuged (<15 s at 10,000 × g) to ensure full coalescence of phase-separated droplets comprising the condensed phase at the bottom of the tube. For concentration measurements, dilutions were made into 6 M Gdm HCl and 20 mM NaPi, pH 6.5. Measurements of the dilute (top) phase were made on samples of 10 $\mu$L removed from each tube and diluted 10-fold. For the condensed (bottom) phase, 2 or 10 $\mu$L were diluted 250- to 500-fold. Absorbance at 280 nm was converted to concentration (milligrams per milliliter) using the Beer–Lambert law with a predicted extinction coefficient $(ϵ)$ of 23,950 ${\text{M}}^{-1}{\text{cm}}^{-1}$ (61) using molecular masses of 25,833, 24,768, 25,161, and 25,833 Da for WT Ddx4, 14FtoA, 24RtoK, and charge scrambled Ddx4, respectively. The reported concentrations and errors are means and SDs of triplicate measurements, respectively. The procedure for fitting to the Flory–Huggins model is described in SI Materials and Methods and Fig. S7.

Details of the NMR experiments are provided in SI Materials and Methods.