Significance
Computational and structural studies of putative Diels–Alderases and the reactions that they catalyze have provided testable models of the reaction coordinates and mechanisms of catalysis; however, there has yet to be a direct experimental interrogation of these hypotheses. Herein, the -secondary deuterium kinetic isotope effects at all sites of rehybridization on the nonenzymatic and SpnF-catalyzed [4+2]-cycloaddition during biosynthesis of spinosyn A are reported. Results implicate an intermediary state between formation of the first and second carbon–carbon bonds and provide evidence that conformational restriction of the substrate may play a role in catalysis.
Keywords: Diels–Alderase, isotope effect, enzyme, spinosyn, Bayesian analysis
Abstract
The Diels–Alder reaction is one of the most common methods to chemically synthesize a six-membered carbocycle. While it has long been speculated that the cyclohexene moiety found in many secondary metabolites is also introduced via similar chemistry, the enzyme SpnF involved in the biosynthesis of the insecticide spinosyn A in Saccharopolyspora spinosa is the first enzyme for which catalysis of an intramolecular -cycloaddition has been experimentally verified as its only known function. Since its discovery, a number of additional standalone -cyclases have been reported as potential Diels–Alderases; however, whether their catalytic cycles involve a concerted or stepwise cyclization mechanism has not been addressed experimentally. Here, we report direct experimental interrogation of the reaction coordinate for the -carbocyclase SpnF via the measurement of -secondary deuterium kinetic isotope effects (KIEs) at all sites of rehybridization for both the nonenzymatic and enzyme-catalyzed cyclization of the SpnF substrate. The measured KIEs for the nonenzymatic reaction are consistent with previous computational results implicating an intermediary state between formation of the first and second carbon–carbon bonds. The KIEs measured for the enzymatic reaction suggest a similar mechanism of cyclization within the enzyme active site; however, there is evidence that conformational restriction of the substrate may play a role in catalysis.
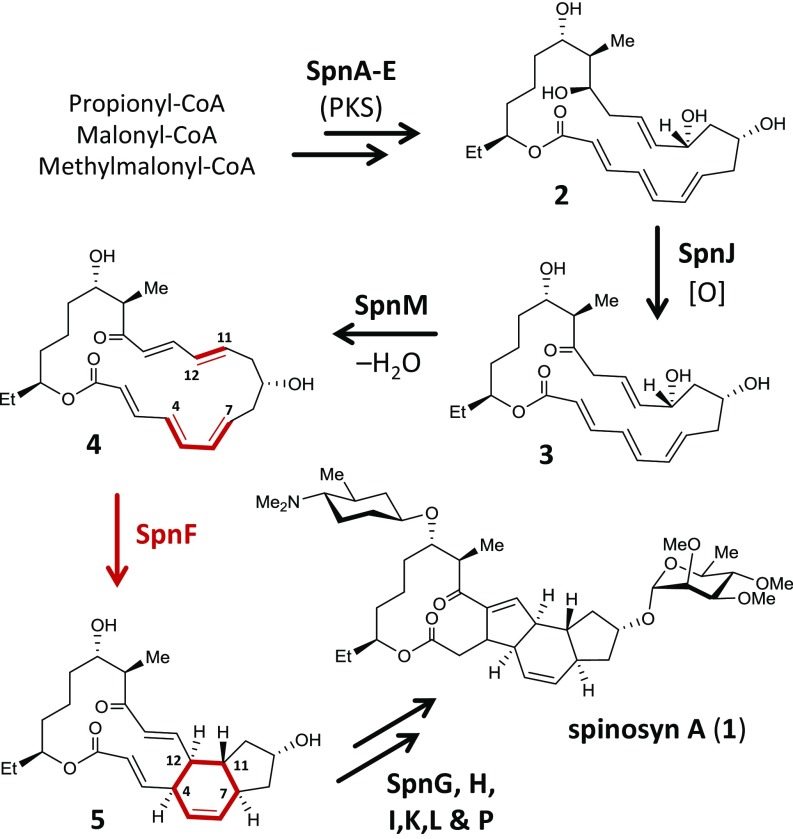
The enzyme SpnF from Saccharopolyspora spinosa catalyzes an intramolecular -cycloaddition (4 5) during biosynthesis of the insecticide spinosyn A (1) (Fig. 1) (1, 2). At the time of its discovery, the search for a naturally selected Diels–Alderase had already led to the characterization of several enzymes proposed to catalyze -cycloadditions (3). In all cases, however, these potential Diels–Alderases were found to be multifunctional, often catalyzing a priming reaction that activates the substrate toward cyclization. Thus, the detailed mechanisms of cyclization and the catalytic roles played by the enzymes were unclear and difficult to address. In contrast, the priming reaction (3 → 4) during spinosyn A biosynthesis is catalyzed by the separate enzyme SpnM (1). The resulting 1, 4-dehydration product 4 can then undergo stereospecific cyclization in aqueous solution with a half-life of min at 300 K; however, in the presence of SpnF, a rate enhancement (i.e., ) of ∼500-fold is observed, making SpnF the first reported example of a standalone -carbocyclase (1). This separation of activities has made SpnF an ideal system for mechanistic study.
Fig. 1.
Biosynthetic pathway of spinosyn A in S. spinosa (1, 2). SpnA–E together constitute a polyketide synthase (PKS) system.
Since the discovery of SpnF, a number of additional enzymes, such as VtsJ (4), PyrI4 (5), PyrE3 (5), TclM (6), TbtD (7), and AbyU (8), have been characterized as uniquely catalyzing -cycloadditions; however, investigation of these enzymes has been limited primarily to crystallographic and computational studies in large part because of the structural complexity of their substrates and the limited options available to study the mechanisms of biological cycloaddition reactions (3). For the purposes of the following discussion, we regard an intermediate as a local minimum in the free energy along the reaction coordinate and a concerted cyclization as one lacking any such intermediate. Consequently, there has yet to be a direct experimental interrogation of the reaction coordinates that defines whether the catalytic cycles of these -carbocyclases proceed via concerted or stepwise mechanisms.
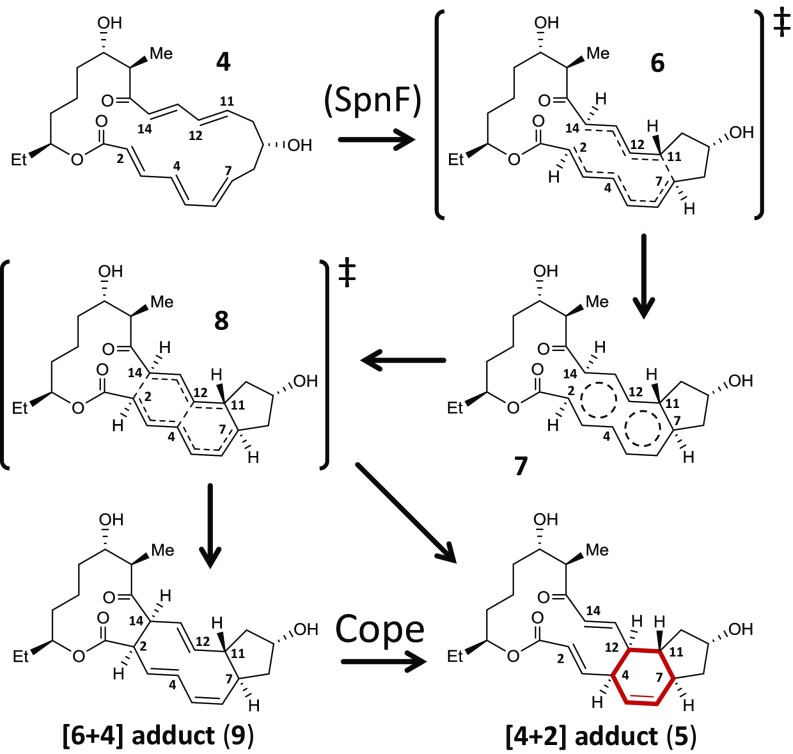
Development of a convergent synthetic strategy (2) has made it possible to prepare isotopologs of the SpnF substrate, allowing study of the SpnF reaction via the measurement of secondary deuterium kinetic isotope effects (KIEs). Previous chemical model studies have indicated that concerted formation of both C–C bonds in a -cycloaddition reaction (e.g., the C4–C12 and C7–C11 bonds in 1) should result in inverse deuterium KIEs of about 5% at all four carbons undergoing to rehybridization (9, 10). In contrast, if cyclization is stepwise, with the first step most rate-limiting, then unit to normal isotope effects would be expected for carbons involved in the second bond formation (9, 11). Since a stepwise intramolecular cyclization for the SpnF-catalyzed cycloaddition (Fig. 2) is expected to proceed with C7–C11 bond formation first, the C4D and C12D secondary deuterium KIEs are of particular interest in determining the sequence of bond formation. With this goal in mind, we prepared four site-specifically deuterated isotopologs of 4 (C4D, C7D, C11D, and C12D) and measured the corresponding secondary deuterium KIEs on both the nonenzymatic and enzyme-catalyzed reactions. The C2D and C14D isotopologs were also prepared to assess the possible involvement of these two carbon centers in the cyclization reaction as predicted by a recent computational investigation (12).
Fig. 2.
Mechanistic proposal for the -cycloaddition of the SpnF substrate 4. Lewis structures represent putative local minima (intermediates) and maxima (transition states) along the generalized free energy curves of the bifurcating reaction coordinate.
Results and Discussion
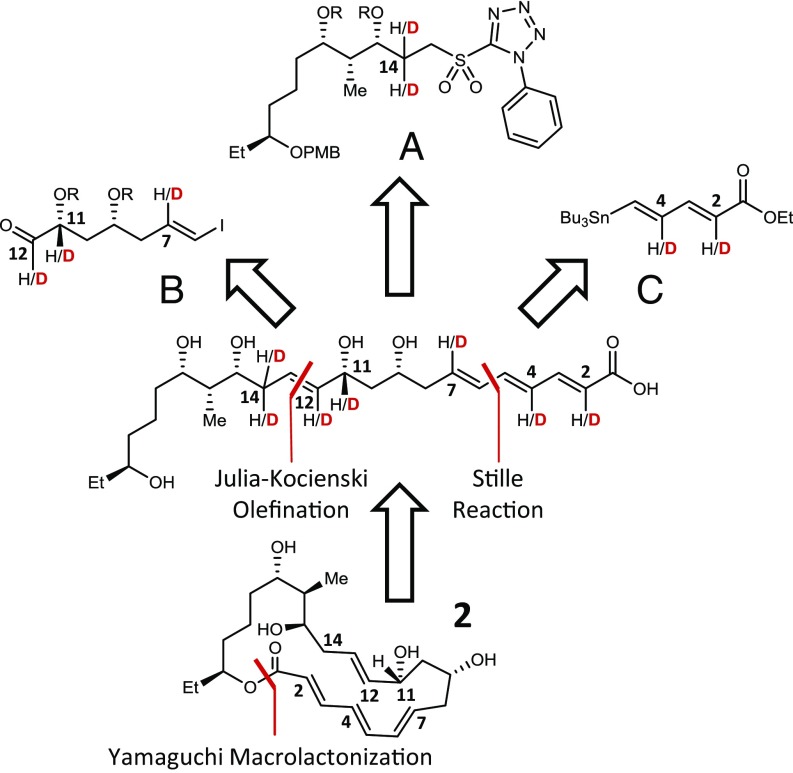
The site-specific KIEs were measured using the method of internal competition (14) and whole-molecule MS to monitor changes in the isotopolog enrichment of residual substrate (15–17). As discussed in SI Appendix, SI Text, this approach requires using isotopically enriched substrates to enhance observable changes in isotopolog populations and minimize any measurement bias caused by natural abundance labeling. Natural abundance and site-specifically deuterated isotopologs of the macrolactone 2 were prepared by connecting the three fragments A, B, and C via two C–C bond coupling reactions as shown in Fig. 3. A Julia–Kocienski olefination between fragments A and B yielded the -(E) olefin, and a palladium-catalyzed Stille coupling with fragment C led to the C-5/C-6 linkage. Subsequent cyclization of the resulting linear polyketide by Yamaguchi macrolactonization completed the assembly of 2. The corresponding SpnM substrate (3) was then prepared and isolated from reactions with the biosynthetic enzyme SpnJ (18). This modular synthetic approach facilitated preparation of the six isotopologs of 3 by incorporating the appropriately deuterated fragments (A–C) as detailed in SI Appendix, SI Text.
Fig. 3.
Modular, retrosynthetic design for the preparation of natural abundance and site-specifically deuterated isotopologs of 2. Carbons are numbered according to their final position in the macrolactone. Full synthetic schemata and protocols are provided in SI Appendix, SI Text and Figs. S5–S7.
Addition of SpnM to a mixture of natural abundance 3 and a site-specifically deuterated isotopolog in /DMSO at 30 °C generated the isotopically enriched 4 in situ. After complete consumption of 3, residual 4 was isolated by HPLC from six reaction aliquots spanning ∼10–90% conversion of 4 to 5 in the presence of sufficient SpnF to ensure that reaction flux is predominantly through the enzyme-catalyzed reaction. Parallel experiments were also performed in the absence of SpnF to study the nonenzyme-catalyzed cyclization. The observed isotopolog ratio of each isolated sample of residual SpnF substrate (4) was then determined by electrospray ionization time-of-flight MS by taking the ratio of the and peak intensities for the sodiated ion of 4 and correcting for natural abundance labeling (19). Experimental and analytical details are provided in Materials and Methods. At least three experimental trials, each consisting of approximately six isolated samples of residual 4, were performed for all site-specific KIEs measured.
Since the expected secondary KIEs are all near unity, the ratio of isotopolog concentrations in the residual starting material (heavy over light) can be expressed as a function of the fraction of reaction parameterized in terms of the isotope effect and initial enrichment ratio according to (20)
| [1] |
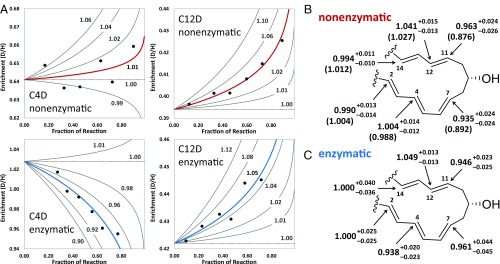
We used a hierarchical Bayesian regression analysis using Markov chain Monte Carlo (MCMC) (21, 22) rather than least squares fitting of Eq. 1 to model uncertainty in the measured KIEs caused by both within- and between-experiment variation while at the same time, estimating posterior probability distributions for the KIEs. Details regarding this analysis, including construction of priors, are described in Materials and Methods. Fig. 4 lists posterior point estimates of the site-specific KIEs as well as examples of enrichment plots for the C4D and C12D labeling patterns. The full dataset and simulated posterior marginal probability distributions of the KIEs are provided in SI Appendix, Figs. S3 and S4 and Tables S2 and S3.
Fig. 4.
Summary of the secondary deuterium KIEs on the enzymatic and nonenzymatic cyclization of 4. (A) Examples of enrichment plots from experimental trials for the C4D and C12D KIEs for both the nonenzymatic and enzymatic reactions. Black circles denote the observed enrichments (D/H, heavy over light) in the isolated residual substrate. Fitted lines (red/blue) are drawn using the median values of the posterior marginal probability distributions for the initial enrichment and KIE corresponding to the experimental trials shown (Materials and Methods). (B) Overall site-specific KIEs for the nonenzymatic reaction. Values are reported as the median (50th percentile) of the simulated posterior marginal probability distribution for each KIE along with the 68% highest posterior density interval (equivalent to ±1 SD about the median of a Gaussian distribution). Isotope effects computed from the gas-phase model system (13) at 300 K are shown in parentheses. (C) Site-specific KIEs for the SpnF-catalyzed cyclization with values reported as in B. The full simulated posterior marginal probability distributions of each KIE as well as all enrichment plots are shown in SI Appendix, Figs. S3 and S4.
Given a quasisteady state, the KIE on the cyclization of 4 to 5 in elementary reactions (steps) can be expressed as the weighted average
| [2] |
where is the effective KIE associated with progression from the reference state (i.e., 4 free in solution) to the th transition state, and is Ray’s sensitivity index for the th step (23–25). Each sensitivity index can be written as a reciprocal sum of forward and reverse commitments and reflects the degree to which a step may be considered “rate-limiting” (24, 25). Applied to the nonenzymatic reaction, the roughly 5% inverse values for and are indicative of partial C7–C11 bond formation in the transition state of the most rate-limiting step. Likewise, the values centered near unity for , , and suggest little to no rehybridization at these positions in this transition state compared with the reference state (4). The ∼4% normal value for may be explained by redistribution of electron density along the C11–C15 -system, leading to a loosening of the C12–H bonding environment (9, 11, 26).
These results are consistent with recent computational models of the reaction (12, 13, 27, 28). In particular, a simplified gas-phase model of the nonenzymatic reaction investigated by Hess and Smentek (13) identified a reaction coordinate with a single potential energy saddle point (similar to 6 in Fig. 2) followed by two apparent inflection points forming a caldera-like region. Subsequent computations by the Houk and Singleton laboratories using variational transition-state theory identified a local free energy minimum described as a -aromatic species (depicted as structure 7 in Fig. 2) residing about the caldera between two variational transition states along the reaction coordinate (12). The first of these transition states (6) is similar to that identified by Hess and Smentek (13), and the trajectory of 7 can bifurcate on progression through the second transition state (8) to form either a - or -cycloadduct (i.e., 5 vs. 9), where the latter then converts to 5 via a facile Cope rearrangement (12). The second of these transition states (8) is ∼2.3 kcal/mol lower in free energy compared with the first (12). This implies that the sensitivity index at 300 K for the first transition state is nearly 50-fold greater than that for the second (24, 25). In other words, conversion of 4 to 7 via 6 is predicted to be significantly rate-limiting in the nonenzymatic reaction.
The KIEs calculated from Hess and Smentek’s gas-phase models of 6 vs. 4 (13) are also shown in Fig. 4 and are directionally consistent with the observed values. Because of uncertainty in the measurements, there are ∼65 and 25% posterior probabilities that the and isotope effects, respectively, are between 0.90 and 0.95; however, the probability that they are less than 0.90 is no greater than 10% (SI Appendix, Fig. S3). Therefore, the reduced magnitude of and vs. the computed values suggests that the actual transition state (represented by 6) is likely earlier than that predicted by the computational gas-phase model. The KIEs are not consistent, however, with a pericyclic -transition state for a synchronous concerted cyclization, which would predict inverse effects at all four sites of rehybridization (9, 10, 29). In so far as the -aromatic state can be considered an intermediate following 6, these observations suggest that nonenzymatic cyclization of 4 may indeed be stepwise, albeit not in the usual sense of a biradical or dipolar intermediate. It should be emphasized, however, that the KIE measurements do not address existence of the -cycloadduct (9) along the reaction coordinate, because they only provide information regarding the first, more rate-limiting elementary reaction.
The enzymatic KIEs can also be interpreted in terms of Eq. 2, where corresponds to the isotope effect on for SpnF (14, 25). If substrate binding were the most rate-limiting (i.e., ), then roughly unit isotope effects would have been expected at all six positions. If product dissociation were the most rate-limiting (i.e., ), then the observed KIE would reflect the equilibrium isotope effect on rehybridization (23, 25), and four of six KIEs would be at least 5% inverse regardless of whether the product released is a - or -cycloadduct (9, 29). That these outcomes were not observed suggests that the intermediary steps of the catalytic cycle dominate the observed enzymatic isotope effects.
Unlike the nonenzymatic cyclization, computational study of the SpnF-catalyzed reaction has been hampered, because a structure of the SpnF–substrate complex is not yet available. Nevertheless, the enzymatic results largely mirror those for the nonenzymatic reaction with the exception of , which is notably inverse, whereas the value of is comparable with that of the nonenzymatic case as shown in Fig. 4. While the posterior marginal probability that is greater than 90%, the ∼5% normal value for argues against significant C4–C12 bond formation in the transition state of the most rate-limiting step. Structural investigations of the -carbocyclases SpnF, AbyU, and PyrE3 all implicate the formation of a closed complex on substrate binding into a largely hydrophobic active site (8, 30, 31). Therefore, the inverse value for may reflect conformational restriction of 4 within a low-volume active site of the Michaelis complex, resulting in a stiffer bonding environment for the C4–H center and an inverse binding isotope effect (32).
Conclusions
As the number of recognized -carbocyclases continues to grow, experimental interrogation of reaction coordinates proposed from structural and computational studies will be necessary for a complete mechanistic understanding of these enzymes. The experimental results and computational predictions are collectively most consistent with the hypothesis that the nonenzymatic cyclization of 4 involves an intermediary state before complete C4–C12 bond formation. A possible candidate for such an intermediate (i.e., local free energy minimum) is the -aromatic state (e.g., 7) identified in recent computational studies (12). The results also suggest that the SpnF-catalyzed reaction is similar to that of the nonenzymatic cyclization but likely involves a reduction in the entropy of activation after the substrate is bound in the active site, thereby facilitating catalysis and the observed rate enhancement (). These observations combined with prior structural investigations (8, 30, 31) suggest that -carbocyclases in general may operate, in part, by reducing the conformation space available to the cyclizing species in a closed, induced fit complex, a criteria worthy of consideration for de novo protein design/reengineering to develop Diels–Alderases in the future.
Materials and Methods
Synthesis of Deuterated Compounds.
Complete synthetic protocols and schemata (SI Appendix, Figs. S5–S7) for all deuterated compounds are provided in SI Appendix, SI Text.
Sample Preparation.
The -secondary deuterium KIE at each site of interest was measured using the method of internal competition (14) in at least three separate experimental trials. In each trial, site-specifically labeled and unlabeled SpnM substrates (3), which are stable, were mixed together (1.5 mM total concentration) in 50 mM Tris buffer (pH 8.0) containing 10% DMSO at 30 °C before adding SpnM. Initial ratios of the isotopologs were generally close to , although they ranged from no less than to no greater than . Reaction mixtures also included 0.47 mM p-methoxyacetophenone as an internal standard to standardize the observed HPLC peak integrations. The species 4 was generated in situ by the addition of SpnM to 16 M, which converts all of the observable SpnM substrate (3) to SpnF substrate (4) within ∼4 min. During this time, a by-product of the SpnM reaction with the same mass as 4 also forms; however, controls showed that, after its formation, this by-product is both stable and baseline-separated from 4 by HPLC.
No SpnF was present during measurement of nonenzymatic KIEs, and reaction aliquots were taken after all of the SpnM substrate had been consumed at six different time points ranging from ∼10 to 90% total reaction (∼90-min time course). Proportionately larger aliquots were taken at later time points to compensate for the reduced concentration of residual substrate. During measurement of enzymatic KIEs, SpnF was added after all of the SpnM substrate had been consumed and immediately before taking the initial quench. SpnF was added in sufficient quantity, so that the final quench at ∼80% total reaction was taken at min after adding SpnF (rationale is in SI Appendix, SI Text). In all other respects, the nonenzymatic and enzymatic samples were treated identically.
On removal, aliquots were quenched by mixing with MeCN containing 5% DMSO at 0 °C, which arrests both enzymatic and nonenzymatic cyclization. Protein was removed by centrifugation, and the residual substrate (4) was isolated using C18 reversed-phase HPLC (Varian Microsorb-MV; 100-5 C18 mm) with UV detection at 254 nm. The column was eluted with water (A) vs. MeCN (B) using the following gradient: start at 25% B, linear to 50% B in 35 min, linear to 70% B in 3 min, isocratic at 70% B for 2 min, and linear return to 25% B in 2 min. A solvent blank was run interposed between each HPLC separation to prevent memory effects. Isolated 4 was concentrated in a speed vacuum concentrator and redissolved in a mixture of MeCN and water for MS analysis. Aliquots of the isolated samples were also reanalyzed by HPLC to ensure that they were free of all other reaction products and by-products. Fractions of reaction were determined from HPLC peak integrations as described in SI Appendix along with an assessment of error in variables (SI Appendix, SI Text). Total sample sizes and outlier criteria are provided in SI Appendix, SI Text.
Isotopolog Enrichments.
Isolated residual substrate was analyzed by MS at the Laboratory for Biological Mass Spectrometry at Texas A&M University using a Waters SYNAPT G2 HDMS System in the positive ion high-sensitivity mode. Samples were first diluted using a 1:1 solution of MeOH: and injected at a flow rate of 0.5 L/min with signal averaging over 1-s intervals. Three 3-min continuous direct infusions were run in series for each sample. The first two 3-min infusions were used to flush the instrument to prevent memory effects. Data from these flushes were discarded. Signal intensities obtained from the third 3-min acquisition were averaged at each mass over the ∼175 spectra acquired to obtain a final spectrum for analysis. Control experiments did not show any evidence of ion fragmentation in the mass spectrometer, even at higher source ionization energies. All samples isolated in a given experimental trial were analyzed together without retuning of the instrument. Details regarding processing of MS spectra, correcting for natural abundance labeling, and an analysis of bias because of isotope effects from natural abundance labeling are provided in SI Appendix, SI Text. An example MS spectrum is shown in SI Appendix, Fig. S1.
Statistical Analysis.
Each of the 12 measured KIEs was analyzed independently of the others using a hierarchical Bayesian regression model (33, 34). If is the number of independent experimental trials for a given KIE, then the model involves parameters. At the highest level is the KIE of interest denoted , for which a log-normal prior was constructed with median 0 and variance 0.0325, which reparameterizes to
| [3] |
The distribution in Eq. 3 has a median of unity and ensures that the prior probability of lying on a positive interval is equal to the prior probability that it is on . This can be interpreted physically as treating positive and negative differences in the free energy of activation between two isotopogs equally. The variance of the log-normal distribution (0.0325) places ∼68% of the prior probability mass between KIEs of 0.83 and 1.20, consistent with previous reports of -secondary deuterium KIEs on rehybridization reactions at 300 K (9, 10, 29, 35–38). The prior also allows for the possibility of large KIEs, consistent with previous estimates of theoretical maxima (11, 29, 39) on the intervals and with a combined probability of 25%. Extreme KIEs that exceed the predicted maxima have a prior probability less than 5% with this prior. A sensitivity analysis described in SI Appendix, SI Text shows that the posterior inferences for were insensitive to changes in the scale of this prior, unless it was increased so as to include extreme values with significant probability.
Between-experiment variation is modeled by characterizing the th trial with its own observed isotope effect and initial enrichment . The prior probability distribution of is treated as uniform on , consistent with the experimental design, and is modeled as dependent on according to
| [4] |
where the error term is a truncated Gaussian random variable with scale and mode 0. The prior distributions for (conditional on and ) and are then given by
| [5a] |
| [5b] |
Based on previous recommendations for hierarchical analyses with small numbers of groups (40), a half-Cauchy distribution on with scale 0.2 was used for , which admits the possibility for large variation between experiments with significant probability. Sensitivity analysis indicated that doubling the scale from 0.2 to 0.4 had no meaningful impact on the posterior marginal probability intervals for . Finally, within-experiment variation is modeled as the SD about the regression, denoted , and the prior distribution for was uniform on support . The joint prior distribution is then given by
| [6] |
where denotes the vector of parameters, and denotes the vector of parameters.
The likelihood function is equal to the probability of the observed data conditional on the parameters. The likelihood function was thus constructed by modeling the th enrichment from the th experimental trial as
| [7] |
where the function is given by Eq. 1, is the th fraction of reaction in the th trial, and is the th th realization of the random Gaussian variable with mean zero and variance . Therefore, if and are vectors of the fractions of reaction and enrichment measurements in the th experimental trial, respectively, then the likelihood function based on the th experimental trial is given by
| [8] |
The likelihood function over all independent experimental trials is then just the product
| [9] |
where and are the fractions of reaction and enrichment vectors over all experimental trials. The posterior joint distribution of the parameters conditional on the observations is given by Bayes’ Theorem and is proportional to the product of the prior joint distribution in Eq. 6 and likelihood function in Eq. 9: that is,
| [10] |
because the distribution of is assumed to provide no information regarding the distribution of given (33).
MCMC (33, 34, 41, 42) was used to sample from the posterior joint distribution in Eq. 10 using the affine-invariant ensemble sampling algorithm proposed by Goodman and Weare (21) and implemented in Python as the emcee package (22). The emcee sampler uses an ensemble of walkers to generate separate MCMC chains. A total of 200 walkers were used for all experiments except the C7D enzymatic KIE, where the number was 246. Starting positions for the walkers were based on a Gaussian ball about the maximum likelihood estimate of the parameters under a linear approximation. Each walker was iterated 5,000 times after an initial equilibration period (burn-in) of 1,000 iterations, which were discarded. This produced a total sample size of at least points, which were used without thinning to construct the simulated posterior joint distribution. Effective sample sizes were calculated for each parameter from the autocorrelation times (22, 42) and found to be at least 10,000 for each parameter (SI Appendix, Tables S2 and S3), which is consistent with recommendations for interval estimation (34). Potential scale reduction factors (43) were calculated for each parameter and found to be less than 1.06 in all cases (SI Appendix, Tables S2 and S3), consistent with equilibration. In all cases, the mean acceptance fraction was between 0.3 and 0.5, indicating that the walkers were neither becoming trapped nor representative of a random walk (22). Visual inspection of randomly selected walker chains (SI Appendix, Fig. S2) indicated the absence of any apparent drift or trapping, which is in line with the quantitative evaluations. SI Appendix, Table S2 provides summary statistics for all parameters based on the simulated posterior joint distributions obtained in the analysis of each nonenzymatic KIE. SI Appendix, Table S3 does the same for each enzymatic KIE. Simulated posterior marginal distributions for each KIE (i.e., the parameter) as well as sampled curves from the posterior joint distribution are shown in SI Appendix, Figs. S3 and S4.
Computed KIEs.
Computational methods used to calculate KIEs are described in SI Appendix, SI Text.
Supplementary Material
Acknowledgments
We thank Ken Houk and Dan Singleton for helpful discussions during preparation of this manuscript. This work was supported by NIH Grant R01 GM040541 and Welch Foundation Grant F-1511.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1710496114/-/DCSupplemental.
References
- 1.Kim HJ, Ruszczycky MW, Choi Sh, Liu Yn, Liu Hw. Enzyme-catalysed [4 + 2] cycloaddition is a key step in the biosynthesis of spinosyn A. Nature. 2011;473:109–112. doi: 10.1038/nature09981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kim HJ, et al. Chemoenzymatic synthesis of spinosyn A. Angew Chem Int Ed. 2014;53:13553–13557. doi: 10.1002/anie.201407806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jeon BS, Wang SA, Ruszczycky MW, Liu Hw. Natural [4 + 2]-cyclases. Chem Rev. 2017;117:5367–5388. doi: 10.1021/acs.chemrev.6b00578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hashimoto T, et al. Biosynthesis of versipelostatin: Identification of an enzyme-catalyzed [4 + 2]-cycloaddition required for macrocyclization of spirotetronate-containing polyketides. J Am Chem Soc. 2015;137:572–575. doi: 10.1021/ja510711x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tian Z, et al. An enzymatic [4 + 2] cyclization cascade creates the pentacyclic core of pyrroindomycins. Nat Chem Biol. 2015;11:259–265. doi: 10.1038/nchembio.1769. [DOI] [PubMed] [Google Scholar]
- 6.Wever WJ, et al. Chemoenzymatic synthesis of thiazolyl peptide natural products featuring an enzyme-catalyzed formal [4 + 2] cycloaddition. J Am Chem Soc. 2015;137:3494–3497. doi: 10.1021/jacs.5b00940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hudson GA, Zhang Z, Tietz JI, Mitchell DA, van der Donk WA. In Vitro biosynthesis of the core scaffold of the thiopeptide thiomuracin. J Am Chem Soc. 2015;137:16012–16015. doi: 10.1021/jacs.5b10194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Byrne MJ, et al. The catalytic mechanism of a natural Diels-Alderase revealed in molecular detail. J Am Chem Soc. 2016;138:6095–6098. doi: 10.1021/jacs.6b00232. [DOI] [PubMed] [Google Scholar]
- 9.Storer JW, Raimondi L, Houk KN. Theoretical secondary kinetic isotope effects and the interpretation of transition state geometries. 2. The Diels-Alder reaction transition state geometry. J Am Chem Soc. 1994;116:9675–9683. [Google Scholar]
- 10.Beno BR, Houk KN, Singleton DA. Synchronous or asynchronous? An “experimental” transition state from a direct comparison of experimental and theoretical kinetic isotope effects for a Diels-Alder reaction. J Am Chem Soc. 1996;118:9984–9985. [Google Scholar]
- 11.Henderson RW, Pryor WA. Secondary hydrogen isotope effect for the transition from olefin to free radical. Int J Chem Kinet. 1972;4:325–330. [Google Scholar]
- 12.Patel A, et al. Dynamically complex [6 + 4] and [4 + 2] cycloadditions in the biosynthesis of spinosyn A. J Am Chem Soc. 2016;138:3631–3634. doi: 10.1021/jacs.6b00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hess BA, Jr, Smentek L. Concerted, highly asynchronous, enzyme-catalyzed [4 + 2] cycloaddition in the biosynthesis of spinosyn A; computational evidence. Org Biomol Chem. 2012;10:7503–7509. doi: 10.1039/c2ob25827g. [DOI] [PubMed] [Google Scholar]
- 14.Cleland WW. Use of isotope effects to elucidate enzyme mechanisms. Crit Rev Biochem. 1982;13:385–429. doi: 10.3109/10409238209108715. [DOI] [PubMed] [Google Scholar]
- 15.Cassano AG, et al. Inaccuracies in selected ion monitoring detemination of isotope ratios obviated by profile acquisition: Nucleotide 18O/16O measurements. Anal Biochem. 2007;367:28–39. doi: 10.1016/j.ab.2007.03.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Harris ME, et al. Kinetic isotope effects for RNA cleavage by 2′-O-transphosphorylation: Nucleophilic activation by specific base. J Am Chem Soc. 2010;132:11613–11621. doi: 10.1021/ja103550e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Berti PJ, Blanke SR, Schramm VL. Transition state structure for the hydrolysis of NAD+ catalyzed by diphtheria toxin. J Am Chem Soc. 1997;119:12079–12088. doi: 10.1021/ja971317a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim HJ, Pongdee R, Wu Q, Hong L, Liu Hw. The biosynthesis of spinosyn in Saccharopolyspora spinosa: Synthesis of the cross-bridging precursor and identification of the function of SpnJ. J Am Chem Soc. 2007;129:14582–14584. doi: 10.1021/ja076580i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang B, et al. Isotopologue distributions of peptide product ions by tandem mass spectrometry: Quantitation of low levels of deuterium incorporation. Anal Biochem. 2007;367:40–48. doi: 10.1016/j.ab.2007.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bigeleisen J, Wolfsberg M. Theoretical and experimental aspects of isotope effects in chemical kinetics. Adv Phys Chem. 1958;1:15–76. [Google Scholar]
- 21.Goodman J, Weare J. Ensemble samplers with affine invariance. Commun Appl Math Comput Sci. 2010;5:65–80. [Google Scholar]
- 22.Foreman-Mackey D, Hogg DW, Lang D, Goodman J. emcee: The MCMC hammer. Publ Astron Soc Pac. 2013;125:306–312. [Google Scholar]
- 23.Stein RL. Analysis of kinetic iosotpe effects on complex reactions utilizing the concept of the virtual transition state. J Org Chem. 1981;46:3328–3330. [Google Scholar]
- 24.Ray WJ., Jr Rate-limiting steps: A quantitative definition. Application to steady-state enzymic reactions. Biochemistry. 1983;22:4625–4637. doi: 10.1021/bi00289a003. [DOI] [PubMed] [Google Scholar]
- 25.Ruszczycky MW, Anderson VE. Interpretation of V/K isotope effects for enzymatic reactions exhibiting multiple isotopically sensitive steps. J Theor Biol. 2006;243:328–342. doi: 10.1016/j.jtbi.2006.06.022. [DOI] [PubMed] [Google Scholar]
- 26.Hout RF, Levi BA, Hehre WJ. A method for the calculation of normal-mode vibrational frequencies using symmetry coordinates. Application to the calculation of secondary deuterium isotope effects on carbocations. J Comp Chem. 1983;4:499–505. [Google Scholar]
- 27.Medvedev MG, et al. Quantifying possible routes for SpnF-catalyzed formal Diels-Alder cycloaddition. J Am Chem Soc. 2017;139:3942–3945. doi: 10.1021/jacs.6b13243. [DOI] [PubMed] [Google Scholar]
- 28.Gordeev EG, Ananikov VP. Computational study of a model system of enzyme-mediated [4 + 2] cycloaddition reaction. PLoS One. 2015;10:e0119984. doi: 10.1371/journal.pone.0119984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gajewski JJ, Peterson KB, Kagel JR, Huang YCJ. Transition-state structure variation in the Diels-Alder reaction from secondary deuterium kinetic isotope effects. The reaction of nearly symmetrical dienes and dienophiles is nearly synchronous. J Am Chem Soc. 1989;111:9078–9081. [Google Scholar]
- 30.Fage CD, et al. The structure of SpnF, a standalone enzyme that catalyzes [4 + 2] cycloaddition. Nat Chem Biol. 2015;11:256–258. doi: 10.1038/nchembio.1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zheng Q, et al. Enzyme-dependent [4 + 2] cycloaddition depends on lid-like interaction of the N-terminal sequence with the catalytic core in PyrI4. Cell Chem Biol. 2016;23:352–360. doi: 10.1016/j.chembiol.2016.01.005. [DOI] [PubMed] [Google Scholar]
- 32.Schramm VL. Binding isotope effects: Boon and bane. Curr Opin Chem Biol. 2007;11:529–536. doi: 10.1016/j.cbpa.2007.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gelman A, et al. Bayesian Data Analysis. 3rd Ed CRC; Boca Raton, FL: 2014. [Google Scholar]
- 34.Kruschke JK. Doing Bayesian Data Analysis. 2nd Ed Elsevier; London: 2015. [Google Scholar]
- 35.Singleton DA, Thomas AA. High-precision simultaneous determination of multiple small kinetic isotope effects at natural abundance. J Am Chem Soc. 1995;117:9357–9358. [Google Scholar]
- 36.Gajewski JJ, Peterson KB, Kagel JR. Transition-state structure variation in the Diels-Alder reaction from secondary deuterium kinetic isotope effects: The reaction of a nearly symmetrical diene and dienophile is nearly synchronous. J Am Chem Soc. 1987;109:5545–5546. [Google Scholar]
- 37.Seltzer S. The mechanism of the Diels-Alder reaction of 2-methylfuran with maleic anhydride. J Am Chem Soc. 1965;87:1534–1540. [Google Scholar]
- 38.Van Sickle DE, Rodin JO. The secondary deuterium isotope effect on the Diels-Alder reaction. J Am Chem Soc. 1964;86:3091–3094. [Google Scholar]
- 39.Streitwieser A, Jr, Jagow RH, Fahey RC, Suzuki S. Kinetic isotope effects in the acetolyses of deuterated cyclopentyl tosylates. J Am Chem Soc. 1958;80:2326–2332. [Google Scholar]
- 40.Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006;1:515–533. [Google Scholar]
- 41.MacKay DJC. Information Theory, Inference, and Learning Algorithms. Cambridge Univ Press; Cambridge, UK: 2003. [Google Scholar]
- 42.Kass RE, Carlin BP, Gelman A, Neal RM. Markov chain Monte Carlo: A roundtable discussion. Am Stat. 1998;52:93–100. [Google Scholar]
- 43.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Stat Sci. 1992;7:457–472. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.