Robust mechanobiological behavior emerges in heterogeneous myosin systems

Significance

Myosin proteins operate in complex coordinated systems to power muscle. There is a diversity of myosins that enable muscle responses with tuned force–velocity characteristics. Myosin structures may be altered and repurposed for nanotechnologies. We developed a computational model to compare myosin systems when multiple myosin types operate together (i.e. heterogeneous) or only a single type is present (i.e. homogeneous). The model predicts that modifying myosin chemical attachment and detachment rates may improve the robustness of a system to operate for a broad range of force conditions. In vitro experiments were conducted for force-loaded heterogeneous systems to validate computational predictions. The model suggests that in comparison with homogenous systems, heterogeneous systems have potentially advantageous and unique trade-offs for system robustness.

Abstract

Biological complexity presents challenges for understanding natural phenomenon and engineering new technologies, particularly in systems with molecular heterogeneity. Such complexity is present in myosin motor protein systems, and computational modeling is essential for determining how collective myosin interactions produce emergent system behavior. We develop a computational approach for altering myosin isoform parameters and their collective organization, and support predictions with in vitro experiments of motility assays with α-actinins as molecular force sensors. The computational approach models variations in single myosin molecular structure, system organization, and force stimuli to predict system behavior for filament velocity, energy consumption, and robustness. Robustness is the range of forces where a filament is expected to have continuous velocity and depends on used myosin system energy. Myosin systems are shown to have highly nonlinear behavior across force conditions that may be exploited at a systems level by combining slow and fast myosin isoforms heterogeneously. Results suggest some heterogeneous systems have lower energy use near stall conditions and greater energy consumption when unloaded, therefore promoting robustness. These heterogeneous system capabilities are unique in comparison with homogenous systems and potentially advantageous for high performance bionanotechnologies. Findings open doors at the intersections of mechanics and biology, particularly for understanding and treating myosin-related diseases and developing approaches for motor molecule-based technologies.

Biological systems are often dauntingly complex, with collective interactions of integrated molecular components, such as myosin motor proteins, producing emergent functionalities (1–4). Myosins work by converting chemical to mechanical energy through cyclical interactions with motile actin filaments (5) and aid muscle contraction (6), cytoskeleton reconfiguration (7), and active transport (8), while also being well-suited for bionanotechnologies (9–12). Myosin isoform variances (13, 14) impact physiological functioning (15–19) and provide an opportunity for altering myosin structures synthetically for tuned performance in designed systems (20). Modeling myosin systems is challenging since each myosin’s behavior is coupled to the aggregate interactions of all myosins interacting with a moving filament (21–24). When considering multiple myosin types (i.e., heterogeneous) interacting with a single filament (Fig. 1A), which is prevalent in muscle (25, 26), complexity is further increased. Here, we seek to develop an integrated computational and experimental approach to model diverse myosin populations, to reveal design principles governing favorable system performance.

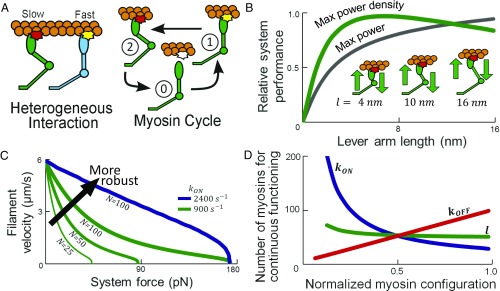
Fig. 1.

System behavior depends on myosin structure and behavior. (A) Heterogeneous myosin systems have contrasting isoforms interacting with a single filament, and myosins may cycle at different rates. (B) Maximum power output/density for systems of myosins with varied l. (C) Force–velocity when myosin number N or k_on varies; robustness improves as system dissociation is less likely. (D) Myosins required for continuous unloaded functionality with parameters perturbed independently from l = 10 nm, k_on = 900 s⁻¹, and k_off = 1,600 s⁻¹ normalized to l = 20 nm, k_on = 1,800 s⁻¹, and k_off = 3,200 s⁻¹.

Assay experiments have provided strong evidence for the hyperbolic force–velocity relationship of muscle, such that filament velocity decreases as force output increases. Computational approaches provide a basis for modeling experimental findings to predict system behaviors when myosin structure and system parameters are altered (27–30), with both analytical and simulation approaches used to predict system level behavior (Movies S1–S3). System-level analyses must be conducted based on the statistically expected behavior of all myosins within a system, since individual myosins behave stochastically. As long as simulations include a suitable number of myosins interacting with a filament (typically when two are attached to the filament on average), time-averaged assumptions are valid (31). Parameters used to describe myosins are based on differences in isoform structure and behavior, and through modeling can provide a basis for predicting performance in homogeneous and heterogenous systems with properties including force output, filament velocity, energy consumption, and system robustness (32, 33).

Robustness (i.e., capacity to retain system functioning once perturbed) may be calculated as a system’s capacity to operate with positive filament velocity, based on the stall force and average number of myosins in contact with the filament. The number of attached myosins is proportional to the average system energy consumption, where systems generally require greater amounts of energy to retain consistent contact between myosins and the filament to ensure the system does not dissociate when no myosins are attached (33). Experiments have demonstrated that heterogeneous myosin combinations bypass the law of averages when considering unloaded assay velocities in relation to relative concentration of two different types of myosin (34, 35). Here we hypothesize that modeling and exploring heterogeneous systems according to loaded force–velocity–energy relationships will enable discoveries of system configurations with advantageous trade-offs.

Our modeling begins by considering homogenous systems with existing experimental evidence as validation for force–velocity–energy performance predictions. Findings are used to investigate criteria to ensure a system remains functional (e.g., at least two myosins heads remain attached on average) as a measure of robustness. Robustness as a metric provides a basis for isolating potentially favorable conditions when mixing isoform types heterogeneously. New experiments are conducted to measure the heterogeneous force–velocity curve for model validation, followed by determining whether advantageous heterogeneous system configurations exist in comparison with achievable performance using only homogenous configurations. The approach opens doors for understanding myosin’s role in causing and treating disease, while additionally supporting the development of highly advantageous myosin nanotechnologies that exploit myosin biomechanical complexity favorably.

Results

Myosin Structure and System Behaviors.

The developed analytical model for describing steady-state myosin interactions with a filament traveling at velocity v was informed by the swinging lever arm theory (36, 37). Three parameters represent structural differences among isoforms: lever arm length l, chemical attachment rate to a nearby filament binding site k_on, and chemical detachment rate when negatively strained k_off (38–43). These parameters influence the behaviors mediating three myosin states: (0) detached with no force generation, (1) power-stroking with positive force generation that promotes filament motility, and (2) drag-stroking with negative force generation that impedes filament motility (Fig. 1A and Fig. S1). The model assumes myosins: operate collectively with a single myosin filament; use one ATP per cycle; are linear elastic elements with force proportional to the displacement of a myosin head relative to a hinge; and interact with the filament at binding sites spaced every 36 nm (44). These assumptions are validated by comparing the predicted time-averaged force–velocity behavior of chicken skeletal muscle (CS) myosins (l = 10 nm; k_on = 900 s⁻¹; k_off = 1,600 s⁻¹) with empirical data (SI Text, section S1).

Extrapolated parameter values are used to examine performance of designed synthetic myosins or naturally available isoforms (Fig. S2). In the current work, modeled myosins have l = 2 nm to l = 16 nm; lever arms longer than l = 16 nm bend significantly and are potentially not advantageous for actuation-based systems (45). The kinetics for myosins range considerably, with attachment and detachment rates varying 100-fold across isoforms (15, 16, 34, 46); plausible ranges of 100 s⁻¹ ≤ k_on ≤ 4,000 s⁻¹ and 100 s⁻¹ ≤ k_off ≤ 4,000 s⁻¹ are therefore used.

A system’s behavioral response is modeled by assuming a discrete number of myosins N interact with a motile actin filament that may have an additional applied force F_app. The operating velocity v_op, which is the expected filament velocity when all forces are balanced over time, is found by solving ${\mathit{F}}_{\mathrm{app}}={\displaystyle {\sum }_{\mathit{i}=1}^N\langle {\mathit{f}}_{\mathit{i}}\left({\mathit{v}}_{\mathrm{op}}\right)\rangle }$, where $\langle \mathit{f}\left(\mathit{v}\right)\rangle$ describes an isoform’s time-average force contribution. System power output may be solved through the force balance and is useful as a metric to determine whether extrapolations in myosin parameters have beneficial influences on system performance (SI Text, section S2).

Maximum system power was found by producing an entire force–velocity curve for each considered l, and varying F_app until the highest power output possible is recorded; power density is found by dividing by l added to an additional offset of 15 nm (Fig. 1B). A high power density occurs for l similar to the conserved ∼10 nm l of natural muscle myosin (44), and further increases to l lower power density, suggesting that evolutionary processes may have converged on the length because of its advantages. Findings suggest when designing high performance force-based myosin systems that alterations should modulate myosins based on kinetics rather than l, as additional changes in l for differing packing density assumptions do not suggest a significant performance increase (SI Text, section S2 and Fig. S3).

Optimized systems should retain consistent functioning for varied stimuli, as a kind of system robustness (32), and this occurs when there is typically at least one myosin attached to the system and the filament moves with a positive velocity relative to the myosins. Therefore, we define robustness as the range of force stimuli that ensures positive filament trajectories (i.e., F_app is less than the system stall force F_stall) for a continuously operating system. F_stall may be increased by adding more myosins to the system (47), which increases robustness (Fig. 1C). A system is considered to operate continuously when it is highly unlikely to dissociate during periods when no myosins are attached and the actin filament diffuses. Natural muscular systems sustain robustness because a high number of myosins interact with each filament. However, potential nanotechnologies may contain much smaller and/or static myosin populations, thus motivating a different approach to achieve high robustness and performance, such as increasing k_on (Fig. 1C). The increase in k_on improves robustness since there are more myosins attached to a filament on average. Having a greater number of myosins attached ensures continuous functioning over a broader range of force conditions, although each myosin may consume ATP at a faster rate since adding more myosins may result in significantly lower force generation required per myosin and, therefore, a faster filament velocity.

We propose that optimally configured systems contain a minimal number of myosins for continuous system functionality while not stalling, therefore ensuring low system ATP consumption and required volume. Experimental evidence suggests that continuous system behavior is generally maintained if at least two myosins are attached on average (31), and also ensures at least one myosin is typically in contact with the filament. The minimum number of myosins required for continuous system functionality is N_req = 2 / r(v), with r(v) being the duty ratio. N_req varies as isoform kinetics are altered, but not significantly for differences in l (Fig. 1D), further supporting the notion that altering l does not significantly improve system performance in these scenarios. Increases in k_off linearly increase N_req while an increase in k_on nonlinearly decreases N_req, with a smaller decrease occurring at higher k_on. These results suggest that determining the optimal isoform configuration requires careful tuning of myosin kinetics, since trade-offs among attachment and detachment rates will differ for varying system responses to applied forces.

System Behavioral Regimes.

The complex tradeoffs underlying system robustness may be simplified by expressing emergent system behaviors with energy considerations (33), in particular, by defining energy requirements E_req for continuous functioning over a range of forces and velocities that is compared with myosin isoform parameters using the equation: ${\mathit{E}}_{\mathrm{req}}\ge \frac{2\cdot \mathit{v}}{\mathit{l}\sin \mathrm{\theta }+v\cdot {\left({\mathit{k}}_{\mathrm{OFF}}\right)}^{-1}}.$ System energy consumption is based on the number of myosins and assuming myosins use one ATP per cycle. When E_req is compared with a system’s used energy E_sys, a critical system force F_crit (the lowest system force for a system to have continuous functioning) is found when E_sys (v_crit) = E_req (v_crit) to provide F_crit = F (v_crit) (SI Text, section S3).

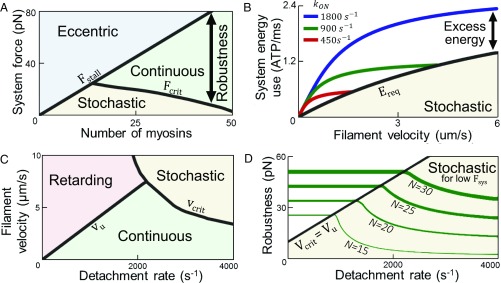
F_crit along with the stalling force, F_stall, define varied emergent system behaviors. When F_sys < F_crit, the system is considered stochastic since there is a greater than 10 percent chance of no myosins being attached to the filament. If F_crit < F_sys < F_stall, the system is considered continuous and is typically in the desired functional system state. When F_stall < F_sys, the system is considered eccentric as the force applied to the system is greater than maximum the force myosins produce, and results in a filament moving in the opposite direction of the myosin power stroke (Fig. 2A). Robustness Y_sys is quantified as the force range for continuous functioning with positive filament velocity and myosin force production that promotes motility according to Y_sys = F_stall − F_sys (v_crit). In Fig. 2A, Y_sys increases as more myosins are added to the system since F_stall is linearly poportional to the number of myosins. There is also an increase in Y_sys due to the greater E_sys resulting from more myosins being available to maintain continuous contact with a filament for a given operating velocity.

Fig. 2.

Robust functioning depends on system energy and velocity. (A) Eccentric, stochastic, and continuous behaviors emerge for varied myosin numbers and system forces. Robustness is the force range a system remains continuous. (B) Energy–velocity for unloaded systems of 50 myosins with varied attachment rates. E_req is the minimum energy for continuous functioning. (C) Retarding, stochastic, and continuous behaviors when detachment rate varies for homogeneous systems of 30 myosins. (D) Robustness as myosin number and detachment rate varies; systems are less robust when critical velocity v_crit is below the unloaded velocity v_u.

An alternate way of increasing Y_sys without increasing system size by adding more myosins is accomplished through increasing k_on (Fig. 2B). As k_on increases, E_sys increases as myosins consume ATP at a higher rate as they cycle more frequently, which, in turn, increases the number of myosins attached to the filament. Once E_sys exceeds E_req, the excess energy no longer increases Y_sys. After E_sys surpasses the energy required for unloaded system functioning, which is the fastest filament velocity for a homogeneous continuous system, further increases do not improve system survivability since it is already continuous. When a system reaches this energy threshold (i.e., the critical velocity is equal or greater than the unloaded velocity), Y_sys increases only as more myosins are added to the system due to the system being able to handle higher forces before stall.

Altering myosin k_off as system size remains constant influences Y_sys through altered energy requirements and attainable filament velocities (Fig. 2C). The unloaded velocity v_u is assumed to act as the maximum system velocity for calculating Y_sys, until the critical velocity becomes limiting as an indicator of when at least one myosin in the system is attached to the filament only 90% of the time. Y_sys may be increased by adding more myosins to the system (Fig. 2D). If there are not enough total myosins in the system to operate continuously at v_u, it is necessary to raise Y_sys by decreasing k_off.

In contrast, increases in k_on raise Y_sys and move the system toward a continuous functionality while v_u remains constant (Fig. S4), and may account for why myosin k_on and k_off have a positive correlation in natural isoforms (34). Across the observed influences of all parameters on homogeneous functioning, increased Y_sys always requires an (often detrimental) increased energy consumption, increased volume, or decreased v_u when Y_sys is not already equal to F_stall. These trade-offs and limitations for homogeneous systems motivate the consideration of heterogeneous systems that may favorably bypass limitations of homogeneous systems imposed by energy requirements.

Nonlinear Emergent Response in Heterogeneous Myosin Systems.

When myosins are mixed heterogeneously (Fig. 1A), it is possible to have myosin populations of two different isoform types behaving in contrasting emergent regimes while promoting an overall emergent systems behavior of continuous functioning. For instance, when fast myosin populations (i.e., high v_u) and slow myosin populations (i.e., low v_u) are mixed, the filament velocity may exceed the v_u of the slow isoform. The slow myosin population then contributes retardation forces to filament motility, although the filament maintains a positive velocity due to the force contributions of the fast myosin population. Retardation behavior occurs for the slow myosin population as the increased average attached time of myosins results in more force output during their drag stroke. The response of having one myosin population in a retarding regime while the other promotes continuous behavior could lead to an overall system response with favorable properties, such as increased robustness, while mitagating trade-offs with unfavorable properties, such as the required number of myosins or energy consumption.

Assessing the emergent response of heterogeneous systems requires consideration of myosin populations in both continuous and retarding regimes. These regimes are plotted in Fig. 3A for unloaded homogeneous systems with varied k_off. Nonlinearities promote higher velocity gains per force in the retarding regime, although the effect is reduced for myosins with low k_off. In heterogeneous systems, it is likely that only the myosin population with the lower k_off operates in the retarding regime. When systems are unloaded, the hyperbolic force–velocity relationship promotes a higher gain in velocity per force for the fast myosin population in comparison with the slow myosin population. The relationship suggests that force contributions of the fast myosins would outweigh the retardation of slow myosins, therefore promoting higher v_u than calculating averages would assume (i.e., calculating v_u as the mean v_u of all myosin types).

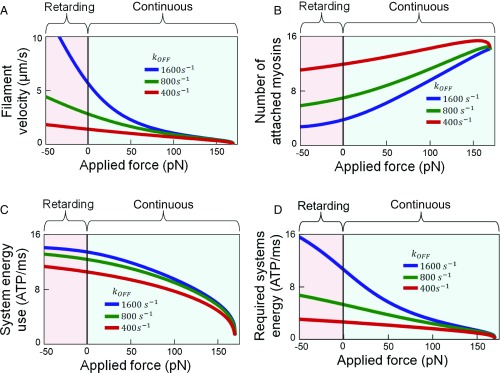
Fig. 3.

Homogeneous systems behave nonlinearly across force-based regimes. (A) Force–velocity for 100 myosins identical to CS myosin except for altered k_off. (B) Number of attached myosins. (C) System energy use and (D) required energy for these systems operating with retarding and continuous behaviors. There is a large nonlinear increase in required system energy for high k_off isoforms compared with low k_off isoforms.

Bypassing the law of averages suggests heterogeneous system responses that differ from homogeneous system capabilities, and are potentially beneficial when considering other nonlinearties that emerge from myosin heterogeneity such as energy–velocity relationships. A similar nonlinear relationship is demonstrated when considering the system performance with respect to the number of attached myosins N_att (Fig. 3B). Here, the values saturate in the retarding regime while N_att decreases nonlinearly with reduced force in the continuous regime. In heterogeneous systems, driving one myosin population toward the retarding regime may lower the overall number of myosins required for continuous system functioning for a given force.

System energy saturates in the retarding regime and is similar across isoforms of different k_on (Fig. 3C). Nonlinearities across regimes have profound effects when considering more complex system relationships such as required energy for continuous functionality E_req (Fig. 3D). Although all isoforms require similar E_req near stalling, when systems operate at low forces and high velocities, there is a sharp increase in E_req when myosins of high k_off are present, therefore limiting robustness when systems are limited by the number of required myosins for continuous functioning. These findings suggest there is an opportunity for designed heterogeneous systems to exploit nonlinearties in parameter relationships to improve performance with respect to one criteria (e.g., high filament velocity) while avoiding the negative trade-offs associated with changes to other performance variables (e.g., number of required myosins).

Testing Predictions of Heterogenous Response with in Vitro Experiments.

The response of heterogeneous systems with contrasting myosin isoforms is predicted by assuming myosins interact with a single filament that travels at the same steady-state velocity v relative to all myosins within a system, regardless of their isoform type. The force contributions of the first myosin isoform population $F_{\mathrm{A}}\left(v\right)={\displaystyle \sum _{i=1}^N}{f}_{\mathit{i}}\left(v\right)$ are aggregated with the second population $F_{\mathrm{B}}\left(v\right)={\displaystyle \sum _{i=1}^N}{f}_i\left(v\right)$ to find an operating velocity v_op that balances steady-state force contributions with an applied filament force such that F_app (v_op) = F_A (v_op) + F_B (v_op) (Movie S4).

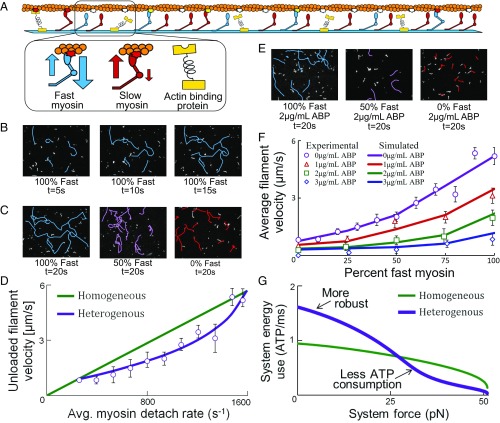
To validate our models of heterogeneous systems, in vitro experiments were conducted by combining fast/slow myosin isoforms and measuring their loaded response with α-actinin (48), an actin-binding protein that exerts a passive retarding force on actin (Fig. 4A and Movies S5–S9). α-Actinin is necessary for investigating the velocity response of heterogeneous systems over their entire force–velocity curves, otherwise the minimum reachable velocity of heterogeneous systems is limited to that of the slow isoform. Before conducting loaded and heterogeneous experiments, the homogeneous response of each system is measured in isolation to determine the minimum myosin concentration that enables continuous motility for each isoform. The filament velocity of CS myosin (fast myosin: k_on ≈ 90 s⁻¹; k_off ≈ 1,600 s⁻¹; Fig. 4B) and β pig cardiac muscle (PC) myosin (slow myosin: k_on ≈ 125 s⁻¹; k_off ≈ 250 s⁻¹) and their mixing (Fig. 4) were used to reverse engineer parameters describing each isoform (SI Text, section S4).

Fig. 4.

Heterogeneity produces advantageous energy efficiency and robustness. (A) Assay schematic of actin binding proteins (ABP) with fast/slow myosins. (B) Microscopy of tracked filaments for CS myosin (fast), and (C) as the relative concentration of PC myosin (slow) is increased. (D) Velocity for homogenous systems with varied detachment rates k_off and heterogeneous systems with average k_off of slow/fast myosins. Heterogeneous measurements (circles) obtained by varying PC (k_off = 250 s⁻¹) and CS (k_off = 1,600 s⁻¹) myosin concentrations. (E) Microscopy of tracked filaments for heterogenous myosins systems with ABP. (F) Filament velocity for systems of slow/fast myosins with ABP measured experimentally and simulated. (G) Energy–force for 30 myosin systems that are homogeneous (k_on = 900 s⁻¹, k_off = 1,600 s⁻¹) or heterogenous (50% k_on = 3,600 s⁻¹, k_off = 3,600 s⁻¹ and 50% k_on = 225 s⁻¹, k_off = 500 s⁻¹). Unique robustness and energy tradeoffs emerge with heterogeneity.

Heterogeneous system response is measured by proportionally mixing slow and fast myosins at different ratios while maintaining a constant total concentration. The measured and modeled system velocity was plotted with the average detachment rate of all myosins as an independent variable that is a predictor of v_u (Fig. 4D). In homogenous systems, k_off is expected to scale linearly with v_u (43), but for heterogeneous systems, the average k_off based on myosin composition does not scale linearly, and agrees with computational predictions that these systems should deviate from a law of averages. As predicted by the model, results are suggestive of the PC isoform operating in a retarding regime as the CS isoform operates in a continuous regime.

When α-actinin is introduced, filament motility is impeded (Fig. 4E). α-Actinin concentration is increased until a point when no filaments are motile and is indicative of the system stall force (48). There was no significant difference in stall force measurements between these myosin types (Fig. S5). The nonlinear force–velocity curve for heterogeneous systems is maintained as α-actinin is added in greater concentrations (Fig. 4F). Measurements agree well with the heterogeneous myosin model when molecular simulations (33) are used to decouple the α-actinin force contributions via a molecular rupture model (49) (SI Text, section S5, Figs. S6 and S7, and Movie S10). Results suggest the heterogeneous myosin model predictions are plausible over a range of forces, and the rule of averages is bypassed for loaded systems, building upon previous experiments that only considered unloaded heterogeneous systems (34, 35).

The computational model was then used to combine slow (k_on = 225 s⁻¹, k_off = 500 s⁻¹) and fast myosins (k_on = 3,600 s⁻¹, k_off = 3,600 s⁻¹) with highly contrasting kinetics in equal proportions for comparison with a homogenous system (k_on = 900 s⁻¹, k_off = 1,600 s⁻¹) that has a similar force–velocity curve and v_u of about 6 μm/s (SI Text, section S6 and Fig. S8). The heterogeneous system draws higher energy at v_u in comparison with the homogenous system and less energy at forces near stall that is potentially advantageous for systems with low numbers of myosins interacting with each actin filament. The advantage emerges due to the high energy consumption at unloaded conditions that ensures contact is maintained between myosins and the filament when at least two myosins are attached on average at v_u. The heterogeneous system beneficially operates with lower energy consumption at low velocities when the system is not limited by N_req. For the system of 30 myosins each in Fig. 4G, the homogenous system has a robustness Y_sys = 34.0 pN, while the heterogeneous system is higher with Y_sys = 40.8 pN. The nonlinear heterogeneous energy response is not achievable by homogenous systems (Fig. S9), since they do not have the same nonlinear parameter interactions that emerge from interactions of myosin populations in the retarding and continuous regime. These advantages are particularly important in volume-limited applications, such as actuation systems, where high performance is necessary based on myosin density.

Discussion

The developed model predicts complex system behaviors for myosin systems with varied isoform combinations. Results demonstrate unique system-wide behavior achieved through exploiting biomechanical pathways of two contrasting myosin isoform populations operating with a single filament. Namely, heterogeneous systems may attain higher robustness while retaining similar stall force and maximum filament velocities as homogeneous systems containing the same number of myosins. The greater robustness occurs as more myosin heads are proportionally attached for heterogeneous systems. These results are significant as they demonstrate potentially advantageous myosin systems within the bounds of trade-offs that typically limit attainable performance, such as hyperbolic force–velocity trade-offs and limitations in robustness for a given energy consumption. Findings demonstrate merits in using computational methods to integrate experimental findings to support the understanding of complex systems of motor molecules and their emergent behavior.

Experimental validation supports model accuracy for systems level behavior, and improves on past validation efforts when considering force–velocity, power, energy, and robustness (33, 44). The model is well-validated for homogeneous configurations when assuming myosins operate as linear elastic elements with one ATP consumption per cycle. The rule-based simulation provides a basis for decoupling behavior contributions from contrasting myosin isoforms and actin-binding proteins in a heterogenous system (17, 34, 35), and accurately predicts filament velocity for these complex assay systems. The model using α-actinin as molecular force sensors has expanded beyond past studies that only predicted α-actinin behavior’s influence on homogeneous myosin systems (50). Here, modeling parameters are fit by considering 26 different molecular combinations provided in Fig. 4F that suggest the model captures the complex force–velocity behavior over a broad range of conditions. These predictions provide a greater range of validity for mixed myosin force–velocity models in comparison with unloaded heterogeneous myosin assays that cannot measure force–velocity responses with filiment velocities lower than provided by a pure mixture of the slowest isoform.

Future modeling accuracy may be achieved by considering force dependencies of myosin kinetics and higher fidelity models of actin-binding proteins that possibly account for differences between experiment and models (49, 51, 52). Here, molecules were assumed to follow their most likely mechanochemical pathway, but there are multiple pathways to follow depending on a molecule’s state of attachment/detachment and stochasticity. Modeling these pathways could potentially improve accuracy, such as including the small chance of myosins detaching before their drag-stroke or force-dependent detachment. Further biochemical pathways for α-actinin may also be considered, such as stochastic release before bond rupturing. However, pathways with low chances of occurring are not expected to play a significant role for the force–velocity ranges of importance in this study that concentrates on systems-level phenomenon. Our assumptions are supported when considering detachment events because there are typically few myosins detaching before their drag stroke unless the system is nearing stall, and α-actinins generally have low kinetic detachment rates on the order of 10 s⁻¹ (53).

The level of agreement between model and experiment suggests the model provides a direction for thinking about system behavior that is experimentally well-validated across a broad range of isoform types. The approach provides an integration of models and experiments with insights for understanding emergent system behavior while highlighting potentially favorable system-wide configurations. Such approaches are crucial for building upon experiments that are necessarily limited in the number of parameters they may consider at once. Current findings illustrate the benefits of using computational approaches for analysis and synthesis of diverse experimental findings to decipher the complex behavior of myosin systems when considering the many achievable combinations of individual myosin parameters and system states.

The study provides a basis for a general methodology for examining aggregate biomechanical effects in complex biological systems, with potential applications for improved medical treatments and development of bionanotechnologies through understanding molecular heterogeneity. In particular, the current effort finds that contrasting isoforms operating in a single system can produce beneficial system-wide behavior not possible to achieve with either isoform independently. The coupled computational and experimental methods provide a basis for developing approaches in synthetic and systems biology to further investigate and design highly complex biomechanical systems.

Methods

Myosin Mathematical Modeling.

A three-state myosin mechanochemical model was developed that consists of (i) an unbound myosin attaching to an actin filament traveling at steady-state velocity v based on the myosin’s attachment rate k_on, (ii) the positive force generation of an attached myosin head that travels ${\mathrm{\delta }}_{+}=\mathit{l}-\sin \left(\theta \right)$ distance, and (iii) a negatively displaced myosin head traveling ${\mathrm{\delta }}_{-}\left(\mathit{v}\right)=\frac{\mathit{v}}{{\mathit{k}}_{\mathrm{off}}}$ distance before detaching according to the myosin’s detachment rate constant k_off.

The time-average force $\langle \mathit{f}\left(\mathit{v}\right)\rangle$ a myosin exerts depends on the time-average displacement of an attached myosin head x_e, stiffness κ, duty ratio r (i.e., percentage of time a myosin is attached), and total distance an actin moves relative to a myosin per cycle ${\mathrm{\Delta }}_{\mathrm{c}}\left(\mathit{v}\right),$ with

$$\langle \mathit{f}\left(\mathit{v}\right)\rangle =\mathrm{\kappa }\cdot \mathit{r}\left(\mathit{v}\right)\cdot {\mathit{x}}_{\mathrm{e}}\left(\mathit{v}\right);\hspace{1em}\text{where}\{\begin{array}{c}\mathrm{\kappa }=\frac{{\mathit{e}}_{\mathrm{atp}}}{\left({\delta }_{+}^2+{\delta }_{\mathrm{o}}^2\right)}\\ \mathit{r}\left(\mathit{v}\right)=\frac{{\delta }_{+}+{\mathrm{\delta }}_{-}\left(\mathit{v}\right)}{{\mathrm{\Delta }}_{\mathit{c}}\left(\mathit{v}\right)}\\ {\mathit{x}}_{\mathrm{e}}\left(\mathit{v}\right)=\frac{{\mathrm{\delta }}_{+}^2-2\cdot {\left({\mathrm{\delta }}_{-}\left(\mathit{v}\right)\right)}^2}{2\left({\mathrm{\delta }}_{+}+{\mathrm{\delta }}_{-}\left(\mathit{v}\right)\right)}\end{array}.$$ [1]

Additional equations and explanations are in SI Text, section S1.

Emergent System Behavior.

A system contains N number of independently configured myosins that each contribute a velocity-dependent time-average force f(v). When a force is applied to the filament F_app, there is a single operating filament velocity v_op found through numerical iteration when the applied force is balanced with myosin contributions:

$${\mathit{F}}_{\mathrm{app}}={\displaystyle {\sum }_{i=1}^N\langle {\mathit{f}}_i\left({\mathit{v}}_{\mathrm{op}}\right)\rangle }.$$ [2]

Emergent system behavior varies with a system’s operating velocity that depends on the structure of myosin isoforms and their organization. Regimes with qualitatively distinct systems behavior are differentiated based on the directionality of a system’s force and average number of attached myosins. A system tends to operate with continuous functionality if at least two myosins are attached on average N_att (v), and implies a system energy E_sys (v) relationship of

$${\mathit{E}}_{\mathrm{sys}}\left(\mathit{v}\right)\ge \frac{2\cdot \mathit{v}}{\mathit{l}\sin \mathrm{\theta }+\mathit{v}\cdot {\left({\mathit{k}}_{\mathrm{OFF}}\right)}^{-1}}$$ [3]

with a critical velocity v_c occurring at equality and representing the minimum velocity where continuous system functionality is expected. At lower velocities, the system is assumed to have a high likelihood of dissociation due to periods when no myosins are attached to the filament. Further details for determining emergent system behaviors are in SI Text, sections S2 and S3.

Motility Assay Experiments.

Experiments with in vitro motility assay experiments varied the relative concentrations of CS muscle and β PC myosins while holding the total myosin concentration constant (34, 35). Filament velocities were measured by tracking motile filaments recorded as image stacks at 30 fps with a Nikon Eclipse TE2000-U microscope. Filament velocity was determined for each isoform separately to determine the minimum concentration required to ensure continuous system functionality; the total myosin concentration was subsequently fixed at 100 µg/mL. Filament loading was accomplished by introducing α-actinin and increasing its concentration to 3 µg/mL, therefore enabling predictions of isometric myosin force from the index of retardation (48). Experimental methods and protocols are detailed in SI Text, section S4.

Rule-Based Molecular Simulations.

Filament velocities in motility assays with α-actinin were modeled with rule-based molecular simulations that have comparable quantitative predictions to the analytical model (1, 33). α-Actinin is assumed to generate force as a passive spring and detaches from the filament according to a maximum allowable displacement. The force contributions of individual molecules are summed for each time step and averaged until SE is negligible. Rules and parameters for describing myosin and α-actinin behavior were developed by comparing simulation results with empirical data and fitting model parameters to empirical measurements. The simulation provides a means for determining the applied force of α-actinins based on their concentration and the filament velocity, where the force contributions of α-actinins is equivalent to the sum of forces of homogenous or heterogeneous myosin systems. Simulation and modeling details are presented in SI Text, section S5 in addition to comparisons with the analytical model adapted for heterogeneous systems in SI Text, section S6.