A common challenge facing rhythmic biological processes is the adaptive regulation of central pattern generator (CPG) activity in response to sensory feedback. We apply dynamical systems tools to understand several properties of a closed-loop respiratory control model, including the coexistence of normal and pathological breathing, robustness to changes in metabolic demand, spontaneous autoresuscitation in response to hypoxia, and the distinct mechanisms that underlie rhythmogenesis in the intact control circuit vs. the isolated, open-loop CPG.
Keywords: autoresuscitation, central pattern generator, closed-loop control model, hypoxia, respiratory rhythm
Abstract
How sensory information influences the dynamics of rhythm generation varies across systems, and general principles for understanding this aspect of motor control are lacking. Determining the origin of respiratory rhythm generation is challenging because the mechanisms in a central circuit considered in isolation may be different from those in the intact organism. We analyze a closed-loop respiratory control model incorporating a central pattern generator (CPG), the Butera-Rinzel-Smith (BRS) model, together with lung mechanics, oxygen handling, and chemosensory components. We show that 1) embedding the BRS model neuron in a control loop creates a bistable system; 2) although closed-loop and open-loop (isolated) CPG systems both support eupnea-like bursting activity, they do so via distinct mechanisms; 3) chemosensory feedback in the closed loop improves robustness to variable metabolic demand; 4) the BRS model conductances provide an autoresuscitation mechanism for recovery from transient interruption of chemosensory feedback; and 5) the in vitro brain stem CPG slice responds to hypoxia with transient bursting that is qualitatively similar to in silico autoresuscitation. Bistability of bursting and tonic spiking in the closed-loop system corresponds to coexistence of eupnea-like breathing, with normal minute ventilation and blood oxygen level and a tachypnea-like state, with pathologically reduced minute ventilation and critically low blood oxygen. Disruption of the normal breathing rhythm, through either imposition of hypoxia or interruption of chemosensory feedback, can push the system from the eupneic state into the tachypneic state. We use geometric singular perturbation theory to analyze the system dynamics at the boundary separating eupnea-like and tachypnea-like outcomes.
NEW & NOTEWORTHY A common challenge facing rhythmic biological processes is the adaptive regulation of central pattern generator (CPG) activity in response to sensory feedback. We apply dynamical systems tools to understand several properties of a closed-loop respiratory control model, including the coexistence of normal and pathological breathing, robustness to changes in metabolic demand, spontaneous autoresuscitation in response to hypoxia, and the distinct mechanisms that underlie rhythmogenesis in the intact control circuit vs. the isolated, open-loop CPG.
sensory feedback is essential to guide the timing of rhythmic motor processes. How sensory information influences the dynamics of a central pattern-generating circuit varies from system to system, and general principles for understanding this aspect of rhythmic motor control are lacking. To complicate matters, the mechanism underlying rhythm generation in a central circuit when considered in isolation may be different from the mechanism underlying rhythmicity in the intact organism.
Despite decades of investigation, there remains little consensus about the mechanisms underlying sustained oscillations during respiratory rhythmogenesis in the brain stem. On one hand, it has been proposed that oscillations in the pre-Bötzinger complex (pBC) arise mainly from synchronized activity of endogenously bursting cells that interact in a highly coupled network and drive a population of amplifying follower cells (Smith et al. 2000). On the other hand, it has also been suggested that oscillations arise from network-dependent interactions of conditionally bursting cells (Feldman et al. 2013). More elaborate models have proposed that interactions between multiple brain stem areas are essential for generating and shaping breathing rhythms (Lindsey et al. 2012; Rybak et al. 2007; Smith et al. 2007). Without presuming to adjudicate between these alternatives, here we investigate an alternative hypothesis, namely that respiratory rhythms arise from the interplay of central rhythm generation circuits, biomechanics, and feedback from peripheral signaling pathways.
Our understanding of respiratory rhythmogenesis derives in large part from the pioneering work of Smith, Feldman, Ramirez, and others who demonstrated that the pBC can autonomously sustain respiratory-like oscillations in isolated brain stem slice preparations (Ramirez et al. 1997; Smith et al. 1991). However, it has long been observed that the mechanisms underlying oscillations in a central pattern generator (CPG) may differ fundamentally in the intact organism vs. a deafferented, isolated central circuit (Bässler 1986; Koshiya and Smith 1999). Here we investigate rhythmogenesis in a simple model of closed-loop respiratory control, incorporating biomechanics, oxygen handling, metabolism, and chemosensation. We show that eupnea-like oscillations arise from a distinct mechanism in the intact (closed loop) vs. isolated (open loop) systems. Specifically, we show the following: 1) During eupneic oscillations in the closed-loop model, the time-varying excitatory drive to the CPG (the control parameter gtonic) remains entirely in a domain that corresponds to quiescent behavior in the open-loop model with constant gtonic. 2) The frequency of respiratory oscillations in the isolated CPG system is controlled by the time constant for a persistent sodium current (τh), whereas the frequency of eupneic oscillations in the intact system is relatively insensitive to changes in τh. 3) In contrast, the frequency of breathing in the closed-loop model can be controlled by manipulating the frequency content of the time-varying excitatory drive feedback signal.
This report is organized as follows: We develop the model and analyze its behavior using averaging and open-loop/closed-loop control analysis; we demonstrate bistable states corresponding to coexistence of eupnea and tachypnea; and we show that imposed bouts of hypoxia, or sustained interruption of the chemosensory pathway monitoring arterial blood oxygen levels, can precipitate a dramatic transition from eupnea to tachypnea. However, for moderate bouts of hypoxia, or brief interruptions of chemosensory feedback, the endogenous properties of the ionic conductances in a standard CPG model (Butera et al. 1999a) can lead to spontaneous autoresuscitation.
A preliminary version of the model was presented at the 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (Diekman et al. 2012).
METHODS
Model Equations
Central pattern generator.
We adopt the Butera-Rinzel-Smith (BRS) model (“model 1” in Butera et al. 1999a) of bursting pacemaker neurons in the pBC as our CPG. We represent the CPG with a single BRS unit described by the membrane potential V and dynamical gating variables n [delayed-rectifying potassium (IK) activation], and h [persistent sodium (INap) inactivation]. Two “instantaneous” gating variables p∞ (INap activation) and m∞ [fast sodium (INa) activation] are set equal to their voltage-dependent asymptotic values; the INa inactivation gate is set equal to (1 − n). In addition, the model includes leak (IL) and tonic excitatory (Itonic) currents. The governing equations for the CPG are
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where C = 21 pF, gK = 11.2 nS, gNaP = 2.8 nS, gNa = 28 nS, gL = 2.8 nS, EK = −85 mV, ENa = 50 mV, EL = −65 mV, Etonic = 0 mV, θn = −29 mV, σn = −4 mV, θp = −40 mV, σp = −6 mV, σh = −48 mV, σh = 6 mV, θm = −34 mV, σm = −5 mV, = 10 ms, and = 10,000 ms.
Motor pool activity.
The membrane potential (V) of the CPG is an input to the respiratory musculature through synaptic activation of a motor unit (α):
| (11) |
| (12) |
where ra = rd = 0.001 mM−1 ms−1 sets the rise and decay rate of the synaptic conductance and [T] is the neurotransmitter concentration with Tmax = 1 mM, VT = 2 mV, and Kp = 5 mV (Ermentrout and Terman 2010).
Lung volume.
The motor unit drives changes in lung volume (volL):
| (13) |
where vol0 = 2 liters is the unloaded lung volume and E1 = 0.4 liter and E2 = 0.0025 ms−1 were chosen to give physiologically reasonable lung expansions (West 2008). The respiratory musculature acts as a low-pass filter: low-frequency bursting of the CPG drives discrete fluctuations in lung volume, but tonic spiking does not. This behavior is analogous to tetanic muscle contraction in response to high-frequency nerve stimulation (Kandel et al. 1991).
Lung oxygen.
External air at standard atmospheric pressure (760 mmHg) with 21% oxygen content will have a partial pressure of oxygen Pexto2 = 149.7 mmHg. When the lungs expand external air is inhaled, and we assume this fresh air mixes instantaneously with the air already in the lungs. The partial pressure of oxygen in the lung alveoli () will increase at a rate determined by the lung volume and the pressure difference between external and internal air. When the lungs are not expanding , there is no mixing of air. During both lung expansion and contraction, oxygen is being transferred to the blood at a rate determined by the time constant τLB = 500 ms and the difference between and the partial pressure of oxygen in the arterial blood (). Thus the change in is given by
| (14) |
where [x]+ denotes max(x, 0).
Blood oxygen.
Our model for blood oxygenation is given by
| (15) |
where the fluxes of oxygen from the lungs to the blood (JLB) and from the blood to the tissues (JBT) have units of moles of O2 per millisecond and the denominator converts changes in the number of moles of O2 in the blood to changes in . JLB depends on the difference in oxygen partial pressure between the lungs and the blood:
| (16) |
and is calculated with the ideal gas law PV = nRT, where n is the number of moles of O2, R = 62.364 l·mmHg·K−1·mol−1 is the universal gas constant, and T = 310 K is temperature.
JBT accounts for both dissolved and bound oxygen in the blood:
| (17) |
The concentration of dissolved oxygen in the blood is directly proportional to (known as Henry’s law), where the constant of proportionality is the blood solubility coefficient βo2 = 0.03 ml O2·liter blood−1·mmHg−1 for blood at 37°C. At physiological partial pressures ( from ~80 to 110 mmHg), the amount of dissolved O2 is far too small to meet the body’s metabolic demand for oxygen. The vast majority of oxygen stored in the blood is bound to hemoglobin (Hb). Hb has four cooperative oxygen binding sites, leading to the nonlinear (sigmoidal) Hb saturation curve :
| (18) |
| (19) |
where K = 26 mmHg and c = 2.5 are phenomenological parameters taken from Keener and Sneyd (2009).
The parameter M in Eq. 17 represents the rate of metabolic demand for oxygen from the tissues and unless stated otherwise is set at 8 × 10−6 ms−1. The conversion factors ζ and η in Eq. 15 and Eq. 17 depend on the concentration of Hb, [Hb] = 150 g/l, and the volume of blood, volB = 5 l, respectively. We assume a molar oxygen volume of 22.4 liters and that each fully saturated Hb molecule carries 1.36 ml of O2 per gram:
| (20) |
| (21) |
Chemosensation.
Peripheral chemoreceptors in the carotid bodies detect reductions in and transmit impulses to the central nervous system through the carotid sinus nerve. In humans, these chemoreceptors are responsible for the increase in ventilation that occurs in response to arterial hypoxemia (Hlastala and Berger 2001). Carotid body afferent fibers can adjust their firing rate rapidly (even within a respiratory cycle) due to small changes in blood gases (West 2008). There is a nonlinear relationship between the activity of carotid chemosensory nerve fibers and , with very little nerve activity until is reduced below 100 mmHg and then steep firing rate increases as is reduced further (Hlastala and Berger 2001; West 2008). We modeled this hypoxia chemosensory pathway with a sigmoidal relationship between and the conductance representing external drive to the CPG (gtonic). Increasing oxygen deficiency increases the respiratory drive:
| (22) |
where ϕ = 0.3 nS, θg = 85 mmHg, and σg = 30 mmHg. This conductance serves to “close the loop” in our respiratory control model, since Itonic = gtonic(V − Etonic) is a term in the CPG voltage Eq. 1.
The closed-loop model (Fig. 1) has the same overall structure as the model in Diekman et al. (2012). The blood oxygenation component of the model has been substantially revised to better reflect the basic physiology of oxygen transport and ensure conservation of mass.
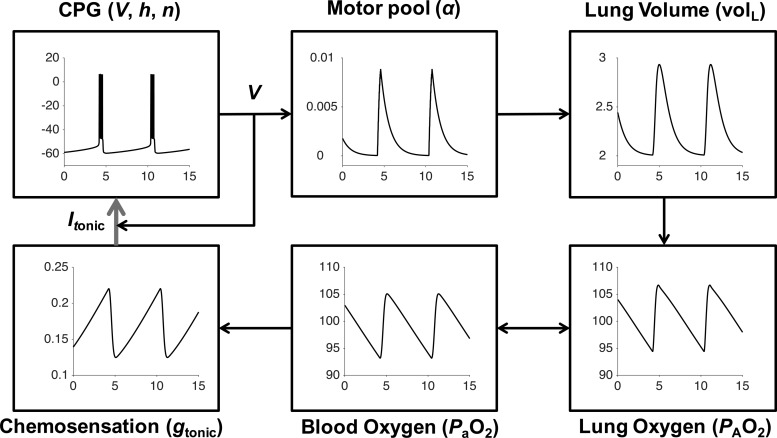
Fig. 1.
Schematic of closed-loop respiratory control model including neural, mechanical, and chemosensory components. Bursting oscillations of the brain stem CPG membrane potential (V) activate motor neurons (α) to cause increases in lung volume (volL) and inspiration. Inhaled air increases alveolar oxygen partial pressure (). Oxygen enters the bloodstream through gas exchange. Arterial oxygen partial pressure () is monitored by chemoreceptors that regulate input drive current (Itonic) to the CPG by modulating excitatory synaptic conductances (gtonic). This respiratory control circuit can maintain levels in the desired range around 100 mmHg.
Computational Platform
Numerical simulations were performed in MATLAB R2016a (MathWorks, Natick, MA) using the ode15s solver with absolute tolerance ≤ 10−9 and relative tolerance ≤ 10−6. Bifurcation diagrams were constructed with XPPAUT (Ermentrout 2002). MATLAB code used to generate all figures (except Fig. 11) is available in ModelDB (McDougal et al. 2017) under accession number 229640 at http://modeldb.yale.edu/229640, along with XPP code used to construct the bifurcation diagrams in Figs. 4 and 10.
Fig. 11.
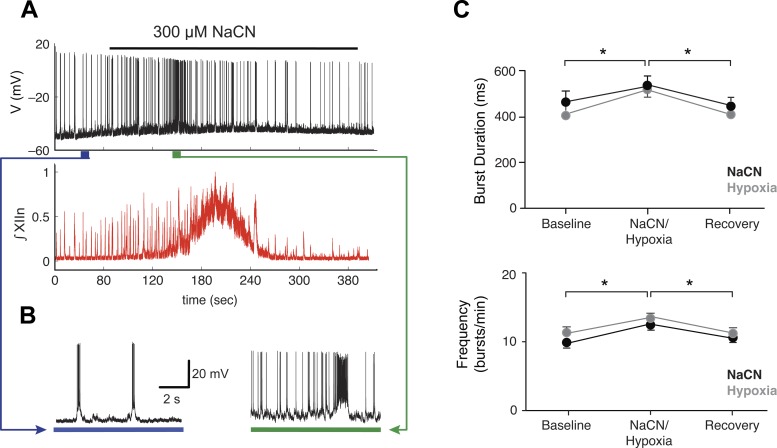
Hypoxia induces a barrage of spiking in vitro. A: application of 300 μM sodium cyanide (NaCN), a pharmacological analog of hypoxia, led to increased spiking in an individual pBC inspiratory cell recorded in current clamp (top) and increased network activity measured as hypoglossal nerve (XIIn) rootlet discharge (bottom) in a brain stem slice preparation. At the peak of the stimulation, phasic, coordinated drive is abolished. B: firing pattern of pBC cell before (left) and after (right) NaCN challenge. The depolarization and increased spiking that occur in response to the hypoxic perturbation in vitro are qualitatively similar to the responses observed in our closed-loop model. C: summary data from 9 experiments showing burst duration (top) and frequency (bottom) changes for baseline, NaCN treatment, hypoxia treatment, and recovery (n = 9, *P < 0.05 ANOVA, Tukey’s least significant difference as post hoc test, baseline vs. hypoxia or NaCN; error bars are SE). NaCN and hypoxia challenges do not result in statistically significantly different responses and produce an equivalent perturbation of the breathing rhythm in our in vitro slice preparations.
Fig. 4.
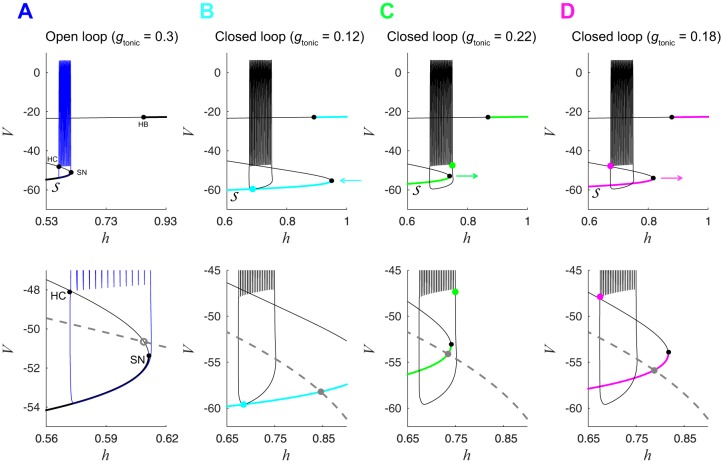
Closed-loop fast subsystem undergoes bifurcations differently than the open-loop fast subsystem. A, top: bifurcation diagram of open-loop fast subsystem with bifurcation parameter h and gtonic = 0.3 nS. Black curve shows stable (thick lines) and unstable (thin lines) fixed points of the fast subsystem. Solid black dots indicate saddle-node (SN), Hopf (HB), and homoclinic (HC) bifurcations of the fast subsystem. Blue trace is the bursting trajectory from the open-loop system projected onto the h-V plane. Bottom: zoomed-in view of image at top, also showing the h-nullcline (dashed gray line). Open gray dot is an unstable fixed point of the full CPG subsystem ; the bursting trajectory circumnavigates this unstable fixed point. Additional unstable fixed points located at (h = 0.20, V = −39) and (h = 0.02, V = −24) are not shown. B–D, top: bifurcation diagrams of closed-loop fast subsystem during silent phase (B), at the onset of spiking (C), and at the termination of spiking (D). Black trace is the closed-loop bursting trajectory, and gray curves show how shifts as gtonic varies during closed-loop bursting (the locations shown correspond to the points labeled B–D in Fig. 3). B: cyan dot shows the location of the trajectory at the minimum gtonic value (0.12 nS) observed during closed-loop bursting. Lower portion of and corresponding SN point are shifted to the right relative to the open-loop system, and the CPG is not spiking. Cyan arrow indicates that will move to the left as the trajectory evolves and gtonic increases through the remainder of the silent phase of the burst. C: green dot shows the location of trajectory at the maximum gtonic value (0.22 nS) observed during closed-loop bursting. Lower portion of and SN point are shifted to the left relative to B, and the CPG is about to start spiking. Green arrow indicates that will move to the right as the trajectory evolves and gtonic decreases, during the spiking phase of the burst. D: magenta dot shows the location of the trajectory at gtonic = 0.22, which is near the HC bifurcation that terminates spiking. Lower portion of is shifted to the left relative to B and to the right relative to C. Magenta arrow indicates that will continue to move to the right until reaching the minimum gtonic configuration shown in B. B–D, bottom: solid gray dots are stable fixed points of the full CPG subsystem . The trajectory does not circumnavigate these fixed points but exhibits bursting due to the movement of , the fast subsystem’s steady-state curve.
Fig. 10.
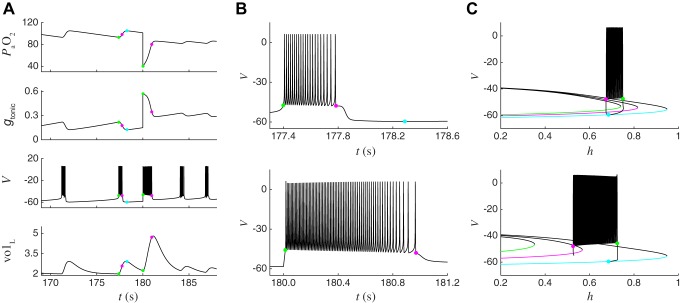
Hypoxia-induced barrage of spiking leads to an autoresuscitative lung expansion and is explained by the effect of hypoxia on the location of the homoclinic bifurcation that terminates spiking. A: traces from the closed-loop model during eupneic bursting (t < 180 s) and after a hypoxic perturbation (t > 180 s). At t = 180 s, (top) was set to 40 mmHg, which causes a large and immediate increase in gtonic (2nd from top). The increase in gtonic elicits a barrage of spiking (V, 3rd from top) that drives a much bigger increase in lung volume (volL, bottom) than occurs during a typical breath. This large breath causes a substantial increase in , which reduces gtonic sufficiently for the system to recover from the perturbation and return to eupneic bursting. Green and magenta dots indicate the values of system variables at initiation and termination of spiking during the last burst before the perturbation and the first burst after the perturbation, respectively. Cyan dot indicates the minimum gtonic point during eupneic closed-loop bursting. B: expanded view of voltage trace from A during the last burst before the hypoxic perturbation (top) and during the barrage of spiking induced by the perturbation (bottom). The burst induced by the perturbation is longer and consists of higher-frequency spiking than the burst before the perturbation. C: bifurcation diagram of BRS model fast subsystem during the last burst before the hypoxic perturbation (top) and during the barrage of spiking induced by the perturbation (bottom). Top: black trace is the trajectory during closed-loop bursting, projected onto the V-h plane. Green, magenta, and cyan curves show the location of the fast subsystem steady states in its leftmost position, which occurs at the initiation of spiking (green, gtonic = 0.22 nS), at the homoclinic bifurcation that terminates spiking (magenta, gtonic = 0.18 nS), and at its rightmost position, which occurs at the gtonic minimum point (cyan, gtonic = 0.12 nS). Note that these 3 curves are the same as those shown in Fig. 4, B–D. Bottom: black trace is the trajectory during the barrage of spiking induced by the perturbation, projected onto the V-h plane. Green and magenta curves show the location of the fast subsystem steady states in its leftmost position, which occurs at the initiation of spiking (green, gtonic = 0.57 nS), and at the homoclinic bifurcation that terminates spiking (magenta, gtonic = 0.35 nS). Cyan curve is the same as at top. The drastic reduction in due to the hypoxic perturbation has shifted the green curve much further to the left (cf. top and bottom), enabling the CPG to fire more spikes (and at a higher frequency) before reaching the homoclinic bifurcation.
Animal Experiments
We used in vitro experiments to determine whether hypoxia exposure of pBC neurons mimicked some of the features observed in our model. We cut rhythmically active slices from Sprague-Dawley rat pups (postnatal days 0–5) anesthetized with 4% isoflurane in a ventilated hood. Once the animal reached a surgical plane of anesthesia (no withdrawal to tail or toe pinch), the skull and spinal column were exposed via a midline incision, a scalpel was used to decerebrate the pup, and the thorax/spinal column was transected at T1/T2. The spinal column and brain stem were then immersed in ice-cold artificial cerebrospinal fluid containing the following (in mM): 124 NaCl, 25 NaHCO3, 3 KCl, 1.5 CaCl2·2H2O, 1.0 MgSO4·7 H2O, 0.5 NaH2PO4·H2O, and 30 d-glucose, bubbled with carbogen (95% O2-5% CO2). We rapidly performed dorsal and ventral laminectomies to expose the neuraxis while preserving the cranial nerve rootlets. Rhythmically active brain stem slices were cut from the brain stem with a vibratome (Leica VT1000). We then transferred the slices to a low-volume chamber mounted on an upright microscope with IR-DIC optics and superfused the slice continuously with 95% O2-5% CO2 for at least 30 min before beginning our experiments. Extracellular potassium concentration was raised to 9 mM to generate a breathing rhythm comparable to an awake human (10–20 breaths/bursts per minute). We used whole cell patch-clamp recordings to assess the behavior of pBC neurons and the role that hypoxia/anoxia played in stimulating autoresuscitative transitions in these neurons. The in vitro slice preparation and electrophysiological recordings were performed as described previously (Koizumi et al. 2008; Smith et al. 1991). Briefly, inspiratory cells were acquired by making a tight seal (≥5 GΩ), breaking through to whole cell, and then switching to current clamp for hypoxia/sodium cyanide (NaCN). To test the role that hypoxia plays in altering rhythmic drive, we switched the gas used to bubble the perfusate to a hypoxic gas mixture (94% N2, 1% O2, 5% CO2) or added NaCN (300 μM) to the perfusate. Application of either hypoxia or NaCN challenge was for 1–3 min. All animal procedures were approved by the Institutional Animal Care and Use Committee of Case Western Reserve University.
RESULTS
Distinct Mechanisms Underlie Bursting in Isolated CPG and Closed-Loop Systems
The closed-loop model described in methods produces a stable eupnea-like breathing rhythm of ~10 breaths/min (Fig. 2A). The CPG components of the model comprise a three-dimensional (3D) subsystem (voltage, fast potassium activation gate n, and persistent sodium inactivation gate h) corresponding to the BRS INap pacemaker model. The isolated pacemaker can also produce a eupnea-like fictive breathing rhythm for a range of (fixed) excitatory conductances, with roughly 10 bursts/min when gtonic = 0.3 nS (Fig. 2B). However, despite similar timing of bursting in the intact and isolated systems, we find that distinct mechanisms underlie rhythmogenesis in these two scenarios. To establish this result, we perform the following analyses.
Fig. 2.
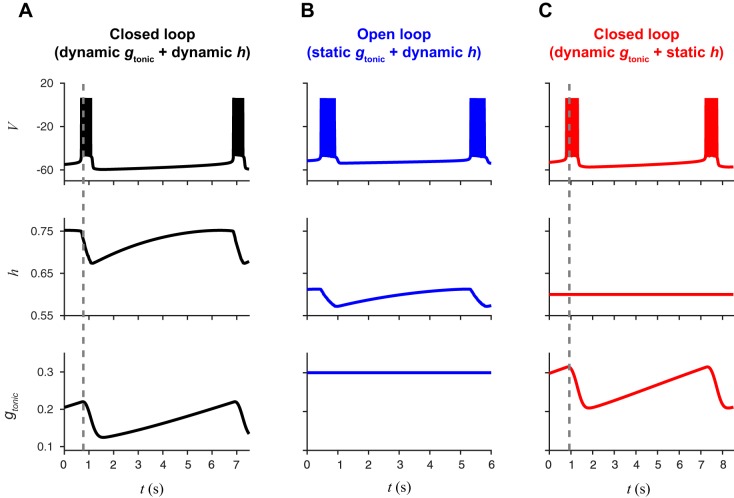
Closed-loop bursting persists in the absence of the isolated CPG bursting mechanism. A: black traces show bursts of action potentials (V, top) in the closed-loop model with persistent sodium channel inactivation (h, middle) as a dynamic variable and a dynamic gtonic (bottom) in response to changes in . B: blue traces show bursting in the open-loop model with h as a dynamic variable and gtonic set as a static parameter. C: red traces show bursting in a version of the closed-loop model where h is set as a static parameter. This illustrates that the dynamical mechanism responsible for bursting in the open-loop model (slow h dynamics) is not required for bursting in the closed-loop model.
-
1)
Compare the range of gtonic supporting bursting in the isolated (open loop) model vs. the values of gtonic attained during eupneic bursting in the intact model. We find that during eupneic bursting for the intact system the values of gtonic remain within the “quiescent” range for the isolated BRS model.
-
2)
Study the dynamics of bursting superimposed on the bifurcation structure of the (v, n, h) subsystem. Both the intact and isolated systems exhibit a fixed point near a saddle-node bifurcation; however, in the isolated system the fixed point is unstable (allowing spontaneous bursting) and in the intact system it is stable (requiring phasic chemosensory drive to support bursting).
-
3)
Compare the effect of accelerating or retarding the dynamics of the h gate in the isolated vs. the intact model. We find that rescaling causes proportionate changes in burst period in the isolated model but has little effect in the intact model. Moreover, the intact model supports eupneic bursting even when is infinitely large (h is held fixed as a constant).
-
4)
Study the sensitivity of burst timing to sensory input by rescaling the time course of gtonic. We find that rescaling the time course of gtonic proportionately changes the burst period.
Closed-loop bursting with “quiescent” gtonic.
Our model of closed-loop respiratory control includes neural, mechanical, and chemosensory components and is capable of producing a stable oscillatory solution that represents normal eupneic breathing. The operation of the closed-loop model is illustrated in Fig. 1. Bursts of action potential firing (V) of pBC neurons in the brain stem CPG activate a pool of motor neurons (α) that contract the diaphragm, causing the lungs to expand in volume (volL) and intake air. Inhaled oxygen increases the partial pressure of oxygen in the lung () and enters the bloodstream through gas exchange between alveoli and capillaries.
Peripheral chemoreceptors in the carotid body detect changes in the partial pressure of oxygen in the blood () and convey this information to the central nervous system by regulating the amount of excitatory input drive gtonic to the brain stem CPG. This chemosensory feedback closes the respiratory control loop and maintains levels around 100 mmHg.
If the connection between and the CPG is interrupted, then gtonic takes a fixed value and the isolated CPG corresponds to the canonical BRS model of pBC neurons in a well-studied regime (Best et al. 2005; Butera et al. 1999a, 1999b; Dunmyre et al. 2011). We refer to this as the “open-loop” system. For a range of gtonic values, bursting arises through fast activation and slow inactivation of a persistent sodium current, INaP. The timescale of bursting is controlled by the inactivation variable h, which must deinactivate sufficiently after a burst before the next burst can begin. With a maximal time constant of 10 s, both the closed-loop model and the open-loop model (with gtonic = 0.3 nS) exhibit burst periods of ~6 s (Fig. 2, A and B).
In the open-loop system, the dynamics of h are essential for bursting: if h were held constant, then the model can exhibit quiescence or repetitive spiking but is not capable of bursting. For example, with h held constant at 0.6, the isolated BRS model exhibits hyperpolarized quiescence for gtonic < 0.31, tonic spiking for 0.31 < gtonic < 1.64, bistability of tonic spiking and depolarized quiescence for 1.64 < gtonic < 2.57, and depolarized quiescence for gtonic > 2.57. In contrast, the dynamics of h are not essential for bursting in the closed-loop system, since fluctuation of gtonic in response to changes in also operates on the timescale of eupneic breathing. A reduced version of the closed-loop model where h is held constant at 0.6 produces bursting with a period of ~7 s (Fig. 2C). Thus closed-loop bursting does not require the dynamical mechanism responsible for bursting in the isolated CPG.
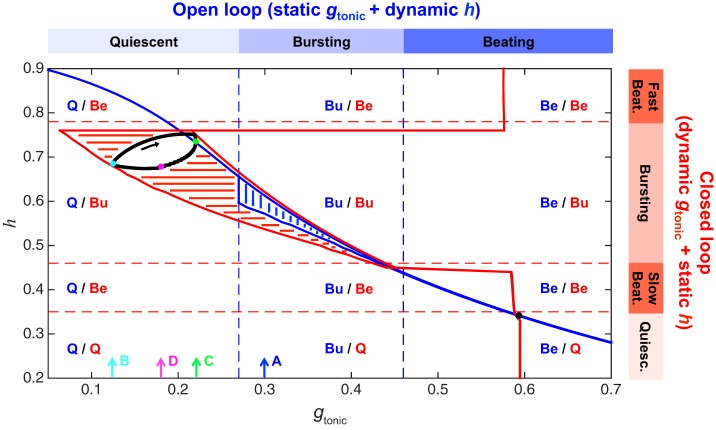
Additional evidence that distinct mechanisms underlie bursting in the open- and closed-loop models comes from the surprising observation that the closed-loop limit cycle exists entirely within the quiescent regime of the isolated CPG system. To compare the operation of the circuit in these different configurations, we conducted a series of simulations of the open-loop (static gtonic, dynamic h) model over a range of gtonic values and the reduced closed-loop (dynamic gtonic, static h) model over a range of h values (Fig. 3). The open-loop model exhibits quiescence if gtonic < 0.28 nS, bursting if 0.28 < gtonic < 0.44 nS, and beating if gtonic > 0.44 nS. The reduced closed-loop model exhibits quiescence if h < 0.3, slow beating if 0.3 < h < 0.45, bursting if 0.45 < h < 0.75, and fast beating if h > 0.75. One might naively predict that the limit cycle corresponding to eupneic bursting in the full closed-loop model (dynamic gtonic, dynamic h) would exist in the region corresponding to bursting in both the static gtonic and static h models (i.e., region labeled Bu/Bu in Fig. 3). Instead, we find that the closed-loop trajectory exhibits h values in the bursting region of the reduced closed-loop model but gtonic values that lie entirely within the quiescent region of the open-loop model (Fig. 3). Thus we observe a novel form of excitability in the canonical BRS model: a time-varying gtonic produces bursting despite the gtonic values remaining within the quiescent region (i.e., the maximum gtonic value observed during bursting in the closed-loop model is less than the minimum gtonic needed to obtain bursting in the open-loop model).
Fig. 3.
Closed-loop bursting exists in the quiescent regime of the isolated CPG system. Blue contour and vertical hatching indicate the range of values the dynamic variable h (x-axis) traverses as the static parameter gtonic (x-axis) is varied in the open-loop model. For example, with gtonic fixed at 0.3 nS, the CPG is bursting and h oscillates between 0.57 and 0.61. Blue dashed vertical lines demarcate regions of quiescence (Q), bursting (Bu), and beating (Be) in the open-loop model. Red contour and horizontal hatching indicate the range of values the variable gtonic traverses as the parameter h is varied in the version of the closed-loop model with dynamic gtonic and static h. For example, with h fixed at 0.6, the CPG is bursting and gtonic oscillates between 0.21 and 0.32 nS. Red dashed horizontal lines demarcate regions of quiescence, slow beating, bursting, and fast beating in this model. Black curve is the bursting trajectory of the full closed-loop model (with dynamic gtonic and dynamic h) projected onto the gtonic-h plane. Note that this limit cycle exists in the Q/Bu region, indicating that the gtonic values traversed during closed-loop bursting lie entirely within the range of gtonic values that produce quiescence in the open-loop model. Black arrow indicates the direction of flow on the closed-loop limit cycle. Cyan, green, and magenta dots (along with cyan, green, and magenta arrows labeled B, C, and D on the gtonic axis) denote 3 locations on the closed-loop limit cycle that are further illustrated in Fig. 4, B–D (where the same color scheme is used). Blue arrow labeled A corresponds to gtonic = 0.3 nS, which is the value used to further illustrate the open-loop limit cycle in Fig. 4A.
Bifurcation analysis.
To understand the distinct mechanisms of closed-loop bursting in more detail, Fig. 4 walks through the dynamics in a series of projections onto the V-h plane. The ability of the closed-loop system to exhibit bursting with a time-varying gtonic that is always less than the value of static gtonic required for bursting can be understood by considering the bifurcation structure of the BRS equations. Bursting consists of oscillations on two timescales: a slow alternation between silent and active phases and rapid spiking oscillations during the active phase. Models of bursting can be decomposed into a fast subsystem responsible for generating spikes and a slow subsystem that modulates spikes and the resting membrane potential (Ermentrout and Terman 2010). In the BRS model, h evolves on a slower timescale than V and n. Thus Eqs. 1 and 2 form the fast subsystem, which we denote , and Eq. 3 is the slow subsystem, which we denote . Different classes of bursting can be identified based on the types of bifurcations that occur in the fast subsystem to cause transitions between the silent and active phases when the slow variable is treated as a bifurcation parameter (Bertram et al. 1995; Rinzel 1987).
The BRS model is an example of “fold/homoclinic” bursting, where spiking initiates at a fold bifurcation and terminates at a homoclinic bifurcation (Izhikevich 2007). This type of bursting has also been called “square-wave” bursting since the shape of the membrane potential profile resembles a square wave (Fig. 2A). The steady states of the fast subsystem, i.e., points satisfying , form an S-shaped curve in the V-h plane that we denote . The lower branch of is stable and meets the middle branch of unstable fixed points at the lower knee (h = 0.61, V = −51.4), where a fold bifurcation occurs as shown in Fig. 4A. Another fold bifurcation, which is not shown in the figure, occurs at the upper knee (h = −1.56, V = −29.7), where the middle and upper branches of meet. The upper branch becomes stable through a subcritical Hopf bifurcation at (h = 0.92, V = −22.8). The branch of unstable periodic orbits that are born at this Hopf bifurcation coalesce with a branch of stable periodic orbits at the saddle node of periodic orbit bifurcation located at h = 1.17 (not shown). The stable branch of periodic orbits ends at the homoclinic bifurcation on the middle branch of at h = 0.57. During the silent phase of bursting, the trajectory is along the lower branch of at a stable fixed point of the fast subsystem. The hyperpolarized membrane potential causes the persistent sodium channel to deinactivate and h to increase. As h increases, the trajectory moves slowly to the right until the stable fixed point is destroyed at the fold bifurcation. At this point, the trajectory jumps up to the stable branch of periodic solutions and spiking begins. The depolarized membrane potential during spiking causes the persistent sodium channel to inactivate and h to decrease. As h decreases, the period of the limit cycle—and therefore the time between spikes—increases until spiking ends when the limit cycle merges with the invariant manifold of a saddle point at the homoclinic bifurcation. At this point, the trajectory jumps down to the stable branch of , ending the active phase of that burst and beginning the silent phase of the next burst. Throughout both phases of open-loop bursting, all fixed points of the full system (Eqs. 1–3) are unstable. This is indicated by all intersections of the h-nullcline (defined as ) occurring on unstable portions of (Fig. 4A, bottom).
In contrast, during closed-loop bursting the h-nullcline always intersects the stable lower branch of (Fig. 4, B–D, bottom). These stable fixed points of the full CPG subsystem correspond to gtonic taking values that would lead to stable quiescence in the isolated BRS model. However, in the closed-loop model, when the CPG is quiescent (as in Fig. 4B) then starts to fall, which causes gtonic to increase. Slowly increasing gtonic gradually shifts to the left, allowing the trajectory to jump up at the lower knee fold bifurcation and start spiking, even though the CPG fixed point remains stable (Fig. 4C). The spiking of the CPG eventually causes to increase, which in turn causes gtonic to decrease and shifts to the right, leading to the homoclinic bifurcation that terminates spiking (Fig. 4D). Thus, although the same bifurcations occur in the fast subsystem during both open- and closed-loop bursting, the time-varying nature of gtonic in the closed-loop system changes the way in which the bifurcations are approached in comparison to the open-loop system.
Sensitivity of burst timing to sensory input and internal dynamics.
We find that the timing of bursts in the closed-loop system is governed by chemosensory feedback rather than the intrinsic bursting mechanism of the isolated CPG (slow inactivation of INaP through the h gate). To assess the influence of h dynamics in controlling burst properties, we simulated the open-loop and closed-loop models with ranging from 8 to 45 s (Fig. 5). The interburst interval (IBI), burst duration, and number of spikes per burst all varied linearly as a function of in the open-loop model, whereas in the closed-loop model these burst properties were much less sensitive to changes in . To assess the influence of the timescale for chemosensory input in controlling burst properties, we recorded the gtonic values observed during closed-loop eupneic bursting with = 10 s and then played back compressed (γ < 1) or elongated (γ > 1) versions of this gtonic waveform as a forcing signal to the BRS model (with = 10 s). For γ = 1, the forced BRS exhibited identical burst properties to the closed-loop model, as one would expect. For γ = 0.8, the system entrained 1:1 to the forcing and exhibited smaller IBIs, burst durations, and number of spikes per burst. For γ < 0.8, the system could not keep up with the forcing and lost 1:1 entrainment, instead only bursting once for every two peaks of the gtonic waveform. For γ > 1, IBI increased linearly with γ, whereas burst duration and number of spikes per burst increased up to γ = 2 before leveling off or even decreasing. These simulations highlight the differential roles of h dynamics and gtonic fluctuations in the closed-loop system, with gtonic controlling the overall period of bursting (dominated by IBI) and h controlling spiking during the burst. Thus it is the timescale of chemosensory input that determines burst timing in the closed-loop system and not the timescale of the internal CPG dynamics.
Fig. 5.
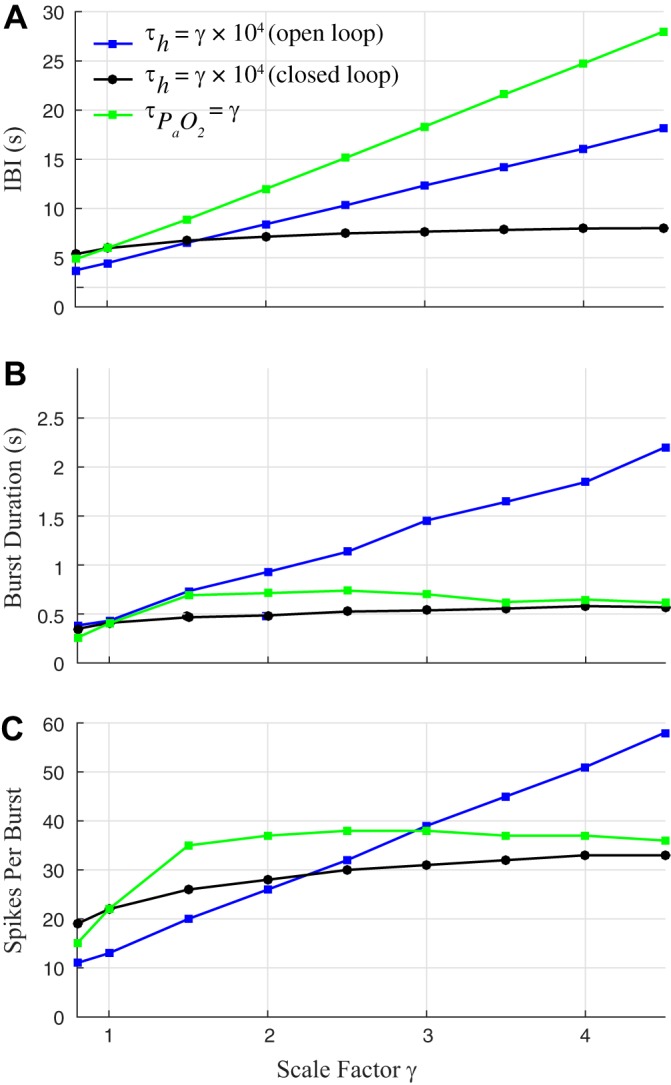
Chemosensory feedback (not the isolated CPG bursting mechanism) governs burst timing in the closed-loop system. A–C: effect of persistent sodium channel inactivation time constant and timescale of chemosensory feedback () on burst properties. Blue lines and black lines: , is increased from 8 to 45 s, where γ = 1 corresponds to the default BRS model setting of , = 10, 000 ms. Green line: is modulated by forcing the BRS model with compressed (γ < 1) and elongated (γ > 1) versions of the gtonic waveform observed during closed-loop bursting (γ = 1). A: interburst interval (IBI) increases linearly in the open-loop system as is increased (blue) and in the forced system as is increased (green). IBI is much less sensitive to in the closed-loop system (black). B and C: burst duration (B) and number of spikes per burst (C) are more sensitive to increases in in the open-loop system (blue) than in the closed-loop system (black). In the forced system, burst duration and number of spikes per burst increase sharply, then level off, and eventually decrease slightly as is increased (green).
Bistability of eupnea and tachypnea in the closed-loop model.
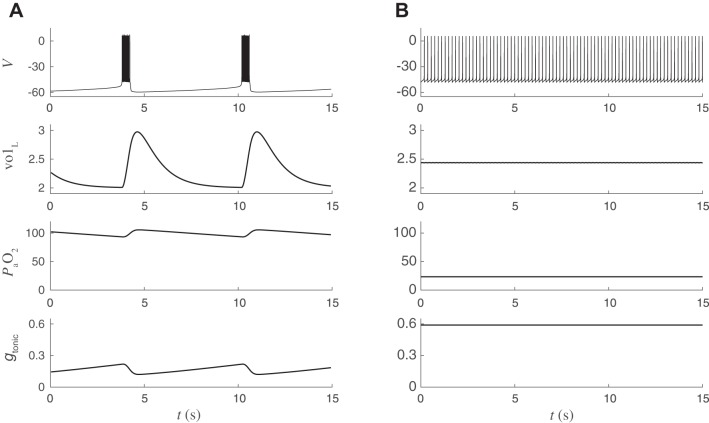
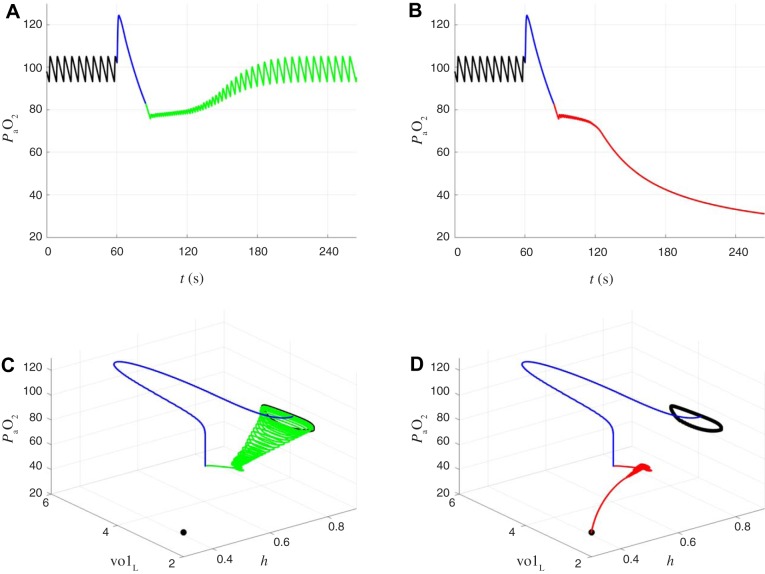
In the closed-loop model, the stable bursting rhythm that represents eupneic breathing coexists with a stable beating rhythm that represents pathologically rapid and shallow “tachypneic” breathing. This bistability is evident in Fig. 6, which shows two simulations of the closed-loop model with identical parameter values but different initial conditions. In Fig. 6A, spikes during the active phase of CPG bursting drive lung expansions that bring in new air, causing an increase in . During the silent phase of the burst, the lungs relax as air is exhaled and decreases. The oscillation in between 90 and 110 mmHg produces an oscillation in gtonic between 0.12 and 0.22 nS, which in turn leads to CPG bursting that maintains eupnea. In contrast, Fig. 6B shows that tonic spiking of the CPG fails to drive lung expansions large enough to support effective gas exchange, resulting in a level well below the desired range. The low produces a high gtonic, which reinforces tonic spiking, trapping the system in a pathological state.
Fig. 6.
Coexistence of 2 stable periodic orbits (bistability) in the closed-loop respiratory control model. A and B: simulations with identical parameter values but different initial conditions. From top to bottom: CPG voltage (mV), lung volume (liters), arterial oxygen (mmHg), chemosensory-dependent input to CPG (nS). x-Axis is time (s). A: “eupneic” bursting. The central BRS circuit responds to time-varying chemosensory input by producing a regular breathing rhythm at ~10 breaths/min. Lung volume varies between 2 and 3 liters. Blood oxygen () varies between 90 and 110 mmHg. B: different initial conditions lead to pathological “tachypneic” spiking. The CPG receives elevated tonic input causing sustained spiking at several hertz, leading to ineffective motor output. Lung volume fluctuates by <0.1 liters, and blood oxygen is approximately constant at a pathologically reduced level (25 mmHg).
To better understand the nature of the bistability between normal and reduced levels observed in the closed-loop model, we analyzed a reduced version of the open-loop model obtained by approximating the dynamics of the control variable , using the method of averaging (Sanders et al. 2007). If the dynamics of the control variable evolve on a slow timescale, then our analysis is formally equivalent to an averaging analysis of the closed-loop model decomposed into fast and slow variables. We find that during eupneic bursting the intrinsic slowness of the variables (measured as the maximum rate of change divided by the range of the variable) span multiple temporal scales, with , volL, and being an order of magnitude slower than h and α, which in turn are an order of magnitude slower than v and n (Table 1). Since is both a slow variable and the control variable, we reduce the closed-loop system to this single component and obtain a reduced model of the form
| (23) |
where y = and is defined by averaging the expression for the flux, given a fixed value (see Eqs. 27 and 28 in appendix). This 1D model facilitates understanding the dynamics of the control variable. In particular, decreases when , increases when , and remains constant when . values for which are fixed points of our reduced (1D) slow subsystem. In Fig. 7A we show for three different values of the metabolic demand M. With M = 0.4 × 10−5 ms−1, the system has a stable fixed point at = 90 corresponding to eupnea, a stable fixed point at = 40 mmHg corresponding to tachypnea, and an unstable fixed point at = 80 mmHg that acts as a boundary between the two stable states. With M = 0.8 × 10−5 ms−1, the same three fixed points exist but the unstable fixed point and the stable eupneic fixed point are now closer to each other. With M = 1.6 × 10−5 ms−1, only one fixed point exists and it is the stable tachypneic fixed point. Figure 7B shows the location of the fixed points as a function of M. As M is increased, the unstable fixed point and the stable eupneic fixed point move toward one another until they collide and annihilate each other in a saddle-node bifurcation. Thus the reduced model obtained through averaging predicts that, as M is increased, the closed-loop system will eventually lose bistability and display tachypneic tonic spiking for all initial conditions. Indeed, simulations of the full model confirm that for high values of M the closed-loop system no longer exhibits eupneic bursting (Fig. 8).
Table 1.
Comparing “relative speed” of closed-loop model variables
| x | maxt∈[0,T]{|x′(t)|} | maxt∈[0,T]{x(t)} | mint∈[0,T]{x(t)} | vx |
|---|---|---|---|---|
| 0.0278 | 105.7054 | 93.3442 | 0.0022 | |
| volL | 0.0022 | 2.9744 | 2.0078 | 0.0023 |
| 0.0349 | 107.2739 | 94.5528 | 0.0027 | |
| h | 0.0035 | 0.7551 | 0.6734 | 0.0427 |
| α | 7.0518 × 10−4 | 0.0090 | 3.5427 × 10−5 | 0.0783 |
| v | 76.2152 | 6.3719 | −59.7198 | 1.1532 |
| n | 1.7849 | 0.9386 | 4.6197 × 10−4 | 1.9027 |
The dimensionless quantity vx of each variable in the model along the eupneic bursting limit cycle of period T is calculated with Eq. 24.
Fig. 7.
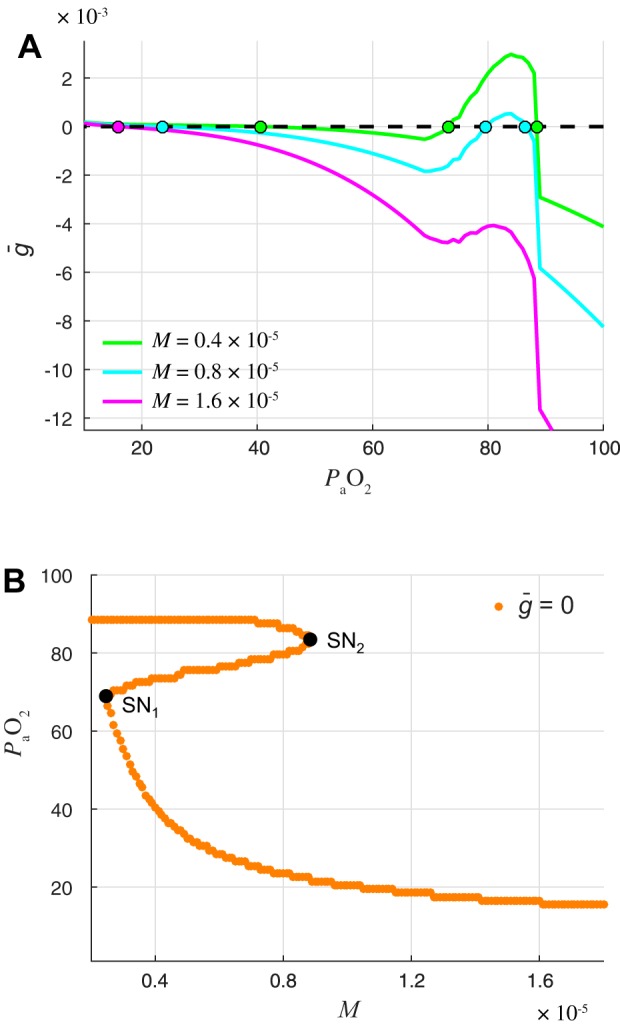
Reduced slow subsystem predicts that eupnea is lost at high metabolic demand through saddle-node bifurcation. A: phase line of averaged slow subsystem (Eq. 23) showing the approximate rate of change of () as a function of . The curves show when will increase and decrease for 3 different values of the metabolic demand M. Colored dots are fixed points of the averaged slow subsystem . Zero crossings with positive and negative slopes are unstable and stable fixed points, respectively. When M = 0.4 × 10−5 ms−1, the system has a stable fixed point corresponding to eupneic bursting ( = 89 mmHg), a stable fixed point corresponding to tachypneic spiking ( = 41 mmHg), and an unstable fixed point ( = 74 mmHg). When M = 0.8 × 10−5 ms−1, the system still has 2 stable fixed points, but the stable eupneic fixed point ( = 87 mmHg) and the unstable fixed point ( = 80 mmHg) have moved closer together. When M = 1.6 × 10−5 ms−1, the system has only 1 fixed point, which corresponds to stable tachypneic spiking ( = 17 mmHg). B: location of fixed points in averaged slow subsystem. The curve shows the value of fixed points as a function of metabolic demand M. For intermediate M values, the system has 3 branches of fixed points. The upper branch is stable and corresponds to eupnea, the middle branch is unstable, and the lower branch is stable and corresponds to tachypnea. At M = 0.25 × 10−5 ms−1, the lower stable branch and unstable middle branch collide and these fixed points are destroyed in a saddle-node bifurcation (SN1), leaving only the stable upper branch (eupnea) for M < SN1. Similarly, at M = 0.88 × 10−5 ms−1, the upper stable branch and unstable middle branch collide in another saddle-node bifurcation (SN2), leaving only the stable lower branch (tachypnea) for M > SN2.
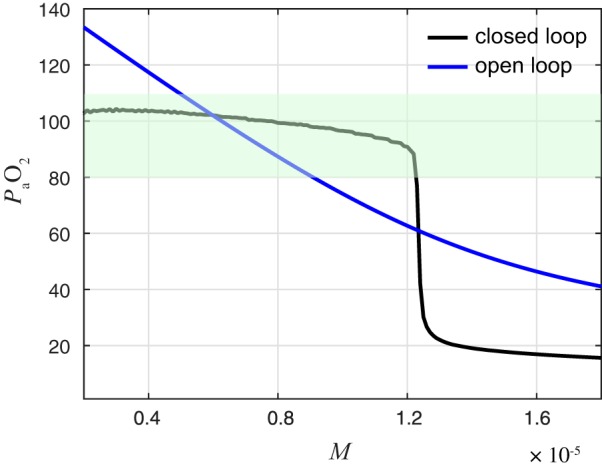
Fig. 8.
Sensory feedback increases the robustness of eupnea with respect to metabolic demand. Mean levels in systems with (closed loop) and without (open loop) chemosensory feedback as a function of M. Green band indicates a nominal range of normoxia from 80 to 110 mmHg. The enhanced robustness of the closed-loop system is evident in the shallower slope of the black curve relative to the blue curve at the operating point of = 100 mmHg and in the wider range of M values for which the black curve stays within the normoxic limits.
Enhanced Robustness of Closed-Loop System
The incorporation of chemosensory feedback leads to the closed-loop system being more robust to changes in metabolic demand than the open-loop system. Figure 8 illustrates the enhanced robustness of the full closed-loop system in two ways. First, the vs. M curve has a shallower slope near the desired operating point of = 100 mmHg, where is 70% less in the closed loop than in the open loop. Thus the closed-loop model is locally robust to increases in metabolic demand (cf. Robustness and Flexibility). Second, the range of M values for which stays within the acceptable range of 80–110 mmHg is larger in the closed loop (1 × 10−7 < M < 1.23 × 10−5 ms−1) than it is in the open loop (0.49 × 10−5 < M < 0.91 × 10−5 ms−1). This is a more global, or functional, measure of the robustness.
As M is increased from 0.2 × 10−5 to 1.5 × 10−5 ms−1, the mean levels decrease from 102 to 90 mmHg in the closed-loop model and from 135 to 62 mmHg in the open-loop model. The ability of the closed-loop system to maintain levels within a narrower range reflects increased robustness of the closed-loop system to variations in metabolic demand. However, if the metabolic demand becomes too great (M > 1.2 × 10−5 ms−1), mean levels in the closed-loop model drop precipitously as the system transitions from eupnea to tachypnea. Our averaging analysis predicts that this transition would occur at M = 0.82 × 10−5 ms−1, since that is the value of M at which saddle-node bifurcation occurs in the reduced system (cf. Fig. 7B). The fact that this transition occurs at a higher value of M than predicted by analysis of the reduced system illustrates another type of robustness present in the closed-loop system.
Autoresuscitation After Transient Perturbations
The closed-loop system exhibits surprising resilience to transient perturbations. Because of the bistable nature of the closed-loop system, perturbations can take the system out of the basin of attraction for eupnea and into the basin of attraction for tachypnea. We find that the closed-loop system is able to recover to eupnea after perturbations, even when the perturbation creates transient levels below 75 mmHg. This “autoresuscitation” phenomenon arises from properties intrinsic to the BRS conductances (Diekman et al. 2012). We demonstrate and analyze autoresuscitation using two different types of perturbations. First, we consider perturbations where instantaneously drops to an abnormally low level. This type of perturbation, which we refer to as an imposed hypoxic event, is rather nonphysiological but is mathematically convenient. The second type of perturbation we consider is more physiologically plausible and models intermittent disruption of chemosensory feedback. In this scenario, we temporarily disconnect gtonic from and hold gtonic at a constant value. All the system variables continue to evolve under this value of gtonic for τ seconds, until we reconnect the loop and again make gtonic a function of .
Perturbation I: imposed hypoxic event.
We defined eupneic and tachypneic “ranges” based on the long-term behavior that results from different initial conditions. First, we simulated the open-loop model over a range of gtonic values corresponding to different levels. The gtonic values were chosen using the chemosensation sigmoid (Eq. 22) for a range of values with 0.1-mmHg spacing. Each simulation was allowed to reach steady state before “closing the loop” and observing whether those initial conditions led to eupnea or tachypnea in the closed-loop system. Closed-loop simulations with initial conditions corresponding to below 75.6 mmHg resulted in tachypnea, and those with initial conditions corresponding to above 78.1 mmHg resulted in eupnea (Fig. 9). These ranges of values are henceforth referred to as the tachypneic range and the eupneic range, respectively. The dividing line between these two ranges was approximately gtonic = 0.38, which corresponds to = 76.85 mmHg (Fig. 9). However, the restored closed-loop system could recover from transient perturbations that brought below this dividing line. For example, at t = 180 s we set = 40 mmHg and then immediately released the system back to its normal dynamics. We see that the trajectory escapes the tachypneic range and returns to eupnea. Then, at t = 360 s we set = 30 mmHg and again immediately released the system back to its normal dynamics. The trajectory is not able to escape the tachypneic range after this more severe perturbation. The system does not recover to eupnea and instead descends into tachypnea.
Fig. 9.
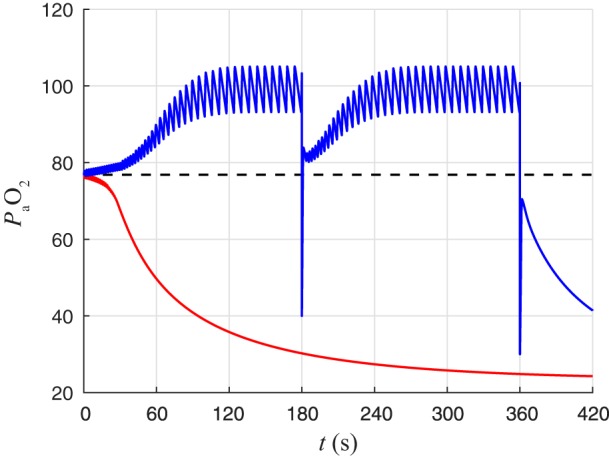
Transient response of CPG in closed-loop system can lead to “autoresuscitation” after hypoxic perturbations. The open-loop system was simulated with gtonic = 0.3800 nS (red curve) and gtonic = 0.3791 nS (blue curve) until it reached steady state. At t = 0, we “closed the loop” and allowed gtonic to vary as a function of throughout the remainder of the simulation. From these initial conditions, the blue trajectory approaches eupnea, whereas the red trajectory approaches tachypnea. Dashed line indicates that initial conditions determined from steady states of open-loop simulations with gtonic values corresponding to levels above (below) this line will approach eupnea (tachypnea). At t = 180 s, was set to 40 mmHg momentarily and then immediately went back to being determined by the system dynamics. This hypoxic perturbation takes the trajectory to levels below the steady-state dividing line, but the transient response allows the system to recover to eupnea. At t = 360 s, was set to 30 mmHg momentarily and then immediately went back to being determined by the system dynamics. The transient response again leads to an abrupt initial increase in following the perturbation, but it is not enough to get over the dividing line and the trajectory ultimately approaches tachypnea.
When the system is able to recover from transient hypoxic perturbations, it is because of the barrage of spiking activity brought on by the reduction in levels and ensuing sudden increase in gtonic. The relationship between , gtonic, V, and volL is illustrated in Fig. 10A. The active phase of a eupneic burst is 0.39 s in duration and consists of 21 spikes, corresponding to a spiking frequency of 54.5 Hz during the active phase (Fig. 10B, top). In contrast, the burst immediately following the hypoxic perturbation is 0.96 s in duration and consists of 69 spikes, corresponding to a spiking frequency of 72.2 Hz (Fig. 10B, bottom). The enhanced spiking during this burst leads to a vigorous expansion of volL (Fig. 10A, bottom) that brings extra oxygen into the lungs, ultimately raising (Fig. 10A, top) to a level high enough that gtonic decreases (Fig. 10A, second from top) before the system becomes trapped in the tachypneic state. The barrage of spiking that facilitates autoresuscitation after hypoxic perturbation can be understood in terms of the bifurcation structure of the fast subsystem of the BRS model (Fig. 10C). As shown in Fig. 4, the curve of fast subsystem fixed points moves as gtonic fluctuates in the closed-loop model. During the silent phase of a burst, decreases and gtonic increases, which shifts the curve leftward until the trajectory jumps up and begins to exhibit limit cycle oscillations corresponding to repetitive spiking. During the active phase, h decreases until the periodic orbits collide with the middle branch of unstable fixed points and are destroyed in a homoclinic bifurcation. Importantly, the period of the orbits increases logarithmically as they approach the homoclinic (Gaspard 1990); thus spiking occurs at a higher frequency when the trajectory is further from the bifurcation point. Figure 10C, top, shows the trajectory of a typical eupneic burst, and the location of the curve of steady states, at the time the trajectory jumps up (green dot). Figure 10C, bottom, shows the trajectory of the spiking barrage following hypoxic perturbation. Note that when the trajectory jumps up, the curve of fixed points is located much further to the left in the (V, h) plane because of the drastic reduction in . Since the trajectory is further from the homoclinic bifurcation when it begins spiking, the system exhibits spikes for a longer time and at a higher frequency than it does during the active phase of a typical burst.
Response to transient hypoxia in vitro.
Although a sudden drop in may seem nonphysiological, it can be simulated in vitro by adding NaCN, a pharmacological analog of hypoxia, to the brain stem slice perfusate. Alternatively, hypoxia can be imposed by reducing the amount of O2 in the gas used to bubble the perfusate. We find that both of these in vitro hypoxic challenges induce a similar barrage of spiking in brain stem slices containing the pBC as occurs in the closed-loop model in response to a hypoxic clamp perturbation. Figure 11A shows a barrage of spikes in an individual pBC cell (Fig. 11A, top) and increased hypoglossal nerve rootlet discharge (Fig. 11A, bottom) after bath application of 300 μM NaCN. Figure 11C shows summary data from nine experiments with increased burst duration and frequency during NaCN or hypoxia treatment, followed by a return to baseline bursting activity after the treatment. The changes in burst duration and frequency are significant (P < 0.05) across baseline, NaCN or hypoxia, and recovery. There is a delay between the initiation of the treatment and the effect seen in the individual neurons or the network output (XII) due to the “dead space” volume of the perfusion system.
The carotid chemoreceptors and their inputs to the nucleus tractus solitarii and the rest of the inspiratory rhythm-generating circuit are absent in the reduced in vitro slice preparation. The cellular mechanisms by which neurons and glia participating in the respiratory neural network sense local changes in oxygen is unknown; however, D’Agostino et al. (2009) have shown that hemeoxygenase is expressed in neurons in the rostral ventrolateral medulla, which includes the pBC and other respiratory-related neurons, and this may serve as a marker for hypoxia-sensitive cells within the pBC. Other cellular mechanisms that may serve as hypoxia sensors in pBC include second messengers as modifiers of KATP channels (Mironov et al. 1998; Mironov and Richter 2000), changes in mitochondrial NADH (Mironov and Richter 2001), and L-type calcium channels (Mironov and Richter 1998). Even changes in the excitability of upstream projecting neurons, for example from the nucleus tractus solitarii to the pBC (Takakura et al. 2007), could impact the behavior of our model with changes in oxygen tension.
Perturbation II: interruption of chemosensory feedback.
To explore the autoresuscitation phenomenon further, we modeled intermittent failure of the chemosensory pathway that transmits information about blood oxygen content to the CPG (Fig. 12). Specifically, we simulated the closed-loop system in the eupneic state and then transiently disconnected gtonic from by setting gtonic to a constant value of 0.1 nS for durations ranging from 1 to 60 s. This intervention puts the CPG in the quiescent regime, and gradually declines, reaching values <50 mmHg for durations >35 s. We then reconnected the chemosensory feedback, which caused an abrupt increase in gtonic and a barrage of spiking that quickly raised . We observed that if the duration of the chemosensory failure was short enough the system would recover to eupnea (Fig. 12, A and C) but if the duration of the failure was sufficiently long the system would descend into tachypnea (Fig. 12, B and D). For chemosensory failure durations near the critical value separating these two states, trajectories transiently exhibited an activity pattern consisting of bursts with a smaller number of spikes and shorter IBIs before transitioning to a steady state of eupneic bursting (as in Fig. 6A) or tachypneic tonic spiking (as in Fig. 6B). In the next section, we show that this intermediate bursting pattern corresponds to an unstable limit cycle with a stable manifold acting as a boundary between respiratory system recovery and failure.
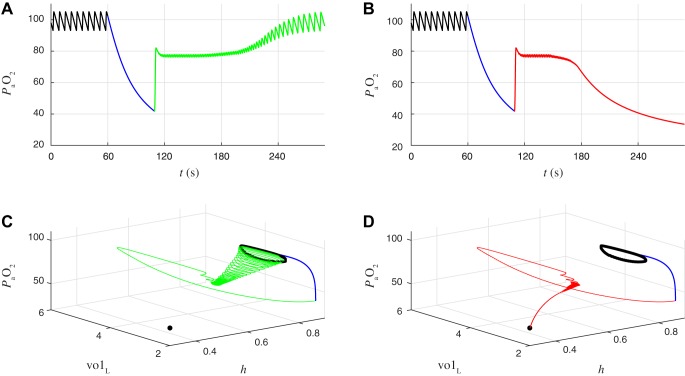
Fig. 12.
Recovery to eupnea vs. tachypneic failure after transient interruption of chemosensory feedback. A: time course of before (black), during (blue), and after (green) interruption of chemosensory feedback. Black, eupneic breathing in closed-loop model; blue, chemosensory feedback is interrupted by holding gtonic fixed at 0.1 nS for 49.2466 s; green, chemosensory feedback is reestablished by again making gtonic a function of . System recovers to eupnea. B: same as A, except the gtonic = 0.1 nS clamp (blue) is held for 0.1 ms longer. After reestablishing chemosensory feedback the system ultimately descends into tachypnea (red) rather than recovering to eupnea. C: eupneic recovery from A projected onto (h, volL, ) coordinates. During the gtonic clamp (blue curve), the CPG is quiescent and decreases to 42 mmHg. After release of the clamp (green curve), gtonic increases rapidly, causing a barrage of spiking and a large expansion of lung volume that rapidly increases to 82 mmHg. From t = 120 to 180 s the system exhibits bursts of spiking with shorter interburst intervals and shorter burst durations than eupneic breathing. This leads to intermediate values (76–80 mmHg) as the interburst intervals and burst durations gradually lengthen and the system returns to eupneic breathing. D: tachypneic failure from B projected onto (h, volL, ) coordinates. Same as C, except that during the intermediate oscillations from t = 120 to 180 s the interburst intervals and burst durations gradually shorten and the system descends into tachypnea (red curve).
Boundary between eupnea and tachypnea.
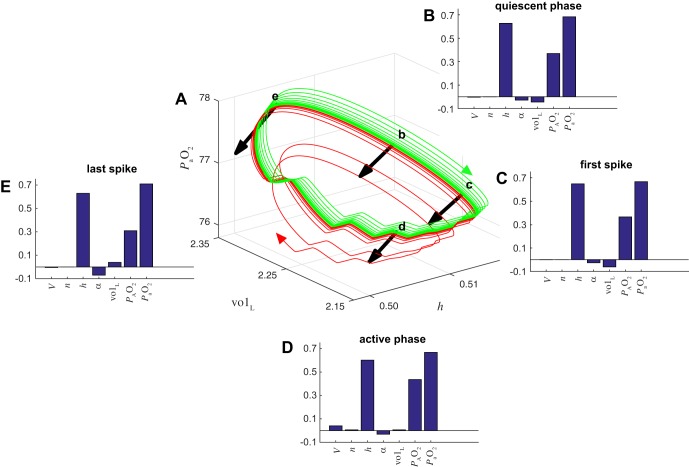
When pushed to the boundary separating eupnea and tachypnea, the failure or survival of the system depends on the interplay of biomechanics (e.g., lung expansion and contraction) and excitability in central circuits (including h-gate dynamics) and cannot properly be understood in terms of the central dynamics in isolation. The model has seven dynamical variables; therefore trajectories move in a 7D space. The two attractors (tachypneic spiking and eupneic bursting) are separated by a smooth 6D separatrix that is the stable manifold of a metastable set living on the boundary. Simulations suggest that this set is a saddle limit cycle, with a 6D stable manifold and a 2D unstable manifold. The intersection of these two sets of points is a 1D unstable limit cycle. We computed Floquet multipliers, μ, for this limit cycle and found one unstable direction (μ > 1), five stable directions (μ < 1), and one neutral direction (μ = 1) (see appendix for details). The components of the eigenvector associated with the unstable direction provide information about the impact of each system variable on the fate of trajectories on the boundary. We analyzed the eigenvectors at the four locations on the boundary limit cycle indicated by the black arrows in Fig. 13A: approximately halfway through the quiescent phase of the burst (arrow b), shortly before the first spike of the active phase (arrow c), between spikes during the active phase (arrow d), and shortly after the last spike of the active phase (arrow e). The size of the eigenvector components indicate how susceptible the system is to being pushed off of the boundary limit cycle by perturbations in each of the system’s variables. We find that the system is most sensitive to perturbations in h, , and at all four locations (Fig. 13, D and E). Since eigenvectors are only defined up to an arbitrary change in sign, we chose the convention that the component is positive in order to orient the eigenvectors consistently around the limit cycle (we ensured this by multiplying the vectors by −1 when necessary). The sign of each eigenvector component then indicates whether small increases in that variable push the system toward eupnea or tachypnea, with positive components being “proeupneic” and negative components being “protachypneic.” We find that the h and components are proeupneic at all four locations on the limit cycle, whereas α has a small protachypneic effect at all four locations. The effect of perturbations in volL is small and varies with location. The system is not sensitive to perturbations in V and n, except during the active phase when V is slightly proeupneic (Fig. 13D).
Fig. 13.
Floquet eigenvectors at the eupnea-tachypnea boundary limit cycle. A: trajectories from the closed-loop model that either recover to eupnea (green) or descend to tachypnea (red) after chemosensory interruption, projected onto (h, volL, ) coordinates. These are the same trajectories as shown in Fig. 12, C and D, replotted here for the time window between t = 130 and 155 s, when they are near an unstable limit cycle on the boundary between eupnea and tachypnea. Black arrows illustrate the eigenvectors associated with the unstable Floquet multiplier at 4 locations along the boundary limit cycle. To aid the clarity of the illustration, the eigenvectors were multiplied by −1 so that the arrows point toward tachypnea rather than eupnea. B–E: eigenvector components at the locations labeled b–e in A. The signs of the components were chosen such that positive values are consistently “proeupneic” and negative values are consistently “protachypneic” (see text for details).
Extent of Autoresuscitation
To quantify the extent of the autoresuscitation regime, we simulated a range of durations for the interruption of chemosensory feedback. Figure 14 shows levels 3 min after reestablishing chemosensory feedback, with dark and bright colors indicating low and high , respectively. In the absence of chemosensory feedback, we assume that the drive to the CPG no longer fluctuates and set gtonic to constant values between 0 and 0.6 nS when disconnected from . If this value was sufficiently close to 0.3 (the nominal gtonic value used for open-loop simulations as shown in Fig. 2A), the CPG exhibited a bursting pattern that kept levels sufficiently high, such that the system always maintained eupnea when the chemosensory feedback was reconnected. Values of gtonic below this range correspond to cases qualitatively similar to the simulations shown in Fig. 12. Values of gtonic above this range correspond to gtonic being set to a high value in the absence of chemosensory feedback. Here the CPG responds with a barrage of spiking at the beginning of, rather than after, the perturbation. This initial barrage raises and can help the system avoid tachypnea if the perturbation is short enough in duration (Fig. 15). The boundary separating eupnea and tachypnea in this case is again associated with the unstable limit cycle analyzed in Fig. 13.
Fig. 14.
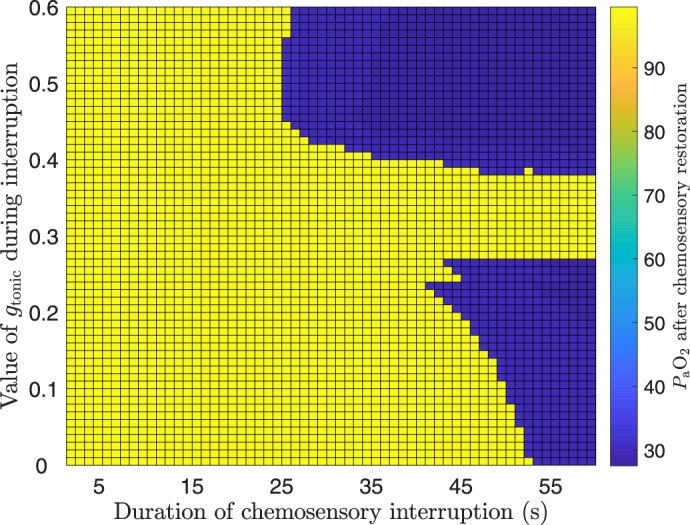
Autoresuscitation occurs for both high and low default gtonic levels. Pseudocolors indicate levels in the restored closed-loop system after transient interruption of chemosensory feedback for a range of durations (x-axis, s) and severities (y-axis, nS). The severity of the failure corresponds to the value at which gtonic was held constant during the chemosensory interruption. levels shown were measured 3 min after chemosensory feedback was reestablished and were calculated as the midrange of over a 10-s window. The capability of the system to autoresuscitate is observed whether the CPG is quiescent because of low input drive (low gtonic values) or hyperexcited because of high input drive (high gtonic values) during the absence of chemosensory feedback. For default gtonic values in an intermediate range, the system recovers to eupnea despite arbitrarily long interruptions of feedback.
Fig. 15.
Recovery to eupnea vs. tachypneic failure after transient interruptions of chemosensory feedback assuming high input drive to the CPG during the interruptions. These simulations are analogous to those shown in Fig. 12, except here gtonic is set to 0.5 nS (high drive to CPG) rather than 0.1 nS (low drive to CPG) in the absence of chemosensory feedback. A: time course of before (black), during (blue), and after (green) interruption of chemosensory feedback. Black, eupneic breathing in closed-loop model; blue, chemosensory feedback is interrupted by holding gtonic fixed at 0.5 nS for 24.5 s; green, chemosensory feedback is reestablished by again making gtonic a function of . System recovers to eupnea. B: same as in A, except that the gtonic = 0.5 nS clamp (blue) is held for 0.1 s longer. After reestablishing chemosensory feedback the system ultimately descends into tachypnea (red) rather than recovering to eupnea. C: eupneic recovery from A projected onto (h, volL, ) coordinates. The interruption of chemosensory feedback causes a sudden increase in gtonic since the constant value it is set to during the interruption (0.5 nS) is higher than the values traversed by gtonic during eupneic bursting (0.12–0.22 nS). This change triggers a barrage of spiking and a large expansion of lung volume that rapidly increases to 124 mmHg. During the remainder of the gtonic clamp, the CPG exhibits tonic spiking that does not drive effective lung expansions and decreases to 83 mmHg. After release of the clamp, the system exhibits bursts of spiking with shorter interburst intervals and shorter burst durations than eupneic breathing. This leads to intermediate values (76–80 mmHg) as the interburst intervals and burst durations gradually lengthen and the system returns to eupneic breathing (green trace). D: tachypneic failure from B projected onto (h, volL, ) coordinates. Same as in C, except that during the intermediate oscillations from t = 90 to 120 s the interburst intervals and burst durations gradually shorten and the system descends into tachypnea (red trace).
DISCUSSION
Modeling Rationale
To understand the generation and stabilization of vital rhythms, such as breathing, one must consider both central and peripheral systems working in concert. Thus one confronts oscillating, nonlinear, closed-loop control systems, which are notoriously difficult to analyze in a general setting (Shimkin 2009). We therefore chose to work with a model that does not include all known aspects of respiratory control but represents enough salient aspects of the physiology to capture the principal conundrum of interest—the interaction of a stable CPG circuit with phasic sensory feedback provided by peripheral chemosensation.
Because breathing is such a fundamental physiological function, one expects there to be multiple interwoven and layered control mechanisms interacting to stabilize and modulate breathing rhythms. For instance, chemosensation allows changes in both oxygen and carbon dioxide concentrations in the bloodstream to dramatically affect the breathing rhythm. Both hypercapnia and hypoxia sensitivity are important, and dysregulation of either—for instance in the perinatal period, when the immature network is still developing—can contribute to pathological apneas (Martin et al. 2012). To formulate our model, we select one element from each step in a closed-loop control circuit: sensitivity to blood gases (hypoxia in our case), central pattern generation, motor output driving gas exchange, metabolic demand, and, as the final “control variable,” the arterial partial pressure of dissolved oxygen. Despite its relative poverty when compared with the full complexity of respiratory control, our simple model nevertheless exhibits these fundamental features of interest: 1) bistability between a normal “eupneic” state and a pathological “tachypneic” state; 2) interaction of intrinsic rhythmicity of central circuitry (BRS model) and global rhythmicity of the closed-loop system; and 3) spontaneous activity providing a mechanism of “autoresuscitation” following bouts of imposed hypoxia or interruption of chemosensory feedback.
We do not claim to have developed a minimal model for robust breathing, in the sense that we do not rule out the possibility of a lower-dimensional closed-loop control model exhibiting the same fundamental behaviors. Rather, we think of our model as minimalist, in the sense that it incorporates enough physiological realism to shed light on natural respiratory control yet remains simple enough to be amenable to mathematical analysis. Thorough analysis of any such system requires a constellation of approaches, including control-theoretic techniques, dissection of fast and slow timescales, bifurcation analysis, and numerical simulation. We apply these tools to better understand the mechanisms of generation and stabilization of robust breathing rhythms.
Alternative Bistable States and Interpretations
We interpret the nonbursting, regular spiking or “beating” regime of the CPG in the closed-loop model as tachypnea because it produces rapid and shallow fluctuations in lung volume that are not sufficient to maintain normoxia (Diekman et al. 2012). These lung fluctuations have extremely small amplitude, and in other closed-loop models the beating regime has been interpreted as apneusis, or “holding the breath” after inspiration (Ben-Tal and Smith 2008). Altering the shape of the gtonic chemosensation sigmoid, by setting the parameters ϕ = 0.2 nS and θg = 100 mmHg in Eq. 22, results in a closed-loop model that has bistability between two different bursting regimes of the CPG: one with 20 spikes per burst and a period of 5.8 s and the other with only 3 spikes per burst and a period of 1.4 s. These bursting patterns produce lung volume fluctuations of 0.9 and 0.07 liter, respectively, with the former maintaining around 100 mmHg and the latter around 30 mmHg. Thus this version of the closed-loop model again exhibits bistability of eupnea and tachypnea, where here the tachypnea regime consists of multispike bursts occurring at a higher frequency than eupnea. Although this is perhaps a more natural concept of tachypnea than the beating regime, we chose to use the beating regime as our model of tachypnea (i.e., we set ϕ = 0.3 nS) for this study in order to make the difference between the coexisting physiological and pathological states more pronounced. Raising instead of lowering the maximal value of the chemosensation sigmoid, i.e., setting ϕ = 5 nS (and θg = 50 mmHg), results in a closed-loop model with bistable eupneic bursting and a depolarized (−30 mV) quiescent state of the CPG. We interpret this quiescent state, for which lung volume is constant at 3.1 liters, as apneusis. Finally, we also considered a bell-shaped curve instead of a sigmoid for the relationship between gtonic and and observed bistability between eupneic bursting and a hyperpolarized (−60 mV) quiescent state of the CPG. We interpret this quiescent state, for which lung volume is constant at 2.0 liters, as apnea. While we have not observed coexistence of more than two stable states in any of these versions of the closed-loop model, we cannot rule out the possibility of higher-order multistability.
Control Theory and Averaging Analysis
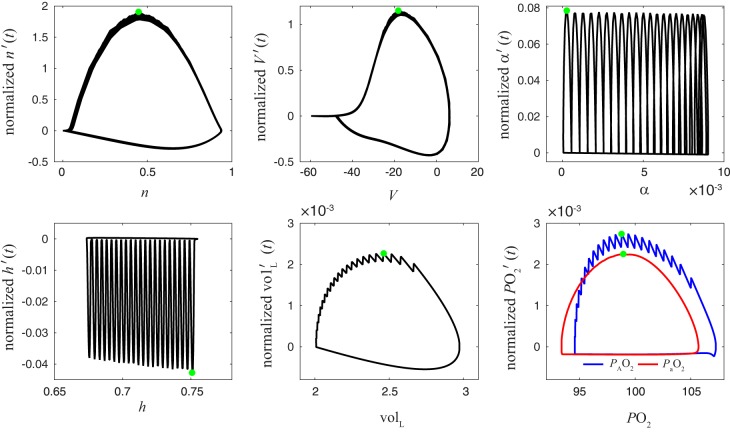
Control theory is a promising framework for studying respiratory control; however, it requires the part of control theory that involves nonlinear, nonstationary control (i.e., control of limit cycle trajectories), and possibly also stochastic control—which means that the control theoretical framework needed is not yet complete (Cowan et al. 2014; Roth et al. 2014). In our closed-loop model, is the natural “control variable”: it carries the signal that regulates the activity of the CPG (as opposed to or lung volume being the feedback signals). Although there is no canonical way to partition fast and slow variables in a high-dimensional system of ordinary differential equations (Clewley et al. 2005), empirical investigation (Fig. 16) suggests that is also a reasonable candidate for consideration as the slow variable. Identification of a slow variable suggests analysis via averaging. In this case, averaging gives a qualitative insight into the nature of the bistability between eupnea and tachypnea, interpreted along the “phase line” (Fig. 7). However, the resulting behaviors are not fixed points but limit cycles, and the averaging analysis with a single slow variable does not give full quantitative agreement. An averaging analysis considering multiple slow variables (Wang and Rubin 2016), which lies beyond the scope of the present report, may be able to more faithfully capture the chain of dependencies present in the closed-loop model.
Fig. 16.
Phase plots showing the relative speed of each variable during closed-loop bursting identify as a slow variable. x-Axis is x and vertical y-axis is the rate of change x′(t) normalized by the range of x, where x = n, V, α, h, volL, , . Green dots indicate the maximal speed vx of each variable (−vx is shown for x = h). Note the significantly different timescales involved: , , and volL are slower than h and α, which themselves are slower than V and n.
It is both conceptually and mathematically convenient that the slow variables coincide with the control variables for this system, and we suggest that it may be useful to look for this feature in other motor control systems, such as those involved in legged locomotion (Full and Koditschek 1999).
Closed-Loop Respiratory Control Models
Although the literature on computational modeling of the respiratory system is vast (Lindsey et al. 2012), the model analyzed here is, to our knowledge, the first to embed a conductance-based CPG capable of firing action potentials into a closed-loop respiratory control model. Most computational studies have focused on respiratory pattern generation rather than the neural response to changes in blood gases (Ben-Tal and Tawhai 2013). Furthermore, much of the work that treats the respiratory system from a control-theoretic perspective (Grodins 1963) predates the identification of the pBC as the main location of the rhythmic pattern generation circuitry (Smith et al. 1991). In early dynamical models of the respiratory control loop, neuronal activity was represented by time delays between different compartments (Grodins et al. 1954, 1967) or as a black-box rhythm generator (Cheng et al. 2010; Khoo 1990). Later models incorporated neuronal dynamics using a generic limit cycle oscillator (Eldridge 1996) or firing rate models of excitatory and inhibitory neurons (Longobardo et al. 2005) as the respiratory pattern generator. Ben-Tal and Smith (2008) developed the first closed-loop model with a rhythm generator based on the persistent sodium current (INaP) that plays a major role in bursting of brain stem pBC neurons. The Ben-Tal model used a reduced description of the BRS model that did not include the ionic currents needed to produce action potentials. Instead, the activity level is described by a variable that represents the average spike rate of the pBC population, which can be related to the average voltage by a linear transformation. Two closed-loop models with detailed respiratory neuronal networks are the O’Connor et al. (2012) and Molkov et al. (2014) models. Both include the pBC as well as other brain stem neuronal populations involved in pattern generation, such as the Bötzinger complex and the ventral respiratory column. However, neither model simulates action potential-like spikes. The O’Connor model employed interacting populations of integrate-and-fire neurons where spikes are implied by voltage threshold crossings. The Molkov model used an activity-based neuron formalism in which the voltage variable represents an average voltage for the population and the population firing rate is described by a function of the voltage variable. As discussed in the previous section, in our model we find that replacing the full conductance-based model with a lower-dimensional model obtained by averaging reproduces the qualitative but not quantitative aspects of the full model.
It is possible that several of the features of the closed-loop model explored in this report, such as bistability and spontaneous autoresuscitation, would still be present in a version of the model where the ionic currents responsible for action potential firing of the CPG have been removed. We choose to retain the spikes, as it has been shown that reduced models of bursting cells (the R15 neuron in Aplysia californica) that do not consider the effects of action potentials on the underlying slow-wave oscillation in membrane potential may wrongly predict transitions between quiescent, bursting, and beating activity modes compared with the full model (Butera et al. 1996). In the BRS model, creating a “spikeless” reduced model by removing the transient sodium current INa yields a slow-wave membrane potential oscillation with a period that is approximately twice that of the full model (Ermentrout and Terman 2010). The full model has a shorter period relative to the reduced model because action potentials intensify the inactivation of the pacemaking persistent sodium current INaP.
Physiology of Autoresuscitation
Autoresuscitation occurs when the confluence of chemosensory drive and centrally generated drive causes a restart of the respiratory network. Typically, this restart occurs after the decreased oxygen tension is sensed via the carotid bodies and low O2 drives the hypoxic ventilatory response, consisting of two distinct phases: phase 1, an acute increase in minute ventilation early after hypoxic exposure, and phase 2, a later response characterized by ventilatory depression. In most mammals, the hypoxic ventilatory response is fully mature by 2 wk of postnatal life (Prabhakar et al. 2007). However, in neonatal mammals with immature chemosensory feedback, the reduced drive to the CPG is likely the key failure point that reduces the probability of restarting the respiratory rhythm in response to severe hypoxia (i.e., anoxia). Serotonergic and adrenergic neuromodulatory inputs appear to play a key role and are developmentally regulated (Erickson and Sposato 2009; Givan and Cummings 2016). Other complications of neonatal life, including infection (Siljehav et al. 2014), confound our understanding of the points of failure in the respiratory control system. As yet we do not have a mechanistic understanding of why autoresuscitation sometimes fails and sometimes succeeds. Our model provides greater understanding of the state changes that are required for resuscitation and an impetus for future experiments dedicated to elucidating the key control points that can force the respiratory network into restart after a hypoxic challenge.
Development
Developmental changes in the respiratory rhythm-generating and pattern formation networks have been described, but we do not yet know the impact that these changes have on the core of the rhythm-generating circuit. For example, burst-generating currents, including INaP and Ca2+-activated nonselective cation (ICAN) currents, are modulated during development (Del Negro et al. 2005). Furthermore, fetal Hb is known to have a higher binding affinity for oxygen, and the time course by which fetal Hb shifts to predominantly adult Hb would impact autoresuscitation (Rutland et al. 1983; Teitel and Rudolph 1985). Developmental changes in chemosensation also are key modifiers of autoresuscitation, as mentioned above. Carotid body resetting—after the relatively hypoxic environment in utero—occurs over the first weeks of life (Prabhakar et al. 2007), and the chronic intermittent hypoxic events common in neonates can alter the gain of carotid body chemosensors (Pawar et al. 2008). In our closed-loop model, changes in the gain of the hypoxia-sensitive pathway would correspond to changes in the slope of the sigmoid connecting to gtonic (the parameter σg in Eq. 22). Additionally, hypoxia alters gene transcription and reactive oxygen species-mediated signaling. Relatively little is known about how the respiratory control circuit changes, as a whole, over the course of development from the perinatal period to adulthood.
In our closed-loop model, the ability of the system to recover from an interruption in chemosensory feedback failure depends on the constant value assumed for gtonic when disconnected from (Fig. 14). If this value is in the range that produces bursting in the isolated CPG (between 0.25 and 0.4 nS), then the closed-loop system always returns to eupnea after chemosensory interruption. Based on this observation, we speculate that there may be at least two distinct components of carotid body input to the brain stem: an excitatory drive that is independent of chemosensory feedback and a modulatory pathway to confer additional robustness. The former would be an example of open-loop control and may be dominant during early stages of development, whereas the latter would reflect closed-loop control and may be more prominent in later stages of development.
Periodic Breathing
In the closed-loop model, a stable bursting limit cycle (eupnea) coexists with a stable tonic spiking limit cycle (tachypnea). On the boundary between the basins of attractions of two different stable limit cycles, one may “generically” expect to find an unstable limit cycle solution—just as we have observed (Benes et al. 2011). Indeed, in many neuronal models, the transition between bursting and spiking exhibits complicated dynamics (Ermentrout and Terman 2010). Recently, it has been shown that a common dynamical phenomenon, the torus canard, separates bursting and spiking regimes in several neuronal models (Burke et al. 2012; Kramer et al. 2008). Torus canards have been found in classes of neuronal models where the active phase of bursting terminates in a saddle-node bifurcation of periodic orbits (a fold-cycle bifurcation) in the fast subsystem, such as subcritical-Hopf/fold-cycle, circle/fold-cycle, and fold/fold-cycle bursters. In contrast, the BRS model is a fold/homoclinic (square wave) burster, i.e., the active phase of bursting terminates at a homoclinic bifurcation. In the BRS model, there is a fold-cycle bifurcation in the fast subsystem; however, the active phase of bursting does not terminate there, and it is not clear whether the torus canard phenomenon is possible in the closed-loop model presented here. Although the single-neuron version of the BRS model exhibits fold/homoclinic bursting, two synaptically coupled BRS model neurons exhibit fold/fold-cycle (or top hat) bursting (Best et al. 2005). A recent study (Roberts et al. 2015) has linked the transitions between bursting and spiking in the coupled BRS model to folded singularities and canards. Thus we expect that torus canards may be present in a version of the closed-loop model where the CPG is a network of BRS neurons rather than a single representative neuron. In systems with torus canards, trajectories can make extended visits to the neighborhood of an attracting limit cycle and a repelling limit cycle in alternation (Benes et al. 2011). Such dynamics in a respiratory control loop might provide a model of periodic breathing, a phenomenon commonly observed in premature infants where pauses in breathing of up to 10 s are followed by a series of rapid, shallow breaths before breathing returns to normal (Mohr et al. 2015; Patel et al. 2016). The typical phenotype of periodic breathing—apneas interspersed with tachypneic episodes—is also seen in adults as Cheyne-Stokes breathing. Hypoxic episodes have been implicated in the early stages of Cheyne-Stokes breathing and may be essential to the initiation of these episodes and the downward spiral into pathophysiological rhythms (Guntheroth 2011).
Robustness and Flexibility
Lyttle et al. (2017) recently introduced a dynamical systems framework for characterizing the robustness and flexibility of motor control systems. They defined robustness as the ability of a system to maintain performance despite perturbations (or parameter variation) and flexibility as the ability of a system to deploy alternative strategies that improve performance by adjusting behavioral output in response to perturbations. A third concept, sensitivity, measures the extent to which the dynamics of system components change in response to perturbations. Using a model of an invertebrate feeding apparatus, Lyttle et al. (2017) demonstrated that motor control systems can achieve robustness and flexibility by dynamically switching between coexisting modes in response to changing demands. One of these modes is characterized by low sensitivity to perturbations and parameter variations and the other mode by high sensitivity.
Interpreting our respiratory control model in this framework raises interesting questions. We have shown that the closed-loop system is more robust to changes in metabolic demand (M) than the open-loop system, because it is able to maintain blood oxygen within acceptable limits (80–110 mmHg) over a wider range of M values (Fig. 8). However, once M exceeds a certain value (1.24 × 10−7 ms−1) drops precipitously in the closed-loop model, and for M values above this threshold the levels in the open-loop model are higher than they are in the closed-loop model. This suggests that respiratory system performance might improve if the system were to modulate its sensitivity by reducing the gain of chemosensory feedback (σg) as metabolic demand increases, paradoxically enabling it to postpone a collapse in by switching to more of an open-loop control regime. Additional feedback mechanisms on a longer time scale could potentially confer such flexibility.
As another point of comparison, Fig. 10 illustrates the mechanism by which sensory feedback allows the closed-loop respiratory system to respond to what Lyttle et al. (2017) call a “challenge,” that is, a perturbation that tends to decrease the system’s performance (in this case, maintenance of adequate levels). Imposing a hypoxic challenge leads to the system producing a longer and stronger motor response that effectively counteracts the perturbation, within certain amplitude limits. The role of sensory feedback in Lyttle et al. (2017) is qualitatively similar. In that system, applying a mechanical load opposing the pulling in of food during the swallowing phase of an ingestive motor pattern activates a proprioceptive input to the CPG that selectively extends a portion of the underlying limit cycle trajectory. In response, the CPG produces a longer and stronger activation of the motor units innervating muscles opposed to the mechanical challenge.
Model Extensions
There are several aspects of the respiratory control network that could be incorporated in future work extending our closed-loop model. These include modeling the pBC as a multiunit network with parametric heterogeneity, which has been shown to increase the robustness of inspiratory oscillations in a network of model conditional pacemaker neurons (Rubin and Terman 2002b); interaction of the pBC with other brain stem nuclei such as the ventral respiratory column and the retrotrapezoid nucleus, which can lead to a variety of multiphasic rhythms (Rubin et al. 2009); changes in cellular properties in response to hypoxia (Mironov et al. 1998; Mironov and Richter 1998); and additional sensory feedback pathways involving carbon dioxide sensing (Molkov et al. 2014) and lung/chest/abdominal stretch receptors (Coleridge and Coleridge 1994; Paintal 1973; Schläfke and Koepchen 1996; Widdicombe 1982).
These extensions would introduce challenges in the mathematical analysis of the resulting model. For example, inclusion of lung volume feedback modulation of inspiratory drive yields a closed-loop model with a mechanical control problem nested within the blood gas homeostatic control problem. Moreover, additional sensory feedback pathways may not converge on the same input (gtonic) used as the control variable in the present report. Incorporating multiple control pathways will significantly complicate the averaging analysis, just as systems with multiple slow variables are more challenging to analyze through fast-slow dissection than systems with a single slow variable (Bertram and Rubin 2017). However, what we would expect to carry over to a more elaborate model is that the timing of the sensory feedback, or different components of sensory feedback, would still be expected to play the predominant role in setting the timing of respiration rather than intrinsic properties of the CPG in isolation.
GRANTS
This work originated as an externally mentored postdoctoral project through the Mathematical Biosciences Institute [National Science Foundation (NSF) Grant DMS-1440386] and was partially supported by NSF Grants DMS-1413770 (P. J. Thomas), DMS-1412877 (C. O. Diekman), and DMS-155237 (C. O. Diekman).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
C.O.D., P.J.T., and C.G.W. conceived and designed research; C.O.D. and C.G.W. performed experiments; C.O.D., P.J.T., and C.G.W. analyzed data; C.O.D., P.J.T., and C.G.W. interpreted results of experiments; C.O.D., P.J.T., and C.G.W. prepared figures; C.O.D., P.J.T., and C.G.W. drafted manuscript; C.O.D., P.J.T., and C.G.W. edited and revised manuscript; C.O.D., P.J.T., and C.G.W. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Catherine A. Mayer and Paulina Getsy for technical assistance with the in vitro experiments, Joseph C. LaManna for helpful technical discussions, and Patricia O'Callaghan for a critical reading of the manuscript.
APPENDIX
To better understand the nature of the bistability between normal and reduced levels, we performed a fast-slow decomposition of the closed-loop system, treating as the slow variable and then approximating its dynamics with the method of averaging (Sanders et al. 2007).
Fast-Slow Decomposition
The application of singular perturbation methods developed by Fenichel and others (Fenichel 1979; Jones 1995; Rubin and Terman 2002a; Wiggins 1994) has led to rapid advances in understanding the geometry of bursting dynamics in numerous neural oscillators admitting a timescale separation between “slow” and “fast” variables (Bertram and Rubin 2017; Borisyuk and Rinzel 2005; Coombes and Bressloff 2005; Izhikevich 2000; Rinzel and Ermentrout 1989). The global structure of the flows in such systems is determined by the “slow” variables, for instance the persistent sodium gating variable h in the isolated BRS model (Best et al. 2005). In the case of a respiratory control loop, we embed the BRS model into a system including timescales for gas exchange, lung mechanics, and metabolic consumption of O2. What is, or what are, the “slow variables” in such a control system?
The closed-loop model is a 7D system of ordinary differential equations that includes timescales for a variety of processes (neuronal dynamics, lung mechanics, gas exchange, and metabolic consumption of oxygen), and several different partitions of the system into fast and slow subsystems are possible. To place disparate variables on a common basis, we calculated the maximum relative speed of the variable vx, defined as the maximum rate of change divided by the range of the variable. Formally,
| (24) |
where x′(t) is the time derivative dx/dt. The smaller vx is, the “slower” we consider x to be. We find that during eupneic bursting the intrinsic slowness of the variables spans multiple temporal scales, with , volL, and being an order of magnitude slower than h and α, which in turn are an order of magnitude slower than v and n (Fig. 16 and Table 1).
Averaging Analysis
To set up an averaging calculation to obtain the approximate dynamics of the control variable, y = , we write the closed-loop model in the following form:
| (25) |
| (26) |
where x = (V, h, n, α, volL, ) play the role of the dependent variables. The control variable, y = , is held constant and the dependent variables are allowed to evolve freely. The dependent subsystem dx/dt = f(x, y) will evolve either to a fixed point or to a (beating or bursting) limit cycle. If the dependent subsystem has a fixed point, then
| (27) |
is the reduced system for the evolution of the control variable, where O*(y) is the (y dependent) value of lung oxygen at the fixed point. If the dependent subsystem has a limit cycle γy(t) with period T(y), we obtain by numerically integrating g[γu(t), u] over one period T(u)
| (28) |
and the averaged equation for the dynamics of the control variable is
| (29) |
Floquet Analysis
The stability of periodic solutions can be determined with Floquet theory (Perko 2001). Suppose we have a period T limit cycle solution x = γ(t) of a system , . The linearization of the dynamics around the limit cycle are A(t) = Dx f[γ(t)], giving the periodically forced linear system
| (30) |
with the fundamental matrix Φ(t) satisfying
| (31) |
Floquet’s theorem says we can write Φ as
| (32) |
where Q(t) is T-periodic and B is a constant matrix. The eigenvalues of eBT are the Floquet multipliers μ1,..., μn, and they describe the cycle-to-cycle growth or decay of perturbations. One multiplier will be unity, corresponding to perturbations along γ(t). If any of the remaining multipliers have |μ| > 1, then the periodic solution is unstable.
In the closed-loop model, Dx is undefined at the transition from inspiration to expiration because the right-hand side of Eq. 14 is nondifferentiable at that point. Thus instead of solving the variational equation we compute Floquet multipliers through perturbation and direct simulation of the system equations alone. We start at a point x0 on the limit cycle and solve the initial value problem from 0 to T with for k = 1,…, 7. The are unit vectors, and ε must be small enough that we stay close to the limit cycle for one period but large enough that we are not overwhelmed by roundoff error. For the limit cycle on the boundary between eupnea and tachypnea the period T is 1,818.5 ms, and we have found ε = 10−7 to work well. We also simulate the unperturbed system, which after one period returns to xT ≈ x0. Let xk be the solution starting from . Then the seven vectors xk–xT form the columns of the (approximate) multiplier matrix, the eigenvalues of which are the Floquet multipliers. With x0 located at arrow b in Fig. 13A (v = −50.9617, n = 0.0041, h = 0.5126, α = 0.0012, volL = 2.2660, = 78.0837, = 77.2000), the following Floquet multipliers μ1,…, μ7 were obtained: 1.37, 1.00, 0.49, −0.01 + 0.01i, −0.01 − 0.01i, 0.00, and 0.00. Since μ1 > 1, we conclude that the limit cycle on the boundary between eupnea and tachypnea is unstable. Associated with each multiplier is an eigenvector ξi satisfying
| (33) |
The components of ξ1 contain information about how influential each of the seven closed-loop variables is in determining whether trajectories perturbed off of the boundary limit cycle will head toward eupnea or tachypnea. To ensure a fair comparison of the components, we rescaled the eigenvectors using scaling factors si defined as the magnitude of the change in each variable during one unperturbed period of the unstable limit cycle. The rescaled eigenvectors ζi are given by
| (34) |
with scaling matrix S = diag(s1, …, s7). The components of ζ1 computed with x0 located at four different points along the boundary limit cycle (arrows b–e in Fig. 13A) are shown in Fig. 13, B–E.
REFERENCES
- Bässler U. On the definition of central pattern generator and its sensory control. Biol Cybern 54: 65–69, 1986. doi: 10.1007/BF00337116. [DOI] [Google Scholar]
- Ben-Tal A, Smith JC. A model for control of breathing in mammals: coupling neural dynamics to peripheral gas exchange and transport. J Theor Biol 251: 480–497, 2008. doi: 10.1016/j.jtbi.2007.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Tal A, Tawhai MH. Integrative approaches for modeling regulation and function of the respiratory system. Wiley Interdiscip Rev Syst Biol Med 5: 687–699, 2013. doi: 10.1002/wsbm.1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benes GN, Barry AM, Kaper TJ, Kramer MA, Burke J. An elementary model of torus canards. Chaos 21: 023131, 2011. doi: 10.1063/1.3592798. [DOI] [PubMed] [Google Scholar]
- Bertram R, Butte MJ, Kiemel T, Sherman A. Topological and phenomenological classification of bursting oscillations. Bull Math Biol 57: 413–439, 1995. doi: 10.1007/BF02460633. [DOI] [PubMed] [Google Scholar]
- Bertram R, Rubin J. Multi-timescale systems and fast-slow analysis. Math Biosci 287: 105–121, 2017. doi: 10.1016/j.mbs.2016.07.003. [DOI] [PubMed] [Google Scholar]
- Best J, Borisyuk A, Rubin J, Terman D, Wechselberger M. The dynamic range of bursting in a model respiratory pacemaker network. SIAM J Appl Dyn Syst 4: 1107–1139, 2005. doi: 10.1137/050625540. [DOI] [Google Scholar]
- Borisyuk A, Rinzel J. Understanding neuronal dynamics by geometrical dissection of minimal models. In: Models and Methods in Neurophysics, Lecture Notes of the Les Houches Summer School 2005, edited by Chow C, Gutkin B, Hansel D, Meunier C, Dalibard J. Amsterdam: Elsevier, 2005, p. 19–72. [Google Scholar]
- Burke J, Desroches M, Barry AM, Kaper TJ, Kramer MA. A showcase of torus canards in neuronal bursters. J Math Neurosci 2: 3, 2012. doi: 10.1186/2190-8567-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butera RJ Jr, Clark JW Jr, Byrne JH, Rinzel J. Dissection and reduction of a modeled bursting neuron. J Comput Neurosci 3: 199–223, 1996. doi: 10.1007/BF00161132. [DOI] [PubMed] [Google Scholar]
- Butera RJ Jr, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons. J Neurophysiol 82: 382–397, 1999a. [DOI] [PubMed] [Google Scholar]
- Butera RJ Jr, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex. II. Populations of coupled pacemaker neurons. J Neurophysiol 82: 398–415, 1999b. [DOI] [PubMed] [Google Scholar]
- Cheng L, Ivanova O, Fan HH, Khoo MC. An integrative model of respiratory and cardiovascular control in sleep-disordered breathing. Respir Physiol Neurobiol 174: 4–28, 2010. doi: 10.1016/j.resp.2010.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clewley R, Rotstein HG, Kopell N. A computational tool for the reduction of nonlinear ODE systems possessing multiple scales. Multiscale Model Simul 4: 732–759, 2005. doi: 10.1137/040615535. [DOI] [Google Scholar]
- Coleridge HM, Coleridge JC. Pulmonary reflexes: neural mechanisms of pulmonary defense. Annu Rev Physiol 56: 69–91, 1994. doi: 10.1146/annurev.ph.56.030194.000441. [DOI] [PubMed] [Google Scholar]
- Coombes S, Bressloff PC, editors. Bursting: The Genesis of Rhythm in the Nervous System. Singapore: World Scientific, 2005. doi: 10.1142/5944. [DOI] [Google Scholar]
- Cowan NJ, Ankarali MM, Dyhr JP, Madhav MS, Roth E, Sefati S, Sponberg S, Stamper SA, Fortune ES, Daniel TL. Feedback control as a framework for understanding tradeoffs in biology. Integr Comp Biol 54: 223–237, 2014. doi: 10.1093/icb/icu050. [DOI] [PubMed] [Google Scholar]
- D’Agostino D, Mazza E Jr, Neubauer JA. Heme oxygenase is necessary for the excitatory response of cultured neonatal rat rostral ventrolateral medulla neurons to hypoxia. Am J Physiol Regul Integr Comp Physiol 296: R102–R118, 2009. doi: 10.1152/ajpregu.90325.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Negro CA, Morgado-Valle C, Hayes JA, Mackay DD, Pace RW, Crowder EA, Feldman JL. Sodium and calcium current-mediated pacemaker neurons and respiratory rhythm generation. J Neurosci 25: 446–453, 2005. doi: 10.1523/JNEUROSCI.2237-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekman CO, Wilson CG, Thomas PJ. Spontaneous autoresuscitation in a model of respiratory control. Conf Proc IEEE Eng Med Biol Soc 2012: 6669–6672, 2012. [DOI] [PubMed] [Google Scholar]
- Dunmyre JR, Del Negro CA, Rubin JE. Interactions of persistent sodium and calcium-activated nonspecific cationic currents yield dynamically distinct bursting regimes in a model of respiratory neurons. J Comput Neurosci 31: 305–328, 2011. doi: 10.1007/s10827-010-0311-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldridge F. The North Carolina respiratory model. A multipurpose model for studying the control of breathing. In: Bioengineering Approaches to Pulmonary Physiology and Medicine, edited by Khoo M. New York: Plenum, 1996, p. 25–49. doi: 10.1007/978-0-585-34964-0_2. [DOI] [Google Scholar]
- Erickson JT, Sposato BC. Autoresuscitation responses to hypoxia-induced apnea are delayed in newborn 5-HT-deficient Pet-1 homozygous mice. J Appl Physiol (1985) 106: 1785–1792, 2009. doi: 10.1152/japplphysiol.90729.2008. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Philadelphia, PA: SIAM, 2002. doi: 10.1137/1.9780898718195. [DOI] [Google Scholar]
- Ermentrout GB, Terman DH. Mathematical of Foundations Neuroscience. New York: Springer, 2010. doi: 10.1007/978-0-387-87708-2. [DOI] [Google Scholar]
- Feldman JL, Del Negro CA, Gray PA. Understanding the rhythm of breathing: so near, yet so far. Annu Rev Physiol 75: 423–452, 2013. doi: 10.1146/annurev-physiol-040510-130049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenichel N. Geometric singular perturbation theory for ordinary differential equations. J Differ Equ 31: 53–98, 1979. doi: 10.1016/0022-0396(79)90152-9. [DOI] [Google Scholar]
- Full RJ, Koditschek DE. Templates and anchors: neuromechanical hypotheses of legged locomotion on land. J Exp Biol 202: 3325–3332, 1999. [DOI] [PubMed] [Google Scholar]
- Gaspard P. Measurement of the instability rate of a far-from-equilibrium steady state at an infinite period bifurcation. J Phys Chem 94: 1–3, 1990. doi: 10.1021/j100364a001. [DOI] [Google Scholar]
- Givan SA, Cummings KJ. Intermittent severe hypoxia induces plasticity within serotonergic and catecholaminergic neurons in the neonatal rat ventrolateral medulla. J Appl Physiol (1985) 120: 1277–1287, 2016. doi: 10.1152/japplphysiol.00048.2016. [DOI] [PubMed] [Google Scholar]
- Grodins F. Control Theory and Biological Systems. New York: Columbia Univ. Press, 1963. [Google Scholar]
- Grodins FS, Buell J, Bart AJ. Mathematical analysis and digital simulation of the respiratory control system. J Appl Physiol 22: 260–276, 1967. [DOI] [PubMed] [Google Scholar]
- Grodins FS, Gray JS, Schroeder KR, Norins AL, Jones RW. Respiratory responses to CO2 inhalation; a theoretical study of a nonlinear biological regulator. J Appl Physiol 7: 283–308, 1954. [DOI] [PubMed] [Google Scholar]
- Guntheroth WG. Cheyne-Stokes respiration: hypoxia plus a deep breath that interrupts hypoxic drive, initiating cyclic breathing. Med Hypotheses 77: 714–716, 2011. doi: 10.1016/j.mehy.2011.07.023. [DOI] [PubMed] [Google Scholar]
- Hlastala MP, Berger AJ. Physiology of Respiration. New York: Oxford Univ. Press, 2001. [Google Scholar]
- Izhikevich EM. Neural excitability, spiking, and bursting. Int J Bifurcat Chaos 10: 1171–1266, 2000. doi: 10.1142/S0218127400000840. [DOI] [Google Scholar]
- Izhikevich EM. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge, MA: MIT Press, 2007. [Google Scholar]
- Jones C. Geometric singular perturbation theory. In: Dynamical Systems, No. 1609 of Lecture Notes in Mathematics, edited by Johnson R. Berlin: Springer, 1995, p. 44–118. [Google Scholar]
- Kandel ER, Schwartz JH, Jessell TM. Principles of Neural Science. New York: Elsevier, 1991. [Google Scholar]
- Keener J, Sneyd J. Mathematical Physiology. II. Systems Physiology. New York: Springer, 2009. [Google Scholar]
- Khoo MC. A model-based evaluation of the single-breath CO2 ventilatory response test. J Appl Physiol (1985) 68: 393–399, 1990. [DOI] [PubMed] [Google Scholar]
- Koizumi H, Wilson CG, Wong S, Yamanishi T, Koshiya N, Smith JC. Functional imaging, spatial reconstruction, and biophysical analysis of a respiratory motor circuit isolated in vitro. J Neurosci 28: 2353–2365, 2008. doi: 10.1523/JNEUROSCI.3553-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koshiya N, Smith JC. Neuronal pacemaker for breathing visualized in vitro. Nature 400: 360–363, 1999. doi: 10.1038/22540. [DOI] [PubMed] [Google Scholar]
- Kramer MA, Traub RD, Kopell NJ. New dynamics in cerebellar Purkinje cells: torus canards. Phys Rev Lett 101: 068103, 2008. doi: 10.1103/PhysRevLett.101.068103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindsey BG, Rybak IA, Smith JC. Computational models and emergent properties of respiratory neural networks. Compr Physiol 2: 1619–1670, 2012. doi: 10.1002/cphy.c110016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longobardo G, Evangelisti CJ, Cherniack NS. Introduction of respiratory pattern generators into models of respiratory control. Respir Physiol Neurobiol 148: 285–301, 2005. doi: 10.1016/j.resp.2005.02.005. [DOI] [PubMed] [Google Scholar]
- Lyttle DN, Gill JP, Shaw KM, Thomas PJ, Chiel HJ. Robustness, flexibility, and sensitivity in a multifunctional motor control model. Biol Cybern 111: 25–47, 2017. doi: 10.1007/s00422-016-0704-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin RJ, Di Fiore JM, Macfarlane PM, Wilson CG. Physiologic basis for intermittent hypoxic episodes in preterm infants. Adv Exp Med Biol 758: 351–358, 2012. doi: 10.1007/978-94-007-4584-1_47. [DOI] [PubMed] [Google Scholar]
- McDougal RA, Morse TM, Carnevale T, Marenco L, Wang R, Migliore M, Miller PL, Shepherd GM, Hines ML. Twenty years of ModelDB and beyond: building essential modeling tools for the future of neuroscience. J Comput Neurosci 42: 1–10, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mironov SL, Langohr K, Haller M, Richter DW. Hypoxia activates ATP-dependent potassium channels in inspiratory neurones of neonatal mice. J Physiol 509: 755–766, 1998. doi: 10.1111/j.1469-7793.1998.755bm.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mironov SL, Richter DW. L-type Ca2+ channels in inspiratory neurones of mice and their modulation by hypoxia. J Physiol 512: 75–87, 1998. doi: 10.1111/j.1469-7793.1998.075bf.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mironov SL, Richter DW. Intracellular signalling pathways modulate KATP channels in inspiratory brainstem neurones and their hypoxic activation: involvement of metabotropic receptors, G-proteins and cytoskeleton. Brain Res 853: 60–67, 2000. doi: 10.1016/S0006-8993(99)02234-9. [DOI] [PubMed] [Google Scholar]
- Mironov SL, Richter DW. Oscillations and hypoxic changes of mitochondrial variables in neurons of the brainstem respiratory centre of mice. J Physiol 533: 227–236, 2001. doi: 10.1111/j.1469-7793.2001.0227b.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohr MA, Fairchild KD, Patel M, Sinkin RA, Clark MT, Moorman JR, Lake DE, Kattwinkel J, Delos JB. Quantification of periodic breathing in premature infants. Physiol Meas 36: 1415–1427, 2015. doi: 10.1088/0967-3334/36/7/1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molkov YI, Shevtsova NA, Park C, Ben-Tal A, Smith JC, Rubin JE, Rybak IA. A closed-loop model of the respiratory system: focus on hypercapnia and active expiration. PLoS One 9: e109894, 2014. doi: 10.1371/journal.pone.0109894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connor R, Segers LS, Morris KF, Nuding SC, Pitts T, Bolser DC, Davenport PW, Lindsey BG. A joint computational respiratory neural network-biomechanical model for breathing and airway defensive behaviors. Front Physiol 3: 264, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paintal AS. Vagal sensory receptors and their reflex effects. Physiol Rev 53: 159–227, 1973. [DOI] [PubMed] [Google Scholar]
- Patel M, Mohr M, Lake D, Delos J, Moorman JR, Sinkin RA, Kattwinkel J, Fairchild K. Clinical associations with immature breathing in preterm infants. Part 2—periodic breathing. Pediatr Res 80: 28–34, 2016. doi: 10.1038/pr.2016.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawar A, Peng YJ, Jacono FJ, Prabhakar NR. Comparative analysis of neonatal and adult rat carotid body responses to chronic intermittent hypoxia. J Appl Physiol (1985) 104: 1287–1294, 2008. doi: 10.1152/japplphysiol.00644.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perko LJ. Differential Equations and Dynamical Systems. New York: Springer, 2001. doi: 10.1007/978-1-4613-0003-8. [DOI] [Google Scholar]
- Prabhakar NR, Peng YJ, Kumar GK, Pawar A. Altered carotid body function by intermittent hypoxia in neonates and adults: relevance to recurrent apneas. Respir Physiol Neurobiol 157: 148–153, 2007. doi: 10.1016/j.resp.2006.12.009. [DOI] [PubMed] [Google Scholar]
- Ramirez JM, Telgkamp P, Elsen FP, Quellmalz UJ, Richter DW. Respiratory rhythm generation in mammals: synaptic and membrane properties. Respir Physiol 110: 71–85, 1997. doi: 10.1016/S0034-5687(97)00074-1. [DOI] [PubMed] [Google Scholar]
- Rinzel J. A formal classification of bursting mechanisms in excitable systems. In: Mathematical Topics in Population Biology, Morphogenesis, and Neurosciences, edited by Teramoto E, Yamaguti M. Berlin: Springer, 1987, Lecture Notes in Biomathematics, Vol. 71. [Google Scholar]
- Rinzel J, Ermentrout G. Analysis of neural excitability and oscillations. In: Methods in Neuronal Modeling, edited by Koch C, Segev I. Cambridge, MA: MIT Press, 1989. [Google Scholar]
- Roberts KL, Rubin JE, Wechselberger M. Averaging, folded singularities, and torus canards: explaining transitions between bursting and spiking in a coupled neuron model. SIAM J Appl Dyn Syst 14: 1808–1844, 2015. doi: 10.1137/140981770. [DOI] [Google Scholar]
- Roth E, Sponberg S, Cowan NJ. A comparative approach to closed-loop computation. Curr Opin Neurobiol 25: 54–62, 2014. doi: 10.1016/j.conb.2013.11.005. [DOI] [PubMed] [Google Scholar]
- Rubin J, Terman D.. Geometric singular pertubation analysis of neuronal dynamics. In: Handbook of Dynamical Systems, Vol. 2: Towards Applications, edited by Fiedler B. Amsterdam: Elsevier, 2002a, p. 93–146. [Google Scholar]
- Rubin J, Terman D. Synchronized activity and loss of synchrony among heterogeneous conditional oscillators. SIAM J Appl Dyn Syst 1: 146–174, 2002b. doi: 10.1137/S111111110240323X. [DOI] [Google Scholar]
- Rubin JE, Shevtsova NA, Ermentrout GB, Smith JC, Rybak IA. Multiple rhythmic states in a model of the respiratory central pattern generator. J Neurophysiol 101: 2146–2165, 2009. doi: 10.1152/jn.90958.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutland PC, Pembrey ME, Davies T. The estimation of fetal haemoglobin in healthy adults by radioimmunoassay. Br J Haematol 53: 673–682, 1983. doi: 10.1111/j.1365-2141.1983.tb07319.x. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Abdala AP, Markin SN, Paton JF, Smith JC. Spatial organization and state-dependent mechanisms for respiratory rhythm and pattern generation. Prog Brain Res 165: 201–220, 2007. doi: 10.1016/S0079-6123(06)65013-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders J, Verhulst F, Murdock J. Averaging Methods in Nonlinear Dynamical Systems. New York: Springer, 2007. [Google Scholar]
- Schläfke M, Koepchen H. A systems view of respiratory regulation. In: Comprehensive Human Physiology, edited by Greger R, Windhorst U. New York: Springer, 1996, p. 2097–2127. doi: 10.1007/978-3-642-60946-6_107. [DOI] [Google Scholar]
- Shimkin N. Nonlinear control systems. In: Encyclopedia of Neuroscience, edited by Binder M, Hirokawa N, Windhorst U. Berlin: Springer, 2009, p. 2886–2889. doi: 10.1007/978-3-540-29678-2_4021. [DOI] [Google Scholar]
- Siljehav V, Shvarev Y, Herlenius E. Il-1β and prostaglandin E2 attenuate the hypercapnic as well as the hypoxic respiratory response via prostaglandin E receptor type 3 in neonatal mice. J Appl Physiol (1985) 117: 1027–1036, 2014. doi: 10.1152/japplphysiol.00542.2014. [DOI] [PubMed] [Google Scholar]
- Smith JC, Abdala AP, Koizumi H, Rybak IA, Paton JF. Spatial and functional architecture of the mammalian brain stem respiratory network: a hierarchy of three oscillatory mechanisms. J Neurophysiol 98: 3370–3387, 2007. doi: 10.1152/jn.00985.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JC, Butera RJ Jr, Koshiya N, Del Negro C, Wilson CG, Johnson SM. Respiratory rhythm generation in neonatal and adult mammals: the hybrid pacemaker-network model. Respir Physiol 122: 131–147, 2000. doi: 10.1016/S0034-5687(00)00155-9. [DOI] [PubMed] [Google Scholar]
- Smith JC, Ellenberger HH, Ballanyi K, Richter DW, Feldman JL. Pre-Bötzinger complex: a brainstem region that may generate respiratory rhythm in mammals. Science 254: 726–729, 1991. doi: 10.1126/science.1683005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takakura AC, Moreira TS, West GH, Gwilt JM, Colombari E, Stornetta RL, Guyenet PG. GABAergic pump cells of solitary tract nucleus innervate retrotrapezoid nucleus chemoreceptors. J Neurophysiol 98: 374–381, 2007. doi: 10.1152/jn.00322.2007. [DOI] [PubMed] [Google Scholar]
- Teitel D, Rudolph AM. Perinatal oxygen delivery and cardiac function. Adv Pediatr 32: 321–347, 1985. [PubMed] [Google Scholar]
- Wang Y, Rubin JE. Multiple timescale mixed bursting dynamics in a respiratory neuron model. J Comput Neurosci 41: 245–268, 2016. doi: 10.1007/s10827-016-0616-6. [DOI] [PubMed] [Google Scholar]
- West JB. Respiratory Physiology: The Essentials. Philadelphia, PA: Lippincott Williams & Wilkins, 2008. [Google Scholar]
- Widdicombe JG. Pulmonary and respiratory tract receptors. J Exp Biol 100: 41–57, 1982. [DOI] [PubMed] [Google Scholar]
- Wiggins S. Normally Hyperbolic Invariant Manifolds in Dynamical Systems, No. 105 in Applied Mathematical Sciences. New York: Springer, 1994. doi: 10.1007/978-1-4612-4312-0. [DOI] [Google Scholar]