Treadmill vs. overground walking: different response to physical interaction

We show that the response of human locomotion to physical interaction differs between treadmill and overground walking. Subjects entrained to a periodic series of ankle plantar flexion torque pulses that shifted their gait cadence, synchronizing ankle push-off with the pulses (so that they assisted propulsion) even when gait cadence slowed. Entrainment was faster overground and, on removal of torque pulses, the entrained gait period persisted more prominently overground, indicating a neural adaptation of locomotor control.

Abstract

Rehabilitation of human motor function is an issue of growing significance, and human-interactive robots offer promising potential to meet the need. For the lower extremity, however, robot-aided therapy has proven challenging. To inform effective approaches to robotic gait therapy, it is important to better understand unimpaired locomotor control: its sensitivity to different mechanical contexts and its response to perturbations. The present study evaluated the behavior of 14 healthy subjects who walked on a motorized treadmill and overground while wearing an exoskeletal ankle robot. Their response to a periodic series of ankle plantar flexion torque pulses, delivered at periods different from, but sufficiently close to, their preferred stride cadence, was assessed to determine whether gait entrainment occurred, how it differed across conditions, and if the adapted motor behavior persisted after perturbation. Certain aspects of locomotor control were exquisitely sensitive to walking context, while others were not. Gaits entrained more often and more rapidly during overground walking, yet, in all cases, entrained gaits synchronized the torque pulses with ankle push-off, where they provided assistance with propulsion. Furthermore, subjects entrained to perturbation periods that required an adaption toward slower cadence, even though the pulses acted to accelerate gait, indicating a neural adaptation of locomotor control. Lastly, during 15 post-perturbation strides, the entrained gait period was observed to persist more frequently during overground walking. This persistence was correlated with the number of strides walked at the entrained gait period (i.e., longer exposure), which also indicated a neural adaptation.

NEW & NOTEWORTHY We show that the response of human locomotion to physical interaction differs between treadmill and overground walking. Subjects entrained to a periodic series of ankle plantar flexion torque pulses that shifted their gait cadence, synchronizing ankle push-off with the pulses (so that they assisted propulsion) even when gait cadence slowed. Entrainment was faster overground and, on removal of torque pulses, the entrained gait period persisted more prominently overground, indicating a neural adaptation of locomotor control.

the demand for effective rehabilitation of human motor function continues to grow with the graying of the population and the rise of age-related disorders. Robot-aided therapy has emerged as a promising method to help meet the need. While upper limb therapy has been successful (Kwakkel et al. 2008; Lo et al. 2010; Volpe et al. 2000; Winstein et al. 2016), lower extremity robotic therapy has proven challenging (Hidler et al. 2009; Hornby et al. 2008; Miller et al. 2010; Winstein et al. 2016). The goal of this study was to better understand the underlying neuromechanical dynamics and control of healthy locomotion to inform the development of effective approaches for robotic walking therapy.

A conventional method of walking therapy consists of providing patients with a repetitive walking pattern, often achieved by manually moving their lower extremities. Following this approach, available therapeutic robots for walking, which are largely “non-back-drivable,” emphasize tracking preplanned kinematic trajectories (Duschau-Wicke et al. 2010a, 2010b). This technique, however, may discourage voluntary participation of patients, since these robots respond poorly (if at all) to patients’ attempts to deviate from the imposed motion. As a result, patients are induced to passively allow the machine to generate the motion (Hidler et al. 2009). Previous research in upper limb rehabilitation has shown that patients must be actively engaged in making movements (Colombo et al. 2007; Maclean et al. 2000, 2002). In addition, this technique of imposing motion may interfere with the natural oscillatory dynamics of human locomotion. Furthermore, lower extremity therapies generally require patients to walk on motorized treadmills, yet motor-driven, treadmill-enforced locomotion may not reflect the “natural dynamics” of human walking. Even without a robot involved, a trial assessing the effect of body weight-supported treadmill training revealed no superior improvements in patients’ functional walking compared with results achieved via progressive home-based training (Duncan et al. 2007, 2011). Indeed, evidence from various studies has emphasized dynamic and mechanical differences between treadmill (TM) and overground (OG) walking (Dingwell et al. 2001; Dingwell and Kang 2007; Lee and Hidler 2008; Riley et al. 2007; White et al. 1998). Building on prior research (Ahn and Hogan 2012a), this study examined how to guide locomotor behavior with minimal encumbrance. Specifically, we applied a periodic series of torque pulses to the ankle joint to 1) assess the sensitivity of locomotor control to treadmill vs. overground contexts; and 2) investigate the neural vs. biomechanical contributions of the locomotor response to these mechanical perturbations.

Prior research by Taga and colleagues (Taga et al. 1991) indicated that human locomotion is achieved as a “global limit-cycle generated by a global entrainment” between the rhythmic behavior of oscillators in both the nervous system and the mechanical periphery. This postulated limit cycle, however, may be inadvertently disrupted by encumbering robots and/or treadmills. A minimally encumbering approach to guide locomotor behavior was proposed by Ahn and Hogan (2012a). In a first study, they presented evidence that unimpaired subjects entrained their gait to a series of periodic mechanical perturbations at the ankle joint delivered by an exoskeletal ankle robot. These perturbations consisted of brief plantar flexion torque pulses with periods that were sufficiently close to subjects’ preferred walking period. While entrainment required the periodic torque pulses to occur at the same constant phase in every stride, it did not constrain convergence to any specific phase. Remarkably, subjects’ gait robustly synchronized with the torque pulses at ankle push-off, giving assistive function to the plantar flexion torque during forward propulsion. A subsequent pilot study showed that neurologically impaired patients also entrained their gait to these mechanical perturbations, maintained that entrainment as the pace of perturbations increased, and sustained the faster cadence when the perturbations were discontinued (Ahn et al. 2011).

A limitation of those studies, however, was that, because the treadmill’s speed was constant, at the subject’s preferred speed, the locomotor cycle was artificially constrained. Shortening of stride period required a concomitant shortening of stride length (and vice versa). To understand how the walking context influences the underlying dynamics of locomotion (aim 1), this study examined the effect of mechanical torque pulses during OG walking, in the absence of a constant speed constraint. We hypothesized that entrained gaits during OG walking would also synchronize with the torque pulses at ankle push-off (hypothesis 1.1), and that convergence during OG walking would require fewer perturbation cycles than during TM walking (hypothesis 1.2).

The perturbation period subjects entrained to and the possible persistence of the entrained stride period during post-perturbation walking may illuminate the neural vs. biomechanical contributions of the locomotor response to the imposed perturbations (aim 2). Ahn and Hogan’s work showed entrainment to both shorter and longer (than preferred) perturbation periods during TM walking, with the perturbations occurring at ankle push-off (Ahn and Hogan 2012a). With constant treadmill speed, faster cadence required shorter step length, and slower cadence required longer step length. Overground, faster cadence might yield faster walking speed, which may be assisted by plantar flexion torque pulses at ankle push-off. In contrast, slower cadence would be opposed by plantar flexion torque at ankle push-off. We expected that convergence to shorter perturbation periods would require fewer perturbation cycles than to longer periods (hypothesis 2.1).

Regarding post-perturbation walking, Ahn and Hogan (2012a) reported that the entrained gait period persisted for 15 treadmill strides after perturbation in 33% of the unimpaired entrained gaits. Similar results were also found with neurologically impaired patients (Ahn et al. 2011). Entrained gaits that were attracted back toward their unperturbed stride period, however, may have been influenced by the constant treadmill speed set before perturbation to establish preferred cadence. Overground, entrained gaits would not be artificially constrained by a constant (belt) speed that could “drag” subjects’ cadence back to its preferred value after pulses were discontinued. Hence, we anticipated that persistence of the entrained gait period would occur more frequently during OG than TM walking (hypothesis 2.2).

These hypotheses were tested with unimpaired human subjects who walked on a motorized treadmill and overground, while wearing an ankle robot that applied a periodic series of brief plantar flexion torque pulses, delivered at periods that were 50 ms shorter or longer than subjects’ preferred stride period. Entrainment was observed in 46 (out of 56) trials across all four experimental conditions. Results emphasized the sensitivity of unimpaired locomotor control to walking context via more frequent and sooner gait convergence during OG than TM walking. Other aspects of gait entrainment, however, were insensitive to the mechanical context and the perturbation period: all entrained gaits synchronized with the torque pulses at ankle push-off, where they provided assistance with propulsion. Moreover, gait entrainment to longer perturbation periods was observed even when the torque pulses assisted forward propulsion, suggesting a neural adaptation that cannot be ascribed to biomechanics alone. Lastly, post-perturbation walking revealed more frequent persistence of the entrained gait period during OG walking. Persistence of the entrained gait was correlated with the number of strides walked at the entrained gait period (i.e., longer exposure to the new coordination pattern), reinforcing the suggestion of an underlying neural adaption of the locomotor process.

METHODS

Participants, Equipment, and Protocols

Fourteen subjects (ages 20–29 yr; eight men and six women; height = 1.73 ± 0.12 m; weight = 67.61 ± 14.41 kg) who reported no neurological or biomechanical impairments participated in this experimental study. All participants gave informed consent in accordance with procedures approved by the Institutional Review Board of the Massachusetts Institute of Technology (MIT). Each subject performed four trials of at least 80 strides, two walking on a Sole Fitness F80 treadmill (with a 0.84 × 1.90 m deck and 0.045 m/s belt speed resolution), and two other trials walking overground in a long corridor at MIT. For both walking conditions, two different perturbation periods were delivered, one that was shorter and one that was longer than the preferred period. In all trials, subjects performed a cognitive distractor task that consisted of listing countries, cities, animals, etc., in alphabetical order (one category at a time). Subjects were instructed to walk at their preferred speed, but they were neither informed that the torque pulses would be delivered periodically, nor asked to “entrain” to these perturbations.

The robot used in these experiments was the Anklebot by Interactive Motion Technologies (Fig. 1). This wearable therapeutic robot, detailed in Roy et al. (2009), attached to the leg via a knee brace and a customized shoe, allowing normal range of motion in all degrees of freedom of the ankle. The design of this device enabled its application to both TM and OG walking. A potentiometer embedded in the knee brace recorded the subjects’ knee angle profile during walking. The Anklebot’s highly back-drivable linear actuators were capable of actuating the ankle in dorsi-/plantar flexion and inversion/eversion while minimally impeding natural movement. Subjects wore one Anklebot on their preferred leg. The effect of unilateral loading of this device on gait symmetry had been previously investigated with stroke patients in Khanna et al. (2010). Their results revealed no significant effects on spatiotemporal parameters of gait, indicating that the robot design did not obstruct ankle motion.

Fig. 1.

An unimpaired human subject wearing the Anklebot, including the knee brace, custom designed shoes, and harness.

Most of the robot’s weight (3.6 kg) is concentrated at the knee and borne by the thigh, leaving the shank or foot free to move and minimizing the added inertia that opposes foot motion during locomotion. In all trials, subjects wore a harness to distribute the weight of the Anklebot over the upper body. The robot was preprogrammed to deliver a periodic series of square plantar flexion torque pulses that were subtle yet perceptible, in the same fashion as in Ahn and Hogan (2012a). The magnitude (10 N·m) and duration (100 ms) of these torque pulses were selected to approximate 10% of maximum ankle torque and 10% of one stride duration in normal adult walking, respectively (Kadaba et al. 1989; Murray et al. 1964; Perry and Burnfield 2010). In addition to exerting the torque pulses, the robot behaved like a torsional spring-and-damper¹ with 5 N·m/rad stiffness, 1 N·m·s/rad damping, referenced to a constant equilibrium position measured from the subject’s upright posture as in Ahn and Hogan (2012a).

Treadmill and Overground Trials

Each TM trial began with subjects gradually increasing the treadmill belt speed until reaching their preferred walking speed. The selected speed was recorded and maintained throughout the duration of any one trial. The first 15 strides were considered transitional strides and not included in subsequent data analysis. Subjects’ preferred stride duration (τ₀) was then measured as the average duration of the subsequent 15 strides. In principle, each trial could have had a different period. As results show below, the preferred periods were largely consistent across the two TM trials (see Table 1). The perturbation period (τ_p) was selected to be 50 ms shorter (τ_p = τ₀ – 50 ms) (TM-shorter) or longer (τ_p = τ₀ + 50 ms) (TM-longer) than subjects’ preferred stride duration. Each trial was divided into three consecutive sections: Before, During, and After. The Before section consisted of 15 strides with no perturbation. The During section comprised a periodic series of 50 consecutive perturbations initiated by the experimenter at random gait phases. In the After section, the robot stopped exerting the torque pulses, but maintained its spring-damper behavior while subjects walked another 15 strides. Subsequently, subjects stopped walking and the trial terminated. Trial duration varied between subjects, on average lasting about 3 min.

Table 1.

Subjects’ preferred stride periods before perturbation in TM and OG trials

	Preferred TM Stride Period		Preferred OG Stride Period
Subject ID	Mean	SD	Mean	SD
S1	1.33	0.041	1.23	0.067
	1.32	0.040	1.26	0.050
S2	1.32	0.039	1.20	0.053
	1.31	0.042	1.27	0.048
S3	1.46	0.024	1.29	0.043
	1.46	0.034	1.29	0.039
S4	1.72	0.030	1.22	0.058
	1.66	0.055	1.23	0.068
S5	1.50	0.032	1.29	0.046
	1.55	0.042	1.31	0.049
S6	1.03	0.014	0.99	0.046
	1.04	0.021	1.00	0.038
S7	1.55	0.019	1.27	0.048
	1.50	0.016	1.26	0.030
S8	1.45	0.024	1.04	0.060
	1.39	0.043	1.03	0.054
S9	1.46	0.051	1.22	0.074
	1.41	0.054	1.19	0.059
S10	1.22	0.014	1.20	0.041
	1.25	0.011	1.20	0.044
S11	1.27	0.023	1.22	0.053
	1.32	0.044	1.24	0.038
S12	1.55	0.019	1.31	0.045
	1.42	0.040	1.29	0.049
S13	1.28	0.017	1.18	0.026
	1.24	0.012	1.20	0.029
S14	1.36	0.043	1.26	0.064
	1.33	0.041	1.21	0.055
All Subjects	1.38	0.032	1.21	0.049

Values are means ± SD in seconds. Values for the two trials are shown for each subject (S1–S14). Boldface values correspond to non-entrained gaits.

OG trials differed from TM trials mainly in that there was no fixed walking speed constraint, i.e., subjects were asked to walk at their preferred speed, which could vary throughout a single trial. After the first 15 transitional strides, subjects’ preferred stride duration was measured as the average duration of the subsequent 15 strides. As for TM trials, the two OG trials showed very similar preferred periods for each subject (see Table 1). OG trials were conducted in the same fashion as TM trials, with shorter (OG-shorter) and longer (OG-longer) perturbation periods (again, with a 50-ms offset from preferred stride period). Throughout OG trials, subjects were followed from a close distance by the experimenters, who moved the computer equipment on a rolling cart.

Data Analysis

All data collected from onboard sensors were recorded at a sampling rate of 200 Hz. Subjects’ stride durations before, during, and after perturbation were compared to evaluate whether mechanical perturbations slowed down or sped up the subjects’ walking cadence. Statistical analyses were performed using JMP Pro statistical software package (SAS Institute) with significance level set at 5%.

Gait cycle.

To assess convergence of stride period to the perturbation period, an estimate of consecutive gait cycles (and stride durations) was needed. The gait cycle was estimated from extrema in the continuous knee angle profile (recorded by a potentiometer embedded in the Anklebot’s knee brace), which was filtered using a fourth-order, zero-lag, low-pass filter with 7-Hz cutoff frequency. Four landmarks were identified: maximum knee flexion during stance phase, maximum knee extension during terminal stance phase, maximum knee flexion during swing phase, and maximum knee extension during terminal swing phase before heel strike. The knee angle profile was normalized from 0 to 100% to define a gait phase for each stride, with 100% defined as the maximum knee extension adjacent to heel strike (0%) (Fig. 2).

Fig. 2.

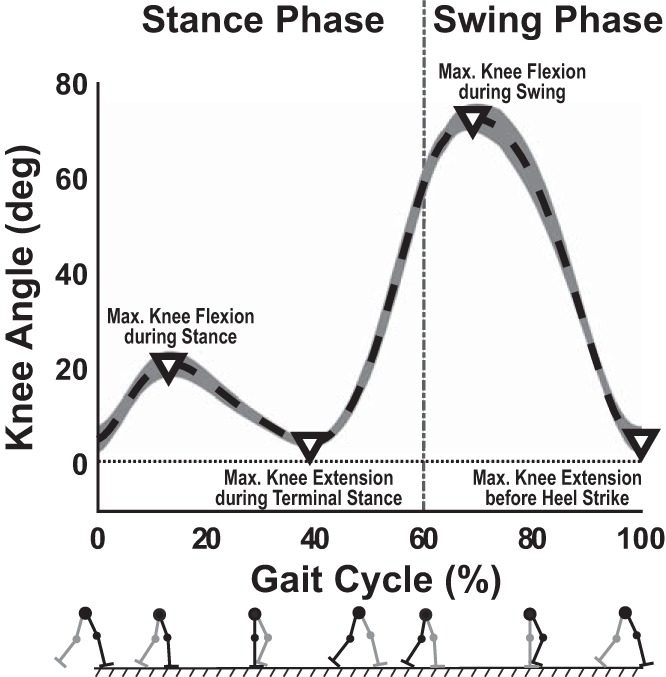
Typical knee angle trajectory [mean (dashed line) ± SD (shading)] vs. gait phase (in percent) over 25 consecutive strides. The trajectory illustrates the four extrema (∇) that defined the gait cycle from 0 to 100%.

Assessment of entrainment.

When a subject’s gait is entrained to the applied torque pulses, the stride period must equal the period of the imposed torque pulses; i.e., entrainment requires each pulse to occur at the same phase of the gait cycle. However, entrainment does not limit convergence to any particular constant phase.

The torque pulse phase was defined as the percentage of the gait cycle at the onset of the torque pulse. The 50 torque pulse phases were calculated in reverse order, starting from the 50th torque pulse. To avoid sudden jumps in the torque pulse phase when the onset of a pulse crossed the 0 or 100% boundaries, wrap-arounds in the gait cycle were allowed (i.e., torque pulse phase values >100% or <0%).

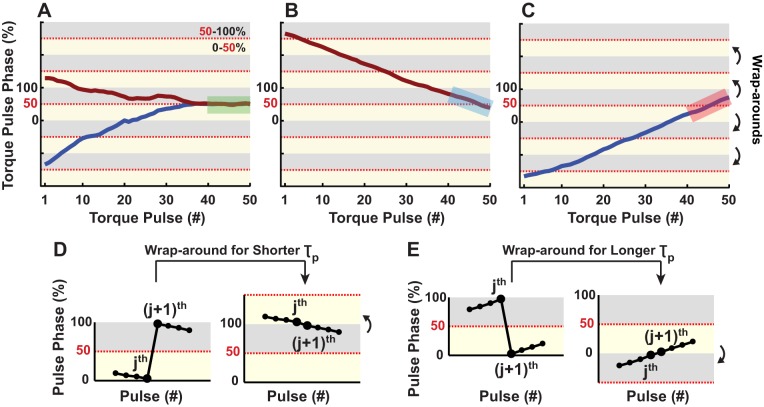
A linear regression of torque pulse phase onto pulse number was applied to the last 10 pulses in each trial; entrainment was indicated if the 95% confidence interval of the slope (m) of this line included zero slope. If the null hypothesis was accepted (H₀: m = 0), then the gait was considered entrained. Trials for which H₀ was rejected were defined as not entrained to longer τ_p (m > 0) or not entrained to shorter τ_p (m < 0). Figure 3, A–C, shows three representative cases of entrained and non-entrained gaits. Figure 3, D and E, shows a schematic representation of wrap-arounds in the gait cycle for shorter and longer τ_p, respectively.

Fig. 3.

Torque pulse phase as a function of torque pulse number, with emphasis on the last 10 torque pulses for three representative scenarios. A: two regression slopes (m) not significantly different from zero, in gaits entrained to shorter (burgundy, m ≈ 0.023) and longer (blue, m ≈ 0.014) τ_p. B: significantly negative regression slope in a gait that did not entrain to shorter τ_p (m ≈ −4.59). C: significantly positive regression slope in a gait that did not entrain to longer τ_p (m ≈ 5.51). Each shaded region in light yellow corresponds to torque pulses occurring within the first half of the gait cycle (0–50%), whereas light gray regions correspond to the second half (50–100%). If the time series crossed these alternating yellow-gray segments, then wrap-arounds in the gait cycle occurred. D and E: schematic representations of these wrap-arounds for shorter and longer τ_p, respectively.

Gait phase convergence.

To evaluate gait phase convergence for each entrained gait across the different experimental conditions, the phase and onset of convergence were determined. First, the standard deviation (σ) of the perturbation phases for the last 10 perturbations was calculated. The converged phase value (φ_conv) was determined such that the greatest number of consecutive perturbations would lie within an interval φ_conv ± 2σ. Lastly, the onset of gait phase convergence was defined as the first perturbation within the indicated interval. When determining the onset of phase convergence, it was allowed for up to three consecutive perturbations to lie outside the interval (φ_conv ± 2σ), provided the subsequent perturbation reentered the interval. For each subject, the onset of convergence was recorded in all entrained trials. The dependent measure, onset of gait phase convergence, was submitted to a within-subjects 2 (TM vs. OG) × 2 (shorter vs. longer) unbalanced ANOVA.

Effect of gait entrainment on stride length and speed.

As previously mentioned, gait entrainment to shorter perturbation periods could be assisted by torque pulses occurring at ankle push-off. Overground, shorter stride period (i.e., faster cadence) could be accompanied by increased stride length and speed, since subjects’ steady-state speed was not constrained. During TM walking, faster cadence required shorter stride length. To better understand the effect of gait entrainment on kinematic parameters in TM vs. OG walking, the estimated change in stride length (and speed) was assessed for the 15 consecutive strides before perturbation and the last 15 consecutive strides during perturbation.

The knee joint has been identified as the lower extremity joint that is most sensitive to changes in cadence (step frequency) (Heiderscheit et al. 2011; Schubert et al. 2014). Under constant speed conditions, an increase in cadence has been associated with reduced stride length and peak knee flexion (Heiderscheit et al. 2011; May and Lockard 2011; Schubert et al. 2014). Given the lack of stride length measurements in this study, the measured knee excursion was used to evaluate the effect of gait entrainment on stride length.²

The effect of gait entrainment on stride length in the two different walking contexts was, therefore, assessed by comparing the average maximum knee flexion per gait cycle before and during perturbation, which were extracted from the continuous time series data. The dependent measure, average maximum knee flexion per gait cycle, was submitted to a within-subjects 2 (before vs. during) × 2 (TM vs. OG) × 2 (shorter vs. longer) unbalanced ANOVA.

Persistence of entrained gait.

Gaits that entrained to the torque pulses could lead to persistent changes in stride duration periods, even after the torque pulses had been discontinued. For all entrained gaits, the absolute difference between the average stride period over the last 15 strides during perturbation and the first 15 strides after perturbation was calculated. The dependent measure, |τ_during − τ_after|, was submitted to a 2 (TM vs. OG) × 2 (shorter vs. longer) unbalanced ANOVA. Post hoc analysis of all entrained gaits was conducted using a linear regression fit of the stride periods over stride number after perturbation. Persistent gaits across the different experimental conditions were identified if the 95% confidence interval of these regression slopes included zero slope.

RESULTS

Entrainment

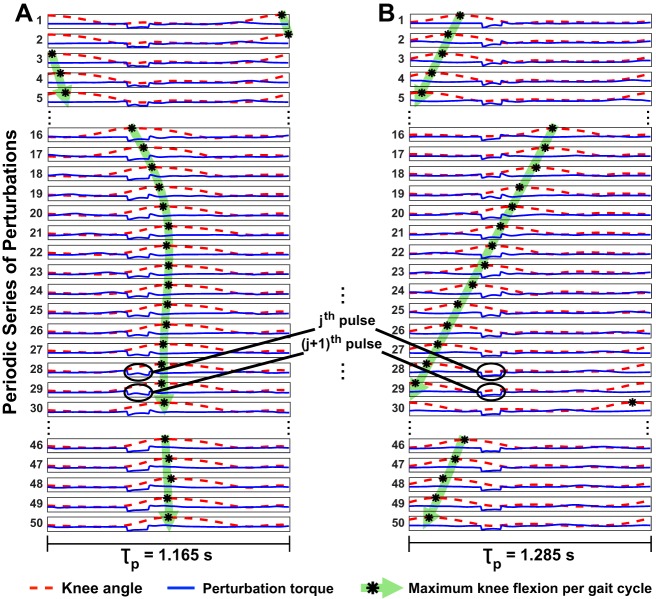
Although subjects could select their preferred cadence for each trial independently, their preferred stride period exhibited small variability across the two trials within each walking environment (see Table 1). Preferred stride periods across all subjects in TM and OG trials were 1.32 ± 0.032 and 1.21 ± 0.049 s, respectively. The relation between the maximum knee flexion (indicated by the asterisk) and the periodic series of torque pulses applied by the Anklebot for representative “entrained” vs. “non-entrained” gaits is shown in Fig. 4. This sequential representation of the perturbation cycles shows that, for entrained gaits (Fig. 4A), landmarks in the gait cycle (e.g., maximum knee flexion) initially drifted with respect to the torque pulse until converging to a specific phase relation. On the other hand, for gaits that did not entrain (Fig. 4B), a similar sequential representation of the perturbation cycles shows that landmarks in the gait cycle never converged to a specific phase relation with respect to the torque pulses.

Fig. 4.

Phase relation between maximum knee flexion per gait cycle and torque pulses along the periodic series of perturbations. Each row represents one perturbation cycle with its period indicated at the bottom and the torque profile depicted in blue. The knee angle profile (dashed line, red curve) during each perturbation cycle is shown in each row with the maximum knee flexion landmark identified. A: representative gait that entrained to shorter τ_p; the maximum knee flexion converged to a specific phase of the perturbation cycle (highlighted in green). B: representative gait that did not entrain to the longer τ_p; the maximum knee flexion drifted continuously relative to the torque pulse (highlighted in green).

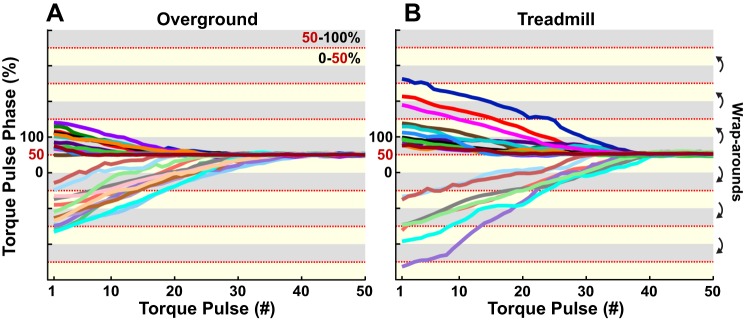
Using linear regression over the last 10 strides rendered a slope that was not significantly different from zero in 46 out 56 total trials, which were considered entrained. One subject did not entrain in any of the four different trials. The remaining six non-entrained trials were all TM-longer trials; i.e., entrainment was not observed in 50% of the TM-longer trials. Figure 5 shows the relation between torque pulse phase and torque pulse number for all entrained gaits during OG (A) and TM (B) walking. A greater number of gaits were entrained during OG (26 out 28) than TM (20 out of 28) walking. Entrained gaits during TM walking exhibited more wrap-arounds in the gait cycle before converging to τ_p; hence the initial phases seen in Fig. 5B seem to have a larger range as torque pulse phases were calculated starting from the last pulse. Importantly, this broader spread of initial phases seen in TM entrained gaits does not represent a different initial distribution compared with those in OG trials (see Fig. 6).

Fig. 5.

Torque pulse phase as a function of torque pulse number for all entrained gaits. Each color represents one subject, with a dark and a light shade for the trials with shorter and longer τ_p, respectively. A: entrained gaits during overground trials. B: entrained gaits during treadmill trials. All gaits synchronized with the torque pulses at ~50% of the gait cycle (i.e., ankle push-off). Each shaded region in light yellow corresponds to torque pulses occurring within the first half of the gait cycle (0–50%), whereas light gray regions correspond to the second half (50–100%). If the time series crossed these alternating yellow-gray segments, then wrap-arounds in the gait cycle occurred.

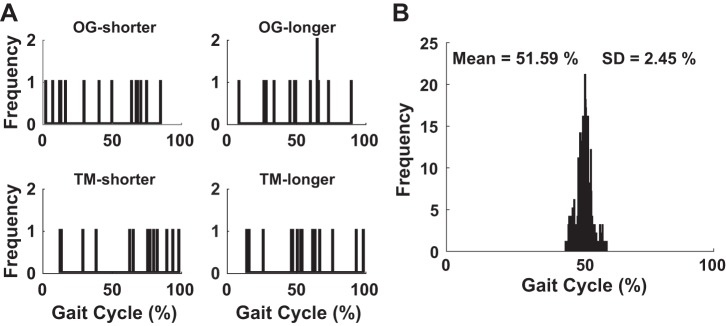
Fig. 6.

Distribution of initial and final gait phase during perturbation. A: histograms of the (random) gait phases at which perturbations were initiated for all subjects and conditions. B: histogram of the gait phases in the last 10 torque pulses for all entrained gaits (i.e., φ_conv).

Converged Gait Phase in Entrained Gaits

Regardless of the gait phases at which perturbations were initiated (Fig. 6A), subjects who entrained synchronized their gaits with the torque pulses at ~50% of the gait cycle (i.e., the phase of ankle push-off), which supports hypothesis 1.1. A histogram of gait phases at the onset of the last 10 torque pulses is shown in Fig. 6B. The mean φ_conv across all entrained gaits was 51.64% (± 2.36%), which was near the boundary between the terminal stance and pre-swing phases. This interval coincides with the maximum ankle plantar flexion torque exerted during normal walking, known as ankle “push-off” (Perry and Burnfield 2010).

Onset of Convergence Across Experimental Conditions

Figure 7 shows the mean onset of phase convergence across subjects for the four conditions. The 2 (TM vs. OG) × 2 (shorter vs. longer) ANOVA evaluating the onset of phase convergence revealed significant main effects for both the walking context and the perturbation period (F_1,42 = 684.83 and F_1,42 = 72.13, P < 0.05, respectively), but no significant interaction (F_1,42 = 0.71). Onset of phase convergence was earlier in OG (mean = 24.12 strides, SD = 10.26) than in TM trials (mean = 35.92 strides, SD = 7.78), in support of hypothesis 1.2. A more rapid gait phase convergence was detected in trials with shorter τ_p (mean = 24.04 strides, SD = 10.71) in comparison to those with longer τ_p (mean = 36.00 strides, SD = 6.79), in support of hypothesis 2.1. The mean ± SD onset of phase convergence across all four experimental conditions is tabulated in Fig. 7.

Fig. 7.

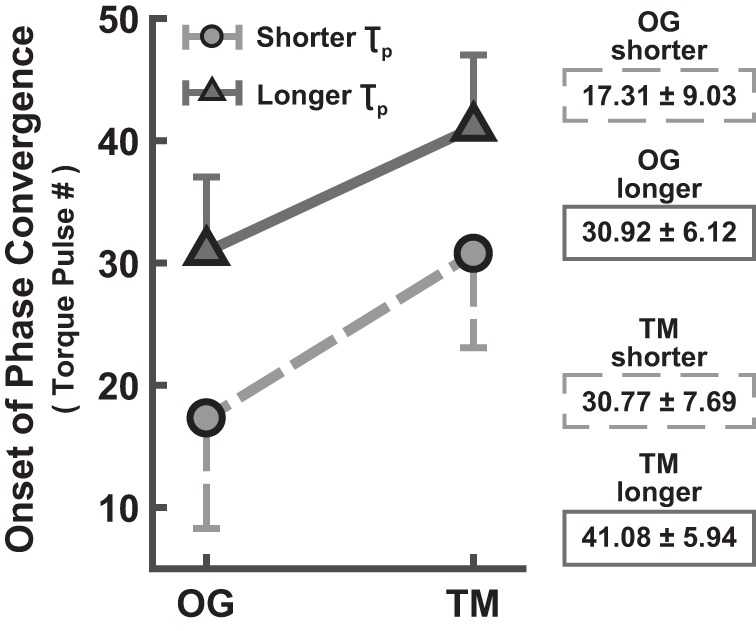
Average torque pulse number at the onset of phase convergence (mean ± SD subjects). Entrained gaits during OG walking converged sooner than those during TM walking. Convergence to shorter τ_p was achieved sooner than to longer τ_p. The bars indicate 1 SD (shown on only one side for better visibility).

Changes in Stride Length and Speed on Entrainment to Shorter τ_p

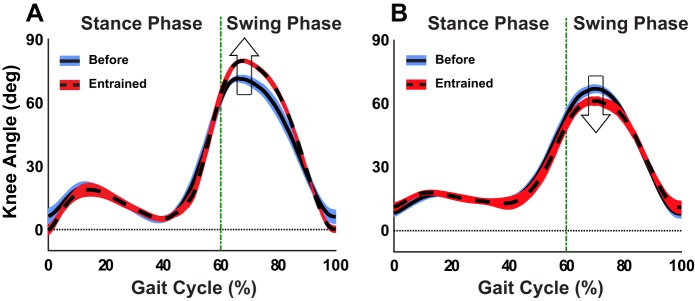
The 2 (before vs. during) × 2 (TM vs. OG) × 2 (shorter vs. longer) ANOVA evaluating the effect of entrainment on maximum knee flexion (or stride length) revealed a significant three-way interaction (F_1,92 = 97.54). There was a significant two-way interaction (F_1,48 = 199.35) between walking context and presence of perturbation for the shorter τ_p condition, as well as significant main effects (F_1,48 = 213.82 and F_1,48 = 50.79, respectively). Figure 8 shows that this interaction was due to the opposite effect of entrainment on peak knee flexion in OG vs. TM. During TM walking, entrainment to shorter τ_p by increasing cadence elicited a significant decrease in peak knee flexion (63.07 to 57.67°), implying a related decrease in stride length to comply with the constant speed constraint. On the other hand, entrainment to shorter τ_p during OG walking resulted in a significant increase in peak knee flexion (70.26 to 80.49°), suggesting an overall increase in stride length and speed. These observed changes in knee excursion are also depicted in Fig. 9 for a representative subject. No other comparisons rendered significant differences.

Fig. 8.

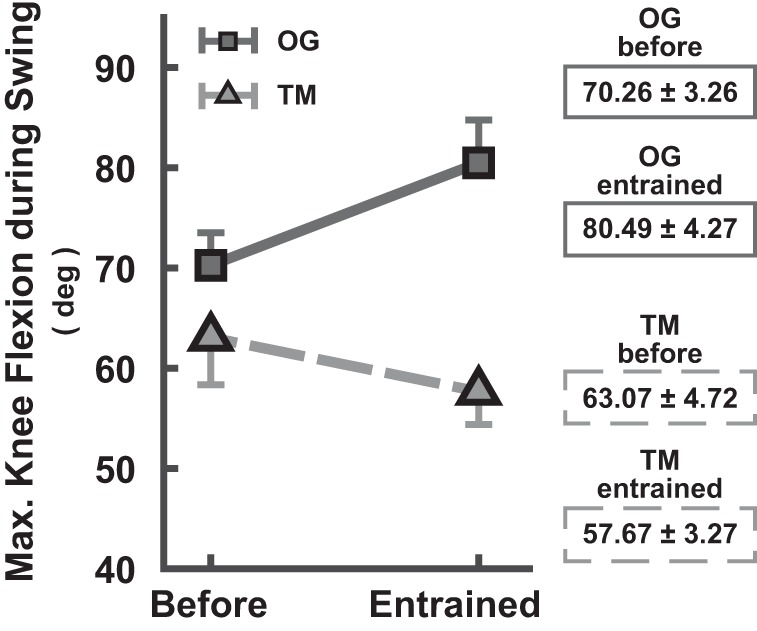
Average maximum knee flexion (in degrees) during swing phase (mean ± SD subjects). On entrainment to shorter τ_p, peak knee flexion increased in OG walking, yet it decreased in TM walking. The bars indicate 1 SD (shown on only one side for better visibility).

Fig. 9.

Knee angle trajectory (mean ± SD) across the gait cycle (in percent) for a representative subject. A: OG-shorter trial. B: TM-shorter trial. In both conditions, the mean knee excursion and SDs are depicted for the 15 consecutive strides before initiating perturbations (solid line) and the last 15 strides during perturbation (dashed line). While entrainment to shorter τ_p elicited a decrease in peak knee flexion (i.e., in stride length) during TM walking (downward arrow), it led to an increase in peak knee flexion (i.e., in stride length and speed) during OG walking (upward arrow).

Post-Perturbation Walking

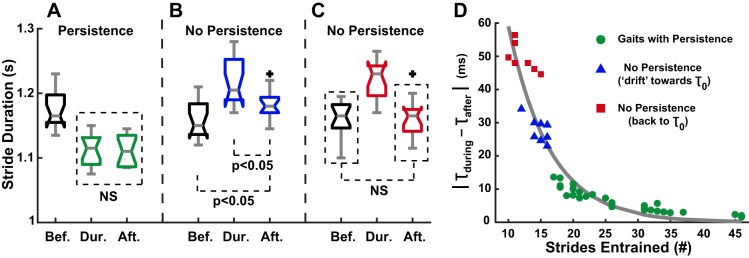
Persistence of the entrained gait period was evaluated by difference in the periods of the last 15 strides during perturbation and the 15 strides immediately after perturbation, |τ_during − τ_after|. The 2 (TM vs. OG) × 2 (shorter vs. longer) ANOVA comparing the difference in stride period revealed significant main effects for both the walking context and the perturbation period (F_1,42 = 32.44 and F_1,42 = 32.48, P < 0.05, respectively). No significant interaction was found (F_1,42 = 1.27). Figure 10 shows the mean stride period difference (in ms) across all entrained gaits for the four conditions. This stride period difference was significantly smaller in OG (mean = 9.17 ms, SD = 8.98 ms) than in TM trials (mean = 29.41 ms, SD = 19.10 ms), which indicated more frequent persistence of the entrained gait period during OG walking, in support of hypothesis 2.2. Entrained gaits to shorter τ_p also showed smaller differences in stride period (mean = 12.34 ms, SD = 14.35 ms) than those with longer τ_p (mean = 26.24 ms, SD  = 18.09).

Fig. 10.

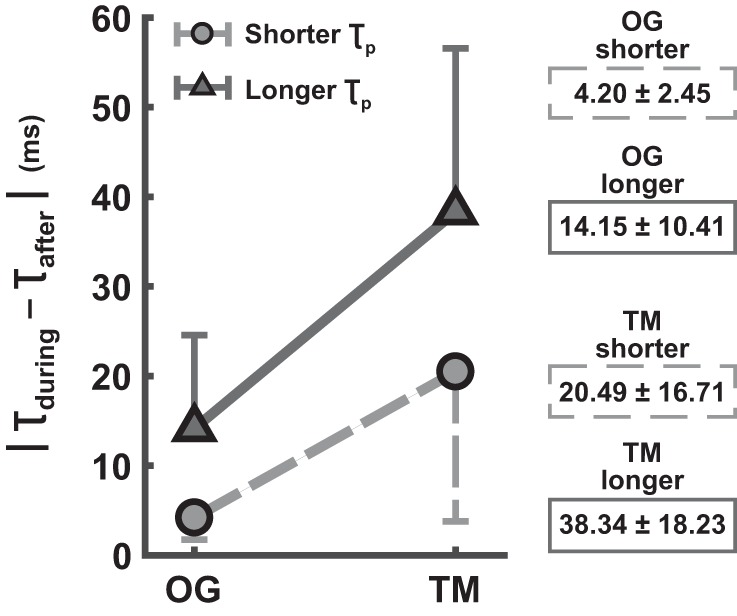
Average (absolute) difference in stride period for entrained gaits during and after perturbation (in ms) (mean ± SD subjects). The entrained gait period persisted after perturbation more frequently during OG walking, evidenced by the significantly smaller difference in stride period. The bars indicate 1 SD (shown on only one side for better visibility).

Using a linear regression over the first 15 strides after perturbation rendered a slope that was not significantly different from zero in 31 out 46 entrained gaits, which were considered cases of persistence. In all, 22 of the persistence cases were in OG walking (out of 26 entrained gaits), and 9 cases were seen in TM walking (out of 20 entrained gaits), thus confirming hypothesis 2.2. The relation between stride period before, during, and after perturbation for a representative subject exhibiting persistence is shown in Fig. 11A. Of the 15 entrained gaits with no significant persistence of the entrained gait, 11 were TM and 4 were OG trials. In 8 of those 15 trials, the stride period after perturbation had begun to return to its preferred value. Figure 11B depicts this stride period relation for a representative subject exhibiting no persistence. In the remaining 7 entrained gaits with no persistence, the subjects’ stride period after perturbation had completely returned to the preferred value within 15 strides. An example of this behavior is shown in Fig. 11C for a representative subject.

Fig. 11.

“Persistence” vs. “no persistence” of the entrained gait period. A: persistence. Representative subject shows entrained gait with no significant difference in stride duration during and after perturbation. B: no persistence. Representative subject shows entrained gait with significant difference in stride duration during and after, as well as before and after, perturbation (i.e., stride period had started to drift back to its preferred value). C: no persistence. Representative subject shows entrained gait with significant difference in stride duration during and after perturbation, but no significant difference before and after perturbation (i.e., stride period had fully returned to its preferred value). This behavior was only observed in TM trials. D: exponential fit of the difference in stride period during and after perturbation as a function of the strides walked at the entrained gait period after convergence: |τ_during − τ_after| = 281·e^{−0.156·strides}, R² = 0.9.

When examining |τ_during − τ_after| with respect to the number of strides walked at the entrained gait period, an exponential trend was seen (Fig. 11D). The more strides walked at the entrained gait, the smaller the difference in stride period during and after perturbation. In all, the 31 gaits exhibiting persistence had been exposed to at least 17 strides at the entrained period after the onset of entrainment.

DISCUSSION

This study aimed to 1) assess the sensitivity of locomotor control to treadmill vs. overground contexts, and 2) investigate the neural vs. biomechanical contributions of the locomotor response to a periodic series of 50 mechanical perturbations in the form of plantar flexion torque pulses. Entrainment was observed in 46 (out of 56) trials across all experimental conditions.

To address aim 1, we assessed the number of perturbation cycles required for gaits to converge to the perturbation period as well as the converged gait phase in TM vs. OG trials. Results revealed that certain aspects of gait entrainment were insensitive to context: all entrained gaits robustly synchronized with the torque pulses at ankle push-off, where they provided assistance with propulsion (confirming hypothesis 1.1). Conversely, other aspects of unimpaired locomotor control were exquisitely sensitive to context: gaits entrained to the perturbation periods more often and more rapidly during OG than TM walking (supporting hypothesis 1.2).

To pursue aim 2, we evaluated gait entrainment to perturbation periods shorter or longer than the preferred stride period, and the possible persistence of the entrained stride period after the perturbation was discontinued. Results concluded gait entrainment to both shorter and longer perturbation periods, even when the torque pulses assisted forward propulsion. This suggests a neural adaptation of locomotor control. Convergence to shorter perturbation periods, however, occurred sooner than to longer periods (confirming hypothesis 2.1). Lastly, the entrained gait period persisted after perturbation in 67% of all entrained gaits, yet more frequently during OG walking (supporting hypothesis 2.2). This persistence was correlated with the number of strides walked at the entrained gait period (i.e., longer exposure to the entrained stride period), which also suggested neural adaptation.

Possible Artifacts

Before discussing these results, we first consider possible artifacts that might have confounded our findings. Could the gait entrainment be an artifact of the wearable equipment used? Anklebot is a wearable robot that weighs 3.6 kg; however, that weight is mostly concentrated at the knee and borne by the thigh, thus minimizing the added inertia that opposes foot motion during walking. Its linear actuators are highly “back-drivable” and have low intrinsic static friction (less than 1 N·m) opposing ankle motion. A previous study on chronic stroke survivors failed to detect significant differences in the kinematic gait patterns with and without the Anklebot on the paretic leg, neither during TM nor during OG walking (Khanna et al. 2010). As the present study tested healthy subjects, we assumed this finding would apply and refrained from further testing. Additionally, the same Anklebot was used in both walking contexts (TM and OG). Thus any locomotor changes induced by the Anklebot would have been observed in both walking contexts and could not account for observed differences.

Might the results be confounded by a differential effect of the same perturbation profile applied to subjects with different height and weight? Even though subjects’ height and weight did not vary considerably (height = 1.73 ± 0.12 m; weight = 67.61 ± 14.41 kg), it is still possible that the perturbations may have had a larger or smaller effect on their gait. Nevertheless, we observed several subjects who entrained their gait to the torque pulses during OG, yet not during TM walking. Hence, our observation of gait entrainment being exquisitely sensitive to context (favoring OG walking) cannot be dismissed as an artifact of differences due to subjects’ differing height and weight.

Could subjects have entrained to the sounds generated by the Anklebot when delivering the mechanical perturbations? The robot made a subtle noise when generating the torque perturbations. Given that humans are sensitive to periodic auditory stimuli (e.g., dancing to a rhythmic beat), might the results presented here be due to entrainment to auditory stimuli rather than to the mechanical perturbations? Previous work by Ahn and Hogan (2012a) reported no change of gait entrainment when subjects wore acoustic noise-canceling headphones through which masking white noise was played. In this experiment, subjects performed a distractor task that required them to speak out loud, which also tended to mask any sound from the robot. Given the similarity of our treadmill results to prior work that controlled for the influence of auditory stimuli, we conclude that the entrainment reported here was a behavioral response to the mechanical perturbations and not to auditory stimuli.

Could the gait entrainment reported here be attributed to voluntary synchronization to the mechanical perturbations? To interfere with voluntary synchronization, subjects were asked to perform a distractor task. Moreover, by analogy with dancing to rhythmic music, if gait entrainment was a result of voluntary synchronization, we would expect the onset of phase convergence to occur within the first few perturbation cycles. Instead, convergence was observed to require an average of 24 and 32 strides in OG and TM trials, respectively. Voluntary adaptation is unlikely to account for these results.

Might our method of estimating the gait cycle have influenced the results presented here? The gait cycle is typically estimated using pressure sensors to identify heel strike (i.e., the moment of initial loading). We used the potentiometer embedded in the Anklebot’s knee brace to measure the knee excursions of the leg wearing the device, from which we estimated key landmarks in each stride. Previous work using the Anklebot compared the reliability of estimating stride period from knee angle data and from a heel pressure sensor; no significant difference was found (Ahn 2011). Moreover, as part of the Anklebot equipment, we have an assortment of knee braces of various sizes. Each subject was provided with a knee brace of their size, and the Velcro straps on it (above and below the knee) were adjusted to ensure a tight fit that centered the potentiometer coaxial with the approximate rotational axis of the knee joint. The harness worn by subjects was mounted to ensure that the knee brace did not shift downwards during walking. Therefore, our results are unlikely to be an artifact of our gait cycle estimation method.

Could differences in subjects’ preferred stride period across the two walking contexts account for our results? At the beginning of each TM and OG trial, subjects chose their preferred speed, which in principle could vary across all four trials. The perturbation periods were always selected based on the current unperturbed stride period. In the case of TM trials, all subjects chose the same TM speed in the two trials. Similarly, in OG trials, subjects also chose the same preferred stride duration in the two trials (with a difference of no more than 50 ms, see Table 1). This implies that there were relatively minor changes during the experiment. Furthermore, entrainment did not depend on subjects’ speed, but rather on the offset between the unperturbed stride period and the perturbation period. Evidence of a narrow basin of attraction of gait entrainment during TM walking was presented in Ahn and Hogan (2012a). Hence, we believe the slight difference in subjects’ preferred stride period in TM and OG walking did not influence our results.

A Nonlinear Limit-Cycle Oscillator Is a Competent Model of Locomotion

Human bipedal locomotion displays features similar to those of a nonlinear limit-cycle oscillator. In fact, nonlinear limit-cycle oscillators have served as models of rhythmic pattern generators, including CPGs (Collins and Richmond 1994; Matsuoka 1987; Rybak et al. 2006; Shik and Orlovsky 1976) and stable bipedal robotic walkers (e.g., “passive walkers”) (Collins et al. 2001; McGeer 1990, 1993). One distinctive characteristic of a nonlinear limit-cycle oscillator is entrainment to an external periodic perturbation over a narrow range of periods (Bennett et al. 2002; Kelso et al. 1981). The experiments presented here demonstrated gait entrainment to periodic mechanical perturbations (specifically, plantar flexion torque pulses at the ankle joint) in both TM and OG walking, together accounting for 46 observations of entrainment in 56 total trials.

Robust entrainment to periodic mechanical pulses shows that a nonlinear limit-cycle oscillator provides a competent (i.e., minimal but sufficient) model of unimpaired locomotor dynamics, confirming prior hypotheses. Admittedly, that model only describes the observational level (Hogan and Sternad 2013). It does not describe the neuromechanical processes that give rise to such behavior. Nevertheless, a limit-cycle model may be useful for applications such as designing devices that interact with humans. Articulating the details of that limit-cycle model requires further work.

Sensitivity of Locomotor Control: Overground vs. Treadmill Entrainment

In the experiments presented here, TM and OG trials were conducted in the same fashion, yet more gaits entrained in OG than in TM walking. In fact, gait entrainment in TM walking was only detected in 50% of the total TM trials, comparable to the 42.5% in previous work by Ahn and Hogan (2012a), although they tested a wider variety of perturbation periods. This difference appears to be due to the fixed-speed constraint in TM trials. In order for subjects to entrain to periodic perturbations 50 ms different from their preferred stride period, they had to change their stride period and/or their stride length. Given that speed was kept constant in TM trials, subjects could only adjust their stride period to match the perturbation period by changing their stride length in proportion. Subjects’ knee excursion patterns before and during perturbation in TM trials suggest they in fact adjusted their stride period via concomitant adjustments to their stride length³ (see appendix). In contrast, in OG trials, subjects adjusted their stride period along with their stride length in a way that also led to changes in their walking speed: faster walking on entrainment to shorter perturbation periods (peak knee flexion increased from 70.26 to 80.49°, Fig. 8). Lastly, we observed another difference between TM and OG walking: not only was entrainment more likely in OG walking, convergence to a constant phase relation happened more quickly, taking an average of 24 and 32 perturbation cycles in OG and TM trials, respectively (Fig. 7).

Locomotor control strategies.

One possible strategy for control of human locomotion is that higher levels of the central nervous system specify a nominal or desired trajectory of the foot, e.g., to place it at a location sufficient to maintain balance or achieve a desired redirection of body momentum, analogous to the “capture point” strategy that has been proposed for robot locomotion (Bauby and Kuo 2000; Englsberger et al. 2011; Popovic et al. 2004; Pratt et al. 2006; Pratt and Tedrake 2006). Previous research on humans has demonstrated robust control of foot trajectory (Ivanenko et al. 2002).

If control to meet a kinematic specification (e.g., foot trajectory) were the predominant mechanism used by the central nervous system, we should not have observed dynamic entrainment to mechanical perturbations. Instead, in some trials, the phase difference between perturbations and gait cycles steadily grew or declined (Fig. 3). The observation that entrainment did not always occur indicates that, for some subjects and conditions, the locomotor controller successfully ignored the modest perturbations we imposed. In those cases, unimpaired locomotion may best be modeled as a kinematic controller driven by central commands.

Another possible strategy for control of human locomotion is that people minimize the energy consumed per unit distance. Indeed, the minimization of energetic cost has been well documented as a key criterion for the selection of walking parameters, such as speed, stride length, and cadence (Bertram and Ruina 2001; Donelan et al. 2001, 2002a, 2002b; Ralston 1958; Srinivasan and Ruina 2006; Umberger and Martin 2007; Zarrugh et al. 1974). Recent work by Selinger and colleagues (2015) showed that not only are humans capable of optimizing energy expenditure, they are also able to adjust their established motor patterns as needed. In their studies, subjects were exposed to torques that resisted the motion of the knee joints, which added an energetic penalty that varied with step frequency, to shift their energetic optimum to higher or lower frequencies. Subjects responded to these imposed penalties by finding new energetic minima at those higher/lower frequencies, even when the cost savings were remarkably low (<5%).

Entrainment to the imposed torque pulses (synchronized at push-off) assisted locomotion and may have reduced energy consumption. In light of the results of Selinger et al. (2015), our observations suggest that the control strategy may have been to minimize energy expenditure.

Robust Synchronization of Torque Pulses with Ankle Push-off

Our results showed that some aspects of gait entrainment were insensitive to context. Specifically, for all entrained gaits, plantar flexion torque pulses synchronized with ankle push-off, independently of the initial torque pulse phase (Fig. 6). While entrainment requires convergence of subjects’ stride duration to the perturbation period, it is not limited to any particular phase. Ahn and Hogan (2012a) showed that unimpaired subjects synchronized with the perturbation at ~50% of the gait cycle in TM walking. The present study confirmed and extended that finding to OG walking. Robust synchronization at ankle push-off suggests that the end of double stance is the “global” attractor of the phase dynamics (for plantar flexion torque pulses) (Ahn and Hogan 2012b).

In normal walking, the maximum ankle plantar flexion torque is exerted at push-off (47–62%), which begins near the end of terminal stance phase and ends during the pre-swing phase (Perry and Burnfield 2010). If subjects adapted their stride period to minimize the possible destabilizing effect of the perturbation, they could have located it anywhere during the swing phase, where it would have the least mechanical effect. Moreover, the swing phase occupies ~40% of the gait cycle, so the entrained phases could have been broadly distributed. In contrast, entrained phases were narrowly distributed around ankle push-off. We, therefore, conclude that stabilization was not the primary driving force behind the observed adaptation. While we present no direct evidence related to energetics, consistent synchronization of the torque pulses with ankle push-off suggests that gaits adapted so that the perturbations mechanically assisted plantar flexion, thus facilitating forward propulsion. Indeed, this mechanical assistance may have induced the increased stride length observed in OG-shorter trials (Fig. 8), along with an increase in steady-state speed.

In several entrained gaits, a torque pulse at push-off was not immediately accompanied by gait synchronization (Fig. 5B). If subjects synchronized their gaits with the perturbation where it assisted propulsion, or did not oppose ankle actuation, then why did they not do so at the first opportunity? Perturbation periods (τ_p) were strictly 50 ms shorter/longer than preferred stride duration (τ₀), but our estimates were inevitably not perfect. As a result, τ_p could deviate from subjects’ walking cadence when perturbations were initiated, requiring greater changes in stride periods. Previous work by Ahn and Hogan (2012a) revealed that entrainment only occurred when τ_p was sufficiently close to subjects’ stride period. Hence, it is possible that τ_p was sufficiently different from a subject’s stride period to preclude gait convergence. In these cases, only nonstationary changes in the preferred walking cadence eventually facilitated entrainment.

Neural Contributions to Locomotion

Ankle plantar flexion torque pulses at push-off can only act as mechanically “assistive” pulses, adding positive work and speeding subjects up (in OG walking) or increasing their stride frequency. Entrainment to shorter perturbation periods required subjects to increase their stride frequency to match the imposed τ_p. Hence, gait entrainment to shorter τ_p might be due to the positive work added by the mechanically assistive perturbations with no neural adaptation required. A simple model presented by Ahn and Hogan (2012b) reproduced this behavior. The fact that entrainment to this type of perturbations occurred more frequently and in fewer strides suggests it was easier for subjects to take advantage of biomechanics.

In contrast, entrainment to longer perturbation periods required a neural response to assistive perturbations. The model of Ahn and Hogan (2012b) was only capable of reproducing entrainment and synchronization at ankle push-off when the perturbation periods were shorter than the preferred stride period. However, the experiments presented here, and those of the prior study (Ahn and Hogan 2012a), also demonstrated gait entrainment to longer τ_p. Entrainment to longer τ_p required subjects to reduce their stride frequency, even though the “mechanically assistive” torque pulses were speeding them up (in OG walking) or increasing their stride frequency. Such entrainment to longer τ_p implicates a neural adaptation that required more than peripheral neuromechanics.

Are these observations indicative of error-based adaptation or learning? We do not believe that the behavioral changes relied on error-based learning mechanisms. One reason is that there was no error-related feedback in the usual sense. Rather, subjects increased or decreased their stride period to converge to a phase where the torque pulses were assistive. Furthermore, in contrast to split-belt walking or upper limb error-based adaptation studies, the subtle perturbations in our study only induced a slightly faster or slower cadence. These changes did not create an error, nor disrupt the kinematic pattern of normal walking after the perturbations were discontinued. Also, persistence improved as more strides were synchronized with the torque pulses, which suggests that a use-dependent learning mechanism drove the adaptation (Diedrichsen et al. 2010).

Persistence of the Entrained Gait in Post-Perturbation Walking

The entrained stride period persisted after perturbation in 67% of the entrained gaits. This observation is significant for characterizing unimpaired locomotor dynamics and informing the type of motor tasks that can evoke longer persistence. Our results also revealed that the difference in stride period during and after perturbation depended on the number of strides walked at the entrained gait period (Fig. 11A). Specifically, the more strides walked at the entrained gait, the smaller the difference in stride period. Overall, the modified stride period persisted in more entrained gaits during OG than TM walking. A previous study evaluating adaptation to walking in a force field revealed similar results indicating that the duration of the after-effects (i.e., the persistence of the adapted motor pattern) was positively correlated with exposure duration (Fortin et al. 2009). Combined, these observations suggest that longer practice of a new motor behavior can help extend persistence, consistent with use-dependent learning.

The effect of perturbations on the natural dynamics of locomotion is an important factor influencing the retention of the new motor behavior in normal conditions (after perturbation). Contrary to our observations, the forgetting rates in related studies are generally fast, often faster than the rates of adaptation to the new motor patterns. For instance, split-belt treadmill training with healthy subjects induced immediate changes (essentially instantaneous adaptation) in stride length and stance time to accommodate the belts running at different speeds (Reisman et al. 2005). Immediately after the belts returned to the same speed, subjects’ stride length and stance time also returned to their initial values (no after-effects). Similarly, other studies have reported deadaptation toward the unperturbed foot trajectory in less than 15 strides (Emken and Reinkensmeyer 2005; Lam et al. 2006). In those studies, the force-field perturbations imposed functional demands that conflicted with the natural locomotor dynamics, such as exaggerated gait asymmetry or increased/decreased foot-ground clearance. Given that those perturbations did not guide subjects toward behavior that is viable or desired under normal conditions, the new motor patterns did not persist on removal of the perturbation (Huber and Sternad 2015).

Consistent with this goal, the subtle plantar flexion torque pulses in our study assisted normal walking when synchronized at ankle push-off. Entraining to these torque pulses only required subjects to change the preferred stride period by 50 ms, which is ~5% of the typical stride period in normal adult walking (Perry and Burnfield 2010). Although we did not record data for the unperturbed leg, we believe that any induced asymmetry was small at most. Even if the unperturbed leg adapted differently, the change in the perturbed leg was close to the typical unperturbed variability of stride duration (coefficient of variation ~3%). It is possible that when “shifted” toward a new limit-cycle attractor, subjects were able to establish new energetically optimal motor patterns in similar fashion as reported by Selinger et al. (2015). Discontinuing this assistance may not have presented a significant incentive for the nervous system to return to its original motor pattern.

Implications for Robot-Aided Locomotor Therapy

A possible explanation for the ineffectiveness of robotic walking therapy is the use of human-interactive robots in ways that may inadvertently suppress the natural oscillatory dynamics of walking. Even without a robot involved, the recovery of functional walking via body weight-supported treadmill training assisted by multiple human therapists was not superior to a home exercise program (Duncan et al. 2007, 2011). Given the manifest practical advantages of using treadmills for clinical locomotor therapy, one open question is how benefits obtained by treadmill training can be transferred to normal OG walking conditions.

Given that the dynamics of unimpaired locomotor control appears exquisitely sensitive to context (i.e., TM vs. OG), the mechanical context of robotic rehabilitation may also affect its success. “Mechanical context” includes not only the walking context, but also whether the therapeutic robot encumbers motion. Hence, we predict that simply using available exoskeletons for OG therapy is unlikely to afford much improvement, as these tend to interfere with the natural dynamics of walking. The Anklebot and also the MIT Skywalker are examples of therapeutic technologies that aim to minimize mechanical interference (Roy et al. 2009; Susko et al. 2016).

Our observation of robust gait synchronization with the torque pulses at ankle push-off suggests that these assistive torque pulses could supply the additional torque needed by patients who cannot produce sufficient propulsion to swing their paretic leg forward, possibly stimulating an increase in stride length to reduce gait asymmetry. We envision that impaired patients could first be entrained to torque pulses at their preferred stride period. Then the perturbation period could be shortened progressively to “drag” them toward faster cadence, while they take advantage of the assistive pulses, as in Ahn et al. (2011). The magnitude and duration of these torque pulses could also be adjusted to each patient’s needs to provide assistance only as needed.

An important outcome measuring the effectiveness of gait rehabilitation is the retention of benefits after training. In this study, the entrained gait period persisted (for 15 strides) after the torque pulses were discontinued, an observation that differed from the rapid deadaptation rates reported in Emken and Reinkensmeyer (2005), Lam et al. (2006), and Reisman et al. (2005). While we cannot determine whether the effects would persist for much longer, previous studies have shown that significant improvements in motor recovery can be achieved over the course of many therapy sessions, even when progress made in one therapy session did not always carry over to the next session (Buerger et al. 2004; Krebs et al. 2003). Altogether, our results and those presented in Fortin et al. (2009) and Selinger et al. (2015) suggest that permissive motor guidance toward viable, functional behavior may render more effective retention of the practiced motor tasks.

GRANTS

J. Ochoa was supported by the Alfred P. Sloan Foundation’s Minority Ph.D. Scholarship and by the Gloria Blake Endowment Fund. N. Hogan was supported in part by the Eric P. and Evelyn E. Newman Fund, National Science Foundation (NSF) Early-Concept Grant for Exploratory Research (NSF-EAGER) Grant 1548501, NSF-National Robotics Initiative (NRI) Grant 1637824, and National Institute of Child Health and Human Development (NICHD) Grant R01-HD087089. D. Sternad was supported by NICHD Grants R01-HD087089 and R01-HD081346, NSF-EAGER Grant 1548514, and NSF-NRI Grant 1637854.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.O. and N.H. conceived and designed research; J.O. performed experiments; J.O. analyzed data; J.O., D.S., and N.H. interpreted results of experiments; J.O. prepared figures; J.O. drafted manuscript; J.O., D.S., and N.H. edited and revised manuscript; J.O., D.S., and N.H. approved final version of manuscript.

APPENDIX

Relation Between Peak Knee Flexion and Cadence at Constant Speed

Entrainment to perturbations with periods that were shorter or longer than preferred stride period required subjects to change their gait period (i.e., stride duration) so that each torque pulse occurred at the same phase of the gait cycle. These changes in stride duration implied concomitant changes in speed, stride length, and/or cadence, in accordance with the known relationship between these kinematic parameters described in Eq. A1.

$$\text{Speed}=\text{Stride\hspace{0.17em}Length}\times \text{Cadence}=\frac{\text{Stride\hspace{0.17em}Length}}{\text{Stride\hspace{0.17em}Duration}}$$ (A1)

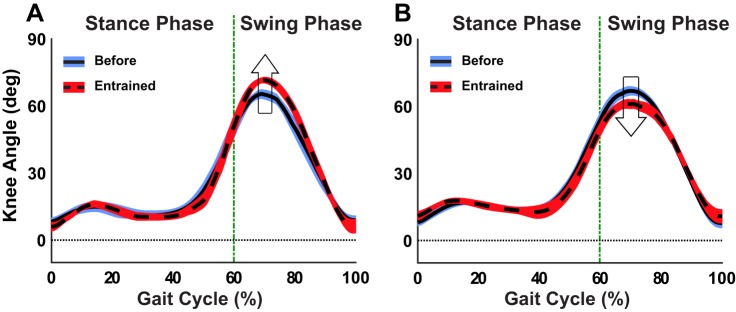
In TM trials, speed was maintained constant throughout each trial. Thus an increase in stride duration on entrainment to longer τ_p must elicit a parallel increase in stride length. Similarly, entrainment to shorter τ_p would require a decrease in stride duration and a concomitant decrease in stride length. Figure A1 shows the correlation between peak knee flexion and stride duration under constant speed conditions for a representative subject who entrained to both longer and shorter τ_p during TM walking. On entraining to longer τ_p by increasing stride duration, the subject’s maximum knee flexion for the last 15 strides during perturbation increased compared with the 15 strides before perturbation (Figure A1A). Similarly, entrainment to shorter τ_p via a decrease in stride duration induced a decrease in maximum knee flexion (Figure A1B). This pattern was observed for all subjects who entrained to both longer and shorter τ_p during TM walking.

Fig. A1.

Knee angle trajectory (mean ± SD) across the gait cycle (in percent) for a selected subject during TM-longer (A) and TM-shorter (B) trials. In both conditions, the mean knee excursion and SDs are depicted for the 15 consecutive strides before perturbations (solid line) and the last 15 strides during perturbation (dashed line). During TM walking, peak knee flexion increased (upward arrow) upon entrainment to longer τ_p via an increase in stride length. Conversely, peak knee flexion decreased (downward arrow) upon entrainment to shorter τ_p via a decrease in stride length, given the constant treadmill belt speed.