Decoding sound level in the marmoset primary auditory cortex

Neurons with nonmonotonic rate-level functions are unique to the central auditory system. These level-tuned neurons have been proposed to account for invariant sound perception across sound levels. Through systematic simulations based on real neuron responses, this study shows that neuron populations perform sound encoding optimally when containing both monotonic and nonmonotonic neurons. The results indicate that instead of working independently, nonmonotonic neurons complement the function of monotonic neurons in different sound-encoding contexts.

Abstract

Neurons that respond favorably to a particular sound level have been observed throughout the central auditory system, becoming steadily more common at higher processing areas. One theory about the role of these level-tuned or nonmonotonic neurons is the level-invariant encoding of sounds. To investigate this theory, we simulated various subpopulations of neurons by drawing from real primary auditory cortex (A1) neuron responses and surveyed their performance in forming different sound level representations. Pure nonmonotonic subpopulations did not provide the best level-invariant decoding; instead, mixtures of monotonic and nonmonotonic neurons provided the most accurate decoding. For level-fidelity decoding, the inclusion of nonmonotonic neurons slightly improved or did not change decoding accuracy until they constituted a high proportion. These results indicate that nonmonotonic neurons fill an encoding role complementary to, rather than alternate to, monotonic neurons.

NEW & NOTEWORTHY Neurons with nonmonotonic rate-level functions are unique to the central auditory system. These level-tuned neurons have been proposed to account for invariant sound perception across sound levels. Through systematic simulations based on real neuron responses, this study shows that neuron populations perform sound encoding optimally when containing both monotonic and nonmonotonic neurons. The results indicate that instead of working independently, nonmonotonic neurons complement the function of monotonic neurons in different sound-encoding contexts.

the nature of cochlear mechanical vibrations leads to decreased peripheral neuron selectivity to sound frequency as sound pressure level increases (Evans 1972; Galambos and Davis 1943; Ruggero 1992). Pure tones delivered at high sound levels, for example, activate a substantially larger fraction of the cochlea than the same tones delivered at lower sound levels (Galambos and Davis 1943). Peripheral representations of sounds therefore vary considerably with increased sound level, leading to as much or more variability in population neural activity in response to changes in sound level as to changes in frequency (Barbour 2011; Chen et al. 2010). Because auditory perceptual discriminability does not vary so dramatically as the level of a sound changes, this level-dependent selectivity in peripheral auditory neural responses must be compensated for by central auditory circuitry.

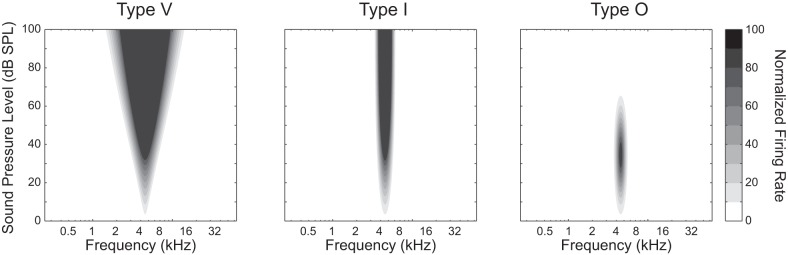
The input-output (IO) functions of auditory neurons in the auditory system measured at their characteristic frequencies (CFs; the sound frequency eliciting the greatest response from a neuron within 10 dB of the neuron’s threshold) fall into two broad categories: 1) monotonic, in which neuronal firing rates increase and can saturate in response to increasing sound level, and 2) nonmonotonic, in which neuronal firing rates are tuned to peak at a specific sound level while decreasing for higher sound levels. Monotonic, or level-untuned, neurons can exhibit either a “type V” frequency-level receptive field (RF) shape with level-varying bandwidths or a “type I” RF shape with a bandwidth invariant to sound level (Barbour 2011; Ramachandran et al. 1999; Watkins and Barbour 2011b) (Fig. 1). Nonmonotonic, or level-tuned, neurons have a “type O” RF shape, whose bandwidth is also invariant with sound level but whose overall rate decreases at the highest sound levels. Both type I and type O neurons are formed from inhibitory processes at high sound levels (Kaur et al. 2004; Ramachandran et al. 1999; Tan et al. 2007; Wehr and Zador 2003) and may represent intermediate calculations in a population code for level-invariant sound representation (Caspary et al. 1994; de la Rocha et al. 2008; Faingold et al. 1991; LeBeau et al. 2001; Wang et al. 2002).

Fig. 1.

Schematic of different types of neurons in the auditory cortex. Type V neurons tend to respond to higher sound levels with higher firing rates and wider frequency bandwidths. At their characteristic frequency, type I neurons increase their firing rate monotonically with sound level. Type O neurons, on the other hand, peak at a particular sound level value; these neurons are described as nonmonotonic, or level-tuned, neurons. [Adapted from Chen et al. (2010).]

Level-tuned responses have been recorded in increasing quantities at progressively more central stages of the mammalian auditory pathway, including the cochlear nuclei (Caspary et al. 1994; Spirou and Young 1991), the inferior colliculus, (Aitkin 1991; Faingold et al. 1991; LeBeau et al. 2001; Ramachandran et al. 1999; Rees and Palmer 1988; Rose et al. 1963; Ryan and Miller 1978; Semple and Kitzes 1985), medial geniculate (Galambos 1952; Galambos et al. 1952; Rouiller et al. 1983), and auditory cortex (Erulkar et al. 1956; Phillips et al. 1985, 1995; Polley et al. 2006; Sadagopan and Wang 2008; Wang et al. 2002; Watkins and Barbour 2011b), but not in the auditory nerve (Galambos and Davis 1943; Kiang et al. 1965). In auditory cortex, the proportion of neurons exhibiting level-tuned behavior is reported to be as high as 80% (Sadagopan and Wang 2008; Watkins and Barbour 2008). The high prevalence of level-tuned neurons in the auditory system and the rarity or absence of any similar type of response in other sensory systems (Peirce 2007; Peng and Van Essen 2005) suggest a specific role for them in auditory coding (Faingold et al. 1991; Ramachandran et al. 1999; Sivaramakrishnan et al. 2004; Tan et al. 2007; Watkins and Barbour 2011a), which is of ongoing interest to researchers.

An attractive theory accounting for the existence of level-tuned neurons is that they represent an intermediate calculation for a level-invariant population code especially suited to the unique peripheral sensory representation in the auditory system (Sadagopan and Wang 2008). In particular, tuned functions are typically considered to be best suited for producing constant outputs at fixed error when combined in a population (Miller et al. 1991; Salinas and Abbott 1994; Theunissen and Miller 1991). Although level-tuned neurons do exhibit constant bandwidth across their full dynamic ranges, this property is shared by type I neurons (Sadagopan and Wang 2008). Type I neurons must also be created centrally, but unlike type O neurons, they retain the monotonic IO function shape found in the auditory periphery. Given that nonmonotonic neurons do not exist in the auditory periphery (Kiang et al. 1965; Sachs and Abbas 1974), yet become the vast majority of neurons in auditory cortex (Tang et al. 2008), we asked whether they alone can encode in a level-invariant manner, and whether type I neurons might play a role in this context. We sought to provide empirical evidence of the level-encoding accuracy of the two types of neurons. To do so, we recorded a large population of monotonic and nonmonotonic neurons from marmoset primary auditory cortex and constructed a series of decoders assessing different neuron subpopulation compositions on their ability to encode sound level accurately under a variety of coding contexts.

MATERIALS AND METHODS

Physiological IO functions.

To evaluate the role of monotonic and nonmonotonic IO functions in encoding sound level, we first obtained the IO functions of a large population of A1 neurons. Neural recording procedures have been described in detail previously (Watkins and Barbour 2011b) and are reviewed briefly here. All animal procedures were approved by the Washington University in St. Louis Animal Studies Committee. Adult marmoset monkeys (Callithrix jacchus) had a head cap placed under anesthesia for head fixation. Following recovery, recordings were performed daily inside a double-walled sound-attenuation booth (IAC 120a-3; Bronx, NY) where the animals sat in a minimally restraining primate chair with their heads fixed in place. A1 location was identified through microcraniotomies using lateral sulcus and bregma landmarks, and was then confirmed physiologically by high tone-driven spike rates (typically peaking 20–70 spikes/s), short latencies (10–15 ms), and a cochleotopic frequency map oriented from low frequencies to high frequencies in the rostral-to-caudal direction parallel to lateral sulcus.

High-impedance tungsten-epoxy electrodes (~5 MΩ at 1 kHz; FHC, Bowdoin, ME) were advanced perpendicularly to the cortical surface within the microcraniotomies. Microelectrode signals were amplified using an AC differential amplifier (AM Systems 1800; Sequim, WA), and action potentials were identified and logged with spike-sorting hardware and software (TDT RX6, Alachua FL; Alpha Omega, Nazareth, Israel). The median action potential waveform signal-to-noise ratio using this setup is 24.5 dB.

Acoustic stimuli were synthesized digitally using custom MATLAB software (The MathWorks, Natick, MA), passed through a digital-to-analog converter (TDT RX6 24-bit DAC), amplified (Crown 40W D75A; Elkhart, IN), and delivered to a calibrated loudspeaker (B&W 601S3; Worthing, UK) located 1 m directly in front of and aligned along the midline of the animal’s head.

Each single unit was analyzed with tones delivered at its CF, defined as the frequency eliciting the greatest response from the neuron within 10 dB of the unit’s threshold. IO functions were measured by pseudorandomly delivering 100-ms CF tones of different sound pressure levels, typically 11 sound pressure levels spaced in 10-dB increments from −15 to 85 dB SPL, separated by at least 700 ms of silence between successive tones. Each stimulus sound pressure level was presented pseudorandomly 10 times. Response firing rates were calculated for the IO function from a time window beginning at the absolute response latency of the neuron and ending 100 ms later. To compensate for the difference in hearing threshold at different tone frequencies, the IO function for each neuron was adjusted by the neural measurement of the threshold audiogram such that reported sound levels were referenced to the overall hearing threshold (Watkins and Barbour 2011b).

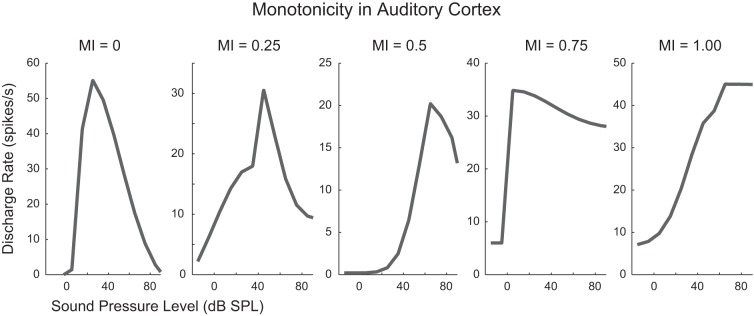
A total of 544 neurons from 7 monkeys were recorded in the manner described above, forming the basic physiological data set from which virtual subpopulations of neurons were constructed. This data set was previously reported in Watkins and Barbour (2011b). IO functions for these neurons were computed by fitting a six-parameter function to their mean rate-level curves (Watkins and Barbour 2011b). To separate monotonic and nonmonotonic neurons, a monotonicity index (MI) was calculated from each of the fitted functions as the ratio of a neuron’s response at the maximum sound level to its maximum response overall, with spontaneous firing rates subtracted out (as shown in Eq. 1) (Watkins and Barbour 2011b). A neuron with an MI in the range 0.5 to 1 was considered monotonic, or level-untuned, whereas a neuron with an MI of less than 0.5 was considered nonmonotonic, or level-tuned. Similar monotonicity measures based on firing rate ratios have been used previously, but without subtracting the spontaneous rates (Clarey et al. 1994; de la Rocha et al. 2008; Doron et al. 2002; Phillips and Cynader 1985; Phillips et al. 1994; Recanzone et al. 2000; Sadagopan and Wang 2008; Sutter and Loftus 2003; Sutter and Schreiner 1995). Other measurements to classify monotonic and nonmonotonic neurons, for example, based on the slope of IO functions, have also been reported previously (Davis et al. 1996; Ramachandran et al. 1999; Schreiner et al. 1992; Schreiner and Sutter 1992).

$$MI=\frac{rat{e}_{\text{maxlevel}}-rat{e}_{\text{spontaneous}}}{\max (rate)-rat{e}_{\text{spontaneous}}}$$ (1)

Consistent with previous reports, these A1 neurons exhibited varying degrees of input-output monotonicity. MIs of the 544 neurons were distributed from very nonmonotonic (MI < 0, indicating suppression below spontaneous spiking rates at the highest sound levels) to very monotonic (MI = 1). More neurons exhibited nonmonotonic IO functions (n = 308) than monotonic (n = 236). Example IO functions from this population demonstrating the variety of IO shapes can be seen in Fig. 2.

Fig. 2.

Examples of degrees of monotonicity in A1 neurons. Sound level to firing rate input-output functions of 5 neurons in primary auditory cortex ranging from very nonmonotonic (MI = 0) to very monotonic (MI = 1) are shown.

Creation of virtual neuron subpopulations.

Our physiologically measured neurons enabled us to form a master population of virtual A1 neurons. For each physiologically measured neuron, a virtual neuron was created with the same IO function. Zero-mean Gaussian noise scaled by the standard deviation of the real neuron’s response at the corresponding sound level was added independently to each rate measurement in each virtual neuron’s IO function to simulate the natural variability in actual neural responses. This method of creating virtual neurons allows for the generation of an infinite number of neural response trials in response to each stimulus and ensures independent noise among different trials. The master virtual neuron population was divided into two pools, one with all monotonic neurons and the other with all nonmonotonic neurons. Note that the current physiological data set did not contain a measurement of the neurons’ spectral RF and thus could not independently distinguish type I neurons from type V neurons. For this reason we only consider IO behavior at the CF in this study.

Neurons were randomly drawn with replacement from these two pools to form subpopulations having different proportions of nonmonotonic to monotonic neurons. To form a 100-neuron subpopulation with 30% nonmonotonic neurons, for example, 30 neurons were drawn from the nonmonotonic pool and 70 neurons were drawn from the monotonic pool. Proportions ranging from 0% nonmonotonic (i.e., all monotonic) to 100% nonmonotonic neurons were tested in 10% intervals. This method of constrained proportions enabled systematic evaluation of different neuronal compositions on sound level encoding. We used subpopulations of different sizes (10, 20, 30, 50, 100, 200, 500, and 1,000 neurons) to assess how performance improves with increased number of neurons and to determine an appropriate group size for sufficient encoding accuracy. To account for sampling variabilities, 500 subpopulations were drawn and evaluated when assessing each neuronal composition and population size combination, and the average performance of these subpopulations was used to indicate the encoding accuracy of each condition.

Assessing encoding ability with optimal linear estimator.

To assess how well a subpopulation of neurons could perform in a given level-encoding context, we modeled the output of a neuron subpopulation with a linear estimator, where the total output of a subpopulation was calculated as a linear summation of the weighted rate-level functions of the contributing neurons, as shown in Eq. 2,

$$y\left(x\right)={\displaystyle \sum _{i=1}^n{w}_i{r}_i\left(x\right)},$$ (2)

where x is the stimulus level in dB SPL, y(x) is the estimated output of the subpopulation of n neurons for an input level of x dB SPL, r_i(x) is the mean firing rate of neuron i given stimulus level x, and w_i is the weight associated with neuron i.

The similarity of the linear estimator output to the target output for a given decoding context quantifies the performance of the estimator. To assess the encoding ability of the neuron subpopulation, we constructed the linear estimator with the best set of weights optimized for the given decoding context and neuron subpopulation, thus constructing an optimal linear estimator (OLE). With weighted linear summation representing a fundamental operation in neural computation (Dayan and Abbott 2001), this method of OLE is commonly used for calculating the output of a group of neuronal units and has been applied to both sensory and motor systems (Poggio and Bizzi 2004; Pouget and Snyder 2000; Salinas and Abbott 1994).

To solve for the set of optimal weights w_i, i = 1, 2, …, n, given the target output function y_target(x) for a level-decoding context, we first represented the set of values of the function y_target(x) at the measured sound levels in vector format y and compiled the firing rates of all neurons at all sound levels into an n × k matrix R, where R =  [r_i,j], and r_i,j is the firing rate of the ith neuron to the jth sound level. The set of optimal weights can then be calculated by multiplying the target output function vector y by the pseudoinverse of the matrix of rate level functions R as in Eq. 3, where pinv represents the operation of pseudoinverse.

$$\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\end{array}\right]=pinv\left[\begin{array}{cccc}{r}_{1,1}& r_{1,2}& \cdots & r_{1,x}\\ r_{2,1}& \ddots & & r_{2,x}\\ ⋮& & \ddots & ⋮\\ r_{n,1}& r_{n,2}& \cdots & r_{n,x}\end{array}\right]\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_x\end{array}\right]$$ (3)

The pseudoinverse yields the maximum likelihood decoder due to the Gaussian noise applied to the neuronal subpopulation (Stark and Woods 2012).

To simulate the effects of neuronal noise upon the weights of neural connection, the process of calculating the optimal weights was repeated 50 times on 50 random instantiations of the noisy encoding each time a subpopulation was evaluated. The calculated sets of weights for each of the 50 noise instantiations were averaged to form a finalized set of weights for that particular subpopulation. These final weights were then multiplied by the individual IO functions to determine the overall decoded output of that particular subpopulation (Fig. 3). The root mean squared error (RMSE) between the decoded and target output functions was calculated as a measurement of the subpopulation’s ability to encode for the level decoding context with the particular target output function. Specifically, the squared errors across different sound levels were averaged, and then the square root was computed. The lowest and highest sound level points (–15 and 85 dB SPL) were omitted in the RMSE calculation to avoid potential edge effects. To summarize the encoding accuracy of the different subpopulations evaluated for each neuronal composition and population size condition, the errors were averaged for different subpopulations, and then the square root of the value was obtained. When the encoding performance of two different conditions was compared, a permutation t-test was used to assess the statistical power of the results (Glerean et al. 2016).

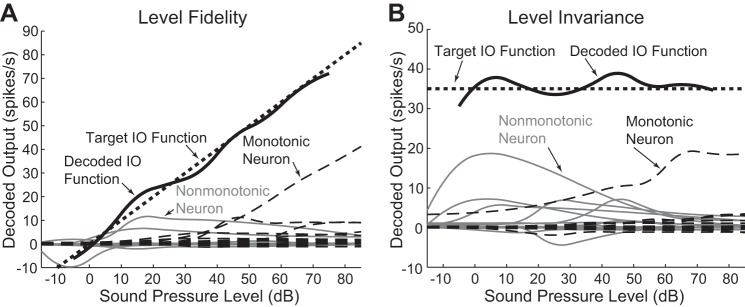
Fig. 3.

Examples of estimator performance. For both a level-fidelity (A) and level-invariant (B) decoding context, an optimal linear estimator (OLE) was constructed for a population of 15 monotonic and 15 nonmonotonic neurons. Individual neuron input-output (IO) functions are shown, scaled by their weight and styled by monotonicity (gray lines for nonmonotonic neurons, dashed lines for monotonic neurons). The decoded IO functions, which are the sum of the weighted individual functions, are shown in black and compared with the target input-output function (dotted lines). The root mean squared errors (RMSEs) for the level fidelity and level invariance estimates are 2.40 and 2.24 spikes/s, respectively.

Sound level decoding contexts: level fidelity and level invariance.

Level fidelity reflects the ability to generate a decoded output that faithfully reflects the input stimulus level. The target output function y_target was set as a line with an intercept of 0 and a slope of 1 so that the magnitude of the desired decoded output (in spikes/s) would be equal to that of the input stimulus in dB SPL (Fig. 3A).

Level invariance reflects the ability to produce a constant representation of a sound across different input sound levels. This type of decoding allows the extraction of other sound features invariantly across different sound levels. In this decoding context, the target output function y_target was fixed at a constant value (y_target = 35), independent of stimulus level (Fig. 3B). The target value of 35 was chosen because it lay in the middle of the input range –15 to 85 dB SPL, thereby allowing for the average performance RMSE values to be comparable with those from a level fidelity context. Note that in the level invariance context, the output does not represent a sound level value. Instead, it represents an abstract sound property of interest. The constant target output value ensures that for the given sound stimuli, which are assumed to differ only in sound level, the same target representation of the sounds is formed.

Simulations with idealized neurons.

To evaluate whether the population coding trends we observed may have been specific to the precise nature of the recorded IO functions, we also conducted simulation experiments using a master population of 500 simulated neurons with idealized IO functions. Within this master population, 250 neurons were monotonic and 250 neurons were nonmonotonic. The monotonic neurons had IO functions with the shape of Gaussian cumulative distribution functions, and the nonmonotonic neurons had IO functions with the shape of Gaussian probability density functions. These IO functions were randomly distributed at different stimulus level locations and were given dynamic ranges, maximum discharge rates, and rate variabilities based on the distributions of these parameters from real A1 neurons reported by Watkins and Barbour (2011b).

RESULTS

Decoder performance improves with neuron population size.

To assess the level-encoding ability of different neuron subpopulations, we modeled the output of a neuron subpopulation in response to CF tones of different sound levels with a linear estimator and quantified how well the output could approach the target output function for a specific decoding context under the OLE. OLEs could provide adequate assessment of neuronal encoding performance in both level-fidelity and level-invariant contexts for physiologically derived neuronal responses, in that the estimated output functions could sufficiently resemble the target output functions in both slope and magnitude. An example of applying OLEs for one neuron subpopulation is shown in Fig. 3 for both decoding contexts.

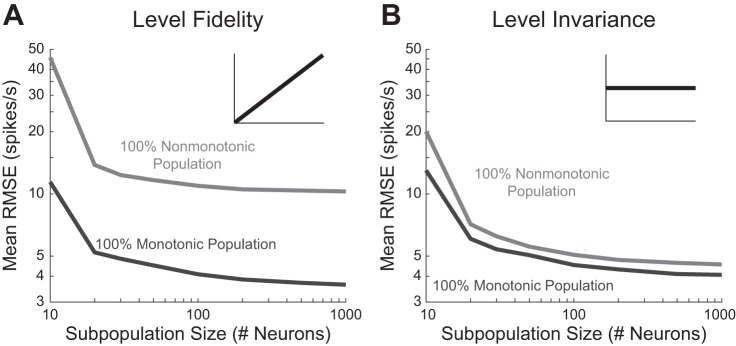
With the tool of OLE, we first asked how the two types of IO functions compare with each other at different decoding contexts when operating in isolation, and how the decoding performance depends on population size. To answer these questions, physiologically derived virtual neuron subpopulations of purely nonmonotonic or monotonic neurons were assessed in population sizes ranging from 10 to 1,000 neurons to form both level-fidelity and level-invariant representations. In all cases, increasing the number of neurons systematically improved decoding performance (Fig. 4). The minimum subpopulation size tested for near-converged performance in all cases was 20 neurons.

Fig. 4.

Effect of population size on decoding performance. Mean RMSEs are shown for populations of varying sizes ranging from 10 to 1,000 neurons, consisting of either only monotonic or nonmonotonic neurons. Populations were presented with both a level-fidelity (A) and a level-invariant (B) decoding context. In all instances, increasing the number of neurons improved decoding performance.

Comparison of the performance of the two neuronal types showed that purely monotonic populations were able to outperform purely nonmonotonic populations in level-fidelity decoding contexts at all population sizes (P < 10⁻⁶ for all subpopulation sizes, permutation t-tests, Bonferroni correction for 16 comparisons including 8 comparisons in each decoding context, one for each subpopulation size) by a large margin. This finding might be expected due to the higher strength of neuronal activity in monotonic neurons in response to more intense sounds, which is a pattern that matches the shape of the target output function for level-fidelity decoding.

In level-invariant decodings, purely monotonic populations still exhibited small yet significant advantages over nonmonotonic populations (P < 10⁻⁶ for all subpopulation sizes of 20 or greater, permutation t-tests, Bonferroni correction for 16 comparisons). This result was surprising because it contradicts the proposed specialized role of nonmonotonic neurons in encoding level-invariant contexts and thereby calls into question a leading theory for their existence.

One detail provides some hint toward the specialization of nonmonotonic neurons in the level-invariant decoding context. When the performance of the same neuronal types is compared across the two decoding contexts, it can be observed clearly that the error incurred by purely monotonic populations increased in the level-invariant context compared with the level-fidelity context, whereas that of purely nonmonotonic populations decreased by a large amount. This opposite direction of change in the two neuronal types indicates a difference in their relative suitability to form the two sound representations.

Mixed populations provide the best decoding accuracy.

One possibility that could potentially resolve the complicated observations in pure neuronal population performance was that nonmonotonic neurons exert their specialized function in level-invariant sound encoding not by operating alone, but by contributing to the decoding together along with monotonic neurons. Given this possibility, we set out to determine how well subpopulation mixtures performed at the same decoding contexts.

To investigate the decoding accuracy of different mixtures of neurons, subpopulations were constructed with constrained proportions of nonmonotonic and monotonic neurons, ranging from 0% to 100% nonmonotonic neurons in 10% increments. Subpopulation sizes ranging from 10 to 1,000 neurons were tested. Consistent with the previous observation, the minimum population size for a consistent trend of performance across neuronal compositions lay between 10 and 20 neurons (Fig. 5).

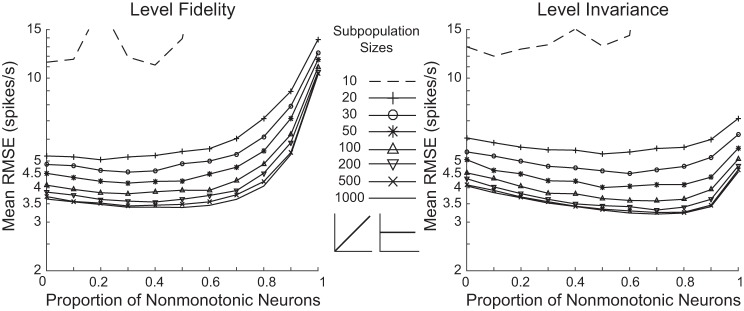
Fig. 5.

Neuronal mixtures provide the best performance compared with either pure population alone. Level-fidelity and level-invariant decoding contexts were tested for neuron subpopulations with varying proportions of nonmonotonic and monotonic neurons. Population sizes ranged from 10 to 1,000 neurons.

As shown previously, purely monotonic populations outperformed purely nonmonotonic populations for the level-fidelity context. The decoding accuracy did not significantly deteriorate, however, when the populations included nonmonotonic neurons instead, up to ~70%, for any population size of 20 or greater. Performance was worse than purely monotonic populations at only nonmonotonic proportions of 70% and higher for 20-neuron populations, as well as 80% and higher for population sizes larger than 20 (P < 10⁻³, permutation t-tests, Bonferroni correction for 240 comparisons including 80 comparisons for the level-fidelity context at 8 population sizes comparing each neuronal composition with purely monotonic population, and 160 comparisons for the level-invariant context, at each of the 8 population sizes, comparing each neuronal composition to either purely monotonic or purely nonmonotonic population; Fig. 5). In fact, for population sizes of 50 or more, one or more neuronal compositions with between 10% to 60% nonmonotonic neurons exhibited significant advantage over purely monotonic population of the same size (nonmonotonic neuron proportion of 30% for 50-neuron population, 20% and 30% for 100-neuron population, 20% ~50% for 200-neuron population, 10%~60% for 500- and 1,000-neuron populations; P < 10⁻⁵ for all cases, permutation t-tests, Bonferroni correction for 240 comparisons). The magnitude of advantage, though, is quite small. In this case, as long as monotonic neurons composed of at least 20%~30% of the population, decoding accuracy was nearly as good as the best obtainable. The performance in the level-fidelity context was thus robust to the inclusion of nonmonotonic neurons in the population within some range.

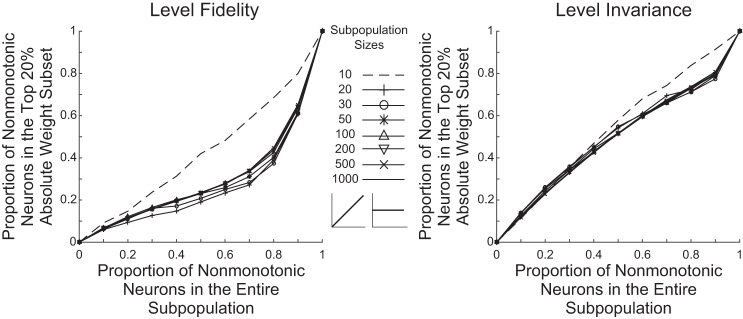
Given the small effect of including nonmonotonic neurons for up to 70~80% of the population size, the question arises whether their weights in the OLE under these conditions were too small to affect the decoding outcome. We first note that the distribution of absolute weights across neurons in a subpopulation was typically not uniform. Instead, the absolute weight distributions were skewed and usually had long-tailed shapes such that a small portion of neurons had large absolute weights and a majority of neurons had small absolute weights. For example, when examining whether at least half of the neurons in a subpopulation have absolute weights within the lowest 20% section of the entire range set by the subpopulation, a large percentage of neuron subpopulations tested at each subpopulation size fit this criterion, indicating a skewed distribution of absolute weights across neurons in neuron subpopulations (Fig. 6). To examine the importance of nonmonotonic neurons for the decoding, we analyzed the neuronal composition of the top 20 percentages of neurons with the largest absolute weight values for each subpopulation. Figure 7 shows the mean proportion of nonmonotonic neurons within this subset averaged across the 500 subpopulations at each neuronal subpopulation size and composition. It can be seen that although nonmonotonic neurons were disproportionally less represented than monotonic neurons within the subsets having the largest absolute weights, they still constituted a large proportion, and that proportion increased with a larger proportion of nonmonotonic neurons in the overall subpopulation. Thus the small effect of including nonmonotonic neurons up to 70~80% on the decoding accuracy of the level-fidelity context was not because that nonmonotonic neurons did not bear sufficient amounts of weights.

Fig. 6.

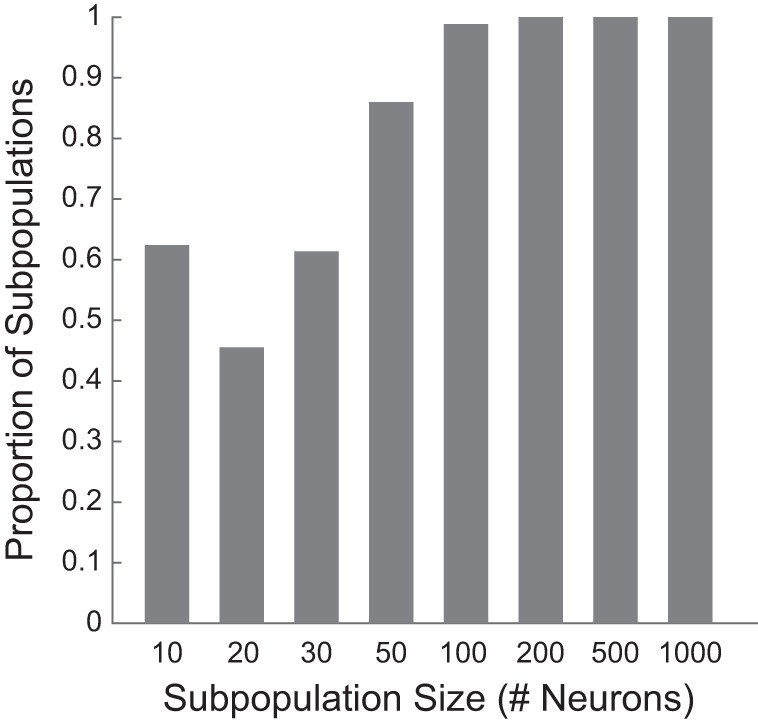
Distributions of the absolute weights among neurons tend to be skewed. For each neuron subpopulation tested, the number of neurons having absolute weights within the lower 20% of the range set by the entire neuron subpopulation was counted. The proportions of subpopulations with more than 50% of neurons meeting this criterion are shown for each subpopulation size for the level-fidelity decoding.

Fig. 7.

Both neuronal types contributed to the encoding in the neuronal mixtures. For each neuron subpopulation tested, the neuronal composition of the top 20% of neurons with the largest absolute weights was examined. The mean proportion of nonmonotonic neurons within this subset is shown for each subpopulation size and overall neuronal composition for both level-fidelity and level-invariant decodings.

For the level-invariant representation, as shown previously, the performance of purely monotonic and purely nonmonotonic populations differed by small margins at all population sizes. Surprisingly, when the two types of neurons were combined in mixed populations, decoding performance improved compared with either pure population alone (Fig. 5). Performance was better than purely nonmonotonic populations for all neuronal compositions of 20 or more neurons (P < 10⁻⁶ for all cases). Performance was better than purely monotonic populations for nonmonotonic neuron proportions of 30%~70% for a 20-neuron population, 20%~80% for a 30-neuron population, 10%~90% for 50-, 200-, 500-, and 1,000-neuron populations, and 20%~90% for a 100-neuron population (P < 10⁻⁵ for all cases). All P values were from permutation t-tests, Bonferroni corrected for 240 comparisons. This trend, while visible in subpopulations as small as 20 neurons, became clearer and more distinctive as the subpopulation sizes grew. The decoding reached optimal performance for larger populations at proportions of 60%~80% nonmonotonic neurons.

To get more insights into the decoding, we again quantified the proportion of nonmonotonic neurons within the top 20% of neurons having the highest absolute weights for each subpopulation for level-invariant decodings (Fig. 7). The proportions of nonmonotonic neurons in the top 20% absolute weight subsets were mostly slightly smaller than their proportions in the entire subpopulations, indicating that both neuronal types contributed within neuronal mixtures for the level-invariant decoding context. Overall, with the performance of both decoding contexts taken into consideration, a nonmonotonic proportion of 60%~70% would be predicted to provide the best overall encoding performance.

Even with idealized populations, nonmonotonic neurons can improve performance.

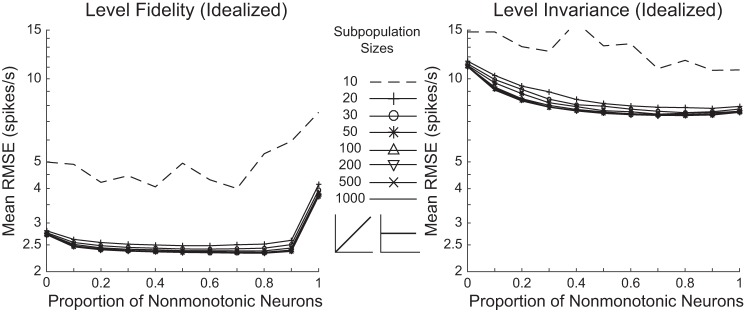
The finding that a mixture of IO functions could be particularly useful for the level-invariant decoding was unexpected and led to questions about which features of the neuronal responses gave rise to this phenomenon. To investigate whether this was a natural feature of combined monotonic and nonmonotonic IO functions or a feature specific to the auditory neuron IOs recorded, we next constructed idealized IO functions with the shapes of Gaussian probability density functions for model nonmonotonic neurons and Gaussian cumulative distribution functions for model monotonic neurons, and then tested their population decoding accuracy. The results can be seen in Fig. 8.

Fig. 8.

Decoding performance of idealized nonmonotonic and monotonic neuron populations. Level-fidelity and level-invariant decoding contexts were tested for subpopulations of neurons with idealized IO function shapes. Populations had varying proportions of nonmonotonic and monotonic neurons, and ranged in size from 10 to 1,000 neurons.

For the idealized neurons, purely monotonic populations were more accurate for the level fidelity context, yet purely nonmonotonic populations were more accurate for the level invariance context (P < 10⁻⁵ for all population sizes of 20 or greater, permutation t-tests, Bonferroni corrected for 320 comparisons, including comparisons of each neuronal composition with either purely monotonic or purely nonmonotonic population, at each of the 8 population sizes, for both decoding contexts). In general, performance of idealized populations was less sensitive to population size.

For the level-fidelity decoding, although idealized nonmonotonic neurons performed worse than idealized monotonic neurons when operating alone, the inclusion of nonmonotonic neurons into the population did not disrupt the encoding performance, consistent with results using real neurons. In this case, neuronal mixtures even exhibited significant although small advantage over purely monotonic populations. This was true for all neuronal mixture compositions for all population sizes of 20 or greater (P < 10⁻⁵ for all cases, permutation t-tests, Bonferroni corrected for 320 comparisons).

For the level-invariant decoding, neuronal mixtures performed significantly better than purely monotonic populations for all population sizes of 20 or larger at all neuronal compositions for the idealized neurons (P < 10⁻⁴ for all cases, permutation t-tests, Bonferroni corrected for 320 comparisons). Compared with purely nonmonotonic populations, neuronal mixtures showed different performance for neuronal compositions in different ranges. Populations with nonmonotonic proportion of 50% or less all performed significantly worse than purely nonmonotonic populations for population size of 20 or greater (P < 10⁻⁵ for all cases, permutation t-tests, Bonferroni corrected for 320 comparisons). Neuronal mixtures with higher nonmonotonic proportions, however, outperformed purely nonmonotonic populations at 80% nonmonotonic proportion for a 30-neuron population, 70% for a 50-neuron population, 60%~90% for 100- and 200-neuron populations, and 50%~90% for 500- and 1,000-neuron populations (P < 10⁻⁵ for all cases, permutation t-tests, Bonferroni corrected for 320 comparisons). Thus, in general, the conclusion that neuronal mixtures provide the optimal outcome in sound-level encoding still holds for the idealized IO functions, although with different details in some aspects.

DISCUSSION

The auditory system faces a unique problem among sensory systems: its peripheral tuning curves become systematically less selective at increasing input sound pressure levels. This frequency-dependent nonlinearity would make downstream level-invariant decoding challenging unless it were inverted in an intermediate step. One proposal for this inversion is to insert strong frequency-dependent inhibition at high sound levels to normalize frequency selectivity across sound level (Sadagopan and Wang 2008). The properties of type O neurons in the auditory system fit this expectation, because they have constant selectivity across sound level, and the nonmonotonic shape of their IO functions might manifest the effects of the proposed inhibition at high sound levels. The unique existence of this type of neuron in the auditory system, as well as their increasing proportion in progressively higher levels of the auditory system, also support this hypothesis (Clarey et al. 1994; Doron et al. 2002; Heil et al. 1994; Nakamoto et al. 2004; Pfingst and O’Connor 1981; Phillips and Hall 1990; Phillips and Irvine 1981; Phillips et al. 1994, 1995; Polley et al. 2007; Recanzone et al. 1999; Shamma and Symmes 1985; Suga 1977; Suga and Manabe 1982; Sutter and Loftus 2003; Sutter and Schreiner 1995; Watkins and Barbour 2011b). The rationale for nonmonotonic neurons being the intermediate calculation for level invariance is that tuned functions can create constant outputs at relatively constant errors, unlike monotonic functions (Salinas and Abbott 1994; Theunissen and Miller 1991). Similarly, monotonic IO functions would intuitively be expected to more accurately combine to construct monotonic target functions, in this case representing absolute sound level accurately. Both of these target functions would need to be encoded by a population of neurons because of the limited dynamic range of any of the constituent neurons (Barbour 2011).

Because the auditory system is capable of eliminating frequency-dependent nonlinearities without creating level-tuned IO functions in the process, i.e., with neurons with type I RF shapes (see Fig. 1), we wanted to directly test the ability of actual auditory cortical IO functions to combine into subpopulations to accurately form both level fidelity and level invariance representations. For these populations, encoding performance tended toward consistency with population sizes of ~20 or greater. As predicted, purely monotonic subpopulations did perform the level-fidelity decoding significantly better than purely nonmonotonic subpopulations. The situation with the level-invariant decoding, however, was more complicated. On one hand, purely nonmonotonic populations performed worse than purely monotonic populations, but on the other hand, the change of the performance of the same neuronal type across different decoding contexts provided some support for the notion of specialized functions of nonmonotonic neurons in level-invariant decoding. This led to the examination of the performance of neuronal mixtures to form these representations, because operating in isolation does not seem to justify the existence of nonmonotonic neurons.

With neuronal mixtures, we found that adding nonmonotonic neurons to a population of monotonic neurons on average did little to improve decoding accuracy for the level-fidelity decoding. Adding monotonic neurons to a population of nonmonotonic neurons, however, did significantly improve decoding accuracy for the level invariance context, up to a point. In other words, a mixture of the two types of IO functions was required for the most accurate level-invariant encoding. Under the optimal neuronal composition with sufficiently large population sizes, the virtual neuron populations were able to achieve a relatively high decoding accuracy similar to those shown in primate psychophysical tests (Sinnott et al. 1992, 1985). For example, virtual neurons on average had an error of ~3 dB in level-fidelity decoding, whereas macaques and vervet monkeys have been shown to discriminate sounds with ~1.5- to 2-dB differences in sound level (Sinnott et al. 1985). To our knowledge, there has been no data available on the sound level discrimination ability of marmoset monkeys to enable a direct comparison.

These findings imply that instead of operating in isolation with one neuronal type, a better coding strategy would be to use a mixture of the two subpopulations for this purpose. This scenario also provides a potential explanation for why nonmonotonic neurons do not completely replace monotonic neurons at higher levels of the auditory system. The variety of IO functions enables the same neurons to be used in different settings for different decoding purposes simply by sending projections of different synaptic strengths to different target output neurons. Because all of these processes are central in origin, they are subject to plastic processes that can effect rewiring as new decoding contexts become behaviorally relevant (Polley et al. 2004; Salinas 2006).

Relative proportions of nonmonotonic neurons actually present in the auditory system vary, presumably as a function of species tested and measurement methodology. Nevertheless, the optimal proportion of nonmonotonic neurons to achieve the most accurate level-invariant encoding with relatively large populations (i.e., 60%~70%) lies at the upper range of the proportions typically estimated from physiological studies. The physical neurons from which the virtual neurons used in this study were derived came from a sampled population of ~60% nonmonotonic neurons. Given that there was nothing in the process of the simulation that would bias results toward such a proportion, this finding provides circumstantial evidence for the population mixtures that encode sound level in actual auditory circuits.

When the same analysis was performed with idealized neurons, the most important conclusion (that neuronal mixtures provided the best encoding) still held true. Thus, even with very different constituent IO functions, some variety in individual neuronal responses generally improved population encoding. This feature appears to be particularly important when the constituent functions are not evenly spaced along the dimension to be encoded but are randomly distributed, leading to local inhomogeneities that can diminish decoding accuracy (Eliasmith and Anderson 2004). The differences in the details of the encoding performance (e.g., the differences of decoding accuracies for purely nonmonotonic and purely monotonic populations in level-invariant decodings) probably arose from some particular features of the real physiological IO functions.

In the current study, only neural firing rate responses were considered, which assumes a rate code for the encoding of sound pressure levels. In the real brain, temporal response features might also be used to carry information about sensory stimuli (Ferster and Spruston 1995; Grothe and Klump 2000). Note also that in the current approach, all virtual neurons were simulated to have independent neural response noises; i.e., the Gaussian noise added to each neural response was independent from other neural responses. In actual brain neural networks, noise correlations between neurons have been shown to vary (Abbott and Dayan 1999; Averbeck et al. 2006; Cohen and Kohn 2011; Ecker et al. 2011) and could have either a beneficial or detrimental effect to information encoding of the neural network, depending on the tuning relationships of the neurons (Averbeck et al. 2006; Ecker et al. 2011). Incorporating the factor of noise correlation would therefore be an important step in future studies to further understand the role of neuronal tuning monotonicity in the encoding of sound levels.

It is worth noting, however, that sound-level encoding is only one of the potential functions of nonmonotonic neurons in the auditory system. There has been evidence from multiple studies that nonmonotonic rate-level functions might arise from neural inhibition processes underlying the encoding of other sound properties, such as spectral information (Phillips et al. 1985; Shamma and Symmes 1985) and sound localization (Barone et al. 1996; Clarey et al. 1994; Imig et al. 1990). Nonmonotonicity in sound level representation thus might be an epiphenomenon secondary to the encoding of other sound properties. Further investigations are needed to fully reveal the complexity of the topic.

Last, it should be noted that the analyses presented are oriented toward understanding the potential role of different neuronal monotonicity in sound-level encoding in primary auditory cortex. It does not rule out the possibility that other auditory brain areas are involved in sound-level encoding or the possibility that rate-level functions of different monotonicity participate the encoding in a different way than observed in the present study.

In conclusion, these experiments partially supported the previously proposed role of nonmonotonic neurons in level-invariant sound encoding, but also revealed an important difference in the encoding scenario compared with the previous theory. We determined that different neuronal types cooperate during the encoding rather than operate in isolation. The result is a novel line of reasoning for the existence of both monotonic neurons and nonmonotonic neurons at high levels of the auditory system, especially primary auditory cortex.

GRANTS

This work was supported by National Institute of Deafness and Other Communications Disorders Grant DC009215 (to D. L. Barbour).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.L.B. conceived and designed research; P.V.W. performed experiments; W.S., E.N.M. analyzed data; W.S., E.N.M., and D.L.B. interpreted results of experiments; W.S. and E.N.M. prepared figures; W.S. and E.N.M. drafted manuscript; W.S., E.N.M., and D.L.B. edited and revised manuscript; W.S., E.N.M., P.V.W., and D.L.B. approved final version of manuscript.