The brain compensates for forces in the body and the environment to control movements, but it is unclear how it does so given the inherent delays in information transmission and processing. We examined how participants cope with delayed forces that depend on their arm velocity 70 or 100 ms beforehand. After adaptation, participants applied opposing forces that revealed a partially correct representation of the perturbation using the current and the delayed information.
Keywords: adaptation, delay, force field, motor primitives, reaching
Abstract
To adapt to deterministic force perturbations that depend on the current state of the hand, internal representations are formed to capture the relationships between forces experienced and motion. However, information from multiple modalities travels at different rates, resulting in intermodal delays that require compensation for these internal representations to develop. To understand how these delays are represented by the brain, we presented participants with delayed velocity-dependent force fields, i.e., forces that depend on hand velocity either 70 or 100 ms beforehand. We probed the internal representation of these delayed forces by examining the forces the participants applied to cope with the perturbations. The findings showed that for both delayed forces, the best model of internal representation consisted of a delayed velocity and current position and velocity. We show that participants relied initially on the current state, but with adaptation, the contribution of the delayed representation to adaptation increased. After adaptation, when the participants were asked to make movements with a higher velocity for which they had not previously experienced with the delayed force field, they applied forces that were consistent with current position and velocity as well as delayed velocity representations. This suggests that the sensorimotor system represents delayed force feedback using current and delayed state information and that it uses this representation when generalizing to faster movements.
NEW & NOTEWORTHY The brain compensates for forces in the body and the environment to control movements, but it is unclear how it does so given the inherent delays in information transmission and processing. We examined how participants cope with delayed forces that depend on their arm velocity 70 or 100 ms beforehand. After adaptation, participants applied opposing forces that revealed a partially correct representation of the perturbation using the current and the delayed information.
to move effectively, the brain must compensate for ongoing kinematic and dynamic changes in the environment and in body state, which are transmitted as afferent signals that propagate through the sensory system. It is widely accepted that to do so, the brain constructs and exploits internal models, i.e., neural structures that constitute the causal link between motor commands, the state of the body, and the forces acting on it (Karniel 2011; Kawato 1999; Shadmehr and Krakauer 2008; Shadmehr and Mussa-Ivaldi 1994; Wolpert and Ghahramani 2000; Wolpert et al. 1995). In a well-established experimental paradigm, participants make point-to-point reaching movements in the presence of perturbations that involve either altered visual feedback or the application of external forces that depend linearly on movement variables such as position and velocity (Shadmehr and Mussa-Ivaldi 1994; Tong et al. 2002). By updating the internal model parameters, the sensorimotor system is able to adapt to these novel environments (Karniel 2011). It was suggested that participants cope with state-dependent force perturbations by adjusting combinations of movement primitives, where each primitive (position, velocity, etc.) produces a force that is linearly related to the respective state. For example, a position primitive is a force that is linearly related to the current hand position. The adjustment of such primitive combinations attempts to increase the weight of the primitive on which the perturbing force depends while decreasing the weights of the others (Shadmehr and Mussa-Ivaldi 1994; Sing et al. 2009; Thoroughman and Shadmehr 2000; Yousif and Diedrichsen 2012).
However, signals from different modalities are transmitted at different rates across the nervous system (Murray and Wallace 2011); hence, the information available for constructing internal models entails delays between signals. This raises the question of how internal models are formed in light of these delays, namely, how the brain represents delayed feedback. Recent studies have demonstrated that when sensory feedback is delayed, the perception of impedance (Di Luca et al. 2011; Leib et al. 2015; Leib et al. 2016; Nisky et al. 2010; Nisky et al. 2008; Pressman et al. 2007) and object dynamics (Honda et al. 2013; Sarlegna et al. 2010; Takamuku and Gomi 2015) are biased. In addition, a delay in the visual feedback of a virtual object affects the proprioceptive state representation (Mussa-Ivaldi et al. 2010; Pressman 2012) and interferes with adaptation to space-based visuomotor perturbations (Held et al. 1966; Honda et al. 2012a). By contrast, participants can adapt to delayed velocity-dependent force perturbations in which the force depends linearly on the hand velocity a certain time beforehand (Levy et al. 2010). In this experiment, after the delayed force was suddenly removed, participants exhibited aftereffects that were shifted in time compared with those after the nondelayed perturbations, suggesting that perhaps some representation of the delay was used.
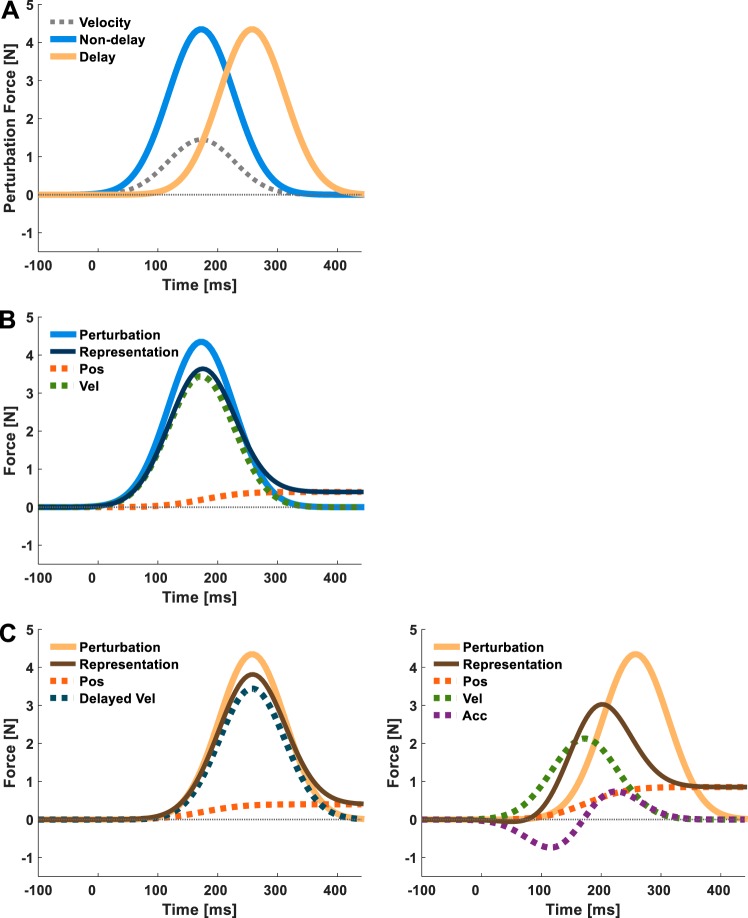
Here, we explored how the brain represents delayed force feedback. We examined adaptation to delayed velocity-dependent force perturbations, compared the effectiveness of different candidate representations in accounting for the observed compensations for the delayed forces, and analyzed the dynamics of the formation of these representations and their aftereffects. We asked healthy participants to perform point-to-point reaching movements and applied forces that were either nondelayed or delayed with respect to movement velocity (Fig. 1A). We examined participants’ internal representations of each type of perturbation by measuring forces they applied in force channel trials, namely trials in which a lateral force was applied on a participant’s hand that was equal and opposite to the force applied by the participant, which were randomly presented throughout the experiment (Scheidt et al. 2000). Based on previous studies (Sing et al. 2009; Yousif and Diedrichsen 2012), we expected that in the nondelayed case, participants would represent the perturbation as a combination of position and velocity primitives and give a higher weight to the velocity primitive (Fig. 1B). For the delayed case, we entertained two competing hypotheses. We reasoned that if participants had access to a representation of delayed velocity, they would learn to use it to predict the force (Fig. 1C, left). Alternatively, if this type of delayed velocity representation was not available, they would formulate a prediction based on the current state and possibly try to approximate the delay as a combination of current state variables (Fig. 1C, right). This state-based representation would be expected to lead to successful coping with small delays (relative to the movement duration) but would be likely to deteriorate for increasing magnitude of delay.
Fig. 1.
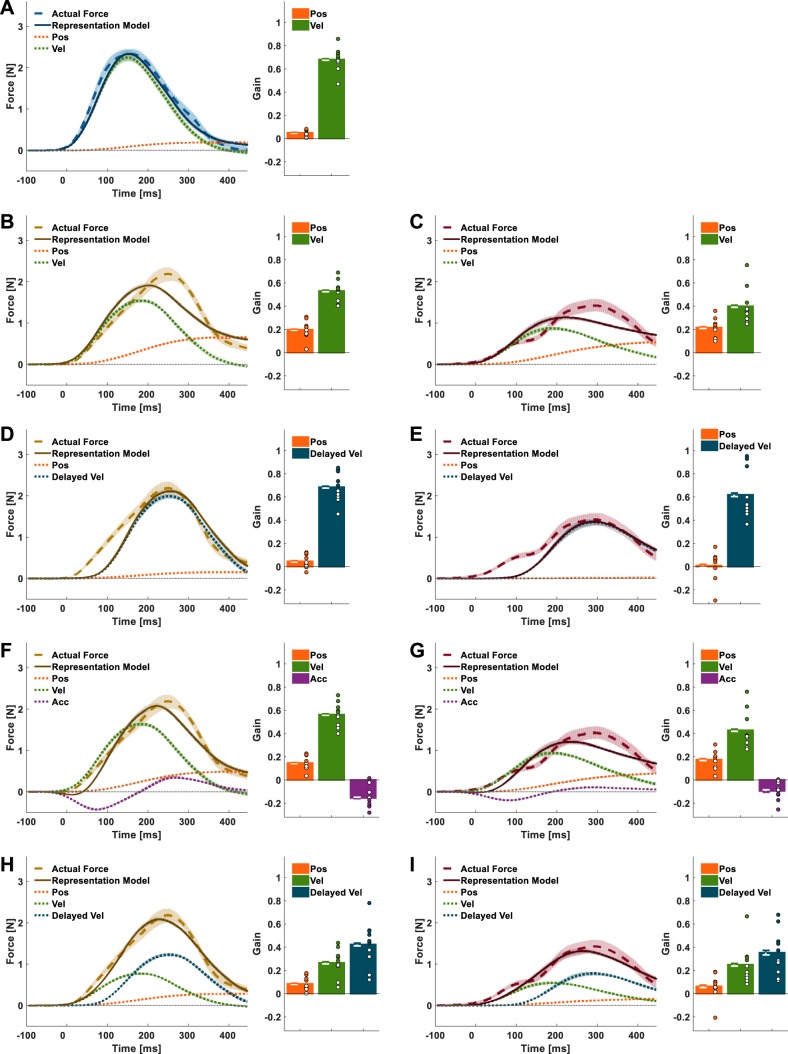
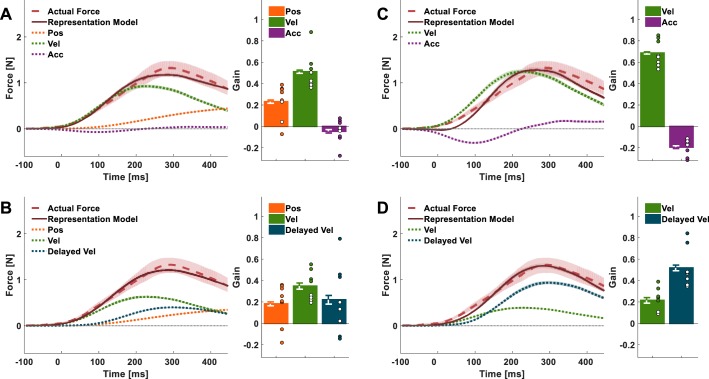
Models of force representation. A: schematic illustration of the force applied by the haptic device during adaptation in the nondelayed (solid blue line) and delayed (solid beige line) conditions, using the same representative velocity trajectory (dotted gray line) in both conditions. B: the representation of nondelayed force (solid dark blue line) is modeled as a combination of position (Pos; dotted orange line) and velocity (Vel; dotted green line). C: possible representations of delayed force (solid brown line). Left: based on representation of position and delayed velocity (Delayed Vel; dotted dark blue line); right: based only on current state; position, velocity, and acceleration (Acc; dotted purple line).
Surprisingly, we found that throughout adaptation to both the 70- and 100-ms delayed velocity-dependent force perturbations, participants formed a representation based on the delayed velocity together with the current position and velocity information. At the higher delay, the temporal separation between the delayed and current velocity trajectories in the representation was greater. The representation of the delayed force generalized to faster movements for which the delayed force field had never been experienced. Importantly, the forces that participants exhibited during the faster movements were also consistent with a combined representation of the current and the delayed velocity.
METHODS
Notations
We use lowercase letters for scalars, lowercase boldface letters for vectors, and uppercase boldface letters for matrices. Uppercase nonboldface letters indicate the dimensions of vectors/matrices of sampled data points and of vectors/matrices that were calculated from sampled data points. The letter n specifies trial index. Lowercase Greek letters indicate regression coefficients; x is the Cartesian space position vector, with x and y as position coordinates (for the right-left and forward-backward directions, respectively). N indicates the number of participants in a group.
Participants and Experimental setup
Thirty-eight healthy volunteers (aged 18–29; 20 females) participated in two experiments; 30 participated in experiment 1 and eight in experiment 2. No statistical methods were used to predetermine sample sizes, but the minimum sample size per condition that we used was the same as the test group in a previous study (Levy et al. 2010) performed in our laboratory, where a satisfactory effect size was reported. The experimental protocols were approved either by the Institutional Helsinki Committee (experiment 1) or by the Human Subjects Research Committee (experiment 2) of Ben-Gurion University of the Negev, Beer-Sheva, Israel, and the methods were carried out in accordance with the relevant guidelines. Both experiments were conducted after the participants signed an informed consent form as stipulated by the associated committee.
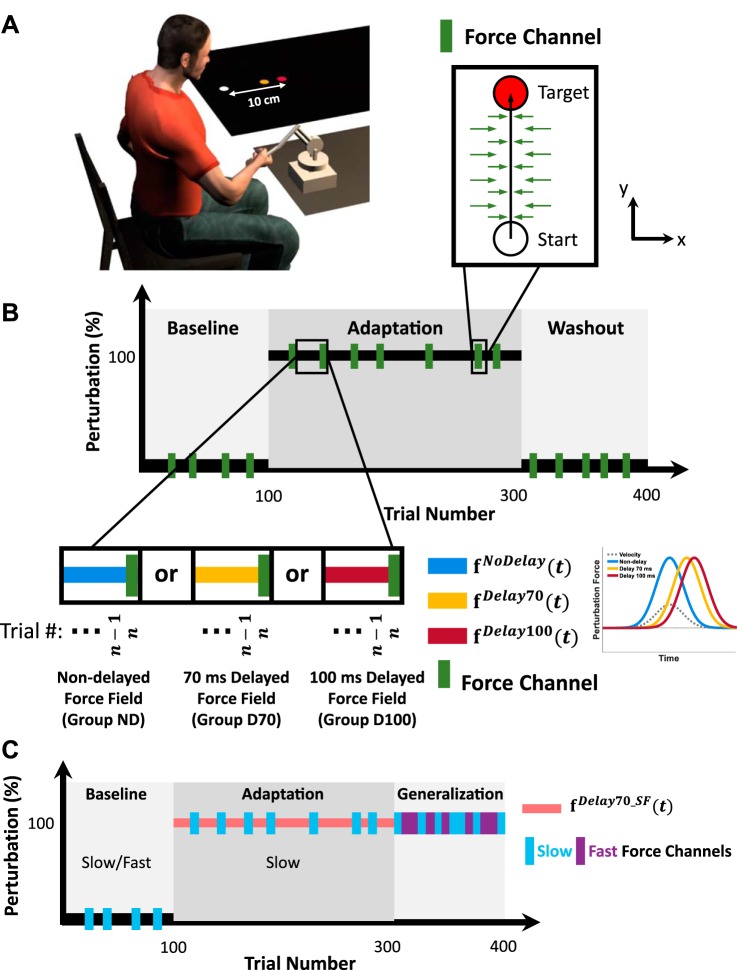
The experiments were administered in a virtual reality environment in which the participants controlled the stylus of a six degrees-of-freedom PHANTOM Premium 1.5 haptic device (Geomagic). Seated participants held the handle of the haptic device with their right hand while looking at a screen that was placed transversely above their hand (Fig. 2A) at a distance of ∼10 cm from participants’ chin. The hand was hidden from sight by the screen, and a sheet covered their upper body. The movement of the haptic device was mapped to the movement of a cursor that indicated the participants’ hand location. Participants were instructed to make point-to-point reaching movements in a transverse plane. Hand position was maintained in the transverse plane by forces generated by the robot that resisted any vertical movement. These forces were implemented by applying a one-dimensional spring and a damper above and below the plane. The update rate of the control loop was 1,000 Hz.
Fig. 2.
Experimental setup and protocols. A: an illustration of the experimental task; the seated participants held the handle of a Phantom Premium 1.5 haptic device (Geomagic). A screen that was placed horizontally covered the hand and displayed the task scene. Participants controlled the movement of a cursor (yellow dot) and performed reaching movements from a start location (white dot) to the target (red dot). B: experiment 1; schematic display of the experimental protocol. The experiment was composed of 3 sessions. During the baseline session (100 trials), no perturbation was applied; during the adaptation session (200 trials), reaching movements were perturbed with a velocity-dependent force field; and during the washout session (100 trials), the perturbations were removed. Three groups of participants performed the experiment, and each experienced different perturbations throughout the adaptation session. Movements of group ND participants were perturbed with a nondelayed velocity-dependent force field (blue bar), and movements of group D70 and group D100 participants were perturbed with a 70- (yellow bar) and 100-ms (red bar) delayed velocity-dependent force field, respectively. Green bars represent force channel trials that appeared pseudo-randomly in ∼11% of the trials. During force channel trials, high-stiffness forces were applied by the haptic device that constrained the hand to move in a straight path, thus making it possible to measure the lateral forces applied by the participants. C: experiment 2; protocol. During the baseline session (100 trials), no perturbation was applied, and participants were trained to reach in 2 velocity ranges: either slow or fast. During the adaptation session (200 trials), movements were perturbed with a 70-ms delayed velocity-dependent force field, and participants were only presented with the slow-reaching type trials. Light blue bars represent force channel trials, during which participants were requested to move in the slow type. The generalization session (100 trials) consisted of only force channel trials that were pseudo-randomly alternated between the slow and the fast (purple) type.
Task
A trial was initiated when the participants placed a yellow cursor 1.6 cm in diameter inside a white circle 2.6 cm in diameter, which was defined as the start area. The cursor center position inside the white circle specified the movement’s initial position. Participants were required to keep the cursor within the start area for 1.5 s. When they did so, a red target also 2.6 cm in diameter appeared on the screen at a distance of 10 cm from the center of the start area along the sagittal axis, instructing the participants to perform a fast-reaching movement and to stop when they saw the cursor reach the target. The target location was constant throughout the entire experiment and across participants. The start area, the cursor, and the target were all displayed during the entire movement (Fig. 2A). Target reach time was defined to be the moment when the center of the cursor was within the target. Movements could be completed if the cursor reached the target or passed the target’s y position. If movements were not completed within 700 ms, they were considered completed at that time. After the movement was completed, the target disappeared, and participants were asked to return to the start area and to prepare for the appearance of the next target.
After completion of each reaching movement, participants were provided with an on-screen text as feedback based on movement duration and accuracy. The purpose of this feedback was to equalize movement durations and velocities as much as possible within and between participants and to make the trajectories and the applied forces consistent and suitable for averaging across trials and participants within a group. In experiment 1, we set a single range of movement duration between 200 and 700 ms. In experiment 2, the feedback on the movement duration served an additional purpose; it enabled us to train participants to move at different velocities and to test the generalization of adaptation of the applied perturbation from slow to fast movements. We defined two trial types in experiment 2: slow and fast. We set the ranges of movement duration for the slow and the fast types to be 550–700 and 350–500 ms, respectively. To inform participants about the required movement duration in each trial, we set a different display background color for each type (slow: cyan; fast: purple) and instructed them before the experiment to move according to the displayed color. In both experiment 1 and experiment 2, for movements where the cursor reached the target within the trial duration range, the word “exact” was displayed. If participants passed the target’s y position during this range, they were requested to “stop on the target.” For movements where participants did not reach the target by the maximum set duration, the words “move faster” were displayed. For movements where participants reached the target in less than the minimum set duration, the words “move slower” were displayed.
Protocol
Experiment 1.
The experiment consisted of three sessions: baseline, adaptation, and washout (Fig. 2B). In the baseline session (100 trials), no perturbation was applied on the hand of the participant. In the adaptation session (200 trials), the participant experienced a velocity-dependent force field in which a force was applied in the rightward direction with a magnitude linearly related to the forward-backward velocity. The washout session (100 trials) was similar to the baseline session and was without perturbations. Forty-five (∼11%) trials (5 trials during baseline, 25 during adaptation, and 15 during washout) were force channel trials. Force channel trials were similar to other trials in the sense that the participants did not receive different instructions; however, in these trials, the haptic device constrained participants’ movement by enclosing the straight path between the center of the cursor at trial initiation and the end location within high-stiffness virtual walls (Gibo et al. 2014; Scheidt et al. 2000). The virtual walls were implemented by applying a one-dimensional spring and a damper around the channel. Although we could not achieve a perfectly straight path in force channel trials, maximum perpendicular displacement from a straight line to the target was kept below 0.77 cm and averaged 0.10 cm in magnitude (considering all the force channel trials in the experiment). The virtual walls served the dual purpose of preventing lateral motions and measuring lateral forces that the participant applied during the reach. We refer to these forces as the actual forces. The rationale for this paradigm was that if participants have an internal model of the perturbing forces and a representation of the forces that they have to apply to be able to reach the target properly, and if this internal model is adapted to the new environment containing a lateral force perturbation, it should be reflected in the forces that they apply on the force channel as a mirrored profile of the representation of the perturbation (Gonzalez Castro et al. 2014; Joiner and Smith 2008; Scheidt et al. 2000). The force channel trials were presented in a pseudo-random and predetermined order that was identical across participants in all the groups of this experiment.
The participants were assigned randomly to three groups: group ND (N = 10), group D70 (N = 10), or group D100 (N = 10). The groups were different from each other in the forces that the participants experienced during the adaptation session (Fig. 2B). Group ND adapted to a nondelayed force field, in which the applied force perturbation, , was temporally aligned with their hand velocity, :
| (1) |
where , and since movements were executed in a two-dimensional plane , and . Group D70 and group D100 adapted to a delayed force field, in which the applied force perturbation, in group D70 and in group D100, was proportional to the movement velocity either 70 or 100 ms before time t, respectively:
| (2) |
where for group D70, τ = 70 ms and , and for group D100, τ = 100 ms and . Similarly to the nondelayed case, and .
Due to the update rate of the control loop (1,000 Hz), during the nondelayed case, there was a delay of 1 ms in the force feedback. The experimentally manipulated delay in the delay conditions was added on top of this delay.
Experiment 2.
One group of volunteers, group D70_SF (N = 8), participated in experiment 2. The experiment consisted of three sessions: baseline, adaptation, and generalization (Fig. 2C). In the baseline session (100 trials), no perturbation was applied on the participant’s hand. The baseline session started with 20 slow-type trials, followed by 20 fast-type trials. In the remaining 60 trials of the session, the slow and fast types were presented in equal number in a pseudo-random and predetermined order that was identical across the participants. In the adaptation session (200 trials), the participant experienced a 70-ms delayed velocity-dependent force field [] in the right direction. All of the trials in the adaptation session were of the slow type. Twenty-nine trials (∼10% of the total number of trials of both the baseline and adaptation sessions: 4 during baseline and 25 during adaptation) were force channel trials, all of them of the slow type. To examine the generalization of adaptation to the delayed force perturbation from slow to fast movements, the generalization session (100 trials) consisted of only force channel trials of both slow- and fast-type trials (Joiner et al. 2011). The slow and fast trials were evenly split in each set of 10 consecutive generalization trials and were presented in a pseudo-random and predetermined order that was identical across the participants.
Data Collection and Analysis
Haptic device position, velocity, and the forces applied were recorded throughout the experiment and sampled at 200 Hz. They were analyzed offline using custom-written MATLAB code (The MathWorks, Natick, MA). To calculate acceleration, the velocity was numerically differentiated and filtered using the MATLAB function filtfilt() with a second-order low-pass Butterworth filter with a cutoff frequency of 10 Hz. For purposes of data analysis, we defined movement onset and movement end time as the first time the velocity rose above and decreased below 5% of its maximum value, respectively. The analysis included the data from 100 ms before movement onset to 200 ms after movement end time.
Adaptation Analysis
To assess adaptation, we calculated the positional deviation from all of the trials that were not force channel trials and the adaptation coefficient at force channel trials subsequent to force field trials. We calculated the positional deviation as the maximum lateral displacement (perpendicular to movement direction). A positional deviation to the right was defined as positive, and a positional deviation to the left was defined as negative. A large positional deviation indicates that the movement was not straight. We calculated the adaptation coefficient φ as the slope of the linear regression between the actual force that the participants applied during a force channel trial n, , and the perturbation force during the preceding force field trial n − 1, , as calculated from the velocity trajectory (Eqs. 1 and 2):
| (3) |
Both and are Ns × 1 column vectors for Ns sampled data points. ψ is the intercept of the regression line and ε the residual error minimized by the regression procedure. Our rationale for this metric was that since reduction in the positional deviation throughout adaptation to a lateral force field can be achieved by various strategies (for example, by increasing arm stiffness), it does not necessarily imply the existence of an internal representation of the perturbation. Rather, the adaptation coefficient indicates that a representation is most likely formed when there is an increasing correlation between the actual forces and the perturbing forces. Thus, during the early stages of adaptation, before an internal representation of the force field has formed, the correlation between the perturbation and the actual force participants apply on the force channel should be low (adaptation coefficient close to zero). As participants adapt and improve their compensation for the perturbation, the adaptation coefficient should approach a value of 1 (Smith et al. 2006).
Representation Analysis
Local peaks of actual forces.
To analyze quantitatively the shape of the actual forces after adaptation to the different force perturbations, we calculated the probability histograms of the number of force peaks (local maxima) in the force trajectory of each single trial. In addition, we calculated the probability histograms of the timing of the local peaks in the actual force trajectories. We first filtered the actual forces from each of the analyzed force channel trials with a second-order low-pass Butterworth zero-lag filter, with a cutoff frequency of 10 Hz implemented with the MATLAB function filtfilt(). We extracted the number of peaks, their values, and their times within the movement from each of the filtered actual force trajectories using the MATLAB function findpeaks(). To exclude peaks that were not related to the representation of the perturbations, and which probably resulted from nonspecific force fluctuations, for each participant we calculated the mean of the maximum applied forces from the force channel trials of the baseline session and set it as the minimum height of a peak.
We calculated probability histograms of number of force peaks in a single trial as , where is the number of trials in which j peaks were detected (5 was the maximum number of peaks in all the trials that were analyzed), N is the number of participants in a group, and Nt = 10 is the number of the trials per participant that were analyzed from the end of the adaptation session.
To calculate the probability histograms of the timing of the local actual force peaks within the movement, we segmented each actual force trajectory into bins of 25 ms each. For each bin, we calculated the probability defined as the number of peaks that were found in that bin over trajectories and participants and divided it by the total number of peaks found for all the trajectories and participants in the group.
Primitives.
We adhered to the assumption that the internal representation of the environment forces during a single movement, , is constructed from a linear combination of L movement primitives and that each primitive corresponds to a specific state variable:
| (4) |
For movements executed in a two-dimensional plane x,y, the vectors and are the represented forces and primitive trajectories in both movement directions. The matrix defines the gains of each primitive that contributes to the representation of the force in each dimension (1st subscript component) and for each dimensional component of the movement (2nd subscript component). For example, the representation of nondelayed velocity-dependent force field was suggested to be constructed from a linear combination of position and velocity primitives (Sing et al. 2009), and accordingly, we can formulate such a representation as follows:
| (5) |
where K and B are the gain matrices of the position and velocity primitives, respectively. Since in our experimental design the participants were required to move in the y direction and the perturbation was applied in the x direction, for each primitive we chose to estimate only the gain component cxy associated with the respective movement and force dimensions. To simplify notations, we designate this gain component as c in the general case. Thus, the internal representation of the forces in the x direction, , can be described as follows:
| (6) |
where piy(t) indicates the y direction trajectory of the ith primitive. Here, we examined the possible contribution of four types of primitives to the representation: position [y(t)], velocity [], delayed velocity [] and acceleration [], and we designate their gains as k, b, bτ, and m, respectively.
The actual lateral force that the participants applied during a force channel trial, , is a proxy for the representation of the forces in the environment, (Sing et al. 2009; Sing et al. 2013). Therefore, to test the predictions in Fig. 1, and to assess which motor primitives participants used to represent the experienced force perturbation in experiment 1, we implemented a repeated-measures linear regression analysis. We fitted a repeated-measures linear regression model to the forces that were applied by the participants during a force channel trial n of Ns sampled data points, (Ns × 1), and various combinations of motor primitives, namely, position, velocity, delayed velocity, and acceleration, from the preceding force field trial n − 1. We chose to fit the model using the primitives of the preceding movements because the movement kinematics were slightly influenced by the force channel. Specifically, we found that the velocity trajectory during force channel trials was slightly skewed toward the beginning of the movement, possibly due to an effect of a feedback component. Therefore, to reduce such distortions as much as possible in the trajectories that could be a result of an online control mechanism, we chose to use the primitives from the preceding force field trial for the regression. Each of the representation models tested was defined as a specific weighted linear combination of the columns of the movement primitives’ matrix with dimensions Ns × L (where L is the number of movement primitives in a model). Each of the columns of is one primitive variable [position , velocity , delayed velocity and acceleration ] constructed from the trajectories of the trials that preceded each of the force channel trials. The weights were determined by an L × 1 gains vector γ, which consists of a combination of one or more of the gains, designated as κ, β, βτ, and μ, associated with each primitive in the model. For example, for a model consisting of only the position and velocity primitives, is the Ns ×2 matrix , and the corresponding γ is a 2 × 1 vector .
For each representation model, the resulting force representation estimation in trial n, a Ns × 1 column vector , was calculated as
| (7) |
The primitives matrix in the regression analysis described in Eq. 7 could consist of different types of state variables (position, velocity, and acceleration), with each having specific units that were also different from the force units. As a result, the gains in γ had noncomparable units. Thus, to assess the weighted contribution of each primitive in a representation model, we calculated normalized gains:
| (8) |
where , , , and are the normalized gains of the position, velocity, delayed velocity, and acceleration primitives, respectively. The normalizing factors , , and were chosen to equate peak perturbing forces between force fields that depend linearly on a single state variable (Sing et al. 2009). was chosen to be equal to the damping constant (Eqs. 1 and 2) for all groups. To determine the other normalizing factors, for each group, we estimated the mean maximum velocity of all participants during force field trials (group ND: ; group D70: ; group D100: ) and approximated a mean maximum velocity-dependent perturbation force (group ND: ; group D70: ; group D100: ). Because participants were required to move a distance (see Protocol), equivalent position-dependent force fields that produce the above peak forces would have an elasticity constant . Accordingly, we set for group ND, for group D70, and for group D100. Similarly, according to the mean maximum acceleration (group ND: ; group D70: ; group D100: ) as was estimated from the acceleration traces, to produce the same amount of maximum force, an equivalent acceleration-dependent force field would have a mass . Thus, we set for group ND, for group D70, and for group D100 (Sing et al. 2013).
The specific combinations of primitives that we considered as models for the representation of the perturbing force field in each of the ND, D70, and D100 groups are specified in Table 1. For the models that included a delayed velocity primitive, for model simplicity, we set the value of the delay to be consistent with the delay in the perturbing force, 70 ms in group D70 and 100 ms in group D100 (see discussion).
Table 1.
Evaluation of the goodness-of-fit with the correlation coefficient (r2) and BIC for the representation models that were examined in each group according to the actual forces at the end of the adaptation session
| Group |
||||||||
|---|---|---|---|---|---|---|---|---|
| ND |
D70 |
D100 |
D70_SF |
|||||
| Representation Model | r2 | BIC (× 104) | r2 | BIC (× 104) | r2 | BIC (× 104) | r2 | BIC (× 104) |
| v (t) | 0.714 | 1.71 | 0.417 | 2.37 | 0.208 | 2.01 | 0.284 | 1.55 |
| p (t), v (t) | 0.732 | 1.65 | 0.648 | 1.80 | 0.468 | 1.58 | 0.459 | 1.30 |
| v (t − τ) | 0.682 | 1.68 | 0.457 | 1.59 | 0.398 | 1.39 | ||
| p (t), v (t − τ) | 0.699 | 1.63 | 0.476 | 1.56 | 0.430 | 1.35 | ||
| p (t), v (t), a (t) | 0.727 | 1.53 | 0.507 | 1.51 | 0.468 | 1.30 | ||
| p (t), v (t), v (t − τ) | 0.768 | 1.34 | 0.574 | 1.34 | 0.476 | 1.28 | ||
BIC, Bayesian information criterion. Values of r2 closer to 1 and smaller values of BIC indicate a better model (values in bold).
The duration and time course of the movement trajectories were roughly similar within and between participants in each group and for each required movement duration (experiment 2) so that no manipulation (such as time scaling) of the data was necessary to make the force trajectories and the primitives consistent and suitable for averaging across trials and participants within a group. To determine the lower cutoff of the duration of the trials that were used for the analysis (force channel trials and each of the preceding force field trials), we calculated the 10th percentile of the trial durations for each group (ND: 545 ms; D70: 585 ms; D100: 610 ms; D70_SF: 560 ms). Trial pairs (successive force field and force channel trials) in which at least one trial was completed faster were removed from the analysis (5.6% of the trial pairs from the overall adaptation trial pairs of all three groups in experiment 1 and 2.3% from the group in experiment 2). To equalize the duration of the displayed trajectories between groups, we used the minimum cutoff duration of the three groups (545 ms).
We used the Bayesian Information Criterion (BIC) (Schwarz 1978) to compare the representation models based on their goodness of fit and parsimony:
| (9) |
where d is the number of predictors associated with the linear regression for each representation model, T is the number of observations, and LogL is the logarithm of the optimal likelihood for the regression model (a smaller value of BIC indicates a better model). The comparison of the representation models was done separately for each group.
For experiment 1, we first conducted this analysis on the last 10 pairs of successive force field and force channel trials in the adaptation session, which were all pooled into a single regression model. We ran the analysis on the entire data set from these trials, combining the actual forces and primitives from each pair in the same regression model and extracting the goodness of fit (r2) and a single BIC value for each model (Table 1). Then, to examine the trial-to-trial dynamics of the different primitives’ normalized gains throughout the experiment, for the best models in each of the groups, we recalculated the regression separately for each force field-force channel trials pair in the experiment. For the latter analysis, we eliminated trials in which we identified high multicollinearity between the primitives. Multicollinearity in a regression analysis occurs when there is a high correlation between predictors in the model, which limits our capability to draw conclusions about the contribution of each predictor in accounting for the variance. To evaluate multicollinearity, for each participant and for each force field-force channel trials pair, we calculated the variance inflation factor (VIF) of the model primitives. Trial pairs in which the VIF was >10 were removed from the analysis (3.9% of trial pairs overall from all three groups) (Myers 1990). Importantly, these trials were removed only for the presentation of the trial-to-trial dynamics of the different primitives’ normalized gains, such that all of the conclusions that were drawn about the fit of the different representation models are also valid without the elimination of these trials.
We compared the normalized gain of the velocity primitive (gβ) from the position/velocity representation model in group ND to the normalized gains of the delayed velocity primitive () from the position/velocity/delayed velocity representation model in groups D70 and D100 during the end of the adaptation. To do so, we calculated the regression again, this time separately for each participant for each of the last 10 force field-force channel trial pairs in the adaptation. We then averaged the resulting normalized gains from these trials for each participant.
For experiment 2 (group D70_SF), we performed the primitives analysis on the last 10 pairs of successive force field and force channel trials in the adaptation session, which were all pooled into a single repeated-measures regression model (similar to the analysis for experiment 1). We first examined the fit of the position/velocity/acceleration and the position/velocity/delayed velocity. However, we were limited in revealing the contributions of the acceleration and delayed velocity primitives from these fits due to their similarity to the position primitive (see results). Thus, we focused on examining the respective representation models that did not include the position primitive, namely, the velocity/acceleration and the velocity/delayed velocity models. To examine the generalization of the fits across velocities and experimental sessions, for each model, we extracted the primitives’ normalized gains from late adaptation trials and then tested their ability to predict the trajectories of the slow and fast trials in the early generalization stage. Thus, we constructed the predicted generalization forces for each movement velocity as the sum of the primitives multiplied by the gains from the models that were fitted to the adaptation trials. Because of the natural decay in the actual forces following adaptation (Joiner et al. 2011), the predicted forces during the early generalization stage were expected to be smaller than the actual forces during late adaptation for the same movement speed. Therefore, we evaluated the decay in our prediction. We calculated the ratio of the mean maximum velocity () to the mean maximum actual force that the participants applied during late adaptation () as . Then, we calculated the ideal maximum actual force that participants would apply during early generalization if there was no decay () from the mean maximum velocity () of each of the slow and fast trials (first 5 trials for each velocity in the generalization session): . Finally, we estimated the decay factor () as , where is the mean maximum actual force during early generalization. As a result of this calculation, when calculating the predicted generalization forces, we set decay factors of and for the slow and fast trials, respectively.
Statistical Analysis
Statistical analyses were performed using custom-written MATLAB functions, the MATLAB Statistics Toolbox, and IBM SPSS.
We used the Lilliefors test to determine whether our measurements were distributed normally (Lilliefors 1967). In the repeated-measures ANOVA models, we used Mauchly’s test to examine whether the assumption of sphericity was met. When it was not, F-test degrees of freedom were corrected using the Greenhouse-Geisser adjustment for violation of sphericity. We denote the P values that were calculated using these adjusted degrees of freedom as Pε. For the factors that were statistically significant, we performed planned comparisons and corrected for familywise error using the Bonfferoni correction. We denote the Bonfferoni-corrected P values as PB.
For the adaptation analysis, we first examined whether there were differences in the positional deviation between stages of the experiment. We evaluated the mean positional deviation of four force field trials for each participant at the following stages of the experiment: late baseline, early adaptation, late adaptation, and early washout. We fit a two-way mixed effects ANOVA model, with the mean positional deviation as the dependent variable, one between-participants independent factor (group: 3 levels; ND, D70, and D100), and one within-participants independent factor (stage: 4 levels; late baseline, early adaptation, late adaptation, and early washout). Mauchly’s test indicated a violation of the assumption of sphericity for the statistical analysis on the mean positional deviation in experiment 1 [,]; thus, we applied the Greenhouse-Geisser correction factor () to the degrees of freedom of the main effect of the experiment stage and to the group-stage interaction effect.
To analyze adaptation according to positional deviation in group D70_SF (experiment 2), we fit a one-way repeated-measures ANOVA model, with the mean positional deviation as the dependent variable and one within-subjects independent factor (stage: 3 levels; late baseline, early adaptation, and late adaptation). Mauchly’s test indicated a violation of the assumption of sphericity [, P < 0.001]; thus, we applied the Greenhouse-Geisser correction factor () to the degrees of freedom of the main effect of the experiment stage.
The second analysis of adaptation was done to test for an increase in the adaptation coefficient between the early and late stages of adaptation. We first computed for each participant the adaptation coefficient φ (Eq. 3) for each of the force channel-preceding force field trial pairs in the adaptation session and averaged these values separately for the first (early adaptation) and the last (late adaptation) five trials of adaptation. After a Lilliefors test for normality, we fit a two-way mixed effect ANOVA model, with φ as the dependent variable, one between-participant independent factor (group: 3 levels; ND, D70, and D100), and one within-subject independent factor (stage: 2 levels; early adaptation and late adaptation). For group D70_SF, we used a two-tailed paired-samples t-test to compare the mean adaptation coefficient during the early adaptation and late adaptation stages.
To compare the movement durations during the end of the adaptation session between the groups, we fit a one-way ANOVA model with the movement duration as the dependent variable and the group as the independent factor (3 levels; ND, D70, and D100).
To compare the normalized gain of the velocity primitive (gβ) from the position/velocity representation model in group ND to the normalized gain of the delayed velocity primitive () from the position velocity/delayed velocity representation model in groups D70 and D100 during the end of the adaptation, we fit a one-way ANOVA model, with the respective normalized gain as the dependent variable and the group as the independent factor (3 levels; ND, D70, and D100).
To compare the mean maximum velocity of the movements in force channel trials during the late adaptation stage of group D70 to group D70_SF, we used a two-tailed independent-sample t-test.
Throughout the paper, statistical significance was set at the P < 0.05 threshold.
Data and Code Availability
The data presented in this manuscript and the computer codes that were used to generate the results are available upon request from the corresponding author.
RESULTS
Experiment 1
In experiment 1, participants performed fast reaching movements from an initial location to a target presented in front of them while holding a haptic device that recorded their movements and applied forces that depended on the state of their hand (Fig. 2A). After a baseline session during which they moved with no external force perturbing their hand, we introduced an adaptation session in which a velocity-dependent force field was presented and persisted throughout the entire session. During washout the perturbation was removed, and the environment was as in baseline (Fig. 2B).
Participants adapted to both nondelayed and delayed velocity-dependent force perturbations by constructing an internal representation of the environment dynamics.
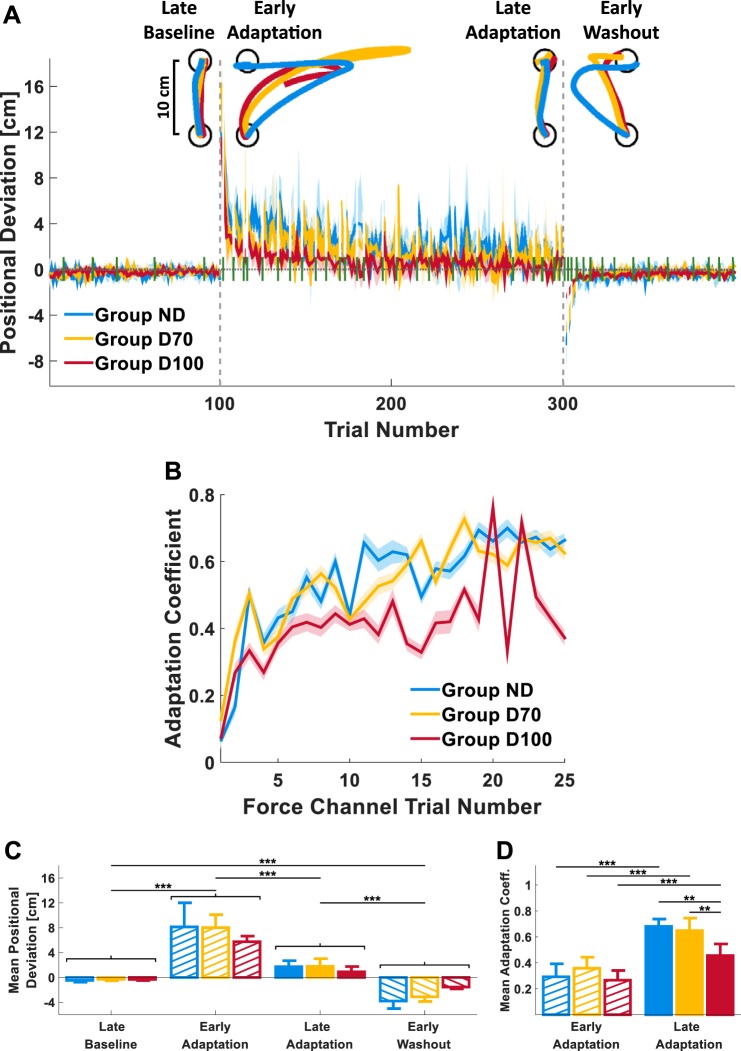
Figure 3 summarizes the analysis of adaptation for group ND (blue), group D70 (yellow), and group D100 (red). Figure 3A presents the mean positional deviation of all trials that were not force channel trials (the latter are indicated by the green bars) for each of the three groups. The positional deviation was defined as the maximum lateral displacement (perpendicular to movement direction), with positive and negative signs for displacements to the right and left, respectively. Individual movements from non-force channel trials of a single participant from each group are presented in Fig. 3A, top, at locations that correspond to the experimental stage from which they were taken. In the last trial of the baseline session, late baseline, participants’ movements were similar to a straight line. In the first trial of the adaptation session, early adaptation, the movements were disturbed by a velocity-dependent force to the right, resulting in a deviation from a straight line in a direction corresponding to the direction of the perturbation. In the last trial of the adaptation session, late adaptation, participants recovered the straight paths they exhibited during baseline. Finally, during the first trial of the washout session, immediately after the removal of the perturbations, early washout, participants from all groups exhibited an aftereffect, i.e., a deviation from the straight line in the opposite direction to the force field that was applied.
Fig. 3.
Experiment 1: adaptation to nondelayed and delayed velocity-dependent force fields. A: time course of the peak positional deviation averaged over all participants in each group (group ND, blue; group D70, yellow; group D100, red). Vertical dashed gray lines separate the baseline, adaptation, and washout sessions of the experiment. Green bars indicate force channel trials. Individual movements of a single participant from each group during a single non- force channel trial from the late baseline (LB), early adaptation (EA), late adaptation (LA), and early washout (EW) stages of the experiment are presented at top. B: time course of the average adaptation coefficient during the adaptation session. The adaptation coefficient represents the slope of the regression line extracted from a linear regression between the actual force participants applied during a force channel trial and the applied perturbation force during the preceding force field trial. Shading represents the 95% confidence interval in both A and B. C: mean positional deviation of four trials from 4 stages of the experiment (LB, EA, LA, and EW) averaged over all participants in each group. D: mean adaptation coefficient of the first (EA) and last (LA) 5 trials pairs of adjacent force field and force channel trials of the adaptation session. Error bars represent the 95% confidence interval. **P < 0.01; ***P < 0.001.
These qualitative observations are also supported by a statistical analysis of the mean positional deviation from four trials during each of the four experimental stages mentioned above (Fig. 3C). For all three groups, the mean positional deviation changed significantly throughout these stages [main effect of stage: F(1.398, 37.747) = 97.580, Pε < 0.001]. It increased considerably from late baseline to early adaptation as a result of the initial exposure to the perturbation (PB < 0.001), and as participants adapted, the mean positional deviation decreased toward zero during late adaptation (PB < 0.001). Immediately after the perturbation was removed during early washout, the observed positional deviation became negative and significantly different from both late adaptation (PB < 0.001) and late baseline (PB < 0.001), implying the existence of an aftereffect. These results indicate that the participants from all three groups adapted to the applied force fields.
The magnitude of the experienced delay in the force (0, 70 and 100 ms) did not affect the overall positional deviation [main effect of group: F(2, 27) = 0.310, P = 0.736] or the change in the positional deviation throughout the stages of the experiment [stage-group interaction effect: F(2.796, 37.747) = 1.880, Pε = 0.153], suggesting that there was no difference in the extent of adaptation between the groups.
On random trials, the haptic device applied a high-stiffness attractor to a straight-line path (force channel trials; Fig. 2B). These trials served to measure the actual forces that the participants applied and to estimate the adaptation coefficient φ from the linear regression between each of these force trajectories and the force trajectories that were applied by the haptic device during the preceding force field trials (Eq. 3). If participants update their internal representation of the external forces, the value of this adaptation coefficient should increase and approach 1 when participants adapt completely. In Fig. 3B, the adaptation coefficients are presented against the sequential numbers of force channel trials in the adaptation session. For all three groups, there was an increase in the adaptation coefficient throughout the adaptation session. The mean adaptation coefficient during late adaptation was significantly higher than during early adaptation [F(1,27) = 131.179, P < 0.001] and was closer to 1 (Fig. 3D), indicating that participants learn to apply lateral forces that oppose the perturbing forces. The magnitude of the experienced delay in the force affected the change in the mean adaptation coefficient from the early to late stages of adaptation [stage-group interaction effect: F(2,27) = 5.170, P = 0.013] such that during late adaptation the mean adaptation coefficient of group D100 was smaller than that of group ND (P = 0.002) and group D70 (P = 0.010).
The adaptation analyses suggest that participants adapted to both 70- and 100-ms delayed velocity-dependent force fields. Both the existence of an aftereffect and the increase in the adaptation coefficient indicate that this adaptation was the result of an adaptive process that used a representation of the external forces. However, the delay had an effect on movement kinematics. By the end of the adaptation session, the movement duration was longer for a higher delay [F(2, 27) = 12.047, P < 0.001 (means ± SD); ND: 364 ± 75.8 ms; D70: 396 ± 72.6 ms; D100: 528 ± 134 ms]. This could have weakened the velocity-dependent perturbing force and may account for the tendency toward decreased positional deviation during both early adaptation and early washout (aftereffect) with the increasing delay, although these effects were not significant. In addition, the significantly smaller adaptation coefficient for the D100 group during late adaptation suggests that the delay partially impeded adaptation to the perturbation and that the representation of the delayed force was not complete.
The actual forces applied following adaptation to the delayed velocity-dependent force fields do not fully correspond to the perturbations.
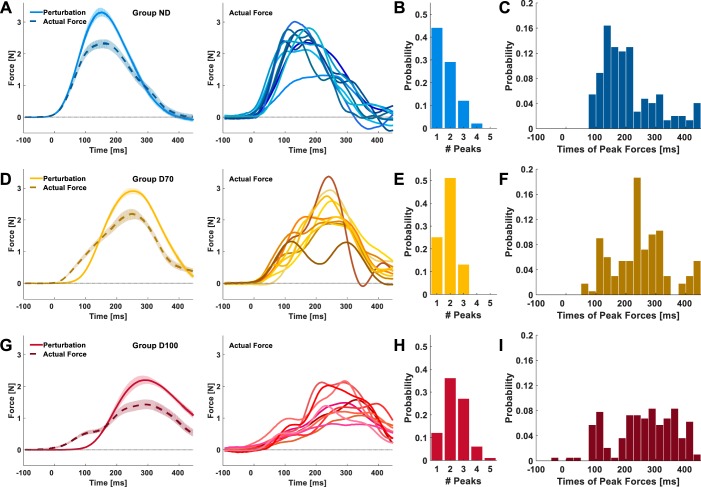
To assess the way participants represented the forces that they adapted to, we examined the actual forces that participants exhibited at the end of the adaptation session (Fig. 4). The mean actual force trajectory exhibited by the group ND participants was roughly a scaled version of the mean perturbation forces applied during the preceding force field trials (Fig. 4A): the onset of the mean actual forces and the time of its peak corresponded to the onset and the peak time of the mean perturbation force, respectively; both trajectories declined together after they reached their respective peak (which was smaller for the mean actual forces trajectory). For the participants in both groups D70 and D100 (Fig. 4, D and G), the onset of their mean actual forces occurred before the onset of the mean perturbation forces, similar to the time within the movement in which the onset of the mean actual forces of group ND participants occurred. However, the peak of their mean actual forces corresponded to the time in which the mean of the perturbation forces for each of these groups (which is a scaled version of the delayed velocity) reached its maximum value. Furthermore, the mean actual forces in both groups did not return to zero. In the mean actual force of group D70, the decrease in the mean actual forces becomes less steep, resulting in a “tail” when approaching the end of the movement (Fig. 4D, left).
Fig. 4.
Experiment 1: actual forces at the end of adaptation. A, D, and G, left: mean perturbation trajectories (solid lines) and mean actual forces (dashed lines) of all of the participants in each group; group ND (A), group D70 (D), and group D100 (G). The forces depicted are the actual forces that participants applied during the last 10 force channel trials of the adaptation session to cope with the applied perturbations presented in the preceding force field trials. Shading represents the 95% confidence intervals. A, D, and G, right: mean actual forces for each participant from the group on the left. B, E, and H: histograms depict the probability distributions of the number of local peaks in the actual force trajectories from late adaptation [ND (B), D70 (E), and D100 (H)]. C, F, and I: distributions of the times of local peaks in the actual force trajectories [ND (C), D70 (F), and D100 (I)].
A closer examination of each participant’s mean actual forces at the end of the adaptation (Fig. 4, A, D, and G, right) revealed a degree of interparticipant variability in the shape of the force trajectories. However, whereas the forces applied by group ND consisted of a single distinct peak, the forces applied by group D70 and group D100 participants consisted of at least two peaks. We quantitatively analyzed the shape of the actual forces following adaptation to the different force perturbations to verify the existence of multiple peaks within a single trajectory. This analysis revealed that for all of the actual force trajectories at the end of adaptation in group ND (Fig. 4B), the highest probability was to find a single peak in the actual force trajectory [P(1) = 0.44]. For group D70 (Fig. 4E) and group D100 (Fig. 4H), the probability of the actual force trajectories with a single peak was lower [D70: P(1) = 0.25; D100: P(1) = 0.12], and was the highest for the actual force trajectories that consisted of two peaks [D70: P(2) = 0.51, D100: P(2) = 0.37]. The histograms of the timing of the local peaks in the actual force trajectories showed that one of the them, usually the dominant peak, occurred around the time of the peak perturbation (which was 70 or 100 ms after the peak of the velocity trajectory), and the other occurred before it and closer to the time of the peak perturbation in group ND (which corresponds to the peak of the current velocity trajectory) (Fig. 4, C, F, and I).
These results indicate that unlike in adaptation to nondelayed velocity-dependent force fields, the actual forces that participants applied to cope with the delayed force fields only partially corresponded to the applied perturbation. Although there seemed to be a component in the actual forces that matched the perturbing force, at least one additional component was present that did not directly relate to the perturbing force.
The representation of the delayed velocity-dependent force perturbations can best be reconstructed by using a combination of current position, velocity, and delayed velocity primitives.
To evaluate the fit of different representation models with the actual forces, we calculated a repeated-measures linear regression between the forces that were applied by the participants during force channel trials from the end of the adaptation session and various combinations of motor primitives, position, velocity, delayed velocity, and acceleration, from the respective preceding force field trials. As mentioned above, the movement duration was different between groups; namely, the durations of the movements from these trials increased with the increasing delay. Nevertheless, since durations were similar within participants and between participants within each group, we did not apply time normalization when averaging the results across trials and participants within a group.
Our evaluation of the ability of different combinations of motor primitives to explain the internal representation of the nondelayed and delayed velocity-dependent force fields is presented in Table 1. The closer the r2 is to 1, and the smaller the value of BIC, the better the model explains the actual forces that the participants applied at the end of the adaptation session. Consistent with previous studies (Sing et al. 2009; Yousif and Diedrichsen 2012), the actual forces applied by the participants in group ND are best fitted by a representation model based on current position and velocity primitives (Fig. 5A) with a large, positive normalized gain for the velocity primitive and a small positive normalized gain for the position primitive than a model based solely on a velocity primitive (Table 1).
Fig. 5.
Experiment 1: actual forces and fitted representation models. The representation models were constructed according to different combinations of motor primitives. A: the actual forces applied by group ND participants are well fitted by a representation model (solid dark blue line) based on position (dotted orange line) and velocity (dotted green line) movement primitives; bar plots present the normalized gain of each primitive estimated from the linear regression between the actual forces and the combination of specific primitive. B–E: the actual forces that were applied by both group D70 (B and D) and group D100 (C and E) only poorly correspond to either a representation model (solid brown lines and solid dark red lines, respectively) based on current position and velocity movement primitives (B and C) or a model based on position and delayed velocity (dotted dark blue lines) movement primitives (D and E). F–I: a representation model based on current position, velocity, and acceleration (dotted purple lines) movement primitives shows a better fit to the actual forces of group D70 and group D100 participants (F and G), but a representation model based on current position and velocity and delayed velocity movement primitives provides the best fit (H and I) (compared with the other models that we tested). Shading and error bars represent the 95% confidence intervals. Dots represent primitive gains of individual participants.
This was not the case for the D70 and D100 groups. The qualitative evaluation of the mean actual forces trajectory (Fig. 4) suggests that a model based on current position and velocity or on current position and delayed velocity would not be able to account satisfactorily for the representation of the delayed velocity-dependent force fields. An examination of these models (Fig. 5, B–E) and their goodness-of-fit evaluation (Table 1) supports this observation. The current position and velocity model failed to capture the shifted peak in the actual forces (Fig. 5, B and C), and the current position and delayed velocity model failed to capture the early initiation of forces (Fig. 5, D and E). This suggests that participants did not represent the delayed velocity-dependent force field through a combination of position and either current or delayed velocity primitives alone.
Next, we examined whether a representation model that included a current position primitive and a state-based approximation of the delayed velocity, using current velocity and acceleration, could provide a better fit for the performance of group D70 and group D100 participants. This model was characterized by a better fit than the representation models mentioned above (Table 1), but an examination of the representation model’s trajectories showed that they still did not coincide with the actual forces very well, especially in the case of the larger delay (Fig. 5, F and G).
We tested an additional simple model that combined current position and velocity as well as delayed velocity movement primitives (Fig. 5, H and I). The components of this combination yielded a representation model that more closely resembled the prominent features of the actual force trajectory than any other model of similar complexity, as evidenced by the r2 and BIC values in Table 1, as well as a visual examination of Fig. 5, H and I. The mean onset of the actual force trajectory was close to the mean onset of the velocity trajectory. The time of the peak of the trajectory was similar to the time in which the delayed velocity trajectory reached a maximum value. Finally, the force tail at the end of the movement hints at the involvement of a position component, although this may have also arisen from feedback. This model appears to provide the best fit to the actual forces that group D70 and group D100 participants applied during force channel trials at the end of the adaptation session (out of all the models we tested in this study) while remaining attractive due to its simplicity. Note, however, that a closer examination of Fig. 5, H and I, reveals that this model does not match the applied forces accurately. We delve into the potential sources of discrepancies and additional, more complex alternative models in the discussion.
The gain of the delayed velocity primitive evolves throughout adaptation to delayed velocity-dependent force perturbations.
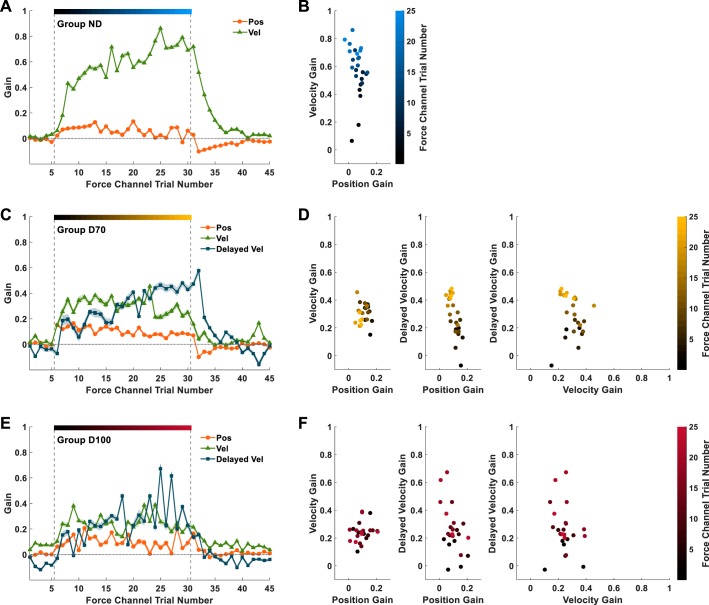
To examine the dynamics of the forming of the internal representation for the nondelayed and both the delayed velocity-dependent force fields, after choosing the best candidate representation model from each group, we calculated the normalized gain of each primitive in these models in each force channel trial. The time course of the evolution of these normalized gains throughout the baseline, adaptation, and washout sessions of the experiment is depicted in Fig. 6.
Fig. 6.
Experiment 1: the dynamics of movement primitives’ normalized gains. The gains are presented for the models that best explain the actual force patterns that each group exhibited during the force channel trials. A: time course of the normalized position (orange dots) and velocity (green triangles) gains throughout the experiment for group ND. Shading represents the 95% confidence interval. Vertical dashed gray lines separate the baseline, adaptation, and washout sessions of the experiment. The color gradient bar represents the progression of force channel trials from early (dark blue) to late (light blue) adaptation. B: the normalized gains from the adaptation session in A are plotted in a position/velocity normalized gain space. Each dot represents the primitives’ gain combination in each trial, and the color codes represent the trial number. C and E: time course of the position, velocity, and delayed velocity (dark blue squares) normalized gains throughout the experiment for group D70 (C) and group D100 (E). D and F: normalized gains from the adaptation sessions in C and E, respectively, are plotted in position/velocity (left), position/delayed velocity (middle), and velocity/delayed velocity (right) normalized gain spaces.
Consistent with the fact that participants did not experience external perturbing forces during baseline, in the last force channel trial in baseline, in group ND (Fig. 6A), group D70 (Fig. 6C), and group D100 (Fig. 6E), the normalized gains of the current position and velocity primitives were close to zero, as well as the normalized gain of the delayed velocity primitive in both the delay groups. For all groups, the first force channel trial of the adaptation session appeared after a single force field trial was presented. After experiencing the perturbation for the first time, group ND participants (Fig. 6, A and B) applied a force that reflected an initial representation consisting of a small contribution of both position and velocity primitives with similar normalized gains. Since the perturbing force depends linearly on the velocity, throughout adaptation, there was a sharp increase in the velocity normalized gain (Fig. 6A, green triangles; Fig. 6B, ordinate) in parallel with a slight decrease in the position normalized gain (Fig. 6A, orange circles; Fig. 6B, abscissa).
In groups D70 and D100 (Fig. 6, C–F), participants started with a similar initial representation consisting of position and velocity normalized gains that were similar to group ND and with no contribution of a delayed velocity primitive. Similar to group ND, the position normalized gains decreased slightly throughout adaptation (Fig. 6, C and E, orange dots; Fig. 6, D and F, left and middle, abscissa). The normalized gains of the velocity primitive (Fig. 6, C and E, green triangles; Fig. 6, D and F, left and right, ordinate and abscissa, respectively) increased slightly during early adaptation and then decreased during late adaptation, such that their final value was similar to that at the beginning. Importantly, in both group D70 and group D100, the normalized gains of the delayed velocity primitive increased (Fig. 6, C and E, dark blue squares; Fig. 6, D and F, middle and right, ordinate). However, they did so more slowly and reached values that were significantly smaller than those of the velocity normalized gain in group ND [main effect of group: F(2, 27) = 12.106, P < 0.001; ND-D70: PB = 0.003; ND-D100: PB < 0.001], which was likely due to the remaining nondelayed velocity primitive in the representation. There was no statistically significant difference between the delayed velocity normalized gains of group D70 and group D100 at the end of the adaptation (PB = 1.000), suggesting that the weighted contribution of the delayed velocity primitive to the representation was not influenced by the delay magnitude.
During washout, the position and velocity normalized gains of group ND showed an early decay response to the removal of the perturbation (Fig. 6A) and then came close to zero in the last force channel trial of the session. In groups D70 and D100, the position and velocity normalized gains exhibited a similar immediate response to that of group ND (Fig. 6, C and E) and eventually approached zero. Interestingly, the delayed velocity normalized gains of both the delay groups remained similar to their mean values at the end of adaptation and even showed a slight increase from the first to the second force channel trials of the washout session. Only then did it drop to a smaller value until approaching zero at the end of the session.
Experiment 2
Generalization of adaptation to a delayed force field from slow to fast movements: support for an internal representation of a delayed velocity-dependent force field as a combination of current position, velocity, and delayed velocity primitives.
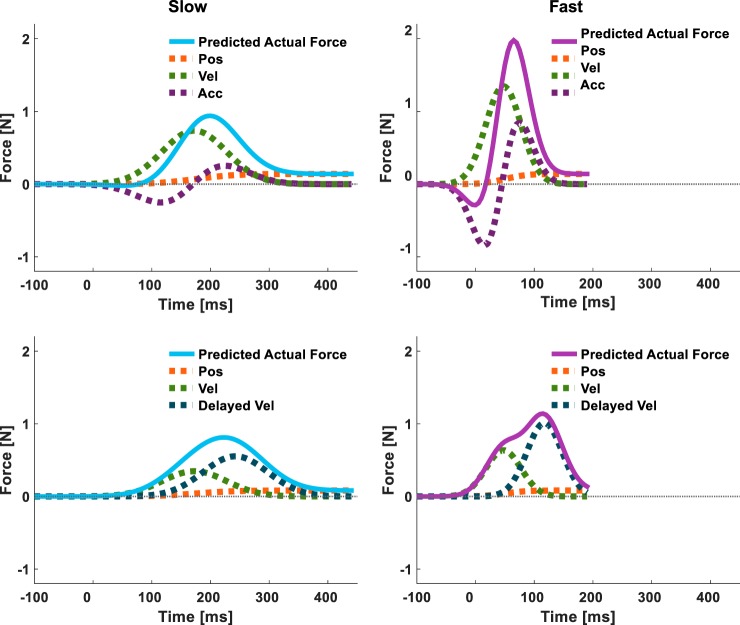
In experiment 1, we showed that the representation model constructed from position, velocity, and acceleration primitives provides a relatively good fit to the actual forces of group D70 participants and that its predicted trajectory is quite similar to that of the position, velocity, and delayed velocity representation model (Fig. 5, F and H). Compared with group D70, the actual forces that group D100 participants applied exhibit clearer dual-peak trajectories (Fig. 4, D and G). These two peaks are likely associated with the current and delayed velocity primitives that are better separated in time. However, based on experiment 1, it is impossible to reject the hypothesis that the clearly distinct delayed velocity primitive was specific to adaptation to a larger delay. Therefore, it remains unclear whether the actual forces that counteracted the 70-ms delayed velocity-dependent force field were the result of a representation composed of current state primitives or a combination of current and delayed primitives. In addition, it remains unclear whether a representation formed at a particular velocity can generalize to a different velocity.
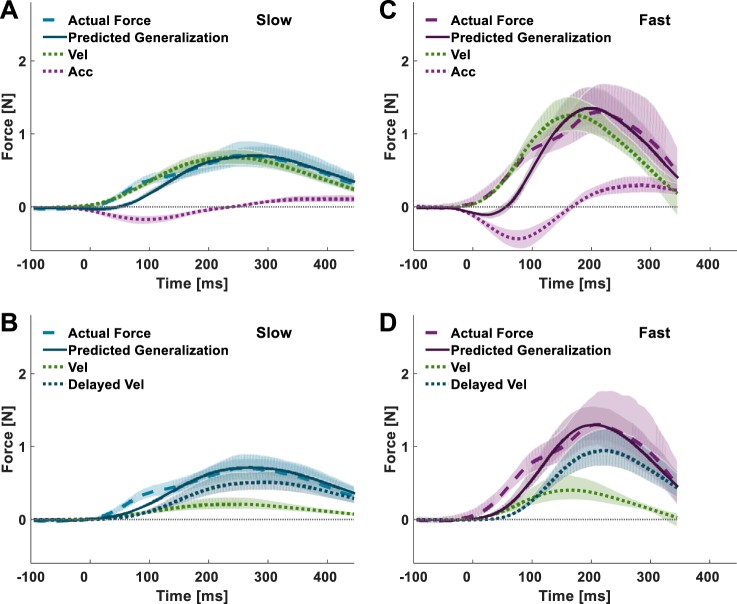
To address these two open questions, we designed experiment 2 as a generalization study to a faster velocity. The predictions of the actual force trajectories during generalization to a faster velocity are different for a representation model composed of position, velocity, and acceleration and a model composed of position, velocity, and delayed velocity (Fig. 7). We simulated the actual forces applied following adaptation to 70-ms delayed velocity-dependent force fields for both the position/velocity/acceleration (Fig. 7, top) and the position/velocity/delayed velocity (Fig. 7, bottom) representation models during slow (Fig. 7, left) and fast movements (Fig. 7, right). We determined the gain of each primitive in our simulation based on their relative contribution in the representation analysis of group D70 in experiment 1 (Fig. 5, F and H). The simulation results showed that during slow movements, the actual force predicted by the position/velocity/acceleration model was similar to the actual force predicted by the position/velocity/delayed velocity model (Fig. 7, solid light blue lines). However, the same representations predicted considerably different actual force trajectories during fast movements (Fig. 7, solid purple lines). The position/velocity/acceleration representation predicted a trajectory with a small initial decrease in the actual force, followed by a steep increase with a single peak. The position/velocity/delayed velocity representation predicted an actual force trajectory that had two positive peaks corresponding to each of the velocity primitives.
Fig. 7.
Predicted actual force during generalization to faster movements. During slow movements (left), the predicted actual forces (solid light blue lines) constructed according to a position/velocity/acceleration representation model (top) are similar to the predicted actual forces of a position/velocity/delayed velocity representation model (bottom). During fast movements (right), the same position/velocity/acceleration representation model predicts substantially different actual force trajectories (solid purple lines) than the actual force trajectories predicted by the position/velocity/delayed velocity representation model; in the former, there is an initial increase in the actual force to the same direction toward which the perturbing force is applied (a negative force), followed by a steep increase in the opposite direction (a positive force), whereas in the latter, the actual force trajectories have 2 positive peaks.
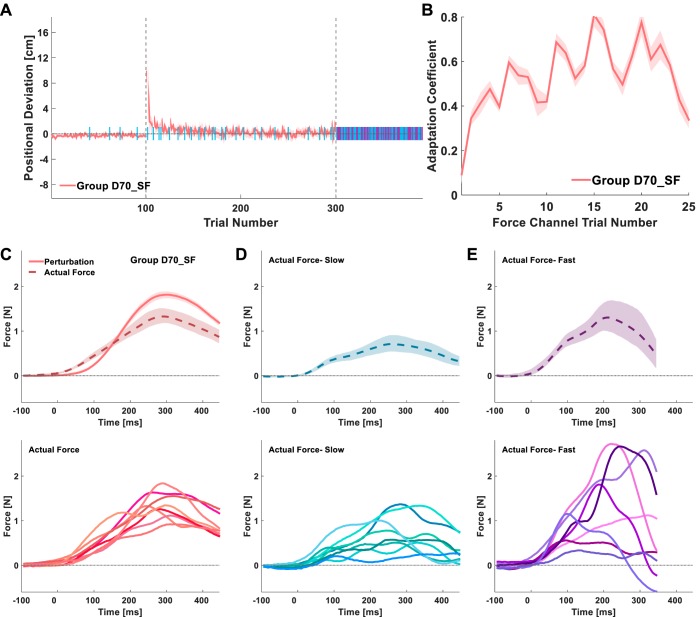
In experiment 2, we tested experimentally how constructing a representation of the 70-ms delayed velocity-dependent force field while executing slow movements would generalize to faster movements. In this experiment, a group of participants (group D70_SF) performed the same task as they did in experiment 1, but under a modified protocol (Fig. 2C). During baseline, participants moved with no external force perturbing their hand, and we trained them to reach the target within two different duration ranges by moving either at low (slow) or high speed (fast). A different display background color signaled the required movement speed. During adaptation, a velocity-dependent force field was presented and persisted throughout the entire session (with the exception of the force channel trials). All the trials in the adaptation session were of the slow type. The applied force influenced the positional deviation of the participants (Fig. 8A), which changed significantly throughout the late baseline, early adaptation, and late adaptation stages of the experiment [main effect of stage: F(1.023, 7.159) = 12.933, Pε = 0.008]. There was an increase in the positional deviation from late baseline to early adaptation as a result of the sudden introduction of the perturbation (PB = 0.017). With repeated exposure to the force, the positional deviation decreased (PB = 0.046) and declined toward zero during late adaptation. These results suggest that group D70_SF participants adapted to the delayed force field.
Fig. 8.
Experiment 2: generalization to faster movements; adaptation results and actual forces. A: time course of the peak positional deviation averaged over all of the participants in group D70_SF. Vertical dashed gray lines separate the baseline, adaptation, and generalization sessions of the experiment. Light blue and purple bars indicate force channel trials. B: time course of the average adaptation coefficient during the adaptation session. C: mean perturbation trajectories (solid pink line) and mean actual forces (dashed pink line) from the end of adaptation of all of the participants in group D70_SF (top). The mean actual forces for each participant are presented at the bottom. D and E: mean actual forces of the first 5 slow (light blue; D) and fast (purple; E) trials in the generalization session averaged over all of the participants in the group (top). The mean actual forces for each participant from each of these trial types are presented at the bottom. Shadings represent the 95% confidence interval.
Similarly to experiment 1, in experiment 2 we also included force channel trials that were presented randomly throughout the baseline and the adaptation sessions. All the force channel trials in these sessions were of the slow type, and they served to measure the actual forces that participants applied to counteract the perturbations. The increase in the adaptation coefficient throughout the adaptation session (Fig. 8B) suggests that the participants formed an internal representation of the perturbation; they exhibited a significantly higher mean adaptation coefficient during late adaptation than during early adaptation [t(7) = −2.691, P = 0.031].
To assess the way participants represented the forces they adapted to, we examined the actual forces that they applied during late adaptation (Fig. 8C). The mean actual force trajectory exerted by group D70_SF participants in experiment 2 was similar in shape to the mean actual force trajectory of group D70 participants in experiment 1 (Fig. 4D). That is, the onset of the mean actual forces occurred before the onset of the mean perturbation forces, and the peak of the mean actual forces corresponded to the time of the peak mean perturbation forces. Because the duration span within which group D70_SF participants were required to move during the adaptation session was smaller than and within the upper range of the movement duration span in group D70, they moved slower. The mean maximum velocity of group D70_SF during late adaptation (means ± 95% CI, 33.234 ± 2.707 cm/s) was significantly lower than that of group D70 [53.025 ± 3.952 cm/s, t(16) = 7.677, P < 0.001]; hence, overall perturbations and actual forces were all downscaled.
To examine the generalization of adaptation to the delayed force perturbation from slow to fast movements, the last session (generalization) consisted only of force channel trials of both slow- and fast-type trials (Joiner et al. 2011). We included the slow force channel trials to compare the actual forces during fast trials with the actual forces during slow trials from the same experimental stage (early generalization). The actual forces (both the group average and individual means) during the slow trials in the early generalization stage (Fig. 8D) showed long-duration trajectories, with an initial increase around the onset of the actual forces during late adaptation (Fig. 8C) and a peak mean force around the time of the peak mean perturbation. This trajectory is consistent with the simulated actual force trajectory of both the position/velocity/acceleration and the position/velocity/delayed velocity representation models (Fig. 7, left, solid light blue lines). The actual forces during the fast trials in the early generalization stage (Fig. 8E) had clear dual-peak trajectories that were consistent with the position/velocity/delayed velocity representation model (Fig. 7, bottom right, solid purple lines). These results suggest that the adaptation of the delayed velocity-dependent force field can generalize to faster movements and that the generalization pattern is consistent with a position/velocity/delayed velocity representation rather than a position/velocity/acceleration representation.
Further support for the use of a delayed velocity primitive rather than an acceleration primitive comes from the evaluation of the fit of the representation models to the actual forces that participants applied during the late stage of adaptation (Fig. 9) and its generalization to slow and fast during the early generalization stage (Fig. 10). The actual forces applied by the participants in group D70_SF during the slow force channel trial of late adaptation was better fitted by a position/velocity/delayed velocity (r2 = 0.476, BIC = 1.28 × 104) than by a position/velocity/acceleration (r2 = 0.468, BIC = 1.30 × 104) representation model. Note, however, that this difference was quite small and was likely the result of the inflation of the position primitive over the acceleration and the delayed velocity primitives (Fig. 9, A and B). Because during slow movements the velocity trajectory is wide, the delayed velocity trajectory does not decline completely by the end of the movement and becomes more similar to the position trajectory. Therefore, the position primitive can capture the delayed increase in the actual force trajectory (Fig. 9B). This may also be why the absolute gain of the acceleration primitive was very small (Fig. 9A). Thus, we also examined representation models that do not include the position primitive, namely velocity/acceleration and velocity/delayed velocity representation models. Here, as in the previous comparison, a representation model that included the delayed velocity primitive provided a considerably better fit to the actual forces (r2 = 0.420, BIC = 1.37 × 104) than a model that included the acceleration primitive (r2 = 0.370, BIC = 1.44 × 104). The former model was able to better account for the early rise in the actual forces and the delayed force peaks than the latter model (Fig. 9, C and D).
Fig. 9.
Experiment 2: actual force and fitted representation models for slow movements during late adaptation. The actual forces (dashed pink) applied by group D70_SF participants during the late adaptation stage and the fitted representation models (solid dark pink) constructed according to different combinations of motor primitives. A and B: the representation model based on current position (dotted orange line), velocity (dotted green line), and acceleration (dotted purple line) movement primitives is similar to the representation model based on current position, velocity, and delayed velocity (dotted dark blue line) movement primitives. C and D: removing the position primitive reveals that a velocity/delayed velocity representation model provides a better fit than the velocity/acceleration model. Shadings and error bars represent the 95% confidence intervals. Dots represent primitive gains of individual participants.
Fig. 10.
Experiment 2: actual force and predicted generalization forces during slow and fast trials. A and B: the predicted generalization forces for group D70_SF during slow trials (solid dark blue line) of the early generalization session are similar between the velocity/acceleration (A) and the velocity/delayed velocity representation models (B), and their fits to the actual forces (dashed light blue line) are comparable. C and D: the predicted generalization forces during fast trials (solid dark purple) of the early generalization session constructed according to the velocity/delayed velocity representation model (D) provide a better fit to the actual forces (dashed purple line) than the predicted generalization forces of the velocity/acceleration representation model (C). Shadings represent the 95% confidence intervals.
In addition, we tested the ability of the models that were fitted to the late adaptation trials to predict the actual forces in the early generalization stage. For the slow trials, both the velocity/acceleration and velocity/delayed velocity models provided similar predicted forces that resembled the actual forces (Fig. 10, A and B). Importantly, for fast trials, the models provided different predicted forces (Fig. 10, C and D); although neither model captured the early rise in the actual forces well, the velocity/acceleration model was markedly worse in terms of fit because it predicted a negative dip in the force (resulting from the negative acceleration) that was clearly absent from the actual force trajectory. Overall, the generalization from slow to fast movements further strengthens our claim that a delayed velocity primitive was used together with a current velocity primitive to adapt to the delayed velocity-dependent force perturbations.
DISCUSSION
To explore how internal models are formed in light of sensory transmission delays, we examined the representation of delayed velocity-dependent force perturbations. Consistent with previous studies, participants adapted to delayed and nondelayed perturbations similarly (Levy et al. 2010; Scheidt et al. 2000). Interestingly, unlike in the nondelayed case where the current position and velocity movement primitives provided a good fit to participants’ actual forces (Sing et al. 2009), models based on the current position with the current or the delayed velocity were insufficient to explain the forces applied in the delayed case. Instead, among the models that we tested, the best model consisted of current position, velocity, and delayed velocity primitives. This representation also generalized to a higher velocity for which the delayed force field had never been experienced.
Previous studies have made conflicting claims about delayed feedback representations. On the one hand, when simultaneity is disrupted during interactions with elastic force fields by force feedback delays, stiffness perception is biased (Di Luca et al. 2011; Leib et al. 2016; Nisky et al. 2010; Nisky et al. 2008; Nisky et al. 2011; Pressman et al. 2008; Pressman et al. 2007). This suggests that the brain does not employ a delay representation that realigns the position signal with the delayed force signal. On the other hand, humans can adapt to delayed velocity-dependent force perturbations (Levy et al. 2010) and adjust their grip force to a delayed load force during both unimanual (Leib et al. 2015) and bimanual (Witney et al. 1999) tool-mediated interactions with objects. By explicitly measuring the forces that participants apply to directly counterbalance delayed force perturbations by using force channels, we provide the first evidence of how delayed state information is exploited for the control of arm movements and suggest that this takes the form of a delayed velocity primitive together with the current state information. We also quantitatively evaluated the relative contribution of the current and delayed state primitives in the representation, determined their evolution and washout dynamics, and examined their generalization.
The vast majority of works exploring the processes by which the sensorimotor system constructs internal representations have examined adaptation to two types of perturbations: visuomotor transformations (Flanagan and Rao 1995; Krakauer et al. 2000) and force fields (Lackner and Dizio 1994; Shadmehr and Mussa-Ivaldi 1994). Adding a delay to the perturbing feedback may be considered an adaptation to two concurrent disturbances, the perturbation and the delayed feedback. Two studies have examined concurrent adaptation to visuomotor rotation and delay (Honda et al. 2012a, 2012b). The results showed that the added delay weakened the adaptation to the rotation (Honda et al. 2012a) but that adaptation to the delayed feedback before the experience of both disturbances together improved adaptation to the rotation for the same and for a larger delay magnitude (Honda et al. 2012b). Similarly, in our study, participants experienced force fields that depended on a delayed state. In addition, the delay deteriorated adaptation, as was evidenced by the increase in movement duration with the increasing delay and the decrease in the adaptation coefficient in the D100 group. Although we did not examine how adaptation to a delayed feedback alone influenced subsequent adaptation to the combined delayed force perturbation, our results may perhaps hint that by constructing a delayed velocity primitive, the participants became more attuned to the delay. The late decline of the gain of the delayed velocity primitive after perturbation removal during washout (experiment 1) suggests that the brain may preserve a representation of the delayed state and might use it in generalizations to different delayed force perturbations. The study of generalization to a higher velocity for the same movement extent (experiment 2) has some similarities to generalization to a higher delay. Thus, our finding that participants continued using a delayed velocity primitive during generalization to a faster movement suggests that they could utilize the acquired information about the delay to other contexts. Interestingly, the prior experience of the delay in Honda et al. 2012b did not affect the adaptation to the no-delay condition. The preservation of the current velocity primitive in our results suggests that it can also be utilized for adaptation to nondelayed velocity-dependent force field.
The coexistence of the delayed and current state primitives in the representation is in line with studies that have found evidence for a mixed representation of the actual delay and a state-based estimation of the delay (Diedrichsen et al. 2007; Leib et al. 2015). Diedrichsen et al. 2007 showed that when two tasks overlap in time, participants use state-dependent control, where the motor command in one task depends on the arm state in the other task, but when they are separated, they use time-dependent control. The delays in our experiments (70 and 100 ms) were within their identified transition range, where a combination of both was used. This combination may result from the similarity between the current and delayed velocity primitives, which hinders the ability to assign the perturbation to one or the other, and larger delays may lead to a better separation (Witney et al. 1999). Nevertheless, the better separation in Witney et al. (1999) may also be related to bimanual coordination. In any case, the delays in our experiment were bounded by the short durations of the ballistic reaches. When analyzing the primitives’ dynamics throughout the experiment in the group that experienced the 100-ms delay (Fig. 6E), the regression analysis of some trials revealed a high correlation between the delayed velocity and the position primitives. Furthermore, larger delays may potentially break down the association between the movement and the perturbing force. Thus, we believe that 100 ms is probably close to the maximal delay magnitude that could be used in our experiment.
Our results indicate a weakening effect of delay magnitude on adaptation to perturbing forces. This highlights the limited ability of the brain to construct an accurate representation of delayed feedback and is consistent with studies that reported decreased aftereffects (Honda et al. 2012b) and greater perceptual biases with increasing delays (Pressman et al. 2007). Both the 70- and 100-ms delay groups in experiment 1 exhibited an increase in the adaptation coefficient and aftereffects, indicating that an internal representation of the perturbing force was formed. However, the increase in the adaptation coefficient was smaller for the 100-ms delay group. This is directly related to our observations that the representation consisted of both current and delayed primitives. Hence, the larger delay resulted in an actual force trajectory that departed further than the applied force perturbation. In addition, when coping with increasing delay, the participants may have increased their arm stiffness to cope with delay-induced instability (Burdet et al. 2001; Milner and Cloutier 1993). Such an increase in stiffness can reduce the effect of the perturbing forces and, consequently, the magnitude of the perturbation-specific representation (Shadmehr and Mussa-Ivaldi 1994) as well as the aftereffect. The findings showed that the aftereffect was smaller when the delay was larger, but this did not reach statistical significance. We also observed a systematic increase in the duration of the movement at the higher delay. In fact, one possible strategy for dealing with a delayed force is to move slower, which results in weaker velocity-dependent perturbations.
The participants’ failure to more accurately represent the delayed forces may have resulted from the absence of well-established priors in the sensorimotor system for such a perturbation. The slow increase in the delayed velocity gain, relative to the current velocity gain (Fig. 6, A, C, and E), is consistent with previous results suggesting that new temporal relationships between actions and their consequences are learned by generating a novel rather than adapting a preexisting predictive response (Witney et al. 1999). The slow process of constructing the new representation may not have been fully complete within the adaptation duration in our study. This seems possible since the gain of the delayed velocity primitive did not clearly reach a plateau and did not decrease instantaneously following the suppression of the perturbation. Determining whether participants could construct an accurate representation if they had more trials or several adaptation sessions over multiple days was beyond the scope of this study. Rather, we focused on comparing the adaptation with nondelayed and delayed perturbations and on the evolution of the current and delayed primitives for the same number of trials.
Our results indicate that the sensorimotor system is likely to use a delayed velocity rather than an acceleration primitive. Despite the fact that the body is continuously exposed to inertial forces, studies have reported slow adaptation and poor generalization of acceleration-dependent compared with velocity-dependent force fields (Hwang and Shadmehr 2005; Hwang et al. 2006), and in fact, force field adaptation studies have focused mainly on primitives depending on position and velocity (Donchin et al. 2003; Sing et al. 2009; Thoroughman and Shadmehr 2000; Yousif and Diedrichsen 2012). However, this may be a consequence of the difficulty of measuring acceleration in experiments. Therefore, the capability of the sensorimotor system to utilize an acceleration primitive when responding to environmental dynamics requires further investigation. We suggest that specifically when coping with a delayed velocity-dependent force feedback, an acceleration primitive is not likely to be used.
Our best model was not perfect in predicting the forces that participants applied at the end of adaptation. The inconsistencies may be related to unmodeled mechanisms, such as increasing arm stiffness, although the fact that both delay groups in experiment 1 exhibited aftereffects and an increase in the adaptation coefficient suggests that increased stiffness was not the main coping mechanism (Burdet et al. 2001; Shadmehr and Mussa-Ivaldi 1994). Other unmodeled factors may include additional higher-order derivatives or lateral movement primitives. In addition, we assumed an accurate delay for the delayed velocity primitive, but the participants may have had a noisy estimation of the delay. We chose not to improve the fit of the model with additional primitives or by optimizing the delay parameter to avoid overfitting. We kept the models that we tested as simple as possible and only examined primitives that were included in our original predictions.
Inferring the gains of the primitives that were used in forming the representation may also be viewed as inferring an implicit estimation of the stiffness (for the position primitive) and viscosity (for the current and delayed velocity primitives) of the environment. Delayed force feedback biases perceptions of stiffness (Di Luca et al. 2011; Leib et al. 2015; Nisky et al. 2008; Pressman et al. 2007), viscosity (Hirche and Buss 2007), and mass (Hirche and Buss 2007; van Polanen and Davare 2016). Such perceptual biases may thus affect the estimation of the correct contribution of each primitive when constructing the representation that generates the actual forces. Perceptual biases do not necessarily align with effects on actions (Goodale and Milner 1992), and specifically in the response to delayed force feedback (Leib et al. 2015). However, future studies should examine the influence of such biases by probing the explicit component of adaptation (Taylor et al. 2014) in both the nondelayed and delayed conditions and extract the primitive gains from the implicit process alone.
Interestingly, the primitive gains continued to change throughout the entire adaptation while performance, as measured by the peak hand deviation from a straight line movement, reached an asymptote after fewer than 100 trials. This suggests that the change in gains was not driven by the error experienced due to hand deviation but may have been a continuous optimization process driven by other variables (Mazzoni and Krakauer 2006; McDougle et al. 2015; Smith et al. 2006).
It remains unclear which signals are used to construct the delayed velocity primitive and the mechanism governing its construction. The second peak in the actual force trajectory may be interpreted as the outcome of a feedback component. However, since the actual forces were measured during force channel trials when no perturbing forces were applied, the delayed increase in the force trajectory is not likely to reflect a reactive component but rather a preplanned force trajectory that was constructed gradually through an updating process of a feedforward control.
The construction of a delayed primitive that is used for action may depend on the presence of the delay in the force feedback. Studies that have examined action with visual feedback delays have reported both perceptual and performance biases that are inconsistent with the capability to represent the delayed signals (Mussa-Ivaldi et al. 2010; Sarlegna et al. 2010; Takamuku and Gomi 2015). However, studies of actions with force feedback delays have found evidence for a delay representation (Leib et al. 2015; Witney et al. 1999). Thus, the formation of a delayed state primitive may depend on the activity of sensory organs that respond to forces, such as the Golgi tendon organ (Houk and Simon 1967) or mechanoreceptors in the skin of the fingers (Zimmerman et al. 2014).
Importantly, the observation that a model that includes the delayed velocity primitive can best account for the actual forces does not necessarily mean that the sensorimotor system uses an actual representation of the delayed velocity. Adaptation can take place by memorizing the shape of the experienced force along the trajectory; however, the brain does not seem to employ such a “rote learning” mechanism when experiencing novel environmental dynamics (Conditt et al. 1997). Alternatively, participants could have estimated the delayed velocity as a function of the time relative to movement duration or according to the extent of motion. However, the fact that the peak actual force during generalization to fast movements was aligned with the delayed velocity suggests that it is more likely that the delayed velocity primitive was constructed as a function of the absolute time. In addition, participants could have represented the perturbing force as an explicit function of time, although it is not clear whether the nervous system is capable of representing time explicitly (Karniel 2011). Humans can adapt to state-dependent but not time-dependent force perturbations while performing movements (Karniel and Mussa-Ivaldi 2003), and time-dependent forces can be misinterpreted as state dependent (Conditt and Mussa-Ivaldi 1999). On the other hand, time and not state representation accounted for the perceived timings of events during a task involving discrete impulsive forces (Pressman et al. 2012). Thus, further studies are required to understand the mechanisms by which delayed state representations are formed.
If participants employed a time representation in our task, either for constructing the delayed velocity primitive or for temporal tuning of the applied force, our best model is consistent with evidence for a neural representation of both time and state. Structures that represent time have been linked to the basal ganglia (Ivry 1996; Rao et al. 2001) and to the supplementary motor area (Halsband et al. 1993; Macar et al. 2006). The cerebellum was suggested to play a role in time representation (Ivry et al. 2002; Spencer et al. 2003) but also in state estimation, especially in light of feedback delays (Ebner and Pasalar 2008), by hosting forward models (Miall et al. 1993; Miall et al. 2007; Nowak et al. 2007; Wolpert et al. 1998). Lobule V of the cerebellum was linked to state-dependent control, whereas the left planum temporale was associated with time-dependent control (Diedrichsen et al. 2007).
Understanding adaptation to environmental dynamics in the presence of delayed causality is critical for understanding forward models and sensory integration. It is also important for studying pathologies with transmission delays such as multiple sclerosis (Trapp and Stys 2009) or disordered neural synchronization such as Parkinson’s disease (Hammond et al. 2007), essential tremor (Schnitzler et al. 2009), and epilepsy (Scharfman 2007), specifically if treatment is attempted by tuning the delay in the feedback loop to control neural synchronization (Popovych et al. 2005; Rosenblum and Pikovsky 2004). Finally, it may also be useful for the design of efficient teleoperation technologies in which feedback is delayed (Nisky et al. 2013; Nisky et al. 2011).
GRANTS
This study was supported by the Binational United States-Israel Science Foundation (grants no. 2011066, 2016850), the Israel Science Foundation (grant no. 823/15), the National Science Foundation (grant no. 1632259), and the Helmsley Charitable Trust through the Agricultural, Biological, and Cognitive Robotics Initiative and by the Marcus Endowment Fund, both at Ben-Gurion University of the Negev. G. Avraham was supported by the Negev and Kreitman Fellowships.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
G.A., F.M., A.K., L.S., F.A.M.-I., and I.N. conceived and designed research; G.A. and F.M. performed experiments; G.A. analyzed data; G.A., F.M., L.S., O.D., F.A.M.-I., and I.N. interpreted results of experiments; G.A. prepared figures; G.A. and I.N. drafted manuscript; G.A., F.M., L.S., O.D., F.A.M.-I., and I.N. edited and revised manuscript; G.A., F.M., L.S., O.D., F.A.M.-I., and I.N. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Amit Milstein and Chen Avraham for assistance in data collection.
REFERENCES
- Burdet E, Osu R, Franklin DW, Milner TE, Kawato M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 414: 446–449, 2001. doi: 10.1038/35106566. [DOI] [PubMed] [Google Scholar]
- Conditt MA, Gandolfo F, Mussa-Ivaldi FA. The motor system does not learn the dynamics of the arm by rote memorization of past experience. J Neurophysiol 78: 554–560, 1997. [DOI] [PubMed] [Google Scholar]
- Conditt MA, Mussa-Ivaldi FA. Central representation of time during motor learning. Proc Natl Acad Sci USA 96: 11625–11630, 1999. doi: 10.1073/pnas.96.20.11625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Luca M, Knörlein B, Ernst MO, Harders M. Effects of visual-haptic asynchronies and loading-unloading movements on compliance perception. Brain Res Bull 85: 245–259, 2011. doi: 10.1016/j.brainresbull.2010.02.009. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Criscimagna-Hemminger SE, Shadmehr R. Dissociating timing and coordination as functions of the cerebellum. J Neurosci 27: 6291–6301, 2007. doi: 10.1523/JNEUROSCI.0061-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin O, Francis JT, Shadmehr R. Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J Neurosci 23: 9032–9045, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebner TJ, Pasalar S. Cerebellum predicts the future motor state. Cerebellum 7: 583–588, 2008. doi: 10.1007/s12311-008-0059-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan JR, Rao AK. Trajectory adaptation to a nonlinear visuomotor transformation: evidence of motion planning in visually perceived space. J Neurophysiol 74: 2174–2178, 1995. [DOI] [PubMed] [Google Scholar]
- Gibo TL, Bastian AJ, Okamura AM. Grip force control during virtual object interaction: effect of force feedback,accuracy demands, and training. IEEE Trans Haptics 7: 37–47, 2014. doi: 10.1109/TOH.2013.60. [DOI] [PubMed] [Google Scholar]
- Gonzalez Castro LN, Hadjiosif AM, Hemphill MA, Smith MA. Environmental consistency determines the rate of motor adaptation. Curr Biol 24: 1050–1061, 2014. doi: 10.1016/j.cub.2014.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends Neurosci 15: 20–25, 1992. doi: 10.1016/0166-2236(92)90344-8. [DOI] [PubMed] [Google Scholar]
- Halsband U, Ito N, Tanji J, Freund HJ. The role of premotor cortex and the supplementary motor area in the temporal control of movement in man. Brain 116: 243–266, 1993. doi: 10.1093/brain/116.1.243. [DOI] [PubMed] [Google Scholar]
- Hammond C, Bergman H, Brown P. Pathological synchronization in Parkinson’s disease: networks, models and treatments. Trends Neurosci 30: 357–364, 2007. doi: 10.1016/j.tins.2007.05.004. [DOI] [PubMed] [Google Scholar]
- Held R, Efstathiou A, Greene M. Adaptation to displaced and delayed visual feedback from the hand. J Exp Psychol 72: 887–891, 1966. doi: 10.1037/h0023868. [DOI] [Google Scholar]
- Hirche S, Buss M. Human perceived transparency with time delay. In: Advances in Telerobotics, edited by Ferre M, Buss M, Aracil R, Melchiorri C, and Balaguer C. Berlin: Springer, 2007, p. 191–209. doi: 10.1007/978-3-540-71364-7_13. [DOI] [Google Scholar]
- Honda T, Hagura N, Yoshioka T, Imamizu H. Imposed visual feedback delay of an action changes mass perception based on the sensory prediction error. Front Psychol 4: 760, 2013. doi: 10.3389/fpsyg.2013.00760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda T, Hirashima M, Nozaki D. Adaptation to visual feedback delay influences visuomotor learning. PLoS One 7: e37900, 2012a. doi: 10.1371/journal.pone.0037900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda T, Hirashima M, Nozaki D. Habituation to feedback delay restores degraded visuomotor adaptation by altering both sensory prediction error and the sensitivity of adaptation to the error. Front Psychol 3: 540, 2012b. doi: 10.3389/fpsyg.2012.00540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houk J, Simon W. Responses of Golgi tendon organs to forces applied to muscle tendon. J Neurophysiol 30: 1466–1481, 1967. [DOI] [PubMed] [Google Scholar]
- Hwang EJ, Shadmehr R. Internal models of limb dynamics and the encoding of limb state. J Neural Eng 2: S266–S278, 2005. doi: 10.1088/1741-2560/2/3/S09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Smith MA, Shadmehr R. Adaptation and generalization in acceleration-dependent force fields. Exp Brain Res 169: 496–506, 2006. doi: 10.1007/s00221-005-0163-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivry RB. The representation of temporal information in perception and motor control. Curr Opin Neurobiol 6: 851–857, 1996. doi: 10.1016/S0959-4388(96)80037-7. [DOI] [PubMed] [Google Scholar]
- Ivry RB, Spencer RM, Zelaznik HN, Diedrichsen J. The cerebellum and event timing. Ann N Y Acad Sci 978: 302–317, 2002. doi: 10.1111/j.1749-6632.2002.tb07576.x. [DOI] [PubMed] [Google Scholar]
- Joiner WM, Ajayi O, Sing GC, Smith MA. Linear hypergeneralization of learned dynamics across movement speeds reveals anisotropic, gain-encoding primitives for motor adaptation. J Neurophysiol 105: 45–59, 2011. doi: 10.1152/jn.00884.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner WM, Smith MA. Long-term retention explained by a model of short-term learning in the adaptive control of reaching. J Neurophysiol 100: 2948–2955, 2008. doi: 10.1152/jn.90706.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karniel A. Open questions in computational motor control. J Integr Neurosci 10: 385–411, 2011. doi: 10.1142/S0219635211002749. [DOI] [PubMed] [Google Scholar]
- Karniel A, Mussa-Ivaldi FA. Sequence, time, or state representation: how does the motor control system adapt to variable environments? Biol Cybern 89: 10–21, 2003. doi: 10.1007/s00422-003-0397-7. [DOI] [PubMed] [Google Scholar]
- Kawato M. Internal models for motor control and trajectory planning. Curr Opin Neurobiol 9: 718–727, 1999. doi: 10.1016/S0959-4388(99)00028-8. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci 20: 8916–8924, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lackner JR, Dizio P. Rapid adaptation to Coriolis force perturbations of arm trajectory. J Neurophysiol 72: 299–313, 1994. [DOI] [PubMed] [Google Scholar]
- Leib R, Karniel A, Nisky I. The effect of force feedback delay on stiffness perception and grip force modulation during tool-mediated interaction with elastic force fields. J Neurophysiol 113: 3076–3089, 2015. doi: 10.1152/jn.00229.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leib R, Mawase F, Karniel A, Donchin O, Rothwell J, Nisky I, Davare M. Stimulation of PPC affects the mapping between motion and force signals for stiffness perception but not motion control. J Neurosci 36: 10545–10559, 2016. doi: 10.1523/JNEUROSCI.1178-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy N, Pressman A, Mussa-Ivaldi FA, Karniel A. Adaptation to delayed force perturbations in reaching movements. PLoS One 5: e12128, 2010. doi: 10.1371/journal.pone.0012128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lilliefors HW. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J Am Stat Assoc 62: 399–402, 1967. doi: 10.1080/01621459.1967.10482916. [DOI] [Google Scholar]
- Macar F, Coull J, Vidal F. The supplementary motor area in motor and perceptual time processing: fMRI studies. Cogn Process 7: 89–94, 2006. doi: 10.1007/s10339-005-0025-7. [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci 26: 3642–3645, 2006. doi: 10.1523/JNEUROSCI.5317-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougle SD, Bond KM, Taylor JA. Explicit and implicit processes constitute the fast and slow processes of sensorimotor learning. J Neurosci 35: 9568–9579, 2015. doi: 10.1523/JNEUROSCI.5061-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miall RC, Christensen LO, Cain O, Stanley J. Disruption of state estimation in the human lateral cerebellum. PLoS Biol 5: e316, 2007. doi: 10.1371/journal.pbio.0050316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miall RC, Weir DJ, Wolpert DM, Stein JF. Is the cerebellum a smith predictor? J Mot Behav 25: 203–216, 1993. doi: 10.1080/00222895.1993.9942050. [DOI] [PubMed] [Google Scholar]
- Milner TE, Cloutier C. Compensation for mechanically unstable loading in voluntary wrist movement. Exp Brain Res 94: 522–532, 1993. doi: 10.1007/BF00230210. [DOI] [PubMed] [Google Scholar]
- Murray MM, Wallace MT. The Neural Bases of Multisensory Processes. Boca Raton, FL: CRC Press, 2011. doi: 10.1201/9781439812174. [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA, Pressman A, Simo LS, Karniel A. Space-Time Separability in the Sensory-Motor System. San Diego, CA: Society for Neuroscience, 2010. [Google Scholar]
- Myers RH. Classical and Modern Regression With Applications. Pacific Grove, CA: Duxbury Classic Series, 1990. [Google Scholar]
- Nisky I, Baraduc P, Karniel A. Proximodistal gradient in the perception of delayed stiffness. J Neurophysiol 103: 3017–3026, 2010. doi: 10.1152/jn.00939.2009. [DOI] [PubMed] [Google Scholar]
- Nisky I, Mussa-Ivaldi FA, Karniel A. A regression and boundary-crossing-based model for the perception of delayed stiffness. IEEE Trans Haptics 1: 73–82, 2008. doi: 10.1109/TOH.2008.17. [DOI] [PubMed] [Google Scholar]
- Nisky I, Mussa-Ivaldi FA, Karniel A. Analytical study of perceptual and motor transparency in bilateral teleoperation. IEEE Trans Hum Mach Syst 43: 570–582, 2013. doi: 10.1109/TSMC.2013.2284487. [DOI] [Google Scholar]
- Nisky I, Pressman A, Pugh CM, Mussa-Ivaldi FA, Karniel A. Perception and action in teleoperated needle insertion. IEEE Trans Haptics 4: 155–166, 2011. doi: 10.1109/TOH.2011.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak DA, Timmann D, Hermsdörfer J. Dexterity in cerebellar agenesis. Neuropsychologia 45: 696–703, 2007. doi: 10.1016/j.neuropsychologia.2006.08.011. [DOI] [PubMed] [Google Scholar]
- Popovych OV, Hauptmann C, Tass PA. Effective desynchronization by nonlinear delayed feedback. Phys Rev Lett 94: 164102, 2005. doi: 10.1103/PhysRevLett.94.164102. [DOI] [PubMed] [Google Scholar]
- Pressman A. Simultaneity in the Human Motor System (PhD thesis). Beer-Sheva, Israel: Ben Gurion University of the Negev, 2012. [Google Scholar]
- Pressman A, Karniel A, Mussa-Ivaldi FA. Simultaneity in perception of knocking. IEEE Trans Syst Man Cybernet 42: 920–930, 2012. doi: 10.1109/TSMCA.2012.2183354. [DOI] [Google Scholar]
- Pressman A, Nisky I, Karniel A, Mussa-Ivaldi FA. Probing virtual boundaries and the perception of delayed stiffness. Adv Robot 22: 119–140, 2008. doi: 10.1163/156855308X291863. [DOI] [Google Scholar]
- Pressman A, Welty LJ, Karniel A, Mussa-Ivaldi FA. Perception of delayed stiffness. Int J Robot Res 26: 1191–1203, 2007. doi: 10.1177/0278364907082611. [DOI] [Google Scholar]
- Rao SM, Mayer AR, Harrington DL. The evolution of brain activation during temporal processing. Nat Neurosci 4: 317–323, 2001. doi: 10.1038/85191. [DOI] [PubMed] [Google Scholar]
- Rosenblum MG, Pikovsky AS. Controlling synchronization in an ensemble of globally coupled oscillators. Phys Rev Lett 92: 114102, 2004. doi: 10.1103/PhysRevLett.92.114102. [DOI] [PubMed] [Google Scholar]
- Sarlegna FR, Baud-Bovy G, Danion F. Delayed visual feedback affects both manual tracking and grip force control when transporting a handheld object. J Neurophysiol 104: 641–653, 2010. doi: 10.1152/jn.00174.2010. [DOI] [PubMed] [Google Scholar]
- Scharfman HE. The neurobiology of epilepsy. Curr Neurol Neurosci Rep 7: 348–354, 2007. doi: 10.1007/s11910-007-0053-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol 84: 853–862, 2000. [DOI] [PubMed] [Google Scholar]
- Schnitzler A, Münks C, Butz M, Timmermann L, Gross J. Synchronized brain network associated with essential tremor as revealed by magnetoencephalography. Mov Disord 24: 1629–1635, 2009. doi: 10.1002/mds.22633. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat 6: 461–464, 1978. doi: 10.1214/aos/1176344136. [DOI] [Google Scholar]
- Shadmehr R, Krakauer JW. A computational neuroanatomy for motor control. Exp Brain Res 185: 359–381, 2008. doi: 10.1007/s00221-008-1280-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sing GC, Joiner WM, Nanayakkara T, Brayanov JB, Smith MA. Primitives for motor adaptation reflect correlated neural tuning to position and velocity. Neuron 64: 575–589, 2009. doi: 10.1016/j.neuron.2009.10.001. [DOI] [PubMed] [Google Scholar]
- Sing GC, Orozco SP, Smith MA. Limb motion dictates how motor learning arises from arbitrary environmental dynamics. J Neurophysiol 109: 2466–2482, 2013. doi: 10.1152/jn.00497.2011. [DOI] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: e179, 2006. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer RM, Zelaznik HN, Diedrichsen J, Ivry RB. Disrupted timing of discontinuous but not continuous movements by cerebellar lesions. Science 300: 1437–1439, 2003. doi: 10.1126/science.1083661. [DOI] [PubMed] [Google Scholar]
- Takamuku S, Gomi H. What you feel is what you see: inverse dynamics estimation underlies the resistive sensation of a delayed cursor. Proc Biol Sci 282: 20150864, 2015. doi: 10.1098/rspb.2015.0864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor JA, Krakauer JW, Ivry RB. Explicit and implicit contributions to learning in a sensorimotor adaptation task. J Neurosci 34: 3023–3032, 2014. doi: 10.1523/JNEUROSCI.3619-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature 407: 742–747, 2000. doi: 10.1038/35037588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong C, Wolpert DM, Flanagan JR. Kinematics and dynamics are not represented independently in motor working memory: evidence from an interference study. J Neurosci 22: 1108–1113, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapp BD, Stys PK. Virtual hypoxia and chronic necrosis of demyelinated axons in multiple sclerosis. Lancet Neurol 8: 280–291, 2009. doi: 10.1016/S1474-4422(09)70043-2. [DOI] [PubMed] [Google Scholar]
- van Polanen V, Davare M. Visuo-Haptic Asynchrony Alters Object Lifting Dynamics and Weight Perception. San Diego, CA: Society for Neuroscience, 2016. [Google Scholar]
- Witney AG, Goodbody SJ, Wolpert DM. Predictive motor learning of temporal delays. J Neurophysiol 82: 2039–2048, 1999. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z. Computational principles of movement neuroscience. Nat Neurosci 3, Suppl: 1212–1217, 2000. doi: 10.1038/81497. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science 269: 1880–1882, 1995. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Miall RC, Kawato M. Internal models in the cerebellum. Trends Cogn Sci 2: 338–347, 1998. doi: 10.1016/S1364-6613(98)01221-2. [DOI] [PubMed] [Google Scholar]
- Yousif N, Diedrichsen J. Structural learning in feedforward and feedback control. J Neurophysiol 108: 2373–2382, 2012. doi: 10.1152/jn.00315.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman A, Bai L, Ginty DD. The gentle touch receptors of mammalian skin. Science 346: 950–954, 2014. doi: 10.1126/science.1254229. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this manuscript and the computer codes that were used to generate the results are available upon request from the corresponding author.