Different roles for inhibition in the rhythm-generating respiratory network

The roles of inhibition within the pre-Bötzinger complex (preBötC) are a matter of debate. Using a combination of modeling and experiment, we demonstrate that inhibition affects synchrony, period variability, and overall frequency of the preBötC and coupled rhythmogenic networks. This work expands our understanding of ubiquitous motor and cognitive oscillatory networks.

Abstract

Unraveling the interplay of excitation and inhibition within rhythm-generating networks remains a fundamental issue in neuroscience. We use a biophysical model to investigate the different roles of local and long-range inhibition in the respiratory network, a key component of which is the pre-Bötzinger complex inspiratory microcircuit. Increasing inhibition within the microcircuit results in a limited number of out-of-phase neurons before rhythmicity and synchrony degenerate. Thus unstructured local inhibition is destabilizing and cannot support the generation of more than one rhythm. A two-phase rhythm requires restructuring the network into two microcircuits coupled by long-range inhibition in the manner of a half-center. In this context, inhibition leads to greater stability of the two out-of-phase rhythms. We support our computational results with in vitro recordings from mouse pre-Bötzinger complex. Partial excitation block leads to increased rhythmic variability, but this recovers after blockade of inhibition. Our results support the idea that local inhibition in the pre-Bötzinger complex is present to allow for descending control of synchrony or robustness to adverse conditions like hypoxia. We conclude that the balance of inhibition and excitation determines the stability of rhythmogenesis, but with opposite roles within and between areas. These different inhibitory roles may apply to a variety of rhythmic behaviors that emerge in widespread pattern-generating circuits of the nervous system.

NEW & NOTEWORTHY The roles of inhibition within the pre-Bötzinger complex (preBötC) are a matter of debate. Using a combination of modeling and experiment, we demonstrate that inhibition affects synchrony, period variability, and overall frequency of the preBötC and coupled rhythmogenic networks. This work expands our understanding of ubiquitous motor and cognitive oscillatory networks.

rhythmic activity is critical for the generation of behaviors such as locomotion and respiration, as well as apparently nonrhythmic behaviors including olfaction, information processing, encoding, learning, and memory (Ainsworth et al. 2012; Buzsaki 2006; Kopell et al. 2010; Marder and Bucher 2001; Missaghi et al. 2016; Skinner 2012). These rhythms arise from central pattern generators (CPGs), neuronal networks located within the central nervous system that are capable of generating periodic behavior because of their synaptic and intrinsic membrane properties (Grillner 2006; Grillner and Jessell 2009; Kiehn 2011; Marder and Bucher 2001).

An increasingly important concept is that a given behavior may involve the interaction between several rhythmogenic microcircuits (Anderson et al. 2016; Ramirez et al. 2016). In the neocortex, multiple rhythms and mechanisms are involved in a variety of cortical processes (Buzsaki 2006). In breathing, which consists of the three dominant respiratory phases—inspiration, postinspiration, and expiration—each phase seems to be generated by its own autonomous, excitatory microcircuit, subpopulations of the overall network that act as rhythm-generating modules (Anderson et al. 2016; Lindsey et al. 2012). The timing between these excitatory microcircuits is established by inhibitory interactions. In locomotion, each side of the spinal cord contains rhythmogenic microcircuits that are similarly coordinated by inhibitory mechanisms to establish left-right alternation (see, e.g., Kiehn 2011). Assembling a behavior by combining different microcircuits may imbue a network with increased flexibility. This strategy could also facilitate the integration and synchronization of one rhythmic behavior with another. Sniffing, olfaction, whisking, and rhythmic activities in hippocampus and locus coeruleus are all rhythmically coupled to the inspiratory rhythm generated in the pre-Bötzinger complex (preBötC) (Ferguson et al. 2015; Huh et al. 2016; Moore et al. 2013; Ramirez et al. 2016; Sara 2009). This small microcircuit, located in the ventrolateral medulla, is the essential locus for the generation of breathing (Gray et al. 2001; Ramirez et al. 1998; Schwarzacher et al. 2011; Smith et al. 1991; Tan et al. 2008).

First discovered a quarter of a century ago, the preBötC is among the best-understood microcircuits (Smith et al. 1991). It continues to generate fictive respiratory rhythm activity when isolated in vitro, reliant on excitatory neurotransmission. Rhythmicity in the preBötC ceases when glutamatergic synaptic mechanisms are blocked, while it persists after the blockade of synaptic inhibition. However, almost 50% of the preBötC neurons are inhibitory (Hayes et al. 2012; Morgado-Valle et al. 2010; Shao and Feldman 1997; Winter et al. 2009). Despite the abundance of inhibitory neurons, the majority of neurons in the preBötC are rhythmically active in phase with inspiration. A small group of ~9% of neurons in the preBötC are inhibited during inspiration and discharge in phase with expiration (Carroll et al. 2013; Morgado-Valle et al. 2010; Nieto-Posadas et al. 2014). A recent optogenetic study by Sherman et al. (2015) showed that stimulation of glycinergic inhibitory preBötC neurons can delay or halt a breath and inhibition of those neurons can increase the magnitude of a breath. This is consistent with pharmacological agonist-antagonist experiments by Janczewski et al. (2013) that found that inhibition can modulate rhythm frequency or trigger apnea but is not essential for rhythm generation. The inhibitory population may thus be an “actuator” that allows descending pathways to control respiration. However, with only a few studies available, the role of these inhibitory preBötC neurons is not well understood.

These experimental findings raise important questions: What is the role of inhibitory neurons within this microcircuit (Cui et al. 2016)? Why does the preBötC generate primarily one rhythmic phase despite the presence of numerous inhibitory neurons? Our modeling study arrives at the conclusion that this microcircuit can only generate one rhythmic phase. Synaptic inhibition seems to primarily serve to titrate the strength of this single rhythm while creating a small number of apparently anomalous expiratory cells. To generate more than one phase, it is necessary to assemble a network in which excitatory microcircuits are segmented, via inhibition, into different compartments. Mutually inhibitory circuits have been proposed for the inspiration-active expiration network (Koizumi et al. 2013; Molkov et al. 2013; Onimaru et al. 2015; Smith et al. 2013) and preBötC-postinspiratory complex (PiCo) networks (Anderson et al. 2016).

The novelty of our theoretical study lies in two conceptually important findings: A single microcircuit is unable to generate more than one phase based on the currently known network structure, and the generation of different phases necessitates the inhibitory interaction between excitatory microcircuits. In light of these findings, we propose that the generation of rhythm and phase arise from separate network-driven processes. In these two processes, inhibition plays fundamentally different roles: Local inhibition promotes desynchronization within a microcircuit, while long-range inhibition establishes phase relationships between microcircuits. Consistent with our proposal is the observation that breathing does not depend on the presence of all three phases at any given time. In gasping and some reduced preparations, the respiratory network generates a one-phase rhythm consisting of inspiration only. Under resting conditions, breathing primarily oscillates between inspiration and postinspiration. This eupneic rhythm also involves a late expiratory phase according to Richter and Smith (2014). Under high metabolic demand or coughing, another phase is recruited in form of active expiration. This modular organization may be a fundamental property of rhythm-generating networks.

MATERIALS AND METHODS

preBötC Network Simulations

We model the preBötC network as a simple directed Erdős-Rényi random graph on N = 300 nodes, where edges are added at random with fixed probability. We denote a directed edge from node j to node i as j → i. The connection probability p = (k_avg/2)/(N − 1) so that the expected total degree, that is, the in-degree plus the out-degree, of a node is k_avg, which we vary. We prefer to parametrize these networks by degree k_avg rather than p, since in this case our results do not depend on N once it is large (Bollobás 1998).

Each node is of type bursting (B), tonic spiking (TS), or quiescent (Q), with corresponding probabilities 25%, 45%, and 30% (Del Negro et al. 2005; Peña et al. 2004). Neurons are inhibitory with probability p_I, another parameter, and all projections from an inhibitory neuron are inhibitory. The sets of excitatory and inhibitory nodes are denoted ${\mathcal{N}}_{\mathrm{E}}$ and ${\mathcal{N}}_{\mathrm{I}}$. Edges are assigned a maximal conductivity g_E for excitatory connections and g_I for inhibitory connections. In our parameter sweeps, we vary these conductivities over the range 2–5 nS. This matches the postsynaptic potential deflections observed in experiments (typical inhibitory postsynaptic potentials: −1.2 to −1.8 mV, excitatory postsynaptic potentials: 1.6 to 2.3 mV; data from Aguan Wei).

We use “model 1” from Butera et al. (1999a) as the dynamical equations for bursting, tonic spiking, and quiescent neurons. All parameters, given in Table 1, are shared among the dynamical types, with the exception of the leak conductance g_L, which is adjusted for the desired dynamics (B, TS, Q). Parameter values besides g_L are taken from Park and Rubin (2013), most of which are the same as or close to the original values chosen by Butera et al. (1999a). With the chosen parameters, the bursting neurons fire 6-spike bursts every 2.4 s and the tonic spikers fire 3.5 spikes/s.

Table 1.

Parameters for network

Parameter	Value
C	21 pF
ENa	50 mV
EK	−85 mV
EL	−58 mV
θm	−34 mV
θn	−29 mV
θm,p	−40 mV
θh	−48 mV
σm	−5 mV
σn	−4 mV
σm,p	−6 mV
σh	5 mV
${\overline{\tau }}_n$	10 ms
${\overline{\tau }}_h$	10,000 ms
gK	11.2 nS
gNa	28 nS
gNa,p	1 nS
Iapp	0 pA
gL(B)	1.0 nS
gL(TS)	0.8 nS
gL(Q)	1.285 nS
Esyn,E	0 mV
Esyn,I	−70 mV
θsyn	0 mV
σsyn	−3 mV
${\overline{\tau }}_{\mathrm{s}\mathrm{y}\mathrm{n}}$	15 ms

Parameters for the network model are taken from the literature (Butera et al. 1999a; Park and Rubin 2013). We modify g_L for quiescent (Q), tonic-spiking (TS), and intrinsically bursting (B) cells. The system of equations is simulated in the given units, so that no conversions are necessary. Parameters with subscript “syn” are for the synaptic dynamics.

The full system of equations is

$$\begin{array}{c}\dot{V}=-\left(I_{\mathrm{L}}+I_{\mathrm{N}\mathrm{a}}+I_{\mathrm{K}}+I_{\mathrm{N}\mathrm{a},\mathrm{p}}+I_{\mathrm{s}\mathrm{y}\mathrm{n}}-I_{\mathrm{a}\mathrm{p}\mathrm{p}}\right)/C\\ \dot{h}=\left[h_{\infty }(V)-h\right]/{\tau }_h(V)\\ \dot{n}=\left[n_{\infty }(V)-n\right]/{\tau }_n(V)\end{array}$$ (1)

with the currents calculated as

$$\begin{array}{c}{I}_{\mathrm{L}}=g_{\mathrm{L}}\left(V-E_{\mathrm{L}}\right)\\ I_{\mathrm{N}\mathrm{a}}=g_{\mathrm{N}\mathrm{a}}{m}_{\infty }^3\left(V\right)\left(1-n\right)\left(V-E_{\mathrm{N}\mathrm{a}}\right)\\ I_{\mathrm{K}}=g_{\mathrm{K}}{n}^4\left(V-E_{\mathrm{K}}\right)\\ I_{\mathrm{N}\mathrm{a},\mathrm{p}}=g_{\mathrm{N}\mathrm{a},\mathrm{p}}{m}_{\mathrm{p},\infty }\left(V\right)h\left(V-E_{\mathrm{N}\mathrm{a}}\right)\end{array}$$

and the activation and time constants are

$$\begin{array}{c}{x}_{\infty }(V)=\frac{1}{1+\exp \left[\left(V-{\theta }_x\right)/{\sigma }_x\right]}\\ {\tau }_x(V)=\frac{{\overline{\tau }}_x}{\cosh \left[\left(V-{\theta }_x\right)/\left(2{\sigma }_x\right)\right]}\end{array}$$

To model network interactions, we model synaptic dynamics with first-order kinetics (Destexhe et al. 1994). The synaptic current neuron i receives is

$$I_{\mathrm{s}\mathrm{y}\mathrm{n},i}={\displaystyle \sum _{j\in {\mathcal{N}}_{\mathrm{E}}:j\to i}{g}_{\mathrm{E}}{s}_{ij}\left(V_i-E_{\mathrm{s}\mathrm{y}\mathrm{n},\mathrm{E}}\right)}+{\displaystyle \sum _{j\in {\mathcal{N}}_{\mathrm{I}}:j\to i}{g}_{\mathrm{I}}{s}_{ij}\left(V_i-E_{\mathrm{s}\mathrm{y}\mathrm{n},\mathrm{I}}\right)}$$

where g_E and g_I are the maximal excitatory and inhibitory synapse conductances. The reversal potentials E_syn,E and E_syn,I for excitatory and inhibitory synapses, shown in Table 1, correspond to the appropriate values for glutamatergic and glycinergic or GABAergic synapses. The variables s_ij represent the open fraction of channels between cells j and i, and they are governed by the differential equations

$$\begin{array}{c}{\dot{s}}_{ij}=\left[\left(1-s_{ij}\right)m_{\infty }^{(ij)}\left(V_j\right)-s_{ij}\right]/{\tau }_{\mathrm{s}\mathrm{y}\mathrm{n}}\\ m_{\infty }^{(ij)}\left(V_j\right)=\frac{1}{1+\exp \left[\left(V_j-{\theta }_{\mathrm{s}\mathrm{y}\mathrm{n}}\right)/{\sigma }_{\mathrm{s}\mathrm{y}\mathrm{n}}\right]}\end{array}$$

Excitatory and inhibitory synapses share the parameters ${\overline{\tau }}_{\mathrm{s}\mathrm{y}\mathrm{n}}$, θ_syn, and σ_syn (Table 1).

Each model run starts from random initial conditions and lasts 100 s of simulation time with 1-ms time resolution. The first 20 s of transient dynamics is removed before postprocessing. Rather than saving all state variables during long runs, we record a binary variable for each neuron that indicates whether or not the neuron fires a spike in the given time step. A spike is registered when V surpasses −15 mV for the first time in the previous 6 ms. This spike raster is then stored as a sparse matrix. The simulation code is configurable to output voltage traces or all state variables; these were examined during development to check that the model and spike detection function correctly.

We examine the effects of network connectivity, inhibition, and synaptic strength on the dynamics of our model by varying k_avg, p_I, g_E, and g_I. To capture the interactions of these parameters, we sweep through all combinations of parameters in the ranges k_avg = 1.0, 1.5,..., 12.0; p_I = 0.00, 0.05,..., 1.00; g_E = 2, 3,..., 5 nS; and g_I = 2, 3,..., 5 nS, with 8 repetitions of each combination. The only randomness in the model is randomness present in the graphs and initial conditions, since the dynamics are deterministic. This amounts to 61,824 graph generation, simulation, and postprocessing steps. Network generation, simulations, and postprocessing were performed with custom code available from K. D. Harris at https://github.com/kharris/prebotc-graph-model. The code was written in Python and C++, and some analysis was performed with MATLAB. Numerical integration used backward differentiation formulas in VODE called via scipy.integrate.ode, suitable for stiff equation systems. We experimented with the tolerance to be sure it resolves all timescales. We used the Hyak cluster at the University of Washington to conduct parameter sweeps. Each simulated 100 s took <3 h and could be performed on a standard consumer machine.

Two-Population Network Model

The preBötC is thought to be connected to another microcircuit, alternately the BötC, PiCo, and lateral parafacial group, in a mutually inhibitory manner (Anderson et al. 2016; Huckstepp et al. 2016; Molkov et al. 2013; Smith et al. 2013) that allows them to generate stable two-phase rhythms as in a half-center oscillator (Marder and Bucher 2001). We study this case with a two-microcircuit model, where each microcircuit is represented by a different population of cells (populations 1 and 2); we arbitrarily refer to the preBötC as population 1.

We use a two-group stochastic block model for the network. The stochastic block model (Holland et al. 1983) is a generalization of the directed Erdős-Rényi random graph, where the connection probability varies depending on the population label of each neuron. Each population has recurrent connections from excitatory to all other cells, with each connection occurring with a fixed probability. As we describe below, we vary probabilities of connections from inhibitory neurons to other neurons in the same population (intragroup) and in the other population (intergroup).

Let N₁ be the number of neurons in population 1 and N₂ the number of neurons in population 2. We assume N₁ = N₂ = 300, so the network has a total of 600 neurons. To generate this network we begin by assigning each neuron to one of the two populations. We then assign each neuron a type: quiescent, tonic, or bursting, using the same method as the single-population model. Afterwards, we randomly assign neurons to be inhibitory with probability p_I = 0.5 (Hayes et al. 2012; Morgado-Valle et al. 2010; Shao and Feldman 1997; Winter et al. 2009); otherwise they are excitatory. We then assign connections to the neurons with probabilities

$$P^{(\mathrm{I})}=\left[\begin{array}{cc}\frac{k_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}}{N_1-1}& \frac{k_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}{N_2}\\ \frac{k_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}{N_1}& \frac{k_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}}{N_2-1}\end{array}\right],P^{(\mathrm{E})}=\left[\begin{array}{cc}\frac{3}{N_1-1}& 0\\ 0& \frac{3}{N_2-1}\end{array}\right]$$

where 0 ≤ k_intra, k_inter ≤ 4. The matrix entries (i, j) are the probability of a connection between an inhibitory or excitatory neuron in population i and a neuron in population j. This model allows us to tune between a half-center network containing only intergroup inhibition and a network with equal amounts of both intra- and intergroup inhibition.

The matrix P^(E) contains the probability of connection for a projecting excitatory neuron. It is diagonal, reflecting the assumption that excitatory neurons only project within the local population, and each excitatory neuron has an average out-degree of 3. The matrix P^(I) describes the probability of connection for inhibitory projecting neurons. The variable k_intra is the expected number of projections per inhibitory neuron to other neurons within its own population, and k_inter is the expected number of projections from an inhibitory neuron to neurons in the other population. We normalize these values in the matrix to ensure that the average in-degree is the sum of the columns and the out-degree is the sum of the rows, both equal to k_intra + k_inter + 3. The total inhibitory degrees then depend on the values of k_intra and k_inter, which affect only the inhibitory connection probabilities. Unless explicitly stated, connections are assigned a fixed conductance of g_E = g_I = 2.5 nS for excitatory and inhibitory connections.

We examine the effects of inhibition both within a population and between populations. To do this, we sweep through the parameters k_intra, k_inter = 0.0, 0.5,..., 4.0 and simulate 8 realizations (i.e., samples from the distribution of random graphs with these parameters) for each parameter pair. This leads to graph generation, simulation, and postprocessing steps. As for the single-population model, all code is available at https://github.com/kharris/prebotc-graph-model.

Slice Experiments

Brain stem transverse slices were prepared from CD-1 mice (P7–12). All experiments were performed with the approval of the Institutional Animal Care and Use Committee of the Seattle Children’s Research Institute. Mice were maintained with rodent diet and water available ad libitum in a vivarium with a 12:12-h light-dark cycle at 22°C. Thickness of slices containing the preBötC varied between 550 and 650 μm. Slices were placed into the recording chamber with circulating artificial cerebrospinal fluid (aCSF) containing (in mM) 118 NaCl, 3 KCl, 1.5 CaCl₂, 1 MgCl, 25 NaHCO₃, 1 NaH₂PO₄, and 30 d-glucose and equilibrated with 95% O₂-5% CO₂, pH 7.4. We maintained the temperature of the bath at 31°C, with an aCSF circulation rate of 15 ml/min. Rhythmic activity of preBötC was induced by slow upregulation of KCl concentration from 3 mM to 8 mM in aCSF. The details of the technique are described in Ramirez et al. (1997a) and Anderson et al. (2016).

We recorded extracellular neuronal population activity in the preBötC region with a protocol that first measured the control activity, then activity following application of a partial excitation block, and finally with an additional complete block of inhibition. We used 700 nM 6,7-dinitroquinoxaline-2,3-dione (DNQX) disodium salt, a selective non-NMDA receptor antagonist that blocks glutamatergic ion channels generating fast excitatory synaptic inputs, to effect the partial excitation block. Picrotoxin (PTX), an ionotropic GABA_A receptor antagonist blocking inhibitory chloride-selective channels, was used at 20 or 50 μM to shut down inhibition. Both concentrations of PTX were equally effective at blocking inhibition. DNQX disodium salt and PTX were obtained from Sigma-Aldrich (St. Louis, MO). After application of either drug, we waited 5 min for the drugs to take effect and used at least 10 min of data to measure the resulting rhythm.

In additional experiments, we supplemented the extracellular population-level data with multielectrode recordings in the contralateral preBötC. Extracellular neural activity from the transverse medullary slice was recorded on a 16-channel commercial linear multiarray electrode (model: Brain Slice Probe, Plexon, Dallas, TX). Each electrode had a recording surface of 15 μm, and interelectrode spacing was fixed at 50 μm. Neural signals were amplified and recorded with the Omni-Plex D system (Plexon). Wide-band data were filtered with a Butterworth low-pass filter, 200-Hz cutoff, and spike sorting was performed off-line and post hoc with Offline Sorter v4.1.0 (Plexon). Specifically, individual unit waveforms were detected and sorted by principal component analysis, visualized in a three-dimensional cluster view. Waveforms were detected and sorted with Offline Sorter with manual cluster cutting single electrode-based feature spaces. Care was taken to follow nonstationarities in waveform shapes in assigning spikes to separate units, and auto- and cross-correlation histograms were examined as a check on sorting results (Lewicki 1998). All neurons with good isolation were kept for analysis.

We kept only those slices that initially showed robust rhythms, as determined by the experimentalist. We performed a total of five multielectrode experiments and discarded one in which the rhythm went away after application of DNQX and never recovered. We recorded extracellularly from 15 slices and excluded 2 outliers from statistical analysis because their rhythms slowed considerably more than the others with DNQX. In vitro slice data were analyzed by hand with Axon pCLAMP (Molecular Devices, Sunnyvale, CA) to extract burst locations and amplitudes, which were exported to a table for analysis with custom Python programs available at https://github.com/kharris/prebotc-graph-model.

Postprocessing

Because of the large number of simulations needed to explore the parameter space, we can examine only a small fraction of the simulations by eye and must rely on summary statistics to characterize the dynamics.

Binning and filtering.

First, the spike raster data are aggregated into 50-ms bins of spike counts to compress the size of the matrix. We denote the spike raster vector time series x^bin(t). The unbinned spike rasters are then convolved with a Gaussian kernel $k(t)={\left(\sigma \sqrt{2\pi }\right)}^{-1}\exp (-\frac{t^2}{{2\sigma }^2})$, where σ = 60 ms, to produce the continuous time series x^filt(t) = (k × x)(t), which is then downsampled to the same time bins. To characterize the overall population output, we compute what we call the integrated trace x^int(t). This is defined as the low-pass-filtered population average, where the population average $\overline{x}(t)=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i(t)}$. We use a second order Butterworth filter with cutoff frequency 4 Hz. The integrated trace is normalized to have units of spikes per second per neuron.

Synchrony statistic.

Our principal aim is to quantify how different networks give rise to varying degrees of synchrony across the population of bursting neurons. We choose to characterize the overall synchrony of the population with one statistic (Golomb 2007; Masuda and Aihara 2004)

$$\chi ={\left(\frac{{〈{\overline{x}}^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}{(t)}^2〉}_t-{〈{\overline{x}}^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)〉}_t^2}{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left[{〈x_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}{(t)}^2〉}_t-{〈x_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)〉}_t^2\right]}}\right)}^{1/2}$$ (2)

where the angle brackets ${〈\cdot 〉}_t$ denote averaging over the time series and ${\overline{x}}^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}}(t)$. The value of χ is between 0 and 1. With perfect synchrony, $x_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)={\overline{x}}^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)$ for all i, then we will find χ = 1. With uncorrelated signals $x_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}(t)$, then χ = 0. Examples of network activity for different values of χ are shown in Fig. 1.

Fig. 1.

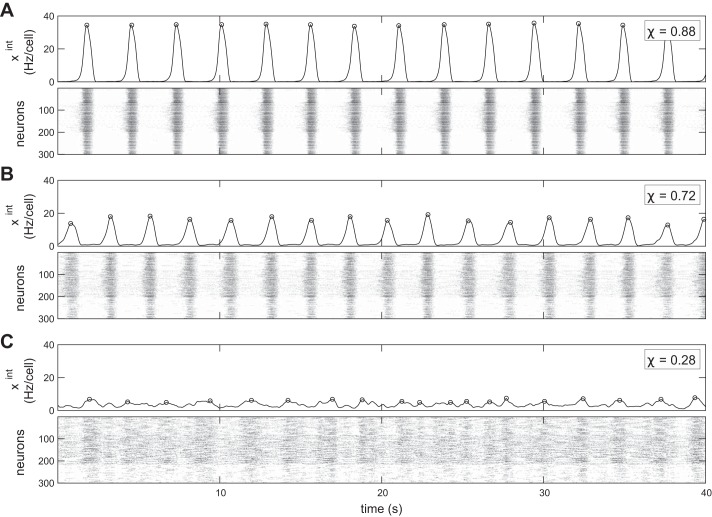
With higher fraction of inhibitory cells, synchrony and burst amplitude decrease and the integrated time series becomes more variable. Three simulations of the respiratory network model: p_I = 0% (A); p_I = 20% (B); p_I = 40% (C). Top: the integrated trace, which is a low-pass-filtered average of the spiking activity of all N = 300 neurons in the network. Bottom: the spike raster of individual neuron activity. In all cases, k_avg = 6, g_E = g_I = 2.0 nS. Detected bursts are marked by open circles on the integrated traces. At lower levels of synchrony, as in C, what constitutes a burst becomes ambiguous.

Burst detection and phase analysis.

The respiratory rhythm is generated by synchronized bursts of activity in the preBötC. To identify these bursts in the integrated traces, we needed a method of peak detection that identifies large bursts but ignores smaller fluctuations. To do this we identify times t* in the integrated time series x_int(t), where x_int(t*) is an absolute maximum over a window of size 600 ms (12 time bins to either side of the identified maximum), and its value is above the 75th percentile of the full integrated time series. This ensures that the detected bursts are large-amplitude, reliable maxima of the time series.

Using the detected burst peak $t_1^{*},t_2^{*},\mathrm{...},\hspace{0.17em}{t}_{n_{\mathrm{b}\mathrm{u}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{s}}}^{*}$, we can examine the activity of individual neurons triggered on those events, the burst-triggered average (BTA). The time between consecutive bursts is irregular, so to compute averages over many events we rescale time into a uniform phase variable ϕ ∈ [−π, π]. A phase ϕ = 0 happens at the population burst, while ϕ = −π ≡ π (mod 2π) occurs between bursts. To define this phase variable, we rescale the half-interval [$\left(t_n^{*}-t_{n-1}^{*}\right)\hspace{0.17em}/\hspace{0.17em}2,t_n^{*}$] preceding burst n to [−π, 0]. Similarly, we rescale the other half-interval [$t_n^{*},\left(t_{n+1}^{*}-t_n^{*}\right)/2$], which follows burst n to [0, π]. Each rescaling is done with linear interpolation of the binned spike rasters. Let Φ(t) denote the mapping from time t to the phase. Then the BTA activity of neuron i is

$$x_i^{\mathrm{B}\mathrm{T}\mathrm{A}}(\varphi )=\frac{1}{n_{\mathrm{b}\mathrm{u}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{s}}}{\displaystyle \sum _{j=1}^{n_{\mathrm{b}\mathrm{u}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{s}}}{\displaystyle {\int }_{-\left(t_j^{*}-t_{j-1}^{*}\right)/2}^{\left(t_{j+1}^{*}-t_j^{*}\right)/2}{x}_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}}}\left(t_j^{*}+t\right)\text{δ}\left[\Phi \left(t_j^{*}+t\right)-\varphi \right]\mathrm{d}\mathrm{t}$$ (3)

where δ(·) is the Dirac delta measure that ensures that $x_i^{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}}$ is sampled at the correct phase.

The BTAs exhibit two characteristic shapes. The first shape is peaked at a particular value of ϕ; these neurons are phasic bursters. Of course, most phasic bursters take part in the overall population rhythm and have their BTA maximum near zero. Cells that are in phase with the population rhythm are inspiratory. However, there are some bursters with a BTA peak near π, and we call these out-of-phase cells expiratory. The second shape is weakly peaked or flat; these neurons are tonic.

We define a complex-valued phase-locking variable z_i as the circular average of the BTA normalized by its integral:

$$z_i=\frac{{\displaystyle {\int }_{-\pi }^{\pi }{x}_i^{\mathrm{B}\mathrm{T}\mathrm{A}}}(\varphi )e^{i\varphi }\mathrm{d}\varphi }{{\displaystyle {\int }_{-\pi }^{\pi }{x}_i^{\mathrm{B}\mathrm{T}\mathrm{A}}}(\varphi )\mathrm{d}\varphi }$$ (4)

Normalization allows us to compare cells with different firing rates. The magnitude of phase-locking (peakedness of $x_i^{\mathrm{B}\mathrm{T}\mathrm{A}}$) is quantified by the magnitude |z_i|. We use the argument arg(z_i) to define the dominant phase of a cell’s activity. These phase-locking variables are similar to the order parameters used to study synchrony (Arenas et al. 2008). We classify cell i as inspiratory, expiratory, tonic, or silent by

• 1.Silent: firing rate is < 0.1 Hz
• 2.Inspiratory: |z_i| > 0.2 and |arg(z_i)| ≤ π/2
• 3.Expiratory: |z_i| > 0.2 and |arg(z_i)| > π/2
• 4.Tonic: otherwise

Two-population phase analysis.

For the two-microcircuit model, we are also interested in the phase relationship between the two populations. To study this, we examine the burst-by-burst phase differences between the two populations’ integrated traces and extract descriptive statistics of the phase differences. The N₁ neurons in population 1 and N₂ neurons in population 2 define two separate groups that we analyze as in Binning and filtering, Synchrony statistic, and Burst detection and phase analysis. Note that because of the symmetry of P^(E) and P^(I), populations 1 and 2 are statistically equivalent. The burst times define two vectors t^1* and t^2*, where $t_j^{i*}$ is the time for the jth peak in the signal of population i = 1 or 2. Population 1 is set as the reference signal for phase analysis. We then define a window with respect to the reference as $W_j=\left[t_j^{i*},t_{j+1}^{i*}\right]$, where i is the chosen reference signal. For each peak $\ell$ in the nonreference signal, which we write as $t_{\ell }^{\overline{i}*}$, we find the reference window W_j so that $t_{\ell }^{\overline{i}*}\in W_j$. In other words, for each peak in the nonreference signal we find the two peaks it lies between in the reference signal; we say that these peaks delineate the reference window. Once we have the reference window to use for the given peak, we define the phase difference between the two signals as

$${\theta }_i=\frac{t_{j+1}^{i*}-t_{\ell }^{\overline{i}*}}{t_{j+1}^{i*}-t_j^{i*}}\in \left[0,1\right]$$

For an accurate description of the overall phase difference between the signals, we use directional statistics (Jammalamadaka and SenGupta 2001), which account for the fact that θ = 0 and 1 are identified. We can imagine that each phase difference is mapped to a circle, where we can then calculate the average position of those phase differences and how spread out the values are on that circle with respect to that average. To do this, we map the θ_i onto the unit circle with the equation ${\zeta }_k=e^{2\pi i{\theta }_k}$. We then take the average of these complex-valued points, ${\zeta }_{\text{avg}}=\frac{1}{n}{\displaystyle {\sum }_{k=1}^n{\zeta }_k}$.

We next calculate two quantities: the average phase difference Φ = arg(ζ_avg)/(2π) and the phase order Ω = |ζ_avg|. The average phase difference Φ is the circular average of the peak-by-peak phase difference between the two signals through time. The phase order Ω tells us how concentrated the phase differences are compared with the average. If ζ_k ≈ ζ_avg for all k, then |ζ_avg| ≈ 1. However, if the values of ζ_k are uniformly spread around the unit circle, we would have a ζ_avg ≈ 0, since opposite phases cancel out. Thus the phase order 0 ≤ Ω ≤ 1, and the closer it is to 1, the more reliable the phase difference is between the two rhythms over time.

Irregularity scores.

We define the irregularity score of sequence x_j as

$$\text{IRS}(x)=\frac{1}{n_{\text{bursts}}}{\displaystyle \sum _{j=1}^{n_{\text{bursts}}}\frac{\left|x_{j+1}-x_j\right|}{\left|x_j\right|}}$$ (5)

Here x_j denotes either the amplitude of the jth detected burst (amplitude irregularity) or the period between bursts j and j + 1 (period irregularity). The irregularity score IRS(x) measures the average relative change in x.

Statistical tests.

We analyzed amplitude, period, amplitude irregularity, and period irregularity, using a linear mixed-effects model. This model captures the repeated measurement structure inherent in our experimental design. In particular, we model the response (amplitude, period, etc.) y_s,d of a slice s to drug d as

$$y_{s,d}=a+a_s+{\mu }_d+{ϵ}_{s,d}$$

where a is a fixed intercept (representing the control level of y), a_s is a zero-mean random effect for each slice, μ_d is a fixed effect for each drug (DNQX or DNQX+PTX), and ϵ_s,d is a zero-mean noise term. We fit this model with the lmerTest package in R, and the code and data used for fitting and analysis are provided in the Supplemental Data, available online at the Journal of Neurophysiology website. In results we report the estimate of the fixed effects (a, μ_d), standard error (SE), degrees of freedom (DF), t value, and P value.

RESULTS

We developed a network model of the preBötC and used this to examine the impact of connectivity and inhibition. Each cell in the network is governed by membrane currents that can produce square-wave bursting via the persistent sodium current I_Na,p (Butera et al. 1999a). We include bursting pacemaker (B), tonic-spiking (TS), and quiescent (Q) cell types in realistic proportions. Through simulations, we examine the effects of network connectivity and the presence of inhibitory cells on rhythm generation. To achieve this, we vary three key parameters over their biologically plausible ranges: 1) the fraction of inhibitory cells p_I, 2) the average total degree k_avg, i.e., the average total incoming and outgoing connections incident to a neuron, and 3) excitatory and inhibitory maximal synaptic conductances g_E and g_I. The parameter k_avg controls the sparsity of synaptic connections present in the network; as k_avg increases, the network becomes increasingly connected.

As we detail below, we compute metrics of synchronous bursting within the microcircuit as these network parameters vary. We then generalize the model to two coupled microcircuits and test whether the added network structure can generate multiphase rhythms. Finally, we also compare these model effects to experiments with preBötC slice preparations, where we use a pharmacological approach to modulate the efficacy of excitatory and inhibitory synapses.

Inhibition and Sparsity Weaken Model Rhythm

We first fix a moderate level of network sparsity, so that each cell receives and sends a total of k_avg = 6 connections on average, and we also fix the synaptic strengths (g_E and g_I = 2.0 nS). In Fig. 1, we show the behavior of the network for varying amounts of inhibitory cells p_I.

In Fig. 1A, the inhibitory fraction p_I = 0, so the network is purely excitatory. In this case it generates a strong, regular rhythm, and the population is highly synchronized. This is clear from both the integrated trace x^int, which captures the network average activity and thus the rhythm (defined in Binning and filtering), and the individual neuron spikes in a raster, which are clearly aligned and periodic across many cells in the microcircuit. To further quantify the levels of synchronized firing, we use the synchrony measure χ, a normalized measure of the individual neuron correlations to the population rhythm, formally defined in Eq. 2. Values of χ ≈ 1 reflect a highly synchronized population, whereas χ ≈ 0 means the population is desynchronized. The cells in Fig. 1A are visibly synchronized from the raster and have synchrony χ = 0.88.

We introduce a greater fraction of inhibitory cells p_I = 0.2 in Fig. 1B. Here we see more irregularity in the population rhythm as well as reduced burst amplitude and synchrony (χ = 0.72). In Fig. 1C, with a still greater fraction of inhibitory cells, p_I = 0.4, the network shows further reduced synchrony (χ = 0.28) and a very irregular, weak rhythm. In this case, the “rhythm” is extremely weak, if it even can be said to exist at all, and could not drive healthy breathing.

Building on these three examples, we next study the impact of inhibition on synchrony over a wider range of network connectivity parameters. Here we vary not only the fraction of inhibitory cells p_I but also the sparsity via k_avg. In Fig. 2, we summarize the effects of inhibition and sparsity on synchrony by plotting χ as those parameters vary. Each point in the plot is the average χ over 8 network realizations with the corresponding parameters. The main tendency is for higher synchrony with higher k_avg, i.e., higher connectivity and less sparsity, and lower synchrony with higher p_I. A similar effect occurs when varying g_E and g_I, where stronger excitation synchronizes and stronger inhibition desychronizes (shown in Fig. 8 for comparison with pharmacological experiments).

Fig. 2.

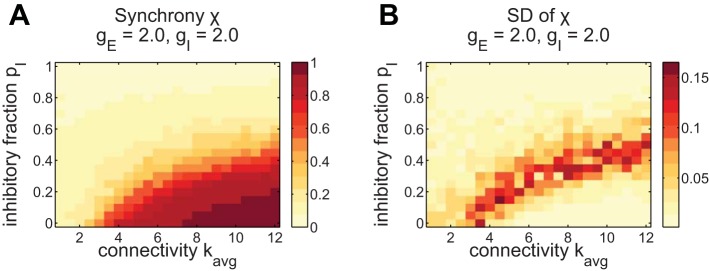
Synchrony decreases with inhibition and sparsity. The highest variability across networks occurs at the synchronization boundary. A: synchrony parameter χ averaged over 8 network realizations, plotted vs. the amount of connections k_avg and the fraction of inhibitory neurons p_I. B: standard deviation of χ over network realizations. Higher standard deviation indicates that the synchrony is not reliable for different networks with those parameters. The area of highest standard deviation occurs at the boundary of low and high synchrony, χ ≈ 0.5. This is indicative of a phase transition between synchronized and desynchronized states.

Fig. 8.

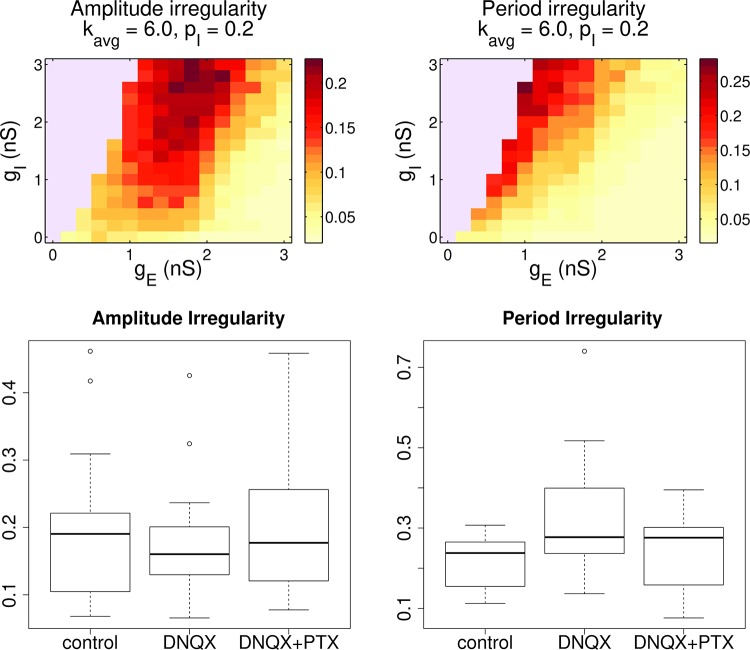
Modulation of inhibition and excitation changes the rhythm in comparable ways for experiments and the model. Top: model: effect of changing conductances g_E and g_I. Burst amplitude and period irregularity decrease with stronger excitation and weaker inhibition. Both of these measures are negatively correlated to the population synchrony, shown in Fig. 7D. Bottom: experiments. This plot summarizes 17 experiments. We extracted bursts from the LFP and measured the amplitude and frequency irregularity of those rhythms. Amplitude irregularity showed no significant trends across conditions. However, period irregularity showed a significant increase from control with DNQX, a decrease from DNQX to DNQX+PTX, and a small increase between control and DNQX+PTX. See Table 2 for the full output of the statistical tests.

Inhibition thus decreases the synchrony within the preBötC microcircuit, which hinders the rhythm. At or above p_I = 50%, the network is desynchronized for all connectivities k_avg. With an inhibitory majority, most inputs a neuron receives are desynchronizing; thus no coherent overall rhythm is possible. This is one of our first major results: In a single microcircuit, constructed with homogeneous random connectivity and with I_Na,p-driven burst dynamics (Butera et al. 1999a), inhibition cannot lead to the creation of a multiphase rhythm. Inhibition only has the effect of desynchronizing bursting neurons and disabling the overall rhythm.

For any type of random connectivity, there is no single network corresponding to a given inhibitory fraction and sparsity level. Rather, each setting of these parameters defines a probability distribution over a whole family of networks, and we can study rhythm generation on sample realizations. This raises the question of how consistent our findings are from one of these networks to the next. To address this, we next depict the standard deviation of χ across the 8 network realizations, shown in Fig. 2B. The standard deviation tells us how much variation in synchrony to expect for different random networks with these parameters, with a higher standard deviation indicating less reliability. The variability in networks is a result of their random generation. The highest standard deviation occurs near the border between synchrony and disorder, where the average χ ≈ 0.5 (see Fig. 2A). Above this border almost all networks exhibit low synchrony, and below it networks consistently show the same levels of high synchrony. Near the transition, random variations in the network structure have a larger effect on synchrony. The increase in standard deviation at the boundary between high and low synchrony is indicative of a “phase transition” between synchronized and desynchronized network states (Arenas et al. 2008).

Inhibition Creates Expiratory Subpopulation

In the preBötC, the majority of cells fire in phase with inspiration, but there are also cells that fire during other phases (postinspiratory or expiratory) along with tonically active cells. A goal of our study is to identify the network and inhibitory effects leading to this variety of cells.

To analyze the time during the ongoing population rhythm at which individual model neurons are active, we identify robust peaks in the integrated trace as population bursts (see Burst detection and phase analysis for details). This allows us to map time into a phase variable φ ∈ [−π, π] and study neuron activity triggered on phase. Each peak in the rhythm occurs as the population bursts in synchrony and sets the phase ϕ = 0. Values of ϕ ≈ 0 correspond to the inspiratory phase, since this corresponds to activity in phase with the overall population rhythm, which for the preBötC is inspiration. A phase near π or −π we call expiratory. We examine cells’ firing rates as a function of phase, which we call the burst-triggered average (BTA, Eq. 3). Using this, we define a phase-locking variable z_i (Eq. 4) for each cell. The magnitude |z_i| reflects how selectively cell i responds to phase, and the angle arg(z) tells the phase it prefers. This allows us to classify cells as inspiratory, expiratory, tonic, or silent. Figure 3A shows the phase-locking variables z_i for an example simulation with parameters that generate a realistic rhythm (k_avg = 6, p_I = 20%, χ = 0.716, with raster and integrated trace in Fig. 1B). In this case we see that most neurons are inspiratory, with a dominant cluster of phase-locking variables centered on |z| ≈ 0.8 and arg(z) ≈ 0. The rest of the cells are distributed approximately uniformly at random in the phase/magnitude cylinder. In this example, the majority of cells are inspiratory, with a smattering of expiratory and tonic cells.

Fig. 3.

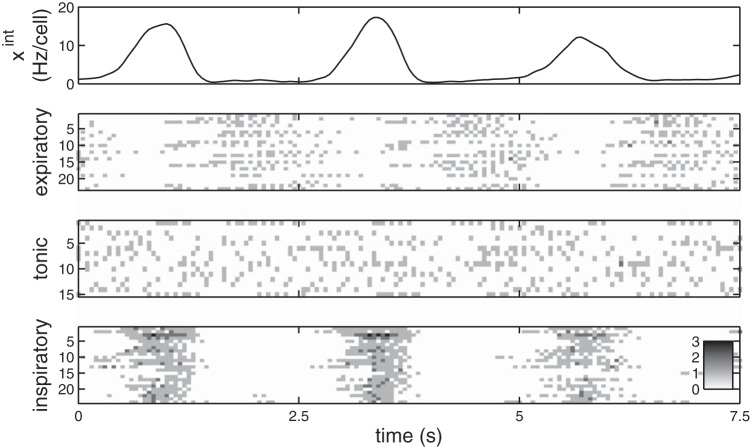
Expiratory cells arise from inhibition but can only occupy a minority without disrupting the inspiratory rhythm. A: neuron phase locking variables for the simulation in Fig. 1B (k_avg = 6, p_I = 20%). Each neuron has an associated complex number z_i with 0 ≤ |z_i| ≤ 1. The magnitude |z_i| is plotted against angle arg z_i. These are used to define inspiratory, expiratory, and tonic neurons via the labeled regions separated by the dashed lines. B: expiratory (antiphase with main rhythm) neurons as a function of network parameters k_avg and p_I. The fraction of expiratory neurons increases with inhibition or as the connectivity becomes weaker. The blue area indicates the absence of any overall rhythm, defined as χ < 0.25. C: example of a simulation with 2-phase activity, with k_avg = 6, p_I = 30%, g_E = 5.0, and g_I = 2.0. A minority of neurons produce a reliable, small bump after every burst. It is aligned near 0.7π, so it is more of a postinspiratory or preexpiratory burst. These expiratory cells are rebound bursting after being disinhibited. This is similar to the “handshake” mechanism of Wittmeier et al. (2008). However, this type of 2-phase rhythm is very rare in simulations.

Figure 3B shows our main results. For any connectivity level k_avg, we find that the number of expiratory neurons increases as the fraction of inhibitory cells p_I increases until the rhythm degrades entirely. Note that there can be a few expiratory neurons even with p_I = 0 for k_avg < 4. However, at this connectivity each cell has fewer than two incoming connections on average. The expiratory cells in that case are isolated from the rest of the network and have in-degree zero, with their phase only reflecting random initial conditions. Comparing Fig. 2A and Fig. 3B, we see that the number of expiratory neurons grows as synchrony decreases.

Another key finding of Fig. 3B is that there are never more than 20% expiratory cells. This means that, in this kind of unstructured microcircuit, it is not possible to create a two-phase rhythm where the expiratory burst is of magnitude similar to the inspiratory burst. Up to ~20% of neurons can be expiratory without destroying the rhythm, defined as maintaining χ ≥ 0.25. Figure 3C shows an example of a rhythm with two phases, where the expiratory or postinspiratory phase recruits only a minority of cells. The expiratory burst in this case is caused by rebound bursting of expiratory cells when they are released from inhibition. However, a two-phase rhythm of this magnitude is rare in our simulations. For example, it does not occur in other network realizations with the same parameters as Fig. 3C.

One of our goals is to understand the network mechanisms that give rise to expiratory cells. In Fig. 4, we show the firing properties of some example expiratory, tonic, and inspiratory classified cells. Expiratory and tonic cells both fire at lower rates than inspiratory cells, which are active in tight bursts. The modeled expiratory cells thus show tonic active behavior that is suppressed by inhibition, as observed in slice (Lieske et al. 2000; Shao and Feldman 1997). Note that some of the tonic cells in Fig. 4 are bursting, just not at a reliable rhythm phase.

Fig. 4.

Example rasters of expiratory, tonic, and inspiratory cells. Expiratory cells exhibit lower firing rates than inspiratory cells, similar to the typical tonic firing observed in slices. As shown, tonic classified cells can be bursting so long as their bursts do not occur reliably at any given phase. The inspiratory cells shown are a random subset. Data are for a representative network with k_avg = 6, p_I = 20% (same as Figs. 1B and 2B).

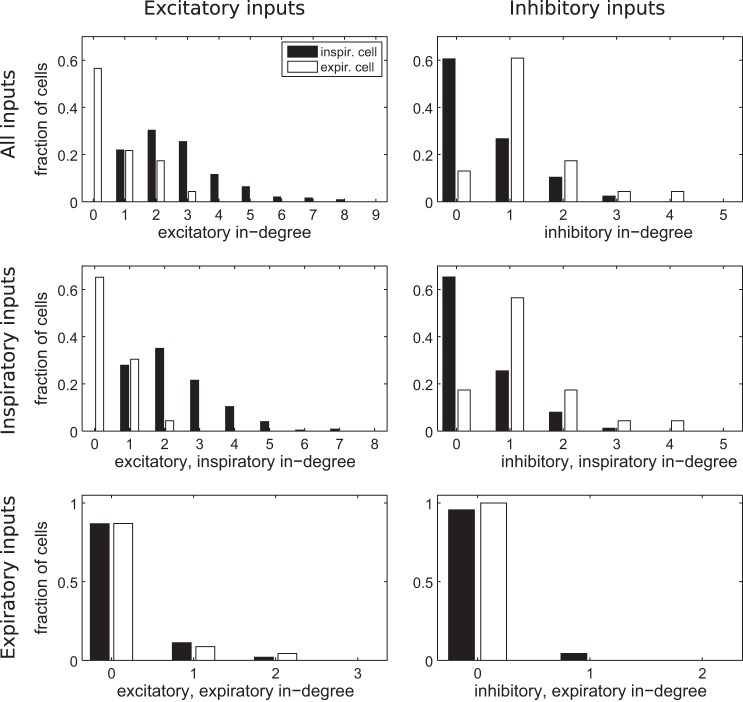
Each neuron’s phase-locking properties are determined by its intrinsic dynamics and the excitatory and inhibitory synaptic currents it receives during various phases of the rhythm. In the model, we find that expiratory cells receive different synaptic inputs than inspiratory cells. We can see this by plotting their input properties in Fig. 5, in this case for a typical simulation in the partially synchronized regime, the same parameters as Fig. 1B. Overall, expiratory cells have less excitatory inputs and more inhibitory inputs than inspiratory cells (Fig. 5, top). We also break down these inputs by the phase of the presynaptic cell. Expiratory cells receive less excitation during the inspiratory phase, and they similarly receive more inhibition during the inspiratory phase (Fig. 5, middle). Given that expiratory cells are the minority, the trends for inputs during the expiratory phase are not as strong (Fig. 5, bottom). This suggests that expiratory cells emerge from random configurations in the network, which partitions itself into different phases based on the types of interactions in each cell’s neighborhood. Excitatory synapses drive the postsynaptic neuron into phase with the presynaptic neuron, while inhibitory synapses drive neurons out of phase.

Fig. 5.

Expiratory cells preferentially receive input from other excitatory, expiratory cells and inhibitory, inspiratory cells. Top: distribution of inputs, excitatory on left and inhibitory on right, colored by whether the receiving cell is inspiratory or expiratory. Expiratory cells receive less excitatory and more inhibitory connections than inspiratory cells. Middle and bottom: these inputs broken down by the phase of the presynaptic neuron, inspiratory (middle) and expiratory (bottom). Expiratory cells preferentially receive excitatory input from other expiratory cells (compare middle left and bottom left). Furthermore, inhibitory input to expiratory cells tends to come from inspiratory cells rather than other expiratory cells (middle right and bottom right). Data are for a representative network with k_avg = 6, p_I = 20% (same as Figs. 1B and 2B). There were 251 inspiratory, 23 expiratory, 15 tonic, and 11 silent cells.

As we have shown in the preceding two sections, the presence of inhibition leads to changes in the population rhythm generated in microcircuits: a degradation of the overall population synchrony as well as an increasing presence of expiratory cells. The average degree k_avg controls the sparsity of connections in the network, and lower values also lead to less synchrony. Moreover, we have shown that cells become expiratory because of the arrival of inhibition during the inspiratory phase as well as excitation during the expiratory phase.

Two-Population Network Shows Benefits of Half-Center Inhibition

In Inhibition and Sparsity Weaken Model Rhythm, we examined the effect of inhibition on rhythmic spiking in a single microcircuit, as would model, for example, an isolated preBötC (e.g., Ramirez et al. 1997a). There we saw that increasing inhibition causes the synchrony and rhythmicity of neural spiking to degrade. Here we extend our analysis to a model of two coupled microcircuits. Each microcircuit, taken separately, is a heterogeneous subnetwork of cells with exactly the same properties and parameterization as for the networks studied above. The two microcircuits are then coupled with mutual inhibition in the manner of a classical half-center pattern generator. We explore the effects of inhibition on the synchrony within each microcircuit, as well as on the phase of the two microcircuits relative to one another.

Figure 6A shows a schematic of our network model. As in the previous sections, each microcircuit (a distinct population of cells) contains both excitatory and inhibitory neurons. For simplicity, since we want to isolate the effects of inhibitory structure, the excitatory neurons only project locally, that is, within the same microcircuit. We vary inhibitory connectivity via the parameters k_inter and k_intra, the intragroup and intergroup average degrees for inhibitory cells. For example, setting k_inter = 0 yields independent populations that do not interact; when k_intra = 0 and k_inter = 0, we have a network version of the classic half-center oscillator, with inhibition purely between the two microcircuits. We will investigate network activity at these two extremes and intermediate levels of connectivity.

Fig. 6.

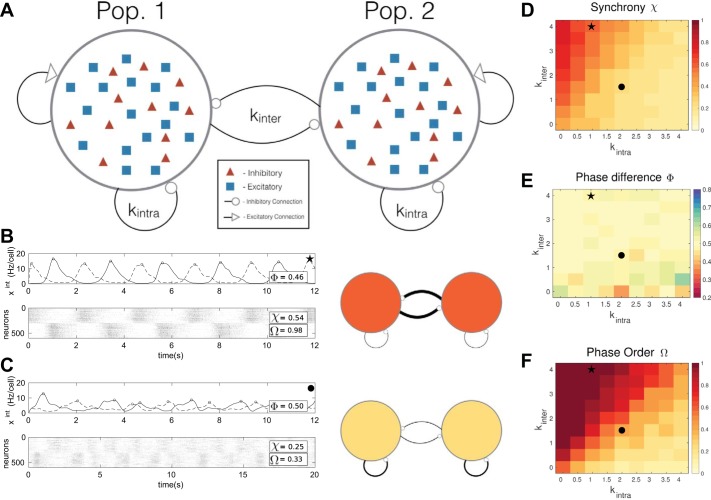
A: schematic of the two-population network. The average amount of excitatory connections on average are fixed, but we vary the expected intragroup and intergroup inhibition k_intra and k_inter. B and C: 2 simulations of the network with different parameters. Each simulation also has a schematic on right demonstrating the differences in inhibitory network strengths. A thicker line indicates more connections, and a darker color indicates a more reliable rhythm. B shows the case k_intra = 1.0 and k_inter = 4.0. C depicts k_intra = 2.0 and k_inter = 1.5. There, we observe less reliable rhythms, with decreased phase order Ω and decreased synchrony χ, despite approximately equal average phase difference Φ. D: average synchrony over 8 realizations for each k_inter and k_intra pair. Higher values of χ occur above the diagonal k_inter = k_intra line. E: average phase difference Φ of rhythmic bursts between the 2 populations. No clear trends are evident, and the value is close to Φ = 0.5, perfectly out of phase, in much of the region. F: average phase order Ω. Higher phase order indicates that the relative phase of bursts in populations 1 and 2, i.e., Φ in E, are reliable. The phase order appears to be proportional to the synchrony, with the highest values above the diagonal. Star and circle symbols in D–F are the network parameters used to produce the rhythms in B and C, respectively.

Figure 6, B and C, illustrate the role of inhibitory connectivity on rhythmic spiking dynamics in two representative cases. The network in Fig. 6, B and C, top (see schematic), has weaker inhibition within each population than between the populations, with parameters k_intra = 1.0 and k_inter = 4.0. The population activity exhibits a strong, regular, and synchronous rhythm with little change in the phase relationship over time. The network in Fig. 6, B and C, bottom, has the opposite connectivity: stronger inhibition within each population and weaker inhibition between (k_intra = 2.0 and k_inter = 1.5). This network demonstrates a weak, sporadic rhythm with a varying phase relationship through time. These suggest that inhibition within microcircuits competes with inhibition between them to determine the strength and phase relationships of rhythms. We now explore this trend across a broad range of connectivity levels.

First, we show how intra- and intergroup inhibition affect the synchrony in the two-population model. To quantify this, we compute the synchrony measures for each population separately (χ₁ and χ₂) and report the average χ = (χ₁ + χ₂)/2. Figure 6D shows the results. As intragroup inhibition k_intra increases, there is a degradation in synchrony. This is consistent with the results from the single-population model, where unstructured local inhibition reduces the strength and regularity of the population rhythm. Figure 6C gives an example of network activity in this regime and is indicated by a circle in Fig. 6, D–F. However, as we add inhibitory connections between the two populations by increasing k_inter, synchrony recovers: overall, we see stronger synchrony above the diagonal where k_inter = k_intra. Figure 6B, indicated by the star in Fig. 6, D–F, illustrates this. Overall, Fig. 6D suggests that intragroup inhibition destabilizes synchrony, while intergroup inhibition can have the opposite effect.

To drive breathing, in which each microcircuit presumably generates a different phase in a motor pattern, the model should produce two rhythms with reliable phase separation. To analyze this, we first compute a measure of the average, over time, of the difference between the phases of each microcircuit, which we call Φ. A value Φ = 1 or 0 indicates that the two rhythms are, on average, in phase, and Φ = 0.5 indicates the two rhythms are, on average, perfectly out of phase (see further details in Burst detection and phase analysis and Two-population phase analysis). Figure 6E shows that Φ ≈ 0.5 over the range of inhibitory connectivity. Thus the two microcircuits appear to be out of phase on average, regardless of connectivity. A glance back at Fig. 6, B and C, reveals that this out-of-phase behavior can arise in different ways: either for two reliable rhythms that are phase locked or for two unreliable rhythms that drift broadly with respect to one another over time. To quantify this difference, we use a phase order metric Ω (Two-population phase analysis), shown in Fig. 6F. Here, Ω = 1 indicates that the phase differences are completely repeatable over time, while Ω = 0 indicates phase differences are completely unreliable, instead being evenly spread over time. In agreement with the two cases illustrated in Fig. 6, B and C, as we increase the inhibition within microcircuits k_intra, phase reliability Ω decreases; conversely, increasing k_inter increases Ω.

These results lead to the important conclusion that it is not a particular number of inhibitory connections in a network that leads to a stable two-phase rhythm but instead the relative strengths of intra- and intergroup connectivity. For a stable two-phase rhythm, there need to be at least as many inhibitory connections between populations as within populations. The key rhythm metrics, synchrony χ and phase order Ω, demonstrate the same effect, because χ and Ω are strongly correlated. This makes sense because the rhythms are generated through synchronous bursting. Note that an irregularity score for the phase differences would yield similar results as Ω, but we prefer Ω since it takes into the account the circular structure of the phase variable. Increasing intragroup inhibition pushes the system to the edge of stability. However, we are able to recover some rhythm stability and phase separation reliability by increasing intergroup inhibition. In summary, we see the same desynchronizing effect of local inhibition as in the single-population model, with some benefit to synchronous rhythms possible from intergroup inhibition.

Partial Synchrony of in Vitro preBötC Rhythms in Multiarray Recordings

We now turn to experiments with the preBötC, to test the model predictions about the role of inhibition in such circuits. We recorded from mouse transverse brain stem slices containing the preBötC, keeping only those that initially exhibited robust rhythms. This yielded a collection of 17 recordings of the population rhythm using a large extracellular local field potential (LFP) electrode. Of these, four were simultaneously recorded with a linear electrode array to capture the behavior of multiple neurons (16, 29, 33, and 29 cells were isolated in individual experiments). From the multiarray data, we extracted individual spikes and calculated the synchrony metric χ as in the model.

Our experiments reveal that a fully synchronized network such as that in Fig. 1A is not realistic under our experimental conditions. This is because preBötC slices exhibit significant cycle-cycle variability (Carroll et al. 2013; Carroll and Ramirez 2013). So real networks are somewhere in the intermediate synchrony range. We confirmed this in multiarray in vitro experiments. An example experiment with 16 cells is shown in Fig. 7A. We observe that there is significant cycle-to-cycle period and amplitude variability in the rhythm, which is reflected in the partial synchrony of the 16 neurons recorded (χ = 0.57). With n = 4 multielectrode control experiments, we measured an average χ = 0.48 (SD 0.055).

Fig. 7.

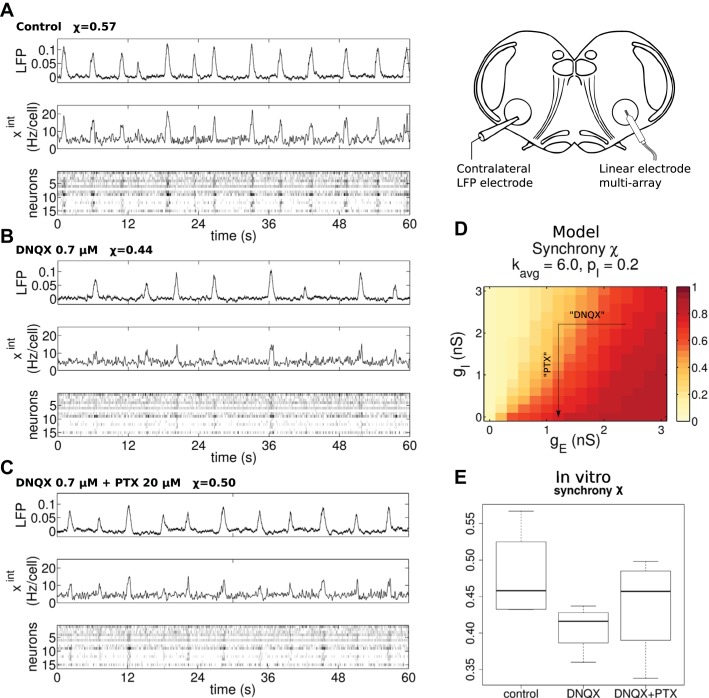
In vitro array recordings from transverse slice preparations exhibit partial synchrony. We performed in vitro preBötC slice experiments, where we measured the rhythm in control, partial excitation block (DNQX 0.7 μM), and partial excitation block with full inhibition block (DNQX 0.7 μM + PTX 20 μM). We recorded the preBötC population activity with a large electrode (LFP, arbitrary units) as well as individual neurons in the contralateral area with an array. The average activity of the isolated units is also shown (x_int, Hz/cell). A: control conditions show a robust population rhythm with some amplitude and period irregularity. B: partial excitation block with DNQX degrades the population synchrony, with decreased burst amplitude, slower rhythm, and more irregular intervals between bursts. C: blocking inhibition with PTX allows the rhythm to recover toward control conditions. D: synchrony in the model, as a function of excitatory and inhibitory synaptic conductances g_E and g_I, increases with stronger excitation and decreases with stronger inhibition, similar to varying connectivity k_avg and inhibitory fraction p_I. The arrow indicates the presumed effects of DNQX and PTX on the model. E: measurements of synchrony from our 4 array recording experiments. Synchrony takes intermediate values in all conditions, decreasing with DNQX and recovering after PTX.

The number of expiratory neurons observed in other experiments is also consistent with the degree of partial synchrony in the model. Multiarray recordings by Carroll et al. (2013) found 5.0% expiratory and 3.9% postinspiratory cells. Counted together, as we are doing, a realistic percentage of expiratory cells is 9%. Referring to Fig. 2A and Fig. 3B, we see that this occurs near the region where χ ≈ 0.6. This value is not far from the experimentally measured average χ = 0.48. However, we did not observe any expiratory cells in our limited set of four multiarray experiments, which is expected based on Carroll et al. (2013).

In Fig. 7, B and C, we also show the behavior of the slice under pharmacological manipulations of the efficacy of excitatory and inhibitory synaptic transmission, shown here for completeness and explored in more detail in Excitatory and Inhibitory Balance Modulates Rhythm Irregularity in Vitro and in Silico. Specifically, we use the glutamatergic antagonist DNQX and the GABA and glycine receptor antagonist PTX (Slice Experiments). After recording the control rhythm, we applied 0.7 μM DNQX to partially block excitation and observed the resulting rhythm. After recording in DNQX conditions, we followed with application of 20 μM PTX. The dosages are chosen so that DNQX partially blocks excitation (Honoré et al. 1988) but does not stop the rhythm, whereas the PTX dosage is high enough to effect near-complete disinhibition (see Fig. 1 in Othman et al. 2012). We see in Fig. 7B that DNQX leads to less synchrony and a visibly degraded, slower rhythm. Moreover, Fig. 7C shows that when this inhibition is reduced by adding PTX the rhythm recovers toward control values of frequency, amplitude, and synchrony.

When varying synaptic conductances in a simulation of the effects of DNQX and PTX, the computational model behaves as one might expect from our earlier results. We generated 8 networks with average degree k_avg = 6 and inhibitory fraction p_I = 20%. Then we varied the maximal conductances of excitatory and inhibitory synapses g_E and g_I while keeping the network structure fixed. We show the synchrony χ as a function of g_E and g_I in Fig. 7D. Increased g_E leads to enhanced synchrony, while, as expected from the results above, increased g_I desynchronizes the population. Thus once again we find that excitation synchronizes and inhibition desynchronizes activity within a microcircuit.

Finally, in Fig. 7E we summarize the synchrony χ across all four multiarray experiments and pharmacological conditions. Clearly, the networks are all partially synchronized. Synchrony χ decreases by ~0.07 (SE 0.02, DF 8, t = −3.414, P = 0.009) with DNQX, with a recovery to near baseline after PTX. These trends are shown in only three of four experiments, so we stress that this is marginally significant according to the mixed-effects model (see Table 2). We next show how proxies for the synchrony that measure regularity of the rhythm can be applied to our larger collection of LFP recordings to further illuminate this trend.

Table 2.

Statistical results for in vitro measurements of amplitude irregularity, period irregularity, amplitude, and period

	Fixed Effect	SE	DF	t Value	Pr(>|t|)
Amplitude irregularity
Intercept	0.197894	0.024664	24.63	8.024	2.48 × 10−8
DNQX	−0.016169	0.018067	34	−0.895	0.377
DNQX+PTX	−0.005418	0.018067	34	−0.3	0.766
Period irregularity
Intercept	0.21622	0.02627	30.38	8.23	3.14 × 10−9
DNQX	0.12076	0.02401	34	5.03	1.57 × 10−5
DNQX+PTX	0.031	0.02401	34	1.291	0.205
Amplitude mean, a.u.
Intercept	0.070486	0.009401	18.72	7.498	4.76 × 10−7
DNQX	−0.01134	0.003552	34	−3.192	0.00304
DNQX+PTX	−0.000614	0.003552	34	−0.173	0.86379
Period mean, s
Intercept	4.0594	1.0299	26.11	3.942	0.00054
DNQX	4.6371	0.8105	34	5.721	1.98 × 10−6
DNQX+PTX	1.9396	0.8105	34	2.393	0.02238
Synchrony χ
Intercept	0.47875	0.02506	6.497	19.104	5.94 × 10−7
DNQX	−0.0715	0.02094	8	−3.414	0.00917
DNQX+PTX	−0.04125	0.02094	8	−1.97	0.08439

The estimated fixed effect for the intercept, DNQX, and DNQX+PTX conditions, as well as standard error (SE), degrees of freedom (DF), t value, and P value for each effect are reported. These data summarize 17 LFP recordings except for the synchrony fit, which comes from 4 multielectrode recordings. a.u., Arbitrary units.

Excitatory and Inhibitory Balance Modulates Rhythm Irregularity in Vitro and in Silico

In Inhibition and Sparsity Weaken Model Rhythm, Inhibition Creates Expiratory Subpopulation, and Two-Population Network Shows Benefits of Half-Center Inhibition, we use a computational model to show how population rhythms depend on levels of inhibitory connectivity within and between microcircuits. We have demonstrated that in vitro preBötC networks are naturally in a partially synchronized state (Partial Synchrony of in Vitro preBötC Rhythms in Multiarray Recordings). We now investigate how in vitro preBötC rhythms behave under the modulation of synaptic conductances with pharmacological techniques. To quantify rhythm quality from the integrated LFP signal, available in all 17 of our recordings, we turn to amplitude and period irregularity. These measure the cycle-to-cycle variability of the sequence of burst amplitudes and interburst intervals (Irregularity scores; Carroll et al. 2013; Carroll and Ramirez 2013).

Our experiments use the synaptic antagonists DNQX and PTX to pharmacologically modulate the efficacy of excitatory and inhibitory synapses in vitro, analogous to lowering g_E and g_I, respectively. This is illustrated by arrows in Fig. 7D. In Fig. 8, we also illustrate the behavior of the amplitude and period irregularity scores in the model as g_E and g_I vary. Comparing Fig. 8 and Fig. 7D, it is apparent that both irregularity scores increase in the model as χ decreases. In the 13 experiments where we have only an LFP signal, this suggests that irregularity can stand in as a proxy for neuron synchrony, which we could only measure with multicell array recordings.

We plot in vitro irregularity across conditions in Fig. 8 with box plots. The results of statistical tests using a linear mixed-effects model are shown in Table 2. To summarize, amplitude irregularity shows no significant trends with the blocking of excitation via DNQX and inhibition via PTX. However, we noted a statistically significant increase (DF = 34, t = 5.03, P = 1.6 × 10−5) in period irregularity of ~0.12 (SE 0.02) after application of DNQX and subsequent decrease with PTX to near baseline. The qualitative effect on period irregularity matches trends present in the computational network model.

The model also predicts that there would be a slight decrease in irregularity with initial application of PTX after control, i.e., a variant of the previous protocol without DNQX. We performed limited experiments with varying doses of PTX and found some small decreases in period irregularity that were not significant (data not shown). However, it did appear that the more irregular control slices showed greater decreases in irregularity with application of PTX, as also would be expected from the model results in Fig. 8.

With regard to the lack of a trend in amplitude irregularity, we note that the “landscapes” of the amplitude and period irregularity scores produced by the computational model (heat maps in Fig. 8) show markedly different regions of high irregularity. In the amplitude irregularity case, the red region of high values is much wider than in the period irregularity case. For amplitude, it is shaped like a plateau rather than the steep slope of period irregularity. This suggests that amplitude irregularity is less sensitive to synaptic modulation, perhaps making trends harder to identify in pharmacological experiments. However, it could also be that bursting in the real preBötC is essentially an “all-or-nothing” phenomenon, with amplitude irregularity a result of noise but not strongly dependent on details of the burst dynamics, in contrast to the model we study. This would make it insensitive to blockers, since once a burst is triggered it is reliable and consistent, similar to the triggering of an action potential. This is interesting in the context of the burstlet hypothesis (Kam et al. 2013).

In Vitro Rhythm Slows After Excitatory Block

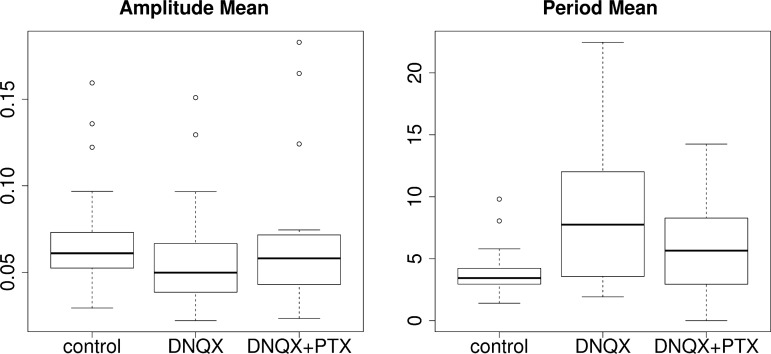
Besides variability, we found in experiments that synaptic blockers also significantly change the overall period and amplitude of rhythmic bursts, as shown in Fig. 9 and Table 2. Mean burst amplitude is decreased by −0.011 units (SE 0.004, DF = 34, t = −3.192, P = 0.003) after DNQX and recovers to baseline with application of PTX. This is consistent with the effect of varying g_E and g_I in the model. In experiments, we also see a significant slowing of the rhythm. The burst period increases with DNQX by 4.6 s (SE 0.81, DF = 34, t = 5.72, P = 2 × 10⁻⁶) and only partially recovers with application of PTX, remaining 1.9 s (SE 0.81, DF = 34, t = 2.39, P = 0.02) above baseline. As described above, while our network model qualitatively predicts the experimental trends for period variability and amplitude modulation in the isolated preBötC, it does not reproduce overall changes in burst period.

Fig. 9.

Effect of DNQX and PTX on in vitro rhythm amplitude and period, similar to Fig. 8. Amplitude decreases with DNQX while period increases, with both recovering to near baseline after addition of PTX. See Table 2 for the result of statistical tests on these data.

Simple modifications to the model capture the period slowing with excitatory blockers. Suppose each respiratory cell receives concurrent input from excitatory and inhibitory pools of tonic neurons (Ramirez et al. 1997b). These cells determine a baseline drive to the preBötC, which we model as a constant current I_app. Tonic external conductances $g_{\text{E}}^{\text{app}}$ and $g_{\text{I}}^{\text{app}}$ have the same effect but complicate our parameter tuning because of modification of the effective leak current. DNQX would then lower the excitatory drive, leading to decreased I_app. A negative drive current then slows the amount of time it takes a neuron to integrate to bursting, lowering the neuron’s intrinsic burst frequency. PTX, by lessening the influence of the inhibitory tonic pool, causes a net disinhibitory effect on the neuron, restoring I_app to near baseline. So far, we have taken I_app = 0 as the baseline, but these differential effects remain regardless of the baseline tonic current. Mimicking DNQX with I_app = −4 pA causes the period to approximately double (not shown but tested for k_avg = 6, p_I = 0.2, g_E = g_I = 3.0 in control, g_E = 1.8 under DNQX).

One consequence of this tonic pool hypothesis is that changing the baseline drive also changes the intrinsic dynamics of neurons. Increased hyperpolarization can cause tonic cells to become bursters and bursters to become silent in the absence of network effects. However, this can benefit synchrony, since when the large pool of originally tonic cells shift into bursting mode they can help maintain a strong rhythm despite the reduced excitatory synaptic drive. In a check for a few network structures, we found that the “main” effects of excitation and inhibition on rhythms persist when we also make these I_app changes.

To recap, our experimental results show that the control preBötC networks lie in the partially sychronized regime. The results also confirm that the relative balance of excitation and inhibition determines the level of synchrony and variability of the rhythm. In experiments, we also find a strong dependence of rhythm frequency on the amount of inhibition, and we have discussed changes to the model that could explain this effect.

DISCUSSION

Network Structure of Respiratory Areas

The preBötC contains neurons that are silent, tonic-spiking, or periodically bursting pacemakers (Peña et al. 2004; Ramirez et al. 2011; Thoby-Brisson and Ramirez 2001). Numerous models are proposed for the preBötC, at the level of single neurons with pacemaker dynamics (Best et al. 2005; Butera et al. 1999a; Park and Rubin 2013; Rubin et al. 2009a; Toporikova and Butera 2011) as well as networks of these neurons (Best et al. 2005; Butera et al. 1999b; Carroll et al. 2013; Carroll and Ramirez 2013; Gaiteri and Rubin 2011; Lal et al. 2011; Purvis et al. 2007; Rubin et al. 2009a, 2009b, 2011; Schwab et al. 2010; Wang et al. 2014). Traditionally, these models have consisted of just the excitatory, essential core of inspiratory neurons. However, Ramirez et al. (1997b) showed that inspiratory cells receive concurrent excitation and inhibition in the inspiratory phase during both in vitro and in vivo recordings from cat preBötC. Furthermore, Morgado-Valle et al. (2010) demonstrated the existence of glycinergic inspiratory pacemakers within preBötC, likely candidates for the inhibitory population presynaptic to those found by Ramirez et al. We have chosen to study the consequences of mixed excitatory and inhibitory cells in this network.

The details of network structure in the preBötC are currently unknown, and molecular markers for rhythmogenic neurons have been found only recently (Wang et al. 2014). Rekling et al. (2000) recorded from pairs of cells and estimated that 13% (3 of 23 pairs) were synaptically connected. However, the distance between the connected neurons of the three pairs is unknown. This, along with the small sample size, makes it difficult to know whether this connectivity is representative for the entire preBötC. Moreover, synaptic transmission was not entirely reliable. Thus the robustness of these excitatory connections is difficult to assess from those exceedingly difficult paired recordings. Hartelt et al. (2008) imaged the dendrites and axons of neurons in the area and found a network with spatially localized, modular structure similar to a small-world network. They estimated that average neuron degrees were between roughly 2 and 6 (Hartelt et al. 2008). Carroll and Ramirez (2013) recorded from in vitro slice preparations and argued for roughly 1% connectivity, using cross-correlation analysis of 10,778 pairs. The number of cells in the preBötC is estimated to be ∼300–600 (Feldman et al. 2013; Hayes et al. 2012; Wang et al. 2014; Winter et al. 2009), although this differs significantly from the estimate of 3,000 neurons by Morgado-Valle et al. (2010). This difference is mainly due to varying functional definitions of what constitutes a preBötC neuron. However, our results should not change much with the network size: Because we parametrize the connectivity by the average degree, the in-degree distribution and thus variability of input signal to a given neuron (proportional to $k_{\text{avg}}^{-1/2}$) will not change significantly.

The exact structure of the preBötC network remains debatable, but it appears clear that the connectivity is relatively sparse. Many original models of the isolated preBötC assume a fully connected network, i.e., a complete graph (Butera et al. 1999b; Purvis et al. 2007; Rubin et al. 2009b). Gaiteri and Rubin (2011) studied a variety of different topologies and their effects on the rhythm. Random graphs have recently become more popular (Carroll et al. 2013; Carroll and Ramirez 2013; Gaiteri and Rubin 2011; Lal et al. 2011; Schwab et al. 2010; Wang et al. 2014); however, only a few of these studies have looked at sparse random networks with average degree < 10 (Carroll et al. 2013; Carroll and Ramirez 2013). We believe this sparse regime is relevant to the irregularity observed in vitro (Carroll et al. 2013).

While a clustered connectivity may be present in the preBötC, where it would have profound effects on rhythm generation (Gaiteri and Rubin 2011), direct evidence for this is limited to the study of Hartelt et al. (2008). Furthermore, the preBötC is a bilateral rhythm generator, with each side coupled to the other principally by excitatory connections (Koizumi and Smith 2008; Lieske and Ramirez 2006), making the two-population model perhaps well suited for the preBötC. There is also evidence for excitatory connections between the expiratory and inspiratory centers (Huckstepp et al. 2015; Onimaru et al. 2009; Tan et al. 2010). We did try adding a few excitatory projections between the two populations, and in our model only a few projections will make the two centers synchronize. Having predominantly excitatory connections between bilateral preBötC areas could further stabilize the rhythm. However, we have chosen to first model the simpler, sparse but unstructured random connectivity as presented. We leave a full exploration of such effects to future work.

Rhythm Patterning by Inhibition

The neural circuits that drive respiration can generate basic rhythms through excitation alone, yet they also include strong inhibitory connections both within and between different microcircuits. Our aim here is to shine light on the role of this inhibition. Through modeling studies that explored thousands of network configurations, we show that inhibition plays two main roles in excitatory rhythm generators that depend systematically on the structure of the underlying connectivity. Unstructured local inhibition within a single excitatory microcircuit, as for our model of an isolated preBötC, destabilizes rhythmic bursting by preventing the synchronization of excitatory neurons. This is in contrast to the spiking models where inhibition facilitates synchrony and relevant, for example, in the gamma oscillation (Börgers and Kopell 2003). Within such a single microcircuit with sparse, random, and homogeneous connectivity, adding inhibitory cells does not create a robust two-phase rhythm (i.e., inspiration and expiration). However, such inhibition does explain the presence of expiratory cells as have been observed experimentally (Carroll et al. 2013; Nieto-Posadas et al. 2014). Our pharmacological experiments in the transverse preBötC slice also support the presence of local inhibition that is destructive to homogeneous synchrony: When we first partially block excitation and then inhibition, we see that levels of period irregularity first increase and then decrease.

The same qualitative effects of local inhibition persist in a two-population inspiratory-expiratory model, suggesting that the synchronizing and desynchronizing roles of excitation and inhibition within a population persist in more complicated systems. Moreover, long-range inhibition between excitatory microcircuits both stabilizes rhythms locally (reflected in their synchrony) and enforces reliable phase separation between microcircuits (phase order), reminiscent of the concept of the half-center (Brown 1911; Sharp et al. 1996; Stuart and Hultborn 2008) This suggests twin roles for inhibition: Within a single microcircuit, it reduces synchrony and introduces some out-of-phase cells; between populations, it facilitates partitioning of the overall rhythm into different phases. As such, inhibition balances against excitation in a way that depends on the overall connectivity of the network.

How strongly do the twin roles for inhibition play out in biological circuits for breathing? Anatomical studies have suggested substantial inhibition within microcircuits, and recordings have shown some cells with expiratory or postinspiratory firing within the predominantly inspiratory preBötC (Carroll et al. 2013; Morgado-Valle et al. 2010; Nieto-Posadas et al. 2014). Intriguingly, our model predicts that the level of local inhibition that is consistent with these observations moves the circuits as a whole toward the boundary between ordered, synchronous and disordered, asynchronous activity. This could be useful for making the network more sensitive to control signals. For instance, descending excitatory inputs that selectively target the inhibitory population could lead to pauses in the rhythm.

This frames two questions: First, what constructive role could such destabilizing inhibition play? Possibly, it could produce a rhythm that has a particular temporal pattern (e.g., ramping) or that could be more flexibly controlled. Second, what role might destabilizing inhibition play in disease states in which rhythms within and between respiratory and other centers degrade?

Physiological studies suggest interesting answers to the first of these questions. Local inhibition within the preBötC has a critical role in shaping the inspiratory pattern (Janczewski et al. 2013; Sherman et al. 2015), as our modeling study also shows. One of the hallmarks of “eupnea” or normal breathing is an augmenting ramplike inspiration that is lost when inhibition is blocked in the isolated preBötC (Lieske et al. 2000). Characterizing the synaptic profile of inspiratory neurons reveals the presence of concurrent inhibition and excitation that likely prevent an effective synchronizing between the excitatory neurons, thereby slowing down the buildup of inspiratory activity. Indeed, we hypothesize that the presence of a local, desynchronizing role of inhibition within the preBötC could also explain an ongoing debate in the field of respiration, i.e., why an isolated preBötC can generate a eupnea-like inspiratory activity pattern in the absence of the other phases of respiratory activity (Lieske et al. 2000; Ramirez and Lieske 2003). The augmenting inspiratory discharge in the isolated preBötC is very sensitive to the blockade of inhibition. In hypoxia, when synaptic inhibition is suppressed, the desynchronizing effect of local inhibition is lost and the isolated preBötC generates an inspiratory burst that is characterized by a fast rise time reflective of a facilitated synchronization. However, the Butera model we implemented does not exhibit these rise time effects at the single-cell level. Instead, the behavior only becomes evident in the population because of the misalignment of individual neuron bursts, and this overall effect is quite weak (data not shown). It is likely that other currents are important for the individual burst characteristics and that future models including these will provide further evidence for a role for local inhibition in shaping inspiratory bursts.

Limitations of Study

There was considerable variability in the control rhythms and the responses to drugs. We believe this is principally due to intrinsic variability of the preBötC network structure across mice, the slicing procedure, which damages the network to varying degrees, and the moderate dose of DNQX. The multielectrode recordings captured between 16 and 33 units. This small sample of cells contributes significant variance to our synchrony measure χ, and we believe this is why we cannot see a significant effect on synchrony. We placed the electrode array where we could record from many inspiratory cells; however, we also found almost as many tonic cells. It is possible that these are cells that are not integrated into the network and therefore could bias χ to lower values. In future work, it would be important to see whether the rhythm also degrades with inhibitory agonists, e.g., muscimol (see Janczewski et al. 2013). However, agonists introduce a tonic input that is rather different from modifying the synaptic efficacies; thus they will have a different effect than antagonists or optogenetic stimulation.

Our slice experiments showed a slowing down with excitation block and no statistically significant variation in amplitude irregularity, both in contrast to the model. Other membrane currents may explain these salient features of our pharmacological studies. We proposed that tonic populations could drive the change in frequency. However, the calcium-activated nonspecific cation (CAN) current is another likely candidate. Since CAN-dependent pacemakers can rely on accumulation of excitatory synaptic events to initiate bursting (Del Negro et al. 2010; Rubin et al. 2009a), excitatory synaptic block will slow this accumulation, leading to an increase of the rhythm period. This mechanism would be similar to the synaptic integrator model of Guerrier et al. (2015), which reproduced the period effects of NBQX (similar to DNQX). As mentioned above, the CAN current is also probably important for generation of augmenting, ramping discharges. Our model excluded CAN for simplicity and because the vast majority of respiratory models use the Butera et al. (1999a) persistent sodium equations. Also, it appears that cadmium-sensitive intrinsic bursting neurons (presumably the same as CAN dependent) are only a minority of the respiratory neurons in the preBötC (Peña et al. 2004). Hayes et al. (2008) present evidence that a low-threshold, inactivating K⁺ current I_A is present in preBötC neurons and significantly affects rhythmogenesis. They conclude that I_A helps control amplitude and frequency irregularity by preventing or delaying those neurons from responding without massive excitatory input. Beyond irregularity, I_A and I_CAN are also important for overall burst shape, duration, interspike intervals, burstiness, etc., which are interesting topics for future study. Finally, synaptic delays can be very important determinants of synchronization strength and phase relationships (Brunel and Hakim 1999). Future models will need to investigate how these many currents interact with excitatory and inhibitory synaptic dynamics in rhythm generation.

Conclusions

Our results contribute to a large body of modeling and experimental work in the field. Because local inhibition has a desynchronizing role, the preBötC cannot generate a two-phase rhythm, consistent with lesioning experiments performed by Smith et al. (2007). Multiarray recordings from >900 neurons that indicate that <9% of the neurons in the preBötC are expiratory (Carroll et al. 2013) also support this finding. Moreover, our modeling study also provides theoretical support for the respiratory network organization recently proposed by Anderson et al. (2016). They propose that each phase of the respiratory rhythm is generated by its own excitatory microcircuit located in a different region of the ventral respiratory group, the inspiratory phase being generated by the preBötC, postinspiration by its own complex (the PiCo) (Anderson et al. 2016), and active expiration by the so-called lateral parafacial/retrotrapezoidal group (Huckstepp et al. 2016; Janczewski and Feldman 2006; Onimaru et al. 2009). This idea is similar in spirit to the microcircuit models of Smith et al. (2013), Molkov et al. (2013), Koizumi et al. (2013), and Onimaru et al. (2015), which contain more areas. However, each of these excitatory microcircuits contains neurons with different anatomical, physiological, and modulatory properties, and each is dependent on excitatory synaptic transmission, able to generate rhythmicity in the absence of synaptic inhibition (Ramirez et al. 2016). Overall, a modular organization of rhythm-generating networks has both evolutionary (Ramirez et al. 2016) and functional implications; the latter may explain, for example, why we can hop on one leg without requiring a major network reconfiguration. We hypothesize that the separation of a rhythmic behavior into several excitatory microcircuits may indeed be dictated by the architecture of these sparsely connected excitatory networks that generate rhythmicity based on excitatory synaptic mechanisms. The addition of local inhibition to each microcircuit adds another layer of complexity to the generation of rhythms that can affect synchrony and controllability. The lessons learned from the respiratory circuit may also apply to networks that generate locomotion or other rhythmic behaviors, where each phase may be composed of separate microcircuits that are interacting with inhibitory connections.

GRANTS

K. D. Harris was supported by a Boeing fellowship and a National Institutes of Health (NIH) Big Data for Genomics and Neurosciences Training Grant. J. Mendoza was supported by a postbaccalaureate fellowship from the University of Washington Institute for Neuroengineering. J.-M. Ramirez, A. J. Garcia III, J. Mendoza, and T. Dashevskiy were supported by NIH Grants R01 HL-126523 and P01 HL-090554. We also acknowledge support of National Science Foundation Career Award DMS-1056125 to E. Shea-Brown and NIH Grant F32 HL-121939 to T. Dashevskiy.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

K.D.H., T.D., J.M., A.J.G., J.-M.R., and E.S.-B. conceived and designed research; K.D.H., T.D., J.M., and A.J.G. performed experiments; K.D.H., T.D., J.M., and A.J.G. analyzed data; K.D.H., T.D., J.M., A.J.G., J.-M.R., and E.S.-B. interpreted results of experiments; K.D.H., T.D., and J.M. prepared figures; K.D.H., T.D., and J.M. drafted manuscript; K.D.H., T.D., J.M., A.J.G., J.-M.R., and E.S.-B. edited and revised manuscript; K.D.H., T.D., J.M., A.J.G., J.-M.R., and E.S.-B. approved final version of manuscript.