Nonlinear Actin Deformations Lead to Network Stiffening, Yielding, and Nonuniform Stress Propagation

Abstract

We use optical tweezers microrheology and fluorescence microscopy to apply nonlinear microscale strains to entangled and cross-linked actin networks, and measure the resulting stress and actin filament deformations. We couple nonlinear stress response and relaxation to the velocities and displacements of individual fluorescent-labeled actin segments, at varying times throughout the strain and varying distances from the strain path, to determine the underlying molecular dynamics that give rise to the debated nonlinear response and stress propagation of cross-linked and entangled actin networks at the microscale. We show that initial stress stiffening arises from acceleration of strained filaments due to molecular extension along the strain, while softening and yielding is coupled to filament deceleration, halting, and recoil. We also demonstrate a surprising nonmonotonic dependence of filament deformation on cross-linker concentration. Namely, networks with no cross-links or substantial cross-links both exhibit fast initial filament velocities and reduced molecular recoil while intermediate cross-linker concentrations display reduced velocities and increased recoil. We show that these collective results are due to a balance of network elasticity and force-induced cross-linker unbinding and rebinding. We further show that cross-links dominate entanglement dynamics when the length between cross-linkers becomes smaller than the length between entanglements. In accord with recent simulations, we demonstrate that post-strain stress can be long-lived in cross-linked networks by distributing stress to a small fraction of highly strained connected filaments that span the network and sustain the load, thereby allowing the rest of the network to recoil and relax.

Introduction

Biological cells exhibit a myriad of complex nonlinear responses to stress or strain, exhibiting stress stiffening and softening, viscous flow, elastic recovery, creep, and plastic deformation, depending on the nature of the applied stress. This wide range of response behaviors results in part from semiflexible actin networks that pervade the cytoskeleton, providing the cell with tensile strength while allowing for morphological changes during cell motion, replication, division, and aptosis (1, 2, 3). A host of actin-binding proteins (ABPs) present in the cell result in cross-linked actin networks that range from isotropically connected, to heterogeneous and highly bundled, depending on the length and concentration of actin filaments and ABPs (4, 5, 6). Cross-linked actin networks also play a principal role in the mechanics and morphology of the extracellular matrix (7), cortex (8), and mitotic spindles (9, 10). Motivated by such physiological significance and spatiotemporal complexity, the mechanical response of in vitro cross-linked actin networks have been extensively studied and remain a topic of debate (1, 11, 12, 13, 14, 15, 16, 17, 18).

Cross-linked actin networks display wide-ranging mechanical responses resulting in part from varying sizes and densities of both ABPs and actin filaments, as well as the compliance and binding affinity of the ABPs and actin filaments (13, 14, 19). Further, the mechanical response has been shown to be highly dependent on the length and timescale of the applied strain and measurement (1, 13, 15, 20, 21, 22, 23). While extensive rheological measurements at both the microscopic and macroscopic scales have been carried out on cross-linked actin networks (24, 25, 26), previous experimental and theoretical work probing the microscale response has been restricted to the linear response limit of small forces and perturbations (20, 21, 27, 28). Thus, the nonlinear response of semiflexible networks and gels at the microscale remains largely unexplored. While several studies have investigated the nonlinear response of cross-linked networks at the macroscale, it has been well established that the microscale response of semiflexible networks is distinct from that at the macroscale, and that the deformations and mobility of single or several filaments does not reflect the macroscopic network response (17, 29, 30, 31, 32). Thus, understanding the nonlinear mechanical response of actin networks at the microscale; the filament motions and deformations that give rise to this response; and how such response propagates to the mesoscopic and macroscopic scales, remain important unanswered questions.

While cross-linked networks display a predominantly elastic response, nearly all networks exhibit some degree of relaxation and fluidity (13, 16, 19, 33). Networks of sterically entangled actin can relax via several mechanisms unique to semiflexible polymers such as bending, stretching, retraction of filament ends, and chain disentanglement (34, 35, 36). However, many of these relaxation mechanisms, most notably disentanglement, are limited in cross-linked networks as many of the molecular crossings are permanent chemical actin-ABP bonds rather than purely steric interactions. Therefore, the source of relaxation in cross-linked networks remains a topic of debate, with studies suggesting the source to be ABP unbinding, cross-link slippage, filament buckling, rupture, or turnover due to treadmilling (16, 26, 37, 38). Previous experimental and theoretical studies have shown that the mechanical response of networks cross-linked with ABPs such as heavy meromyosin (HMM) and α-actinin are controlled principally by dynamic ABP unbinding/rebinding, in contrast to cross-linking with scruin, fascin, and epsin in which the response is dominated by filament buckling and rupture (39, 40). Further, larger and more compliant cross-linkers such as filamin lead to a mechanical response that is dominated by the flexibility of the ABP rather than actin (40, 41). While concentrated cross-linked networks will indeed be influenced by both entanglements and cross-links, at high enough cross-linker ratio (short enough cross-linker length l_c), the dynamics will be governed by the cross-linker length rather than the length between entanglements l_e. Previous experiments on actin cross-linked with HMM reported that the transition between cross-link dominated to entangled dynamics in the linear regime occurred at l_c < 15 μm (comparable to the persistence length of actin l_p ≃ 17 μm) (19, 25). However, the extension of this crossover length scale to the nonlinear regime, in which filaments are deformed far from equilibrium, remains unknown.

Related topics of debate are how applied stresses propagate or distribute throughout cross-linked networks, and the nature of filament and network deformations that give rise to this distribution. While several studies have suggested that stress is distributed evenly throughout the network due to unbinding and rebinding events and reorganization (40, 42, 43, 44, 45), recent studies have also suggested that the stress distribution is highly nonuniform, with the stress being maintained by only a small fraction of the highly strained connected filaments that span the network, with the remainder of the network able to relax (43, 46, 47, 48). Further, induced strains in cross-linked networks are presumed to be affine (uniform) collective deformations at the macroscopic scale, which result in stress-stiffening behavior. However, it has been shown that below a critical strain, γ_c ≃ (l_cl_p)/6, and length scale λ ≃ (l_cl_p)^1/2 (∼10⁻³ and ∼1 μm for the systems under consideration) (49), deformations become nonaffine and heterogeneous, and stress curves exhibit softening rather than stiffening (22, 44, 45, 50, 51). While it is well established that most cross-linked actin filaments display nonlinear stress stiffening followed by softening, the molecular mechanisms that lead to this signature nonlinear elasticity remain debated. Stiffening has been suggested to arise from suppressing bending modes as the filaments extend to align with the strain, as well as from increasing tension as the filaments are stretched by the strain, with the relative contributions from each depending on the ratio of l_c and the polymer bending length scale l_b (∼2.3 nm for actin (44, 49)). For l_b/l_c ≪ 1, bending modes are predicted to dominate and deformations can lead to percolating stress paths, while for l_b/l_c ≃ 0.1, filament stretching and more uniform stress distribution is predicted as bending between cross-links becomes more energetically costly (46, 52). As l_b/l_c approaches 1, stiffening is delayed and suppressed due to the transition from a bending-dominated to a stretching-dominated regime (46). While stiffening has typically been coupled with collective affine network deformations (44, 45, 51), recent simulations have shown that stiffening can arise from discrete highly strained stress paths (i.e., percolating paths of stressed filaments) that are not reflective of the rest of the network, which relaxes its induced stress (43, 46, 47). Further, stiffening has been reported to increase, decrease, or stay the same as l_c is increased depending on the system and the scale of the strain (46, 53).

On the other hand, entangled and weakly cross-linked actin networks have typically only exhibited softening and nonaffine deformation due to allowed bending modes and retraction of free filament ends dominating the stress response (28). Softening, and ultimately yielding, can also arise from stress-alleviating network reorganization on the timescale of the strain, due to intrinsic relaxation mechanisms or strain-induced network breakup (34, 54, 55, 56, 57).

However, our previous nonlinear microrheology measurements have shown that the response of entangled actin at high enough concentrations (c_c > 0.4 mg/mL) is similar to that of cross-linked networks at the microscopic scale when subject to fast enough strain rates (${\dot{\gamma }}_c$ > 3 s⁻¹) over large enough distances (10 μm) (23, 30). Specifically, entangled actin exhibited stress stiffening coupled with filament deformation that was principally affine (in the direction of the strain). However, these key nonlinear features, which arise from spatially varying filament deformations, were only apparent for filaments within ∼l_p of the strain path, decaying to collective linear behavior at larger length scales.

These findings motivate the question as to how chemically cross-linked networks respond to nonlinear microscale strains. Are entangled networks able to mimic all features of cross-linked networks at small enough length scales for large enough strains? Or are there signature features that emerge that distinguish entangled and cross-linked networks, and if so what is the degree of cross-linking necessary to invoke these changes? This work also aims to address the important questions outlined above. Specifically, what is the source of nonlinear stress relaxation of cross-linked actin networks at the microscale, what filament deformations and motions lead to this signature relaxation, and how is stress propagated in this nonlinear regime?

We use optical tweezers to drag a microsphere probe 10 μm at a constant rate through entangled actin networks of varying ABP/actin ratios R = 0–0.07 and measure the force the network exerts to resist the strain. We subsequently hold the trapped probe fixed following the strain and measure how the built-up force evolves or relaxes over time. Simultaneously, we track fluorescent-labeled segments of actin filaments in the network to determine the underlying filament and network deformations that give rise to the stress response and how stress propagates from segment to segment through the network from the site of the microscale strain. To focus on the response of isotropic networks and the mechanics arising exclusively from actin properties and dynamics, we use biotin-NeutrAvidin as our ABP, which is a small, rigid, and nearly permanent cross-linker. We solely probe R values high enough to measure an appreciable difference from R = 0 (R = 0.01) but low enough to not induce bundling (R = 0.07). We fix the actin concentration (c = 0.5 mg/mL) and strain rate ($\dot{\gamma }$ = 7.5 s⁻¹) to be higher than the concentration (c_c) and strain rate $\left({\dot{\gamma }}_c\right)$ necessary for the onset of microscale nonlinear response in entangled actin networks. Thus, measurements directly investigate the dependence of these nonlinear features on cross-linking.

Materials and Methods

Lyophilized unlabeled (A), biotinylated (BA), and Alexa-568-labeled (FA) rabbit skeletal muscle globular actin (G-actin) purchased from Cytoskeleton (AKL99, AB07) and Invitrogen (A12374), respectively, were resuspended to concentrations of 2 mg/mL (A), 1 mg/mL (BA), and 1.5 mg/mL (FA), respectively, in Ca Buffer G (2 mM Tris pH 8.0, 0.2 mM ATP, 0.5 mM DTT, 0.1 mM CaCl₂) and stored at −80°C. Labeled actin segments for tracking were assembled as described in Falzone and Robertson-Anderson (30). Briefly, an equimolar mixture of A and FA was polymerized at 5 μM for 1 h in F-buffer (10 mM Imidazole pH 7.0, 50 mM KCl, 1 mM MgCl₂, 1 mM EGTA, 0.2 mM ATP). Filaments were then sheared through a 26 s gauge Hamilton syringe and immediately mixed with 100% unlabeled actin of the same concentration (5 μM) to form actin filaments with interspersed labeled and unlabeled segments (Fig. 1). Cross-linked actin networks were formed by polymerizing actin to 0.5 mg/mL with variable concentrations of preassembled BA-NeutrAvidin complexes with a twofold molar excess of BA to NeutrAvidin (i.e., BA:NA = 2:1). The molar ratio of NA to actin spans a range of R = 0–0.07 to create networks with average filament lengths between cross-linkers of l_c = l_mon × R⁻¹ = 0.1–0.7 μm, where l_mon ≃ 7 nm is the size of each actin monomer. Carboxylated polystyrene microspheres of diameter a = 4.5 μm (probes; Polysciences, Warminster, PA) were labeled with Alexa-488 BSA (Invitrogen, Carlsbad, CA) to inhibit interaction with the actin network (58) and visualize the probes during measurement. Actin networks for experiments were generated by mixing preassembled discretely labeled actin filaments, unlabeled G-actin, BA:NA cross-linker complexes, and probes in F-buffer for a final actin concentration of 0.5 mg/mL, corresponding to a mesh size of ξ ≃ 0.4 μm and a length between entanglements of l_e ≃ 0.9 μm. The mixture was quickly pipetted into a sample chamber made from a glass slide and coverslip, separated ∼100 μm by double-sided tape. It was then sealed with epoxy and allowed to polymerize and cross-link for 1 h before measurement.

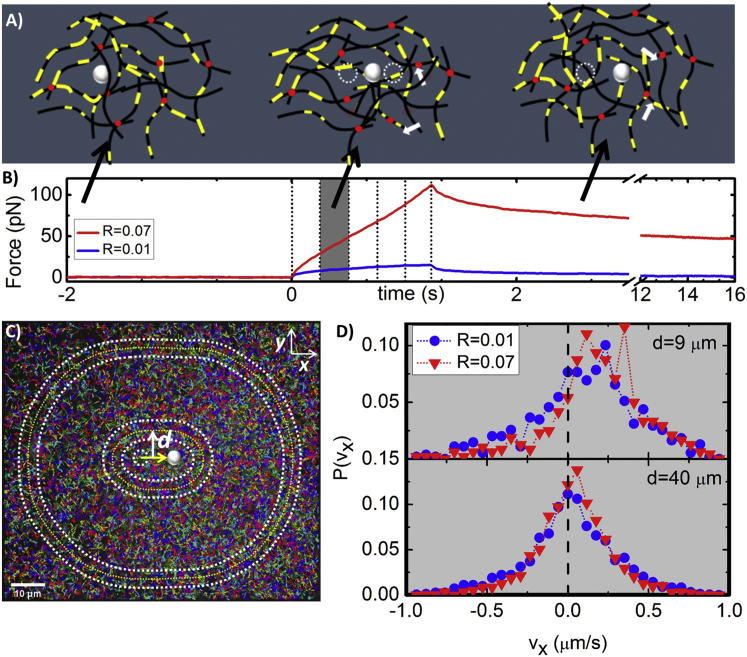
Figure 1.

Schematic of coupled microrheology and particle-tracking experiments. (A) Cartoon of an actin network cross-linked by NeutrAvidin (red dots) and doped with filaments with interspersed labeled segments (yellow) for tracking. Three phases of experiments shown: equilibration (no trap movement), strain (middle, trapped probe (white) moves 10 μm through the network at 8 μm/s), and relaxation (no trap movement, probe remains trapped). White arrows show unbinding/binding of NeutrAvidin during the strain/relaxation phases. (B) Measured force traces for networks with R = 0.01 and 0.07 during three experimental phases. Dashed lines during strain phase indicate the times at which images of labeled filaments are captured. Highlighted region corresponds to time depicted in (D). (C) Sample 122 × 140 μm image displaying all filament tracks (rainbow colors) measured for 85 individual measurements. Data for R = 0.07 is shown. Image is sectioned into concentric annuli, each 4.5 μm wide, with increasing radii d centered on the center of the strain path. (D) Probability distributions of tracked particle velocities parallel to the strain P(v_x) at a single window of time (highlighted in B) for R = 0.01 and 0.07 networks. Distributions for annuli near (d = 9 μm, top) and far (d = 40 μm, bottom) from strain path are shown. To see this figure in color, go online.

The optical trap used in measurements was formed by outfitting a model No. IX71 fluorescence microscope (Olympus, Melville, NY) with a 1064 nm Nd:YAG fiber laser (Manlight, Lannion, France) focused with a 60× 1.4 NA objective (Olympus). A position-sensing detector (Pacific Silicon Sensor, Westlake Village, CA) measured the deflection of the trapping laser, which is proportional to the force acting on the trapped probe over our entire force range. The trap stiffness was calibrated via Stokes drag in water (59) and passive equipartition methods (60). During measurements, a probe embedded in the network is trapped and moved 10 μm at a constant speed of $v=8$ μm/s relative to the sample chamber via steering of a nanopositioning piezoelectric mirror (Physik Instrumente, Auburn, MA), while measuring both the laser deflection and stage position at a rate of 20 $\text{kHz}$ during the three phases of experiment: equilibration (5 s), strain (1.6 s), and relaxation (15 s) (Fig. 1). The probe speed, corresponding to a strain rate of $\dot{\gamma }=3\times \sqrt{2}v/a$ = 7.5 s⁻¹ (61), is $2.5{\dot{\gamma }}_c.$ Displayed force curves are averages of 50 trials using 50 different probes each at different locations in the sample chamber. Drift in force measurements over the time course of the experiment, due to instrument and sample drift, were measured to be <1 pN.

To track labeled filament segments during and following the strain, 122 × 140 μm images were recorded at 2.5 fps with an ORCA flash 2.8 CMOS camera (Hamamatsu, Hamamatsu City, Shizuoka, Japan). Each image contained ∼1.5 × 10⁴ labeled segments and all tracking data shown is a result of ∼85 videos for each condition. The custom particle-tracking code used was based on the MATLAB (The MathWorks, Natick, MA) implementation of Crocker and Weeks’ (62) particle tracking algorithms that obtains the position of each labeled segment and links those positions into tracks in time. To determine the dependence of filament velocities and displacements on distance from the applied strain d, we constructed concentric annuli, each 4.5 μm wide, with increasing radii centered on the center of the strain path (Fig. 1 C). For each annulus, we calculated the velocity distribution and ensemble-averaged velocity of tracked segments in the x and y directions ($\langle v_x\rangle ,$ $\langle v_y\rangle$). We also quantified ensemble-averaged filament displacements ($\langle x\rangle ,$ $\langle y\rangle$) by integrating $\langle v_x\rangle$ and $\langle v_y\rangle$ over time. Filament drift over the time course of the experiment was measured to be <50 nm. All presented data is for $\langle v_x\rangle$ and $\langle x\rangle$ as all $\langle v_y\rangle$ and $\langle y\rangle$ measurements were within the Brownian noise of ∼63 nm, quantified by the average track length per frame during the equilibrium phase. We tested many geometries over which to average filament velocities and displacements, including angular and Cartesian segments. This analysis showed that filament velocities depended most strongly on radial distance d from strain, so all presented data is for filament ensembles within annuli of varying radii d centered on the strain path. For reference, we show in Fig. S1 in the Supporting Material the angular dependence of $\langle x\rangle$, which shows that filament displacements vary by a factor of ∼2 as a function of angle with the maximum displacements at the trailing edge of the strain and the minimum displacement perpendicular to the strain path. However, this angular dependence showed no dependence on the degree of cross-linking so is not included in the discussion and interpretation of our results. To clearly demonstrate the complete spatial dependence of filament trajectories, we also constructed filament displacement vector maps that show the spatially resolved filament displacements during strain and relaxation (Fig. S2).

Confocal imaging of networks was also carried out to confirm network structure and morphology. As shown in Fig. 2, all networks are largely homogeneous with minimal bundling. Images also show that as R increases network mobility decreases and connectivity increases.

Figure 2.

Steady-state network morphology and structure show decreased mobility and increased connectivity of actin networks with increasing R. Images shown are a collapsed time-series of networks taken on an A1R confocal microscope with a 60× objective (Nikon, Melville, NY). Each image is a sum of 2700 frames captured over 3 min (15 fps). 1% of actin filaments in the network are labeled with Alexa-568 to resolve network and filament structure and dynamics. As shown, as R increases, the time-averaged images have more contrast and less Brownian noise demonstrating that filament mobility is suppressed as R increased. Images also demonstrate that all networks are largely homogeneous. Zoomed-in network images in insets show network architecture at the scale of single filaments. Note that minimal bundling is observed.

Results

All presented data is for pulling a probe of diameter a = 4.5 μm a distance x = 10 μm through actin networks that have a mesh size of ξ ≃ 0.4 μm, a length between entanglements of l_e ≃ 0.9 μm, and cross-linker lengths of l_c ≃ 0.1–0.7 μm. Thus, the probe is continuously in contact with a/ξ ≃ 11 network segments, a/l_e ≃ 5 entanglements, and a/l_c ≃ 6–45 cross-links. During each strain, the probe passes through x/ξ ≃ 23 network segments, x/l_e ≃11 entanglements, and x/l_c ≃ 14–100 cross-links. While the perturbation is localized to several microns, because of the many interactions with the network and the fast strain rate $\left(2.5{\dot{\gamma }}_c\right)$, we expect the strain to be able to disrupt the network and induce possible breakup and plastic reorganization if mechanisms for such dynamics exist.

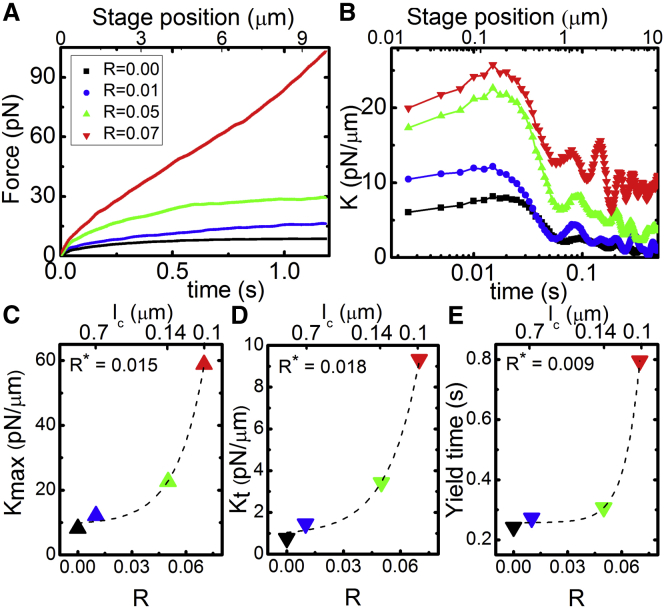
We first characterize the force exerted on the probe and the corresponding filament motions during strain. As shown in Fig. 3, both the magnitude and slope of the induced force increase substantially with increasing R over the entire strain path. While the force response has both viscous and elastic components, we keep the strain rate fixed in all measurements so we expect variations in the viscous (rate-dependent) response to be negligible compared to response variations arising from the elastic component. To quantify the apparent R-dependent elasticity, we evaluate how the differential modulus (K = dF/dx) evolves during strain. We find that all networks exhibit stress stiffening (dK/dt > 0) at short times (t < 0.01 s), followed by softening (dK/dt < 0) and yielding to a steady-state regime over a timescale of t_y ≃ 0.5 s. This signature nonlinear response (i.e., stress stiffening followed by softening) has been reported in a number of studies on cross-linked actin networks, most of which attribute softening to cross-linker unbinding (12, 42, 43, 48, 63). During the stiffening phase, the probe has only moved a fraction of the mesh size (0.08 μm ≃ ξ/5). However, because the probe itself is ∼10ξ, even for displacements <ξ it is still appreciably interacting with the network. Further, the stiffening timescale is comparable to the fastest predicted relaxation timescale for entangled actin, namely the time for length scales comparable to the mesh size (ξ ≃ 0.4 μm for all networks) to relax (29, 36). This mesh time, τ_mesh, is the time it takes for hydrodynamic interactions between filaments to become important (i.e., for each filament to feel the network). The maximum stiffness achieved (K_max) roughly follows an exponential function of R (K_max ∼ exp(R/R^∗)) (Fig. 3 D). Previous studies on HMM-cross-linked actin networks and biotin-cross-linked microtubule networks have similarly reported substantial increase in K_max with increasing R (12, 42). These studies attribute the R dependence to the need to break more cross-linker bonds to enable softening as R increases. The terminal steady-state K value (K_t), as well as the timescale over which the network yields to the terminal regime (yield time, t_y), also both exhibit a similar dependence on R (Fig. 3). Thus, while K softens to a principally viscous terminal regime (K ≃ 0) for the network with no cross-links, the terminal force response becomes exponentially more elastic as R increases. The average R^∗ value for all three quantities is R^∗ ≃ 0.014, corresponding to a cross-linking length of l_c ≃ 0.50 μm, which is smaller than, but quite close to, the predicted entanglement length l_e ≃ 0.9 μm of the network (29).

Figure 3.

Viscoelastic response of actin networks with varying degrees of cross-linking (R = 0–0.07). (A) Average force exerted by actin networks to resist probe motion. (B) Elastic differential modulus K as a function of time as obtained from the derivative of the force in (A) with respect to stage position. All data shows initial stiffening to a maximum value (K_max) before softening and yielding to a terminal steady-state stiffness/elasticity (K_t). (C) Maximum differential modulus (K_max) follows an exponential function K_max ∼ exp(R/R^∗) with a critical cross-linking ratio of R^∗ ≃ 0.015. (D) Terminal modulus K_t versus R increases exponentially with R with R^∗ ≃ 0.018. (E) Yield time, t_y, defined as the time at which K(t) = K(0)/2e, displays a similar exponential dependence on R with R^∗ ≃ 0.009. To see this figure in color, go online.

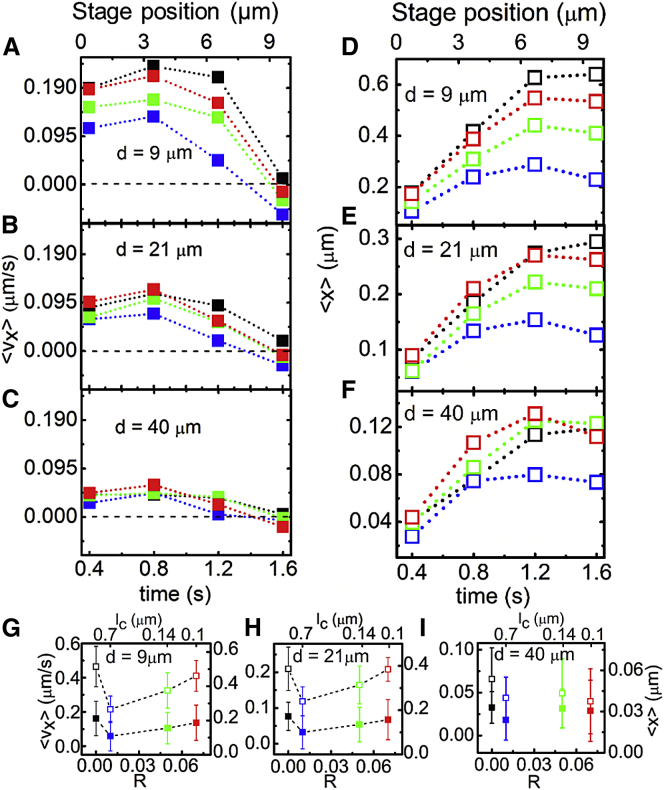
To elucidate the filament and network deformations responsible for the observed stress response, we evaluate the corresponding ensemble-averaged velocities ($\langle v_x\rangle$) and displacements ($\langle x\rangle$) of filament segments at four different time points during the strain and for varying distances from the strain path. As shown in Fig. 4, despite the constant-rate applied strain, the filament strain is highly nonlinear and thus can inform the nonlinear stress response. For all networks, filaments initially accelerate in the direction of the strain up to t ≃ 0.5 s ≃ t_y, after which all filaments exhibit deceleration and eventual halting, with cross-linked networks even displaying varying degrees of recoil.

Figure 4.

Ensemble-averaged velocities $\langle v_x\rangle$ and displacements $\langle x\rangle$ of actin filaments during strain for networks with varying cross-linking ratios R. Ensemble-averaged velocities (A–C) and displacements (D–F) at four different time points during the 1.6 s strain (0.4, 0.8, 1.2, 1.6 s) and for varying distances d from the strain path: (A and D) d = 9 μm, (B and E) d = 21 μm, and (C and F) d = 40 μm. Time-evolution of velocities and displacements show filament acceleration followed by deceleration, halting, and recoil dependent on R and d. (G–I) Time-average of $\langle v_x\rangle$ (solid symbols) and $\langle x\rangle$ (open symbols) values depicted in (A)–(F) versus cross-linker ratio R for varying distances d from the strain path. The nonmonotonic dependence of filament mobility on R, described in the text, is shown by the dashed lines in (G) and (H). To see this figure in color, go online.

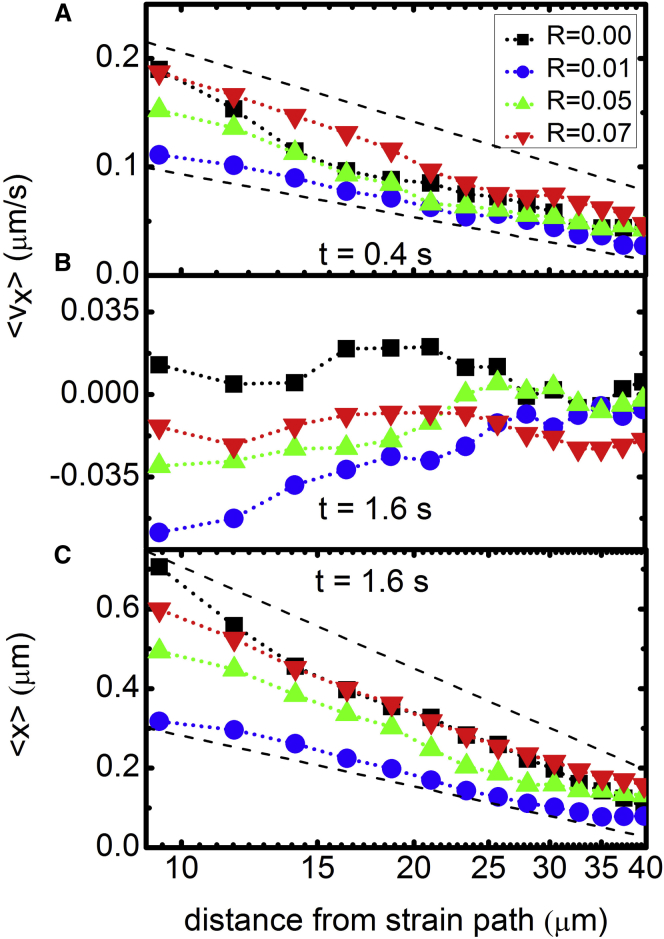
Fig. 4, G and H, also reveals a nonmonotonic dependence of filament deformation on R. R = 0 and 0.07 filaments display the fastest forward velocities and largest displacements during strain, followed by R = 0.05, then R = 0.01. More explicitly, R = 0 segments exhibit high initial velocities and no recoil; R = 0.07 segments also display large initial velocities but with some recoil; and R = 0.05 and 0.01 networks display reduced forward velocities and more recoil. Further, as shown in Fig. 5, the measured velocities and displacements decay roughly exponentially with distance from the strain path. Extrapolating the exponential decays to the point of strain (d = 0) gives zero-position filament speeds of 0.2–0.35 μm/s (∼2–4% of the 8 μm/s probe speed) and displacements of 0.6–1.4 μm (∼10% of the probe strain). The critical decay distances for the velocity and displacement spatial decays are ∼10–18 and ∼11–14 μm, respectively, similar to the actin persistence length (l_p ≃ 17 μm). This decay distance agrees with our previous findings for entangled actin, which show that l_p controls the crossover from discrete to continuum mechanics (30).

Figure 5.

Ensemble-averaged filament velocities (A and B) and displacements (C) as a function of distance from the strain path d display the propagation of induced strain throughout the network at the beginning (A) and end (B and C) of the applied strain (times displayed in plots). Dashed lines in (A) and (C) show exponentially decaying functions of d with critical decay distances of (A) ∼10–18 μm and (C) ∼11–14 μm. Extrapolation of decays to d = 0 give maximum filament velocities of 0.2–0.35 μm/s (A) and displacements of 0.6–1.4 μm (C). (B) Velocities at the end of the strain show that particle deceleration and recoil during strain, responsible for stress softening, exhibit a nonmonotonic dependence on the degree of cross-linking. To see this figure in color, go online.

After we pull the probe through the network, we hold the trapped probe fixed and measure the time-dependent evolution of the built-up force exerted by the network and corresponding filament motion. Fig. 6 shows that only the R = 0 network relaxes to negligible force over the measurement timescale, while all R > 0 networks sustain some force, with the sustained terminal force (F_t) exhibiting a similar exponential dependence as the strain phase dynamics (Fig. 3). By comparing the terminal force (F_t) reached at the end of relaxation (Fig. 6 C) to the maximum force reached during strain (Fig. 3 A), we quantify the relative sustained elasticity versus plasticity. We find that while the R = 0 network only retains 5% of its elastic memory (95% dissipation), 40% of the elasticity is recovered for R = 0.07 (implying 60% plastic deformation). This partial plastic deformation is in line with recent results from microrheology experiments of biotin-streptavidin cross-linked microtubules (42), as well as simulations of HMM-cross-linked actin networks (64). These simulations report that 25–50% of the induced deformation was elastically recoverable, attributing the 50–75% plastic deformation to force-induced cross-linker unbinding and rebinding. Complementary simulations showed that rebinding prevented the network from undergoing complete plastic flow (42).

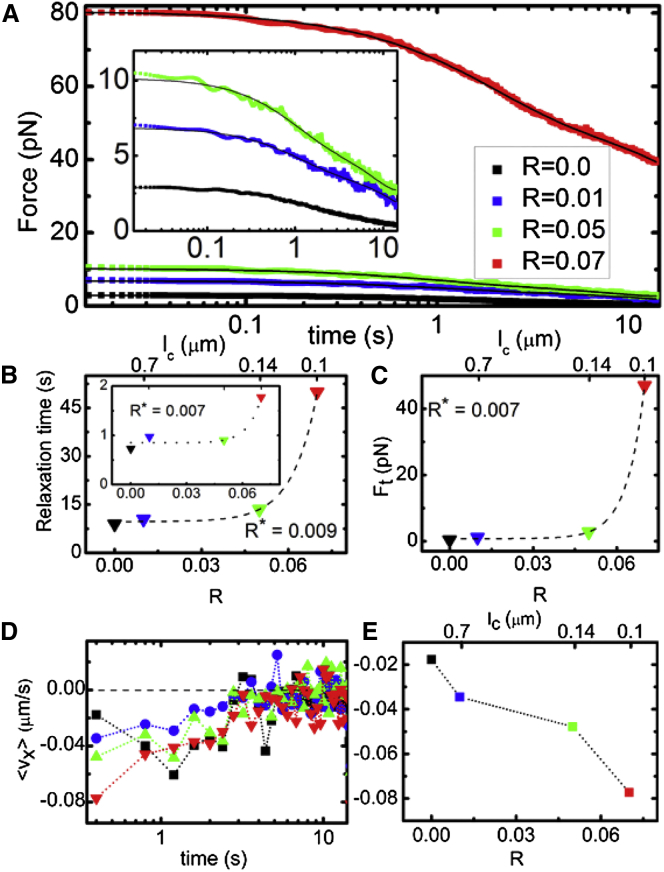
Figure 6.

Relaxation of induced force is strongly suppressed as cross-linker ratio R increases. (A) Time evolution of induced force after the strain. (Solid black lines) Fits of the data to a sum of two exponential decay functions with well-separated decay times t_fast and t_slow. (Inset) Zoomed-in data for R < 0.07. (B) Measured force decay times, t_slow and t_fast (inset), as a function of R, determined from the corresponding fits in (A). (Dashed lines) Fits to exponential functions of cross-linker ratio R (t ∼ exp(R/R^∗)) with critical cross-linker ratios R^∗ listed in corresponding plots. (C) Terminal sustained force F_t, defined as the force reached at the end of the relaxation phase, as a function of R, with an exponential fit (dashed line) that gives R^∗ ≃ 0.007. (D) Ensemble-averaged retraction velocities $\langle v_x\rangle$ during the relaxation phase for filaments closest to the strain path (d = 9 μm) as a function of time for networks of varying R. (E) Retraction velocities immediately following the strain as a function of cross-linker ratio R. Velocities correspond to the data in the first time point of (D). Corresponding retraction distance for R = 0.07 was measured to be ∼0.5 μm, corresponding to 80% recovery of the strain-induced displacement (data not shown). To see this figure in color, go online.

We previously found that entangled networks relaxed via two relaxation mechanisms, which occurred over timescales of ∼1 s (t_fast) and ∼10 s (t_slow) that were attributed to disengagement of actin polymers from dilated entanglements tubes (t_slow) and lateral hopping of entanglement segments between entanglements (t_fast) (23). Similar to these previous measurements, the force decay values for all actin networks are well described by a sum of two exponentials with well-separated timescales, with the timescales for R = 0 similar to our previous measurements. Further, both t_fast and t_slow exhibit similar exponential trends with R as the terminal force F_t, yield time t_y, and stiffening parameters (K_max, K_t) (Figs. 3 and 6).

Fig. 6 D shows the corresponding ensemble-average velocities for 15 different time points following the strain. While all networks retract back toward their starting configurations, the fastest retraction is exhibited by R = 0.07 with corresponding speeds decreasing with decreasing R (Fig. 6 E). However, by comparing the filament displacements during the strain and relaxation phases, we find that filaments recover, at most, ∼80% of their strain-induced displacement (for R = 0.07), thus remaining permanently displaced from their starting positions (i.e., plastic deformation). The maximum retraction is measured to be ∼0.5 μm (for R = 0.07), comparable to the mesh size (ξ ≃ 0.4 μm). Further, the velocities for all R > 0 networks smoothly decrease to zero as t approaches ∼10 s, suggesting collective relaxation of a well-connected network over time. In contrast, the time-evolution of filament velocities for the network without cross-links (R = 0) is much noisier, indicating that the network is only loosely connected, resulting in filament motion that is much less ordered.

Discussion

To frame our interpretations of the diverse data presented above, we first depict the expected results for a purely elastic material versus a viscous material. In our measurements, we use a microscopic probe to apply a local force to the network. The probe pulls on a region of the network, inducing a force on the network that varies as the probe is pulled further. If the network were purely elastic, this force would increase proportionally with the distance the probe is pulled, and once the probe stops, the force would be maintained with no relaxation, as the network is held in a stretched state. Conversely, if the probe were pulled through a purely viscous network, the force would quickly reach a time-independent plateau value, dependent on the probe strain rate, and once the probe stops, the built-up force would instantaneously dissipate to zero. However, for a viscoelastic network in which there are cross-links that give rise to elastic response, as well as steric entanglements and unbinding events that are able to rearrange the network and dissipate energy, the response would be in between these two extremes. Specifically, if cross-links can unbind or if the network entanglements are not all cross-linked (i.e., if l_c > l_e), then the network can partially relax and rearrange, thereby reducing the built-up force—allowing for stress softening and relaxation as well as filament deceleration and recoil. Further, if the entire network is not strained by the probe, rather the stress is maintained by a small fraction of the network comprising a stress path or fiber, then relaxation of the rest of the network will contribute to dissipation and give rise to filament recoil events.

During strain, we see an increasingly elastic response as R increases (Fig. 3). Initial stress stiffening coincides with filament acceleration, which can be explained by filaments being conformationally extended (entropically stretched) in the direction of the strain, as predicted for networks with l_b/l_c ≪ 1 (46, 52). Stiffening ensues until a timescale of τ_mesh ≃ 0.01 s. Because no softening or yielding can occur at times less than the shortest relaxation time of the system (i.e., τ_mesh), for t < τ_mesh, networks stiffen; and after τ_mesh, the networks can relax or yield via intrinsic relaxation mechanisms. Filament deceleration and recoil during strain, which coincides with stress softening, suggests that entanglement release, cross-linker unbinding, and/or filament rupturing, is allowing the segments to momentarily disengage from the rest of the strained network. Recoil becomes less pronounced for increasing R because as R increases, the network has more rigid connections, so a larger fraction of the network is pulled by the moving probe. In other words, a smaller fraction of the total number of cross-links is able to release from the strained path (via disentanglement, unbinding, or rupturing). While filament recoil would suggest that the network can substantially relax induced stress, we find that only for R = 0 does stiffness (K_t ) decay to nearly 0, while all cross-linked networks exhibit substantial sustained elasticity. This sustained elasticity (K_t), as well as the corresponding yielding timescales, increases with increasing R, as previously reported (12, 42). The coupling of filament deceleration and recoil with ample sustained elastic stiffness and suppressed stress yielding suggests that the stress is only maintained by a small fraction of the network, while most of the network is able to disconnect to alleviate its stress. Recent simulations indeed show that cross-linked actin networks distribute stress nonuniformly along percolated paths of connected filaments that make up only a small fraction of the filaments in the network (43).

The stress softening and yielding exhibited by all networks (Fig. 3), as well as post-strain relaxation dynamics (Fig. 6), demonstrate the availability of relaxation mechanisms (65). We previously attributed fast relaxation in entangled actin solutions (occurring over t_fast) to a recently predicted lateral hopping mechanism that can arise in the nonlinear regime, whereby fluctuating filament segments can momentarily evade entanglement confinement because the entanglement density is reduced by nonlinear straining (23, 65, 66). By analogy, similar yielding phenomena in cross-linked networks would imply momentary evasion of cross-linking confinement, which can arise from forced cross-linker unbinding and subsequent rebinding (43, 46, 47). Likewise, t_slow (Fig. 6) can be understood as the time necessary for filaments to completely disengage from constraints, which becomes increasingly more difficult as more permanent cross-links are incorporated into the system.

Cross-linker unbinding or filament rupturing/severing events could both result in the softening and relaxation phenomena we measure. However, there is significant literature demonstrating the principle role that unbinding, as opposed to rupturing, plays in the nonlinear softening response that follows initial stress stiffening (12, 26, 42, 43, 48, 63). As described in Results, many of these studies report results similar to ours, as opposed to studies that support rupturing (39, 40, 67, 68). This literature encompasses a wide range of cross-linked networks, including actin networks cross-linked by HMM (12, 25), which has an extremely high actin binding affinity (>4× stronger than α-actinin and filamin). This affinity is similar to the strong biotin-streptavidin bond, and HMM has been shown to form isotropically cross-linked rather than bundled networks, similar to our biotin-streptavidin networks (12). For reference, typical forces needed to rupture the biotin-streptavidin bond have been measured to be ∼15–60 pN (69) within the range of forces we measure, so force-induced unbinding is indeed feasible.

Further, a recent simulation investigating the competing roles of filament severing/rupturing versus cross-linker unbinding during cyclic strains shows that severing is important for substantial relaxation during cyclic strain, but it has little effect on the initial (first cycle) stress response (68). Conversely, cross-linker unbinding was the underlying mechanism for initial stress softening but did not contribute to continued relaxation during cycles of strain. While unbinding and rebinding resulted in partial relaxation (as we see in Fig. 6), severing was needed to produce complete relaxation. Because we measure sustained elastic stress following strain, as well as substantial softening without cyclic straining, the results of this simulation demonstrate that the response we measure is indeed a result of unbinding/rebinding events rather than filament rupturing. Finally, this study showed that softening and relaxation from filament severing increased with increasing R, whereas we find that increasing R reduces stress softening (higher K_t) and relaxation (greater terminal force F_t and longer relaxation timescales t_y, t_fast, and t_slow). Other simulations on cross-linked actin networks similar to ours further support unbinding/rebinding as the underlying mechanism for the response features we observe (26, 48). These studies show that unbinding and rebinding leads to nonlinear stress stiffening followed by softening and partial force relaxation. They further demonstrate that unbinding leads to the formation of percolated stress fibers that sustain the load, allowing the rest of the network to relax (48). Rebinding was also reported to prevent complete relaxation, such that networks exhibit partial plastic deformation while retaining some degree of elasticity (26). Thus, although filaments elastically retract following strain, they do not return to their original starting positions. Likewise, we find that while filaments retract, they still remain permanently displaced from their starting positions, with the maximum retraction distance comparable to the mesh size (ξ ≃ 0.4 μm). Thus, this plastic deformation likely arises because released segments can rebind with the network when they come in contact with new network segments.

Finally, a 2013 study using magnetic tweezers to probe the viscoelastic response of biotin-streptavidin cross-linked microtubules (42) reported response features similar to ours; namely, stiffening followed by softening during strain and sustained elasticity as well as partial plastic dissipation following the strain. This study carried out complementary simulations to show that softening, network rearrangement, and plastic flow arise from cross-linker unbinding, while sustained elasticity arises from cross-linker rebinding. Further, similar to the results of many cross-linked actin studies, this work reported that when unbinding/rebinding is the principal source of softening, the maximum differential modulus reached during stiffening (K_max), before softening ensues, increases with increasing R (as shown in Fig. 3).

We find that relaxation and yielding timescales, as well as dynamical quantities derived from the underlying relaxation mechanisms (i.e., the degree of stiffening and sustained elastic force), all display roughly exponential dependence on R with an average critical cross-linking ratio R^∗ ≃ 0.011 corresponding to l_c^∗ ≃ 0.6 μm. While extracting definitively functional forms from one of these data sets (Figs. 3, C–E, and 6, B and C) is not sound as there are too few data points, because we have five such data sets that all exhibit markedly similar dependences on R, we do believe that the exponential dependence of relaxation dynamics on cross-linking ratio is robust. We also note that l_c^∗ ≃ 0.6 μm is comparable to, but smaller than, the entanglement length of the network (l_e ≃ 0.9 μm), suggesting that the relaxation mechanisms that are available to entangled networks are suppressed when the cross-linker length becomes smaller than the entanglement length (l_c < l_e) (i.e., nearly every steric filament crossing is chemically linked). A previous rheology study on HMM-crosslinked actin networks interprets the transition that they measure in linear mechanics as due to the same competing length scales (25). At this transition point, relaxation mechanisms are suppressed (Fig. 6) and the elastic contribution to the induced force during strain dominates (Fig. 3, C–E).

To further describe the physics underlying this exponential dependence, we look to theoretical scaling laws derived for the diffusive timescales of a microsphere of radius r in a polymer network of mesh size ξ (70, 71, 72). Specifically, Cheng et al. (70) showed that the reduced probe diffusion coefficient (D/D₀) scales as exp[−β(r/ξ)^z], where β ∼ O(1) and the stretching coefficient z is close to 1. This result (which is a variant on widely used theories that relate probe diffusion to the concentration c of polymer solutions via exp(−βrc^1/2), where β ∼ O(1) (71, 72)) describes how probe mobility and relaxation mechanisms are restricted by the constraining polymer mesh. This scaling implies that the allowed diffusive and relaxation timescales for a probe of fixed size increase roughly exponentially with decreasing network mesh size (i.e., τ ∼ τ_o exp[r/ξ]). We note that while ξ and r parameters are fixed in our experiments, and we are probing the nonlinear regime rather than steady state, we can still use these scaling theories to gain insight into our exponentially R-dependent dynamics. Our experiments nonlinearly strain the network and measure the resulting forces imposed on the filaments and the corresponding relaxation timescales. Thus, our measurements are measuring the mobility and relaxation timescales of individual actin segments in the network rather than the mobility of the probe. Therefore, instead of r in the above relationship we expect the governing probe length scale to be l_e, the length scale of independent network segments. Further, we expect the analogous constraining network length scale for the nonlinear regime to be that of the rigid chemical cross-links (l_c) rather than the liable steric polymer overlaps (quantified by ξ). In this case, actin segment relaxation timescales (Figs. 3 F and 6 B) and associated dynamical quantities determined by these timescales (Figs. 3, D and E, and 6 C) would scale roughly as exp[l_e/l_c]. Given that R ∼ l_c⁻¹, we indeed find this relationship, namely exp[R/R^∗] = exp[l_c^∗/l_c] with l_c^∗ ≃ l_e ≃ 0.6 μm.

We finally look to the strain propagation dynamics to gain insight into how stress is distributed throughout the network. Previous theoretical work investigating the strain field induced in a cross-linked network by a local point perturbation shows that network deformation decays exponentially with distance from the perturbation. In these studies, in which the perturbation scale is infinitesimal, the characteristic decay length is the nonaffinity length scale λ, which depends on l_c and l_p, as described in the Introduction (73). The predicted exponential decay is further explained as demonstrating a crossover from noncontinuum to continuum mechanics at a length scale of λ. Beyond λ, the exponential decay is qualitatively similar to that predicted by continuum elastic theory. Our perturbation scale is much larger than that investigated by these studies, but the exponential decay with distance from the strain is nevertheless preserved. Further, our previous work investigating nonlinear strain propagation in entangled actin networks showed that the analogous crossover length scale from discrete to continuum mechanics was the persistence length l_p (29). Our current results, with exponential decay constants of ∼10–18 and ∼11–14 μm for the velocity and displacement data, respectively (Fig. 5), suggest that this length scale is robust to cross-linking. The crossover from discrete to continuum mechanics can also be seen explicitly in Fig. 5, in which the deformation field is network-dependent for length scales <∼l_p but collapses to a single decay curve for length scales beyond l_p.

The maximum filament deformations derived via extrapolation of the decay curves to d = 0 provide further insight into how the filaments are deformed in response to the strain. Displacements are ∼10% of the applied strain and comparable to the mesh size of the networks, indicating that network crossings restrict free filament motion. However, the fact that filament displacements are larger than the cross-linking lengths for R = 0.05 (l_c ≃ 0.14) and R = 0.07 (l_c ≃ 0.1) indicate that forced cross-linker unbinding allows filaments to move beyond steady-state network constraints. The largest displacement and speed is measured for R = 0, as expected, because steric entanglements are liable to disruption from large forces, enabling filaments to flow in response to the strain.

Conclusions

We have combined force-measuring optical tweezers and fluorescence microscopy, along with novel discrete labeling of actin segments and particle-tracking analysis, to directly couple the nonlinear stress response of cross-linked and entangled actin networks with the underlying molecular and network deformation and rearrangements. We find that the elasticity of the network is highly dependent on the length between cross-linkers, l_c, with the critical cross-linking length in which cross-linking dominates entanglement effects occurring when l_c becomes smaller than the entanglement length l_e. We have demonstrated that the initial stiffening, present for both entangled and cross-linked networks, arises from the acceleration of actin segments near the strain, due to entropic stretching along the strain path. Subsequent filament deceleration and recoil, due to force-induced disentanglement and cross-linker unbinding, leads to stress softening and yielding to a steady-state regime. This terminal regime occurs at timescales longer than the fastest relaxation timescale of the network, and exhibits sustained elastic resistance, enhanced by cross-linker rebinding events, which increases with increasing cross-linker density. Strain-induced filament velocities and displacements exhibit a nonmonotonic dependence on cross-linker density, with both R = 0 and 0.07 exhibiting the fastest speeds and largest displacements while the intermediate R values show less pronounced deformation. We show that the extreme R = 0 strain response is a result of viscous flow and ample network reorganization/yielding, while the R = 0.07 response arises from the highly elastic network being pulled with minimal ability to reorient or relax to relieve the strain. The systems in which reorganization and elasticity are comparable (R = 0.01, 0.05) result in smaller filament deformations and increased recoil. Further, high levels of elastic stress for l_c < l_e are maintained with minimal relaxation, while the corresponding tracked segments exhibit highly elastic retraction following deformation. In agreement with recent simulations, these contradictory results indicate that the stress is maintained by only a small fraction of highly strained connected filaments. Most of the network can then disconnect from the strain path via cross-linker unbinding, and elastically retract.

Author Contributions

B.G. conducted experiments, analyzed data, and wrote the article; S.R. prepared reagents and conducted confocal microscopy experiments; and R.M.R.-A. designed experiments, analyzed and interpreted data, and wrote the article.

Editor: James Sellers.