Disruption of Magnetic Compass Orientation in Migratory Birds by Radiofrequency Electromagnetic Fields

Abstract

The radical-pair mechanism has been put forward as the basis of the magnetic compass sense of migratory birds. Some of the strongest supporting evidence has come from behavioral experiments in which birds exposed to weak time-dependent magnetic fields lose their ability to orient in the geomagnetic field. However, conflicting results and skepticism about the requirement for abnormally long quantum coherence lifetimes have cast a shroud of uncertainty over these potentially pivotal studies. Using a recently developed computational approach, we explore the effects of various radiofrequency magnetic fields on biologically plausible radicals within the theoretical framework of radical-pair magnetoreception. We conclude that the current model of radical-pair magnetoreception is unable to explain the findings of the reported behavioral experiments. Assuming that an unknown mechanism amplifies the predicted effects, we suggest experimental conditions that have the potential to distinguish convincingly between the two distinct families of radical pairs currently postulated as magnetic compass sensors. We end by making recommendations for experimental protocols that we hope will increase the chance that future experiments can be independently replicated.

Introduction

“Our study establishes the use of oscillating magnetic fields as a diagnostic tool that can indicate the involvement of a magnetosensitive radical-pair reaction in birds.” (1) This quotation comes from an article published in 2004 in which it was proposed that the orientational behavior of migratory birds exposed to radiofrequency electromagnetic fields offers a method to confirm that their magnetic compass is based on radical pairs rather than magnetic iron-containing minerals. The radical-pair hypothesis suggests that the yield of a photochemical reaction, with transient radical pairs as intermediates, exhibits a directional magnetic-field dependence that provides the information necessary for compass magnetoreception (2, 3, 4). The exquisite magnetic sensitivity of such chemical transformations arises because the coupled electron and nuclear spins of the radical pair are created in a non-equilibrium state and exhibit quantum oscillations involving non-stationary populations of the electronic singlet and triplet states. These coherences can be influenced by weak magnetic fields interacting with the spins of the unpaired electrons in the two radicals (5, 6).

There is significant but largely circumstantial evidence in support of this hypothesis (4): the avian compass is known to be light dependent (7, 8), a proof-of-principle model radical-pair compass has been demonstrated (9), and cryptochromes, the proposed receptor proteins (2), form magnetically sensitive radical pairs when excited in vitro with blue light (10, 11). However, it is the disorientation of birds exposed to very weak radiofrequency magnetic fields (1, 12) that arguably rules out the competing hypotheses based on superparamagnetic (13) or ferrimagnetic particles (14). Although the interaction of a radical pair with a radiofrequency field can be rationalized as a direct electron paramagnetic resonance (EPR) effect on the coherent singlet-triplet interconversion (15, 16), it is difficult to see how magnetite or other iron-containing particles could be affected by such high-frequency magnetic fields.

However, the use of radiofrequency fields as a diagnostic tool has not been uncontroversial. Conflicting behavioral studies have reached different conclusions as to whether migratory birds are more sensitive to a (monochromatic) magnetic field oscillating at a single radiofrequency or to broadband electromagnetic noise containing a range of radiofrequencies (17, 18). Additionally, doubt has been cast on the physical interpretation of the experiments (4, 19). “Back-of-the-envelope” calculations suggest that the quantum coherence believed to be essential for the disorienting effect would have to persist for at least 100 times longer than the most generous estimates of the spin relaxation times of organic radicals in the warm and noisy environment of a living cell (20).

In light of these uncertainties, we present here a computational investigation of the effects of radiofrequency magnetic fields on biophysically plausible radical pairs. Theoretical studies complementary to the behavioral experiments are currently limited, being severely hampered by the computational challenges. Using a recently developed approach (21), we examine the behavior of radical pairs in silico subject to an approximation to the conditions of the behavioral experiments. On the basis of these simulations, we discuss how it might be possible to discriminate experimentally between different radical pairs and to determine more convincingly than hitherto whether the sensory mechanism is indeed based on radical pairs. Linked to these predictions are some recommendations for experimental protocols that we believe would improve the reproducibility of future behavioral tests.

Radiofrequency field effects

The original study of radiofrequency field effects indicated that both a 7 MHz single-frequency oscillating field and a 0.1−10 MHz broadband noise field could prevent European robins from orienting themselves by means of their magnetic compass (1). Based on this work, several behavioral studies have used radiofrequency fields to probe aspects of the radical-pair hypothesis in birds (12, 17, 22, 23, 24, 25, 26). Perhaps the most significant of these reported a distinct resonance at the electron Larmor frequency—the precession frequency of a free electron spin in the Earth's magnetic field (12). Exceptionally weak oscillating fields at this frequency (1.315 MHz in Frankfurt am Main, Germany, where the measurements were performed) were found to cause magnetic disorientation. At other single frequencies (half and double the Larmor frequency), much stronger fields were required to upset the birds’ orientation (12).

The identification of this unique “Larmor resonance” has been interpreted to mean that one of the radicals in the pair contains a magnetically isolated electron (12). “Isolated” in this context means that the electron spin has no magnetic interactions other than with the geomagnetic field. More specifically, any hyperfine interactions with the nuclear spins of hydrogen or nitrogen atoms in or near the radical must be negligible, as must the exchange and dipolar interactions with the partner radical. In the presence of an external magnetic field, the otherwise degenerate “spin-up” and “spin-down” states of an isolated electron are split apart by an energy that corresponds to the Larmor frequency (Fig. 1 a). A radiofrequency field oscillating at this frequency, driving transitions between these two states, would have a far greater effect on the singlet-triplet interconversion than a field at any other single frequency and therefore, perhaps, would have a more disruptive effect on the operation of the compass sensor (12). Further experimental evidence reported by Ritz et al. (12) supports this conclusion: as expected for a Larmor resonance, doubling the strength of the static magnetic field in which the birds were tested doubled the frequency of the resonance, and the effect disappeared when the Larmor-frequency field was aligned parallel to the geomagnetic field. The latter result is expected for an isolated electron spin because the radiofrequency-induced EPR transition becomes forbidden by symmetry (12, 15). The presence or absence of a Larmor-frequency resonance in behavioral experiments has subsequently been used as evidence that other species do (cockroaches (27), snapping turtles (28), and wood mice (29)) or do not (mole rats (30)) have a radical-pair-based sensor.

Figure 1.

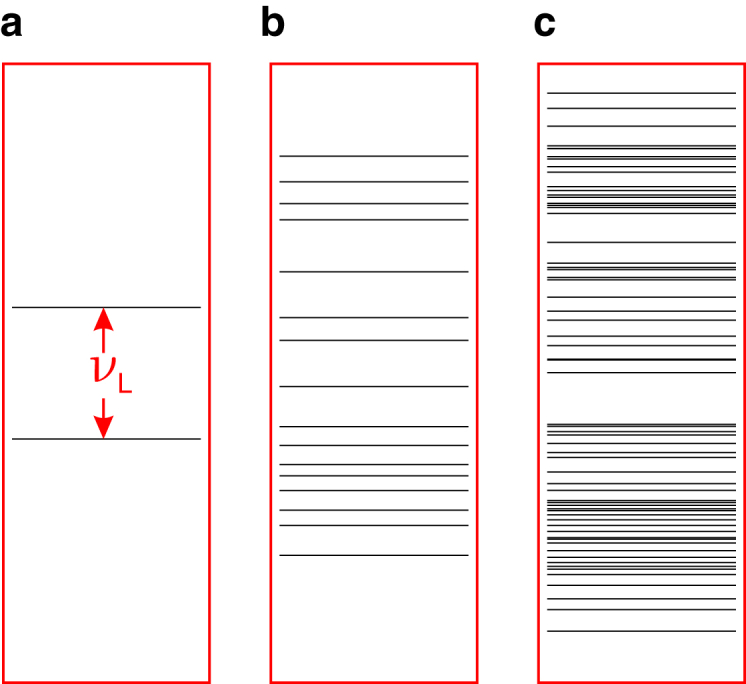
Energy levels of a radical containing different numbers of hyperfine-coupled spin-1/2 nuclei. (a) In the absence of hyperfine, exchange, and dipolar interactions, the electron experiences only the external magnetic field, resulting in a Zeeman splitting equal to the Larmor frequency, ${\nu }_{\mathrm{L}}$. (b) A small number of hyperfine interactions results in a variety of energy-level spacings. (c) A large number of hyperfine interactions gives rise to many energy levels, a situation representative of the majority of organic radicals. Only in case (a) would a radiofrequency field at the Larmor frequency be expected to have a strong effect on the spin dynamics. To see this figure in color, go online.

Several theoretical studies have explored the effect of a single-frequency perturbation on radical pairs containing a magnetically isolated electron in one of the radicals (here denoted Z^•) (31, 32, 33). The consensus is that the anisotropy of the reaction yield—thought to be the source of the directional signal—is considerably attenuated by a Larmor-frequency field provided the spin-coherence lifetime is sufficiently long (31). However, the radical pairs treated in these studies have often been grossly oversimplified. Although such work has offered useful conceptual insights, we are now in a position to extend these investigations to examine more realistic radical pairs subject to more complex time-dependent magnetic fields.

The seemingly complete picture of a Larmor-frequency resonance backed up by computer simulations (albeit ones requiring extraordinarily slow loss of coherence) suffers from the drawback that the existence of a biologically plausible Z^• radical whose unpaired electron experiences only the external magnetic field, remains unsubstantiated (34, 35). The requirement that a radical has no significant hyperfine interactions with magnetic nuclei is a stringent one that severely limits the list of possible candidates. A rough estimate of the maximum permissible magnetic interaction can be obtained from the observation that birds disoriented by a radiofrequency field at the Larmor frequency were not affected by a field of the same amplitude at half the Larmor frequency (12). This implies that the hyperfine field would have to be smaller than the difference between these two frequencies (0.66 MHz), which corresponds to a magnetic interaction of 24 μT. This is an order of magnitude smaller than typical hyperfine interactions in organic radicals.

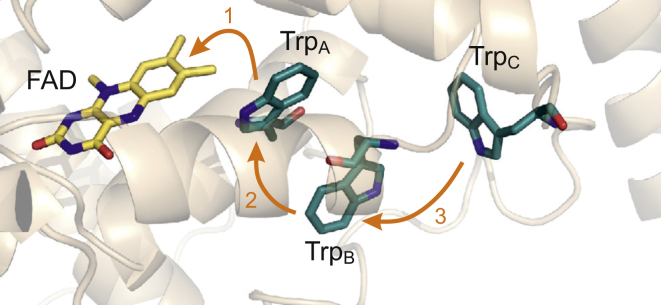
The radical pair in cryptochrome in vivo is thought to include the radical form of the flavin adenine dinucleotide (FAD) cofactor but the identity of the counter-radical is less clear (35). In vitro, the magnetic field effects on Arabidopsis thaliana cryptochrome-1 arise from a radical pair formed from FAD and the terminal tryptophan (Trp) residue of the “tryptophan triad” (Fig. 2) (10). Superoxide $\left({\text{O}}_2^{•-}\right)$ has been suggested as a potential partner for the FAD radical in vivo partly on the basis that the ¹⁶O isotope (99.8% natural abundance) has no nuclear spin and hence no hyperfine interactions (9, 12). However, the details of such a radical pair remain opaque, as a rotating superoxide radical would undergo exceedingly rapid electron spin relaxation (probably ∼1 ns), excluding any possibility of an effect of a weak magnetic field (34, 36, 37). To be suitable as a component of a geomagnetic sensor, an ${\text{O}}_2^{•-}$ radical would have to be rigidly immobilized by strong molecular interactions, which, in all likelihood, would introduce significant hyperfine couplings (34). Furthermore, unless the counter-radical were >∼5 nm away from the FAD radical, there would also be a non-vanishing dipolar coupling of the two electron spins (38). Both of these interactions would alter the spin energy levels of the radical pair and so abolish any resonance at the Larmor frequency (Fig. 1, b and c).

Figure 2.

The FAD chromophore and Trp triad in cryptochrome. After photoexcitation of the flavin, three sequential electron transfers lead to the magnetically sensitive FAD-Trp_C radical pair. The structure is that of AtCry, PDB: 1U3D. Only the flavin part of FAD is shown. To see this figure in color, go online.

This physical intuition seems to be corroborated by more recent behavioral data. Engels et al. (17) found that European robins tested on the campus of the University of Oldenburg, in Germany, were unable to orient magnetically unless shielded from the background electromagnetic noise. Importantly, artificially introduced, band-limited radiofrequency noise caused the robins to be disoriented whether or not the Larmor frequency was included in the frequency band (17). Furthermore, another study, aimed directly at comparing the effects of broadband noise and Larmor-frequency fields, found that radiofrequency noise is far more effective than monochromatic radiofrequency fields at disorienting the birds, in contradiction to the Frankfurt studies (18). The results of the behavioral experiments that have employed radiofrequency fields are summarized in Table S1.

We present here an investigation of the responses of realistic FAD-Z and FAD-Trp radical pairs to monochromatic and broadband radiofrequency fields.

Methods

In the absence of a time-dependent external magnetic field, the coherent spin dynamics of a radical pair is governed by the spin Hamiltonian,

$$\hat{\mathit{H}}={\hat{\mathit{H}}}_1+{\hat{\mathit{H}}}_2+{\hat{\mathit{H}}}_{12}\left(\mathit{r}\right),$$ (1)

where the ${\hat{\mathit{H}}}_1$ and ${\hat{\mathit{H}}}_2$ operators describe the magnetic interactions of radicals 1 and 2, and ${\hat{\mathit{H}}}_{12}\left(\mathit{r}\right)$ contains the inter-radical exchange and dipolar coupling terms, which depend on r, the separation of the two radicals. ${\hat{\mathit{H}}}_{\mathit{i}}$ (i = 1 or 2) includes the Zeeman interaction of the electron spin in radical i (angular momentum operator ${\hat{\mathbf{S}}}_{\mathit{i}}$) with the static geomagnetic field, B₀, and its hyperfine interactions with N_i nuclear spins (angular momentum operators ${\hat{\mathbf{I}}}_{\mathit{ik}}$), parametrized by hyperfine tensors, ${\mathbf{A}}_{\mathit{ik}}$:

$${\hat{\mathit{H}}}_{\mathit{i}}={\gamma }_{\mathrm{e}}{\mathbf{B}}_{\mathbf{0}}\cdot {\hat{\mathbf{S}}}_{\mathit{i}}+\sum _{\mathit{k}\mathrm{=1}}^{{\mathit{N}}_{\mathit{i}}}{\hat{\mathbf{S}}}_{\mathit{i}}\cdot {\mathbf{A}}_{\mathit{ik}}\cdot {\hat{\mathbf{I}}}_{\mathit{ik}}$$ (2)

(${\gamma }_{\text{e}}$ is the magnetogyric ratio of the electron). For radical Z^•, with no hyperfine-coupled nuclei, this expression contains only the Zeeman term that defines the Larmor frequency, ν_L:

$${\nu }_{\mathrm{L}}=\frac{{\gamma }_{\mathrm{e}}\left|{\mathbf{B}}_{\mathbf{0}}\right|}{2\pi },\mathrm{where}\frac{{\gamma }_{\text{e}}}{2\pi }=0\mathrm{.028}\mathrm{MHz}/\mu \mathrm{T}\mathrm{.}$$ (3)

At radical separations >∼2 nm, the coupling Hamiltonian ${\hat{\mathit{H}}}_{12}\left(\mathit{r}\right)$ is dominated by the dipolar interaction:

$$\mathit{D}\left(\mathit{r}\right)=-\frac{3}{2}\frac{{\mu }_0}{4\pi }\frac{{\gamma }_{\mathrm{e}}^2{\hslash }^2}{{\mathit{r}}^3},\mathrm{i}\mathrm{.e}\mathrm{.,}\mathit{D}\left(\mathit{r}\right)\text{/}\mu \mathrm{T}=-\frac{2786}{{\left(\mathit{r}\text{/}\mathrm{nm}\right)}^3}.$$ (4)

A time-dependent external magnetic field enters Eq. 2 as an additional, time-dependent Zeeman term. This severely complicates simulation of even simple spin systems, but an approximate Floquet method significantly simplifies the calculation (21). The basis of the algorithm is to consider degeneracies between states in the extended “Floquet space”, whose energies are shifted by integer multiples of the base frequency in the applied field. These degeneracies therefore correspond to the external fields being resonant with an energy gap in the spin system. Assuming these resonances account for the important physics in the problem, we can exploit the weakness of the time-dependent fields and slow radical-pair recombination to derive a viable perturbation method based on diagonalization of a single Hilbert-space-sized matrix (21).

Although single-frequency fields are straightforward to model, the details of the Floquet method mean that we must mimic the broadband noise using a “comb” of frequency components, spaced (in this case) by 1 kHz (21). The amplitudes, phases, and directions of the different frequency components are randomized, and to compare different conditions, we choose their amplitudes so that all the time-dependent fields we consider, whether single-frequency or broadband, have the same root-mean-square amplitude. This approach is clearly an imperfect representation of the experimental conditions. In a true noise field, there will be non-negligible amplitudes for all frequencies in the band, and these will vary over time. However, our computational approach (21) is currently the only one able to include thousands of frequency components in simulations of radical pairs with large spin systems, and it should give at least a qualitative idea of the effect of these time-dependent magnetic fields.

In the calculations below, the radical pair recombines symmetrically with equal rate constants for the singlet and triplet channels, k = 10³ s⁻¹. The geomagnetic field is set at 50 μT so that the Larmor frequency is 1.4 MHz (Eq. 3). For each set of conditions, we calculate Φ_S, the quantum yield of a signaling state imagined to be formed by recombination of singlet radical pairs; we refer to this quantity as the “singlet yield”. The amplitude of the single-frequency magnetic fields in all cases is B₁ = 5.0 μT. The amplitudes of the components of the broadband noise were chosen randomly in the range −B_1,max to +B_1,max. For example, if there are 10⁴ components in a 10 MHz comb, B_1,max = 86.6 nT, so that the root-mean-square intensity is $5/\sqrt{2}\mathit{\mu }\text{T}=\sqrt{10^4}\mathrm{\times 50}/\sqrt{2}\mathrm{nT}$, and the root-mean-square noise density is $5\mu \mathrm{T}/\sqrt{2}\sqrt{10\mathrm{MHz}}$ = 1.12 nT Hz^−1/2. The radiofrequency fields used here are therefore considerably stronger than those reported in the behavioral experiments; we chose these values so that the qualitative effects on the yields of the products of the radical-pair reactions can easily be seen. The choice of B₁ for the individual frequency components is linked to the choice of radical pair-lifetime τ = 1/k. For a time-dependent field in resonance with a fully allowed transition between two energy levels, one can expect a significant effect on the spin dynamics if ${\gamma }_{\mathrm{e}}{\mathit{B}}_1\tau /2\pi \ge 1$. For B₁ = 50 nT and τ = 1 ms, ${\gamma }_{\mathrm{e}}{\mathit{B}}_1\tau /2\pi$ = 1.4. We also neglect the effects of spin relaxation and thereby assume coherence lifetimes far longer than expected for room-temperature radical pairs (20, 39). We discuss these choices and assumptions later.

As a complement to the spin dynamics simulations we also introduce, as a rough conceptual tool, “action-spectrum histograms” that give an impression of the likely effects of applying weak magnetic fields oscillating at different frequencies. They are obtained by calculating the eigenvalue spectrum of the static Hamiltonian, $\hat{\mathit{H}}$ (Eq. 1), and identifying all pairs of energy levels whose separation falls within a given frequency interval and then summing their “resonance effects” on the yield of the radical-pair reaction. We define resonance effect to be the product of the transition probability and the difference in the populations of the two energy levels at the moment the radical pair is created in a singlet state. The height of the nth histogram bar, covering the frequency interval $\left[\mathit{n}\Delta \nu ,\left(\mathit{n}\mathrm{+1}\right)\Delta \nu \right]$, is thus given by

$$\sum _{{\nu }_{\mathrm{ij}}\mathrm{\in }\left[\mathit{n}\Delta \nu ,\left(\mathit{n}\mathrm{+1}\right)\Delta \nu \right]}\mathit{N}{\left|\langle \mathit{i}|{\hat{\mathit{H}}}_{\perp }|\mathit{j}\rangle \right|}^2\left|\langle \mathit{i}|{\hat{\mathit{P}}}_{\mathrm{S}}|\mathit{i}\rangle -\langle \mathit{j}|{\hat{\mathit{P}}}_{\mathrm{S}}|\mathit{j}\rangle \right|.$$ (5)

In Eq. 5, $|\mathit{i}\rangle$ and $|\mathit{j}\rangle$ are eigenstates of the time-independent spin Hamiltonian $\hat{\mathit{H}}$ (Eq. 1), with an eigenvalue difference ${\mathit{\nu }}_{\mathit{ij}}$, ${\hat{\mathit{P}}}_{\mathrm{S}}$ is the singlet projection operator, ${\hat{\mathit{H}}}_{\perp }$ is the Zeeman Hamiltonian for a weak static magnetic field perpendicular to the geomagnetic field, N is a normalization constant to ensure that the heights of the histogram bars sum to unity, and the sum runs over all pairs of energy levels in both radicals. This expression was averaged over 100 orientations of the geomagnetic field so as to sample the relevant range of interactions.

Results

To address the results of the behavioral experiments and their interpretation, we consider the effects of monochromatic radiofrequencies and broadband radiofrequency noise on both FAD-Z and FAD-Trp radical pairs. For each radical pair, we start with the action-spectrum histogram to get an impression of which frequencies can be expected to elicit large effects. We then present simulations of the singlet yield, Φ_S. As described in the Methods section, these simulations were performed for radical pairs with lifetime τ = 1 ms and root-mean-square radiofrequency field B_1,rms = $5\mathrm{.0}/\sqrt{2}$ μT.

FAD-Z radical pair

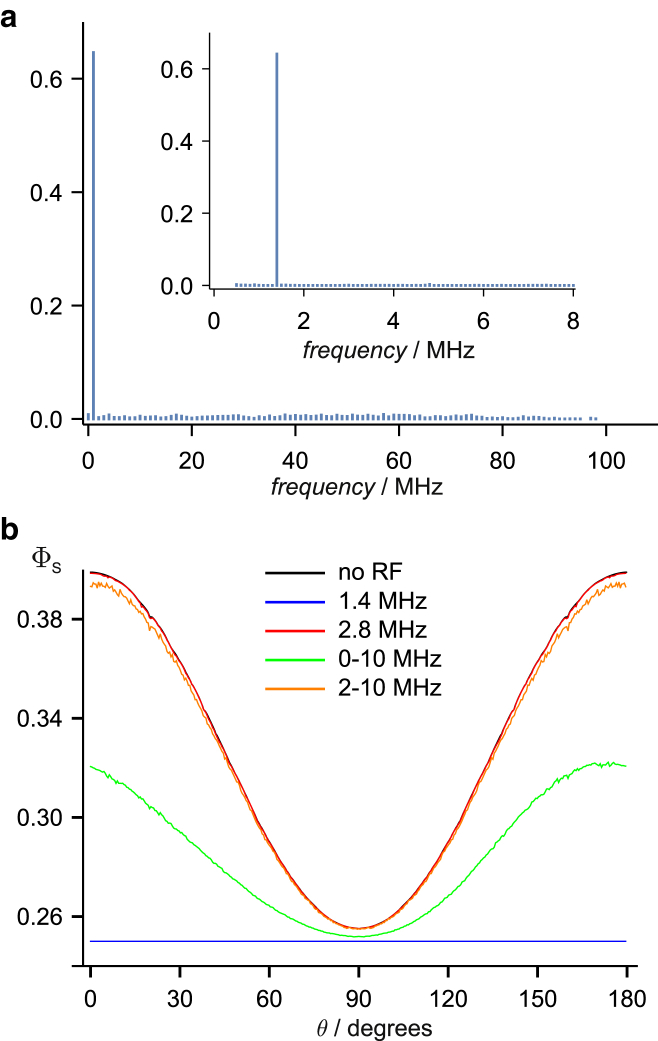
We first examine the radical pair comprised of a flavin anion radical, FAD^•−, and a radical with no hyperfine couplings, Z^•. Following Lee et al. (35), the former contains the seven nuclei with the largest anisotropic hyperfine interactions. Dipolar and exchange interactions between the radicals were not included at this stage. The action-spectrum histogram (Fig. 3 a) is dominated by the bin containing the Larmor frequency (1.4 MHz) as a direct result of the unique energy-level spacing in Z^•. The resonance effects attributable to FAD^•− are spread fairly uniformly over the 100 bins between 1 and 100 MHz, with each individual bar being ∼1% of that at 1.4 MHz. The maximum frequency in the histogram corresponds to the gap between the highest- and lowest-energy eigenstates of the hyperfine Hamiltonian of FAD^•−. Fig. 3 a suggests that a radiofrequency field at the Larmor frequency should have a much stronger effect than any other single frequency. We discuss the likely width of the Larmor resonance in a later section.

Figure 3.

FAD-Z radical pair with no exchange or dipolar interactions. (a) Action-spectrum histogram showing a dominant peak at the Larmor frequency, 1.4 MHz, and much smaller features in the range 0−100 MHz (bin width, 1 MHz). Inset: an expanded portion of the main figure (bin width, 0.1 MHz). (b) The anisotropic singlet yield, Φ_S(θ), in the presence of 1.4 and 2.8 MHz single-frequency fields and 0–10 and 2–10 MHz broadband fields. The 2–10 MHz trace (orange) is very similar to the singlet yield in the absence of a radiofrequency field (black), and the 2.8 MHz simulation (red) is almost indistinguishable from it.

Simulations of the singlet yield, shown in Fig. 3 b, reflect the form of the histogram. In the absence of a time-dependent magnetic field, Φ_S shows a relatively strong, approximately sinusoidal dependence on the direction of the static magnetic field, which is completely flattened by a radiofrequency field at the Larmor frequency. By contrast, a field of the same amplitude oscillating at double the Larmor frequency has a negligible effect. Broadband noise extending from 1 to 10 MHz significantly alters the shape and amplitude of Φ_S; its exact form depends on the (randomly chosen) amplitude, phase, and direction of the component of the noise at 1.4 MHz (Fig. S1). A band of noise that does not contain the Larmor frequency (2–10 MHz) causes a much smaller change in Φ_S. As expected from the histogram, radiofrequency fields oscillating faster than ∼100 MHz were found to have no effect on Φ_S (data not shown).

FAD-X radical pair

As argued above, it is unlikely that a FAD-Z-type radical pair could exist without the “isolated” electron in Z^• experiencing a small local magnetic field due to nearby spins. To test the effect of weak additional interactions, we add just one of the possible interactions to the calculation presented in Fig. 3—a dipolar coupling between the electron spins in Z^• and FAD^•−. This radical pair is denoted FAD-X. We use (somewhat arbitrarily) the interaction appropriate for the separation (1.9 nm) of the FAD and Trp radicals in cryptochrome (dipolar coupling parameter, D = −407 μT). The histogram in Fig. 4 a shows clearly that inclusion of even this single weak interaction abolishes the special resonance at the Larmor frequency and spreads its intensity into the frequency bins between 1 and ∼10 MHz. This is also evident from the complementary singlet yield calculations in Fig. 4 b. Now, single-frequency oscillating fields at 1.4 and 2.8 MHz have the same qualitative effect, which is significantly less pronounced than the effect of both 1−10 MHz and 2−10 MHz broadband noise fields. Evidently, the cumulative effect of the ∼10⁴ frequency components present in the noise outweighs the effect of a single-frequency field, even though the root-mean-square intensity is the same in the two cases. Now that there is no isolated electron spin, inclusion of a component at 1.4 MHz is no longer necessary for the noise to have a strong influence on Φ_S.

Figure 4.

FAD-Z radical pair with a dipolar coupling, D = −407 μT. (a) Action-spectrum histogram comprising frequencies spread over the range 0−100 MHz (bin width, 1 MHz). Inset: an expanded portion of the main figure (bin width, 0.1 MHz). The strong peak at the Larmor frequency (Fig. 3a) has been abolished by the dipolar interaction. (b) The anisotropic singlet yield, Φ_S(θ), in the presence of 1.4 and 2.8 MHz single-frequency fields and 0–10 and 2–10 MHz broadband fields. The 1.4 MHz (blue) and 2.8 MHz (red) traces are very similar to the singlet yield in the absence of a radiofrequency field (black).

FAD-Trp radical pair

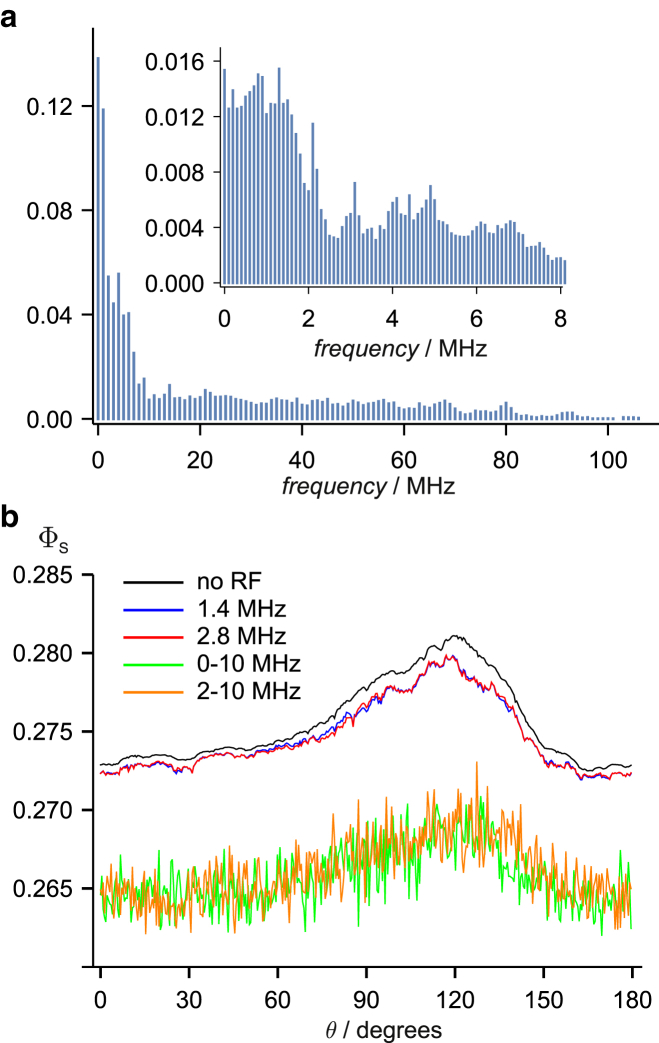
We now examine the behavior of the FAD-Trp radical pair, including the seven largest hyperfine interactions in both FAD^•− and the tryptophan radical, TrpH^•+ (again following Lee et al. (35)). The action-spectrum histogram (Fig. 5 a) has a roughly uniform distribution of bar heights from 1 to ∼100 MHz; no particular frequencies stand out in the way that 1.4 MHz did for FAD-Z (Fig. 3 a). As previously noted by Hiscock et al. (40), the singlet yield (Fig. 5 b) shows a sharp “spike”, arising from avoided energy-level crossings, when the geomagnetic field vector lies in the plane of the tricyclic aromatic ring system of the FAD (θ = 90°). Consistent with the histogram, both 1.4 and 2.8 MHz radiofrequency fields have similarly small effects on Φ_S; the same should be true of any single-frequency field in the range 1–100 MHz. As in the case of the FAD-X radical pair, broadband fields have a more pronounced effect attributable to the simultaneous excitation of resonances throughout the 1 kHz−100 MHz range. Note, however, that the effect of the noise field here is mainly on the “background” part of Φ_S; the spike, which Hiscock et al. (40) suggested could offer a precise compass bearing, has not been strongly affected. Inclusion of dipolar coupling in this 16-spin calculation is impractical, but for a simplified spin system, we find the same qualitative difference between noise and single-frequency fields as found for FAD-X (Fig. 6; also note that the inclusion of dipolar coupling destroys the spike at θ = 90°).

Figure 5.

FAD-Trp radical pair with no exchange or dipolar interactions. (a) Action-spectrum histogram containing frequencies spread roughly uniformly over the range 0−100 MHz (bin width, 1 MHz). (b) The anisotropic singlet yield, Φ_S(θ), in the presence of 1.4 and 2.8 MHz single-frequency fields and 0–10 and 70–80 MHz broadband fields. The 1.4 MHz (blue) and 2.8 MHz (red) traces are very similar to the singlet yield in the absence of a radiofrequency field (black).

Figure 6.

Simplified FAD-Trp radical pair with a dipolar coupling, D = −407 μT. (a) Action-spectrum histogram (bin width, 1 MHz). This plot is more structured than the histogram in Fig. 5a because of the reduced number of nuclear spins. (b) The anisotropic singlet yield, Φ_S(θ), in the presence of 1.4 and 2.8 MHz single-frequency fields and a 0–10 MHz broadband field. The 1.4 MHz (blue) and 2.8 MHz (red) traces are almost indistinguishable. The following hyperfine interactions were included: in FAD^•−, N5, N10, H6, and H8; and in TrpH^•+, N1, H1, H2, and H4. The narrow spike at θ = 90° (Fig. 5b) has been abolished by the dipolar interaction.

Width of Larmor resonance

An important consideration when planning behavioral experiments is the width of the Larmor resonance expected for a FAD-Z-type radical pair. By this we mean, how wide is the range of frequencies that will excite this special resonance? Assuming Z^• experiences only the geomagnetic field, there are two sources of line broadening: the lifetime of the radicals (τ) and the strength of the radiofrequency field (B₁). Their contributions are ∼ $1/\pi \tau$ and ${\gamma }_{\mathrm{e}}{\mathit{B}}_1/2\pi$, respectively. If, as above, we assume that the radiofrequency field only has a significant effect on the spin dynamics when ${\gamma }_{\mathrm{e}}{\mathit{B}}_1\tau /2\pi \ge 1$, then the B₁ contribution clearly dominates. Therefore, if the frequency of the time-dependent field is offset from the Larmor frequency by more than a few multiples of ${\gamma }_{\mathrm{e}}{\mathit{B}}_1/2\pi$ it should have little effect on the radical pair. This prediction is confirmed by simulations of Φ_S for the FAD-Z radical pair subject to 5 μT monochromatic radiofrequency fields of different frequencies (Fig. S2). The attenuation of the anisotropy of Φ_S is greatly reduced when the time-dependent field is off resonance by more than twice ${\gamma }_{\mathrm{e}}{\mathit{B}}_1/2\pi$.

Discussion

Relation to experiment

The calculations described above were performed on the basis that the dependence of the singlet yield, Φ_S, on the local direction of the geomagnetic field would somehow allow a bird to derive a magnetic compass bearing. How this might be achieved in vivo is completely unknown. We can therefore only speculate on the extent to which Φ_S must have changed if a radiofrequency field causes a bird to become magnetically disoriented. Most authors have assumed, somewhat naively in our view, that all, or at least a large part, of the anisotropy of Φ_S would need to be abolished so that little or no directional information would remain. It is difficult to justify such an assumption given the current level of ignorance of what a bird actually perceives when it senses the geomagnetic field and how it processes the directional information. For example, anthropogenic radiofrequency noise with a root-mean-square amplitude that varied from one second to the next could render the output of the sensor so variable as to cause the bird to disregard it until such time as the signal became more stable. Similarly, although to human eyes the spike predicted for FAD-Trp-type radical pairs (40) is still clearly visible in the singlet yield when the radical pairs are subject to broadband radiofrequency noise (Fig. 5 b), this does not necessarily mean that the birds can still use it for orientation in the presence of a highly variable background. We therefore refrain from making definite predictions about whether a given change in Φ_S would or would not be expected to prevent a bird from using its magnetic compass.

We start by comparing the values of the parameters in the above simulations either with those used in the behavioral experiments or with independent estimates. The strength of the monochromatic radiofrequency fields, B₁, was chosen to be 5 μT. To obtain the same root-mean-square intensity for the broadband fields, the amplitudes of the 10⁴ frequency components in a 10-MHz-wide band of radiofrequency noise were chosen to give a root-mean-square noise density of $5\mu \mathrm{T}/\sqrt{2}\sqrt{10\mathrm{MHz}}$ = 1.12 nT Hz^−1/2. The lifetime of the radical pairs, τ, determined by their recombination reactions, was taken as 1 ms. The effective lifetime of the spin coherence in these calculations, τ_coh, is therefore also ∼1 ms. These values were chosen to satisfy ${\gamma }_{\mathrm{e}}{\mathit{B}}_1{\tau }_{\mathrm{coh}}/2\pi$ ≥ 1 so that even a single component of the broadband noise could have an appreciable effect on the spin dynamics. In all the studies of the effects of time-dependent magnetic fields on the behavior of migratory birds, the measured values of B₁ have been significantly smaller than those used here. For example, Ritz et al. (12) and Schwarze et al. (18) reported disorientation of European robins by a 15 nT Larmor-frequency field and by ∼1 pT Hz^−1/2 broadband noise, respectively. Moreover, τ_coh = 1 ms seems implausibly long for the spin-coherence lifetime of an organic radical in a biological setting at physiological temperatures. Molecular dynamics simulations of the motions of flavin and tryptophan radicals in cryptochrome combined with realistic hyperfine, exchange, and dipolar interactions suggest that τ_coh is closer to 1 μs than to 1 ms (20). Taken together, the reported values of B₁ and estimates of τ_coh lead to the conclusion ${\gamma }_{\mathrm{e}}{\mathit{B}}_1{\tau }_{\mathrm{coh}}/2\pi$ ≪ 1, so that experimentally relevant effects of time-dependent fields on Φ_S would be several orders of magnitude smaller than those shown in Figs. 3, 4, 5, and 6. The immediate conclusion, therefore, is that modeling of the sort described above cannot explain any of the reported effects of radiofrequency fields on the ability of migratory birds to orient in the Earth’s magnetic field.

This failure suggests that one or possibly more of the following is true. 1) The assumption that ${\gamma }_{\mathrm{e}}{\mathit{B}}_1{\tau }_{\mathrm{coh}}/2\pi$ must be ≥1 is wrong, and the birds are in fact extraordinarily sensitive to tiny variations in the yield of the signaling state. This does not seem very likely given that the intensity of the Earth’s magnetic field naturally fluctuates by 25–50 nT in any 24 h period (41, 42) without obviously interfering with the ability of migratory birds to use their magnetic compass. 2) The spin-coherence lifetime might be >1 μs by several orders of magnitude. In molecular terms, we cannot begin to imagine how this could come about. The molecular motions responsible for spin relaxation would need to be of extraordinarily low amplitude or exceptionally fast or both (20, 39). 3) The current model of radical-pair magnetoreception is incomplete: there is some aspect of the primary sensing mechanism that makes the sensor respond significantly to exceedingly weak magnetic fields (43). Perhaps the external magnetic fields are locally amplified in some way before they are experienced by the radical pair. 4) The birds are disoriented by an effect of the magnetic component of the radiofrequency field on some other part of the magnetoreception signaling pathway. We are unable to suggest a plausible mechanism for this. 5) The birds are disoriented by an effect of the electric component of the radiofrequency field on the magnetoreception signaling pathway. We cannot offer a plausible mechanism for this either. 6) The birds are prevented from using their magnetic compass by some unknown effect of the radiofrequency field on their motivation, the origin of which is unrelated to magnetoreception.

It is interesting that both snapping turtles (28) and wood mice (29) have been reported to change their orientation in the geomagnetic field when subject to a radiofrequency field. This suggests that, in some cases, time-dependent fields may modify the magnetic information the animals use to orient themselves rather than rendering it useless or unreliable.

It does not seem profitable to speculate further on the alternatives set out above. Rather, we discuss the above results assuming that the disorientation of birds exposed to radiofrequency fields is a genuine effect on the spin dynamics of photo-induced radical pairs and that there is some unknown mechanism that causes the effects to be much larger than would be expected on the basis of the magnitude of ${\gamma }_{\mathrm{e}}{\mathit{B}}_1{\tau }_{\mathrm{coh}}/2\pi$.

Discrimination between different types of radical pairs

We start by attempting to generalize our results for two types of radical pairs. “FAD-Z-type” pairs have no significant coupling between the radicals and Z^• has no significant hyperfine interactions. “FAD-Trp-type” pairs may or may not have radical-radical couplings, but both radicals have significant hyperfine interactions. FAD-X pairs therefore fall into the FAD-Trp category. By “significant” interactions we mean “not negligible compared to 50 μT.” Although we continue to use the FAD, Trp, and Z labels for the sake of clarity, the following is intended to apply more generally to organic radical pairs that fall into one or another of the above categories. When we talk about the “effect” of a particular radiofrequency field condition, we mean the change in the anisotropy of ${\Phi }_{\text{S}}$. To compare like with like, the time-dependent magnetic fields, whether single-frequency or broadband (bandwidth ≥5 MHz), are taken to have the same root-mean-square amplitude. The Larmor frequency is denoted ${\nu }_{\mathrm{L}}$.

A FAD-Z-type radical pair is more strongly affected by a single-frequency field at ${\nu }_{\mathrm{L}}$ than by one at neighboring frequencies, e.g., 0.5 ${\nu }_{\mathrm{L}}$ and 2 ${\nu }_{\mathrm{L}}$. It is more strongly affected by a Larmor-frequency field than by a broadband field, and more strongly affected by a broadband field that includes ${\nu }_{\mathrm{L}}$ than by one that does not. A FAD-Trp-type radical pair is affected to a similar extent by single-frequency fields at ${\nu }_{\mathrm{L}}$ and at neighboring frequencies, e.g., 0.5 ${\nu }_{\mathrm{L}}$ and 2 ${\nu }_{\mathrm{L}}$. Broadband fields have a similar effect whether or not they include ${\nu }_{\mathrm{L}}$. Broadband fields have a stronger effect than a Larmor-frequency field, but neither appears to have a strong effect on the spike that is predicted to arise from avoided level crossings in the absence of dipolar coupling.

A clear distinction between the two types of radical pairs requires comparative experiments, using different single frequencies or different bands of noise or a comparison of single-frequency fields with broadband fields. Observation of a disrupting effect at the Larmor frequency does not prove that the radical pair is of FAD-Z-type unless it can also be shown that a similar response at other frequencies requires a substantially stronger B₁ field. Likewise, a response to a broadband field does not identify the radical pair as FAD-Trp-type unless it occurs for a noise band that excludes ${\nu }_{\mathrm{L}}$ as well as one that includes ${\nu }_{\mathrm{L}}$. A further argument in favor of comparative tests is that the theoretical predictions are on safer ground. Given all the unknowns, it is currently impossible to forecast quantitatively the outcome of a single experiment. However, it ought to be possible to devise experimental conditions with the qualitative expectation—derived from simulations such as those presented here—that the effect of condition A should be similar to that of condition B and larger than that of condition C, and so on.

Diagnostic test for a radical-pair magnetoreceptor

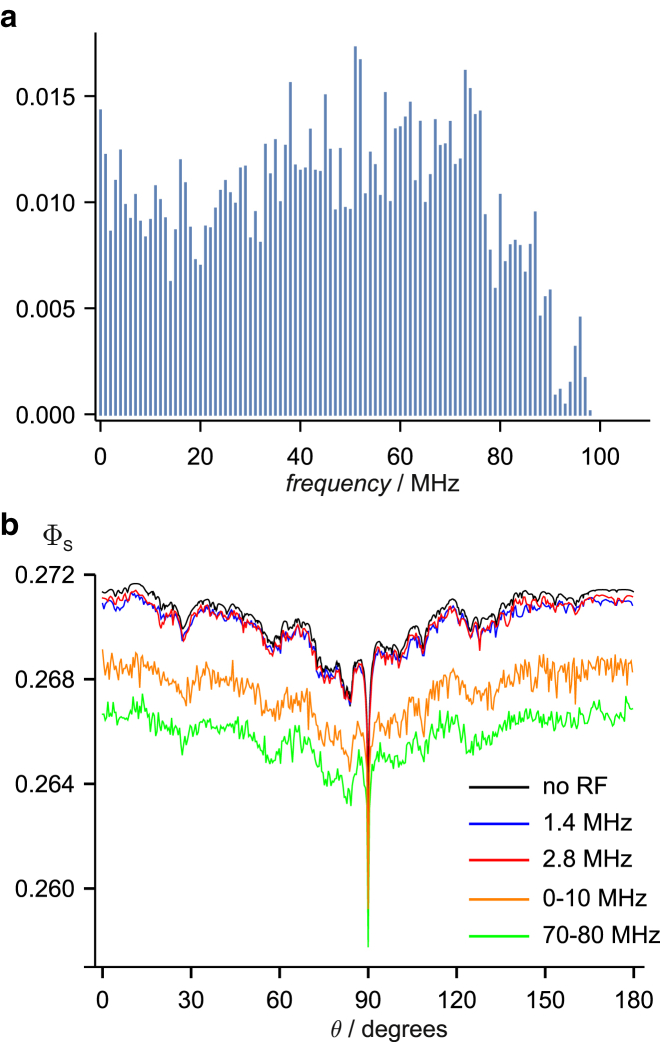
The original motivation for testing migratory birds in radiofrequency fields was to discriminate between a radical-pair mechanism and a magnetite-based mechanism (1). Despite the reports of radiofrequency disruption of the ability of birds to use their magnetic compass, it has still to be convincingly demonstrated that the primary magnetoreceptor is a radical pair. Hitherto, birds have not been tested at radiofrequencies exceeding ∼10 MHz. Looking at the histograms in Figs. 3, 4, 5, and 6, it is apparent that all but very simple or specialized (e.g., FAD-Z-type) radical pairs should be influenced by time-dependent fields at frequencies significantly higher than 10 MHz. Therefore, as an additional test for the existence of a radical pair sensor, we suggest that broadband noise centered at 75 MHz with a 10 MHz bandwidth would be a good choice for future experiments. The majority of biologically plausible organic radicals should have energy-level spacings in this range. Simulations for FAD-Trp, shown in Fig. 5 b, suggest that the effect of a 70–80 MHz band should be similar to those already observed for 0–10 MHz noise. Our simulations indicate that if FAD-Z is the in vivo radical pair, this band of frequencies should be much less effective at disorienting the birds than 0–10 MHz. Indeed, this comparative experiment would effectively discriminate between FAD-Z-type and FAD-Trp-type radical pairs. A control experiment to guard against possible artifacts could employ a 10 MHz band of noise of the same intensity but at a much higher frequency. When 12−15 hyperfine interactions are included in each radical, instead of just the seven strongest (as in Fig. 5), the maximum resonance frequencies for the FAD and Trp radicals are ∼120 and ∼100 MHz, respectively. If there is an appreciable coupling between the radicals, the maximum resonance frequency could be as large as the sum of these frequencies, i.e., 220 MHz. We therefore suggest that 240−250 MHz would be an appropriate negative control condition for future experiments. Additionally, if the maximum resonance frequency could be determined to within, say, 10 MHz it would provide powerful clues to the identity of the radicals. We appreciate that the use of frequencies much higher than 10 MHz may present serious technical challenges.

Width of Larmor resonance

The linewidth of any Larmor resonance observed for a FAD-X-type radical pair potentially contains information on the dipolar interaction and therefore the separation of the radicals. If, as described above (Fig. S2), one only has to step a few multiples of ${\gamma }_{\mathrm{e}}{\mathit{B}}_1/2\pi$ away from the Larmor frequency to be well off resonance, then the local magnetic interactions in Z^• would have to be small compared to B₁. Had this been sought and found in the study of Ritz et al. (12), for example, it would have implied a dipolar coupling <15 nT, corresponding to an unbelievably large distance between the radicals of >57 nm. The results of Ritz et al. (12) put an upper limit of 0.5 ${\nu }_{\mathrm{L}}$ on the linewidth of the Larmor resonance. If this were due entirely to the dipolar interaction, it would imply a distance of >4.8 nm, which also seems rather large.

Experimental protocols

As outlined in the Introduction, there have been conflicting reports of the ability of migratory birds to use their magnetic compass when exposed to radiofrequency fields. Part of the problem is that the experimenter, unable consciously to sense either static or time-dependent magnetic fields, can easily overlook gross artifacts in magnetic-stimulus protocols. To increase the chance that future experiments can be independently replicated, we recommend that both static and time-dependent magnetic fields are carefully recorded before, and ideally during, behavioral experiments, and that both measurements and measurement techniques are reported in detail. The minimum requirements, in our view, are 1) the intensity, direction, and spatial uniformity of the static field; 2) the spectrum of the magnetic and electric components of the radiofrequency field (up to at least 100 MHz), showing clearly any harmonics or other spurious frequencies, the level of background noise, and the bandwidth of artificially generated noise fields; 3) the frequency span of nominally single-frequency fields; and 4) the amplitude of radiofrequency noise (in T Hz^−1/2), whether or not intentionally added. We recommend the following items of high-quality equipment for such measurements: the Rohde & Schwarz (Munich, Germany) FSV signal and spectrum analyzer (10 Hz–3.6 GHz) combined with carefully calibrated antennas such as Schwarzbeck Mess-Electronik’s (Schönau, Germany) EFS 9218 (9 kHz–300 MHz, for electric fields), FMZB 1513 (9 kHz–30 MHz, for magnetic fields), and HFS 1546 (150 kHz–400 MHz, for >30 MHz magnetic fields); and the Narda Safety Solutions (Pfullingen, Germany) EFA-300 field analyzer (5 Hz–32 kHz, for <30 kHz magnetic and electric fields). Static fields should be measured with a tri-axial fluxgate magnetometer (e.g., MEDA FVM400). Only with the accurate measurements provided by such equipment will it be possible to judge whether, for example, the birds’ orientation is disrupted by a particular frequency component or by the radiofrequency noise that accompanies it.

Conventional laboratories are not suitable for carefully controlled magnetic sense experiments because of the distortions to static magnetic fields introduced by the steel reinforcing bars in concrete walls and foundations. The ideal is a dedicated facility built exclusively from non-magnetic materials (typically wood, brass, and aluminum) in a location where the geomagnetic field is undisturbed (e.g., (17, 18)). If necessary, such facilities should be shielded from electromagnetic noise by enclosure in an aluminum Faraday cage or moved to a rural location well away from anthropogenic sources of electromagnetic interference.

Conclusions

The principal conclusion from this study is that the current model of radical-pair magnetoreception is unable to explain any of the reported effects of radiofrequency fields on the ability of migratory birds to orient in the Earth’s magnetic field. To predict appreciable changes in the yield of a signaling state, we had to choose radiofrequency field strengths significantly larger than used in the experiments and assume an unfeasibly long spin-coherence lifetime (which would need to be even longer to see effects of weaker radiofrequency fields). Proceeding on the basis that there is an unknown mechanism that amplifies the predicted effects, we reached several secondary conclusions. 1) Any plausible amount of dipolar coupling between the two radicals abolishes both the resonance effect at the Larmor frequency and the “spike” predicted for FAD-Trp-type radical pairs. 2) In the presence of dipolar coupling, broadband radiofrequency noise has a larger effect on the spin dynamics than does a monochromatic radiofrequency field of the same root-mean-square amplitude. 3) It should be possible to distinguish the two main types of proposed radical-pair detectors by means of behavioral experiments using broadband and/or single-frequency radiofrequency fields. 4) Additional diagnostic tests for a radical-pair magnetoreceptor may shed further light on the existence and identity of the putative radical pair sensor.

Author Contributions

H.G.H., D.E.M., and P.J.H. conceived and designed the study. H.G.H. performed the calculations. All authors discussed the results and conclusions. H.G.H. and P.J.H. wrote the manuscript with advice from H.M. and D.E.M.

Editor: Elsa Yan.