Determination of Cell Membrane Capacitance and Conductance via Optically Induced Electrokinetics

Abstract

Cell membrane capacitance and conductance are key pieces of intrinsic information correlated with the cellular dielectric parameters and morphology of the plasma membrane; these parameters have been used as electrophysiological biomarkers to characterize cellular phenotype and state, and they have many associated clinical applications. Here, we present our work on the non-invasive determination of cell membrane capacitance and conductance by an optically activated microfluidics chip. The model for determining the cell membrane capacitance and conductance was established by a single layer of the shell-core polarization model. Three-dimensional finite-element analyses of the positive and negative optically induced dielectrophoresis forces generated by the projected light arrays of spots were performed, thus providing a theoretical validation of the feasibility of this approach. Then, the crossover frequency spectra for four typical types of cells (Raji cells, MCF-7 cells, HEK293 cells, and K562 cells) were experimentally investigated by using a micro-vision based motion-tracking technique. The different responses of these cells to the positive and negative ODEP forces were studied under four different liquid conductivities by automatic observation and tracking of the cellular trajectory and texture during the cells’ translation. The cell membrane capacitance and conductance were determined from the curve-fitted spectra, which were 11.1 ± 0.9 mF/m² and 782 ± 32 S/m², respectively, for Raji cells, 11.5 ± 0.8 mF/m² and 114 ± 28 S/m² for MCF-7 cells, 9.0 ± 0.9 mF/m² and 187 ± 22 S/m² for HEK293 cells, and 10.2 ± 0.7 mF/m² and 879 ± 24 S/m² for K562 cells. Furthermore, as an application of this technique, the membrane capacitances of MCF-7 cells treated with four different concentrations of drugs were acquired. This technique introduces a determination of cell membrane capacitance and conductance that yields statistically significant data while allowing information from individual cells to be obtained in a non-invasive manner.

IntroDuction

The cell is a fundamental building block of structures in living organisms, representing the complexity of living systems (1). All life activities, such as cellular growth (2), mitosis (3), migration (4), and apoptosis (5), are directly or indirectly correlated with the intrinsic information of cells. Consequently, acquiring such cellular information is critical for characterizing cell function and further assessing a living organism’s status. In general, cell intrinsic information, which can be used to guide biomedical and bioengineering applications, such as disease diagnosis and pharmaceutical development, can be obtained through biochemical techniques (6). For example, the fluorescence method, a typical biochemical approach, is widely used to determine cell intrinsic information (7), owing to its accurate positioning and high specificity. However, this technology has several shortcomings. Specifically, 1) the auto-fluorescence on the surface of living cells strongly influences the fluorescence-based detection of labeled molecules, and 2) the signal/interference ratio of fluorescence images is typically low, and the fluorescence signal is also easy to quench, thus resulting in an inaccurate interpretation of the molecular reaction.

The biophysical properties of cells, such as the intrinsic electrical and mechanical information, can be used to characterize and forecast the cellular status via label-free and non-invasive approaches (8). The mechanism by which infrared light excites cells can be revealed by measuring the capacitance change of the cell membrane; this finding has important implications for the nervous system, cell signaling, and other organs (9). Real-time monitoring of stem-cell differentiation can also be realized by performing real-time, label-free quantitative detection of the differences in cell lineage dielectric properties with impedance sensing (10). On the basis of the different electrophysiological properties of oral squamous cell carcinoma cells with different tumorigenic characteristics, the cellular tumorigenicity can be characterized by monitoring the cell-membrane capacitance change, thus providing a reliable and label-free approach for the discrimination of putative tumorigenic cells in larger populations (11). Consequently, substantial efforts have been dedicated to the research and development of biophysical methods capable of acquiring cell intrinsic information in a non-invasive, label-free, and rapid manner. For instance, patch-clamp technology can accurately record the cell-membrane capacitance of individual cells by detecting ionic channel currents in real time (12). This method is a typical low-noise measurement technique; however, the throughput and parallelization of this approach are restricted by the formation of seals between the micropipette and the cell membrane. This technique is generally difficult, and hence, the measurement efficiency is also low. The microfluidics method is another prevalent technique that can be used to obtain cell-membrane capacitance/conductance through use of custom-designed microfluidics structures (13). However, the measurement efficiency and performance of this scheme depend strongly on the use of microstructures with specific and sophisticated designs tailored to the cell size; the microstructures cannot be altered after they are fabricated by the conventional micro-matching technique. Owing to their non-invasive and non-contact properties, the alternating-current (AC) electrokinetics-based techniques using non-uniform electrical fields generated by the physical metal microelectrodes are promising and have been widely used for measuring the electrical parameters of cells, such as dielectrophoresis (DEP) (14) and electro-rotation (15). This mechanism can determine the cell-membrane/cytoplasm/nucleus capacitance and conductance in large populations by experimentally investigating the displacement-frequency spectra of the cells. In addition, a prerequisite of achieving the target of generating the non-uniform electric field is that the unique conductive metal electrodes must be fabricated through standard micro-lithographic techniques. However, these metal electrodes cannot be changed once they are made and they also cannot be recycled, which means that manipulation of the cells at the desired purpose is difficult and the flexibility and performance of this method is decreased.

Opto-electronic tweezers (OETs) or optically induced DEP (ODEP) have operational principles similar to those in the AC electrokinetics-based method, i.e., they rely on a non-uniform electric field to manipulate objects. However, OETs and ODEP can provide the capabilities of dynamic, parallel, and programmable micro-/nano-scaled manipulation by using virtual electrodes generated by optically projected images in an optical-electrical coupled microfluidics chip (16). Hence, these techniques have been exploited in a series of applications in micro-/nano-material and bio-related fields, such as the rapid manipulation and fabrication of micro-/nano-structures using various nano-materials (17, 18). In the biomedical and bioengineering fields, these techniques have been demonstrated to work well with cells in a non-invasive and non-destructive manner (19, 20). Our team have presented the intrinsic mechanical information of cells (i.e., mass and density) which can be rapidly determined using ODEP and other optically induced electrokinetics (OEK) forces (21, 22). Recently, we have also reported that the cell membrane capacitance of Raji cells can be estimated by experimentally investigating the translational motion of individual cells and acquiring the crossover frequency of the cells (23). However, in the work reported in (23), the theoretical model could only roughly estimate the membrane capacitance of cells, and hence, a much more accurate model is required. Moreover, only limited parametric studies were conducted, and experimental samples were used in that study. For example, the cell-membrane capacitance was obtained using only one value of liquid conductivity, and the statistical properties from multiple types of cells were lacking. Furthermore, the software used in that work did not have the ability to track the translation of multiple cells simultaneously.

To overcome the existing technical barriers to the accurate determination of the cell-membrane capacitance/conductance, this article reports our recent work on the non-invasive determination of cell-membrane capacitance/conductance by tracking four types of cell translation motions in OEK chips through the micro-vision technique. The cell-membrane capacitance/conductance determination model was introduced using a curve-fit function, and finite-element analyses (FEAs) of three-dimensional ODEP force were performed to validate the feasibility of this method. Then, the crossover frequencies of the four types of cells versus four different liquid conductivities were experimentally investigated using an image-processing algorithm to determine the crossover frequency. Here, we examine the corresponding cell-membrane capacitance/conductance determined by the above process, alongside the variations in membrane capacitance of MCF-7 cells treated with four different concentrations of drugs.

Materials and Methods

Chip structure and experimental system

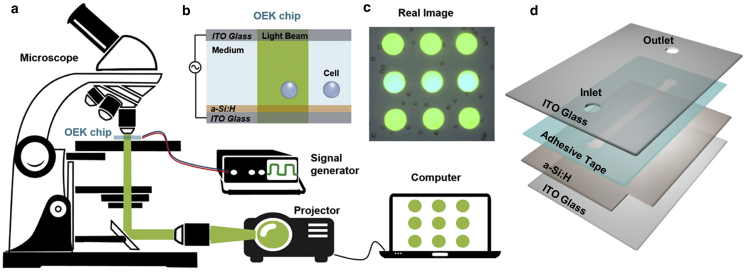
Fig. 1 is a diagrammatic illustration of the experimental setup in this study, and the photograph of the actual system is from our prior work (18). An available graphics software package (Flash Professional CC; Adobe, San Jose, CA) was used to produce the desired virtual electrodes that were projected onto the OEK chip through a liquid-crystal display projector (VPL-F400X; Sony, Tokyo, Japan). A condenser lens (MS plan, 50×; Nikon, Tokyo, Japan) was placed between the liquid-crystal display projector and the OEK chip to focus the optical image onto the OEK chip. The manipulated cells were recorded using a charged coupled device (DH-SV1411FC; DaHeng Image, Beijing, China) mounted on a microscope (Zoom 160; Optem Engineering, Calgary, Alberta, Canada). An AC bias potential applied to the top and bottom indium tin oxide (ITO) glass substrates powered the OEK chip by a function generator (33522A; Agilent, Santa Clara, CA).

Figure 1.

(a) Generalized illustration of the experimental equipment for the OEK platform used to manipulate cells in this study. (b) Schematic configuration of the OEK chip. (c) Captured image of real cells. (d) Exploded view of the OEK chip. To see this figure in color, go online.

A schematic of the OEK chip configuration used in this study is presented in Fig. 1 b. In general, the OEK chip was composed of four layers: a top glass layer with a transparent and conductive ITO film; a thin film of photoconductive hydrogenated amorphous silicon (a-Si:H); a fabricated adhesive tape with the custom-designed microchannel; and a bottom ITO glass layer. To prepare the ITO glass, an 800-μm-thick glass substrate was coated with a 180 ± 10 nm ITO film using sputtering thin-film technology, and two through-holes with diameters of ∼1 mm were mechanically drilled using a glass driller. With the plasma-enhanced chemical vapor deposition technique, a 1-μm-thick a-Si:H layer was deposited onto the ITO surface of the glass. The microstructure was fabricated on double-sided adhesive tape (3M 9009; 3M China, Shanghai, China) utilizing a CO₂-laser engraving machine (FL-570; Hengchunyuan Machinery Equipment, Liaocheng City, China). Fig. 1 c is a still image of cells captured when the optically projected arrays of 3 × 3 spots were used as the virtual electrodes. Fig. 1 d clearly shows the OEK chip structure in exploded view.

Cell preparation

Raji cells, MCF-7 cells, human embryonic kidney (HEK) 293 cells, and K562 cells, were obtained from the cell bank of the Chinese Academy of Sciences. The Raji cells, MCF-7 cells, and K562 cells were maintained in Roswell Park Memorial Institute 1640 medium (Sigma-Aldrich, St. Louis, MO) supplemented with 10% (v/v) fetal calf serum, 1% penicillin (v/v) (100 U/mL), and 1% streptomycin (v/v) (100 μg/mL). The HEK293 cells were maintained in Dulbecco’s modified Eagle’s medium (high glucose) supplemented with 10% (v/v) fetal calf serum, 1% penicillin (v/v) (100 U/mL), and 1% streptomycin (v/v) (100 μg/mL). Some of the MCF-7 cells were further cultured by adding resveratrol dissolved in dimethylsulfoxide to the RPMI-1640 medium to final concentrations of 50, 100, 150, and 200 μg/mL.

The subsequent cell preparation processes for the Raji cells and K562 cells were the same as those used for the MCF-7 cells and HEK293 cells. Hence, we used the Raji cells and HEK293 cells as examples to describe the details of cell treatment in this study. Before each experiment, 1 mL of the Raji cell suspension was centrifuged at 1000 Rpm for 5 min at 4°C with the supernatant discarded. Then, the remaining Raji cells were washed twice with an isosmotic solution consisting of 0.2 M sucrose and bovine serum albumin with adjusted conductivities of 0.01, 0.02, 0.04, and 0.06 S/m. The purpose of adding bovine serum albumin to the isosmotic solution has been discussed and described in our previous work (20). The HEK293 cells were harvested from 50 to 60% confluent cultures after seeding by exposure to 0.25% trypsin-0.53 mM EDTA solution. Then, 1 mL of the HEK293 cell suspension was centrifuged at 1000 Rpm for 10 min at 4°C and washed twice in 0.2 M sucrose and Dulbecco’s modified Eagle’s medium (high glucose) with adjusted conductivities of 0.01, 0.02, 0.04, and 0.06 S/m.

The measured diameters were 12.2 ± 1.1, 16.3 ± 0.6, 16.6 ± 0.6, and 18.4 ± 0.7 μm for the Raji cells, MCF-7 cells, HEK293 cells, and K562 cells, respectively. Furthermore, cell counts were performed using a commercial hemocytometer (Qiujing, Shanghai, China) to allow a cell concentration of 1 × 10⁶ cells/mL to be used for each experiment conducted in this study.

Characterization of the cell-membrane capacitance/conductance determination model

Initially, nearly all of the applied AC bias potential dropped across the a-Si:H layer with no incident light illuminating the OEK chip. The a-Si:H layer behaved as an insulator, owing to its inherently lower conductivity. Instead, if an optical pattern from a computer transmitted by a commercial digital projector was projected onto a particular area of the a-Si:H surface, then the electron-hole pairs were excited and then increased by the migration of electrons from the valence band to the conduction band of the a-Si:H layer, thereby locally enhancing the conductivity of the a-Si:H via the photoconductive effect. Then, the electric field across the liquid chamber sharply increased above the locally illuminated a-Si:H area because the majority of the applied voltage was substantially transformed to the liquid chamber. Hence, a non-uniform electric field was created in the liquid chamber, and any suspended cells located in the vicinity of the non-uniform electric field would experience a force resulting from an interaction between the electrically polarized dipole moments of both the cells and the liquid solution. This force is known as the DEP force and is referred to herein as the “ODEP force” in the OEK chip. The time-averaged ODEP force (i.e., the DEP force) exerted on cells in a fluidic medium is defined as (24)

$$\langle {\overrightarrow{F}}_{\text{DEP}}\rangle =2\pi r^3{\epsilon }_{\text{m}}\mathrm{Re}\left[K\left(\omega \right)\right]\nabla {\left|{\overrightarrow{E}}_{\text{rms}}\right|}^2,$$ (1)

where r is the cell radius; ε_m is the permittivity of the liquid medium; E_rms is the root-mean-square value of the electric field; ω is the angular frequency, ω = 2πf, where f is the applied voltage frequency; and Re[K(ω)] is the real part of the Clausius-Mossotti factor, which reflects the polarization property of the cells against the liquid medium in a non-uniform electric field and is further expressed as

$$\mathrm{Re}\left[K\left(\omega \right)\right]=\mathrm{Re}\left[\frac{{\epsilon }_{\text{p}}^{\ast }-{\epsilon }_{\text{m}}^{\ast }}{{\epsilon }_{\text{p}}^{\ast }+2{\epsilon }_{\text{m}}^{\ast }}\right].$$ (2)

In the above equation, ε^∗ = ε – jσ/ω, where ε and σ are the permittivity and conductivity, respectively; the subscripts “p” and “m” denote the properties of the cell and liquid medium, respectively. Equation 2 indicates that the polarization property for one specific type of cells is directly related to the cell intrinsic information and liquid properties. Furthermore, the DEP force acting on cells can be positive or negative depending on the sign of the Re[K(ω)] value under a specific applied frequency of the AC voltage; i.e., when the value of the Re[K(ω)] is greater than zero, the cells experience a positive DEP force and are attracted to the illuminated areas of the OEK chip; for a negative value of the Re[K(ω)], a negative DEP force is exerted on cells, which will be repelled from the illuminated areas. Hence, in theory, the cells should present three different motions (attraction, repulsion, and no motion) in response to the optical pattern under different frequencies. An alternation between the two typical cellular translation responses (i.e., attraction and repulsion) versus the positive or negative DEP forces occurs when the polarization of the cell matches that of the liquid medium under a specifically applied AC bias potential. Then, the corresponding frequency (i.e., Re[K (ω)] = 0) is defined as the crossover frequency for this cellular motion shift (i.e., the cellular motion would change from attraction to repulsion, or vice versa, at this selected frequency), expressed as

$$f_{\text{crossover}}=\frac{1}{2\pi }\sqrt{\frac{\left({\sigma }_{\text{m}}-{\sigma }_{\text{p}}\right)\left({\sigma }_{\text{p}}+2{\sigma }_{\text{m}}\right)}{\left({\epsilon }_{\text{p}}-{\epsilon }_{\text{m}}\right)\left({\epsilon }_{\text{p}}+2{\epsilon }_{\text{m}}\right)}}.$$ (3)

According to the dielectric multi-shell polarization model, the single layer of the shell-core model has been widely used to represent a biological cell as a sphere of radius r surrounded by a thin membrane with a thickness d. The DEP crossover experiments were typically confined to frequencies well below the Maxwell-Wagner dispersion frequency, and the cell interior can be generally assumed to be much more conductive than the membrane (25). During the experiments, the cells can always retain their integrity. Accordingly, in this study, at all frequencies below the dispersion frequency, typically ∼1 MHz, the following approximations can be performed (25):

$$\begin{array}{c}{\epsilon }_{\text{p}}=\frac{r{\epsilon }_{\text{mem}}}{d}\\ {\sigma }_{\text{p}}=\frac{r{\sigma }_{\text{mem}}}{d}\end{array},$$ (4)

where subscript “mem” refers to the cell membrane. Furthermore, ε_mem/d and σ_mem/d can be rewritten as C_mem and G^∗_mem, which are the cell-membrane capacitance and cell effective total membrane conductance, respectively, as shown in Fig. 2. Then, Eq. 3 can be approximated and expressed in terms of the specific membrane capacitance and conductance as (26)

$$f_{\text{crossover}}=\frac{\sqrt{2}{\sigma }_{\text{m}}}{2\pi r{C}_{\text{mem}}}\sqrt{1-\frac{r{G}_{\text{mem}}^{\ast }}{2{\sigma }_{\text{m}}}-\frac{1}{2}{\left(\frac{r{G}_{\text{mem}}^{\ast }}{{\sigma }_{\text{m}}}\right)}^2}.$$ (5)

Using the theory proposed by Pethig et al. (27) and applying the simple binomial theorem and equivalent infinitesimal substitution method, Eq. 5 can be further approximately defined as,

$$f_{\text{crossover}}=\frac{\sqrt{2}}{2\pi r{C}_{\text{mem}}}{\sigma }_{\text{m}}-\frac{\sqrt{2}{G}_{\text{mem}}^{\ast }}{8\pi C_{\text{mem}}}.$$ (6)

The theory of Eq. 6 states that for one specific type of cells, if the relationship between f_crossover and σ_m can be experimentally obtained, then the cell membrane capacitance/conductance can be determined. We can assume that a plot of f_crossover versus σ_m is linear, with a slope and an f_crossover-axis intercept; then, the cell dielectric parameters can be expressed as follows, on the basis of Eq. 6:

$$\begin{array}{c}{C}_{\text{mem}}=\frac{\sqrt{2}}{2\pi r\times \text{slope}}\\ G_{\text{mem}}^{\ast }=-\frac{4\times {\text{intercept}}_{f_{\text{crossover}}}}{r\times \text{slope}}\end{array}.$$ (7)

In this study, we measured f_crossover for σ_m values of 0.01, 0.02, 0.04, and 0.06 S/m to derive the cell membrane capacitance/conductance dielectric parameters.

Figure 2.

Illustration of a single cell membrane. The phospholipid bilayer is equivalent to a combination of a resistor and capacitor under the action of DEP. To see this figure in color, go online.

Simulation

To test the feasibility of using the positive and negative ODEP forces exerted on the cells, a simulation of the spatial distributions of arrays of 3 × 3 spots inducing the ODEP forces was performed using an FEA simulation software package (COMSOL Multiphysics, version 5.1, COMSOL, Stockholm, Sweden). The diameter of each spot was 60 μm, and the space between any two adjacent spots was 30 μm. The time-harmonic analysis module, assuming a quasi-static current field with three-dimensional views, was used to solve Maxwell’s equations in the sub-domain of the liquid chamber. The corresponding boundary settings were the same as those discussed in our prior work (28). In this simulation example, the dark conductivity of a-Si:H was 1 × 10⁻¹¹ S/m and the photoconductivity was 4 × 10⁻⁵ S/m (experimental values for the a-Si:H film used in our work, as measured by a Keithley 2410 source meter); we used a liquid conductivity of 0.01 S/m as an example to perform the simulation. In addition, the relative dielectric constants of the liquid and a-Si:H were 78 and 11, respectively.

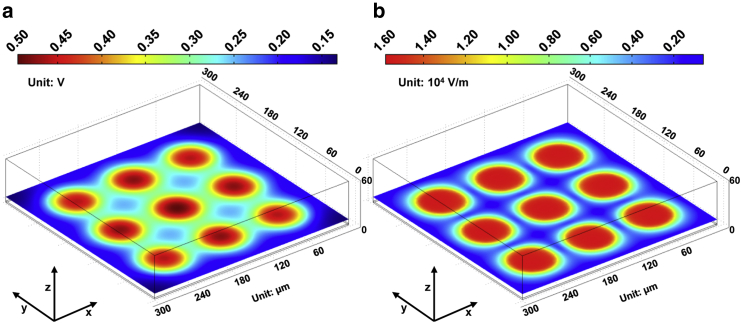
Fig. 3 a shows the FEA results for the voltage distribution at a height of 6 μm above the a-Si:H surface. The voltage changes were ∼0.35 V, and thus the generated ODEP was mainly from the voltage change instead of the shifted voltage. Furthermore, the voltages inside the illuminated areas were higher and the voltage changes around the optical spots were larger, meaning that the cells suspended at these locations would experience greater polarization, because the corresponding electric-field magnitudes would also be higher. Instead, the voltage changes located at the central areas created by any of the adjacent four spots were lower, and hence, the polarization magnitude generated by the optically induced electric field surrounding the cells was also lower, as further validated by the FEA of the electrical field shown in Fig. 3 b. As shown in Fig. 3 b, the changes in the electric-field magnitude around the illuminated areas were considerably larger, and the maximum values of the electric field were located at each of the nine spots. However, the electric-field gradient was also considerably lower at the location of any of the adjacent four spots and away from the illuminated areas. Consequently, the cells initially located at these areas would be stationary regardless of how the externally applied AC voltages and frequencies were changed.

Figure 3.

Simulation results of the spatial distribution of the voltage (a) and the electrical field (b) induced by the optically projected arrays of 3 × 3 spots at a height of 6 μm above the a-Si:H surface, respectively. To see this figure in color, go online.

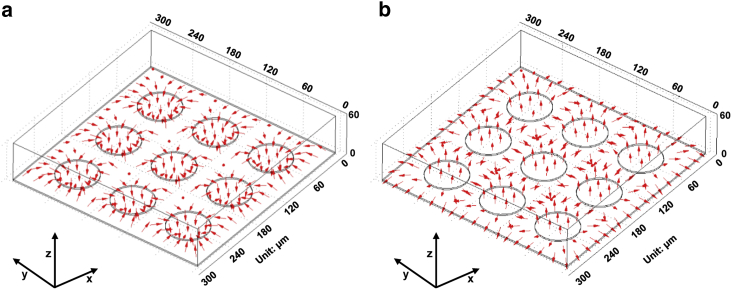
To further ascertain whether the arrays of 3 × 3 spots inducing ODEP forces could generate attracted and repelled motion of cells, respectively, especially at those areas between the two optical spots and among the three or four adjacent spots, the gradient of the square of the electric-field norm was calculated, as shown in Fig. 4. The simulation results in Fig. 4 a demonstrate that the cells would be attracted to the locations of the optical spots, depicted by arrows in this figure. Nevertheless, as shown in Fig. 4 b, if a negative ODEP force was exerted on the cells, then the cells would be repelled from the illuminated areas or pushed toward the central areas constructed by any of the two or four adjacent spots. Accordingly, the simulation in this section theoretically confirms the feasibility of using the arrays of spots to generate the positive/negative ODEP forces.

Figure 4.

Simulation results showing the positive (a) and negative (b) ODEP forces induced by optically projected arrays of 3 × 3 spots at a height of 6 μm above the a-Si:H surface. To see this figure in color, go online.

Results and Discussion

Determination of the cellular crossover frequencies by observing translational behaviors

Fig. 5 shows the experimental process for determining the Raji cell crossover frequency at a liquid conductivity of 0.01 S/m. Movie S1 provides the complete experimental details. Generally, the crossover frequency was acquired on the basis of the different translational motions of the Raji cells under various applied frequencies with a step size of 1 kHz. As shown in Fig. 5 b i, the optically projected arrays of 3 × 3 spots with sizes that were described above under Simulation illuminated the OEK chip, and the initial positions of the Raji cells were shown and recorded. All of the Raji cells in the field-of-view areas, more than 31, moved away from the illuminated areas when an externally applied AC bias potential of 10 kHz and 10 V_pp was switched on, as shown in Fig. 5 b ii. When the frequency was gradually increased, the Raji cells were still repelled from the illuminated areas. The Raji cells were also found to undergo a self-rotational behavior during this process, as characterized in our prior work (23). However, when the frequency was changed to 35 kHz, the Raji cells presented no motion. After the frequency was >35 kHz, the Raji cells began to be slowly attracted to the optical spot edge, as shown in Fig. 5 b iii, thus indicating that the DEP force exerted on the Raji cells changed from a negative DEP force to a positive DEP force at this frequency; therefore, 35 kHz was the crossover frequency of Raji cells under this condition. When the frequency was 300 kHz, the optical patterns disappeared, and the final positions of the Raji cells are shown in Fig. 5 b iv, thus indicating that the Raji cells still experienced a positive DEP force. Then, the optical patterns were projected onto the OEK chip again, and the frequency was set to gradually decrease from 300 kHz with a step of 5 kHz. When the frequency was <35 kHz, the Raji cells that had been attracted to the optical spot were repelled from the optical spots, as shown in Fig. 5 b v. The final positions of the Raji cells after both the AC bias potential and the optical patterns were removed are shown in Fig. 5 b vi. In conclusion, the frequency of 35 kHz was the crossover frequency for the Raji cells suspended in the liquid solution with a conductivity of 0.01 S/m.

Figure 5.

Series of time-lapse (a) animation and (b) microscope images of the different translation responses of Raji cells to positive and negative DEP forces under various applied frequencies at an AC bias potential of 10 V_pp. (i) Initially, the arrays of 3 × 3 spots were optically projected onto the OEK chip. (ii) When the AC bias potential was applied at a frequency of 10 kHz, all of the Raji cells were repelled from the illuminated areas and simultaneously underwent a self-rotation behavior. (iii) When the frequency was adjusted to 35 kHz, the Raji cells exhibited no motion; after the frequency was >35 kHz, the Raji cells began to move to the edges of the optical spot slowly. (iv) At 300 kHz, when the optical spots were removed, the positions of Raji cells were as shown. (v) When the frequency was decreased to <35 kHz, all of the Raji cells that had been attracted to the optical spots moved away from the optical spots. (vi) The final positions of Raji cells. All scale bars represent 60 μm. To see this figure in color, go online.

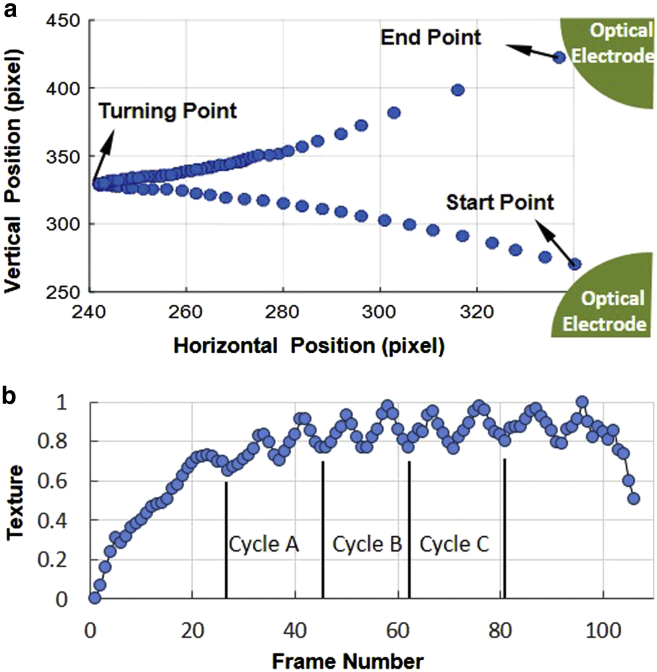
The processes for the experimental acquisition of the crossover frequencies for the four selected types of cells were identical. Thus, we use the Raji cells as an example to discuss and describe the process of determining the cellular crossover frequencies by using the micro-vision technique. The traditional method of determining crossover frequency often uses the naked eye, thus resulting in a low accuracy and high variation. In this study, we applied cell-tracking software to track the cell translation and rotation simultaneously, as shown in Fig. 6. Fig. 6 a shows a cell repelled from the start point to the turning point by an optical electrode and then attracted to another optical electrode again. Throughout the translation process, the rotation of the cell was also recorded by the texture, as illustrated in Fig. 6 b. Hu invariant moments, a certain particular weighted moment of the image pixels' intensities, were calculated to describe the cell’s texture and normalized for convenient comparison. In this manner, the crossover frequency can be determined more accurately and automatically using this method compared with other methods.

Figure 6.

Tracking of cellular translation and rotation on the basis of computer vision algorithms. (a) Two-dimensional trajectory of the Raji cell. (b) Normalized texture varies with the frame number over time. To see this figure in color, go online.

During each experiment, there was a frequency range close to the crossover in which the DEP force was not sufficiently strong to be observed because Re[K(ω)] was approximately zero. To enhance the reliability and validity of the method proposed in this study, 10 repeated experiments for 10 different cells, similar to the experiments in Fig. 5, were conducted to acquire the Raji cell crossover frequency, thus demonstrating that the crossover frequency for Raji cells under this condition was 35 ± 3 kHz. Then, the crossover frequencies for Raji cells under liquid conductivities of 0.02, 0.04, and 0.06 S/m with experimental processes similar to that illustrated in Fig. 5, were also measured as 75 ± 5, 135 ± 10, and 205 ± 15 kHz, respectively. For each of the liquid conductivity conditions, 10 experimental replicates were performed, and the crossover frequencies were successfully acquired. The crossover frequencies for the four types of cells versus the liquid conductivities were also obtained through the experimental approach shown in Fig. 5.

Determination of the cell-membrane capacitance/conductance

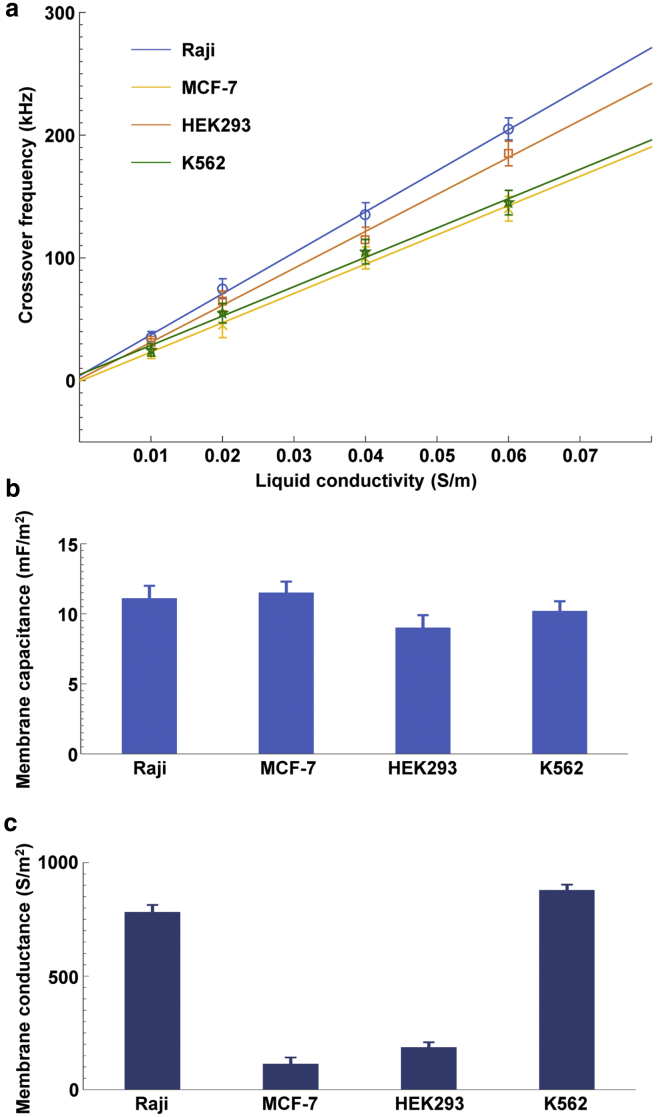
Fig. 7 a is a plot of the measured crossover frequencies of the four cell types as a function of different OEK media. A clear linear relationship between the crossover frequency and medium conductivity was observed for all four cell types. A least-squares polynomial smoothing algorithm fit was used to derive the slope and ordinate intercept for each curve for the four conditions. The crossover frequency increased linearly for each type of cell when the liquid conductivity increased. Furthermore, the slope, i.e., the rate of increase, of each curve for the four cell types had different values. This finding indicated that different types of cells have different intrinsic properties and also that different cell types can be discriminated on the basis of their distinctive crossover frequencies.

Figure 7.

(a) Crossover frequencies for the four cell types—Raji cells, MCF-7 cells, HEK293 cells, and K562 cells—as a function of the liquid conductivities. In all four curves, each data point is indicated as the mean ± SD (n = 10). (b and c) Cell-membrane capacitances (b) and conductances (c) for the four types of cells in this study as determined by the proposed ODEP method. In all four curves, each data point is represented as the mean ± SD (n = 10). To see this figure in color, go online.

The cell membrane capacitance/conductance was determined using Eq. 7 and is shown in Fig. 7, b and c. The cell membrane capacitances acquired for the four cell types were close to the values determined using other previously reported techniques, such as DEP (29, 30, 31), patch-clamp, and electro-rotation (32). Table 1 provides a comparison of the cell-membrane capacitances obtained with the method presented in this study with those obtained by previously described methods.

Table 1.

Comparison of the Cell-Membrane Capacitances Acquired by the ODEP Method with Those Acquired by Other Published Methods

	OEK Method (mF/m2)	Other Methods (mF/m2)
Raji	11.1 ± 0.9	10.7 ± 1.3 (29)
MCF-7	11.5 ± 0.8	12.4 ± 1.8 (30)
HEK293	9.0 ± 0.9	8.8 ± 0.7 (32)
K562	10.2 ± 0.7	9.5 ± 1.0 (31)

Characterization of the membrane capacitances of MCF-7 cells treated with drugs

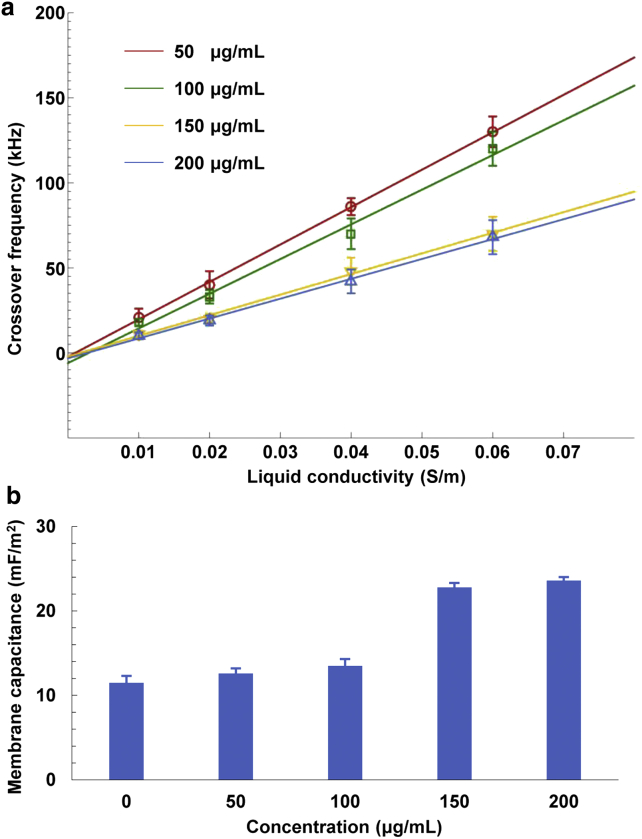
Fig. 8 a shows the experimental results for the acquired crossover frequencies of MCF-7 cells treated with different concentrations of resveratrol in media with different liquid conductivities. The relationship between the crossover frequencies of MCF-7 cells under the four different conditions and the liquid conductivities also presented a linear relationship. In addition, the crossover frequencies of MCF-7 cells treated with drugs exhibited a declining trend compared with those of MCF-7 cells cultured in drug-free medium. The corresponding membrane capacitances were obtained with Eq. 7, as shown in Fig. 8 b. The results indicated that the membrane capacitance of MCF-7 cells treated with drugs was higher than that of MCF-7 cells cultured in drug-free medium. Furthermore, when the concentrations of the drugs were gradually increased, the corresponding membrane capacitances presented a similar trend, thus indicating that drug concentration can be ascertained indirectly by determining the membrane capacitance of treated cells.

Figure 8.

(a) Crossover frequencies for MCF-7 cells treated with four different concentrations of drugs as a function of the liquid conductivities. In all four curves, each data point is represented as the mean ± SD (n = 10). (b) Determined membrane capacitances of MCF-7 cells treated with four different concentrations of drugs. In all four curves, each data point is represented as the mean ± SD (n = 10). To see this figure in color, go online.

The cell membrane typically consists of the lipid bilayer with various embedded proteins. The composition and the morphology of the cell membrane directly affect the cellular functions, such as the membrane capacitance and the selective permeability. Furthermore, the cell-membrane capacitance mainly reflects membrane thickness, composition, and morphologic properties. When the MCF-7 cells were cultured in the drug-free medium, the membrane capacitance could reveal the intrinsic membrane information. The MCF-7 cells treated with the drug resveratrol at four different concentrations possess their own characteristic crossover frequencies, although overlaps exist for some concentrations under one specific given liquid conductivity. However, the membrane capacitances of MCF-7 cells present variations over four different drug concentrations of resveratrol. The reason may be that the added drug affects the cellular morphology, especially the membrane thickness. The decreased thickness of the cell will enhance the membrane capacitance. We are currently focusing our study on investigating this and will report our findings in the future.

This study sought to test the capability of the ODEP mechanism to determine the cell-membrane capacitance/conductance dielectric parameters in a non-invasive manner and potentially to supply an automated and label-free method for separating different cancer cell lines. However, in our current research, the degree of automation in the determination of cell dielectric parameters was still low, owing to the lack of a real-time recognition and observation module for monitoring cellular translational motion during the AC bias potential sweep frequency process and a synchronous triggering module for simultaneously controlling the AC power and charge-coupled devices. We are currently focusing on this topic and further investigating how the function and state of cells in the presence of externally applied factors are reflected by changes in the intrinsic information of cells; we will report our findings in the future.

Conclusion

In this study, the cell membrane capacitances and conductances of Raji cells, MCF-7 cells, HEK293 cells, and K562 cells were successfully determined using optically projected patterns to define virtual electrodes and further induce ODEP forces in an optical-electrical coupled microfluidics chip. The cell membrane capacitances/conductances of the four types of cells were derived by characterizing their ODEP crossover frequencies using micro-vision techniques and compared with the liquid conductivities, which were 11.1 ± 0.9 mF/m² and 782 ± 32 S/m², respectively, for Raji cells, 11.5 ± 0.8 mF/m² and 114 ± 28 S/m² for MCF-7 cells, 9.0 ± 0.9 mF/m² and 187 ± 22 S/m² for HEK293 cells, and 10.2 ± 0.7 mF/m² and 879 ± 24 S/m² for K562 cells. Before performing the experiments, we established a theoretical model of cell-membrane capacitance/conductance determination and then demonstrated that the dielectric parameters of the cells could be easily determined by referring to the curve-fitted spectra of the crossover frequencies of cells versus the liquid conductivities. The FEA of the optically induced electric field and ODEP confirmed the feasibility of using this ODEP mechanism to derive the cell-membrane capacitance/conductance. Furthermore, we demonstrated that the concentration of a drug applied to MCF-7 cells could be determined based on the determined cell-membrane capacitance. The ability to easily determine the cell-membrane capacitance/conductance using the ODEP mechanism proposed in this study may be used in characterizing the current state of cellular growth, assessing stem-cell differentiation, and sorting different types of cells, with many applications in the biomedical, bioengineering, and pharmaceutical development fields.

Author Contributions

W.L. and Y.Z. wrote the article and analyzed data; W.L., W.J.L., and L.L. conceived and designed the experiments; W.L. performed the experiments; and Y.W. and G.-B.L. contributed materials. All authors gave final approval for publication.

Editor: Stephen Evans.