Deciphering Intrinsic Inter-subunit Couplings that Lead to Sequential Hydrolysis of F₁-ATPase Ring

Abstract

Rotary sequential hydrolysis of the metabolic machine F₁-ATPase is a prominent manifestation of high coordination among multiple chemical sites in ring-shaped molecular machines, and it is also functionally essential for F₁ to tightly couple chemical reactions and central γ-shaft rotation. High-speed AFM experiments have identified that sequential hydrolysis is maintained in the F₁ stator ring even in the absence of the γ-rotor. To explore the origins of intrinsic sequential performance, we computationally investigated essential inter-subunit couplings on the hexameric ring of mitochondrial and bacterial F₁. We first reproduced in stochastic Monte Carlo simulations the experimentally determined sequential hydrolysis schemes by kinetically imposing inter-subunit couplings and following subsequent tri-site ATP hydrolysis cycles on the F₁ ring. We found that the key couplings to support the sequential hydrolysis are those that accelerate neighbor-site ADP and Pi release upon a certain ATP binding or hydrolysis reaction. The kinetically identified couplings were then examined in atomistic molecular dynamics simulations at a coarse-grained level to reveal the underlying structural mechanisms. To do that, we enforced targeted conformational changes of ATP binding or hydrolysis to one chemical site on the F₁ ring and monitored the ensuing conformational responses of the neighboring sites using structure-based simulations. Notably, we found asymmetrical neighbor-site opening that facilitates ADP release upon enforced ATP binding. We also captured a complete charge-hopping process of the Pi release subsequent to enforced ATP hydrolysis in the neighbor site, confirming recent single-molecule analyses with regard to the role of ATP hydrolysis in F₁. Our studies therefore elucidate both the coordinated chemical kinetics and structural dynamics mechanisms underpinning the sequential operation of the F₁ ring.

Introduction

Coordination on ring-shaped NTPases is fundamental and crucial for the diverse physiological functions of these cellular molecular machines (1, 2, 3, 4, 5). In well-studied systems such as F_oF₁-ATP synthase, the binding-change mechanism, for example, was proposed early on to illustrate rotary cooperative catalysis around the hexameric F₁-ATPase ring (6, 7). The mechanism indicated that binding and catalytic activities of ATP alternate sequentially on three chemically active sites, formed at the interfaces of the α and β subunits on the ring (8). According to the mechanism, the central γ-shaft across the F₁ ring dictates the coordinated alternation (9, 10, 11, 12). Nevertheless, experimental studies later on showed that upon significant truncations of the γ-shaft, the F₁ motor still rotates directionally (13, 14, 15, 16). Furthermore, recent experiments conducted in the absence of the central γ-shaft demonstrated that the stator F₁-ring also maintains rotary sequential hydrolysis around the three chemical sites (17). These studies consistently indicated that the sequential coordination arises intrinsically from the F₁-ATPase ring, though the stator-rotor interactions would likely enhance the rotary cooperativity.

In this work, we aimed to investigate how the intrinsic sequential operation on the F₁ ring arises due to inter-subunit or site couplings in the absence of the central γ-shaft. We assume that the sequential hydrolysis scheme achieved without the γ-rotor is similar to that detected originally with the rotor. We focused on two typical reaction schemes, one suggested recently for human mitochondrial F₁ (MF₁) (18), and the other determined for bacterial F₁ (BF₁) (19). For an individual ATPase site, formed by one α-β hetero-dimer, the uni-site reaction rates for the product ADP and Pi releases, for example, are particularly low (20, 21). To allow reactions that are as fast as that achieved on the tri-site F₁ ring, it is necessary that the inter-subunit couplings significantly accelerate the respective product releases, yet how that is achieved remains elusive. Inter-subunit coordination has been recognized in particular for ring-like NTPases (1, 2, 22), such as the viral RNA or DNA packaging motor (23, 24), helicases (4, 5, 25), and F₁-ATPase (2, 6, 26). For example, in the viral ϕ29 DNA packaging motor, it was discovered that multiple subunits coordinate ADP release with ATP binding in an alternating fashion during a packaging dwell phase (1, 24, 27), whereas Pi release happens from one site to the next in a burst phase. Nevertheless, it is not clear what inter-subunit interactions support the coordination, and similar puzzles remain for various ring-shaped NTPases. Some suggestions have been made that address, for example, how ATP binding in one site may couple with ADP release in a neighbor site (1, 24, 26, 27), how an arginine-finger insertion from one subunit can induce ATP hydrolysis in the next-neighbor site (23, 24, 27), and how ATP hydrolysis may assist Pi release in the neighbor site (28) or vice versa. A basic scenario is that one chemical event triggers certain conformational changes that propagate through the subunit interfaces to the neighbor site(s), accelerating the site conformational transitions on the forward chemical reaction path, with both kinetic and structural consequences. However, quantitative studies to reveal these couplings and determine the underlying kinetics or structural dynamics are lacking.

Accordingly, the major task of this study is to identify the inter-subunit couplings that essentially support the sequential hydrolysis of the F₁ stator ring, along with quantitative descriptions and physical understanding. Computational modeling and simulations have contributed significantly to the understanding of molecular mechanisms of F₁-ATPase (29, 30, 31, 32, 33, 34, 35, 36, 37, 38). Although most previous computational studies have focused on quantifying the rotary motion of F₁-ATPase (α₃β₃γ), current work has neglected the rotational degree of freedom and studied only a minimal model of the F₁ ring (α₃β₃) for sequential hydrolysis. We started by conducting stochastic kinetics simulations for the three independent ATP hydrolysis cycles, based on the uni-site reaction rates obtained for bovine heart MF₁ (21) and Escherichia coli F₁ (20). Empirically chosen inter-site couplings that are likely to happen upon assembly and operation of the ring were then kinetically incorporated into the stochastic simulation, and the kinetic rates were tuned, in particular, under a constant free-energy condition for ring operation. If a sequential hydrolysis reaction arises in the tri-site reaction as experimentally detected under these couplings, we then regard the couplings as kinetically feasible.

For the kinetically feasible inter-subunit couplings that were identified as key for sequential hydrolysis, we then probed the physical basis of the couplings with structural dynamics investigations. Previously, atomistic molecular dynamics (MD) simulation studies had been performed on the F₁-ATPase system to reveal protein conformation changes from several nanoseconds (30) to tens and hundreds of nanoseconds (37). Nevertheless, micro- to millisecond “long-timescale” dynamics in such a protein machine is still hardly accessible for conventional MD simulations. As mentioned above, the inter-subunit couplings are usually manifested as the neighbor-site conformational responses toward an active site where some triggering chemical event, such as ATP binding or hydrolysis, happens, with a “waiting time” up to milliseconds or above. To allow such a “slow” event to happen in the MD simulation, we accordingly enforced conformational transitions to mimic the ATP binding or hydrolysis event in the corresponding active site by implementing targeted MD (TMD) in sub-microseconds (39, 40, 41). However, the purpose is not to simulate the triggering event per se, but to monitor the ensuing conformational relaxations or responses on the ring. Considering that artifacts or bias might be introduced in the highly accelerated sub-microsecond TMD, we additionally performed coarse-grained (CG) simulations with similar enforcing and relaxation strategies, since CG simulations are supposed to capture comparatively slow motions. As the essential conformational responses appearing in the accelerated atomistic MD simulation could be reproduced on the CG level connecting to the long timescale, the TMD-induced responses are regarded to be as reasonable as those that happen without acceleration.

In practice, we adopted a reaction scenario in which Pi is released after the ADP release in one hydrolysis cycle of F₁ (19, 42). Using stochastic kinetic simulations, we were able to first determine kinetically feasible inter-subunit couplings that support the sequential hydrolysis. Then, we implemented atomistic MD simulations to probe the physical basis of the kinetically important couplings. The bovine MF₁ structure was employed in the MD simulation. Once the TMD was implemented to mimic ATP binding or hydrolysis in one active site, the conformational responses in both neighbor sites were closely monitored. We subsequently found asymmetrical neighbor-site openings that may facilitate the product(s) release or bias the ATP binding for directional coordination. To validate the TMD implementation to a comparatively long timescale, we further implemented targeted elastic network (TEN) simulations in a CG structural model.

Methods

Kinetic Monte Carlo simulation of three chemical sites

For each ATP binding or catalytic site at the α-β interface, there are several chemical states: the empty state without any substrate binding (E); the ATP-bound state and the hydrolysis-ready state (T/T^∗); the post-hydrolysis state right after the reaction, as ATP turns into ADP and Pi (DP); and the ADP-released but Pi-bound state (P). Here, we follow the convention that the ADP releases before the Pi release (19, 42). As such, the uni-site reaction proceeds in cycles as E⇔T/T^∗⇔DP⇔P⇔E. We differentiate T^∗ from T by enhancing the ATP-hydrolysis rate of the T^∗-state above that of the T-state, as if T^∗ arises due to the assembly of the tri-site ring.

The uni-site reaction rates for forward and backward transitions in the bovine heart mitochondrial and bacterial E. coli F₁-ATPase were obtained experimentally (20, 21) (see Tables S1 and S2). We assume that the rate of ADP release from the DP state is the same as that originally listed from the D state, and the rate of Pi release from the P state is the same as that originally listed from the DP state. We also assume that bovine and human MF₁ behave similarly (18), and that E. coli and thermophilic (Bacillus PS3) BF₁ perform alike as well (43).

We used the kinetic Monte Carlo (KMC) method (44) to simulate the chemical kinetics of F₁-ATPase hydrolysis, from the three independent uni-site reactions to the coupled tri-site reactions. In the KMC simulation, one starts with an initial ring configuration (e.g., E-E-E or E-DP-T) of the three chemical sites; each time a transition from one of the three chemical sites was made, either forward or backward along the reaction path, according to rate competitions of all potential transitions in the current ring configuration (i.e., fast transitions get higher chances). When the uni-site reaction rates were adopted for each site, the three sites performed as if they hydrolyzed independently. In any coupled tri-site reaction scheme, inter-subunit couplings were imposed at certain ring configurations, for example, by tuning the product-release rates upon neighbor-site ATP binding (E→T) or hydrolysis reaction (T^∗→DP). In particular, we used four parameters to define the strength of the couplings, and we tuned these parameters for optimal sequential performance (see the Supporting Material).

Atomistic TMD simulations

All the MD simulations were performed using the NAMD 2.10 software (45) with the CHARMM22 force field for protein and the CHARMM27 force field for lipid (46, 47), except for the construction of the E-DP-T structure, for which GROMACS was used (48). The F₁-ATPase structures were obtained from the existing crystal structures: The E-DP-T ring was made from the crystal structure of P-DP-T (Protein Data Bank (PDB): 1E1R) (49); the γ-shaft, when included, was rotated ∼40° accordingly. An E-T-T^∗ structure was obtained directly from the crystal structure (PDB: 2JDI) (50). An E-E-E structure was made from E-T-T, and a T-P-T^∗ structure was obtained from the crystal structure (PDB: 1W0J) (51) (see the Supporting Material).

The PDB structures were then solvated with TIP3P water in a cubic box, and the minimum distance from the protein to the wall was 15 Å. We neutralized the systems with Na⁺ and Cl⁻ to a concentration of 0.15 M. The temperature was set to 310 K and the pressure was 1 bar. The van der Waals and short-range electrostatic interactions used a cutoff of 12 Å. The particle-mesh Ewald method was applied to deal with long-range electrostatic interactions (52). The solvated system was minimized with the steepest-descent algorithm, followed by a 10 ps MD simulation under the canonical ensemble with a time step of 1 fs. Then, a 5 ns equilibrium simulation was performed under the NVT ensemble with a time step of 1 fs, and position restraints were imposed on the heavy atoms of proteins during the simulation. After the constrained simulation, the unconstrained equilibrium simulations, or TMD simulations, were carried out under the NPT ensemble with a time step of 2 fs. During the TMD simulation, the structure was constantly forced toward a moving target conformation (according to the heavy-atom root mean-square deviation (RMSD) value) geometrically designated on the reaction path toward a final target structure (39). Further implementations are found in the Supporting Material.

Performing the elastic-network relaxation dynamics

The elastic network of the ring was obtained by first replacing each amino acid residue in the atomic structure by a single bead, which was placed at the position of the α-carbon atom of the respective residue. These equilibrium positions were denoted by ${\overrightarrow{R}}_i^{\left(0\right)}$ for bead $i$. Then, to determine the pattern of network connections, the distances $d_{ij}^{\left(0\right)}=\left|{\overrightarrow{R}}_i^{\left(0\right)}-{\overrightarrow{R}}_j^{\left(0\right)}\right|$ between equilibrium positions of any two beads $i$ and $j$ were compared with a prescribed interaction radius $r_{int}=10\text{Å}$. If this distance was below $r_{int}$, the two beads were connected by a deformable elastic spring with natural length $d_{ij}^{\left(0\right)}$. The network connectivity was stored in matrix $\mathit{A}$ with entries $A_{ij}=1$, if beads $i$ and $j$ are connected, and $A_{ij}=0$, else. The total elastic energy of the network is $U={\sum }_{i,j;i<j}^N\kappa \left(A_{ij}/2\right){\left(d_{ij}-d_{ij}^{\left(0\right)}\right)}^2$. Here, $N$ is the number of beads in the protein network, $d_{ij}=\left|{\overrightarrow{R}}_i-{\overrightarrow{R}}_j\right|$ is the actual length of a spring connecting beads $i$ and $j$ in some deformed network conformation, with ${\overrightarrow{R}}_i$ being the actual position vector of bead $i$, and $d_{ij}^{\left(0\right)}$ is the corresponding natural length. The spring stiffness constant $\kappa$ is assumed to be the same for all network springs.

When thermal fluctuations and hydrodynamical interactions are neglected, the dynamics of the network can be described by a set of Newton’s equations in the over-damped limit (53, 54, 55). For bead $i$ the equation of motion is

$$\gamma \frac{d}{dt}{\overrightarrow{R}}_i=-\frac{\partial }{\partial {\overrightarrow{R}}_i}U.$$ (1)

On the left side of Eq. 1, $\gamma$ is the friction coefficient assumed to be equal for all network beads. On the right side are the elastic forces exerted by network springs of beads which are connected to bead $i$. Explicitly, the equations read

$$\frac{d}{dt}{\overrightarrow{R}}_i=-\sum _j^N{A}_{ij}\frac{d_{ij}-d_{ij}^{\left(0\right)}}{d_{ij}}\left({\overrightarrow{R}}_i-{\overrightarrow{R}}_j\right)+\sigma {\overrightarrow{f}}_i.$$ (2)

Here, we have removed the dependencies on $\gamma$ and $\kappa$ by an appropriate rescaling of time and, after that, added external forces ${\overrightarrow{f}}_i$ which can act on bead $i$ (if $\sigma =1$).

In the TEN simulations performed, external forces were applied only to the beads of one of the catalytic $\alpha \beta$ -sites to induce the desired transition there. Such forces were updated in each integration step and had the form ${\overrightarrow{f}}_{i,n}=\left(\alpha /N_{\text{s}}\right)\left|{\text{RMSD}}_{n-1}-{\text{RMSD}}^{\ast }\right|{\overrightarrow{d}}_{i,n-1}$, for bead $i$. Here, ${\overrightarrow{d}}_{i,n}$ is the difference vector between positions of bead $i$ in the target and the actual conformation of the forced $\alpha \beta$ -subunit, determined after superposition of the subunits at integration step $n$, and ${\text{RMSD}}^{\ast }={\text{RMSD}}_0-{\text{RMSD}}_0\left(n/S\right)$, with $S$ being the total number of integration steps. $N_{\text{s}}$ is the number of beads of the forced $\alpha \beta$ -subunit, and parameters $\alpha =2500$ and $S=\mathrm{400,000}$ were chosen in the simulations. The set of Eq. 2 was numerically integrated to obtain the positions of network beads at all moments in time. In the simulations, a first-order scheme with a time step of 0.1 was used. In particular, we performed TEN to mimic ATP binding to the E-site of the E-DP-T ring, in comparison with the TMD simulation. Further details can be found in the Supporting Material.

Results

Stochastic simulations identified kinetically feasible inter-subunit couplings that support sequential hydrolysis on the F₁ ring

To probe what type of inter-subunit or site couplings may be responsible for sequential hydrolysis of the F₁ ring, we first conducted the kinetic Monte Carlo (KMC) simulations for three ATP hydrolysis cycles to mimic the chemical kinetics of the three active sites (see Fig. 1; Methods). The three chemical cycles proceed independently when there is no inter-subunit coupling. The coordinated sequential hydrolysis arises kinetically when certain transitions in one hydrolysis cycle are connected with those in another hydrolysis cycle at the right moments via appropriate coupling rules (see Supporting Material).

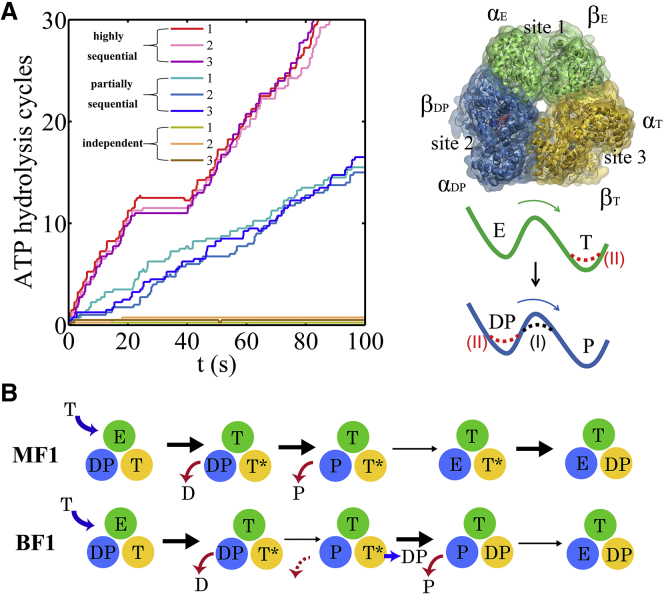
Figure 1.

Stochastic simulations of tri-site hydrolysis reactions on the F₁ ring. (A) The trajectories (left) show the number of hydrolysis cycles for the three chemical sites of BF₁, from the independent (yellow traces, with three different shades shown for the three active sites) to the partially coordinated (blue traces with three shades) and the highly sequential case (red traces with three shades). In the sequential case, each site follows its upstream/counterclockwise site along the ATP hydrolysis reaction path, as detected experimentally. In the independent case, the uni-site reaction rates from E. coli F₁ were used (20). The ring-shaped structure (right) of a key configuration, E-DP-T, is shown (E for the empty state, T for the ATP bound state, DP for the ADP^∗Pi or the hydrolysis state, and P for the Pi bound state), with the most essential inter-subunit coupling illustrated: ATP binding to the E-site facilitates ADP release from the next DP-site. The coupling is imposed in two ways, implementations I and II (see text). Implementation I was used for the BF₁ trajectories shown here. (B) The sequential hydrolysis schemes for MF₁ (top) and BF₁ (bottom), with the essential inter-subunit couplings enabling the schemes indicated. The ATP binding (E→T) to E-DP-T enhances the ADP release (DP→P) for both MF₁ and BF₁; in MF₁, Pi release (P→E) is enhanced right after the ADP release upon ATP binding, whereas in BF₁, Pi release is enhanced either similarly to that in MF₁ and/or later, upon ATP hydrolysis (T^∗→DP). To see this figure in color, go online.

We started by simulating the three independent hydrolysis cycles based on the uni-site reaction rates obtained experimentally, for both MF₁ and BF₁ (20, 21) (see Tables S1 and S2). Each hydrolysis cycle consists of ATP binding (from E, the empty state, to T, the ATP-bound state), hydrolysis (T or T^∗ to DP, the ADP+Pi bound state), and product release (DP to P, the Pi-bound state, and then to E). We then imposed coupling rules onto the three ATP hydrolysis cycles in the KMC simulations (Fig. S1). First, since the three-ATP-bound configuration (3-T) was not detected experimentally (17), we imposed a constraint to prevent 3-T when needed by lowering the third ATP binding rate to the ring (e.g., for ∼100 times the rate inhibition; see Figs. S1, S2, and S3). It turns out that MF₁ explicitly requires the constraint to achieve the sequential performance, since on the dominant reaction path of MF₁ (see Fig. 1 B), a T-E-T^∗ configuration exists that readily turns into 3-T, which can then obtain a large population in the absence of the constraint (e.g., >60%). In BF₁, however, the sequential performance was acceptable without adding the constraint, and the 3-T population would not become dominant (i.e., it remained at <30%). Second, when two sites among the three are bound with ATP, we refer to the T^∗-site as the one that binds ATP earlier, so that it proceeds to an intermediate T^∗ state (or tightly bound state, as in the assembled ring), ready for catalysis (31). We accordingly assigned an elevated ATP hydrolysis rate (e.g., ∼100-fold rate enhancement; see Figs. S1, S2, S3, and S4) for the T^∗-site.

Note that sequential performance was evaluated by a performance score (between 0 and 1), according to the experimentally detected sequential schemes (18, 19). A higher score shows a better sequential performance or consistency with the detected scheme (see Eq. S1 in Supporting Materials and Methods; Figs. S2, S3, and S4). In the case of a high score, one can consistently see high correlations between neighboring sites in their hydrolysis cycles, as one site follows the other closely moving along the hydrolysis reaction path (see Eq. S2 in Supporting Materials and Methods; Fig. S5).

Representative trajectories for the ATP hydrolysis cycles on the three active sites of the BF₁ ring are shown in Fig. 1 A, from an independent case to a partially coordinated and then a highly sequential case. In particular, the highly sequential case demonstrates an overall cycling rate (∼0.3 s⁻¹) comparable to the experimental detection on the rotor-less BF₁ (17). In the full F₁ in the presence of the central rotor, the cycling rates become hundreds to thousands times faster (18, 43).

Since it is not clear whether product binding affinities change during the inter-subunit coupling, we imposed the coupling kinetically in two ways (see Fig. 1 A, right): For implementation I, we enhanced both the product unbinding and binding rates by the same amount to keep a constant binding affinity. For implementation II, we enhanced the product unbinding rate without changing the product rebinding rate, whereas the ATP unbinding rate or the reversal rate of the hydrolysis in the triggering active site was additionally enhanced to keep the overall free energy constant. The trajectories for MF₁ and BF₁ with both implementations I and II are shown in Fig. S6. Regardless of the means of implementation, we found that the key couplings that support the sequential schemes are the same as those summarized below.

ATP binding to the E-DP-T ring facilitates product release from the downstream DP site

Presumably, as ATP binding (E→T) induces an open-to-closed transition in the E-site, the next downstream DP-site (in the counterclockwise direction viewed from the C-terminal side of F₁) can be disturbed and the product (ADP and Pi) release rate can be affected (1, 24, 26). Accordingly, in the kinetic simulation, we allowed the ATP binding to the E-DP-T ring to enhance both the ADP and Pi release rates in the DP-site. In MF₁, >∼10⁵-fold rate enhancement (see Fig. S3) was applied to both the ADP and Pi release (from E-DP-T to T-E-T^∗) to achieve a high sequential performance. In BF₁ (from E-DP-T to T-P-DP), the ADP release rate has to be enhanced > 10³-fold upon the E-site ATP binding (see Fig. S4) to allow the sequential performance; the Pi release rate either can be enhanced along with ADP release upon ATP binding or can occur after T^∗-site ATP hydrolysis (see Fig. S2, B and C), as analyzed below.

The Pi release from the T-P-T^∗ ring can be facilitated either by the upstream-site ATP binding or later by the downstream-site ATP hydrolysis

Based on time-series data analyses from high-speed single-molecule experiments, it was suggested that ATP hydrolysis plays a role in facilitating the neighbor-site Pi release (28). We tested whether this causality coupling between ATP hydrolysis and Pi release could be kinetically feasible, i.e., to support sequential hydrolysis in the KMC simulation. We then found that in BF₁, by enhancing the Pi release rate ∼10³-fold upon ATP hydrolysis in the next T^∗-site (see Fig. S4), sequential hydrolysis could emerge. Alternatively, Pi release in BF₁ can also be enhanced right after ADP release, as in MF₁, to support the sequential performance.

Note that the overall hydrolysis or cycling rates of F₁ achieved in our KMC simulations are comparatively low, e.g., less than one cycle (with three ATPs hydrolyzed) per second, as experimentally detected for BF₁ in the absence of the rotor (17). One can also enhance the coupling strengths to mimic the full F₁ system in the presence of the rotor to achieve high rates, i.e., up to hundreds of cycles per second, as measured for the full F₁ (18, 43). The corresponding kinetic coupling parameters to achieve the low and high rates of F₁ are provided in Tables S3 and S4 for MF₁ and BF₁, respectively.

In brief, from a kinetic perspective, the ATP-binding-facilitated ADP release in the downstream DP-site appears to be an indispensable coupling for sequential performance for both the MF₁ and BF₁ rings. On the other hand, the coupling for promoting Pi release could be attributed either to ATP binding in the upstream site (in MF₁), or to ATP hydrolysis in the downstream T^∗-site, or both (in BF₁). To further probe the physical basis of these kinetically feasible couplings, we performed atomistic MD simulations as illustrated below.

Atomistic MD simulations demonstrated an asymmetrical opening of the neighbor site upon current-site closing/tightening induced by ATP binding/hydrolysis

We performed four sets of TMD simulations (39) mimicking ATP binding or ATP hydrolysis in one chemical site, and we monitored the ensuing mechanical responses from the two neighboring chemical sites. The four sets of simulations include 1) targeting the ATP-binding transition from E-DP-T to T-DP-T^∗ to examine how the downstream DP-site and the upstream T-site are affected, with a control TMD simulation to include the central γ-shaft; 2) targeting the ATP hydrolysis transition from T-P-T^∗ to T-P-DP to examine how the upstream P-site and downstream T-site react; 3) targeting the first-ATP binding transition from E-E-E to E-T-E to examine the responses without ligand bound in the neighbor sites; and 4) targeting the third-ATP binding transition to E-T^∗-T, to see if the 3-T ring remains stable.

ATP binding to the E-DP-T ring opens the downstream DP-site to facilitate ADP release

We obtained an E-DP-T ring from the P-DP-T structure of bovine MF₁ (PDB: 1E1R) (49) and performed the TMD simulation to enforce the α_E-β_E structure to approach the targeted α_T-β_T conformation, so that the original E-site was turned into a T-site and a T-DP-T^∗ ring was obtained (see Fig. 2; Supporting Material, section II.4).

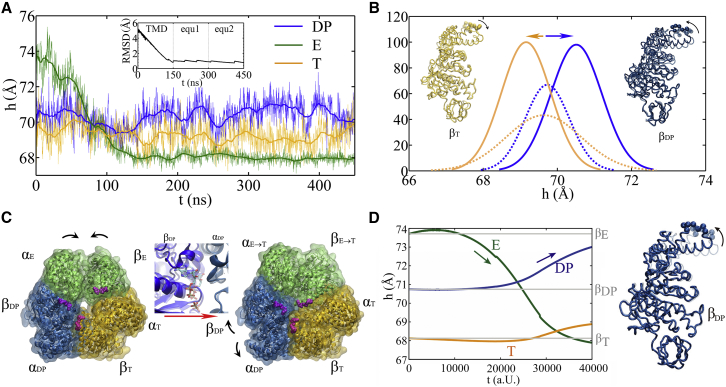
Figure 2.

The TMD simulation enforcing an ATP binding to the E-site in the E-DP-T ring. (A) In the first 150 ns TMD simulation, the E→T transition was gradually enforced; additional simulations were conducted for relaxation as holding the structure toward the final targeted form. The conformational changes of the chemical sites were monitored by the C-terminal protrusions of the β-subunits (green, E-site; blue, DP-site; yellow, T-site). (Inset) RMSD of α_E-β_E dimer with respect to the targeted α_T-β_T. (B) Histograms of the protrusion heights from β_DP (blue lines) and β_T (yellow lines) measured from the TMD simulations (solid curves) and the equilibration simulation in control (dashed curves), respectively (with the average changes indicated by arrows). Side views of the conformational changes on the β_T and β_DP C-terminal protrusions are shown, with spheres indicating the DELSEED motif (with the initial conformation in transparent ribbon and the final in non-transparent ribbon aligned together). (C) Top view from the C-terminal side of the F₁ ring, for both the initial (E-DP-T; left) and the final enforced configurations (T-DP-T^∗; right). The DELSEED motifs are highlighted in magenta spheres. The widening of the DP-site interface between α_DP and β_DP is also shown in the middle. The initial and final structures are aligned together and are shown in transparent and non-transparent representations, respectively, with β_DP colored blue, α_DP colored light blue, and ADP/Pi in stick representation. (D) Results from the TEN simulations of the E-DP-T ring, with the protrusion changes of three sites shown on the left and the structural changes of the downstream β_DP subunit (with the initial in transparent ribbon and the final in non-transparent ribbon aligned together) shown on the right. To see this figure in color, go online.

To determine whether the ATP binding site transited from open to closed as it was enforced to do, we calculated the C-terminal protrusion (i.e., on the DELSEED motif) height, the hinge-bending angle on the β-subunit, and the size of the ATP binding pocket (see Fig. S7). Large values of these measures indicate an open form, whereas small values indicate a closed one. In Fig. 2 A, we see that the β_E-protrusion decreased by ∼6 Å during the TMD simulation, indicating clearly a transition from an open site to a closed one (E→T). In response, the average β_DP protrusion height increased slightly (by ∼1 Å; also see Fig. 2 B) and the β_DP hinge-bending angle also increased (by ∼3°), accompanied by a small increase in the pocket size (∼0.2 Å; see Fig. S8), all indicating a slight opening of the DP-site compared with the results from an equilibrium control simulation. In comparison, the average β_T-protrusion height decreased a little (∼1 Å), though the pocket size of the T-site increased a bit (∼0.2 Å), and the hinge-bending angle of β_T increased slightly (∼1°). Movies made from the simulation show both top and side views of the ring, highlighting how the β-protrusions shifted (Movies S1 and S2).

Since the average magnitudes of the responses were small, we performed an additional TMD simulation for the control, retaining the γ-shaft in the center of the E-DP-T ring. The average β_DP protrusion then increased to ∼2 Å upon the E-site closing (see Fig. S9), whereas the pocket size only increased in the downstream site but decreased in the upstream site. In brief, all three geometric measures consistently suggested that the downstream DP-site opened in response to the ATP binding in the E-site, whereas the upstream T-site did not show such an opening tendency. In particular, one could see that the DELSEED of β_E→T moved toward the center of the ring during the enforced transition (see Fig. 2 C). The trend was maintained in the presence of the γ-shaft, though the γ-shaft occupancy prevents the β_E→T protrusion from interacting directly with that of β_DP, and the β_DP protrusion then increased, largely due to the γ-shaft rotation.

Notably, even without the γ-shaft, one still sees that the DP-site interface widens between α_DP and β_DP upon the enforced ATP binding (see Fig. 2 C). The conformational changes are actually quite significant in the peripheral region of the DP-site (within 10 Å of the bound ADP), with an RMSD of ∼3 Å upon the enforced transition (see Fig. S10 A). The average number of hydrogen bonds in that region also decreased (from ∼25 in the equilibrium MD to ∼20 in the TMD simulation; see Fig. S10 B). In particular, the hydrogen bonds that connect α_DP and β_DP and ones on the β-strand of α_DP frequently broke in the TMD simulation, but not in the equilibrium control simulation. All these features indicate an enlarging of the DP-site interface in response to the enforced ATP binding to the E-site.

To further probe how the DP-site region was able to respond to the enforced E-site to facilitate the ADP release, we also conducted steered MD (SMD) simulations to pull ADP out of the DP-site from the initial E-DP-T ring (before the TMD) and from the final T-DP-T^∗ structure (after the TMD), respectively. Three directions were chosen for the ADP pulling: upward from the top of the DP bound pocket, and outward from and inward to the center of the ring. Correspondingly, we conducted three SMD simulations for each direction, to both the E-DP-T and T-DP-T^∗ rings before and after the TMD simulations (3 × 3 × 2 = 18 SMD simulations; see Fig. S11; Supporting Material, section II.4). The results show that after the TMD simulation or the E-site closing, it was comparatively easy to pull the ADP out of the DP-site, and the contrast was made apparent for pulling along the upward and/or outside pathways. Close inspections along the steered ADP release paths show some structural clues as to how the release could possibly proceed (see Fig. S11).

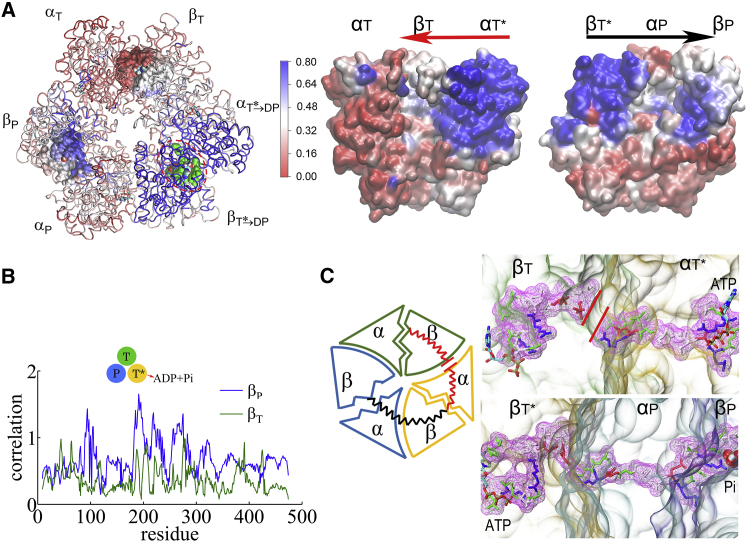
Finally, we probed how the mechanical responses propagate from the ATP-binding E-site to the respective DP- and T-site in the stator F₁-ring, without the γ-shaft. We calculated individual residue correlations with the E-site ATP-binding residues (αI343, αR373, βG161–V164, βY345, βA421, βF424, and βT425), which are mainly on the β_E subunit (see Fig. 3 A) by first evaluating the pairwise cross-correlation values for all residues (see Fig. S12) and then summing up the correlation strengths between each protein residue and those E-site ATP-binding residues. Close to the E-site, the correlations generated were similarly high across α_E->T and β_E->T, respectively (see Fig. 3 A, right). The correlation was still maintained high as being propagated from α_E->T to β_DP, owing to an α-loop region (αQ405–D411) on the top of α_E->T that interacts closely with the DELSEED region (βD394–D400) from β_DP and a helix underneath (βD383–M390). Indeed, upon ATP binding to the E-site, the α_E->T-loop pushes toward the β_DP helix and DELSEED region and moves slightly outward, away from the center, allowing the β_DP protrusion to increase and the DP-site to slightly open. On the other hand, the propagation from β_E->T to α_T and to β_T was over a comparatively long distance, and the correlation decayed noticeably reaching toward β_T. Since the ADP/ATP binding site mainly locates on the β-subunit, it is reasonable to see that the upstream T-site was affected less than the downstream DP-site by the E-site ATP binding.

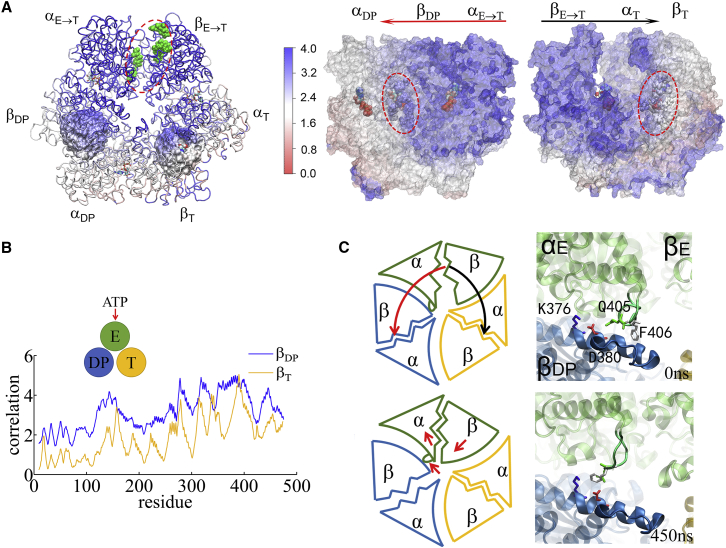
Figure 3.

Conformation correlation with the ATP-binding-pocket residues in the TMD simulation of the E-DP-T ring. (A) Correlation map of the full ring during the enforced E→T transition starting from E-DP-T, colored according to correlation values (blue/white/red, high/medium/low) between individual residues and the E-site ATP binding residues (green spheres in the top view on the left). An inside view (right) shows the conformation propagation or correlation from α_E→T to β_DP and to α_DP (left), and from β_E→T to α_T and to β_T (right), with the bound ADP+Pi and ATP at the DP-site and the T-site, respectively, circled. (B) The residue-wise correlation from β_DP (blue) and β_T (yellow). (C) A close inspection of the C-terminal region of α_E→T to β_DP during the TMD simulation is shown, with cartoon schematics on the left and zoom-in structural views on the right. To see this figure in color, go online.

ATP hydrolysis in T-P-T^∗ facilitates Pi release from the upstream P-site

To mimic ATP hydrolysis in the T-P-T^∗ ring (PDB: 1W0J) (51), we enforced the T^∗-site to a targeted DP-site conformation, obtained from the crystal structure (PDB: 1E1R) (49). Interestingly, one notices that in the crystal structure of T-P-T^∗, the P-site Pi is located around the βP-loop, a marginally stabilized position according to a recent MD study probing the free energy of Pi release (37). It was indicated that the doubly charged Pi group has a tightly bound state located ∼7 Å inside, whereas the P-loop bound state is a less stabilized intermediate state close to the exit of the Pi release channel.

Since the ring structure T-P-T^∗ is obtained from bovine MF₁, the marginally stabilized positioning of Pi in this structure, by itself, suggests a coupling scenario consistent with our proposal for MF₁ (see Fig. S1 C): the Pi release from the P-site of T-P-T^∗ (to T-E-T^∗) has been facilitated right along with the ADP release (from T-DP-T^∗ to T-P-T^∗) upon ATP binding in the upstream site (E-DP-T to T-DP-T^∗; see Fig. 1 C, top).

Moreover, we captured in the TMD simulation of the T-P-T^∗ ring a complete Pi release event from the P-site upstream of the enforced T^∗-site. Within 50 ns of the TMD simulation, the protrusion of the T^∗-site dropped slightly, showing a tightening of the site key to the ATP hydrolysis (T^∗→DP). Meanwhile, one notices an up to ∼3 Å rise of the β_P protrusion for the P-site (see Fig. 4 A; Fig. S13), indicating an opening response of the P-site within 50 ns that consequently led to the Pi release. The finding that the Pi release was facilitated upon the enforced hydrolysis nicely confirms the prediction from the recent experimental data analyses (28), conducted for BF₁ (thermophilic Bacillus PS3).

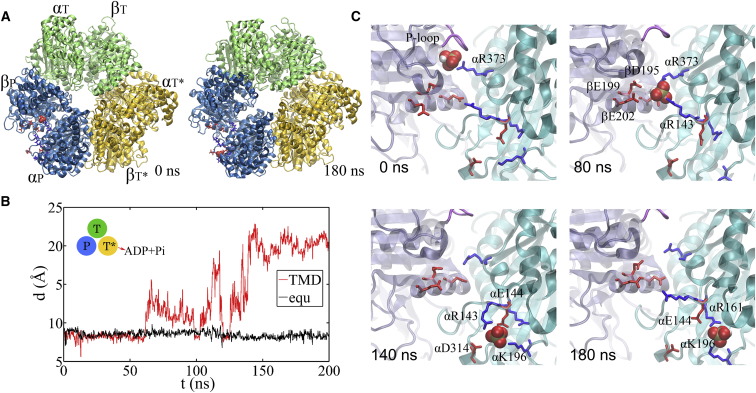
Figure 4.

TMD simulation enforcing an ATP hydrolysis transition to the T^∗-site in the T-P-T^∗ ring. (A) Top views of the ring at an early and a late stage of the simulation (green, T-site; blue, P-site; yellow, T^∗-site). (B) The distance between Pi and an inside reference (Cα of αR373) in the TMD and an equilibrium (equ) control simulation of the T-P-T^∗ ring. (C) The full pathway of Pi release captured in the TMD simulation. β_P is colored in ice blue, its P-loop in magenta, and α_P in cyan. The key charged residues are colored in blue (positively charged) and red (negatively charged). The Pi group (spheres) hopped from the arginine finger αR373 to αR143 (∼80 ns), and then to αK196 (∼140 ns) and αR161 (∼180 ns) before the final release. Three negatively charged residues from β_P (D195, E199, and E202) also helped the Pi release through repulsion. To see this figure in color, go online.

Remarkably, our TMD simulation demonstrated a complete charge-hopping pathway of the Pi release through three arginine residues and one lysine residue (see Fig. 4 B; Movies S3 and S4), which has not been revealed before. The Pi group was initially positioned through hydrogen bonding with both the P-loop from the β_P subunit and the first arginine finger residue, Arg373, from the α_P subunit. In response to the enforced hydrolysis transition, T^∗→DP, the P-loop from β_P retracted slightly from Pi. Meanwhile, Arg143, the second arginine finger from α_P, which frequently switched its side chain between Arg373 and Glu144, captured Pi after ∼50 ns of the simulation, so that Pi dissociated from Arg373. In addition, three negatively charged residues from the β_P subunit, Asp195, Glu199, and Glu202, helped to repel Pi away from β_P. Later on, Pi was further transferred to Lys196 (∼140 ns) and Arg161 (∼180 ns) on α_P and then released fully from the F₁ ring at the end of the 200 ns TMD simulation. In contrast, in an equilibrium control simulation of the T-P-T^∗ ring (for 200 ns), Pi was kept stable in association with the P-loop and Arg373, whereas the Arg143 side chain was trapped with Asp314 most of time (see Fig. 4 C; Movie S5).

To understand why the conformational transition T^∗→DP impacts the P-site that is upstream to the enforced T^∗-site, we examined again the residue-wise correlations on the T-P-T^∗ ring during the enforced transition (see Fig. 5). In particular, we see that the overall correlation decayed quickly right away from the T^∗-site. Nevertheless, one notices that the local region of the P-site correlates well with the T^∗-site residues. A close examination shows that the correlation propagates from the hydrolysis site on β_T^∗→DP, via an inactive site at the interface of β_T^∗→DP and α_P, and then extends along a narrow region of a β-sheet structure in the middle part of α_P (αArg164–Arg171, αIle345–Leu352, and αLeu369–Arg373), and finally reaches the P-site at α_P-β_P. The connection with the corresponding residues in α_T^∗→DP was, however, broken toward the β_T direction due to a gap region right at the α _T^∗→DP-β_T interface, where another inactive site is located (see Fig. 5 C). A movie was made to show the dynamics of the conformation propagation from the T^∗-site to the P-site (see Movie S6).

Figure 5.

Conformation correlation with the ATP hydrolysis pocket in the TMD simulation of the T-P-T^∗ ring. (A) Correlation map (left) of the full ring during the enforced T^∗→DP transition starting from T-P-T^∗, colored according to the correlation values (blue/white/red, high/medium/low) between individual residues and the T^∗-site ATP binding/hydrolysis residues (green spheres). An inside side view (right) shows the conformation propagation or correlation from α_T^∗→DP to β_T to α_T, and from β_T^∗→DP to α_P to β_P. (B) Residue-wise correlation from β_P (blue) and β_T (green). (C) A close structural view of the connecting residues along the two propagation pathways from α_T^∗→DP to β_T to α_T (top right) and from β_T^∗→DP to α_P to β_P (bottom right). A gap region is indicated by two red lines on the former path (top right). The cartoon schematics illustrating the two pathways is shown on the left. To see this figure in color, go online.

The first ATP binding opens the next downstream E-site more than the upstream E-site

To investigate whether asymmetrical responses arise on the early tri-site reaction path, we conducted the TMD simulation to a fully empty ring E-E-E (see Figs. S14 and S15; Supporting Material). First, we enforced an E→T transition on one pair of α_E-β_E (blue site) in the E-E-E ring; we then observed trends of mechanical responses similar to those in the E-DP-T configuration: The downstream E-site (yellow site) opened compared to the equilibrium control simulation, whereas the upstream E-site (green site) did not (see Fig. 6 A; Fig. S15). Further calculations on the cross-correlations also show an asymmetrical pattern (Fig. S16). Nevertheless, the three E-sites in the E-E-E ring were not identical (see Fig. 6; Fig. S14), e.g., one of the sites (green site) appears to open more than the other two as its protrusion height and pocket radius stay comparatively large in the equilibrium simulation. Accordingly, we conducted an additional run of the TMD simulation to see if the responses were sensitive to the initial configuration of the E-site. Again, by enforcing an E→T transition to another E-site (green site), the downstream site (now blue) opens more than the upstream site (yellow site), though one would notice that the opening bias appears small and large fluctuations are sampled in the MD simulations (see Figs. S14 and S15). Anyhow, it is also interesting to notice that the yellow E-site, being the downstream site in the first TMD run (see Fig. 6 A), demonstrated a much larger increase of the protrusion height than in the second TMD run, in which it became the upstream site of the enforced ATP binding site. Hence, we concluded that without ligand binding in the neighboring active sites, the asymmetrical responses toward the ATP binding already exist in the ring.

Figure 6.

TMD simulations enforcing an E→T transition to one of the E-sites in an empty E-E-E ring. (A) The E-site being forced into a T-site is colored blue (left) or green (right) in two TMD runs. The β-protrusions from both neighboring E-sites, sampled from the TMD simulation (solid curves) and a control equilibrium simulation (dashed curves), are shown, with arrows indicating the opening or closing trend. (B) A top view of the E-E-E ring illustrating when one of the E-sites is forced to open, the next/downstream E-site would open in response, whereas the previous/upstream E-site would not. (C) An early reaction pathway starting from an empty F₁-ring (E-E-E) shows a bias after the first ATP binding. The bias likely facilitates the second ATP binding to the downstream E-site and further leads to the E-DP-T configuration (instead of T-DP-E). To see this figure in color, go online.

Indeed, the asymmetrical responses triggered by the first ATP binding to the ring can bring a bias in recruiting the second ATP. We found through the KMC simulation that if the second ATP is recruited to the downstream site with a slight bias over the upstream site (e.g., a binding-rate ratio of ∼10), then the reaction intermediate quickly converges to E-T^∗-T, and then to E-DP-T (see Fig. 6 C), rather than to the “reversal configurations” T-T^∗-E and then T-DP-E. Once the E-DP-T configuration is reached, the chemical cycles repeat, as demonstrated in Fig. 1 C, for both MF₁ and BF₁.

The third ATP binding to the ring destabilizes both neighboring ATP-bound sites

In the KMC simulation, the 3-T configuration in BF₁ was absent due to the coordinated tri-site kinetic, i.e., T-T-T was simply not on the dominant reaction pathway. In contrast, the 3-T configuration in MF₁ needs to be explicitly prohibited to support sequential performance, by reducing the third ATP binding rate (∼10 to 100-fold; see Fig. S3 A). In the MD simulation, nevertheless, we enforced a third ATP binding to the E-T^∗-T ring (i.e., an intermediate on the MF₁ reaction path) to probe the mechanical (in-)stabilities. We noticed an abnormal increase of the pocket size in the upstream T-site, even though the β_T protrusion dropped (see Figs. S17 and S18). Notably, the bound ATP from the downstream T^∗-site released in one of the two TMD simulation trials, though the T^∗-site did not open significantly. Hence, the enforced third ATP binding appears unfavorable, as it triggers significant distortions or even destabilizes the bound ATP. In brief, an E-T^∗-T ring would either resist the third ATP binding or likely convert to T-E-T^∗ (rather than T-T^∗-E) if the third ATP binding succeeds by chance.

The TEN simulation induces the asymmetric neighbor-site opening upon ATP binding, as the atomistic TMD does

Note that ATP binding and hydrolysis, along with the induced mechanical responses, involve substantial conformational changes with a characteristic time of up to micro- to milliseconds, which may not be easily sampled by equilibrium atomistic MD. To check whether the accelerated TMD and ensuing responses at the sub-microsecond timescale bear artifacts or capture the essential motions from the original slow dynamics, we also conducted CG simulations of the F₁ ring. We employed the single-bead-per-residue elastic network (EN) description (56), which has been widely used to describe the slow or micro- to millisecond functional domain motions of protein (57, 58, 59). To make an easy comparison, we implemented targeted dynamic schemes in the EN model as well and then monitored closely the neighbor site-responses (see Supporting Material) (53, 54, 55). In particular, the forced E→T transition starting from the E-DP-T ring, and that starting from the E-E-E ring, were conducted at the CG level. Upon the E-DP-T to T-DP-T^∗ transition, the C-terminal β-protrusion of the DP-site increased, indicating an opening, whereas the T-site did not show such an opening (see Fig. 2 D and Fig. S19). Upon the E-E-E to E-T-E transition, the asymmetric responses revealed were similar to those triggered by the TMD simulation, in which the downstream site showed opening, whereas the upstream site did not (see Fig. S20). Hence, regarding the conformational responses due to the inter-subunit coupling on the F₁ ring, agreement between the CG model and the atomistic-level description is obtained. The agreement indicates that the responses under the fast enforcement in the TMD simulations persist when enforcement takes place slowly in the TEN. It also suggests that the conformational responses upon ATP binding or hydrolysis may not be very slow or rate limiting. Instead, it may be the wait for ATP binding or hydrolysis that lasts long enough to be essentially rate limiting in the overall cycle.

Discussion

To reveal kinetics essentials and structural dynamics mechanisms supporting high coordination of a prototypical ring-shaped NTPase, we investigated computationally the inter-subunit couplings that lead to intrinsic sequential performances of the F₁-ATPase ring in the absence of the central γ rotor. We first explored which types of inter-subunit couplings are kinetically feasible to allow sequential hydrolysis of the three active sites on the F₁-ring through the stochastic Monte Carlo simulations. We imposed the primary couplings of the three independent ATP hydrolysis cycles by essentially enhancing the ADP and Pi release rates in one site (i.e., above the uni-site reaction rates) upon a certain neighbor-site ATP binding or hydrolysis event in another site. We found that to support sequential hydrolysis in MF₁, the ADP release needs to be accelerated >∼10⁵-fold upon upstream-site ATP binding to the E-DP-T ring, and similarly for the ensuing Pi release from the same site; in BF₁, on the other hand, the ADP release needs to be accelerated for above ∼10³ fold, while the Pi release can be accelerated either along with the ADP release and/or upon downstream-site ATP hydrolysis in the T-P-T^∗ ring. To elucidate the physical basis of these kinetically feasible couplings with structural detail, we next performed atomistic TMD simulations to enforce the conformational transition of the ATP binding or hydrolysis to one of the three chemical sites, and we monitored the following mechanical responses from the two neighbor sites. We found essentially the features below from the combined stochastic kinetic and structural dynamics simulations.

The primary inter-subunit coupling that supports sequential hydrolysis with a directional bias is the ATP-binding-facilitated downstream-site product release, arising from the asymmetrical site opening inherent to the architecture of the trimer-of-heterodimer ring

Consistently, we found in the atomistic simulation of the E-DP-T ring that the downstream DP-site opens in response to the enforced E-site closing that mimics ATP binding. The site opening was partially characterized by a slight increase of the β-protrusion, the hinge bending angle, and the pocket size of the binding. Further examinations show notable conformational changes along with weakening of the hydrogen-bond network in the peripheral region of the DP-site. All these allosteric impacts induced by the E-site closing would likely facilitate ADP release from the DP-site. When the central γ-rotor was included in the TMD simulation, the β_DP-protrusion increase was notably enhanced. Close examination of the cross-correlation of the E-DP-T ring in the absence of the γ rotor shows that the ATP-binding-induced conformational changes propagate asymmetrically from the E-site to the DP- and T-sites via the α_E-β_DP and β_E-α_T-β_T paths, respectively. The asymmetrical downstream site opening is also preserved upon the induced site closing that mimics the first ATP binding to the empty E-E-E ring. The asymmetrical responses thus appear to be inherent to the architecture of the trimer-of-the-heterodimer (α-β) ring, in particular, as α- and β-subunits differ and alternate around the ring, whereas the chemical active site largely locates on β. The inclusion of the γ-rotor into the center of the ring is able to enhance the asymmetrical responses significantly, which either promotes ADP release (and the initial Pi release) or biases the second ATP binding to the downstream site. In particular, the bias for the second ATP binding downstream allows the sequential hydrolysis to proceed directionally (counterclockwise viewed from the C-terminal side).

Sequential hydrolysis is also supported by proper timing and acceleration of Pi release, which follows ADP release either quickly upon upstream-site ATP binding or later upon downstream-site ATP hydrolysis; Pi release is completed in charge hopping in the simulation

On the other hand, Pi release can be facilitated via two different mechanisms (see Fig. 1 C), either upstream-site ATP binding that induces ADP release first (MF₁ (18)) or downstream T^∗-site ATP hydrolysis (BF₁ (19)). Direct support for the first mechanism comes from the bovine heart MF₁ structure per se (T-P-T^∗; PDB: 1W0J) (51), in which the Pi group in the P-site (after ADP release) is located nearby the P-loop, a marginally stabilized state, rather than in the innermost tightly bound state (37). That is, ATP binding to the ring (from E-DP-T to T-DP-T^∗) not only destabilized ADP from the DP-site, but also destabilized the bound Pi, so that Pi moved from the tightly bound state to the marginally stabilized state. The release of Pi thereafter then becomes comparatively easy.

Nevertheless, our equilibrium MD simulation of the T-P-T^∗ ring was not yet able to capture the Pi release from the P-site within hundreds of nanoseconds. In the equilibrium simulation, the Pi group was associated with the β P-loop as well as the arginine finger αArg373. The other arginine finger, αArg143, was trapped initially by association with αAsp314 in the P-site. Nicely, in contrast, a complete Pi-release event was revealed in the TMD simulation, as the P-site mechanistically responded to the enforced hydrolysis in the T^∗-site. The P-loop retracted and Arg143 was able to switch occasionally toward Arg373, whereas the three negatively charged residues from β_P also repelled Pi to assist the release. Consequently, the chance that Pi is caught by Arg143 and dissociates from the P-loop increases significantly, and P-loop dissociation becomes critical for further charge hopping, and the final release of Pi.

Compared with the significant open-to-closed conformational changes in the ATP binding site, ATP-hydrolysis-induced conformational changes are rather subtle. We found that the inactive site at the β_T^∗-α_P interface, along with a β-sheet region on α_P, actually bridged the mechanistic pathway to propagate the subtle conformational changes from the T^∗-site to the P-site, whereas the other way of propagation was broken through the inactive site at the α_T^∗-β_T interface. In brief, ATP hydrolysis does not generate substantial responses on the protein ring; rather, it triggers local directional conformational propagation via the inactive site and a restricted structural element. Besides, in the T-P-T^∗ ring, the P-site upstream of the T^∗-site is more open and likely much more flexible than the downstream T-site; hence, it appears easier for the mechanical responses to propagate upstream than downstream.

We also found additional couplings or constraints that would help the sequential hydrolysis. An explicit constraint to prevent the third ATP binding to the MF₁ ring (or inhibit the 3-T population) would improve the sequential performance, since the 2-T (T-E-T^∗) configuration is on the dominant reaction path of MF₁. The 2-T configuration can easily turn into 3-T without the constraint, thus interfering with the sequential scheme. The TMD simulation enforcing a third ATP binding to the E-T^∗-T ring consistently demonstrated significant destabilization of the neighboring sites. On the other hand, the BF₁ ring achieves sequential performance without the explicit constraint to exclude 3-T, as such a 2-T configuration is not on the dominant reaction path. In addition, we effectively enhanced the ATP hydrolysis rate in the T^∗-site, when a second ATP binds to the ring to form a T-site. The rate enhancement in the hydrolysis-ready intermediate T^∗-site ensures that hydrolysis takes place sufficiently fast and the site that binds ATP early can hydrolyze early most of the time. Anyhow, these constraints or couplings were not very stringently imposed, and there was a significant chance that the reactions went off-path to configurations such as 3-T or 2-DP, which might also account for some non-optimal mechanochemical couplings detected early (60).

Tight coupling is expected between ATP binding and ADP release, and the strength of the coupling can be substantially enhanced by the central γ-rotor; the coupling between ATP hydrolysis and Pi release is notable even in the absence of the γ-rotor

The rotary sequential hydrolysis of F₁-ring is basically supported by chemical free energy through the three ATP cycles, which are coordinated with certain phase differences. The coordination also demands free-energy input and dissipation (61). The kinetic rate enhancements in the inter-subunit couplings require lowering activation barriers of the facilitated transitions, e.g., for the hydrolysis product (ADP or Pi) release. For such couplings, either the product binding affinity (or the dissociation constant) is maintained, or the product-rebinding rate remains constant, which requires free-energy compensation from the neighboring unit. For example, to enhance the ADP release rate ∼10⁵-fold (in MF₁), it requires up to ∼12 k_BT to destabilize the DP-site (with a constant ADP-rebinding rate), and the energy compensation should come from the neighbor-site ATP binding (e.g., by also destabilizing the ATP binding to the T-site). Since the chemical free energy is mostly dissipated through the rotational degree of freedom in the presence of the γ-rotor (62, 63), one expects that the γ-rotor would play a significant role in strongly coupling the ATP binding to the next-site ADP release, both structurally and energetically. Current studies indeed show that the β_DP-protrusion responds more significantly to the enforced ATP binding in the presence of the γ-rotor than in its absence.

In comparison, the ATP-hydrolysis-facilitated Pi release (rate enhancement ∼10³-fold) appears to require less energetic compensation in the coupling if there is any, so we could actually capture the Pi release event in the absence of the γ-rotor. As such, we infer that the central γ-rotor dictates the inter-subunit coupling more significantly in the ATP binding step than in the ATP hydrolysis step, which leads to stronger inter-subunit couplings or higher coordination in the original F₁-ATPase with the rotor than in the stator ring only. As a matter of fact, considering the recent MD studies on the γ-shaft rotation and the Pi release (37), together with our current simulation results, we suggest that the initial stage of the Pi release can also be facilitated by the γ-shaft rotation that accompanies the ATP binding and the ADP release. Complete Pi release can be further promoted by the neighbor-site ATP hydrolysis in the bacterial F₁, which can couple with the additional γ-shaft rotation.

According to our study, one can further tune the inter-subunit coupling kinetics to allow a significant increase in the overall cycling rate of F₁, approaching experimentally measured values for the full F₁ system with the rotor (see Tables S3 and S4). Hence, one can see that the rotor effectively plays a role in strengthening and further modulating the inter-subunit couplings on the ring, and consequently in promoting the overall hydrolysis rate. Based on current work, it would be promising to determine how exactly the central γ-rotor contributes to the F₁ inter-subunit coordination for the respective steps of ATP binding and hydrolysis. Indeed, the ATP binding and hydrolysis transitions, along with their coordination in the ring assembly, have only been phenomenologically modeled in current work, and they deserve more substantial investigation in future work.

Conclusions

Combining stochastic simulations of tri-site chemical kinetics of the F₁ stator ring with targeted atomistic MD and coarse-grained EN simulations, we inferred the most crucial inter-subunit couplings leading to sequential hydrolysis on the F₁ ring: ATP binding facilitates ADP release from a downstream DP-site, along with Pi release from the same site, whereas complete Pi release can be further facilitated by ATP hydrolysis downstream. The couplings come from asymmetrical neighbor-site opening/loosening upon current site closing/tightening produced by the ATP binding/hydrolysis. The dominant conformational asymmetry, demonstrated upon ATP binding, appears to be embedded in the trimer-of-heterodimer ring, owing largely to the alternating arrangement of α- and β-subunits. Additionally, a minor structural dynamics asymmetry is revealed upon subtle conformational transition under ATP hydrolysis, which impacts the neighbor sites differently via subtle structural variations. The mechanistic propagation around the ring is therefore modulated also by the ligand (ATP, ADP, or Pi) bound status in the neighboring sites. Furthermore, preventing a third ATP from binding to the assembled ring, as well as allowing a hydrolysis-ready intermediate in the ring to have an elevated hydrolysis rate, also supports the sequential hydrolysis on the F₁ ring. Though the overall cycling rate in our simulation of the bacterial F₁ ring matches with the experimental detection of the rotor-less system, it should be noted that the full F₁ in the presence of the rotor rotates and cycles much faster, revealing a central role played by the rotor in enhancing inter-subunit coupling on the ring. The large discrepancy between the cycling rates of mitochondrial and bacterial species of F₁ in the rotor-less case does not necessarily show in the presence of the rotor, indicating further inter-subunit modulation from the rotor. It would be highly interesting to pursue whether comparable coupling scenarios apply to evolutionarily connected ring-shaped protein enzymes working on a central substrate of protein or nucleic acid.

Author Contributions

J.Y. designed the research. L.D. and H.F. performed the research. L.D. and H.F. analyzed the data. J.Y., H.F., and L.D. wrote the article.

Editor: Hiroyuki Noji.

Supporting Citations

References (64, 65, 66) appear in the Supporting Material.

Supporting Material

Movie S1. Top View of DP-Site Opening Induced by E-Site ATP Binding

The top view showing the DP-site opening upon the enforced ATP binding to the E-site in the E-DP-T ring. The TMD simulation and ensued relaxation lasted ∼ 450 ns (see Fig. 2). The α-β dimers forming the E, DP and T-site are colored in green, blue, and yellow, respectively, with the DELSEED residues highlighted in magenta spheres (the initial positions in pink).

Movie S2. Side View of DP-Site Opening Induced by E-Site ATP Binding

The side view of the same simulation as in Movie S1. For clarity, only the β subunits were shown (βE, βDP and βT in green, blue and yellow), with the DELSEED residues on the β protrusions in spheres. The βE protrusion drops as the E-site was enforced to close, while the βDP protrusion increases in response.

Movie S3. Zoom-In View of P-Site Pi Release Induced by T∗-Site Hydrolysis

The zoom-in view of the Pi release upon the enforced ATP hydrolysis transition in the T^∗-site of the T-P-T^∗ ring. The TMD simulation lasted ∼ 200 ns (see Fig. 4). The βP subunit is colored in iceblue and its P-loop colored in magenta; the αP subunit is colored by cyan. The key charged residues are colored in blue (positively charged) or red (negatively charged). The Pi group started in association with the P-loop and Arg373 (an arginine finger from αP), and then released through charge hopping from Arg373 to Arg143, then to Lys196 and Arg161.

Movie S4. Top View of P-Site Pi Release Induced by T∗-Site Hydrolysis

The top view of the same simulation as in Movie S3. The α-β dimers forming T, P, and T^∗-site are colored by yellow, green, and blue, respectively. The P-loop from βP still colored in magenta and the key charged residues from αP are colored according to their charges (blue for positive and red for negative).

Movie S5. Top View of T-P-T∗ Ring in an Equilibrium Control

The top view of a controlled equilibrium simulation (200 ns) of the T-P-T^∗ ring. The color scheme is the same as Supporting Movie 4. In contrast with the TMD simulation (shown in Movie S4), the Pi group did not release and kept in association with the P-loop and Arg373.

Movie S6. Zoom-In View of Conformation Propagation from T∗-Site to P-Site

The zoom-in view of the conformation propagation from the T^∗-site to the P-site. The βT^∗ subunit is colored by gray, αP is colored by green and βP is colored by yellow. The residue with high correlation to the T^∗ pocket are shown. The correlation propagates from the hydrolysis site on βT^∗→DP, via an inactive site at the interface of βT^∗->DP and αP, and then extends along a narrow region of a beta-sheet structure in the middle part of αP (αArg164 to Arg171, αIle345 to Leu352, and αLeu369 to Arg373), and finally reaches to the P-site at αP-βP.