On the differing growth mechanisms of black-smoker and Lost City-type hydrothermal vents

Abstract

Black smokers and Lost City-type springs are varieties of hydrothermal vents on the ocean floors that emit hot, acidic water and cool, alkaline water, respectively. While both produce precipitation structures as the issuing fluid encounters oceanic water, Lost City-type hydrothermal vents in particular have been implicated in the origin of life on the Earth. We present a parallel-velocity flow model for the radius and flow rate of a cylindrical jet of fluid that forms the template for the growth of a tube precipitated about itself and we compare the solution with previous laboratory experimental results from growth of silicate chemical gardens. We show that when the growth of the solid structure is determined by thermal diffusion, fluid flow is slow at the solid–liquid contact. However, in the case of chemical diffusive transport, the fluid jet effectively drags the liquid in the pores of the solid precipitate. These findings suggest a continuum in the diffusive growth rate of hydrothermal vent structures, where Lost City-type hydrothermal vents favour contact between the vent fluid and the external seawater. We explore the implications for the road to life.

1. Introduction

Black smokers (figure 1a) [1,3] and Lost City-type springs (figure 1b) [4,5] are varieties of hydrothermal vents on the ocean floors that emit hot, acidic water and cool, alkaline water, respectively. While both produce precipitation structures as the issuing fluid encounters oceanic water, Lost City-type hydrothermal vents in particular have been implicated in the origin of life on the Earth. Fluid flow in black-smoker and Lost City-type undersea hydrothermal vents is remarkably different. While black smokers are largely characterized by high-temperature flow focused in channels, the Lost City-type vents exhibit a more distributed flow of colder fluids. One of the basic questions about these flows is what determines the fluid–solid–structure interaction. We show that black-smoker growth is driven by thermal diffusion, while Lost City-type hydrothermal vent growth is driven by much slower chemical diffusion, leading to more contact between the issuing and the environmental fluids in this case. Thus, the cool alkaline vents that geochemists favour as the environment for proto-life also make most sense from a physics standpoint, because the fluid dynamics and precipitation produces a self-organized and self-assembled complex system that allows the controlled exchange of ions with the environment across a semipermeable membrane. We explore the consequences for the origin of life [6].

Figure 1.

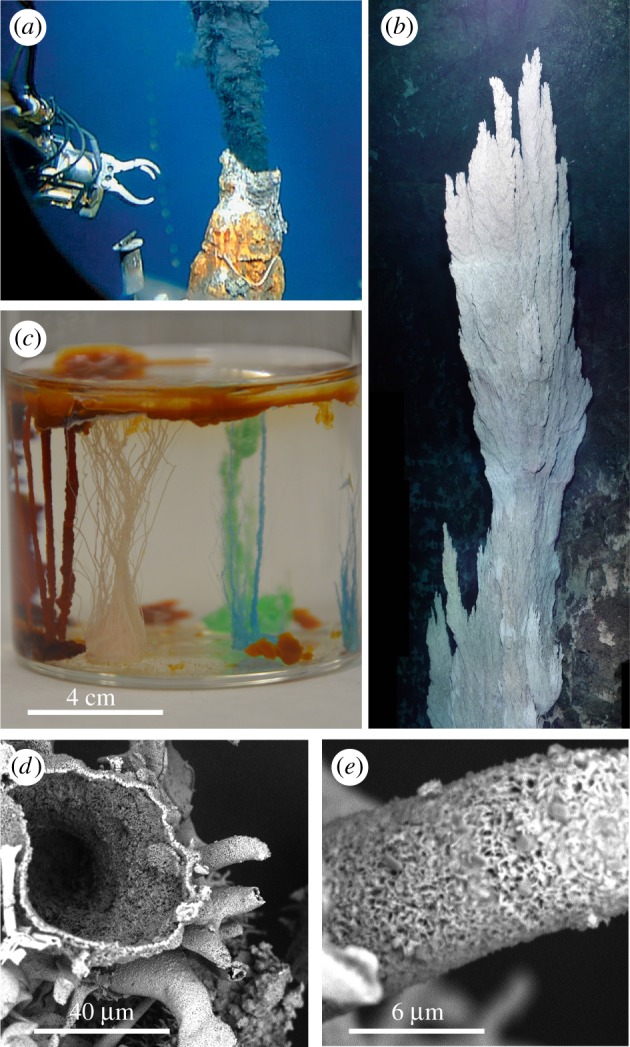
Fluid-jet-templated precipitated tubes: (a) oceanic hydrothermal vent of the black-smoker type [1]; the robot arm claw is opened about 15 cm. (b) Lost City hydrothermal vent; this feature, named Ryan, is some 13 m in height [2]. (c) Chemical garden in a laboratory beaker showing the tubular growths of a variety of metal salts placed in a solution of sodium silicate. (d) Overall scanning electron microscopy view of a group of tubes growing from a zinc sulfate seed. (e) Close-up scanning electron microscopy view of one tube displaying its outer wall microstructure.

Previous work on hydrothermal vents has shown that black smokers emitting high-temperature fluids of 350–400^°C display channelled flow through well-defined conduits surrounded by a relatively low permeability solid structure, up to 3×10⁻¹³ m², with porosity of 0.15–0.40 [7]. For vents emitting lower temperature fluids of less than 150^°C, the flow has been observed to be more distributed in a porous chimney with permeabilities up to 5×10⁻¹² m² and slightly larger porosities, in the range 0.30–0.45 [7]. For vents such as those at Lost City hydrothermal field, the temperature of the issuing fluid is even lower, around 40–90^°C, and the flow of fluid is completely distributed [2]. We expect the large temperature contrasts to enhance the loss of heat by conduction and thus to provide a thermal control on the precipitation rate; at lower temperatures, chemical diffusion will determine transport and the rate of precipitation process. These observations suggest that we explore the roles of both heat and chemical transport in these precipitate deposits. In order to do so, we first investigate laboratory systems ranging from chemical gardens [8] to ice brinicles [9]. We also develop a parallel-velocity flow model for the radius and flow rate of a cylindrical jet of fluid that forms the template for the growth of a tube precipitated about itself and compare the solution with these laboratory results. We then build upon these laboratory and theoretical results to understand the flow behaviour and growth rates in hydrothermal vents.

In chemical gardens and other chemobrionic systems, liquids of differing composition form precipitation products with many self-organized morphologies [8]. Beyond the laboratory, chemobrionic systems are encountered in circumstances as varied as iron corrosion products [10], and the hydration of Portland cement [11], as well as hydrothermal vents on the ocean floor [12] and brinicles under sea ice [9]. One of the most characteristic morphologies seen in such systems is that of a tube of material that precipitates around a jet of fluid (figure 1). In the typical case, there is some volume of quiescent fluid into which a jet of another fluid impinges. A reaction between the two fluids occurs along the zone of contact, which implies that the jet acts as a template for the tube growth.

Figure 1 displays fluid-jet-templated precipitated tubes from a classical chemical garden experiment. In figure 1c, we see an array of tubes from four metal salts—iron(II) chloride, nickel chloride, copper sulfate, zinc sulfate—grown in sodium silicate solution. In figure 1d,e, we show scanning electron micrographs of a group of zinc sulfate tubes and of the external wall of one zinc sulfate tube, displaying its complex microstructure. Recent work has examined aspects of tube growth including the range of possible reactants from silicates, carbonates, phosphates, hydroxides, sulfides or polyoxometallates [13–17], the range of tube wall microstructures [18–21] and tubes arising from corrosion [22], cement hydration [23,24], brinicles [25] and hydrothermal vents [26].

The mathematical modelling of chemical gardens and chemobrionic systems has sought to quantify this tube growth. In contrast to classical jets and plumes [27–29], which expand considerably as they rise, in a chemical garden the jet or plume has constant radius. This dissimilarity arises from the usual viscosity difference and precipitation reaction between the internal and external fluids in a chemical garden. The classical solutions for laminar jets and plumes where the inside and outside fluids have similar properties are therefore not applicable to the present flow. However, like classical jets and plumes, we expect the solution for the flow in a chemical garden to allow the possibilities of purely buoyant flow (pure plume) and fully forced flow by a pump (pure jet), as well as the continuum between these limits. Below we derive an approximate solution that encompasses such behaviours.

One of the simplifications that has been introduced for this purpose is to decouple the fluid mechanics from the chemistry. This decoupling can only be valid when the timescale of fluid motion is quite remote from the timescale of the chemistry. Nonetheless, it is a useful starting point. A full solution of this simplified problem requires two-dimensional numerics, but here we present an approximate one-dimensional analytical solution which is a good basis for an understanding of the different effects, and we show that it is a very good approximation to the experimental results obtained for this system [30].

Consider a non-reactive jet or plume of one viscous fluid rising in another fluid of finite vertical and lateral extent (figure 2). Momentum and mass conservation are governed by

$$\begin{array}{rl}0& =-\mathbf{\nabla }p+\mu {\mathbf{\nabla }}^2\mathbf{\text{u}}+\rho \mathbf{\text{g}}\\ \mathrm{and}\mathbf{\nabla }\hspace{0.17em}\cdot \hspace{0.17em}\mathbf{\text{u}}& =0,\end{array}\}$$ 1.1

where, u is the velocity vector, p is pressure, g is the gravitational acceleration, and μ and ρ are the viscosity and density of the fluid, respectively. The first relation demonstrates a balance between pressure, viscous and buoyancy forces and is valid for slow, low Reynolds number flows for which the acceleration of the fluid is negligible; this is the classical Stokes equation. The solution of equations (1.1) requires appropriate boundary conditions at the interface of the two fluids and for the environment, which we discuss below. For an axisymmetric configuration, the inner jet fluid forms a cylindrical jet of radius R, surrounded by external environmental fluid recirculating in a toroidal cell of radius R_c>R. This complex flow requires a two-dimensional solution of equations (1.1). However, a simple approximate solution may be obtained by assuming a parallel-velocity flow and ignoring end effects at the top and bottom of the domain.

Figure 2.

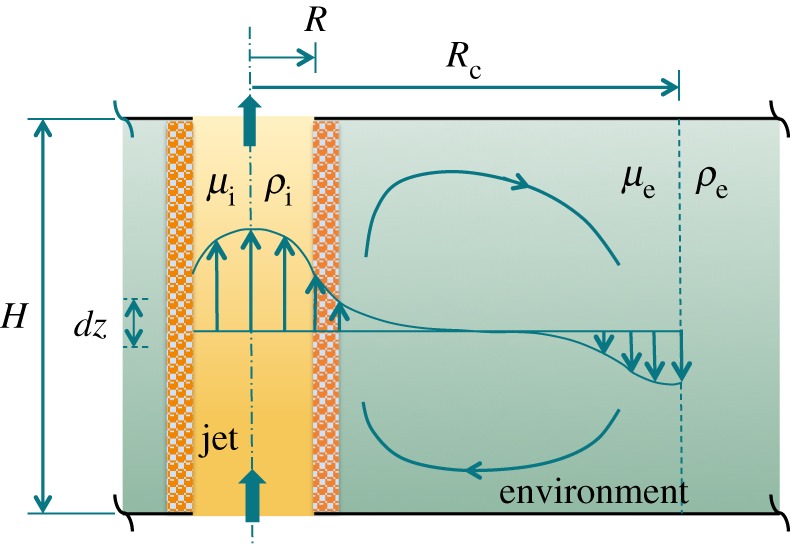
Sketch of the model set-up with a fluid jet and recirculation of the fluid in the environment around it. (Online version in colour.)

Consider then the one-dimensional motion of an inner fluid of density ρ_i and viscosity μ_i in an environmental fluid with density ρ_e>ρ_i and viscosity μ_e. While continuity imposes no variation of the vertical velocity w with vertical position z (i.e. ∂w/∂z=0), the vertical component of Stokes’ equation requires that

$$0=-\frac{\mathrm{\partial }P}{\mathrm{\partial }z}+\mu \frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)+\mathrm{\Delta }\rho g,$$ 1.2

in each fluid. Here, P=p+ρ_egz is the reduced pressure and Δρ=ρ_e−ρ (thus, for the internal fluid Δρ_i=ρ_e−ρ_i and for the external fluid Δρ_e=0). The radial component of Stokes’ equation implies ∂P/∂r=0 in each fluid, so that there is no pressure variation in the radial direction.

The boundary conditions at the interface between the two fluids express continuity of vertical velocity, pressure and shear stress: at r=R, P_i=P_e, w_i=w_e, and τ_i=μ_i∂w_i/∂r=μ_e∂w_e/∂r=τ_e. We also impose zero net vertical flow of the external fluid: ${\int }_R^{R_{\mathrm{c}}}r{w}_{\mathrm{e}}(r)\hspace{0.17em}\mathrm{d}r=0$. We should note that for a two-dimensional model we would also impose at the edge of the recirculating cell, r=R_c, either zero velocity (for a solid wall) or continuity of stress (for a fluid). However, given the simplification of the problem to one dimension, we need to drop this boundary condition. The radius of the cell R_c is therefore defined here by one requirement only, that of no net vertical flow in the environment; in reality R_c is a function of the aspect ratio of the environment but cannot be specified by a simple one-dimensional approximate flow. Integration of equations (1.2) in the radial direction, taking into account the boundary conditions and the symmetry condition ∂w/∂r|_r=0=0 , gives the vertical velocity in the jet

$$w_{\mathrm{i}}=\mathrm{\Delta }{\rho }_{\mathrm{i}}g[\frac{R^2-r^2}{4{\mu }_{\mathrm{i}}}+\frac{R^2}{4{\mu }_{\mathrm{e}}}(2\mathrm{\hspace{0.17em}ln}\frac{R_{\mathrm{c}}}{R}-1)]-\frac{\mathrm{d}P}{\mathrm{d}z}[\frac{R^2-r^2}{4{\mu }_{\mathrm{i}}}-\frac{R^2}{4{\mu }_{\mathrm{e}}}(1-\frac{1}{2}{\left(\frac{R_{\mathrm{c}}}{R}\right)}^2)].$$ 1.3

This result is equivalent to using lubrication theory. The volumetric flow rate in the jet is then

$$Q_{\mathrm{i}}=\frac{\mathrm{\Delta }{\rho }_{\mathrm{i}}g\pi R^4}{8{\mu }_i}[1+4\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}(\mathrm{\hspace{0.17em}ln}\frac{R_{\mathrm{c}}}{R}-\frac{1}{2})]+\frac{\mathrm{d}P}{\mathrm{d}z}\frac{\pi R^4}{8{\mu }_{\mathrm{i}}}[-1+2\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}-\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}{\left(\frac{R_{\mathrm{c}}}{R}\right)}^2].$$ 1.4

We can identify four limiting behaviours in equation (1.4), according to the dominant driving force for flow, either pressure or buoyancy, and according to the viscosity of the outside fluid, either finite, for a liquid, or infinite, representing a solid. Let us consider some limiting cases.

• (i) When ${\mu }_{\mathrm{e}}\to \mathrm{\infty }$,

  $$Q_{\mathrm{i}}=(\mathrm{\Delta }{\rho }_{\mathrm{i}}g-\frac{\mathrm{d}P}{\mathrm{d}z})\frac{\pi R^4}{8{\mu }_{\mathrm{i}}};$$ 1.5

  i.e. when the outside fluid is solid, we recover Poiseuille flow driven by a pressure gradient −dP/dz and a density difference Δρ_ig.
• (ii) When μ_e=μ_i,

  $$Q_{\mathrm{i}}=\frac{\mathrm{\Delta }{\rho }_{\mathrm{i}}g\pi R^4}{8{\mu }_{\mathrm{i}}}[1+4(\mathrm{\hspace{0.17em}ln}\frac{R_{\mathrm{c}}}{R}-\frac{1}{2})]+\frac{\mathrm{d}P}{\mathrm{d}z}\frac{\pi R^4}{8{\mu }_{\mathrm{i}}}[1-{\left(\frac{R_{\mathrm{c}}}{R}\right)}^2].$$ 1.6

  As R_c>R, the flow rate is larger than in (i), as expected.

• (iii) Lastly, when $R_{\mathrm{c}}\to \mathrm{\infty }$, $Q_{\mathrm{i}}\to \mathrm{\infty }$. This result is unphysical. The assumption of one-dimensional vertical flow breaks down when the environment is wide: several convecting cells develop such that R_c≤H. In this case, a one-dimensional model is insufficient and we must look to a two-dimensional model that requires numerical solution or obtain R_c from experimental observation.

Equation (1.4) may be compared with experimental results. For this, it is useful to write it in non-dimensional form

$$\frac{8{\mu }_{\mathrm{i}}}{\mathrm{\Delta }{\rho }_{\mathrm{i}}g\pi {R_{\mathrm{c}}}^4}{Q}_{\mathrm{i}}=R^{\prime 4}[1+4\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}(\mathrm{\hspace{0.17em}ln}\frac{1}{R^{\prime }}-\frac{1}{2})+\frac{1}{\mathrm{\Delta }{\rho }_{\mathrm{i}}g}\frac{\mathrm{d}P}{\mathrm{d}z}(-1+2\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}-\frac{{\mu }_{\mathrm{i}}}{{\mu }_{\mathrm{e}}}\frac{1}{R^{\prime 2}})],$$ 1.7

where R′=R/R_c. Thouvenel et al. [30] performed experiments on growing chemical-garden tubes in the laboratory that correspond to the case of coupled buoyancy- and pressure-driven flow in a viscous environment. They plotted data shown in figure 3 and a comparison with both Poiseuille flow and an expression they derived that differs from the first term of equation (1.4) in having 1 rather than $\frac{1}{2}$ inside the innermost parentheses, and does not have the second term. In figure 3, we show that almost all of the measurements lie, within experimental error, on the red line predicted by equation (1.7) if, in addition to the experimental parameters provided by Thouvenel et al. [30], we suppose that the pump provided a minimal pressure gradient. We suspect that some of the remaining ‘noise’ is because the pump was under no obligation to deliver a fixed pressure, the pressure required being far below its maximum, and so the pressure gradient may differ somewhat between different runs. In these experiments, the environment is narrow compared with the height (R_c/H=0.04) so that the one-dimensional approximation is very good. We expect this approximate solution to become less accurate as $R_{\mathrm{c}}/H\to 1$.

Figure 3.

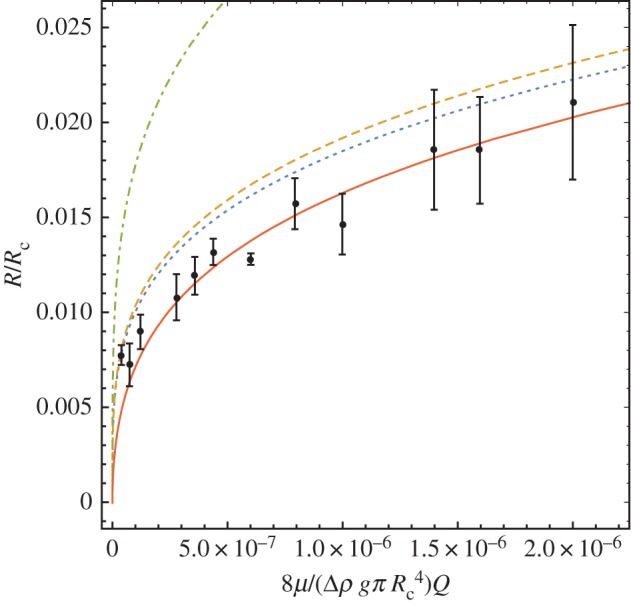
Variation of tube radius with flow rate for chemical gardens. Thouvenel et al.’s experimental data [30] for R_c=11 mm, Δρ_i= 115.75 kg m⁻³, μ_i=0.942 mPa s, μ_i/μ_e= 0.942/1.74=0.541, g=9.81 m s⁻² are shown with the prediction from Thouvenal et al. (dashed line) and that of Poiseuille flow, equation (1.5) with dP/dz=0 (dot-dashed line), together with equation (1.4) with dP/dz=0 (dotted line) and with dP/dz=−3 Pa m⁻¹ (solid line). (Online version in colour.)

In order to compare and contrast these data, let us now look at another set of experimental results from laboratory experiments on a rather different fluid-jet-templated tube. Brinicles are tubes of ice that form around plumes of cold heavy brine that descend from the lower surfaces of floating sea ice in the Antarctic and Arctic [9,25]. Although these ice tubes are formed of a different material in different circumstances to either chemical gardens or hydrothermal vents, they constitute a further instance of the same fluid-jet-templated tube growth, and we shall see that we can gain insight into hydrothermal vents by comparison. Martin [31] performed experiments to grow these ice tubes in the laboratory; his results are shown in figure 4. As in figure 3, blue is the basic Poiseuille flow solution, and most data lie near that curve (three data points are off the curve; we discuss these below). This indicates that for brinicles, the inner flow does not ‘feel’ the outer fluid, but only the presence of the wall, so that effectively the outside fluid is solid and Poiseuille flow applies. To understand this difference between the two sets of experimental results, consider the difference in scale and in wall thickness between the chemical garden experiments and the brinicle experiments. The wall thickness should scale with $\sqrt{Dt}$, but in a chemical garden the D is a chemical diffusivity, while in a brinicle it is a thermal diffusivity, typically 100× larger. So a brinicle should increase in thickness faster. We can check this prediction with chemical garden data from Stone [32]: $t\sim 100\hspace{0.17em}min$, thickness approximately 1–2 mm and brinicle data from Martin [31] t∼6–10 min, thickness around 5 mm. Hence, the radial diffusivity is for chemical gardens approximately D∼0.001²/(100⋅60)=1.7×10⁻⁹ m² s⁻¹ and for brinicles D∼0.005²/(6⋅60)=7×10⁻⁸ m² s⁻¹. So, yes, brinicles grow by thermal diffusion, approximately 100× larger than the chemical diffusion in chemical gardens. In both systems, the inner fluid drags the outer fluid as it moves. This dragging becomes less efficient as the viscosity and thickness of the precipitate increases. The structure of the solid depends on the relative amount of residual fluid it contains. During brinicle growth, the most abundant component in the external fluid—water—is solidifying so that the residual salty brine left in the pores has a small volume fraction. By contrast, the dilute chemical solutions from which a chemical garden tube grows will form a network of saturated pores with larger volume fraction. Thus, we expect the faster growing wall to have a less porous structure and to act as a solid sooner than the slower one. Hence the difference in scales and morphologies between chemical gardens and brinicles, and the pure Poiseuille behaviour we find in the brinicle compared to the ‘liquid-wall’ behaviour in the chemical gardens. Both these behaviours are encompassed by equation (1.4) or equivalently (1.7).

Figure 4.

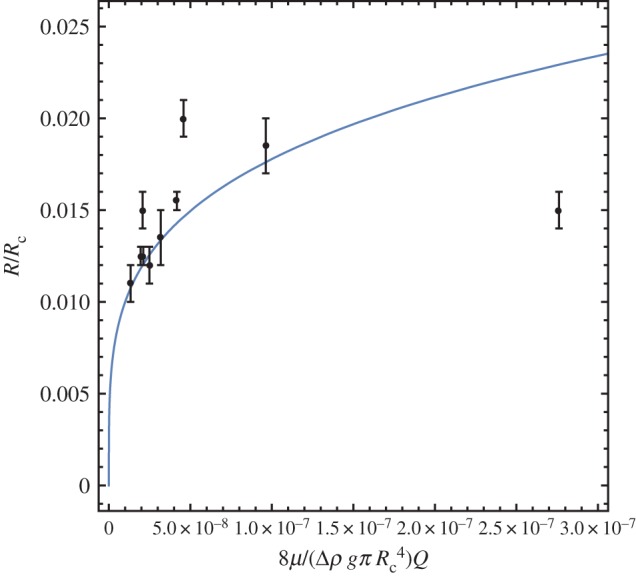
Variation of tube radius with flow rate for brinicles. Martin’s experimental data [31] for R_c=10 cm, Δρ_i=0.15 g cm⁻³, μ_i= 1.03 c P, μ_i/μ_e=1, g=981 cm s⁻² are shown with the prediction from Poiseuille flow, equation (1.4) with dP/dz=0 and ${\mu }_{\mathrm{e}}\to \mathrm{\infty }$. (Online version in colour.)

We may compare these chemical gardens with laboratory experiments of Turner & Campbell [33] in which mineral tubes are grown not by chemical reaction but by phase change. Unfortunately, they do not provide the data that would allow us to plot a graph like figure 3 or figure 4, but in their fig. 2 they show an image after 50 min, allowing us to estimate a growth of thickness around 1 cm, giving an approximate diffusivity of D∼0.01²/(50⋅60)=3×10⁻⁸ m⁻² s⁻¹, which reflects a combined effect of thermal and chemical diffusion.

It is important to note that our theoretical expression equation (1.4) or equivalently (1.7) is valid for the continuous flow regime; the so-called jetting. Different regimes have been described for varying buoyancy, and as well as this continuous flow jetting regime, there exist non-continuous flow regimes at lower buoyancy, popping and budding [34,8]. The Steinbock chemical garden measurements that we use in figure 3 are all for jetting, but some of Martin’s brinicle measurements in figure 4 are for another regime, popping, where there is periodic formation of an end cap. These brinicles grown in the popping regime are those that correspond to the three data points that are some way off the Poiseuille curve in figure 4.

Let us now compare laboratory experiments with natural precipitation membranes. In hydrothermal vents on the ocean floor, precipitation membranes grow at the boundary between seawater and mineral-rich liquid flowing out of the vent. Both hot acidic black-smoker and cooler alkaline Lost City-type vents have been found. The latter grow much more slowly than the former. A black smoker attains a thickness of 7 cm in 5 days [35], while a Lost City-type vent needs 2 years to achieve a thickness of 10 cm [36]. Thus for a black smoker, D∼0.07²/(5⋅24⋅60⋅60)=1.1×10⁻⁸ m² s⁻¹ while for a Lost City-type vent D∼0.1²/(2⋅365⋅24⋅60⋅60)=1.6×10⁻¹⁰ m² s⁻¹, a factor of nearly 100. We can have radial growth of a tube driven by thermal diffusion or chemical diffusion. Thermal diffusion is fast so that a solid wall is rapidly formed, compared to chemical diffusion. Additionally, high temperatures normally allow higher concentrations of dissolved chemicals, so that the structure of the precipitating solid contains less residual fluid and is therefore less porous. This growth-rate argument is supported by the observations of lower permeabilities and porosities in black-smoker walls [7]. We therefore expect transport across the wall for hot black-smoker vents to be slower than for colder Lost City-type vents. This means that for hot vents there should be less contact between surrounding environmental and issuing fluids; the chimney becomes solid faster and so hot vents are more isolated from the surroundings. This conclusion is compatible with geological evidence that the active lifetime of a black smoker is tens of years, but of a Lost City-type vent is up to 100 000 years [37].

There is increasing evidence for the idea that life on the Earth may have originated at these cool, alkaline vents [38]. Life needs a source of free energy from the environment [39], and extant cells pump ions across the cell membrane using chemiosmosis [40]. It is proposed that some 4 billion years ago at sites similar to today’s Lost City vents chemical reactions began to take advantage of natural ion gradients across membranes like those we have been studying here [41]. There is strong evidence for the geochemical aspects of this possible route to life [42]. The present work adds to this accumulating evidence [43] the physical reasons why warm alkaline vents are a better prospect than hotter vents to allow the necessary controlled exchange with their environment from osmotic pumping across the semipermeable membranes of these natural chemical gardens.

Data accessibility

All the supporting data are supplied in the article.

Authors' contributions

Both authors contributed in an integrated fashion to this work.

Competing interests

We declare we have no competing financial interests.

Funding

S.S.S.C. acknowledges the financial support of the UK Leverhulme Trust project RPG-2015-002. J.H.E.C. acknowledges the financial support of the Spanish project FIS2016-77692-C2-2-P.