Abstract
Obtaining reliable estimates about health outcomes for areas or domains where only few to no samples are available is the goal of small area estimation (SAE). Often, we rely on health surveys to obtain information about health outcomes. Such surveys are often characterised by a complex design, stratification, and unequal sampling weights as common features. Hierarchical Bayesian models are well recognised in SAE as a spatial smoothing method, but often ignore the sampling weights that reflect the complex sampling design. In this paper, we focus on data obtained from a health survey where the sampling weights of the sampled individuals are the only information available about the design. We develop a predictive model-based approach to estimate the prevalence of a binary outcome for both the sampled and non-sampled individuals, using hierarchical Bayesian models that take into account the sampling weights. A simulation study is carried out to compare the performance of our proposed method with other established methods. The results indicate that our proposed method achieves great reductions in mean squared error when compared with standard approaches. It performs equally well or better when compared with more elaborate methods when there is a relationship between the responses and the sampling weights. The proposed method is applied to estimate asthma prevalence across districts.
Keywords: Integrated nested Laplace approximations, Model-based inference, Small area estimation, Spatial smoothing, Survey weighting
1. Introduction
In public health we are often interested in the question whether there are disparities in illness, behavioural risk factors or health conditions across areas. An increasing amount of information on individuals is collected in this respect. Bayesian methods in disease mapping based on census or population registry data are well developed and used in a fairly standard manner (see e.g., Elliott et al., 2001; Waller and Gotway, 2004; Lawson, 2013 for a review of the methods). Such population registry or census data obtains information pertaining to each member of the population of an area. Historically, focus was on the construction of cancer atlases and on mapping rare diseases based on registry data (see e.g., Kemp et al., 1985; Mason, 1995).
Since it is nearly always impossible to measure the health outcome of interest in every individual in the population, a survey is used to record information from a random sample of individuals from the population (Cochran, 1977). Such surveys are often characterized by a complex design, with stratification, clustering and unequal sampling weights as common features. Policy makers are often interested in a specific characteristic, such as the total number of diseased cases or the prevalence, per area. In small area estimation (SAE) one investigates how to obtain these area specific characteristics from survey data covering more than only the area of interest by using spatial smoothing methods.
In SAE, one needs to choose whether to base inference on design-based, model-based or design-based model-assisted approaches. In design-based inference the values of the health outcomes are assumed fixed, and inference is based on the randomization distribution of the sample inclusion indicators. Often a model is used in the construction of a design-based estimator (known as design-based model-assisted approaches). A popular design-based estimator is the Horvitz–Thompson (HT) estimator (1952) and its extensions that weigh sampled individuals with the associated sampling weight. These estimators play a dominant role in sample surveys, however, they often fail in SAE because the sample size per area could be very small or even zero inflating the mean squared error tremendously. This makes design-based estimators unreliable or not feasible to use (Rao, 2011). Additionally, because of the spatial nature of the problem, understanding the geographical distribution of the health outcome is important. Model-based approaches that perform spatial smoothing, both those based on empirical and hierarchical Bayesian methodology, have shown to be more relevant in the handling of spatially correlated health survey data. In model-based approaches one conditions on the selected sample and the inference is based on the underlying model of the health outcome. Examples include Fay and Herriot (1979) which proposed a linear empirical Bayes model to estimate the income for small areas, while Datta and Ghosh (1991) considered a hierarchical Bayesian formulation instead. A number of extensions have been made, see Rao (2003) and Jiang and Lahiri (2006) for an overview. For binary data, MacGibbon and Tomberlin (1989) developed an empirical Bayes model using a logistic regression model with fixed and random effects. Stroud (1994), Ghosh et al. (1998) and Farrell (2000) described hierarchical Bayesian approaches to estimate small area proportions.
While model-based SAE is conceptually appealing, complex survey designs with the accompanying survey weights cause a difficulty in their practical implementation. Only relatively few approaches acknowledge the survey sampling mechanism and account for it in the model. Kott (1989) and Prasad and Rao (1999) described a design-consistent model-based estimator. Kott (1989) proposed an estimator which is a weighted combination of the HT estimator and the sample means of the different areas. Prasad and Rao (1999) proposed a pseudo-empirical best linear unbiased prediction estimator for the small area mean based on area level data. You and Rao (2002, 2003) used unit level data instead. Malec et al. (1997) described a hierarchical Bayesian model for binary survey data. They examined the use of sampling weights as a linear covariate in the model, after the inclusion of several post-stratification variables. Chen et al. (2014) proposed the use of a weight-adjusted Bayesian estimator that takes into account the effective sample size. Mercer et al. (2014) described a simulation study in which several methods for spatial smoothing in SAE, taking into account the sampling weights, are compared.
In this article, we describe a spatial predictive model-based approach to SAE for a binary health outcome in a complex survey with given sampling weights. We assume that the sampling weights on the sampled individuals are the only information available about the survey design. The goal is to estimate the prevalence of the health outcome for all small areas in the spatial domain. A hierarchical Bayesian model is used in which the health outcomes are regressed on the sampling weights. A nonparametric regression on the weights is used to minimise possible bias of the regression function. Additionally, both unstructured and structured spatial random effects are introduced to model the geographical distribution of the health outcomes. The population distribution of the sampling weights is unknown as well, hence we must model the weights themselves to be able to perform predictions. Our proposed method extends ideas described in Si et al. (2015) that are useful for surveys outside the SAE context. We use integrated nested Laplace approximations in R for model estimation (Rue et al., 2009). The methods described in this article add a hierarchical Bayesian model-based prediction approach for data with associated sampling weights to the SAE literature.
The structure of the paper is as follows. In Section 2 we introduce notations and describe the traditional design-based approach to perform SAE from a health survey. Several model-based approaches summarized in Mercer et al. (2014) that are used here for comparison purposes in the simulation study are also described in Section 2. We describe our proposed model-based approach in Section 3, and provide some details on the implementation of the models in standard software. A simulation study comparing our methods to other design- and model-based methods is provided in Section 4. In Section 5, we analyse the 2001 Belgian Health Interview Survey to estimate asthma prevalence across districts. We conclude the paper with a discussion in Section 6.
2. Notation and conventional method of analysis
2.1. Notation
Let Yik be a binary health outcome for individual i in small area k (i = 1, …, Nk and k = 1, …, K) with Nk the population size in area k. We assume that Nk is known for each area. A sample of size nk is drawn from each area k, where some of the nk could be zero. Denote the sampled values by yik. Let and represent the total population and sample size, respectively. We shall focus on estimating the true prevalence, Pk, in each area k, namely
| (1) |
Let Rik denote the binary variable indicating whether the ith individual in area k is sampled (Rik = 1) or not (Rik = 0). We use sk to indicate the set of sampled individuals in area k and for those that are not sampled.
To reflect the sampling design, weights wik are attached to each respondent’s outcome. The weights are proportional to the inverse probability of inclusion in the sample for unit i in area k. These weights can reflect both or a combination of the complex survey design and post-stratification adjustments. In this paper, we assume that the sampling weights on the sampled individuals are the only information available on the design of the survey. This assumption seems limited (e.g., one cannot adjust for cluster sampling) but it is standard in publicly available datasets that only sampling weights are available with few to no information on the survey design. We further assume that all sampled individuals respond to the survey. A typical dataset will have the structure as presented in Table 1. Throughout this article, we use the normalized weights, denoted by , defined by
| (2) |
The weights are called normalized because they sum up to the sample size nk in area k.
Table 1.
Structure of datasets used in this article.
| Response | Area | Sample weight |
|---|---|---|
| y11 | 1 | w11 |
| y21 | 1 | w21 |
| ⋮ | ⋮ | ⋮ |
| y12 | 2 | w12 |
| ⋮ | ⋮ | ⋮ |
2.2. Horvitz–Thompson estimator
Design-based methods evaluate properties of estimators under the randomization distribution and assume that the measurements are fixed values. Inference is based on all possible samples that could be selected from the target population of interest under the considered sampling design. A common design-based estimator in SAE is the Horvitz–Thompson (HT) estimator (Horvitz and Thompson, 1952) given by
| (3) |
The variance of has the form
| (4) |
The HT estimator is a design-unbiased estimator of Pk. It is a so-called direct estimator because it uses only the responses from the area of interest (Rao, 2003). Most surveys are not designed to yield appropriate direct estimates for all areas as the sample size in some areas can be too small to produce reliable or stable estimates. Another disadvantage is that no estimate can be obtained in those areas that are not included in the sample. In the next section, we present indirect estimates that borrow strength across the different areas by using the responses from all sampled areas.
Other design-based methods use a model for the construction of the estimators. The synthetic estimator (Gonzalez, 1973), for example, uses a linear model on several covariates fit by ordinary least squares to predict the mean for a particular area. Pfeffermann (2013) gives an overview of commonly used methods and new developments in the field of design-based small area estimation.
2.3. Model-based methods
We now focus on several model-based methods described in Mercer et al. (2014). The simplest approach, called naive binomial (NB), is to ignore the design and use the model
| (5) |
where , β0 is an overall effect, are independent random effects taking into account extra heterogeneity amongst areas k, and vk are spatially dependent random effects. It is assumed that vk follows the commonly used intrinsic conditional autoregressive (ICAR) model (Rue and Held, 2005)
| (6) |
where ne(k) denotes the set of neighbours of area k and mk is the number of neighbours. For identifiability reasons of the overall intercept β0, the sum of the random effects vk is constrained to zero (Eberly and Carlin, 2000). In this article, we take the common approach to consider two areas as neighbours if they share a common boundary.
In model (5), the design weights of the survey are ignored. To account for the design, Mercer et al. (2014) proposed to model the empirical logistic transform of , namely using the model
| (7) |
where the variance is set equal to Model (7) is further referred to as the logit-normal (LN) model.
As an alternative, Mercer et al. (2014) considered the arcsine square-root transformation as proposed by Raghunathan et al. (2007). This transformation, , is an approximate variance stabilizing transformation for binary data. The model, called the arcsine (AS) model, is
| (8) |
where the variance is equal to with the so-called effective sample size calculated as .
Some authors proposed the use of a weighted likelihood to take into account the sampling design, also referred to as pseudo-likelihood (PL) (e.g., see Skinner, 1989 and Congdon and Lloyd, 2010). Mercer et al. (2014) also considered a pseudo-likelihood approach by assuming that has a binomial likelihood, namely
| (9) |
Finally, Mercer et al. (2014) described a recent approach proposed by Chen et al. (2014) that combines the pseudo-likelihood approach with the effective sample size. The model, called the effective sample size (ES) model, is
| (10) |
where . The rationale behind this model is that both numerator and denominator are adjusted for the sampling design.
For more details on the models described in this section, we refer to Mercer et al. (2014). Models (5), (7), (8), (9) and (10), in which global and local information is borrowed within the same model via independent and ICAR random effects for each region, are called convolution models (Besag et al., 1991).
3. Proposed methods
In this section, we propose a hierarchical model for the observed outcomes yik (Section 3.1), and explain how to use this model to make predictions for non-sampled individuals in order to obtain an estimator of Pk (Section 3.2).
3.1. Hierarchical model
A predictive model-based approach proposed by Royall (1970) is used to specify an estimator for Pk. The estimator is given by
| (11) |
where the first term sums outcome values of the sampled individuals, and the second term is a sum of the predicted values over the non-sampled individuals in area k. Royall (1970) argued that this modelbased approach is more efficient than the design-based approaches, when the model to predict is correctly specified.
Several authors proposed the use of weight-smoothing models to predict by modelling the health outcome as a smooth-varying function of the survey weights (or probability of inclusion), and showed that these models give better estimates as compared to the HT estimator. For continuous data, Zheng and Little (2003, 2005) estimated the finite population total based on a non-parametric regression as a function of the inclusion probabilities in the likelihood framework. Chen et al. (2010) used a Bayesian p-spline predictive estimator to estimate the finite population proportion. Their model is a binary p-spline probit regression model with the inclusion probability as covariate.
We extend these ideas to small area estimation. The normalized sampling weights are used as a covariate in the model for the observed outcomes yik. We employ Bayesian hierarchical models consisting of three stages. At the first stage, the likelihood of the binary outcome is specified, namely
| (12) |
At the second stage, the latent process ηik is modelled as a function of the sampling weights and allows for between-area variation by using both spatially independent and spatially dependent random effects (Besag et al., 1991). Two versions are considered:
where . Similar as described in Section 2.3, β0 is an overall effect, uk are independent random effects and vk are spatially dependent random effects following the ICAR model.
Zheng and Little (2003, 2005) and Chen et al. (2010) used penalized splines to construct the nonparametric function f (·) in (13) and (14). Si et al. (2015) avoided parametric assumptions or specific functional forms for the f (·) function and used a Gaussian process (GP) prior. To specify f (), we investigate both approaches, namely penalized splines using B-spline basis functions and a GP·prior using a random walk model of order one (RW1).
For notational convenience, let denote the sorted set of unique values of all observed weights in the sample, where L is the number of unique values. A RW1 model is a smoothing model constructed by assuming that the increments, , follow a multivariate normal distribution with mean zero. The distribution of is thus proportional to
| (15) |
with variance parameter . For 1 < l < L, the conditional distribution of the (l + 1)th normalized weight depends only on and , while the boundary weights and depend on their only neighbour point. To specify the RW1 model in (14) one simply replaces by πik in (15).
In the penalized spline case, the function f (·) is of the form
| (16) |
where B1(·), …, BB(·) are the B-spline basis functions of degree d (Eilers and Marx, 1996). The smoothness of f (·) is achieved by imposing a penalty on the regression coefficients θ of the form , where λ is a smoothing parameter and Dq is the qth order differencing matrix (Eilers and Marx, 1996). For a detailed description of B-splines, see for example Hastie et al. (2001) and Ruppert et al. (2003). We implement B-spline basis functions of degree two (d = 2) with a second order difference penalty (q = 2). We choose B = 20 to ensure enough flexibility and we use quantile-based knots. For fitting purposes, the penalized spline in (16) is expressed in general linear mixed model representation (Ruppert et al., 2003):
| (17) |
where βw is an unknown coefficient, zb(·) is a transformed spline basis of the B-spline basis functions and (see the Supplementary Materials for more information, Appendix A).
In the last stage one needs to assign proper hyperprior distributions for the unknown parameters in stage 2, namely for β0, , , and . Vague priors are used for all parameters. A normal prior with large variance is used for β0. Similar as Mercer et al. (2014) and Chen et al. (2014), we assign Gamma (0.5, 0.008) priors on the precision parameters and . This gives a 95% range on the σu and σv scale of (0.056, 4.036). It is well-known that by taking both these hyperpriors to be vague, only the sum of the random effects (ui + vi) and not their individual values are identified (Gelfand et al., 2010). A common choice for the prior on the precisions and is Gamma(0.001, 0.001). However, as discussed in Wakefield (2009) this prior puts most of the prior mass of σw and σα to the right of the prior distribution and is therefore not recommended. To avoid this and as recommended by Wakefield (2009), we use Gamma(1, 0.01) priors for both precisions and . These priors yield a 95% range on the σw and σα scale of (0.052, 0.628). We investigate in Sections 4 and 5 the sensitivity of our results to other prior distributions.
3.2. Prediction of health outcome for non-sampled individuals
Once estimates of β0, uk, vk and for model 1 are obtained, in (12) is estimated by
| (18) |
with a similar expression used for model 2 (replacing ) with πik. However, note that for the non-sampled individuals no information on wik, or equivalently on , is available, and thus it is not possible to obtain estimates of for individuals in . In this section, we propose (i) a method to estimate weights for the non-sampled individuals i in sampled area k; and (ii) a method to estimate Pk for non-sampled areas k.
In previous work of Zheng and Little (2003, 2005) and Chen et al. (2010) it was assumed that the inclusion probabilities (sampling weights) were known for all units in the population. These three papers assumed a probability-proportional-to-size sampling in which the inclusion probability is proportional to a size variable (e.g., dwelling size) measured for all population units. Alternatively, Si et al. (2015) proposed to model the sampling process by a Bayesian model to obtain weights for non-sampled individuals.
In each area k, we map the unique values of the observed weights wik to form Lk strata, where Lk is the number of unique wik values in area k. Si et al. (2015) referred to these strata as poststratification cells since they are constructed based on the weights in the sample. It is assumed that the Lk poststratification cells observed in the sample in area k are the only possible strata in the population of this area. Si et al. (2015) argued that this assumption is generally not correct (for example, if weights are constructed by multiplying factors for different demographic variables, there may be some empty cells in the sample corresponding to unique products of factors that would appear in the population but not in the sample) but it allows one to proceed with (18) without additional knowledge of the process by which the weights were constructed.
For each k, let nlk denote the sample size in poststratification cell l (l = 1, …, Lk) in area k. It is assumed that the supplied weights wik are proportional to the inverse of the inclusion probabilities. Assuming independent sampling, the sampling process probabilities for an individual i in area k is given by a Bernoulli process, with probability
| (19) |
where ck is a positive normalizing constant to ensure that the expected number of observed individuals corresponds with the actual sample size nk. Denote by Nlk the (unknown) population size in stratum l and area k. Since all individuals i in stratum l have the same weight, wik ≡ w(l)k, the expected value of nlk is E(nlk) = ckNlk/w(l)k. Because , it follows that and as a result . Therefore, it is assumed that the vector in area k follows a multinomial distribution conditional on nk,
| (20) |
for each k, where the Nlk are unknown parameters. Because the Nlk are unnormalized in the above parametrization, we normalize them after fitting such that they sum to the population size in area k:
| (21) |
Knowledge of can be used in (11), which can be written as
| (22) |
where and is obtained from (18) with weight . Eq. (22) is the point estimate of Pk. The contributions of the Lk different cells to the estimation of Pk is clear from (22).
Inference of is based on the posterior distribution of . The posterior is obtained by drawing B posterior samples from the posterior distributions of and for l = 1, …, Lk. Substituting these samples in (22) yields B posterior draws of . The Bayesian 100 × (1 − α)% credible interval (CI) of is constructed by taking the α/2 and 1 − α/2 quantiles of the posterior distribution.
Finally, we propose a procedure to estimate Pk in those areas where no individuals have been sampled (the so-called off-sample areas). Consider an area k∗ that has not been sampled and thus has no observations available. To obtain estimates of plk*, we consider all unique weights that are observed in the sample, . These weights are used in (18) to get estimates of plk* and the estimate of Pk* is of the form
| (23) |
3.3. Implementation
The Bayesian hierarchical model for the outcomes (12)–(17) and the multinomial model (20) described in Sections 3.1 and 3.2 are fitted using the integrated nested Laplace approximations (INLA) approach by Rue et al. (2009). INLA yields a computationally convenient alternative to Markov chain Monte Carlo (MCMC) techniques. This method combines Laplace approximations and numerical integration in a very efficient manner to carry out a Bayesian analysis. A multinomial likelihood, needed to fit the multinomial model (20), is not directly available in INLA. Instead, we employ the multinomial-Poisson transformation of Baker (1994) to fit model (20). The sum-to-zero constraint of the random effects vk is default when using INLA. Sampling using this constraint is achieved by considering the intrinsic Gaussian Markov random field representation of the ICAR model for which, in addition, a linear constraint is assumed (Rue and Held, 2005 and Rue et al., 2009; See the Supplementary Materials, Appendix A, for more detailed information).
We used R version 3.2 (R Core Team, 2014) to fit the models using the INLA package (Martino and Rue, 2009). Sampling from the posterior distributions obtained from INLA is done via the inla.posterior.sample() function. More details on the implementation and example code are given in the Supplementary Materials (see Appendix A). In the Supplementary Materials, an R script to perform the analyses and a simulated dataset are attached.
4. Simulation study
4.1. Simulation setup
In this section we describe the setup of the simulation study to evaluate the performance of the different small area estimators described in this article. As geography, we took the administrative district division of Belgium (see Fig. 1 and Section 5). The total region consists out of 43 districts. Population sizes stratified by five-year age-groups and gender (yielding a total of J = 36 strata) at each district are available. The total population size is around ten million. Let xa denote the indicator for the different age-groups (xa = 1 for ages 0–4, xa = 2 for ages 5–9, …, xa = 18 for ages 85+). Let xg be a gender indicator taking the values 0 or 1. Let Yi(j)k denote the response value of the ith individual belonging to the jth stratum in district k.
Fig. 1.
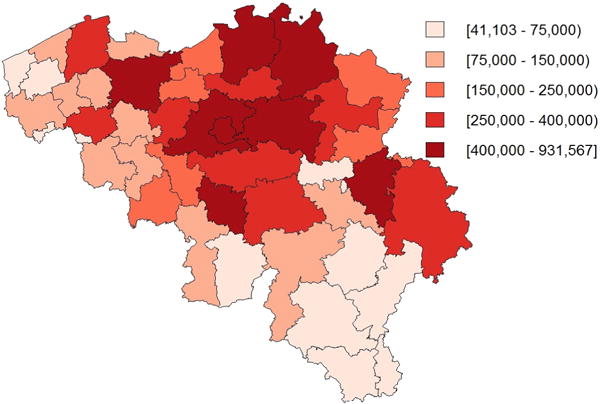
Map of Belgium divided in the 43 administrative districts with accompanying population size in each district.
In each district k and for i = 1, …, Nk, binary outcomes were simulated, namely Yi(j)k ∼ Bin(pjk) where pjk = Pr(Yi(j)k = 1) is the prevalence of a certain health outcome for individuals belonging to stratum j in area k. The following six models were considered for the prevalences pjk:
-
(P1)
pjk = 0.20,
-
(P2)
logit(pjk) = logit(0.10) + 0.15xa,i(j)k,
-
(P3)
logit(pjk) = logit(0.10) + 0.15xa,i(j)k − 0.50xg,i(j)k,
-
(P4)
logit(pjk) = logit(0.20) + uk + vk,
-
(P5)
logit(pjk) = logit(0.10) + 0.15xa,i(j)k + uk + vk,
-
(P6)
logit(pjk) = logit(0.10) + 0.15xa,i(j)k − 0.50xg,i(j)k + uk + vk.
The effects are spatially unstructured effects. The vk are spatially correlated effects that are sampled from a zero mean ICAR model with a variance of 0.20. The random effects of this ICAR model were generated using INLA. In (P1) the prevalence is constant over all strata and districts. In (P2) the prevalence increases with age and is spatially independent. In (P3) the prevalence also increases with age and is spatially independent, but women have a smaller prevalence than men. Models (P4), (P5) and (P6) additionally assume that the prevalences vary across districts.
A survey sample was taken from the simulated population by the following procedure:
-
(1)
Select districts from which samples are drawn. First, we simulated a random number, narea, from the set {39, 40, 41, 42, 43}. Next, we sampled narea from the 43 districts with probability-proportional-to-size sampling where the size variables are the population sizes of the districts. In this manner, districts with a large population size were sampled with probability one, whereas districts with a small population size had a probability smaller than one. Note that a small number of off-sample areas were created in this manner.
-
(2)
The total sample size was randomly sampled by drawing a random number from the set {4000, 4001, …, 6000}. Next, a multinomial distribution with probabilities proportional to the district population size was used to draw sample sizes in each selected district, denoted by nk.
-
(3)
The sample sizes in the J strata of area k, denoted by njk, were generated from a multinomial distribution with total sample size nk and probabilities qjk. Four scenarios were considered and the probabilities qjk were constructed using the hypothetical sampling proportions in different age groups as presented in Table 2. In scenario (S1) simple random sampling (SRS) is performed which implies that qjk = Njk/Nk. In scenario (S2), the hypothetical sampling proportion of the [0–20[ year-old males is 0.20. In this [0–20[ year-old males subgroup simple random sampling is performed which implies that for the strata j belonging to this subgroup, where is the population size in district k of the [0–20[ year-old males subgroup. For the other subgroups in Table 2, the probabilities qjk were calculated in a similar manner. Finally, we randomly sampled njk individuals in strata j in area k from the simulated population.
Table 2.
Different scenarios presenting the hypothetical sampling proportions for different age and gender groups. These sampling proportions are used to construct probabilities qjk used for the sampling of individuals from the generated population (see text). SRS: simple random sampling.
| Scenario | [0–20[ y. | [20–35[ y. | [35–50[ y. | [50–65[ y. | 65+ y. | |
|---|---|---|---|---|---|---|
| Male | (S1) | SRS | SRS | SRS | SRS | SRS |
| (S2) | 0.20 | 0.12 | 0.10 | 0.06 | 0.02 | |
| (S3) | 0.16 | 0.12 | 0.12 | 0.06 | 0.04 | |
| (S4) | 0.15 | 0.12 | 0.07 | 0.06 | 0.10 | |
| Female | (S1) | SRS | SRS | SRS | SRS | SRS |
| (S2) | 0.20 | 0.12 | 0.10 | 0.06 | 0.02 | |
| (S3) | 0.16 | 0.12 | 0.12 | 0.06 | 0.04 | |
| (S4) | 0.15 | 0.12 | 0.07 | 0.06 | 0.10 |
For a simulated sample, the survey design weight of a sampled individual i of area k, , is equal to the inverse of the probability of inclusion πik of this individual in the sample. The calculation of the probabilities of inclusion is presented in the Supplementary Materials (see Appendix A). The survey design weights were adjusted with a post-stratification factor fps to form the final weights used in the analysis, namely , with the strata of the post-stratification defined by the age-groups [0–10[, [10–20[, [20–30[, [30–40[, [40–50[, [50–60[, [60–70[, [70–80[, 85 and gender.
In sampling scenario (S1) there is no relationship between the values of the weights wik and age. In scenarios (S2) and (S3) the values of the weights wik increase with the age groups considered in Table 2 and the weights in scenario (S2) are more dispersed than in scenario (S3). In scenario (S4) lower weights are obtained for the age groups [0–20[, [20–35[ and 65+, and higher weights for the age groups [35–50[ and [50–65[. Plots of the distribution of the generated weights wik are given in the Supplementary Materials (see Appendix A).
For each combination of a prevalence model and a sampling scenario (6 × 4 combinations) we ran S times through steps (1)–(3) to obtain S simulated datasets. Each simulated dataset contains only the outcome, the area indicator and the final weight wik. Two direct and nine indirect estimators were used to estimate the small-area prevalences from the simulated datasets. As direct estimators we used the unweighted mean (UM) and the HT estimator given in (3). The five indirect estimators described in Section 2.3 were used, namely the NB-estimator in (5), the LN-estimator in (7), the AS-estimator in (8), the PL-estimator in (9) and the ES-estimator in (10). Finally, we calculated the prevalence using the indirect estimator (11), or equivalently (22), using the models presented in (13) and (14), respectively further referred to as model-based model 1 (M1) and model-based model 2 (M2). We then further used a random walk model (RW1) or penalized splines (PS). For all indirect estimators we included both independent and spatial ICAR random effects into the model.
To evaluate the different estimates we compared two statistics: the estimated squared bias and the estimated mean squared error (MSE). Denote by Pk the true proportion in area k (which stays constant across the simulations) and denote by the estimated proportion from the sth simulated dataset. The statistics were calculated as:
We also calculated the nominal coverage and the average length of the 95% credible intervals of the prevalence estimates.
4.2. Simulation results
The squared bias and mean squared error results are presented in Tables 3 and 4 with all results based on one hundred simulations (S = 100).
Table 3.
The average squared bias and mean squared error for 11 estimators based on 100 simulated datasets using the prevalence models (P1), (P2), (P3) and the four sampling scenarios. Figures in bold denote the row minimum.
| UM | HT | NB | LN | AS | PL | ES | M1 | M2 | M1 | M2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RW1 | RW1 | PS | PS | |||||||||
| Bias2 (×103)
| ||||||||||||
| (P1) | (S1) | 0.02 | 0.03 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (P1) | (S2) | 0.04 | 0.05 | 0.00 | 0.04 | 0.01 | 0.00 | 0.01 | 0.00 | 0.01 | 0.00 | 0.00 |
| (P1) | (S3) | 0.04 | 0.05 | 0.00 | 0.02 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (P1) | (S4) | 0.02 | 0.02 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (P2) | (S1) | 0.03 | 0.03 | 0.03 | 0.04 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 |
| (P2) | (S2) | 4.01 | 0.09 | 4.06 | 0.04 | 0.04 | 0.03 | 0.03 | 0.66 | 0.22 | 0.14 | 0.13 |
| (P2) | (S3) | 1.76 | 0.05 | 1.75 | 0.04 | 0.02 | 0.02 | 0.02 | 0.15 | 0.07 | 0.05 | 0.05 |
| (P2) | (S4) | 0.26 | 0.06 | 0.21 | 0.03 | 0.02 | 0.02 | 0.02 | 0.10 | 0.09 | 0.12 | 0.12 |
| (P3) | (S1) | 0.04 | 0.04 | 0.03 | 0.04 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 |
| (P3) | (S2) | 3.05 | 0.10 | 3.13 | 0.04 | 0.02 | 0.02 | 0.02 | 0.57 | 0.22 | 0.11 | 0.09 |
| (P3) | (S3) | 1.32 | 0.05 | 1.33 | 0.04 | 0.01 | 0.02 | 0.02 | 0.13 | 0.07 | 0.05 | 0.04 |
| (P3) | (S4) | 0.17 | 0.05 | 0.12 | 0.03 | 0.01 | 0.02 | 0.02 | 0.07 | 0.07 | 0.08 | 0.08 |
|
| ||||||||||||
| MSE (×103) | ||||||||||||
|
| ||||||||||||
| (P1) | (S1) | 2.81 | 2.82 | 0.09 | 0.09 | 0.48 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 |
| (P1) | (S2) | 2.72 | 3.95 | 0.09 | 0.29 | 0.79 | 0.28 | 0.27 | 0.15 | 0.23 | 0.11 | 0.11 |
| (P1) | (S3) | 2.55 | 3.01 | 0.08 | 0.12 | 0.53 | 0.12 | 0.12 | 0.16 | 0.16 | 0.10 | 0.10 |
| (P1) | (S4) | 2.81 | 3.09 | 0.09 | 0.11 | 0.52 | 0.10 | 0.10 | 0.16 | 0.15 | 0.09 | 0.09 |
| (P2) | (S1) | 3.66 | 3.68 | 0.17 | 0.16 | 0.63 | 0.17 | 0.16 | 0.40 | 0.40 | 0.37 | 0.37 |
| (P2) | (S2) | 7.18 | 6.44 | 4.17 | 0.65 | 1.59 | 0.73 | 0.75 | 1.18 | 0.88 | 0.44 | 0.41 |
| (P2) | (S3) | 4.90 | 4.56 | 1.88 | 0.30 | 0.96 | 0.31 | 0.33 | 0.54 | 0.47 | 0.29 | 0.28 |
| (P2) | (S4) | 3.71 | 4.04 | 0.34 | 0.20 | 0.74 | 0.21 | 0.21 | 0.63 | 0.62 | 0.60 | 0.60 |
| (P3) | (S1) | 3.22 | 3.24 | 0.14 | 0.14 | 0.54 | 0.14 | 0.13 | 0.34 | 0.34 | 0.31 | 0.32 |
| (P3) | (S2) | 5.81 | 5.84 | 3.23 | 0.61 | 1.47 | 0.64 | 0.69 | 1.07 | 0.78 | 0.35 | 0.32 |
| (P3) | (S3) | 4.09 | 4.12 | 1.42 | 0.26 | 0.85 | 0.25 | 0.27 | 0.49 | 0.38 | 0.23 | 0.22 |
| (P3) | (S4) | 3.41 | 3.74 | 0.24 | 0.13 | 0.67 | 0.18 | 0.18 | 0.51 | 0.48 | 0.46 | 0.45 |
Table 4.
The average squared bias and mean squared error for 11 estimators based on 100 simulated datasets using the prevalence models (P4), (P5), (P6) and the four sampling scenarios. Figures in bold denote the row minimum.
| UM | HT | NB | LN | AS | PL | ES | M1 | M2 | M1 | M2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RW1 | RW1 | PS | PS | |||||||||
| Bias2 (×103)
| ||||||||||||
| (P4) | (S1) | 0.03 | 0.03 | 0.52 | 0.71 | 0.41 | 0.52 | 0.55 | 0.52 | 0.52 | 0.52 | 0.52 |
| (P4) | (S2) | 0.04 | 0.04 | 0.58 | 0.79 | 0.43 | 0.48 | 0.58 | 1.37 | 1.35 | 0.58 | 0.58 |
| (P4) | (S3) | 0.03 | 0.04 | 0.56 | 0.74 | 0.41 | 0.52 | 0.57 | 1.02 | 0.81 | 0.56 | 0.56 |
| (P4) | (S4) | 0.02 | 0.02 | 0.50 | 0.69 | 0.37 | 0.48 | 0.52 | 0.62 | 0.66 | 0.50 | 0.50 |
| (P5) | (S1) | 0.03 | 0.03 | 0.73 | 0.92 | 0.56 | 0.73 | 0.75 | 0.65 | 0.65 | 0.69 | 0.69 |
| (P5) | (S2) | 4.08 | 0.12 | 4.74 | 0.91 | 0.59 | 0.73 | 0.74 | 3.58 | 2.30 | 0.94 | 0.91 |
| (P5) | (S3) | 1.93 | 0.06 | 2.59 | 0.90 | 0.58 | 0.76 | 0.74 | 3.09 | 1.65 | 0.81 | 0.81 |
| (P5) | (S4) | 0.28 | 0.04 | 1.03 | 0.91 | 0.54 | 0.70 | 0.73 | 1.43 | 1.29 | 0.76 | 0.76 |
| (P6) | (S1) | 0.02 | 0.02 | 0.65 | 0.86 | 0.50 | 0.65 | 0.68 | 0.58 | 0.58 | 0.61 | 0.61 |
| (P6) | (S2) | 3.27 | 0.08 | 3.92 | 0.81 | 0.50 | 0.62 | 0.63 | 2.90 | 1.89 | 0.80 | 0.77 |
| (P6) | (S3) | 1.54 | 0.06 | 2.19 | 0.81 | 0.52 | 0.68 | 0.66 | 2.69 | 1.32 | 0.72 | 0.72 |
| (P6) | (S4) | 0.23 | 0.06 | 0.89 | 0.81 | 0.47 | 0.60 | 0.64 | 1.26 | 1.04 | 0.67 | 0.67 |
|
| ||||||||||||
| MSE (×103) | ||||||||||||
|
| ||||||||||||
| (P4) | (S1) | 2.65 | 2.66 | 1.49 | 1.57 | 1.50 | 1.49 | 1.50 | 1.49 | 1.49 | 1.48 | 1.49 |
| (P4) | (S2) | 2.60 | 3.75 | 1.56 | 2.11 | 2.01 | 2.04 | 2.03 | 2.23 | 2.34 | 1.56 | 1.56 |
| (P4) | (S3) | 2.46 | 2.86 | 1.50 | 1.73 | 1.63 | 1.66 | 1.65 | 2.01 | 1.91 | 1.51 | 1.51 |
| (P4) | (S4) | 2.55 | 2.80 | 1.45 | 1.62 | 1.54 | 1.54 | 1.54 | 1.77 | 1.74 | 1.45 | 1.44 |
| (P5) | (S1) | 3.47 | 3.49 | 2.12 | 2.18 | 2.15 | 2.12 | 2.12 | 2.24 | 2.24 | 2.23 | 2.23 |
| (P5) | (S2) | 6.98 | 5.71 | 5.81 | 3.13 | 3.28 | 3.20 | 3.14 | 4.69 | 3.89 | 2.56 | 2.57 |
| (P5) | (S3) | 4.80 | 4.18 | 3.70 | 2.48 | 2.56 | 2.49 | 2.47 | 4.04 | 3.30 | 2.27 | 2.28 |
| (P5) | (S4) | 3.52 | 3.67 | 2.29 | 2.27 | 2.25 | 2.22 | 2.21 | 3.15 | 2.95 | 2.30 | 2.30 |
| (P6) | (S1) | 3.08 | 3.09 | 1.82 | 1.90 | 1.86 | 1.82 | 1.82 | 1.92 | 1.92 | 1.92 | 1.92 |
| (P6) | (S2) | 5.93 | 5.57 | 4.86 | 2.99 | 3.12 | 3.05 | 3.02 | 4.03 | 3.55 | 2.25 | 2.25 |
| (P6) | (S3) | 4.27 | 3.94 | 3.18 | 2.19 | 2.27 | 2.20 | 2.18 | 3.47 | 2.89 | 2.03 | 2.04 |
| (P6) | (S4) | 3.30 | 3.49 | 2.01 | 2.01 | 1.98 | 1.94 | 1.94 | 2.71 | 2.60 | 2.01 | 2.01 |
We first discuss the results of the scenarios in which the small area prevalences are not spatially varying (Table 3). For scenario (P1) all estimators have a low squared bias. The MSE of the two direct estimators is large due to the increased variance associated with these estimators. The variance and thus the MSE of the indirect estimators is smaller, showing the benefit of spatial smoothing methods. For the prevalence model (P2) and (P3), except in the SRS case (S1), the unweighted mean and the naive binomial – methods ignoring the survey weights – have a large squared bias. Again, the MSE of the direct estimators is large. For sampling scenarios (S2) and (S3), it is observed that the proposed model-based approach using the penalized splines performs best in terms of MSE. This can be expected, since these scenarios imply a relationship between the design weights and the responses, namely both the prevalences and the values of the weights increase with age, and models (13) and (14) exploit that relationship. For (S4), on the contrary, our proposed methods perform less good than the methods LN, PL and ES. In this scenario there is no clear relationship between the design weights and the responses and thus using a model of the form (13) or (14) has no benefit above the other indirect methods. We further observed a small decrease in the mean squared error between sampling scenarios (S2) and (S3) due to the influence of the less dispersed weights of the latter scenario.
The results with spatially varying prevalences are summarized in Table 4. It is observed that the HT estimator has a small bias over all scenarios. The unweighted mean is unbiased for (P4) and in the SRS scenarios (S1). The indirect estimators have a larger squared bias than the HT estimator since these methods shrink the small area prevalences towards the overall population prevalences through the spatial random effects. The estimators ignoring the survey weights, UM and NB, have larger bias for (S2), (S3) and (S4). In terms of MSE, the naive binomial and the proposed model-based approach using the penalized splines perform the best for (P4). For (P5) and (P6) again the proposed model-based approach performs well. Whereas for (S4) the methods PL and ES perform somewhat better.
The results of the nominal coverage and average length of the 95% credible intervals are shown in Table 5. We only present the results of settings (P4), (P5) and (P6) here. Results for (P1), (P2) and (P3) are qualitatively similar (Supplementary Material). The HT estimator has a nominal coverage around 95% for all scenarios. The unweighted mean and naive binomial have poor coverages for the combinations (P5) and (P6) with (S2) and (S3) due to the bias of the estimators in these settings. The nominal coverage of the LN, AS, PL and ES methods have an undercoverage in some scenarios. The proposed model-based approach using the random walk does not perform well. The model-based approach using the penalized splines, on the other hand, has a coverage around 95% in all scenarios. The average length of the CIs of the indirect estimators is smaller than the length of the HT estimator CIs.
Table 5.
The nominal coverage and length of the 95% credible intervals for 11 estimators based on 100 simulated datasets using the prevalence models (P4), (P5), (P6) and the four sampling scenarios. The results are averaged over all districts.
| UM | HT | NB | LN | AS | PL | ES | M1 | M2 | M1 | M2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RW1 | RW1 | PS | PS | |||||||||
| Nominal coverage
| ||||||||||||
| (P4) | (S1) | 0.96 | 0.96 | 0.95 | 0.94 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 |
| (P4) | (S2) | 0.96 | 0.94 | 0.94 | 0.89 | 0.92 | 0.91 | 0.90 | 0.80 | 0.80 | 0.94 | 0.94 |
| (P4) | (S3) | 0.95 | 0.95 | 0.94 | 0.92 | 0.95 | 0.93 | 0.93 | 0.85 | 0.88 | 0.94 | 0.94 |
| (P4) | (S4) | 0.96 | 0.96 | 0.95 | 0.94 | 0.95 | 0.94 | 0.94 | 0.91 | 0.92 | 0.95 | 0.95 |
| (P5) | (S1) | 0.95 | 0.95 | 0.95 | 0.94 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 |
| (P5) | (S2) | 0.70 | 0.95 | 0.63 | 0.88 | 0.88 | 0.89 | 0.88 | 0.64 | 0.78 | 0.96 | 0.96 |
| (P5) | (S3) | 0.84 | 0.95 | 0.80 | 0.92 | 0.92 | 0.92 | 0.92 | 0.72 | 0.85 | 0.96 | 0.95 |
| (P5) | (S4) | 0.94 | 0.95 | 0.92 | 0.94 | 0.95 | 0.94 | 0.94 | 0.84 | 0.87 | 0.94 | 0.94 |
| (P6) | (S1) | 0.95 | 0.95 | 0.94 | 0.94 | 0.96 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 |
| (P6) | (S2) | 0.73 | 0.93 | 0.66 | 0.87 | 0.86 | 0.87 | 0.86 | 0.65 | 0.78 | 0.95 | 0.96 |
| (P6) | (S3) | 0.86 | 0.95 | 0.81 | 0.92 | 0.92 | 0.92 | 0.92 | 0.72 | 0.85 | 0.95 | 0.95 |
| (P6) | (S4) | 0.94 | 0.95 | 0.92 | 0.93 | 0.95 | 0.94 | 0.94 | 0.85 | 0.87 | 0.94 | 0.94 |
|
| ||||||||||||
| Average length | ||||||||||||
|
| ||||||||||||
| P4) | (S1) | 0.18 | 0.18 | 0.15 | 0.15 | 0.16 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| (P4) | (S2) | 0.18 | 0.21 | 0.15 | 0.16 | 0.16 | 0.15 | 0.15 | 0.13 | 0.14 | 0.15 | 0.15 |
| (P4) | (S3) | 0.18 | 0.19 | 0.15 | 0.15 | 0.16 | 0.15 | 0.15 | 0.14 | 0.15 | 0.15 | 0.15 |
| (P4) | (S4) | 0.18 | 0.19 | 0.15 | 0.15 | 0.16 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| (P5) | (S1) | 0.20 | 0.20 | 0.17 | 0.18 | 0.18 | 0.17 | 0.17 | 0.18 | 0.18 | 0.18 | 0.18 |
| (P5) | (S2) | 0.19 | 0.25 | 0.16 | 0.18 | 0.18 | 0.18 | 0.17 | 0.14 | 0.17 | 0.20 | 0.20 |
| (P5) | (S3) | 0.19 | 0.22 | 0.16 | 0.17 | 0.18 | 0.17 | 0.17 | 0.15 | 0.17 | 0.19 | 0.19 |
| (P5) | (S4) | 0.20 | 0.21 | 0.17 | 0.18 | 0.18 | 0.17 | 0.17 | 0.17 | 0.17 | 0.18 | 0.18 |
| (P6) | (S1) | 0.19 | 0.19 | 0.16 | 0.17 | 0.17 | 0.16 | 0.16 | 0.17 | 0.17 | 0.17 | 0.17 |
| (P6) | (S2) | 0.18 | 0.24 | 0.15 | 0.17 | 0.17 | 0.17 | 0.16 | 0.14 | 0.17 | 0.19 | 0.19 |
| (P6) | (S3) | 0.19 | 0.22 | 0.15 | 0.16 | 0.17 | 0.16 | 0.16 | 0.13 | 0.17 | 0.18 | 0.18 |
| (P6) | (S4) | 0.19 | 0.20 | 0.16 | 0.17 | 0.17 | 0.16 | 0.16 | 0.15 | 0.16 | 0.17 | 0.17 |
In general, the two methods ignoring the sampling weights (unweighted mean and naive binomial) produce poor estimates due to the bias of these methods. The HT estimator is unbiased but has a large variance, making it unsuitable for practical usage. The indirect estimators accounting for the weights produce estimates with both small bias and small mean squared errors. The model-based approach using the penalized splines described in Section 3 is preferred when there is a relationship between the survey weights and the responses, otherwise, the LN, PL and ES methods are preferable. The performance of the penalized splines is better than the random walk models. For the penalized spline model-based approach the difference in performance between models (13) and (14) is negligible.
In the Supplementary Material (see Appendix A), we present the results with respect to the sensitivity of the results to other prior distributions. It was observed that the obtained results are insensitive to other (vague) prior distribution choices. In addition, we also present in the Supplementary Material (see Appendix A) the results with respect to the off-sample areas separately. These results are presented separately to be able to evaluate the described approaches with respect to the estimation and prediction in areas where no data is available. The conclusions from this off-sample analysis are similar as the conclusions discussed above.
5. Application to belgian health interview survey
Next, we focus our attention on empirical data measuring the prevalence of asthma across the 43 districts shown in Fig. 1 using the 2001 Belgian Health Interview Survey (HIS). Data were collected in response to the question “Have you experienced asthma in the previous year?”. In total, 12,003 individuals responded to this question. The number of respondents per district varied between 50 and 2949, and 4 districts were not selected in the survey. In total 612 (5.1%) individuals responded positive to the question. The 2.5% and 97.5% quantiles of normalized weights calculated via (2) are 0.35 and 2.49, respectively. The minimum and maximum normalized weights are 0.06 and 10.49, respectively.
We calculated the small areas prevalences of asthma using the eleven estimators that were considered in the simulation study in Section 4. Fig. 2 presents the violin plots of the predicted prevalences of asthma by district using the different estimators. It is clear that the direct estimators (unweighted mean and HT estimator) have a large amount of heterogeneity amongst the districts with predicted asthma prevalences ranging from 0.0 to 0.10. This variability is substantially reduced by using the nine indirect approaches that use Bayesian hierarchical models. The shape and location of the violin plots are similar for the indirect estimators with the arcsin square root transformation and pseudo-likelihood binomial approach showing the most heterogeneity amongst districts. The results of the model-based approaches are fairly similar. In the Supplementary Materials (see Appendix A), we give the point estimates and associated CI per district.
Fig. 2.
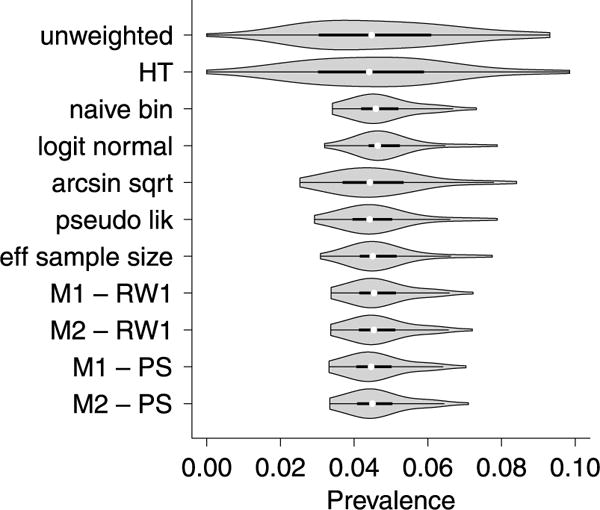
Violin plot of the predicted prevalence estimates of asthma, using various approaches, across the 43 districts in Belgium estimated from the Health Interview Survey of 2001.
In Fig. 3, we display maps of the predicted prevalences calculated using the unweighted mean, the HT estimator, the naive binomial approach and the proposed model-based approaches as described in Section 3 (lower panels). It is observed that the naive binomial approach yields quite similar results as the proposed model-based approaches. We expected this result, since the goal of the sampling design of the HIS (Demarest et al., 2001) is to obtain a sample which is as close as possible to simple random sampling. The estimated prevalences are highest in the districts of Nivelles and Soignies, with predicted prevalences (using the model-based model 1 with PS estimator) of 7.04% [95% CI: 5.00 – 9.98] and 6.25% [95% CI: 4.23 – 9.50], respectively. Fig. 4 presents the estimated cell probabilities obtained via model (13) with PS (left panel) and the estimated cell size proportions (right panel) for the district of Nivelles. The 95% credible intervals of are calculated using (18) with the parameter estimates replaced by their posterior samples. It is observed that the relationship between the normalized weights and probability on asthma is non-linear. The credible intervals of are somewhat inflated near the boundary values of since the variability of is inflated near the boundary. In the Supplementary Materials (see Appendix A) we also present the estimated cell size proportions obtained via model (13) with RW1. It can be observed that the PS approach is better able to capture a non-linear trend. Under RW1 the estimated probabilities are smaller than PS for small weights and approach a constant probability around 0.07 after a small initial drop. The strata size proportions depend on the normalized weights in an irregular structure since the sample sizes in the strata are different. Fig. 5 presents prevalence maps where the results are obtained via four spatial smoothing methods that account for the spatial weights that are described in Mercer et al. (2014). There are no important differences between these maps and the maps produced by the model-based approaches (Fig. 3) as described in Section 3. The results of the model-based approaches are not influenced by the choice of the prior distributions (see Supplementary Materials, Appendix A).
Fig. 3.
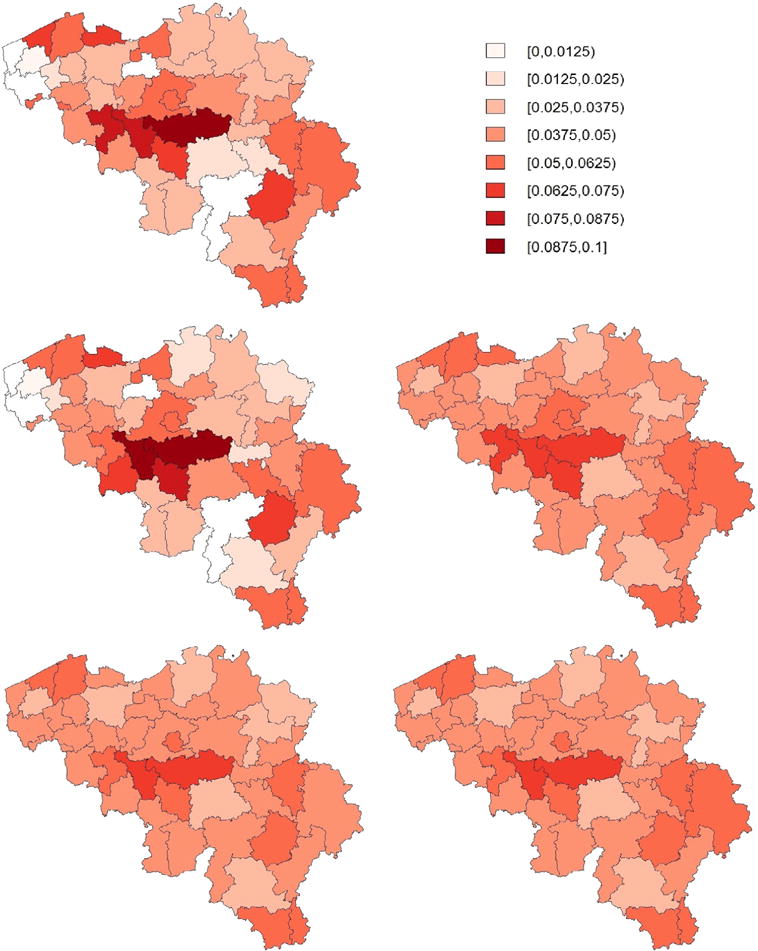
Predicted asthma prevalences by district in Belgium using the 2001 Belgian Health Interview Survey. The obtained estimates are the unweighted mean (top left), the Horvitz–Thompson estimator (middle left), the naive binomial approach (middle right), the model-based approach using model (13) with RW1 (bottom left) and the model-based approach using model (13) with PS (bottom right).
Fig. 4.
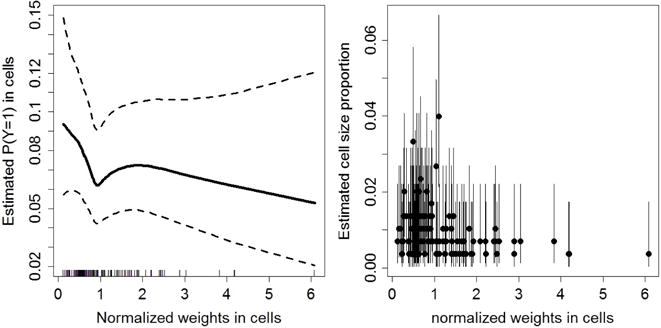
Estimated cell probabilities obtained via (13) with PS together with the 95% credible intervals (left panel) and cell size proportions obtained via (20) (right panel) for the district of Nivelles using the model-based approach. In the right panel, the dots indicate the posterior mean and the black vertical lines are the 95% credible intervals.
Fig. 5.
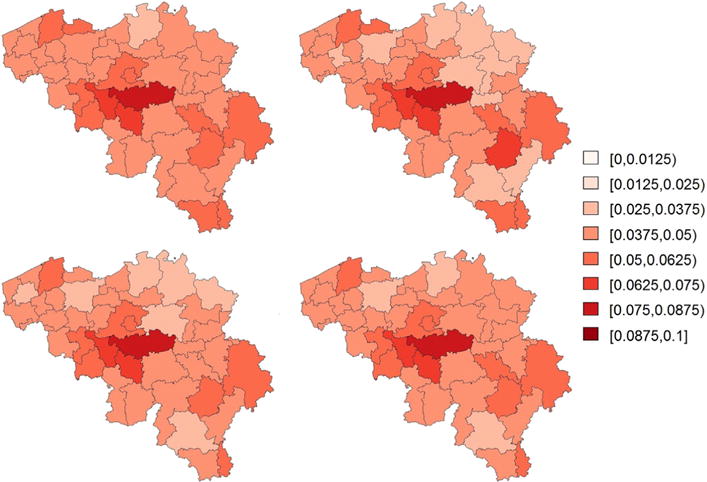
Predicted asthma prevalences by district in Belgium using the 2001 Belgian Health Interview Survey. The obtained estimates are obtained via four estimators described in the overview paper of Mercer et al. (2014): the logit normal estimator (top left), the arcsin square root transformation estimator (top right), the pseudo-likelihood binomial estimator (botom left) and the effective sample size adjusted estimator (bottom right).
6. Discussion
We have presented a predictive model-based approach for the estimation of small area estimates from a health survey in which the survey weights of the sampled individuals are the only information available on the survey design. Our approach uses a hierarchical Bayesian model in which the health outcomes are regressed via a non-parametric function on the normalized survey weights to obtain predictions of the outcome for the non-sampled individuals. The hierarchical model accounts for the spatial distribution by using both spatially unstructured and spatially structured random effects. Simultaneously, the survey weights themselves are modelled to estimate the survey weights of the non-sampled individuals. In the simulation study, the benefits of using indirect methods that account for the survey weights based on hierarchical models are clearly observable. The simulation study indicates that our proposed model-based approach performs well, especially when there is a relationship between the responses and the sampling weights. The 95% credible intervals of the described model-based approach provide good nominal coverage results with short average interval lengths. The results are not sensitive to different choices of prior distributions for the hyperparameters. The proposed methodology is based on Si et al. (2015) describing similar approaches to estimate the finite population mean from a survey. We extended their work to the context of small area estimation.
Both a first-order random walk and a penalized spline were considered for the regression of the health outcome on the survey weights. A first-order random walk can be seen as the Bayesian counterpart of P-splines in which abrupt jumps between two successive spline parameters βm − βm − 1 are penalized (Brezger and Lang, 2008). A first-order random walk was preferred over a second-order random walk since it was observed that the second-order random walk yielded unstable results for some datasets in the simulation study. Overall, we observed in the simulation study that the penalized spline approach outperforms the random walk. Knot selection for the penalized spline, both in terms of number of knots and placement of the knots, is out of the scope of the manuscript. Techniques described in, for example, Ruppert et al. (2003) could be used for this purpose. A sensitivity analysis (results not shown) indicated that our choice of B = 20 was sufficient for the analyses presented here.
To implement our methods we used the inla package within the R computing environment. In this paper, we have observed that inla is very accurate and yields trustworthy results. However, in general we advise researchers to check their results carefully, especially for rare binary events and small sample sizes, since inla can produce inaccurate results in these cases (Fong et al., 2010). The procedure to obtain estimates for off-sample areas is easily implemented in inla by extending the data with the appropriate set of weights and treat the response data as missing. In this manner, predictions for these responses are done as part of the model fitting. We opted for implementing the estimation for the mean and the distribution estimation for the weights separately to make sure that we can make use of standard inla functions. Part of the uncertainty is not accounted for in this manner, however, from the simulation study we observed that the nominal coverage of the 95% credible intervals of the proposed methods are satisfactory.
This paper presented methodology for binary distributed health outcomes. Generalization to other distributions of the health outcome could be done without much effort. The model is also easily extended to include additional predictors. In addition, this proposed methodology can also be used for surveys in which the variables on which the sampling design is based are known. Suppose for example that the survey design selects people according to age, gender and educational level. It seems unlikely that census data per small area which is fully cross-classified over these three variables is available (only marginals but no full cross-classifications). The proposed approaches described in the paper are useful in this example by modelling the health outcome on these three variables and simultaneously making inference about the unknown population sizes in the cross-classified cells. This is a topic that is currently under investigation. Investigating how the proposed models can be used and how they perform for the calculation of subgroup means is another interesting topic of future research.
Another possible extension is replacing the spatially structured random effects by a smooth, non-parametrically specified trend. This was first proposed by Opsomer et al. (2008). This would be useful when more specific information on the spatial locations (more specific than the small area of interest) of the sampled individuals is available.
The hierarchical model approaches described in this paper borrow strength from neighbouring areas. These models are useful to detect hot spot clustering. However, their ability to detect localized hot spots (clusters) is questionable because the models include a global smoothing mechanism (Lawson and Denison, 2002). In the literature, some authors described Bayesian approaches addressing the hot spot (cluster) identification problem. We refer to Lawson and Denison (2002) for an overview.
The described approaches assume that all unique values of the weights have been observed. Si et al. (2015) argued that this is a possible concern of the proposed methods when it is known that some large weights in the population have not occurred in the sample. In this case, this should be taken into account in the setup of the model. A second concern arises in multi-purpose health surveys in which many health outcomes are of interest. Our proposed methods should be repeated separately for each outcome. This is computationally intensive, however, we believe that in the modern era where cluster and parallel computing is available this should not be a major obstacle.
Supplementary Material
Acknowledgments
Support from a doctoral grant of Hasselt University is acknowledged (BOF11D04FAEC to YV). Support from the National Institutes of Health is acknowledged [award number R01CA172805 to CF]. Support from the University of Antwerp scientific chair in Evidence-Based Vaccinology, financed in 2009–2015 by a gift from Pfizer, is acknowledged [to NH]. Support from the IAP Research Network P7/06 of the Belgian State (Belgian Science Policy) is gratefully acknowledged (FEDRA P7/06). This research is supported in part by funding under grant NIH R01CA172805 [CF, RK, AL].
Appendix A. Supplementary material
Supplementary material related to this article can be found online at http://dx.doi.org/10.1016/j.spasta.2016.09.004.
References
- Baker SG. The multinomial-Poisson transformation. Statistician. 1994;43(4):495–504. [Google Scholar]
- Besag J, York JC, Mollie A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Statist Math. 1991;43:1–59. [Google Scholar]
- Brezger A, Lang S. Simultaneous probability statements for Bayesian P-splines. Stat Model. 2008;8:141–186. [Google Scholar]
- Chen Q, Elliott MR, Little RJA. Bayesian penalized spline model-based inference for finite population proportion in unequal probability sampling. Surv Methodol. 2010;36(1):23–34. [PMC free article] [PubMed] [Google Scholar]
- Chen C, Wakefield J, Lumley T. The use of sample weights in Bayesian hierarchical models for small area estimation. Spat Spat-Temporal Epidemiol. 2014;11:33–43. doi: 10.1016/j.sste.2014.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochran WG. Sampling Techniques. John Wiley & Sons, Inc; Hoboken: 1977. [Google Scholar]
- Congdon P, Lloyd P. Estimating small area diabetes prevalence in the US using the behavioral risk factor surveillance system. J Data Sci. 2010;8:235–252. [Google Scholar]
- Datta GS, Ghosh M. Bayesian prediction in linear models: Applications to small area estimation. Ann Statist. 1991;19:1748–1770. [Google Scholar]
- Demarest S, Tafforeau J, Van Oyen H, Bruckers L, Molenberghs G, Tibaldi F, Van Steen K. Health Interview Survey 2001: Protocol for the Sampling Design. Wetenschappelijk Instituut Volksgezondheid, Afdeling Epidemiologie; Brussel: 2001. [Google Scholar]
- Eberly LE, Carlin BP. Identifiability and convergence issues for Markov chain Monte Carlo fitting of spatial models. Stat Med. 2000;19:2279–2294. doi: 10.1002/1097-0258(20000915/30)19:17/18<2279::aid-sim569>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Eilers PHC, Marx BD. Flexible smoothing with B-splines and penalties (with discussion) Statist Sci. 1996;11:89–121. [Google Scholar]
- Elliott P, Wakefield J, Best N, Briggs D, editors. Spatial Epidemiology: Methods and Applications. Oxford University Press; Oxford: 2001. [Google Scholar]
- Farrell PJ. Bayesian inference for small area proportions. Indian J Stat. 2000;62:402–416. [Google Scholar]
- Fay RE, Herriot RA. Estimates of income for small places: An application of James–Stein procedures to census data. J Amer Statist Assoc. 1979;74(366):269–277. [Google Scholar]
- Fong Y, Rue H, Wakefield J. Bayesian inference for generalized linear mixed models. Biostatistics. 2010;11(3):397–412. doi: 10.1093/biostatistics/kxp053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand AE, Diggle PJ, Fuentes M, Guttorp P, editors. Handbook of Spatial Statistics. Chapman & Hall/CRC; Boca Raton: 2010. [Google Scholar]
- Ghosh M, Natarajan K, Stroud T, Carlin B. Generalized linear models for small-area estmation. J Amer Statist Assoc. 1998;93(441):55–93. [Google Scholar]
- Gonzalez ME. Proceedings of the Social Statistics Section. American Statistical Association; Washington, D.C.: 1973. Use and evaluation of synthetic estimators; pp. 33–36. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Springer-Verlag; New York: 2001. [Google Scholar]
- Horvitz DG, Thompson DJ. A generalization of sampling without replacement from a finite universe. J Amer Statist Assoc. 1952;47:663–685. [Google Scholar]
- Jiang J, Lahiri P. Mixed model prediction and small area estimation. TEST. 2006;1:1–96. [Google Scholar]
- Kemp I, Boyle P, Smans M, Muir CS. Incidence and epidemiological perspective Lyon. 1985. Atlas of cancer in Scotland, 1975–1980. (IARC publication no 72). [PubMed] [Google Scholar]
- Kott P. Robust small domain estimation using random effects modelling. Surv Methodol. 1989;9:1–12. [Google Scholar]
- Lawson AB. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology. second. Chapman & Hall/CRC; Boca Raton: 2013. [Google Scholar]
- Lawson AB, Denison DGT. Spatial Cluster Modelling. Chapman & Hall/CRC; Boca Raton: 2002. [Google Scholar]
- MacGibbon B, Tomberlin TJ. Small area estimates of proportions via empirical Bayes techniques. Surv Methodol. 1989;15:237–252. [Google Scholar]
- Malec D, Sedransk J, Moriarity CL, LeClere FB. Small area inference for binary variables in the National Health Interview Survey. J Amer Statist Assoc. 1997;92(439):815–826. [Google Scholar]
- Martino S, Rue H. Implementing approximate Bayesian inference using integrated nested Laplace approximation: A manual for the INLA program. 2009 Available from: http://www.r-inla.org/download.
- Mason TJ. The development of the series of U.S. cancer atlases: Implications for future epidemiologic research. Stat Med. 1995;14:473–479. doi: 10.1002/sim.4780140508. [DOI] [PubMed] [Google Scholar]
- Mercer L, Wakefield J, Chen C, Lumley T. A comparison of spatial smoothing methods for small area estimation with sampling weights. Spat Stat. 2014;8:69–85. doi: 10.1016/j.spasta.2013.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opsomer J, Claeskens G, Ranalli MG, Kauermann G, Breidt FJ. Non-parametric small area estimation using penalized spline regression. J R Stat Soc Ser B Stat Methodol. 2008;70:265–286. [Google Scholar]
- Pfeffermann D. New important developments in small area estimation. Statist Sci. 2013;28:40–68. [Google Scholar]
- Prasad NGN, Rao JNK. On robust small area estimation using a simple random effects model. Surv Methodol. 1999;25:67–72. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2014. URL http://www.R-project.org. [Google Scholar]
- Raghunathan T, Xie D, Schenker N, Parsons V, Davis W, Dood K, Feuer E. Combining information from two surveys to estimate county-level prevalence rates of cancer risk factors and screening. J Amer Statist Assoc. 2007;102:474–486. [Google Scholar]
- Rao JNK. Small Area Estimation. John Wiley & Sons, Inc; Hoboken: 2003. [Google Scholar]
- Rao JNK. Impact of frequentist and Bayesian methods on survey sampling practice: A selective appraisal. Statist Sci. 2011;26:240–256. [Google Scholar]
- Royall RM. On finite population sampling theory under certain linear regression models. Biometrika. 1970;57:377–387. [Google Scholar]
- Rue H, Held L. Gaussian Markov Random Fields. Chapman and Hall/CRC Press; Boca Ratton: 2005. [Google Scholar]
- Rue H, Martino S, Chopin N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J R Stat Soc Ser B Stat Methodol. 2009;71:1–35. [Google Scholar]
- Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge: University Press; 2003. [Google Scholar]
- Si Y, Pillai NS, Gelman A. Bayesian nonparametric weighted sampling inference. Bayesian Anal. 2015;10:605–625. [Google Scholar]
- Skinner C. Analysis of Complex Surveys. Wiley; Chichester: 1989. pp. 59–87. (Chapter). Domain means, regression and multivariate analysis. [Google Scholar]
- Stroud T. Bayesian inference from categorical survey data. Canad J Statist. 1994;22:33–45. [Google Scholar]
- Wakefield J. Multi-level modelling, the ecologic fallacy, and hybrid study designs. Int J Epidemiol. 2009;38:330–336. doi: 10.1093/ije/dyp179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waller IA, Gotway CA. Applied Spatial Statistics for Public Health Data. John Wiley & Sons, Inc.; Hoboken: 2004. [Google Scholar]
- You Y, Rao JNK. A pseudo-empirical best linear unbiased prediction approach to small area estimation using survey weights. Canad J Statist. 2002;30:431–439. [Google Scholar]
- You Y, Rao JNK. Pseudo hierarchical Bayes small area estimation combining unit level models and survey weights. J Statist Plann Inference. 2003;111:197–208. [Google Scholar]
- Zheng H, Little RJA. Penalized spline model-based estimation of finite population total from probability-proportional-to-size samples. J Off Stat. 2003;19:99–117. [Google Scholar]
- Zheng H, Little RJA. Inference for the population total from probability-proportional-to-size samples based on predictions from a penalized spline nonparametric model. J Off Stat. 2005;21:1–20. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


