Mechanical Model of Dexterous Continuum Manipulators with Compliant Joints and Tendon/External Force Interactions

Abstract

Dexterous continuum manipulators (DCMs) have been widely adopted for minimally- and less-invasive surgery. During the operation, these DCMs interact with surrounding anatomy actively or passively. The interaction force will inevitably affect the tip position and shape of DCMs, leading to potentially inaccurate control near critical anatomy. In this paper, we demonstrated a 2D mechanical model for a tendon actuated, notched DCM with compliant joints. The model predicted deformation of the DCM accurately in the presence of tendon force, friction force, and external force. A partition approach was proposed to describe the DCM as a series of interconnected rigid and flexible links. Beam mechanics, taking into consideration tendon interaction and external force on the tip and the body, was applied to obtain the deformation of each flexible link of the DCM. The model results were compared with experiments for free bending as well as bending in the presence of external forces acting at either the tip or body of the DCM. The overall mean error of tip position between model predictions and all of the experimental results was 0.62±0.41mm. The results suggest that the proposed model can effectively predict the shape of the DCM.

I. Introduction

Minimally invasive procedures are popular in current clinical diagnoses and treatments because of improved safety and faster recovery as compared to open surgery [1]. Typically, such surgeries require specific tools such as biopsy forceps or ring curettes to enter a small space and perform the surgery. Traditional rigid tools cannot provide enough flexibility and maneuverability to reach all necessary targets without adversely interacting with the surrounding tissue.

In this paper, we focus on two motivating minimally invasive lesion-removal applications in confined anatomical space. Each procedure—treatment of osteolysis and skull base surgery—utilizes a dexterous continuum manipulator (DCM) with a large lumen for manipulation and tool insertion. The less invasive treatment of osteolysis (defected bone tissue) behind the acetabular cup during hip revision surgery is performed through the screw holes of the well-fixed acetabular implant [2]. Conventional rigid tools only allow removing less than 50% of the defected tissues [3]. At the skull base, cholesterol granulomas in the petrous apex will cause hearing loss without complete removal. Drainage and ring curettes are usually used cooperatively to perform the aeration; conventionally, an unsteerable drainage tube and a rigid curette inserted through the limited entry port cannot perform complete removal. The performance of both motivating minimally invasive surgeries is limited because the reachable workspace through the small entry port is severely restricted by a rigid tool.

Previously, we have developed a notched DCM with a large lumen machined with a series of compliant joints to assist these two typical surgeries [2]–[4], where the skull base surgery is taken as an example shown in Fig. 1. Preliminary kinematic models of the variable-curvature DCM described free space movement with acceptable accuracy [5]. However, the empirical kinematic model was not accurate in the presence of external forces. Previous work [6] developed a physical model assuming revolute joints to describe the deformation of DCM. However, this did not effectively capture friction, only worked well for the bending phase, and underestimated the hysteresis. The hysteresis, likely caused by the friction in the bending and unbending cycle described in [7], should be addressed carefully. Rather than a kinematic model, a mechanical model may be more suitable to predict DCM deformation, especially in the presence of tendon interaction and external forces.

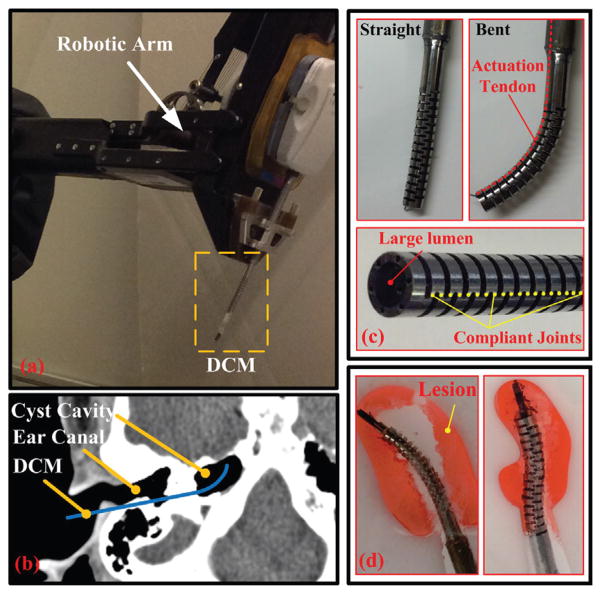
Fig. 1.

DCM integrated with a robotic arm for an example application to skull base surgery [4]: (a) DCM attached to a robotic arm; (b) DCM path to the petrous apex through the tympanic bone for skull base surgery; (c) the straight and bent DCM with large lumen. Also shown is the location of compliant joints; (d) lesion (red color) removal using a 2D phantom of a cross section of petrous apex, where DCM is interacting with the boundary of phantom.

The literature documents several mechanical models using the principle of virtual work [8], [9], Cosserat rod theory [10], [11], and other approaches [12], [13] without considering the friction. Kato et al. [14] built a model to describe the deformation of an endoscope considering the friction force. However, these modeling methods mainly focus on robots with a continuum rod or tube as the backbone significantly different from our DCM with notched tube as the backbone and cannot be used directly to describe our notched DCM with compliant joints. Du et al. [15] designed a similar manipulator with V-shaped units, and proposed a kinematic model based on Timoshenko beam theory, but did not explore the effects of friction force and external forces. York et al. [16] designed a needle-sized robot and built a static model with friction force to describe only the free bending. To our knowledge, the existing literature lacks models of notched DCMs with compliant joints subjected to the tendon force, friction force, and external forces and did not predict the hysteresis of DCM.

In this paper, we propose a partition method for notched DCMs with compliant joints and then build a general and comprehensive 2D mechanical model for tendon actuated DCMs. The model considers the geometric structure to describe the deformation accurately in the presence of tendon interaction and external forces. Section II reviews the DCM and its workspace and capabilities. Section III introduces a partition approach for the notched DCM. Section IV reviews Cosserat rod theory and calculates the parameters for general flexible and rigid links, and describes the particular mechanical model. Section V presents the experimental results to validate the proposed model. Section VI discusses the sources of error, and illustrates the variation of notches. Finally, Section VII presents the conclusions. The main contribution of this paper is the development of a general modeling approach for notched 2D DCMs including the tendon force, friction force, and external force.

II. Overview of DCM With Compliant Joints

A. Structure

The 2D DCM was first developed in [2] for less invasive removal of osteolysis, and later was extended for skull base surgery (Fig. 1). The DCM is made of two superelastic nitinol tubes, which are cut axially through the outer wall of the inner tube and the inner wall of the outer tube to create a through channel. They are then assembled with an interference fit and cut using electrical discharge machining (EDM) to create crossed notches, thereby forming compliant joints. Actuation tendons are inserted inside the through channels and fixed to the tip of the DCM. When the actuation tendon is pulled or released, the DCM is bent or recovered.

B. Workspace and Payload Capability

Previously, we showed that a kinematic model with pin joints at the center of compliant joints has an acceptable accuracy for the treatment of osteolysis application [5]. Based on this, a group theoretic convolution framework was adapted to describe the workspace [17]. Assuming arbitrary external forces and no self-collisions, the workspace approximates a banana-shaped distribution covering about 1200mm² [17]. This workspace is for a particular pose of the base of the DCM; when integrated with a robotic arm, the workspace can be increased by translating and rotating the base of the DCM.

Given a specific notch pattern and length as described in [2], the DCM applied 1N tip force on a stationary object when its tendon was pulled 25N. As a very conservative estimate, the payload capability at the tip of DCM, therefore, can be larger than 1N.

III. Partition Approach of DCM with Compliant Joints

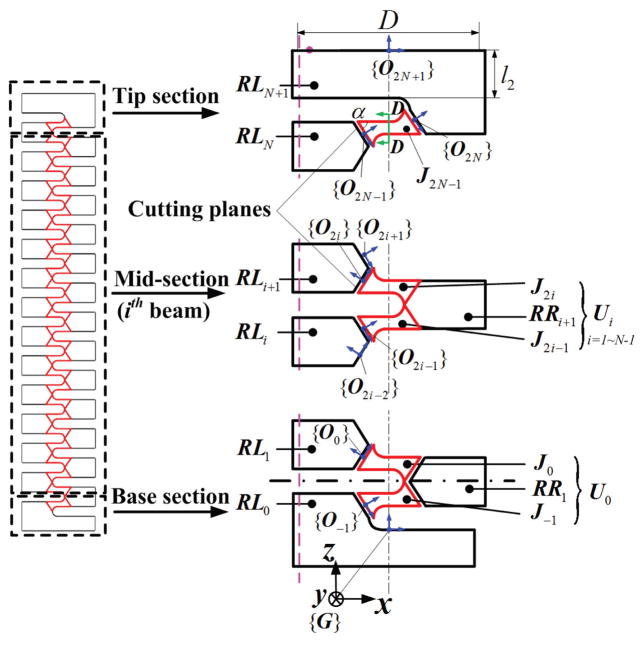
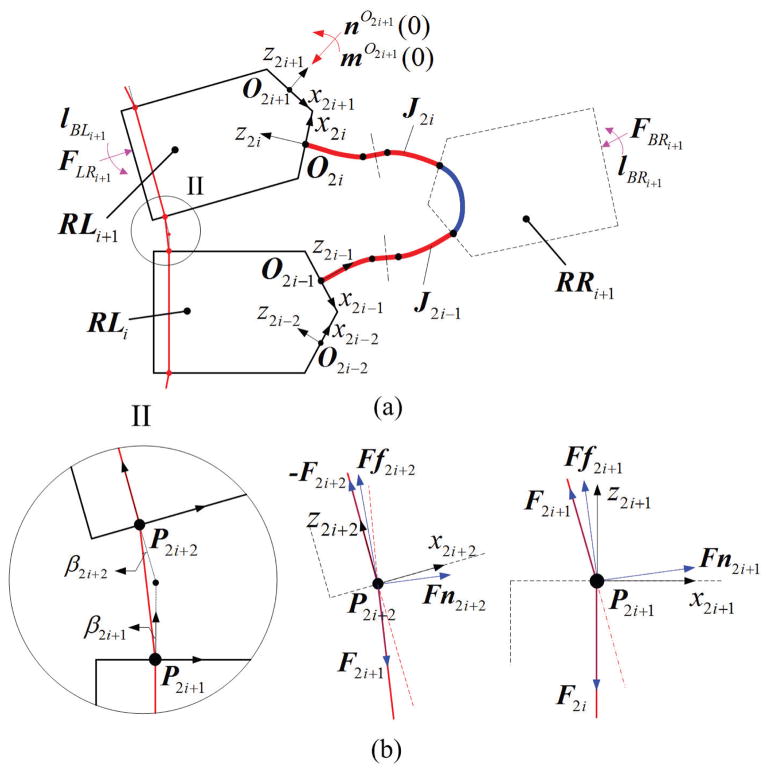
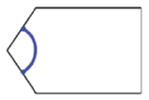
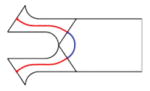
Consider a notched DCM with 2N+1 compliant joints, such as that (N=13) described in Section II for example. It has a series of rectangular crossed notches with round corners to create compliant joints (Fig. 2). Our approach partitions the DCM into both flexible and rigid links and uses beam theory to calculate the deformation of flexible links. The computed deformation of each link approximates the deformation of the DCM. We assume the DCM is built from three interconnected sections: tip, mid, and base (Fig. 2). Each section is composed of a left rigid link (RL_i), and flexible links (J_2N−1 and U_i): the tip section includes J_2N−1; the mid-section includes U-shaped link U_i; the base section includes U₀. Each typical U-shaped link U_i includes both a right link (denoted as RR_i+1) and flexible links (denoted J_2i−1 and J_2i).

Fig. 2.

Diagram of partition method: The cutting planes are defined and the red and black parts stand for the flexible links and the rigid links, respectively.

Because the half circle structure (Fig. 2, near the cross section D-D) is shared by two flexible links, we partition the DCM at each joint by using two cutting planes: parallel to Y axis in {G} (Fig. 2) and going through the middle points of the left and right half circles. This choice of portioning defines the largest flexible link possible. The deduction of α, the angle between the cutting plane and the notch plane (Fig. 2), is introduced in Section IV-B (1). Notably, J_2i−1, J_2i and RR_i+1 can be integrated into a single U-shaped link U_i (Table I).

TABLE I.

Description of separated links

Link	J2i−1	J2i	RRi+1	Ui
Projection & neural axis
Angular rate of change	u;j*(s)	−u;j*(s)	${\mathit{u}}_{RR}^{\ast }(s)$	${\mathit{u}}_U^{\ast }(s)$

IV. Mechanical Model With Tendon Actuation And Parameters Calculation

Based on the partition, we aim to use beam theory to describe the deformation of flexible links (Part B–F). The D-H method will integrate the rigid links and define the kinematics of the three sections to obtain the whole DCM deformation (Part G).

A. Review of Classic Cosserat Rod Theory

Cosserat rod theory is a good choice to model the links because it considers the shear and axial force, especially for short beams like the flexible links (Fig. 2). For classic Cosserat rod beam theory, ordinary differential equations (ODEs) are derived from the rod kinematics, equilibrium equations, and constitutive laws [10], [11]. For an arbitrary arc length s of the beam, the homogeneous transformation matrix from the base is:

$${\mathit{g}}_i(s)=\left[\begin{array}{cc}{\mathit{R}}_i(s)& {\mathit{p}}_i(s)\\ 0& 1\end{array}\right]$$ (1)

For the typical U-shape link U_i in Fig. 2:

$$\begin{array}{l}{\stackrel{.}{\mathit{p}}}_i(s)={\mathit{R}}_i(s){\mathit{v}}_i(s)\\ {\stackrel{.}{\mathit{R}}}_i(s)={\mathit{R}}_i(s){\widehat{\mathit{u}}}_i(s)\\ {\stackrel{.}{\mathit{n}}}_i(s)=-{\mathit{f}}_i(s)\\ {\stackrel{.}{\mathit{m}}}_i(s)=-{\stackrel{.}{\mathit{p}}}_i(s)\times {\mathit{n}}_i(s)-{\mathit{l}}_i(s)\end{array}$$ (2)

where v_i(s) and u_i(s) are linear rate and angular rate of change of g_i(s), expressed as follows:

$$\begin{array}{l}{\mathit{v}}_i(s)={\mathit{v}}_i^{\ast }(s)+{\mathit{K}}_{se}^{-1}(s)·{\mathit{R}}_i{(s)}^T·{\mathit{n}}_i(s)\\ {\mathit{u}}_i(s)={\mathit{u}}_i^{\ast }(s)+{\mathit{K}}_{bt}^{-1}(s)·{\mathit{R}}_i{(s)}^T·{\mathit{m}}_i(s)\end{array}$$ (3)

Here, K_se(s) and K_bt(s) are the stiffness matrices for shear/extension and bending/torsion respectively.

$$\begin{array}{l}{\mathit{K}}_{se}(s)=\text{diag}(GA(s),GA(s),EA(s))\\ {\mathit{K}}_{bt}(s)=\text{diag}(E{I}_{xx}(s),E{I}_{yy}(s),E{J}_{zz}(s))\end{array}$$ (4)

where E is the Young’s modulus and G is the shear modulus; A(s) is the area of the cross section; I_xx (s) and I_yy(s) are the second moments of area; J_zz(s) is polar moment of inertia. Because the DCM only deforms in the bending plane, EI_yy(s) = +∞ and EJ_zz(s) = +∞.

If an external force or moment is applied at the mid-point of an arbitrary segment, then n_i(s) and m_i(s) (Eq. 2–3) in the left and right side of the specific arc length, σ, can be calculated as follows:

$$\begin{array}{l}{\mathit{n}}_i({\sigma }^{-})={\mathit{n}}_i({\sigma }^{+})+{\mathit{F}}_{{BR}_i}\\ {\mathit{m}}_i({\sigma }^{-})={\mathit{m}}_i({\sigma }^{+})+{\mathit{l}}_{F_{{BR}_i}}+{\mathit{l}}_{{BR}_i}\end{array}$$ (5)

Here, F_BRi is an external force at any point (denoted as Point B); l_BRi is the moment at Point B; and l_FBRi is the moment resulting from F_BRi.

According to Eq. 2, given the structural parameters and the boundary conditions, the ODEs can be solved. The critical structural parameters for flexible and rigid links, ${\mathit{v}}_i^{\ast }(s),{\mathit{u}}_i^{\ast }(s)$, I_xx(s) and A(s) will be discussed and calculated in Subsection B–D. The boundary conditions for each section will be given in Subsection F.

B. Geometrical Parameters of Flexible Links - J_2i−1 and J_2i

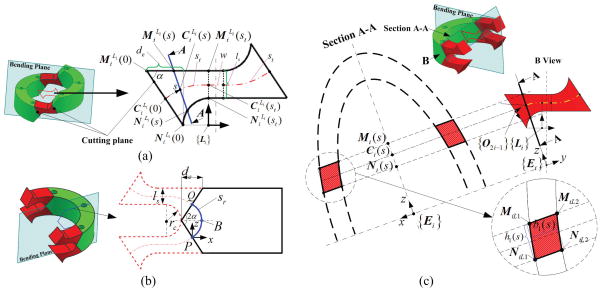
The DCM can only deform in the 2D bending plane, so we can project J_2i−1 to the bending plane (Fig. 3(a)).

Fig. 3.

Diagram of flexible link (red color), rigid link (green color) and the flexible link’s cross section: (a) Projection of flexible link to the bending plane; (b) Projection of rigid link to the bending plane: the blue line indicates the virtual neutral axis with arc length, s_r. P and Q are the intersection points between the neural axis and two cutting planes with the angle, 2α; (c) Diagram of cross section for the flexible link, J_2i−1.

(1) Determination of cutting plane and parameters

In order to determine the cutting plane, we choose the middle point of circular notch ${\mathit{N}}_i^{L_i}(0)$ as one point in the cutting plane and then calculate the angle α between the cutting plane and notch plane (Fig. 3(a)). We make two assumptions: 1) the neutral axis of flexible link lies at the structural center; 2) the tangent vector of the neutral axis is perpendicular to the beam cross section at the initial reference configuration before the deformation.

With regard to the first segment (Fig. 3(a)), d_e is defined as $\Vert {\mathit{M}}_i^{L_i}(0)-{\mathit{M}}_i^{L_i}(s_l)\Vert -r_c$. Points for the base edge and top edge at the coordinate {L_i} with respect to the arc length s of neural axis are expressed as

$${\mathit{M}}_i^{L_i}(s)={\left[\begin{array}{lll}0\hfill & -r_c·cos(\pi /2·t)\hfill & r_c·sin(\pi /2·t)\hfill \end{array}\right]}^T$$ (6)

$${\mathit{N}}_i^{L_i}(s)={\left[\begin{array}{lll}0\hfill & -\left(d_e+r_c\right)·(1-t)\hfill & r_c+l_s\hfill \end{array}\right]}^T$$ (7)

where t = s / s_t (0 ≤ s ≤ s_t, 0 ≤ t ≤ 1), l_s is the height of second segment. Based on the assumption 1, the neutral axis can be calculated as ${\mathit{C}}_i^{L_i}(s)=0.5·({\mathit{M}}_i^{L_i}(s)+{\mathit{N}}_i^{L_i}(s))$.

Based on the assumption 2, the unit tangent vector denoted as ${\mathit{e}}_{C_i}^{L_i}(s)$ of neutral axis ${\mathit{C}}_i^{L_i}(s)$ and the unit tangent vector denoted as ${\mathit{e}}_{M_i{N}_i}^{L_i}(s)$ of the cross section should conform to ${\mathit{e}}_{M_i{N}_i}^{L_i}(0)·{\mathit{e}}_{C_i}^{L_i}(0)=-1$ at ${\mathit{C}}_i^{L_i}(0)$ where s = 0, so d_e can be calculated. The curvature of neutral axis can be derived as

$${\kappa }_1^{\ast }(s)=\Vert {\stackrel{.}{\mathit{C}}}_i^{L_i}(s)\times {\ddot{\mathit{C}}}_i^{L_i}(s)\Vert$$ (8)

By integrating the arc length, s_t can be calculated as

$$s_t=\int ds=\int \sqrt{{(d{C}_i^{L_i}{(s)}_y)}^2+{(d{C}_i^{L_i}{(s)}_z)}^2}$$ (9)

Next the angle α between the notch plane and cutting plane (Fig. 3(a)) can be calculated as

$$\alpha =arctan\left((r_c+l_s)/d_e\right)$$ (10)

which finally defines the location of cutting plane.

The second segment with arc length w and height l_s is a straight line, so the curvature ${\kappa }_2^{\ast }(s)=0$. Due to the rotational symmetry to the first segment, the curvature of the third segment is ${\kappa }_3^{\ast }(s)=-{\kappa }_1^{\ast }(s)$. Then, for J_2i−1, ${\mathit{u}}_J^{\ast }(s)$, the angular rate of change of g(s) in Eq. 3, can be expressed as Eq. 11 and its linear rate of change is ${\mathit{v}}_J^{\ast }(s)=[0,0,1]$.

$${{\mathit{u}}_J}^{\ast }(s)=\{\begin{array}{ll}{\left[{\kappa }_1^{\ast }(s)00\right]}^T\hfill & 0\le s\le s_{\mathrm{t}}\hfill \\ {\left[000\right]}^T\hfill & s_t<s<s_t+w\hfill \\ \left[-{\kappa }_1^{\ast }(2·s_t+w-s)00\right]\hfill & s_t+l_s\le s\le 2·s_t+w\hfill \end{array}$$ (11)

Also due to the mirror symmetry, the angular and linear rate of change for J_2i is $-{\mathit{u}}_J^{\ast }(s)$ and ${\mathit{v}}_J^{\ast }(s)$.

(2) Calculate I(s) and A(s)

The moment of inertia I(s) and cross sectional area A(s) are used to calculate the stiffness (Eq. 4). Because the deformation only happens in the bending plane, the stiffness along the Y and Z axes are I_yy (s) = (s)I_zz = +∞.

The cross section for the first segment is the intersection of Section A-A and DCM forming an elliptical ring (Fig. 3(c)). We simplify this cross section to a parallelogram. The first segment has two symmetric flexible parts to Y-Z plane in the local coordinates {E_i}, and its moment of inertia, I₁(s), and area, A₁(s), are calculated as:

$$\begin{array}{l}{I}_1(s)=2·b_1(s)·h_1{(s)}^3/12\\ A_1(s)=b_1(s)·h_1(s)\end{array}$$ (12)

The third segment has rotational symmetry to the first segment, therefore, its moment of inertia is I₃ (s) = I₁ (2 · s_t + w − s) and its cross-sectional area is A₃ (s) = A₁ (2 · s_t + w − s).

The cross section of the second segment is a rectangle. This segment’s moment of inertia and cross-sectional area are $I_2(s)=2·b_2(s)·l_s^3/12$ and A₂ (s) = b₂ (s) · l_s respectively. Here, l_s is the height of the cross section, and b₂ (s) is the width of the cross section.

The moment of inertia and the cross-sectional area of the whole link J_2i−1 can be expressed as follows:

$$\begin{array}{l}{I}_{xx}(s)=\{\begin{array}{ll}{I}_1(s)\hfill & 0\le s\le s_{\mathrm{t}}\hfill \\ 2·b_2(s)·l_s^3/12\hfill & s_t<s<s_t+w\hfill \\ I_1(2·s_t+w-s)\hfill & s_t+l_s\le s\le 2·s_t+w\hfill \end{array}\\ A(s)=\{\begin{array}{ll}{A}_1(s)\hfill & 0\le s\le s_{\mathrm{t}}\hfill \\ b_2(s)·l_s\hfill & s_t<s<s_t+w\hfill \\ A_1(2·s_t+w-s)\hfill & s_t+l_s\le s\le 2·s_t+w\hfill \end{array}\end{array}$$ (13)

C. Geometrical Parameters of Rigid Links- RR_i+1

We assume the rigid link, RR_i+1, has a rotational and shear stiffness of +∞, and RR_i+1 ’s curvature is first-order continuous with respect to its arc length. Therefore, the rigid link, RR_i+1 in the link U_i (one link in the mid-section) is defined as an arc starting at P and ending at Q with an infinite stiffness (Fig. 3(b)).

The curvature, κ_PQ, at Point P and Q is the same as ${\kappa }_1^{\ast }(s_t)$ in Eq. 8. Point B (Fig. 3(b)) is the mid-point of the arc with an unknown curvature, κ_B. We linearize the curvature at any specific arc length s as:

$${\kappa }_r(s)=\frac{d\theta }{ds}=\frac{d\theta }{dy}·sin\theta ={\kappa }_{PQ}+\frac{{\kappa }_B-{\kappa }_{PQ}}{\alpha }\left(\theta -\frac{\pi }{2}+\alpha \right)$$ (14)

$$\frac{r_c+l_s}{2}=\int dy={\int }_{\frac{\pi }{2}-\alpha }^{\frac{\pi }{2}}\frac{sin\theta }{{\kappa }_r(s)}d\theta$$ (15)

Projecting the half arc $\stackrel{⌢}{\mathit{PB}}$ onto the Z axis (Fig. 3(b)), we can obtain the Eq. 15. Then substitute Eq. 14 to Eq. 15, κ_B can be calculated, as well as κ_r(s). The arc length, s_r, is derived by integrating inverse curvature (Eq. 14) from P to B.

Deriving Eq. 14 defines the curvature with respect to the specific arc length in Eq. 16. The resulting angular rate of change of g(s) with respect to s can be expressed in Eq. 17.

$${\kappa }_r(s)={\kappa }_{PQ}·e^{\frac{{\kappa }_B-{\kappa }_{PQ}}{\alpha }·s}$$ (16)

$$u_{RR}^{\ast }={\left[\begin{array}{lll}{\kappa }_r\hfill & 0\hfill & 0\hfill \end{array}\right]}^T$$ (17)

D. Geometrical Parameter of U-shaped Links - U_i

As shown in Table I, each typical link, U_i, is composed of J_2i−1, J_2i and RR_i+1. We denote the structural parameter of U_i as follows:

$${{\mathit{u}}_U}^{\ast }(s)=\{\begin{array}{ll}{{\mathit{u}}_J}^{\ast }(s)\hfill & 0\le s\le 2·s_t+w\hfill \\ {{\mathit{u}}_{RR}}^{\ast }(s)\hfill & 2·s_t+w<s<2·s_t+w+s_r\hfill \\ -{{\mathit{u}}_J}^{\ast }(s)\hfill & 2·s_t+w+s_r\le s\le 4·s_t+2·w+s_r\hfill \end{array}$$ (18)

$${\mathit{v}}_U^{\ast }(s)={[\begin{array}{lll}0\hfill & 0\hfill & 1\hfill \end{array}]}^T$$ (19)

Finally, we derive the structural parameters of each link, which are used in Eq. 3–4 when solving the ODEs in Eq. 2.

E. Model Assumptions and DCM Configuration

The proposed mechanical model assumes: 1) deformation only occurs in the bending plane (X-Z plane), meaning the rotational stiffness along the X/Z axis is +∞; 2) the clearance between the tendon and the channel is ignored; 3) the tendon is defined as a string, which cannot resist bending and/or torsion; and 4) the non-actuating cable is not tensioned and imparts neither force nor friction on the DCM. These assumptions will be used in the following deductions.

We consider a typical section configuration with odd compliant joints (Fig. 2). To be more general, there are four types of section configurations with even or odd compliant joints.

F. Tendon Coupled Model

We use Cosserat rod theory to describe each section, given the proximal tendon force, external force and enough boundary conditions, the deformation of each link can be solved, then the whole deformation of DCM can be derived. In order to build the real boundary conditions, the tendon interaction will be illustrated below.

(1) The tip section

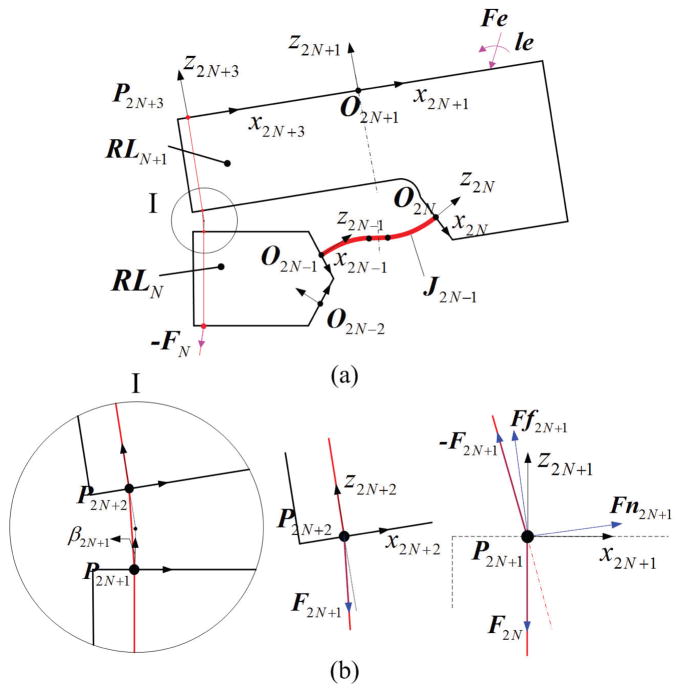
Fig. 4(a) shows the bending plane of the tip section, where the start and end coordinates of the flexible link are defined as {O_2N−1} and {O_2N}.

Fig. 4.

Diagram of tip sections coupled with the tendon: (a) shows the projection of tip section; (b) show the free body diagrams of tendon at P_2N+2 and the sharp corners P_2N+1, where β_2N+1 is denoted as the relative angle between two segments of tendon.

a) Tendon interaction at P_2N+2

The tendon is fixed at P_2N+3, then goes through the channel and notch, and interacts with the rigid link RL_N+1 at P_2N+2 and P_2N+1 (Fig. 4). The interaction at P_2N+1 is only applied to the rigid part RL_N, affecting the deformation of the next beam in the mid-section, not J_2N−1 or U_N in the tip section. The N-th beam therefore, is subjected to F_2N+1 at P_2N+2.

b) Section property and boundary conditions

For J_2N−1 in Fig. 4(a), the total arc length s_l is 2 · s_t + w, where s_t can be calculated in Eq. 9. Then the initial parameters are defined as ${\mathit{v}}_N^{\ast }(s)={[\begin{array}{lll}0\hfill & 0\hfill & 1\hfill \end{array}]}^T$ and ${\mathit{u}}_J^{\ast }(s)$ in Eq. 11.

The boundary conditions, two at s = 0 and two at s = s_t (for Eq. 2), for the top section are defined as follow:

$$\begin{array}{l}{\mathit{p}}_N(0)={[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \end{array}]}^T\\ {\mathit{R}}_N(0)={\mathit{I}}_3\\ {\mathit{n}}_N(s_l)=-{\mathit{F}}_{2N+1}+\mathit{Fe}\\ {\mathit{m}}_N(s_l)={\mathit{r}}_{O_{2N}{P}_{2N+2}}\times (-{\mathit{F}}_{2N+1})+{\mathit{r}}_{O_{2N}{P}_E}\times \mathit{Fe}+\mathit{le}\end{array}$$ (20)

where p_N(0) and R_N(0) are the position and orientation at the s = 0 ; n_N(s_l) and m_N(s_l) are the internal force and moment at the s = s_l. Here Fe and le are the external force and moment applied at the rigid link RL_N+1, r_O2NP2N+2 and r_O2NPE are the distance for the point of force to {O_2N}.

So given Eq. 23 and the distal tendon force F_2N+1, the ODEs in Eq. 2 can be solved to derive the beam configuration.

(2) The mid-section

The mid-section is composed of a series of U-shaped link U_i. The bending plane of U_i in the mid-section starts at O_2i−1 and ends at O_2i (Fig. 5(a)).

Fig. 5.

Diagram of mid-section coupled with the tendon: (a) shows the mid-section with U_i; (b) show the free body diagrams of tendon at the sharp corners- P_2i+2 and P_2i+1, where β_2i+2 and β_2i+1 are denoted as the relative angle between two segments of tendon.

a) Tendon interaction at P_2i+3 and P_2i+2

The tendon interacts with RL_i+1 at P_2i+3 and P_2i+2 respectively, assuming that the tendon channel in the rigid link remains straight (Fig. 5). Since the friction force is proportional to the normal force, we assume no friction for the tendon inside the rigid link channel. Only the contact points at the border of the channel have a normal force component and, therefore, friction force. Take P_{2i +2} as an example: we assume that the direction of normal force lies in the middle of two tendon tensions −F_2i+2 and F_2i+1, then the friction force is perpendicular to the normal force. If we denote the angle between −F_2i+2 and z_2i+2 as β_2i+2, then the angle between Ff_2i+2 and z_2i+2 is β_2i+2/2. So we can obtain the free body diagram of RL_i+1 and tendon at P_2i+2 (Fig. 5(b)). Similarly we can also get the free body diagram of RL _i+1 and tendon at P_2i+3 (P_2N+1). The force balance equations for the tendons are:

$$\begin{array}{l}{\mathit{P}}_{2i+3}:-{\mathit{F}}_{2i+3}+\mathit{F}{\mathit{f}}_{2i+3}+\mathit{F}{\mathit{n}}_{2i+3}+{\mathit{F}}_{2i+2}=0\\ {\mathit{P}}_{2i+2}:-{\mathit{F}}_{2i+2}+\mathit{F}{\mathit{f}}_{2i+2}+\mathit{F}{\mathit{n}}_{2i+2}+{\mathit{F}}_{2i+1}=0\end{array}$$ (21)

where Ff_2i+3 and Ff_2i+2 are the friction force; and Fn_2i+3 and Fn_2i+2 are the normal force. Thus, U_i is subjected to Fn_2i+3, Ff_2i+3, Fn_2i+2 and Ff_2i+2. It is noticeable that F_2i+3 is equal to F_2N+1.

b) Section property and boundary conditions

The total length of U_i is s_l = 4·s_t + 2·l_s +s_r(Fig. 5(a)). ODEs are the same with Eq. 2, where i=1~N−1, and the reference configuration ${\mathit{v}}_i^{\ast }(s)$ and ${\mathit{u}}_i^{\ast }(s)$ can be obtained from Eq. 18–19. The boundary conditions are

$$\begin{array}{l}{\mathit{p}}_i(0)={[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \end{array}]}^T\\ {\mathit{R}}_i(0)={\mathit{I}}_3\\ {\mathit{n}}_i(s_l)=\underset{I}{\underbrace{{\mathit{T}}_{O_{2i+1}}^{O_{2i-1}}·{\mathit{n}}_{2i+1}^{O_{2i+1}}(0)}}+\underset{II}{\underbrace{\mathit{F}{\mathit{n}}_{2i+3}+\mathit{F}{\mathit{f}}_{2i+3}}}\\ +\underset{\mathit{III}}{\underbrace{\mathit{F}{\mathit{n}}_{2i+2}+\mathit{F}{\mathit{f}}_{2i+2}}}+\underset{IV}{\underbrace{{\mathit{F}}_{L{R}_{i+1}}}}\\ {\mathit{m}}_i(s_l)=\underset{I}{\underbrace{{\mathit{m}}_{i+1}^{O_{2i+1}}(0)}}+\underset{II}{\underbrace{{\mathit{r}}_{O_{2i}{O}_{2i+1}}\times ({\mathit{T}}_{O_{2i+1}}^{O_{2i-1}}·{\mathit{n}}_{i+1}^{O_{2i+1}}(0))}}\\ +\underset{\mathit{III}}{\underbrace{{\mathit{r}}_{O_{2i}{P}_{2i+3}}\times (\mathit{F}{\mathit{n}}_{2i+3}+\mathit{F}{\mathit{f}}_{2i+3})}}\\ +\underset{IV}{\underbrace{{\mathit{r}}_{O_{2i}{P}_{2i+2}}\times (\mathit{F}{\mathit{n}}_{2i+2}+\mathit{F}{\mathit{f}}_{2i+2})}}+\underset{V}{\underbrace{{\mathit{l}}_{L{R}_{i+1}}}}\end{array}$$ (22)

Here in the right side of n_i(s_l), the first term is the force transformed from the last link, the middle terms are the forces at P_2i+3 and P_2i+2, the last term is the external force applied at RL_i+1; while in the right side of m_i(s_l), term I is the moment transformed from the last link, term II is the moment transformed from the force in the last link, terms III and IV are the moments from the forces at P_2i+3 and P_2i+2, term V is the external moment applied at RL_i+1. And r_O2iP2i+3 and r_O2iP2i+2 are the distances for the point of force to O_2i.

Given Eq. 22, the ODEs in Eq. 2 can be solved when we substitute Eq. 21 for Eq. 22. Therefore, the normal force, friction force and beam configuration can be derived.

(3) The base section

Fig. 5(a) with i=0 also shows the bending plane of base section, where the start point and end point of flexible link are defined with O₋₁ and O₀. The tendon interacts with the rigid link at P₂ and P₃. So the elastic link is subject to the normal force Fn₂ and Fn₃, and the friction force Ff₂ and Ff₃. This section has the same boundary conditions with Eq. 22 where i=0. As shown in Fig. 5(b), F₀ is the proximal force we usually apply, whose magnitude can be solved as

$$F_0=F_1·\left|\frac{cos({\beta }_1/2)+sin({\beta }_1/2)·{\mu }_c}{cos({\beta }_1/2)-sin({\beta }_1/2)·{\mu }_c}\right|$$ (23)

where β₁ the angle between −F₁ and F₀.

G. DCM Kinematics

Because we have assumed that the DCM is composed of a series of interconnected left rigid links (RL_i) and flexible links (J_2N−1 or U_i). A series of transformation matrices based on the D-H method define the homogenous matrix from the tip to the base as

$$\left[\begin{array}{cc}{\mathit{R}}_{2N+1}^G& {\mathit{p}}_{2N+1}^G\\ 0& 1\end{array}\right]=\underset{I}{\underbrace{\left({\mathit{T}}_{-1}^G·{\mathit{T}}_0^{-1}\right)}}·\underset{II}{\underbrace{\left(\prod _{i=1}^j{\mathit{T}}_{O_{2i-1}}^{O_{2i-2}}·{\mathit{T}}_{O_{2i}}^{O_{2i-1}}\right)}}·\underset{\mathit{III}}{\underbrace{\left({\mathit{T}}_{2N}^{2N-1}·{\mathit{T}}_{2N+1}^{2N}\right)}}$$ (24)

Here, ${\mathit{R}}_{2N+1}^G$ and ${\mathit{p}}_{2N+1}^G$ are the tip position and orientation in the global coordinates {G}; terms I–III are the transformation matrices of base section, mid-sections and tip section, respectively; ${\mathit{T}}_{O_{2i}}^{O_{2i-1}}$ is the transformation matrix of each link U_i in the mid-section expressed using Eq. 25, which can be derived from the solution of each link in Subsection F- (1)–(3); ${\mathit{T}}_{O_{2i-1}}^{O_{2i-2}}$ is the transformation matrix of each left rigid link RL_i.

$${\mathit{T}}_{O_{2i}}^{O_{2i-1}}=\left[\begin{array}{cc}{\mathit{R}}^{O_{2i-1}}(s_l)& {\mathit{p}}^{O_{2i-1}}(s_l)\\ 0& 1\end{array}\right]$$ (25)

According to the above deduction, given the distal tendon force F_2N+1, Eq. 25 can be derived by numerically solving the statics of each section of DCM, finally the proximal force F₀ can be calculated using Eq. 23, and the shape of DCM can be calculated using Eq. 24 based on kinematics, respectively.

H. Consideration of Friction Force

We consider both static and kinetic friction. Subramani et al. [18] proposed a method for modeling the friction force in catheter-like manipulators. We extend their method to match the structure of our DCM. Here we use a Coulomb model of the friction force. We assume that the static friction coefficient equals the kinetic friction coefficient, μ_c, which is constant for all the cases.

In our model when the DCM is bent, we assume the friction force is always toward the base section with the kinetic friction +μ_c · Fn_i. Before starting to release the tendon, it is assumed that there is no relative movement between the tendon and the channel, and the friction force at the contact point remains +μ_c · Fn_i.

When the DCM starts to unbend by releasing the tendon tension, the direction of the friction force at all contact points will not change to −μ_c ·Fn_i immediately. The tension of the tendon will release from the proximal to the distal end. Therefore, the friction force gradually changes from the first contact point P₁ (Fig. 5(b) with i=0) to the last contact point P_2N+1 (Fig. 4(b)) point by point. At the m-th contact point, before the start of relative movement between the tendon and channel, it will stick to the original position only with the change of static friction starting from +μ_c · Fn_i; while when it starts to slide along the channel, the direction of friction force will become negative, then the friction force will be −μ_c ·Fn_i. After the relative slide occurs at all the contact points, the friction force of all the contact points will be −μ_c · Fn_i. So for all the contact points, the friction forces will be

$$F{f}_i=\{\begin{array}{ll}-{\mu }_c·F{n}_i\hfill & i<m\hfill \\ \eta ·{\mu }_c·F{n}_i\hfill & i=m,-1\le \eta \le 1\hfill \\ +{\mu }_c·F{n}_i\hfill & i>m\hfill \end{array}$$ (26)

where i is the i-th contact point (i =1~ 27), m is the m-th contact point which has the transition situation; η is a coefficient indicating the change of static friction before the relative movement. By adjusting η, the friction force is calculated, then the boundary conditions in Subsection F can be derived.

V. Experimental Validation and Results

Young’s modulus of nitinol is highly nonlinear with temperature and dependent on manufacturing processes; additionally, the developed model assumes an infinite stiffness for the rigid links. Therefore, we calibrated an equivalent Young’s modulus and friction coefficient using an experimental setup described in the following subsection. We performed experiments to compare the model with experimental deformations of the DCM for the following scenarios: 1) with tip force only, 2) with tendon force only, and 3) with tendon force and external tip/body force.

A. Experimental Setup

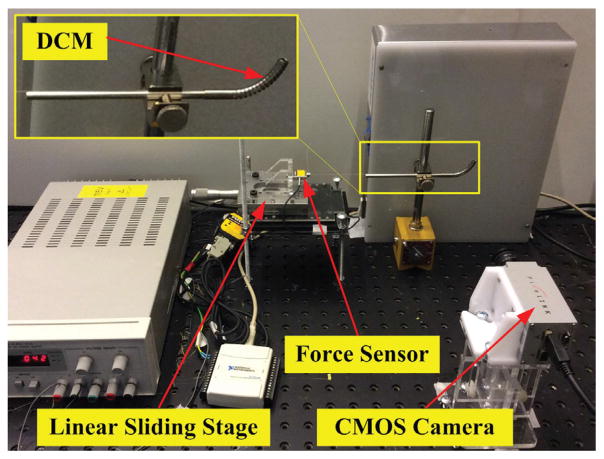
The DCM was fixed to a magnetic support block. The actuation tendon, a 0.25mm steel stripe (McMaster, USA), was attached to the distal tip of the DCM. The proximal side of the tendon was attached to a force sensor (Futek LSB200, USA) fixed to the linear stage (M-UMR8.25A, Newport, USA) with 0.01mm accuracy. A CMOS camera (PixeLINK PL-B774F, USA) was mounted on an optical platform table.

During the experiments, the linear stage was controlled manually to pull/push the tendon with a slow speed (nearly <0.06mm/s) to guarantee a quasi-static scenario, and the tendon force was transferred to the computer using the data acquisition card. When the force reached a desired value, the DCM image was captured by the camera. The images were then processed to calculate the shape of the DCM using a 2D/3D registration method [19]. A DCM made from nested nitinol tubes with 14 pairs of notches [2] was used for the experiments.

B. Calibration of the Equivalent Young’s Modulus

To find the equivalent Young’s modulus E in Eq. 4 for the DCM, we carried out six groups of experiments with a series of weights - 10g, 20g, 50g, 70g, 100g and 150g. Each weight was applied from the tip at the position [−0.5d_t,0,0] in the local coordinates {O_2N+1}. Each group was repeated ten times. Next, using the model described in Section IV, we found an equivalent Young’s modulus that provided the best match between the simulated DCM shapes and the experimental results by minimizing the errors shown below.

$$e_{\mathit{total}}=argmin(\sum _{n_1=1}^{N_1}\sum _{n_2=1}^{N_2}\sum _{k=1}^{30}{e}_k^{(n_1,n_2)})$$ (27)

Here $e_k^{(n_1,n_2)}$ is the Euclidean distance between the experimental results and simulation results at the k-th point of the n₂-th shape in the n₁-th group; e_total is the sum of errors. The deformation shape of the DCM was measured at its centerline.

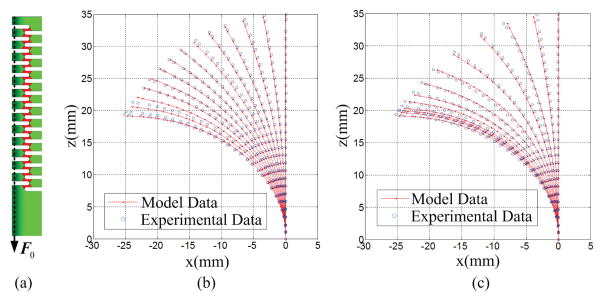
The experiments with 20g, 70g and 150g were used to implement the optimization approach, finally determining an equivalent Young’s modulus 22GPa. Then the experiments with 10g, 50g, and 100g were used to provide the test data. Results indicate that the model with the equivalent Young’s modulus can predict the shapes with the mean error 0.40±0.18mm.

C. Calibration of the Friction Coefficient

The tendon was tensioned from 0 to 13N in 1N increments. Next, the tendon was released back to 0N in 1N decrements. The procedure was repeated 5 times. We determined a best friction coefficient that minimized the Euclidean distance as described in Eq. 27.

The experimental shapes with tendon force from 1N to 13N in 2N increments for the bending and unbending cycles were used to determine the best friction coefficient of 0.66. Then the experimental shapes with tendon force from 0N to 12N in 2N increments were used to test the model. Shape comparison for the calibration and test are shown in Fig. 7. The total mean error was 0.61±0.43mm. We observed that during the bending phase, the DCM shape changed gradually with the gap between the shapes increasing uniformly. During the unbending phase, the gap between shapes did not decrease uniformly. From Fig. 7, the shape at 13N is not a typical circle with constatnt curvature. This agrees with the analysis of Murphy et al. [20].

Fig. 7.

Shape comparison between the model data and experimental data with free bending and unbending phases: (a) shows the applied force; (b) shows the comparison with free bending phase; (c) shows the comparison with unbending phase.

D. Tendon Force Distribution Along the Channel

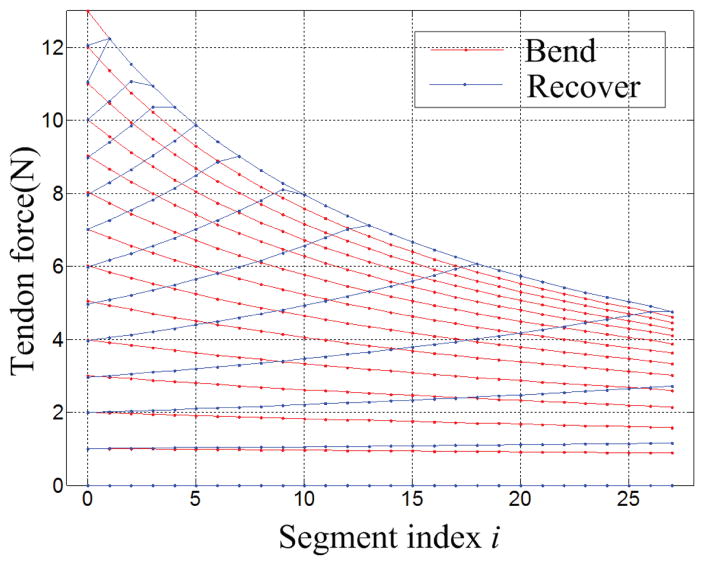
The shape of the DCM during the free bending and unbending cycles is different (Fig. 7). This might be due to the friction force affecting the tendon distribution and leading to the different deformation for each joint during the bending/unbending cycle. Simulation results for tendon force distribution F_i(i =0–27) (defined in Section IV-F) along the 27 segments from the proximal to the distal end of the DCM during the bending/unbending cycle suggest tendon force profiles are significantly different when comparing loading (DCM bending) and unloading (DCM recovery) cycles (Fig. 8). During the loading cycle, the force profile from the proximal to distal segment simultaneously increases along all segments. However, during the unloading cycle, the tendon force reduces incrementally (one segment at a time) from the proximal to the distal segment. When the maximum force 13N is applied to the tendon in the proximal end, the force in the proximal end is more than twice the force in the distal end.

Fig. 8.

Display of tendon force distribution along the channel when DCM is bent and unbent

E. Experiments with the External Tip Force and External Force on the DCM Body

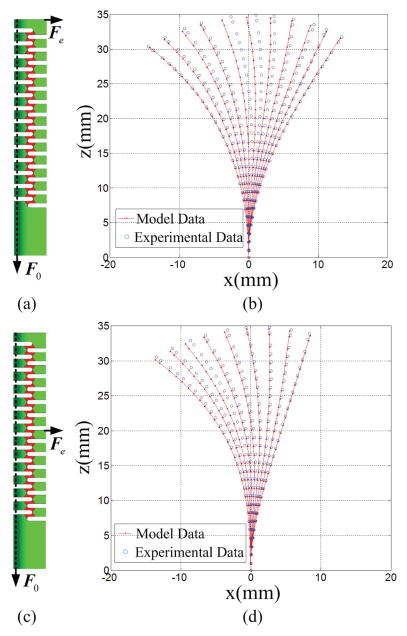
We performed the experiments incorporating an external force. The weight, 50g, was hung from the tip of the DCM (Fig. 9(a)). The tendon was pulled from 0N to 10N five times in 1N increments. Results are shown in Fig. 9(b). The total mean error was 0.75±0.42mm. The weight, 100g, was hung from the 7-th flexible link (Fig. 9(c)); the weight application was at the point q_E15, which can be transformed to the neutral axis of flexible link at Point Q defined in Fig. 3(b). Since the force was applied to the beam body, Eq. 5 was considered to reflect this additional force. In the experiment, the tendon force varied from 0N to 8N in 1N increments five times (Fig. 9(d)). The total mean error was 0.83±0.44mm.

Fig. 9.

Shape comparison between the model data and experimental data with the external tip force: (a) & (c) show the applied force; (b) & (d) show the shape comparison.

VI. Discussion

A. Sources of Error

Results in Section V show that the proposed model can predict the shape of the DCM with high accuracy. The model was relatively accurate for all three scenarios discussed in Section V. The following describes some of the main sources of error:

1. The friction model utilizing Coulomb friction assumes that the coefficient of static friction equals that of kinetic friction μ_c; this has shown good accuracy when predicting the deformation, but is still not accurate enough to describe the real situation. Advanced friction models, such as the Dahl or LuGre models [21], show the potential to describe the friction more accurately.

2. The assumption that the friction coefficient between the sharp corner and cable is the same at each contact point is not appropriate due to possible inconsistent contact conditions resulting in different μ_c at contact points. Ideally, friction would be reduced as much as possible using a PTFE-coated cable or potential ultrasonic vibration technology [22].

3. The wider discrepancy between model and experimental data in some cases when the DCM is subject to a tip force (Fig. 9(b)) may result from the tendon-channel gap. This gap changes the contact conditions and relative angles, β_2i+1 and β_2i+2 (Fig. 5(b)), between the tendon and the rigid link, especially in the almost straight configuration. This, in turn, impacts the propagation of tendon force from the tip to the base, therefore leading to the inaccurate deformation of the entire DCM. One potential solution is to use a larger diameter cable decreasing the tendon-channel gap; however, such a cable must remain flexible enough to bend with the DCM.

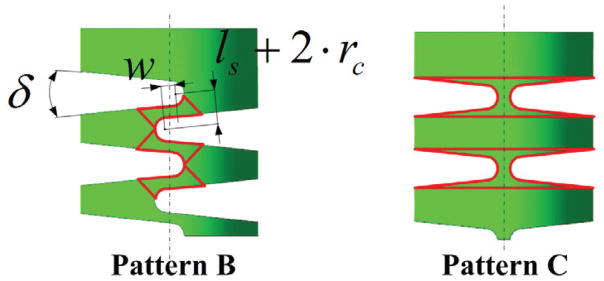
B. Variation of Notches

The partition approach and mechanical model in this paper are also suitable for other compliant joints such as pattern B & C shown in Fig. 10. Pattern B is with more general compliant joints created by the adjacent crossed and angular notches; while Pattern C is the one transformed from Pattern B by moving the left notches to the left of centerline and the right notches to the upper right when decreasing w and l_s. Both of the patterns can also be analyzed by the partition method and mechanical model proposed in Section III–IV. The partitioned rigid and flexible links are shown in Fig. 10. In addition, the calibration approach in Section V can also be adopted to derive the equivalent Young’s modulus and friction coefficient.

Fig. 10.

Variation of notches: Pattern B shows the DCM cut off by the cross angular notch; Pattern C shows the DCM cut off by the uncrossed and symmetrical V-shaped notch.

VII. Conclusion

The paper proposed an effective partition approach and derived a mechanical model of any tendon driven notched DCM with compliant joints. This model predicted the deformation of the DCM in the presence of the tendon force, external tip force, and the body force and/or combinations therein. It also shows the potential to describe the DCM with varying notches.

The comparison of experiments and simulations showed that the model can predict the shape of the DCM accurately during free bending/unbending and loaded bending/unbending cycles. Results indicated that the mean tip error of all the experiments was 0.62±0.41mm, about 1.77±1.17% of the total manipulator length. The model and its simulation results enabled an explanation of the hysteresis. The effect of varying friction coefficients was also discussed and evaluated.

The model developed in this paper can be used to design or optimize the DCM and/or associated similar tools. It can be used for model-based external force prediction based on intrinsic force sensing technology and control of the DCM with compliant joints. Also, the effects from the friction force can also be compensated for in the control algorithm.

Fig. 6.

Experimental Setup: DCM, CMOS camera, linear sliding stage was fixed to the optical table to avoid the vibration; the tendon was fixed to the force sensor and then actuated gradually to keep the quasi-static scenario.

Biographies

Anzhu Gao received the B.S., M.S. degrees in mechatronics engineering from Harbin Institute of Technology in China, in 2009, 2011, respectively. He worked as an engineer from 2011 to 2013. He is currently a Ph.D. student at the Shenyang Institute of Automation, State Key Laboratory of Robotics, Chinese Academy of Sciences, and also University of Chinese Academy of Science. He worked as a visiting student with the Laboratory for Computational Sensing and Robotics from 2014~2015. His research interests include medical robots, continuum robots.

Ryan J. Murphy received the Ph.D. degree in mechanical engineering from Johns Hopkins University, in 2015. He is currently with the Biomechanical- and Image-Guided Surgical Systems Laboratory, part of the Laboratory for Computational Sensing and Robotics. He is also a Senior Professional Staff Member with the Johns Hopkins University Applied Physics Laboratory, Laurel, MD. His research interests include medical robots, robot and computer-assisted surgery, robot kinematics and dynamics, systems and software engineering, and biomechanics.

Hao Liu received the B.S., M.S., and Ph.D. degrees in mechanical engineering from the Harbin Institute of Technology in China, in 2004, 2006, and 2010, respectively. He is currently an Associate Professor with the Shenyang Institute of Automation, Chinese Academy of Sciences. His research interests include surgical robots, medical sensors, surgical navigation, and robot control.

Iulian Iordachita (M’08–SM’14) received the B.Eng. degree in mechanical engineering, the M.Eng. degree in industrial robotics, and the Ph.D. degree in mechanical engineering from the University of Craiova, Romania, in 1984, 1989, and 1996, respectively. He is currently a Research Faculty Member with the Mechanical Engineering Department, Whiting School of Engineering, Johns Hopkins University, a Faculty Member with the Laboratory for Computational Sensing and Robotics, and the Director of the Advanced Medical Instrumentation and Robotics Research Laboratory. His current research interests include medical robotics, image guided surgery, robotics, smart surgical tools, and medical instrumentation.

Mehran Armand received the Ph.D. degree in mechanical engineering and the Ph.D. degree in kinesiology from the University of Waterloo, ON, Canada, with a focus on bipedal locomotion. He is currently a Principal Scientist and holds joint appointments with Mechanical Engineering and Orthopaedic Surgery. Prior to joining JHU/APL in 2000, he completed postdoctoral fellowships at JHU Orthopaedic Surgery and Otolaryngology-head and neck surgery. He currently directs the collaborative Laboratory for Biomechanical and Image-Guided Surgical Systems, Laboratory for Computational Sensing and Robotics, JHU/Whiting School of Engineering.