A modified risk set approach to biomarker evaluation studies

Summary

There is tremendous scientific and medical interest in the use of biomarkers to better facilitate medical decision making. In this article, we present a simple framework for assessing the predictive ability of a biomarker. The methodology requires use of techniques from a subfield of survival analysis termed semicompeting risks; results are presented to make the article self-contained. As we show in the article, one natural interpretation of semicompeting risks model is in terms of modifying the classical risk set approach to survival analysis that is more germane to medical decision making. A crucial parameter for evaluating biomarkers is the predictive hazard ratio, which is different from the usual hazard ratio from Cox regression models for right-censored data. This quantity will be defined; its estimation, inference and adjustment for covariates will be discussed. Aspects of causal inference related to these procedures will also be described. The methodology is illustrated with an evaluation of serum albumin in terms of predicting death in patients with primary biliary cirrhosis.

1. Introduction

Recently, the use of biomarkers has been strongly advocated for in clinical research (Pepe et al., 2001; Biomarkers Working Group, 2001). The promise of biomarkers is that their measurement can be used to develop better patient management procedures during the medical decision-making process. This is related to the use of biomarkers as surrogate endpoints for medical studies. Surrogate endpoints are proposed based on biological considerations within a progression model of disease. One example is CD4 count levels in AIDS; the CD4 count can potentially serve as a surrogate endpoint for death. Another example from cancer studies is using tumor shrinkage as a surrogate endpoint for survival or disease-free survival. We note that the ultimate goal of surrogate endpoints is to have an outcome measure that is strongly predictive of the true clinical endpoint that can also be clinically actionable.

The viewpoint taken in this paper is that the biomarker will be used clinically to trigger further decisions in practice. As an example, consider prostate cancer. Typically, prostate-specific antigen (PSA) has been used for detection of prostate cancer. If a man has a PSA measurement between 4 and 10 ng/mL, then this leads to a prostate needle biopsy. If the biopsy is positive for prostate cancer, the patient either undergoes surgical removal of the prostate (radical prostatectomy) or is monitored periodically for elevations in PSA (watchful waiting). Thus, the PSA measurement being thresholded at 4 ng/mL is often used to trigger a medical intervention. While PSA is known for being a relatively sensitive biomarker, it is not known as being a very specific measurement. As a result, many biopsies yield negative results for tumor, even when the PSA is between 4–10 ng/mL.

In many applications, associations between biomarker and a outcome is typically assessed through regression models. Here and in the sequel, we will focus on the response variable being a time to event that is potentially subject to right censoring. One commonly used model is the proportional hazards model (Cox, 1972; Gail et al., 1981). There are many studies in which univariate and possibly multivariate PH regression models are fit in which one of the covariates is the biomarker of interest.

The approach we take in this paper is to treat the time at which biomarker positivity occurs as a time to event such as that commonly used in the area of survival analysis. We then wish to study the association between the time to biomarker positivity and the time to the clinical endpoint of interest. We formulate the observed data as data structure that we term semi-competing risks data (Fine et al., 2001; Ghosh, 2006, 2009; Ghosh et al., 2012). Based on this framework, we define a quantity known as the predictive hazard ratio (Bryant et al., 1997). They argued eloquently for its use in assessing the dependence between time to a landmark event with time to a clinical endpoint. The predictive hazards ratio is quite compatible with the semi-competing risks data structure. One of its crucial features is that the region of interest is when the time to biomarker positivity occurs before the important clinical event. From our view, use of the predictive hazard ratio has several appealing features:

1. It utilizes a risk set structure based on the notion of biomarker positivity. We define this concept in Section 2.2. Such a concept is consistent with the binary way in which clinicians use biomarkers.

2. There exists a well-established theory and asymptotic results to provide inference about the predictive hazard ratio.

3. The predictive hazard ratio is very flexible in adjusting for covariates.

The structure of this paper is as follows. In Section 2, we review the data structures as well as semi-competing risks data. The proposed methodology is described in Section 3. We illustrate the application of the methodology with application to data from a primary biliary cirrhosis study in Section 4. Finally, the paper concludes with discussion in Section 5.

2. Preliminaries and Background

2.1. Data Structures and Limitations of Standard Analyses

We start by making the following definitions. Let a ∧ b denote the minimum of two numbers a and b. Define I(A) to be the indicator function for the event A. Let T be the time to a clinical event and C time to independent censoring. Let Z(t) be the longitudinal process for the biomarker. We will use boldface when we wish to use the full biomarker process up to time t, and Z(t) to denote the value of the biomarker at time t. We observe the data $\{Y_i,{\delta }_i^Y,(Z_i(t);t\le Y_i)\}$, i = 1, …, n, n independent and identically distributed observations from {Y, δ^Y, Z_i(·)}, where Y = T ∧ C and δ^Y = I(T ≤ C).

A standard analysis that is done here is to typically model the event time using a time-dependent regression model, such as the Cox proportional hazards with time-dependent covariates (Gail et al., 1981):

$$\lambda (t|\mathbf{Z}(s):0\le s\le t)={\lambda }_0(t)\text{ exp}\{\beta Z(t)\},$$ (1)

where λ₀(t) denotes the baseline hazard function, and β represents the parametric regression co-efficient. Estimation in such a model can be done using the partial likelihood, which in standard in many software packages. While there exist asymptotic results to guide the user in terms of estimation and inference for the estimates of the parameters in the Cox model, we can argue as in Pepe et al. (2006) that measures of association in a survival regression do not convey appropriate information about biomarker utility in terms of classification or prediction.

2.2. Risk Set and clinical relevance

In the Cox model (1) described in the previous section, the full covariate process is used as predictor variables. Estimation of β proceeds by comparing the biomarker value for the individuals who have the event relative to the biomarker value for individuals that are at risk for having the event. This is calculated and summed at all observed event times, and the value of β that solves the estimating equation corresponding to (1) is the estimated hazard ratio.

For the purposes of biomarker evaluation in the medical decision making setting, adopting a landmark approach has a lot of appeal. By this, we mean that individuals should be considered at risk only if their biomarker exceeds a threshold. For example, in the prostate cancer setting, patients are flagged for further biopsy when their PSA levels exceeds 4 ng/ML. We define the event of the biomarker exceeding a threshold as biomarker positivity. Thus, we simply convert the covariate process Z(t) into another failure time variable X (possibly censored) based on a positivity criterion. Hence, the observed data become $(X_i,{\delta }_i^X,Y_i,{\delta }_i^Y)$, i = 1, …, n, n independent and identically distributed observations from (X, δ^X, Y, δ^Y), where X = S ∧ T ∧ C, δ^X = I(S ≤ T ∧ C), Y = T ∧ C and δ^Y = I(T ≤ C).

The proposed framework defines a new random variable S that is the time to biomarker positivity. Note that we have censored S, the time of biomarker positivity, by the minimum of T and C and not just by C. From the biomarker point of view, it is of no use if S is larger than T. In this instance, the biomarker becoming positive will occur after the clinically relevant event does, so its being positive provides no practical utility in aiding the management of the patient. In addition, in most clinical settings, the biomarker becoming positive will trigger some type of medical intervention. This suggests that the region of practical interest for the joint distribution of (S, T) occurs when S < T. This is what was argued in Bryant et al. (1997). This type of data is called semi-competing risks data because of the inherent asymmetry in the dependence and censoring structures for S and T.

To summarize the effect of the biomarker, we will use what Bryant et al. (1997) term the predictive hazard ratio. The model being assumed is that of Clayton (1978) and Oakes (1982) and can be formulated as the following:

$$\theta =\frac{{\lambda }_T(t|S=s)}{{\lambda }_T(t|S\ge s)},$$ (2)

where ${\lambda }_T(t|A)={\text{lim}}_{\mathrm{\Delta }t\to 0}\frac{d}{dt}\mathit{\text{Pr}}(T<t+\mathrm{\Delta }t|T\ge t,S\in A)$, and A is a subset of the interval (0, ∞). The right-hand side of (2) is the predictive hazard ratio and depends on both s and t. However, the left-hand side does not.

There will be uncountably infinite joint distributions for (S, T) that are consistent with the model (2). One trivial example is to assume the model for the entire joint distribution of (S, T). We discuss possible conceptual problems with this approach within a causal framework in §3.3.

Note that model (2) also enjoys a risk set interpretation. However, we have defined ‘at-risk’ in a manner that is completely different from the notion for model (1). Now we are comparing times of the event for individuals whose are biomarker positive at time s relative to those who are not yet biomarker positive. This modification of the risk set naturally falls into a bivariate survival model framework, and model (2) provides one such model. Because we want the event of the biomarker being positive to occur before the actual event, we focus on the wedge region S < T. An appeal of the proposed methodology is the fact that the biomarker positivity event, being binary, will correspond to how clinicians use biomarker measurements in practice.

To estimate θ, we follow the approach of Fine et al. (2001). They provided a closed form estimator of θ using modified weighted concordance estimating functions from Oakes (1982, 1986) along with an asymptotic variance estimator. For i = 1, …, n and j = 1, …, n, define X̃_ij = X_i ∧ X_j, Ỹ_ij = Y_i ∧ Y_j, C̃_ij = C_i ∧ C_j and D_ij = I(X̃_ij < Ỹ_ij < C̃_ij). Fine et al. (2001) proposed the following closed-form estimator for θ:

$$\hat{\theta }=\frac{{\sum }_{i<j}W({\tilde{X}}_{ij},{Ỹ}_{ij})D_{ij}{\mathrm{\Delta }}_{ij}}{{\sum }_{i<j}W({\tilde{X}}_{ij},{Ỹ}_{ij})D_{ij}(1-{\mathrm{\Delta }}_{ij})},$$

where W(u, v) is a weight function that converges uniformly to w(u, v), a bounded deterministic function, and Δ_ij = I{(X_i − X_j)(Y_i − Y_j) > 0}, i, j = 1, …, n. They also prove the consistency and asymptotic normality of θ̂ using a combination of U-statistic theory. Here and in the sequel, we will take the weight function to be unity.

The variances for the limiting distribution of these random variables are fairly complicated. Here, we will use a resampling method proposed by Jin, Ying and Wei (2001) and used in Ghosh (2009). The algorithm proceeds as follows:

1. We generate n Exponential random variables (G₁, …, G_n) and calculate θ̂*, where

   $${\hat{\theta }}^{*}=\frac{{\sum }_{i<j}{D}_{ij}{\mathrm{\Delta }}_{ij}{G}_i{G}_j}{{\sum }_{i<j}{D}_{ij}(1-{\mathrm{\Delta }}_{ij})G_i{G}_j},$$

2. Repeat step 1 M times.

3. Estimate the variance of θ̂ based on the empirical variance of θ̂*.

This resampling procedure is quite fast. In practice, we usually take M = 1000. It is very similar in concept to the bootstrap (Efron and Tibshirani, 1986). In terms of theoretical justification, it can be proven using arguments as in Ghosh (2009) that the conditional distribution of θ̂* − θ̂ given the detail is asymptotically the same as the unconditional distribution of θ̂ − θ. This result formally justifies the use of the resampling algorithm described above.

Remark

As pointed out by a referee, the focus on biomarker positivity does not address the issue of the biomarker being negative and that being an important indicator of the event not happening. We can adapt the methods by defining the event time to be the largest time when the biomarker does not exceed the threshold, have δ^X = 1 and define δ^Y to be one minus the observed event indicator for T.

2.3. Related Work

In this proposal, we have used a redefinition of the risk set in order to develop methods for evaluating the efficacy of a biomarker. There is related literature in this area by authors who have used receiver operating characteristic curves with survival data for evaluating biomarkers (e.g., Heagerty et al., 2000; Heagerty and Zheng, 2005; Saha and Heagerty, 2010; Zheng et al., 2012).

Before describing these proposals, we define ROC curves in the case of a binary disease status D that takes values of zero for control (not diseased) and one for case (diseased). Assume that higher values of the biomarker correspond to a greater probability of having disease. Define the false positive rate based on a cutoff c to be FP(c) = P(Z(t) > c|D = 0), and the true positive rate is TP(c) = P(Z(t) > c|D = 1). Note that we have suppressed dependence of FP(c) and TP(c) on t. The true and false positive rates can be summarized by the receiver operating characteristic (ROC) curve, which is a graphical presentation of {TP(c), FP(c) : −∞ < c < ∞}. The ROC curve shows the tradeoff between increasing true positive and false positive rates. Tests that are have {TP(c), FP(c)} values close to (0,1) indicate perfect discriminators, while those with {TP(c), FP(c)} values close to the 45° degree (diagonal) line in the (0, 1) × (0, 1) plane are tests that are unable to discriminate between the D = 0 and D = 1 populations.

In the case of disease status being an event time, there are choices as to how to define cases and controls. Heagerty and Zheng (2005) define several schemes using the counting process N(t) = I(T ≤ t). One group focuses on define cases cumulatively versus in an incident manner. For the true positive rate, this would correspond to P(Z(t) > c|N(t) = 1) versus P(Z(t) > c|dN(t) = 1), respectively. There is also the issue of what time point to use in the conditioning event; this corresponds to the static versus dynamic classification that described in Heagerty and Zheng (2005). A more recent extension by Saha and Heagerty (2010) incorporates various types of competing risk events and develops extensions based on new definitions of being at risk for events. Zheng et al. (2012) have taken the methodology of Saha and Heagerty (2010) and developed modelling procedures based on the induced prognostic accuracy measures.

All of these proposals evaluate the biomarker conditional on disease status. By contrast, our approach using (2) can be viewed as a model for

$$\frac{P\{dN(t)=1|Z(t)>c\}}{P\{dN(t)=1|\mathbf{Z}(s)<c:0\le s\le t\}}$$ (3)

so that our approach can be thought of as prospective rather than the retrospective approach that the ROC-based proposals take. In addition, there is a very different concept of at-risk relative to what has been described in this section. If we apply Bayes rule, we see that (3) is equal to

$$\frac{P(Z(t)>c|dN(t)=1)}{{\int }_0^{t}P(Z(u)>c|dN(u)=1)f_{Z(s)}(u)du}$$

The numerator is the incident true positive rate in the sense of Heagerty and Zheng (2005), but the denominator is a complicated integral that is a function of the one minus incident true positive rate as well as the trajectory of the biomarker process. This is substantially different than the ROC-based methods described in the section.

3. Proposed Methodology

3.1 Biomarker Evauation

As alluded to in Section 2, we convert the problem of biomarker evaluation into one of estimating the predictive hazard ratio. We will assume throughout the paper that positivity occurs when the biomarker reaches above a cutoff value c. Define S as the time to this event. We then create the bivariate survival dataset as described in Section 2.2 and calculate the estimate of θ ≡ θ(c) as well as the associated 95% confidence intervals. We then vary the values of c and plot the estimates of the dependence parameter and the associated 95% CI. This then provides a useful method of presenting results on the discriminative ability of the biomarker. In particular, one might consider regions of the plot in which θ̂ is highest. If there is no such region, then this suggests that the choice of biomarker cutoff has minimal effect on its predictive power. A related inferential problem is that one might wish to see if the biomarker predicts better than ‘random chance.’ Within our framework, this corresponds to testing H₀ : θ = 1 and can be done by checking if the associated confidence interval contains 1 or not.

It should also be noted that the event time S can be defined in many ways. One way is to define it as the time to a biomarker above a cutoff. However, it could also be defined based on multiple biomarker measurements or a statistic thereof. For example, one could calculate some type of moving average and define S to be the time at which the moving average is above a certain cutoff. Alternatively, one could calculate a slope based on a moving window of measurements and determine S based on time to when the slope is above a cutoff. The proposed framework is quite flexible in how the biomarker gets utilized to calculate the value of S.

If we examine the structure of the model in Section 2.2., we see that it has a connection to a conditional version of the C-index (Harrell et al., 1996). This is a measure of predictive accuracy that is commonly used for evaluating predictions from survival models, and its connection to time-dependent ROC curves has been established in Section 2.4. of Heagerty and Zheng (2005). It can be shown for (2), we have the following relationship:

$$P((X_i-X_j)(Y_i-Y_j)>0|{\tilde{X}}_{ij}\le {Ỹ}_{ij})=\frac{\theta }{2(1+\theta )}.$$ (4)

The original C-index proposal of Harrell et al. (1996) examines concordance of predicted values with observed values. It is also a rank-invariant measure. For our setting, S plays the role of the prediction, and we are assessing its concordance with T in the presence of dependent censoring. This is in fact the relationship that motivates the estimator in Fine et al. (2001). In (4), the left-hand side is a conditional version of the C-index that respects the constraint S ≤ T. This reinforces the idea that there is a prediction interpretation to the model (2) that is being used here.

3.2 Covariate Adjustment

In many scientific settings, the distribution of the biomarker will depend on other covariates, such as gender, race and other confounding factors. Thus, it is important to be able to adjust for covariates in the analysis.

The issue of covariate adjustment becomes quite complex in the current modelling framework. There are many possible ways in which covariates can affect the joint distribution of (S, T). First, the distribution of the biomarker can depend on other variables. Examples of such variables would include age and gender. In this scenario, one would formulate models for the distribution of Z(t) conditional on covariates; examples of such models include linear mixed-effects models (Laird and Ware, 1982). Based on the fitted values from such a model, we then define S based on a covariate-adjusted biomarker positivity criterion and apply the methods as described before. Such an approach is quite straightforward to implement.

One concern then becomes that the variability in the covariate-adjusted dependence parameter estimate comes from two sources: (a) the variance in the estimate of the biomarker covariate adjustment model; (b) the variance in the dependence parameter estimate. There are two modes of inference we can employ. The first is termed conditional and ignores step (a) in the variability estimation. For this approach the standard error calculation described in §2.2. is sufficient; this is what is used in the examples presented in §4. The other mode of inference is unconditional and attempts to incorporate both sources of variability from (a) and (b). We can use the nonparametric bootstrap, repeat the two-stage estimation process, and use the bootstrapped empirical distribution of the dependence parameter estimators to calculate variance estimates and construct confidence intervals. Such an approach will lead to wider confidence intervals relative to those shown in Figures 2 and 3.

An alternative method of covariate adjustment is to assume that the predictive hazard ratio depends on covariates. If one assumes that the variables being considered are effect modifiers of the predictive hazard ratio so that the association between biomarker positivity and the event of interest depends on the combination of variables, then one could compute stratum-specific predictive hazard ratio estimators, where the strata are defined by the combination of covariate levels.

4. Numerical Example: PBC data

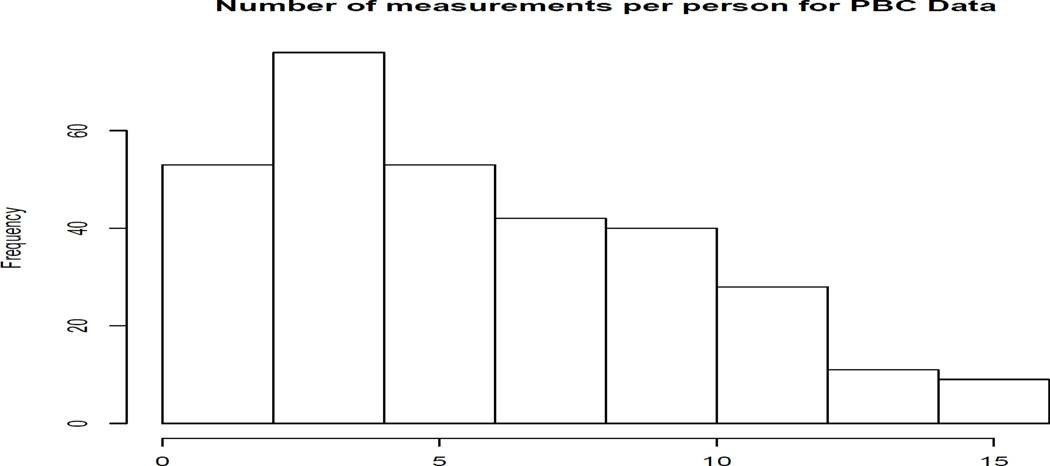
The data we consider in this paper are from a famous primary biliary cirrhosis study that is available as an appendix in Fleming and Harrington (1991). We work with an extended version of the dataset that was analyzed by Murtaugh et al. (1994). These data involve repeated visits by the patients who were diagnosed with PBC and seen at the Mayo Clinic between January 1974 and May 1984. In particular, there are 312 subjects generating a total of 1945 measurements. The distribution of visits per person can be found in Figure 1. In Murtaugh et al. (1994), the goal of the study was twofold. One was to update the Mayo model for predicting survival in subjects with PBC using repeated measurements. The model consists of the following variables: age, bilirubin, prothrombin time, albumin and edema. To illustrate the procedures developed here, we will focus on bilirubin, which is a biochemical measurement indicative of liver activity.

As in prior analyses of these data, we will transform the albumin measurements to a log scale in order to reduce skewness. If we fit a proportional hazards model using only the albumin measurement at baseline, then the log hazard ratio is 5.4, with an associated standard error of 0.6. This yields a statistic that is strongly associated with risk of death (p-value < 2 × 10⁻¹⁶). Next, we consider a time-dependent PH model with log(albumin) as the covariate. It turns out that the estimated log hazard ratio does not change much from before, but the standard error is reduced to 0.33. As suggested by the arguments of Pepe et al. (2006), such a strong association does not necessarily mean that albumin is useful for prediction purposes.

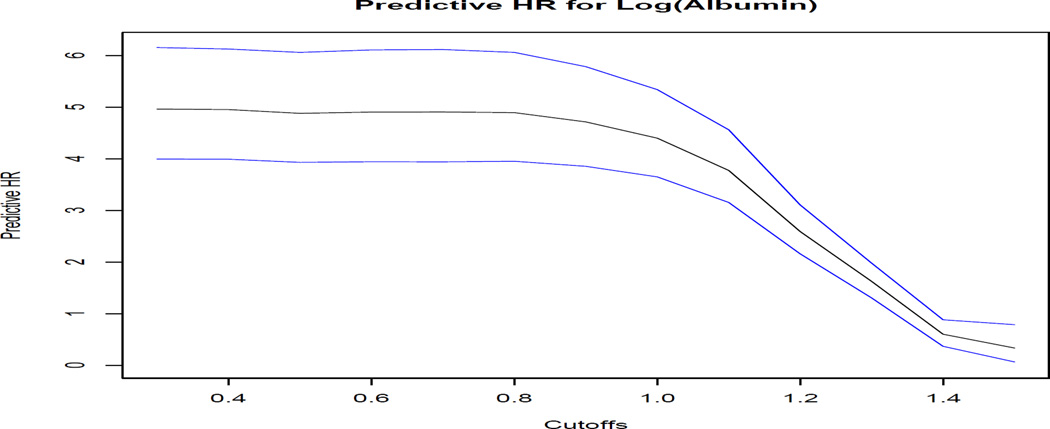
The results of the predictive hazard ratio along with the associated 95% pointwise CIs are provided in Figure 2 below.

Based on the plot, we find that there is a noticeable decrease in the predictive hazard ratio corresponding a cutoff of one for albumin on the natural logartihm scale. Also, we see that the predictive hazard ratio is smaller for all cutoff values considered relative to the regression coefficients from the proportional hazards models that we previously fit. In particular, for cutoff values around 1.4, albumin has no predictive value, which contrasts with the seemingly large hazard ratios provided by the Cox proportional hazards analyses. This is consistent with the argument by Pepe et al. (2006) that strong regression coefficients do not immediately imply strong prediction performance.

Next, we consider adjustment with covariates. We refer back to the Mayo model studied in Murtagh et al. (1994) and consider adjustment of albumin for other covariates from that model. Next, we fit a linear model regressing albumin on a logarithmic scale as a function of age at baseline, gender, edema, prothrombin time and bilirubin. The latter two covariates are log-transformed. This leads to the following regression equation for albumin:

$$\text{log}(\widehat{\text{Albumin}})=2.01-0.001\text{Age}-0.03\text{Female}-0.276\text{log}(\text{Protime})-0.11\text{Edema}-0.049\text{log}(\text{Bili}).$$

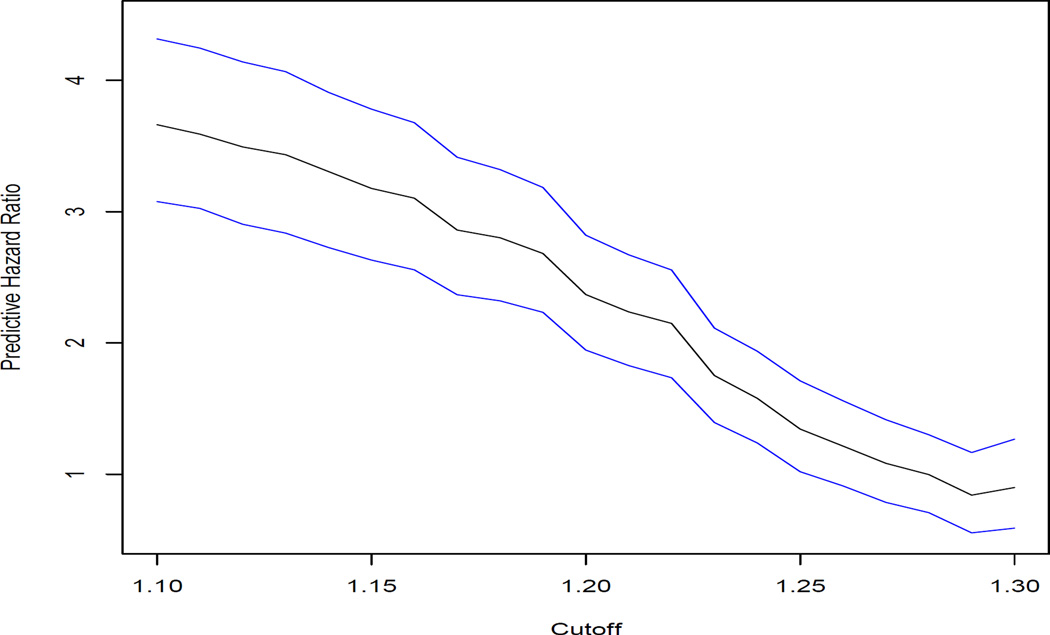
If we adjust albumin using this regression equation and compute the predictive hazard ratio, the results are presented in Figure 3. The shape of the curve is different from that for unadjusted albumin in Figure 2. There is no cutoff at which the curve has a steep decrease relative to that in Figure 2.

We again see that the predictive hazard ratio estimates are smaller than from the Cox proportional hazards model that was initially fit. For cutoff values of 1.2 or greater, we again find that the predictive hazard ratio is consistent with the null hypothesis of no association. This suggests less strength of evidence for the use of albumin in a medical decision making context than what is suggested by the proportional hazards model.

5. Discussion

For the evaluation of biomarkers, it is necessary to consider prediction performance. In this article, we have presented a simple approach to prediction assesment of biomarker rules using dependent censoring methodology from survival analysis. The methodology is quite easy to implement, and code implementing the predictive hazard ratio estimation can be downloaded as supplementary material. One appealing feature is that the proposed methodology has an interpretation in terms of predictive ability.

One limitation of the methodology is that it requires fairly intensively collected longitudinal biomarker measurements in order to define S. In the motivating dataset, measurements were intended to be collected annually. There were several assumptions in the methodology. First, there biomarker was not assumed to go above the cutoff between visits. If that were the case, then S then becomes considered as current status data, because the tumor measurement is made only at six months. Thus, the information available about S here is whether or not it occurred before six months. Development of semi-competing risks procedures in such a framework is quite challenging and beyond the scope of the current article. Another issue is incorporating multiple biomarkers. A simple approach would be to develop a risk score that is a one-dimensional summary of the measurements and to then apply the methodology in this paper. However, there may exist more powerful methods of modelling multiple biomarkers. A third issue is that biomarkers might be subject to measurement error or truncation due to assay limits, and extending the methodology proposed in this paper to handle that situation is important.

A crucial point that has not been discussed in the paper is the choice of cutoff value for c. The example in the paper illustrated that for certain cutoff values, we would fail to reject the null hypothesis of no association between albumin positivity and death, either unadjusted or adjusted for covariates. In practice, the choice of cutoff depends on the relative costs of making mistakes, namely false positives and false negatives. Gail and Pfeiffer (2005) have developed a decision-theoretic framework based on the ROC curves in the screening context, and it would be useful to see if their methodology is extendible to the current setting. Finally, in many settings, longitudinal serum or tissue samples have been collected prospectively in many studies. This allows for the use of nested case-control designs for assessing the discriminative ability of biomarkers (Baker et al., 2002). Conceptually, this involves following subjects prospectively in order to determine disease status; based on the disease status, the distribution of biomarkers between cases and controls are then compared. It would be of interest to extend the predictive hazard ratio to this setting as well.

There is code available for implementing the methods in this paper and for the example in Section 4. It is available at www.bepress.com/debashis_ghosh/.