Summary
Unobserved environmental, demographic and technical factors canadversely affect the estimation and testing of the effects ofprimary variables. Surrogate variable analysis, proposed to tacklethis problem, has been widely used in genomic studies. To estimatehidden factors that are correlated with the primary variables,surrogate variable analysis performs principal component analysiseither on a subset of features or on all features, but weightingeach differently. However, existing approaches may fail to identifyhidden factors that are strongly correlated with the primaryvariables, and the extra step of feature selection and weightcalculation makes the theoretical investigation of surrogatevariable analysis challenging. In this paper, we propose an improvedsurrogate variable analysis, using all measured features, that has anatural connection with restricted least squares, which allows us tostudy its theoretical properties. Simulation studies and real-dataanalysis show that the method is competitive with state-of-the-artmethods.
Keywords: Batch effect, High-dimensional data, Principal component analysis, Surrogate variable analysis
1. Introduction
In regression analysis, the existence of unobserved factors can cause biases in estimating parameters. Suppose that the true relationship in the data is
where  is a vector of outcome measurements,
is a vector of outcome measurements, 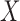 is a matrix of the observed covariates including the primary variables, and
is a matrix of the observed covariates including the primary variables, and 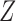 is a matrix of the unobserved factors. We are interested in estimating the regression parameter
is a matrix of the unobserved factors. We are interested in estimating the regression parameter 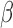 . Since
. Since  is not observed, in practice we use the misspecified model
is not observed, in practice we use the misspecified model
which can negatively impact inference on 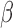 .
.
With the development of high-throughput technologies in biomedical sciences, high-dimensional data are routinely collected and analysed to find biologically meaningful features. Unobserved factors can cause adverse effects, including inflation of Type I error and/or power loss (Stegle et al., 2010). Although in practice great efforts are made to control confounders, such efforts may be insufficient to avoid all confounding issues (Leek et al., 2010).
Principal component analysis on the original or residualized features after removing the effects of observed dependent variables has often been used to identify hidden factors, and has been successful in identifying and controlling for population stratification in genome-wide association studies (Price et al., 2006). However, principal component analysis-based approaches are less effective for gene expression studies, where the hidden factors can affect a subset of features with relatively large effects (Leek & Storey, 2007). To overcome this limitation, surrogate variable analysis has been proposed (Leek & Storey, 2007, 2008; Teschendorff et al., 2011; Chakraborty et al., 2012) for microarray data. Leek & Storey (2007) initially developed a two-step approach which involves first identifying a subset of features that may be affected by hidden factors but not by primary variables, and then performing principal component analysis on the selected features. Later, they modified the approach to a weighted principal component analysis, where each feature is weighted according to its probability of being affected by the hidden factors only (Leek & Storey, 2008). Surrogate variable analysis has been extended to factor analysis (Friguet et al., 2009) and mixed-effect models (Listgarten et al., 2010). Recently, assuming that negative control genes are known, Gagnon-Bartsch & Speed (2012) proposed a surrogate variable method.
Surrogate variable analysis has been successfully applied to many genomic studies (Dumeaux et al., 2010; Teschendorff et al., 2010), but existing methods may fail to identify hidden factors. Strong correlation between hidden factors and primary variables can prevent the two-step and weighted principal component-based surrogate variable methods from identifying features that are affected by hidden factors only. If negative control genes are affected by primary variables or if the observed variation in negative control genes does not reflect unwanted variations in the entire genome, the methods for removing unwanted variation can also fail to identify true hidden factors.
In this paper, we propose a simple and straightforward method for identifying hidden factors and adjusting for their effects. Our approach, called direct surrogate variable analysis, is based on the observation that naïve estimators of the effects of the primary variables are biased when the effects of hidden factors are ignored in the analysis, but the bias can be estimated and removed using singular value decomposition on residuals. We derive the asymptotic properties of our estimators using techniques recently developed for the ultrahigh-dimensional regime (Lee et al., 2014) and the connection between our estimating procedure and the restricted least-squares method (Greene & Seaks, 1991). An R package (R Development Core Team, 2017) implementing the proposed approach, dSVA, can be downloaded from the comprehensive R archive network.
2. Methods
2.1. Direct surrogate variable analysis
Suppose that 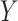 is an
is an 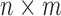 matrix of measured features, where
matrix of measured features, where 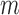 is the number of features and
is the number of features and 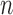 is the number of samples. For gene expression data,
is the number of samples. For gene expression data, 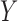 represents RNA expression levels on
represents RNA expression levels on 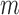 genes. Further, suppose that
genes. Further, suppose that 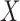 is an
is an 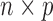 matrix of observed covariates, including an intercept, and
matrix of observed covariates, including an intercept, and 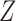 is an
is an 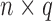 matrix of unobserved hidden factors. The following model represents the true relationship between
matrix of unobserved hidden factors. The following model represents the true relationship between 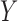 and
and 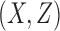 :
:
| (1) |
where 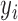 denotes the
denotes the 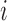 th column of
th column of 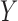 ,
, 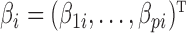 is a
is a 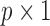 vector of regression coefficients associated with
vector of regression coefficients associated with 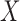 ,
, 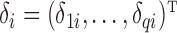 is a
is a 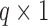 vector of regression coefficients associated with
vector of regression coefficients associated with 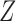 , and
, and 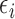 is an
is an 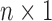 random vector which follows
random vector which follows 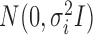 . We further define
. We further define 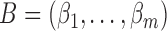 and
and 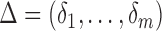 , which are
, which are 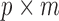 and
and 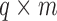 matrices of regression coefficients associated with
matrices of regression coefficients associated with 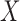 and
and 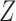 , respectively. In this model,
, respectively. In this model, 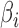 and
and 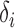 are assumed to be fixed. Later, to generate large numbers of
are assumed to be fixed. Later, to generate large numbers of 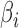 and
and 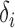 values for the simulation studies, we use a specified correlation between
values for the simulation studies, we use a specified correlation between 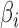 and
and 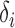 . However, we emphasize that the proposed method is frequentist:
. However, we emphasize that the proposed method is frequentist: 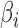 and
and 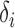 are considered fixed and unknown.
are considered fixed and unknown.
In practice, since 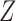 is not observed, we effectively use the misspecified model
is not observed, we effectively use the misspecified model
| (2) |
instead of (1). Under (2), the least-squares estimator of 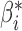 is
is
| (3) |
with residual vector
| (4) |
where 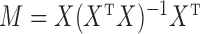 is the projection matrix onto the column space of
is the projection matrix onto the column space of 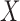 . Equations (3) and (4) indicate that
. Equations (3) and (4) indicate that 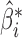 is a biased estimator of
is a biased estimator of 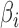 with bias
with bias 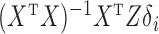 . The conditional mean of the residual vector given
. The conditional mean of the residual vector given 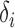 is
is 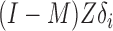 , which allows us to estimate
, which allows us to estimate 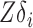 via, for example, singular value decomposition.
via, for example, singular value decomposition.
Suppose that singular value decomposition is performed on the residual matrix 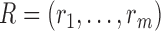 , where
, where 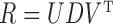 , with
, with 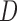 being a diagonal matrix of ordered singular values, and
being a diagonal matrix of ordered singular values, and 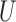 and
and 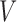 being matrices of left- and right-singular vectors. The first
being matrices of left- and right-singular vectors. The first 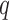 left-singular vectors can be viewed as estimators of linear combinations of the columns of
left-singular vectors can be viewed as estimators of linear combinations of the columns of 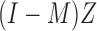 , which we denote by
, which we denote by 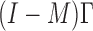 where
where 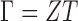 , with
, with 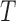 being a
being a 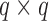 orthonormal matrix. Let
orthonormal matrix. Let 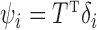 . For any
. For any 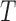 , the matrices
, the matrices 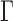 and
and 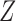 have the same column space, so
have the same column space, so 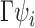 is identical to
is identical to 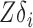 . With an additional assumption that the row vectors of
. With an additional assumption that the row vectors of 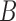 and the row vectors of
and the row vectors of 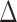 are asymptotically orthogonal after mean centring, we can estimate
are asymptotically orthogonal after mean centring, we can estimate 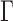 and use it to remove the bias in
and use it to remove the bias in 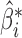 . The proposed method is as follows.
. The proposed method is as follows.
Step 1.
Carry out singular value decomposition on the residual matrix
. Let
be the matrix comprising the first
columns of
that are equivalent to the
left-singular vectors corresponding to the
largest singular values.
Step 2.
Obtain
and
from the model
. Since
and
are orthogonal to each other,
from this model equals that from model (3).
Step 3.
Let
and
. We propose to estimate the surrogate variables
as
where
is a projection matrix with
.
Step 4.
Estimate and test
from the model
(5)
This method requires estimation of  , the number of surrogate variables, which can be obtained by permutation (Buja & Eyuboglu, 1992) or by analytical-asymptotic approaches (Johnstone, 2001; Leek, 2011). In this paper, we use the method of Buja & Eyuboglu (1992) for all numerical work. Since
, the number of surrogate variables, which can be obtained by permutation (Buja & Eyuboglu, 1992) or by analytical-asymptotic approaches (Johnstone, 2001; Leek, 2011). In this paper, we use the method of Buja & Eyuboglu (1992) for all numerical work. Since 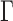 and
and 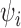 can be always rescaled, they are not identifiable, so we set
can be always rescaled, they are not identifiable, so we set 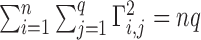 , where
, where 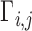 is the
is the 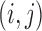 th element of
th element of  , and adjust
, and adjust  to satisfy this restriction. In the Supplementary Material we show that
to satisfy this restriction. In the Supplementary Material we show that 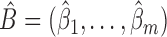 from (5) in Step 4 is the same as
from (5) in Step 4 is the same as
| (6) |
in which 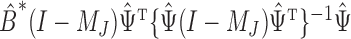 is an estimate of the bias of the naïve estimator
is an estimate of the bias of the naïve estimator 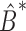 . In § 2.3, we show that (6) is related to the restricted least-squares method.
. In § 2.3, we show that (6) is related to the restricted least-squares method.
2.2. Consistency of the proposed estimators
Important questions are under what conditions does the proposed 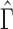 span the same column space as
span the same column space as 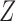 , and whether
, and whether 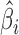 is a consistent estimator of
is a consistent estimator of 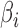 . For high-dimensional data, the number of features,
. For high-dimensional data, the number of features, 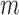 , can be substantially larger than the number of samples,
, can be substantially larger than the number of samples, 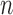 , and thus asymptotic results derived from the traditional low-dimensional setting where
, and thus asymptotic results derived from the traditional low-dimensional setting where 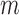 is fixed are inappropriate (Johnstone & Lu, 2009; Jung & Marron, 2009; Lee et al., 2010). Lee et al. (2014) considered a regime in which both
is fixed are inappropriate (Johnstone & Lu, 2009; Jung & Marron, 2009; Lee et al., 2010). Lee et al. (2014) considered a regime in which both  and
and 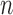 increase to infinity with
increase to infinity with 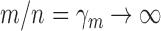 . This regime is well-suited to high-throughput biomedical data, where the number of genes is in the tens of thousands and the number of samples is in the range of several dozens to hundreds. We work in this regime and investigate the asymptotic properties of the proposed method under the spiked-eigenvalue model of Johnstone (2001).
. This regime is well-suited to high-throughput biomedical data, where the number of genes is in the tens of thousands and the number of samples is in the range of several dozens to hundreds. We work in this regime and investigate the asymptotic properties of the proposed method under the spiked-eigenvalue model of Johnstone (2001).
Before presenting our main results, let us define some additional notation. Suppose that 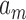 and
and 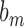 are two sequences. We write
are two sequences. We write 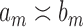 if
if 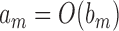 and
and 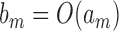 , and write
, and write 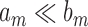 if
if 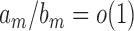 . We also define
. We also define 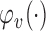 to be the function that returns the
to be the function that returns the 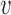 th largest singular value of an input matrix. Without loss of generality we assume that
th largest singular value of an input matrix. Without loss of generality we assume that 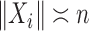 and
and 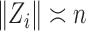 , where
, where 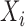 and
and 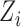 are the
are the 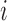 th columns of
th columns of 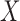 and
and 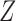 , respectively, and
, respectively, and  is the vector norm. We introduce the following conditions.
is the vector norm. We introduce the following conditions.
Condition 1.
Both
and
increase to
with
.
Condition 2.
Let
, where
. Then
,
, and
for
.
Condition 3.
Let
, where
is the standard deviation of
and
. Then either of the following is satisfied: (i)
; or (ii)
,
and
.
Condition 4.
Let
be the matrix with
columns formed by concatenating
and
. Then
is nonsingular with
and
.
Condition 5.
Suppose that
and
are the
th elements of
and
, respectively, and that
and
. For all
,
Condition 2 assumes the spiked-eigenvalue model (Johnstone, 2001), which ensures that the effects of hidden factors are large enough to be identified by singular value decomposition. Condition 3 comprises the sphericity conditions on nonspiked singular values (Lee et al., 2014). The relative growth rates of 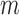 and
and 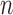 play a key role in this condition. For example, when
play a key role in this condition. For example, when 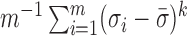 is greater than zero,
is greater than zero, 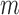 must grow at a faster rate than
must grow at a faster rate than 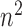 to satisfy the first condition in Condition 3. The second part of Condition 3 relaxes the assumption on
to satisfy the first condition in Condition 3. The second part of Condition 3 relaxes the assumption on 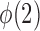 but adds an assumption on
but adds an assumption on 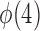 . Condition 5 requires that the row vectors of
. Condition 5 requires that the row vectors of 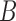 and the row vectors of
and the row vectors of 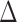 be asymptotically orthogonal after mean centring.
be asymptotically orthogonal after mean centring.
Theorem 1.
Suppose that Conditions 1–5 are satisfied. Then the columns of
span the same column space as the columns of
with probability
, and
for
.
Theorem 1 shows that the proposed method produces consistent estimates of 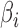 and the hidden factors. The proof can be found in the Supplementary Material.
and the hidden factors. The proof can be found in the Supplementary Material.
2.3. Relationship to the restricted least-squares method
We now show the connection between the proposed method and the restricted least-squares procedure of Greene & Seaks (1991). Suppose that 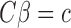 is a linear restriction on
is a linear restriction on 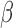 . The restricted least-squares estimator
. The restricted least-squares estimator 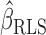 of
of 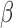 is the solution of
is the solution of
It can be shown that 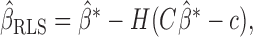 where
where 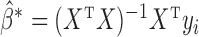 is the ordinary least-squares estimator and
is the ordinary least-squares estimator and  .
.
When estimating  , we impose a restriction on
, we impose a restriction on  and
and  , and hence on
, and hence on 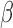 and
and 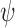 , such that they are asymptotically orthogonal after mean centring. While this is not a linear restriction as in the restricted least-squares procedure, the similarity of the two approaches can be illustrated as follows. Let
, such that they are asymptotically orthogonal after mean centring. While this is not a linear restriction as in the restricted least-squares procedure, the similarity of the two approaches can be illustrated as follows. Let 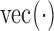 be a function on a matrix which stacks the columns of the matrix into one long vector. Then model (2) for all
be a function on a matrix which stacks the columns of the matrix into one long vector. Then model (2) for all  features can be re-expressed as
features can be re-expressed as
where 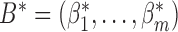 ,
, 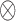 is the Kronecker product, and
is the Kronecker product, and 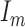 is the
is the 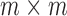 identity matrix. We further define
identity matrix. We further define 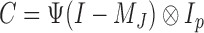 and
and 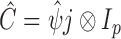 . The solution of
. The solution of
is 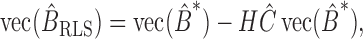 where
where
Now 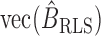 can be written as
can be written as
which leads to
| (7) |
Clearly, 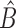 in (6) and
in (6) and 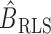 in (7) are identical if
in (7) are identical if 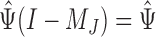 . Hence the proposed method and the restricted least-squares method are identical if the row means of
. Hence the proposed method and the restricted least-squares method are identical if the row means of 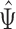 are zero. Gene expression data are commonly normalized so that the row means of
are zero. Gene expression data are commonly normalized so that the row means of 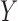 are equal (Bolstad et al., 2003); this makes the row means of the residual matrix
are equal (Bolstad et al., 2003); this makes the row means of the residual matrix 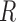 , and consequently the row means of
, and consequently the row means of 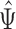 , all zero. Thus, this zero-mean condition is easily satisfied by gene expression data. If
, all zero. Thus, this zero-mean condition is easily satisfied by gene expression data. If 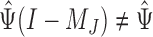 , then
, then 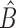 and
and 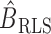 will be different.
will be different.
Since  is a random matrix, our procedure is not the same as the restricted least-squares procedure, which assumes that the restriction matrix
is a random matrix, our procedure is not the same as the restricted least-squares procedure, which assumes that the restriction matrix 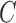 is fixed. However, the discussion above highlights the similarity between the two approaches. The restricted least-squares estimator can have smaller mean squared error than the ordinary least-squares estimator if the restriction is satisfied (Greene & Seaks, 1991). From our simulations, we observe that our estimators tend to have smaller mean squared errors than the estimators from the true regression model, where the restriction is not utilized.
is fixed. However, the discussion above highlights the similarity between the two approaches. The restricted least-squares estimator can have smaller mean squared error than the ordinary least-squares estimator if the restriction is satisfied (Greene & Seaks, 1991). From our simulations, we observe that our estimators tend to have smaller mean squared errors than the estimators from the true regression model, where the restriction is not utilized.
3. Numerical studies
3.1. Simulation studies
We performed simulations to compare the proposed approach with existing methods in a wide range of scenarios. For each simulated dataset, 5000 features and 100 samples were generated from the regression model
where 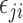 was generated from
was generated from 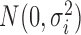 with
with 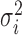 following an ig
following an ig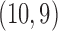 distribution, which yields
distribution, which yields 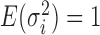 and
and 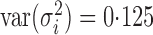 .
.
A total of 864 simulation settings are summarized in Table 1. The binary and continuous 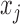 were simulated respectively from
were simulated respectively from
Table 1.
Simulation parameters; the total number of simulation settings is 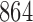
| Parameter | Values |
|---|---|
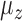
|
0, 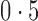 , 1 , 1 |
Percentage of nonzero 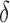
|
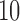 , , 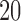 , , 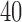 , , 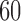
|
Percentage of nonzero 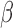
|
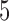 , , 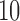 , , 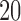
|
Overlap among nonzero 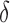
|
total overlap, independent |
| Number of hidden factors | 2, 4 |
Type of 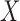
|
binary, continuous |
Correlation between nonzero 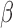 and nonzero and nonzero 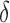
|
0, 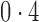 , , 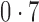
|
and the first two hidden factors were simulated from
When the number of hidden factors is four, i.e., 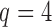 ,
, 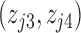 were independently generated from
were independently generated from 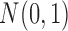 . The parameter
. The parameter 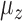 determines the correlation between the primary variable,
determines the correlation between the primary variable, 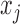 , and the first hidden factor,
, and the first hidden factor, 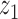 . Three different values of
. Three different values of 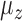 were considered: 0,
were considered: 0, 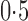 and 1. The regression coefficients
and 1. The regression coefficients 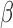 and
and 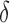 were generated from the distribution
were generated from the distribution
where 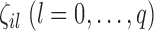 are indicator variables,
are indicator variables, 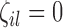 or
or 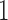 , that determine which of the
, that determine which of the 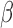 and
and 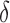 have nonzero values. To mimic real biological data where the primary variables and hidden factors are not associated with all features, we assumed that 5%, 10% or 20% of the
have nonzero values. To mimic real biological data where the primary variables and hidden factors are not associated with all features, we assumed that 5%, 10% or 20% of the 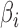 were nonzero and that 10%, 20%, 40% or 60% of the
were nonzero and that 10%, 20%, 40% or 60% of the 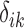 were nonzero. The value of
were nonzero. The value of 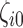 was independently assigned. For
was independently assigned. For 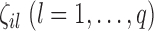 , we considered situations in which nonzero
, we considered situations in which nonzero  values were totally overlapping,
values were totally overlapping, 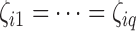 , or independently selected. In the first situation, each feature either had no associated hidden factors or was associated with all
, or independently selected. In the first situation, each feature either had no associated hidden factors or was associated with all 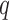 hidden factors. The correlation between the nonzero
hidden factors. The correlation between the nonzero 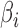 and the nonzero
and the nonzero 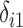 , namely
, namely 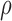 , was set to
, was set to 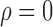 ,
, 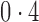 and
and 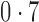 , representing scenarios in which Condition 5 ranged from being satisfied to severely violated.
, representing scenarios in which Condition 5 ranged from being satisfied to severely violated.
Nine different methods were compared: direct surrogate variable analysis; regression model (1), where the hidden factors are assumed to be known and included in the analysis; a no-adjustment model, i.e., regression model (2), where the hidden factors are ignored in the analysis; the iteratively reweighted surrogate variable analysis of Leek & Storey (2008); the two-step surrogate variable analysis of Leek & Storey (2007); principal component analysis on the residuals; principal component analysis on the original measurements of the features; latent effect adjustment after primary projection (Sun et al., 2012); and four-step remove unwanted variation (Gagnon-Bartsch et al., 2017). Latent effect adjustment after primary projection uses an outlier detection approach after initial data projection to adjust for hidden factors. We treated the second method as a gold standard. In both principal component analyses, top principal components were selected and treated as surrogate variables.
For the four-step remove unwanted variation method, we assumed that 6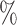 of features were negative control genes, close to the proportion of housekeeping genes in the genome (Gagnon-Bartsch & Speed, 2012). We considered situations in which negative control genes were selected only among features with
of features were negative control genes, close to the proportion of housekeeping genes in the genome (Gagnon-Bartsch & Speed, 2012). We considered situations in which negative control genes were selected only among features with 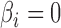 , i.e., high-quality control genes, or were randomly selected among all features, i.e., poor-quality control genes. In the second case, the assumption of negative control genes was violated. A method to estimate the number of surrogate variables for the four-step remove unwanted variation method has been developed (Gagnon-Bartsch et al., 2017). We used this method in conjunction with the method of Buja & Eyuboglu (1992) to estimate
, i.e., high-quality control genes, or were randomly selected among all features, i.e., poor-quality control genes. In the second case, the assumption of negative control genes was violated. A method to estimate the number of surrogate variables for the four-step remove unwanted variation method has been developed (Gagnon-Bartsch et al., 2017). We used this method in conjunction with the method of Buja & Eyuboglu (1992) to estimate 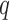 for the four-step remove unwanted variation method; for all other methods, the approach of Buja & Eyuboglu (1992) was used to estimate
for the four-step remove unwanted variation method; for all other methods, the approach of Buja & Eyuboglu (1992) was used to estimate 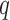 .
.
For each simulation set-up, 200 datasets were generated and the performance of each method was evaluated based on (i) empirical false discovery rates, where the significant findings were determined by the Benjamini & Hochberg (1995) procedure for a targeted false discovery rate of 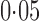 ; (ii) the mean squared errors of the
; (ii) the mean squared errors of the 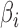 ; and (iii) the area under the receiver operating characteristic curve. For calculation of the false discovery rate and the area under the receiver operating characteristic curve, we define true and false positives as follows. If
; and (iii) the area under the receiver operating characteristic curve. For calculation of the false discovery rate and the area under the receiver operating characteristic curve, we define true and false positives as follows. If 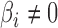 and a statistical test for
and a statistical test for 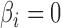 is significant after applying the Benjamini–Hochberg procedure, it is a true positive. If the test is significant when
is significant after applying the Benjamini–Hochberg procedure, it is a true positive. If the test is significant when 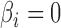 , it is a false positive. In addition to the mean false discovery rates, we calculated the proportion of datasets with an empirical false discovery rate greater than
, it is a false positive. In addition to the mean false discovery rates, we calculated the proportion of datasets with an empirical false discovery rate greater than 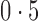 .
.
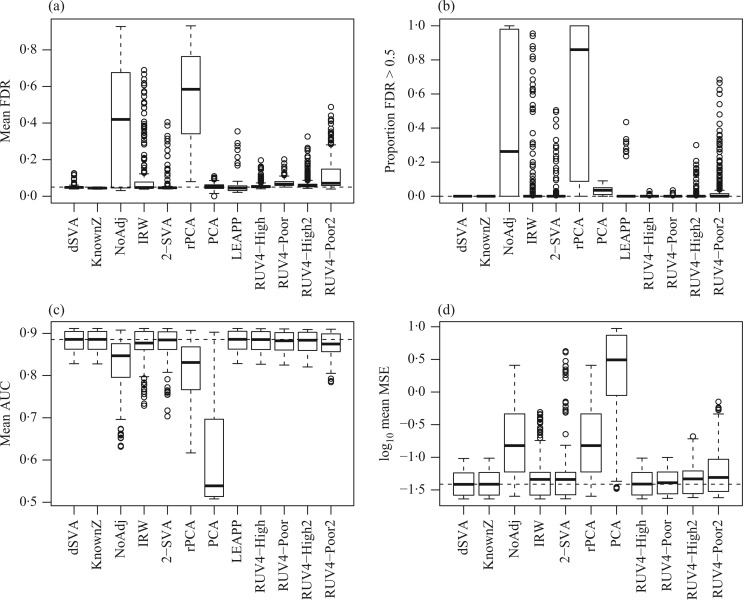
Figure 1 shows simulation results from a scenario where Condition 5 was satisfied, i.e., 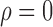 . Direct surrogate variable analysis performed well, as the observed area under the receiver operating characteristic curve and the mean squared errors are similar to those obtained from the approach assuming that the hidden factors are known, and the observed false discovery rates are only slightly inflated in a few simulation settings. Among 288 simulation settings, only four had mean false discovery rates higher than
. Direct surrogate variable analysis performed well, as the observed area under the receiver operating characteristic curve and the mean squared errors are similar to those obtained from the approach assuming that the hidden factors are known, and the observed false discovery rates are only slightly inflated in a few simulation settings. Among 288 simulation settings, only four had mean false discovery rates higher than 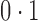 . As expected, the no-adjustment and principal component analysis-based approaches performed very poorly. When the negative control gene assumption was satisfied, the remove unwanted variation method performed only slightly worse than direct surrogate variable analysis: in ten of the simulation settings, the mean empirical false discovery rates were larger than
. As expected, the no-adjustment and principal component analysis-based approaches performed very poorly. When the negative control gene assumption was satisfied, the remove unwanted variation method performed only slightly worse than direct surrogate variable analysis: in ten of the simulation settings, the mean empirical false discovery rates were larger than 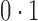 ; however, when this assumption was violated, the remove unwanted variation method had substantially inflated false discovery rates. The latent effect adjustment after primary projection method had mean empirical false discovery rates above
; however, when this assumption was violated, the remove unwanted variation method had substantially inflated false discovery rates. The latent effect adjustment after primary projection method had mean empirical false discovery rates above 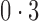 in some simulation settings. Since this method was not developed to estimate
in some simulation settings. Since this method was not developed to estimate 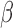 , we did not obtain the mean squared errors. When the method developed for four-step remove unwanted variation was used to estimate the number of surrogate variables, the overall performance of the remove unwanted variation method declined substantially, indicating that the method of Buja & Eyuboglu (1992) performs better in estimating the number of surrogate variables. We compared different approaches to estimating
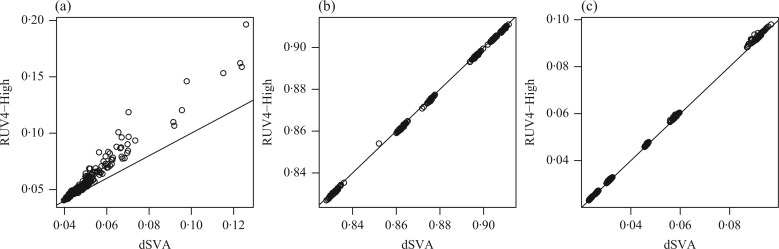
, we did not obtain the mean squared errors. When the method developed for four-step remove unwanted variation was used to estimate the number of surrogate variables, the overall performance of the remove unwanted variation method declined substantially, indicating that the method of Buja & Eyuboglu (1992) performs better in estimating the number of surrogate variables. We compared different approaches to estimating 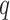 , and the method of Buja & Eyuboglu (1992) outperformed the others; see the Supplementary Material. In Fig. 2, we directly compare the two top-performing approaches: direct surrogate variable analysis and the four-step remove unwanted variation method with high-quality control genes. Direct surrogate variable analysis clearly does better in controlling the false discovery rates.
, and the method of Buja & Eyuboglu (1992) outperformed the others; see the Supplementary Material. In Fig. 2, we directly compare the two top-performing approaches: direct surrogate variable analysis and the four-step remove unwanted variation method with high-quality control genes. Direct surrogate variable analysis clearly does better in controlling the false discovery rates.
Fig. 1.
Comparisons of the proposed and competing methods when 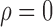 . Each bar summarizes results from 288 different simulation settings, and in each setting 200 datasets were generated to calculate: (a) mean empirical false discovery rates, FDR; (b) the proportion of datasets with empirical FDR higher than
. Each bar summarizes results from 288 different simulation settings, and in each setting 200 datasets were generated to calculate: (a) mean empirical false discovery rates, FDR; (b) the proportion of datasets with empirical FDR higher than 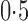 ; (c) the mean area under the receiver operating characteristic curve, AUC; and (d) the mean squared errors, MSE. The methods compared are: dSVA, direct surrogate variable analysis; KnownZ, hidden factors known and included in the model; NoAdj, no adjustment for hidden factors; IRW, iteratively reweighted surrogate variable analysis; 2-SVA, two-step surrogate variable analysis; rPCA, principal component analysis on the residuals; PCA, principal component analysis on the original measured features; LEAPP, latent effect adjustment after primary projection; RUV4-High, four-step remove unwanted variation method with high-quality control genes; RUV4-Poor, four-step remove unwanted variation method with poor-quality control genes; RUV4-High2, RUV4-High with
; (c) the mean area under the receiver operating characteristic curve, AUC; and (d) the mean squared errors, MSE. The methods compared are: dSVA, direct surrogate variable analysis; KnownZ, hidden factors known and included in the model; NoAdj, no adjustment for hidden factors; IRW, iteratively reweighted surrogate variable analysis; 2-SVA, two-step surrogate variable analysis; rPCA, principal component analysis on the residuals; PCA, principal component analysis on the original measured features; LEAPP, latent effect adjustment after primary projection; RUV4-High, four-step remove unwanted variation method with high-quality control genes; RUV4-Poor, four-step remove unwanted variation method with poor-quality control genes; RUV4-High2, RUV4-High with 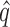 from Gagnon-Bartsch et al. (2017); RUV4-Poor2, RUV4-Poor with
from Gagnon-Bartsch et al. (2017); RUV4-Poor2, RUV4-Poor with 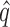 from Gagnon-Bartsch et al. (2017).
from Gagnon-Bartsch et al. (2017).
Fig. 2.
Comparison of direct surrogate variable analysis, dSVA, and the four-step remove unwanted variation method with high-quality control genes, RUV4-High, when 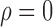 : (a) mean empirical false discovery rate; (b) mean area under the receiver operating characteristic curve; (c) mean squared errors.
: (a) mean empirical false discovery rate; (b) mean area under the receiver operating characteristic curve; (c) mean squared errors.
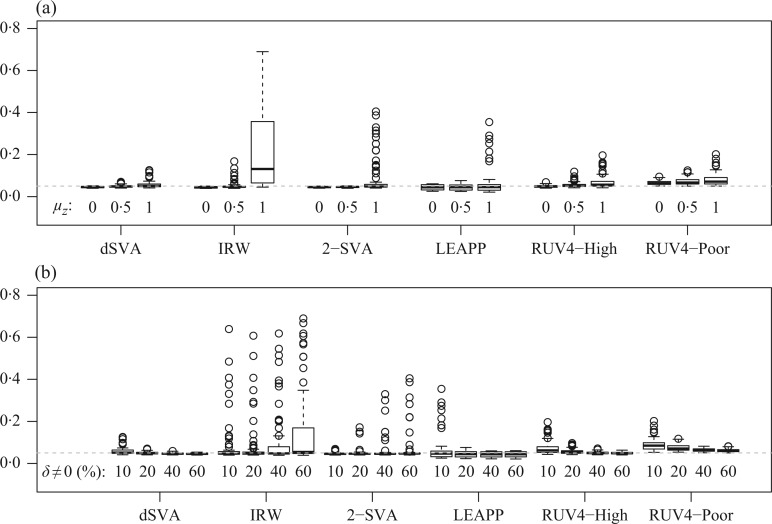
To investigate the effect of each simulation parameter on the performance of the methods when 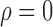 , we created plots for each parameter value. Since the no-adjustment and principal component analysis-based methods performed substantially worse than the other methods, we did not include them in these plots. Among the parameters,
, we created plots for each parameter value. Since the no-adjustment and principal component analysis-based methods performed substantially worse than the other methods, we did not include them in these plots. Among the parameters, 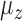 and the percentage of nonzero
and the percentage of nonzero 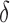 had large effects on the performance of some methods. Figure 3(a) shows boxplots of the false discovery rates with different
had large effects on the performance of some methods. Figure 3(a) shows boxplots of the false discovery rates with different 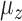 values. The iteratively reweighted and two-step surrogate variable analysis approaches had well-controlled false discovery rates when
values. The iteratively reweighted and two-step surrogate variable analysis approaches had well-controlled false discovery rates when 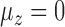 and
and 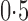 , but had inflated rates when
, but had inflated rates when 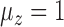 . Therefore, these two methods cannot efficiently estimate the hidden factors in the presence of a strong correlation between
. Therefore, these two methods cannot efficiently estimate the hidden factors in the presence of a strong correlation between 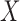 and
and 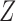 . Figure 3(b) shows that when the percentage of nonzero
. Figure 3(b) shows that when the percentage of nonzero 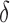 was
was 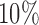 , direct surrogate variable analysis had slightly inflated false discovery rates, perhaps because direct surrogate variable analysis uses all features, instead of selecting features with nonzero
, direct surrogate variable analysis had slightly inflated false discovery rates, perhaps because direct surrogate variable analysis uses all features, instead of selecting features with nonzero 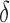 . Since the four-step remove unwanted variation approach uses a small fraction of features to estimate the hidden factors, it had more inflated false discovery rates when the percentage of nonzero
. Since the four-step remove unwanted variation approach uses a small fraction of features to estimate the hidden factors, it had more inflated false discovery rates when the percentage of nonzero 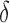 was small. The performances of the different methods in terms of areas under the receiver operating characteristic curves and mean squared errors were largely similar.
was small. The performances of the different methods in terms of areas under the receiver operating characteristic curves and mean squared errors were largely similar.
Fig. 3.
Comparison of mean empirical false discovery rates when 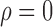 for: (a)
for: (a) 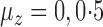 or
or 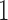 ; and (b) different proportions of nonzero
; and (b) different proportions of nonzero 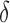 ; 10%, 20%, 40% or 60%. In each simulation setting, 200 datasets were generated to obtain the mean empirical false discovery rates. The methods compared are: dSVA, direct surrogate variable analysis; IRW, iteratively reweighted surrogate variable analysis; 2-SVA, two-step surrogate variable analysis; LEAPP, latent effect adjustment after primary projection; RUV4-High, four-step remove unwanted variation method with high-quality control genes; RUV4-Poor, four-step remove unwanted variation method with poor-quality control genes.
; 10%, 20%, 40% or 60%. In each simulation setting, 200 datasets were generated to obtain the mean empirical false discovery rates. The methods compared are: dSVA, direct surrogate variable analysis; IRW, iteratively reweighted surrogate variable analysis; 2-SVA, two-step surrogate variable analysis; LEAPP, latent effect adjustment after primary projection; RUV4-High, four-step remove unwanted variation method with high-quality control genes; RUV4-Poor, four-step remove unwanted variation method with poor-quality control genes.
Additional simulation results are presented in the Supplementary Material. Our proposed approach was observed to perform well even when 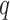 was overestimated and Condition 5 was moderately violated. Overall, our simulation study shows that the proposed method can outperform existing methods in diverse scenarios.
was overestimated and Condition 5 was moderately violated. Overall, our simulation study shows that the proposed method can outperform existing methods in diverse scenarios.
3.2. Application to real data
We downloaded the Hapmap dataset GSE5859 from the National Center for Biotechnology Information gene expression omnibus website to investigate differentially expressed genes between European and Asian populations (Spielman et al., 2007). This dataset contains 8793 genes, or features, and 208 samples from three continental populations: 102 European, 65 Chinese, and 41 Japanese. The affy package (Gautier et al., 2004) was used for background correction and quantile normalization (Bolstad et al., 2003). In the Supplementary Material we perform an analysis without quantile normalization as a sensitivity analysis. Similar to the original study, we restricted the analysis to 4044 reliably expressed genes in at least 80% of the samples in one population (Spielman et al., 2007).
The original study showed that nearly 70% of genes were differentially expressed across the European and Asian samples (Spielman et al., 2007), but it was subsequently discovered that the calendar year in which each sample was processed was a strong confounding factor (Akey et al., 2007; Leek et al., 2010), and many of the positive findings could potentially be false. In this analysis, we considered a scenario where the researchers did not record the calendar year of sample collection and investigated whether the proposed surrogate variable analysis could capture the year effect. We treated year as a categorical response variable and estimated the proportion of variability that can be explained by the surrogate variables.
Table 2 shows the proportion of the variability explained by surrogate variables estimated by four different methods. Since the estimated variability would increase with the number of surrogate variables, for a fair comparison we used 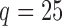 for all the methods, which was estimated by the method of Buja & Eyuboglu (1992). Both direct surrogate variable analysis and the remove unwanted variation method performed well, as 70% and 73% of the variability was explained by the surrogate variables estimated from these respective methods. In contrast, the surrogate variables from the iteratively reweighted and two-step surrogate variable analysis approaches explained only 41% and 64% of the variability in year, respectively. We also considered different combinations of the populations. Direct surrogate variable analysis and the four-step remove unwanted variation method again consistently outperformed the other methods.
for all the methods, which was estimated by the method of Buja & Eyuboglu (1992). Both direct surrogate variable analysis and the remove unwanted variation method performed well, as 70% and 73% of the variability was explained by the surrogate variables estimated from these respective methods. In contrast, the surrogate variables from the iteratively reweighted and two-step surrogate variable analysis approaches explained only 41% and 64% of the variability in year, respectively. We also considered different combinations of the populations. Direct surrogate variable analysis and the four-step remove unwanted variation method again consistently outperformed the other methods.
Table 2.
Proportion of variability in year explained by the estimated surrogate variables; for a fair comparison, the same number of surrogate variables was used in all the methods
| Type | Number of surrogate variables | dSVA | IRW | 2-SVA | RUV4 |
|---|---|---|---|---|---|
| EUR vs (JPT + CHI) | 25 |
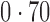
|
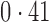
|
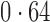
|
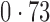
|
| JPT vs (EUR + CHI) | 25 |
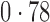
|
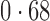
|
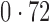
|
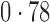
|
| CHI vs (EUR + JPT) | 25 |
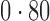
|
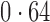
|
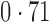
|
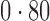
|
| JPT vs CHI | 16 |
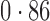
|
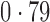
|
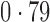
|
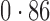
|
EUR, JPT and CHI, individuals of European, Japanese and Chinese ancestry, respectively; dSVA, direct surrogate variable analysis; IRW, iteratively reweighted surrogate variable analysis; 2-SVA, two-step surrogate variable analysis; RUV4, four-step remove unwanted variation method.
Without any hidden variable adjustment, 73% and 65% of genes were found to be differentially expressed between the European and Asian populations at false discovery rates of 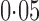 and
and 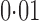 , respectively. As pointed out elsewhere, it seems implausible that so many genes would be differentially expressed between the two populations (Akey et al., 2007). When direct surrogate variable analysis was applied, only 29% and 18% of genes were found to be significant at false discovery rates of
, respectively. As pointed out elsewhere, it seems implausible that so many genes would be differentially expressed between the two populations (Akey et al., 2007). When direct surrogate variable analysis was applied, only 29% and 18% of genes were found to be significant at false discovery rates of 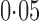 and
and 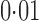 , respectively. Li et al. (2010) have reported that approximately 20% of genes in lymphoblastoid cell lines are differentially expressed between Hapmap2 European and African samples at a false discovery rate of
, respectively. Li et al. (2010) have reported that approximately 20% of genes in lymphoblastoid cell lines are differentially expressed between Hapmap2 European and African samples at a false discovery rate of 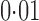 . Given that the genetic difference between the European and African populations is greater than that between the European and Asian populations, 18% of genes differentially expressed between the European and Asian populations seems a reasonable estimate.
. Given that the genetic difference between the European and African populations is greater than that between the European and Asian populations, 18% of genes differentially expressed between the European and Asian populations seems a reasonable estimate.
When we applied two-step surrogate variable analysis and the four-step remove unwanted variation method to the Hapmap data, 15% and 18% of genes, respectively, were declared to be differentially expressed between the European and Asian populations at false discovery rate 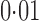 . In contrast, 65% of genes were found to be significant by iteratively reweighted surrogate variable analysis at the same false discovery rate, indicating that this method fails to identify the effects of the hidden factors. When we included year as a covariate in the regression analysis, only 28 genes, i.e.,
. In contrast, 65% of genes were found to be significant by iteratively reweighted surrogate variable analysis at the same false discovery rate, indicating that this method fails to identify the effects of the hidden factors. When we included year as a covariate in the regression analysis, only 28 genes, i.e., 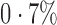 of the tested genes, were significant at false discovery rate
of the tested genes, were significant at false discovery rate 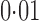 , because year was nearly nested within each population. All Asian samples were processed in 2005 and 2006, but only three European samples were processed in those two years. Among these 28 genes, 15 were significant according to direct surrogate variable analysis. On the other hand, 12 and 14 genes, respectively, were significant by two-step surrogate variable analysis and the four-step remove unwanted variation method.
, because year was nearly nested within each population. All Asian samples were processed in 2005 and 2006, but only three European samples were processed in those two years. Among these 28 genes, 15 were significant according to direct surrogate variable analysis. On the other hand, 12 and 14 genes, respectively, were significant by two-step surrogate variable analysis and the four-step remove unwanted variation method.
We carried out an additional analysis using the same dataset to identify genes differentially expressed by gender. Since genes in sex chromosomes can be used as positive control genes, this additional analysis can be used to directly evaluate the performance of each method. The results show that our method had comparable or slightly better performance than the competing methods; see the Supplementary Material for details.
4. Discussion and conclusion
Surrogate variable analysis was originally proposed for gene expression data, but it has since been applied to epigenetic data as well (Teschendorff et al., 2011; Maksimovic et al., 2015). Recently, surrogate variable analysis has been extended to {prediction} and clustering problems. For example, Parker et al. (2014) developed frozen surrogate variable analysis to remove batch effects for prediction problems, and Jacob et al. (2016) extended the remove unwanted variation method to unsupervised learning. Direct surrogate variable analysis was mainly developed for differential expression analysis, but it can be extended to other types of -omics data, as well as to prediction problems, by adopting the approaches used in frozen surrogate variable analysis. We leave such extensions for future research. One key assumption of the proposed method is Condition 5, which requires that the vector of 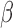 values across
values across 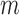 genes and the vector of
genes and the vector of 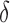 values across
values across 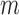 genes be asymptotically orthogonal after mean centring. We think that this is reasonable for many biomedical datasets. In our real-data analysis, for example, batch effects are purely technical issues and their effect sizes would not be correlated with those of population differences. Moreover, our method is robust with respect to moderate violations of this condition. In simulation studies, for instance, our method shows better false discovery rate control than the competing methods when
genes be asymptotically orthogonal after mean centring. We think that this is reasonable for many biomedical datasets. In our real-data analysis, for example, batch effects are purely technical issues and their effect sizes would not be correlated with those of population differences. Moreover, our method is robust with respect to moderate violations of this condition. In simulation studies, for instance, our method shows better false discovery rate control than the competing methods when 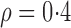 . A similar assumption is implicitly used in existing methods. For example, in their simulation studies, Sun et al. (2012) generated
. A similar assumption is implicitly used in existing methods. For example, in their simulation studies, Sun et al. (2012) generated 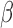 and
and 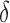 independently. They also suggested that when
independently. They also suggested that when 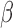 and
and 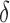 are correlated, it will be difficult to identify
are correlated, it will be difficult to identify 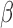 .
.
Principal component analysis was used to correct for batch effects and the effects of hidden confounders prior to the introduction of surrogate variable analysis. This approach has proven very successful for genome-wide association studies (Price et al., 2006). However, our simulation results show that naïve use of principal components for hidden factor adjustment can result in severe power loss, because the top principal components identified can be highly correlated with the primary variables when the effects of the primary variables are not too weak. When this is the case, principal component analysis should be avoided.
Supplementary Material
Acknowledgement
We thank the editor, associate editor and referees for their valuable comments and suggestions, which have greatly helped to improve the quality of the paper. This research was supported by the U.S. National Institutes of Health.
Supplementary material
Supplementary material available at Biometrika online includes proofs of the theoretical results as well as additional simulation and real-data analysis results.
References
- Akey J. M., Biswas S., Leek J. T. & Storey J. D. (2007). On the design and analysis of gene expression studies in human populations. Nature Genet. 39, 807–8. [DOI] [PubMed] [Google Scholar]
- Benjamini Y. & Hochberg Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Statist. Soc. B 57, 289–300. [Google Scholar]
- Bolstad B. M., Irizarry R. A., Åstrand M. & Speed T. P. (2003). A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 19, 185–93. [DOI] [PubMed] [Google Scholar]
- Buja A. & Eyuboglu N. (1992). Remarks on parallel analysis. Mult. Behav. Res. 27, 509–40. [DOI] [PubMed] [Google Scholar]
- Chakraborty S., Datta S. & Datta S. (2012). Surrogate variable analysis using partial least squares (SVA-PLS) in gene expression studies. Bioinformatics 28, 799–806. [DOI] [PubMed] [Google Scholar]
- Dumeaux V., Olsen K. S., Nuel G., Paulssen R. H., Børresen-Dale A. L. & Lund E. (2010). Deciphering normal blood gene expression variation—The NOWAC postgenome study. PLoS Genet. 6, e1000873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friguet C., Kloareg M. & Causeur D. (2009). A factor model approach to multiple testing under dependence. J. Am. Statist. Assoc. 104, 1406–15. [Google Scholar]
- Gagnon-Bartsch J. A., Jacob L. & Speed T. P. (2017). Removing Unwanted Variation: Exploiting Negative Controls for High Dimensional Data Analysis. IMS Monographs Cambridge: Cambridge University Press, in press. [Google Scholar]
- Gagnon-Bartsch J. A. & Speed T. P. (2012). Using control genes to correct for unwanted variation in microarray data. Biostatistics 13, 539–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier L., Cope L., Bolstad B. M. & Irizarry R. A. (2004). Affy-analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 20, 307–15. [DOI] [PubMed] [Google Scholar]
- Greene W. H. & Seaks T. G. (1991). The restricted least squares estimator: A pedagogical note. Rev. Econ. Statist. 73, 563–7. [Google Scholar]
- Jacob L., Gagnon-Bartsch J. A. & Speed T. P. (2016). Correcting gene expression data when neither the unwanted variation nor the factor of interest are observed. Biostatistics 17, 16–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnstone I. M. (2001). On the distribution of the largest eigenvalue in principal components analysis. Ann. Statist. 29, 295–327. [Google Scholar]
- Johnstone I. M. & Lu A. Y. (2009). On consistency and sparsity for principal components analysis in high dimensions. J. Am. Statist. Assoc. 104, 682–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung S. & Marron J. S. (2009). PCA consistency in high dimension, low sample size context. Ann. Statist. 37, 4104–30. [Google Scholar]
- Lee S., Zou F. & Wright F. A. (2010). Convergence and prediction of principal component scores in high-dimensional settings. Ann. Statist. 38, 3605–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Zou F. & Wright F. A. (2014). Convergence of sample eigenvalues, eigenvectors, and principal component scores for ultra-high dimensional data. Biometrika 101, 484–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek J. T. (2011). Asymptotic conditional singular value decomposition for high-dimensional genomic data. Biometrics 67, 344–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek J. T., Scharpf R. B., Bravo H. C., Simcha D., Langmead B., Johnson W. E., Geman D., Baggerly K. & Irizarry R. A. (2010). Tackling the widespread and critical impact of batch effects in high-throughput data. Nature Rev. Genet. 11, 733–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek J. T. & Storey J. D. (2007). Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 3, e161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek J. T. & Storey J. D. (2008). A general framework for multiple testing dependence. Proc. Nat. Acad. Sci. 105, 18718–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J., Liu Y., Kim T., Min R. & Zhang Z. (2010). Gene expression variability within and between human populations and implications toward disease susceptibility. PLoS Comp. Biol. 6, e1000910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J., Kadie C., Schadt E. E. & Heckerman D. (2010). Correction for hidden confounders in the genetic analysis of genec expression. Proc. Nat. Acad. Sci. 107, 16465–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maksimovic J., Gagnon-Bartsch J. A., Speed T. P. & Oshlack A. (2015). Removing unwanted variation in a differential methylation analysis of Illumina HumanMethylation450 array data. Nucleic Acids Res. 43, e106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker H. S., Bravo H. C. & Leek J. T. (2014). Removing batch effects for prediction problems with frozen surrogate variable analysis. PeerJ 2, e561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A. L., Patterson N. J., Plenge R. M., Weinblatt M. E., Shadick N. A. & Reich D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genet. 38, 904–9. [DOI] [PubMed] [Google Scholar]
- R Development Core Team (2017). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing: ISBN 3-900051-07-0, http://www.R-project.org. [Google Scholar]
- Spielman R. S., Bastone L. A., Burdick J. T., Morley M., Ewens W. J. & Cheung V. G. (2007). Common genetic variants account for differences in gene expression among ethnic groups. Nature Genet. 39, 226–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegle O., Parts L., Durbin R. & Winn J. (2010). A Bayesian framework to account for complex non-genetic factors in gene expression levels greatly increases power in eQTL studies. PLoS Comp. Biol. 6, e1000770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y., Zhang N. R. & Owen A. B. (2012). Multiple hypothesis testing adjusted for latent variables, with an application to the AGEMAP gene expression data. Ann. Appl. Statist. 6, 1664–88. [Google Scholar]
- Teschendorff A. E., Menon U., Gentry-Maharaj A., Ramus S. J., Weisenberger D. J., Shen H., Campan M., Noushmehr H., Bell C. G., Maxwell A. P.. et al. (2010). Age-dependent DNA methylation of genes that are suppressed in stem cells is a hallmark of cancer. Genome Res. 20, 440–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teschendorff A. E., Zhuang J. & Widschwendter M. (2011). Independent surrogate variable analysis to deconvolve confounding factors in large-scale microarray profiling studies. Bioinformatics 27, 1496–505. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.