Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Aug 31;29(18):7969–7975. doi: 10.1021/acs.chemmater.7b03032

Setting Directions: Anisotropy in Hierarchically Organized Porous Silica

Florian Putz †, Roland Morak ‡, Michael S Elsaesser †, Christian Balzer §, Stephan Braxmeier §, Johannes Bernardi ∥, Oskar Paris ‡,*, Gudrun Reichenauer §,*, Nicola Hüsing †,*
PMCID: PMC5627989  PMID: 28989232

Abstract

graphic file with name cm-2017-030327_0004.jpg

Structural hierarchy, porosity, and isotropy/anisotropy are highly relevant factors for mechanical properties and thereby the functionality of porous materials. However, even though anisotropic and hierarchically organized, porous materials are well known in nature, such as bone or wood, producing the synthetic counterparts in the laboratory is difficult. We report for the first time a straightforward combination of sol–gel processing and shear-induced alignment to create hierarchical silica monoliths exhibiting anisotropy on the levels of both, meso- and macropores. The resulting material consists of an anisotropic macroporous network of struts comprising 2D hexagonally organized cylindrical mesopores. While the anisotropy of the mesopores is an inherent feature of the pores formed by liquid crystal templating, the anisotropy of the macropores is induced by shearing of the network. Scanning electron microscopy and small-angle X-ray scattering show that the majority of network forming struts is oriented towards the shearing direction; a quantitative analysis of scattering data confirms that roughly 40% of the strut volume exhibits a preferred orientation. The anisotropy of the material’s macroporosity is also reflected in its mechanical properties; i.e., the Young’s modulus differs by nearly a factor of 2 between the directions of shear application and perpendicular to it. Unexpectedly, the adsorption-induced strain of the material exhibits little to no anisotropy.

1. Introduction

Natural materials frequently exhibit multiple levels of structural hierarchy combined with a directional orientation of the constituting components, resulting in exceptional properties, e.g., hydration-triggered morphology changes as found in pine cones or anisotropic mechanical properties as found in trabecular bone.1−7 The pine cone example3 demonstrates impressively how the combination of large accessible surface area and tailored hierarchical structuring leads to active or responsive properties. In this context, anisotropy is a fundamental parameter for the functionality of many biological materials. With respect to materials science, anisotropic, hierarchical structures with large accessible surface area could offer a multitude of direction-dependent properties that are, e.g., useful in separation science, for an angular dependent interaction with light, or even to generate a material with an anisotropic mechanical behavior.

Although being highly desirable, so far there are only few applicable methods for synthesizing porous materials with anisotropic features on multiple length scales. Typical processes that have been applied to form anisotropic macroporous structures include anodic oxidation,8 wood templating,9−11 unidirectional solidification,12 extrusion,13 freeze casting, or directional ice templating.14,15 Mesoporous powders and coatings with a 2D hexagonal arrangement of cylindrical pores, such as MCM-41 or SBA-15, are inherently anisotropic in the mesoscopic regime, and additional macroscopic alignment by shear has been reported.16,17 Furlan and Lattuada presented a preparation method using pre-aligned paramagnetic nanocolloids as additional templates that permit control over the microstructure of silica monoliths obtained by sol–gel processing combined with phase separation by means of an external magnetic field.18 Aizenberg et al. have applied unidirectional shrinkage to synthesize anisotropic inverse opal structures, to name two recent examples.19 However, as mentioned above, these prior research efforts to form porous structures with unidirectionally oriented pores have primarily focused on the design of either the mesopore or the macropore level, but not on the combination of both structural levels in hierarchically organized meso-/macroporous monolithic networks.

One possible bottom-up route toward the formation of such multilevel porous architectures relies on the processing of condensable, network forming precursors (e.g., sol–gel processing of silanes) in the presence of porogens or phase separation-inducing agents.20−22 In the case of silica, these materials consist of a unique macroporous network of struts, each strut comprising cylindrical mesopores on a 2D hexagonal lattice with similar mesopore characteristics as SBA-15. On the basis of these hierarchically organized silica monoliths, we here report a straightforward, facile approach to simultaneously create anisotropy on both the meso- and macropore level. We present an investigation of shear-induced macroscopic anisotropy in self-assembled, hierarchically organized silica gels in comparison to their nonsheared counterparts, taking advantage of the dynamics of the sol–gel transition and of chemical reactions continuing after gelation. In particular, we discuss the structural implications of shearing on the porous network and their impact on the mechanical properties and the adsorption-induced strain characteristics of the porous monolith. This knowledge is intended as the basis for future applications of hierarchically organized porous systems with anisotropic features in separation science, but also in designed switchable components, for instance as actuators, thermal insulation, or acoustic mechanical components.

2. Experimental Section

Synthesis of Hierarchically Organized, Monolithic Silica Gels

Tetrakis(2-hydroxyethyl)orthosilicate (an ethylene glycol modified silane; EGMS) with a SiO2 content of 20 wt % was prepared from TEOS (Merck Millipore) and ethylene glycol (VWR Chemicals) as described by Brandhuber et al.23 Wet gel preparation was conducted by adding EGMS to a homogeneous mixture of aqueous P123 (Sigma-Aldrich) in 1 M HCl with a composition by weight (Si/P123/HCl) of 8.4/30/70. Stirring for 1 min yielded a clear, viscous liquid that was poured in PP containers, and allowed to gel and age at 313 K for 7 days. Demolding of the wet gels was followed by a repeated washing procedure (5 times within 72 h) with ethanol to remove the surfactant and residual ethylene glycol. Afterward, the as-prepared wet gel bodies were dried supercritically with CO2 (Tc = 304.18 K; Pc = 7.38 MPa). In the case of sheared samples, the procedure as described above was modified after stirring. The viscous liquid sol was filled into a plastic syringe (Henke-Sass, Wolf GmbH, 5 mm diameter), which was then sealed and placed in an oven to gel for 1–2 h at 313 K. By pressing the stamp, a shear force was applied, leading to a directed flow of the gel inside the syringe. Within the syringe, on both sides sealed, the gels were aged for 7 days at 313 K in the mother liquor. Further processing steps were performed according to the description above.

Electron Microscopy

Scanning electron microscopy (SEM) images were taken using a ZEISS FE-SEM ULTRA PLUS applying its in-lens secondary electron detector at an accelerating voltage of 2 kV. The microstructure of the samples was studied by transmission electron microscopy (TEM) with a TECNAI F20 field emission electron microscope operated at an accelerating voltage of 200 kV. Images were recorded with a Gatan Orius SC600 CCD camera.

Small-Angle X-ray Scattering (SAXS)

Samples for SAXS were prepared by cutting an about 1 mm thick central slice parallel to the cylindrical sample axis using a diamond saw. SAXS measurements were performed with a Nanostar laboratory instrument (Bruker AXS, Karlsruhe, Germany) using Cu–Kα radiation and a Våntec 2000 detector at a sample–detector distance of 711 mm. The beam was monochromatized and focused by a graded multilayer mirror and defined by two scatterless pinholes of 300 μm in diameter. 2D SAXS patterns were corrected for background and transmission and either sector averaged to obtain the intensity I(q) as a function of the scattering vector length q (q = 4π sin θ/λ, θ being half the scattering angle and λ = 0.154 nm the X-ray wavelength) or azimuthally averaged to obtain the intensity I(χ) as a function of the azimuthal detector angle χ. The lattice parameter of the 2D hexagonal mesopore lattice was determined from the position of the first-order Bragg peak by a = 4π/(√3 q10), and the mesopore radius R was estimated from the integrated intensity of the first three Bragg peaks by assuming a circular pore cross section and a steplike corona model.24 The domain size of the periodically arranged pores was estimated by applying the Scherrer formula corrected for instrumental resolution D = 2πK/(ΔqS – ΔqRes), with K = 0.9.25 The peak widths were determined by Lorentzian fits, where ΔqS is the full-width at half-maximum (fwhm) of the main Bragg peak from the respective silica samples and ΔqRes is the fwhm of the resolution function determined from a rat-tail tendon sample.26 The mesopore volume fraction from SAXS is then calculated by ϕmeso = (2π√3)·(R2/a2). Finally, the degree of preferred orientation (DPO) of the mesopore cylindrical axis with respect to the macroscopic sample cylinder axis was determined from the ratio of the peak area to the total area under the I(χ) curves, i.e.

graphic file with name cm-2017-030327_m001.jpg

This parameter takes the value zero for completely random orientation (no azimuthal peak) and one for perfect parallel orientation of the mesopore axes (corresponding to the strut direction) with respect to a macroscopic coordinate system.

Determination of Young’s Modulus

The Young’s modulus E was determined from the longitudinal sound velocity vL, the bulk density ρ, and the characteristic Poisson’s number ν of amorphous silica (ν = 0.20 ± 0.05) (see, e.g., ref (27)): E = ρvL2·(1 – 2ν)(1 + ν)/(1 – ν).

The longitudinal sound velocity was determined at a frequency of 0.5 MHz via a run time experiment in an impulse-echo setup.28 The mechanical properties were investigated on cylindrically shaped monoliths both in axial and in radial directions of the cylinder in order to identify potential anisotropy. The bulk density ρ was determined from mass and geometric dimensions of the monolith cylinders after degassing them for at least 1 day at 110 °C. Noteworthy, the wavelength of the sound waves used in the experiment is significantly larger than any structural heterogeneity within the bulk material, and therefore, the sound waves perceive the samples as effectively homogeneous media.

Water Vapor Adsorption Measurement and in Situ Dilatometry

The H2O adsorption isotherm (17 °C) of the sheared sample was determined by a commercial sorption instrument (SPS-11, ProUmid, Ulm, Germany). The corresponding linear strain of a cylindrical sample (length: 4.7 mm, diameter: 3.1 mm) was measured by a self-designed dilatometric setup placed in a vacuum chamber. The relative humidity within the chamber was controlled via the stepwise dosing of water vapor from a high purity water reservoir. Measurements of the sample’s linear strain during H2O adsorption were performed in the axial as well as in the radial direction of the monolithic cylinder. The spatial resolution of the length sensor used in this setup is approximately ±200 nm. Prior to each measurement, the sample was degassed in vacuum at 50 °C for at least 3 h.

3. Results and Discussion

Hierarchically organized, highly porous silica monoliths can be fabricated by using a combination of polymerization-induced phase separation and sol–gel processing of tetrakis(2-hydroxyethyl)orthosilicate, a tailor-made silane that allows for hydrolysis and condensation reactions in a purely aqueous environment. Addition of condensable silanes to a preformed lyotropic liquid crystal (LC) phase of a nonionic block copolymer (P123) in aqueous hydrochloric acid results in clear gels that turn opaque after gelation, indicating an additional phase separation on a larger length scale. Structural investigations of the resulting supercritically dried gels by small-angle X-ray scattering (SAXS), scanning electron microscopy (SEM), and transmission electron microscopy (TEM) confirm that a hierarchically organized, low-density network is formed, comprising periodically 2D hexagonal organized cylindrical mesopores with a repeating unit distance of about 11 nm and a cellular silica network with macropores in the range of 1 μm in diameter (Figure 1a–d). While the channel-like mesopores show a high degree of anisotropy due to their arrangement on a 2D hexagonal lattice, the network of mesoporous struts is entirely disordered, leading to isotropic macroporosity.29,30 In the following, these samples are used as a reference.

Figure 1.

Figure 1

Open in a new tab

Reference (a–d) and sheared (e–h) silica gel monoliths as well as a schematic representation of the shear-induced alignment process (i–l). (a) and (e) are optical photographs of the resulting gel bodies; (b) and (f) are representative SEM images illustrating the anisotropic alignment of the sheared sample; (c) and (g) are SEM images with increased magnification; and (d) and (h) are representative TEM images showing the high spatial orientation of the mesopores within the struts. The alignment process (i–l) starts with the synthesis of a liquid-crystalline silica/P123 composite alcogel in a syringe (i). During aging, extrusion is started (j), resulting in an alignment of the silica network (k). Afterward, the sheared gel is left for aging, resulting in network formation along the aligned silica struts, but also by formation of novel smaller connections between the struts, leading to an aligned, anisotropic silica network (l).

To obtain hierarchically organized porous silica monoliths exhibiting anisotropy on the level of meso- and macropores, the above-described synthesis is complemented by a shearing step. For this, the liquid-crystalline silica/P123 composite is pregelled in a syringe and then exposed to shear by pressing the syringe’s stamp, causing part of the gel to flow through the nozzle. Afterward, the nozzle of the syringe is closed and the gel is left for aging. Drying of the sheared gel by supercritical extraction with CO2 is performed the same way as for the reference samples. SEM and TEM images of the sheared gels are shown in Figure 1e–h, while the shearing step is schematically depicted in Figure 1i–l. SEM images of reference and sheared samples (Figure 1b,f) clearly show the impact of the shearing step on the macroporous strut network, i.e., a preferential arrangement of the struts in the direction of the applied shearing force. Noteworthy, the macroscopic appearance (Figure 1a,e) and the structural properties of sheared and reference samples, such as density (reference: 0.411 g cm–3, sheared: 0.409 g cm–3), specific surface area (reference: 215 m2 g–1, sheared: 211 m2 g–1), mesopore volume (reference: 0.279 cm3 g–1, sheared: 0.282 cm3 g–1), etc., are essentially identical (see Figure S1 and Table S1).

The efficacy of shearing a preformed gel network relies on the fact that the gelation event in sol–gel processes still leaves a large number of monomers and oligomers in the gel unreacted. Gelation is defined as the point at which the sol loses fluidity; i.e., no flow of the gel is observed when the container is turned. Thus, with time, the aligned struts in the sheared gel will experience further condensation reactions in parallel to a stiffening of the strut network. Therefore, the correct timing between the preliminary gelation step and the shearing process is crucial for a pronounced alignment of the network constituting struts. In a series of experiments, we subjected the gel bodies to shear before, just after and up to several hours after gelation (i.e., always prior to phase separation), and after the gels turned opaque, hence after phase separation. Phase separation is defined as the point at which the gel changes from transparent to opaque, indicating the formation of structures, e.g., macropores, larger than the wavelength of light. These experiments revealed that, on the one hand, gelation is a prerequisite for an alignment, however, on the other, that the degree of condensation is already too advanced after phase separation.32

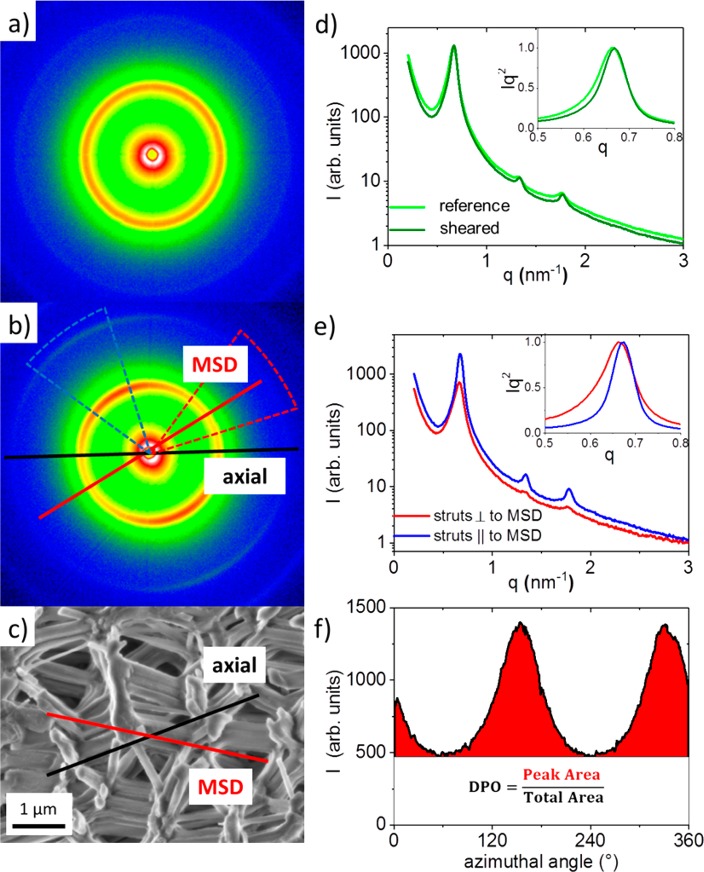
For quantitative analysis of the anisotropy of the strut network, we evaluated the SAXS patterns of reference and sheared samples (Figure 2a,b, respectively). In this context, the expressions “axial” and “radial” refer to the macroscopic dimensions of the cylindrical sample, whereas the “main strut direction” (MSD) corresponds to the preferred orientation of struts within the monolith. The reference sample shows the expected homogeneous Debye–Scherrer rings from the 2D hexagonal pore lattice. This indicates that the hexagonally ordered cylindrical mesopores within the investigated sample volume take all angular orientations with the same probability. In contrast, the sheared sample shows an azimuthal modulation exhibiting the lowest intensity at an angle of roughly 35° with respect to the axial direction of the cylindrical sample and the highest intensity perpendicular to it. This means that a larger fraction of struts is oriented preferentially at an average inclination angle of 35° with respect to the cylinder axis. In the Supporting Information (Figure S2), it is shown that this tilt angle is homogeneous along the cross section of the sample with a switching of direction in the middle. This indicates rotational symmetry around the cylindrical sample axis, suggesting that the anisotropy of the strut network is correlated to the flow field during the shear-induced alignment. The “degree of preferred orientation” (DPO) quantifies the amount of struts oriented in MSD. The DPO defined as the ratio of the peak area to the total area in the azimuthal intensity (Figure 2f) would be zero for a complete random alignment of the struts (no azimuthal peak) and one for all struts being oriented preferentially in parallel. Figure 2f shows that, on average, roughly 40% of the strut volume shows a preferred orientation, supporting the qualitative impression obtained from the related SEM images (Figure 1f). Interestingly, the DPO is considerably smaller (20–25%) in the center of the cylindrical sample, meaning that the anisotropic strut arrangement is more pronounced at the edges.

Figure 2.

Figure 2

Open in a new tab

2D scattering patterns of (a) the reference sample and (b) the sheared sample. (c) Representative SEM image of the sheared sample showing the preferred orientation of struts (main strut direction, MSD), which is about 35° tilted from the macroscopic sample cylinder axis, i.e., the axial direction. (d) Comparison of the radially averaged scattering profiles from (a) and (b). (e) Scattering curves from the sheared sample integrated in a narrow sector (±20°) around the intensity minimum (MSD direction) as well as around the intensity maximum (perpendicular to the MSD direction). The insets in (d) and (e) show the main Bragg-reflection in a Kratky Plot31 normalized to the same height. (f) Azimuthal integration in a narrow q-range around the main Bragg peak of the sheared sample. The degree of preferred orientation (DPO) is defined by the area of the peak divided by the total area under the azimuthal intensity distribution.

The radially averaged 2D patterns (Figure 2d) provide information on the mesopore order and the mesopore size. Quantitative comparison of the structural characteristics (Table 1) reveal that pore lattice parameter, mesopore diameter, and mesopore volume fraction are essentially identical for the reference and sheared samples; this also applies to struts parallel (∥) and perpendicular (⊥) to MSD in the sheared sample. What is striking, however, is that the first Bragg peak originating from struts parallel to the direction of preferred orientation is considerably narrower than the one from struts perpendicular to it (inset of Figure 2e). Assuming microstrains of the pore lattice being negligible, the inverse peak width is directly related to the thickness of the struts. Applying the Scherrer equation,25 we find the strut population perpendicular to the MSD considerably thinner than the strut population in MSD (see Table 2). This result corroborates the qualitative observation from SEM images (Figure S3).

Table 1. Comparison of Structural Parameters for Reference and Sheared Samples Obtained from SAXSa.

  lattice parameter [nm] pore radius [nm] strut width [nm] DPO mesopore volume fraction
struts ∥ MSD 10.84 ± 0.04 3.42 ± 0.02 601 ± 30 0.40 ± 0.08 0.361 ± 0.009
struts ⊥ MSD 10.96 ± 0.04 3.35 ± 0.02 137 ± 7 0.40 ± 0.08 0.334 ± 0.010
reference 10.98 ± 0.04 3.43 ± 0.02 196 ± 10 0 0.354 ± 0.006
Open in a new tab
a

Here, the ∥ direction corresponds to the main strut direction (MSD), and ⊥ is the corresponding direction perpendicular to the MSD.

Table 2. Young’s Moduli E Calculated from Longitudinal Sound Velocity Assuming a Poisson’s Ratio of ν = 0.2 ± 0.05a.

  ρ [g/cm3] E [MPa]
reference 0.411 ± 0.007 627 ± 62
sheared ∥ 0.409 ± 0.032 627 ± 98
sheared ⊥ 0.409 ± 0.032 335 ± 68
Open in a new tab
a

In the case of the sheared sample, ∥ denotes the mechanical properties along the axial direction of the cylindrical monolith and ⊥ along its radial direction.

To explore the impact of the strut orientation on the mechanical properties of the bulk material, we performed sound velocity measurements on cylindrical monoliths of reference and sheared samples, both in axial and in radial directions. Notably, the force applied during the gelation of the sheared samples was orientated in the axial direction of the cylinder. The results were evaluated with respect to the Young’s modulus E and summarized in Table 2. As expected, the Young’s modulus of the reference sample is identical in axial and radial directions, once again supporting the concept of an isotropic macropore network. However, for the sheared sample, E differs nearly by a factor of 2 between the direction of shear application, i.e., the axial direction of the cylinder, and perpendicular to it, i.e., in the radial direction of the cylinder. Note that this anisotropy of the elastic modulus is of similar magnitude as that found in human trabecular bone from different anatomical locations.7

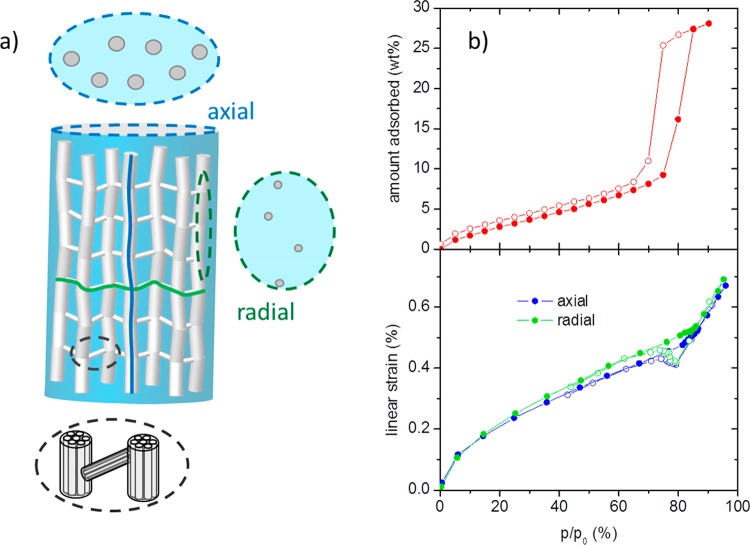
The difference of Young’s moduli in axial and radial directions can be qualitatively explained when assuming in a zero-order approach that the struts are either fully aligned in the direction of the axis or perpendicular to it (Figure 3a). In this case, the modulus along the axis of the cylinder is given essentially by the Young’s modulus of the individual mesoporous strut (in axial strut direction) weighed by the strut density (see schematic projection in Figure 3a). In the radial direction of the monolith, the connected structure is given by an alternation of horizontally and vertically oriented struts. Therefore, the modulus in this direction is given by a superposition of the moduli of the individual struts in the radial direction and axial direction; hereby, the areal density in the related plane is dominated by the cross section of the thin struts providing the horizontal connection of the structure in Figure 3a.

Figure 3.

Figure 3

Open in a new tab

(a) Schematic of the microstructure of a sheared sample of cylindrical shape; the dashed circles represent cross sections in two different directions (blue and green) and a magnification (black). (b) Adsorption (top) and strain isotherms (bottom) of the sheared sample during H2O adsorption at 17 °C. Full symbols denote adsorption, open symbols denote desorption. The strain isotherms have been measured on cubic samples (cut from the cylindrical monoliths) in the two different directions.

With respect to recent studies on the adsorption-induced deformation of hierarchical structured silica33 and the development of humidity driven cantilevers,34 we also investigated the mechanical response of the sheared sample to adsorption by in situ dilatometry. Again, we used monolithic pieces to measure the linear strain of the bulk material in the cylinder’s axial and radial directions. The respective adsorption and strain isotherms of water vapor at 17 °C and N2 at 77 K and adsorption isotherms are given in Figure 3b and S1, respectively. The shape of the obtained strain isotherms (including the small “dip” at the pressure of capillary evaporation) corresponds well to previous dilatometric studies on this type of material33 and is in qualitative agreement with theoretical predictions.35 However, in contrast to the Young’s modulus, the impact of the anisotropy on adsorption-induced strain in different orientations of the cylindrical monolith is quite small.

This apparently counterintuitive observation can be explained when analyzing the situation in detail (compare Figure 3a):35 The adsorption-induced strain of the macroscopic material results from the strain of the mesoporous struts forming the macroporous network. This strain is inherently anisotropic, i.e., an individual strut exhibits different adsorption-induced strains along and perpendicular to the cylindrical mesopores. The quantitative differences between both strain components vary with the filling state of the mesopores but are rather small prior to capillary condensation and close to saturation pressure of the adsorbate. From the scheme in Figure 3a, it is obvious that, in the axial direction of the cylindrical sample (blue line), the axial strain characteristic of an individual strut will be dominating. On the other hand, in the radial direction of the cylindrical sample (green line), the strain of the monolithic sample is a mixture of the individual strut’s axial and radial strains; however, the majority of the path is given by the thin struts oriented horizontally in Figure 3a. Therefore, here also, the axial strain of an individual strut will have a major impact.

4. Conclusions

In summary, hierarchically organized silica gel monoliths with an anisotropic cellular macroporous network comprising 2D hexagonal organized mesopores have been prepared by a facile shear-induced alignment process. SEM images qualitatively indicate that the network forming struts are tilted in the shearing direction, and SAXS analysis quantitatively confirmed that roughly 40% of the strut volume shows a preferred orientation. The anisotropy of the sample’s macropore structure is reflected in its mechanical properties: the Young’s modulus for the sheared sample differs nearly by a factor of 2 between the direction of shear application and perpendicular to it. Contrarily, the adsorption-induced strain of the material exhibits only minor anisotropy. This result is in line with the current understanding of adsorption-induced deformation and leads to the conclusion that anisotropy of adsorption-induced actuation is more difficult to achieve than anisotropic mechanical properties.

Acknowledgments

We thank Anna M. Waag (Bavarian Center for Applied Energy Research) for performing N2 adsorption measurements combined with in situ dilatometry.

Glossary

Abbreviations

MSD

main strut direction

DPO

degree of preferred orientation

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemmater.7b03032.

  • Nitrogen adsorption analysis with in situ dilatometry, adsorption and strain isotherms, position resolved SAXS patterns, and SEM image (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

We acknowledge financial support from the Austrian Science Foundation FWF (Project I 1605-N20) and the German Science Foundation DFG (Project GZ: RE1148/10-1).

The authors declare no competing financial interest.

Supplementary Material

cm7b03032_si_001.pdf (2.1MB, pdf)

References

  1. Wegst U. G.; Bai H.; Saiz E.; Tomsia A. P.; Ritchie R. O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. 10.1038/nmat4089. [DOI] [PubMed] [Google Scholar]
  2. Dawson C.; Vincent J. F.; Rocca A.-M. How pine cones open. Nature 1997, 390, 668–668. 10.1038/37745. [DOI] [Google Scholar]
  3. Van Opdenbosch D.; Fritz-Popovski G.; Wagermaier W.; Paris O.; Zollfrank C. Moisture-Driven Ceramic Bilayer Actuators from a Biotemplating Approach. Adv. Mater. 2016, 28, 5235–5240. 10.1002/adma.201600117. [DOI] [PubMed] [Google Scholar]
  4. Zysset P. K. A review of morphology–elasticity relationships in human trabecular bone: theories and experiments. J. Biomech. 2003, 36, 1469–1485. 10.1016/S0021-9290(03)00128-3. [DOI] [PubMed] [Google Scholar]
  5. Odgaard A.; Kabel J.; van Rietbergen B.; Dalstra M.; Huiskes R. Fabric and elastic principal directions of cancellous bone are closely related. J. Biomech. 1997, 30, 487–495. 10.1016/S0021-9290(96)00177-7. [DOI] [PubMed] [Google Scholar]
  6. Fratzl P.; Weinkamer R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. 10.1016/j.pmatsci.2007.06.001. [DOI] [Google Scholar]
  7. Augat P.; Link T.; Lang T. F.; Lin J. C.; Majumdar S.; Genant H. K. Anisotropy of the elastic modulus of trabecular bone specimens from different anatomical locations. Med. Eng. Phys. 1998, 20, 124–131. 10.1016/S1350-4533(98)00001-0. [DOI] [PubMed] [Google Scholar]
  8. Lee W.; Ji R.; Gösele U.; Nielsch K. Fast fabrication of long-range ordered porous alumina membranes by hard anodization. Nat. Mater. 2006, 5, 741–747. 10.1038/nmat1717. [DOI] [PubMed] [Google Scholar]
  9. Tampieri A.; Sprio S.; Ruffini A.; Celotti G.; Lesci I. G.; Roveri N. From wood to bone: multi-step process to convert wood hierarchical structures into biomimetic hydroxyapatite scaffolds for bone tissue engineering. J. Mater. Chem. 2009, 19, 4973–4980. 10.1039/b900333a. [DOI] [Google Scholar]
  10. Fritz-Popovski G.; Van Opdenbosch D.; Zollfrank C.; Aichmayer B.; Paris O. Development of the fibrillar and microfibrillar structure during biomimetic mineralization of wood. Adv. Funct. Mater. 2013, 23, 1265–1272. 10.1002/adfm.201201675. [DOI] [Google Scholar]
  11. Deshpande A. S.; Burgert I.; Paris O. Hierarchically Structured Ceramics by High-Precision Nanoparticle Casting of Wood. Small 2006, 2, 994–998. 10.1002/smll.200600203. [DOI] [PubMed] [Google Scholar]
  12. Okada K.; Isobe T.; Katsumata K.-i.; Kameshima Y.; Nakajima A.; MacKenzie K. J. Porous ceramics mimicking nature—preparation and properties of microstructures with unidirectionally oriented pores. Sci. Technol. Adv. Mater. 2011, 12, 064701. 10.1088/1468-6996/12/6/064701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Xu Z.; Zhang Y.; Li P.; Gao C. Strong, conductive, lightweight, neat graphene aerogel fibers with aligned pores. ACS Nano 2012, 6, 7103–7113. 10.1021/nn3021772. [DOI] [PubMed] [Google Scholar]
  14. Deville S.; Saiz E.; Nalla R. K.; Tomsia A. P. Freezing as a path to build complex composites. Science 2006, 311, 515–518. 10.1126/science.1120937. [DOI] [PubMed] [Google Scholar]
  15. Zhang H.; Hussain I.; Brust M.; Butler M. F.; Rannard S. P.; Cooper A. I. Aligned two-and three-dimensional structures by directional freezing of polymers and nanoparticles. Nat. Mater. 2005, 4, 787–793. 10.1038/nmat1487. [DOI] [PubMed] [Google Scholar]
  16. Yamauchi Y. Field-Induced alignment controls of one-dimensional mesochannels in mesoporous materials. J. Ceram. Soc. Jpn. 2013, 121, 831–840. 10.2109/jcersj2.121.831. [DOI] [Google Scholar]
  17. Shan F.; Lu X.; Zhang Q.; Wu J.; Wang Y.; Bian F.; Lu Q.; Fei Z.; Dyson P. J. A facile approach for controlling the orientation of one-dimensional mesochannels in mesoporous titania films. J. Am. Chem. Soc. 2012, 134, 20238–20241. 10.1021/ja309168f. [DOI] [PubMed] [Google Scholar]
  18. Furlan M.; Lattuada M. Fabrication of anisotropic porous silica monoliths by means of magnetically controlled phase separation in sol–gel processes. Langmuir 2012, 28, 12655–12662. 10.1021/la302407j. [DOI] [PubMed] [Google Scholar]
  19. Phillips K. R.; Vogel N.; Hu Y.; Kolle M.; Perry C. C.; Aizenberg J. Tunable anisotropy in inverse opals and emerging optical properties. Chem. Mater. 2014, 26, 1622–1628. 10.1021/cm403812y. [DOI] [Google Scholar]
  20. Feinle A.; Elsaesser M.; Hüsing N. Sol–gel synthesis of monolithic materials with hierarchical porosity. Chem. Soc. Rev. 2016, 45, 3377–3399. 10.1039/C5CS00710K. [DOI] [PubMed] [Google Scholar]
  21. Hartmann M.; Schwieger W. Hierarchically-structured porous materials: from basic understanding to applications. Chem. Soc. Rev. 2016, 45, 3311–3312. 10.1039/C6CS90043G. [DOI] [PubMed] [Google Scholar]
  22. Nakanishi K.; Amatani T.; Yano S.; Kodaira T. Multiscale Templating of Siloxane Gels via Polymerization-Induced Phase Separation. Chem. Mater. 2008, 20, 1108–1115. 10.1021/cm702486b. [DOI] [Google Scholar]
  23. Brandhuber D.; Torma V.; Raab C.; Peterlik H.; Kulak A.; Hüsing N. Glycol-modified silanes in the synthesis of mesoscopically organized silica monoliths with hierarchical porosity. Chem. Mater. 2005, 17, 4262–4271. 10.1021/cm048483j. [DOI] [Google Scholar]
  24. Jähnert S.; Müter D.; Prass J.; Zickler G. A.; Paris O.; Findenegg G. H. Pore structure and fluid sorption in ordered mesoporous silica. I. Experimental study by in situ small-angle x-ray scattering. J. Phys. Chem. C 2009, 113, 15201–15210. 10.1021/jp8100392. [DOI] [Google Scholar]
  25. Scherrer P. Bestimmung der Größe and der inneren Struktur yon Kolloidteilchen mittels Röntgenstrahlen. Nachr. Ges. Wiss. Goettingen, Math.-Phys. Kl. 1918, 98–100. [Google Scholar]
  26. Paris O.; Li C.; Siegel S.; Weseloh G.; Emmerling F.; Riesemeier H.; Erko A.; Fratzl P. A new experimental station for simultaneous X-ray microbeam scanning for small-and wide-angle scattering and fluorescence at BESSY II. J. Appl. Crystallogr. 2007, 40, s466–s470. 10.1107/S0021889806045444. [DOI] [Google Scholar]
  27. Scherer G. W. Dilatation of porous glass. J. Am. Ceram. Soc. 1986, 69, 473–480. 10.1111/j.1151-2916.1986.tb07448.x. [DOI] [Google Scholar]
  28. Gross J.; Reichenauer G.; Fricke J. Mechanical properties of SiO2 aerogels. J. Phys. D: Appl. Phys. 1988, 21, 1447–1451. 10.1088/0022-3727/21/9/020. [DOI] [Google Scholar]
  29. Brandhuber D.; Huesing N.; Raab C. K.; Torma V.; Peterlik H. Cellular mesoscopically organized silica monoliths with tailored surface chemistry by one-step drying/extraction/surface modification processes. J. Mater. Chem. 2005, 15, 1801–1806. 10.1039/b417675h. [DOI] [Google Scholar]
  30. Flaig S.; Akbarzadeh J.; Peterlik H.; Hüsing N. Hierarchically organized silica monoliths: influence of different acids on macro-and mesoporous formation. J. Sol-Gel Sci. Technol. 2015, 73, 103–111. 10.1007/s10971-014-3500-8. [DOI] [Google Scholar]
  31. Glatter O.Data treatment. In Small Angle X-ray Scattering; Academic Press: New York, 1982. [Google Scholar]
  32. Weinberger M.; Puchegger S.; Rentenberger C.; Puchberger M.; Hüsing N.; Peterlik H. Mesoporous dendrimer silica monoliths studied by small-angle X-ray scattering. J. Mater. Chem. 2008, 18, 4783–4789. 10.1039/b806931j. [DOI] [Google Scholar]
  33. Balzer C.; Morak R.; Erko M.; Triantafillidis C.; Hüsing N.; Reichenauer G.; Paris O. Relationship between pore structure and sorption-induced deformation in hierarchical silica-based monoliths. Z. Phys. Chem. 2015, 229, 1189–1209. 10.1515/zpch-2014-0542. [DOI] [Google Scholar]
  34. Ganser C.; Fritz-Popovski G.; Morak R.; Sharifi P.; Marmiroli B.; Sartori B.; Amenitsch H.; Griesser T.; Teichert C.; Paris O. Cantilever bending based on humidity-actuated mesoporous silica/silicon bilayers. Beilstein J. Nanotechnol. 2016, 7, 637–644. 10.3762/bjnano.7.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Balzer C.; Waag A.; Gehret S.; Reichenauer G.; Putz F.; Huesing N.; Paris O.; Bernstein N.; Gor G.; Neimark A. Adsorption-Induced Deformation of Hierarchically Structured Mesoporous Silica - Effect of Pore-Level Anisotropy. Langmuir 2017, 33, 5592–5602. 10.1021/acs.langmuir.7b00468. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm7b03032_si_001.pdf (2.1MB, pdf)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES