Sinogram Blurring Matrix Estimation from Point Sources Measurements with Rank-One Approximation for Fully 3D PET

Abstract

An accurate system matrix is essential in PET for reconstructing high quality images. To reduce storage size and image reconstruction time, we factor the system matrix into a product of a geometry projection matrix and a sinogram blurring matrix. The geometric projection matrix is computed analytically and the sinogram blurring matrix is estimated from point source measurements. Previously we have estimated a two dimensional (2D) blurring matrix for a preclinical PET scanner. The 2D blurring matrix only considers blurring effects within a transaxial sinogram and does not compensate for inter-sinogram blurring effects. For PET scanners with a long axial field of view (FOV), inter-sinogram blurring can be a major problem influencing the image quality in the axial direction. Hence estimation of a four dimensional (4D) blurring matrix is desirable to further improve the image quality. Four dimensional blurring matrix estimation is an ill-conditioned problem due to the large number of unknowns. Here we propose a rank-one approximation for each blurring kernel image formed by a row vector of the sinogram blurring matrix to improve the stability of the 4D blurring matrix estimation. The proposed method is applied to simulated data as well as real data obtained from an Inveon microPET scanner. The results show that the newly estimated 4D blurring matrix can improve the image quality over those obtained with a 2D blurring matrix and requires less point source scans to achieve similar image quality compared with an unconstrained 4D blurring matrix estimation.

I. Introduction

Positron Emission Tomography (PET) can produce three-dimensional functional images of a living subject through the injection of a radioactive tracer. Compared with other imaging modalities, such as x-ray computed tomography (CT) and magnetic resonance imaging (MRI), PET has a relatively low spatial resolution. The degradation of image resolution in PET is caused by many factors. Some of these factors are related to the radioactive decay of positrons, such as positron range [1], photon noncolinearity [2], and object scatters [3]. Other factors arise when coincidence photons interact with detectors, such as inter-crystal penetration and inter-crystal scatter [4]. In addition, noise in detector electronics can also cause mispositioning of annihilation photons.

To improve PET image resolution, the degradation factors need to be modeled in image reconstruction. The system model can be obtained by different approaches, including analytical calculation, Monte Carlo simulation, and real measurements. Some of the analytical methods are based on a parameterization of the detector response function [5]–[9]; others focus on multi-ray tracing implementations [10]–[12]. Most of the analytical methods only modeled inter-crystal penetration and could not consider inter-crystal scatter. Inter-crystal scatter is an important factor influencing system modeling and hence the quality of the reconstructed image. As shown in [13], a large percentage of the total paired coincidences are affected by inter-crystal scatter. It demonstrated that the inclusion of inter-crystal scatter in system modeling had the potential to increase model accuracy. Monte Carlo methods have been used to model inter-crystal scatter in addition to other physical factors. Examples include using simulated point source data to construct the system matrix [14], [15], as well as the estimation of detector response functions [16]–[18].

Estimating the system model from real measurements has also been investigated. In contrast to Monte Carlo methods, real data contain all physical factors that occur in a PET scanner and hence are more realistic. Point source or line source measurements are often used. The data can be used to estimate the blurring effect either in the projection space or in the image domain. As for the modeling in the projection space, Alessio et al [19], [20] and Panin et al [21] modeled the detector response function in the radial and axial directions based on parametric approximations. Tohme and Qi [22] proposed to estimate the radial and angular blurring kernel using a maximum likelihood method. As for modeling in the image domain, Reader et al [23] first approximated the image domain blurring kernel as a shift-invariant 3D Gaussian function. More complicated space-variant models were proposed later [24]–[30]. A recent review paper [31] gives a more detailed description of these methods.

In this paper, we focus on the maximum likelihood estimation of the blurring effect in the projection domain based on real data measurements. This is an extension of the sinogram blurring matrix estimation proposed by Tohme and Qi [22], where the sinogram blurring effect was limited to the in-plane radial and azimuthal angle directions. We refer to such sinogram blurring matrix as 2D blurring matrix.¹ However, in fully 3D PET data, the sinogram blurring effect can occur in all four dimensions: radial, azimuthal angle, axial, and polar angle (commonly referred to as ring difference in PET data) as illustrated in Fig. 1. For scanners with a short axial field of view (FOV), 2D blurring kernel can be sufficient because photon penetration does not cause significant blurring in the axial direction. However, for scanners with a large axial FOV, blurring effects in the axial and polar angle directions can be substantial and should be considered. For example, the Inveon microPET scanner (Siemens, Knoxville, TN) has a axial FOV of 12.7 cm and ring diameter of 16.1 cm. The maximum axial oblique angle is 38.3 degrees and is comparable to the transverse oblique angle of a line of response (LOR) at 5 cm radial offset, where crystal penetration causes substantial degradation in the radial resolution. To show the effect of axial blurring, we simulated two point sources at radial offset 0 cm and 5 cm, respectively, using the SimSET package (please see Section III.A for details) [32] and plotted the axial profiles of the 3D sinograms in different segments² in Fig. 2. Clearly the axial blurring increases with increasing ring difference and also depends on the point source location.

Fig. 1.

The sinogram blurring effects included in the 4D blurring kernel: (a) radial blurring; (b) azimuthal-angle blurring; (c) axial blurring; (d) polar-angle blurring. The geometry represents an Inveon scanner. Blocks shown in (a) and (b) are in transaxial direction; Blocks shown in (c) and (d) are in axial direction.

Fig. 2.

Axial profiles of the 3D sinogram of two simulated point sources. (a) A point source at the radial center. (b) A point source at radial offset = 5 cm.

The advantage of using 4D blurring kernel instead of 2D blurring kernel has been demonstrated previously using the microPET II scanner [34]. Compared with the 2D kernel, a 4D kernel contains a larger number of unknowns and requires more point source measurements to reduce the uncertainty in the estimation. This increases the difficulty of the experimental setup. In our experiment, a robotic arm was used and it took 3 days to acquire 4,000 point source scans. To improve the robustness of the 4D kernel estimation and hence reduce the number of measurements, here we propose a rank-one approximation for each sinogram blurring kernel image to reduce the number of unknown parameters. Low-rank constraint is an efficient way to enforce sparsity in the estimation process when performing matrix estimation. The nuclear norm is widely used to enforce rank minimization [35], [36]. To enforce the rank-one constraint, we adopt the method of power factorization which performs well with good initials [37], [38].

The main contributions of this paper include (1) the application of a 4D sinogram blurring matrix to a commercial pre-clinical PET scanner (Siemens Inveon D-PET) and (2) the development of a new 4D kernel estimation method based on rank-one approximation and comparing it with the unconstrained 4D blurring kernel. This paper is organized as follows. Section II presents the theory of the kernel estimation as well as the rank-one approximation. Section III describes the Monte Carlo simulations and real data measurements used in the evaluation. Experimental results are shown in section IV, followed by discussions in section V. Finally conclusions are drawn in Section VI.

II. Theory

A. PET data model

In PET image reconstruction, the measured data y ∈ ℝ^{M × 1} can be modeled as a collection of independent Poisson random variables and its mean ȳ ∈ ℝ^{M × 1} is related to the unknown image x ∈ ℝ^{N × 1} through an affine transform

$$\overline{\mathit{y}}=\mathit{P}\mathit{x}+\mathit{s}+\mathit{r}$$ (1)

where P ∈ ℝ^{M × N} is the detection probability matrix, s ∈ ℝ^{M × 1} denotes the expectation of scattered events, and r ∈^{M × 1} denotes the expectation of random coincidences. M is the number of lines of response (LOR) and N is the number of pixels in image space. The reconstructed image quality strongly depends on the accuracy of the detection probability matrix P, which can be decomposed to [39]

$$\mathit{P}=\mathit{\text{NABGR}},$$ (2)

where N ∈ ℝ^{M × M} and A ∈ ℝ^{M × M} are the standard diagonal matrices containing the normalization and attenuation factors, respectively. G ∈ ℝ^{M × N} is the geometric projection matrix whose (i, j)^th element denotes the probability of a photon pair produced in voxel j reaching the front faces of detector pair i in the absence of attenuation and photon-pair non-collinearity. It can be computed based on the solid angle effect [10]. B ∈ ℝ^{M × M} is the sinogram blurring matrix which models photon pair non-collinearity, inter-crystal scatter and photon penetration. Each element b_{k, i} represents the probability of recording a pair of coincident photons that impinge upon the front faces of detector pair i by detector pair k. R ∈ ℝ^{N × N} models the image domain blurring effects, such as positron range.

B. Estimating sinogram blurring matrix from point source scans

In this study, we focus on the estimation of B from real point source scans. Let S denote the total number of point source scans and y_i,s and g_j,s denote the measured projection and calculated geometric projection (with consideration of positron range) of the s^th point source scan, respectively. Based on (1) and (2), we can write the expectation of the s^th point source measurement data as

$$E(y_{i,s})=n_i\sum _{j=1}^M{b}_{i,j}{g}_{j,s},$$ (3)

where b_i,j denotes the blurring contribution from LOR j to LOR i, and n_i is the normalization factor of LOR i. The object attenuation, scatters and randoms in the point source measurements are negligible and are not considered here [40]. Given a set of point source scans, b_i,j can be estimated iteratively using the maximum likelihood expectation maximization (ML EM) algorithm as described in [22]. The update equation for b_i,j is

$$b_{i,j}^{n+1}=\frac{b_{i,j}^n}{n_i{\sum }_{s=1}^S{g}_{j,s}}\sum _{s=1}^S\frac{y_{i,s}{g}_{j,s}}{{\sum }_{j\prime =1}^M{b}_{i,j\prime }^n{g}_{j\prime ,s}}.$$ (4)

It is worth noting that using the above equation, each row of B, denoted by b_i,*, can be estimated independently of other rows. This substantially reduces the memory requirement in the kernel estimation procedure and the process can be easily parallelized on multiple computers. In comparison, it is more straightforward to compute one column of B at a time by using analytical calculation (e.g., [6]) or Monte Carlo methods (e.g, [18], [39]). As each column of B represents the contributions of events originated in a given LOR to all other LORs, we commonly refer to it as a donor-based blurring kernel; conversely, we refer to each row of B as a receiver-based blurring kernel because it represents the contributions of events to a particular LOR from all other LORs.

C. Rank-one approximation of 4D blurring kernels

To improve the robustness of the 4D kernel estimation, we propose a rank-one approximation. Specifically, we consider one row of B at a time. We arrange b_i,* into a D × D matrix B_i, where the (k, l)th element contains the contribution to LOR i from the LOR formed by detector k and detector l, and D is the number of detectors. The rank-one approximation is to approximate this D × D matrix by a tensor product of two D × 1 vectors p and q:

$${\mathit{B}}_i={\mathit{p}}_i{\mathit{q}}_i^T.$$ (5)

Vectors p and q can be considered as receiver-based detector response functions.

Previously rank-one approximation has been used to compute donor-based blurring kernels using Monte Carlo simulation of collimated photons [18], [39], in which case the tensor product is easy to understand because the detections of two coincident photons are independent of each other. However, enforcing rank-one constraint on donor-based blurring kernels in the kernel estimation is difficult because donor-based blurring kernels (columns of B) are coupled in the update equation (4) and all the elements of B have to be estimated simultaneously. This would not only increase the memory requirements by orders of magnitude, but also prolong the computational time because of the difficulty in parallelization. For fast kernel estimation, we propose to enforce rank-one constraint on receiver-based kernels. We note that if the donor-based kernels were shift invariant, B would be a block Toeplitz matrix and then receiver-based kernels and donor-based kernels would have the same rank. We shall show later using computer simulation that the approximation is reasonable for a real 3D PET scanner.

Using the rank-one approximation, the log-likelihood function in terms of p_i and q_i is

$$L({\mathit{p}}_i,{\mathit{q}}_i)=\sum _{s=1}^S{y}_{i,s}\text{ log}(n_i\sum _{l=1}^D\sum _{k=1}^D{p}_{i,l}{q}_{i,k}{g}_{h(k,l),s})-n_i\sum _{l=1}^D\sum _{k=1}^D{p}_{i,l}{q}_{i,k}{g}_{h(k,l),s},$$ (6)

where h(k, l) is the mapping from the detector pair index (k, l) to the linear index of the LOR formed by detectors k and l in the sinogram. Equation (6) is a biconvex function, i.e., it is a convex function of q_i (p_i) for a fixed p_i (q_i). Our strategy to solve this ML problem is to update p_i and q_i alternately using the ML EM update equation. Fixing q_i, the update equation of p_i is

$$p_{i,l}^{n+1}=\frac{p_{i,l}^n}{n_i{\sum }_{s=1}^S{\sum }_{k=1}^D{q}_{i,k}^n{g}_{h(k,l),s}}\sum _{s=1}^S\sum _{k=1}^D\frac{q_{i,k}^n{g}_{h(k,l),s}{y}_{i,s}}{{\sum }_{l\prime =1}^D{\sum }_{k\prime =1}^D{p}_{i,l\prime }^n{q}_{i,k\prime }^n{g}_{h(k\prime ,l\prime ),s}},$$ (7)

and fixing p_i, the update equation of q_i is

$$q_{i,k}^{n+1}=\frac{q_{i,k}^n}{n_i{\sum }_{s=1}^S{\sum }_{l=1}^D{p}_{i,l}^{n+1}{g}_{h(k,l),s}}\sum _{s=1}^S\sum _{l=1}^D\frac{p_{i,l}^{n+1}{g}_{h(k,l),s}{y}_{i,s}}{{\sum }_{l\prime =1}^D{\sum }_{k\prime =1}^D{p}_{i,l\prime }^{n+1}{q}_{i,k\prime }^n{g}_{h(k\prime ,l\prime ),s}}.$$ (8)

The above estimation is similar to the power factorization method in compressed sensing. Though it is a non-convex problem, it can perform well when the number of measurements is large [37], [38].

D. Simplification by exploiting symmetries

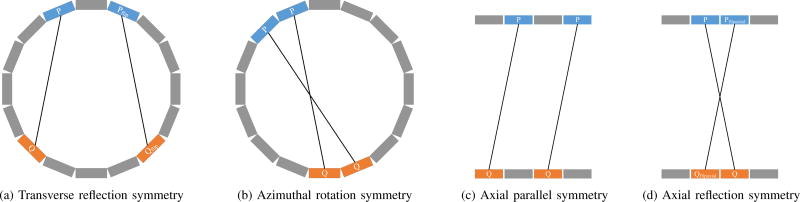
The following symmetries are used to reduce the number of unknowns in the kernel estimation: transverse reflection symmetry, azimuthal rotation symmetry, axial parallel symmetry, and axial reflection symmetry, as illustrated in Fig. 3. Note that the azimuthal rotation symmetry is only valid for rotation angles corresponding to one or multiple detector blocks. As a result, we need to estimate the blurring kernels for the number of azimuthal angles that is equal to the number of transaxial crystals in a detector block. For the axial parallel symmetry, we consider p (and q) to be the same for all parallel axial planes because of the following two reasons: (1) the axial gap between blocks in the Inveon scanner is much smaller than the transaxial block gap and the axial crystal pitch is constant; (2) all the axially parallel LORs share the same axial incident angle. For the transverse reflection and axial reflection symmetries, the p and q vectors also need to be flipped in the reflected direction. After exploiting these symmetries, the update equations in (7) and (8) are modified to include summation over all the sinogram elements sharing the same blurring kernel.

Fig. 3.

The symmetries used in the implementation. (a) Transverse reflection symmetry: the p and q vectors are flipped in the transaxial direction for radial bins symmetric to the center radial bin; (b) azimuthal rotation symmetry: the p and q vectors are the same after every 20 (number of transaxial crystals in one block) azimuthal-angle bins; (c) axial parallel symmetry: the p and q vectors are the same for all parallel axial planes; (d) axial reflection symmetry: the p and q vector are flipped in the axial direction.

In addition, as the inter-crystal blurring only happens in a few adjacent crystals, the p and q vectors are only nonzero in a small neighbourhood near the LOR of interest. In our experiment, we set the window size of p and q to 11 (transaxial) × 11 (axial). Therefore, the total number of unknown parameters to be estimated for each blurring kernel is 2 × 11 × 11 = 242 with the rank-one approximation. In comparison, the number of unknown parameters without the rank-one approximation is 14,641. As we will demonstrate later, the rank-one approximation substantially improves the robustness of the 4D kernel estimation, especially when the number of point source measurements is limited.

III. EXPERIMENTAL METHODS

A. Monte Carlo Simulation

Computer based Monte Carlo simulation was performed to study the accuracy of the rank-one approximation and the effectiveness of the 4D kernel in reconstruction. An Inveon microPET [41] was simulated using the SimSET (v2.9.2 package with the standard default block setting). The Inveon scanner has a ring diameter of 16.1 cm with a transaxial FOV of 10 cm and an axial FOV of 12.7 cm. The system contains 4 detector rings with 16 detectors per ring. Each detector consists of an array of 20 × 20 crystals with a crystal size of 1.51 × 1.51 × 10 mm³ and a crystal pitch of 1.59 mm in both transaxial and axial directions. Reconstructed images are represented by a 200×200×159 matrix with a voxel size of 0.5×0.5×0.796 mm³.

1) Point source simulation

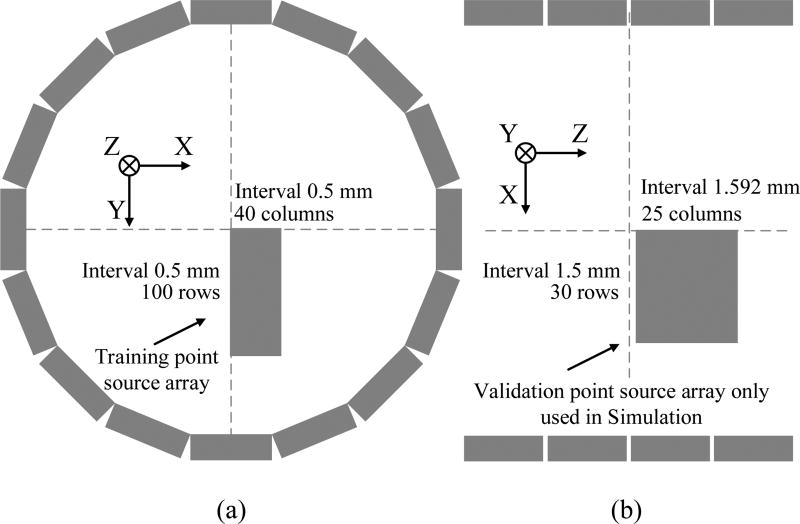
To study the blurring kernel estimation, 4,000 points were simulated inside the Inveon scanner arranged on a rectangular grid as shown in Fig. 4(a). The grid is located in the 79^th image plane, and has 100 rows and 40 columns with a 0.5-mm spacing between adjacent points in both the horizontal and vertical directions. A total of 300 million events were simulated at each point location to match the real point scans to be described later. In the blurring kernel estimation, the geometric projection g_j,m was obtained by forward projecting simulated point source images using the geometrical system matrix G, which was computed by the multi-ray tracing method as described in [10] with the detector sampling points located only on the surface of the crystal and without considering the photon penetration effect. We estimated the 2D blurring kernels and 4D blurring kernels with and without rank-one approximation. To demonstrate the improvement in robustness by using the rank-one approximation, we also estimated the 4D kernels using only 100 point sources located along the y-axis in Fig. 4(a).

Fig. 4.

(a) The training source positions used in the simulation and real point source scans. The point source array has 100 rows and 40 columns. The distance between the neighboring point sources is 0.5 mm both vertically and horizontally. (b) The validation source positions used in simulation. The array has 30 rows and 25 columns. The distance between neighboring points is 1.5 mm in the radial direction and 1.59 mm in the axial direction.

To measure the accuracy of the kernel estimation, we simulated another set of point source array in the x-z plane for validation as shown in Fig. 4(b). The validation set has 30 rows and 25 columns with an axial spacing (z direction) of 1.59 mm and radial spacing (x direction) of 1.5 mm. Note that the oblique sinograms of the radially and axially offset point sources cover LORs outside the non-zero support of the training set sinogram even after applying all the symmetries. Thus they can assess potential problems of over-fitting the training data. The accuracy of the estimated kernel was measured by the RMSE defined as

$$\text{RMSE}=\sqrt{\frac{{\sum }_i{(y_i-{\hat{y}}_i)}^2}{{\sum }_i{y}_i^2}},$$ (9)

where y_i and ŷ_i denotes the SimSET simulated sinogram and the predicted sinogram for a point source.

2) Phantom simulation

To study the effect of 4D kernels on image reconstruction, a hot rod phantom and a NEMA phantom were simulated. The simulated hot rod diameters are 1 mm, 1.3 mm, 1.8 mm, 2.3 mm, 2.7 mm, and 3.2 mm, respectively. It was oriented orthogonal to the scanner axis to assess the axial resolution in reconstructed images. The position of the center of the phantom had an axial offset of 16.7 mm and a radial offset of 21 mm. A uniform water cylinder was used as the attenuation media. A total of 96 million counts were recorded. The NEMA phantom was placed at the center of the FOV. The diameter of the four hot spheres were 2.5 mm, 3.25 mm, 4.25 mm, and 5.5 mm, respectively. Twenty realizations were simulated and about 90 million events were collected in each dataset.

The MLEM algorithm was used in all reconstructions. Attenuation and normalization were included in the system matrix and only true events were considered. For the hot rod phantom, profiles were taken to compare the image resolution. For the NEMA phantom, volumes of interest (VOIs) matching the individual sphere sizes were drawn to evaluate the contrast. Sixty background ROIs were drawn on 5 transaxial slices with an axial separation of 20 mm. The background ROI size was chosen to match the size of each hot sphere. Contrast recovery coefficient vs. standard deviation (CRC-STD) curves were plotted to compare the image quality. The background STD was computed as

$$\text{STD}=\frac{1}{K_b}\sum _{k=1}^{K_b}\frac{\sqrt{\frac{1}{R-1}{\sum }_{r=1}^R{(b_{r,k}-{\overline{b}}_k)}^2}}{{\overline{b}}_k},$$ (10)

where b_r,k is the mean of the k^th background ROI in realization r, ${\overline{b}}_k=1/R{\sum }_{r=1}^R{b}_{r,k}$ is the average of the ROI means over R = 20 realizations, and K_b = 60 is the number of background ROIs in each image.

B. Real data

1) Point source measurements

A ²²Na point source (0.3 mm, 132 µCi) encapsulated in Lucite was scanned at 4,000 locations inside the Inveon FOV at the same positions as shown in Fig. 4(a). The process was automated by using a 3D robotic arm (DENSO Robotics, Long Beach, CA). The point source was scanned for 1 minute at each location, generating an average of 16.7 million events per point. The data were used to estimate 4D blurring kernels with and without the rank-one approximation as described in the Monte Carlo simulation. Since the positron range of the point source is much smaller than the scanner resolution, we did not explicitly model the positron range, but used a 0.5-mm voxel, which is slightly larger than the physical size of the point source, to partially compensate the positron range effect in the geometric projection and set R to the identity matrix.

A ultra micro hot rod phantom was scanned in the Inveon scanner oriented perpendicular to the axial direction at the center of the FOV. The rod diameters are 0.75 mm, 1 mm, 1.35 mm, 1.7 mm, 2.0 mm, and 2.4 mm, respectively. The phantom was filled with 100 µCi ¹⁸F-FDG and scanned for 15 min. A total of 142 million counts were detected. Random events were estimated using the singles rates provided by the scanner and no attenuation and scatter correction were performed.

Furthermore, a ¹⁸F-FDG scan of a mouse was obtained. The injected dose was 230 µCi and 1.06 billion events were detected during a 60-minute scan. Random correction was performed by the scanner. No correction was performed for attenuation and scatters. All real data were reconstructed into a 256×256×159 matrix with a voxel size of 0.194×0.194×0.796 mm³, which is the default high-resolution setting on the Inveon scanner. The MLEM algorithm was used in all reconstructions. For quantification, myocardium and the left ventricle were manually segmented in six adjacent slices based on the reconstructed image of the unconstrained 4D blurring kernel. We kept a 2-pixel gap between the blood pool and myocardium ROIs to exclude some partial volume voxels. The contrast between the myocardium and the blood pool in the left ventricle was quantified to compare image quality.

C. Practical considerations

To reduce the memory requirement and accelerate the kernel estimation procedure, sparse matrix format was used for all point source projections. Furthermore, any value less than 1% of the maximum value in a sinogram was set to zero. The 4D kernel estimation was implemented in C and the total computation time was 360 hours on 10 computers with dual 8-core Intel Xeon E5-2650 processors using 4,000 points, and 20 hours using 100 points.

When using the rank-one approximation, the objective function is a biconvex function of the unknown parameters p and q, which means that there may exist local maxima. When using 4,000 points, a uniform initial image was sufficient to obtain good results. However, when only 100 points were used in the kernel estimation, a better initial image is required for kernels of large ring differences (>15). In this case, we used the kernel estimated for ring difference of 10 as the initial values for ring differences greater than 10. A small positive value was added to make all initial values of p and q positive.

After the blurring kernels were estimated, we re-computed the sinogram normalization factors taking the newly estimated blurring matrix into account. This was done by taking the ratio between a measured sinogram of a uniform cylinder and the forward projection of the same cylinder. It can also be computed using the ML estimation procedure proposed by Bai et al [42].

D. Methods to compare

For comparison, all the phantom data and real mouse data were reconstructed using no blurring kernel, 2D kernel, and 4D kernel with and without rank-one constraint. In addition, we include a 3D sinogram blurring kernel by combining the 2D kernel with a spatially invariant axial blurring kernel. The axial blurring kernel was estimated using the counts distribution of the center point source along the axial direction in the direct planes.

IV. RESULTS

A. Kernel accuracy evaluation

Fig. 5(a) compares the sinogram RMSE maps for the validation point sources. First, we can see that all 4D and p-q kernels have less RMSE than the 3D kernel does. Second, when 4,000 point sources are used, both the unconstrained 4D kernel and p-q kernel estimations work well with relatively low RMSE. However, when only 100 point sources are used, the unconstrained 4D kernel results in very large RMSE for a subset of the validation points, because the oblique sinograms of those point sources contains non-zero LORs outside the support of the training set. In comparison, the p-q kernel with 100 points still works well and increases the RMSE only slightly. This clearly demonstrates the robustness of the p-q kernel estimation and the benefit of the rank-one approximation.

Fig. 5.

(a) The sinogram RMSE maps for the validation point sources. The maximum RMSE value of the 4D,100 case reaches 140 and is thresholded to allow better comparison with other kernels. The location of the point sources in each map corresponds to the array shown in Fig. 4(b). (b) RMSE of different segments for the validation point sources.

To further investigate the kernel accuracy, we plot the sinogram RMSE as a function of the segment (i.e., ring difference) in Fig. 5(b). Note that here the relative RMSE is calculated with respect to the L-2 norm of the sinogram in each segment, so the values are different from those shown in Fig. 5(a). We see that the p-q kernel results in lower RMSE than the unconstrained 4D kernel using either 4,000 points or 100 points. The sharp increase of RMSE for segments greater than 20 is due to missing data in fully 3D PET. For those large oblique angles, PET data may not cover a radially off-centered point at all azimuthal angles. Therefore, the amount of useful data for estimating blurring kernels of those large segments is less than the amount of data in lower segments. The 4D kernel with 100 points exhibits large RMSE for segments greater than 23, which is also the reason for the large RMSE shown in Fig. 5(a). The large sinogram RMSE of the 4D kernel with 100 points will result in severe artifacts in the phantom reconstructions to be shown later.

B. Simulated phantom reconstruction

Fig. 6 shows the reconstruction results of the simulated hot spot phantom. Vertical profiles along the rods of three different sizes are shown. From the images and profiles we can see that the 4D and p-q kernels result in higher axial resolution than either the 2D or 3D kernels. With the rank-one approximation, the robustness of the 4D kernel estimation is substantially improved as the p-q kernel estimated from only 100 points provides similar image quality as that estimated from 4000 points. In comparison, the unconstrained 4D kernel estimated from the same 100 points results in noticeable artefacts in the reconstructed image. The severe artifact is caused by the poor kernel quality estimated from limited data and it matches the region of the validation point sources that exhibit large RMSE in Fig. 5.

Fig. 6.

Reconstruction of the simulated hot rod phantom using different blurring kernels (MLEM, 500 iterations). (a) A central sagittal slice of the hot rod phantom; (b) vertical profiles through the smallest rods; (c) vertical profiles through the second smallest rods; (d) vertical profiles through the fourth smallest rods.

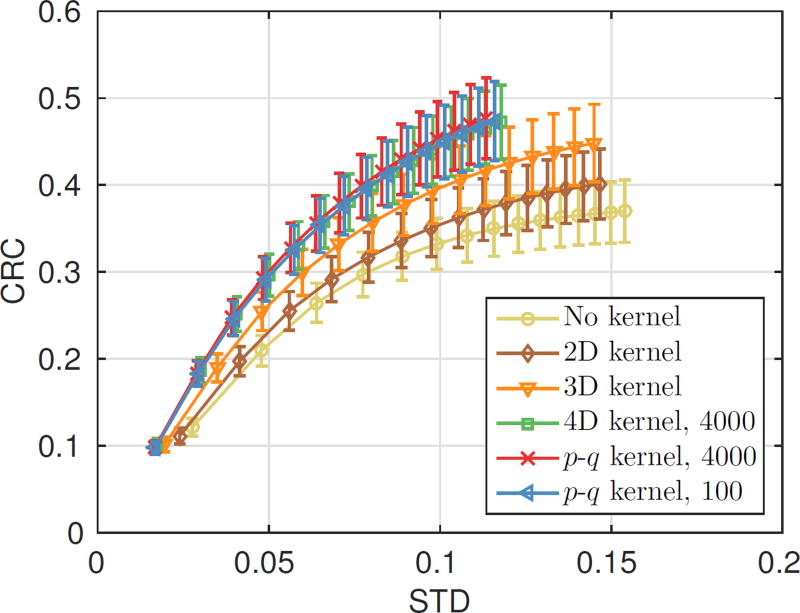
Fig. 7 shows the center transaxial and coronal slices of the reconstructed NEMA phantom images. The CRC-STD curve is also shown in Fig. 8 for the smallest hot sphere. The curves for the other three larger spheres are similar and are included in the supplemental material. We can see that the reconstruction using the 2D blurring kernel is better than the reconstruction without blurring kernel and the reconstructions using 4D kernels and p-q kernel are better than that using the 2D kernel and 3D kernel. The p-q kernel using 100 points has similar performance to the p-q kernel and 4D kernel estimated from 4,000 points.

Fig. 7.

The central transaxial and coronal slices of the reconstructed NEMA phantom using different blurring kernels for one noisy realization (MLEM, 70 iterations).

Fig. 8.

The CRC-STD curve for the smallest hot sphere (diameter = 2.5 mm) plotted at every 10 iterations. A total of 150 MLEM iterations are shown in each curve. The error bars were estimated from 20 realizations.

C. Real data reconstruction

Fig. 9 shows a sagittal slice of the reconstructed ultra micro hot rod phantom and vertical profiles through selected rods. Similar to the Monte Carlo simulation results, we can see that 4D kernels improve the axial resolution of reconstructed image and the robustness of the 4D kernel estimation is improved by using the rank-one approximation.

Fig. 9.

Reconstructed ultra micro hot rod phantom using different blurring kernels (MLEM, 500 iterations). (a) a sagittal slice of the reconstructed images (b) vertical profiles through selected hot rods shown in (a).

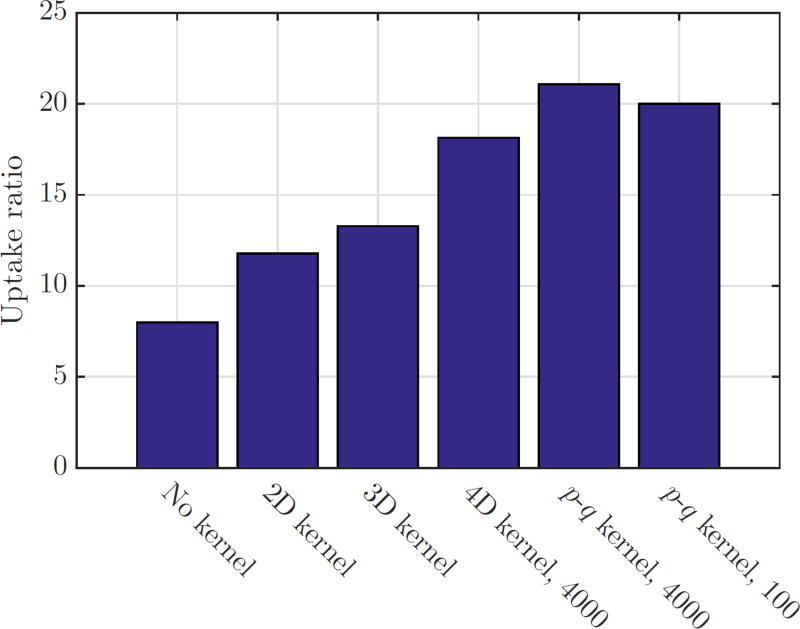
Fig. 10 shows a coronal slice of the whole-body mouse reconstruction. Vertical profiles through the heart region are plotted in Fig. 11. We can see that 4D blurring kernels improve the contrast of the myocardium. The ratios between the myocardium and left ventricle are shown in Fig. 12, which clearly shows the benefits of using 4D kernels and the rank-one approximation.

Fig. 10.

A coronal slice of the mouse reconstruction using different blurring kernels (MLEM, 240 iterations). The bottom row shows a zoomed-in view of the heart region. The blue line indicates the location where the vertical profile in fig. 11 is taken.

Fig. 11.

Comparison of vertical profiles through the mouse heart.

Fig. 12.

The uptake ratios between the myocardium and the blood pool in different reconstructed images.

V. DISCUSSION

Compared with the 2D blurring kernel estimation, 4D kernel greatly increases the number of unknowns in the estimation. Overfitting can be a serious problem without using prior information, especially when the measurement data are limited. From the update equation (4), we can see that a necessary condition for b_i,j to be estimable is Σ_s g_j,s > 0. After applying all the symmetries, this necessary condition is met for all LORs when 4,000 point sources are used. In the case of 100 point sources, this necessary condition is also met for almost all LORs from segment 1 to segment 24 (ring difference less than 73), which is why the kernel estimation still works. However, due to the limited amount of data, some estimated blurring kernels at large segments (24 and above) are heavily affected by noise and scattered events and contain erroneously large b_i,j values in isolated bins. These erroneous b_i,j values result in large sinogram RMSE in segments 24–27 as shown in fig. 5, which in turn results in reconstruction artifacts shown in fig. 6. Using the rank-one approximation, the number of unknowns is reduced, which improves the robustness of the estimation. Even with the same limited data, the estimated p-q kernels are still reasonable and produce reconstructed images with good quality.

When reducing the number of points from 4,000 to 100, we chose 100 points on the y-axis. This is a convenient choice using the existing data, but may not be the optimal configuration. A previous study [43] has examined the effect of point source configuration on 2D kernel estimation and found that for a given total acquisition time a finer sampling grid yields better estimation of 2D kernels. For 4D or p-q kernel estimation, it may be beneficial to include point sources at different axial position to improve the kernel accuracy for the most oblique segments. This will be a subject of future study.

Comparing reconstructed images, we found that all 4D kernels (constrained and unconstrained) improve the axial resolution of the reconstruction. This is because photon penetration along the axial direction becomes more prominent in a PET scanner with a long axial FOV (relative to its ring diameter). For the Inveon scanner that was used in this study, the maximum oblique angle is 38.3 degree. We expect the impact of 4D kernels will be even greater for future PET scanners with even longer axial FOV (larger oblique angle), e.g., the 2-m long total-body PET scanner [44]. We noticed a slight edge-enhancement artifact in the piecewise-constant NEMA phantom images (Fig. 7), but not in real animal images. This phenomenon is common to all resolution models [31] and methods to mitigate this effect have been investigated [45].

VI. CONCLUSION

In this paper, we evaluated the 4D kernel estimation using an Inveon PET scanner and proposed a rank-one approximation to improve the robustness of the 4D kernel estimation. Both computer simulation and real data show that the 4D kernel can improve the axial resolution of reconstructed image and the rank-one approximation can substantially reduce the number of point source measurements that is required as well as the involved computational burden. We expect that the application of a 4D blurring kernel will be more important for future PET scanners with a longer axial FOV.