Quantum-like dynamics applied to cognition: a consideration of available options

Abstract

Quantum probability theory (QPT) has provided a novel, rich mathematical framework for cognitive modelling, especially for situations which appear paradoxical from classical perspectives. This work concerns the dynamical aspects of QPT, as relevant to cognitive modelling. We aspire to shed light on how the mind's driving potentials (encoded in Hamiltonian and Lindbladian operators) impact the evolution of a mental state. Some existing QPT cognitive models do employ dynamical aspects when considering how a mental state changes with time, but it is often the case that several simplifying assumptions are introduced. What kind of modelling flexibility does QPT dynamics offer without any simplifying assumptions and is it likely that such flexibility will be relevant in cognitive modelling? We consider a series of nested QPT dynamical models, constructed with a view to accommodate results from a simple, hypothetical experimental paradigm on decision-making. We consider Hamiltonians more complex than the ones which have traditionally been employed with a view to explore the putative explanatory value of this additional complexity. We then proceed to compare simple models with extensions regarding both the initial state (e.g. a mixed state with a specific orthogonal decomposition; a general mixed state) and the dynamics (by introducing Hamiltonians which destroy the separability of the initial structure and by considering an open-system extension). We illustrate the relations between these models mathematically and numerically.

This article is part of the themed issue ‘Second quantum revolution: foundational questions’.

1. Introduction

Throughout the history of psychological research, a key objective has been to understand the general principles which guide decision-making. Important advances have been made and today most psychologists would agree that the principles of classical probability theory (CPT) can characterize human decision-making in many cases [1–3]. The problem arises because, in some cases, behaviour seems persistently at odds with the prescription of CPT. Tversky & Kahneman are best known for initiating a highly influential empirical research programme identifying so-called paradoxes, that is, decision results which appear paradoxical from the perspective of CPT, but several other researchers have engaged with similar research ([4–6], see also [7–9]). Such results have led to intense debate regarding the role of CPT in psychological theory, and also more generally the extent to which we are justified in considering human decision-making as rational. Tversky & Kahneman's position has been that decision-making is best understood on the basis of heuristics and biases (see the above references). However, an alternative approach is to consider whether a description of behaviour with a formal probabilistic framework is possible, but perhaps CPT is too limited to provide a comprehensive framework—either CPT needs to be extended with additional probabilistic principles or a more general probabilistic framework should be adopted.

Quantum probability theory (QPT) can provide such an extension. We call QPT the rules for how to assign probabilities to events from quantum mechanics, without any of the physics. QPT is, in principle, applicable in any situation where there is a need to quantify uncertainty. However, whether QPT will provide a suitable descriptive framework clearly depends on whether the structure of the situation that requires modelling is consistent with that of QPT. The paradigmatic results that have been offered as challenging the descriptive adequacy of CPT in decision-making (and cognition generally) involve violations of the law of total probability (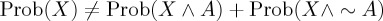), conjunction or disjunction fallacies (e.g. 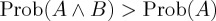) and order effects (e.g. 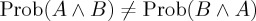). QPT is particularly suitable for accommodating such results, because QPT is a framework for probabilistic assigning sensitive to context; changes in context can lead to interference effects, which allow QPT to violate, for example, the law of total probability or commutativity in conjunction. Indeed, a number of researchers have been engaged with the exploration of QPT in psychological modelling for such situations that are problematic for CPT [10–13]. Most of these researchers take the view that a complete picture of decision-making requires us to invoke both CPT and QPT principles, possibly the former for better practised, familiar situations.

QPT cognitive models have taken two forms. First, some models have involved static representations. The modeller aims to provide a representation of the available information, including an assumed mental state, such that the application of QPT rules leads to probabilities consistent with the observed behaviour [10,14–19].

Second, some models have allowed dynamical change, so that, for example, the mental state changes as a result of the available information and the evolution of the mental state (and corresponding probabilities) are set up in a way that matches the observed behaviour [11,20–22]. The difference between static and dynamical models partly relates to modelling objectives, with dynamical models sometimes presented as having a greater process component, whereas static models tend to be focused on the just representation and relevant computational principles (cf. [23,24]). The denomination ‘dynamical’ here does not intend to model any physical processes in the brain substrate itself. Quantum-like modelling in cognition is essentially a phenomenological approach that not only provides the kinematical evolution of states in a person's belief space, but also can detail the various transfers of these probability amplitudes. The denomination ‘dynamical’ captures the fact that, in the model, the cognitive evolution is driven by parameters in the Hamiltonian and Lindbladian operators, which should be psychologically interpretable and of which the relative parameter amplitudes can be used to assess the importance of constituent transfer processes.

The focus of the present work is cognitive QPT dynamical models. Notwithstanding their descriptive success, it is typically the case that many simplifying assumptions are made when specifying the relevant dynamical processes. How important are such simplifications and what kind of modelling assumptions do they entail? If one is to allow QPT dynamics in their full complexity, what is the ensuing modelling flexibility and is it likely that this flexibility will be relevant in cognitive modelling? It is worth bearing in mind that QPT is one of the most technically sophisticated theories developed by the human mind. As we shall see in this work, even for simple situations, QPT dynamical systems can provide an extremely rich structure.

2. Overview of some dynamical quantum probability theory cognitive models

In this section, we will provide a brief overview of the kind of dynamical QPT models that have been proposed in cognitive theories. The overview is not meant to be comprehensive; rather, it is meant to illustrate the kind of simplifications which are characteristic of all QPT cognitive applications involving dynamics. This overview will also serve to briefly introduce the main QPT concepts, so that some of the main ideas of the paper can remain reasonably accessible to non-specialists, though we will not attempt a systematic introduction to all the technical concepts in the paper (for recent tutorials, see [25,26]).

We start with the dynamical model of Pothos & Busemeyer [13] concerning the so-called disjunction effect in the Prisoner's Dilemma (PD) [27]. Participants were given a PD game, with the twist that in some trials (labelled as bonus trials), the opponent's action was communicated prior to the participant's action. When participants were told that the opponent was going to cooperate (C), the probability to defect (D) was high, because that was how the payoff matrix was arranged. Participants were also likely to D when told the opponent was going to D. Interestingly, when participants were not given any information about the opponent's action, the probability to D, Prob(D), dropped. This result shows a violation of the law of total probability, because 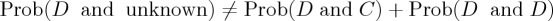, where in the conjunctions the first premise is for the participant's action and the second is for the opponent's (note that, for all so-called violations of CPT principles, it is always possible to create a CPT model consistent with any finding, as long as post hoc conditionalizations are allowed, but we are not considering such approaches presently).

The QPT model for this disjunction effect is based on the idea that participants have some initial representation of the probabilities of defecting or cooperating, assuming knowledge of the opponent cooperating or defecting. This mental representation corresponds to the state vector in QPT. Then, the information relevant to the decision (notably the different payoffs, but also a process of cognitive dissonance) is taken into account through an assumed thought process, which changed the mental state with time. Eventually, this dynamical evolution was stopped and the mental state would be examined regarding the relative probabilities of defecting or cooperating.

The key ingredient in this QPT model was the Hamiltonian operator. In QPT, evolution of a system is specified through Schrödinger's equation, according to which 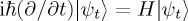, where H denotes the Hamiltonian operator and 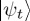is the state vector, a vector in multidimensional complex vector space (with some additional convergence properties) called Hilbert space, which embodies all the information that is possible to learn about the state vector. More precisely, provided with a dot product is a finite-dimensional Hilbert space. The Hamiltonian operator is a Hermitian operator (an operator is Hermitian if it is equal to the complex conjugate of its transpose). The constant is a scaling constant (in QPT it has a specific meaning; in psychological applications it is often just set to 1). The solution of Schrödinger's equation is 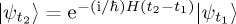, where 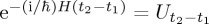is a unitary operator; unitary operators have the property that their conjugate transpose is equal to their inverse.

In this model, the overall Hamiltonian was specified in 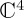, but the structure of this space was such that a part was separable, in , and a part was not separable (note that, in physics, it is typically the case that separability concerns 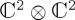, but the structure of the problem we consider lends itself better to ). In fact, most QPT dynamical cognitive models are specified so that they have a part which is separable, that is, it can be written as , and a part which is not separable, so that it can only be specified in 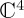. There is a reason why this is the case: most of the current, interesting empirical findings which are driving the application of QPT in cognition involve a binary decision. It makes sense to model binary decisions in a two-dimensional space (such as 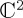). Also, modelling in such a separable way retains consistency with the law of total probability, when (binary) decisions under two conditions are involved. Using the PD example, suppose that there is one Hamiltonian which corresponds to the dynamical evolution of the mental state, given knowledge that the opponent is cooperating, H_C, and another one, given knowledge that the opponent is defecting, H_D. Suppose also that P_D denotes the projector operator for the measurement of whether the opponent intends to D or not; in QPT, a projector applied onto a mental state is like a query corresponding to the particular question represented by the projector. Then, 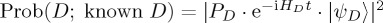and 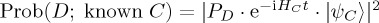, where and 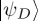encode the mental states depending on whether the participant knows the opponent will C or D. Crucially, in the unknown case, we could assume 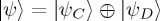and H = H_C⊕ H_D, where now 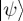and H are defined in 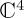. Then, 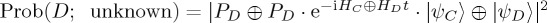. But, 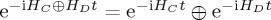, an identity which can be fairly easily reproduced using the Taylor expansions for each exponential. We can write 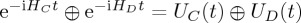, where U_C and U_D are the relevant unitary operators (which are functions of time). Then, . In other words, if the structure of the Hamiltonian is separable, then the law of total probability has to be obeyed by QPT, in the same way as it holds for CPT. To allow for violations of the law of total probability to develop, we would need a Hamiltonian along the lines 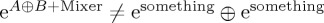, where each of A and B are defined in a 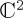space and the Mixer in .

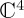The modelling approach of Pothos & Busemeyer [13] was exactly to specify the dynamics in a way that a part was separable and another part (the mixing element) was not separable. The role of the mixing element is primarily to transfer amplitude from one 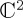space to another, so that interference effects arise which allow violations of the law of total probability. Although we will consider options for mixing elements in this work, our initial focus are the building blocks of the dynamics, in this case H_C and H_D. These are just 2 × 2 Hermitian matrices. What are the options for their structure and how do they affect the state's evolution?

In general, for the space of 2 × 2 complex Hermitian matrices, a basis consists of the identity matrix and the three Pauli matrices, 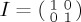, , 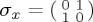, 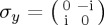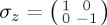. That is, any 2 × 2 complex Hermitian matrix can be generated as a linear combination of these four matrices. Note that a common notation is H = I + n · σ, where the dot now indicates a dot product and n and σ are vectors with three components; n = (n_x, n_y, n_z) needs to be normalized. It is a minor loss in generality to restrict ourselves to traceless H = n · σ, and we shall do so in this work (see also §3). In practice, as noted, the Hamiltonians proposed in current QPT cognitive models have a much simpler form.

Ignoring any mixing elements for now, Pothos & Busemeyer [13] proposed for both H_C and H_D a Hamiltonian of the form 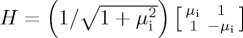, which can be written as 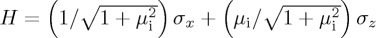. Note that the parameter µ_i was interpreted as the gain for different actions (D or C). In Trueblood & Busemeyer's [28] work on order effects in inference, the building block of the dynamics was a Hamiltonian of the form 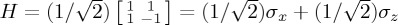. Yearsley & Pothos [29] follow this trend (of not considering σ_y) and argued that, in specifying a general Hamiltonian for a two-state system (any binary decision) in psychological modelling, a reasonable choice is just H = ωσ_x, ignoring both I and two out of the three Pauli spin matrices. Atmanspacher & Filk [30] developed a QPT model for bistable perception, that is, the shifts in interpretation that can occur when an ambiguous figure (such as the Necker cube) is presented. The dynamics in Atmanspacher & Filk's [30] work concerned the time development of the perception process and the Hamiltonian they employed was just H = σ_x.

In closing this section, we review the two key points so far. First, for many of the models, the structure A ⊕ B + Mixer, with A and B Hamiltonians in 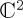, makes sense, because the model can show how the classical result (law of total probability) can be recovered and what exactly is the role of the quantum contribution (the Mixer), which allows interference effects (interference effects and violations of the law of total probability are exactly the effects which motivate a QPT approach in the first place). In all cases we reviewed above, the building block of the dynamics was a simple binary decision (and so a representation in 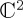). Second, all QPT dynamical models have been descriptively successful, so it does not appear that any further complexity in the Hamiltonian is needed. Indeed, these simple Hamiltonians enable analytical solutions for the relevant unitary operators and the probabilities for the relevant actions. However, there is a question of how (if at all) any additional complexity in the Hamiltonian can serve any explanatory objectives. The purpose of the next section is to introduce a generic binary decision situation and illustrate the contribution to the dynamics from each component of the Hamiltonian. To clarify, we do not seek to provide a specific model for a specific empirical situation; but rather we seek to present the possible framework for dynamical modelling in QPT, for a simple, generic situation. We hope that our presentation will help inform choices regarding the development of specific dynamical models in ways that appear less ad hoc, as is arguably the case with some of the current dynamical approaches.

3. The impact of different Hamiltonian components: Bloch representation

Attempting to understand the impact of different Hamiltonian choices on the dynamics by direct inspection of analytical solutions is often fruitless; in a subsequent section, we will explore some of these analytical solutions and it will become clear that the algebraic complexity quickly obscures any intuition (we will pursue though illustrations based on numerical analysis). A useful tool in this context is the Bloch sphere, which is a geometrical representation for the dynamics of a two-state quantum system. Pure states (the contrast with mixed states will be explored later) correspond to points on the Bloch sphere given by the following identification:

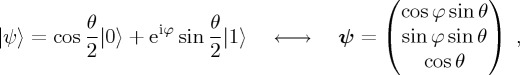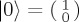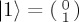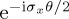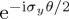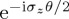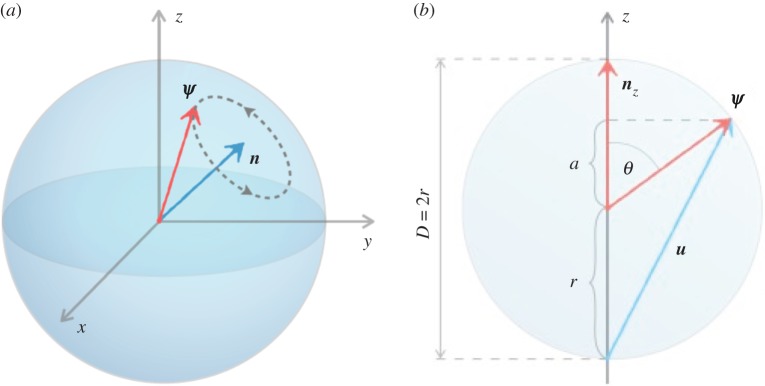
where and are a fixed computational basis. Importantly, the unitary operators , and correspond to rotations of the state vector by angle θ, around rotation axes which correspond to each of the x, y, z axes. That is, in the Bloch sphere representation, each of the Pauli matrices corresponds to a rotation of the state vector about a particular axis, but rotations about an arbitrary axis n = a_xn_x+ a_yn_y + a_zn_z can also be specified, which correspond to a unitary operator 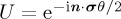(figure 1a; note that n must be normalized).

Figure 1.

(a) The Bloch sphere representation, illustrating the dynamical evolution (rotation) of a state ψ, around a rotation axis n. (b) The length that corresponds to Prob_A(t), 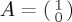, in the Bloch sphere representation (with r = 1). (Online version in colour.)

Suppose we are modelling a binary decision, such that the two relevant options are 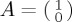and 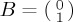, and suppose we are interested in Prob_A(t) (it is not necessary to explore Prob_B(t) separately because, using CPT or QPT rules, the probabilities for mutually exclusive and exhaustive probabilities have to sum to 1). In the Bloch sphere representation, the north z-direction corresponds to 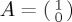and the south z-direction to 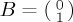. Note also that operator σ_z corresponds precisely to this observable 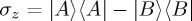(albeit with the eigenvalues 1 and −1 instead of 0 and 1 as used in the above notation for ket vectors). With some algebra, one can show that Prob(A) = (1 + ψ · n_z). This has a nice graphical interpretation, 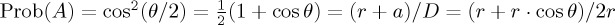, which in words is the proportion of the projection on the vertical diameter of the vector u from the south pole to the point on the sphere corresponding to the state 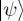(figure 1b). As a technical note of interest, the state can be represented as 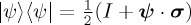(note that ψ and 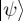both indicate a particular state, but ψ emphasizes the vector form of the state; note also that 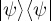is the representation of a state as a density matrix and we will consider this later).

For a fixed state vector A, there are Hamiltonians which generate the same dynamical evolution of Prob_A(t). It is useful to briefly illustrate this, because it motivates the discussion of the more general case. Let us consider the situation when 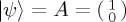. Then, 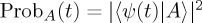, where 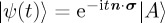, and n · σ is a general Hamiltonian. Since 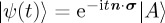, then 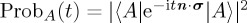. Now consider an alternative Hamiltonian, produced by rotating n by an angle a about the z-axis; the new Hamiltonian would be given by n′ · σ. The corresponding unitary operator is given by 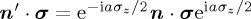. Noting that 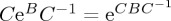(this identity is independent of whether B and C commute and can be easily verified with a Taylor expansion), we have 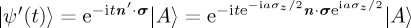. So, 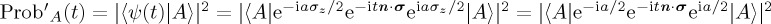. 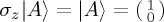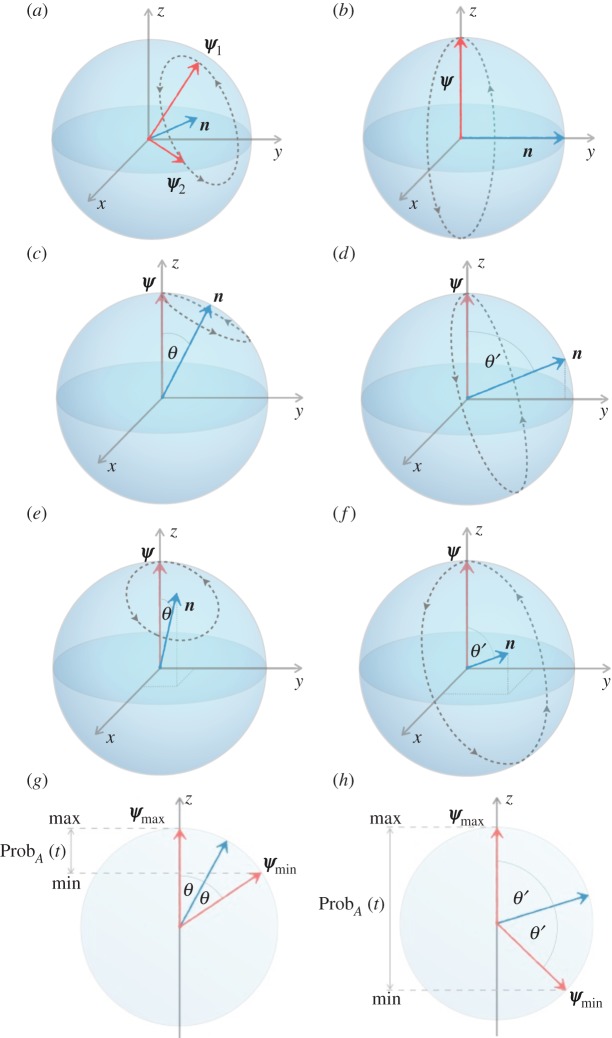The last equality employs the fact that , and then the three operators e^ia/2, e^−itn·σ and e^−ia/2 commute. So we conclude 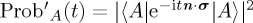, exactly as before. In the Bloch representation, it corresponds to the same behaviour of projection of the evolved state vector on the z-axis (cf. figure 2c with e and figure 2d with f). Note that this analysis relies on the particular relation between the state and the form of considered Hamiltonians. In general, the Hamiltonian will have impact on the dynamics of Prob_A(t). This is best illustrated with the Bloch sphere, in terms of the effect of each of σ_x, σ_y and σ_z on the rotation of the state vector.

Figure 2.

(a) For Hamiltonian H = n · σ, the state of the system traces a circle whose centre is n. Probability Prob_A(t) exhibits oscillatory behaviour. (b) A simple form of dynamics regarding Prob_A(t) (projection along the z-axis), where H = σ_y. Probability Prob_A(t) oscillates between 0 and 1. (c) Hamiltonian of the form H = n_yσ_y+ n_zσ_z; rotation axis n in the yz-plane at angle θ to z-axis. (d) Hamiltonian of the form H = n_yσ_y+ n_zσ_z; rotation axis n in the yz-plane at angle θ′ to z-axis. (e) Hamiltonian of the form H = n_xσ_x+ n_yσ_y+ n_zσ_z; rotation axis n at angle θ to z-axis (i.e. it obtains from that in c by rotation about z-axis). Note that the dependence of Prob_A(t) is the same as in case c, for this initial state. (f) Hamiltonian of the form H = n_xσ_x+ n_yσ_y+ n_zσ_z; rotation axis n at angle θ′ to z-axis (i.e. it obtains from that in d by rotation about z-axis). Note that the dependence of Prob_A(t) is the same as in case d, for this initial state. (g) Probability Prob_A(t) in c and e oscillate between the maximum value equal to 1 and minimal value equal to (1/2)(1 + cos 2θ) = cos²θ. (h) Probability Prob_A(t) in d and f oscillates between the maximum value equal to 1 and minimal value equal to (1/2)(1 + cos 2θ′) = cos²θ′. (Online version in colour.)

We always consider Prob_A(t), 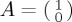. Consider a comparison between 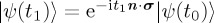and 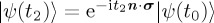, where t₂> t₁. As time increases, we can think of ψ as tracing the circumference of a disc whose centre is n. So, if 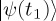is set as in figure 2a, then an increase in t will translate at first into an increased Prob_A(t), followed by a decrease; eventually, it will return to the initial value. If all we are interested in is changes in Prob_A(t) with time (or some other equivalent quantity), then the simplest choice is to consider the Hamiltonian H = σ_y and initial state 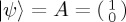as in figure 2b. In such a case, the projection along the z-axis varies all the way from +1 to −1 and so Prob_A(t) varies from 1 to 0. The main quantum-like feature of such a form of dynamics is oscillatory behaviour.

What would be the effect of introducing a rotation component along the z-axis, so that the Hamiltonian now looks like H = n_yσ_y+ n_zσ_z? As the rotation axis moves in the yz-plane from the y-axis to the z-axis, the amplitude of the oscillation is reduced and the average Prob_A(t) is increased. Therefore, in moving from a Hamiltonian of the form H = σ_y to one of the form H = n_yσ_y+ n_zσ_z, one basically increases the minimum possible value for Prob_A(t); the greater n_z relative to n_y, the higher the minimum possible value for Prob_A(t) (cf. figure 2b, c and d). The impact of introducing a σ_x component, so that the Hamiltonian is now of the more general form H = n_xσ_x+ n_yσ_y+ n_zσ_z, is subtler still. As indeed shown in figure 2b–d, the critical factor affecting the amplitude of oscillations is the angle between n and the z-axis, so that, when 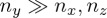(i.e. the rotation axis n is approximately in the xz-plane), one obtains max ≈ 1 and min ≈ 0; the frequency of oscillations depends on the length of vector n. Comparing figure 2c with e and figure 2d with f, one can see that rotating n towards the x-axis does not change the overall amplitude, though specific aspects of the oscillation may change. Note that the Bloch sphere picture ignores the irrelevant overall phase of the state vector, and hence this component in the general Hamiltonian may be harmlessly neglected for a single qubit, simplifying the Hamiltonian to H = n · σ. (As a word of caution, for more complex systems, the overall phase of a subsystem may lead to non-trivial interference effects; however, for the present considerations of a single qubit, we can ignore it.)

Overall, this section shows that each possible component of the Hamiltonian, σ_x, σ_y and σ_z, can have a very distinctive effect on the dynamics of the state vector and, in a general case, there is no theoretical reason to exclude any components. Of course, in specific cases, it may be that simpler Hamiltonians are descriptively adequate. In the next sections, we explore these themes further and illustrate numerically the kind of dynamical curves produced by different modelling options.

4. A hierarchy of models for dynamical evolution

In this section, we present a first set of numerical illustrations regarding the impact of different choices for the Hamiltonian on Prob_A(t), 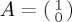. Before we do this, there is a source of complexity which we have yet to consider, concerning the way the state vector is specified. The elementary way to specify a state vector of a two-state QPT system is as a vector in a two-dimensional Hilbert space, 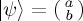, called a pure state, with a, b in 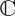. In the context of an intention to create a QPT model for a cognitive situation, such a pure state would represent the belief or mental state of the average or typical participant (that is, we assume that an ensemble of participants can be represented by a single ‘typical’ participant, who can characterize all individuals, approximately speaking). In QPT terms, to employ a pure state means that we cannot assert with more precision knowledge of the state the system is in. However, QPT offers an alternative way to represent information about the state of a system, using mixed states (represented by density matrices).

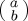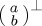A mixed state is meant to represent classical uncertainty of the particular (quantum) state of a system. For example, suppose that the individuals in our sample could be assumed to be in one of two orthogonal states, and . Then, the state of the system would be written as 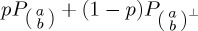, where 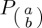indicates the projector along the 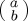ray and analogously for 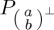. The variable p is analogous to a classical probability that any particular individual will be in state 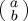. Alternatively, we could assume that participants are in one of two non-orthogonal states, so that the state of the system is 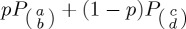. In general, a mixed state can be represented by any positive, semi-definite operator ρ, such that tr(ρ) = 1 and ρ^†= ρ. For illustration, we show the mixed state explicitly assuming a decomposition into two orthogonal states in 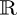; we have 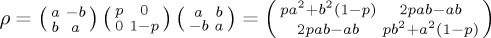. The corresponding expression for a, b in 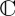is 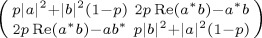, noting that * indicates the complex conjugate.

One can readily see that the number of parameters required to represent a state rises as we go from a pure state (two parameters if in 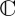, one if real) to a constrained (orthogonal) mixed state (three parameters if in 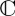, two if real). For a general mixed state with a particular decomposition into pure states, we need to count five parameters, working in 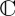(three if real), when two psychologically interpretable component states are aimed for. In a population sample, it will not always be possible to accommodate individual differences as variations from a single typical pure state. It is not uncommon for the population sample to have two distinct groupings that can be thought of as opposite in some way, e.g. risk-seeking versus risk-averse individuals in a gambling task. In such cases, it is computationally desirable to represent the relevant mental state for the decision making task as a mixed state of two orthogonal pure states. That is, the mixed state reflects our classical uncertainty of which of two pure states each participant is in. The assumption of orthogonality is partly as well an issue of keeping the total number of parameters low. The non-orthogonal mixed state is applicable when the population sample can be divided into two groups, but cannot be considered as orthogonal in some meaningful way. For example, in a gambling task, the population sample may reflect a group of participants particularly high in risk seeking and one particularly high in reward sensitivity. In such a case, the two groups are different, but it would be inappropriate to consider them as opposite, because risk seeking may partly reflect reward sensitivity.

One key problem undermining the utility of mixed states in psychology is, however, that their decomposition is not unique. This degeneracy reduces the number of parameters to three if in 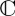(two if real), and no specification of the component vectors is assumed. If we have grounds to assume that our participant sample can be represented by two orthogonal states, then a decomposition as above can be used. However, unfortunately, there are usually alternative decompositions, involving more pure states, which result in the same mixed state. Therefore, the use of a mixed state is better seen as a general statement of the inhomogeneity of a sample, rather than as a specific statement of what is the form of this inhomogeneity. Importantly, in using a mixed state, the dynamics remains of the Schrödinger type but the outcome probabilities can be affected (in general, the maximum amplitude of oscillations is reduced). Note that, using the Bloch sphere representation, pure states are points on the surface of the sphere, but mixed states are situated within the sphere, with the maximally uniformed state (represented by the identity matrix I/2) represented by the centre of the sphere. As such, it can be intuitively seen that configurations within the Bloch sphere would, in general, produce oscillations with a smaller maximum amplitude compared to those on the surface of the Bloch sphere. We finally remark that mixed states can be used for cognitive experiments when the participants sample is, for example, a mixture of two groups of typical participants with non-orthogonal mental states. Alternatively, such states could be employed if there is just one typical participant whose mental state is itself a mixture of two non-orthogonal choices. To fully describe these situations, we would need five, not three, parameters, which would not just encode the mixed state per se, but also account for the non-orthogonal decomposition. As an interesting footnote, in physics, there is a well-developed approach for distinguishing between two non-orthogonal states by ‘generalized measurement’ through positive operator-valued measures (POVM). The idea behind it is that a mixed state always corresponds to some larger-dimensional pure state, traced over the extra degrees of freedom. These POVMs thus correspond to a projection measurement in a larger-dimensional encompassing space. Applications of POVMs in psychology are very new; see e.g. Khrennikov et al. [31] or [32]. One obvious application of POVMs is for violations of repeatability, because applying a POVM twice can easily lead to a different result (as opposed to regular projectors P with their characteristic property P² = P).

Regarding our illustration, for simple Hamiltonians it is possible to produce analytical solutions using the identity 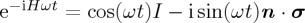, where n · σ = n_xσ_x + n_yσ_y + n_zσ_z. These correspond to the famous Rabi oscillation expressions, where ω is the Rabi frequency, which we consider as a scaling constant (for time, or whichever other quantity t corresponds to) and I is the identity matrix. In its more general form, when X² = (1+h²)I, the unitary propagator can be shown to satisfy

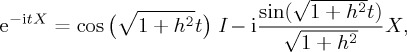with h another constant which we shall relate to mixing strength in 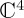in the next section. Table 1 summarizes the unitary propagator for simple Pauli matrix-based Hamiltonians and gives the corresponding outcome probabilities for state 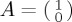starting from initial vector 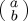in 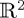, with 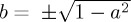. The outcome probabilities for state A over time are obtained using the QPT standard expression 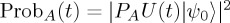, where P_A is the projector over the A eigenstate. We notice that the outcome probabilities Prob_A(t) are periodic functions with periodicity π in most cases. Moreover, we notice that by itself the Pauli matrix σ_z does not engender a time dynamics; indeed one can easily see that the diagonal structure of the Pauli matrix σ_z only produces a trivial phase to the state over time.

Table 1.

Hamiltonians expressed with Pauli matrices, with their respective time propagators (ω = 1) and outcome probabilities for pure state initial vector 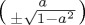in .

Hamiltonian	unitary time propagator, e−iHt	ProbA(t)
σx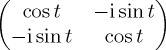
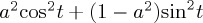σy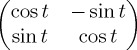
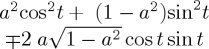σz		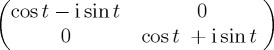a2

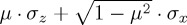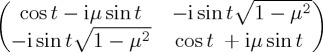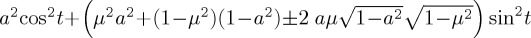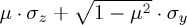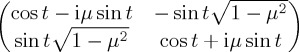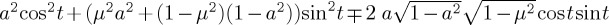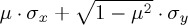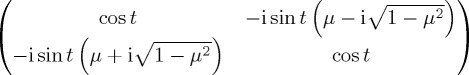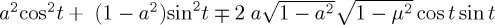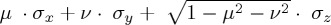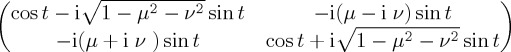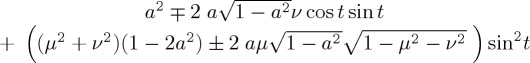The reason why we have assumed a pure state in 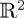for table 1 is that this is indeed the most common approach in QPT cognitive models, as a simplifying assumption. A pure, real starting state is not a theoretical requirement and particular data sets or theoretical considerations may motivate the need to adopt a more general representation for the initial state (as above). Still, even for a pure, real starting state, the complexity of the expressions in table 1 quickly increases with more complex Hamiltonians. A pertinent question is this: Assuming a modelling objective corresponding to a binary observable (which is reasonably common in cognitive models and otherwise), what would a modeller gain by considering these more complex Hamiltonians? Is there any particular reason to consider a single Pauli spin matrix—apart from σ_z, which leads to flat dynamics? We provide a series of illustrative graphs, for the restricted case represented in table 1.

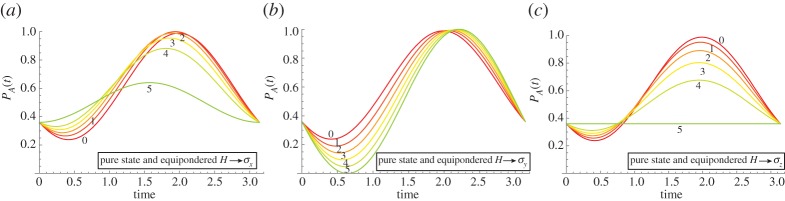
The first point is that, if we are concerned just with projection along 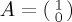and adopt the simplest possible Hamiltonian (corresponding to just a single Pauli matrix), then the choice of Hamiltonian informs the maximum amplitude of the oscillations, as can be seen in figure 3, employing an initial state 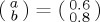. Note that, as pointed out above too, the Hamiltonian based on σ_z does not produce any evolution, while the Hamiltonian based on σ_y reaches maximum values of 0 and 1 at 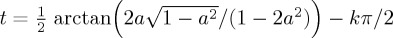. The evolution of Prob_A(t) when the Hamiltonian is just σ_x attains a maximum value of 1 − a² at t = π/2 when 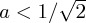(if 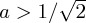, this will be a minimum instead). One should notice that it is necessary to vary the initial state in order to see these differences in dynamical evolution from these three Hamiltonians. Should one only choose a uniformed initial state, 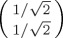, then there is no change in the temporal evolution of both σ_x and σ_z.

Figure 3.

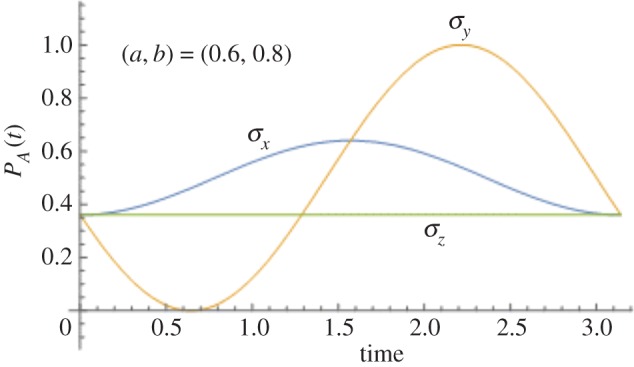
The change of Prob_A(t) over time, where 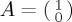, when the initial state is 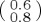. (Online version in colour.)

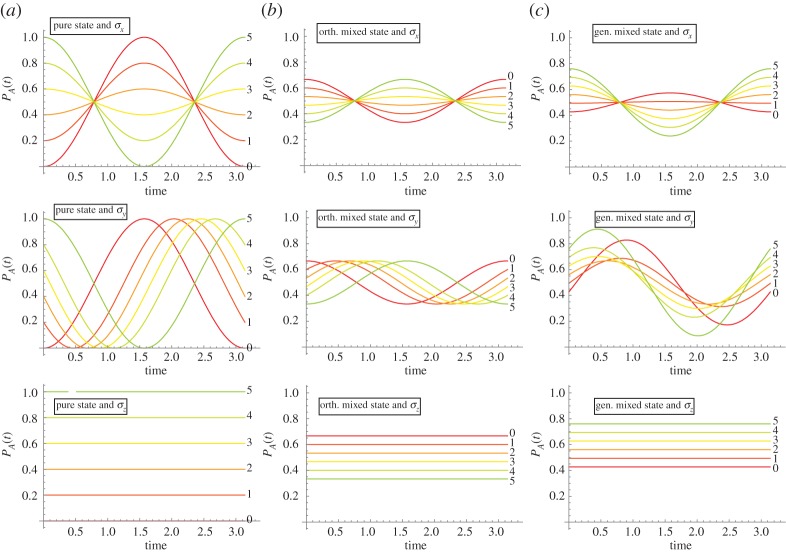
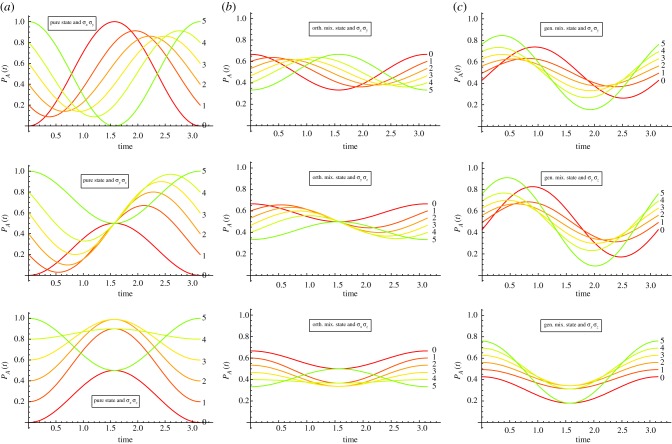
An important question for modellers is whether the state should be modelled as a pure state or a mixed state. We have already seen that this choice translates to a difference in the number of free parameters required to specify the initial state (and associated assumptions regarding the homogeneity of the ensemble of systems used for data collection; in psychology studies, this ensemble would typically correspond to a population sample). Does the dynamical evolution change in consistent ways as we move from pure states to mixed states? We noted above that, in general, mixed states lead to dampened oscillations and this point is illustrated in figure 4, where we compare pure state evolution with orthogonal mixture evolution and ‘general’ mixture evolution. For the orthogonal mixture, an ad hoc value of p = 1/3 has been adopted and the time dependence shows the expected dampened oscillation. One can verify that giving equal classical weights p = 0.5 to the two orthogonal components will also extinguish all temporal dependence for a σ_x Hamiltonian similarly as for general mixtures with a σ_z Hamiltonian. For the general mixture, a classical weight of p = 1/3 was also adopted and the second component was set to (−0.8, 0.6).

Figure 4.

Outcome probability for state A based on a Hamiltonian dynamics due to σ_z, σ_y and σ_z on descending rows. For initial pure state 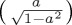in (a), an orthogonal mixed state with weight 1/3 for 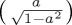and 2/3 for 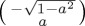in (b) and initial general mixed state with weight 1/3 for 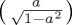and 2/3 for 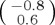in (c). For all cases, a² = 0 to 1 in five steps of 0.2 (i = 0–5). (Online version in colour.)

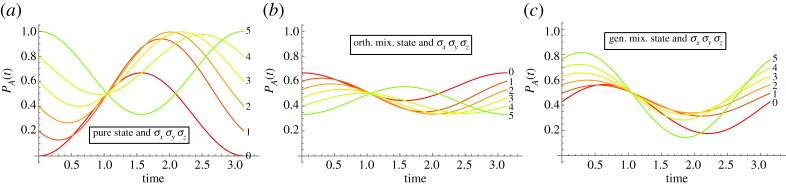
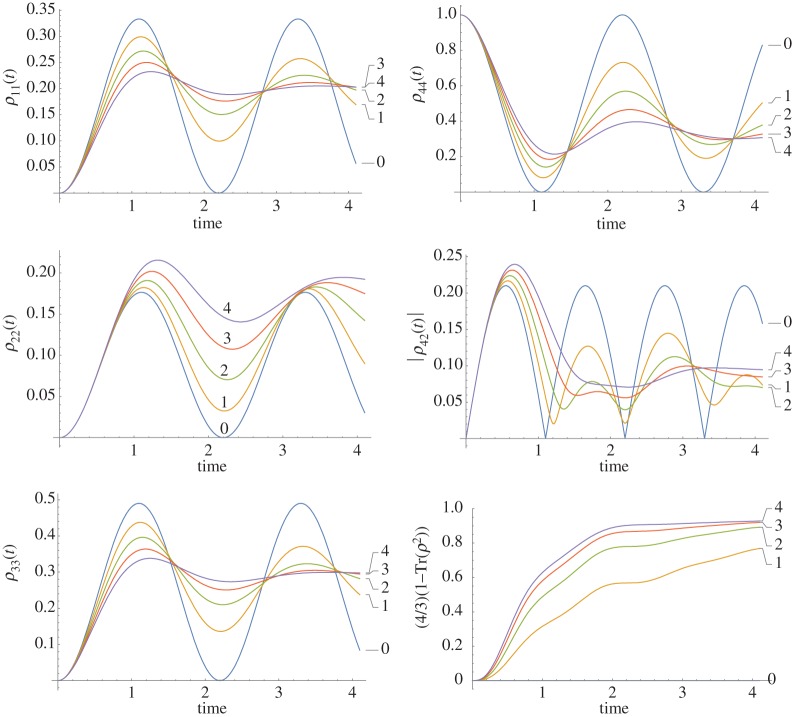
Appendix A shows the time evolution when two Pauli matrices are combined to create a Hamiltonian. When combining Pauli matrices, the resulting time evolution does not retain the distinctive features of dynamics that are characteristic of each separate Pauli component. This indistinctive temporal behaviour can be observed in the σ_x–σ_y composition and the σ_y–σ_z composition. In the σ_x–σ_z composition, however, the time of extrema t = π/2 of the pure σ_x case is retained. The overall similarity of the combined two Pauli case Hamiltonians is due to the fact that, in such combinations, there will always be a counter-diagonal Pauli matrix (either σ_x or σ_y). In the next section, we will study this ‘mixing’ behaviour by counter-diagonal elements in the extended dynamical model for bivariate paradigms.

The final issue concerns the extent to which considering the most general 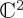Hamiltonian, involving components from all three Pauli matrices, can modify temporal dynamics. With our previous observation, the triple Pauli combination will not add essential features to the temporal behaviour of the probability outcome of A, because the counter-diagonal position in the Hamiltonian was already covered by double Pauli combinations (figure 5).

Figure 5.

Outcome probability for state A based on Hamiltonian dynamics due to combined 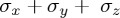. (a) For initial pure state 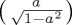, (b) orthogonal mixed state with weight 1/3 for 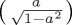and 2/3 for 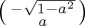and (c) initial general mixed state with weight 1/3 for 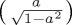and 2/3 for 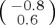. For a² = 0–1 in steps of 0.2 (i = 0–5). (Online version in colour.)

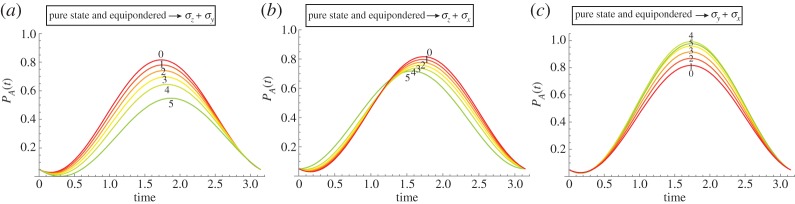
In figure 6, we juxtapose the temporal behaviour of the outcome probability for the equiponderate Hamiltonian 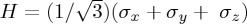evolving into each of the three single Pauli matrices separately.

Figure 6.

Outcome probability for state A based on a Hamiltonian dynamics due to combined σ_x + σ_y + σ_z and stepwise transition to single (a) σ_x, (b) σ_y and (c) σ_z for μ² = 0 –1 and ν² = 0–1 in steps of 0.2 (i =0–5). For initial pure state (0.6,0.8). (Online version in colour.)

While setting real-valued initial vectors is a typical simplifying assumption in cognitive modelling, the following reasoning is valid for all types of initial vector. By their make-up, we observe that the mixing of vector components can be achieved by combining either σ_x or σ_y with σ_z. Therefore, when both are used together without σ_z, no mixing of the components takes place any more, but only component swapping occurs. Swapping dynamics causes (a,b) → (b,a), while mixing dynamics causes 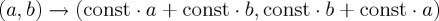. This effect is clear in figure 7, where we parametrized the Hamiltonian to evolve from equiponderate composition to σ_y + σ_z, σ_x + σ_z and σ_x + σ_y composition. Using a contrasted initial vector (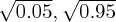), we observe that both the xz and yz Hamiltonians lead to component mixing (smaller oscillation amplitude), while the xy Hamiltonian swaps the probability mass (large oscillation amplitude).

Figure 7.

Outcome probability for state A based on a Hamiltonian dynamics due to combined σ_x + σ_y + σ_z and stepwise transition to (a) σ_y + σ_z, (b) σ_x + σ_z and (c) σ_x + σ_y by letting μ² = 0–1 and ν² = 0–1 in steps of 0.2 (i = 0–5). For initial pure state (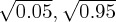). (Online version in colour.)

5. Violations of the law of total probability in dynamical models

Section 4 was intended to illustrate the temporal evolution that is possible with basic Hamiltonian dynamics and the range of technical modifications available for cognitive modelling. As noted, most QPT cognitive models are built using 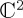components, that is, components corresponding to a choice involving two alternatives. We note that, in the literature, Hamiltonian-driven cognitive models with an odd dimension n, e.g. n = 3 [33], or with not Pauli-based Hamiltonians, n = 5 [20] and n = 8 [34], have been proposed.

A main source of interest for QPT dynamical models is how a separable 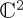structure consistent with the law of total probability can be extended to produce interference effects which allow deviations from the law of total probability. The essential idea is that, as long as the dynamics has a separable structure of the form H₁⊕ H₂ (where each of H₁ and H₂ acts on separate 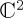spaces), then, whatever the specific form for the evolution of the composite state vector 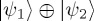, the resulting probabilities will obey the law of total probability. But, like Markovian dynamics, QPT dynamics on the composite system allows extensions of the form H₁ ⊕ H₂ + H_mix. In QPT, H_mix acts on 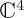and can result in evolved state vectors not of the form 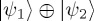, and which violate the law of total probability. What are the possible forms for H_mix and what kind of dynamics is produced?

We proceed in this discussion in the context of a generic decision framework, which can easily be adapted to more specific situations—including the Prisoner's Dilemma paradigm of Pothos & Busemeyer [13]. Example framework: Imagine a gambling task with sequential steps. The gamble is organized such that if you are on a winning streak your payoff for the gamble on the next step is determined by one bankroll function, while if you are on a losing streak your payoff for the gamble is determined by another bankroll function. The experimental paradigm thus has two distinct and non-overlapping conditions: win and lose. The decision-makers are asked to decide whether to proceed with the next step in the sequence, given knowledge that they have either been in a winning streak, or a losing streak, or the outcome of previous steps is left unknown. The experimental paradigm thus involves a binary decision: stop or continue. Classically, the probabilities to stop or continue in the last ‘unknown’ condition would be given by the law of total probability on probabilities to stop or continue from each of the corresponding known win and known lose conditions. In an analogous QPT model, the Hamiltonian would be H_win⊕ H_lose. A more elaborate QPT model would, however, allow for violations of the law of total probability and utilize a Hamiltonian of the form H_win⊕ H_lose+ H_mix.

We consider next what is a simple form of H_mix, such that the Hamiltonian can produce violations of the law of total probability, while still allowing for analytical solutions for the probabilities. The latter is clearly not a cognitive modelling requirement, but it facilitates the discussion of the temporal behaviour of the outcome probabilities.

Recall that we pointed out that a simple class of analytically expressible propagators follows the identity

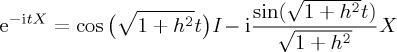when X satisfies X²= (1 + h²)I. While, in the simple 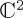space, Hamiltonians corresponding to any combination of the Pauli matrices will readily satisfy this condition, this is not the case for general Hamiltonians with a mixing component in 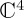space. We recall that, in general, H_mix can be any Hermitian matrix operating in the 2 × 2 off-diagonal space, but the Pauli-based version will allow analytical expression. We can write such a Pauli-based general Hamiltonian as 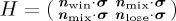, where we have normalization conditions on the weighing vector for the Hamiltonian composition in both subspaces of win and lose, n_win · n_win = 1 = n_lose · n_lose. Notice that we do not assume normalization of n_mix, as its norm will be defining for the strength of the mixing dynamics. For simple calculational notation, it is convenient to employ Feynman's slash notation, so that the Hamiltonian can be rewritten as 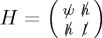, where 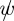is short hand for n_w · σ, and 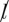stands for n_l · σ; finally, 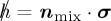. Using this slash notation and following Pauli matrix algebra, we have 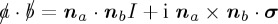, where, in the above equation and for these computations, the dot indicates the vector dot product and the cross the vector cross product. We can now express the condition for when we would be able to use the simple analytical expression for the time propagator for a Pauli matrix-based Hamiltonian.

Noting that 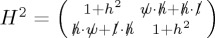, we will now require this expression to be of the form (1 + h²)I₄:

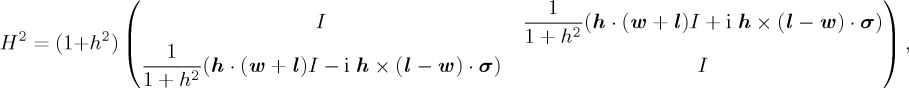where we have used 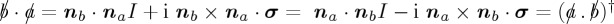and self-adjointness of the Pauli matrices. We therefore have to meet the following two conditions:

or explicitly

Thus, n_mix should be orthogonal to the sum of n_win and n_lose, and parallel to their difference. This is satisfied by n_mix = m(n_lose − n_win), where m is a free parameter, and thus

This final expression allows us to finally write the required mixing Hamiltonian as

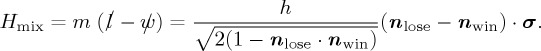Note that h is a mixing variable dependent on the free parameter m and the relative orientation of n_lose and n_win. One retrieves the non-mixing case by taking the limit h → 0.

The end result H_mix has a simple psychological expression. The degree of mixing—and thus interference—in the dynamics of the unknown condition could be reduced either by diminishing the free parameter m, or also implicitly by narrowing the difference between n_lose and n_win. This is an interesting aspect of this particular dynamical construction based on Pauli matrices. Recall that n_lose characterizes the cognitive dynamics in a losing streak and n_win in the winning streak. This structure for the dynamics suggests that interference—and thus the degree of non-classicality—increases when there is a greater discrepancy in the dynamics for the two known conditions. On the other hand, experimental paradigms may be such that the disjunctive—or ‘unknown’—condition may lead to a cognitive shift in the belief state of the decision-maker even if the dynamics in both subspaces are almost identical because she deems the condition of one subspace more probable than the other. This latter situation should then be captured by increasing the free parameter m when fitting with experimental data. Finally, we note that, besides monitoring the strength of the mixing, h also modifies the temporal rate at which the dynamics evolves, with higher values of h leading to relatively faster progression of the unitary operator.

Given this simplified dynamics, Prob_A(t) can now be computed analytically for a range of Pauli-based Hamiltonians in space as well. The corresponding expressions can be complicated for the general case; nevertheless, we think there is merit in producing them, for reference purposes and for transparency regarding the classical and non-classical terms (and, indeed, the extent to which they can be separated) in Prob_A(t). The expression of Prob_A(t) for an initial general mixture and its analytical calculation is delayed to appendices A and B. We will only discuss the pure state expression in more detail here, but will still also provide the formalism for the mixed states.

To facilitate interpretation, we choose the basis corresponding to the condition—i.e. w (win) or l (lose)—and the decision that is taken—i.e. c (continue) or s (stop)—leading to a representation (ψ_cw ψ_sw ψ_cl ψ_sl)^† of the belief state.

Now, for example, in the w-space (in the space concerning the dynamics when a participant knows she has been winning), we could have a mixed state composed of two pure states, corresponding to each of the two participant groups (recall, in this picture, we are assuming that the population sample is best described by two distinct groups; clearly, this would be an approximation in some cases). The pure states appearing in the general mixed state will be parametrized, respectively, by p_cw (probability to choose c given condition w) and (probability to choose s given condition w). Note that the prime indicates quantities belonging to the second group (out of two). The respective weight of both distinctly featured subgroups in the decision-maker sample is again denoted by p and 1 − p.

W states: a linear combination of and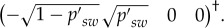

So, the above two pure states capture the two (assumed) groups that the mixed state is composed of. Note that a more intuitive notation for the w-states might be something like 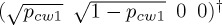and 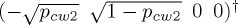, indicating that we have two groups of participants, with different tendency to continue playing. However, it is algebraically more convenient to express one group of participants in terms of the probability to continue and the other in terms of the probability to stop. Notice that when 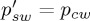, the two distinct groups of decision-makers assumed in the population sample are represented by orthogonal belief states. As long as the reader remembers that cw is the index for group 1 and sw′ for group 2, then the algebra should be straightforward.

Similarly, we define, in the l-space, p_cl (probability to choose c given condition l) and (probability to choose s given condition l).

L states: a linear combination of 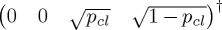and .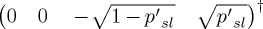

In the disjunctive condition, the decision-maker has no information on the condition and will attribute a weight p_w to believing w to be the condition (or weight 1 − p_w for the possibility that l is the condition). The initial belief state of the decision-maker is then a superposition 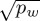times the w-state and times the l-state. We choose square roots with plus sign, ignoring possible phase difference in order to keep things as simple as possible. We suppose a similar predisposition to occur in the second subgroup but then parametrized by .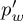

Unknown states: a combination of 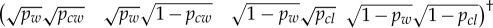and .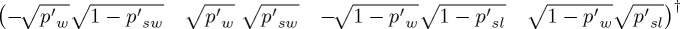

We proceed 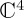in as in 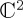(§4). The initial mixed state is obtained by weighing the respective projectors for both participant groups: 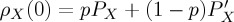, where X can be any of w, l or u (note that the unknown state is produced as a combination of the w and l states; as above, we just indicate here where the projectors for the mixed state should come from).

The Schrödinger evolution for the density operator implies 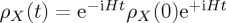and the outcome probability of obtaining a ‘continue’ decision—i.e. probability to decide to c—under condition X is obtained by taking the trace 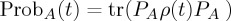, with projector P_A now equal to the matrix Diag(1 0 1 0). Note that this is the same as taking the partial trace of ρ(t) over the second index (w or l) and then applying the two-dimensional projector P_A of §4. In the appendices A and B, we provide some details of the calculation of Prob_A(t), given the mixed initial state in the u-condition. From this expression, all simpler cases can be derived.

We discuss now the outcome probability to continue in the u-condition for an initial pure state. A priori in the u-condition one expects the presence of distinct terms stemming from the w-condition and from the l-condition, augmented with a third type of terms stemming from the mixing. This anticipated subdivision is, however, only partially realized (see equation below), because all the trigonometric functions in the u-condition show an accelerated temporal behaviour by a factor to the time variable t in these functions. Therefore, only if no mixing occurs in the ‘unknown’ condition—either through vanishing m or coincidence of the n_X vectors—do the terms appropriate to the distinct w and l cases add up in the unknown cases regarding the probability to continue. If mixing takes place, then it is also the case that these dedicated w and l terms will be affected, in terms of accelerated time development. In any case, one can attempt to subdivide the expression for Prob_A(t) into three main summands: one with pre-factor p_w indicating it is the w-contribution (i.e. the contribution from the known win dynamics); one term with pre-factor 1 − p_w indicating it is the l-contribution; and finally an interference term preceded by the factor 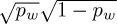exclusively produced by the mixing dynamics. One should, however, notice that both in the l- and w-parts, the 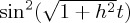terms have factors that depend purely on second-order n_M components (recall, M stands for mixer). These terms in the w-contribution result from probability amplitude transfer from the l-subspace to the w-subspace and vice versa as determined by the mixing Hamiltonian (analogously for the l-contribution).

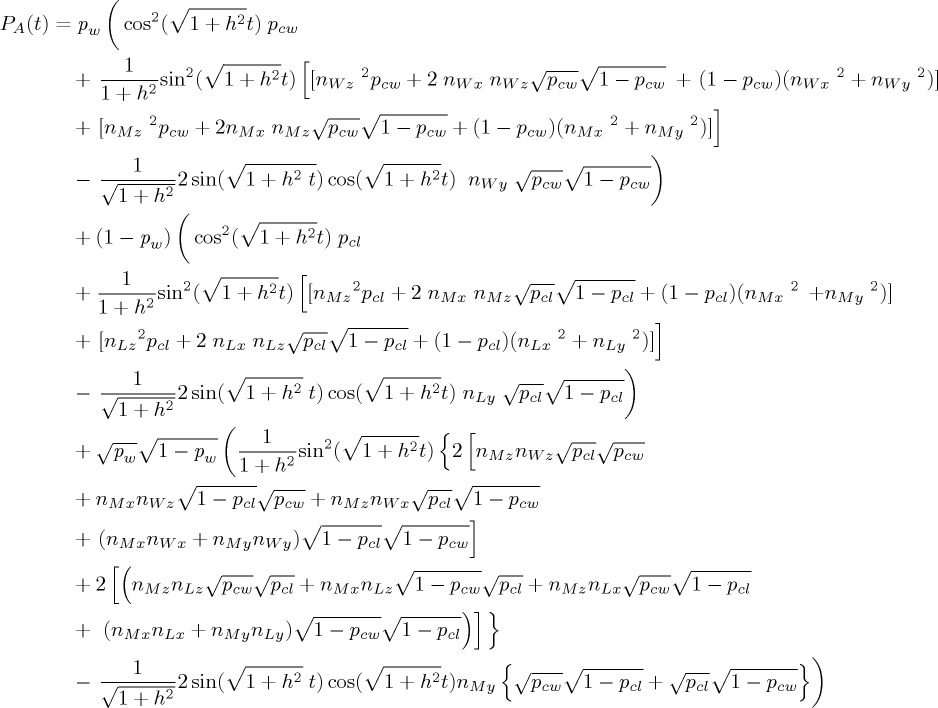In figure 8, the effect of increasing the mixing parameter m is shown for a u-state defined by p_w = 0.6, p_cw = 0.7 and p_cl = 0.1, and its subspace w-dynamics and l-dynamics are defined by the Hamiltonian vectors w = {0.09, 0, 1}, l = {−0.5, 0, 1} (where their normalized expression is n_X= X/|X|). This corresponds to a belief state which slightly biases the w-state over the l-state, and which reflects a preference to decide c in the w-condition while avoiding the c decision in the l-condition. The Hamiltonian subspace dynamics express a similar bias for c when w through our specific choice of w, and aversion for c when l through our specific choice of l.

Figure 8.

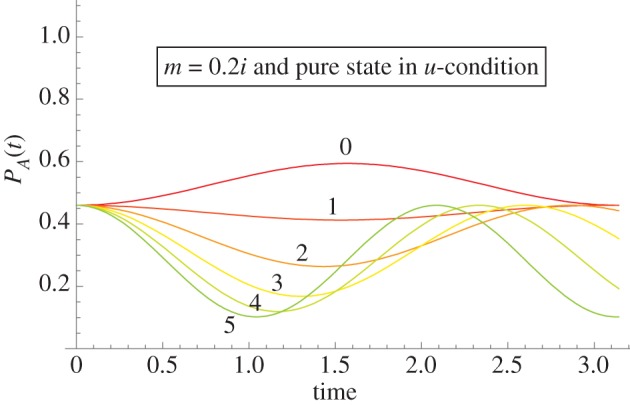
Outcome probability to continue based on Hamiltonian dynamics with Pauli matrix combination w = {0.9,0,1} in w-space and l = {−0.5,0,1} in l-space, and with an initial pure state in the u-condition specified by p_w = 0.6, p_cw = 0.7 and p_cl = 0.1. The mixing parameter is varied, m = 0–1 in steps of 0.2 (i = 0–5). (Online version in colour.)

For higher values of the mixing parameter m, the oscillation frequency of Prob_A(t) increases and, in this case, depresses the probability for decision c in the u-condition. When no mixing occurs (m = 0), the probability Prob_A(t) corresponds to the classically weighted sum of probabilities for decision c in the respective conditions of w and l.

With the Hamiltonian scheme, we can easily evaluate the degree of violation of the law of classical total probability, as a function of the mixing strength. The classical total probability to decide for c at time t consists of adding the probability for the decision to happen in the two mutually exclusive conditions w and l, where we weigh each condition with its probability to occur, respectively, p_w and p_l:

where we have rendered explicit the conditional w and l in the index of P_A. Any quantum violation of the law of classical total probability can be observed by comparing Prob_Tot,A(t) with P_A|u(t), where we recall u indicates the unknown condition.

The violation of the classical total probability can be expressed using the ‘unpacking factor’ by Tversky & Koehler [7], which is the idea of unpacking an event into subevents with disjoint probabilities. The factor needs to be assessed relative to 1:

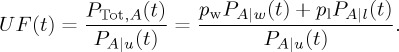This quantity will be larger than 1 for destructive interference of beliefs under conditions ‘w OR l’ and smaller than 1 in the case of constructive interference of beliefs under ‘w OR l’. Both regimes are covered by the present Hamiltonian scheme. For the mutually exclusive conditions w and l, the disjunction fallacy is of the fully subadditive type in figure 9 with p_w = 0.6 and occasionally of superadditive type in figure 10 with p_w = 0.1.

Figure 9.

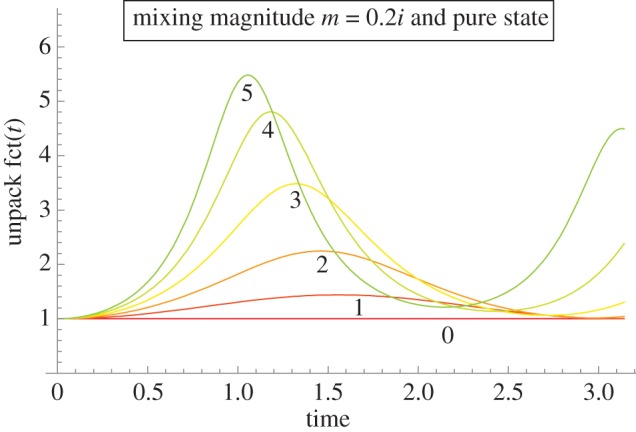
Evolution of the unpacking factor over time showing destructive interference for Hamiltonian dynamics with Pauli matrix superposition w = {0.9,0,1} in w-space and l = {−0.5,0,1} in l-space, and with an initial pure state in the u-condition specified by p_w = 0.6, p_cw = 0.7 and p_cl = 0.1. The mixing parameter is varied, m = 0–1 in steps of 0.2 (i = 0–5). (Online version in colour.)

Figure 10.

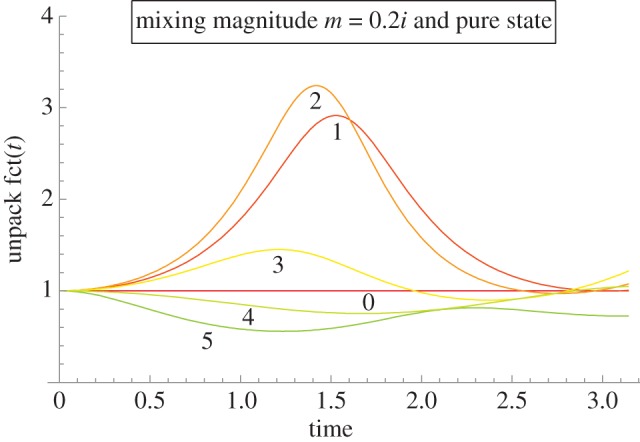
Evolution of the unpacking factor over time showing both destructive and constructive interference for Hamiltonian dynamics with Pauli matrix superposition w = {0.9,0,1} in w-space and l = {−0.5,0,1} in l-space, and with an initial pure state in the u-condition specified by p_w= 0.1, p_cw = 0.7 and p_cl = 0.1. The mixing parameter is varied, m = 0–1 in steps of 0.2 (i = 0–5). (Online version in colour.)

In the next section, the dynamical scheme is expanded to take into account damping through Lindblad evolution.

6. Dynamics of an open quantum system

The Schrödinger equation represents by far the most common approach to dynamics in cognitive modelling (for exceptions, see [35,36]). A distinctive characteristic of such dynamics is their imperative periodicity and, for some cases at least, this periodicity will be the main theoretical motivation for employing such dynamics in the first place (as well as the potential for violations of the law of total probability, as discussed). Empirically, however, there may be cases when a strict requirement for periodicity is undesirable (even when there are other reasons motivating a QPT approach). Additionally, Schrödinger dynamics entail an assumption that the system under consideration is isolated from its environment. Psychologically, such an assumption may be occasionally tenable, e.g. when a participant is immersed in a psychological task that is being performed in relative isolation to the participant's beliefs and general knowledge (of course, even if common, such an assumption is hardly trivial, cf. [37]). Equally, it is simple to think of situations when cognitive processing in a psychological task cannot be considered isolated, e.g. when a participant is asked to reflect on what her answers on a task mean for her personally.

Various contexts of decision-making include mood, physical and emotional condition of the participant, interaction with other people's opinions and interference with other (probably latent) tasks of the participant. These contexts can be interpreted as environment. The significance of environment in mental processing can be so large that it solely defines the final result, regardless of inherent motivations of the participant (described by the Hamiltonian). For example, a relatively unimportant choice faced in an extremely noisy environment (e.g. under the pressure of more vital tasks) can be easily imagined to be made randomly, with equal probability of any option. This uniform mixture of possible opinions would correspond to a classical mental state, given by a normalized identity matrix. Other examples for such open-system modelling occur in political science, in the complex dynamics of election campaigns where potential voters are submerged in a high-intensity information flow from various external sources [38,39], or they occur in connectionist approaches describing the decision-maker embedded in her surrounding environment [40].

In this paper, we consider one particular form of open quantum system equation, namely, the Lindblad equation. This is motivated, first of all, by the simplicity of the equation itself (it basically has one parameter, Γ) and the interpretation (the greater the parameter Γ, the stronger is the coupling to the environment). Namely, the Markovian approximation, used in the derivation of this equation, corresponds to the possibility to neglect the impact of the long-term memory of the problem in question in comparison to the whole environment.

In QPT, if a quantum system is assumed to interact with a classical environment, then the Lindblad equation must be employed, which can be seen as a modification to the Schrödinger equation. The idea is that our quantum state is coupled to numerous other, also quantum, states, comprising the (classical) environment. The total dynamics of this huge system (represented by a tensor product of the quantum system of interest and the many-dimensional environment) is also governed by a Hamiltonian, and the dynamics of our system are extracted by taking a trace over all environmental degrees of freedom.

The general form of the Lindblad equation is [41,42]

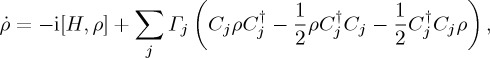where the Planck constant is set to one, C_j are arbitrary operators and the constants Γ_j are positive and interpreted as inverse relaxation times (the higher the value of these constants, the faster the extinction of oscillatory behaviour). The C_j are called ‘collapse operators’ or ‘quantum jump operators’. Note that the solution of the above equation ρ(t) remains a positive density matrix with trace 1 if started with such ρ(0) (so this general form of dynamics preserves trace in the same way as Schrödinger dynamics does). A simple form (with one non-zero j), which will be used in all subsequent considerations, can be given as

The key aspect of the Lindblad equation is that, whereas the standard Schrödinger equation produces incessant periodic oscillations in all probabilities for all observables (unless the state is an eigenvector of H), the Lindblad equation eventually produces a ρ(t) with only diagonal non-zero terms (for the part of ρ(t) that it affects). Indeed, this exactly corresponds to a statement that diagonal density matrix ρ(t) is a classical mixture of eigenstates. In other words, for such a ρ, all quantum structure has been lost and any residual uncertainty simply corresponds to classical uncertainty (of which particular state the system is in). This process of extinguishing quantum structure is called decoherence. It can be seen more clearly in the Lindblad form how the size of Γ determines the strength of decoherence, which can be thought of as the strength of the interaction with the environment.

When physicists talk about decoherence of a quantum system, this means losing coherence, that is, loosely speaking, the degree of quantum structure, which can be quantified as follows. In a pure state, the degree of purity of the state is maximal and decoherence is zero (note that the higher the decoherence of a system, the more classical it will be). In a totally classical state, purity is minimal, and decoherence maximal. One interpretation of decoherence in decision-making may be that it is a measurement without an actual measurement procedure, but rather by means of interaction with the environment. The classical stable state to which the dynamics converges may be interpreted as the final opinion of the decision-maker. The main problem with this interpretation is that very often this asymptotic stable state would be a uniform mixture, that is, expressing total classical uncertainty or complete personal indifference. That is, the question of the time of measurement remains open for many open-system approaches, as is the case in the standard unitary evolution approach.

Even though interpretations of decoherence (and open quantum systems in general) in psychology have yet to be established, we present here for completeness a basic approach to its quantification. One measure of decoherence is 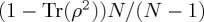, where N is the space dimension. This measure is zero (the minimum) when the state is pure and one (the maximum) for a density matrix ρ with equal (diagonal) elements 1/N. Note that 1 − Tr(ρ²) can be easily seen (remembering that trace is basis-independent) to be zero when the state is pure and to attain its maximum value only for a density matrix ρ with diagonal elements equal to 1/N. In any basis, the maximally mixed state ρ is the identity matrix I multiplied by 1/N. So, the diagonal elements of ρ² are 1/N² and 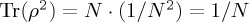. Such a maximally mixed state (1/N)I is always a (stable) solution to our Lindblad equation, because I commutes with any operator—in particular, with H and J_z—and very often it is the only stable solution (see below for an exception). In general, we can represent any density matrix ρ = (1/N)I + μ, where μ is a (not positive) traceless matrix. Then,, and we can see that the decoherence, 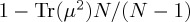, is maximal only if μ is zero.

Note that J_z is the same observable for an arbitrary-dimensional Hilbert space as σ_z/2 is for a two-dimensional one. That is, J_z is a z-axis spin operator. Generally speaking, if we employ in the Lindblad equation J_z, we end up asymptotically with a ρ that is diagonal in the J_z basis, i.e. the basis in which J_z is also diagonal (if we employed another operator instead of J_z, then we could also end up with a diagonal ρ). This is what is meant by saying that the system ρ has become classical. Still, it may so happen that some degrees of freedom are decoherence-free [43]. As long as we are interested in the J_z observable, it is natural to employ J_z. Computing explicitly the Lindblad term for the simple case, we have 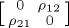, which again illustrates (to a first approximation) how the differential equation for ρ includes terms producing a gradient towards zero for the off-diagonal terms. For a four-dimensional system (, which has been much of the focus of this paper, or the non-separable version), we can specify J_z in the Lindblad equation as 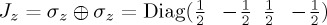. Then, the last term in the Lindblad equation would be

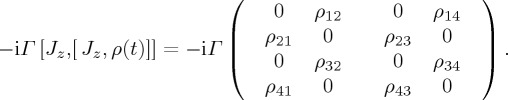Non-diagonal zeros indicate the absence of decoherence between the first (cw) and the third (cl) basis vector, as well as between the second (sw) and the fourth (sl). But note that a general diagonal J_z would still preserve the direct sum structure, assuming that the Hamiltonian part was separable.

Note that our case is an unusual one, because we deal with a direct sum Hamiltonian, with a mixing term. If there were no mixing term, the two subspaces would be evolving independently. For example, if the initial state was in the ‘winning’ subspace, it would remain there. It may decohere to the mixed state 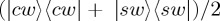, which looks exactly as if maximally mixed for the 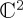case, but which is not totally mixed for our 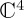case (because the basis states of the ‘lose’ subspace are missing in this mixture and the measure of decoherence is 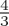(1 − 2/4) = 0.66). Moreover, if we imagine decoherence affecting only one of the subspaces, e.g. J_z= σ_z⊕ 0, this would mean that the ‘losing’ subspace is decoherence-free. Starting with a pure state in a ‘losing’ subspace, we would remain in the ‘losing’ subspace (oscillating incessantly if the initial state was not an eigenstate) and preserve the purity, with the measure of decoherence remaining zero.

Moving back to our concrete form of Hamiltonian, we note that for the 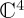Hamiltonian with the mixing term as described in §5, and with parameters n_w = (0, 0.8, 0.6), n₁ = (0.8, 0.6, 0) and m = 1, there exists a non-trivial (not I/4) stable state solution

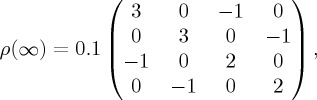which commutes with both J_z and H, [J_z,ρ] = 0, [H,ρ] = 0. Obviously, these two commutation relations are sufficient for the solution ρ to be time-independent. It was possible to find such a solution in our case, because both H and J_z are degenerate (note that H² and 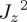are proportional to I). In order for non-trivial ρ to be diagonalizable together with H, and with J_z, it needs to have the same eigenvectors as H and J_z. While our H and J_z do not commute, they are not diagonalizable in one same basis, and if at least one of them was not degenerate, this would imply that no ρ (other than I/4) could commute with both of them. This could easily happen if we relax some conditions. Consider, for example, another natural form of H_mix which would just be the identity matrix I₂, mixing 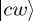and 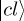as well as 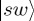and . 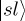Then, the 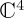Hamiltonian would have four distinct eigenvalues, 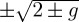, where we denoted 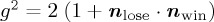, and none of the eigenvectors is an eigenvector of J_z, hence the only stable mixed state is I/4.

As it is the case with H and J_z considered throughout the paper, we can see directly from the form of J_z that it has invariant subspaces and , and it is easily seen that H must be degenerate from the fact that H² is proportional to I (in effect 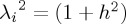, following §5; thus, all 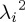are identical for all four i, which leaves only two values for the four eigenvalues λ_i of the Hamiltonian). Indeed, H also has two twice degenerate eigenvalues, which allows for a choice of eigenvectors such that they would also be eigenvectors of ρ.

For this stationary state ρ, we can either directly calculate the measure of decoherence to be 0.9333, or represent 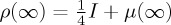, where μ is a traceless operator responsible for pertaining of coherence

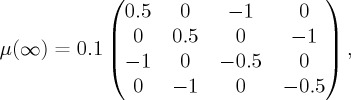and calculate (1 − Tr(ρ²))N/(N − 1) = 1 − Tr(µ²)N/(N − 1) = 1 – 4·0.1²·(0.5² + (−1)²)·4/3 = 0.933. For other values of parameters, the situation is similar.

For a more general picture, we may look for a stable state solution satisfying commutative relations [H,ρ] = 0 and [J_z,ρ] = 0 (note that [J_z,[J_z,ρ]] = 0 if and only if [J_z,ρ] = 0). From the commutation relation [J_z,ρ] = 0, we obtain the form of the solution

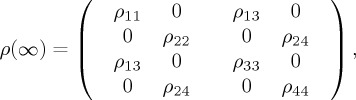with the condition that all elements are real numbers. Plugging this form into the equation [H,ρ] = 0, we obtain the following one-parametric solution (m is fixed as mixing strength):

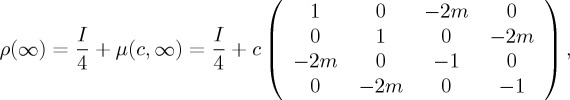where c is a real number, 0 ≤ c ≤ 1/2. Note that the solution is independent of n_w and n_l, but the parameter c depends on the difference . The solution ρ(∞) has two eigenvalues:

which must be between zero and one. This means that c must satisfy

We notice that the larger the mixing parameter m, the more narrow is the range of possible values for c.

Till now, we did not discuss what initial state will converge to what stable state. Obviously, if we start with a uniform mixture I/4 (c = 0), or any other stable state with c > 0, we are bound to stay in this initial state, because it is stationary. Suppose that a particular initial state ρ(0) stabilizes to a particular 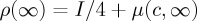(with some concrete c). Since the Lindblad equation is linear in the density matrix ρ, the linear combinations of its solutions are also solutions. If we consider now a weighted mixture of ρ(0) and I/4, with the weight 0 < a < 1, the resulting stable state would be the mixture 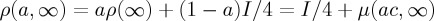. So, the effect of adding a uniform mixture to an initial state results in a decrease of the non-trivial part of the solution, μ, which gets multiplied by the factor a. From an interpretive point of view, this sustains the idea that a group of participants with a fraction 1 − a of indifferent deciders will proportionally diminish the belief difference of the whole group.

If we consider the initial state to be a mixture of two states, with respective weights a and 1 − a, the stable state would have the non-trivial term 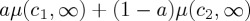, which is proportionally weighing the outcomes we have for each of the states separately.

To obtain a connection between the parameter c and the initial state ρ(0), we note that there is a basis in which: (i) our general stable state solution is diagonal; (ii) J_z remains diagonal; and (iii) the Hamiltonian H is block-diagonal. This means that we have independent evolution of certain initial states initially prepared in one or the other two-dimensional subspace. Roughly speaking, we have a situation opposite to having two decoherence-free subspaces (no decoherence within a subspace but decoherence between the subspaces): namely, in our case, we have two subspaces which, individually, always decohere completely, but there is no interaction (and no decoherence) between these two subspaces. So, if the initial state belonged exclusively to one of the subspaces, it remains there and tends to the stable state 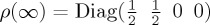in the basis described in this paragraph, which has 66% decoherence (minimal possible). The resulting expression for the parameter c is

The measure of decoherence is 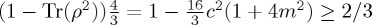. If we want less decoherence, we can increase m (which defines the initial Hamiltonian) or c (which is defined from the initial state).

Figure 11 illustrates how decoherence grows with time, depending on the strength of the Lindblad term. Starting with the initial state 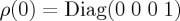, we looked at decoherence across a range of the Γ parameter (0, 0.5, 1, 1.5 and 2), numerically solving the Lindblad equation. Figure 11 plots the evolution of the elements ρ₁₁(t), ρ₂₂(t), ρ₃₃(t), ρ₄₄(t), |ρ₄₂(t)| and the decoherence measure as described above. One can see that the decoherence measure grows from 0 to 0.933, more steeply when Γ is greater. For Γ = 0, decoherence is always zero, and the oscillating pattern repeats forever. For other values of Γ, we observe diagonalization (but not complete!) of the density matrix, attested, in particular, by quenching of the non-diagonal element |ρ₄₂(t)|.

Figure 11.

Dynamics of the density matrix under decoherence. Curves are numbered (0 1 2 3 4) as corresponds to Γ parameter (0, 0.5, 1, 1.5, 2). (Online version in colour.)

Moreover, figure 11 demonstrates efficient mixing between all four basic states, starting from a pure state (0 0 0 1). This mixing is due to the mixing part of the Hamiltonian, H_mix. If H_mix were set to zero, the oscillations would be observed just between ρ₄₄(t) and ρ₃₃(t), leaving ρ₁₁(t) and ρ₂₂(t) constant zero.

7. Concluding comments

The richness of dynamical options in QPT cannot be comprehensively covered in a brief paper and there are textbooks better suited for an in-depth presentation. Here, we aimed to focus on situations which have been of interest to cognitive scientists, notably corresponding to binary decisions. We used the eigenstates of the Pauli σ_z matrix to correspond to the outcomes of a binary decision of psychological interest. Then, we have a series of key questions: What are meaningful options for specifying a general Hamiltonian for the evolution of a corresponding state? How should the state be represented in the first place? In what way could we extend the dynamics so that a more realistic picture for the influences on the mental state is provided?

Regarding the first question, the Bloch sphere presentation was meant to illustrate that the evolution of states induced by Hamiltonians can be given geometric interpretation. In particular, we have argued that, for the initial state , evolution of probabilities Prob_A(t) depends only on the polar angle of the vector n defined by the Hamiltonian H = n · σ. In view of the fact that the main features of the probabilistic behaviour are insensitive to the particular distribution of weights between σ_x and σ_y, one may simplify the picture by considering only σ_z and σ_y components in the Hamiltonian. Regarding σ_x + σ_z and σ_y + σ_z, the resulting Hamiltonian mixes amplitudes across the state, that is, it combines amplitude in each slot of the mental state with amplitude from other slots. However, σ_x + σ_y merely swaps amplitude from one slot to another. Noting that each Pauli matrix in the Hamiltonian introduces a free parameter, it seems an appropriately parsimonious approach to not introduce a third Pauli matrix in the specification of the Hamiltonian in the first instance. Relatedly, we simplified the specification of the Hamiltonian, by not including the identity matrix, as it only affects an overall phase in the mental state. Again, the Bloch sphere presentation illustrates why this is not necessary in simple cases, but note that this would play a role, for example, in the case of superpositions in the unknown case in .

The mental state representation itself is not a simple problem: when there is an assumption that inhomogeneity in the population sample may affect outcome probability behaviour, then a density matrix approach should be employed, even if particular decompositions of the density matrix cannot be assumed. In this work, and unlike the standard approach in physics, we have motivated two approaches in specifying a mixed state, as a mixture of either two orthogonal pure states or two non-orthogonal pure states (to capture an insight of two-cluster structure in the population). While this may appear an intuitive approach in psychology, bear in mind the cautionary notes regarding parameters and the non-uniqueness of density state decomposition. From the point of view of modelling in psychology, the transition between these different approaches to mental state representation can be operationally determined, in terms of the complexity of the data set and the additional parameters that are needed in the different cases. Readers should also be aware that a seemingly innocuous increase in the complexity of the mental state—by mixing—can translate to much greater complexity regarding probabilities, compared to the situation of dealing with pure states.

We have devised a novel Hamiltonian mixing scheme in that allows an analytical expression of the outcome probability. We were able to specify H_mix in such a way that mixing will diminish with a greater similarity of the dynamics in the two ‘known condition’ subspaces; this can plausibly be endowed with psychological meaning, in particular situations. Additionally, it may be the case that mixing can be theoretically motivated even in cases of almost identical subspace dynamics; this can be achieved through increasing the free parameter m.

One of the main motivations in adopting modelling with QPT over CPT is the former's possibility to formally express the violation of the classical law of total probability in various experimental paradigms [22]. Comparing the total probability P_Tot,A(t) with P_A|u(t), which can reflect a result from quantum interference, we observed the law's violation in the unpacking factor and displayed both subadditive and superadditive regimes. It is this problem which motivated the use of direct sum space structure in many QPT cognitive dynamical models, instead of the more common tensor structures. Here, we saw how we can specify a simple mixer, which has a powerful interpretation regarding the transition from consistency with the law of total probability to violations of the law of total probability. Readers should again be cautioned regarding the algebraic complexity of such directions, especially when the mental states are represented with mixed operators. Of course, one can always employ numerical methods to address any such problems.

Finally, we addressed the issue of the time periodicity in conventional—Schrödinger type—quantum-like modelling and provided an interpretative framework to extend such dynamics. Unitary dynamics assumes that participants adopt a task in isolation. Such an assumption may be warranted in some cases (e.g. when an experimenter takes great care to ensure that participants approach a task regardless of any other knowledge or biases they might have), but this will clearly not be a general assumption. An area of quantum cognition, which has received little attention, concerns the transition from unitary to open-system dynamics, whereby the latter can be understood as decision situations which take place in the broader context of a participant's knowledge and experience. Importantly, this distinction has empirical traction, in the simple sense that unitary dynamics are perpetually oscillating, whereas open-system dynamics stabilize to a particular state. We have shown how open-system Lindblad dynamics can be simply implemented for the dynamical system of interest and illustrated the diminishing of oscillatory behaviour in the dynamics.

In conclusion, QPT provides a rich set of technical tools for dynamics. Current work in quantum cognition has only employed a small subset of these tools. It is hoped that this paper will facilitate the adoption of more complex dynamical tools and so open the doors for richer empirical predictions.

Appendix A

See figure 12.

Figure 12.

Outcome probability for state A based on a Hamiltonian dynamics due to σ_z, σ_y and σ_z on descending rows. For initial pure state 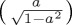in (a), an orthogonal mixed state with weight 1/3 for 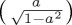and 2/3 for 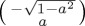in (b) and initial general mixed state with weight 1/3 for 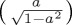and 2/3 for 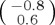in (c). For all cases, a² = 0–1 in five steps of 0.2 (i = 0–5). (Online version in colour.)

Appendix B

Analytical expression Prob_A(t) for general Hamiltonian form H_win⊕ H_lose+ H_mix.

Data accessibility

Supplementary software is available via the website of Phil. Trans. A: Mathematica notebook ‘PhilTransA-2DimHamiltonian-BBBP2017’ for the two-dimensional Hilbert space Hamiltonian dynamics. Mathematica notebook ‘PhilTransA-4DimHamiltonian-BBBP2017’ for the four-dimensional Hilbert space Hamiltonian dynamics. Mathematica notebook ‘PhilTransA-4DimLindbladian-BBBP2017’ for the four-dimensional Hilbert space Lindbladian dynamics.

Authors' contributions

All authors helped draft the manuscript, critically revised all parts and gave final approval for publication. In particular, J.B. provided the Hamiltonian dynamics and diagrams and developed the mixing Hamiltonian, I.B. developed the Lindblad dynamics and diagrams and the decoherence formalism, P.B. detailed the discussion of the 3D vectorial representation and designed the Bloch sphere diagrams, and E.M.P. provided the initial outline of the manuscript, positioning the work in state-of-the-art context and overall critical revision.

Competing interests

We have no competing interests.

Funding

J.B. was supported by Leverhulme Trust grant RPG-2015-311 and Center Leo Apostel for Interdisciplinary Studies – Vrije Universiteit Brussel. I.B. was supported by H2020-MSCA-IF-2015 grant no. 696331. E.M.P. was supported by Leverhulme Trust grant RPG-2015-311 and I.B. by H2020-MSCA-IF-2015 grant 696331.