Genetic risk models: Influence of model size on risk estimates and precision

Abstract

Disease risk estimation plays an important role in disease prevention. Many studies have found that the ability to predict risk improves as the number of risk single-nucleotide polymorphisms (SNPs) in the risk model increases. However, the width of the confidence interval of the risk estimate is often not considered in the evaluation of the risk model. Here, we explore how the risk and the confidence interval width change as more SNPs are added to the model in the order of decreasing effect size, using both simulated data and real data from studies of abdominal aortic aneurysms and age-related macular degeneration. Our results show that confidence interval width is positively correlated with model size and the majority of the bigger models have wider confidence interval width than smaller models. Once the model size is bigger than a certain level, the risk does not shift markedly, as 100% of the risk estimates of the one-SNP-bigger models lie inside the confidence interval of the one-SNP-smaller models. We also created a confidence interval-augmented reclassification table. It shows that both the more effective SNPs with larger odds ratios and the less effective SNPs with smaller odds ratios contribute to the correct decision of whom to screen. The best screening strategy is selected and evaluated by the net benefit quantity and the reclassification rate. We suggest that individuals whose upper bound of their risk confidence interval is above the screening threshold, which corresponds to the population prevalence of the disease, should be screened.

Introduction

Personalized genomics is currently a widely discussed topic [Bloss, et al. 2011]. Personalized genomics companies and many publications [Evans, et al. 2009; Morrison, et al. 2007; Wray, et al. 2007] have provided disease risk prediction models based on genetic predictors. However, these risk reports seldom take the confidence interval of the risk estimate into account [Kalf, et al. 2014]. For example, 23andMe presented to its customers a point estimate of the risk and the average risk of the disease in the population, as well as how much higher the estimated risk was than the average risk. 23andMe did not present confidence intervals of the provided risk estimates. And in many publications, especially when risk estimates are based on odds ratios derived by meta-analysis, the confidence intervals of the risk estimates are not presented nor considered in the evaluation of the risk model. Many studies have applied regression models to a set of risk single-nucleotide polymorphisms (SNPs) to make predictions. Using the area under the curve (AUC) metric to evaluate their risk models, they conclude that the more risk SNPs in the risk model, the larger the AUC will be, thus, the better the ability to predict the risk [De Jager, et al. 2009; van Dieren, et al. 2012]. However, as we illustrate here, as the number of risk SNPs in the model increases, the confidence interval of the risk estimate can widen. In fact, a risk estimate with a larger confidence interval from a larger model with more SNPs may not be practically better than a similar risk estimate with a smaller confidence interval from a smaller model based on fewer SNPs. When presenting and evaluating risk estimates, it is important to consider the level of uncertainty in the risk estimate.

In this study, we explore the changes of risk estimates and their 95% confidence interval widths as more SNPs, in the order of decreasing effect size, are added into the model, based on both simulated and real data. We also created a reclassification table to evaluate the effect of the added SNPs predictors, taking the confidence interval of the risk estimate into account. Finally, we selected the best screening strategy based on the net benefit quantity and the reclassification rate.

Methods

Data Description

In this study, we use three data sets to evaluate and compare our risk models. The first data set is a simulated one. We simulated a data set of 100,000 people assuming a genetic model based on 19 independent risk SNPs with odds ratios and allele frequencies matching those observed in a large meta–analysis of age–related macular degeneration (AMD) [Fritsche, et al. 2013], using the Multiple Gene Risk Prediction Performance (mgrp) R package [Pepe, et al. 2010]. In the large meta–analysis of AMD, the 19 SNPs were shown to be highly related to AMD. AMD is a progressive neurodegenerative disease, which constitutes one of the primary causes of visual impairment and irreversible blindness in the elderly of western countries [Klein, et al. 2011]. In our simulation, we assumed that the disease is dichotomous with a prevalence of 0.055, which is similar to the prevalence of AMD.

The second data set is from a study of abdominal aortic aneurysms (AAA). AAA is the most common form of aortic aneurysm. In general, the prevalence of AAA (2.9 to 4.9 cm in diameter) ranges from 1.3% for men aged 45 to 54 years to up to 12.5% for men 75 to 84 years of age. Comparable prevalence figures for women are 0% and 5.2%, respectively [Rooke, et al. 2012]. Up to 10% of the male population who are more than 65 years old has AAA, and 80–90% of ruptures lead to sudden death [Assar and Zarins 2009]. Our goal was to classify the population into high-risk and low-risk categories, where “high risk” is defined as having a risk higher than the population prevalence. Our motivation was to identify people with high AAA risk for targeted ultrasound screening. The samples were genotyped at 731K SNPs using the Illumina OmniExpress platform (dbGaP Study Accession numbers: phs000381.v1.p1, phs000408.v1.p1 and phs000387.v1.p1). AAA cases and controls were identified by electronic phenotyping [Borthwick, et al. 2015]. After imputation and quality control [Verma, et al. 2014], 2,626 samples (733 cases and 1,893 controls) were available. The imputed data are part of the eMERGE Network Imputed GWAS data for 41 Phenotypes (the dbGaP eMERGE Phase 1 and 2 Merged data Submission with an accession number phs000888.v1.p1). By modeling in a much larger electronic medical record (EMR)-based clinical data set, seven easy-to-measure clinical predictors (age, smoking status, sex, systolic blood pressure, diastolic blood pressure, height and weight) were chosen for use in our risk models [Smelser, et al. 2014]. Based on prior literature [Biros, et al. 2011; Bown, et al. 2011; Elmore, et al. 2009; Galora, et al. 2013; Giusti, et al. 2008; Harrison, et al. 2013; Helgadottir, et al. 2012; Jones, et al. 2013; Jones, et al. 2008; Saracini, et al. 2012],15 SNPs present in the imputed data were selected with odds ratios in the literature ranging from 0.41 to 2.16 (Supplementary Table I).

The third data set is from a study of the genetics of AMD [Weeks, et al. 2000; Weeks, et al. 2004]. In our analysis, for 1,015 unrelated individuals (882 cases and 133 controls) high quality genotypes were available at 14 of the 19 SNPs mentioned above, and these 14 were used as predictors in the AMD data analysis. The cases in our study were defined according to the diagnosis criteria of “Model C” in Weeks, et al. [2004]. Under Model C, cases are those who are definitely or probably affected with AMD or with a related maculopathy. Model C also included individuals with end-stage disease, in the absence of any other documentation of macular pathology. The controls had no AMD symptoms with an age at last eye exam ≥ 65.

Data analysis

First, for all the three data sets, we used logistic regression to fit the risk models. To avoid over fitting, we used four-fifths of the data as the training data set and the rest of the data as the testing data set. The training and testing data sets are not only used to recommend a single best prediction model, but are also applied to explore the behavior of models with different sizes, when each model is built using an ordered set of risk SNPs. We did not include any covariates besides the SNPs when analyzing the AMD and simulated data sets (Since the simulated data are set up to be similar to the AMD data, this makes the results from these more comparable). When analyzing the AAA data set, we included seven easy-to-measure clinical predictors (age, smoking status, sex, systolic blood pressure, diastolic blood pressure, height and weight). We let M be the total number of risk SNPs. Using the training data set, we fit the largest model using logistic regression with all of the M SNPs to estimate an odds ratio for each SNP. We ordered the M SNPs in decreasing order of effect size using odds ratios as an estimate of effect size after inverting any odds ratios < 1. So SNP 1 has the largest estimated effect size, SNP 2 has the next largest estimated effect size, etc. After ordering the SNPs in this manner, starting by fitting a model of size 1 using SNP 1, we then fit successively larger models using the training data set, increasing the model size K by adding in the next SNP from our ordered list (Supplementary Table I, Supplementary Table II). For each model, all of the effect sizes were re-estimated – these are the natural logarithm of odds ratios: β parameters. Then we estimated risks for each individual in the testing data set by plugging in the β’s as estimated from the training set using K SNPs. When estimating risks from a case/control sample using logistic regression, the resulting risk estimate is not the absolute risk, but rather depends on the case/control ratio in the sample itself. Accordingly, for the case/control data sets, risk estimates were adjusted using the methods described in Pyke et al. [1979]. For each person in the testing data set, we recorded the risk estimate, its 95% confidence interval, the model size, and the SNP genotypes.

We then explored how the risk shifts as the model size increases using bean plots and risk trajectory plots. To quantify the magnitudes of the risk shifts, we recorded the maximum of the absolute risk shifts (MRS) between model k and all bigger models for each individual. We recorded the maximum, across all individuals, of the MRS when additional SNPs were added to the model k which we refer to as the “maxMRS”; and the 95^th percentile of the MRS which we refer to as the “95PMRS”. To investigate the relationship of the confidence interval width and the model size, we used Spearman’s rank correlation test and bean plots.

For the AAA and AMD data sets, we evaluated the risk models using reclassification tables, taking the confidence interval into account, classifying individuals into high-risk and low-risk groups based on a threshold T corresponding to the population prevalence (we assumed the prevalence was 0.033 for AAA and 0.055 for AMD). In the traditional reclassification tables (which do not take the confidence intervals into account), assignment to either the low or the high risk classes is defined solely based on the chosen risk threshold T. In order to take the risk confidence intervals into account, we created confidence interval augmented (CI-augmented) reclassification tables where we defined the LOW*/HIGH* risk classes to contain individuals whose risk estimates were lower/higher than T and whose confidence interval did not overlap T. Individuals in these two classes had risk estimates that were unambiguously either below or above T (Figure 1). Then we added two more classes, denoted as “{−T}” and “{+T}” which contain individuals with risk estimates with confidence intervals that overlap the threshold T. The individuals in the {−T} class had risk estimates < T, while those in the {+T} class had risk estimates ≥ T. For individuals in these two classes, it is not clear if their true risk is above or below T. As the CI-augmented approach classifies the individuals into four categories (LOW*, {−T}, {+T}, HIGH*), there are three possible screening strategies: 1. screen the individuals in HIGH* risk class only (defined as {T,1]); 2. screen the individuals in both {+T} class and HIGH* risk class (defined as {+T,1]); 3. screen the individuals in {−T}, {+T} and HIGH* risk class (defined as {−T,1]). We calculated the net benefit [McGeechan, et al. 2014], which provides a measure of the number of people correctly screened as having the outcome, adjusted for the number of people incorrectly screened as having the outcome. The net benefit formula is:

$$\mathit{Net}\mathit{benefit}=\frac{\mathit{True}\mathit{positives}}{n}-\frac{\mathit{False}\mathit{positives}}{n}\left(\frac{T}{1-T}\right),$$

where n is the sample size, and T is the threshold as indicated above. Then we calculated the reclassification rate of [0,−T}⬄{+T,1] and the reclassification rate of LOW*⬄{−T,1] according to the screening strategies 2 and 3. The reclassification rate of lower risk group⬄higher risk group means the proportion of individuals reclassified from the lower risk group to the higher risk group or from the higher risk group to the lower risk group. We also evaluated the rate of correct reclassifications for the three screening strategies. Correct reclassification means reclassifying cases from the lower risk group to the higher risk group, or reclassifying controls from the higher risk group to the lower risk group. We used the net benefit and the rates of correct reclassification to select the best screening strategy. Furthermore, in order to explore the influence of model size on the confidence interval width, we recorded how many confidence interval widths increased and decreased when additional SNPs were added to the initial model.

Figure 1.

Illustration of the risk estimates falling in the four LOW*, {−T}, {+T}, and HIGH* risk classes, which are defined as a function of the risk estimate value (grey dot) and its confidence interval. The horizontal line indicates the threshold T.

Results

First, in each data set, we examined how much the risk shifted when one more SNP with the next largest odds ratio (after all odds ratios were inverted to be > 1) was added to the model. To explore the risk shift at the individual level, we plotted representative risk trajectories as SNPs were added to the model in the order of decreasing effect sizes (Figure 2). As expected, the risks shift less when SNPs with the smaller odds ratios are added. Figure 2 shows, at the individual level, movement in risk among the smaller models has a marked flattening of the risk trajectories as the models get larger. We also found that individuals with higher initial risks tend to have their risks shift more than those with lower initial risks as the model size increases. In the simulated data set (Figure 2a), when the three initial risk are 0.027, 0.068 and 0.161, the maxMRS’s based on model 1 are 0.15, 0.27 and 0.39, and the 95PMRS’s based on model 1 are 0.05, 0.11 and 0.21, respectively. In AAA and AMD data set, the 95PMRS’s based on model 1 are also bigger when the initial risks are bigger (Figure 2b,c).

Figure 2.

Risk trajectories as categorized by the initial risk for (a) the simulation study, (b) the AAA data set, and (c) the AMD data set. Each part contains the trajectories of 30 individuals randomly chosen from the testing data set. The odds ratios of the added SNPs are shown on the top of each sub figure. The horizontal black line is the disease prevalence (0.055 for the simulated data set and the AMD data set; 0.033 for the AAA data set). The maxMRS.m1 is the maxMRS based on model 1, while the 95PMRS.m1 is the 95PMRS based on model 1, where MRS = max(absolute risk shifts between the current model and all bigger models for a given individual); maxMRS = max(MRS) across all individuals; and 95PMRS = the 95^th percentile of the MRS.

We then explored the risk shift at the population level, as more SNPs are added into the risk model. Table I shows that the risks do not shift markedly once the model size is bigger than a certain level. For example, if we let the ‘maxMRS-selected model’ be the smallest model with a maxMRS < 0.06, then in all the three data sets, the 95PMRS of the models bigger than the maxMRS-selected model were all smaller than 0.025. Furthermore, if we let M_i represent the model with i SNPs, in all the three data sets, when the model size is bigger than the maxMRS-selected model, 100% of the M_i+1 risk estimates lay inside the corresponding M_i confidence interval (Figure 3a–c) and 100% of the M_i+1 confidence intervals overlap with the corresponding M_i confidence interval (Figure 3d–e). In addition, when the model size is bigger than the maxMRS-selected model, all the M_i+1 confidence intervals overlapped more than 50%, 90% and 95% with the corresponding M_i confidence intervals, in the simulation data set, AAA data set and AMD data set, respectively (data not shown). Consistent with these observations, Figure 4 shows that when the model size was greater than the maxMRS-selected model, the risk shift distributions did not change markedly as the model sizes grew.

Table I. The maxMRS and 95PMRS measures^* in the simulation data set, the AAA data set and the AMD data set.

The bold values indicate the “maxMRS-selected model” which is the smallest model with maxMRS less than 0.06.

	Simulation data set		AAA data set		AMD data set
# of SNPs in Model	maxMRS	95PMRS	maxMRS	95PMRS	maxMRS	95PMRS
1	0.395	0.113	0.221	0.075	0.381	0.227
2	0.311	0.076	0.222	0.070	0.322	0.158
3	0.286	0.067	0.182	0.063	0.307	0.136
4	0.214	0.060	0.133	0.051	0.297	0.128
5	0.209	0.053	0.147	0.041	0.222	0.104
6	0.185	0.050	0.098	0.038	0.164	0.079
7	0.176	0.046	0.070	0.027	0.142	0.066
8	0.163	0.041	0.058	0.022	0.096	0.050
9	0.150	0.036	0.042	0.016	0.064	0.035
10	0.119	0.032	0.039	0.014	0.032	0.021
11	0.103	0.029	0.030	0.011	0.022	0.010
12	0.099	0.025	0.021	0.009	0.007	0.004
13	0.087	0.022	0.020	0.006	0.002	0.001
14	0.069	0.019	0.017	0.005
15	0.060	0.016	0.002	0.001
16	0.043	0.012
17	0.025	0.007
18	0.011	0.003

^*MRS = max(absolute risk shifts between the current model and all bigger models for a given individual); maxMRS = max(MRS) across all individuals; 95PMRS = the 95^th percentile of the MRS.

Figure 3.

Percentages of M_i+1 risks inside the M_i confidence intervals (a–c), and percentages of M_i+1 confidence intervals that overlap with the M_i confidence intervals (d–f), where model M_i+1 is one SNP larger than model M_i. The grey bar shows the maxMRS-selected models.

Figure 4.

The distribution of risk shifts as a function of the number of SNPs in the updated model. The plots were generated by the beanplot command in the R package of the same name [Kampstra 2008]. The dark horizontal lines show individual observations, and the red line indicates the mean. The label above the plot is the added SNP’s odds ratio in the model. The circled model is the maxMRS-selected model.

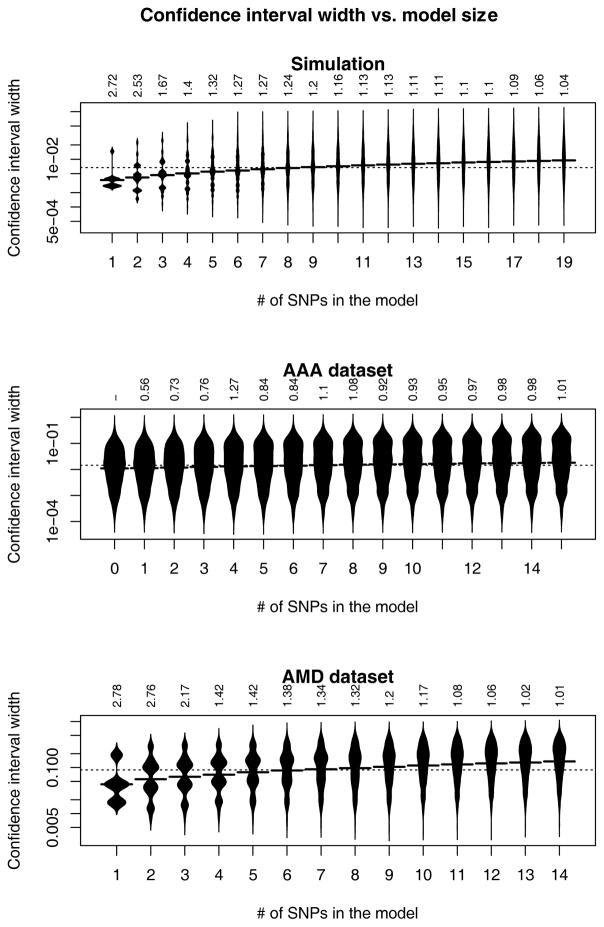
We then explored the influence of the model size on the confidence interval width. Figure 5 shows that the confidence interval width was positively correlated with model size in all the three data sets. For all the three data sets, the Spearman’s rank correlation test gives p values smaller than 0.001, indicating positive correlation between the confidence interval width and model size. Table II also shows the influence of the model size on the confidence interval width. More estimates have wider confidence intervals in the updated model than in the initial model. For the AAA data set, comparing M₀ with M₈, 84.8% of the estimates have wider confidence intervals in the updated model compared to the initial model; while comparing the M₈ with M₁₆, 96.0% of the estimates have wider confidence intervals in the updated model compared to the initial model. For the AMD data set, comparing M₁ to M₁₀, 90.0% of the estimates have wider confidence intervals in the updated model compared to the initial model; while comparing M₁₀ to M₁₄, 100% of the estimates have wider confidence intervals in the updated model compared to the initial model.

Figure 5.

The distribution of the confidence interval widths by model size. The confidence interval width axis uses the log scale. The label above the bean plot is the added SNP’s odds ratio in the model. The horizontal line in the middle of each bean plot shows the mean value.

Table II. CI-augmented reclassification tables for the AAA data set and the AMD data set.

“LOW*”/“HIGH*” class records the number of samples with both risk estimates and the two confidence interval bounds lower/higher than the threshold, which is the prevalence of the corresponding disease. “{−threshold}” class records the number of samples with risk estimates lower than the threshold, but the higher confidence interval bounds above the threshold. “{+threshold}” class records the number of samples with risk estimates higher than the threshold, but the lower confidence interval bounds below the threshold. “% reclassified” is the percentage of samples that are reclassified from LOW*/HIGH* risk class to HIGH*/LOW* class. “−=” means the confidence interval width in the updated model is narrower than or equal to the width in the initial model. “+” means the confidence interval width in the updated model is wider than the initial width.

a. CI–augmented reclassification table for the AAA data set, when the initial model only has the clinical predictors (Model 1) and the updated model added 7 most effective SNPs (Model 8).
Outcome: Unaffected with AAA											Outcome: Affected with AAA
	Updated Model: clinical predictors plus 7 SNPs								[0, −0.033}⬄{+0.033,1] >% Reclassified	LOW* ⬄ {−0.033,1] >% Reclassified		Updated Model: clinical predictors plus 7 SNPs								[0, −0.033}⬄{+0.033,1] >% Reclassified	LOW* ⬄ {−0.033,1] >% Reclassified
Initial Model: clinical predictors	LOW* [0,0.033}		{−0.033}		{+0.033}		HIGH* {0.033,1]				Initial Model: clinical predictors	LOW* [0,0.033}		{−0.033}		{+0.033}		HIGH* {0.033,1]
	−=	+	−=	+	−=	+	−=	+				−=	+	−	+	−=	+	−=	+
LOW* [0,0.033}	99	323	0	19	0	1	0	0	2.1	4.5	LOW* [0,0.033}	2	17	0	4	0	0	0	0	13.9	17.4
{−0.033}	5	1	0	12	0	8	0	1		3.7	{−0.033}	0	2	1	5	0	5	0	0		1.0
{+0.033}	0	0	5	7	0	9		4	11.9		{+0.033}	0	0	1	4	0	8	0	3	4.3
HIGH*{0.033,1]	0	0	0	4	3	10	1	92			HIGH* {0.033,1]	0	0	1	2	2	9	6	152

b. CI–augmented reclassification table for the AAA data set, when the initial model has clinical predictors plus the 7 most effective SNPs (Model 8) and the updated model has the clinical predictors plus all the 15 SNPs (Model 16).
Outcome: Unaffected with AAA											Outcome: Affected with AAA
	Updated Model: clinical predictors plus 15 SNPs								[0, −0.033}⬄{+0.033,1] >% Reclassified	Low*⬄{−0.033,1] >% Reclassified		Updated Model: clinical predictors plus 15 SNPs								[0, −0.033}⬄{+0.033,1] >% Reclassified	Low*⬄{−0.033,1] >% Reclassified
Initial Model: clinical predictors plus 7 SNPs	LOW* [0,0.033}		{−0.033}		{+0.033}		HIGH* {0.033,1]				Initial Model: clinical predictors plus 7 SNPs	LOW* [0,0.033}		{−0.033}		{+0.033}		HIGH* {0.033,1]
	−=	+	−=	+	−=	+	−=	+				−=	+	−=	+	−=	+	−=	+
LOW* [0,0.033}	29	379	0	15	0	0	0	0	0.6	3.5	LOW* [0,0.033}	0	17	0	4	0	0	0	0	5.1	19.0
{−0.033}	0	1	3	40	0	3	0	0		0.6	{−0.033}	0	0	1	15	0	2	0	0		0.0
{+0.033}	0	0	0	4	0	26	0	0	3.1		{+0.033}	0	0	0	3	0	21	0	0	1.6
HIGH* {0.033,1]	0	0	0	0	0	10	0	88			HIGH* {0.033,1]	0	0	0	0	0	8	0	151

c. CI–augmented reclassification table for the AMD data set, when the initial model only has one SNP (Model 1) and the updated model has 10 most effective SNPs (Model 10).
Outcome: Unaffected with AMD											Outcome: Affected with AMD
	Updated Model: 10 SNPs								[0,0.055}⬄{+0.055,1] >%Reclassified	LOW*⬄{−0.055,1] >%Reclassified		Updated Model: 10 SNPs								[0,0.055}⬄{+0.055,1] >%Reclassified	LOW*⬄{−0.055,1] >%Reclassified
Initial Model: 1 SNP	LOW [0,0.055}		{−0.055}		{+0.055}		HIGH* {0.055,1]				Initial Model: 1 SNP	LOW* [0,0.055}		{−0.055}		{+0.055}		HIGH* {0.055,1]
	−=	+	−=	+	−=	+	−=	+				−=	+	−=	+	−=	+	−=	+
LOW* [0,0.055}	8	12	0	5	0	6	0	1	21.9	37.5	LOW* [0,0.055}	6	28	0	21	0	23	0	4	32.9	58.5
{*0.055}	0	0	0	0	0	0	0	0		15.0	{−0.055}	0	0	0	0	0	0	0	0		2.0
{+0.055}	0	0	0	0	0	0	0	0	55.0		{+0.055}	0	0	0	0	0	0	0	0	15.6
HIGH* {0.055,1]	3	0	1	7	1	5	0	3			HIGH* {0.055.1]	4	0	1	27	8	38	2	125

d. CI–augmented reclassification table for AMD data set, when the initial model has 10 most effective SNPs (Model 10) and the updated model has the clinical predictors plus all the 14 SNPs (Model 14).
Outcome: Unaffected with AMD											Outcome: Affected with AMD
	Updated Model: 14 SNPs								[0.−0.055}⬄{+0.055,1] >% Reclassified	LOW*⬄{−0.055,1] >% Reclassified		Updated Model: 14 SNPs								[0.−0.055}⬄{+0.055,1] >% Reclassified	LOW*⬄{−0.055,1] >% Reclassified
Initial Model: 10 SNP	LOW* [0,0.055}		{−0.055}		{+0.055}		HIGH* {0.055,1]				Initial Model: 10 SNP	LOW* [0,0.055}		{−0.055}		{+0.055}		HIGH* {0.055,1]
	−=	+	−=	+	−=	+	−=	+				−=	+	−=	+	−=	+	−=	+
LOW* [0,0.055}	0	20	0	3	0	0	0	0	0.0	13.0	LOW* [0,0.055}	0	30	0	8	0	0	0	0	2.3	21.1
{−0.055}	0	0	0	13	0	0	0	0		0.0	{−0.055}	0	0	0	47	0	2	0	0		0.0
{+0.055}	0	0	0	1	0	11	0	0	6.2		{+0.055}	0	0	0	1	0	68	0	0	0.5
HIGH* {0.055,1]	0	0	0	0	0	1	0	3			HIGH* {0.055,1]	0	0	0	0	0	23	0	108

Furthermore, we determined the reclassification rates based on the screening strategies 2 and 3. The reclassification rates with bigger-effect SNPs in Table IIa and IIc are higher than that with smaller-effect SNPs in Table IIb and IId. But the small-effect SNPs can still affect the reclassifications. Table IIb shows that in the AAA data set, adding 8 less effective SNPs to the maxMRS-selected model, 19.0% of cases and 0.6% controls were correctly reclassified; while 0% of cases and 3.5% of controls were mistakenly reclassified. Table IId shows that in AMD data set, adding 4 less effective SNPs to the maxMRS-selected model, 21.1% of the cases and 0% of the controls were correctly reclassified; while 0% of the cases and 13.0% of the controls were mistakenly reclassified. We also found the correctly reclassified rate of LOW*⬄{−T,1] is much higher than [0, −T}⬄{+T,1] for cases, and the correctly reclassified rate of LOW*⬄{ −T,1] is lower than [0, −T}⬄{+T,1] for controls, in both the AAA data set and the AMD data set.

Finally, we evaluated the net benefit quantities of the three screening strategies. Table III shows that in both of the two data sets, the screening strategy of screening the individuals in the {−T,1] category provides the biggest net benefit quantity among the three strategies. The full models of both AAA and AMD data sets with {−T,1] screening strategy have the biggest net benefit quantity.

Table III. Net benefit of the classification of each model in the AAA data set and the AMD data set for the three screening strategies.

The threshold T is the population disease prevalence.

	AAA			AMD
Screening strategies	Model 1	Model 8	Model 16	Model 1	Model 10	Model 14
Screen individuals in {T,1]	0.201	0.191	0.180	0.601	0.386	0.318
Screen individuals in {+T,1]	0.220	0.218	0.216	0.601	0.587	0.590
Screen individuals in {−T,1]	0.236	0.238	0.242	0.601	0.730	0.753

Discussion

Due to rapid progress and advancements in sequencing technology, it is now feasible, yet still expensive, to accurately type all genetic variants for an individual. To construct a risk estimate from these variants, we could attempt to use all of them or we could order them by estimated effect size, and use only the strongest predictors. But then the question is how many of these should be used. Clearly, as the effect size shrinks, adding a single small effect predictor to the risk model will not shift the risk by much. We explored here how the risk estimate and its certainty change as variants of decreasing effect size are added into the risk model, using simulated data and real data of two different complex diseases (AAA and AMD).

If we order SNPs by decreasing effect sizes and build risk models of increasing size by adding in the next SNP, we first observe that the risk shifts between successive models become more and more modest (Figure 4, Figure 2, Table I) and the confidence intervals of the risk estimates tend to become larger (Figure 5, Table II). Then, we observe that when the model size is large enough, if one more variant is added, the majority of the updated risk estimates will lie within the confidence interval of the preceding estimate and the confidence intervals of the new and old estimates will overlap substantially (Figure 3). However, as we add multiple small-effect SNPs to the model simultaneously, these SNPs can still affect the reclassifications (Table II, Table III).

Our data also suggest that models with slightly larger AUCs are not necessarily better than those with smaller AUCs, if one takes into consideration risk shifts and confidence interval widths. Table I and II b,d shows that when the model size is bigger than ‘MaxMRS-selected model’, the risks shifts become modest and the confidence intervals become wider. Thus, with similar risk estimates and wider confidence interval widths, full models are not necessarily superior to maxMRS-selected models. However, Table IV shows that the AUCs of the full models are only slightly larger than the AUCs of the maxMRS-selected models. This suggests that only considering the AUC but ignoring risk shifts and confidence intervals may not be adequate.

Table IV. AUCs (area under the curve) of the maxMRS-selected model and the full model in the simulation data set, AAA data set, and AMD data set.

The numbers in each cell are the mean value and the standard deviation (shown in the parenthesis) of the AUCs in the 10 replicates.

	Simulation	AAA	AMD
MaxMRS-selected model	0.758 (0.006)	0.871 (0.017)	0.741 (0.021)
Full model	0.760 (0.006)	0.873 (0.016)	0.742 (0.022)

We recommend that all individuals with risk estimates above the threshold T or who have risk estimates with confidence intervals that overlap T (e.g., those in the {−T,1] category) should be screened. There are two reasons for this. First, the strategy of screening the individuals in the {−T,1] category gives the biggest net benefit among all three screening strategies. Second, for the cases, the correctly reclassified rate of LOW*⬄{ −T,1] is much higher than [0, −T}⬄{+T,1], although for the controls, the correctly reclassified rate of LOW*⬄{ −T,1] is lower than [0, −T}⬄{+T,1], in both the AAA data set and the AMD data set. Where screening costs much less compared to failing to detect the disease, screening the individuals in {−T,1] is the most appropriate strategy. However, it is important to remember that clinical cost-benefit analyses are complex and the assumption here is that screening is beneficial, although it is not necessarily so (for various diseases) if the “cost” of intervention risks are taken into account.

The results (Table III) are based on setting the threshold (T) to the population disease prevalence. The purpose of setting T to the population disease prevalence is to recommend screening for anyone whose risk was higher than what it would be if they were sampled from the general population. However, for many diseases, people may not undergo screening unless their estimated risk is relatively high. So we re-evaluated the net benefit, setting T to higher values of 10% and 20%. Supplementary Table III shows that when the thresholds are 10% and 20%, for both AAA and AMD data sets, the strategy of screening individuals in the {−T,1] category still provides the biggest net benefit quantity among the three strategies, and the full models with {−T,1] screening strategy still have the biggest net benefit quantity.

In our study, all the results are generated by one single split with 80% individuals in the training data set and 20% individuals in the testing data set. We then generated 5 more 80/20 random splits of the training and testing data sets to illustrate the results change. Table V shows the maxMRS-selected models of each split. In the simulation data set, the maxMRS-selected models in the 5 testing data sets are similar; while in the AAA and AMD data sets, the maxMRS-selected models in the 5 testing data sets are variant. This is because the sample size in the simulation data set is large (100,000), while the sample sizes in the AAA and AMD data sets are small (2,626 and 1,015, respectively). Therefore, the max-MRS selected models should be built using data sets with large sample sizes. Otherwise, the max-MRS selected models may be greatly affected by the splitting of the training and testing data sets. When the sample size is small and the maxMRS-selected model sizes are variant, we would recommend using the median value of the maxMRS-selected model sizes as the final model.

Table V. The number of SNPs in the maxMRS-selected models of five times 80/20 random splits in simulation data set, AAA data set, and AMD data set.

The “-” symbol indicates that the maxMRS based on the full model is bigger than 0.06. The numbers of SNPs in the maxMRS-selected model of the five splits are sorted by an increasing order in each data set.

Cross-validation	Simulation	AAA	AMD
1	16	8	10
2	16	8	11
3	17	9	12
4	17	13	-
5	17	14	-

In our results, the relationship of the risks and the confidence interval widths is consistent with the binomial distribution property that the confidence interval width increases as the risk estimate rises to 0.50 and decreases as the risk estimate increases beyond 0.5. Since the disease prevalence in the simulation study, AAA study, and AMD study were 0.055, 0.033 and 0.055, respectively, most of the risk estimates were much lower than 0.5, in all three data sets. In the simulation data set, AAA data set and AMD data set, only three, one, and eight individuals had risk estimates bigger than 0.5, respectively. In all the three data sets, most of the confidence intervals increased as the risk increased, or decreased as the risk decreased, when one more SNP with the next largest effect size was added to the model. But there were still some confidence intervals that increased as the risks decreased in the three data sets and some confidence intervals that decreased as the risks increased in the AAA data set only. These two scenarios are because of two reasons. The first one is that the confidence interval widths are not only related to the risk size, but are also related to the model size. Even though the risks estimated by larger models are smaller, the confidence intervals can still become bigger if the model sizes are bigger. The second reason is that when the risk estimate exceeds 0.50, the confidence interval width decreases as the risk increases, and vice versa.

The risk trajectory plot (Figure 2) shows that the higher-initial-risk individuals have their risks shifted more than the lower-initial-risk individuals as more SNPs are added to the model. This observation is mainly because of two reasons. First, the risk trajectories that start with a low initial risk suffer from a lower bound effect – they can not move very far in the down direction. Second, since the disease prevalence in the three data sets is as low as 0.055, 0.033 and 0.055, respectively, the majority of people must be in the low risk category.

Other previous studies classified individuals using both the risks and the confidence intervals. Goddard and Lewis [2010] developed a strategy, which has been implemented in the R package REGENT [Crouch, et al. 2013], to classify individuals into risk classes using the risk and the confidence interval of an average individual to anchor the classification. With N SNPs, there are 3^N genotypes. The “average individual” is the individual with a genotype relative risk closest to the average risk, which is the sum across all the 3^N genotypes of the products of their frequencies and relative risks of disease. An estimate with confidence interval overlapping the confidence interval of the “average individual” is classified as “Average” risk. An estimate with confidence interval below the confidence interval of the “average individual” is categorized as “low” risk. In a similar manner, they also define “moderate” and “high” risk categories. Scott et al. [2013] applied the reclassification method and the REGENT R package to predict the risk of rheumatoid arthritis and its age of onset with smoking. In Goddard and Lewis [2010], they observed that when one uses confidence interval-based risk classification, one can run into the situation where an individual with a lower risk is classified into the high risk group because their confidence interval was larger than an individual with a slightly higher risk who had a narrower confidence interval. This phenomenon also happens in our AAA and AMD data sets. We recorded the smallest risk estimate among those whose upper bounds of the confidence intervals are higher than the threshold. Then, we counted the number of estimates that are higher than this smallest risk estimate, but with confidence intervals that do not cross the threshold. Using the smallest model (model 1) and the biggest model (model 16) of the AAA data set, models 1, 11, and 14 of the AMD data set, there are 12, 24, 0, 19 and 9 estimates that meet these criteria, respectively.

Hart et al. [2013] also built a logistic regression model for risk estimation and took confidence intervals into account. They used logistic regression to create a new actuarial risk assessment instrument (ARAI). They categorized the individuals to two groups based on the ARAI score. They evaluate the ARAI at both group level and the individual level. Their results at the individual level are similar to our results. The mean width of the 95% confidence intervals for individual risk estimates in the high risk score category was much bigger than that of subjects in the low risk category. Confidence intervals for individual risk estimates overlapped completely within groups, and almost completely across groups.

In our study, the numbers of SNPs used in the simulation data set, AAA data set, and AMD data set are small (19, 14, and 15 risk SNPs, respectively), based on using the subset of significantly associated risk SNPs. Of course, in genome-wide studies, it might be of interest to use more or all of the available SNPs. In such a case, statistical methods, such as Penalized regression equipped with variable selection [Austin, et al. 2013] and Bayesian Alphabet methods [Gianola 2013], can be applied to the SNP selection; prediction is then based on the selected SNPs. Wimmer et al. [2013] compared methods performing variable selection to methods that retain all predictors in the model, e.g. ridge regression best linear unbiased prediction (RR-BLUP). They concluded that when the sample size is much larger than the number of causal mutations contributing to the trait, SNP-selection based prediction outperforms RR-BLUP. However, when the number of SNPs is big compared to sample size, each of small to modest effect size, like many complex disease scenarios, RR-BLUP is superior to the SNP-selection based prediction. Thus, under the situation that sample size is smaller than the number of causal mutations contributing to the traits, methods distributing effects across the genome would provide more precise predictions than those that perform model selection, and our proposed SNP-selection based prediction according to width of confidence intervals might be less than optimal. It would be of interest to extend this work to the context of penalized shrinkage models and traits with larger numbers of established risk SNPs.

Consideration of risk estimate uncertainty is important because if the disease risk estimates, as well as the confidence intervals are provided, people can make more informed decisions regarding their screening decisions [Weeks and Ott 1990]. For example, suppose an individual has a risk estimate below the threshold, but the upper bound of the confidence interval is much higher than the threshold. If only the risk estimate is provided, there will be an unfounded confidence in the estimate and the individual may feel safe, and therefore may choose to not undergo screening. But if both the risk estimate and its confidence interval are provided, the individual may no longer feel safe, and probably will undergo screening. For another example, consider an individual with a risk estimate slightly higher than the threshold and the lower bound of the confidence interval also above the threshold. If only the risk estimate is provided, this individual may not undergo screening, because the risk estimate is only slightly higher than the threshold. However, if the confidence interval shows that it has 95% certainty that the individual has high risk of getting the disease, then this individual may decide to undergo screening. On the other hand, since it is difficult to clearly convey risk estimates in such a way that they are understood and interpreted correctly, it may be even more difficult to clearly communicate the information embodied in the confidence intervals around those risk estimates [Lautenbach, et al. 2013]. Careful consideration of how to best communicate these measures of risk estimate uncertainty is merited, lest such communications lead to increased disease-related anxieties and poorer risk perceptions [Han 2013; Han, et al. 2011].