Abstract
Many modern statistical problems can be cast in the framework of multivariate regression, where the main task is to make statistical inference for a possibly sparse and low-rank coefficient matrix. The low-rank structure in the coefficient matrix is of intrinsic multivariate nature, which, when combined with sparsity, can further lift dimension reduction, conduct variable selection, and facilitate model interpretation. Using a Bayesian approach, we develop a unified sparse and low-rank multivariate regression method to both estimate the coefficient matrix and obtain its credible region for making inference. The newly developed sparse and low-rank prior for the coefficient matrix enables rank reduction, predictor selection and response selection simultaneously. We utilize the marginal likelihood to determine the regularization hyperparameter, so our method maximizes its posterior probability given the data. For theoretical aspect, the posterior consistency is established to discuss an asymptotic behavior of the proposed method. The efficacy of the proposed approach is demonstrated via simulation studies and a real application on yeast cell cycle data.
Keywords: Bayesian, Low rank, Posterior consistency, Rank reduction, Sparsity
1. Introduction
In various fields of scientific research such as genomics, economics, image processing, astronomy, etc., massive amount of data are routinely collected, and many associated statistical problems can be cast in the framework of multivariate regression, where both the number of response variables and the number of predictors are possibly of high dimensionality For example, in genomics study, it is critical to explore the relationship between genetic markers and gene expression profiles in order to understand the gene regulatory network; in a study of human lung disease mechanism, the detailed CT-scanned lung imaging data enable us to examine the systematic variations in airway tree measurements across various lung disease status and pulmonary function test results. To formulate, suppose we have n independent observations of the response vector yi ∈ ℝq and the predictor vector xi ∈ ℝp, i = 1, …, n. Consider the multivariate linear regression model
| (1) |
where Y = (y1, …, yn)⊤ ∈ ℝn×q is the response matrix, X = (x1, …, xn)⊤ ∈ ℝn×p is the predictor matrix, C ∈ ℝn×q is the unknown regression coefficient matrix, and E = (e1, …,en)⊤ ∈ ℝn×q is the error matrix with ei's being independently and identically distributed (i.i.d.) with mean zero and covariance matrix Σe, a q × q positive definite matrix. Following Bunea et al. [8, 9], Chen et al. [11] and Mukherjee et al. [28], we assume Σe = σ2Iq. We further assume the response variables and the predictors are all centered, and there is no intercept term. In what follows, we use to denote the jth row of a generic matrix A and ãℓ the ℓth column of A, e.g., C = (c1, …, cp)⊤ = (c̃1, …, c̃q). A fundamental goal of multivariate regression is thus to estimate and make inference about the coefficient matrix C so that meaningful dependence structure between the responses and predictors can be revealed.
When the predictor dimension p and the response dimension q are large relative to the sample size n, classical estimation methods such as ordinary least squares (OLS) may fail miserably. The curse of dimensionality can be mitigated by assuming that C admits certain low-dimensional structures, and regularization/penalization approaches are then commonly deployed to conduct dimension reduction and model estimation. The celebrated reduced rank regression (RRR) [2, 24, 32] achieved dimension reduction through constraining the coefficient matrix C to be rank deficient, building upon the belief that the response variables are related to the predictors through only a few latent directions, i.e., some linear combinations of the original predictors. As such, low-rank structure induces and models dependency among responses, which is the essence of conducting multivariate analysis. Bunea et al. [8] generalized the classical RRR to high dimensional settings, casting reduced-rank estimation as a penalized least squares problem with the penalty being proportional to the rank of C. Yuan et al. [37] utilized the nuclear norm penalty, defined as the ℓ1 norm of the singular values. See also, Chen et al. [11], Mukherjee and Zhu [29], Negahban and Wainwright [30], and Rohde and Tsybakov [33].
It is worth noting that low-rankness in C is of intrinsic multivariate nature; when combined with row and/or column-wise sparsity, it can further lift dimension reduction and facilitate model interpretation. For example, in the aforementioned genomics study, it is plausible that the gene expression profiles (responses) and the genetic markers (predictors) are associated through only a few latent pathways (linear combinations of possibly highly-correlated genetic markers), and moreover, very likely such linear associations only involve a small subset of genetic markers and/or gene profiles. Therefore, recovering a low-rank and also sparse coefficient matrix C in model (1) hold the key to reveal such interesting connections between the responses and predictors. Chen et al. [10] proposed a regularized sparse singular value decomposition (SVD) approach with known rank, in which each latent variable is constructed from only a subset of the predictors and is associated with only a subset of the responses. Chen and Huang [12] proposed a rank-constrained adaptive group Lasso approach to recover a low-rank coefficient matrix C with sparse rows; for each zero row in C, the corresponding predictor is then completely eliminated from the model. Bunea et al. [9] also proposed a joint sparse and low-rank estimation approach and derived its nonasymptotic oracle error bounds. Both methods required to solve the nonconvex rank-constrained problem by fitting models of various ranks. Recently, Ma et al. [27] proposed a subspace assisted regression with row sparsity method which was shown to achieve near optimal nonasymptotic minimax rates in estimation.
While all the aforementioned regularized regression techniques produce attractive point estimators of the coefficient matrix C, it remains a difficult problem to assess the uncertainty of the obtained estimators. To overcome this limitation, there has already been a rich literature on Bayesian approaches of the reduced rank regression. From a Bayesian perspective, the unknown parameter is considered as a random variable, and thus the statistical inference can be made by the posterior distribution. The first attempt to develop the Bayesian reduced rank regression was made by Geweke [20]. The coefficient matrix is assumed to be C = AB⊤ with A ∈ ℝp×r and B ∈ ℝq×r, where r < min(p, q) is assumed to be known. Then, by assigning Gaussian prior for each elements of A and B, the induced posterior achieves the low-rank structure of the prespecified rank. As an alternative, Lim and Teh [26] proposed to start from the largest possible rank r = min(p, q), assign a column-wise shrinkage Gaussian prior on each columns of A and B. The posterior for redundant columns of A and B is forced to be concentrated around zero, so the (approximate) rank reduction can be accomplished. The main challenge of this Bayesian approach is the choice of the hyperparameters of the Gaussian priors in order to control the amount of shrinkage. There have been several attempts to overcome this challenge by assigning priors on the hyperparameters, so that they can be determined in the estimation procedure. For instance, Salakhutdinov and Mnih [34] proposed to utilize the Wishart distribution as the hyperprior. Similar hierarchical Bayesian methods were also proposed in the context of matrix completion, matrix completion deals with missing values, but we do not [4, 40]. However, none of the aforementioned studies dealt with the sparsity of the coefficient matrix C. Recently, Zhu et al. [41] introduced a Bayesian low-rank regression model with high-dimensional responses and covariates. To enable sparse estimation under low rank constraint with a prefixed rank, they utilized a sparse singular value decomposition (SVD) structure [10] with Gaussian-mixtures of gamma priors on all the elements of the decomposed matrices. Then, the sparsity of C was achieved using Bayesian thresholding method. For a survey on Bayesian reduce rank models, see Alquier [1] and the references therein.
We develop in this article a novel Bayesian simultaneous dimension reduction and variable selection approach. Our method aims to tackle several challenges regarding both the estimation and inference in the sparse and low-rank regression problems. First, the proposed method enables us to simultaneously estimate the unknown rank and remove irrelevant predictors, in contrast to several existing methods in which rank selection has to be resolved by comparing fitted models of various ranks or by some ad hoc approach such as scree plot. In addition, we also seek potential column sparsity of the coefficient matrix, so that it is applicable to problems with high-dimensional responses where response selection is highly desirable (to be elaborated below). Second, by careful construction of the prior distribution, our method alleviates the many difficulties brought by the use of nonsmooth and non-convex penalty functions and by the tuning parameter selection procedure in penalized regression analysis. From a Bayesian perspective, the penalty function can be viewed as a negative logarithm of the prior density function [25, 31, 36]. We develop a general prior for C mimicking the rank penalty and the group ℓ0 row/column penalty, to achieve simultaneous rank reduction and variable selection through the induced posterior distribution, yet the computation is kept tractable and efficient, where the group ℓ0 penalty directly restricts the number of nonzero rows and columns. Since the tuning parameters are considered as random variables in our Bayesian formulation, the optimal ones are selected to achieve the highest posterior probability given the data. Furthermore, using our Bayesian approach, the credibility intervals for the regression coefficients and their functions can be easily constructed using the Markov Chain Monte Carlo (MCMC) technique. In contrast, there has been little work on quantifying the estimation uncertainty in regularized regression approaches.
We now formally state our assumptions or prior beliefs about the coefficient matrix C in model (1).
A1. (Reduced rank) r* ≤ r, where r* = rank(C) indicates the rank of C and r = min(p, q).
A2. (Row-wise sparsity) p* ≤ p, where and denotes the jth row of C, where card(·) denotes the cardinality of a set.
A3. (Column-wise sparsity) q* ≤ q, where and c̃ℓ denotes the ℓth column of C.
A1 states that C is possibly of low rank. In A2, excluding the jth predictor from model (1) is equivalent to setting all entries of the jth row of C as zero. Therefore, the first two assumptions concern rank reduction and predictor selection. The third assumption is about “response selection”, i.e., if the ℓth column of C is zero, the ℓth response is modeled as a noise variable. While such structural assumption can be treated as optional depending on the specific application, we stress that there are many circumstances where response selection is highly desirable [10]. For example, in many applications the dimension of the responses can be very high, and there may exist noise variables that are not related to any predictors in the model. In addition, eliminating irrelevant predictors dramatically reduces the number of free parameters of the model and thus it improves the accuracy of parameter estimation [5]. In addition, allowing possible response selection provides more flexibility and generality in the multivariate linear regression framework, since the case of selecting all responses can be viewed as a special case.
The remainder of the paper is organized as follows. In Section 2, we briefly introduce a general penalized regression approach for conducting sparse and low-rank estimation. In Section 3, we develop our new Bayesian approach, and explore the connections between the penalized least squares and our Bayes estimators. The full conditionals are obtained in Section 4, and we describe the posterior optimization algorithm and posterior sampling technique. In Section 5, we study the posterior consistency of the proposed method. Simulation studies and a real application on yeast cycle data are presented in Section 6 and Section 7. Some concluding remarks are given in Section 8.
2. Penalized regression approach
In the regularized estimation framework, the unknown coefficient matrix C in model (1) can be estimated by the following penalized least squares (PLS) method,
| (2) |
where denotes the Frobenius norm and 𝒫λ(C) is a penalty function with non-negative tuning parameter λ controlling the amount of regularization. It is natural to construct a penalty function of an additive form,
where , and induce the low-rankness, row-wise sparsity and column-wise sparsity in C, with tuning parameters λ1, λ2 and λ3, respectively. There are numerous choices of the penalty functions. Note that the rank of matrix C is same as the number of non-zero singular values, i.e., rank(C) = card ({k: sk(C) > 0}) = r*, where sk(C) denotes the kth singular value of C. Hence, rank reduction can be achieved by penalizing the singular values of C, i.e.,
| (3) |
where ρ1 is a sparsity-inducing penalty function. In particular, choosing ρ1(|a|) = 1 (|a| ≠ 0) corresponds to directly penalizing/restraining the rank of C, and that ρ1(|a|) = |a|β1 gives the Schatten-β quasi-norm penalty when 0 < β1 < 1 and the convex nuclear norm penalty λ1‖C‖* when β1 = 1, where denotes the nuclear norm. For promoting rowwise/column-wise sparsity, selecting or eliminating parameters by groups is needed, which can be achieved by penalizing the row/column ℓ2 norms of C,
| (4) |
| (5) |
where denotes the ℓ2 norm. Choosing ρ2(|a|) = 1 (|a| ≠ 0) corresponds to directly counting and penalizing the number of nonzero rows, and ρ2(|a|) = |a| corresponds to the convex group Lasso penalty [38]. Other methods include group SCAD [16] and group MCP [7, 39]; see Fan and Lv [18] and Huang et al. [22] for comprehensive reviews. In principal, rank reduction and variable selection can be accomplished by solving the PLS problem (2) with any sparsity-inducing penalties ρ1, ρ2 and ρ3.
The pros and cons of using convex penalties in model selection are well understood. In low-rank estimation, Bunea et al. [8] showed that while the convex nuclear norm penalized estimator has similar estimation properties to those of the nonconvex rank penalized estimator, the former requires stronger conditions and is in general not as parsimonious as the latter in rank selection. For sparse group selection, it is known that the convex group Lasso criterion often leads to over-selection and substantial estimation bias, and adopting nonconvex penalties may lead to superior properties in both model estimation and variable selection under milder conditions [23, 27]. Unfortunately, the nonconvexity of a penalized regression criterion also imposes great challenges in both understanding its theoretical properties and solving the optimization problem in computation. Therefore, trading off computation efficiency and statistical properties is critical in formulating penalized estimation criterion, and it is particularly relevant when dealing with large data applications. The problem of tuning parameter selection can also be troublesome, especially so for the problem of interest here as it requires multiple tuning parameters. Furthermore, it is still a largely unsolved problem on how to make statistical inference and attach error measures to any penalized estimator. All these concerns motivate us to tackle the sparse and low-rank estimation problem in a Bayesian fashion, to achieve a computationally efficient implementation and be able to make valid inference about the composite low-dimensional structure of C.
3. Bayesian sparse and low-rank regression
From a Bayesian perspective, the PLS estimator in (2) can be viewed as the maximum a posteriori (MAP) estimator from the following posterior density function,
where f(Y | C) denotes the likelihood function and π(C | λ) denotes the prior density function of C given the tuning parameter λ. Since the MAP estimator of C is free of σ2, without loss of generality, throughout this paper we assume that σ2 = 1. Motivated by the connections between PLS and MAP and by the penalty function defined in (3)-(5), it is natural to consider the following prior,
| (6) |
where ε > 0 is a suitably small value and λ = (λ1, λ2, λ3). Note that as ε → 0, this prior converges to the following penalty function under the MAP estimation:
In penalized regression, this £0 penalty corresponds to directly penalize the rank, the number of nonzero rows, and the number of nonzero columns of C, which leads to an intractable combinatory problem. Similarly, in Bayesian framework, even though this setup directly targets on the desired structure of C, there are several difficulties in using such a prior distribution. Since the prior density function in (6) involves the singular values of C, it induces an improper posterior distribution, as it is generally difficult to be considered as a probability density function of C. Moreover, the non-differentiability of indicator function induces a discontinuous posterior density function.
To overcome the first difficulty, i.e., avoiding direct use of the singular values, we propose an indirect modeling method through decomposing the matrix C. We write C = AB⊤, where A is a p × r matrix, Bisaq×r matrix, and r is an upper bound of the true rank r* of C, e.g., a trivial one is r = min(p, q). Apparently such a decomposition is not unique, as with any nonsingular r×r matrix Q, C = AB⊤ = AQQ−1B⊤ = ÃB̃⊤ where à = AQ and B̃ = B (Q−1)⊤. Interestingly, the following lemma reveals that the low-rankness and the row/column sparsity of C can all be represented as certain row/column sparsity of A and B, and more importantly, the representations are invariant to any nonsingular transformation.
Lemma 1. Let C ∈ ℝp×q, and suppose C = AB⊤ for some A ∈ ℝp×r, B ∈ ℝq×r with r = min(p, q). Let ãk and b̃k denote the kth column of A and B, respectively. Let and denote the jth row of A and the ℓth row of B, respectively. Then
{j: ‖cj‖2≠0} ⊂ {j: ‖aj‖2≠0}.
{ℓ: ‖c̃ℓ‖2 ≠ 0} ⊂ {ℓ: ‖bℓ‖2 ≠ 0}.
The first statement in the above lemma suggests the following rank-reducing prior,
| (7) |
where ε > 0 and λ1 > 0. For a sufficiently small ε, this prior induces sparsity on columns of A and B simultaneously and thus reduces the rank of C. Similarly, Lemma 1 suggests the following row-wise and column-wise sparsity-inducing priors,
| (8) |
| (9) |
where ε > 0, λ2 > 0 and λ3 > 0. Combining (7), (8) and (9) leads us to the following prior,
| (10) |
where λ = (λ1, λ2, λ3).
The discontinuity problem still presents in (10) due to the indicator functions. We address this problem by approximating ℓ0-norm by a well-behaved smooth function. Let D be a m × n matrix. Define
| (11) |
where D = (d1, …, dm)⊤, 0 ≤ β ≤ 1 and ω > 0. We have
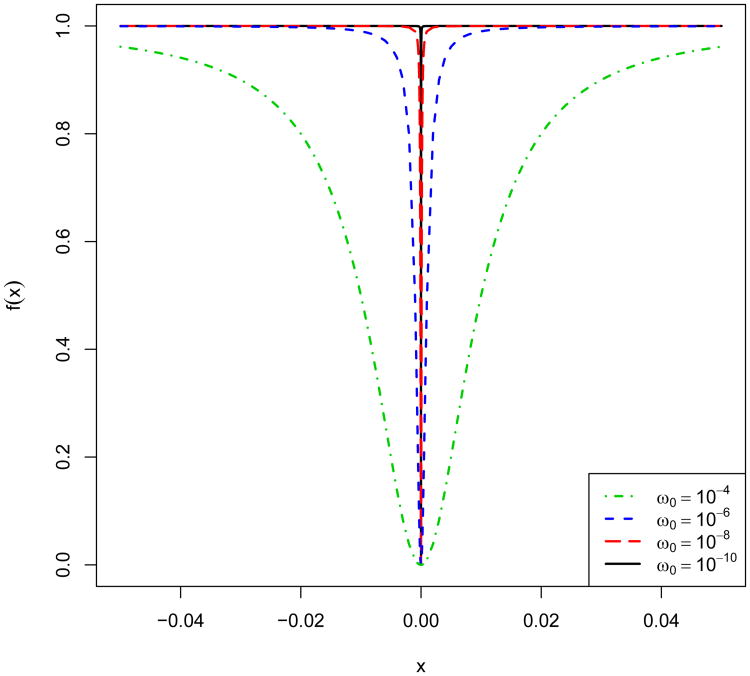
as ω → 0, where we define (0)0 = 0. This implies that the proposed penalty approximates the group ℓβ-norm penalty when ω is sufficiently small. In particular, when β = 0 and ω is chosen to be a small positive constant ω0, (11) gives an approximate group ℓ0-norm penalty and produces approximately sparse solutions, while it is continuous as well as differentiable with respect to D. In all our numerical studies, we set ω0 = 10−10 and utilize tolerance level 10−5 to determine zero estimates. Fig. 1 shows the plots of f(x) = x2/(x2 + ω0) for varying ω0 = 10−k, k = 4, 6, 8,10. Indeed, when w0 = 10−10, the function closely mimics the ℓ0 penalty.
Figure 1.
Plot of f(x) = x2/(x2 + ω0) for ω0 = 10−k (k = 4, 6, 8, 10).
We now propose the following prior distribution for our Bayesian Sparse and Reduced-rank Regression (BSRR) method,
| (12) |
where λ = (λ1, λ2, λ3) and λi, ≥ 0 (i = 1, 2, 3). The BSRR posterior is then given as
| (13) |
and the MAP estimate (Âmap, B̂map) is defined as
Since C = AB⊤, the MAP estimator for C, named BSRR estimator, is given by ĈBSRR = Âmap(B̂map)⊤.
The following lemma tells us the BSRR model can be expressed as a hierarchical Bayesian model by introducing auxiliary variables.
Lemma 2. Define d = (d1,1, …, d1,r, d2,1,…, d2,p, d3,1,…, d3,q). Let π (A, B, d | λ) be a density function of (A, B, d) such that
| (14) |
where m1 = r, m2 = p and m3 = q. Let πBSRR(A, B | λ) denote the BSRR prior defined in (12). Then, for any positive λ and ω0, we have that
The proof of Lemma 2 can be shown by differentiating Eq. (14) with respect to di,j's, letting them to be zero, and finding the solutions of the equations. Based on Lemma 2, we introduce the following hierarchical Bayesian representation of the sparse reduced-rank regression model (HBSRR),
| (15) |
| (16) |
| (17) |
where m1 = r, m2 = p, m3 = q, d = {diag(D1), diag(D2), diag(D3)}, λ = (λ1, λ2, λ3), and di,mi > 0 (i = 1, 2, 3). Let (Âmode, B̂mode, d̂mode) be the mode of the induced posterior π(A, B, d | Y, λ) from the above hierarchical model. Recall that ĈBSRRindicates the BSRR estimator. Then, using Lemma 2, it is straightforward to show that ĈBSRR = Âmode (B̂mode)⊤, almost surely. This enables us to easily find ĈBSRR using the HBSRR. Since all full conditional distributions of the HBSRR are well-known distributions such as Gaussian and gamma, the estimation procedure can be conducted by standard Bayesian estimation algorithms.
4. Bayesian analysis
Since our posterior distribution is complex, the Bayesian inference procedure requires the implementation of iterated conditional modes (ICM) algorithm [6] or Markov chain Monte Carlo (MCMC) sampling techniques, to obtain Bayes estimators such as posterior mode, posterior mean, or credible set. We derive full conditional distributions from the joint posterior of HBSRR. Then, we describe the implementation of ICM and MCMC, and discuss the determination of the tuning parameter from a Bayesian perspective.
4.1. Full conditionals
To derive the full conditionals of the HBSRR, we write
| (18) |
Here we use the notation C(j) to denote the submatrix of a generic matrix C by deleting its jth row, and C(j̃) by deleting its jth column. Using (15), (16) and (18), the full conditional distribution of aj (j = 1,…, p) is determined to be
| (19) |
where
with Ir denoting the r × r identity matrix. Similar to (18), we have
The full conditional distribution of bℓ, for ℓ = 1,…, q, is given by
| (20) |
where
From (16) and (17), it is straightforward to show that the full conditionals for elements of D are written as
where k = 1,…, r, j = 1,…, p, and ℓ = 1, …, q.
4.2. Iterated conditional modes
All full conditionals in Section 4.1 are well-known distributions (normal or gamma distribution), and the modes are thus well-known. Consequently, using the full conditionals, we construct the following ICM algorithm to find the BSRR estimate ĈBSRR:
|
|
| Algorithm 1 ICM algorithm for ĈBSRR |
|
|
| Step 1) Set initial values (Â, B̂, d̂) = (A(0), B(0), d(0)). |
| Step 2) Update (Â, B̂, d̂) = (A(t+1), B(t+1), d(t+1)) by |
| for k = 1, …, r; j = 1, …, p; ℓ = 1, …, q. |
| Step 3) Repeat step 2 until convergence. |
| Step 4) Return ĈBSRR = ÂB̂⊤. |
|
|
To set an initial value (A(0), B(0), d(0)), we propose to utilize the OLS estimate Ĉols = (X⊤X)−X⊤Y. Let Ĉols = USV⊤ be the sigular value decomposition of Ĉols. Then, (A(0), B(0), d(0)) can be defined as
for k = 1, …, r, j = 1, …, p and ℓ = 1, …, q.
4.3. Posterior sampling
Using the HBSRR, we introduce indirect sampling method to obtain the posterior samples for C, so that they can be used to construct the credible set for the BSRR estimate ĈBSRR. Recall that (Âmode, B̂mode, d̂mode) denotes the posterior mode of the HBSRR. Then,
Consequently, we can obtain the posterior sample of C from the following posterior
Note that d̂mode can be obtained by the proposed ICM algorithm in the previous section. First, to generate MCMC samples from the above posterior distribution of (A, B), we consider a Gibbs sampler that iterates through the following steps:
update aj for j = 1, …, p;
update bℓ for ℓ= 1, …, q.
The explicit forms of full conditionals of aj and bℓ, respectively, are given in (19) and (20). In each Gibbs step, we update aj and bℓ by generating samples from
where d̂mode = {diag(D̂1), diag(D̂2), diag(D̂3)}. Let be a set of obtained MCMC samples from the above sampling procedure. Then a set of posterior samples for C can be obtained by .
4.4. Tuning parameter selection
In practice, we are usually interested in selecting a tuning parameter λ = (λ1, λ2, λ3) (or hyperparameter) from the set of candidates ℒ = {λ1, …, λK}. We assume that there is no preferred model, i.e., π(λk) = 1/K for k = 1, …, K. In general, the tuning parameter is determined via a grid search strategy from a lower bound λL = (0+, 0+, 0+) to a given upper bound λU which is the smallest value to induce the marginal null model (i.e., all estimates are zero). Hence, the set ℒ is well-defined. Let m(Y | λk) = ∫ f(Y | A, B)Π(dA, dB | λk) be a marginal likelihood for a given λk. Then, we can show that m(Y | λk) is proportional to the posterior probability of λk given Y, that is
| (21) |
From the above viewpoint, we define the optimal λk* such that
Let C be the p × q coefficient matrix with rank(C) = r*. Without loss of generality, suppose that the first p* rows and q* columns of C are non-zero and the remaining rows and columns of C are zero. Then, the matrix C can be decomposed as
where Ir*. denotes the identity matrix of order r*, CA is a (p* −r*) × r* nonzero matrix, CB is a r* × q* nonzero matrix, and OA is the (p−p*) × r* zero matrix, and OB is the r* × (q − q*) zero matrix. The key to above parameterization of C is that the matrix CA and CB are uniquely determined. It can be seen that for given (r*, p*, q*), the number of free parameters in C is dim(CA) + dim(CB) = r*(p* + q*−r*). Suppose that a given tuning parameter λ = λk results in an estimator with (rk, pk, qk). Define θ = {vec(CA)⊤, vec(CB)⊤}⊤ such that θ ∈ Θ ⊂ ℝrk(pk+qk−rk), where vec(⋅) denotes the vectorization of a matrix. Then, the marginal likelihood can be rewritten as
| (22) |
where gn(θ | Y, λ) = (nqk)−1 {ln f(Y | θ) + ln π (θ | λk)}. Let θ̂ be the mode of gn(θ | Y, λ). By the Laplace approximation, the marginal likelihood in (22) can be expressed as
| (23) |
where
By taking the logarithm of the formula (23) and ignoring the term of O(1) and higher order terms, we have the following approximation of log marginal likelihood
| (24) |
Let Ĉk be the BRRR estimate for given λk. Then, by substituting it in (24) and multiplying by −2, (24) reduces to the BRRR version of Bayesian information criterion [35],
| (25) |
According (21), we know that minimizing the BIC corresponds to maximizing the posterior probability of λk given Y. Hence, we regard the tuning parameter λ* as the optimum if λ* = argminλk∈ℒ BIC(λk).
5. Posterior consistency
In Bayesian analysis, the posterior consistency assures that the posterior converges to point mass at the true parameter as more data are collected [13, 15, 21]. Here, we discuss the posterior consistency for the proposed BSRR method, following Armagan et al. [3]. We allow the number of predictors p to grow with sample size n, and the number of true non-zero coefficients p* is assumed to be finite. Henceforth, we denote p as pn. Similarly the response matrix Y and predictor matrix X are denoted by Yn and Xn, respectively. Unlike pn, the number of response variables q is assumed to be fixed in our analysis.
Suppose that, given Xn and C*, Yn is generated from
where with a positive definite matrix Σ (assumed to be known) and C* is a (pn × q) matrix such that card , card and rank(C*) = r*. Further, we make the following assumptions.
pn = o(n), but p* < ∞ and q* ≤ q < ∞.
0 < Smin < lim infn→∞ Sn, min/√n ≤ lim supn→∞ Sn, max/√n < Smax < ∞, where Sn, min and Sn, max denote the smallest and the largest singular values of X, respectively.
, where indicates the (j, ℓ)th element of C*.
Our main results are presented in Theorems 3 and 4 below.
Theorem 3. Under assumptions I and II, if the prior Π(A, B) satisfies the following condition:
for all and and some ρ > 0, where τmin and τmax denote, respectively, the smallest and the largest eigenvalue of Σ, then the posterior of (A, B) induced by the prior Π(A, B) is strongly consistent, i.e., for any ε > 0,
as n → ∞.
Theorem 4. Under assumptions I, II and III, the prior defined in (12) yields a strongly consistent posterior if ln n for finite δi > 0, i = 1, 2, 3.
In Theorem 3, we establish a sufficient condition on a prior distribution in order to achieve posterior consistency. Theorem 4 then shows that our BSRR prior in (12) satisfies the sufficient condition in Theorem 3, and consequently, our BSRR method possesses the desirable posterior consistency property. The proofs of both theorems are shown in the supplementary materials.
6. Simulation studies
To examine the performance of our BSRR method, we conduct Monte Carlo experiments under several possible scenarios. For purposes of comparison, we also consider the following two reduced priors:
| (26) |
| (27) |
We denote the Bayesian methods using (26) and (27) as RR (Row-wise-sparse and Reduced-rank) method and RC (Row-and-Column-wise sparse) method, respectively. Our BSRR method aims to recover all the low-dimensional structures in A1–A3, but RR and RC methods, respectively, do not consider the column-wise sparsity of C in A3 and the reduced rank structure of C in A1. Therefore, the RR method is analogous to the joint rank and predictor selection methods proposed by Chen and Huang [12] and Bunea et al. [9]. The RR and RC methods can be derived from BSRR method with setting λ3 = 0 and λ1 = 0 in (13), respectively. Hence, the BSRR estimate ĈBSRR as well as RR and RC estimates, ĈRR and ĈRC, are obtained by the proposed algorithm in Section 4.2. Similarly, the unknown tuning parameter λ for each model is estimated by the proposed BIC in (25).
We generate data from the multivariate regression model Y = XC + E. For the n × p design matrix X, its n rows are independently generated from 𝒩p(0, Γ), where Γ = (Γij)p×p with Γij = (0.5)|i−j|. The p × q coefficient matrix C is defined as , where sk = 5 + (k − 1)ȳ15/r*ɉ; the entries of Ck are all zero expect in its upper left p* × q* submatrix, which is generated by , where z1 ∈ ℝp*, z2 ∈ ℝq*, and all their entries are i.i.d samples from uniform([−1, −0.3] ∪ [0.3,1]). The rows of the noise matrix E are independently generated from 𝒩p(0, Σe), where Σe = (Σij)q×q with Σij = σ2(0.5)|i−j| and σ2 is chosen according to the signal to noise ratio(SNR) defined by sr* (XC)/s1(PXE) with PX = X(X⊤X)−X⊤.
In the first scenario, we generate models of moderate dimensions (i.e., p, q < n) in three setups:
(a1) p = q = 25, n = 50, r* = 3, p* = 10, q* = 10. This setup favors our BSRR method.
(a2) p = q = 25, n = 50, r* = 3, p* = 10, q* = 25. As all the responses are revelent in the model, this setup favors the RR method.
(a3) p = q = 25, n = 50, r* = 10, p* = 10, q* = 10. This favors the RC method, which does not enforce rank reduction.
In the second scenario, we generate high-dimensional data (i.e., p, q > n) using similar settings as above,
(b1) p = 200, q = 170, n = 50, r* = 3, p* = 10, q* = 10.
(b2) p = 200, q = 170, n = 50, r* = 3, p* = 10, q* = 170.
(b3) p = 200, q = 170, n = 50, r* = 10, p* = 10, q* = 10.
The estimation accuracy is measured by the following three mean squared errors (MSEs):
where s(C) denotes the vector of singular values for a matrix C. To assess the variable selection performance, we use false positive rate (FPR) and false negative rate (FNR) such that FPR% = 100FP/(TN + FP) and FNR% = 100FN/(TP + FN), where TP, FP, TN and FN denote the numbers of true nonzeros, false nonzeros, true zeros and false zeros, respectively. The rank selection performance is evaluated by the percentage of correct rank identification (CRI%). All measurements are estimated by the Monte Carlo method with 500 replications.
Tables 1 and 2 summarize the simulation results. As expected, in the cases (a1) and (b1), where rank reduction, predictor selection and response selection are all preferable, the BSRR method performs much better than the other two reduced methods. In cases (a2) and (b2), rank reduction and predictor selection are preferable while response selection is not necessary. The performance of the BSRR method is very similar to the RR method which assumes the correct model structure. In the cases (a3) and (b3), rank reduction becomes unnecessary when response and predictor selections are performed. While the BSRR method slightly underestimates the true rank (r* = 10), its variable selection performance (FPR and FNR) is comparable to that of the RC method which assumes the correct model structure. The results are consistent for different SNR levels. Therefore, our BSRR approach provides a flexible and unified way for simultaneously exploring rank reduction, predictor selection and response selection.
Table 1.
Summary of the simulation results for examples (a1)–(a3).
| Case | SNR | Method | MSEest | MSEpred | MSEdim | FPR% | FPR% | CRI% | r̂ |
|---|---|---|---|---|---|---|---|---|---|
| (a1) | 0.50 | BSRR | 7.42 | 109.63 | 17.59 | 0.41 | 0.24 | 100.00 | 3.00 |
| RR | 14.74 | 220.78 | 49.13 | 28.91 | 0.26 | 98.80 | 3.01 | ||
| RC | 16.26 | 212.42 | 198.35 | 3.53 | 0.02 | 0.00 | 9.73 | ||
| 0.75 | BSRR | 2.73 | 40.11 | 5.40 | 0.02 | 0.02 | 100.00 | 3.00 | |
| RR | 5.14 | 81.80 | 10.06 | 28.55 | 0.06 | 100.00 | 3.00 | ||
| RC | 5.50 | 71.34 | 64.30 | 0.43 | 0.00 | 0.00 | 9.30 | ||
| 1.00 | BSRR | 1.48 | 21.69 | 2.85 | 0.00 | 0.02 | 100.00 | 3.00 | |
| RR | 2.60 | 42.38 | 3.93 | 28.57 | 0.00 | 100.00 | 3.00 | ||
| RC | 2.89 | 37.46 | 33.57 | 0.06 | 0.00 | 0.00 | 9.07 | ||
|
| |||||||||
| (a2) | 0.50 | BSRR | 17.00 | 255.77 | 50.98 | 0.01 | 0.68 | 100.00 | 3.00 |
| RR | 17.48 | 259.70 | 56.60 | 0.01 | 0.44 | 100.00 | 3.00 | ||
| RC | 38.16 | 470.79 | 535.99 | 0.03 | 0.01 | 0.00 | 10.00 | ||
| 0.75 | BSRR | 6.01 | 96.44 | 9.77 | 0.00 | 0.24 | 100.00 | 3.00 | |
| RR | 6.15 | 97.63 | 11.59 | 0.00 | 0.08 | 100.00 | 3.00 | ||
| RC | 16.43 | 204.44 | 232.50 | 0.00 | 0.02 | 0.00 | 10.00 | ||
| 1.00 | BSRR | 3.06 | 50.14 | 3.70 | 0.00 | 0.10 | 100.00 | 3.00 | |
| RR | 3.12 | 50.62 | 4.32 | 0.00 | 0.04 | 100.00 | 3.00 | ||
| RC | 8.93 | 112.27 | 128.20 | 0.00 | 0.00 | 0.00 | 10.00 | ||
|
| |||||||||
| (a3) | 0.50 | BSRR | 0.03 | 0.38 | 0.15 | 0.36 | 0.00 | 18.20 | 9.10 |
| RR | 0.07 | 0.87 | 0.12 | 28.69 | 0.00 | 23.00 | 9.16 | ||
| RC | 0.03 | 0.36 | 0.07 | 1.64 | 0.00 | 98.00 | 9.98 | ||
| 0.75 | BSRR | 0.02 | 0.19 | 0.10 | 0.80 | 0.00 | 19.40 | 9.12 | |
| RR | 0.03 | 0.40 | 0.09 | 28.82 | 0.00 | 21.40 | 9.14 | ||
| RC | 0.01 | 0.15 | 0.03 | 3.50 | 0.00 | 98.20 | 9.98 | ||
| 1.00 | BSRR | 0.01 | 0.12 | 0.09 | 1.73 | 0.00 | 20.00 | 9.12 | |
| RR | 0.02 | 0.24 | 0.08 | 29.16 | 0.00 | 21.20 | 9.13 | ||
| RC | 0.01 | 0.09 | 0.02 | 4.38 | 0.00 | 98.40 | 9.98 | ||
Table 2.
Summary of the simulation results for examples (b1)–(b3).
| Case | SNR | Method | MSEest | MSEpred | MSEdim | FPR% | FNR% | CRI% | r̂ |
|---|---|---|---|---|---|---|---|---|---|
| (b1) | 0.50 | BSRR | 0.03 | 3.12 | 0.47 | 0.00 | 0.06 | 98.00 | 3.00 |
| RR | 0.35 | 44.87 | 21.49 | 4.72 | 0.08 | 30.40 | 3.69 | ||
| RC | 0.06 | 6.67 | 5.68 | 0.04 | 0.02 | 0.00 | 9.14 | ||
| 0.75 | BSRR | 0.01 | 1.37 | 0.23 | 0.00 | 0.04 | 99.20 | 3.00 | |
| RR | 0.15 | 19.28 | 8.68 | 4.72 | 0.02 | 27.20 | 3.73 | ||
| RC | 0.02 | 2.29 | 1.90 | 0.00 | 0.02 | 0.00 | 8.66 | ||
| 1.00 | BSRR | 0.01 | 0.79 | 0.17 | 0.00 | 0.00 | 99.80 | 3.00 | |
| RR | 0.07 | 9.97 | 3.54 | 4.72 | 0.02 | 51.20 | 3.49 | ||
| RC | 0.01 | 1.22 | 0.94 | 0.00 | 0.00 | 0.00 | 8.20 | ||
|
| |||||||||
| (b2) | 0.50 | BSRR | 0.30 | 44.79 | 4.78 | 0.00 | 0.79 | 99.60 | 3.00 |
| RR | 0.31 | 45.36 | 6.04 | 0.00 | 0.16 | 99.40 | 3.00 | ||
| RC | 1.29 | 128.08 | 168.35 | 0.00 | 0.03 | 0.00 | 10.00 | ||
| 0.75 | BSRR | 0.12 | 18.79 | 0.82 | 0.00 | 0.38 | 99.20 | 3.00 | |
| RR | 0.12 | 18.77 | 1.09 | 0.00 | 0.00 | 99.20 | 3.00 | ||
| RC | 0.56 | 55.61 | 72.10 | 0.00 | 0.07 | 0.00 | 10.00 | ||
| 1.00 | BSRR | 0.07 | 10.44 | 0.27 | 0.00 | 0.26 | 99.60 | 3.00 | |
| RR | 0.07 | 10.36 | 0.36 | 0.00 | 0.00 | 99.40 | 3.00 | ||
| RC | 0.30 | 30.43 | 39.46 | 0.00 | 0.06 | 0.00 | 10.00 | ||
|
| |||||||||
| (b3) | 0.50 | BSRR | 0.00 | 0.02 | 0.01 | 0.02 | 0.00 | 19.40 | 9.13 |
| RR | 0.00 | 0.21 | 0.02 | 4.68 | 0.00 | 27.20 | 9.22 | ||
| RC | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 98.20 | 9.98 | ||
| 0.75 | BSRR | 0.00 | 0.01 | 0.01 | 0.03 | 0.00 | 19.20 | 9.13 | |
| RR | 0.00 | 0.10 | 0.01 | 4.67 | 0.00 | 24.60 | 9.19 | ||
| RC | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 98.40 | 9.98 | ||
| 1.00 | BSRR | 0.00 | 0.01 | 0.01 | 0.02 | 0.00 | 19.20 | 9.13 | |
| RR | 0.00 | 0.06 | 0.01 | 4.66 | 0.00 | 22.40 | 9.16 | ||
| RC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 98.60 | 9.99 | ||
7. Yeast cell cycle data
Transcription factors (TFs), also called sequence-specific DNA binding proteins, regulate the transcription of genes from DNA to mRNA by binding specific DNA sequences. In order to understand the regulatory mechanism, it is important to reveal the network structure between TFs and their target genes. The network structure can be formulated using the multivariate regression model in (1), where the row and column of the response matrix, respectively, correspond to genes and samples (arrays, tissue types, time points), and the design matrix includes the binding information representing the strength of interaction between TFs and the target genes. The regression coefficient matrix then describes actual transcription factor activities of TFs for genes. In practice, many TFs are not actually related to the genes and there exists dependency among the samples due to the design of experiment.
Here, we analyze an Yeast cell cycle data [14] using BSRR. The dataset is available in the spls package in R. The response matrix Y consists of 542 cell-cycle-regulated genes from an α factor arrest method, where mRNA levels are measured at every 7 minutes during 119 minutes, i.e., n = 542 and q = 18. The 542 × 106 predictor matrix X contains the binding information of the target genes for a total of 106 TFs, where Chromatin immunoprecipitation (ChIP) for the 542 genes was performed on each of these 106 TFs. In our analyses, Y and X are centered.
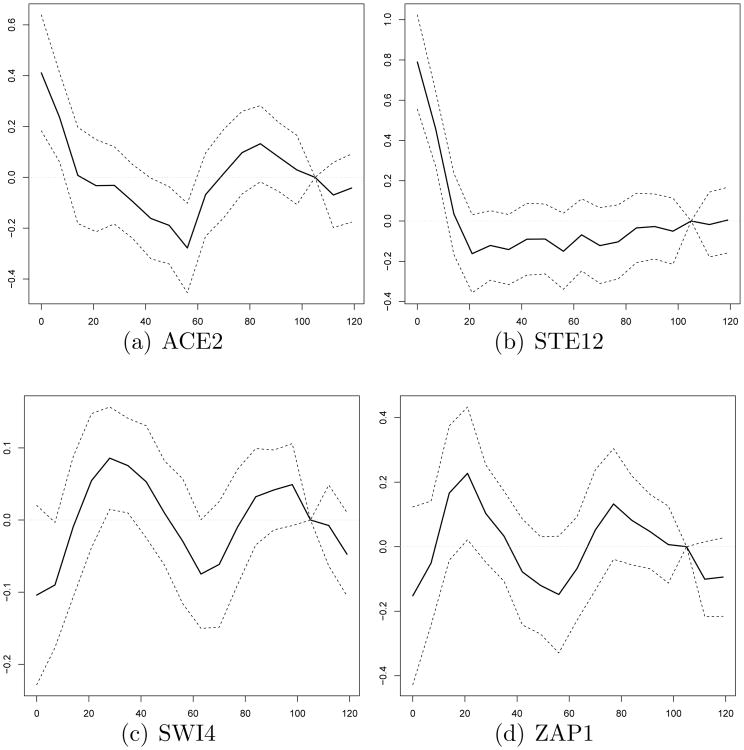
We apply the BSRR method to the dataset. We use the proposed BIC to choose the tuning parameter and obtain λ̂1 = 5, λ̂2 = 1.5 and λ̂3 = 1.5. As a result, 26 TFs are identified at 17 time points (105 min is eliminated) with the estimated rank r̂ = 4. Fig. 2 displays the obtained parameter estimates and 95% credible bands for randomly selected 4 TFs among the 26 TFs; see figures in the supplementary materials for all TFs. The same data set was also analyzed by the adaptive SRRR method of Chen and Huang [12]. In the adaptive SRRR, 32 TFs were identified at 18 time points with the optimal rank r̂ = 4 determined by a cross validation method. Among their selected 32 TFs, 21 TFs were also identified by our BSRR method. To compare variable selection performance between two methods, we define the following two models:
Figure 2.
The parameter estimates and 95% credible bands for randomly selected 4 TFs from the BSRR, where x-axis indicates time (min) and y-axis indicates estimated coefficients.
where X1 contains the information of the 542 genes for the 32 TFs identified by the adaptive SRRR, X2 contains the information of the 542 genes for the 26 TFs identified by BSRR, C1 is the 32 × 18 matrix with rank(C1) = 4, and C2 is the 26 × 18 matrix with rank(C2) = 4. To conduct a fair comparison, we consider the following reduced rank priors in Geweke [20] for the models M1 and M2, respectively:
| (28) |
| (29) |
where A1 is a 32 × 4 matrix, B1 is an 18 × 4 matrix, A2 is an 26 × 4 matrix, B2 is a 18 × 4 matrix and we set τ = 0.0001 to be a non-informative (flat) prior, so that the parameter estimates are determined nearly by the observations (Y1, X1) and (Y2, X2). As the Bayesian model selection criterion, using the priors in (28) and (29), we utilize the deviance information criteria (DIC) defined by
where denotes the posterior mean. If DIC1 > DIC2, then it implies that the model M2 is more strongly supported by the given data than the model M1. Let and be MCMC samples from the posteriors π1(A1, B1 | Y, X1) and π2(A2, B2 | Y, X2), respectively. Note that the MCMC samples can be easily generated from multivariate normal distributions by using the Gibbs sampler. Define , for m = 1, 2. Then the DIC can be estimated by the following Monte Carlo estimator:
Based on 1,000 MCMC samples (after 1,000 burn-in iterations) with 100 replication, we obtain and with Monte Carlo errors 1.29 and 1.14, respectively. Since , this result supports the model M2. Consequently, this implies that our BSRR method has better variable selection performance than the adaptive SRRR for Yeast cell cycle data. Recall that the response at 105 min was eliminated in the BSRR method. Table 3 displays the parameter estimates and 95% credible intervals (CIs) at 105 min from the model M2. Since all CIs include zero, this demonstrates that the response elimination at 105 min in the BSRR is valid. In other words, none of TFs activates at 105 min.
Table 3.
Parameter estimates (Est) with 95% credible intervals (CIs) at 105 min from the model M2.
| TF | Est | CIs | TF | Est | CIs |
|---|---|---|---|---|---|
| ACE2 | −0.03 | (−0.13, 0.10) | RME1 | 0.05 | (−0.08, 0.17 |
| ARG81 | −0.05 | (−0.19, 0.09) | RTG3 | 0.01 | (−0.09, 0.11) |
| FKH2 | 0.06 | (−0.01, 0.13) | SFP1 | −0.05 | (−0.15, 0.05) |
| HIR1 | 0.10 | (−0.06, 0.26) | SOK2 | −0.03 | (−0.07, 0.02) |
| HIR2 | 0.07 | (−0.06, 0.21) | STB1 | 0.01 | (−0.05, 0.06) |
| IME4 | −0.02 | (−0.13, 0.08) | STE12 | −0.04 | (−0.21, 0.12) |
| MBP1 | −0.04 | (−0.13, 0.05) | SWI4 | 0.02 | (−0.03, 0.08) |
| MCM1 | −0.03 | (−0.11, 0.04) | SWI5 | −0.06 | (−0.21, 0.09) |
| MET4 | 0.06 | (−0.02, 0.13) | SWI6 | −0.01 | (−0.08, 0.07) |
| NDD1 | 0.05 | (−0.08, 0.17) | YAP7 | 0.03 | (−0.04, 0.10) |
| NRG1 | 0.02 | (−0.06, 0.11) | YFL044C | 0.04 | (−0.06, 0.15) |
| PHD1 | −0.02 | (−0.09, 0.04) | YJL206C | 0.08 | (−0.05, 0.22) |
| REB1 | 0.03 | (−0.03, 0.09) | ZAP1 | −0.03 | (−0.15, 0.09) |
8. Discussion
We have developed a Bayesian sparse and low rank regression method, which achieves simultaneous rank reduction and predictor/response selection. There are many directions for future research. We have mainly focused on the ℓ0 type sparsity-inducing penalties to construct prior distribution. The method can be extended to use other forms of penalties for inducing diverse lower-dimensional structures. The low-rank structure induces dependency among the response variables, and hence the error correlation structure is not explicitly considered in the current work. Incorporating the variance component into our model might improve the efficiency of the coefficient estimation. In a Bayesian framework, this can be accomplished by assigning an appropriate prior on the variance component; the choice of the prior should be carefully treated due to the lack of unimodality of the posterior [31]. In practice, the response variables could be binary or counts. It is thus pressing to utilize a general likelihood function with the proposed BSRR prior. The proposed ICM algorithm converges relatively fast, and in each iteration the main cost is to inverse a matrix of dimension min(n, p) owning to Woodbury matrix identity. However, this approach would still be inefficient when both p and n are extremely large. One way is to conduct some pre-screening procedure [17, 19] before implementation of the proposed method. It would also be interesting to study on-line learning and the divide-and-conquer strategies of the proposed model. We have established the posterior consistency of the proposed sparse and low-rank estimation method under a high-dimensional asymptotic regime, which characterizes the behavior of the posterior distribution when the number of predictors pn increases with the sample size n. The theoretical analysis of the Bayesian (point) estimator itself could be of interest rather than the entire posterior distribution [1].
Supplementary Material
Acknowledgments
The authors are grateful to the Associate Editor and two referees for their helpful comments on an earlier version of this paper. Chen's research was partially supported by U.S. National Institutes of Health grant U01-HL114494 and U.S. National Science Foundation grant DMS-1613295.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Alquier P. Bayesian Methods for Low-Rank Matrix Estimation: Short Survey and Theoretical Study. Springer; Berlin Heidelberg: 2013. pp. 309–323. [Google Scholar]
- 2.Anderson TW. Estimating Linear Restrictions on Regression Coefficients for Multivariate Normal Distributions. The Annals of Mathematical Statistics. 1951;22:327–351. [Google Scholar]
- 3.Armagan A, Dunson DB, Lee J, Bajwa WU, Strawn N. Posterior consistency in linear models under shrinkage priors. Biometrika. 2013;100:1011–1018. [Google Scholar]
- 4.Babacan SD, Luessi M, Molina R, Katsaggelos AK. Low-rank matrix completion by variational sparse Bayesian learning. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2011:2188–2191. [Google Scholar]
- 5.Bahadori MT, Zheng Z, Liu Y, Lv J. Scalable Interpretable Multi-Response Regression via SEED. arXiv:1608.03686. 2016 [Google Scholar]
- 6.Besag J. On the Statistical Analysis of Dirty Pictures. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1986;48:259–302. [Google Scholar]
- 7.Breheny P, Huang J. Penalized methods for bi-level variable selection. Statistics and Its Interface. 2009;2:369–380. doi: 10.4310/sii.2009.v2.n3.a10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bunea F, She Y, Wegkamp MH. Optimal selection of reduced rank estimators of high-dimensional matrices. The Annals of Statistics. 2011;39:1282–1309. [Google Scholar]
- 9.Bunea F, She Y, Wegkamp MH. Joint variable and rank selection for parsimonious estimation of high dimensional matrices. The Annals of Statistics. 2012;40:2359–2388. [Google Scholar]
- 10.Chen K, Chan KS, Stenseth NC. Reduced rank stochastic regression with a sparse singular value decomposition. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2012;74:203–221. [Google Scholar]
- 11.Chen K, Dong H, Chan KS. Reduced rank regression via adaptive nuclear norm penalization. Biometrika. 2013;100:901–920. doi: 10.1093/biomet/ast036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen L, Huang JZ. Sparse Reduced-Rank Regression for Simultaneous Dimension Reduction and Variable Selection. Journal of the American Statistical Association. 2012;107:1533–1545. [Google Scholar]
- 13.Choi T, Ramamoorthi RV. Remarks on consistency of posterior distributions. Institute of Mathematical Statistics Collections. 2008;3:170–186. [Google Scholar]
- 14.Chun H, Keles S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2010;72:3–25. doi: 10.1111/j.1467-9868.2009.00723.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Diaconis P, Freedman D. On the Consistency of Bayes Estimates. The Annals of Statistics. 1986;14:1–26. [Google Scholar]
- 16.Fan J, Li R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- 17.Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fan J, Lv J. A selective overview of variable selection in high dimensional feature space. Statistica Sinica. 2010;20:101–148. [PMC free article] [PubMed] [Google Scholar]
- 19.Fan J, Song R. Sure independence screening in generalized linear models with NP–dimensionality. The Annals of Statistics. 2010;38:3567–3604. [Google Scholar]
- 20.Geweke J. Bayesian reduced rank regression in econometrics. Journal of Econometrics. 1996;75:121–146. [Google Scholar]
- 21.Ghosh JK, Delampady M, Samanta T. An Introduction to Bayesian Analysis: Theory and Methods. Springer-Verlag; New York: 2006. [Google Scholar]
- 22.Huang J, Breheny P, Ma S. A Selective Review of Group Selection in High Dimensional Models. Statistical Science. 2012;27(4):481–499. doi: 10.1214/12-STS392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang J, Horowitz JL, Ma S. Asymptotic properties of bridge estimators in sparse high-dimensional regression models. The Annals of Statistics. 2008;36:587–613. [Google Scholar]
- 24.Izenman AJ. Reduced-rank regression for the multivariate linear model. Journal of Multivariate Analysis. 1975;5:248–264. [Google Scholar]
- 25.Kyung M, Gilly J, Ghosh M, Casella G. Penalized regression, standard errors, and Bayesian lassos. Bayesian Analysis. 2010;5:369–412. [Google Scholar]
- 26.Lim YJ, Teh YW. Variational Bayesian approach to movie rating prediction. Proceedings of KDD Cup and Workshop. 2007 [Google Scholar]
- 27.Ma Z, Ma Z, Sun T. Adaptive Estimation in Two-way Sparse Reduced-rank Regression. arXiv:1403.1922. 2014 [Google Scholar]
- 28.Mukherjee A, Chen K, Wang N, Zhu J. On the degrees of freedom of reduced-rank estimators in multivariate regression. Biometrika. 2015;102:457–477. doi: 10.1093/biomet/asu067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mukherjee A, Zhu J. Reduced rank ridge regression and its kernel extensions. Statistical Analysis and Data Mining. 2011;4:612–622. doi: 10.1002/sam.10138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Negahban S, Wainwright MJ. Estimation of (near) low-rank matrices with noise and high-dimensional scaling. The Annals of Statistics. 2011;39:1069–1097. [Google Scholar]
- 31.Park T, Casella G. The Bayesian Lasso. Journal of the American Statistical Association. 2008;103:681–686. [Google Scholar]
- 32.Reinsel GC, Velu PP. Multivariate reduced-rank regression: Theory and Applications. Springer-Verlag; New York: 1998. [Google Scholar]
- 33.Rohde A, Tsybakov AB. Estimation of high-dimensional low-rank matrices. The Annals of Statistics. 2011;39:887–930. [Google Scholar]
- 34.Salakhutdinov R, Mnih A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo. In: Cohen WW, Mccallum A, Roweis ST, editors. Proceedings of the 25th International Conference on Machine Learning (ICML-08) 2008. pp. 880–887. [Google Scholar]
- 35.Schwarz G. Estimating the Dimension of a Model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- 36.Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1996;58:267–288. [Google Scholar]
- 37.Yuan M, Ekici A, Lu Z, Monteiro R. Dimension reduction and coefficient estimation in multivariate linear regression. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2007;69:329–346. [Google Scholar]
- 38.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006;68:49–67. [Google Scholar]
- 39.Zhang CH. Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics. 2010;38:894–942. [Google Scholar]
- 40.Zhou M, Wang C, Chen M, Paisley J, Dunson D, Carin L. Nonpara-metric Bayesian matrix completion. 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop. 2010:213–216. [Google Scholar]
- 41.Zhu H, Khondker Z, Lu Z, Ibrahim JG. Bayesian Generalized Low Rank Regression Models for Neuroimaging Phenotypes and Genetic Markers. Journal of the American Statistical Association. 2014;109:997–990. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.