Monitoring fetal maturation—objectives, techniques and indices of autonomic function

Abstract

Objective

Monitoring the fetal behavior does not only have implications for acute care but also for identifying developmental disturbances that burden the entire later life. The concept, of ‘fetal programming’, also known as ‘developmental origins of adult disease hypothesis’, e.g. applies for cardiovascular, metabolic, hyperkinetic, cognitive disorders. Since the autonomic nervous system is involved in all of those systems, cardiac autonomic control may provide relevant functional diagnostic and prognostic information.

Approach

The fetal heart rate patterns (HRP) are one of the few functional signals in the prenatal period that relate to autonomic control and, therefore, is key to fetal autonomic assessment. The development of sensitive markers of fetal maturation and its disturbances requires the consideration of physiological fundamentals, recording technology and HRP parameters of autonomic control.

Main Results

Based on the ESGCO2016 special session on monitoring the fetal maturation we herein report the most recent results on: (i) functional fetal autonomic brain age score (fABAS), Recurrence Quantitative Analysis and Binary Symbolic Dynamics of complex HRP resolve specific maturation periods, (ii) magnetocardiography (MCG) based fABAS was validated for cardiotocography (CTG), (iii) 30 min recordings are sufficient for obtaining episodes of high variability, important for intrauterine growth restriction (IUGR) detection in handheld Doppler, (iv) novel parameters from PRSA to identify Intra IUGR fetuses, (v) evaluation of fetal electrocardiographic (ECG) recordings, (vi) correlation between maternal and fetal HRV is disturbed in pre-eclampsia.

Significance

The reported novel developments significantly extend the possibilities for the established CTG methodology. Novel HRP indices improve the accuracy of assessment due to their more appropriate consideration of complex autonomic processes across the recording technologies (CTG, handheld Doppler, MCG, ECG). The ultimate objective is their dissemination into routine practice and studies of fetal developmental disturbances with implications for programming of adult diseases.

Introduction

Fetal developmental disturbances cannot be compensated for in later life and have implications that may burden an individual over its total lifespan. Therefore, the early identification of such disturbances is of outstanding importance. Fetal heart rate patterns, as one of the few signals obtainable, are predestinated for early functional prenatal diagnosis. It requires the sophisticated consideration of autonomic physiological and pathophysiological behavior, of appropriate recording technology, of the system theoretic aspects underlying heart rate variability (HRV) patterns, and of clinical studies. Herein, we report recent advances of original work by the contributors at the ESCGO 2016 special session on ‘Fetal maturation’. These results were furthermore discussed with respect to establishing an overarching research network.

After an introduction on the physiological fundamentals and clinical importance, topical HRV indices, namely those based on Recurrence, Binary Symbolic Dynamics, phase rectified signal analysis (PRSA), and a functional fetal autonomic brain age score (fABAS) are introduced and evaluated with regards to the assessment of the maturation age and the identification of maturation disturbances.

For routine applications the advantages and limitations of the different recording technologies, namely cardiotocography (CTG), handheld Doppler, magnetocardiography (MCG), and electrocardiography (ECG) should be taken into a complementary consideration. With the ultimate objective of describing synergies for widespread fetal diagnosis in routine applications, several topical approaches across HRV indices, recording techniques, as well as physiological and medical aspects are presented as follows:

• Physiological fundamentals and clinical importance

• Joint data set for the analysis of MCG based HRV indices (Recurrence Quantitative Analysis, Binary Symbolic Dynamics, and functional brain age score (fABAS))

• Recurrence quantitative analysis (MCG)

• Binary symbolic dynamics of fetal heart rate in the course of gestation (MCG)

• Validation of MCG based fABAS in CTG recording

• The feasibility of detecting intrauterine growth restriction (IUGR) from Doppler-based HRV markers in low-resource settings

• Quantitative diagnosis of IUGR fetuses: PRSA indices method and interpretation

• Fetal ECG recording technique - state-of-the-art and own case-study

• Altered correlation between maternal and fetal HRV in pre-eclampsia (ECG)

• Resume, outlook

Physiological fundamentals and clinical importance

Developing the autonomic ability to adapt to varying amounts of supply and demand in the organism is one of the key necessities during fetal maturation. This maturational process of autonomic regulation in utero reaches a pace that may never be observed again later in life. We only start to anticipate that this maturation deems to be highly sensitive to acute and chronic influences with long-lasting consequences. One may assume that any disturbance of normal intrauterine development inevitably leads to changes in autonomic capacities. The concept of ‘fetal programming’ also known as ‘developmental origins of adult disease hypothesis’ applies for several diseases such as cardiovascular, metabolic, hyperkinetic, cognitive, and behavioral disorders (Barker 1998, Van den Bergh et al 2005). Therefore, monitoring the fetal behavior does not only have implications for acute perinatal care but also with respect to identifying developmental disturbances that burden the entire later life and that may not completely be compensated by later postnatal therapies.

Autonomic aptitude is mirrored in cardiovascular regulation. Since the autonomic nervous system is involved in the control in almost all organ systems, the cardiac autonomic control, that is assessable from heart rate pattern, may provide relevant functional diagnostic and prognostic information.

The relation between the exponential increase of cardiac output and asymptotic growth of ventricular size demonstrates that the capability to adapt the single stroke volume is a function of advancing gestational age (DeVore 2005). Considering these limitations, one may anticipate that the fetal heart rate (fHR) is not only the major continuous regulative of the developing autonomic nervous system (ANS) but the access point to understand fetal autonomic maturation. The related fetal heart rate patterns (HRP) are one of the few accessible functional signals in the prenatal period and, therefore, predestinated for a respective evaluation. The development of sensitive markers of fetal maturation and its disturbances requires a well thought out consideration of physiological fundamentals, recording technology and HRP parameters of autonomic control.

Continuous antenatal heart rate tracing is based on two physical principles: (i) Doppler ultrasound based cardiotocography (CTG) delivering a reasonable temporal resolution for daily clinical practice. Although individual heart beats cannot be identified, heart rate acceleration and deceleration patterns can be described. Global visual assessment of the CTG trace allows to spot severe fetal distress due to hypoxaemia, infection or anaemia but is subject to high intra- and interobserver variability and a high rate of false-positive results. Algorithms for computerized analysis i.e. according to the Dawes/Redman algorithm aid in reducing these shortcomings. The algorithm is adapted to the capacities of temporal resolution a Doppler based signal is able to deliver. The short-term variation (STV) was established as a standard parameter of clinical surveillance in high risk pregnancies (Pardey et al 2002, Serra et al 2008, 2009), (ii) In comparison to the CTG, electrophysiological methods such as fetal electrocardiography (fECG) or fetal magnetocardiography (fMCG) allow the precise QRS complex detection and beat-to-beat heart rate variability (fHRV) analysis necessary for resolving fast vagal activity and applying established linear and complex HRV analysis.

The link between CTG and fMCG/fECG based results is an important issue for further methodological developments and clinical application. STV is mainly correlated with fMCG based SDNN (standard deviation of normal-to-normal heartbeat intervals) and fLF HRV (power of normal-to-normal beat intervals in the fetal low frequency band of 0.08–0.2 Hz, interpreted as overall, mainly sympathetic) power, but to a minor part only with indices of vagal activity (RMSSD: root means square of successive interbeat interval differences, fHF: power of normal-to-normal beat intervals in the fetal high frequency band of 0.4–1.7 Hz) (Seliger et al 2015). STV poorly describes fetal maturation over gestation (coefficient of determination R² = 0.21) compared to R² = 0.65 by fABAS of the identical data set (Hoyer et al 2014).

Besides the physiological changes with increasing GA, the fetal neuro-behavioral state (state of fetal activity) must be taken into account when interpreting fHRP. Rest/activity cycles have been described from about 23 weeks GA onwards and the progressive synchronization of neuro-behavioral variables like fHRP, body movements and eye-movements are markers of developmental integrity of the fetus (Nijhuis et al 1982, Pillai and James 1990). FMCG results are mainly consistent with those CTG results and provide additional information. Indices of both, sympathetic activation and vagal modulation increase with increasing fetal age. The ‘active awake’ fetal neuro-behavioral state marks a different quality of sympathetic activation that is characterized by a significantly higher mean fHR, a shift in sympatho-vagal balance and reduced complexity of the time series of heartbeats (sympathetic triad) (Schneider et al 2008). Characteristic intervals of maturation appear: The transitional period between the second and the third trimesters of pregnancy is characterized by the appearance of physiological decelerations, a steeply enhancing vagal regulation followed by an increase in overall variability and complexity (Van Leeuwen et al 1999, 2003, Hoyer et al 2009). Beyond 30 weeks GA, development is characterized by the diversification of fHRV parameters according to the stabilization of the fetal neuro-behavioural states and a strong relation between heart rate accelerations and intentional body movements (Schmidt et al 2014).

Multiple novel HRV indices were proposed with respect to particular questions, but cross-validation remains an issue. The consideration of universal principles of evolution, adaptation and self-organization, such as used in a functional fetal autonomic brain age score (fABAS) may not only improve the accuracy of diagnosis of developmental problems but also provide implications for novel therapeutic strategies (Hoyer et al 2013b).

Joint data set for the analysis of MCG based HRV indices

From the Jena Fetal Monitoring Data Base only normal healthy fetuses were analysed. For each analysis (recurrence plot analysis: n = 316, binary symbolic dynamics: n = 398; validation of MCG based age score fABAS in CTG recording: n = 390) the entire data set of normal cases of the data base at the time of analysis was used. According to the permanently growing data base, different numbers of recordings resulted, whereby the larger sets contained smaller ones. All data sets are medically and technically comprehensively described (Study Group ‘Prenatal Monitoring of Fetal Maturation’, Department of Obstetrics, Division of Prenatal Diagnostics and Fetal Physiology; Biomagnetic Center, Hans Berger Department of Neurology, both Jena University Hospital) according to the study protocol approved by the Local Ethics Committee (standard procedure designed in a prospective study in 2006, DFG, HO 1634 12–2, Schn 775/2–3). All subjects gave their written consent to perform the study. The here investigated subsets used in the following three sections include recordings of normal singleton fetuses in a non-stress situation, aged between 19 and 40 weeks of gestation (WGA), healthy according to standard obstetric observation methods. In all these cases standard maternity documents were revised at the time of investigation to confirm gestational age according to last menstrual period verified by first trimester fetal crown-rump-length and the normal course of the ongoing pregnancy. Exclusion criteria: (maternal) known heart diseases, diabetes mellitus of the mother, maternal medication affecting cardiac function/rhythm, abuse of nicotine, alcohol or drugs, previous administration of synthetic glucocorticoids, uterine contractions during the recording. (fetal) known chromosomal abnormalities, sonographically identified malformations, fetal cardiac arrhythmias.

All magnetocardiographic (MCG) recordings were taken over 30 min sampled at 1024 Hz in a magnetically shielded room at the Biomagnetic Center, Department of Neurology, Jena University Hospital using the vector-magnetograph ARGOS 200 (ATB, Chieti, Italy) during daytime. The pregnant women were positioned supine or with a slight twist to either side to prevent compression of the inferior vena cava by the pregnant uterus. The Dewar containing the magnetometers was positioned with its curvature above the fetal heart after sonographic localization as close to the maternal abdominal wall as possible without direct contact.

The fetal heart beats were detected and normal-to normal (NN) beat intervals series calculated. The NN series were screened for artifacts, arrhythmias and non-stationarities. The rate of interpolated artifacts was below 2%. Additionally, to the analysis of the entire 30 min recordings, 10 min sections of active (according to 2F) and quiet (according to 1F) sleep and active awakeness (according to 4F) were selected after a consensus decision by three independent obstetricians blinded to the heart rate analysis according standard criteria previously described (Hoyer et al 2013b). This procedure was done in a standardized way independently of the recording subsets and the subsequent HRV analyses.

Recurrence plot analysis of fetal heart rate variability—dependence on gestational age

Results on multiscale entropy and multiscale multifractal analysis indicating dependencies of fetal heart rate variability (HRV) on gestational age (GA) were published earlier (Hoyer et al 2013a, Gieraltowski et al 2015). Here, we present new results on fetal heart rate variability development with GA using recurrence plot (RP) analysis.

Recurrence is a basic property of the dynamics of physical systems observed in phase space and occurs when the system comes close to a state from which it began evolution time. Recurrence is not the same as periodicity as recurrent phenomena do not have to occur regularly in the time and, in principle, recurrence may occur after an arbitrarily long time. The tool to study recurrence properties is the Recurrence Plot (Marwan et al 2007) that was introduced by Ruelle in 1987 and very shortly later used for biological research by Webber (1991). To obtain the Recurrence Plot, the m-dimensional phase space trajectory of the signal studied must be reconstructed first using Takens delay coordinates with the proper Takens delay and embedding dimension. Then, for each ith element of the time series a search is made for all the other elements of the series that approach that point by not more than a certain distance in phase space (recurrence). A distance matrix is constructed the i,j elements of which are 1 (black) when recurrence occurred for the given pair of indices and 0 otherwise. As a result, a plot containing several kinds of structures (Marwan et al 2006) is obtained including lines parallel to the diagonal, vertical lines and often more complicated patterns. The properties of the RP can be studied using recurrence quantitative analysis (RQA) (Marwan et al 2002) as done below. Many different RQA parameters have been defined but here only the following parameters will be discussed: recurrence rate (RR) (the number of 1’s in the RP), Determinism DET (the number of black points of the RP that form lines parallel to the main diagonal, a measure of the periodicities in the signal, related to unstable periodic orbits UPO (Bradley et al 2002)) and Entropy (Shannon entropy of the lines parallel to the diagonal, a measure of how disordered are the line segments).

The fetal HRV data analyzed by recurrence plots consisted of 316 MCG recordings 30 min long. 10 min sections were extracted from the 30 min recordings that had a well-defined sleep state: quiet (n = 92) and active (n = 292).

Methods

Recurrence plots (RP) were computed for each 30 min recording without windowing. Standard recurrence quantitative analysis (RQA) was calculated using the Matlab package (Marwan et al 2002): recurrence rate RR, determinism DET, entropy of diagonal lines Entropy, the length of vertical lines V and trapping time TT were calculated. First, the recurrence diagram tolerance parameter was adjusted so that RR = 5% was obtained for each individual recording as recommended in the literature (Javorka et al 2009) for adult and children heart rate variability. We checked that setting the tolerance parameter so that RR = 2.5% or RR = 7.5% yielded results of worse quality (i.e. more extreme outlier artefacts or a very weak dependence on GA). For each recording, the Takens delay was found using mutual information and the embedding dimension—by the False Nearest Neighbors method.

Results

Of all the RQA parameters only determinism (DET) and Entropy yielded interesting results. The first step was to check whether the active and quiet sleep fetal HRV may be distinguished by RQA. It was found that both for DET versus GA and Entropy versus GA the results calculated using the 10 min recordings, for the two sleep states, practically coincide. This opened the possibility to analyze the 30 min recordings for which the state may have been active, quiet or mixed.

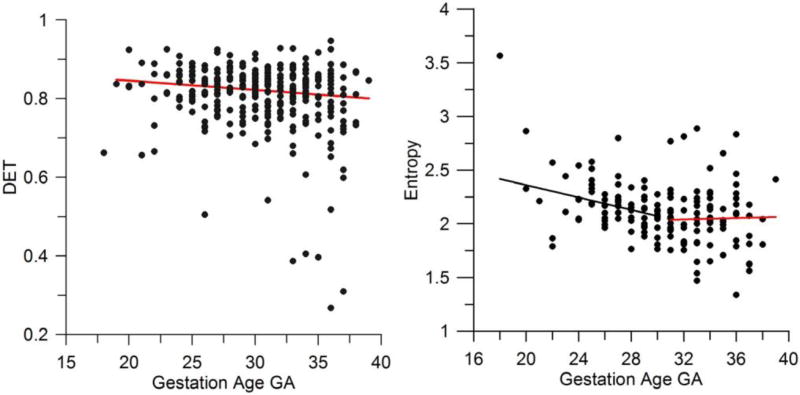
It was then found that both DET and Entropy for the 30 min recordings decrease with GA. A rather large spread between the results for the RQA measures for a given gestation week was obtained. The spread seems to be a feature of the analysis of fetal heart rate variability (see also the next the section on symbolic dynamics below) and may be found in other papers presenting results in this area. Note that the overall decrease of DET with GA is rather small. The red line in the left panel of figure 1 is only for the convenience of the eye to better see the trend. The spread is too large to consider this regression line a prediction. Note that for a number of cases, the values of DET obtained are definitely lower than for the rest of the cases studied. Careful inspection of the fHRV recordings revealed that for these particular cases larger MCG noise was present than for the rest. Overall, however, the DET appears to decrease with GA throughout the whole range 18–36 weeks. However, the decrease of Entropy is stronger and at the week 30–32, Entropy definitely levels off (figure 1, right panel). The spread of the results is again large so that the black and red lines given in the right panel of figure 1 are for the convenience of the eye only, to better visualize the trend or its lack.

Figure 1.

(left panel) Determinism versus gestational age; (right panel) entropy versus gestational age.

Discussion and conclusions

The RQA parameter Determinism is a measure of the occurrence of periodicities in the time series analyzed. It is also related to unstable periodic orbits (UPO) in the data (Bradley et al 2002)—a feature of the deterministic dynamics of the system. Entropy of the diagonal lines in the RP is a measure of the disorder of the periodicities that determine the parameter DET. The observed behavior of the RQA parameters indicates that, as the autonomic nervous system (ANS) regulation of heart rate variability grows with GA, the initial simple (deterministic) properties of the heart rate variability due to the self-oscillatory action of the conduction system of the fetal heart become dominated by a more complex (disordered) variability. This variability is due to the effect of the ANS on the fetal heart rate. At the same time, entropy of the diagonal lines decreases indicating a less complex structure of the periodicities in HRV. Inspection of the recordings of fetal HRV for this range of GA reveals features of long-term correlations and these are responsible for the decrease of Entropy. Such an increase of long-term correlations was observed at later GA in Hoyer et al (2012) and it is possible that it is related to fetal movement (see Schmidt et al (2014)). The process appears to be complete at about GA 30 weeks after which the entropy stays approximately constant. The results confirm earlier findings indicating a transition in the properties of fetal heart rate variability slightly after the gestation age of 30 weeks: the transition at approximately 31 weeks GA may be seen in the number of fHR accelerations lasting between 70–100 ms per 30 min (figure 5 in Hoyer et al 2009), in the number of fHR accelerations related to fetal movement (figure 5 in Schmidt et al (2014)), in the complexity measure trajectory divergence rate ρ (figure 2 in Van Leeuwen et al (1999)) and in the properties of the fHR power spectrum, especially in the total power, the LF and HF bands but not in the LF/HF ratio (figure 2 in Van Leeuwen et al (2003)).

Binary symbolic dynamics of fetal heart rate in the course of gestation

Many standard measures of fetal HRV show a linear relationship with gestational age (GA) of the fetus (Van Leeuwen et al 2013), i.e. the measures increase with progressing GA. The analysis symbolic dynamics provides a powerful approach of the analysis of heart rate dynamics that complements standard measures of HRV (Cysarz et al 2013). It consists of a coarse grained description of the original time series. Each instance of the original time series is replaced by a symbol according to a transformation rule. The symbolic time series, i.e. the coarse grained description, focusses on dynamical aspects of the system under investigation (Kurths et al 1995, Porta et al 2001). In adults, this approach may be used to assess the functioning of cardiac autonomic regulation (Guzzetti et al 2005). Different transformations have been developed to assess dynamical features of the time series under investigation (Cysarz et al 2013). Binary symbolic dynamics uses only two symbols to reflect dynamical features (Cysarz et al 2000, Wessel et al 2007, Cysarz et al 2012). Nevertheless, relevant dynamical features are retained and it is possible to quantify e.g. fetal heart rate complexity (Van Leeuwen et al 2007). The dynamical features of fetal heart rate vary with GA of the fetus and, hence, the analysis of binary symbolic dynamics reflected changes of fetal cardiac autonomic functioning with progressing age (19th–39th week of gestation) as represented by a strong linear relationship of the measures of symbolic dynamics with GA (Cysarz et al 2015).

The latter results have been obtained using 5 min fetal MCG recordings without knowledge of the fetal behavioral state. Here, we analyzed selected 30 min fetal MCG recordings of the Jena Fetal Monitoring Data Base (N = 398, 237 females, 161 males, 19th–39th week of gestation). Furthermore, 10 min segments of the recordings have been classified according to heart rate patterns correlated to quiet sleep (1F, N = 157, 90 females) and heart rate patterns correlated to active sleep (2F, N = 342, 201 females). The normal-to-normal beat series NN_i served as the basis for further calculations. The 30 min recordings contained on average 4145 ± 507 NN intervals and the 10 min segments 1376 ± 111 NN intervals. The binary symbolic series S_T,i of each recording was formed using the sequence of successive differences ΔNN_i+1 = NN_i+1 − NN_i:

$$S_{\tau ,i}=\{\begin{array}{c}0:|\mathrm{\Delta }{\text{NN}}_{i+1}|<\tau \hfill \\ 1:|\mathrm{\Delta }{\text{NN}}_{i+1}|\ge \tau \hfill \end{array}$$

The threshold τ was set to 5 ms taking into account the lower variability in fetal NN interval series (Cysarz et al 2015).

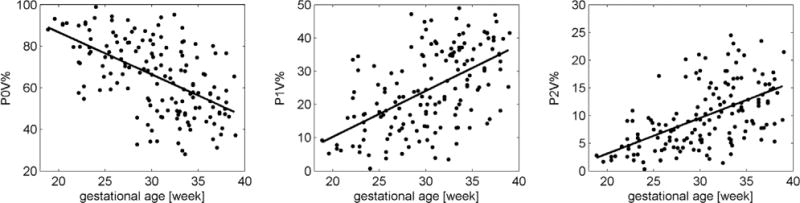
Subsequently, all binary patterns of length 3 (i.e. 2³ = 8 binary patterns) were categorized with respect to the amount of variations in the succession of the symbols in the pattern: 0 V patterns: no variation of the symbols (binary patterns 000 and 111), 1 V patterns: one variation in the succession of the symbols (binary patterns 100, 110, 001, 011) and, 2 V patterns: two variations in the succession of the symbols (binary patterns 010 and 101). P0V%, P1V% and P2V% quantify the percentage of occurrence of each category. The linear relationships between these measures and week of gestation have been quantified using the coefficient of determination (R²).

Generally, the average NN interval increased with progressing age (p < 0.001). All linear relationships presented in table 1 were statistically significant (p < 0.001). Figure 2 shows the changes of P0V%, P1V% and P2V% with progressing GA during quiet sleep (1F). Regardless of the analyzed data set P0V% had always a negative slope indicating a decrease of occurrence of 0 V binary patterns with increasing GA. On the other hand, P1V% and P2V% had positive slopes indicating an increase of occurrence of 1 V and 2 V binary patterns with increasing GA. The constant of the linear relationship of P0V% is approx. 100, the constant of P1V% and P2V% is close to 0. Hence, extrapolating this relationship to fetal heart rate at an early GA suggests that its dynamics is probably dominated by 0 V symbolic patterns, i.e. the heart rate dynamics is very simple because mainly variations below the threshold τ occur. With increasing age the dynamics gets more complex as 1 V and 2 V symbolic patterns occur more often. At the end of pregnancy, 0 V and 1 V symbolic patterns appear with the same probability on average (approx. 40% each) whereas 2 V patterns occur less often (approx. 20%).

Table 1.

Parameters of linear relationship with respect to gestational age.

Data set	Parameter	R2	Slope (95% CI)	Constant (95% CI)
1F (quiet sleep)	P0V%	0.32	−2.03 (−2.50, −1.56)	127.28 (112.73, 141.84)
	P1V%	0.30	1.38 (1.05, 1.72)	−17.45 (−27.73, −7.16)
	P2V%	0.28	0.65 (0.48, 0.81)	−9.93 (−14.85, −4.82)
2F (active sleep)	P0V%	0.26	−1.78 (−2.09, 1.46)	110.95 (101.16, 120.74)
	P1V%	0.23	1.10 (0.88, 1.31)	−3.72 (−10.31, 2.85)
	P2V%	0.26	0.68 (0.56, 0.80)	−7.22 (−11.05, −3.40)
30 min	P0V%	0.32	−1.87 (−2.14, −1.60)	115.74 (107.51, 123.97)
	P1V%	0.29	1.18 (0.99, 1.36)	−7.36 (−13.02, −1.69)
	P2V%	0.31	0.69 (0.59, 0.79)	−8.38 (−11.52, −5.24)

Figure 2.

Occurrence of binary patterns without variations (P0V%), one variation (P1V%) and two variations (P2V%) versus gestational age during quiet sleep (1F).

P0V% during quiet sleep (1F) showed the steepest slope (−2) indicating an average 2% decrease of 0 V symbolic patterns per gestational week. 1 V symbolic patterns increase faster compared to 0 V patterns because the positive slope is steeper. The coefficient of determination was strongest for quiet sleep (1F) and the 30 min data sets whereas during active sleep (2F) slightly poorer relationships were observed.

The present coefficients of determination of P0V%, P1V% and P2V% were lower compared to findings of a previous study (previous study: R² > 0.40) (Cysarz et al 2015). The higher coefficients of determination in the previous study were probably caused by two factors: (i) the data sets were shorter (5 min versus 10 min or 30 min), i.e. likely less variability within each data set, and (ii) the previous study dealt also with the individual fetal maturation and, hence, 215 data sets from only 11 fetuses were considered whereas in the present analysis each data set reflects a different fetus. Furthermore, the coefficient of determination of P0V%, P1V% and P2V% increased by taking into account the average NN interval of each data set. The present results may also be improved by taking into account the average NN interval of each data set, i.e. they partially depend on the increase of NN intervals with progressing GA. In comparison to parameters from the time domain (skewness of the NN distribution, pNN5) P0V, P1V and P2V seem to perform almost equally whereas they perform worse compared to a complexity measure (generalized mutual information at coarse graining level 3) (Hoyer et al 2013a, 2013b, 2014).

The construction of binary symbolic dynamics omits a lot of information from the original time series. Nevertheless, relevant dynamical information is retained and the analysis of binary symbolic dynamics is able to reflect progressing maturation of the cardiac autonomic functioning with progressing age of the fetus. It should be elucidated whether the parameters from this analysis contribute to the calculation of the fetal autonomic brain age score (Hoyer et al 2013b, 2014).

Validation of MCG based age score fABAS in CTG recording

As introduced above, FHR traces based on CTG lack on the precise identification of individual heart beat intervals due to technological reasons. Therefore, we addressed the question to which extent results obtained from beat precise fMCG can be transferred to CTG recordings. From the Jena Fetal Monitoring Data Base 390 MCG recordings over 30 min sampled at 1024 Hz were selected with respect to a range of 24–40 WGA matched to the CTG dataset. We investigated the heart beat interval series and the respective time series resampled at 4 Hz. Only normal beat intervals (NN) were considered. The frequency of corrected artificial beats was below 2% (details see e.g. Hoyer et al (2013a, 2013b)).

The CTG dataset consists of 50 normal cases of a longitudinal prospective study, collected at the obstetrics outpatient clinic of a tertiary care hospital (Hospital de S João, Porto University) and comprises 358 recordings (mean ± SD, 7.6 ± 1.5; min–max, 5–11) obtained through external monitoring with Hewlett-Packard M1350A or M1351 fetal monitors at 4 Hz sampling, with GA in the range of 24–40 weeks. Tracings with signal loss above 33%, or signal quality (percentage of points identified by the fetal monitor as having good or very good signal quality) below 80% were excluded (Amorim-Costa et al 2016). The fetal behavioral states were classified similar to that of fMCG recordings mentioned above in the Jena study group ‘Prenatal Monitoring of Fetal Maturation’.

fABAS was previously introduced as a linear equation with factors that reflect universal developmental characteristics, namely increasing fluctuation amplitude, increasing complexity and pattern formation, assessed from HRP (table 2, Hoyer et al (2013b)). The coefficients of those factors were estimated by linear regression with respect to the chronological age of the fetuses.

Table 2.

HRV indices that constitute factors of fABAS, from Hoyer et al (2013b).

HRV index	Calculation	Interpretation
Fluctuation amplitude
Amplitude	20–95 inter-quantile distance (difference between the 20th and 95th percentile of detrended NN interval series)	Fluctuation range of heart beat intervals above an approximated baseline
Complexity
gMSE(3)	Generalized mutual information at coarse graining level 3 of NN series	Complexity of sympatho-vagal modulation
Pattern formation
Skewness	Skewness of NN interval series	Asymmetry, decline of deceleration and formation of acceleration patterns
pNN5	Percentage of differences between adjacent NN intervals > 5 ms	Formation of vagal modulations
VLF/LF	Ratio between VLF (0.02–0.08 Hz) and LF (0.08–0.2 Hz) power	Baseline fluctuation in relation to sympatho-vagal modulations

The cross-validation of fABAS was done with respect to: (i) the transfer of fABAS obtained from fMCG heart beat interval series (MCG_NN) to the corresponding time series resulting from resampling at 4 Hz (MCG_res) in order to create a data time base similar to that of CTG; (i) the transfer of fABAS from the resampled time series (MCG_res) to the CTG data; and (ii) the transfer of fABAS from CTG to MCG_res. For that purpose, fABAS was fitted to respective learning sets and the resulting model was applied to the respective validation (test) set. The fits were performed by linear regression to estimate the coefficients of the factors of fABAS with respect to predicting the chronological age of the fetuses. The goodness of fit was provided as standard error (SE, in weeks) and coefficient of determination (R²).

From the 390 MCG recordings, a total of 142, 346 and 24 segments were classified as 1F, 2F and 4F, respectively, as previously described in the paper section ‘Joint data set for the analysis of MCG based HRV indices’. A similar procedure was followed regarding the 358 CTG recordings, resulting in the classification of 153, 294 and 23 segments as 1F, 2F and 4F, respectively. The 4F state segments were not analyzed due to their small number. The cross-validation results are summarized in table 3.

Table 3.

Standard error (SE) and coefficient of determination (R²) of fitted models (learn sets) and the respective validation sets. (Beat interval series: MCG_NN; resampled time series: MCG_res; and CTG).

		Learn set			Validation (test) set
		SE (weeks)	R2		SE (weeks)	R2
30 min	MCGNN	2.68	0.498	MCGres	2.724	0.481
	MCGres	2.647	0.510	CTG	3.719	0.345
	CTG	3.587	0.391	MCGres	2.724	0.481
1F	MCGNN	2.739	0.498	MCGres	2.742	0.497
	MCGres	2.722	0.504	CTG	3.891	0.294
	CTG	3.671	0.368	MCGres	2.721	0.505
2F	MCGNN	2.929	0.395	MCGres	2.966	0.380
	MCGres	2.928	0.395	CTG	3.902	0.257
	CTG	3.766	0.308	MCGres	3.026	0.354

The MCG cross-validation (learn set: MCG_NN → test set: MCG_res) shows almost similar goodness (regarding SE and R²) in the learning and the test data sets in each state. This result is consistent with previous findings, showing that equidistant resampling did not disturb the assessment of autonomic modulations compared to analyzing beat interval series (Hoyer et al 2011, 2012). This result is also plausible with respect to the origin of the autonomic modulators.

The validation of MCG based models on CTG data (learn set: MCG_res → test set: CTG) shows a clearly reduced goodness, namely increased SE and decreased R² in the CTG data in all states. The loss of goodness in the CTG may have been caused by the lack of precise heart beat detection and/or the higher amount of random disturbances according to the lower signal quality. FHR obtained by external CTG is based on Doppler ultrasound autocorrelation, which provides a less precise assessment of FHR variability and different complexity than fMCG or other technologies with beat-to-beat basis.

The increasing goodness found in the opposite direction, namely the validation of CTG based models on MCG data (learn set: CTG → test set: MCG_res) seems surprising at first glance. One possible explanation might be that the higher error rate in the CTG based models may have been mainly caused by random effects, while the systematic part is identified almost on the level of the MCG based models. The goodness values of the test sets MCG_res (validation step: learn set: CTG → test set: MCG_res) are similar to those of the learning sets MCG_res (see validation step: learn set: MCG_res → test set: CTG). This result can be explained by almost similar gestational age-related patient characteristics of the Jena MCG data base and the Porto CTG data base, while the differences are mainly caused by the recording technology and respectively lower data quality (Gonçalves et al 2006, 2013, 2015). Despite the higher random residuals, CTG based fABAS seems to identify similar gestational age systematics compared to MCG based fABAS. This result might help to design clinical studies that include both, CTG and MCG recordings.

We conclude that fABAS is an appropriate candidate for standardized assessment of functional brain developmental age and developmental disturbances across different recording technologies. In addition, the precise detection of individual beats clearly improves the accuracy of the gestational age assessment which is related with fetal maturation.

The feasibility of detecting intrauterine growth restriction from Doppler-based HRV markers in low-resource settings

Intrauterine growth restriction is a pathological slow-down in fetal growth (Pollack and Divon 1992, Resnik 2002). Fetuses affected by intrauterine growth restriction (IUGR) do not reach their full growth potential, leading to increased risk of severe health problems during pregnancy, delivery and after birth. The prevalence of IUGR is particularly high in developing countries (estimated at 10% (Black et al 2008)) where resources, both trained clinical personnel and adequate equipment, are rare, resulting in poor screening and referral rates. One approach is to equip frontline healthcare workers with low-cost easy-to-use tools, empowering midwives to detect risk early for a timely referral.

The fetal cardiac signal is one of the most accessible physiological signals in the antenatal period and is routinely used in clinical practice to monitor the wellbeing of the fetus. Methods to record the fetal cardiac activity include auscultation (stethoscope), handheld Doppler, cardiotocography (CTG), fetal ECG (both using abdominal and scalp electrodes), and fetal MCG. Their low cost, portability and ease-of-use make handheld 1D Dopplers a potential candidate for use in resource-poor environments.

To assess the feasibility of such proposition, initial research assessed whether markers reflecting the impact of growth retardation on the fetal cardiovascular system, computed from a Doppler-derived heart rate signal, would be suitable for the detection of IUGR antenatally (Stroux 2015, Stroux et al 2016).

Several articles have investigated the detection of growth restriction (Schneider et al 2006, Ferrario et al 2007, Buscicchio et al 2010, Lobmaier et al 2010, Huhn et al 2011, Graatsma et al 2012, Fanelli et al 2013, Hoyer et al 2013b) with heart rate variability markers being the most extensively researched measures of fetal wellbeing. Studies reporting on differences in markers between IUGR and normal fetuses have however been largely underpowered, any generalisation beyond the subjects studied was therefore not viable.

An extensive cardiotocography archive of fetal heart rate variables was instead analysed towards the development of an IUGR prediction model. Short-term and long-term variability computed according to Dawes and Redman (Pardey et al 2002) were readily available in the database.

The archive of fetal heart rate variables was collected at the John Radcliffe hospital in Oxford between 1990 and 2011 using the Sonicaid FetalCare system (Huntleigh Healthcare Ltd) for the recording and analysis of the cardiotocograms. Ethics approval was granted by NRES Committee South Central, Oxford A (REC Reference 13/SC/0153). Fetuses with a birth weight under the third percentile (adjusted Yudkin birth weight centile (Yudkin et al 1987)) were selected into the study dataset as IUGR cases. A group of healthy controls was matched for gestational age and gender. With a total of 1163 cases and 1163 control records, the study dataset was the largest reported on to date.

Results confirmed that both short-term and long-term variability differs significantly in growth-restricted compared to healthy fetuses (Wilcoxon rank sum test, p < 0.01). To avoid the bias of varying trace lengths, variability markers averaged over periods of active sleep only were also tested (p < 0.01), as well as the overall time spent in high variability per hour (p < 0.01). Available heart rate variability markers together with surrogate information on sleep states were ultimately used to build an IUGR prediction model (described in detail in Stroux (2015)). Tests on held-out data clearly demonstrated the clinical utility of the multi-variate classifier for early-onset IUGR (fetuses ≤ 34 weeks of gestation), which is of particular importance in settings where IUGR prevalence is high due to addressable factors such as malnutrition or substance abuse.

Given the encouraging outcomes a key consideration is the feasibility of implementing such a screening model in the settings anticipated. The trace length required to make meaningful predictions may be a limiting factor in an environment where both time and examination space can be scarce. In rural settings in particular midwife or expectant mother typically have to travel substantial distances for an assessment taking place at home or in a low resource health post (Stroux et al 2016). Recordings of 60 min, the standard maximum trace length in CTG monitors, may therefore not be feasible.

The previous investigation into an IUGR prediction model has shown that variability measures are better predictors of IUGR when derived from active sleep episodes (Stroux 2015). Active sleep (associated with rapid-eye-movement (REM)) and quiet sleep (associated with no rapid-eye-movement (non-REM)) are the two most distinctive biological sleep states. Behavioural states are reflected in the fetal heart trace and screened for by the Dawes/Redman system as part of its automated CTG analysis. The assignment of states is based on the long-term variability of the fetal heart rate, described in detail by Pardey et al (2002).

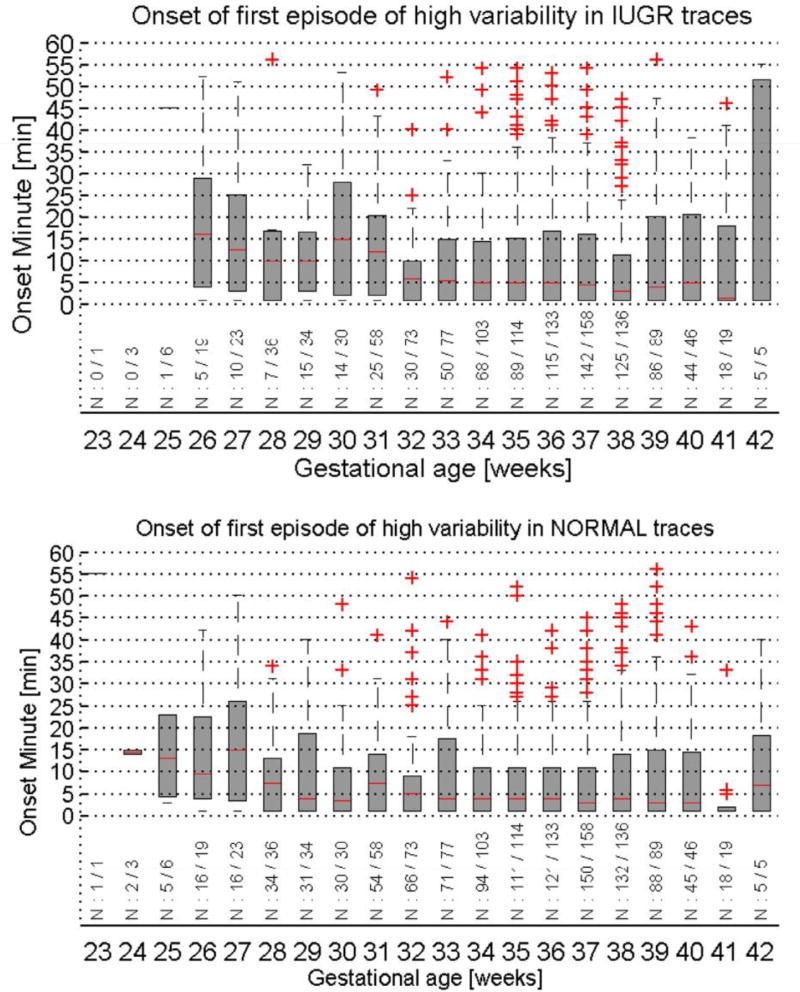
The time of onset of the first active sleep episode in recorded traces was reviewed using the same dataset described above (figure 3). An easily made assumption that a high episode only occurs much later in a majority of IUGR recordings, given the higher number of long recordings found in the database, did not apply. In 61% of IUGR and 84% of normal traces an episode of high heart rate variability occurred within 30 min of starting the recording. When taking into account the percentage of fetuses that did not enter a period of active sleep at all within 60 min (27% IUGR, 6% normal), monitoring for only 30 min would capture 83% of the expected high variability episodes in IUGR and 89% in healthy fetuses.

Figure 3.

The median and interquartile range of the onset time of the first episode of high heart rate variation in recorded traces (top: IUGR traces, bottom: healthy controls). Box plots are shown per gestational age, below each boxplot the number of traces with a high variation episode out of the total number of traces for the gestational age group is indicated.

This observation allows the assumption that in a majority of cases monitoring of the fetus for a maximum of 30 min will be sufficient for IUGR risk assessment. In a setting where time is precious as midwives and patients often have to travel far to provide antenatal care, and where parallel assessment is not feasible as patient encounters typically occur at home, this is a very valuable insight.

To further augment the IUGR risk assessment algorithm and to select and prioritise patients for IUGR screening, additional indicators should be taken into account. The risk for fetal growth retardation increases with maternal complications, as well as due to socio-economic factors (Bamfo and Odibo 2011, Lausman et al 2012). Indicators that may be recorded during midwife-patient encounters include: constitutionally small mother or low pre-pregnancy weight, extremes of maternal age (<16 years, >35 years), maternal hypertension, poor maternal weight gain and malnutrition, low socio-economic status, smoking, alcohol and drug abuse, or signs of severe infection in regions prevalent with growth-related diseases such as Zika.

Given the encouraging results demonstrating the clinical utility of developed Doppler-based IUGR detection model (Stroux 2015), together with the prospect of being able to monitor for only half the anticipated time, make Doppler-based risk screening for early-onset IUGR a proposition worth-while pursuing.

Ongoing work attempts to translate reported findings from CTG to handheld Doppler with the goal of implementing such a screening tool combining low-cost transducers with smart phones for point-of-care recording and remote analysis (Stroux et al 2016).

Quantitative diagnosis of IUGR fetuses: PRSA indices method and interpretation

Monitoring FHR signal became of common clinical use when cardiotocographic (CTG) recordings were introduced and computerized analysis allowed to classify FHR variability by standard traditional parameters (De Haan et al 1971). A still open problem is that, up to now, FHR analysis has given unsatisfactory results predicting fetal morbidity (Van Geijn 1996). Different factors determined this result: the choice of parameters related to FHR morphologic or time domain variations only and the lack of patho-physiological information. Further weak points are the search for a single figure of merit able to discriminate normal and pathological fetuses and the limited or improper use of classification techniques (Magenes et al 2014).

Since 1996 we started a new approach based on multiparameter analysis, considering FHR as a complex signal in which different mechanisms even nonlinear are involved (Signorini et al 2003). This novel approach opened a new route to classify FHR signal through nonlinear parameters, which could reveal further information about fetal condition. Our goal was to identify a set of indices strictly related to physiological mechanisms responsible of heart rate control and to obtain information about relationships between these parameters and fetal conditions (normal or IUGR) in a multivariate approach.

Methods

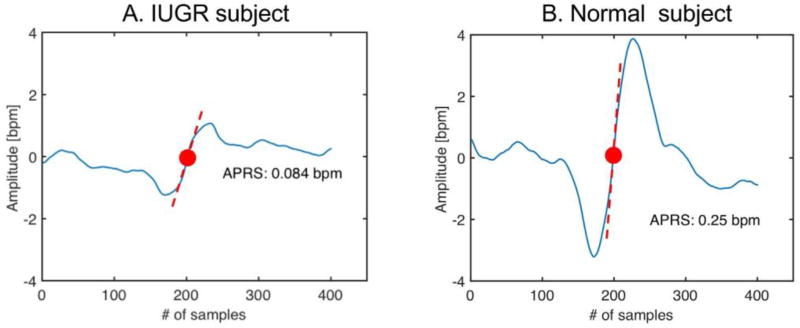
Our fetal monitoring system reads samples at the frequency of 2 Hz. We computed parameters from classical time domain analysis as short-term variability (STV), long term irregularity (LTI) and Delta (Arduini et al 1993). The adopted approach excluded intervals were accelerations and/or decelerations appeared. As nonlinear indices, Entropy estimators were considered. Approximate entropy (ApEn) (Pincus 1995) and sample entropy (SampEn) (Richman and Moorman 2000) were both calculated as a function of m (difference in signal length, m = 1 to 3), r (std of the signal r = 0.10, 0.15, 0.2) and N (signal length, N = 300). Both ApEn and SampEn measured the signal regularity/irregularity providing a family of indices evidencing predictability degree of time series. Another estimation of complexity was made by Lempel and Ziv parameters that quantify repetition of similar patterns in FHR (Lempel and Ziv 1976). More recently, the phase rectified signal analysis (PRSA) was introduced to detect and quantify quasi-periodic oscillations in non-stationary signals affected by noise and artifacts, by synchronizing the phase of all periodic components (Bauer et al 2006). This method demonstrated its usefulness in FHR signal analysis, when episodes of increasing and/or decreasing FHR appear: occurrence or absence of such periods can be related to fetus healthy status. For this reason, we introduced the PRSA method to quantify fetal well-being states. The PRSA curve is obtained from FHR series. The procedure for constructing the curve is described in Bauer et al (2006). First anchor points are selected if the right average of a chosen window is larger than the left one and vice versa. Then, windows are synchronized by their anchor points (middle point of the curve) and averaged to obtain PRSA. The great advantage to this approach is that a 30–40 min HRV signal can be condensed in a single waveform, showing the average dynamic pattern of the recording. Figure 4 illustrates two examples of PRSA curve, computed respectively on a normal fetus (left) and on a IUGR fetus (right). Red dots represent the anchor point. Dashed red lines are the slopes of the curves in the anchor points. In the FHR signal we employed 200 s windows (400 samples).

Figure 4.

PRSA curves obtained from increases in heart rate in FHR recordings from a Normal fetus (left) and from a IUGR fetus (right). The PRSA curves are in blue. Anchor points are the red dots. Red dashed lines represent the slopes in the anchor points (APRS parameter).

Starting from the PRSA curve, several parameters can be computed that describe its shape and, indirectly, quantify the overall dynamics in the HRV series. Depending on the slope sign of the PRSA curve, a novel parameter has been defined as acceleration or deceleration phase rectified slope (APRS or DPRS) (Fanelli et al 2013). Through this estimation, a quantification of FHR oscillations related to cardiovascular control can be obtained. PRSA oscillations can also be related to Autonomic Control activity.

Results

Table 4 summarizes results obtained from methods shortly described and applied to a selected population of normal and IUGR fetuses. Recordings were collected in collaboration with Azienda Ospedaliera Universitaria Federico II, Napoli, Italy. This set consisted 61 Healthy and 61 Intra Uterine Growth Restricted—IUGR fetuses, at gestational age 32–35 weeks. The two groups were selected ‘a posteriori’, after delivery, on the basis of Apgar scores, weight and abdominal circumference: IUGR fetuses were selected by weight below the 10th percentile for their gestational age, abdominal circumference below the 10th percentile and Apgar <8.

Table 4.

Results of the analysis performed in a population of 61 normal and 61 IUGR fetuses. FHR signals were collected through CTG recordings.

	Parameter	Healthy (mean ± std)	IUGR (mean ± std)	t-test	p-value
	Time
Variability in time domain (clinical use)	Delta (ms)	41.5 ± 6.4	29.6 ± 9.3	b	6.3* 10−7
	STV (ms)	6.7 ± 2.24	4.29 ± 1.62	c	1.22* 10−9
	LTI (ms)	21.46 ± 6.53	17.17 ± 5.37	c	1.5* 10−11
	Nonlinear
Complexity and nonlinearity	ApEn(1, 0.1)	1.33 ± 0.13	1.21 ± 0.11	b	5.14* 10–7
	Lempel ziv complexity (2, 0)	1.00 ± 0.08	0.94 ± 0.09	a	0.000 78
	SampEn(1, 0.1)	1.3 ± 0.19	1.13 ± 0.15	b	2.08* 10−7
	PRSA
Signal oscillations	APRS	0.17 ± 0.041	0.12 ± 0.042	c	7.76* 10−12
	DPRS	−0.18 ± 0.046	−0.12 ± 0.042	c	1.08* 10−13

The upper part of table 4 reports time domain indices (STV, LTI and Delta), middle part shows results for Entropy and complexity parameters, lower part reports PRSA derived parameters (APRS, DPRS). Populations were compared by a paired T-test (* = 0.001% marks the level of statistical significance).

Results show that all selected parameters succeed (last two columns in table 4, some of them with a high level of statistical significance) in separating Normal and IUGR groups. Variability in short time domain (STV), together with long term irregularity measured in FHR, both provide a very good separation of the two conditions. Entropy estimators also demonstrate their reliability in FHR analysis.

PRSA-derived parameters, APRS and DPRS, seem the most selective indices for the two group separation. APRS allows to reject the null hypothesis with a p-value of 7.76 * 10⁻¹². DPRS behaves even better (p-value = 1.08 * 10⁻¹³). These two indices summarize respectively the global rate of change (slope) of increase (APRS) and decrease (DPRS) of FHR signal in the whole recording.

Discussion and conclusions

The main focus of our work is to identify a set of indices that can help early identification of diseases arising during gestation. Most parameters so far examined are highly significant in discriminating healthy fetuses from IUGRs, in particular nonlinear ones have shown good performance. However, if considered as ‘stand-alone’ parameter, each of them can provide only a single feature extracted from the FHR signal.

The truth is that a single index cannot summarize by itself the features of pathophysiological processes driving the fetus development towards IUGR condition. In fact, many controlling mechanisms can affect FHR and they may act linearly and/or nonlinearly on it in pathological situations. Only a multivariate approach, considering both linear and nonlinear parameters, can really improve the discrimination of healthy and pathological fetuses. Preliminary results of a multivariate approach based on the above described indices, together with power spectral density (PSD) analysis parameters (not reported in table 4; detailed description in Signorini et al (2003)), show that a simple Logistic Regression model using 4 parameters (2 linear and 2 nonlinear, respectively LTI, High Frequency PSD component, Lempel Ziv Complexity and ApEn) can reach very high levels of Accuracy (92.5%), Sensitivity (93.5%) and Specificity (91.5%) (Magenes et al 2016).

Fetal ECG recording technique—state-of-the-art and own case-study

Overview

The fetal ECG (FECG) is a promising alternative to the FMCG that can be recorded either invasively or non-invasively. Invasive FECG technology, the so-called fetal scalp electrode (FSE), uses an electrode attached to the presenting part of the fetal scalp. FSE has three major drawbacks that discourage its use: (i) its restricted usability (i.e. it can only be used during labor stages, after the rupture of membranes); (ii) its associated risk of infection, due to its invasiveness; and (iii) the reduced number of available leads (which prevents a 3D analysis of the myocardium electrical activity). The only FSE commercial equipment available to date that in addition to FHR analysis performs FECG waveform analysis is the STAN^® monitor (Neoventa Medical, Mölndal, Sweden). STAN performs both fetal heart rate and morphological analysis through a proxy measure for the fetal ST deviation (Clifford et al 2014). Despite being readily available, a Cochrane study (Neilson 2006) reviewed six randomized trials and found no significant improvement in primary outcomes when using STAN’s ST metric. Similarly, another randomized trial (Belfort et al 2015) showed no improvement in perinatal outcome as well as no decrease operative-delivery rates. Therefore, FSE’s premise is under current debate; see Neilson (2006), Belfort et al (2015) and Saccone et al (2016).

The latter technique, i.e. non-invasive FECG (NI-FECG), is applied using regular ECG surface electrodes attached onto the maternal abdomen. This straightforward recording scheme provides considerable advantages compared to FSE and FMCG such as its applicability without expert supervision, multiple channel availability and the possibility of long-term recording at low-cost. NI-FECG can be used during both antepartum (usually from ≥20 weeks onward) and intrapartum periods. In addition, the technique allows the monitoring of fetal QRS (FQRS) complexes in a beat-to-beat manner, therefore enabling the use of more sophisticated FHRV metrics (similarly to the FMCG). This latter feature associated with long-term recordings is particularly relevant to evaluate the fetal circadian heart activity, behavioral states and periods of breathing movements, thus, providing additional information on the fetal/maternal circadian rhythm. Analogously to the FMCG, the NI-FECG allows a deeper characterization of the electrophysiological activity by means of morphological analysis of its signal’s waveform. Promising early works on extracting morphological information from NI-FECG recordings have been published by Clifford et al (2011), Andreotti et al (2016a) and Behar et al (2016b).

Challenges in NI-FECG analysis

NI-FECG’s undemanding recording setup comes at cost of a generally low signal-to-noise ratio (SNR) for the FECG signal, which is buried into noise (mainly the maternal ECG). Moreover, around the 28th–32nd weeks of gestation (WGA), the fetus is almost completely covered by the vernix caseosa, a layer which electrically insulates the fetus, thus, recording the FECG signal during this period is very difficult. For further information on the signal processing challenges involved in NI-FECG, the reader is referred to (Sameni and Clifford 2010, Clifford et al 2014, Behar et al 2016a). Aside from these concerns related to implementation, little is known about the pathophysiological factors that influence the signal quality of the NI-FECG. A few contributions have partially analyzed the dependency of signal quality on some factors, such as gestational age and body-mass-index (Pieri et al 2001, Graatsma et al 2009, Reinhard et al 2012, Van Laar et al 2014, Van Leeuwen et al 2014). However, most of those studies considered a limited group of patients, or the conveyed information is incomplete to fully understand when the NI-FECG may have good quality. Moreover, most researchers focus on late stages of pregnancy, during which the vernix is likely to have dissolved.

For this reason, in this contribution, we aim at providing a more accurate description of the variables involved with focus on WGA 20–28 weeks.

Case study: NI-FECG signal quality for recordings below 28th gestational week

Data was acquired at the Department of Obstetrics and Gynecology at the University Hospital of Leipzig (local ethics committee approval 348–12–24092012). Multichannel recordings (n = 175, each with 20 min duration, 1 maternal and 7 abdominal channels) from 62 singleton pregnancies (67% physiological) from early stage pregnancies (mean/standard deviation: 24.1 ± 3.4 weeks) were used as described in Andreotti et al (2014). Patients showed different placental positions (42% posterior, 29% anterior, fundal 16%, sideways 2% and 11% others), levels of amniotic fluid (80% normal, 15% under, 5% over norm), fetal presentations (41% vertex, 29% breech, 7% should, 23% unknown) and BMIs (26.3 ± 5.1 kg). Five equidistant 5s segments extracted from each recording's channel were carefully annotated by four experts for their FECG amplitude (labelled as not present, low, moderate or high amplitude) and SNR levels (i.e. unacceptable, bad, adequate, good or excellent), so that at least 3 annotations for each segment of the whole data were available. A subset of 500 segments was annotated by every observer twice to evaluate intra-observer reliability. A consensus was then obtained using majority voting. Intra and inter-rater agreement was evaluated using the AC₂ statistics by Gwet (2008). To assess the associations between the clinical information and consensus FECG and SNR annotations a bivariate statistical analysis was carried out, using either ordinal-ordinal correlations (Spearman’s ρ), nominal-ordinal/interval (Eta-coefficient—η) and nominal-nominal associations (Cohen’s w).

Results showed a very good average intra-rater (AC₂ > 0.86) and inter-rater (AC₂ > 0.90) agreement. As shown in table 5(a), a highly significant dependency but weak correlation was found between FECG and SNR metrics (ρ = 0.14, p < 0.001). Some effects presented in table 5, e.g. the reduction of amniotic fluid levels with an increase in WGA, can be physiologically explained. Meanwhile, the cause for other effects such as the association between fetal and placental position are less evident. From table 5(b) it is noticeable that a strong and significant association was found between the lead configuration and FECG amplitude, which confirms the previous results. Strong associations between placental position and SNR level (η = 0.76, p < 0.01) and moderate association for placental position and FECG (η = 0.30, p < 0.001) were encountered. Further analysis showed slightly inferior SNR results for patients with anterior/fundal placentas, which can be justified by the higher relative permittivity of the placenta compared to muscles/amniotic fluid (shown in Peyman et al (2011)). FECG levels were weaker for sideways and praevia/bipartia positions. Different from the results obtained by Graatsma et al (2009), fetal position showed a highly significant association for both SNR and FECG parameters, as shown in table 5(b). Indeed results show higher visibility consensus levels for fetuses in vertex position. Lastly, regarding the levels of amniotic fluid, despite significant dependency no association was found. The counterintuitive results for the interval-scaled variable WGA against nominal variables (fetal and placental position) showing high association with no significance, indicate that the dataset is limited in number for providing such analyses. This is because the correlation coefficient (η) for interval-nominal variables requires that the frequencies of each class of the categorical variable must be large enough to give statistical stability to the means of these classes.

Table 5.

Measures of association between clinical parameters for clinical data regarding WGA 20–28. In (a) are presented the correlation coefficients for interval/ordinal scaled variables, while in (b) the results for nominal associations. Omitted associations (—) in (a) are due to unfeasibility or to the fact that they are present in (b), or vice versa. (a) Effect size for interval-ordinal and ordinal-ordinal variables (both using ρ). (b) Effect size for nominal-nominal (w) and nominal-ordinal/interval (η) variables.

Parameter	WGAd	Amniotic fluid	SNR consensus	FECG consensus
Amniotic fluid	−0.28c	—	—	—
SNR consensus	—	−0.02	—	—
FECG consensus	—	−0.03a	0.14c	—

Parameter	Channel #	WGA	Placenta position	Amniotic fluid	Fetal position
WGA	—	—	—	—	—
Placenta position	—	0.99	—	—	—
Amniotic fluid	—	—	0.07c	—	—
Fetal position	—	0.99	0.42c	0.25c	—
SNR consensus	0.34	—	0.76b	—	0.79c
FECG consensus	0.78c	—	0.30c	—	0.23c

Note: significance level denoted as significant

^a(p < 0.05), very significant

^b(p < 0.01) and highly significant

^c(p < 0.001).

^dRepeated terms were excluded prior to effect size calculation.

Aside from the few publications herein listed, the current NI-FECG commercial equipment have yet to show evidence of their ability to extract and detect fetal signals. For this purpose, randomized trials to compare NI-FECG recordings with other gold-standards such as CTG and FSE are required. Unfortunately, bivariate analysis does not cover inter-dependencies between multiple variables. For assessing how these variables interact, a more elaborate multivariate analysis is further required. However, due to the limited number of recordings available for this work, such analysis is unfeasible and remains for future works.

Reduced materno-fetal correlations of heart rate pattern in pre-eclampsia

Maternal cardiovascular oscillations are known as a convenient tool of hemodynamic regulation (Ivanov 2009, Musa et al 2016). Pre-eclampsia (PE) is a gestational disease featured by placental ischemic syndrome, sympathetic overactivity, hypovolemia and systemic vasculopathy (Rosser 2013, Musa et al 2016). Since respiratory sinus arrhythmia (RSA) captures the parasympathetic effect on the heart rate variability (HRV) the question of the lack of vagal tone in the scenario of PE becomes a rather current issue. RSA was found to have a modulating impact on heart rate, cardiac output, blood pressure and vascular tone of end-organ (Singh et al 2014).

Fetal and maternal hemodynamics are anatomically distinct but periods of their cardiac synchrony are known. RSA was determined as a crucial regulatory mechanism of the synchronization (Ivanov 2009). Fetal RSA plays an important role in the adaptive response to chronic placental insufficiency (Arias-Ortega et al 2015). The umbilical vein could be approached as a ‘mirror’ of the oscillatory processes in the ‘mother-placenta-fetus’ system since the cord is not an innervated tissue. The driver with a frequency of 0.5 Hz was determined in the umbilical vein spectrum of the blood flow velocities. The maternal origin of this controlling signal was supported. The absence of 0.5 Hz peak was found to be associated with pulsatile flow pattern and low Apgar score (Lakhno 2016). Therefore, the amplitude of this peak could be relevant to maternal cardiovascular oscillations. The AIM of the investigation was to determine the role of RSA in the regulation of fetal circulatory system in the case of healthy pregnancy and in PE.

Materials and methods

The maternal and fetal HRV values were studied and umbilical venous blood flow velocity spectral analysis was performed in 106 patients at 32–38 weeks of gestation. 30 of them had a healthy pregnancy and were included in Group I. In Group II, 44 pregnant women with mild-moderate PE were observed. 32 patients with severe PE were monitored in Group III. Maternal and fetal RR interval time series were obtained from maternal abdominal wall with the application of the fetal non-invasive ECG monitor Cardiolab Babycard (Kharkiv, Ukraine). The registration was carried out over 10 min. Blind source separation, adaptive noise cancellation and Kalman filtering techniques were used to reduce artifact rate. The sampling rate was 1000 Hz. The root mean square of successive heartbeat interval differences (RMSSD) was used as a measure of RSA both in mother and fetus. The values of cardiac index (CI) and total peripheral vascular resistance (TPVR) were measured by bioimpedance cardiography and the type of central maternal hemodynamics (CMH) was determined in the study population. The results were analyzed using statistics software package Excel 2010 (Microsoft Corporation, Redmond, WA, United States of America). For the analysis of relationship between X and Y, correlations coefficients were estimated using Spearman’s test.

Results

The maternal and fetal HRV parameters demonstrated a suppressed autonomic nervous regulation with abnormally elevated variables of the sympathetic domain region in PE. The mean maternal sympatho-vagal balance (LF-to-HF ratio) values were 0.9 ± 0.3, 2.2 ± 0.6 and 4.5 ± 1.1 respectively in Group I, Group II and Group III. It was revealed a weak relationship between sympatho-vagal balance and CI, sympatho-vagal balance and TPVR in Group I (table 6). The strength of correlation was not different in mild-moderate PE. The correlation was strong in the same pairs in severe PE.

Table 6.

Statistically significant (p < 0.05) Spearman’s correlations between the maternal sympatho-vagal balance and CI, maternal sympatho-vagal balance and TPVR in the study population.

Pairs of parameters (X versus Y)	Group I	Group II	Group III
Sympatho-vagal balance versus CI	R = −0.30	R = −0.34	R = −0.63
Sympatho-vagal balance versus TPVR	R = 0.32	R = 0.38	R = 0.70

The investigation of relationship between the maternal and fetal RMSSD values and the amplitudes of 0.5 Hz peak revealed following correlations (table 7). The most considerable positive correlation was determined in healthy pregnancy between maternal RMSSD and 0.5 Hz peak amplitude, maternal and fetal RMSSDs. The positive weak correlation between maternal RMSSD and the amplitude of 0.5 Hz frequency peak was determined in Group II. The positive weak correlation between maternal and fetal RMSSDs in women with mild-moderate PE was also found. No considerable relationship was revealed between maternal RMSSD and the amplitude of 0.5 Hz frequency peak, maternal and fetal RMSSDs in the patients with severe PE.

Table 7.

Statistically significant (p < 0.05) Spearman’s correlations between maternal RMSSD and amplitude of 0.5 Hz peak, maternal and fetal RMSSDs in the study population.

Pairs of parameters (X versus Y)	Group I	Group II	Group III
Amplitude of the RSA-associated peak (0.5 Hz) versus the maternal RMSSD	R = 0.64	R = 0.36	R = 0.20
Maternal RMSSD versus fetal RMSSD	R = 0.51	R = 0.32	R = 0.18

Conclusion

The increased maternal sympathetic tone in mild-moderate PE could represent a compensatory mechanism directed towards maintaining of end-organ perfusion. The severe PE was characterized by dramatically increased sympatho-vagal balance, hypokinetic type of CMH and a hypoperfusion of end-organ. The relationship between maternal and fetal RMSSDs, maternal RMSSD and the umbilical vein 0.5 Hz peak amplitude was found only in healthy pregnancy. The revealed relations supported the possible coupling between maternal hemodynamic fluctuations (found as 0.5 Hz peak in the umbilical vein) and fetal hemodynamics in healthy pregnancy. Maternal and fetal RSA were involved in the relationship. The regulatory dissociation between maternal and fetal HRV was found in pre-eclamptic patients. The sympathetic overactivity and the lack of vagal regulation lead to the loss of link between maternal and fetal correlations of heart rate pattern in severe PE.

Resume—outlook

In this paper, the latest advancements in the assessment of normal fetal maturation and its disturbances were presented across original indices of heart rate patterns and different recording technologies.

Fetal MCG allows a stable fetal heart beat detection with a high sampling precision and signal-noise ratio and low error rate, appropriate for the analysis of vagal and sympathetic rhythms over the entire second and third trimester of pregnancy. Due to its high cost, however, fMCG is available only in a few research centers worldwide. On the contrary, fECG recording devices are cheap and mobile, but due to physiological reasons, fECG is only recordable over particular periods of pregnancy and partly suffers from a high error rate. CTG is well established in clinical practice worldwide, analysis standards exist and its routine use has generated a wealth of experience. However, CTG does not allow the identification of individual heart beats and suffers from gaps in the continuous heart rate trace.

Innovative HRV indices such as fABAS, RQA, entropy, binary symbolic dynamics and PRSA significantly extend the diagnostic value of the established ones like STV and LTV, time and frequency domain indices, as well as complexity measures on different time scales. Since the different HRV indices consider different aspects of the complex autonomic control, it was furthermore concluded that multivariate approaches are necessary to develop sensitive and specific scores.

Lessons learnt from clinical experience are that severe disturbances of intrauterine milieu or maturation like chronic hypoxaemia, chorioamnionitis after preterm premature rupture of the membranes, fetal anaemia or acute distress during labour, cause changes in autonomic regulatory capacities that may be picked up by current clinical standards of fetal surveillance. Moreover, several conditions such as maternal diabetes, substance abuse, dietary deficiencies (Gustafson et al 2013) or late intrauterine growth restriction are suspected to result in long term influences on both humoral and autonomic regulation. The subtle methods of recording and assessment presented here, at least, carry the potential to complement clinical management pathways and link intrauterine with postnatal assessment for a better understanding of these mechanisms in the future.

The ultimate goal is the early identification of fetuses at risk to improve prenatal care in clinical practice. The complimentary results on HRV indices/scores and recording technologies allow the design of a comprehensive diagnostic system. Several research and clinical groups are interested in a respective multicenter study by providing access to their data bases or HRV indices.

The objective of a related ongoing project is the advancement of fABAS with respect to precise and robust use in research and clinical application (DFG: HO 1634 12–2, Schn 775/2–3). Its primary aim is to transfer fABAS from MCG to other modalities (ECG, CTG), secondary is the further development of other promising HRV indices/scores of maturation disturbances and fetuses at risk. We intend to make the resulting fABAS system and other scores available for the international scientific community. Respective international collaborations were discussed between the coauthors that attended the ESGCO 2016 special session. Based on pilot studies, multicenter prospective studies could be designed and planned.

Abbreviations

ANS

Autonomic nervous system

CMH

Central maternal hemodynamics

CI

Cardiac index

CTG

Cardiotocography

DET

Determinism

ECG

Electrocardiogram

fABAS

Fetal autonomic brain age score

fECG

Fetal ECG

fHF

Power of normal-to-normal beat intervals in the fetal high frequency band of 0.4–1.7 Hz

fHR

Fetal heart rate

fHRV

Fetal heart rate variability

fLF

Power of normal-to-normal beat intervals in the fetal low frequency band of 0.08–0.2 Hz

fMCG/MCG

(Fetal) magnetocardiography

FQRS

Fetal QRS

FSE

Fetal scalp electrode

GA

Gestational age

HRP

Heart rate pattern

HRV

Heart rate variability

IUGR

Intrauterine growth restriction

MECG

Maternal ECG

NI-FECG

Non-invasive fetal ECG

PE

PRE-eclampsia

PRSA

Phase rectified signal analysis

REM

Rapid eye-movement

RMSSD

Root mean square of successive heart beat interval differences

RP

Recurrence plots

RQA

Recurrence quantitative analysis

RSA

Respiratory sinus arrhythmia

SDNN

Standard deviation of normal-to-normal heart beat intervals

STV

Short-term variability

TPVR

Total peripheral vascular resistance

UPO

Unstable periodic orbits

WGA

Weeks of gestational age