Integrated Computational Approach to the Electron Paramagnetic Resonance Characterization of Rigid 3₁₀-Helical Peptides with TOAC Nitroxide Spin Labels

Abstract

We address the interpretation, via an integrated computational approach, of the experimental continuous-wave electron paramagnetic resonance (cw-EPR) spectra of a complete set of conformationally highly restricted, stable 3₁₀-helical peptides from hexa- to nonamers, each bis-labeled with nitroxide radical-containing TOAC (4-amino-1-oxyl-2,2,6,6-tetramethylpiperidine-4-carboxylic acid) residues. The usefulness of TOAC for this type of analysis has been shown already to be due to its cyclic piperidine side chain, which is rigidly connected to the peptide backbone α-carbon. The TOAC α-amino acids are separated by two, three, four, and five intervening residues. This set of compounds has allowed us to modulate both the radical···radical distance and the relative orientation parameters. To further validate our conclusion, a comparative analysis has been carried out on three singly TOAC-labeled peptides of similar main-chain length.

Introduction

Electron paramagnetic resonance (EPR) of spin-labeled compounds emerged as a powerful spectroscopy in biological structure determination. In particular, it allows one to measure distances between two paramagnetic centers, often spin labels, covalently linked to well-defined positions in the biomacromolecule of interest. However, methodologies to assess distances by EPR are limited because (i) they work well for frozen solutions at low temperatures and (ii) distance ranges between 0.8 and 1.5 nm are difficult to determine.^1,2 Physiological conditions, such as liquid solutions at room temperature, pose additional challenges. To first order, the dipolar interaction between spins, so far the most reliable indicator for distance, is averaged out in isotropic solution, and the isotropic exchange interaction, J, being of the short-distance (several tenths of nanometer) type, is difficult to interpret in terms of separation between spins. Moreover, in a liquid environment, the spin···spin interaction information, be it dipolar or exchange interaction, needs to be extracted from the line shape. More specifically, the differences in line shape of the spectra of the system of interest in the presence and the absence of the spin···spin interaction have to be analyzed, which is particularly challenging for small spin···spin interactions, i.e., long distances.

In previous papers,³⁻⁵ the authors have synthesized, conformationally characterized, and experimentally investigated by EPR a complete series of four 3₁₀-helical peptides, based on α-aminoisobutyric acid (Aib), with pairs of TOAC (4-amino-1-oxyl -2,2,6,6-tetramethylpiperidine-4-carboxylic acid) nitroxide spin labels separated by two, three, four, and five residues (see Table 1 for the exact amino-acid sequences and the number of covalent bonds (n_CB) between the side-chain oxygens of the two TOAC labels). The nitroxide-containing TOAC is as strongly helicogenic⁶ as the well-known Aib residue,^7,8 in that they are both members of the same class of C_α-tetrasubstituted α-amino acids. Moreover, the TOAC side chain is rigidly connected to the α-carbon of the peptide main chain so that the motion of the TOAC label relative to the peptide is reduced to a minimum.

Table 1. Chemical Formulas and Acronyms for the Peptides Investigated.

	peptide	acronym	nCBc	radical state
(i)	Z-(Aib)5-TOAC-Aib-OMea	HEPTA6		mono
(ii)	Z-(Aib)6-TOAC-Aib-OMe	OCTA7		mono
(iii)	Fmoc-Aib-TOAC-(Aib)7-OMeb	NONA2		mono
(iv)	Fmoc-(Aib)2-TOAC-(Aib)2-TOAC-Aib-OMe	HEPTA3,6	16	bis
(v)	Fmoc-TOAC-(Aib)3-TOAC-Aib-OMe	HEXA1,5	19	bis
(vi)	Fmoc-Aib-TOAC-(Aib)4-TOAC-Aib-OMe	OCTA2,7	22	bis
(vii)	Fmoc-Aib-TOAC-(Aib)5-TOAC-Aib-OMe	NONA2,8	25	bis

^aZ, benzyloxycarbonyl; OMe, methoxy.

^bFmoc, fluorenyl-9-methyloxycarbonyl.

^cNumber of covalent bonds between the side-chain oxygens of the two TOAC labels.

As reference compounds for our EPR analysis, we have also investigated three size-matched singly TOAC-labeled peptides. The four bis-labeled peptides have been classified according to the magnitude of the exchange interactions: (i) class I (J ≃ 800 MHz), with HEPTA_3,6 (two intervening residues) and HEXA_1,5 (three intervening residues), which shows a large exchange interaction and five-line EPR spectra, and (ii) class II (J < 9 MHz), with OCTA_2,7 (four intervening residues) and NONA_2,8 (five intervening residues), which exhibits a small exchange interaction and three-line EPR spectra. In general, in these Aib/TOAC peptides we have found a stronger coupling than that in the corresponding Ala/TOAC peptides investigated some time ago.⁹ This result is not surprising in view of the known, much less strong, helix-supporting properties of Ala versus Aib.⁷

In this work, a detailed study is presented of the aforementioned mono- and bis-labeled peptides employing an established integrated computational approach (ICA)^10,11 based on the definition and solution of a proper stochastic Liouville equation (SLE) for the system under investigation.¹² The ICA is a multiscale procedure that aims at calculating “ab initio” EPR spectra of molecules in solution. The idea of multiscale is applied to both space and “time”. Spatial multiscaling (i.e., coarse graining) is employed to access mainly structural properties of the molecule, such as magnetic tensors (via quantum mechanical calculations), dissipative properties (via hydrodynamics modeling where only the shape of the molecule counts), potentials of mean force (using classical mechanics), etc. The time coarse graining is the procedure leading to the complexity reduction of the description of the dynamics of the system. In particular, the idea is to describe the degrees of freedom relevant to the EPR spectroscopy in detail, whereas the irrelevant ones are treated on a simplified level. The interaction of the relevant coordinates with the irrelevant ones becomes unknown and probability theory is used to model such an interaction. Under the assumption of Markovian motion of the relevant degrees of freedom, the SLE employed in the ICA is formulated. Although the selection of the relevant degrees of freedom is usually left to some heuristic reasoning, with the need of comparison with experiments to prove its correctness, some of the authors are working on a more deterministic procedure for the time coarse graining.¹³

The overall computational protocol that constitutes ICA is involved and more complex than the conventional analysis of EPR spectra. Conventional analysis employs a multicomponent fit of the spectra where dynamics is substituted by the diagonalization of the spin Hamiltonian in different orientations of the molecule with respect to the laboratory frame in which the magnetic field is defined. In these conventional approaches, dynamics is simulated by line broadening contributions, which are fitted as well. In the ICA the dynamics is exactly coupled to spin relaxation, making it possible to directly calculate the line shape. Also, the theory is able to treat all motional regimes, without resorting to different approximations for motional narrowed or slow motion regimes. Finally, the main objective of ICA is predictivity. In small to medium sized molecules the present theoretical knowledge and computational power allows us to calculate most of the needed structural properties ab initio leaving a limited number of complicated, yet important, properties unknown that still require fitting. Previously, the ICA protocol was applied to the interpretation of EPR spectra of peptides similar to the ones studied here.

By ICA, the backbone-secondary structure was determined for these peptides in different solvents.^3,4,14 Also, the ICA method proved its sensitivity to internal motions, e.g., in the interpretation of EPR measurements of tempo-palmitate in both isotropic and nematic environments.¹⁵ Also insights into radical polymerization of methacrylic monomers was gained by ICA, in a study in which all parameters were calculated with the exception of a frequency connected to the growth of the polymer. The latter parameter was obtained from fitting the experimental spectra.¹⁶ These examples show the scope of ICA and the power of the interplay between EPR experiments and proper theoretical/computational modeling. In the following, it will be shown that the coupled experimental/ICA approach is a powerful analytical tool to determine the exchange interaction J between electron spins.

As mentioned above, the coupling constant J is also a parameter of the SLE of the biradicals that needs to be determined. To keep in line with the philosophy of the ICA, J would, in principle, have to be calculated ab initio. Quantum mechanical methods to calculate J in biradicals are based on the computation of the difference in energy between the singlet and triplet states. Approches based on density functional theory,¹⁷⁻¹⁹ configuration interaction,^20,21 and asymptotic methods^22,23 were applied to the calculation of J in case studies of biradicals where the interaction is weak. In those studies, “weak” refers to exchange interactions on the order of 1.0–0.1 cm^–1. This range corresponds to energy differences of 10^–3 to 10^–4 kcal/mol between singlet and triplet states. Such an accuracy is not reached in “routine” quantum mechanical calculations, where accuracies are usually on the order of 10^–1 kcal/mol.²⁴ Higher accuracy can be obtained with configuration interaction-based methods, but at present this type of calculation cannot be carried out in reasonable times on medium-large molecules, like the peptides studied in this work. Moreover, a coupling constant much smaller than the limits above-mentioned is expected for the octa- and nonapeptides (by inspection of their experimental EPR spectra). As will be shown in the Results, the magnitude of the coupling is on the order of 0.1 G, i.e., 10^–3 cm^–1. This, in turn, means that, if J had to be accessed by quantum mechanical calculations, energies more accurate than 10^–6 kcal/mol would be required: a still prohibitive limit.

A second route, the one that has been adopted here, is to determine J by fitting the experimental data. A point of strength of the SLE-based approach is that it exactly accounts for line broadening. Sensitivity on such a feature of the cw-EPR spectrum is particularly important in the present study becacuse, as shown in previous work on bis-labeled C₆₀-fullerene molecules,²⁵ the sign of the exchange interaction affects differently the high- and low-field parts of the EPR spectrum. As discussed in Results and Discussion, the sensitivity is sufficient to distinguish the sign even if J is small compared to the isotropic hyperfine coupling constant of the unpaired electron with the ¹⁴N nucleus. This property is a special advantage of the SLE-based approach to determine J from experimental measurements, also compared to other computational approaches.

The integrated computational approach allows the calculation of most of the parameters entering the SLE at a sufficient quality level to avoid the difficulties of complex multidimensional fitting procedures. As will be shown later in the text, a very limited set of fitting parameters will be employed, namely J, and a constant broadening (intrinsic line width, γ) accounting for secondary effects on spectral lines arising from details neglected in the model. By constant broadening we mean a contribution that affects all peaks in the spectrum by the same amount, to be distinguished from the homogeneous broadening due to the coupling of molecular dynamcs to spin relaxation that can affect differently the peaks due to the tensorial nature of the dissipative properties and of the magnetic tensors.

Experimental Section

Details of the chemical syntheses in solution, and the analytical and conformational characterizations of the TOAC mono- and bis-labeled peptides HEPTA₆, OCTA₇, NONA₂ (labeled as NONA₉ in ref (4)), HEXA_1,5, HEPTA_3,6, OCTA_2,7, and NONA_2,8 have been already reported.³⁻⁵

Modeling

The Stochastic Liouville Equation

Aib-based short peptides can be treated as rigid bodies from the point of view of the cw-EPR spectroscopy in solution.^3,4,14 The relevant (slow) coordinates of the molecules are simply the three Euler angles, Ω, that describe the overall orientation of a molecule-fixed reference frame (MF) with respect to a laboratory-fixed (LF) frame. The remaining degrees of freedom, i.e., peptide internal dynamics and solvent, are treated at the level of a thermal bath, providing only fluctuation–dissipation to the angular momentum of the molecule. Within this level of description, the time behavior of the coordinate Ω is stochastic. To describe its time evolution, the quantity ρ (Ω, t|Ω₀, 0) is introduced, i.e., the conditional probability density of finding the molecule with an orientation Ω at a time t, if it was in Ω₀ at some reference time. In this case, the high-friction approximation regime is used, under which the angular momentum is thought to relax in a time scale much faster with respect to the Euler angles so that it can be projected out. Under this assumption, the time evolution of ρ(Ω,t) = ρ(Ω,t|Ω₀,0) is

1

which is valid in an isotropic medium. In eq 1, Ĵ(Ω) is the angular momentum operator, describing the infinitesimal rotation of the molecule, and D is the rotational diffusion tensor. If (i) MF is chosen as the frame that diagonalizes D and (ii) assuming a nearly axially symmetric rotational diffusion tensor, then the diffusive operator Γ̂ reads

2

with D_∥ = D_ZZ the principal value of the rotational diffusion tensor about the direction nearly parallel to the axis of the 3₁₀-helix and D_⊥ = (D_XX + D_YY)/2 the average of the other two principal values for the rotation about two perpendicular axes, both nearly perpendicular to the helix axis. Ĵ² and Ĵ_Z² are, respectively, the square of the total angular momentum and the square of its projection onto the Z-axis of MF. Because the relaxation-time scales characteristic for Ω are likely to be comparable with the spin-relaxation rates, the quantum mechanical evolution of the spin pseudovariables σ and the classical rotational motion need to be treated in a coupled way. The stochastic Liouville equation¹² provides the correct framework to describe in a complete and exact way the full set of relaxations in the system.

3

where now the probability density is an operator (density matrix), Ĥ is the spin Hamiltonian, Ĥ^× a superoperator that returns the commutator of Ĥ and ρ̂, and L̂ is the stochastic Liouvillean. Because in this work we deal with both mono- and bis-labeled peptides, and each spin label bears an unpaired electron coupled with one nitrogen nucleus, the general shape of the spin Hamiltonian (in units of frequency) is

4

where β_e is the Bohr magneton and ℏ is the reduced Planck constant. The first term is the Zeeman interaction of each electron spin with the magnetic field B₀, depending of the g_i tensor; the second term is the hyperfine interaction of each ¹⁴N/unpaired electron, defined with respect to the hyperfine tensor A_i; the third and fourth terms are the electron exchange and spin···spin dipolar interactions, respectively. J is the exchange constant, whereas the tensor T is modeled here according to the point-dipole approximation

5

where μ₀ is the vacuum magnetic permeability, r is the distance vector between the position of the two electrons, r is its modulus, and ⊗ stands for the dyadic product. Though, in principle, to evaluate the tensor T, the distributions of the unpaired electrons in their orbitals should be taken into account, the two N–O moieties in the bis-labeled radicals of this study are sufficiently separated (>7 Å) to allow to consider the electrons as point charges.³ In the calculations, the electrons are placed in the center of the N–O bond. In eq 4, tensors g_i and A_i are taken diagonal in their local frames μ_iF (μ = g, A) rigidly fixed on the ith nitroxide, and Ω_μi is introduced as the time-independent set of Euler angles that transforms MF to μ_iF. Operators Ŝ_i and Î_i are defined in LF. For monoradicals, n_probes = 1 and the third and fourth term of the Hamiltonian are not present, whereas for biradicals, n_probes = 2 and the full eq 4 must be considered. Finally, the dependence of the spin Hamiltonian on Ω is implicit due to the fact that Zeeman, hyperfine, and dipolar interactions are modulated by tensorial quantities that are constant in MF but change in LF, which is the reference where the spin operators are defined.^12,26

The EPR spectrum is obtained as Fourier–Laplace transform of the correlation function for the X-component of the magnetization, defined as

6

where I is the nuclear spin. Following standard definitions,¹² the spectral line shape is obtained as

7

where P_eq = 1/8π² is the (isotropic) distribution in the Ω space. Here, ω is the sweep frequency, ω₀ = g₀β_eB₀/ℏ = γ_eB₀, and g₀ is the trace of the g_i tensor divided by three. The starting vector |v⟩ of eq 7 is related to the allowed EPR transitions and it is actually an operator acting on the spin degrees of freedom.¹²

To summarize, the peptide is described as a diffusive rotor and the TOAC probes are rigidly fixed. Parameters are (i) the principal values of the diffusion tensor D_XX, D_YY, D_ZZ, (ii) the principal values of g and A tensors, and (iii) the Euler angles Ω_μ describing the orientation of the magnetic local tensors with respect to MF. In the case of biradicals, the exchange interaction J and the dipolar tensor T must be added to the set.

Structure and Magnetic Tensors

The geometrical optimization of all of the peptides has been carried out using the Gaussian 03 software package²⁷ at the DFT level of theory in acetonitrile solvent, which is modeled at the level of the polarizable continuum model (PCM).²⁸ The hybrid counterpart PBE0 of the conventional functional PBE with the standard 6-31G(d) basis set has been employed. On the basis of previous studies on TOAC-labeled, Aib-rich peptides,^3−5,14 the backbone of the peptides is fixed in the 3₁₀-helix conformation, and a twist geometry for the piperidine rings is assumed.

Hyperfine and Zeeman tensors have been computed by the same functional and using the N06 basis set.²⁹ No vibrational averaging correction has been applied to the isotropic hyperfine term, A_iso = tr{A}/3. Rather, A_iso was extracted from the experimental spectra considering that it corresponds to one-half of the width of the spectrum, i.e., the separation between the highest and the lowest field line in the spectra, which is justified as no external orienting field is present. Also, because all the experiments have been conducted in the same conditions of temperature and solvent, A_iso was the same for all of the radicals. With respect to the quantum mechanically calculated A_iso, the value extracted from the spectra is 0.5 G smaller. This difference is compatible with the correction that one obtains with vibrational averaging of the hyperfine-coupling constant (see, e.g., Table 5 of ref (10)).

In biradicals, as described above, the spin···spin dipolar interaction tensor has been calculated within the point-dipole approximation in eq 5, taking the vector connecting the centers of the two N–O bonds as a measure of the distance between the electrons. For the reasons mentioned in the Introduction, J has been kept as a free parameter of the calculations, to be fitted over the experimental data.

Dissipative Properties

The evaluation of the diffusion properties of the peptides has been based on a hydrodynamic approach.³⁰ The molecule is described as a set of rigid fragments (made of atoms or groups of atoms) connected via bonds about which rotation is possible and is immersed in a homogeneous isotropic fluid of known viscosity. The tensor D can be conveniently partitioned into translational (TT), rotational (RR), internal (II), and mixed (TR, TI, RI) blocks. It is thus obtained as the inverse of the friction tensor Ξ using Einstein’s relation^31,32

8

where k_B is the Boltzmann constant and T is the absolute temperature. The friction tensor for the constrained system of spheres (the real molecule), Ξ, is calculated from the friction tensor of nonconstrained extended atoms, as described in ref (30).

Because the peptides are here described as rigid molecules, their generalized diffusion tensor is represented by a 6 × 6 matrix. Moreover, due to the translational invariance of the magnetic field in the cw-EPR experiments that have been conducted, one may project out the translational part of the diffusion tensor. Thereby, the diffusion tensor is reduced to a 3 × 3 matrix made up only of the rotational tensor, D = D_RR. For all of the peptides, the diffusion tensors have been calculated with this set of parameters: viscosity 0.343 cP,³³ temperature 293 K, an effective radius of 2 Å for all of the non-hydrogen atoms, and stick boundary conditions.

Results and Discussion

The calculations of the cw-EPR spectra have been carried out with the E-SpiRes software package.¹¹ Relevant parameters are reported in Tables 2 and 3, respectively, for the three monolabeled and for the four bis-labeled peptides (a rough estimate on the relative error of all the parameters is between 0.1% and 1%, as reported in section 3 of the Supporting Information). Because there was no g-calibration in the experimental spectra, a fixed correction g_corr, has been applied to match the field position of the center of the theoretical spectra to their experimental counterparts. As stated in the previous section, A_iso has been measured directly from the experimental spectra because the librational effects have not been accounted for in the quantum mechanical (QM) calculations. We also recall that a limited set of parameters has been adjusted via a nonlinear least-squares procedure, that is, the value of J in biradicals, and an intrinsic line width, which provides a constant broadening to the spectral lines. The last parameter is added to take into account secondary effects of 3D-structure/dynamics on the spectrum neglected by the stochastic model. The values obtained for J are reported in Table 3, along with the geometric distance between the two nitroxide moieties.

Table 2. Dissipative, Geometric, and Magnetic Parameters Employed in the Calculations of the cw-EPR Spectra of Mono-Labeled Peptides.

	HEPTA6	OCTA7	NONA2
Calculated Parameters
D/109 Hza	1.03, 1.08, 2.75	1.36, 1.38, 3.78	1.08, 1.11, 3.35
g – ge/10–3 a	6.41, 3.66, −0.29	6.48, 3.71, −0.22	6.97, 4.14, 0.16
Ωg/dega	–2.0, 89.9, −1.6	–107.5, 12.5, 170.2	153.0, 182.1, 249.4
A – Aiso/Gaussa	–9.24, −9.10, 18.34	–9.22, −9.08, 18.33	–9.10, −8.94, 18.01
ΩA/dega	77.7, 172.1, −70.6	151.5, 10.4, 162.7	146.0, 174.5, −102.7
Parameters from Experimental Setup/Spectra
ω/109 Hzb	9.784351	9.784351	9.786595
gcorr/Gaussc	+11.5	+11.5	+11.5
Aiso/Gaussd	14.74	14.74	14.74
Fit Parameters
γ/Gausse	0.73	0.70	0.58

^aPrincipal values of tensors and their transformation angles with respect to MF.

^bSpectrometer frequency.

^cShift correction.

^dIsotropic part of the hyperfine interaction tensor.

^eIntrinsic line width.

Table 3. Dissipative, Geometric and Magnetic Parameters Employed in the Calculations of cw-EPR Spectra of bis-Labeled Peptides.

	HEXA1,5	HEPTA3,6	OCTA2,7	NONA2,8
Calculated Parameters
D/109 Hza	0.89, 0.92, 1.69	0.83, 0.87, 2.04	1.01, 1.03, 1.93	0.51, 0.53, 1.48
g1 – ge/10–3 a	6.90, 4.20, 0.02	6.83, 4.08, 0.13	6.97, 4.14, 0.16	6.70, 3.90, −0.10
Ωg1/ dega	–87.4, 116.4, −147.9	171.5, 7.6, −28.0	154.0, 182.1, 249.4	153.0, 182.1, 249.4
A1 – Aiso/Gaussa	–9.10, −8.94, 18.01	–9.24, −9.10, 18.34	–9.10, −8.94, 18.01	–9.10, −8.94, 18.01
ΩA1/dega	–157.2, 45.6, −139.3	171.5, 24.5, −98.3	146.0, 174.5, −102.7	146.0, 174.5, −102.7
g2 – ge/10–3 a	6.41, 3.66, −0.29	6.97, 4.14, 0.16	6.88, 4.10, 0.18	6.48, 3.71, −0.22
Ωg2/dega	37.4, 87.2, 133.3	–40.3, 137.6, 169.3	–107.5, 12.5, 170.2	–107.5, 12.5, 170.2
A2 – Aiso/Gaussa	–9.24, −9.10, 18.34	–9.10, −8.94, 18.01	–9.22, −9.08, 18.33	–9.22, −9.08, 18.33
ΩA2/dega	37.4, 87.2, 133.3	–40.3, 137.6, 169.3	151.5, 10.4, 162.7	6.3, 90.0, −180.0
r/Åb	11.9	7.0	15.0	12.9
Parameters from Experimental Setup/Spectra
ω/109 Hzc	9.787400	9.787091	9.786611	9.785979
gcorr/Gaussd	+11.5	+11.5	+11.5	+11.5
Aiso/Gausse	14.74	14.74	14.74	14.74
Fit Parameters
J/Gaussf	250	>300	–0.38	0.31
γ/Gaussg	1.16	0.92	0.42	0.44

^aPrincipal values of tensors and their transformation angles with respect to MF.

^bGeometric distance.

^cSpectrometer frequency.

^dShift correction.

^eIsotropic part of the hyperfine interaction tensor.

^fExchange interaction.

^gIntrinsic line width.

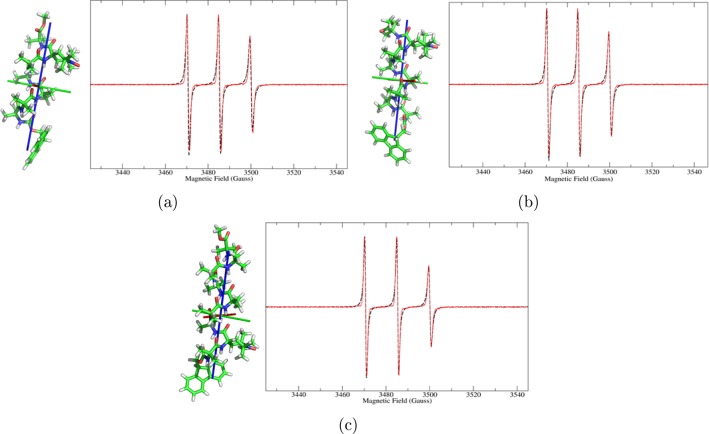
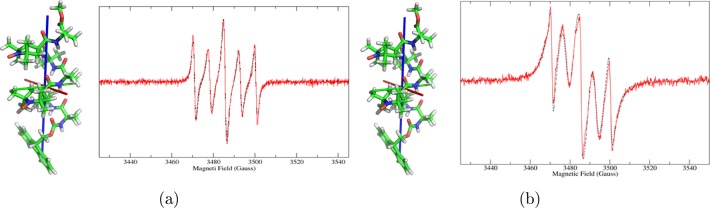
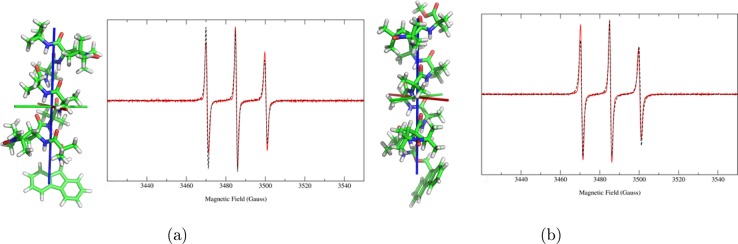
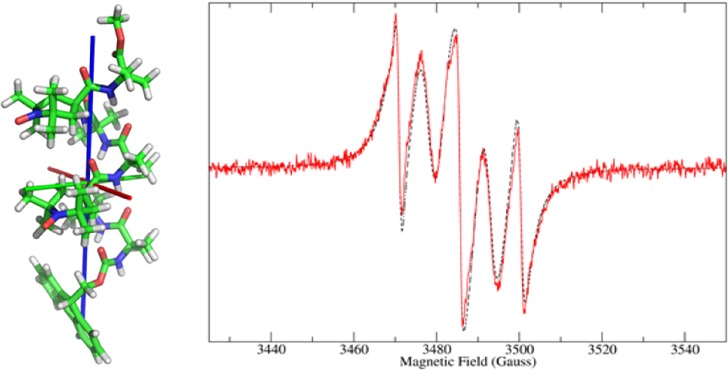
Figure 1 compares experimental and calculated spectra for the monolabeled peptides, whereas Figures 2 and 3 show the comparison for the four bis-radicals. The good agreement of the theoretical lineshapes with the experimental data obtained using a very limited set of parameters underlines the good performance of the stochastic model employed, despite its simplicity.

Figure 1.

Experimental (red, solid line) and calculated (black, dashed line) cw-EPR spectra of the three monoradical peptides, and their QM-minimized structures: (a) HEPTA₆, (b) OCTA₇, and (c) NONA₂. The principal axes of rotational diffusion are also shown (X, red; Y, green; Z, blue).

Figure 2.

Experimental (red, solid line) and calculated (black, dashed line) cw-EPR spectra of the bis-radical peptides, and their QM-minimized structures: (a) HEXA_1,5 and (b) HEPTA_3,6. The principal axes of rotational diffusion are also shown (X, red; Y, green; Z, blue).

Figure 3.

Experimental (red, solid line) and calculated (black, dashed line) cw-EPR spectra of the bis-radical peptides, and their QM-minimized structures: (a) OCTA_2,7 and (b) NONA_2,8. The principal axes of rotational diffusion are also shown (X, red; Y, green; Z, blue).

A comment can be made on the values obtained for J. On one hand, the spectra of HEXA_1,5 and HEPTA_3,6 exhibit five lines, with the two extra lines with respect to the normal monoradical pattern placed exactly at ±A_iso/2 and with high intensity (Figure 2). Following Luckhurst,³⁴ this finding shows that J/A_iso ≫ 1. In fact, for HEXA_1,5 the fit returned 250 G, whereas for HEPTA_3,6, the only possible estimation is that J ≥ 300 G, because beyond this value the calculated spectrum starts to become insensitive to variations of the value of the exchange interaction. In section 1 of the Supporting Information we show how a theoretical spectrum loses sensitivity on J and its sign as the absolute value is increased. To obtain a good agreement with the experimental spectra, the assumption that a certain percentage of monoradical peptide would be present in the sample has been made (e.g., due to partial degradation of the samples).²⁵ In particular, 20% and 4% components of monoradical for HEXA_1,5 and HEPTA_3,6, respectively, have been used. The high fraction of monoradical in HEXA_1,5 seems too high given the chemical purity of the sample and may indicate a dynamic process, as discussed before.⁵

On the other hand, the experimental spectra of OCTA_2,7 and NONA_2,8 show only three peaks, suggesting a weak exchange interaction between the two unpaired electrons. Also, due to the large distance of the unpaired electrons (15 and 13 Å, respectively; see Table 3), the dipolar interaction is not able to contribute to the broadening of the peaks. Thus, it was not possible to estimate, if present, the quantity of monoradical with a significant accuracy. Calculations have been performed with the bis-radical contribution only, neglecting any possible contamination from the monoradical.

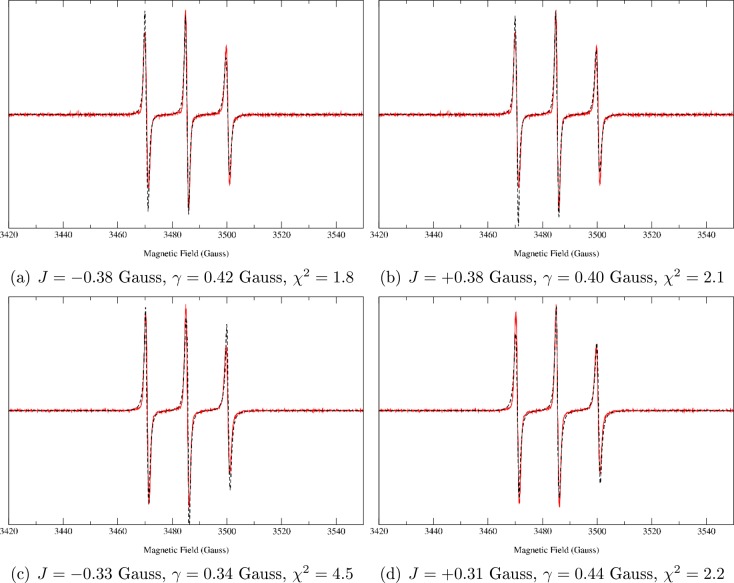
To evaluate the value of J, two fits have been run starting from either a positive or a negative value of the coupling constant. Values reported in Table 3 correspond to the best χ² value. For the sake of completeness, the spectra calculated with both positive and negative values of J (together with the intrinsic line width, γ, and the χ²) are shown in Figure 4 for the two peptides. The spectra show that a small but decisive difference is noticeable between the two calculations with an opposite sign of J. Thus, not only is the SLE approach sensitive to a small (in absolute value) J, but also it is able to catch its sign. Although the first information is in some way “hidden” in the spectral pattern, the sign is intrinsically related to the broadening, which is exactly taken into account in our approach, within the limits of the precision of the chosen model for the dynamics. Such a conclusion is supported statistically, as is discussed in detail in section 2 of the Supporting Information. For the small value of |J| observed for OCTA_2,7 and NONA_2,8, i.e., class II biradicals with three-line EPR spectra, we need to ascertain that the absolute value of J and its sign are significant. Obviously, both J and the intrinsic line width (γ) used in the fitting routine broaden the lines; however, J broadens each one of the EPR lines to a different degree, whereas γ broadens each line by the same amount, enabling us to distinguish the effect of J and γ to some degree (this is shown in section 2 of the Supporting Information where the spectra are fitted keeping γ = 0). In section 2 of the Supporting Information we describe the procedure to determine the statistical significance of J. In particular, we compare two models, one fixing J = 0 and fitting the spectra only with γ, and the second model with both γ and J as fitting parameters. The F-test shows that the latter model is significantly better than the former one. Moreover, the error on the fitting of both parameters is of the order of 1%. Thus, also the sign of J is significant.

Figure 4.

Comparison among experimental (red, solid line) and theoretical (black, dashed line) cw-EPR spectra of (a,b) OCTA_2,7, and (c,d) NONA_2,8 bis-radical peptides fitted using a negative or a positive initial guess for the J coupling constant (the intrinsic line width has also been fitted). χ² for the fittings are also reported.

On the basis of these observations, i.e., the good outcome of the F-test, the small error in the fitting parameters (even if a moderate (expected) correlation exists between the two), and their different physical meaning, we believe that the ICA applied to the interpretation of experimental spectra of bis-radicals is a reliable method to obtain J values and their sign from experimental spectra, even in the case of very weak coupling.

Conclusions

A combination of different computational methods, from quantum mechanical calculations to stochastic modeling, provides a useful approach to interpret cw-EPR spectra of bis-radical labeled peptides.^3,4 It is thus possible to combine convergent and complementary computational techniques to obtain geometrical and dynamical information. The DFT geometry optimization procedure has led to a 3₁₀-helical structure for all of the peptides studied in this work, consistent with previous theoretical and experimental studies.³⁻⁵ For the systems OCTA_2,7 and NONA_2,8 we have found that the principal values of the hyperfine tensors (A₁ and A₂) are equal.

A remarkable finding is that HEXA_1,5 has a large J, whereas NONA_2,8, has a much smaller J coupling, although they have similar distances between the nitroxide groups (Table 3). As discussed previously, the magnitude of J in these two compounds rather follows the respective number of covalent bonds between the nitroxides (Table 1), suggesting, as discussed previously,⁵ that the J-interaction is through bond, rather than through space.

In Figure 3a,b, differences between the theoretical and experimental spectra are noticed in the low- and high-field peaks. We first recall that line broadening depends on the anisotropy of the magnetic and diffusion tensors, and on the orientation of their principal axes with respect to the molecule. The dipolar interaction tensor also plays a role in biradicals. Imperfections in the modeling of these quantities (related to the accuracy of the employed computational approaches to determine the mentioned parameters) may provide a slight difference in the line broadening observed in the theoretical spectra with respect to that seen in the experimental ones. Furthermore, an effect not accounted for in our modeling is the hyperfine interaction of each unpaired electron with the 12 protons of the methyl groups adjacent to the nitroxide group of TOAC. Such a coupling contributes to the broadening of the peaks and, if unresolved, gives a Gaussian line shape. As the intrinsic line shape in our fitting routine is Lorentzian, we expect a deviation of the fitted with respect to the experimental spectrum, particularly at the foot of the line.

We account partially for the coupling with the protons, together with other secondary effects, with the intrinsic line width fitting parameter, γ, which provides a constant line broadening. To quantify the comprehensive goodness of the approach, based on detailed features of the spectra, we measured the areas of the two (integrated) peaks at low and high field in Figures 3a,b. The difference between experiment and calculation is respectively 20% and 10%. ICA provides an overall good agreement with experimental data with an extremely reduced need of parameter fitting. Of course, secondary effects are neglected, leading to a not perfect detailed matching of the theoretical spectra with the experimental ones.

To conclude, we stress that the ICA proved again to be a powerful theoretical/computational approach to extract relevant molecular properties from experimental EPR spectra. This is due to both the nearly predictive level of the computational protocol, especially for small-medium molecules, and the ability of the SLE approach to correctly couple molecular motions to spin relaxation. In the present study, in particular, the approach allowed us to access the value of the coupling constant J in bis-radicals, in both its absolute value and its sign. Such a result is relevant in the EPR-based analysis of molecular structures and molecular processes that are studied by means of site-directed spin labeling with two radical probes. As discussed in the Introduction, there are limitations on the quantum mechanical determination of J if it is smaller than 1 G. Moreover, it has to be recalled that when the absolute value of J is larger than the broadening of the peaks, it can be directly measured from the spectrum. However, the sign is not determined, because it enters in the broadening of the peaks, not in their splitting. These limits pose, at the moment, our ICA in an important position as an analytical tool for the extraction of such an important molecular property as J is from a macroscopic observation, i.e., a solution cw-EPR spectrum.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.7b01050.

• Simulations showing the effect of the sign of J (Figure S1), statistical analysis of the significance of the sign and the magnitude of J (Figure S2), and estimation of errors of all parameters used in the simulations (PDF)

The authors declare no competing financial interest.