GENERATIVE METHOD TO DISCOVER EMPHYSEMA SUBTYPES WITH UNSUPERVISED LEARNING USING LUNG MACROSCOPIC PATTERNS (LMPS): THE MESA COPD STUDY

Abstract

Pulmonary emphysema overlaps considerably with chronic obstructive pulmonary disease (COPD), and is traditionally subcategorized into three subtypes: centrilobular emphysema (CLE), panlobular emphysema (PLE) and paraseptal emphysema (PSE). Automated classification methods based on supervised learning are generally based upon the current definition of emphysema subtypes, while unsupervised learning of texture patterns enables the objective discovery of possible new radiological emphysema subtypes. In this work, we use a variant of the Latent Dirichlet Allocation (LDA) model to discover lung macroscopic patterns (LMPs) in an unsupervised way from lung regions that encode emphysematous areas. We evaluate the possible utility of the LMPs as potential novel emphysema subtypes via measuring their level of reproducibility when varying the learning set and by their ability to predict traditional radiological emphysema subtypes. Experimental results show that our algorithm can discover highly reproducible LMPs, that predict traditional emphysema subtypes.

1. INTRODUCTION

In computer vision, topic models are popular tools capable of explaining complex macro-structures contained in an image via the use of “visual words” (i.e. visual primitives) [1, 2]. Topics (e.g., a human face) are defined via the learning of common co-occurence of visual words (e.g., two eyes, a nose, and a mouth) in documents (e.g., a set of portrait images). Visual topics convey very rich structural information that is able to extract the essence of image data content toward image interpretation and detection of more abstract visual concepts. Visual topics have been applied to medical image analysis for image-type classification and image retrieval [3]. Discovery of topics may also benefit disease subtypes discovery [4], and disease phenotyping.

In the context of radiological emphysema subtypes, which were initially defined at autopsy and have poor inter-rater agreement even in expert hands [5], we propose a learning framework to discover in a set of training CT scans (analogous to documents) some lung macroscopic patterns (LMPs, analogous to topics) of lung texture prototypes (LTPs, analogous to visual words) to encode emphysema subtypes. As introduced in [6], topics are learned with a probabilistic “mixed-membership” model called the Latent Dirichlet Allocation (LDA), which enables multiple topics per document. We assume that each subject is a mixture of multiple emphysema subtypes that can be explained by LMPs, and each LMP is closely related to a specific set and proportion of LTPs.

2. METHOD

This section is organized as follows: 1) Preprocessing (lung and emphysema segmentation and LTP labeling); 2) Unsupervised discovery of LMPs; and 3) Evaluation metrics of LMPs.

2.1. Emphysema Segmentation and LTP labeling

Following our previous works on quantifying emphysema subtypes on CT scans [7, 8] we pre-analyze each CT scan and generate two masks: the emphysema mask within the lung via HMMF regularized segmentation [7], and a LTP label mask, via assignment of 3D patches to the most similar LTP within a set of 100 LTPs generated using texton features [8].

2.2. Unsupervised Lung Macro Pattern (LMP) discovery

We assume that our dataset of M CT scans (documents) is generated from N_lmp LMPs (topics) using N_ltp LTPs (words). LTP label is the observed variable, while the structure of the LMPs and their occurence in a CT scan are the two hidden (unobserved) variables. Discovering of the LMP topics is solved as the maximization of the posterior probabilities of the hidden variables given the observations. LDA is used as the probabilistic generative process of the observed data. Concretely, a LMP i is equipped with a probability distribution φ over the LTPs, using a Dirichlet with parameter β: φ_i ~ Dir(β) and a CT scan j is equipped with a probability distribution θ of LMPs, using a Dirichlet with parameter α: θ_j ~ Dir(α). α and β are Dirichlet prior hyperparameters.

The joint distribution of observed LTP and hidden LMP random variables is written as [6]:

$$P(\mathbf{LTP},\mathbf{LMP},\mathit{\theta },\mathit{\phi },\alpha ,\beta )=\prod _{i=1}^{N_{\mathit{lmp}}}P({\mathit{\phi }}_i;\beta )\times \prod _{j=1}^{M}P({\mathit{\theta }}_j;\alpha )\times \prod _{t=1}^{N_{\mathit{ltp}}}P(\mathbf{LM}{\mathbf{P}}_{\mathbf{j},\mathbf{t}}\mid {\mathit{\theta }}_j)P(\mathbf{LT}{\mathbf{P}}_{\mathbf{j},\mathbf{t}}\mid {\mathit{\phi }}_{\mathbf{LM}{\mathbf{P}}_{\mathbf{j},\mathbf{t}}})$$ (1)

where LTP_j,t is the observed value of LTP t in document j. φ_i, θ_j and LMP_j,t are hidden variables to be inferred. The generative LDA process is described as follows:

1. For a LMP i, a multinomial parameter φ_i is sampled from Dirichlet prior φ_i ~ Dir(β);

2. For a scan j, a multinomial parameter θ_j over the N_lmp LMPs is sampled from Dirichlet prior θ_j ~ Dir(α).

3. For a LTP t in scan j, its LMP is sampled from discrete distribution LMP_j,t ~ Multinomia(θ_j).

4. The value LTP_j,t of LTP t in scan j is sampled from the distribution of LMP_j,t, LTP_j,t~Multinomia(φ_LMPj,t).

Learning these various distributions (the set of LMPs and their associated LTP probabilities) is a Bayesian inference problem. As in [9], we used the Gibbs Sampling approach to maximize Eq. 1.

2.2.1. Localized LDA model

We perform LMP learning on local regions of interests rather than the whole lung. Each scan is quantized into a M^* × N_ltp-dimensional vector, where M^* is the number of (local) document-level regions of interest (DROI) per scan. We chose overlapping DROIs of size between 1.5 and 4 times the patch size used for LTP labeling (PROI = 25×25×25 mm), and extracted an average of 50 DROIs per scan to achieve a balance between lung volume coverage and computational complexity of LDA. To infer emphysema-like topics, we only use the DROIs which have at least 1% of overlap with the HMMF emphysema mask for generating the LMPs.

2.2.2. Setting the number of LMPs

A common problem with LDA-based topic discovery models is that they do not guarantee global optimality, which can lead to instability and lack of reproducibility. To tackle this problem, we follow [10] which improved LDA for “community detection in networks” using the Infomap [11] graph partition to initialize the number of topics. Infomap is able to find stable clusters given a similarity graph using information compression technique. In contrast to standard unsupervised clustering algorithms, Infomap does not require the user to guess the number of clusters.

After extracting training ROIs at a given DROI size, we use Infomap to set N_lmp as follows: For each LTP, we generate the histogram of their frequency of occurrence over all the DROIs. We calculate the histogram intersections [12] as the measure of similarity of each pair of LTPs that co-appear in at least one DROI. To enforce sparsity in the similarity graph, we threshold similarity values below a threshold T. We then used Infomap to infer N_lmp based on this similarity graph. This sets the number of topics to discover and best guess of word composition of each topic. We then refine the estimation of the topics solving the LDA using Gibbs Sampling [9] to get the final LMPs. The hyper-parameters α and β were empirically set to 0.5 and 0.01. The threshold T is tested from 0 to 1 with 0.1 increments and we retain the maximal obtained value N_lmp to initialize Gibbs Sampling.

2.3. Evaluation metrics of LMPs

We evaluate the discovered LMPs based on their reproducibility over training sets and association with traditional radiological subtypes.

Given two sets of LMPs (topics) C and C′ learned on two distinct training sets, we propose the following metric to measure their reproducibility R:

$$R(C,C^{\prime })=\underset{\pi }{max}\frac{1}{N_{\mathit{lmp}}}\sum _{k=1}^{N_{\mathit{lmp}}}\text{sim}(C_k,C_{{\pi }_k}^{\prime })$$ (2)

where sim(C_k, C′_πk) measures the similarity between LMPs C_k and $C_{{\pi }_k}^{\prime }$ and π denotes the permutation of indices leading to optimal matching of compared LMPs, using the Hungarian method [13]. We define two metrics for the similarity measurement, simA for measuring common LTP components in LMPs C_k and $C_{{\pi }_k}^{\prime }$, and simB for measuring overlap of LMP labeling on a common test set, as follows:

$$\text{simA}\left(c_k,{c^{\prime }}_{{\pi }_k}\right)=\frac{min\left(C_k,{C^{\prime }}_{{\pi }_k}\right)\mathbf{1}}{\text{mean}\left(C_k\mathbf{1}+{C^{\prime }}_{{\pi }_k}\mathbf{1}\right)}$$ (3)

where 1 is a column vector with all 1s (C_k1 = sum(C_k)).

$$\text{simB}\left(C_k,{C^{\prime }}_{{\pi }_k}\right)=\mathbf{I}(L_{C_k}=L_{{C^{\prime }}_{{\pi }_k}})$$ (4)

where I is the 0–1 loss function, and L_Ck denotes LMP label masks using the LMPs C_k.

Noting MROI the ROIs used to label CT scans with LMPs, their size should not exceed the size of DROI and not be smaller than the size of PROI. We tested MROI of size between 1 and 3 times the PROI size. For each MROI, we get a normalized histogram of LTPs, and calculate its similarity with the LMPs composition using Euclidean distance. Each MROI is assigned to the LMP with the highest similarity.

The association of LMPs with traditional emphysema subtypes is measured as the intraclass correlation (ICC) of the percentage of emphysema subtypes (CLE, PLE, PSE) and non-emphysema (NE) between the visually assessed ground-truth reported in [5] and the predicted values from LMPs using a constrained multivariate regression [8].

3. EXPERIMENTS

Quality of generated topics was measured via: (1) measure of reproducibility of LMPs learned in two distinct training sets. (2) visual inspection of LMP samples; (3) Ability of LMPs to predict the traditional radiological emphysema subtypes. We performed two sets of experiments which are now described.

3.1. Synthetic Data

We first tested our algorithm on synthetic data generated as follows:

1. Generate a set of M =300 documents with N = 1000 words per document. There are N_ltp=100 vocabularies.

2. Choose θ_i ~Dir(α), where i ∈{1, …, M} and Dir(α) is a Dirichlet distribution with α= 0.1;

3. Choose φ_k~Dir(β), where k∈{1, …,N_lmp} and β=0.01;

4. Use φ to generate a set of K = 3, 5, 10 topics made of vocabularies.

5. Use θ_i to generate a set of M = 300 documents with N words per document. Generation of the synthetic data is performed as follows: For each word position i, j, where j ∈ {1, …, N}, and i ∈ {1, …, M}:

   1. Choose a topic z_i,j ~ Multinomial(θ_i);

   2. Choose a word w_i,j ~ Multinomial(φ_zi,j).

We measured the similarity of the composition of the topics discovered by the LDA algorithm (using the known number of topics and random initialization) and the ground truth synthetic topics using the similarity metric R (using simA). The results for R_K where K is the number of topics to discover, are: R₃ = 1, R₅ = 1, R₁₀ = 0.99.

3.2. MESA COPD Study

We used N=203 out of 317 CT scans from the MESA COPD Study [5] by excluding the scans without emphysema. MESA COPD Study were acquired at full inspiration with either a Siemens 64-slice scanner or a GE 64-slice scanner, and reconstructed using B35/Standard kernels with axial resolutions within the range [0.58, 0.88]mm, and 0.625mm slice thickness. All CT scans were visually labeled by expert radiologists in [5] into global extents of each of the three traditional radiological emphysema subtypes over the lung volume.

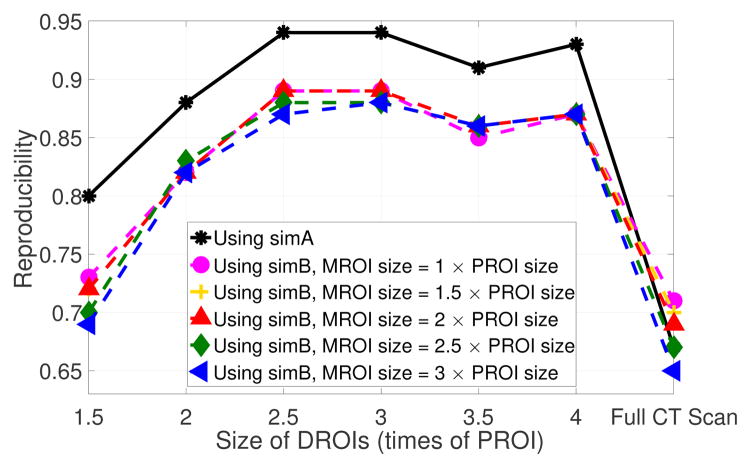
We split the study into three parts with 68, 68, 67 CT scans each, using the first two subsets as independent training sets and the third as a test set. We trained on the first two sets to generate two sets of LMPs and obtained N_lmp= [10, 8, 6, 6, 6, 6, 7] and N_lmp=[9, 7, 6, 6, 6, 6, 6] LMPs in each training run, using DROI sizes of [1.5,2,2.5,3,3.5,4,∞] times the LTP labeling patch ROI (PROI) size and where the ∞ means that the full lung volume field was used. Reproducibility of the learned LMPs is illustrated in Fig. 1. From the results using simA, we can see that highest reproducibility is achieved for the learned LMPs with DROI size (62.5 × 62.5 × 62.5)mm and (75 × 75 × 75)mm. In general, the LMPs learned on the full scan were not as good as those learned on DROIs. This verifies that spatial information is helpful for learning LMPs. From the results using simB, reproducibility follows a similar trend as with simA in terms of DROI size effect: the highest reproducibility is achieved with DROI size (62.5 × 62.5 × 62.5)mm and (75 × 75 × 75)mm. On the other hand, the size of MROI has no significant effect on the reproducibility of LMP labeling.

Fig. 1.

Reproducibility of LMPs with different DORIs sizes, and the reproducibility of labeling MROIs with different DROIs sizes in the validation set (N=67).

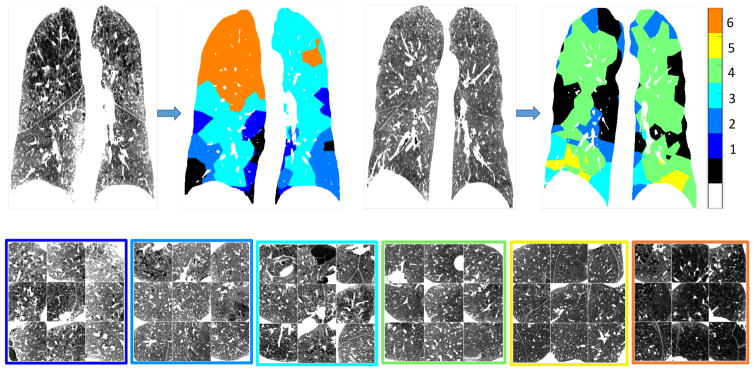
For visual illustration, we show in Fig. 2 some randomly selected MROIs (size = 75×75×75 mm) for each of the six LMPs learned from the first training set with DROI size=75×75×75 mm. These illustrations show that the MROIs are generally homogeneous within a LMP, and visually distinct between LMPs.

Fig. 2.

Examples of LMPs from 1 to 6. In the legend, ‘white’ is the background, ‘black’ is the area not covered by emphysema mask, and the other 6 colors are the 6 LMPs. Each MROI has the size of (75 × 75 × 75)mm.

Finally, we used the six generated LMPs, from the first training set with DROI size=75 × 75 × 75 mm, to predict the traditional radiological emphysema subtypes using a constrained multivariate regression [8]. We conducted three-fold cross-validations on the whole cohort to evaluate the ICC against visual labeling by radiologists, and the results are reported in Table 1. The 6-dimensional LMPs predicted traditional radiological subtypes better than the radiologist interrater reproducibility for CLE, PLE and NE. For PSE, however, the ICC of LMPs was not satisfactory. To investigate this issue, we augmented the LMPs by visually picking up the two LTPs within the disease LTPs (most occuring in disease subjects) that looked the most like PSE. Adding these 2 PSE-like LTPs to the LMPs corresponds to forcing the topic discovery process to consider these two LTPs as being topics on their own. The resultant ICC for PSE increased to 64%.

Table 1.

ICC of predicted of visual radiological subtypes. Three-fold cross validation on MESA COPD Study with 203 subjects.

Method	CLE	PLE	PSE	NE
LMPs	0.85	0.65	0.23	0.89
Augmented LMPs	0.86	0.65	0.64	0.89
LTPs	0.92	0.72	0.69	0.95
Inter-rater	0.74	0.59	0.67	0.76

4. DISCUSSION & CONCLUSION

In this paper, we have shown that topic discovery via Infomap and LDA can generate up to six highly reproducible emphysema-specific lung macroscopic patterns (LMPs) from a series of 100 pre-learned lung texture prototypes (LTPs), which are associated to traditional radiological emphysema subtypes. The PSE emphysema subtype was not properly discovered by the algorithm but easily added to the LMPs via picking up two visually-compatible LTPs. In future work, we will investigate how to add constraints on the LDA topic discovery process to preserve rare but important LTPs, such as PSE. In the longer term, we will also explore whether LMPs can be used to guide the discovery of novel clinical emphysema subtypes.