Variation in Recombination Rate and Its Genetic Determinism in Sheep Populations

Abstract

Recombination is a complex biological process that results from a cascade of multiple events during meiosis. Understanding the genetic determinism of recombination can help to understand if and how these events are interacting. To tackle this question, we studied the patterns of recombination in sheep, using multiple approaches and data sets. We constructed male recombination maps in a dairy breed from the south of France (the Lacaune breed) at a fine scale by combining meiotic recombination rates from a large pedigree genotyped with a 50K SNP array and historical recombination rates from a sample of unrelated individuals genotyped with a 600K SNP array. This analysis revealed recombination patterns in sheep similar to other mammals but also genome regions that have likely been affected by directional and diversifying selection. We estimated the average recombination rate of Lacaune sheep at 1.5 cM/Mb, identified ∼50,000 crossover hotspots on the genome, and found a high correlation between historical and meiotic recombination rate estimates. A genome-wide association study revealed two major loci affecting interindividual variation in recombination rate in Lacaune, including the RNF212 and HEI10 genes and possibly two other loci of smaller effects including the KCNJ15 and FSHR genes. The comparison of these new results to those obtained previously in a distantly related population of domestic sheep (the Soay) revealed that Soay and Lacaune males have a very similar distribution of recombination along the genome. The two data sets were thus combined to create more precise male meiotic recombination maps in Sheep. However, despite their similar recombination maps, Soay and Lacaune males were found to exhibit different heritabilities and QTL effects for interindividual variation in genome-wide recombination rates. This highlights the robustness of recombination patterns to underlying variation in their genetic determinism.

Meiotic recombination is a fundamental biological process that brings a major contribution to the genetic diversity and the evolution of eukaryotic genomes (Baudat et al. 2013). During meiosis, recombination enables chromosomal alignment resulting in proper disjunction and segregation of chromosomes, avoiding deleterious outcomes such as aneuploidy (Hassold et al. 2007). Over generations, recombination contributes to shaping genetic diversity in a population by creating new allelic combinations and preventing the accumulation of deleterious mutations. Over large evolutionary timescales, divergence in recombination landscapes can lead to speciation; the action of a key factor in the recombination process in many mammals, the gene PRDM9, has been shown to have a major contribution to the infertility between two mouse species, making it the only known speciation gene in mammals today (Mihola et al. 2009).

Genetics studies on recombination were first used to infer the organization of genes along the genome (Sturtevant 1913). With advances in molecular techniques, more detailed physical maps and eventually whole-genome assemblies are now available in many species. The establishment of highly resolutive recombination maps remains of fundamental importance for the validation of the physical ordering of markers obtained from sequencing experiments (Groenen et al. 2012; Jiang et al. 2014). From an evolutionary perspective, the relevant distance between loci is the genetic distance and recombination maps are essential tools for the genetic studies of a species, for estimation of past demography (Li and Durbin 2011; Boitard et al. 2016), detection of selection signatures (Sabeti et al. 2002; Voight et al. 2006), QTL mapping (Cox et al. 2009), and imputation of genotypes (Howie et al. 2009) for genome-wide association studies (GWAS) or genomic selection. Precise recombination maps can be estimated using different approaches. Meiotic recombination rates can be estimated from the observation of markers’ segregation in families. Although this is a widespread approach, its resolution is limited by the number of meioses that can be collected within a population and the number of markers that can be genotyped. Consequently, highly resolutive meiotic maps have been produced in situations where large segregating families can be studied and genotyped densely (Shifman et al. 2006; Mancera et al. 2008; Groenen et al. 2009; Rockman and Kruglyak 2009; Kong et al. 2010) or by focusing on specific genomic regions (Cirulli et al. 2007; Stevison and Noor 2010; Kaur and Rockman 2014). In livestock species, the recent availability of dense genotyping assays has fostered the production of highly resolutive recombination maps (Tortereau et al. 2012; Johnston et al. 2016, 2017), particularly by exploiting reference population data from genomic selection programs (Sandor et al. 2012; Ma et al. 2015; Kadri et al. 2016).

Another approach to study the distribution of recombination on a genome is to exploit patterns of correlation between allele frequencies in a population (i.e., linkage disequilibrium, LD) to infer past (historical) recombination rates (McVean et al. 2002; Li and Stephens 2003; Chan et al. 2012). Because the LD-based approach in essence exploits meioses accumulated over many generations, it can provide more precise estimates of local variation on recombination rate. For example, until recently (Pratto et al. 2014; Lange et al. 2016) this was the only known indirect approach allowing the detection of fine-scale patterns of recombination genome-wide in species with large genomes. Several highly recombining intervals (recombination hotspots) were detected from historical recombination rate maps and confirmed or completed those discovered by sperm-typing experiments (Crawford et al. 2004; Myers et al. 2005). One important caveat of LD-based approaches is that their recombination rate estimates are affected by other evolutionary processes, especially selection that affects LD patterns unevenly across the genome. Hence, differences in historical recombination between distant genomic regions have to be interpreted with caution. Despite this, historical and meiotic recombination rates usually exhibit substantial positive correlation (Rockman and Kruglyak 2009; Brunschwig et al. 2012; Chan et al. 2012; Wang et al. 2012).

The LD-based approach does not allow the study of individual phenotypes to directly identify loci influencing interindividual variation in recombination rates. In contrast, family-based studies in human (Kong et al. 2008; Chowdhury et al. 2009), Drosophila (Stevison and Noor 2010; Chan et al. 2012) mice (Shifman et al. 2006; Brunschwig et al. 2012), cattle (Sandor et al. 2012; Ma et al. 2015; Kadri et al. 2016), and sheep (Johnston et al. 2016) have demonstrated that recombination exhibits interindividual variation and that this variation is partly determined by genetic factors. Two recombination phenotypes have been described: the number of crossovers per meiosis (genome-wide recombination rate, GRR herein) and the fine-scale localization of crossovers (Individual Hotspot Usage, IHU). GRR has been shown to be influenced by several genes. For example, a recent GWAS found evidence for association with six genome regions in cattle (Kadri et al. 2016). Among them, one of the genomic regions consistently found associated with GRR in mammals is an interval containing the RNF212 gene. In contrast to GRR, the IHU phenotype seems mostly governed by a single gene in most mammals: PRDM9. This zinc-finger protein has a key role in recruiting SPO11, thereby directing DNA double-strand breaks (DSBs) that initiate meiotic recombination. Because PRDM9 recognizes a specific DNA motif, the crossover events happen in hotspots carrying this motif. However, this PRDM9-associated process is not universal as it is only active in some mammals; canids, for example, do not carry a functional copy of PRDM9 and exhibit different patterns for the localization of recombination hotspots (Auton et al. 2013).

As mentioned above, recombination was studied recently in sheep (Johnston et al. 2016), which lead to the production of precise genome-wide recombination maps, revealed a similar genetic architecture of recombination rates in sheep as in other mammals, and identified two major loci affecting individual variation. Quite interestingly, one of the QTL identified in this study, localized near the RNF212 gene, was clearly demonstrated to have a sex-specific effect. This study was performed in a feral population of sheep that is quite distantly related to continental populations (Kijas et al. 2012) and has not been managed by humans for a long time. To understand how recombination patterns and genetic determinism can vary across populations, in this work we conducted a study in another sheep population, the Lacaune, from the south of France. The Lacaune breed is the main dairy sheep population in France, its milk being mainly used for the production of Roquefort cheese. Starting in 2011, a large genotyping effort started in the breed to implement a genomic selection program (Baloche et al. 2014), and young selection candidates are now routinely genotyped for a medium-density genotyping array (∼50K SNP). This constitutes a large data set of genotyped families that can be used to study recombination, although limited to one sex as only males were used for genomic selection in this population. This data set offers an opportunity to study variation in recombination and its genetic determinism between very diverged populations of the same species. Hence, a first objective of this study was to elucidate whether these two sheep populations had similar distribution of recombination on the genome and whether they shared the same genetic architecture of the trait, and in particular the same QTL effects.

The second objective of this study was to compare different approaches to study recombination from independent data in the same population. To this end, in addition to the pedigree data, we exploit a sample of 51 unrelated individuals genotyped with a high-density genotyping array (∼500K SNP). While, the family data were used to establish meiotic recombination maps, the sample of densely genotyped individuals was used to create historical recombination maps of higher resolution. This offered the opportunity to evaluate to what extent sheep ancestral recombination patterns match contemporary ones.

Materials and Methods

Study population and genotype data

In this work, we exploited two different data sets of sheep from the Lacaune breed: a pedigree data set of 8085 related animals genotyped with the medium-density Illumina Ovine Beadchip including 54,241 SNPs, and a diversity data set of 70 unrelated Lacaune individuals selected as to represent population genetic diversity, genotyped with the high-density Illumina Ovine Infinium HD SNP Beadchip (Moreno-Romieux et al. 2017; Rochus et al. 2017).

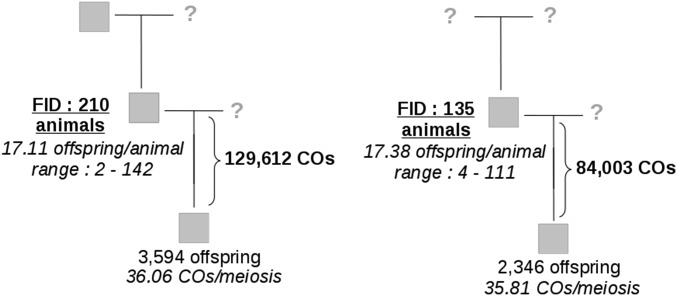
Standard data cleaning procedures were carried out on the pedigree data set using plink 1.9 (Chang et al. 2015) excluding animals with call rates below 95% and SNPs with call frequency < 98%. After quality controls, we exploited genotypes at 46,813 SNPs and 5940 meioses. For these animals, we only selected the sires that had their own sire known and at least two offspring and the sires that did not have their own sire known but at least four offspring. Eventually, 345 male parents, called focal individuals (FIDs) hereafter, met these criteria: 210 FIDs had their father genotype known while the remaining 135 did not (Figure 1).

Figure 1.

Families used to infer crossover (CO) events. COs were identified in meioses of 345 focal individuals (FIDs). Two-hundred and ten FIDs had their father known (left) while 135 FIDs did not (right).

Recombination maps

Meiotic recombination maps from pedigree data:

Detection of crossovers:

Crossover locations were detected using LINKPHASE (Druet and Georges 2015). From the LINKPHASE outputs (recombination_hmm files), we extracted crossovers boundaries. We then identified crossovers occurring in the same meiosis < 3 Mb apart from each other (that we call double crossovers) and considered them as dubious. This number was chosen as it corresponded to clear outliers in the distribution of intercrossover distances. They are also quite unlikely under crossover interference. We applied the following procedure: given a pair of double crossovers, we set the genotype of the corresponding offspring as missing in the region spanned by the most extreme boundaries and reran the LINKPHASE analysis. After this quality control step, we used the final set of crossovers identified by LINKPHASE to estimate recombination rates. This data set consisted of 213,615 crossovers in 5940 meioses.

Estimation of recombination rates:

Based on the inferred crossover locations, meiotic recombination rates were estimated in windows of 1 Mb and between marker intervals of the medium SNP array using the following statistical model, inspired by Cheung et al. (2007). For small genetic intervals such as considered here, the recombination rate (termed c in the following), is usually expressed in centimorgans per megabase and the probability that a crossover occurs in one meiosis in an interval j (measured in morgans) is $0.01c_j{l}_j$ where $l_j$ is the length of the interval expressed in megabases. When considering M meioses, the expected number of crossovers in the interval is $0.01c_j{l}_{j}M.$ When combining observations in multiple individuals, we want to account for the fact that they have different average numbers of crossovers per meiosis (termed $R_s$ for individual s). To do so, we multiply the expected number of crossovers in the interval by an individual-specific factor equal to ($R_s/R$), where R is the average number of crossovers per meiosis among all individuals. Finally, for individual s in interval j, the expected number of crossovers is $0.01c_j{l}_j{M}_s{R}_s/R.$ Given this expected number, a natural distribution to model the number of crossovers observed in an interval is the Poisson distribution so that the number y${}_{\text{sj}}$ of crossovers observed in the interval j for an individual s is modeled as:

$$y_{sj}|c_j\sim \text{Poisson}(0.01c_j{l}_j{M}_s{R}_s/R).$$ (1)

To combine crossovers across individuals, the likelihood for $c_j$ is the product of Poisson likelihoods from Equation 1.

We then specify a prior distribution for $c_j:$

$$c_j\sim \Gamma \left(\alpha ,\beta \right)$$. (2)

To set α and β, first raw $c_j$ estimates are computed using the method of Sandor et al. (2012) across the genome and then a γ distribution is fitted to the resulting genome-wide distribution (Supplemental Material, Figure S1 in File S11). Combining the prior (2) with the likelihoods in Equation (1), the posterior distribution for $c_j$ is:

$$c_j|y_{•j}\sim \Gamma (\alpha +{\displaystyle \sum _s{y}_{sj}},\beta +0.01l_j{\displaystyle \sum _s{M}_s{R}_s/R}).$$ (3)

As the localization of crossovers was usually not good enough to assign them with certainty to a single genomic interval, final estimates of $c_j$ are obtained as follows:

1. For each crossover overlapping interval j and localized within a window of size L, let $x_c$ be an indicator variable that takes value 1 if the crossover occurred in interval j and 0 otherwise. Assuming that, locally, recombination rate is proportional to physical distance, set $P\left(x_c=1\right)=\min \left(l_j/L,1\right).$

2. Using the probability in step 1, sample $x_c$ for each crossover overlapping interval j and set $y_{sj}={\displaystyle {\sum }_c{x}_c}.$

3. Given $y_{sj},$ sample $c_j$ from Equation (3).

For each interval considered, perform step 2 and 3 above 1000 times to draw samples from the posterior distribution of $c_j$, thereby accounting for uncertainty in the localization of crossovers.

Historical recombination maps from the diversity data:

The diversity data contains 70 Lacaune individuals genotyped for a high-density (HD) SNP array comprising 527,823 autosomal markers (Rochus et al. 2017). Nineteen of these individuals are FIDs in the pedigree data. To perform the LD-based analysis on individuals unrelated to the pedigree study, these individuals were therefore removed from the data set and the subsequent analyses performed on the 51 remaining individuals. Population-scaled recombination rates were estimated using PHASE (Li and Stephens 2003). For computational reasons and to allow for varying effective population size along the genome, estimations were carried out in 2 Mb windows, with an additional 100 kb on each side overlapping with neighboring windows, to avoid a border effect in the PHASE inference. PHASE was run on each window with default options, except that the number of main iterations was increased to obtain larger posterior samples for recombination rate estimation (option -X10) as recommended in the documentation.

From the PHASE output, 1000 samples were obtained from the posterior distribution of:

• The background recombination rate: ${\rho }_w=4{\mathit{N}}_w{\mathit{c}}_w,$ where $N_w$ is the effective population size in the window, $c_w$ is the recombination rate comparable to the family-based estimate.

• An interval-specific recombination intensity ${\lambda }_j,$ for each marker interval j of length $l_j$ in the window, such that the population scaled genetic length of an interval is: ${\delta }_j={\rho }_w{\lambda }_j{l}_j.$

The medians were used as point estimates of parameters ${\lambda }_j$ and ${\delta }_j,$ computed over the posterior distributions $\left\{{\lambda }_j^{\left(k\right)},{\lambda }_j^{\left(k\right)}{\rho }_w^{\left(k\right)}{l}_j;k\in \left[1,1000\right]\right\}.$

Intervals that showed an outlying ${\lambda }_j$ value compared to the genome-wide distribution of ${\lambda }_j$ were considered as harboring a crossover hotspot. Specifically, a mixture of Gaussian distribution was fitted to the genome-wide distribution of ${\log }_{10}\left({\lambda }_j\right)$ using the mclust R package (Fraley and Raftery 2002; Fraley et al. 2012), considering that the major component of the mixture modeled the background distribution of ${\lambda }_j$ in nonhotspot intervals. From this background distribution, a P-value was computed for each interval that corresponded to the null hypothesis that it does not harbor a hotspot. Finally, hotspot-harboring intervals were defined as those for which false discovery rate (FDR) (${\lambda }_j$) < 5%, estimating FDR with the Storey and Tibshirani (2003) method, implemented in the R qvalue package. This procedure is illustrated in Figure S2 in File S11.

Combination of meiotic and historical recombination rates and construction of a high-resolution recombination map:

To construct a meiotic recombination map of the HD SNP array requires that the historical recombination rate estimates be scaled by four times the effective population size. Due to evolutionary pressures, the effective population size varies along the genome, so it must be estimated locally. This can be done by exploiting the meiotic recombination rate inference obtained from the pedigree data analysis, as explained below.

Consider a window of 1 Mb on the genome; using the approach described above, we can sample values $c_{jk}$ (window j, sample k) from the posterior distribution of the meiotic recombination rate $c_j.$ Similarly, using output from PHASE, we can extract samples ${\rho }_{jk}$ from the posterior distribution of the historical recombination rates (${\rho }_j={\rho }_w{\lambda }_j$). Now, considering that ${\rho }_j=4N{e}_j{c}_j$ where $N{e}_j$ is the local effective population size of window j, we get $\log \left({\rho }_j\right)=\log \left(4N{e}_j\right)+\log \left(c_j\right).$ This justifies using a model on both c${}_{\text{jk}}$ and ${\mathrm{\rho }}_{\text{jk}}$ values:

$$y_{ijk}=\mu +x_{ijk}\alpha +{\beta }_j+{\nu }_{ij}+e_{ijk}$$ (4)

where $y_{ijk}$ is $\log \left(c_{jk}\right)$ when i = 1 (meiotic-recombination rate sample) and $y_{ijk}$ is $\log \left({\rho }_{jk}\right)$ when i = 2 (historical recombination rate sample). In this model, μ estimates the log of the genome-wide recombination rate, x${}_{\text{ijk}}$=1 if i = 2 and 0 otherwise, so that α estimates log(4Ne), where Ne is the average effective population size of the Lacaune population, $\mu +{\beta }_j$ estimates log(c${}_{\text{j}}$) combining population and meiotic recombination rates, and $\alpha +\left({\nu }_{2j}-{\nu }_{1j}\right)$ estimates log(4Ne${}_{\text{j}}$). μ and ${\alpha }_i$ were considered as fixed effects while ${\beta }_j$ and ${\nu }_{ij}$ were considered as independent random effects. Using this approach allows us to combine, in a single model, LD- and pedigree-based inferences, while accounting for their respective uncertainties as we exploit posterior distribution samples.

Model 4 was fitted on 20 samples of the posterior distributions of $c_j$ and ${\rho }_j$ for all windows of 1 Mb covering the genome, with an additional fixed effect for each chromosome, using the lme4 R package (Bates et al. 2015). Windows lying < 4 Mb from each chromosome end were not used because inference on $c_j$ was possibly biased in these regions (see Results). After estimating this model, historical recombination rate estimates of HD intervals were scaled within each window by dividing them by their estimated local effective population size (i.e., $\exp \left(\widehat{\alpha }+\widehat{{\nu }_{2j}}-\widehat{{\nu }_{1j}}\right)$ for window j). For windows lying within 4 Mb of the chromosome ends, historical recombination rate estimates were scaled using the genome-wide average effective population size exp($\widehat{\alpha }$). This led eventually to estimates of the meiotic recombination rates, expressed in centimorgans per megabase, for all intervals of the HD SNP array, which we termed a high-resolution recombination map.

For each interval of the medium-density SNP array, we computed the number of significant hotspots detected as explained above and the hotspot density (number of hotspots per unit of physical distance). After having corrected for the chromosome effect, the GC content effect and for windows farther than 4 Mb of the chromosome end, we fitted a linear regression model to estimate the effect of hotspot density on the meiotic recombination rate.

Comparison with Soay sheep recombination maps and integration of the two data sets to produce new male recombination maps in sheep:

To compare the recombination maps in Lacaune with the previously established maps in Soay sheep (Johnston et al. 2016), we downloaded the raw data from the dryad data repository (doi: 10.5061/dryad.pf4b7) and the additional information available on https://github.com/susjoh/GENETICS_2015_185553. As the approach used in Johnston et al. (2016) to establish recombination maps differs from the one used here, we chose to apply the method of this study to the Soay data to perform a comparison that would not be affected by differences in the methods. As the Lacaune data consist only of male meioses, we also only considered male meioses in the Soay data. The final Soay data set used consisted of 3445 individuals, among which were 299 male FIDs, defined as in the Lacaune analysis. After detecting crossovers with LINKPHASE, one FID exhibited a very high average number of crossover per meiosis (> 100) and was not considered in the analyses (Soay individual ID: RE4844), leaving 298 FIDs. The final data set consisted of 88,683 crossovers in 2609 male meiosis and was used to estimated meiotic recombination maps using the exact same approach as described above, both on intervals of 1 Mb and on the same intervals as the ones considered in the Lacaune meiotic maps on the medium-density SNP array. Note that the Soay sheep are not necessarily polymorphic for the same markers as the Lacaune, but that our method is flexible and can nonetheless estimate recombination rates in intervals bordered by monomorphic markers: in such a case adjacent intervals will have the same estimated recombination rate. As the two populations were found to have very similar meiotic recombination maps (see Results), the two sets of crossovers were finally merged to create a combined data set of 302,298 crossovers in 8549 male meioses and to estimate new male sheep recombination maps, again on 1 Mb intervals and on intervals of the medium-density SNP array.

GWAS on recombination phenotypes: GRR

The set of crossovers detected was used to estimate the GRR of each FID in the family data set from their observed number of crossovers per meiosis, adjusting for covariates: year of birth of the parent, considered as a cofactor with 14 levels for years spanning from 1997 to 2010, and insemination month of the offspring’s ewe, treated as a cofactor with seven levels for months spanning from February to August. We used a mixed model for estimating the population average GRR μ, covariates fixed effects β, and individual breeding values $u_s,$ while controlling for nongenetic individual-specific effects $a_s:$

$$y_{so}=\mu +x_{so}\beta +a_s+u_s+e_{so}$$

with $u_s\sim N\left(0,A{\sigma }_s^2\right),$ $a_s\sim N\left(0,I{\sigma }_a^2\right)$, and $e_{so}\sim N\left(0,I{\sigma }_e^2\right),$ where $y_{so}$ is the number of crossovers in the meiosis between FID s and offspring o, A is the pedigree-based relationship matrix between FIDs, and $x_{so}$ the line of the corresponding design matrix for observation $y_{so}.$ We fitted this model using BLUPf90 (http://nce.ads.uga.edu/software/) and extracted: (i) estimates of variance components ${\sigma }_e^2,$ ${\sigma }_{\mathrm{a}}^2$, and ${\sigma }_s^2,$ which allows the estimation of the heritability of the trait (calculated as ${\sigma }_s^2/\left({\sigma }_s^2+{\sigma }_a^2+{\sigma }_e^2\right)$) and (ii) prediction $\stackrel{\sim }{u_s}$ of GRR deviation for each FID.

Genotype imputation

Nineteen of the 345 FIDs are present in the diversity data set of HD genotypes. For the 336 remaining FIDs, their HD genotypes at 507,784 SNPs were imputed with BimBam (Servin and Stephens 2007; Guan and Stephens 2008) using the 70 unrelated Lacaune individuals as a panel. To impute, BimBam uses the fastPHASE model (Scheet and Stephens 2006), which relies on methods using clusters of haplotypes to estimate missing genotypes and reconstruct haplotypes from unphased SNPs of unrelated animals. BimBam was run with 10 expectation-maximization (EM) starts, each EM was run for 20 steps on panel data alone, and an additional step was run on cohort data, with a number of clusters of 15. After imputation, BimBam estimates an average number of alleles for each SNP in each individual, termed mean genotype, computed from the posterior distribution of the three possible genotypes. This mean genotype has been shown to be efficient for performing association tests (Guan and Stephens 2008). In subsequent analyses, we used the mean genotypes provided by BimBam of the 345 FIDs at all markers of the HD SNP array. To assess the quality of genotype imputation at the most associated regions, 10 markers of the HD SNP array, one in the chromosome 6-associated region and nine in the chromosome 7-associated region (see Results) were genotyped for 266 FIDs for which DNA samples were still available. We evaluated the quality of imputation for the most significant SNPs by comparing each possible genotype’s posterior probability estimated by BimBam to the error rate implied by calling it. We observed a very good agreement between the two measures (Figure S3 in File S11), which denoted good calibration of the imputed genotypes at top GWAS hits.

Single- and multi-QTL GWAS on GRR

We first tested association of individual estimated breeding values $\stackrel{\sim }{u_s}$ (EBVs) with mean genotypes at 503,784 single SNPs imputed with BimBam. We tested these associations using the univariate mixed model approach implemented in the Genome-wide Efficient Mixed Model Association (Gemma) software (Zhou and Stephens 2012). To account for polygenic effects on the trait, the centered genomic relationship matrix calculated from the mean genotypes was used. The P-values reported in the results correspond to the Wald test.

To go beyond single SNP association tests, we also estimated a Bayesian sparse linear mixed model (Zhou et al. 2013) as implemented in Gemma. This method allows the consideration of multiple QTL in the model, together with polygenic effects at all SNPs. The principle of the method is to have, for each SNP l, an indicator variable ${\gamma }_l$ that takes value 1 if the SNP is a QTL and 0 otherwise. The strength of evidence that a SNP is a QTL is measured by the posterior probability $P\left({\gamma }_l=1\right),$ called posterior inclusion probability (PIP). Note that all SNPs are included in the model when doing so. Inference of the model parameters is performed using an iterative MCMC algorithm: the number of iterations was set to 10 million and inference was made on samples extracted every 100 iterations. When a genome region harbors a QTL, multiple SNPs in the region can have elevated PIPs. To summarize the strength of evidence for a region to carry a QTL, we calculated a rolling sum of PIPs over 50 consecutive SNPs using the rollsum function of the R zoo package (Zeileis and Grothendieck 2005). Given that the average physical distance between SNPs on the high-density SNP array is ∼5 kb, this procedure interrogates the probability of the presence of a QTL in overlapping windows of ∼250 kb.

For the univariate analysis, the FDR was estimated using the ash package (Stephens 2017), and SNPs corresponding to an FDR < 10% were deemed significant and annotated. For the multivariate analysis, regions where the rolling sum of PIPs were > 0.15 were further annotated. The annotation of the QTL regions consisted of extracting all genes from the Ensembl annotation v87 along with their Gene Ontology (GO) annotations and interrogating for their possible involvement in recombination.

Variant discovery and additional genotyping in RNF212: identification and assignation of the RNF212 sheep genome sequence

The RNF212 gene was not annotated on the Ovis aries v3.1 reference genome. Nevertheless, a full sequence of RNF212 was found in the scaffold01089 of O. orientalis [assembly Oori1, National Center for Biotechnology information (NCBI) accession NW_011943327]. By BLAST alignment of this scaffold, ovine RNF212 could be located with confidence on chromosome 6 in the interval OAR6:116426000–116448000 of the Oari3.1 reference genome (Figure S4 in File S11). This location was confirmed by BLAST alignment with the bovine RNF212 gene sequence. We also discovered that the Oari3.1 unplaced scaffold005259 (NCBI accession JH922970) contained the central part of RNF212 (exons 4–9) and could be placed within a large assembly gap. Moreover, we also observed that automatically annotated noncoding RNA in the RNF212 interval matched the exonic sequence of RNF212 (Figure S4 in File S11).

Variant discovery in RNF212 in the Lacaune population

Based on the genomic sequence and structure of the RNF212 gene annotated in O. orientalis (NCBI accession NW_011943327), a large set of primers were designed using PRIMER3 software (Table S1 in File S11) for amplification of each annotated exon and some intron parts corresponding to exonic regions annotated in Capra hircus (Chir_v1.0). PCR amplification (GoTaq; Promega, Madison, WI) with each primer pair was realized on 50 ng of genomic DNA from four selected homozygous Lacaune animals exhibiting the GG and AA (nonimputed) genotypes at the most significant SNP of the medium-density SNP array of the chromosome 6 QTL (rs418933055, P-value 2.56e−17). Each PCR product was sequenced via the BigDye Terminator v3.1 Cycle Sequencing kit and analyzed on an ABI3730 sequencing machine (Applied Biosystems, Foster City, CA). Sequenced reads were aligned against the O. orientalis RNF212 gene using CLC Main Workbench Version 7.6.4 (QIAGEN, Valencia, CA) to identify polymorphisms.

Genotyping of mutations in RNF212

The genotyping of 266 genomic DNAs from Lacaune animals for the four identified polymorphisms within the ovine RNF212 gene was done by Restriction Fragment Length Polymorphism after PCR amplification using dedicated primers (Table S1 in File S11) (GoTaq; Promega), restriction enzyme digestion (BsrBI for SNP_14431_AG; RsaI for SNP_18411_GA; and Bsu36I for both SNP_22570_CG and SNP_22594_AG; New England Biolabs, Beverley, MA), and resolution on a 2% agarose gel.

Data availability

Genotype data and pedigree information on Lacaune individuals after quality controls are deposited on Zenodo (Astruc et al. 2017) as well as high-density genotypes of 70 unrelated Lacaune individuals (Moreno-Romieux et al. 2017). Computer code and scripts needed to reproduce all results are available on Github (https://github.com/BertrandServin/sheep-recombination) and described in supporting material File S10. Additional data, including output from PHASE, LINKPHASE, BimBam, and Gemma, are provided on the Zenodo repository (DOI: 10.5281/zenodo.821569) (Petit et al. 2017).

Results

High-resolution recombination maps

Meiotic recombination maps: genome-wide recombination patterns:

We studied meiotic recombination using a pedigree of 6230 individuals, genotyped for a medium-density SNP array (50K) comprising ∼54,000 markers. After quality controls, we exploited genotypes at 46,813 SNPs and identified 213,615 crossovers in 5940 meioses divided among 345 male parents (FIDs) (see Materials and Methods). The pedigree information available varied among FIDs (Figure 1); 210 FIDs had their father genotype known while the remaining 135 did not. Having a missing parent genotype did not affect the detection of crossovers as the average number of crossovers per meiosis in the two groups was similar (36.1 with known father genotype and 35.8 otherwise) and the statistical effect of the number of offspring on the average number of crossovers per meiosis was not significant (P > 0.23). This can be explained by the fact that individuals that lacked father genotype information typically had a large number of offspring (17.4 on average, ranging from 4 to 111), allowing us to infer correctly their haplotype phase from their offspring genotypes only. Overall, given that the physical genome size covered by the medium-density SNP array is 2.45 Gb, we estimate that the mean recombination rate in our population is ∼1.5 cM/Mb.

Based on the crossovers identified, we developed a statistical model to estimate meiotic recombination rates (see Materials and Methods) and constructed meiotic recombination maps at two different scales: for windows of 1 Mb and for each interval of the medium-density SNP array. As this statistical approach allowed us to evaluate the uncertainty in recombination rate estimates, we provide them in File S1 and File S2, along with the recombination rate estimates in each interval, their posterior variance, and 90% credible intervals. Graphical representation of the meiotic recombination maps of all autosomes are given in File S3.

The recombination rate on a particular chromosome region was found to depend highly on its position relative to the telomere and to the centromere for metacentric chromosomes, i.e., chromosomes 1, 2, and 3 in sheep (Figure S5 in File S11). Specifically, for acrocentric and metacentric chromosomes, recombination rate estimates were elevated near telomeres and centromeres, but very low within centromeres. In our analysis, recombination rate estimates were found to be low in intervals lying within 4 Mb of chromosome ends. While this could represent genuine reduction in recombination rates near chromosome ends, it is also likely due to crossovers being undetected in our analysis as only a few markers are informative to detect crossovers at chromosome ends. In the following analyses, we therefore did not consider regions lying within 4 Mb of the chromosome ends.

From local recombination rate estimates in 1-Mb windows or medium SNP array intervals, we estimated chromosome-specific recombination rates (Figure S6 in File S11). Difference in recombination rates between chromosomes was relatively well-explained by their physical size, with larger chromosomes exhibiting smaller recombination rates. Even after accounting for their sizes, some chromosomes showed particularly low (chromosomes 9, 10, and 20) or particularly high (chromosomes 11 and 14) recombination rates. In low recombining chromosomes, large regions had very low recombination, between 9 and 14 Mb on chromosome 9 and 36, 46 Mb on chromosome 10, and between 27 and 31 Mb on chromosome 20. In highly recombining chromosomes, recombination rates were globally higher on chromosome 14, while chromosome 11 exhibited two very high-recombination windows between 7 and 8 Mb and between 53 and 54 Mb. In addition, we found, consistent with the literature, that GC content was quite significantly positively correlated with recombination rate both in medium SNP array intervals (P-value < 10⁻¹⁶, r = 0.20) and in 1 Mb intervals (P-value < 10⁻¹⁶, r = 0.28).

Estimation of historical recombination rates and identification of crossover hotspots:

We used a different data set, with 51 unrelated individuals from the same Lacaune population genotyped for the Illumina HD SNP array (600K) comprising 527,823 autosomal SNPs after quality controls. Using a multipoint model for LD patterns (Li and Stephens 2003), we estimated, for each marker interval of the HD SNP array, historical recombination rates ρ (see Materials and Methods). Compared to meiotic maps, these estimates offer a greater precision as they in essence exploit meioses cumulated over many generations. However, the historical recombination rates obtained are scaled by the effective population size ($\rho =4N_{e}c$, where Ne is the effective population size and c the meiotic recombination rate), which is unknown and may vary along the genome due to evolutionary pressures, especially selection. Thanks to the higher precision in estimation of recombination rate, LD-based recombination maps offer the opportunity to detect genome intervals likely to harbor crossover hotspots. A statistical analysis of historical recombination rates (see Materials and Methods) identified ∼50,000 intervals exhibiting elevated recombination intensities (Figure S2 in File S11) as recombination hotspots, corresponding to an FDR of 5%. From our historical recombination map, we could conclude that 80% crossover events occurred in 40% of the genome and that 60% of crossover events occurred in only 20% of the genome (Figure S7 in File S11).

High-resolution recombination maps combining family and population data:

Having constructed recombination maps with two independent approaches and having data sets in the same population of Lacaune sheep, we first evaluated to what extent historical crossover hotspots explain meiotic recombination, and second estimated the impact of evolutionary pressures on the historical recombination landscape of the Lacaune population. We present our results on these questions in turn.

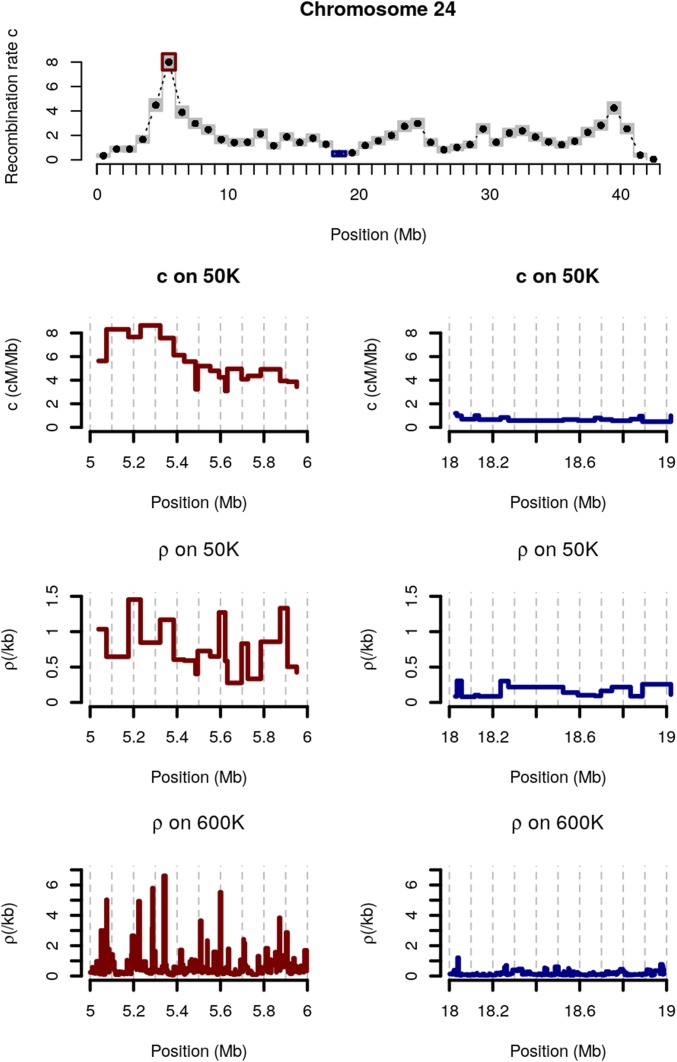
We studied whether variation in meiotic recombination can be attributed to the historical crossover hotspots detected from LD patterns only. For each interval between two adjacent SNPs of the density array, we (i) extracted the number of significant historical hotspots and (ii) calculated the historical hotspot density (in number of hotspots per unit of physical distance). We found both covariates to be highly associated with meiotic recombination rate estimated on family data [r = 0.15 with hotspot density (P < 10⁻¹⁶) and r = 0.19 with the number of hotspots (P < 10⁻¹⁶)]. These correlations hold after correcting for chromosome and GC content effects [respectively, r = 0.14 (P < 10⁻¹⁶) and r = 0.18 (P < 10⁻¹⁶)]. Figure 2 illustrates this finding in two 1-Mb intervals from chromosome 24: one that exhibits a very high recombination rate (7.08 cM/Mb) and the second a low one (0.46 cM/Mb). In this comparison, the highly recombining window carries 36 recombination hotspots while the low recombinant one exhibits none. As the historical background recombination rates in the two windows are similar (0.7/kb for the one with a high recombination rate, and 0.2/kb for the other), the difference in recombination rate between these two regions is largely due to their contrasted number of historical crossover hotspots.

Figure 2.

Comparison between population-based recombination rate and meiotic recombination rate for two 1-Mb windows on Sheep chromosome 24. Top: meiotic recombination rate along chromosome 24. Two windows with high (left, red) and low (right, blue) meiotic recombination rates estimates are zoomed in. Each panel represents, from top to bottom: meiotic recombination rate estimates (c) in SNP intervals of the 50K SNP array, population-based recombination rate estimates (ρ) in SNP intervals of the 50K SNP array, and population-based recombination rate estimates (ρ) in SNP intervals of the High-Density (600K) SNP array.

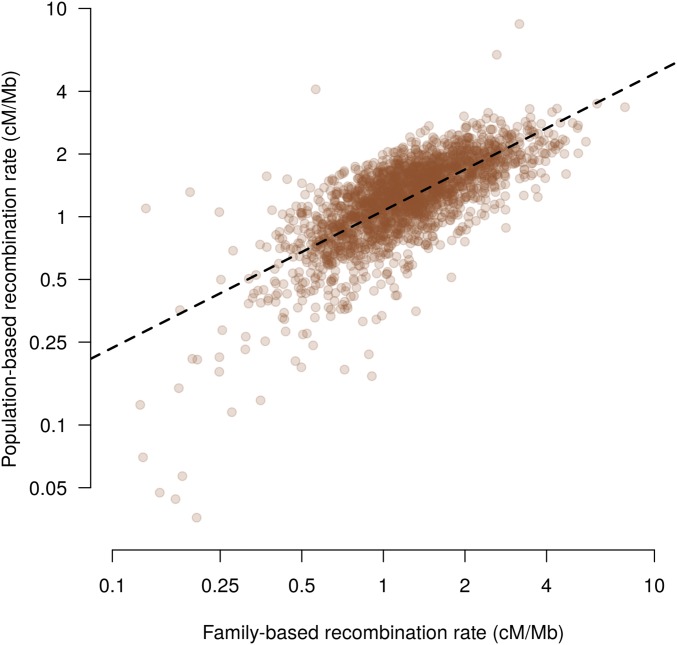
To study more precisely the relationship between historical and meiotic recombination rates, we fitted a linear mixed model (see Materials and Methods) that allowed us to estimate the average effective population size of the population, the correlation between meiotic and historical recombination rates, and to identify genome regions where historical and meiotic recombination rates were significantly different. We found the effective population size of the Lacaune population to be ∼7000 individuals and a correlation of 0.73 between meiotic and historical recombination rates (Figure 3). We discovered seven regions where historical recombination rates were much lower than meiotic ones and three regions where they were much higher (FDR < 0.02, Figure S8 in File S11 and Table 1).

Figure 3.

Population-based and meiotic recombination rates in windows of 1 Mb. The dashed line is the regression for population-based recombination rate on the family recombination rate. Values are shown on a logarithmic scale.

Table 1. Genome regions where meiotic and population-based recombination rates differ significantly.

Chromosome	Window Span (Mb)	$q_w$	P-Value	${\rho }_s/c$
3	103–104	0.06	1.6 10−5	0.28
3	109–110	0.04	1.8 10−5	0.28
6a	36–38	0.14	1.2 10−7	0.22
10a	29–30	0.77	8.8 10−5	0.31
10	36–37	0.01	2.1 10−5	0.29
10	42–44	< 0.01	1.2 10−14	0.11
13a	63–64	0.33	7.4 10−6	0.31
12	4–5	0.92	7.4 10−6	3.7
20a	28–29	0.01	1.7 10−5	3.6
23	10–11	0.97	5.1 10−6	3.8

${\rho }_s/c:$ ratio of population to meiotic recombination rate. $q_w:$ proportion of genome regions with lower meiotic recombination rate. Details on the estimation of these parameters are given in the text. Regions with P-values $<$10⁻⁴ were considered outliers (FDR = 0.02).

^aRegions corresponding to potential selection signatures.

Seven of these 10 regions have extreme recombination rates compared to other genomic regions. To quantify to what extent a window is extreme, we indicate in Table 1, for each window, the proportion of the genome with a lower recombination rate (q${}_{\text{w}}$). For six of these seven regions, the historical recombination rate is more extreme than the meiotic rate: four regions have very low meiotic recombination rate and even lower historical recombination rates (the two regions on chromosome 3 and two regions on chromosome 10, between 36 and 37 Mb and between 42 and 44 Mb), while two regions have very high meiotic recombination rates and even higher historical recombination rates (on chromosome 12 and on chromosome 23). For these six regions, the discrepancy between meiotic recombination and historical recombination estimates can be explained by the fact that we used a genome-wide prior in our model to estimate meiotic recombination rates that has the effect of shrinking our estimates toward the mean. Because historical estimates were not shrunk in the same way, for these six outlying regions the two estimates did not concur and it is possible that our meiotic recombination rate estimates were slightly overestimated (or, respectively, underestimated).

Out of the four remaining outlying windows, three had a low historical recombination rate but did not have particularly extreme meiotic recombination rates, so that the effect of shrinkage is not likely to explain the discrepancy between meiotic and historical recombination rates. Indeed, these three regions corresponded to previously identified selection signatures in sheep: a region on chromosome 6 spanning two intervals between 36 and 38 Mb contains the ABCG2 gene, associated with milk production (Cohen-Zinder et al. 2005), and the LCORL gene associated to stature [recently reviewed in Takasuga (2016)]. This region has been shown to have been selected in the Lacaune breed (Fariello et al. 2014; Rochus et al. 2017). A region spanning one interval on chromosome 10, between 29 and 30 Mb, contains the RXFP2 gene, which is associated with polledness and horn phenotypes (Johnston et al. 2013), is found to be under selection in many sheep breeds (Fariello et al. 2014), and a region on chromosome 13 between 63 and 64 Mb that contains the ASIP gene is responsible for coat color phenotypes in many breeds of sheep (Norris and Whan 2008), and again was previously demonstrated to have been under selection. For these three regions, we explain the low historical recombination estimates by a local reduction of the effective population size due to selection.

Finally, one of the three regions with a high historical recombination rate, on chromosome 20 between 28 and 29 Mb, had a low meiotic recombination rate, so that the effect of shrinkage cannot explain the discrepancy. This region harbors a cluster of olfactory receptor genes and its high historical recombination rate could be explained by selective pressure for increased genetic diversity in these genes (i.e., diversifying selection), a phenomenon that has been shown in other species [e.g., pig (Groenen et al. 2012), human (Ignatieva et al. 2014), and rodents (Stathopoulos et al. 2014)]. Finally, we used the meiotic recombination rates to scale the historical recombination rate estimates and produce high-resolution recombination maps on the HD SNP array (File S4).

Improved male recombination maps by combining Lacaune and Soay sheep data:

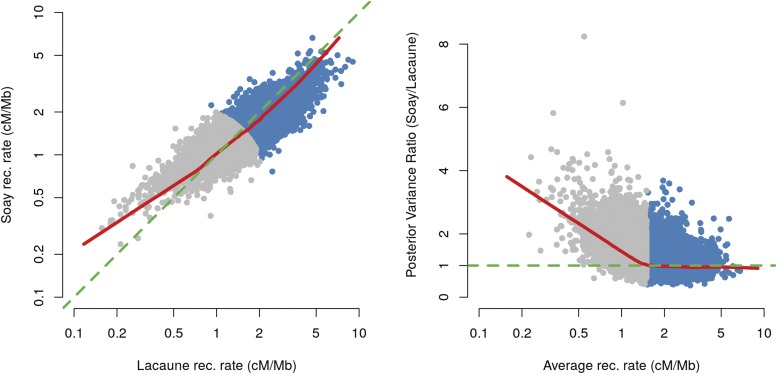
Recently, recombination maps have been estimated in another sheep population, the Soay (Johnston et al. 2016). Soay is a feral population of ancestral domestic sheep living on an island located northwest of Scotland. The Lacaune and Soay populations are genetically very distant, their genome-wide Fst, calculated using the sheep HapMap data (Kijas et al. 2012), being ∼0.4. Combining our results with results from the Soay offered a rare opportunity to study the evolution of recombination over a relatively short timescale as the two populations can be considered to have been separated at most dating back to domestication, ∼10,000 years ago. The methods used in the Soay study are different from those used here, but the two data sets are similar, although the Soay data has fewer male meioses (2604 vs. 5940 in the present study). To perform a comparison that would not be affected by differences in estimation methods, we ran the method developed for the Lacaune data to estimate recombination maps on the Soay data. As the Soay study showed a clear effect of sex on recombination rates, we estimated recombination maps on male meioses only. Figure 4 presents the comparison of recombination rates between the two populations in marker intervals of the medium-density SNP array. The left panel shows that the two populations exhibit very similar recombination rates (r = 0.82, P < 10⁻¹⁶), although Soay recombination rates appear higher for low recombining intervals (c < 1.5 cM/Mb in gray on the figure). We explain this by the shrinkage effect of the prior, which is more pronounced in the Soay as the data set is smaller: the right panel on Figure 4 shows that the posterior variance of the recombination rates are clearly higher in Soays for low recombining intervals while they are similar for more recombining intervals. Overall, our results on the comparison of the recombination maps in the two populations are consistent with the two populations having the same amplitude and distribution of recombination on the genome, at the scale of the medium-density SNP array. Therefore, we analyzed the two populations together to create new male recombination maps based on 302,298 crossovers detected in 8549 meioses (File S5). Combining the two data sets together led to a clear reduction in the posterior variance of the recombination rates, i.e., an increase in their precision (Figure S9 in File S11).

Figure 4.

Comparison of recombination (rec.) rates in Soay and Lacaune populations. Left: scatterplot of posterior means of rec. rates (on a log scale). The green line is the line y = x and the red line is a lowess smoothed line (f = 0.05). Right: Scatterplot of the ratio of posterior variance (Soay/Lacaune) as a function of the average of the posterior mean rec. rates in the two populations (on a log scale). The green line corresponds to equal variances and the red line is a lowess smoothed line (f = 0.05). Points in gray on both panels correspond to intervals with average rec. rate < 1.5 cM/Mb.

Genetic determinism of genome-wide recombination rate in Lacaune sheep

Our data set provides information on the number of crossovers for a set of 5940 meioses among 345 male individuals. Therefore, it allows us to study the number of crossovers per meiosis (GRR) as a recombination phenotype.

Genetic and environmental effects on GRR:

We used a linear mixed model to study the genetic determinism of GRR. The contribution of additive genetic effects was estimated by including a random FID effect with covariance structure proportional to the matrix of kinship coefficients calculated from pedigree records (see Materials and Methods). We also included environmental fixed effects in the model: year of birth of the FID and insemination month of the ewe for each meiosis. We did not find significant differences between the FID year of birth; however, the insemination month of the ewe was significant (P = 1.3 10⁻³). There was a trend in increased recombination rates from February to May followed by a decrease until July and a regain in August, although the number of inseminations in August is quite low, leading to a high SE for this month (Figure S10 in File S11). Based on the estimated variance components (Table 2), we estimated the heritability of GRR in the Lacaune male population at 0.23.

Table 2. Genetic parameters of the interindividual variation in GRR.

Number of Sires	Additive Genetic Variance	Phenotypic Variance	Heritability
345	6.86 (0.75)	29.73 (0.84)	0.23 (0.02)

GWAS identifies three major loci affecting GRR in Lacaune sheep:

The additive genetic values of FIDs, predicted from the above model were used as phenotypes in a GWAS. Among the 345 FIDs with at least two offspring, the distribution of the phenotype was found to be approximately normally distributed (Figure S11 in File S11). To test for association of this phenotype with SNPs markers, we used a mixed model approach correcting for relatedness effects with a genomic relationship matrix (see Materials and Methods). Using our panel of 70 unrelated Lacaune, we imputed the 345 FIDs for markers of the HD SNP array. With these imputed genotypes, we performed two analyses. The first was an association test with univariate linear mixed models, which tested the effect of each SNP in turn on the phenotype (results in File S6); the second fitted a Bayesian sparse linear mixed model, allowing multiple QTL to be included in the model (results in File S7).

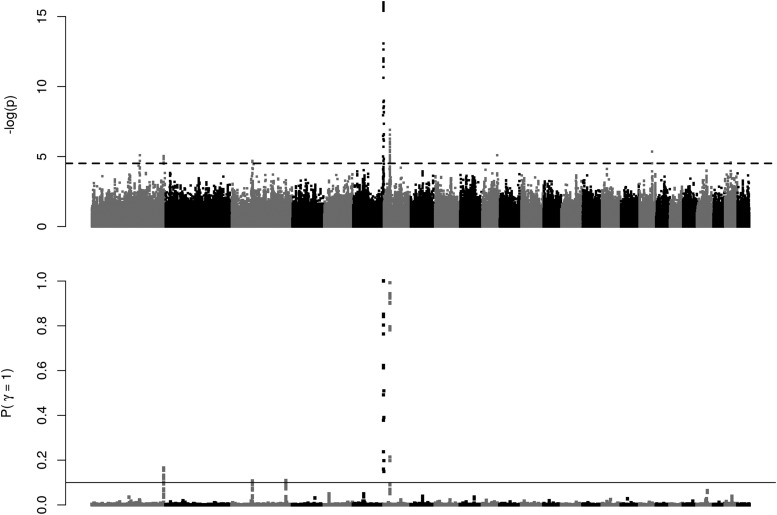
Figure 5 illustrates the GWAS results: the top plot shows the P-values of the single SNP analysis and the bottom plot the posterior probability that a region harbors a QTL, calculated on overlapping windows of 20 SNPs. The single SNP analysis revealed six significant regions (FDR < 10%): two on chromosome 1, one on chromosome 6, one on chromosome 7, one on chromosome 11, and one chromosome 19. Regions of chromosomes 6 and 7 exhibited very low P-values whereas the other three showed less-intense association signals. The multi-QTL Bayesian analysis was conclusive for two regions (regions on chromosome 6 and chromosome 7) while the rightmost region on chromosome 1 was suggestive (Table 3). Two additional suggestive regions were discovered on chromosome 3. Use of the multi-QTL approach of Zhou et al. (2013) led to estimate that, together, QTL explain ∼40% of the additive genetic variance for GRR, with a 95% credible interval ranging from 28 to 53%.

Figure 5.

Genome-wide association study identifies three main QTL for GRR. Top: −log10 (P-value) for single SNP tests for association. The genome-wide significance level (FDR = 5%) is represented by the horizontal dotted line. Bottom: posterior probability that a region of 20 SNPs harbors a QTL, using a Bayesian multi-QTL model. FDR, false discovery rate; GRR, genome-wide recombination rate.

Table 3. SNPs associated with GRR (P-values correspond to the single-SNP Wald test).

Rs Number	Chr	Position (bp)	Minor Allele	p	β	P-Value	pQTL
rs430436336	1	180044043	A	0.11	2.19	8.08 10−6	0.006
rs400472211	1	268670581	A	0.33	0.86	9.41 10−6	0.03
rs418551122	3	75216491	A	0.3	0.76	2.42 10−5	0.04
rs407545143	3	201298545	G	0.24	1.13	9.36 10−4	0.07
rs411987057	6	116517201	C	0.22	−2.3	1.31 10−16	0.19
rs401206888	6	116440663	G	0.14	−1.95	2.04 10−16	0.16
rs412583165	6	116525709	G	0.27	−2.38	9.80 10−17	0.15
rs429477322	6	116509403	A	0.18	−2.17	3.94 10−16	0.11
rs161854895	6	116491013	G	0.22	−2.17	2.53 10−16	0.11
rs398811467	6	116472870	A	0.13	−1.94	2.51 10−16	0.14
rs407110999	7	22859168	G	0.25	1.37	8.71 10−7	0.1
rs413147562	7	22798236	A	0.23	1.61	1.20 10−7	0.71

β corresponds to the effect of SNP (in number of crossover per meiosis) on GRR and pQTL is the probability of the SNP to be a QTL estimated using a Bayesian Sparse Linear Mixed Model (see Materials and Methods). Chr, chromosome; GRR, genome-wide recombination rate.

The most significant region was located on the distal end of chromosome 6 and corresponded to a locus frequently associated with variation in recombination rate. In our study, the significant region contained 10 genes: CTBP1, IDUA, DGKQ, GAK, CPLX1, UVSSA, MFSD7, PDE6B, PIGG, and RNF212. For each of these genes except RNF212, which was not annotated on the genome (see below), we extracted their gene GO of the Ensembl v87 database, but none was clearly annotated as potentially involved in recombination. However, two genes were already reported as having a statistical association with recombination rate: CPLX1 and GAK (Kong et al. 2014). CPLX1 has no known function that can be linked to recombination (Kong et al. 2014) but GAK has been shown to form a complex with cyclin-G, which could impact recombination (Nagel et al. 2012). However, RNF212 can be deemed a more likely candidate due to its function and given that this gene was associated with recombination rate variation in human (Kong et al. 2008; Chowdhury et al. 2009), cows (Sandor et al. 2012; Ma et al. 2015; Kadri et al. 2016), and mice (Reynolds et al. 2013). RNF212 is not annotated in the sheep genome assembly oviAri3; however, this chromosome 6 region corresponds to the bovine region that contains RNF212 (Figure S4 in File S11). We found an unassigned scaffold (scaffold01089, NCBI accession NW_011943327) of O. orientalis musimon (assembly Oori1) that contained the full RNF212 sequence and that could be placed confidently in the QTL region. To confirm RNF212 as a valid positional candidate, we further studied the association of its polymorphisms with GRR in results presented below.

The second most significant region was located between 22.5 and 23.1 Mb on chromosome 7. All significant SNPs in the region were imputed, i.e., the association would not have been found based on association of the medium-density array alone. It matched an association signal on GRR in Soay sheep (Johnston et al. 2016). Consistent with our finding, in the Soay sheep study, this association was only found using regional heritability mapping and not using single SNP associations with the medium-density SNP array. This locus could match previous findings in cattle (association on chromosome 10 at ∼20 Mb on assembly btau3.1); however, the candidate genes mentioned in this species (REC8 and RNF212B) were located 2 and 1.5 Mb away from our strongest association signal, respectively. In addition, none of the SNPs located around these two candidate genes in cattle were significant in our analysis. Eleven genes were present in the region: OR10G2, OR10G3, TRAV5, TRAV4, SALL2, METTL3, TOX4, RAB2B, CHD8, SUPT16H, and RPGRIP1. The study of their GO, extracted from the Ensembl v87 database, revealed that none of them were associated with recombination, although SUPT16H could be involved in mitotic DSB repair (Kari et al. 2011). However, another functional candidate, CCNB1IP1, also named HEI10, was located between positions 23,946,971 and 23,951,850 bp, ∼500 kb from our association peak. This gene is a good functional candidate as it has been shown to interact with RNF212: HEI10 allows the elimination of the RNF212 protein from early recombination sites and the recruitment of other recombination intermediates involved in crossover maturation (Qiao et al. 2014; Rao et al. 2016). Again, SNPs located at the immediate proximity of HEI10 did not exhibit significant associations with GRR. Hence, our association signal did not allow us to pinpoint any clear positional candidate among these functional candidates (see Figure S12 in File S11). However, it was difficult to rule them out completely for three reasons. First, with only 345 individuals, our study may not be powerful enough to localize QTL with the required precision. Second, the presence of causal regulatory variants, even at distances of several 100 kb, is possible. Finally, the associated region of HEI10 exhibited apparent rearrangements with the human genome, possibly due to assembly problems in oviAri3. These assembly problems could be linked to the presence of genomic sequences coding for the T-cell receptor α chain. This genome region is in fact rich in repeated sequences, making its assembly challenging. Overall, identifying a single positional and functional candidate gene in this gene-rich misassembled genomic region was not possible based on our data alone.

Our third associated locus was located on chromosome 1 between 268,600 and 268,700 kb. In cattle, the homologous region, located at the distal end of cattle chromosome 1, has also been shown to be associated with GRR (Ma et al. 2015; Kadri et al. 2016). In these studies, the PRDM9 gene has been proposed as a potential candidate gene, especially because it is a strong functional candidate given its proven effect on recombination phenotypes. In sheep, PRDM9 is located at the extreme end of chromosome 1, ∼275 Mb, 7 Mb away from our association signal (Ahlawat et al. 2016). Hence, PRDM9 was not a good positional candidate for association with GRR in our sheep population. However, the associated region on chromosome 1 contains a single gene, KCNJ15, which has been associated with DNA DSB repair in human cells (Słabicki et al. 2010).

Finally, the two regions on chromosome 3 were analyzed. The first was located between 75,162 and 75,319 kb and contains only one annotated gene coding for the receptor for follicle-stimulating hormone (FSHR). Although it does not affect recombination directly, it is necessary for the initiation and maintenance of normal spermatogenesis in males (Tapanainen et al. 1997). The second region on the chromosome 3 was located between 201,198 and 201,341 kb but does contain any annotated gene.

Mutations in the RNF212 gene are strongly associated to genome-wide recombination rate variation in Lacaune sheep:

The QTL with the largest effect in our association study corresponded to a locus associated with GRR variation in other species and harboring the RNF212 gene. As it was a clear positional and functional candidate gene, we carried out further experiments to interrogate specifically polymorphisms within this gene. As stated above, we used the sequence information available for the RNF212 gene from O. orientalis, which revealed that RNF212 spanned 23.7 kb on the genome and may be composed of 12 exons by homology with bovine RNF212. However, mRNA annotation indicated multiple alternative exons. Surprisingly, the genomic structure of ovine RNF212 was not well-conserved with goat, human, and mouse syntenic RNF212 genes (Figure S4 in File S11). As a first approach, we designed primers for PCR amplification (see Materials and Methods) and sequencing of all annotated exons and some intronic regions corresponding to exonic sequences of C. hircus RNF212. By sequencing RNF212 from four carefully chosen Lacaune animals homozygous for GG or AA at the most significant SNP of the medium-density SNP array on chromosome 6 QTL (rs418933055, P-value 2.56 10⁻¹⁷), we evidenced four polymorphisms within the ovine RNF212 gene (two SNPs in intron 9 and two SNPs in exon 10). The four mutations were genotyped in 266 individuals of our association study. We then tested their association with GRR using the same approach as explained above (results in File S8) and computed their LD (genotypic r²) with the most associated SNPs of the high-density genotyping array (see Figure S13 in File S11) (Table 4). Two of these mutations were found to be highly associated with GRR, their P-values being of the same order of magnitude (P < 10⁻¹⁶) as the most associated SNP (rs412583165), and one of them was even more significant than the most significant imputed SNP (P = 6.25 10⁻¹⁷ vs. P = 9.8 10⁻¹⁷). We found a clear agreement between the amount of LD between a mutation and the most associated SNPs and their association P-value (see Figure S13 in File S11). Overall, these results showed that polymorphisms within the RNF212 gene were strongly associated with GRR, and likely tagged the same causal mutation as the most associated SNP. This confirmed that RNF212, a very strong functional candidate, was also a very strong positional candidate gene underlying our association signal.

Table 4. Association of GRR with mutations in the RNF212 gene.

Mutation Name	Base Change	Positions on OA Musimon Genome (Scaffold 01089)	Predicted Positions on v3.1 Sheep Genome (OAR6)	p	β	P-Value	pQTL
RNF212_14431_AG	A $>$G	132229	116438514	0.18	−3.98	6.25 10−17	0.23
RNF212_18411_GA	G $>$A	136209	116442624	0.17	−5.58	4.93 10−15	0.02
RNF212_22570_CG	C $>$G	140368	116446753	0.18	−3.94	4.61 10−16	0.09
RNF212_22594_AG	A $>$G	140392	116446777	0.17	0.57	0.54	0.004

Association of mutations in the RNF212 gene with GRR in 345 individuals. Positions on different reference sequences as well as predicted positions on OAR v3.1 are indicated. p: allele frequency β: allele substitution effect. pQTL: probability that the SNP is a QTL after fitting a Bayesian sparse linear mixed model on the region (see details in the text). OA, O. aries reference genome; GRR, genome-wide recombination rate.

The genetic determinism of recombination differs between Soay and Lacaune males

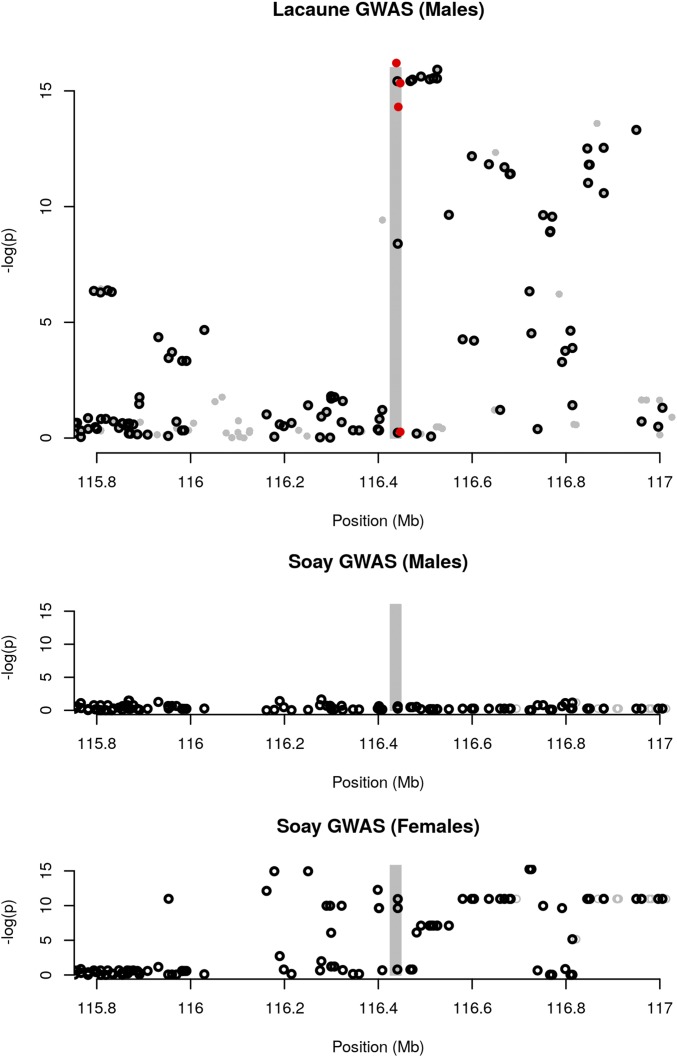
GWAS in the Soay identified two major QTL for GRR, with apparent sex-specific effects. These two QTL were located in the same genomic regions as our QTL on chromosome 6 and chromosome 7. The chromosome 6 QTL was only found to be significant in Soay females, while we detected a very strong signal in Lacaune males. Although the QTL was located in the same genomic region, the most significant SNPs were different in the two GWAS (Figure 6). Two possible explanations could be offered for these results: either the two populations have the same QTL segregating and the different GWAS hits correspond to different LD patterns between SNPs and QTL in the two populations, or the two populations have different causal mutations in the same region. Denser genotyping data, for example by genotyping the RNF212 mutations identified in this work in the Soay population, would be needed to have a clear answer. For the chromosome 7 QTL, the signal was only found using regional heritability mapping (Nagamine et al. 2012) in the Soay, and after genotype imputation in our study, which makes it even more difficult to discriminate between a shared causal mutation or different causal mutations at the same location in the two populations.

Figure 6.

Comparison of GWAS results for the chromosome 6 QTL in Lacaune Males (top), Soay Males (middle), and Soay Females (bottom) The shaded area highlights the predicted position of the RNF212 gene. Circle dots are markers tested in both populations. Red dots are the new mutations within the RNF212 gene discovered in this study and genotyped in the Lacaune population. GWAS results in the Soay are from Johnston et al. (2016). GWAS, genome-wide association study.

Discussion

In this work, we studied the distribution of recombination along the sheep genome and its relationship to historical recombination rates. We showed that contemporary patterns of recombination are highly correlated to the presence of historical hotspots. We showed that the recombination patterns along the genome are conserved between distantly related sheep populations but that their genetic determinism of genome-wide recombination rates differ. In particular, we showed that polymorphisms within the RNF212 gene are strongly associated to male recombination in Lacaune, whereas this genomic region shows no association in Soay males. Hence, combining three data sets, two pedigree data sets in distantly related domestic sheep populations and a densely genotyped sample of unrelated animals, revealed that recombination rate and its genetic determinism can evolve at short timescales, as we discuss below.

Fine-scale recombination maps

In this work, we were able to construct fine-scale genetic maps of the sheep autosomes by combining two independent inferences on recombination rate. Our study on meiotic recombination from a large pedigree data set revealed that sheep recombination exhibits general patterns similar to other mammals (Shifman et al. 2006; Chowdhury et al. 2009; Tortereau et al. 2012). First, sheep recombination rates were elevated at the chromosome ends, both on acrocentric and metacentric chromosomes. In the latter, our analysis revealed a clear reduction in recombination near centromeres. Second, recombination rate depended on the chromosome physical size, consistent with an obligate crossover per meiosis irrespective of the chromosome size. These patterns were consistent with those established in a very different sheep population, the Soay (Johnston et al. 2016), and indeed when reanalyzing the Soay data with the same approach as used in this study, the results showed a striking similarity between recombination rates in the two populations. Hence, our results show that recombination patterns were conserved over many generations, despite the very different evolutionary histories of the two populations and clear differences in the genetic determinism of GRR in males of the two populations. This similarity allowed us to combine the two data sets to create more precise male sheep recombination maps than any of the two studies taken independently.

Our historical recombination maps revealed patterns of recombination at the kilobase scale, with small, highly recombining intervals interspaced by more wide, low recombining regions. This result was consistent with the presence of recombination hotspots in the highly recombinant intervals. A consequence was that, as observed in other species, the majority of recombination took place in a small portion of the genome: we estimated that 80% of recombination takes place in 40% of the genome. Kaur and Rockman (2014) suggested the use of a Gini coefficient as a measure of the heterogeneity in the distribution of recombination along the genome to facilitate interspecies comparisons. When calculated on the historical recombination data, the Lacaune sheep has a coefficient of 0.52, which is similar to what is observed in Drosophila but lower than that measured in humans or mice. However, the coefficient calculated here is likely an underestimate due to our limited resolution (a few kilobases on the HD SNP array) compared to the typical hotspot width (a few hundred base pairs). Overall, we identified 50,000 hotspot intervals, which was twice the estimated number of hotspots in humans (International HapMap Consortium et al. 2007). This difference can be explained by different nonmutually exclusive reasons. First, it is possible that what we detect as crossover hotspots are due to genome assembly errors, and we indeed found a significant albeit moderate effect (odds ratio = 1.4) of the presence of assembly gaps in an interval on its probability of being called a hotspot. Second, our method to call hotspots could be too liberal. Indeed, a more stringent threshold (FDR = 0.1%) would lead to ∼25,000 hotspots, which would be similar to what is found in humans. Third, selection has been shown to impact hotspot discoveries, although not with the methods that we used here (Chan et al. 2012). Finally, there exists the possibility that sheep historically exhibit more recombination hotspots than humans. In any case, the strong association between meiotic recombination rate and density in historical hotspots showed that our historical recombination maps were generally accurate. We tried to find enrichment in sequence motifs in the detected hotspots or specify their position relative to TSS (data not shown), but with no success mainly due to (i) the relative large hotspot intervals (∼5 kb) compared to typical hotspot motifs and (ii) the quality of the sheep genome assembly, which still contains many small gaps that make such analyses difficult. Ultimately, these questions would need an improved genome assembly and better resolution of crossover hotspots, which should be addressed in the future from LD-based studies on resequencing data.

We combined, using a formal statistical approach, meiotic- and LD-based recombination rate estimates. Using an approach conceptually similar to that of O’Reilly et al. (2008) led us to assess the impact of selection events on the sheep genome, in particular suggesting the possibility of an effect of diversifying selection at olfactory receptor genes. Based on this comparison, the correlation between historical and meiotic recombination rates was found to be high (r 0.7), but less than could be expected from previous results in humans, where the correlation was 97% on 5 Mb (Myers et al. 2006). However, it was closer to that of worms(Rockman and Kruglyak 2009), mice (Brunschwig et al. 2012), or Drosophila (Chan et al. 2012), 69, 47, and 50%, respectively. Again, more precise estimates of both meiotic and historical recombination rates could change this number but other causes can be put forward.

A first explanation could come from the fact that the model we used to estimate historical recombination rates is based on the assumption of a constant effective population size, both in the past and along the genome. To allow for varying population size along the genome, we estimated the model in 2-Mb intervals, but there is still a possibility that varying population size in the past affected our historical recombination rate estimates, as the method has been shown to be somewhat influenced by demography, although much less so for the identification of crossover hotspots (Li and Stephens 2003). Also, as already mentioned above, selection has been shown to have a substantial impact on the estimation of recombination rates with other approaches (Chan et al. 2012), although it has not been evaluated for the Li and Stephens (2003) model to our knowledge.

Second, our meiotic recombination maps are based on male meioses only, while historical recombination rates are averaged over both male and female meioses. The fact that male and female recombination differ substantially, particularly in sheep (Johnston et al. 2016), could also explain this relatively lower correlation.

Third, it is also possible that selective pressure due to domestication and later artificial breeding had the impact of modifying extensively LD patterns on the sheep genome, degrading the correlation between the two approaches. Indeed, the historical recombination estimates summarize ancestral recombinations that took place in the past and it is possible that recombination hotspots that were present in an ancestral sheep population are no longer active in today’s Lacaune individuals. This could arise, for example, if domestication led to a reduction in the diversity of hotspots defining genes, such as PRDM9, and hence a reduction in the number of motifs underlying hotspots, which would in turn change the distribution of recombination on the genome. For example, this has been shown in humans, where patterns of recombination differ between populations due to their different diversity at PRDM9 (Baudat et al. 2010; Berg et al. 2010, 2011). Eventually, such a phenomenon would degrade the correlation between present day recombination (measured by the meiotic recombination rates) and past recombination (measured by historical recombination rates). Further studies on the determinism of hotspots in sheep, their related genetic factors, and their diversity would be needed to elucidate this question.

Despite these different effects, the substantial correlation between meiotic and historical recombination rates motivates the creation of scaled recombination maps that can be useful for interpreting statistical analysis of genomic data. As an illustration of the importance of fine-scale recombination maps for genetic studies, we found an interesting example in a recent study on the adaptation of sheep and goats (Kim et al. 2016). In this study, a common signal of selection was found using the integrated Haplotype Score (iHS) statistic (Voight et al. 2006) in these two species (Figure 5 in Kim et al. (2016)). This signature precisely matches the low recombining regions that we identified on chromosome 10. However, the iHS statistic has been shown to be strongly influenced by variation in recombination rates, and in particular to tend to detect low recombining regions as selection signatures (O’Reilly et al. 2008; Ferrer-Admetlla et al. 2014). Precise genetic maps such as the one we provide in this work could thus help in annotating and interpreting such selection signals.

Determinism of recombination rate in sheep populations

As mentioned in the introduction, two phenotypes have been studies with respect to the recombination process, but only one was studied here, GRR. We found that our data were not sufficient to study the Individual Hotspot Usage, which requires either a larger number of meioses per individual (Sandor et al. 2012; Ma et al. 2015; Kadri et al. 2016) or denser genotyping in families (Coop et al. 2008).

Our approach to study the genetic determinism of GRR in the Lacaune population was first to estimate its heritability, using a classical analysis in a large pedigree. This analysis also allowed us to extract additive genetic values (EBVs) for the trait in 345 male parents, which we used for a GWAS in a second step. The EBVs are, by definition, only determined by genetic factors, as environmental effects on GRR are averaged out. Indeed, we found that the proportion of variance in EBVs explained by genetic factors in the GWAS was essentially one. A consequence was that, although this sample size could be deemed low by current standards, the power of our GWAS was greatly increased by the high precision on the phenotype. We estimated the heritability of GRR at 0.23, which was similar to estimates from studies on the same phenotype in ruminants [e.g., 0.22 in cattle (Sandor et al. 2012) or 0.12 in male Soay sheep (Johnston et al. 2016), but see below for a discussion on the comparison with Soay sheep]. We had little information on the environmental factors that could influence recombination rate, but did find a suggestive effect of the month of insemination on GRR; in particular, we found increased GRR in the month of May. Confirmation and biological interpretation of this result would need dedicated studies, but it was consistent with the fact that fresh (i.e., not frozen) semen is used for insemination in sheep and that the reproduction of this species is seasonal (Rosa and Bryant 2003).

The genetic determinism of GRR discovered in our study closely resembles what has been found in previous studies, especially in mammals. Two major loci and two suggestive ones affected the recombination rate in Lacaune sheep. The two main QTL are common to cattle and Soay sheep. The underlying genes and mutations for these two QTL are not yet resolved, but the fact that the two regions harbor interacting genes [RNF212 and HEI10 (Qiao et al. 2014; Rao et al. 2016)] involved in the maturation of crossovers makes these two genes likely functional candidates. Indeed, these two genes were identified as potential candidates underlying QTL for GRR in mice (Wang and Payseur 2017). The third gene identified here, KCNJ15, is a novel candidate, and its role and mechanism of action in the repair of DSBs needs to be confirmed and elucidated. Interestingly, these three genes are linked to the reparation of DSBs and crossover maturation processes. Finally, the fourth candidate FSHR has well-documented effects on gametogenesis but has not previously been linked to recombination.

In our study, 60% of the additive genetic variance in GRR remained unexplained by large-effect QTL and were due to polygenic effects. This could be interpreted in the light of recent evidence that has shown that other mechanisms, involved in chromosome conformation during meiosis, explain a substantial part of the variation in recombination rate between mouse strains (Baier et al. 2014) and bovids (Ruiz-Herrera et al. 2017). Furthermore, the variations at the major mammal recombination loci (RNF212, CPLX1, and REC8 or the Human inversion 17q21.31) explain only 3 to 11% (Ritz et al. 2017) of the phenotypic variance among individuals. Elucidating the genetic determinism of these different processes would thus require much larger sample sizes or different experimental approaches (Baier et al. 2014; Ruiz-Herrera et al. 2017).

The combination of data sets from the Lacaune population and one from the recent study of recombination in Soay sheep (Johnston et al. 2016) allowed us to study the evolution of recombination at relatively short timescales. One of the most striking differences between our two studies is that the two QTL that were detected to be in common had no effect in Soay males, whereas they had strong effects in Lacaune males. However, the two populations had very similar polygenic heritability; accounting for the fact that the Lacaune QTL explain ∼40% of the additive genetic variance, we could estimate the polygenic additive genetic variance in Lacaune males at 0.16, very similar to the 0.12 found in Soay males. Combined with our results that the two populations exhibit very similar male recombination maps, both in terms of intensity and genome distribution, the combination of the two studies shows that recombination patterns are conserved between populations under distinct genetic determinism, highlighting the robustness of mechanisms that drive them. We note that this robustness concerns recombination at a relatively broad scale (in the order of 10–100 kb), so it does not necessarily mean that the two breeds share recombination hotspots. Further work is needed to get a more detailed picture of the genetic control of recombination in sheep and will likely require the combination of multiple inferences from genetics, cytogenetics, molecular biology, and bioinformatics analyses.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300123/-/DC1.