A Parallel-Plate Flow Chamber for Mechanical Characterization of Endothelial Cells Exposed to Laminar Shear Stress

Abstract

Shear stresses induced by laminar fluid flow are essential to properly recapitulate the physiological microenvironment experienced by endothelial cells (ECs). ECs respond to these stresses via mechanotransduction by modulating their phenotype and biomechanical characteristics, which can be characterized by Atomic Force Microscopy (AFM). Parallel Plate Flow Chambers (PPFCs) apply unidirectional laminar fluid flow to EC monolayers in vitro. Since ECs in sealed PPFCs are inaccessible to AFM probes, cone-and-plate viscometers (CPs) are commonly used to apply shear stress. This paper presents a comparison of the efficacies of both methods. Computational Fluid Dynamic simulation and validation testing using EC responses as a metric have indicated limitations in the use of CPs to apply laminar shear stress. Monolayers subjected to laminar fluid flow in a PPFC respond by increasing cortical stiffness, elongating, and aligning filamentous actin in the direction of fluid flow to a greater extent than CP devices. Limitations using CP devices to provide laminar flow across an EC monolayer suggest they are better suited when studying EC response for disturbed flow conditions. PPFC platforms allow for exposure of ECs to laminar fluid flow conditions, recapitulating cellular biomechanical behaviors, whereas CP platforms allow for mechanical characterization of ECs under secondary flow.

Introduction

Vascular endothelial cells (ECs) line the circulatory system and have unique functions within vascular biology. Endothelial dysfunction is recognized as an early event in the pathogenesis of cardiovascular disease⁸. EC monolayers, located at the interface between circulating blood in the lumen and the vessel wall are constantly subjected to shear stresses caused by blood flow¹⁶. Such mechanical stimuli elicit various cellular responses, including changes in gene expression and protein alterations that determine cellular activity¹⁰. Moreover, mechanical stimuli, through mechanotransduction, cause ECs to exhibit a change in their phenotypical, morphological, and mechanical properties^4,15,25,32. This includes the alignment of filamentous actin (F-actin) in the direction of fluid flow, stiffness increases of the cell, and changes in surface topography characteristics. The actin cytoskeleton is imperative in the cell’s ability to both generate and sense external forces. Recently, it has been shown that actin filaments act as mechanosensors, and transmit mechanical tension to other proteins²⁴. The actin cytoskeleton therefore plays an integral role in mechanotransductory pathways. To more fully understand these pathways, cellular responses to physiological stimuli, such as shear stress, must be explored¹³.

Atomic Force Microscopy (AFM) has become a popular tool to study the mechanical responses of cells^11,27,30. In AFM contact mode, a laser is reflected off the back of a thin cantilever with a tip fixed to the front of the free end. Contact between the tip and a sample causes deflection of the cantilever, which is interpreted by a position-sensitive diode that tracks the laser’s reflection and provides a feedback. This deflection is interpreted though the application of a contact model that uses the geometry of the tip and the AFM measurements to calculate the viscoelastic properties of the sample. AFM is a powerful tool to study EC mechanotransductory responses to shear stresses since its ability to measure stiffness is useful for interrogating the conformational changes and the physiological state of a cell^17,29.

Cone-and-plate viscometers are used in the application of shear stress onto adherent cells for AFM purposes^6,9,26. Typically, ECs are seeded onto polystyrene slides, and then subjected to shear stress from fluid flow induced by the rotating cone. The use of slides allows easy access to the cell monolayer by an AFM probe, making it a convenient tool for characterizing mechanical properties of the monolayer after fluid flow conditions.

Applied shear stress, τ, from a cone-and-plate device can be accurately modeled with eq. 1:

$${\tau }_{r\theta }=\frac{\mu \varpi }{\alpha }(1+2.58(\frac{{\stackrel{\sim }{R}}^{\frac{2}{3}}}{3.5+\stackrel{\sim }{R}})-0.86(\frac{{\stackrel{\sim }{R}}^{\frac{5}{2}}}{{(3.5+\stackrel{\sim }{R})}^2}\left)\right)$$ (1)

where R̃ is the effective Reynolds Number, μ is the viscosity of the fluid, ω is the angular velocity of the cone, and α is the cone angle¹⁸.

Alternatively, parallel plate flow chambers (PPFCs) are also used to create fluid shear stresses on various cell types, including adherent cell monolayers such as ECs. By ensuring fully developed laminar shear stress, PPFCs can simulate fluid flow that ECs experience in a physiological environment³. Commercially available PPFCs are often sealed units. Hence, the EC monolayer cannot be physically contacted by the AFM probe. To this end, we designed an AFM-compatible PPFC based on the governing equations that describe laminar flow between two parallel plates.

By simplifying and rearranging terms in the Navier-Stokes equations (eq. 2), we can describe shear stresses on parallel plates

$$\frac{d^{2}u}{{\mathit{\text{dy}}}^2}=\frac{1}{\mu }\frac{\mathit{\text{dP}}}{\mathit{\text{dx}}}$$ (2)

where (dP/dx) is the pressure gradient parallel along the plates, and μ is the fluid viscosity, u is fluid velocity, and y is a height position with respect to either the center plane or the bottom plate. Integrating twice, and applying boundary conditions (eq. 3), yields:

$$u=\frac{1}{2\mu }\left(\frac{\mathit{\text{dP}}}{\mathit{\text{dx}}}\right)[{\left(\frac{h}{2}\right)}^2-y^2]$$ (3)

By integrating over the height of the chamber, h, and noting that wall shear stress, τ, is described as τ=μ(du/dy), we can express shear stress between stationary parallel plates as a function of volumetric flow of the fluid, Q, as shown in eq. 4:

$${\tau }_{\mathit{\text{wall}}}=\frac{6\mu Q}{{\mathit{\text{bh}}}^2}$$ (4)

where τ_wall is the shear stress at the plate where the EC monolayer is located. This equation is used to determine the magnitude of shear stresses within a PPFC.

Physiologically, these forces from the wall shear stress are transmitted by the cellular cortex, the most peripheral region of the cytoplasm. Thus, the cellular cortex is integral to cell mechanics and mechanotransduction, and is a target of study for AFM²⁰. Since AFM compatible PPFC devices are not commercially produced, here we present a PPFC specifically for AFM and related applications to investigate the role of shear stresses on ECs.

Materials and methods

Design of PPFC Ensures Laminar Flow over EC Monolayers

The design of many PPFCs are not compatible with an atomic force microscope, as it does not allow the EC monolayer to be exposed to the probe needed for analysis^5,16. To effectively study the EC response to shear via AFM, there must be a reliable means of applying shear stress from laminar fluid flow to the EC monolayer that can be accessible to the AFM.

A new PPFC was designed to create a laminar flow profile along the EC monolayer, demonstrated by the Reynolds’ Number (Re), shown in eq. 5:

$$\mathrm{\text{Re}}=\frac{Q\rho }{\mu b}$$ (5)

where Q is the volumetric flow rate of the fluid, ρ is the density of the fluid, μ is the dynamic viscosity of the fluid, and b is the width of the chamber²¹. Generally, Re < 1400 is considered laminar. Calculations show that at the maximum volumetric flow rate applied, Re is sufficiently below this threshold. For cone-and-plate experiments, an equivalent τ_wall was selected to compare the EC response to each of these two devices. The corresponding angular velocity yielded a R̃ value of 0.143, which is considered laminar (Table 1).

Table 1.

Volumetric flows and Reynold number (Re) at various shear stresses for the PPFC and the Cone-and-Plate

PPFC			Cone-and-Plate
τ (dyn cm−2)	Q (mL min−1)	Re	τ (dyn cm−2)	Velocity (rad sec−1)	R̃
1.000	1.783	1.298	1.000	1.746	0.018
2.000	3.566	2.597	2.000	3.490	0.036
3.000	5.348	3.895	3.000	5.320	0.054
4.000	7.131	5.194	4.000	6.971	0.072
5.000	8.914	6.492	5.000	8.706	0.089
6.000	10.697	7.791	6.000	10.438	0.107
7.000	12.479	9.089	7.000	12.165	0.125
8.000	14.262	10.388	8.000	13.888	0.143
9.000	16.045	11.686	9.000	15.606	0.160
10.000	17.828	12.985	10.000	17.319	0.178
11.000	19.610	14.283	11.000	9.027	0.198
12.000	21.393	15.582	12.000	20.729	0.213

Positioning of the inlet was set at a sufficient distance from the slide to ensure that fully developed laminar flow occurs before reaching the EC monolayer. This distance is calculated in eq. 6:

$$L_{\mathit{\text{entry}}}=0.04h\ast \mathrm{\text{Re}}$$ (6)

where Re is the Reynolds number, h is the distance between parallel plates, and L_entry is the length from inlet to fully developed laminar flow¹². Minimum L_entry is calculated to be 0.07 mm, well below the 25.91 mm from the inlet to the slide (Fig. 1a,b). Therefore, the EC monolayer is ensured to see fully developed laminar flow, under conditions more closely resembling the correct in vivo microenvironment. Lastly, the ratio of the width of the plate, b, to height, h, must be greater than 20 to ensure that at least 85% of the surface is exposed to a homogenous shear stress³. Aspect ratio is calculated to be 198, well above the minimum recommended aspect ratio (b=25.15 mm, h=0.13 mm).

FIGURE 1.

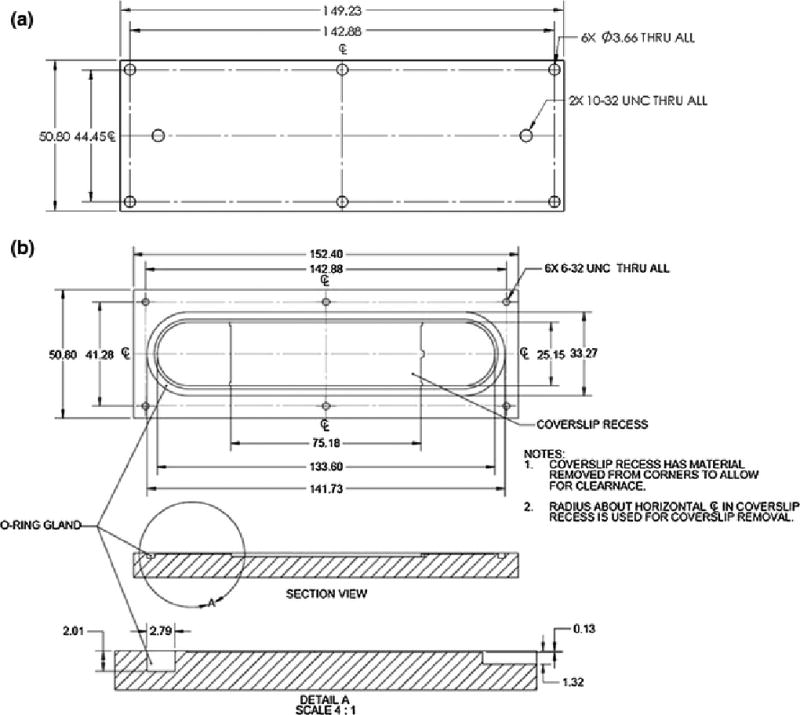
Schematic diagram of the PPFC (a) top plate and (b) base. Base has a recess to accommodate a coverslip. The recess has material removed from corners to allow for clearance, and that the radius about the horizontal centerline is used for removal of the coverslip containing the EC monolayer.

To prevent leakage of the PPFC, an O-ring gland was designed in accordance with ISO 3601 (Fluid Power Systems- O-rings) for an AS568A-154 Silicone O-ring (Parker Hannifan, Hauppauge, NY). To ensure biocompatibility of the PPFC with adherent cells, 316L stainless steel (Southern Tool Steel, Chattanooga, TN) was selected for the parallel plates, and Silicone was selected for the O-ring material. Engineering Drawings (Fig. 1a,b) show dimensions of each component. Both components of the PPFC were fabricated using a computer numerically controlled milling machine (Hardinge, Inc. Elmira, NY). Coated Carbide end mills were used to form the 316L stainless steel giving it its desired dimensional attributes.

Ensuring Laminar Flow over EC monolayers using cone-plate methods

The cone-and-plate device positions a rotating cone such that the tip of the cone is on the same plane as the cells. The rotation of the cone creates streamlines in the fluid that are assumed to resemble concentric circles, i.e. azimuthal², with some secondary flow in the radial direction. The velocity profile and shear rate below the cone are similar to Couette flow². Therefore, the cone-and-plate device can be used to create an effectively laminar flow profile of EC monolayers, simulating the microenvironment within linear areas of the vasculature, such as capillaries³¹. Laminar flow in these platforms is largely dependent on the effective Reynolds number, R̃, which is a unitless comparator of viscus and inertial forces in the system as calculated by eq.1. When R̃ ≥ 0.5, turbulent components start to develop, transitioning into fully turbulent flow. When R̃ = 4, fully turbulent flow exists⁹. R̃ can be described as:

$$\stackrel{\sim }{R}\equiv \frac{r^2\omega {\alpha }^2}{12\nu }$$ (7)

where r is the radius of the cone, ω is the angular velocity of the cone, α is the cone angle, and ν is the kinematic viscosity of the fluid¹⁸. To minimize this effective Reynold’s number the cone-and-plate system the cone angle is minimized. This allows the same levels of shear stress to be imparted on the cells using a lower angular velocity but also magnifies error in cone positioning¹⁸. On the extreme end, a cone with a very low cone angle will not give enough space beneath it to fit the cells. We selected parameters such that the EC monolayers are subjected to laminar fluid flow (R̃ =0.143). A 40 mm stainless steel cone with a cone angle of 0.0176 radians was controlled by the Discover HR-2 Hybrid Rheometer to impart a shear stress. The rheometer maintained a constant height for the cone which was calibrated before every experiment.

Endothelial Cell Culture

Primary human umbilical vein endothelial cells (HUVECs), a generous gift from Dr. Shahin Rafii from the Weill Cornell Medical College, were cultured in tissue culture treated polystyrene flasks (Corning, Corning, NY) in Medium 199/EBSS (Hyclone, Logan, Utah), supplemented with 20% fetal bovine serum (Hyclone), endothelial mitogen (Biomedical Technologies, Inc., Stoughton, MA), heparin (Sigma-Aldrich, St. Louis, MO), L-glutamine (Gibco, Grand Island, NY), HEPES buffer (Gibco, Grand Island, NY), and penicillin/streptomycin (Corning, Corning, NY). HUVECs were then seeded onto gelatin coated polystyrene slides (Nalge Nunc International, Naperville, IL) (75mm × 25mm) and incubated at 37°C for 24 hours. Several experiments from HUVECs obtained from three different umbilical cords were used for this study.

Applying Shear Stress to EC Monolayers

All PPFC components were placed in an autoclave instrument sterilization bag, and then subjected to an instrument sterilization protocol (135°C for 25 minutes). In a biosafety cabinet, the O-ring was inserted into the gland, a slide with a HUVEC monolayer was inserted into the base inlay, barbed fittings were attached to the inlet and outlet of the top plate, and then the top plate was fitted onto the bottom plate assembly. A 10 mL syringe was filled with media, and a 1/8 in ID tubing was attached to the syringe luer and PPFC inlet. Media was gently added through the inlet until the internal volume was filled, and then the tube was clamped. The syringe plunger was removed and covered with parafilm, which acted as a reservoir. Next, a peristaltic pump was attached to the PPFC such that the inlet of the pump was connected to the outlet of the PPFC, and the outlet of the PPFC fed into the reservoir. All tubing was then unclamped and fluid flow allowed shear stresses to be applied to the HUVEC monolayer, where ECs were exposed to shear stresses of 0.8 Pa (8 dyn cm⁻²) for 15 hours. Immediately after an experiment was terminated, the PPFC was disassembled, and static and sheared monolayers were fixed with 4% paraformaldehyde (37°C for 20 minutes) for AFM measurements and imaging.

For cone-and-plate devices, HUVECs were cultured as described above, and then subjected to the same shear stresses as the PPFC for 15 hours. The slides were held in place by a custom 3-D printed base plate through the use of friction and capillary action. The plate was housed in a media containing 80 mm dish centered on a Peltier plate which controlled temperature at 37°C. The dish was covered with a custom 3-D printed top plate and parafilm around the edges to prevent evaporation from the system. A cone diameter of 40 mm was selected to ensure that both coverslips in the system lie under the cone and therefore are exposed to shear stresses.

Quantification of EC Alignment

To quantify EC alignment in both systems, bright field images were taken of the fixed monolayers using a Zeiss Axio Vert.A1 (Carl Zeiss, Thornwood, NY), lengths and widths of 20 randomly selected cells per experiment in the monolayer were measured using ImageJ, and then the aspect ratios of cells were calculated. To determine whether or not there is any significant change in phenotype when exposed to shear stresses, a Wilcoxon Rank Sum test was used to compare aspect ratios of both control and sheared monolayers for the PPFC and the cone-and-plate device (α=0.001).

F-Actin Alignment Quantification

F-actin was labeled with rhodamine phalloidin to demonstrate changes in cytoskeletal structure. DAPI nuclear counter-stain was used to identify individual cells and VE-Cadherin was stained with Alexa 488 to show that the primary cells are distinctly endothelial. Cells were imaged on an inverted Zeiss Axio Observer microscope. Quantification of actin filament alignment was performed on a grayscale image of the actin filaments using ImageJ to determine principle direction of fiber alignment¹. Using the ImageJ Oval-Profile plugin, authored by Bill O’Connell, pixel intensities from a 2D fast Fourier transform (FFT) were summed along the radius of a projected circle for 0 through 360 degrees. Normalized intensity summations were plotted against the angle of acquisition. Maximums were then taken of the alignment plot to determine fiber orientation within the image. Maxima of alignment plots represent the principle angle of fiber alignment. Magnitude and shape of these peaks describe to what degree fibers are aligned. For example, multiple alignment angles will appear as a plateau on the alignment plot. For each experiment, five ROIs per condition were selected, yielding a minimum of 30 cells imaged per experiment.

Atomic Force Microscopy Measurements

An MFP-3D-Bio AFM (Asylum Research, Santa Barbara, CA) was used to take 90 × 90 μm force maps (Fig. 2a–d) of selected regions of interest within each sample. Each force map includes a 32×32 grid of separate force curves which were each acquired using a trigger point of 200 pN and indenting 250 nm at a rate of 600 nm s⁻¹. Force curves can be fitted with different theoretical models in order to accurately estimate the elastic modulus of cell components²³. Thus, in order to calculate cortical stiffness, the first 100 nm of indentation in the force curves were fitted with the Hertz-Sneddon model with a pyramidal indenter³³. Data was collected on a minimum of 12 cells per condition for each experiment, as each ROI contained at least three cells from the monolayer. In addition to determining stiffness distributions of these monolayers, AFM imaging (Fig. 3a–d) was performed. 90×90 μm images were taken at .10Hz with a spacing of 0.352 μm between lines. All stiffness measurements were taken with TR400PB silicon nitride pyramidal tips with a height of 3 μm and a semi-included angle of 35 degrees (Olympus, Tokyo, Japan), and AFM images were taken using a MLCT probe (Bruker, Billerica, MA). Asylum Research’s software (Igor Pro 6.34A) was used for thermal tune calibration of the cantilever spring constant.

FIGURE 2.

Representative force maps of a HUVEC monolayer taken with a TR400PB silicon nitride tip of static (a) and sheared using the designed PPFC (b). Force maps were also taken of static (c) and cone-and-plate sheared (d) HUVEC monolayers.

FIGURE 3.

AFM images a HUVEC monolayer taken with a MLCT probe of static (a) and sheared using the designed PPFC (b). Images were also taken of static (c) and cone-and-plate sheared (d) HUVEC monolayers.

Results

EC response to shear stress in the PPFC was compared to both previous findings and the cone-and-plate method. Comparisons between cone-and-plate models were to determine the relative efficacy of each system in terms of the EC response to laminar fluid flow. The EC response to laminar flow is well characterized. Specifically, there are three parameters used to determine changes to the physical state of the cell: actin stress fiber alignment in the direction of the fluid flow³², elongation of the cell in the direction of fluid flow⁴, and an increase in stiffness measured by AFM²⁵.

Computational Fluid Dynamics Simulation of PPFC and Cone-and-Plate devices

To confirm the fully developed laminar flow seen on the slide, Computational Fluid Dynamic (CFD) simulations were performed using the SolidWorks Flow Simulation tool to determine flow characteristics of both methods. The PPFC simulation of the experimental system consists of a volume flow outlet and a pressure inlet boundary condition. For cone-plate simulations, the fluid/air boundary condition was assumed to be at atmospheric pressure, the angular velocity of the fluid at the cone-fluid interface is assumed equal to that of the cone, and the converged solutions are solved relative to the rotating frame (the cone). The fundamental difference between laminar and turbulent flow is that turbulent flow is characterized by the random, chaotic behavior of velocity, pressure, and shear stress, whereas laminar flow consists of parallel streamlines and thus no chaotic behavior of fluid characteristics. Fluid velocity, u, can be described in terms of time averaged values, u̅, superimposed with the fluctuations, u’: (u = u̅+u'). To model velocity in the x direction (u) with these fluctuations, we say that u=u(x,y,z,t). Then we can say u̅ is described as eq. 8:

$$\overline{u}=\frac{1}{T}{\int }_{t_0}^{t_0+T}u(x,y,z,t)\mathit{\text{dt}}$$ (8)

where T, the time interval, is considerably longer than the time of the longest fluctuations. This means that the time-averaged fluctuations are equal to zero, since the fluctuations have an equal distribution on either side of zero, shown in eq. 9:

$$\overline{u\text{'}}=\frac{1}{T}{\int }_{t_o}^{t_o+T}(u-\overline{u})\mathit{\text{dt}}=\frac{1}{T}({\int }_{t_o}^{t_o+T}\mathit{\text{udt}}-\overline{u}{\int }_{t_o}^{t_o+T}\mathit{\text{dt}})=\frac{1}{T}(T\overline{u}-T\overline{u})=0$$ (9)

However, the square of these fluctuations must be a value greater than zero. Therefore, the turbulence intensity, described by eq. 10, can be used to describe these fluctuations.

$$I=\frac{\sqrt{{(u\text{'})}^2}}{\overline{u}}$$ (10)

where I is the turbulence intensity, which is described by the root-means-squared of the fluctuations over the time-averaged mean velocity. Typically, turbulence intensities below 1% are considered laminar. CFD simulations of turbulence intensities in the PPFC (Fig. 4a) indicate that fully developed laminar flow occurs at the slide. Turbulence intensities on the slide, where EC monolayers exist, range from 0.04 to around 0.29%, below the 1% threshold for fluid flow to be considered laminar. Moreover, velocities remain uniform at the slide (Fig. 4b). Thus, a PPFC will ensure uniform shear stresses caused by laminar fluid flow on the EC monolayer. The minimum turbulence intensity over the EC within the cone-plate system is 1.28%. However, the majority of the surface area where ECs are seeded has turbulence intensities over 5%, which indicate that the majority of ECs in the monolayer are subjected to turbulent flow. Since turbulence intensities were greater than 1% for all areas on the EC monolayer, and therefore cannot be considered laminar (Fig. 4c). Furthermore, there is an increase in velocity the distance from the center of the cone increases (Fig. 4d). However, this is accounted for by the cone angle, meaning uniform shear stress is assumed¹⁸.

FIGURE 4.

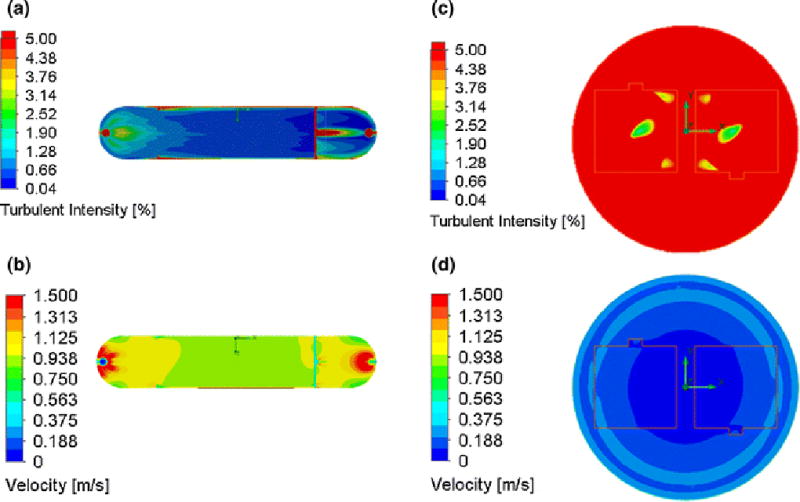
Contour plots of Turbulent Intensities within the PPFC (a) and the cone-and-plate device (c). Intensities less than 1% are considered laminar. The PPFC subjects EC monolayers to exclusively laminar flow, whereas the cone-and-plate device does not. Contour plots of Velocities within the PPFC (b) and the cone-and-plate device (d). EC monolayers in the PPFC are subjected more uniform velocities (and therefore shear stresses) than the cone-and-plate devices. Boundary conditions for the PPFC are as follows: inlet pressure (due to hydrostatic pressure from reservoir) is 103134 Pa, and the outlet of the PPFC has a volumetric flow rate of 15 mL/min, corresponding to the maximum flow rate. The lid which indicates where liquid/air interface occurs is 101325 Pa, the fluid velocity at the boundary between the cone and fluid is equal to the velocity of the cone, −18.33rad/sec.

EC Response to Flow Conditions

EC monolayers were fixed to preserve the phenotypical structure, as ECs which are no longer subjected to shear stress tend to revert to their original cobblestone morphology. Although it is possible to collect stiffness measurements on live cells that have been sheared, force maps will be at a much lower resolution and thus not be as representative of a sheared monolayer. Static samples measured with AFM to determine relative stiffness changes caused by the fixation process, which shows that cortical stiffness increases with the fixation by 15%. However, since the comparison between cortical stiffness is relative, any consistent stiffness changes that result from the fixation process should not affect results.

Analysis of the FFT alignment plots from 2D FFTs taken from IF images (Fig. 5a,b,c) indicate that application of shear stress to the HUVEC monolayer via cone and plate causes an increase in actin alignment of 15.03% along the principal axis of alignment (Fig. 5d). Interestingly, alignment plots from FFT analysis resulted in a broad peak, with a relatively flat shoulder. This indicates that more than one axis of alignment exists. Since actin elongates in the direction of fluid flow, a possible explanation for the multiple axes of alignment may be that there is an angular quality to the fluid flow velocity, and therefore shear stress, τ, at any point along the monolayer. FFT analysis of PPFC revealed that f-actin aligned to a greater extent, showing a 208.10% increase in alignment units along the direction of fluid flow (Fig. 5e). It should be noted, that while actin is significantly aligned with the maximum along direction of fluid flow, the fibers are not exclusively parallel. Rather, actin fibers are aligned with a distribution about the principle axis of elongation.

FIGURE 5.

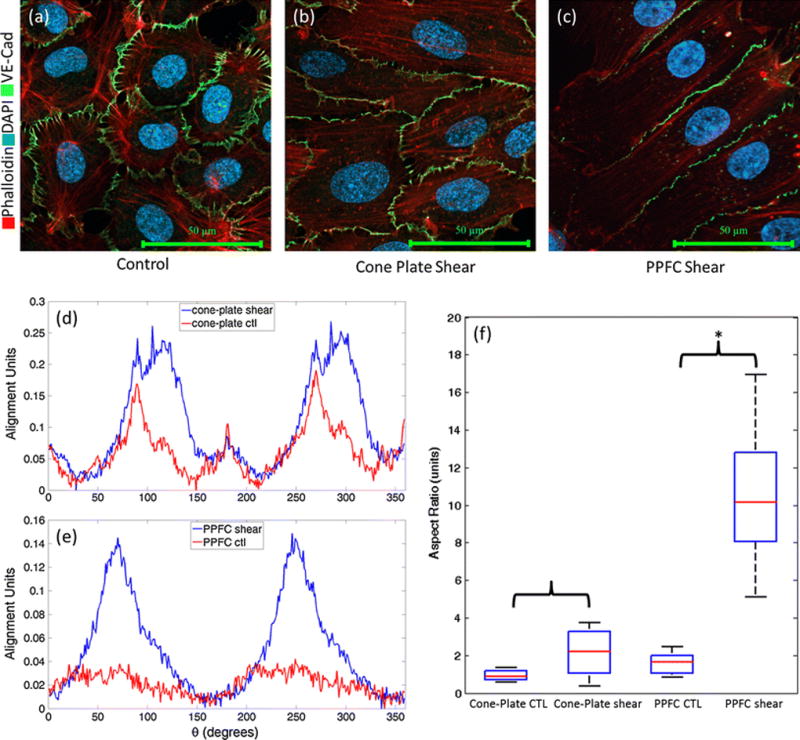
Representative IF images of control (a) and sheared HUVECs using cone-and-plate (b) and PPFC (c). VE-Cadherin Staining is shown in green, phalloidin in red, and nuclear counterstain in blue. Alignment plots representative of the data set (n=10 images) from 2D FFT analysis from Cone-and-Plate (d) and PPFC (e) IF images. Note the broad shoulder on the sheared cone-and-plate data, indicating multiple axis of alignment. Aspect ratios of EC monolayers exposed to both Cone-and-Plate and PPFC (f). Aspect ratios were determined to be 0.99+/−0.42 for control samples, and 2.12+/−1.16 for shear samples using the cone-and-plate device. The PPFC yielded aspect ratios of 11.38+/−4.99 for sheared sample and 1.60+/−0.56 for control samples. * denotes statistically significant results.

Bright field images were taken of the slides, and aspect ratios of 20 cells per experiment were quantified. For each cell, length in pixels was divided by width in pixels. Aspect ratios for sheared cells were 11.38±4.99, whereas aspect ratios for control cells were 1.60±0.56 (Fig. 5f). A Wilcoxon rank sum test (α=0.001) was performed, showing that there is a statistically significant increase in the aspect ratio when HUVECs are subjected to shear stresses (p<0.001). This confirms the change in phenotype ECs undergo when exposed to shear stresses¹². However, aspect ratios in cone-and-plate experiments were determined to be 0.99±0.42 for control samples, and 2.12±1.16 for shear samples. Therefore, cell elongation occurred during shear stress is not significant (p=0.022).

After force maps (Fig. 2a–d) were acquired, stiffness measurements below 500 Pa (below the lever stiffness threshold) were omitted. To account for inherent variance in stiffness measurements, experimental controls were paired with the conditioned sample. Statistical analysis was employed to determine the significance of our results. Since these distributions are not Gaussian, nonparametric statistical analysis was necessary. Hence, a Kruskal-Wallis test was performed to determine if the two populations are of the same distribution (α=0.001). A one-sided Wilcoxon Rank Sum test was then performed to determine if the median stiffness of the shear stress-activated ECs was greater than that of the control (α=0.001). Analysis showed that stiffness increased with statistical significance (p<0.001) by 44±5% (Fig. 6), confirming increases in cortical stiffness from previous studies²⁵. For cone-and-plate stiffness distributions, an 18 ± 2% increase in stiffness occurs when HUVECs are subjected to shear stress (Fig. 6). There was a statistically significant increase (p<0.001) when exposed to shear stress. However, the magnitude of this stiffness increase was greatly attenuated when compared to PPFC experiments. Although we observe an increase in stiffness in vitro, it should be noted that the “stiffer” cells are more physiologically relevant, as ECs are constantly subjected to fluid flow. Rather, there is a decrease in stiffness when ECs are no longer under fluid flow conditions.

FIGURE 6.

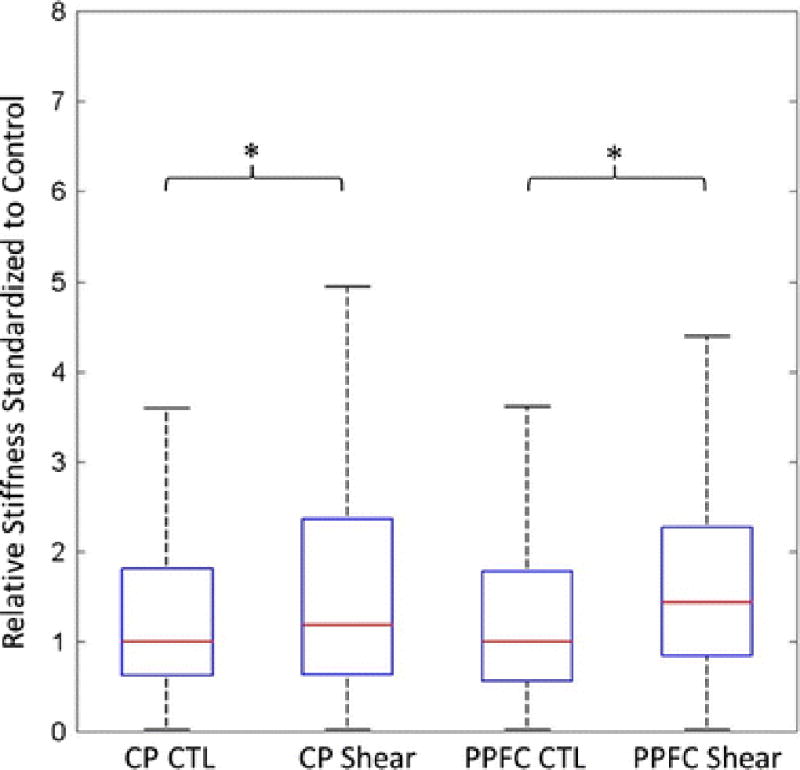
Box-and-whisker plots of median stiffness from the three different cords standardized against the corresponding control. This standardization removes shifts in stiffness between experimental replicates caused by variation in the ECs before each trial. The median stiffness increased in the shear group using both methods of shear. * denotes statistical significance.

Discussion

Validation of PPFC Design

Parallel plate flow chambers subject adherent cells to laminar flow conditions and can be used to evaluate the cellular response to well quantifiable fluid shear stresses. We present a PPFC design for AFM applications, and subsequent biological testing that provides robust evidence that it produces uniform laminar fluid flow across the EC monolayer. Therefore, this device is a reliable means of subjecting EC monolayers to a desired level of shear stress. Moreover, this device can confidently be used as a means of comparing these two common methods for applying shear stress across EC monolayers. The unique microenvironment in vivo, where ECs are constantly subjected to shear stresses, should be recapitulated in vitro to more accurately represent in vivo behavior.

Effects of Laminar and Disturbed flow on EC monolayers

EC response to shear stress in the PPFC was compared to the cone-and-plate method. Comparisons between cone-and-plate models were done to determine the relative efficacy of each system in inducing responses from the ECs. ECs subjected to shear stress using cone-and-plate methods did not induce the typical EC response to shear stresses as effectively as PPFC experiments: actin alignment was determined to be multidirectional to a greater extent, and no significant change in phenotype occurred. It is likely that secondary flow created by the system caused this discrepancy. Although cone-and-plate device streamlines are assumed to be azimuthal, flow profiles with a cone-and-plate device are only approximately azimuthal, and primary flow itself is not a solution to Navier-Stokes equations². Fluid Simulation shows more evidence that cone-and-plate devices will not yield laminar fluid flow on the EC monolayer (Fig. 4c). Based on turbulence intensities, secondary or turbulent flow occurs at all areas of the EC monolayer. Since there will be an inherent secondary flow component when cone-and-plate devices are utilized, they are therefore not ideal for studying EC monolayers under laminar flow conditions.

When secondary flow exists, it causes an unequal magnitude of shear stress across the monolayer²⁶. Since cellular responses to fluid flow are dependent on the magnitude of shear stress applied⁴, this may indicate that AFM measurements are dependent on position. In other words, AFM stiffness or image measurements intended for EC characterization at specified shear stress have an inherent inaccuracy when using the cone-and-plate. Fluid simulations confirm unequal velocities, and thus unequal shear stresses, on the coverslip when secondary flow exists (Fig. 4d). Non-laminar flow within capillaries in vivo causes many known diseases and conditions, such as the preferential localization of atherosclerotic lesions, occurrence of in-stent restenosis, and is a precursor to venous inflammation⁷. Previous work has shown that EC stiffness significantly decreases with the progression of atherosclerosis¹⁴. As turbulent blood flow plays an essential localizing role in plaque formation²², the lesser magnitude of apparent stiffness increase seen in cone-and-plate devices may be correlated with the disease. Shear stresses applied using the cone-and-plate models would be therefore may be better suited for studying the EC response in disturbed flow conditions.

Cellular Microenvironment and Actin Dynamics

The mechanism by which cell niches create specialized microenvironments of chemical and biophysical signals remains to be fully understood. Mechanotransduction of biophysical cues have been implicated as a key factor in the cell’s interpretation of its microenvironment²⁸. One such microenvironmental cue is the wall shear stress from fluid flow over tissues. Disturbed and laminar fluid flow over ECs has been studied in vitro to investigate its implications in vascular disease development and progression. Precise relationships between fluid flow characteristics and endothelial cell phenotype can be elucidated via in vitro models of the ECs’ microenvironment¹⁹. Our device can be used to test these changes in microenvironment and can be potentially used to create disturbed flow for high flow rates. Shear stress mediated EC dysfunction, in regions where the arterial tree is exposed to disturbed flow, is a critical early event in atherosclerosis⁷. The ability to monitor these effects on cell and tissue stiffness via AFM will be a crucial step to deriving a mechanism of treatment for this disease.

The study of the actin cytoskeleton is not exclusive to biochemical pathways. Determining the mechanical properties of actin filaments will allow for deeper insight into how cells respond to external forces, and the mechanisms of mechanotransduction. For example, actin filaments can be analogous to a beam of length L. If compressive forces above a critical load (P_cr) were to be applied to this beam, the beam itself will begin to buckle. If we were to look at this with respect to the elastic curve we find that P_cr=(π²n²EI)/L² where n is dependent on end conditions. Shorter filament will thus need a greater critical load to buckle. In other words, shorter filaments within the cell will allow for increased resistance to forces such as shear stress. Furthermore, an increase in filament width would also require greater critical loads to buckle. Filament length changes may be crucial in certain biophysical pathways. Previous studies have shown that controlled shear stress can induce the differentiation of mouse embryonic stem cells into vascular endothelial cells in vitro by an unknown molecular pathway. This change occurred through stimulation of the mechanosensors, such as cell surface receptors and the actin cytoskeleton, from shear stress²⁸. Studying the mechanical response to external stimuli may further the understanding of actin dynamics with respect to external forces or other microenvironmental cues. Moreover, understanding the changes in cellular mechanical properties and how these changes relate to actin dynamics will help to clarify specific cytoskeletal responses and could elucidate their roles in mechanotransduction.

Conclusions

Parallel plate flow chambers can be used more effectively than cone-and-plate systems to study EC responses to fully developed laminar flow conditions. Since cone-and-plate devices are inherently prone to developing secondary flow characteristics, they are best utilized while studying cellular responses under disturbed flow conditions. Using a PPFC will allow researchers to gain insight into complex mechanotransductory pathways which are influenced by typical microenvironmental cues within small diameter blood vessels such as shear stress.