Field-controlled structures in ferromagnetic cholesteric liquid crystals

Diverse structures are demonstrated in a unique liquid crystal helimagnet under magnetic and electric fields.

Abstract

One of the advantages of anisotropic soft materials is that their structures and, consequently, their properties can be controlled by moderate external fields. Whereas the control of materials with uniform orientational order is straightforward, manipulation of systems with complex orientational order is challenging. We show that a variety of structures of an interesting liquid material, which combine chiral orientational order with ferromagnetic one, can be controlled by a combination of small magnetic and electric fields. In the suspensions of magnetic nanoplatelets in chiral nematic liquid crystals, the platelet’s magnetic moments orient along the orientation of the liquid crystal and, consequently, the material exhibits linear response to small magnetic fields. In the absence of external fields, orientations of the liquid crystal and magnetization have wound structure, which can be either homogeneously helical, disordered, or ordered in complex patterns, depending on the boundary condition at the surfaces and the history of the sample. We demonstrate that by using different combinations of small magnetic and electric fields, it is possible to control reversibly the formation of the structures in a layer of the material. In such a way, different periodic structures can be explored and some of them may be suitable for photonic applications. The material is also a convenient model system to study chiral magnetic structures, because it is a unique liquid analog of a solid helimagnet.

INTRODUCTION

Liquid crystals (LCs), that is, orientationally ordered fluids, present a fascinating class of soft materials and are widely exploited in modern LC displays and other devices (1). The combination of the richness of the LC phases with different degrees of orientational and partial positional orders, and relatively easy experimental observation of their structures makes them ideal model systems to study the fundamental physical and mathematical concepts (2–6). The possibility of controlling their orientation using external fields is one of their most important properties.

In the simplest, nematic LC phase, elongated molecules, on average, orient along the common direction called director n. Ordinary nematic LCs are uniaxial, and although the polar order in the nematic phase was theoretically considered long ago (7, 8), its experimental realization is recent. It has been shown that magnetic nanoplatelets suspended in nematic LCs exhibit polar magnetic ordering. This finding has two important implications. First, it has opened new opportunities for exciting experimental studies of ferromagnetism in liquids. Second, a liquid crystalline material, controllable by small magnetic fields, has been finally realized. Although ferromagnetism in solid materials has been known for a long time and is still widely studied for its importance in applications, it is rare in liquids (9–12). So far, the ferromagnetic nematic LC systems have been shown to form magnetic domains separated by domain walls unique to the polar LC phase (11–13), and they exhibit strong magneto-optic, converse magnetoelectric (14), and magnetoviscous effects (15). Biaxial ferromagnetic liquid crystalline colloids have also been designed, in which the direction of the magnetic order differs from that of the nematic director (16).

If molecules forming nematic phase are chiral or a chiral dopant is added to nematic LCs, the resulting LC phase will be chiral (Fig. 1A). Chiral nematic LCs, also called cholesteric LCs (CLCs), form a rich variety of topological configurations and defect structures when confined in layers (4, 17–19), droplets, microchannels, or shells (20–23). On the other hand, field-induced structures, which appear in bulk or thick layers, are very interesting also from the application point of view (for example, as filters or lasers) (24, 25).

Fig. 1. Ferromagnetic CLC in homeotropic LC cells.

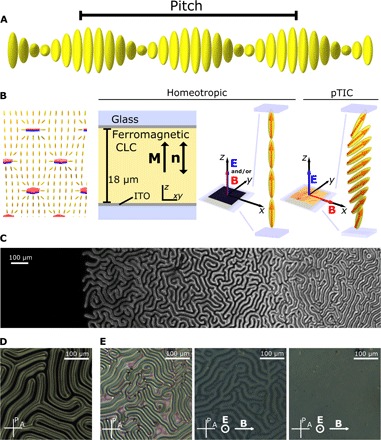
(A) Schematic of director orientation in bulk CLC. (B) Schematic of magnetic nanoplatelets in a nematic LC. Magnetic orientation of the platelets is denoted by red (N) and blue (S) colors. Schematic of ferromagnetic CLC in a homeotropic cell. Red arrows represent the orientation of M, and yellow cylinders represent the orientation of n. During the filling of the LC cell, parallel electric and magnetic fields were applied so that the director and the magnetization were uniformly oriented and the sample was magnetically monodomain. When B is perpendicular to E, pTIC structure appears. (C) CLC in a wedge cell with perpendicular (homeotropic) anchoring. (D) Fingerprint structure of ferromagnetic CLC in the case of d/P = 0.94. In the dark regions, which separate the fingers, the director and the magnetization are uniformly oriented. (E) Fingerprint structure (left), structure immediately after the unwinding (middle), and structure 15 min later (right) in the case of d/P = 1.74.

In a suspension of magnetic nanoplatelets in CLCs, similarly as in a suspension in nematic LCs, ferromagnetic ordering of the platelets appears, which makes the suspensions sensitive also to small magnetic fields (26). This material is a liquid analog of a solid helimagnet (27), in which topologically stable two-dimensional (2D) field structures called skyrmions can be observed (28, 29). In thin films, they can be produced or annihilated by spin-polarized currents (30) or laser pulses (31), whereas in bulk, a skyrmion lattice appears as a special phase in magnetic field at temperatures close to the transition to magnetically disordered phase. In this phase, the lattice, made of hexagonal arrangement of spin whirls, which are parallel to magnetic field, is stabilized by Gaussian thermal fluctuations (28). The structures in solid helimagnets are small (of nanometer size), mostly appear at low temperatures, and are therefore experimentally difficult to study. However, the structures in ferromagnetic CLCs are larger and can be probed by direct 3D imaging. It has been shown recently that the ferromagnetic CLCs, confined in thin films, exhibit 3D topological solitons, named hopfions, which can be manipulated by magnetic field (32).

Here, we focus on thicker layers of ferromagnetic CLCs and demonstrate that the sensitivity to both electric and small magnetic fields opens up access to and control of diverse magnetic structures. Some of these are polar variants of the structures observed in ordinary CLCs, whereas some are unique to the ferromagnetic phase.

RESULTS

The system

The suspension of barium hexaferrite (BaHF) monodomain ferromagnetic nanoplatelets in CLC with positive dielectric anisotropy was prepared similarly as the suspensions in nematic LCs (see Materials and Methods) (14). Magnetic moments of the nanoplatelets are perpendicular to the plane of the platelets, and their surface was treated so that, when suspended in the LC, they preferably orient with the magnetic moments parallel to n. The ferromagnetic CLCs can therefore be described by two coupled order parameters: the director n and the density of magnetic moments, that is, the magnetization M. The coupling is such that parallel orientation of the order parameters is energetically the most favorable. The pitch P, which describes the periodicity of the helical structure in bulk CLCs, was the same in suspension (Fig. 1A), within experimental error, as in pure CLC. We used typical LC cells (thickness, 18.3 μm; Instec Inc.) in which an LC is placed between two glass plates with surfaces treated so that the preferred orientation of n at the surface was perpendicular to the substrate (homeotropic) (Fig. 1B). When a CLC is confined to such a layer, the surface promotes uniform orientation of n, which competes with helical ground state of the bulk CLCs. Depending on the confinement ratio between the thickness of the layer d and the pitch P, n is either uniformly oriented perpendicularly to the layer (d/P < 1), completely wound (d/P > 1.5), or composed of wound structures (called cholesteric fingers) separated by uniform regions (1 < d/P < 1.5) (Fig. 1C) (17, 18). The wound structures can be unwound by the electric field (17). The ferromagnetic CLC behaves similarly. In the uniformly oriented region, topological solitons may spontaneously appear during the quench from the isotropic phase or they can be generated using a spatially modulated laser beam (32). Here, we focused on the other two regions: the isolated cholesteric fingers and the completely wound state.

We filled the cells with the suspension in the presence of electric and magnetic fields, which were both applied perpendicularly to the layer. The electric field (ac, 1 kHz, 10 V) was large enough to unwind the CLCs, whereas the magnetic field (24 mT) ensured that the uniformly oriented ferromagnetic CLC was magnetically monodomain (Fig. 1B).

We analyzed the samples by polarizing optical microscopy (POM). Uniformly oriented configuration appeared dark between crossed polarizers. After the magnetic field was switched off, the sample remained dark, indicating that the structure remained uniformly oriented. When a small magnetic field (a few millitesla) was applied in the plane of the layer, it became homogeneously brighter. The brightness increased with the increasing magnetic field. Rotating the sample between crossed polarizers caused changes in the intensity but never resulted in a completely dark state. This is typical for a translationally invariant configuration (TIC), in which bend and splay deformations are accompanied by the twist (Fig. 1B). A nonpolar variant of TIC is observed, for example, in ordinary CLCs with negative dielectric anisotropy (17).

We switched off the magnetic field and then the electric field. In the cell with d/P = 0.94, cholesteric fingers formed, which were separated by uniform regions (Fig. 1D). In the cell with d/P = 1.74, fingerprint texture, typical for CLCs, appeared (Fig. 1E). After a longer period of time (a day), we unwound the samples using the electric field. The magnetic orientation was again probed by a small magnetic field applied in the plane of the layer. Initially, the magneto-optic response was inhomogeneous (Fig. 1E). Features of the response resembled the fingerprint pattern of the wound structure, in which the sample remained overnight. This indicates that in the wound configuration, the concentration of magnetic nanoplatelets became inhomogeneous, the concentration being higher in the regions where n is less deformed (that is, in the middle of the fingers and the regions outside the fingers). Distinct inhomogeneities in the magneto-optic response faded out after the sample had remained uniformly oriented in the external electric field for about 20 min (Fig. 1E). The homogenization of the concentration is a result of the translational diffusion of the platelets. This shows that the initial magnetic monodomain structure was preserved and that the winding/unwinding transition is reversible.

Periodic structures

The magnetic and electric fields, when perpendicular to each other, stabilize polar TIC (pTIC) (Fig. 1B). pTIC is homogeneous in the plane of the layer, in the middle of the layer M and n are tilted toward B, whereas they deviate from the field direction when they are closer to the surface of the layer.

The pTIC structure can be calculated by numerical minimization of the Oseen-Frank free energy with field coupling terms. We assume constant temperature and pressure, uniform concentration of particles, constant external magnetic field B = μ₀H, and electric displacement field D (14, 32)

$$\mathit{F}={\displaystyle \int }({\mathit{f}}_{\text{CLC},\text{elast}}+\frac{1}{2{\mathrm{\epsilon }}_0}\mathbf{D}\cdot {\underset{¯}{\mathbf{\epsilon }}}^{-1}\cdot \mathbf{D}-\mathbf{B}\cdot \mathbf{M}-\frac{1}{2}\mathrm{\gamma }{\mathrm{\mu }}_0{(\mathbf{n}\cdot \mathbf{M})}^2)\mathit{d}\mathit{V}-\int \frac{1}{2}\mathit{W}{(\mathbf{n}\cdot {\mathbf{n}}_{\mathrm{s}})}^2\mathit{d}\mathit{S}$$ (1)

The first term is the Frank elastic energy: ${\mathit{f}}_{\text{CLC},\text{elast}}=\frac{1}{2}{\mathit{K}}_1{(\nabla \cdot \mathbf{n})}^2+\frac{1}{2}{\mathit{K}}_2{(\mathbf{n}\cdot (\nabla \times \mathbf{n})+{\mathit{q}}_0)}^2+\frac{1}{2}{\mathit{K}}_3{(\mathbf{n}\times (\nabla \times \mathbf{n}))}^2-\frac{1}{2}{\mathit{K}}_{24}\nabla \cdot (\mathbf{n}(\nabla \cdot \mathbf{n})+\mathbf{n}\times (\nabla \times \mathbf{n}))$, where K_i are elastic constants and q_o = 2π/P describes periodicity. The second and third terms describe coupling with the external fields. Here, $\underset{¯}{\mathbf{\epsilon }}={\mathrm{\epsilon }}_{\perp }\underset{¯}{\mathbf{I}}+{\mathrm{\epsilon }}_{\mathrm{a}}\mathbf{n}\otimes \mathbf{n}$ is the dielectric tensor, where ε_⊥ is the dielectric constant perpendicular to the director and ε_a is the dielectric anisotropy of the nematic LC. In the electric term equality, ${\mathrm{\epsilon }}_0\mathbf{E}={\underset{¯}{\mathbf{\epsilon }}}^{-1}\mathbf{D}$ was taken into account. Note that the electric term is quadratic in the field, whereas the magnetic term is linear. The fourth term describes coupling between n and M, where γ is the coupling constant and μ₀ is the vacuum permeability. In the last term, the surface term W is the strength of the surface anchoring and n_s is the preferred direction of n at the surface of the LC cell. The pTIC is homogeneous in the plane of the LC cell, so n and M depend only on coordinate z. Numerical minimization of the free energy in such a case yields the structures shown in Fig. 1B.

pTIC is stable when either of the fields is large enough. If B is turned off, the sample will be uniformly aligned perpendicularly to the layer for voltages larger than the threshold voltage U > U_t. If U is turned off, the sample will remain in pTIC for B > B_t. By reducing B and/or U, pTIC becomes unstable. We observed two types of destabilization. In the inhomogeneous case, which is typical for ordinary CLCs, localized wound director field structures (cholesteric fingers) nucleate at spacers or other irregularities of the sample or grow from the areas outside of the electrodes. In the homogeneous case, the instability arises from a fluctuation of the director field and a periodic structure, which evolves continuously from TIC, occurs almost simultaneously across the sample. Both processes compete, though the growth of the fingers is usually slower.

We focused on the instabilities, which lead to the formation of periodic structures. The resulting structures depended on the confinement ratio and on the exact configuration of pTIC, from which they evolved and which was determined by the combination of B and U. We investigated two cases. In the first case, we slowly reduced U at constant B, and in the second case, we did the reverse—we slowly reduced B at constant U. In each experiment, we assigned critical values, either U_t(B) or B_t(U), of external fields, where the structural transition started to occur.

For the small confinement ratio, d/P = 0.94, both cases gave similar result. In the absence of the magnetic field, the fingers nucleated inhomogeneously when U was reduced (Fig. 1D and fig. S1). The additional magnetic field caused the fingers to be oriented perpendicularly to B and to appear homogeneously in the whole observed region at B < 0.5 mT (Fig. 2A). They can be continuously wound and unwound by switching off/on the magnetic field. Whereas winding and unwinding of the structure by the magnetic field are fast, the inhomogeneous nucleation of fingers takes minutes (fig. S1).

Fig. 2. POM images of structures that evolve from pTIC when either B or U is slowly reduced (0.16 mT/0.7 s and 10 mV/1.5 s).

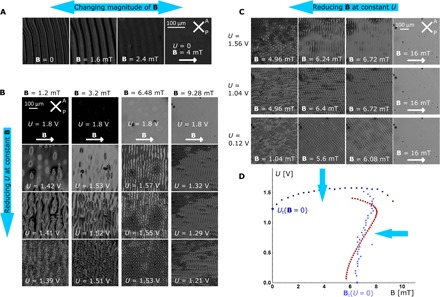
(A) d/P = 0.94 and B is reduced. (B) d/P = 1.74 and U is reduced at constant B. (C) d/P = 1.74 and B is reduced at constant U. (D) Blue dots denote experimentally obtained values of U_t(B) and B_t(U), where the pTIC becomes unstable, and red dots denote theoretical prediction of B_t(U) obtained by stability analysis. In cases where U > 1.56 V, the direct transition from the pTIC to the fingerprint configuration was not observed; however, nucleation of cholesteric fingers was present.

For the confinement ratio, d/P = 1.74, the situation is more complex. Figure 2B shows the patterns that occur when U was slowly reduced at constant B. If B was very small, the transition occurred inhomogeneously in a manner similar to that in the pure CLC. At larger values of B, stripe-like pattern formed, with the stripes oriented perpendicularly to B. The stripes evolved into cholesteric fingers, which at the end formed a zigzag-like pattern.

Figure 2C shows the case in which B was slowly reduced at constant U. At higher voltages (>1.5 V), a stripe-like 1D pattern occurred similar to that from the previous experiment. When U was very small or zero, a characteristic diamond pattern formed. Angle α between the stripes of the pattern and the direction of B was slightly above 50°. By increasing U, angle α also increased. At higher voltages, the pTIC became unstable at higher B_c than at zero voltage. All of the observed periodic structures can be transformed back to the initial pTIC structure by increasing the corresponding field.

For this confinement ratio and for small B, the inhomogeneous evolution of fingers prevails over the homogeneous destabilization. For increasing B, the evolution of fingers becomes slower and homogeneous destabilization starts to prevail. In structural transitions, inhomogeneous nucleation and homogenous destabilization are signatures of the first- and second-order transitions, respectively (17). Therefore, in our case, by increasing B, the structural transition from pTIC to 2D/3D wound structures, which is initially of the first order, is getting weaker, going toward the second order. However, it is experimentally difficult to prove whether the transition became truly of the second order or not.

Reversal of the magnetic field and pTIC2

Because pTIC is polar, it is particularly interesting to observe what happens when the direction of B is suddenly reversed. Here, we demonstrate two special cases, which are observed in the sample with d/P = 1.74 (Fig. 3, A and B). In the first case, we set the voltage above the threshold voltage, and in the second case, the applied voltage was very small or zero, and the magnetic field was above the threshold field B_t.

Fig. 3. Reversal of magnetic field in the case of d/P = 1.74.

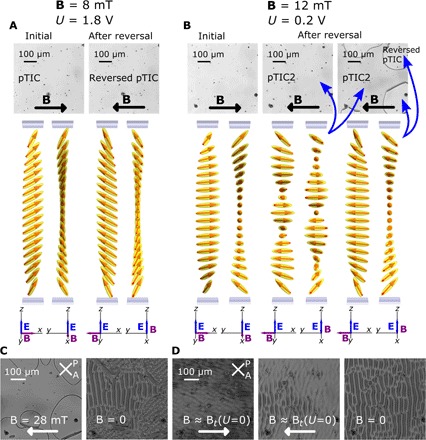
(A and B) The POM images show the homogeneous magneto-optic response. Schematics below the images show the calculated corresponding director and magnetic field configurations. Every configuration is represented from two side views: (A) U > U_t(B) and (B) U ≪ U_t(B). Here, two resulting TICs were observed: the pTIC2 (the second image and the region outside the lines in the third image) and the reversed pTIC (within the lines in the third image). (C) Evolution of structures from pTIC2 outside and reversed pTIC within the lines after B is turned off. (D) Response of the sample on the reversal of B at magnitudes around B_t and U = 0. The third image shows the stable structure that evolves continuously from monodomain pTIC2 at B = 0.

In the first case, the intensity of the POM image did not change significantly. The resulting pTIC is the initial pTIC rotated by π along the z axis (Fig. 3A). The transition from the first structure to the second structure was continuous, and it went through the homeotropic configuration.

The second case is more interesting. Immediately after the switching, the intensity of the magneto-optic response changed; however, it remained homogenous (Fig. 3B). After a while, lines that formed around the spacers started to propagate across the layer. The regions, which grew within the lines, had the same brightness as the initial pTIC, whereas the region outside the lines was slightly darker. The propagation of the lines slowed down as they grew and eventually stopped. The equilibrium size of the areas within the lines depended on the magnitude of B and the density of spacers or other irregularities from which they grew or got pinned. We performed two experiments to see how the structures in the two regions differ.

In the first experiment, we turned off the voltage and then slowly turned off B (Fig. 3C). In the region within the lines, we observed the previously described diamond pattern texture, and in the region outside the lines, we observed new stripe-like texture. This indicates that the pTIC within the lines was initial pTIC rotated by π, whereas outside the lines, a new pTIC2 had formed. In the case where the field reversal was performed at B ≈ B_t, only the stripe-like pattern formed (Fig. 3D).

In the second experiment, we unwound the sample with U at B = 0. The structure within the lines continuously and homogeneously transformed to the uniform orientation of n, as in the case of the original pTIC. However, in the region outside the lines, the transformation was inhomogeneous and several defect lines formed during the transition (that is, the transition was not continuous) (fig. S2).

From these observations, it is evident that we obtained two different resulting TICs: pTIC and pTIC2. Configuration of the pTIC2, as obtained from numerical minimization of the free energy (Eq. 1), is represented in Fig. 3B. Although in pTIC the projection of n and M on the plane of the LC layer rotates by π, in the case of pTIC2 it rotates by about 2.4π along the z direction, which correspond to 0.5 and 1.2 of helical periods, respectively. Comparison of the configurations calculated numerically showed that at small magnetic fields, the energy of pTIC2 is smaller, whereas at larger magnetic fields (above 10 mT), the pTIC is energetically more favorable (fig. S3). Although pTIC2 has lower energy at small fields, pTIC does not transform to pTIC2 spontaneously. The reason is probably because the height of the energy barrier between the structures is much larger than the thermal energy k_BT. That is, in order for the structure to change from pTIC to pTIC2, the system must go through configurations with much larger energy. By reversing the magnetic field, we “open the path” in the configuration space, which leads to pTIC2. pTIC2 is also observed when a voltage is reduced to 0 at constant small B (fig. S4).

Numerical calculations of periodic instabilities and structures

The periodic structures form when pTIC or pTIC2 becomes unstable. We have numerically calculated fluctuations, which cause the instabilities for the cases that correspond to the measurements. First, we calculated the structure of pTIC at given B and U by the numerical minimization of the free energy (Eq. 1) and then checked its stability toward periodic fluctuations of the orientations of n and M, that is, $\mathrm{\delta }{\mathrm{\varphi }}_{\mathit{i}}=\mathrm{\delta }{\mathrm{\varphi }}_{\mathit{i}0}(\mathit{z}){\mathit{e}}^{-\mathit{i}{\mathbf{q}}_{\mathit{x}\mathit{y}}\cdot {\mathbf{r}}_{\mathit{x}\mathit{y}}}+\mathit{c}.\mathit{c}.$. Here, ϕ_i are the four angles describing the orientation of n and M, the xy plane is the plane of the layer, and B is parallel to the x axis (see Materials and Methods). The results show that the pTIC structure becomes unstable toward one or two fluctuations with the wave vectors q_xy, which depends on the confinement ratio and the combination of B and U (fig. S5). Stripe-like 1D patterns result from one periodic fluctuation, with maximum amplitude centered in the middle of the cell and with the wave vector q_xy parallel to B. For d/P = 0.94, the instability evolves in a finger-like structure, schematically shown in Fig. 4A. This structure is a polar variant of the nonsingular cholesteric finger of the first kind. We calculated it by numerical minimization of the 2D free energy (Eq. 1) using periodically perturbed pTIC as a starting configuration (see Materials and Methods). A nonpolar variant of this has been observed in CLC with negative dielectric constant in rubbed homeotropic cell (33). Similarly, one fluctuation centered at the middle of the cell destabilizes the pTIC in the case of the confinement ratio d/P = 1.74 and voltages above 1.5 V. However, in this case, the 1D periodic pattern (Fig. 4B) is not stable but further evolves in a zigzag-like finger structure. The structure that evolves from pTIC2 is stable. This structure, calculated numerically, shows that undulation of the cholesteric structure is accompanied by the onset of two twisted regions, with magnetization pointing in opposite directions located alternatingly close to the bottom and upper plates of the LC cell (Fig. 4C).

Fig. 4. POM images and cross section in the xz plane of calculated structures with 1D periodicity.

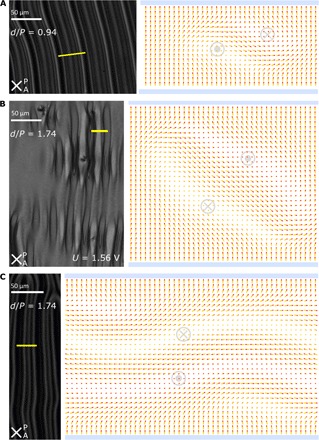
(A) d/P = 0.94 (structure that evolves from pTIC when external fields are switched off). (B) d/P = 1.74 (transient structure that evolves from pTIC at constant U = 1.5 when B is switched off. In the POM image, evolution of fingers in different stages can be observed, whereas the simulation shows the last stage of evolution.) (C) d/P = 1.74 (structure that evolves from pTIC2 when external fields are switched off). The direction of out-of-plane orientation of the magnetization is shown in some typical regions by gray circles surrounding “x” or the dot. The yellow lines on POM images denote the regions that correspond to the accompanying calculated structures.

The diamond pattern observed at small voltages evolves as a consequence of two fluctuations—the first is located closer to the upper plate of the LC cell, whereas the second is located closer to the bottom plate—with the 2D wave vectors q_1,xy = (q_x, q_y) and q_2,xy = (q_x, −q_y), respectively. The pTIC structure, perturbed by these fluctuations, is shown in Fig. 5.

Fig. 5. Schematic of 2D periodic instability, which causes diamond pattern in the case of d/P = 1.74 and U = 0.

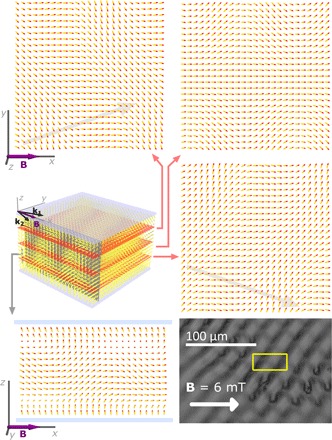
The structure evolves continuously from pTIC by two critical fluctuations. The maximal amplitude of the first fluctuation is located closer to the top, and that of the second fluctuation is located closer to the bottom of the layer. Schematics show the structure at the instability. Gray arrows behind the first and third schematics show the calculated wave vectors of the fluctuation, which is dominant in the corresponding region. The yellow rectangle on the POM image denotes the region that corresponds to the three in-plane cross sections.

DISCUSSION

The experiments show that controlling the TICs is the key to obtaining a variety of structures, because periodic patterns homogeneously evolve from a stable pTIC. This mechanism importantly differs from the case of inhomogeneous nucleation of cholesteric fingers, which leads to an irregular pattern usually observed in the CLCs. The exact structure of the pTIC determines what kind of periodic structure evolves when the fields are reduced or switched off. In ordinary CLCs with positive dielectric anisotropy, nonpolar TIC is observed as a transient configuration when electric field is switched off and it cannot be controlled (17). On the other hand, a stable TIC was observed in CLCs with negative dielectric anisotropy in the high-confinement regime, that is, d/P < 1, in which the director structure in the absence of the external electric field is unwound (33). This system exhibits a rich phase diagram of director structures when the confinement ratio and electric field are varied, but is limited to a high-confinement regime. In the ferromagnetic CLCs, TIC is polar and also stable in the low-confinement regime, in which the structure in the absence of the fields is completely wound.

The instabilities discussed in this paper differ from those extensively studied in ordinary CLC (34–39). In those studies, 1D and 2D periodic instabilities appeared when an electric or magnetic field was applied along the helical axis of the sample, which was in the ground helical state (Fig. 1A). In that case, the field was perpendicular to the director, and above some threshold field, the helical structure periodically deformed. Similar electrohydrodynamic instabilities appear in low-frequency ac electric field (35), and their behavior has been thoroughly researched also in the presence of magnetic field (40). In all those cases, the external fields destabilized the homogeneous helical ground structure in the layer of the CLC, where orientation and homogeneity are defined by the parallel anchoring at the boundaries of the layer. Contrary to that, we study the instabilities of the unwound structure and use the external fields to control how it winds.

Combining magnetic and electric fields in polar magnetic system offers interesting new possibilities, because the two fields affect the system in a different way. The advantage of the magnetic field is that it can be applied in a noncontact way in any direction, whereas the direction of the electric field is determined by the position of the electrodes. Because the system is ferromagnetic, it is sensitive also to the sign of the magnetic field, whereas the response of the system to the electric field is quadratic. Therefore, applying the two fields at some angle with respect to each other is not the same as applying one field in the direction of their sum, as is the case in the ordinary CLCs. Consequently, much larger configuration space can be explored using the combination of both fields. Here, we explored only a small portion of it.

In the case of isolated fingers (d/P = 0.94), the magnetic field can be used to control the direction of the 1D periodicity. The finger structure is a polar variant of the fingers observed in the CLCs with negative dielectric anisotropy, in which homogenous periodic evolution of fingers was induced by rubbing homeotropic substrates of the LC cell (33). In that case, within each finger, two pairs of λ^1/2 and λ^−1/2 nonsingular disclinations evolve, which, in the ferromagnetic case, differ in the direction of M.

The diamond pattern observed in the case of d/P = 1.74 and low or zero voltage resembles a transient state in the ordinary CLC, observed in the moving nematic-cholesteric front in the directional melting experiment (41). In the latter case, the structure of the director field is unknown. The stability analysis in our case showed that a combination of two periodic fluctuations located closer to the LC cell substrates causes the formation of the structure. The origin of the instability of pTIC is mainly the competition between the elastic energy, which favors the twisted state, and the field terms, which are the smallest when n and M are oriented along the corresponding fields. When d/P is close to 1, the thickness can only accommodate one finger and only one fluctuation destabilizes the structure, whereas at d/P ≈ 2, two fingers can, in principle, form on top of each other, which results in one destabilizing fluctuation splitting into two. In this case, the instabilities begin, where the pTIC structure exhibits the largest twist that is closer to the substrates.

On the other hand, pTIC2 is already wound by about 1.2 of the twist periods, which fits better within the thickness. However, because of the perpendicular anchoring at the LC cell surface, the structure is frustrated, which leads to undulating configuration. Undulating structures have been observed in ordinary CLCs in the case of parallel anchoring at the LC cell surface, in which frustration of the structure was caused by the electric or magnetic field (37–39, 42).

CONCLUSIONS

We demonstrated that the phase diagram of chiral ferromagnetic nematic structures is rich and different paths in the electric-magnetic fields phase diagram can be used to access a variety of interesting configurations. In comparison to the ordinary CLCs, in which the electric field offers important but limited possibilities for the control of the structures (1, 17, 24, 42), the novelty of ferromagnetic CLCs is that a combination of electric and small magnetic fields can be used to reach a certain structure in the field phase diagram. Moreover, in this system, magnetic field weakens the first-order structural transition from unwound to wound phase so that homogeneous destabilization prevails over the inhomogeneous one, which, consequently, leads to the formation of periodic structures. Whereas the electric field affects the ferromagnetic CLC in a manner similar to the ordinary CLC, there are two important differences in the response of the two systems to magnetic fields. In the ordinary CLCs, magnetic fields, typically of the order of 1 T, are needed to observe a response, which is quadratic in the field, whereas the ferromagnetic CLCs respond to small magnetic fields (of the order of 10 mT) and their response is linear in the field.

The ferromagnetic CLCs can be used as model systems to study possible structures in solid helimagnets. However, there are differences between the solid and liquid ferromagnets. The most important is that the latter can adapt their shape to a container and can flow, which affects the formation of the structures and magnetic domains (43). As shown here and in studies of Zhang (26) and Ackerman and Smalyukh (32), the structures in liquid crystalline systems are much easier to manipulate, which gives much larger variety of configurations. Periodic structures, which can be manipulated by electric and magnetic fields, have potential for photonic applications similar to those of ordinary CLCs (1).

MATERIALS AND METHODS

Sample preparation

CLC was prepared from liquid crystalline mixture E7 (Merck) doped with chiral dopant S811 [0.9 weight % (wt %) for P = (10.5 ± 0.02) μm and 0.5 wt % for P = (19.5 ± 0.05) μm]. The LC has positive dielectric anisotropy, that is, it is energetically favorable for the director to align along the direction of external E. Pitches were measured by the Grandjean-Cano method.

Ferromagnetic suspension was prepared by mixing 200 μl of CLC in the isotropic phase with 150 μl of the suspension of scandium-substituted BaHF single-crystal nanoplatelets (44) in tert-butanol (the nanoplatelet concentration was 15 g/liter). The thickness of the platelets was about 5 nm, and the distribution of the platelet diameter was approximately log normal, with a mean of 70 nm and an SD of 38 nm. The nanoplatelets are magnetically monodomain, with the magnetic moment perpendicular to the plane of the platelets. Dodecylbenzenesulfonic acid was used as a surfactant. It favors a perpendicular orientation of n at the surface of the particles, so the platelets in CLC orient with the surface normal parallel to n (that is, with magnetic moments parallel to n). We kept the mixture in the isotropic phase heated up to 85°C for 1 day so that the tert-butanol evaporated. The mixture was then quenched from the isotropic phase to the cholesteric phase by pipetting the mixture to the edge of a glass container that was cooled to approximately 18°C. The suspension was centrifuged at a_r ≈ 13,000g for 30 min. We left the suspension in a gradient of magnetic field for 3 days to further reduce the number of aggregates. The aggregate-free part was filled in homeotropic LC cells (thickness, 18 μm; Instec Inc.) with indium tin oxide (ITO)–coated surfaces in external magnetic field (B = 24 mT) and external electric field (U = 10 V), which were both applied perpendicularly to the plane of the cell substrates so that in the ITO area the sample was uniformly oriented. We left the sample in the external field for half an hour to obtain magnetically monodomain sample in the uniformly oriented area. From the measured value of magnetization, we estimated the volume concentration of the platelets to be 1.5 × 10^{− 3}. All the measurements were performed at 25°C. We measured the pitches of the suspensions, and their values were the same as those in pure CLC, within experimental error.

Stability analysis and calculation of the structures

Distortion of n and M in an external field was calculated by numerical minimization of the free-energy density per area (that is, Eq. 1) with respect to four angles ϕ_i (i = 1 to 4) describing the orientation of n = (sin ϕ₁ cos ϕ₂, sin ϕ₁ sin ϕ₂, cos ϕ₁) and M/M₀ = (sin ϕ₃ cos ϕ₄, sin ϕ₃ sin ϕ₄, cos ϕ₃).

We chose the z axis of the coordinate system to be perpendicular to the cell surface (that is, in the direction of the electric field) and the x axis to be along the direction of the magnetic field. The distorted director and magnetization are in the case of pTIC structure only functions of z. The starting configuration at the beginning of the minimization was the uniform orientation of M and n along z. In the case of calculation of pTIC2, we first calculated pTIC at given B and U, then reversed the magnetic field, and did the minimization again, starting with the calculated pTIC configuration.

Taking into account ∇ × E = 0 and ∇ ⋅ D = 0, the electric part of the free-energy density can be written as

$$\frac{1}{2}\mathbf{D}\cdot {\underset{¯}{\mathbf{\epsilon }}}^{-1}\mathbf{D}=\frac{{\mathit{D}}_{\mathit{z}}^2}{{\mathrm{\epsilon }}_0}\frac{1}{{\mathrm{\epsilon }}_{\mathrm{a}}{\text{cos}}^2{\mathrm{\varphi }}_1+{\mathrm{\epsilon }}_{\perp }}$$ (2)

where D_z is a constant related to the applied voltage

$$\mathit{U}=\frac{{\mathit{D}}_{\mathit{z}}}{{\mathrm{\epsilon }}_0}{\displaystyle \underset{0}{\overset{\mathit{d}}{\int }}}\frac{\mathit{d}\mathit{z}}{{\mathrm{\epsilon }}_{\mathrm{a}}{\text{cos}}^2{\mathrm{\varphi }}_1+{\mathrm{\epsilon }}_{\perp }}$$ (3)

The stability analysis of the pTIC structure against small periodic fluctuations in the xy plane, $\mathrm{\delta }{\mathrm{\varphi }}_{\mathit{i}}=\mathrm{\delta }{\mathrm{\varphi }}_{\mathit{i}0}(\mathit{z}){\mathit{e}}^{-\mathit{i}{\mathbf{q}}_{\mathit{x}\mathit{y}}\cdot {\mathbf{r}}_{\mathit{x}\mathit{y}}}+\mathit{c}.\mathit{c}.$, was performed by numerical calculation of eigenvalues and eigenvectors of the fluctuations. At a given field, we calculated the smallest nontrivial eigenvalue and q_xy at which it appears. If this eigenvalue is negative, the structure is not stable. We determined the threshold field as the magnetic field at which it becomes negative (fig. S5).

The 1D periodic metastable structures were calculated by numerical minimization of the free energy in the xz plane using the conjugate gradient method to find local minimum. Starting configuration was the pTIC or pTIC2 structure perturbed by the fluctuation, which caused instability.

In the calculations, the following values were taken: K₃ = 15 pN, K₂ = 0.42 K₃, K₁ = 0.6 K₃, γ = 400, M = 120 A/m, W = 10⁻⁵ J/m², ε^⊥ = 4, ε_a = 14, d = 18.3 μm. The values of elastic constants K₃ and K₁ were taken as measured by optic Frederiks transition in equivalent suspension in the nematic phase of E7 without chiral dopant. The values are similar to those of E7 at the same temperature (25°C). The value of K₂ was taken from Chen et al. (45).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/10/e1701336/DC1

fig. S1. Inhomogeneous nucleation of cholesteric fingers in the case of d/P = 0.94 in the absence of external fields.

fig. S2. Comparison of the response of pTIC and pTIC2 to the electric field.

fig. S3. Phase diagrams showing stability of pTIC versus pTIC2 as obtained from 1D model.

fig. S4. POM images of structures that evolve from pTIC in the case of constant B and d/P = 1.74.

fig. S5. The eight smallest nontrivial eigenvalues of fluctuations as a function of external magnetic field showing the destabilization of the pTIC structure.