A web application for evaluating Phase I methods using a non-parametric optimal benchmark

Abstract

Background/aims

In evaluating the performance of Phase I dose-finding designs, simulation studies are typically conducted to assess how often a method correctly selects the true maximum tolerated dose (MTD) under a set of assumed dose-toxicity curves. A necessary component of the evaluation process is to have some concept for how well a design can possibly perform. The notion of an upper bound on the accuracy of MTD selection is often omitted from the simulation study, and the aim of this work is to provide researchers with accessible software to quickly evaluate the operating characteristics of Phase I methods using a benchmark.

Methods

The non-parametric optimal benchmark is a useful theoretical tool for simulations that can serve as an upper limit for the accuracy of MTD identification based on a binary toxicity endpoint. It offers researchers a sense of the plausibility of a Phase I method’s operating characteristics in simulation. We have developed an R shiny web application for simulating the benchmark.

Results

The web application has the ability to quickly provide simulation results for the benchmark, and requires no programming knowledge. The application is free to access and use on any device with an internet browser.

Conclusion

The application provides the percentage of correct selection of the MTD and an accuracy index, operating characteristics typically used in evaluating the accuracy of dose-finding designs. We hope this software will facilitate the use of the non-parametric optimal benchmark as an evaluation tool in dose-finding simulation.

Introduction

Historically, the primary objective of a dose-finding trial in oncology has been to identify the maximum tolerated dose (MTD) from a range of pre-defined dose levels. Numerous designs¹ have been proposed for identifying the MTD from a set of doses, in which dose-limiting toxicity (DLT) is measured as a binary outcome (DLT; yes/no), based on protocol-specific adverse events. The MTD is commonly defined as the dose having an associated probability of DLT closest to an acceptable target DLT rate. In assessing performance of methods, simulation studies of finite sample behavior are typically conducted under a set of hypothesized true dose-toxicity relationships, characterized by the assumption that toxicity is monotonically increasing with dose. The simulations generate the operating characteristics that are used to evaluate the safety and accuracy of the method.^2,3 Accuracy is typically summarized by the percentage of simulated trials in which the method correctly identified the true MTD. Safety is typically summarized by the expected number of DLTs at each dose level and the percentage of patients treated above the MTD, which reflects the risk of overdosing. The problem of determining how some method performs relative to another can be a difficult question to answer. Under one assumed set of true dose-toxicity curves, we may come to a conclusion that does not hold another assumed set of curves. This can be the case for Bayesian designs where the impact of prior information, and how it aligns with some chosen truth, can be difficult to assess. It happens that such information can favor performance in certain hypothetical dose-toxicity situations and hinder performance in others. The choice of which curves to show then becomes subjective.

A necessary component of the evaluation process is to have some concept for how well a design can possibly perform. This gives researchers an idea of the plausibility of performance in simulation for a particular method. The non-parametric optimal benchmark⁴ serves as an upper bound for accuracy in simulation studies. The authors⁴ showed that it is not generally possible to do better than the benchmark based on the observations themselves. For a design to be “super-optimal”,⁵ it requires some form of extraneous knowledge, such as an informative prior distribution. Furthermore, a design such as “always choose dose level 3” is one that is impossible to beat, even with no observations, in situations in which level 3 is the true MTD. This is not considered an admissible design. If considering only admissible designs, then the benchmark can be taken as an upper bound across a broad range of scenarios. The details of the benchmark are provided elsewhere,⁴ so we only briefly recall them here.

Methods

Suppose that the binary indicator Y_j takes value 1 if patient j experiences a DLT at dose d_i; 0 otherwise. In simulating DLT outcomes, we can consider each patient j to possess a latent toxicity tolerance⁶ v_j that is uniformly distributed on the interval [0,1]. In a real study, the latent tolerance is not observeable, but it can be used as a computer simulation tool to compare the behavior of designs on the same patients. Based on the simulated outcome v_j of patient j and the probability of DLT R(d_i) at the dose d_i administered to patient j, it can be determined whether a patient would experience a DLT at this level. A patient will have a DLT outcome if the simulated uniform latent variable is less than or equal to the true DLT probability of the dose assigned to the patient. That is,

$$Y_j=\{\begin{array}{lll}1\hfill & \text{if}\hfill & v_j\le R(d_i)\hfill \\ 0\hfill & \hfill & \text{otherwise}\hfill \end{array}.$$

For instance, suppose a patient receives dose level 1 with an assumed DLT probability of 0.05, suppose this patient has a toxicity tolerance of v₁ = 0.735. This patient does not have a DLT outcome because the latent tolerance v₁ = 0.735 > R(d₁) = 0.05.

During the course of a Phase I trial, each patient receives a dose and is observed for the presence or absence of DLT only at that dose. Therefore, we can only observe partial information. For instance, consider a trial investigating six available dose levels. Suppose a patient is given dose level 4 and experiences a DLT. The monotonicity assumption driving dose-finding design implies that a DLT would necessarily be observed at dose levels 5 and 6. We will not have any information regarding whether the patient would have experienced a DLT for any dose below level 4. Conversely, should dose level 3 be deemed safe for an enrolled patient, we can then infer that he or she would also experience a non-DLT at dose levels 1 and 2. However, any information concerning whether the patient would have had a DLT had he or she been given any dose above level 3 is unknown.

In simulating trial data, we can generate each patient’s latent outcome from which we can observe DLT at all available dose levels. For example, consider a set of true DLT probabilities R(d₁) = 0.05; R(d₂) = 0.07; R(d₃) = 0.20; R(d₄) = 0.35; R(d₅) = 0.55; and R(d₆) = 0.70. Suppose patient j has a latent tolerance of v_j = 0.238. Therefore, he or she will experience a non-DLT at dose levels 1; 2; and 3 because v_j > R(d_i) for i = 1,2,3, and will experience a DLT at levels 4; 5; and 6 because v_j < R(d_i) for i = 4,5,6. Complete information is not obtainable from a real trial due to the fact that we cannot, in reality, observe a patient’s toxicity tolerance. We can however generate complete vectors of toxicity information for a simulated trial of n patients and use them to estimate the DLT probabilities by using the sample proportion R̂(d_i) of observed DLTs at each dose. These estimates can then be used to select the MTD, defined as the dose with an estimated DLT probability closest to the target DLT rate θ. Table 1 presents the complete toxicity vectors of 20 simulated patients for the assumed true DLT probabilities above. The last row of Table 1 gives the sample proportions of the simulated trial. After 20 patients, the recommended dose is level 3, with an estimated DLT probability of R̂(d_i) = 0.15, which is closest to a target DLT rate of θ = 0.20. It can easily be shown that the sample proportion is an unbiased estimator of the true DLT probability at each dose, and that the variance of the sample proportion achieves the Cramer-Rao lower bound. In this sense, the benchmark can be considered optimal.⁴ We have developed an R Shiny Web Application, which we now describe, for simulating the operating characteristics of this benchmark.

Table 1.

Simulated Phase I trial of complete information for a sample of 20 patients under an assumed set of true DLT probabilities.

Patient	Tolerance	True DLT probability at dose level i
j	vj	0.05	0.07	0.20	0.35	0.55	0.70
1	0.606	0	0	0	0	0	1
2	0.703	0	0	0	0	0	0
3	0.891	0	0	0	0	0	0
4	0.441	0	0	0	0	1	1
5	0.115	0	0	1	1	1	1
6	0.247	0	0	0	1	1	1
7	0.686	0	0	0	0	0	1
8	0.968	0	0	0	0	0	0
9	0.967	0	0	0	0	0	0
10	0.464	0	0	0	0	1	1
11	0.958	0	0	0	0	0	0
12	0.441	0	0	0	0	1	1
13	0.008	1	1	1	1	1	1
14	0.843	0	0	0	0	0	0
15	0.221	0	0	0	1	1	1
16	0.500	0	0	0	0	1	1
17	0.294	0	0	0	1	1	1
18	0.143	0	0	1	1	1	1
19	0.671	0	0	0	0	0	1
20	0.506	0	0	0	0	1	1
Sample Proportions		0.05	0.05	0.15	0.30	0.55	0.70

Results

The operating characteristics of the benchmark can be evaluated over many simulation runs and can be considered an upper bound for accuracy. One way to assess a method’s accuracy is by simply observing the percentage of trials in which it correctly identifies the true MTD. This is referred to as the percentage of correct selection. A more thorough assessment will involve looking at the entire distribution of the selected doses in order to see how often a method recommends doses other than the correct one as the MTD. For instance, in order to adhere to certain ethical considerations presented by Phase I trials, it is appropriate to evaluate how often a method selects doses above the MTD (i.e. overly toxic doses). It is important to have some measure of accuracy that represents the distribution of doses selected as the MTD. For instance, the accuracy index of Cheung⁷ given by

$$A_n=1-k\times \frac{{\mathrm{\sum }}_{i=1}^k\mid R(d_i)-\theta \mid \times \text{Probability}\text{of}\text{selecting}\text{dose}i}{{\mathrm{\sum }}_{i=1}^k\mid R(d_i)-\theta \mid }$$

is a weighted average summary of the distribution of MTD recommendation, where n is the sample size and k is the number of dose levels being studied. Its maximum value is 1 with larger values (close to 1) indicating that the method possesses high accuracy.

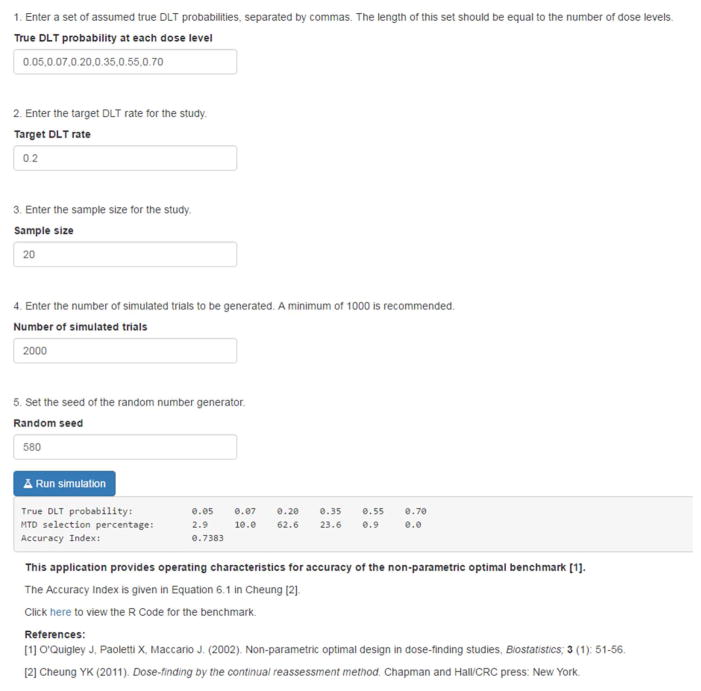
The web application is written in the R programming language⁸ and is made freely available using the Shiny package.⁹ Access to the application online is available at https://uvatrapps.shinyapps.io/nonparbnch/. The R code for the application can be downloaded by clicking the link on the web application or by locating the ‘R code’ section at http://faculty.virginia.edu/model-based_dose-finding/. The application has a simple web interface, where the user specifies five input parameters; (1) True DLT probability at each dose level, a comma delimited vector of assumed DLT probabilities, (2) Target DLT rate, (3) Sample size, (4) Number of simulated trials, and (5) Seed of the random number generator. The output of the application produces three components for evaluating the accuracy operating characteristics for the benchmark; (1) True DLT probability, the entered vector of assumed true DLT probabilities, (2) MTD selection percentage, the percentage of simulated trials in which each dose was selected as the MTD, and (3) Accuracy Index, Cheung’s summary of accuracy given above. The MTD selection percentage and the Accuracy Index can vary depending on the number of simulated trials run, so it is recommended that a minimum of 1000 trials be run in a simulation study.^2,3 The results can be reproduced exactly by another user by entering the exact same set of input parameters, provided that the same random seed is used.

As an illustration of how the optimal can be used to assess design performance, we present simulation results in Figure 1 for a true toxicity scenario in which R(d₁) = 0.05; R(d₂) = 0.07; R(d₃) = 0.20; R(d₄) = 0.35; R(d₅) = 0.55; and R(d₆) = 0.70. The target DLT rate is 20%, indicating dose level 3 to be the true MTD in this scenario. The random seed is set at 580. In each of the 2,000 simulated trials, complete information was generated for a fixed sample size of n = 20 patients, from which the sample proportions were calculated. These values were used to select the MTD as the dose that minimizes the absolute distance between the estimated DLT probability and the target DLT rate of θ = 0.20 at the end of each trial. The distribution of MTD selection was calculated by tabulating the proportion of simulated trials in which each dose was selected as the MTD. The simulation results assess how well the benchmark is performing in terms of accuracy in two ways. One is by simply observing the distribution of MTD selection and the percentage of correct selection. The second is the accuracy index. The results provide the true probability of DLT at each dose {0.05, 0.07, 0.20, 0.35, 0.55, 0.70}, the selection percentage for each dose as the MTD after 2,000 simulated trials {2.9, 10.0, 62.6, 23.6, 0.9, 0.0}, and the accuracy index A₂₀ = 0.7383. The percentage of correct selection is the selection percentage for the true MTD, which is 62.6%.

Figure 1.

Simulation results for the non-parametric optimal benchmark using the new R shiny web application.

Conclusion

In this brief communication, we have presented software in the form of an R shiny web application for a non-parametric optimal benchmark for evaluating dose-finding methods in a timely and reproducible fashion. Having a benchmark can give statisticians a tool for assessing the plausibility of a design’s operating characteristics, serving as an upper limit of how accurate a method can possibly be, given a particular simulation scenario. It should be noted that the benchmark does not account for patient allocation, so it does not output operating characteristics such as percent of experimentation or the expected number of DLTs at each dose level. It cannot be used as a tool for evaluating how well a method can perform in terms of safety. Therefore, the benchmark is not sufficient for a complete evaluation of the operating characteristics for a particular design. Furthermore, it can only be used as simulation tool and cannot be used in practice as a dose escalation design since it assumes knowledge of the true underlying dose-toxicity curve. We have demonstrated the software through one illustrative example, but indeed any specific situation can easily be generated using the application. The results from 10,000 simulated trials takes less than 2 seconds to generate. We hope the availability of this software will facilitate the use of the benchmark in evaluating the operating characteristics of dose-finding methods.