Essentiality Is a Strong Determinant of Protein Rates of Evolution during Mutation Accumulation Experiments in Escherichia coli

Abstract

The Neutral Theory of Molecular Evolution is considered the most powerful theory to understand the evolutionary behavior of proteins. One of the main predictions of this theory is that essential proteins should evolve slower than dispensable ones owing to increased selective constraints. Comparison of genomes of different species, however, has revealed only small differences between the rates of evolution of essential and nonessential proteins. In some analyses, these differences vanish once confounding factors are controlled for, whereas in other cases essentiality seems to have an independent, albeit small, effect. It has been argued that comparing relatively distant genomes may entail a number of limitations. For instance, many of the genes that are dispensable in controlled lab conditions may be essential in some of the conditions faced in nature. Moreover, essentiality can change during evolution, and rates of protein evolution are simultaneously shaped by a variety of factors, whose individual effects are difficult to isolate. Here, we conducted two parallel mutation accumulation experiments in Escherichia coli, during 5,500–5,750 generations, and compared the genomes at different points of the experiments. Our approach (a short-term experiment, under highly controlled conditions) enabled us to overcome many of the limitations of previous studies. We observed that essential proteins evolved substantially slower than nonessential ones during our experiments. Strikingly, rates of protein evolution were only moderately affected by expression level and protein length.

Introduction

Rates of protein evolution exhibit a bewildering diversity, spanning approximately three orders of magnitude. Whereas the sequence of certain proteins remains basically unaltered over large evolutionary periods, others can quickly accumulate an important number of amino acid replacements (Zuckerkandl and Pauling 1965; Dickerson 1971; Li et al. 1985). Protein rates of evolution depend mostly on the selective constraints (purifying selection) to which they are subjected, with different proteins evolving under very different constraints, and hence presenting different rates of evolution. What factors determine the strength of the selective constraints acting on protein evolution, and their relative importance, remains a fundamental question in Evolutionary Biology, and has been the arena of heated debates among those adducing an adaptive value to observable changes in proteins and those invoking the Neutral Theory to explain the observed variations in the rates of evolution among proteins.

Initial attempts to explain the variability of protein rates of evolution focused on the different importance and functional density of proteins. Kimura and Ohta (1974) deduced from the Neutral Theory of Molecular Evolution (Kimura 1968, 1983) that proteins or protein domains that are functionally less important ought to evolve faster than those that are functionally more important, as a lower fraction of mutations are expected to be neutral in important proteins. Zuckerkandl (1976) postulated that the strength of purifying selection acting on a protein depends on the proportion of amino acids involved in the protein’s function (i.e., its “functional density”). Wilson et al. (1977) proposed that the rate of evolution of a protein should be influenced by the effect of a substitution on the function of the protein and the probability that an organism can survive and reproduce without that protein (dispensability). Limited by the amount of data available at that time, however, these hypotheses could only be supported by anecdotal examples.

In the last years, the development of diverse high-throughput techniques has allowed scientists to investigate the effects of multiple factors on the rates of protein evolution (for review, see Herbeck and Wall 2005; Koonin 2005; Koonin and Wolf 2006; Pál et al. 2006; Rocha 2006; Choi and Hannenhalli 2013; Alvarez-Ponce 2014; Zhang and Yang 2015). Surprisingly, rates of protein evolution seem to be mostly determined by levels and patterns of gene expression (Pál et al. 2001; Rocha and Danchin 2004; Drummond et al. 2005, 2006; Wilke and Drummond 2006; Drummond and Wilke 2008). Unexpectedly, the rates of evolution of essential genes (those whose knock-out results in lethality or sterility) are only slightly lower than those of nonessential genes, particularly once covariation of both rates of evolution and essentiality with expression levels is corrected for. In fact, early analyses in rodents found no significant differences between the rates of evolution of essential and nonessential genes once genes involved in the immune system, which are known to often evolve under positive selection, were removed from the analysis (Hurst and Smith 1999). Similarly, in yeasts no differences were observed between essential and nonessential genes, and only a weak positive correlation was detected between rates of protein evolution and dispensability (Hirsh and Fraser 2001), which vanished once expression levels were corrected for (Pál et al. 2003). Several subsequent analyses in bacteria (Jordan et al. 2002; Dötsch et al. 2010; Wei et al. 2013; Ish-Am et al. 2015; Luo et al. 2015), yeasts (Hirsh and Fraser 2003; Yang et al. 2003; Chen and Xu 2005; Wall et al. 2005; Zhang and He 2005; Kim and Yi 2007; Plotkin and Fraser 2007; Wang and Zhang 2009; Xia et al. 2009; Theis et al. 2011; Vishnoi et al. 2011; Waterhouse et al. 2011), Caenorhabditis (Castillo-Davis and Hartl 2003; Cutter et al. 2003; Luz and Vingron 2006), Drosophila (Larracuente et al. 2008; Waterhouse et al. 2011), and mammals (Liao et al. 2006; Waterhouse et al. 2011; Luisi et al. 2015) have shown that essential and lowly dispensable genes do evolve slower than nonessential and highly dispensable genes. However, the differences are usually very small, and sometimes negligible once covariation with expression levels is corrected for (Rocha and Danchin 2004; Drummond et al. 2006). Nonetheless, some authors have advised caution regarding this claim, as a stronger effect of essentiality can be observed when using certain statistical techniques (Wall et al. 2005; Plotkin and Fraser 2007; Wei et al. 2013). In Escherichia coli, all analyses in which the confounding effect of expression level has been controlled for have shown that essentiality has a very small effect (Rocha and Danchin 2004; Drummond et al. 2006), or an effect that is weak compared with that of expression level and its surrogates (Wei et al. 2013).

Thus far, analyses of the effect of essentiality and dispensability on rates of protein evolution have relied on rates of evolution estimated by comparison of different, often phylogenetically distant, species. It has been argued, that this approach may have entailed a number of limitations. First, most analyses have relied on estimates of essentiality and dispensability obtained under the favorable conditions of the lab, which may not resemble the conditions under which the compared species diverged (Brookfield 1992; Hurst and Smith 1999; Pál et al. 2006; Wolf 2006). Thus, many of the genes that are not essential in the lab may be essential under some of the conditions faced in nature (but see Wang and Zhang 2009). Second, essentiality itself is an evolving feature, and hence genes that are essential in one species may be dispensable in closely related species (Gerdes et al. 2003; Roemer et al. 2003). Therefore, estimates of essentiality in one species are only approximate estimates of essentiality over the divergence period studied. Indeed, Zhang and He (2005) found that the differences between essential and nonessential genes in yeast increased significantly when rates of protein evolution were estimated from closely related species. Third, during the divergence of essential genes, many mutations are filtered by natural selection, particularly deleterious or slightly deleterious mutations (Kimura et al. 1963; Kimura 1968; Lanfear et al. 2014). When comparing different species, only fixed mutations are accounted for, whereas many are lost neutrally or by purifying selection depending on the effective population size, providing a poor picture of the tolerance of the organism to mutations in its genes. Fourth, high rates of protein evolution can be the result of both positive selection or relaxed purifying selection, and the former can only be detected under certain conditions (Anisimova et al. 2001). Fifth, the combined and correlated effect of many factors on protein evolution (i.e., expression levels, protein lengths, network position, etc.) makes it difficult to isolate the individual effect of essentiality (Koonin and Wolf 2006; Larracuente et al. 2008; Alvarez-Ponce 2014). This limitation, although alleviated by the use of multivariate analyses, remains unresolved, as no single approach seems to be able to completely disentangle the factors influencing the rates of protein evolution (Drummond et al. 2006; Wolf et al. 2006; Ingvarsson 2007; Kim and Yi 2007; Plotkin and Fraser 2007; Alvarez-Ponce 2014). Finally, deleterious mutations may have been restored by compensatory mutations, within the same gene or in interacting genes, diluting the effects of mutations on essential proteins (Codoñer and Fares 2008; Lovell and Robertson 2010). It is likely that, combined, these limitations may have led to an underestimation of the effect of essentiality on protein rates of evolution.

Are organisms less tolerant of amino acid replacements in essential proteins than in nonessential proteins? Here, we address this question by studying evolution on a much shorter evolutionary time-scale, and under controlled conditions that resemble those in which essentiality was previously determined. For that purpose, we performed two parallel evolution experiments using E. coli under controlled conditions, maintaining a very small effective population size (close to 1), over a period comprising 5,500–5,750 generations of evolution. This is expected to alleviate, to a great extent, many of the problems described earlier (see the “Discussion” section). Contrary to what has been previously observed, we found that essentiality is a very strong determinant of protein rates of evolution: nonessential proteins evolved 27–65% faster than essential ones. Remarkably, gene expression and protein length had only a moderate impact, if any, on protein rates of evolution in our experiments.

Results

Accumulation of Mutations in Two Parallel Experimental Evolution Lines of E. coli

Our evolution experiment started with a colony of the strain of E. coli K12 MG1655 lacking the repair gene mutS (ΔmutS strain). Using this strain enabled a faster rate of evolution (∼1,000 times faster than a standard E. coli K12 MG1655 strain; Bjedov et al. 2007; Turrientes et al. 2013), which enabled our lines to accumulate a large number of mutations in a relatively short time. From a colony of this strain, two lineages were created (lines A and B). Each line was systematically passaged on rich Luria–Bertani (LB) medium, by re-streaking a single colony every ∼24 h on a fresh Petri dish. A total of 260 passages were conducted for line A, and 250 for line B (equivalent to ∼5,720 and ∼5,500 E. coli generations, respectively). A “living” record of the evolution experiment was built for each of these evolution lines by preparing a glycerol stock that included samples of the evolving populations isolated every ∼10 passages (i.e., every 220 generations). A total of seven colonies were sequenced, including line A after 100, 200, 250, and 260 passages, and line B after 150, 200, and 250 passages (fig. 1).

Fig. 1.—

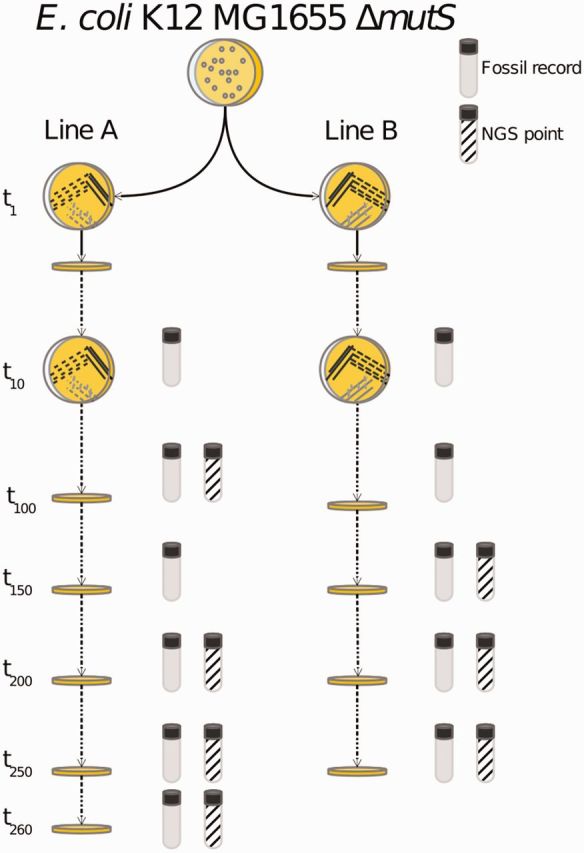
Mutation accumulation experiment scheme. In each passage, part of one colony was picked and used to found the new generation. Genomes for line A were sequenced after 100, 200, 250, and 260 passages. For line B, genomes were sequenced after 150, 200 and 250 passages.

When comparing each genome to the ancestral ΔmutS genome (Sabater-Muñoz et al. 2015), a total of 291 substitutions were identified in genome A100 (line A after 100 passages), 552 in genome A200, 695 in A250, and 733 in A260. With very few exceptions, substitutions at any time point included those for the previous points, consistent with the clonal propagation scheme used: A200 is a descendant of A100, A250 is a descendant of A200, and A260 is a descendant of A250. Likewise, a total of 724 substitutions were identified in genome B150, 1,041 in B200 and 1,281 in B250. The mutation spectra at the end of the experiments are summarized on supplementary table S1, Supplementary Material online. A total of 126 genes were lost in line A (47 due to large deletions, 16 by nonsense mutations, and 63 by frameshift mutations), and 90 were lost in line B (8 due to large deletions, 20 due to nonsense mutations, and 62 due to frameshift mutations). Seven of the genes lost in line A and five of the genes lost in line B were deemed essential by Gerdes et al. 2003. Genes lost in line B include mutT, ogt and gph, responsible for DNA repair, which may explain why line B evolved much faster than line A. This makes the results for line B particularly relevant for our purposes. A Gene Ontology enrichment analysis of lost genes reveals that they are enriched in unclassified proteins (in terms of biological process, molecular function and cellular component). In addition, lost genes in line A are 33.7-fold enriched in genes involved in histidine biosynthesis.

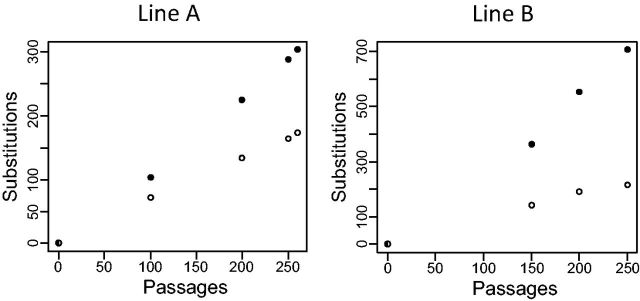
Consistent with previous observations in an E. coli strain deficient for the DNA repair machinery (Lee et al. 2012), 98% of point mutations accumulated in line A were transitions. However, in line B this fraction was only 45%, due mostly to a very high incidence of A→C and T→G mutations (supplementary table S2, Supplementary Material online). At the end of the experiments, the genome of line A had accumulated a total of 174 synonymous and 304 nonsynonymous substitutions, and that of line B had accumulated 215 synonymous and 705 nonsynonymous substitutions. Both synonymous and nonsynonymous substitutions accumulated in a molecular clock fashion during the experiments, with no signs of saturation of either synonymous or nonsynonymous genome sites (fig. 2). In the remainder of this article, we focus on the mutational landscapes at the end of the experiment (i.e., genomes A260 and B250), as they contain the highest number of mutations and are therefore the most informative to study protein rates of evolution; nevertheless, the tables include the results for all intermediate genomes.

Fig. 2.—

Accumulation of synonymous (white) and nonsynonymous (black) mutations in two parallel mutation accumulation lines.

The evolution of both lines exhibited significant parallelisms. A total of 10 genes were lost in parallel in both lines. In order to evaluate the statistical significance of this overlap, we performed a permutation test. In each permutation, two lists of E. coli genes (one of size 126 and another of size 90) were obtained randomly, and the number of genes present in both lists was recorded. This process was repeated 10,000 times. The average number of overlapping genes was only 2.54, and only one of the permutations exhibited an overlap higher than or equal to 10 genes (P = 0.0001), indicating that the observed degree of overlap is significantly higher than would be expected if genes were lost at random. Similar results were obtained when the analysis was restricted to nonessential genes (number of genes lost in both lines: 8, average number of overlapping genes in the simulations: 2.62, P = 0.0041).

A total of 40 substitutions (17 synonymous and 23 nonsynonymous) occurred convergently at the same positions in both mutation accumulation lines. To assess the statistical significance of this number, we compiled a list of all mutations affecting coding regions in line B (e.g., mutation 1 implied substitution of codon “AAT” by codon “AAG” at position 428 of gene aaeB), and we randomized the position of these mutations a total of 2,500 times. In each randomization, each mutation was randomly reassigned to any position of the genome with the same initial codon (e.g., in randomization 1, mutation 1 was randomly reassigned to codon 97 of gene pgpC, which before the mutation was an “AAT” codon), and it was counted the number of mutations that were shared between the randomized genome and line A. On average, both sets of mutations exhibited an overlap of only 0.333 mutations (ranging from 0 to 4), indicating that the observed degree of convergence is much higher than would be expected if mutations had accumulated randomly.

Essential Proteins Evolved Substantially Slower than Nonessential Proteins during Our Short-Term Evolution Experiments

The genome of our ancestral line (the ΔmutS colony that we used as parental genome) contains a total of 4,237 putatively functional protein-coding genes. Out of these, 611 (14.4%) were determined to be essential (i.e., deletion of these genes results in lethality or inability of cells to divide), and 2,981 were deemed nonessential by Gerdes et al. (2003). The rest could not be classified for different reasons (Gerdes et al. 2003). The coding regions of essential and nonessential genes in our ancestral line exhibit virtually identical nucleotide compositions (supplementary table S3, Supplementary Material online).

We inferred the strength of purifying selection acting on protein-coding genes from the nonsynonymous to synonymous divergence ratio (ω = d_N/d_S, where d_N is the number of substitutions per nonsynonymous position, and d_S is the number of substitutions per synonymous site). Assuming that synonymous mutations are neutral, values of ω < 1, ω = 1, or ω > 1 are indicative of purifying selection filtering out nonsynonymous substitutions, genes evolving neutrally, or positive selection, respectively. The small number of substitutions observed in our relatively short evolution experiments does not allow calculating d_N/d_S values for individual genes, as many genes have accumulated no substitutions, and no gene has accumulated enough substitutions to infer d_N/d_S accurately. Therefore, we decided to group genes in two categories, essential and nonessential, and to calculate the overall d_N/d_S within each group. For that purpose, two concatenomes were generated: one for essential and another for nonessential genes. Genes that had been lost at the end of our experiments (126 in line A and 90 in line B) were not included in our analyses.

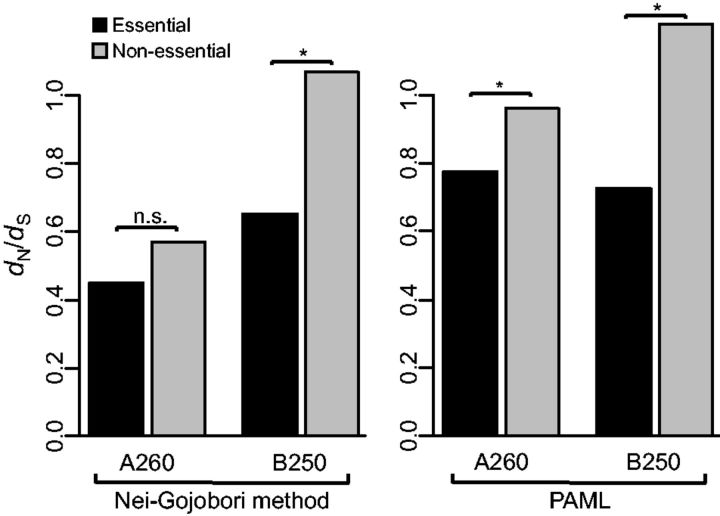
Comparison of the parental genome and the evolved genomes revealed higher d_N/d_S values for nonessential genes than for essential genes in both evolving lines, A and B. For genome A260, d_N/d_S was 0.451 for essential genes and 0.572 (i.e., 27% higher) for nonessential genes. For genome B250, d_N/d_S was 0.651 for essential genes and 1.071 (i.e., 65% higher) for nonessential genes (table 1 and fig. 3). A Fisher’s exact test showed that ω = 1.071 is not significantly >1 (P = 0.443) for B250 nonessential genes, indicating that positive selection cannot be invoked. Therefore, our results indicate that essential genes evolved under stronger purifying selection than nonessential genes.

Table 1.

Rates of Evolution of Essential and Nonessential Genes

Genome	Essential genes (n = 611)								Nonessential genes (n = 2,981)								P-value
	Nonsyn. difs.	Nonsyn. pos.	d N	Syn. difs.	Syn. pos.	d S	d N/dS (N–G)	d N/dS (PAML)	Nonsyn. difs.	Nonsyn. pos.	d N	Syn. difs.	Syn. pos.	d S	d N/dS (N–G)	d N/dS (PAML)	LRT
A100	11	373,440.6	2.95×10−5	9	119,780.4	7.51×10−5	0.392	0.681	86	2,251,207.0	3.82×10−5	61	722,587.8	8.44×10−5	0.453	0.462	3.1×10−126***
A200	27	373,442.4	7.23×10−5	21	119,778.6	1.75×10−4	0.412	0.715	184	2,251,206.0	8.17×10−5	107	722,589.1	1.48×10−4	0.552	0.500	>0.999
A250	35	373,443.9	9.37×10−5	26	119,777.1	2.17×10−4	0.432	0.749	235	2,251,205.0	1.04×10−4	131	722,590.6	1.81×10−4	0.576	0.970	0.017*
A260	38	373,444.3	1.02×10−4	27	119,776.8	2.25×10−4	0.451	0.775	244	2,251,205.0	1.08×10−4	137	722,590.4	1.90×10−4	0.572	0.964	<10−156***
B150	38	374,720.9	1.01×10−4	26	120,213.1	2.16×10−4	0.469	0.586	291	2,256,565.0	1.29×10−4	111	724,430.1	1.53×10−4	0.842	1.107	5.5×10−9***
B200	61	374,719.6	1.63×10−4	34	120,214.4	2.83×10−4	0.576	0.667	449	2,256,549.0	1.99×10−4	150	724,445.8	2.07×10−4	0.961	1.137	<10−156***
B250	71	374,717.9	1.89×10−4	35	120,216.1	2.91×10−4	0.651	0.728	574	2,256,543.0	2.54×10−4	172	724,452.3	2.37×10−4	1.071	1.211	7.1×10−11***

*P < 0.05;

**P < 0.01;

***P < 0.001.

Nonsyn. difs., nonsynonymous differences; Nonsyn. pos., nonsynonymous positions; d_N = nonsynonymous differences per nonsynonymous position; Syn. difs., synonymous differences; Syn. pos., synonymous positions; d_S = synonymous differences per synonymous position; N–G, Nei–Gojobori method; FET, Fisher’s exact test; LRT, likelihood ratio test.

Fig. 3.—

Evolutionary rates of essential and nonessential proteins at the end of the evolution experiments. Statistical support was determined using the Fisher’s exact test. *P < 0.05. n.s., nonsignificant.

At the end of the evolution of line B (genome B250), essential genes had accumulated a total of 35 synonymous and 71 nonsynonymous substitutions, and nonessential genes had accumulated a total of 171 synonymous and 574 nonsynonymous substitutions (table 1). The ratio of nonsynonymous to synonymous substitutions is significantly higher for nonessential genes (574/171 = 3.34) than for essential genes (71/35 = 2.03; Fisher’s exact test, P = 0.029), consistent with our interpretation that the latter evolve under stronger selective constraints. A similar, but less acute, trend is observed for genome A260 (essential genes accumulated 27 synonymous and 38 nonsynonymous substitutions, whereas nonessential genes accumulated 137 synonymous and 244 nonsynonymous substitutions), although the difference in ω between essential and nonessential genes was not significant (38/27 = 1.407; 244/137 = 1.781; Fisher’s exact test: P = 0.406). This might be due, at least in part, to the fact that line A has accumulated fewer mutations than line B, which may be limiting the power of the test. When we repeated our analyses using the model M0 (implemented in the codeml program, PAML package; Yang 2007), we observed that the d_N/d_S ratios of nonessential genes were significantly higher than those of essential genes in all genomes except genome A200 (genome A260: P < 10 ⁻¹⁵⁶; genome B250: P = 2.1 × 10 ⁻⁸; table 1 and fig. 3). In order to discard the possibility that our results might have been biased by the patterns of evolution of long proteins (which contribute disproportionally to our concatenated alignments), we repeated our analyses after removing the longest proteins (the top 33.33%). Similar results were obtained, with the likelihood ratio test revealing slower rates of evolution for essential proteins in all genomes except A260 (supplementary table S4, Supplementary Material online).

In order to discard the possibility that the faster rates of evolution of nonessential proteins may be due to confounding factors such as these proteins having a different amino acid composition, or their encoding genes having a different codon composition, we compiled a list of all mutations affecting coding regions in line B (as above), and we performed the following randomization a total of 2,500 times. First, each mutation was randomly reassigned to any position of the genome with the same initial codon (as above). Second, we obtained a concatenome for essential genes, and another for nonessential genes, as described earlier. Third, the d_N/d_S of essential and nonessential genes were compared. The median of the ratio ω_nonessential/ω_essential was 1.017 (i.e., in the randomized alignments nonessential proteins evolved only 1.7% faster than essential ones), and only in 34 of the 2,500 randomizations the ratio was higher than or equal to the ratio observed in our evolution experiment (ω_nonessential/ω_essential = 1.65; table 1), indicating that the ratio observed in our experiment is not expected under a random distribution of mutations among essential and nonessential genes (P = 34/2,500 = 0.014). When we used the mutations accumulated in line A in our analyses, the median ω_nonessential/ω_essential ratio was 0.999 (i.e., in the randomized alignments essential proteins evolved 0.1% faster than nonessential ones), and the ratio was higher than the observed in our experiment (1.27; table 1) in 455 of the simulations (P = 455/2,500 = 0.182). The lack of significance in the permutation test in the case of line A may be due to reduced statistical power resulting from the smaller number of mutations accumulated in this line. These observations indicate that the faster rates of evolution of nonessential proteins observed in our experiments is not due to a different amino acid or codon composition.

Little Evidence for an Effect of Levels of Gene Expression and Protein Abundance on the Rates of Protein Evolution

For each E. coli gene, we obtained its mRNA abundance from Covert et al. (2004) and the abundance of the encoded protein from the PaxDB database (Wang et al. 2015). Consistent with previous reports (Cutter et al. 2003; Pál et al. 2003; Zhang and He 2005), we observed that essential E. coli genes are significantly more highly expressed than nonessential genes (median mRNA abundance: 338.20 for essential genes, 132.23 for nonessential genes; Mann–Whitney’s U test, P = 1.30 × 10 ⁻³³). We also observed that essential genes tend to encode proteins that are more highly abundant than those encoded by nonessential genes (median protein abundance: 30.80 for essential genes, 4.88 for nonessential genes; P = 4.05 × 10 ⁻²²). This, combined with the fact that, in all organisms studied so far including E. coli, mRNA and protein abundances negatively correlate with rates of protein evolution (Pál et al. 2001; Rocha and Danchin 2004; Drummond et al. 2005, 2006), raises the possibility that our observation that essential proteins evolve slower than nonessential proteins is a byproduct resulting from the higher expression level of essential genes. That is, it is possible that essential proteins evolve slower due to their high levels of expression rather than to their essentiality per se. However, two pieces of evidence demonstrate that this is not the case.

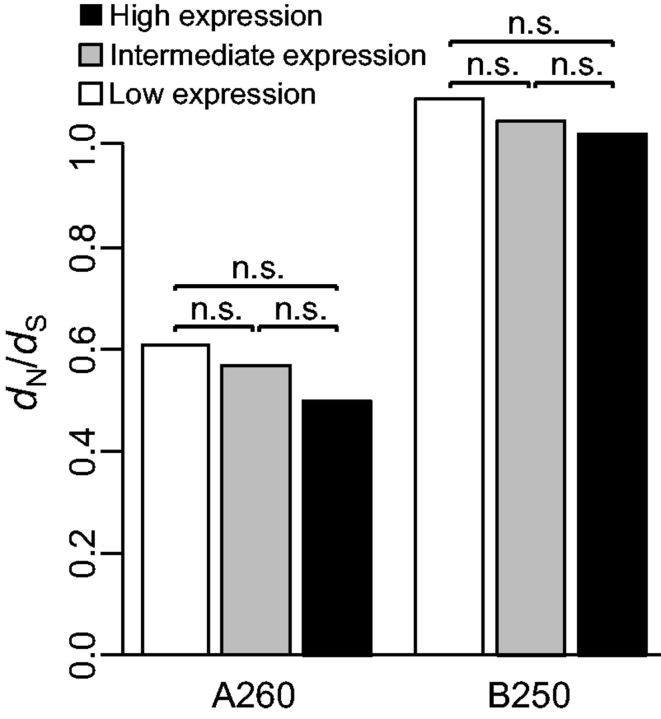
First, in our evolution experiment there was only little evidence for slower rates of evolution in highly expressed genes than in lowly expressed genes. We classified all E. coli genes into three categories with the same number of genes (n = 1,327 each) according to their expression levels (mRNA abundances: 0–78.43 for lowly expressed genes; 78.47–290.77 for intermediately expressed genes; 290.87–4,902.43 for highly expressed genes). Respectively, highly, intermediately and lowly expressed genes exhibit aggregated d_N/d_S values of 0.499, 0.567, and 0.610 in genome A260, and 1.024, 1.051, and 1.093 in genome B250 (supplementary table S5, Supplementary Material online and fig. 4). The nonsynonymous/synonymous substitutions ratios for highly and lowly expressed genes are not significantly different (Fisher’s exact test; P = 0.416 for A260; P = 0.770 for B250). Classification of genes according to their protein abundances yielded similar results (supplementary table S6, Supplementary Material online). Similar results were obtained when we compared the top 10% highly expressed genes with the bottom 10% expressed genes, and when we compared the top 20% highly expressed genes with the bottom 20% expressed genes (supplementary table S7, Supplementary Material online). However, when we compared the top 50% highly expressed genes with the bottom 50% expressed genes, lowly expressed genes were found to evolve significantly slower in genome A260 (according to both the Fisher’s exact test and the likelihood ratio test) and in genome B250 (according to the likelihood ratio test, but not according to the Fisher’s exact test; supplementary table S7, Supplementary Material online).

Fig. 4.—

Evolutionary rates of highly, intermediately and lowly expressed genes. Statistical support was determined using the Fisher’s exact test. N.s., nonsignificant.

Second, the rates of evolution were higher for a group of nonessential genes with virtually the same distribution of mRNA abundances as the 595 essential genes with available expression data. We ranked all genes according to their expression level. For each essential gene in the list, we randomly selected the nonessential gene that was immediately above, or that immediately below in the ranking. In the genome A260, essential and nonessential genes exhibit a d_N/d_S of 0.439 and 0.495, respectively (i.e., nonessential genes evolved 12.6% faster). In the genome B250, essential and nonessential genes display a d_N/d_S of 0.651 and 1.055, respectively (i.e., nonessential genes evolved 62.1% faster) (supplementary table S8, Supplementary Material online). Similar results were obtained when protein abundance was used as controlling variable (nonessential genes evolved 18.6% and 95.3% faster in genomes A260 and B250, respectively; supplementary table S9, Supplementary Material online). For genome B250, the nonsynonymous/synonymous substitutions ratio is significantly higher for nonessential genes (Fisher’s exact test; P = 0.034). Therefore, the observed differences in the evolutionary rates of essential and nonessential proteins are independent from their differences in expression levels and protein abundances.

Little Evidence for an Effect of Protein Length on Rates of Protein Evolution during Our Mutation Accumulation Experiments

It has been previously suggested that protein length is an important determinant of rates of protein evolution. However, both the strength and the sign of the correlation varies from one analysis to another (Marais and Duret 2001; Lipman et al. 2002; Drummond et al. 2006; Liao et al. 2006; Ingvarsson 2007; Alvarez-Ponce 2012; Shin and Choi 2015), hinting at a complex, and perhaps multifactorial, relationship between evolutionary rate and protein length (reviewed in Alvarez-Ponce 2014).

Essential proteins are significantly shorter than nonessential proteins in E. coli (median length: 219 and 305 amino acids; Mann–Whitney’s U test, P = 1.62 × 10 ⁻²⁴), thus raising the possibility that our observation that essential proteins evolve slower could be due to their particular length. However, we found that protein length had little effect, if any, on proteins’ rates of evolution during our evolution experiment. We divided proteins into three categories according to their length (short: <199 amino acids, n = 1,414; intermediate: 200–350 amino acids, n = 1,414; long: >351 amino acids, n = 1,409). Respectively, short, intermediate, and long proteins had a d_N/d_S of 0.809, 0.402, and 0.609 in genome A260; and 0.994×, 0.985, and 1.099 in genome B250 (supplementary table S10, Supplementary Material online). The nonsynonymous/synonymous substitutions ratios are not significantly different for any of the possible comparisons (short vs. intermediate, intermediate vs. long, or short vs. long) (Fisher’s exact test; P ≥ 0.051 for genome A260; P ≥ 0.597 for genome B250). Similar results were obtained when we compared the top 10% longest proteins with the top 10% shortest proteins, and when we compared the top 20% longest proteins with the top 20% shortest ones (supplementary table S11, Supplementary Material online). When we compared the top 50% longest proteins with the top 50% shortest ones, the Fisher’s exact test revealed no significant differences, and the likelihood ratio test was significant only for genome A260. In this genome, long proteins evolved 10% faster than short ones (supplementary table S11, Supplementary Material online). It should be noted, however, that in some comparisons long genes evolved faster than short ones, whereas in other comparisons short genes evolved faster (depending on the line and threshold used; supplementary table S11, Supplementary Material online), and therefore the link between protein length and rates of evolution remains unclear.

In addition, we obtained a list of nonessential genes with a length distribution nearly identical to that for essential genes (using a procedure identical to that described earlier for mRNA and protein abundances). For genome A260, d_N/d_S is slightly smaller for nonessential genes (0.440) than for essential ones (0.451). However, for genome B250, nonessential genes evolved 77.5% faster (supplementary table S12, Supplementary Material online). This indicates that the faster rate of evolution observed in nonessential genes is independent of protein length, at least in the evolution of line B.

Our Observations Are Not Confounded by Gene Functions

Genes involved in “informational” processes (replication, transcription and translation) tend to evolve slower than those involved in “operational” ones (metabolism, cellular processes and signaling) (Alvarez-Ponce and McInerney 2011). In addition, “informational” genes tend to be essential (Alvarez-Ponce and McInerney 2011). Given the potential that this could have biased our analyses, we classified all E. coli genes into two categories, informational or operational, and analyzed the differences between essential and nonessential genes within each category. In both A260 and B250 genomes, essential informational genes (n = 158) exhibit a substantially lower d_N/d_S ratio than nonessential informational (n = 421) ones, and essential operational genes (n = 333) exhibit substantially lower d_N/d_S ratios than nonessential operational ones (n = 1,791; supplementary table S13, Supplementary Material online). However, the differences are only statistically significant for operational genes (i.e., the case in which more genes were available for analysis; likelihood ratio test, genome A260: 2Δℓ = 298.51, P = 7.0 × 10 ⁻⁶⁷; genome B250: 2Δℓ = 33.25, P = 8.1 × 10 ⁻⁹). Differences are not statistically significant for the other 3 comparisons, probably due to reduced statistical power (supplementary table S13, Supplementary Material online).

We next classified E. coli genes into different COG functional categories (Galperin et al. 2015) and compared the rates of evolution of essential and nonessential proteins within each category (supplementary table S13, Supplementary Material online). For genome B250, d_N/d_S could be calculated separately for essential and nonessential genes for a total of 13 functional categories, and essential genes evolved slower in 11 of these categories, which represents a significant departure from the 6.5 categories expected by chance (Binomial test, P = 0.022). A similar analysis of the A260 genome reveals no statistically significant differences (P > 0.999), which is consistent with the smaller number of mutations accumulated in line A, for which we may have reduced statistical power. Taken together, these results suggest that our observation that essential proteins evolved slower than nonessential ones is not due to covariation of functional category with both essentiality and rates of evolution.

Our Observations Are Not Confounded by the Concatenome Approach Used

As mentioned earlier, the small number of mutations accumulated in each gene during our evolution experiments prevented us from calculating a separate d_N/d_S ratio for each gene; instead, we decided to generate two concatenomes (one for essential, and another for nonessential genes). We considered the possibility that this approach might be biasing our results, somehow amplifying the differences between essential and nonessential genes. To discard this possibility, we identified the most likely ortholog of each E. coli gene in the closely related bacterium Salmonella enterica, and we obtained a CDS alignment for each pair of orthologs (see the “Material and Methods” section). We (1) calculated the d_N/d_S ratio for each alignment individually, and (2) obtained two concatenomes (one for essential and another for nonessential genes) and we calculated the d_N/d_S ratio for each concatenome.

When rates of evolution were estimated separately for each gene, the median d_N/d_S ratio of nonessential genes was 12% higher than the median d_N/d_S ratio for essential genes (median for essential genes: 0.041, median for nonessential genes: 0.045). A Mann–Whitney U test revealed significant differences (P = 0.008). When rates of evolution were estimated on the concatenomes, the d_N/d_S ratio of essential genes was 17% higher for nonessential genes than for essential ones (ratio for essential genes: 0.063, ratio for nonessential genes: 0.074). Regardless of the approach used, the percent increase was substantially lower than the 27%–65% increase observed in our evolution experiments (table 1 and fig. 3). Taken together, these observations indicate that our results are not biased by the concatenome approach used.

Discussion

Essential genes maintained substantially lower d_N/d_S ratios than nonessential genes during our evolution experiments (table 1 and fig. 3). This effect was replicated in two mutation accumulation lines that evolved independently, and was clearly independent of gene expression levels, protein abundances, protein lengths and gene functions (supplementary tables S8, S9, S12, and S13, Supplementary Material online). This demonstrates that organisms tolerate less amino acid changing mutations in essential proteins than in nonessential ones. Our observation contrasts with previous results based on comparison of highly divergent genomes, which suggest that in the long term essential proteins evolve only slightly slower than nonessential ones. Therefore, if essential proteins do not evolve substantially slower than nonessential proteins across long evolutionary distances, this might be due to the simultaneous action of a number of confounding factors (expression levels, population dynamics, positive selection, compensatory mutations, changes in genes’ essentiality, etc.) that obscure the effects of essentiality.

The approach adopted in our experiments—relatively short-term experiments, under highly controlled lab conditions, in which we maintained a very small effective population size—probably allowed us to overcome many of the limitations of previous studies based on highly divergent genomes, thus providing a better picture of the effect of essentiality on protein sequence evolution. First, gene essentiality is an evolving parameter (Gerdes et al. 2003; Roemer et al. 2003), and it has been argued that this may have hindered the detection of a relationship between essentiality and protein rates of evolution (Zhang and He 2005). However, the number of generations intervening in our experiment (∼5,500–5,750) was much smaller than the number of generations usually intervening when comparing the genomes of two species. Therefore, most likely, the set of essential genes was virtually the same at the beginning and the end of the experiment.

Second, available essentiality data sets have been obtained under lab conditions that may not resemble the conditions under which species’ divergence took place (Hurst and Smith 1999; Pál et al. 2006; Wolf 2006). Our experiment, however, was conducted in the lab, under conditions that are very similar to those in which essentiality was determined by Gerdes et al. (2003).

Third, evolutionary dynamics is largely affected by effective population size (N_e) (Kimura et al. 1963; Kimura 1968; Lynch and Conery 2003; Lynch 2007; Lanfear et al. 2014), but in nature this parameter changes over time and is difficult to measure (for review, see Charlesworth 2009). We have maintained a controlled, small N_e during our experiments. In each passage, a small number of cells from the same colony were used to found the following generation. Therefore, our E. coli populations were subject to periodic population bottlenecks, which are known to reduce effective population size (Wright 1931; Charlesworth 2009). This is expected to result in a Muller’s ratchet dynamics, a phenomenon that refers to the irreversible accumulation of deleterious mutations in small populations (Muller 1964). In populations with large N_e, natural selection acts efficiently, removing deleterious mutations and driving beneficial mutations to fixation. Conversely, in small populations, genetic drift out-powers natural selection, thus making the fate of most nonlethal mutations (including beneficial, neutral and deleterious mutations) largely determined by drift (Kimura et al. 1963; Kimura 1968; Lanfear et al. 2014) and reducing the gap between the mutation rate and the fixation rate. Remarkably, the low N_e maintained during our experiments, together with the short time spanned, makes positive selection and compensatory mutations (which are often fixed by positive selection; Hartl and Taubes 1996; Charlesworth and Eyre-Walker 2007)—two of the confounding factors known to affect analyses based on comparison of highly divergent genomes—highly unlikely.

Finally, a number of genomic factors, and particularly gene expression level, protein abundance, and perhaps protein length, are known to have a strong impact on rates of protein evolution (Marais and Duret 2001; Pál et al. 2001; Lipman et al. 2002; Rocha and Danchin 2004; Drummond et al. 2006; Liao et al. 2006; Ingvarsson 2007; Alvarez-Ponce 2012). Therefore, establishing any other factor as a true determinant of protein rates of evolution requires demonstrating that its effect on sequence evolution is independent of (i.e., not due to covariation with) these factors. Previous efforts have mostly relied on multivariate analysis techniques, but all available techniques rely on a number of assumptions (e.g., depending on the technique, linear or at least monotonic relationships among the analyzed variables, independence between certain variables, and equal measurement error for the different variables), some of which may not always be met. It is therefore highly debated what techniques should be used to isolate the independent effects of individual variables on rates of protein evolution (Drummond et al. 2006; Wolf et al. 2006; Ingvarsson 2007; Kim and Yi 2007; Plotkin and Fraser 2007; Alvarez-Ponce 2014). Strikingly, we observed that genes with different (low, intermediate and high) mRNA abundances, protein abundances, and protein lengths evolved at similar rates (supplementary tables S5–S7, S10 and S11, Supplementary Material online and fig. 4), indicating that these factors had only a moderate effect on protein evolution during our experiments. In addition, our observation that nonessential proteins evolved faster than essential ones remained unaltered when controlling for expression levels and protein length (supplementary tables S8, S9 and S12, Supplementary Material online). Therefore, our observation that essential genes evolved slower than nonessential genes during our experiment cannot be due to covariation of both essentiality and protein rates of evolution with these factors.

The very small N_e maintained during our mutation accumulation experiments is very different from the one typically observed in natural populations, thus raising the possibility that our observations do not reflect those observed in nature. It should be noted, however, that many natural populations evolve under small population sizes. For instance, microbial infection or colonization of new niches often start with a very small number of individuals (sometimes single individuals; Rubin 1987; Mueller et al. 2005; Ruiz-González et al. 2011), and endosymbiotic bacteria exist in very small populations (Moran and Baumann 1994; Woolfit and Bromham 2003). It is unclear how the low N_e maintained in our experiments may have affected the difference between the evolutionary rates of essential and nonessential proteins. On the one hand, a low N_e may increase the rates of evolution of both essential and nonessential genes, thus reducing the differences between essential and nonessential genes. If this was the case, our observations that essential and nonessential proteins evolve at substantially different rates would be even more striking. On the other hand, in small populations, only lethal and highly deleterious mutations will be removed by purifying selection—the fate of most other mutations will be determined by drift. Only in essential genes, a fraction of nonsynonymous mutations are expected to be lethal. Should this be the case, the small N_e maintained in our experiments may be amplifying the differences between essential and nonessential genes. However, this latter possibility is not supported by the fact that, in endosymbiotic bacteria—which are thought to have small N_e—proteins of all categories, including those participating in basic cellular processes, accumulate a high number of radical nonsynonymous mutations (Wernegreen 2011). Another notable difference between our experiment and evolution occurring in nature is the rich nutritional conditions under which our experiments took place. This may explain the relatively high number of genes lost during our experiment: In such rich conditions, many genes may become nonessential.

The surprisingly weak effect of levels of gene expression on the rates of protein evolution (supplementary tables S5 and S6, Supplementary Material online and fig. 4) may be explained by the extremely small N_e maintained during our experiments. The translational robustness hypothesis proposes that proteins are under selection to be able to fold properly despite translation errors. This translational robustness is encoded in protein sequences, and should be stronger for highly expressed proteins—as misfolding will be more deleterious for highly expressed proteins—resulting in a negative expression level-evolutionary rate correlation (Drummond et al. 2005; Wilke and Drummond 2006; Drummond and Wilke 2008). Nevertheless, translation errors are rare, affecting only ∼5 in 10,000 amino acids (Parker 1989), and thus mutations reducing translational robustness are not expected to be lethal. Nonlethal mutations can be fixed in small populations by genetic drift (Kimura et al. 1963; Kimura 1968). If, as our observations suggest, N_e indeed affects the strength of the correlation between protein rates of evolution and expression level and protein abundance, this may explain why this correlation is stronger in microorganisms (which usually have very high N_e) than in multicellular organisms (which have a much smaller N_e; Lynch 2007; Charlesworth 2009), in which expression breadth—the number of tissues in which a gene is expressed—seems to be a better predictor of rates of protein evolution than expression level (Duret and Mouchiroud 2000; Wright et al. 2004; Zhang and Li 2004; Liao et al. 2006; Pál et al. 2006; Ingvarsson 2007; Alvarez-Ponce 2012; Alvarez-Ponce and Fares 2012). Likewise, this may explain why the correlation is weaker in endosymbiotic bacteria than in their free-living close relatives (Toft and Fares 2009). Another possibility is that a single amino acid replacement—very few genes accumulated more than one nonsynonymous mutation during our relatively short evolution experiments—is not enough to significantly decrease the translational robustness of a protein. Alternatives to the translational robustness hypothesis include the misinteraction avoidance hypothesis (according to which highly expressed proteins are subject to stronger selective pressures to avoid unspecific interactions; Levy et al. 2012; Yang et al. 2012) and the mRNA folding requirement hypothesis (according to which highly abundant mRNA require a stronger folding and are thus subject to stronger selective pressures; Park et al. 2013). In any case, a single mutation is unlikely to alter the relevant parameters (misinteraction rate or mRNA folding energy) significantly. Nonetheless, it is possible that, in a much longer evolution experiment, a stronger relationship between d_N/d_S and expression levels might have been observed.

A number of comparative genomics analyses have revealed a correlation between protein lengths and rates of evolution; however, both the strength and the sign of this correlation depend on the organism (Marais and Duret 2001; Lipman et al. 2002; Lemos et al. 2005; Bloom et al. 2006; Liao et al. 2006; Ingvarsson 2007; Larracuente et al. 2008; Alvarez-Ponce and Fares 2012; Chang and Liao 2013), and other analyses have suggested little or no correlation (Drummond et al. 2006; Warringer and Blomberg 2006; Alvarez-Ponce 2012). The correlation between protein lengths and rates of evolution has been attributed to the Hill-Robertson effect (Hill and Robertson 1966). In long sequences, multiple mutations can interfere with the fixation (of beneficial mutations) or elimination (of deleterious mutations) of each other, resulting in a reduced efficacy of natural selection (Ingvarsson 2007). Nonetheless, during our experiments natural selection was probably inefficient for all genes, regardless of their length, due to small N_e. Furthermore, the simultaneous existence of multiple segregating sites is highly unlikely, due to both small N_e and the small number of intervening generations. Other hypotheses that have attempted to explain the correlation between protein lengths and rates of evolution due to Hill-Robertson interference require the existence of introns (Comeron and Kreitman 2000, 2002; Larracuente et al. 2008), and are thus not relevant to our experiment in E. coli.

The hypermutant lines that we used in our evolution experiments exhibit mutation spectra that differ from those of normal E. coli strains (supplementary table S2, Supplementary Material online). This potential caveat, nonetheless, is alleviated by the fact that our results are robust to using the Goldman and Yang model (Goldman and Yang 1994) (implemented in the model M0 of PAML; Yang 2007). One of the parameters of this model is κ, the transition/transversion ratio. Furthermore, codon-based maximum likelihood models are often robust to violation of model assumptions (Zhang et al. 2005; Kosiol et al. 2007; Jordan and Goldman 2012; Zhai et al. 2012; Gharib and Robinson-Rechavi 2013). In addition, hypermutability resulting from loss of certain components of the DNA repair machinery is common (and sometimes adaptive) in natural populations of bacteria (for review, see Jayaraman 2011). Such bacteria may have mutational biases similar to those of our ΔmutS E. coli. Well-known systems where DNA reparation genes have been lost include endosymbiotic bacteria (Moran 1996).

In summary, our evolution experiments allowed us to overcome many of the limitations of previous analyses that were based on comparison of highly divergent genomes and have made it possible to test one of the main predictions of the Neutral Theory of Molecular Evolution that had remained hitherto under intense debate: essential genes do evolve slower than nonessential genes (Kimura and Ohta 1974; Wilson et al. 1977). Our observations, thus, shed considerable light on a controversy that has been open for decades.

Material and Methods

Experimental Evolution

Escherichia coli K12 substr. MG1655 ΔmutS was obtained from I. Matic (INSERM U571, Paris, France) via the J. Blazquez’s group at Centro Nacional de Biotecnología (CSIC, Madrid, Spain). Two parallel mutation accumulation lines were created (A and B). Cells were grown aerobically on solid rich LB media (1% bacto-tryptone, 1% NaCl, 0.5% yeast extract; Pronadisa #1551; 1.5% bacto-agar European grade; Pronadisa #1800) at 37 °C. Every ∼24 h, a few cells from the same colony were transferred to a fresh Petri dish. Part of the colony was stored on 25% glycerol at −80 °C every ∼10 passages. The evolution experiment is summarized in figure 1.

Genome Sequencing and Identification of DNA Substitutions

Whole genome sequencing of the ancestral strain, E. coli K12 substr. MG1655 ΔmutS, has been reported elsewhere (Sabater-Muñoz et al. 2015) (BioSample SAMN03742160 from the BioProject PRJNA285176). The other seven genomes were sequenced, assembled and annotated as follows. Glycerol stocks from passages 100, 200, 250, and 260 (line A) and passages 150, 200, and 250 (line B) were recovered in 10 ml liquid LB for 24 h at 37 °C, and cells pelleted by centrifugation at 12,000 rpm to perform genomic DNA extraction. This extraction was performed using the QIAmp DNA mini kit for the QiaCube automatic extractor [Qiagen, Venlo (Pays Bas), Germany]. DNAseq libraries were constructed using the TrueSeq DNA polymerase chain reaction-free HT sample preparation kit (Illumina) and labeled with individual indices to allow running them in a single lane. Quality and quantity of libraries were assessed using the 2100 Bioanalyzer (Agilent). Sequencing was carried out using the paired-end Illumina HiSeq2000 platform using a 2 × 100 cycles configuration. DNA extraction, library construction and sequencing were carried out by LifeSequencing SL (Valencia, Spain). We used the breseq v 0.24rc4 pipeline (Deatherage and Barrick 2014) for aligning the Illumina reads against our ancestral strain and to identify SNPs and indels (using bowtie2; Langmead and Salzberg 2012). The Individual runs of breseq with the seven evolved lines were run with default parameters.

Protein Rates of Evolution

For each gene and evolved genome (A100, A200, A250, A260, B150, B200, and B250), an alignment of the ancestral (from the parental genome) and the evolved sequences was generated. The small number of substitutions attained in our evolution experiment (table 1) hinders the usual calculation of an individual d_N/d_S value per gene, as many genes have accumulated no substitutions, or not enough substitutions for proper estimation of the strength of purifying selection. Therefore, we based our d_N/d_S calculations on sets of genes (e.g., essential genes, nonessential genes, lowly expressed genes, intermediately expressed genes, and highly expressed genes). For that purpose, alignments for each gene set were concatenated. The 126 genes that were lost in genome A260 were eliminated from the alignments corresponding to line A, and the 90 genes lost in genome B250 were eliminated from the alignments corresponding to line B.

For each alignment, the number of synonymous substitutions and positions and the number of nonsynonymous substitutions and positions were determined using the Nei–Gojobori method (Nei and Gojobori 1986) as implemented in DnaSP version 5.10 (Librado and Rozas 2009). The degree of nonsynonymous divergence (d_N) was computed by dividing the number of nonsynonymous substitutions by the number of nonsynonymous sites. Similarly, d_S was computed by dividing the number of synonymous substitutions by the number of synonymous sites. The small number of mutations accumulated during our evolution experiments made unnecessary the application of a model of evolution. Unless stated otherwise, d_N/d_S ratios reported throughout the article are based on estimates of the Nei–Gojobori method.

Additionally, analyses were also conducted using the model M0 implemented in the codeml program of the PAML package version 4.4d (Yang 2007). These supplementary results are provided in the relevant tables and in figure 3. In order to avoid the problem of local optima, all computations were run multiple times, using different starting d_N/d_S ratios (d_N/d_S = 0.05, 0.1, 0.5, 1, and 5). For each genome, the d_N/d_S ratios of essential versus nonessential genes were compared by the following: (1) estimating d_N/d_S and the likelihood under model M0 for essential and nonessential genes; (2) estimating the likelihood for nonessential genes assuming a fixed d_N/d_S equal to the one estimated for essential genes; and (3) comparing the likelihood of both nested models (with d_N/d_S to be estimated vs. a fixed d_N/d_S) using a likelihood ratio test, assuming that twice the difference between the likelihoods of both models follows a χ² distribution with one degree of freedom.

Interspecific Comparisons

For each E. coli gene, the most likely ortholog in S. enterica enterica (serovar Typhimurium, strain LT2) was identified a best reciprocal hit approach. Each E. coli protein sequence was blasted against the proteome of S. enterica, and the best hit was blasted against the proteome of E. coli. If the best hit in the second BLAST search was the original E. coli sequence, both genes were considered to be orthologs. This method has been shown to exhibit very high accuracy (Wolf and Koonin 2012). For each pair of orthologous genes, the protein sequences were aligned using ProbCons 1.12 (Do et al. 2005), and the resulting alignments were used to guide the alignment of the CDSs using an in-house script. For each individual CDS alignment, and for two concatenomes (one for essential and another for nonessential genes), the Nei–Gojobori method, implemented in PAML (Yang 2007), was used to estimate the d_N/d_S ratio.

Essentiality

Essentiality data were obtained from Gerdes et al. (2003). They systematically induced gene inactivation using a transposon, and they grew the mutants aerobically on an enriched LB medium that was very similar to the one used in our experiment.

Gene Expression and Protein Abundance Data

Levels of mRNA abundance were obtained from Covert et al. (2004). Measurements correspond to wild-type E. coli cells growing in aerobic conditions. For each gene, we averaged the abundances across three biological replicates. Protein abundance data was retrieved from the PaxDb database, version 4 (Wang et al. 2015).

Gene Functional Categories

For each E. coli gene, the Cluster of Orthologous Genes (COG) to which it belongs, and the functional category to which this COG belongs, was derived from the COG database (Galperin et al. 2015). Genes were then classified into two classes: “informational” (categories “A,” “B,” “J,” “K,” and “L”) and “operational” (categories “C,” “D,” “E,” “F,” “G,” “H,” “I,” “M,” “N,” “O,” “P,” “Q,” “T,” “U,” “V,” “W,” “Y,” and “Z”). Gene Ontology enrichment analyses were performed using the Gene Ontology website (www.geneontology.org; last accessed July 2016).