Inevitability of Genetic Parasites

Abstract

Almost all cellular life forms are hosts to diverse genetic parasites with various levels of autonomy including plasmids, transposons and viruses. Theoretical modeling of the evolution of primordial replicators indicates that parasites (cheaters) necessarily evolve in such systems and can be kept at bay primarily via compartmentalization. Given the (near) ubiquity, abundance and diversity of genetic parasites, the question becomes pertinent: are such parasites intrinsic to life? At least in prokaryotes, the persistence of parasites is linked to the rate of horizontal gene transfer (HGT). We mathematically derive the threshold value of the minimal transfer rate required for selfish element persistence, depending on the element duplication and loss rates as well as the cost to the host. Estimation of the characteristic gene duplication, loss and transfer rates for transposons, plasmids and virus-related elements in multiple groups of diverse bacteria and archaea indicates that most of these rates are compatible with the long term persistence of parasites. Notably, a small but non-zero rate of HGT is also required for the persistence of non-parasitic genes. We hypothesize that cells cannot tune their horizontal transfer rates to be below the threshold required for parasite persistence without experiencing highly detrimental side-effects. As a lower boundary to the minimum DNA transfer rate that a cell can withstand, we consider the process of genome degradation and mutational meltdown of populations through Muller’s ratchet. A numerical assessment of this hypothesis suggests that microbial populations cannot purge parasites while escaping Muller’s ratchet. Thus, genetic parasites appear to be virtually inevitable in cellular organisms.

Introduction

All or nearly all cellular life forms appear to harbor diverse genetic parasites including transposable elements, plasmids, viruses, and others (Koonin and Dolja 2013). Genetic parasites are non-cellular replicators that possess their own genomes but to various degrees depend on the host cells for information processing systems, in particular translation (Raoult and Forterre 2008). Parasite–host interaction and co-evolution undoubtedly are major aspects of all evolution of life that to a large extent drive evolutionary transitions (May and Anderson 1990; Messinger and Ostling 2009; Koskella and Brockhurst 2014; Leggett et al. 2014; Gorter et al. 2015; Koonin 2016). A major aspect of this co-evolution is the perennial arms race whereby cellular hosts evolve multiple mechanisms of defense to which the parasites respond by evolving counter-defense systems (Forterre and Prangishvili 2009; Stern and Sorek 2011; Forterre and Prangishvili 2013). However, cooperation between hosts and parasites is the other side of the co-evolution coin. Parasitic genetic elements can be beneficial to the host by providing resistance to superinfection but also in other, still incompletely characterized ways (Bao and Roossinck 2013; Shirogane et al. 2013). Importantly, genetic material of parasitic elements is often recruited for host functions. Indeed, sequences derived from transposable elements constitute large fractions of the genomes of diverse eukaryotes, (e.g., up to 90% of many plant genomes) and are considered to be important drivers of genome evolution (Kazazian 2004; Hua-Van et al. 2005; Jurka et al. 2007; Goodier and Kazazian 2008; Huda and Jordan 2009; Lopez-Flores and Garrido-Ramos 2012). Although genomic parasites are not quite as prominent in prokaryotes, there are few bacterial or archaeal genomes that are free of selfish, parasitic elements including transposons and prophages (Casjens 2003; Busby et al. 2013). A major role of viruses in the host biology has also been demonstrated in prokaryotes as illustrated by the transfer of photosystem genes by cyanophages (Sullivan et al. 2006; Lindell et al. 2007), the utilization of defective prophages as vehicles for horizontal gene transfer known as Gene Transfer Agents (Lang et al. 2012), and more generally by the recruitment of viral genes for diverse host functions (Cortez et al. 2009).

The relationships between genomic parasites and their hosts are highly differentiated such that the parasites span a wide range of “selfishness,” i.e., the cost incurred on the host by the parasite reproduction (Jalasvuori 2012; Jalasvuori and Koonin 2015; Koonin and Starokadomskyy 2016). At one end of the spectrum are benign elements that are incapable of autonomous replication and only replicate with the host genome, so that the only cost associated with the element is that of the replication itself which is near negligible compared to the total energy expenditure of the host (Lynch and Marinov 2015). At the opposite end are lytic viruses that replicate to extremely high copy numbers and rapidly kill the host. In between are selfish elements with various degrees of autonomy including transposons that have the capacity to proliferate within the host genomes, low and high copy number plasmids and others. There are multiple, tight evolutionary links between selfish elements that differ in terms of the cost to the host, such as lytic viruses and transposons (Koonin and Dolja 2014). Moreover, the same element often alternates between different life styles, e.g., between low cost prophages and high cost lytic viruses, as in the thoroughly studied case of temperate bacteriophages (Canchaya et al. 2003; Los and Wegrzyn 2012; Casjens and Hendrix 2015), or between a bacteriophage and a plasmid (Briani et al. 2001). The same cellular organism typically hosts various classes of parasitic selfish elements resulting in complex ecosystems of interacting replicators (Koonin and Starokadomskyy 2016).

Because parasites exist at all levels of biological organization and apparently accompany (nearly) all cellular life forms, the question of whether parasites are inherent to life becomes pertinent. The inevitability of the emergence of parasites has figured prominently in theoretical studies on the origin of life (Szathmary and Demeter 1987; Szathmary 1992; Maynard Smith and Szathmary 1995; Koonin and Martin 2005; Takeuchi and Hogeweg 2012). In particular, considerable effort has been dedicated to understanding how pre-cellular communities of simple replicators could survive the onslaught of “cheaters” that replicate faster than “cooperators” by not coding for resources required for replication but rather exploiting resources produced by the cooperators. A major and striking theoretical result is that a spatially homogeneous population of replicators is prone to takeover by cheaters (parasites) and hence is generally doomed to collapse (Takeuchi and Hogeweg 2007). The only path to stability for a population of replicators in the face of the parasite onslaught appears to be compartmentalization: generally, parasites can be eliminated from a population or at least kept in check if the rate at which the parasite is transferred to new hosts is insufficient to compensate for the loss of the parasite (Takeuchi and Hogeweg 2007; Takeuchi et al. 2011; Takeuchi and Hogeweg 2012). Thus, the primordial parasite-host arms race could have been a key driver of the evolution of biological complexity (Koonin 2016).

Assuming that selfish genetic elements evolved within the simplest, pre-cellular replicator systems (Koonin et al. 2006), the emergence of cells resulted in a steep new barrier to the spread of parasites, which thereafter needed to undergo horizontal gene transfer (HGT) to infect new hosts. The question, then, emerges: can cellular organisms purge parasites by lowering their HGT rates? Parasites are lost at two levels: at the genome level, the intrinsic loss bias observed in prokaryotic genomes leads to attrition of non-beneficial genes (Kuo and Ochman 2009, 2010); at the population level, purifying selection eliminates the hosts with the larger parasitic load (Lynch 2006b). In the case of relatively passive elements, fitness costs are likely associated with the additional energy required for DNA replication, increased genomic instability, and interference with functional genes. Although these costs are presumably small for many if not most non-viral selfish elements (Lynch 2007), the relatively low copy numbers of such elements in prokaryotic genomes imply that host populations are able to keep them under control (Lynch 2006b; Wolf and Koonin 2013). The intuitive idea that a combination of proliferation, loss, transfer, and selection governs the internal dynamics of genomes can be formalized to obtain an expression that defines the conditions for parasites to survive in a population. In this work, we derive such an expression and evaluate its consistency with genomic data. To this end, we estimate characteristic duplication, loss and transfer rates for transposons, plasmids and virus-related elements, as well as “non-selfish” genes, in bacterial and archaeal genomes. As predicted by the theory, we find that the estimated transfer rates are large enough to compensate for losses. Similar qualitative patterns of loss and transfer are observed for genetic parasites and non-selfish genes, which suggest that the causes that underlie the long-term persistence of parasites are not essentially different of those that allow long-term persistence of most other genes. According to this view, genetic parasites with a higher effective loss rate (which includes the negative contribution to the fitness of the host) require a higher transfer rate to survive, which might explain the division between parasites that possess or lack autonomous transfer mechanisms. Moreover, the existence of the latter class of parasites raises the question whether cells could curtail genetic transfer to levels incompatible with the persistence of such parasites.

In prokaryotes, the processes that lead to the acquisition of external genetic material have been traditionally divided according to the mechanism by which DNA enters the cell, the origin of such DNA, and the consequences of its acquisition. Thus, transformation is associated to the intake of DNA from close relatives, which leads to homologous recombination, whereas conjugation and transfection are related to the transfer of heterologous DNA from plasmids and phages. Recent research reveals a more complex picture, whereby any of these DNA uptake mechanisms can result in homologous and/or non-homologous recombination (Darmon and Leach 2014; Hanage 2016). For example, large heterologous sequences can be acquired through transformation as long as flanking homology regions exist, as it has been observed with pathogenicity islands in S. pneumoniae (Coffey et al. 1998; Johnston et al. 2013). Therefore, transformation can be not only a source of genetic innovation (Croucher et al. 2011; Johnston et al. 2014) but also a means of transmission of genetic parasites. Conversely, plasmids and prophages are capable of mobilizing other (non-parasitic) genes, some of which can share homology with the resident genes if the infection occurs between related lineages. For these reasons, we refer to HGT as a catchall term that comprises the entry of DNA into a cell and its subsequent incorporation into the genome via homologous or non-homologous recombination.

Horizontal gene transfer (HGT) is a dominant process in the evolution of bacteria and archaea that is the source of most innovations and adaptations to new environments (Lerat et al. 2005; Dagan et al. 2008; Koonin and Wolf 2008; Treangen and Rocha 2011; Puigbo et al. 2014). Apart from the acquisition of new genes that is crucial in the long term but can be beneficial only sporadically in evolving microbial populations, HGT appears to be important for a more immediate reason. In the absence of recombination, finite populations are subject to irreversible deterioration through accumulation of deleterious mutations, a process known as Muller’s ratchet, that eventually leads to the collapse of a population via mutational meltdown (Muller 1964; Felsenstein 1974; Pamilo et al. 1987; Charlesworth et al. 1993). Even if, in some cases, Muller’s ratchet can be partly offset by compensatory mutations (e.g., in the case of rapidly mutating RNA viruses), it still causes a dramatic drop in the fitness of susceptible populations (Lazaro et al. 2003). Muller’s ratchet is more powerful than neutral drift and can keep acting in regimes where selection is able to counteract the drift. Specifically, population genetics models show that, in a population of size N, Muller’s ratchet drives the accumulation of mutations with the cost s’ such that $\hspace{0.17em}N{s}^{\text{'}}>1>N{s}^{\text{'}}{e}^{-U/s\text{'}}$, where U is the rate at which such mutations occur (Gordo and Campos 2008). Therefore, with the possible exceptions of extremely fast mutating organisms or populations subject to severe bottlenecks, the main contribution to Muller’s ratchet comes from slightly deleterious mutations. In line with its major evolutionary impact, avoidance of Muller’s ratchet is thought to be one of the key driving forces in the evolution of sex (Kondrashov1988, 1993; Gordo and Campos 2008; Hartfield and Keightley 2012). Mathematical modeling suggests that in microbes, a sufficiently high rate of environmental DNA (eDNA) uptake is a key condition for the long-term survival of microbial populations facing Muller’s ratchet (Takeuchi et al. 2014).

Here, we test the hypothesis that cells cannot tune their horizontal transfer rates to be below the threshold required for parasite persistence without compromising their long-term survival. Among all the proposed benefits of HGT, we considered prevention of genome degeneration through Muller’s ratchet because it constitutes a baseline (i.e., a minimum requisite) for the HGT rate that can be analytically estimated from population genetics models and tested through comparative genomics. The analysis of available data suggests that most microbial populations cannot purge parasites and escape from Muller’s ratchet at the same time. Susceptibility to selfish elements thus becomes a cost that cells have to pay to maintain an evolutionary regime that does not lead to mutational meltdown.

Results

A Condition for the Persistence of Parasites

Genomic parasites can be broadly defined as DNA sequences whose presence does not provide any primary benefit to the host (Doolittle and Sapienza 1980; Orgel and Crick 1980). Upon intake from an eDNA pool or direct transmission, genomic parasites often integrate into the host genome, where they experience proliferation and loss. In order to dissect the evolutionary processes that affect the fate of genomic parasites, we modeled the stochastic dynamics of their copy number in a population of hosts (see Supplementary Material online). In our model, the parasite copy number is determined by four processes: proliferation, loss, HGT, and purifying selection. The first three processes act at the genome level whereas selection acts at the population level by reducing the fitness of hosts that harbor parasites. In the most general version of the model, the rate of each process depends on the parasite copy number, so that r_k, d_k, and h_k are, respectively, the proliferation, loss, and HGT rates in a host with k copies; and s_k is the fitness cost to the host. For simplicity, we assume that the rates are linear with the copy number, so r_k = rk, d_k = dk, and s_k = sk. Because the probability of incorporating a parasite via HGT depends on how abundant such a parasite is in the population, we set h_k = h 〈k〉, where 〈k〉 is the population average for the copy number. Mathematically, this model defines a multitype branching process whose stationary behavior is described by its generating matrix A (Moody 1988; Bichsel et al. 2013).

$$\mathrm{A}=\mathrm{\hspace{0.17em}}\left(\begin{array}{ccccc}-{\mathrm{\Theta }}_0& d& 0& 0& \cdots \\ h〈k〉& -{\mathrm{\Theta }}_1& 2d& 0& \cdots \\ 0& r+h〈k〉& -{\mathrm{\Theta }}_2& 3d& \cdots \mathrm{\hspace{0.17em}}\\ 0& 0& 2r+h〈k〉& -{\mathrm{\Theta }}_3& \cdots \\ 0& 0& 0& 3r+h〈k〉& \cdots \\ ⋮& \mathrm{\hspace{0.17em}}⋮& ⋮& ⋮& \ddots \mathrm{\hspace{0.17em}}\end{array}\right)$$ (1)

where ${\mathrm{\Theta }}_k=k\left(r+d+s\right)+h\mathrm{\hspace{0.17em}}〈k〉$.

A large population of hosts evolves according to the following dynamical equation:

$$\frac{d\mathbf{p}}{dt}=\mathrm{\hspace{0.17em}}\mathrm{A}\hspace{0.17em}\mathbf{p}+s\mathrm{\hspace{0.17em}}\left({\sum }_{k}k\mathrm{\hspace{0.17em}}{p}_k\right)\mathrm{\hspace{0.17em}}\mathbf{p}$$ (2)

where the components p₀, p₁, …, p_k of the vector p represent the fraction of the population harboring 0, 1, …, k copies of the parasite. The stationary composition of the population is described by the eigenvector p* associated with the largest real eigenvalue of A.

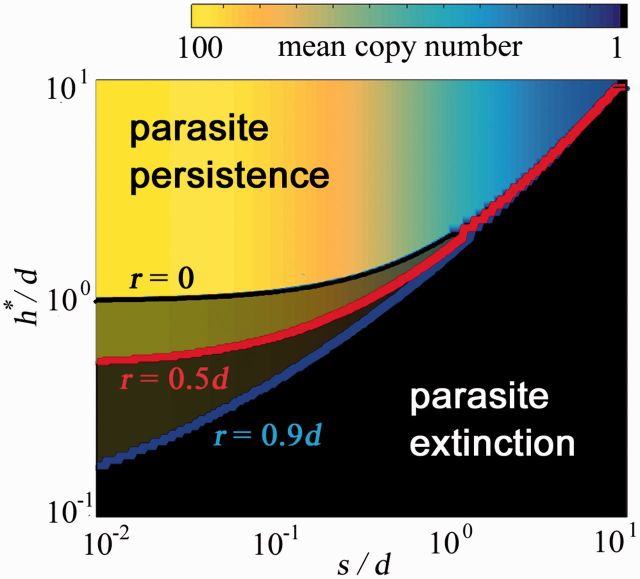
Depending on the parameter values, two outcomes are possible for the parasite. In the subcritical regime, the parasite becomes extinct (i.e., the stationary composition is $p_0^{*}=1$ and $p_{k>0}^{*}=0$), whereas in the supercritical regime the parasite persists. A comprehensive exploration of the model shows that the two regimes are separated by a critical value of the HGT rate, $h_{PP}^{*}$, so that parasites only persist if $h>h_{PP}^{*}$ (fig. 1 and table 1). In general, the value of $h_{PP}^{*}$ has to be numerically computed. In a few special cases, however, simple analytical expressions can be readily obtained.

Fig. 1.—

Critical HGT rate for parasite persistence ($h_{\text{PP}}^{*}$) as a function of the cost/deletion ratio (s/d). The ratio between the critical HGT rate and the deletion rate ($h_{\text{PP}}^{*}$/d) is plotted for three different values of the proliferation rate (r = 0, black line; r = 0.5d, red line; and r = 0.9d, blue line). Parasite persistence is only possible if the HGT rate is greater than the critical value represented by the curve. The background color indicates the mean copy number as a function of s and h for the particular case d = 0.01.

Table 1.

Summary of the Persistence Conditions and their Validity

Critical HGT rate	Validity	Regime
h*PP = d – r	s = 0	Neutral regime
h*PP ≈ d – r + s d/(d – r)	s ≪ d – r	Loss-driven regime
h*PP = f(r,s,d) = de	s ∼ d	Mixed regime
h*PP ≈ s + d s/(r + s)	s ≫ d – r	Selection-driven regime

Parasites can persist in a population if their HGT rate is larger than the critical value reported in the table, h > $h_{\text{PP}}^{*}$. Other designations: d, loss (or deletion) rate; r proliferation (duplication) rate, s fitness cost, d_e effective loss bias. See supplementary fig. S1 in the Supplementary Material online for a comparison of these approximations and the exact numerical results.

Because the fitness cost imposed by parasites varies from quasi-neutrality, as in the case of many transposable elements, to highly deleterious or lethal effects, as for lytic viruses, we focused on the effect that the fitness cost s has on parasite survival (see “Methods” section and Supplementary Material online). In the particular case of a neutral parasite, the exact expression for the critical HGT rate is $h_{PP}^{*}=d-r$. Obviously, this expression can be interpreted in terms of the intrinsic loss bias: in the absence of fitness cost, transmission of a parasite through HGT must at least compensate for the loss bias in order to prevent extinction of the parasite. The previous expression holds approximately even when fitness cost is taken into account, as long as the cost is small compared to the loss rate (table 1). In this regime, intrinsic loss of the parasite at the genomic level is more relevant than selection dynamics which explains why the critical HGT rate is determined by the intrinsic loss bias, whereas selection mostly affects the maximum copy number that the parasite can reach (see Supplementary Material online for formal details). Conversely, if the fitness cost is much larger than the genomic loss rate, parasite persistence requires that HGT compensate for the combined effects of loss and selection. Because elimination of the parasites through purifying selection is more efficient in hosts with high copy numbers, high proliferation rates do not contribute to parasite persistence in this selection-driven regime, for which the critical HGT rate approximates $h_{PP}^{*}\approx s$. Finally, in the intermediate regime of comparable cost and loss rate, the expression for the critical HGT rate involves all the model parameters in a non-trivial way and has to be calculated numerically. Extensive simulations show that the critical HGT rates in this mixed regime lie between the deletion-driven and selection-driven cases as summarized in table 1. Specifically, the critical HGT rate increases with the fitness cost, whereas the quantitative effect of the proliferation rate becomes less and less relevant as the fitness cost increases (see supplementary fig. S1, Supplementary Material online).

For practical purposes, let us define the effective loss bias d_e for a genetic element (parasitic or not) as a parameter that represents the combined effects of duplication, losses through deletion and losses through purifying selection affecting infected hosts. For a purely neutral genetic element, the effective loss bias is equal to the difference between loss and duplication rates. For a costly genetic element, the effective loss bias corresponds to the loss bias that would be estimated by fitting a neutral model to the observed distribution of the parasite copy numbers. In terms of the effective loss bias, the critical HGT rate becomes $h_{PP}^{*}=d_e$ and the condition for the persistence of parasites can be simply expressed as h ≥ d_e.

Persistence of Parasites in the Light of Comparative Genomic Data

Given a set of closely related genomes, the underlying phylogenetic tree, and the parasite copy number in each genome, it is possible to obtain maximum likelihood estimates of the effective loss bias and the gene transfer rate under the assumption that parasites follow the duplication-loss-transfer dynamics described above. We used the previously described approach (Puigbo et al. 2014) to obtain such estimates for the mobile genetic elements (MGE which collectively comprise the mobilome) as well as other categories of genes in 35 groups of bacteria and archaea (see “Methods” for details). The clusters of closely related prokaryotic genomes (Alignable Tight Genome Clusters, ATGC) (Novichkov et al. 2009; Puigbo et al. 2014) were employed as the data set for this analysis. This data set is particularly suitable for the purpose of the present analysis because it provides, for each group of genomes, sets of orthologous genes for which the copy number can be accurately assessed, as well as high quality phylogenetic trees. Throughout the present analysis, we used mobile genetic elements as a proxy for selfish elements, i.e., genomic parasites.

The loss bias for selfish elements typically takes values from 1 to 10 times the fixation rate of point mutations per site, with a median of 6.2 (fig. 2A). No significant differences were found among transposable elements, conjugative plasmids and viruses (Kruskal–Wallis test P = 0.059, see supplementary fig. S4A, Supplementary Material online). When compared to gene families that do not belong to the mobilome (with the highly dynamic “defense” category also excluded), mobile elements show a significantly higher effective loss bias (median for the other genes is 0.6; Mann–Whitney test P < 10⁻²⁰). Among “non-selfish” gene families, those encoding components of the translation system show the smallest effective loss bias, followed by enzymes of nucleotide and coenzyme metabolism (see supplementary fig. S5, Supplementary Material online). These differences are probably due to the effect of purifying selection on genomes which results in high effective loss rates for the selfish genes of the mobilome, followed by defense genes, and significantly lower loss rates for the rest of the genes. Different taxa (ATGC) display a large variation in the effective loss bias, consistent with a non-uniform propensity of host genomes to harbor parasites (see supplementary fig. S6, Supplementary Material online). The higher loss bias of the MGE is also apparent at the taxon level (medians 7.6 and 1.8 for MGE and other genes, respectively; Mann–Whitney test P = 3 × 10⁻⁴).

Fig. 2.—

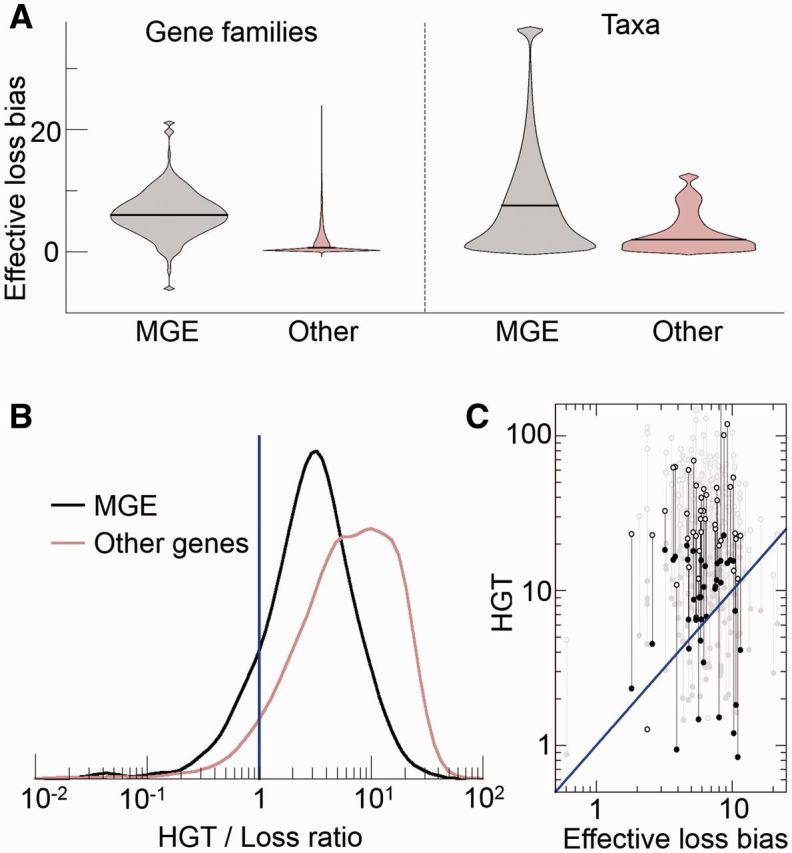
Quantitative assessment of the effective loss bias (A) and the parasite persistence condition (B, C) in genomic data. (A) Violin plots with the distribution of effective loss biases affecting MGE (grey) and other genes (brown). Black, horizontal lines represent the median of the distribution. The plots on the left side were obtained by grouping genetic elements (ATGC COGs) with the same COG or Pfam assignment; in the plots on the right side, the elements are grouped according to the taxa (ATGC) they belong to. The loss bias is measured in relation to the fixation rate of point mutations per site. (B) Distribution of the ratio between the HGT rate and the effective loss bias for MGE (black) and other genes (brown). Both groups of genes show transfer-to-loss ratios significantly greater than one (vertical blue line), which is the critical ratio for parasite persistence (medians 2.9 and 6.6 for MGE and other, non-selfish genes, Wilcoxon sign test P-values < 10⁻²⁰ in both cases). The distributions were smoothed using a Gaussian kernel. (C) The individual HGT rates and effective loss biases for every family of the mobilome. For clarity, the subset of the MGE unrelated to phages is plotted in black, whereas the more numerous phage-related elements are depicted in grey. Full and open circles correspond, respectively, to the conservative and upper bound estimates of the relative HGT rate (the distributions in A correspond to the geometric mean of both values). In B and C, the blue line indicates the critical HGT rate required for parasite persistence.

When compared to other gene categories, transfer rates are also substantially higher for MGE (median 18.7 versus 4.2 for the rest of families; Mann–Whitney test P < 10⁻²⁰). Transfer rates vary among different classes of MGE (Kruskal–Wallis test P = 0.010, see supplementary fig. S4B, Supplementary Material online), with transposons (median 15.0) showing lower transfer rates than plasmids (median 24.8, Mann–Whitney test P = 0.019) and phages (median 20.3, P = 0.006). The transfer rates for most selfish elements as well as other, non-selfish gene families fulfill the condition for the persistence of parasites. Despite the uncertainty in the estimation of the relative HGT rates, the HGT rates clearly are at least comparable to the loss biases but typically, are approximately 2–10 times greater, thus permitting persistence of the respective genetic elements (fig. 2B and C). Notably, when gene families are grouped by taxa, a strong positive correlation is observed between the median HGT rates of MGE and non-mobile gene families (Spearman’s rho = 0.89, P < 10⁻⁴, see supplementary fig. S7, Supplementary Material online).

A Lower Bound for the Minimum HGT Rate Required by Cells

The condition for the persistence of parasites implies that in principle it would be possible for hosts to completely purge selfish elements by lowering their HGT rates below a critical threshold. In finite populations, however, the need of HGT to counteract mutational meltdown sets a limit for the lowest eDNA intake rate that can be put into effect without compromising genome integrity (Takeuchi et al. 2014). To derive a condition for such a minimum HGT rate, we built upon the results of previous theoretical analyses that dealt with the mutation accumulation dynamics in finite populations (Rouzine et al. 2008; Neher and Shraiman 2012; Takeuchi et al. 2014). Following Takeuchi et al. (2014), we considered a Wright–Fisher process in a well-mixed population of effective size $N_{\mathrm{e}}$ that experiences deleterious mutations with the cost s’ at a rate U. Each genome is composed of l blocks which are considered the units of HGT. Cells die and contribute to the eDNA pool in an inverse proportion to their relative fitness. HGT is implemented as a replacement of genome blocks by equivalent blocks randomly picked from the eDNA pool at a rate H (per genome). Long term survival of the master sequence (the genome with no deleterious mutations) is guaranteed if master sequences are continuously produced via HGT and recombination from those bearing a single mutation. In terms of the model, such a condition can be expressed as $H\hspace{0.17em}{P}_{10}{n}_1>1$, where P₁₀ is the probability that the master sequence is recovered from the eDNA pool and n₁ is the number of individuals bearing a single mutation. Moreover, recovering the master sequence from the eDNA pool (the term P₁₀) requires that the locus with the mutation is the one that experiences recombination (which occurs with probability $l^{-1}$) and that an allele of that locus with no mutations is randomly drawn from the eDNA pool. Assuming that the population is large ($N_{\mathrm{e}}\gg 1$) and mutations are randomly distributed along the genome, it is possible to obtain estimates for P₁₀ and n₁ (see Supplementary Material online):

$$P_{10}=l^{-1}\mathrm{\hspace{0.17em}}\left(1-l^{-1}\right)\mathrm{\hspace{0.17em}}{e}^{-l^{-1}U/s\mathrm{\text{'}}}$$ (3)

$$n_1=N_e\mathrm{\hspace{0.17em}}(U/s\mathrm{\text{'}}){\mathrm{\hspace{0.17em}}e}^{-U/s\mathrm{\text{'}}}$$ (4)

Combining (3) and (4) and taking into account that, typically, $l\gg 1$, we obtain the condition for the master class persistence, $H\hspace{0.17em}{N}_e\hspace{0.17em}{l}^{-1}\left({U/s}^{\text{'}}\right)\hspace{0.17em}{e}^{-U/s\text{'}}>1$. Because the HGT rate per transfer unit is $h=H/l$, it follows that HGT can rescue a population from the effects of Muller’s ratchet if $h>h_{MR}^{*}$, which defines another critical HGT rate (under the assumption that the population is not far from the regime of susceptibility to Muller’s ratchet, i.e., U > s’):

$$h_{MR}^{\mathrm{*}}={\left(N_e\mathrm{\hspace{0.17em}}\left({U/s}^{\mathrm{\text{'}}}\right)e^{-U{/s}^{\mathrm{\text{'}}}}\right)}^{-1}$$ (5)

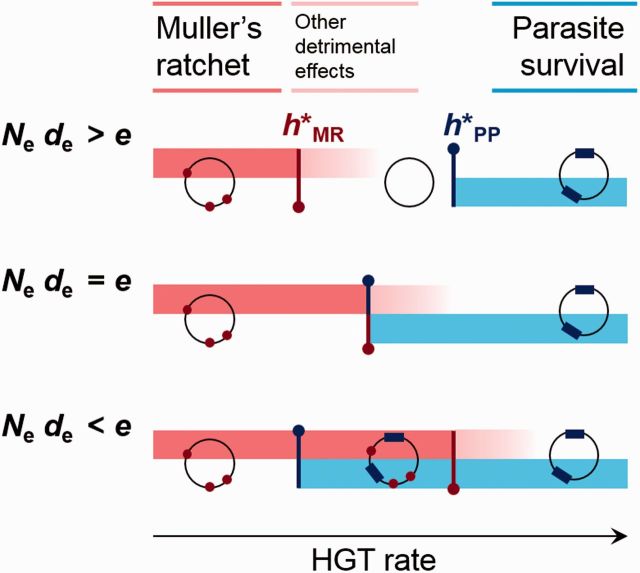
If this rate is greater than the critical HGT rate required for parasites to persist, hosts would not be able to eliminate parasites and avoid mutation accumulation at the same time (fig. 3). Such a trade-off makes parasite persistence inevitable in hosts facing the burden of Muller’s ratchet whenever the condition $h_{MR}^{*}>h_{PP}^{*}$ holds. Using Equation (5) for $h_{MR}^{*}$, we obtain the following condition for the persistence of parasites

$$N_e\mathrm{\hspace{0.17em}}{d}_e\mathrm{\hspace{0.17em}}\left(\frac{U}{s^{\mathrm{\text{'}}}}\right)e^{-\frac{U}{s^{\mathrm{\text{'}}}}}<1.$$ (6)

Fig. 3.—

The rate of HGT determines the susceptibility of a population to Muller’s ratchet and parasites. If the HGT rate lies below the critical value $h_{\text{MR}}^{*}$, the accumulation of mutations leads to genome degeneration (red regions). Because HGT provides benefits to the population beyond counteracting Muller’s ratchet, $h_{\text{MR}}^{*}$ gives only an absolute minimum to the HGT level compatible with genome maintenance. Therefore, some detrimental effects will also be observed if the HGT rate is only slightly greater than the critical value $h_{\text{MR}}^{*}$ (light red shaded regions). On the other side, if the HGT rate is greater than $h_{\text{PP}}^{*}$, genomic parasites can persist in the population (blue regions). The critical HGT rates $h_{\text{MR}}^{*}$ and $h_{\text{PP}}^{*}$ depend on the effective population size (N_e) and the effective loss bias (d_e), as illustrated in the figure. Only if the condition N_ed_e > e holds, the hosts can exist free of parasites while preventing mutational meltdown (this is represented as a “clean” genome in the range of intermediate HGT in the upper scenario). In any other case, susceptibility to parasites becomes an inevitable cost that cells must pay to escape Muller’s rathcet.

When attempting to dissect this expression, one faces the problem of estimating the average fitness effect of deleterious mutations involved in Muller’s ratchet (the parameter s’). However, because $\left(U{/s}^{\text{'}}\right)e^{-{U/s}^{\text{'}}}\le e^{-1}$, it is possible to write a simplified but more restrictive condition which does not depend on such a parameter:

$$N_e\mathrm{\hspace{0.17em}}{d}_e<e$$ (7)

Here, the effective loss bias d_e can be substituted by the simpler expressions in table 1 for the appropriate regimes.

Inevitability of Genetic Parasites

What do genomic data tell us about the inevitability of parasites? To address this question, we compared the effective loss bias estimated for MGE with the minimum HGT rate required to prevent Muller’s ratchet, and checked whether the latter was high enough to compensate for the former, as stated by Equation (7). Because our estimates of the loss bias are relative to the mutation rate, we can write the conservative condition for the persistence of parasites as N_eu(d_e/u) < e, and then combine the estimated loss bias d_e/u ∼6.2 with estimates for N_eu to quantitatively appraise N_ed_e. Based on within-species nucleotide variation data, the values of N_eu in prokaryotes range from approximately 0.003–0.2, with an average of approximately 0.05 (Lynch 2006a). The assessment of the condition N_ed_e < e based on those values suggests that parasite elimination and prevention of Muller’s ratchet are incompatible (table 2). Because population size estimates based on neutral variation might be down-biased by selection on silent sites, we also considered a conservative upper limit for N_e of the order 10¹⁰, which combined with a typical mutation rate per base pair per generation of the order of 10⁻¹⁰ for prokaryotes (Drake et al. 1998; Lynch 2006a), results in N_eu ∼ 1. Although the value of N_ed_e obtained under this conservative estimate does not fulfill the condition for the inevitability of parasites, it is within the same order of magnitude as e (table 2). Thus, organisms seem to exist not far from the edge of the condition beyond which parasites become inevitable. Furthermore, N_ed_e estimates for genes that do not belong to the mobilome typically are well below e, which implies that the minimum HGT rate required to escape Muller’s ratchet also guarantees the survival of most of these genes.

Table 2.

Inevitability of Parasites in the Light of Effective Loss Bias and Population Size Estimates

Estimate source for Ne	N e u	N e d e (mobil.)	N e d e (other)
Neutral nucleotide variation (average)	0.05	0.3*	0.03*
Neutral nucleotide var. (upper limit)	0.2	1.2*	0.1*
Conservative upper limit Ne = 1010	1	6.2	0.6*

The population size estimates are from Lynch(2006a).

Prevention of Muller’s ratchet and elimination of parasites are incompatible if $N_{\mathrm{e}}{d}_{\mathrm{e}}<2.7$.

*Taking into account the variance of the estimated loss bias across gene families, condition $N_e{d}_e<2.7$ holds with P < 10⁻²⁰ (Wilcoxon signed rank test).

A second line of evidence indicating that the condition for the inevitability of parasites actually holds comes from the study of recombination rates. Although the relevant data are limited in scope, estimates for the ratio between recombination and mutation rates in several prokaryotes are typically of the order of one (Posada et al. 2000; Feil et al. 2001; Sarkar and Guttman 2004; Lynch 2006a; Vos and Didelot 2009), with a median of approximately 1.5 (Q1–Q3 equal to 0.5 and 7, respectively) when pooling data from Lynch (2006a) and Vos and Didelot (2009). Notably, these values are not far from the effective loss bias of selfish elements according to the estimates above. Moreover, given that DNA intake precedes recombination, the intake rate is bound to be at least as high as the recombination rate (i.e., around 1–10 times the nucleotide mutation rate). As a result, the intake of DNA by prokaryotic cells would more than suffice to compensate for the effective loss bias of parasitic elements.

Discussion

Mutation accumulation and invasion by selfish elements are two forces that act against genome optimization and streamlining in finite-size populations. In asexual organisms, eDNA intake followed by recombination is the only way to counteract the mutation burden imposed by Muller’s ratchet (Takeuchi et al. 2014). However, eDNA intake can also be exploited by selfish elements to spread across the population, which turns eDNA intake (and horizontal gene transfer in general) into a double-edged sword for cells. By combining simple mathematical models with genomic data, we show that the rate of HGT required for cells to escape Muller’s ratchet is typically high enough to allow mildly deleterious parasites to persist in most populations. Therefore, if cells are to avoid genome degeneration through mutation accumulation, persistence of parasites becomes (virtually) inevitable. Although we centered our argument on the requirement for cells to escape Muller’s ratchet, other benefits associated with HGT, such as acquisition of determinants of antibiotic or virus resistance, or biochemical pathways that are advantageous in a particular environment, additionally constrain the possibility to lower the HGT rates below the threshold of parasite elimination, strengthening this general conclusion.

The conditions required for the short- and long-term persistence of genetic parasites have been a recurrent topic in theoretical population biology after the discovery of selfish elements (Charlesworth and Charlesworth 1983; Langley et al. 1983; Kaplan et al. 1985; Moody 1988). We revisited a general model that takes into account the effects of HGT, duplication, losses and selection to describe the fate of a selfish element in a host population (Moody 1988; Basten and Moody 1991; Bichsel et al. 2013; Iranzo et al. 2014). Despite its simplicity, this model has been shown to fit well the abundance distributions of insertion sequences in bacterial genomes (Iranzo et al. 2014), and its neutral version has been used to infer the evolutionary dynamics of gene content (Csuros and Miklos 2006; Csuros 2010). In agreement with previous findings, persistence of parasites is only possible if horizontal transfer compensates for the effective loss of parasitic elements via deletion and purifying selection. In the case of neutral or quasi-neutral elements, such as transposons, the key factor affecting the critical transfer rate is the intrinsic loss bias, i.e., the difference between the proliferation and loss rates for the given element, the latter determined to a large extent by the genome-wide deletion rate (Kuo and Ochman 2009, 2010). On the other end of the replicator selfishness spectrum, long term survival of highly deleterious parasites, such as lytic viruses, requires that, on average, viruses infect at least as many host cells as they kill per unit of time (which is equivalent to the condition R₀ > 1 for the basic reproductive ratio used in epidemiology (Heffernan et al. 2005).

As predicted by the model, our reconstruction of the evolutionary events in the ATGCs shows that the estimated transfer rates for different mobile genetic elements (transposons, plasmids, and prophages) surpass their effective loss rates, indicating that despite occasional losses in particular lineages, these elements can stably persist in the biosphere for long evolutionary times. Moreover, we found that the critical transfer rate for persistence, calculated from the estimated effective loss rates, is close to or smaller than the theoretical estimate for the minimum HGT rate required to counteract Muller’s ratchet, which connects parasite persistence to prevention of mutational meltdown (third scenario in fig. 3).

The results of this work rely, to a greater or lesser extent, on certain model assumptions that we summarize here for clarity. First, we assumed that the dynamics of genetic parasites can be described by a generalized birth–death–transfer model (see Supplementary Material online for details). In the most general version of such model, parasites proliferate within a genome, are lost from a genome, and infect new genomes at rates that depend on their genomic and population abundances, whereas host genomes experience differences in fitness that depend on their parasite load. For simplicity, we made all rates directly proportional to the parasite copy number which is equivalent to the assumption that each copy of the parasite behaves independently of the rest. This assumption is empirically supported by the observation that the linear birth–death–transfer model provides a good fit for the copy number distributions of a large number of MGE in bacterial genomes (Iranzo et al. 2014). Arguably, large parasite copy numbers might produce non-linearities in the fitness function (e.g., due to increased genomic instability associated with multiple repeats) or lead to a saturation of the infection rate. However, because our aim was to explore the transition between the regimes of parasite extinction and parasite survival, rather than instances of intense parasite proliferation, such large copy number effects are irrelevant for the present study.

Second, the Muller’s ratchet model that we used to calculate $h_{PP}^{*}$ assumes, in its original formulation (Takeuchi et al. 2014), a multiplicative effect of slightly deleterious mutations on fitness. However, because the approximations applied in the derivation of equations (3)–(6) only consider the classes of genomes with one and zero mutations, equivalent expressions would be obtained in the case of additive fitness. Furthermore, using equation (7) instead of (6), we worked with a simplified expression that is independent of the particular value of the fitness cost. An additional limitation of the original Muller’s ratchet model is that it is formulated for a constant size population. The inclusion of bottlenecks or size fluctuations would reinforce the impact of Muller’s ratchet, which implies that a higher HGT rate would be necessary to prevent genome degeneration, thus facilitating the persistence of parasites. In practice, because the model is implemented for a Wright–Fisher population, size fluctuations can be captured using the effective population size N_e as we did in the expressions above.

One potential amendment to the approach implemented here would involve explicit modeling of the dynamics of the genes that facilitate HGT (such as, for instance genes involved in conjugation). However, the great majority of prokaryotic genomes show clear signs of substantial HGT, suggesting that such an addition, although interesting in itself, is not essential.

Although parasite transmission implies the transfer of non-homologous genetic material, whereas prevention of Muller’s ratchet requires homologous recombination, both phenomena can result from the same basic processes, especially in the case of transposons and other parasites that do not encode an autonomous transfer machinery (Darmon and Leach 2014; Hanage 2016). This notion is empirically supported, for example, by the association between the uptake of MGE and homologous material from core loci observed in antibiotic resistant strains of S. pneumoniae (Hanage et al. 2009). In a similar vein, sub-lineages within the S. aureus major lineage ST239 show unusually high variation in recombination in both core loci and MGE, suggesting that the lineage-specific levels of eDNA acquisition and recombination simultaneously affect MGE and core genes (Castillo-Ramirez et al. 2012). Although we have not explicitly invoked mobilization by MGE as a source of HGT for the cell, a significant correlation between the transfer rates of MGE and other genes was observed. Such correlation suggests the intriguing possibility that, apart from their persistence underpinned by the minimal essential HGT rate, the spread of MGE might be an important factor of microbial evolution that helps prokaryotes regain core genes that are occasionally lost during evolution.

Our results imply that prevention of Muller’s ratchet and maintenance of selfish elements are coupled through HGT. Accordingly, any prokaryotic genome that is free of genetic parasites is also expected to show signs of genome degeneration. This trend is indeed strikingly apparent in microbes whose life style leads to curtailment of HGT, such as obligate endosymbiotic bacteria (Moran 1996; Mamirova et al. 2007; Moran et al. 2008). The genus Wolbachia, a group of anciently host-restricted intracellular bacteria with reduced genomes (∼1 Mbp) and very small effective population sizes, seems particularly suitable to test the hypothesis. Arthropod-associated strains of Wolbachia (e.g., those from Culex aculeatus and Drosophila melanogaster) are known to coinfect hosts and undergo HGT (Bordenstein and Wernegreen 2004; Baldo et al. 2006). These strains also host numerous prophages and functional copies of insertion sequences, suggestive of an ongoing activity of genetic parasites (Wu et al. 2004; Cerveau et al. 2011; Duron 2013). In contrast, the strains from filarial nematodes (Brugia malayi and Onchocerca ochengi) are transmitted in a strict vertical manner that (virtually) excludes HGT (Bandi et al. 1998), and their genomes are characterized by the lack of prophages and functional insertion sequences (Foster et al. 2005; Cordaux 2009). Based on the coupling between parasite maintenance and Muller’s ratchet prevention, we predict that this second group of Wolbachia should exhibit signs of the effects of Muller’s ratchet, such as accumulation of mildly deleterious mutations. The other side of the coin is exemplified by Mycoplasma-related endobacteria: an association between parasite maintenance and avoidance of genome degeneration has been invoked to explain their evolutionary longevity as endosymbionts of mycorrhizal fungi (Naito and Pawlowska 2016).

The estimates of the HGT/loss ratio indicate that not only genetic parasites but also most of the non-parasitic genes lie above the critical threshold (fig. 2B and C) and hence typically persist in the population even in the absence of purifying selection. This observation suggests a fresh outlook on the “selfish gene” concept (Doolittle and Sapienza 1980; Orgel and Crick 1980; Dawkins 2006). The ability of genes to evolve along trajectories distinct from those of the respective vehicles (hosts), is often viewed as a trait that evolved via gene-level selection (hence the perceived selfishness of the genes). The present results imply that the apparent ability of genes to persist via HGT even when they are neutral or slightly deleterious to the host is a by-product of the organism-level selection which maintains the level of eDNA intake sufficient to escape Muller’s ratchet. Then, extensive gene loss and genome streamlining that are most typical of parasitic and symbiotic bacteria but appear to also occur in some free-living microbes (Lynch 2006b; Wolf et al. 2012; Wolf and Koonin 2013) could be either signs of genome degeneration along the path to extinction driven by Muller’s ratchet or a manifestation of strong selection whereby certain categories of genes become deleterious to the organism. The present estimates also imply that the path to becoming a parasite is, in principle, open to any gene that is not strongly deleterious, without a need to evolve efficient propagation mechanisms from the start.

Blurring the lines between a genuine genomic parasite and a non-functional sequence, such as a pseudogene, implied by the present results, raises the question whether there exists a qualitative difference between these two types of entities. The major distinction appears to be that, upon entering a new cell, a parasite adds an intact, replication-competent copy of its genome to the host genome, whereas non-parasitic, non-functional elements are likely to lose their integrity by either integrating with the genome via homologous (or in rare cases, illegitimate) recombination or degrading. From this perspective, the critical barrier that limits the conversion of non-functional DNA into genuine selfish elements is the acquisition of mechanisms that allow them to maintain their integrity in the cells they enter. In agreement with this view, there is a broad spectrum of such mechanisms which include devices that facilitate the mobility of the elements (as in transposons), those that contribute to replication (as in self-synthesizing transposons and viruses) or those that make the host cell addicted to the element as in the case of toxin-antitoxin or restriction–modification (R–M) systems (Kobayashi 2001; Van Melderen and Saavedra De Bast 2009; Koonin and Starokadomskyy 2016).

The trade-off between genome degeneration and parasite persistence constrains the strategies available to hosts and parasites in their everlasting race. Provided that the HGT rate cannot be reduced below a critical value without affecting the genome integrity, the remaining options for the host are (i) increasing the mutational bias towards deletions, thus pushing up the critical HGT rate for parasite persistence above the minimum needed to escape Muller’s ratchet (fig. 3), (ii) decreasing the mutation rate u, thus lowering the minimal HGT rate required for Muller’s ratchet avoidance (fig. 3), and (iii) evolving defense systems that discriminate between benign and parasitic elements upon DNA intake. The first strategy is consistent with the general observation that, in prokaryotes, deletions are more frequent than insertions and the rate of gene loss exceeds the rates of gene acquisition and gene duplication (Andersson and Andersson 1999, 2001; Mira et al. 2001; Kuo and Ochman 2009). Accordingly, it has been proposed that such a strong deletion bias could even be an adaptive trait that is selected for the beneficial effect of parasite elimination (Lawrence et al. 2001). However, our present analysis of effective loss rates in prokaryotic genomes shows that, despite the generalized loss bias, HGT rates are still high enough for parasites (and more generally, neutral sequences) to survive. Actually, because high deletion rates represent a burden for the maintenance of transitorily non-essential genes, an upper bound to the loss bias should exist that a cell can attain without compromising its long-term survival. The utility of the second choice, lowering the mutation rate, is limited by the power of genetic drift (Lynch 2011; Sung et al. 2012). Finally, the third possibility for hosts is to achieve discrimination between harmless and deleterious DNA when it enters the cell, thus decoupling the parasite onslaught from the “benign” HGT that could result in acquisition of beneficial genes. Such self-non-self discrimination is a stiff challenge but can be partially achieved by R–M systems that target unmodified virus DNA but not DNA modified similarly to the host genome (Pleska et al. 2016) and CRISPR-Cas systems at least some of which appear to specifically target actively replicating DNA (Amitai and Sorek 2016). In a less specific manner, the bias of transformation toward the intake of shorter DNA molecules also has been proposed as a means to combat the spread of parasites (Croucher et al. 2016).

Parasites can advance their long-term survival through three fundamentally distinct but not mutually exclusive strategies: (i) lowering the critical transfer rate that the parasites need to survive, which can be achieved by reducing the cost they inflict onto the host, (ii) increasing proliferation rate of the parasitic element inasmuch as this does not result in significant extra cost to the host, and (iii) raising the parasite transfer rate and making it independent of the host by evolving autonomous transmission mechanisms (this is the only alternative for highly deleterious elements). The two extreme strategies employed by MGE are represented by transposons (low cost, non-autonomous transmission) and lytic viruses (high cost, autonomous transmission), respectively. Temperate viruses employ bet-hedging by taking advantage of the first strategy, while keeping the ability to autonomously transmit under conditions where the survival of the host is compromised (Maslov and Sneppen 2015). Indeed, some prophages provide benefits to their host, and superinfection inhibition can be interpreted as a means to avoid further reduction of the host fitness. Eventually, the “reduced costs” strategy is bounded by the energy cost associated to the replication of the additional genetic material (Lynch and Marinov 2015) which likely sets a limit to the size of non-beneficial elements that do not encode autonomous transfer mechanisms.

An intriguing conclusion from the present analysis is that cell–parasite systems seem to exist near the edge of parasite inevitability. This phenomenon could be a co-evolutionary by-product of the long-term competition between cells and parasites: to avoid the spread of parasites, cells would tend to lower their HGT rates as much as possible without falling below the Muller’s ratchet threshold, which would keep the actual HGT rate not far above that threshold_. Parasites then would evolve such that the minimum HGT rate needed for persistence drops below the HGT rate realized by cells. This race would lead to a situation with both critical HGT rates close to each other and hence to life on the edge of parasite inevitability.

The “inevitability of parasites” can be interpreted as a null model, a starting point underlying the arms race between cells and selfish elements. This starting condition highlights the necessity for cells to evolve defense mechanisms that allow them to maintain HGT rates compatible with the preservation of the genome integrity while limiting the intake of genetic parasites. Parasites, conversely, face the challenge of counteracting such self vs. non-self discrimination mechanisms or evolving their own means for autonomous transfer. Remarkably, this co-evolutionary race centered on controlling HGT, on the host side, and escaping the HGT control, on the parasite side, is a major source of evolutionary innovation and exaptation, as HGT mechanisms originally evolved by selfish elements as means of their spread end up being used by cells for their own benefit, in particular, anti-parasite defense (Koonin and Krupovic 2015a, 2015b).

Materials and Methods

The Condition for Parasite Persistence

The condition for parasite persistence was derived by modeling the dynamics of a selfish element in a population of hosts (see Supplementary Material online). Specifically, we obtained the stationary distribution of the element copy number by numerically solving the non-linear system defined by equation (2), with the value of A given by equation (1). To this end, we used iterative techniques and matrix analysis tools implemented in Matlab. Due to computational constraints, we set the size of matrix A so that the maximum copy number was limited to 10³ copies.

The limiting case of a neutral element (s = 0) can be analytically solved within the framework of birth and death processes. In this scenario, the fraction of genomes harboring k copies of the element, p_k, becomes (Karev et al. 2002):

$$p_k^{\mathrm{*}}={\left(1-r/d\right)}^{b/r}\mathrm{\hspace{0.17em}}\frac{{\left(r/d\right)}^k}{k!}\mathrm{\hspace{0.17em}}\frac{\Gamma \left(k+b/r\right)}{\Gamma \left(b/r\right)}$$

where $b=h〈k〉$ is the average rate at which new elements arrive in the genome via HGT. An analytical condition for the persistence of parasites was obtained in this case by calculating the mean copy number from these expressions, substituting $b=h〈k〉$, and solving the resulting fixed point equation (Iranzo et al. 2014).

Approximate conditions in the limits of small and large fitness cost can be obtained by applying perturbation theory to the generating matrix A. Such derivations are comprehensively developed in the Supplementary Material online.

Estimation of Duplication, Loss and Transfer Rates from Genomic Data

Genomic data were obtained from an updated version of the ATCG database that clusters genomes from bacteria and archaea into closely related groups (Novichkov et al. 2009; Puigbo et al. 2014). We analyzed 35 of the largest ATGCs (34 bacterial and one archaeal group) that each included 10 or more genomes. For each of those ATGCs, Clusters of Orthologous Genes shared among genomes of the same ATGC (ATGC COGs) were identified (Kristensen et al. 2010) and rooted species trees were generated as described previously (Puigbo et al. 2014).

Maximum likelihood estimates of the duplication, loss and transfer rates for all ATGC COGs belonging to the mobilome were estimated using the program COUNT (Csuros 2010). For each ATGC and given a phyletic profile and a phylogenetic tree, COUNT optimizes duplication, loss and transfer rates, as well as branch lengths, according to a stochastic birth–death–transfer model. The program options were set such that duplication-loss and transfer-loss ratios were constant for all branches of the tree; duplication, loss, and transfer rates were sampled from discretized gamma distributions with four categories for duplication and loss rates and three categories for the transfer rate. The phyletic profiles of all COGs (MGE and non-MGE) within an ATGC were used as the input for COUNT. As the output, we collected branch lengths (in units of expected number of loss events per branch), the parameters of the three gamma distributions, and the posterior probabilities that each ATGC COG belongs to each possible set of categories of the gamma distributions. Posterior probabilities were processed to obtain maximum likelihood estimates for every rate in the model (in units of expected number of losses). In order to find a conversion factor between loss-based and nucleotide divergence-based timescales, we divided the total branch length as provided by COUNT (in units of expected losses) by the total branch length of the original tree (in units of nucleotide divergence), and multiplied all rates by this conversion factor. Notice that, because COUNT uses a neutral birth–death–transfer model, the value we calculate for the loss rate is actually an effective value (i.e., it is a composite of the true loss rate and the effects of selection). Accordingly, the difference between the loss and duplication rates as given by COUNT provides an estimate for the effective loss bias that can be compared with the theory.

In order to perform a statistical analysis of the rates, ATGC COGs belonging to the same COG/pfam were considered instances of the same family. Families with less than five instances were discarded. For the remaining families, we calculated descriptive statistics (median, mean, SEM and SD) for the duplication (D), loss (L), and transfer (T) rates, as well as for the loss bias (L − D). We used two estimates of the mean copy number of a family in the pool of DNA available for HGT: (i) the mean copy number in ATGCs that contain at least one genome with at least one copy of the family (henceforth denoted as 〈k⁺〉); and (ii) the mean copy number in the total set of genomes (denoted as 〈k〉). Because the condition for the persistence of parasites makes reference to the total transfer rate per mean copy number, we added up ATGC COG-specific transfer rates for all instances of the same family and divided the result by the two estimates of the mean copy number. Note that the rate based on 〈k〉 gives an upper bound for the relative HGT, whereas the value derived from 〈k⁺〉 is a more conservative estimate.

Viral elements were identified by filtering domains whose annotations contain the key terms “virus,” “(bacterio)phage,” and/or “terminase.” Domains annotated as “transposase” were classified as belonging to transposable elements. The rest of the domains were manually inspected to identify those related to conjugative plasmids. These three groups were analyzed separately in a first step, and then all MGE were merged for the subsequent analysis.