Accurate quantification of within- and between-host HBV evolutionary rates requires explicit transmission chain modelling

Abstract

Analyses of virus evolution in known transmission chains have the potential to elucidate the impact of transmission dynamics on the viral evolutionary rate and its difference within and between hosts. Lin et al. (2015, Journal of Virology, 89/7: 3512–22) recently investigated the evolutionary history of hepatitis B virus in a transmission chain and postulated that the ‘colonization–adaptation–transmission’ model can explain the differential impact of transmission on synonymous and non-synonymous substitution rates. Here, we revisit this dataset using a full probabilistic Bayesian phylogenetic framework that adequately accounts for the non-independence of sequence data when estimating evolutionary parameters. Examination of the transmission chain data under a flexible coalescent prior reveals a general inconsistency between the estimated timings and clustering patterns and the known transmission history, highlighting the need to incorporate host transmission information in the analysis. Using an explicit genealogical transmission chain model, we find strong support for a transmission-associated decrease of the overall evolutionary rate. However, in contrast to the initially reported larger transmission effect on non-synonymous substitution rate, we find a similar decrease in both non-synonymous and synonymous substitution rates that cannot be adequately explained by the colonization-adaptation-transmission model. An alternative explanation may involve a transmission/establishment advantage of hepatitis B virus variants that have accumulated fewer within-host substitutions, perhaps by spending more time in the covalently closed circular DNA state between each round of viral replication. More generally, this study illustrates that ignoring phylogenetic relationships can lead to misleading evolutionary estimates.

Importance

Pathogen strains carrying mutations that confer a selective advantage are expected to become fixed within a population. For the hepatitis B virus (HBV), however, mutations that confer adaptation within a single host are generally not passed on to the next host, which suggests that there are conflicting selective constraints for within-host survival versus transmission. Determining the strategy that HBV uses to reconcile these different fitness requirements is of general interest to evolutionary virologists as it can help explain why rates of molecular change are dependent on the evolutionary time scale on which they are measured. By using methods that appropriately take the shared ancestry into account we find that, contrary to what was previously reported, strains that are less adapted to their current host, perhaps by undergoing fewer rounds of viral replication, are preferentially transmitted.

1. Introduction

Reliable estimates of evolutionary rates are critical for testing hypotheses in molecular epidemiology, involving, for example, the timing of viral emergence (Faria et al. 2016) or associating past demographic changes with ecological factors (Bryant et al. 2007; Markov et al. 2012; Trovão et al. 2015; Gill et al. 2016; Al-Qahtani et al. 2017; Cuypers et al. 2017). Various statistical descriptions of sequence divergence through time, collectively referred to as ‘clock models’, have been proposed to estimate the rate of nucleotide substitution (see Ho and Duchêne 2014 for a comprehensive overview). These models require calibration information in order to root phylogenies in time. If a significant amount of evolutionary change has accumulated over the sampling time span, the difference in sample isolation dates can be used to calibrate the tick rate of the molecular clock (Rambaut 2000; Drummond et al. 2003b; Biek et al. 2015). Over the years, it has become clear that the estimated rate of evolution depends on the evolutionary timescale (Ho et al. 2011, 2005; Aiewsakun and Katzourakis 2016), implying that the rate of change estimated from recently collected samples may not be applicable to deeper evolutionary time scales. This so-called time-dependency of evolutionary rates is also central to the debate about the evolutionary origins of hepatitis B virus (HBV), where discrepancies in evolutionary rate estimates complicate distinguishing between competing scenarios. Specifically, when the molecular clock is calibrated using recent sampling dates, the estimated evolutionary rates appear too high to be compatible with the ‘out of Africa’ hypothesis (Fares and Holmes 2002), whereas this hypothesis finds support when calibration relies on human-HBV co-divergence information (Paraskevis et al. 2013).

In addition to model misspecification (Ho et al. 2011), unaccounted for evolutionary constraints and saturation problems (Holmes 2003; Wertheim and Kosakovsky Pond 2011; Duchêne et al. 2014; Bielejec et al. 2014), a mismatch between the within- and between-host evolutionary rate (Zhou and Holmes 2007) can also contribute to the time dependency of molecular clock estimates. Indeed, transient within-host polymorphisms lead to inflated within-host substitution rate estimates because it is typically assumed that all polymorphisms are fixed (Duffy et al. 2008). When sampling occurs close to transmission, such effects may not impose a strong rate mismatch because there is little opportunity to accumulate many host-specific substitutions. HBV patients, however, usually only develop liver disease decades after infection, and, consequently, most patients are only sampled late in infection. Furthermore, a rate mismatch will confound dating efforts in phylogenies calibrated by dated tips for which the sampling time period covers only a small fraction of the total evolutionary history. This may be particularly true for HBV, which is assumed to have co-evolved with modern humans for the past ∼40,000 years (Paraskevis et al. 2013), while samples are available only for the last few decades (with the notable exception of a HBV genotype C2 sequence recovered from a 16th century Korean mummy, Kahila Bar-Gal et al. 2012).

Known transmission chains provide unique opportunities to investigate what causes may underlie a difference between within- and among-host evolutionary rates. This has recently attracted considerable attention for the human immunodeficiency virus-1 (HIV-1), for which three hypotheses have been put forward to explain a lower evolutionary rate between hosts (Lythgoe and Fraser 2012). According to the ‘store-and-retrieve’ hypothesis, variants that avoid participating in the within-host evolutionary arms race better preserve the key phenotypic characteristics that enable to efficiently establish new infections and are hence more likely to do so. As ‘stored’ variants undergo fewer rounds of replication than actively replicating lineages they accumulate fewer mutations and the between-host rate will be lower than the within-host rate (Pybus and Rambaut 2009; Lythgoe and Fraser 2012). Alternatively, the rate discrepancy can also be explained by frequent transmission before the virus is subjected to strong immune-driven selection (‘stage-specific selection’) (Maljkovic Berry et al. 2007) or by the frequent reversion of adaptive mutations (‘adapt-and-revert’) (Herbeck et al. 2011). Importantly, these hypotheses make different predictions about the extent to which transmission affects the synonymous (μ_S) and non-synonymous (μ_N) contribution to the evolutionary rate. Specifically, when more slowly evolving variants have a transmission advantage, transmission will equally affect μ_S and μ_N whereas it is expected that μ_N contributes less to the overall rate at the between-host than at the within-host level under the two alternative scenarios. By investigating the signal in sequence data, different studies were able to attribute the HIV-1 rate slow-down to the reservoir dynamics (Alizon and Fraser 2013; Vrancken et al. 2014).

Lin et al. (2015) analysed the evolutionary dynamics in a known HBV transmission chain and found evidence for an evolutionary rate decline with increasing transmission, supporting the idea that different evolutionary processes act at the within- and between-host level (Zhou and Holmes 2007). They also observed a higher impact of transmission on the non-synonymous component of the evolutionary rate. To explain this, the authors consider the different stages of the virus life cycle, in which transmission is followed by colonization and then adaptation to the new host, and which pose conflicting phenotypic demands to the virus. They propose that variants that are well-adapted to the previous host may be less fit in the new host and therefore be outcompeted by variants that do not carry the specific adaptive changes. Although conceptually identical to the ‘adapt-and-revert’ hypothesis, Lin et al. (2015) coin this the ‘colonization-adaptation-transmission’ (CAT) model to emphasise the need for a continual switching between a set of phenotypes during the course of infection.

Here, we revisit this dataset and embed the sequence data in a full probabilistic Bayesian phylogenetic framework (BEAST, Drummond et al. 2012) to evaluate the robustness of their inferences against methods that properly take the correlation structure due to shared ancestry into account, which is ignored by pairwise comparisons to calculate evolutionary rates as used in the original study. Specifically, pairwise measurements may count substitutions on particular branches multiple times, which can impact rate estimates with unpredictable biases (Drummond et al. 2003a).

2. Materials and Methods

We follow a workflow previously applied to a known HIV transmission chain (Vrancken et al. 2014) and first examine the congruence between the timings of coalescent events, the clustering patterns and the known sequence of timed transmission events in a standard time-measured phylogenetic analysis (further referred to as the ‘unconstrained’ analysis). Next, we explicitly test for a transmission-associated evolutionary rate decline using a mixed-effects (ME) molecular clock model while imposing transmission compatibility in our genealogical inference. Finally, we estimate the contribution of synonymous and non-synonymous substitutions to the overall evolutionary rate at the within- and between-host levels.

2.1 Datasets

We analyse the known HBV transmission chain data that was recently described by Lin et al. (2015). This chain covers seven vertical transmission events: from a grandmother (GM) to her five children (three daughters, D1, D2, D3, and two sons, S1 and S2), and from two of the daughters (D2 and D3) to the granddaughters (GD2 and GD3). We used the available complete genomes generated by cloning and Sanger sequencing of HBV variants from all members of this chain. We refer to Supplementary Fig. S1 for more details on the family relations, the times of infection (which equal the birth dates) and the sampling times and to Lin et al. (2015) for a more complete description of the data. Sequences were aligned using Muscle (Edgar 2004) and manually edited in AliView (Larsson 2014).

All sequence data were used in the ‘unconstrained’ analyses and in the analyses in which among lineage rate variation is captured using the ME relaxed clock model. For the direct comparison of the contribution of μ_S and μ_N to the within- and between-host evolutionary rates, we focused on subsets of the data. Specifically, only patients for which samples of multiple time points are available (all daughters and granddaughters) were included in the within-host evolutionary rate estimation, while only the sample closest to the transmission event of each patient was included in the between-host rate estimation (Table 1).

Table 1.

Overview of the data and phylogenetic model combinations.

	Transmission history	Among lineage rate comparison			Transmission-effect on μS and μN
	Unaware (‘unconstrained’)	Trunka	Trunka	Branchb	Within-host	Between-host
	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
Data	All	All	All	All	D1–3, GD2–3	Earliest sample
Coalescent model	Skygrid	Skygrid	Constantc	Constantc	Constant	Constantc
Clock model	ucld	ME	ME	ME	Strict	Strict
HPMd	–	–	–	–	Coalescent, clock	–

ucld, uncorrelated relaxed clock model where branch rates are drawn from a discretised lognormal distribution.

^aThe fixed effect that allows for a possibly different substitution rate on a subset of branches is specified on the transmitted lineages (‘trunk’).

^bThe fixed effect that allows for a possibly different substitution rate on a subset of branches is specified on the branches that accommodate one or more transmission events (‘branch’).

^cThis refers to the within-patient coalescent process under the transmission model, which is shared among all individuals of the transmission chain.

^dThe parameters for which information is pooled through hierarchical prior specification.

2.2 Bayesian phylogenetic inference

We parameterised the substitution process using an HKY substitution model (Hasegawa et al. 1985) and modelled among-site rate variation using a discretised Γ-distribution (Yang 1993) in the ‘unconstrained’ analyses and when estimating the within- and between-host rates. The skygrid model (Gill et al. 2013) was used as a flexible tree prior for all ‘unconstrained’ analyses. For the among host evolutionary rate estimations and for contrasting evolutionary rates among lineages, we accommodate the transmission history as in Vrancken et al. (2014). Briefly, the transmission model combines temporal constraints (the most recent common ancestor or MRCA of all donor and recipient lineages is constrained to predate the time of transition) with host transition compatibility requirements (correct host jumps are required upon transmission) to ensure the viral genealogy is fully compatible with the known transmission history. As detailed previously, this model does not make any assumptions about the transmission bottleneck. Because of the sparse within-host sampling, we resorted to the coalescent model with the fewest parameters (constant population size) to describe the demographic process within-hosts. We used different molecular clock models in our analyses. Evolutionary rates were estimated using an uncorrelated relaxed clock with rates drawn from a lognormal distribution (Drummond et al. 2006) in the ‘unconstrained’ analyses. The ME model was used to test for a transmission-associated rate slow-down for a specified set of internal branches. This clock model combines random effects on branch-specific evolutionary rates modelled according to an uncorrelated relaxed clock process with estimable fixed effects on pre-specified subsets of branches (akin to fixed local molecular clock modelling) (Vrancken et al. 2014). Finally, the simplest strict clock model was used for the independent estimations of the between- and within-host evolutionary rates. To obtain informative estimates for the sparser within-host data, we allow for sharing of information about population sizes and strict clock parameters in these analyses by specifying hierarchical phylogenetic models (HPM) (Suchard et al., 2003).

We follow Lin et al. (2015) in considering only the non-overlapping regions to obtain estimates of synonymous (μ_S) and non-synonymous (μ_N) substitution rates. Briefly, this involves summarising estimates of the absolute number of synonymous (S) and non-synonymous (N) substitutions (Minin and Suchard 2008; O’Brien et al. 2009; Lemey et al. 2012) as rates by dividing the total S and N counts by the alignment length and the total tree length in time units (Vrancken et al. 2014).

Posterior estimates under the full probabilistic model were obtained using Markov Chain Monte Carlo sampling as implemented in BEAST (Drummond et al. 2012), which was used in conjunction with BEAGLE (Ayres et al. 2012). Convergence and mixing properties of the chains were inspected using Tracer v1.6 (http://tree.bio.ed.ac.uk). Maximum clade credibility trees were summarised using the TreeAnnotator tool in BEAST and visualised in FigTree v1.4.2 (http://tree.bio.ed.ac.uk). An overview of the dataset and phylogenetic model combinations is presented in Table 1.

3. Results

3.1 Conflicts between the genealogy and the transmission history

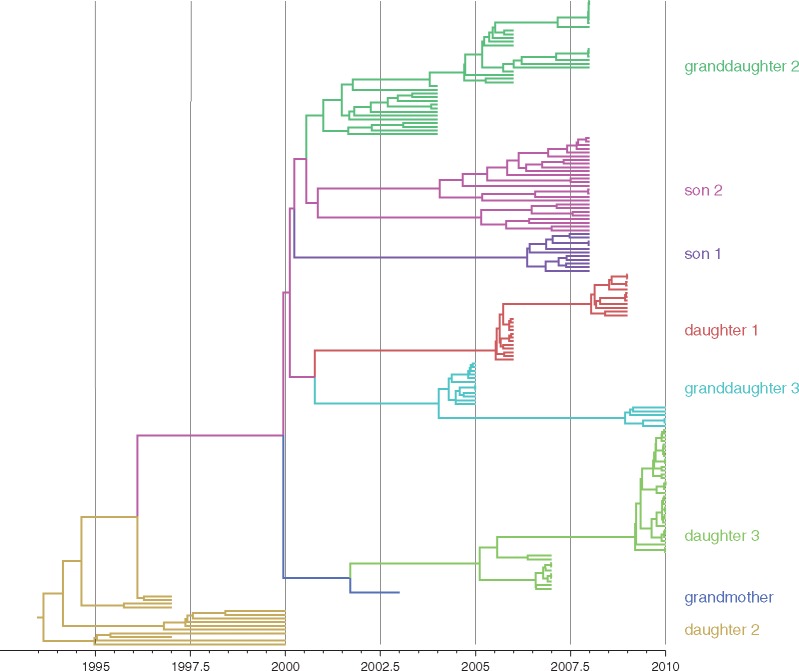
To investigate the level of compatibility between the viral genealogy and the known transmission history, we superimpose the known transmission history onto the reconstructed viral genealogy and summarise transmission compatibility of each transmission event as described previously by Vrancken et al. (2014). The estimated t_MRCA of the viral genealogy, 1992 (95% HPD: 1990–1994) in the ‘unconstrained’ analysis (model 1, Table 1) shows that calibrating the molecular clock with samples collected from the more recent part of the history—the sampling time span covers only the last 13 years of the virus history that goes back at least 66 years—results in a misleadingly high estimate of the evolutionary rate (1.86 × 10⁻³ substitutions/site/year, 95% HPD: 1.47–2.19 × 10⁻³). As a consequence all donor–recipient lineages coalesce too early in time to be compatible with the known transmission history (Fig. 1). This is further aggravated by a host transition conflict involving GM, D2, and GD2. The basal clustering of the sequences from D2, which are the oldest sequences sampled from the transmission chain, makes a scenario of transmission from GM to D2, and subsequently from D2 to GD2, implausible (Fig. 1).

Figure 1.

HBV phylogeny estimated from the transmission chain data under the ‘unconstrained’ model. We refer to Table 1 for details on the model setup. To facilitate identifying incompatibilities with the transmission history, we colored the tips and internal branches using a discrete asymmetric trait analysis with the patients as discrete states (Lemey et al. 2009; Edwards et al. 2011). The patient-color links are as indicated next to the tree.

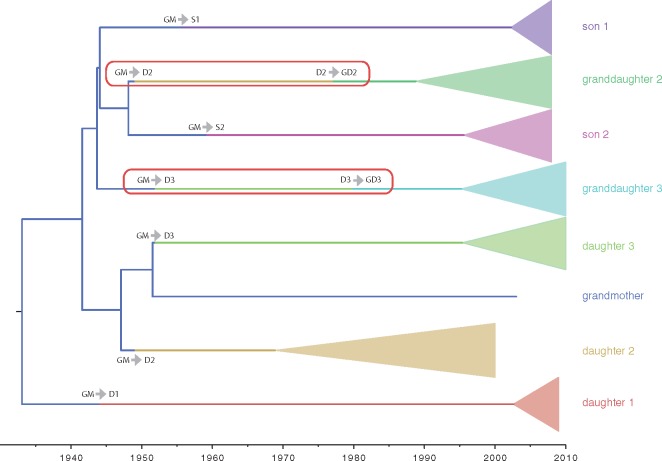
The general incompatibility between the viral genealogy and the transmission history underscores the need to incorporate external information into the analysis in order to obtain realistic parameter estimates (model 2, Table 1). Interestingly, imposing compatibility between the viral genealogy and the known chain of infections through time requires the hypothesis that D2 and D3 were infected by two variants. In both cases, the variant that was eventually transmitted to GD2 and GD3, respectively, was either not sampled or did not lead to any progeny (Fig. 2).

Figure 2.

HBV phylogeny estimated from the transmission chain data while imposing compatibility with the transmission history. We refer to Table 1 for details on the model setup. The same color representation of patients is used as in Fig. 1. Each transmission event on a branch is represented by a color change. Multiple host jumps over the same branch are highlighted by red boxes.

3.2 Evolution slows at transmission

To test for a transmission-associated rate slow-down, we applied a ME molecular clock model that allows for a different rate along the lineages that are transmitted from the index case all the way down into the different recipients compared to the rate on the branches that represent within patient evolution (model 3, Table 1 and Supplementary Fig. S2A). This allows testing whether the lineages that are being transmitted are the ones that accumulate fewer mutations as compared to the ‘dead-end’ within-host branches. Although the taxa specific to each family member always formed monophyletic clades when enforcing transmission history compatibility, we now explicitly enforced this to make sure that the fixed effect was always associated with the branches that link the within-host populations. In agreement with the original study, we find a transmission-associated decrease in the evolutionary rate and recover strong support for a lower rate on the transmitted lineages, which we express as the natural logarithm of the Bayes factor estimate (ln BF, see Table 2). We also applied an ME model that specifies a rate effect on the branches that connect different hosts (model 4 in Table 1 and Supplementary Fig. S2B) and find strong support for a lower rate on branches that accommodate a transmission event (Table 2). The estimated rate on this subset of branches is also somewhat lower than that for the transmitted lineages (Table 2 and Supplementary Fig. S3). To test for the significance of this rate difference, we further considered an analysis combining fixed effects on the transmitted lineages and the transmission-accommodating branches. The ln BF in support of a lower substitution rate on the latter class of branches is 3.96, which is usually considered as strong evidence (Kass and Raftery 1995).

Table 2.

Overview of ME model evolutionary rate analyses.

Demographic model	Fixed-effects specification		Within-host	ln BFa	Fold changeb
	‘Trunk’	‘Branch’
Transmission model	0.76 (0.33–1.25)	n.a.	8.91 (6.02–11.8)	>10.57	11.7
	n.a.	0.57 (0.24–0.99)	8.36 (5.82–11.1)	>8.26	14.7
Skygrid (‘unconstrained’)	8.1 (3.5–13.5)	n.a	19.1 (14.7–23.7)	5.56	2.4

The mean evolutionary rate and HPD intervals are expressed as the number of nucleotide substitutions (10⁻⁴) per site per year. ‘Trunk’ refers to the ME model specification in which a possibly different substitution rate operates on the transmitted lineages (this corresponds to model 3 in Table 1). ‘Branch’ refers to the ME model specification in which a possibly different substitution rate operates on the branches that accommodate one or more transmission events (this corresponds to model 4 in Table 1).

^aThe natural logarithm of the Bayes factor estimate in favour of a slower evolutionary rate on the transmitted lineages or the branches that accommodate one or more transmission events compared to the within-host rate.

^bThe fold change of the mean evolutionary rate estimate over the within-host lineages with respect to the mean evolutionary rate estimate over the between-host lineages.

We also checked whether the well-supported non-zero rate difference could be an artefact of imposing the transmission model constraints by combining the ‘trunk’ ME model with the skygrid tree prior (model 2, Table 1) instead of the transmission model (model 3, Table 1). This shows that imposing the transmission model constraints decreases the substitution rate, but the ln Bayes factor support >5 for a rate difference (Table 2) reassures that the temporal and host transition constraints do not introduce the effect although they make the difference more pronounced.

3.3 Synonymous and non-synonymous substitution rates are similarly affected by transmission

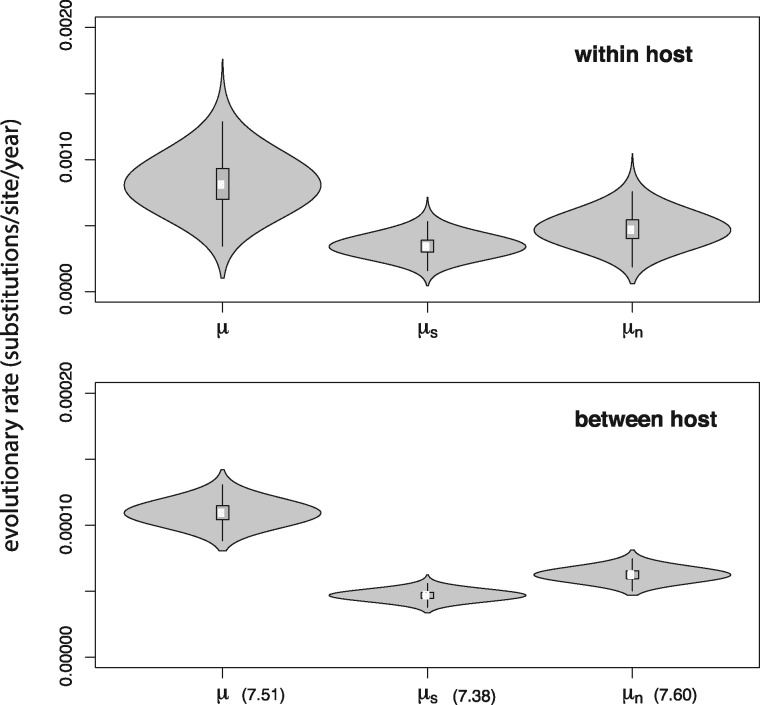
To gain insight into the mechanisms underlying the rate difference, we used a robust counting approach (Minin and Suchard 2008; O’Brien et al. 2009; Lemey et al. 2012) to estimate the synonymous (μ_S) and non-synonymous (μ_N) contribution to the evolutionary rate in the non-overlapping reading frames. Figure 3 shows the posterior probability densities for the overall rate μ, μ_S and μ_N for both the within- and between-host analysis. The scale of the Y-axis illustrates the rate difference between both biological scales, with within-host rate estimates being an order of magnitude higher than between-host estimates (10⁻³ compared to 10⁻⁴). Importantly, Fig. 3 also shows that μ_S and μ_N are affected similarly by transmission, which stands in contrast with the reported larger effect of transmission on μ_N by Lin et al. (2015).

Figure 3.

Substitution rate estimates within and between hosts. We refer to Table 1 for the model setup for the within- and between-host rate estimates. Numbers between parentheses indicate the fold decrease of the mean relative to the within-host mean rate estimate.

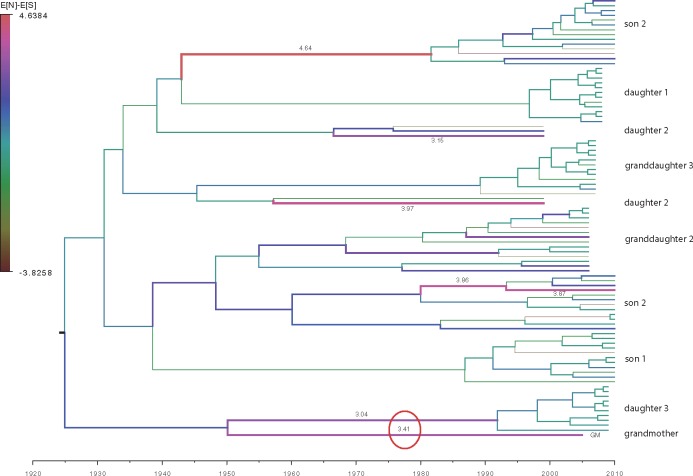
We suspect that this discrepancy can be attributed to the use of different estimation procedures. Due to shared ancestry, pairwise comparisons will count substitutions over particular branches multiple times, potentially biasing the distance estimates that involve such branches (Lemey et al. 2009). To explore whether such biases are present, we coloured all branches of the maximum clade credibility tree inferred under the transmission model by their associated difference in expected number of N and S mutations (Fig. 4). This shows that a select number of branches have a pronounced positive difference between N and S counts. The most notable of these is the branch leading to the GM because substitutions along this branch are expected to be counted in five (GM→D1, D2, D3, S1, S2) of the seven (the other two are D2→GD2 and D3→GD3) distance estimates between clades separated by one transmission event, and it is this category that accounts for the previously detected effect (see Fig. 3 in Lin et al. 2015). The substitutions along this branch are also not counted for within-host estimates because only a single sequence is available for the GM. We note that the difference in expected N and S counts over this branch is highly similar to the estimated difference in an unconstrained analysis (Supplementary Fig. S4).

Figure 4.

HBV phylogeny estimated from the transmission chain data using the non-overlapping parts of the open reading frames. The tree was inferred using only the first sample per patient and the transmission model (model 6, Table 1). The width and color of branches accord to the difference in the expected number of non-synonymous and synonymous mutations (E[N]-E[S]) they accommodate. For clarity, only values >3 are shown. The difference on the branch leading to the GM is highlighted with a red circle.

4. Discussion

In this study, we revisited the impact of transmission on the HBV substitution rate in a known transmission chain previously examined by Lin et al. (2015). Here, we analysed the genetic data using models that appropriately take into account shared ancestry. This is important because, as shown by our results, ignoring the evolutionary relationships can introduce unpredictable biases and lead to misleading results.

Using a standard demographic model as tree prior, we found that the divergence time estimates of donor–recipient lineages are in conflict with the timed series of known transmission events. This is likely explained by peculiarities of the HBV biology and the fact that the HBV patients were chronically infected for decades before the virus population was sampled (range, 25–80 years). The latter is important because, while the HBeAg prevents the immune system from mounting a response during early chronic infection, this virus antigen is usually not expressed at later stages (Harrison et al. 2011). The preCore 1986 G→A substitution is a hallmark for the HBeAg^- status, and was found in 76.7 per cent of the sampled lineages (Supplementary Table S2). Therefore, the evolutionary divergence that accumulated over the sampling period to some extent reflects fast HBeAg^- status associated evolution and the too recent divergence time estimates can at least be partly explained by the impact of the immune system on the HBV evolutionary rate.

In addition to anomalous timings, the ‘unconstrained’ analysis also revealed a discordant clustering pattern (Fig. 1). As was noted by Lin et al. (2015), this can be a consequence of the quick reversion of mutations that were adaptive in the previous host environment, such that infection is initiated by similar variants in all individuals. The decades of evolution between infection and the first sampling event in immunologically similar hosts too may have resulted in homoplasies that confound the inferred clustering patterns, making them incompatible with the transmission history.

Next, we explicitly tested for a transmission-associated evolutionary rate decline using a ME molecular clock model while imposing coalescent compatibility under the transmission model. The ME clock model allows for among-branch rate variation in the same way as a standard relaxed clock model. Two observations reassure us that this provides sufficient flexibility to adequately capture the variation in within-host rates that is most likely linked to the HBeAg status. First, the estimated substitution rate over the transmitted lineages and branches that accommodate a transmission event, which likely represent the HBeAg⁺ periods of infection, is consistently at the lower end of the rate estimate spectrum (Table 2). Second, the 95 per cent HPD interval of the between-host rate largely overlaps with those estimated from data sets restricted to HBeAg⁺ carrier sequences (Harrison et al. 2011).

Like Lin et al. (2015), we find a transmission-associated decrease in the evolutionary rate, and recover strong Bayes factor support for a lower rate on the transmitted lineages (Table 2). Because the switch from HBeAg⁺ to HBeAg^- usually occurs between the ages of 15 and 35 years (Merican et al. 2000), which is more or less the donor age at transmission in this chain (Supplementary Table S1), it is very likely that the donor was HBeAg⁺ for some transmission events. Since HBV evolves slower during the HBeAg⁺ stage of infection, and our sampling partly reflects faster HBeAg^- evolution, it could be that the rate difference detected by the ME clock model between the transmitted lineages or branches that accommodate a transmission event, on the one hand, and the branches that represent within-host evolution, on the other hand, is linked to the HBeAg status and not to impact transmission. However, we find strong support (ln BF = 3.96) for a lower substitution rate on the branches that accommodate a transmission event than on the transmitted lineages (Table 2 and Supplementary Fig. S3). This indicates that in addition to a potential effect of HBeAg⁺ evolution on the ‘trunk’ or transmitted lineages, we find support for a specific effect of slower evolution associated with transmission.

Because HBV usually is transmitted by HBeAg⁺ carriers, it has been suggested that the slower evolution during the HBeAg⁺ phase appropriately approximates the long-term substitution rate of the virus and could be used for studying events over longer periods of time (Simmonds 2001). However, they are still an order of a magnitude higher than the rate estimates obtained by calibrating the molecular clock using human-virus co-divergence data (2.2 × 10⁻⁶, 95%HPD: 1.5–3.0 × 10⁻⁶, Paraskevis et al. 2013), suggesting that saturation and long-term purifying selection (Holmes 2003; Wertheim and Kosakovsky Pond 2011; Duchêne et al. 2014; Bielejec et al., 2014) may play a role at longer evolutionary time scales. This time-dependency of substitution rates has permeated the field of molecular evolution and advocates the use of internal calibrations to obtain more appropriate divergence times over longer time scales (Worobey et al. 2008, 2010; Paraskevis et al. 2013; Duggan et al. 2016).

The difference in evolutionary rates was also apparent in the direct comparison of the within- and between-host estimates (Fig. 3), where we evaluated the effect of transmission on μ_S and μ_N. The interpretation of the impact of transmission on μ_S and μ_N measurements critically depends on the assumption that synonymous changes are less affected by selection than non-synonymous changes. Synonymous changes are not per se selectively neutral, for example, due to their impact on the secondary RNA and DNA structure, and the compact nature of the HBV genome may further aggravate this. However, it has been shown for HIV-1, which also has a compact genome, that the sites that affect the secondary RNA structure are under strong purifying selection, which indicates that this class of sites contributes little to the substitution rate (Sanjuán and Bordería 2011). In addition, available data for single-stranded viruses indicate that synonymous changes have markedly lower selection coefficients than amino acid changing mutations (Cuevas et al. 2012).

In contrast to Lin et al. (2015), we found that μ_S and μ_N experience a similar decline, and we indicate how ignoring the tree structure can bias pairwise divergence estimates. Under the CAT model put forward by Lin et al. (2015), it is expected that the non-synonymous changes that have accumulated within a host have reverted by the time of sampling in the new host, and are thus not accounted for in the between host substitution rate measurements. Because synonymous changes are expected to be less affected by selection, the CAT model predicts that transmission should have a more pronounced impact on the non-synonymous component of the substitution rate. This conflicts with our results, which instead are in line with the recently proposed hypothesis by Lythgoe et al. (2017); that is, HBV variants mitigate the trade-off between more efficient replication within single hosts and decreased transmissibility between hosts by spending a long time in the covalently closed circular DNA (cccDNA) state, which can persist for prolonged periods of time (Yang and Kao 2014), between rounds of replication. In this way, the viral generation time increases and, hence, the opportunity to accumulate deleterious adaptive mutations decreases (Lythgoe et al. 2017). To account for the differences in evolutionary rates within and between hosts, we further propose that viruses that have undergone fewer rounds of replication, and therefore had less opportunity to accumulate mutations, are more likely to be transmitted (similar to what has been proposed for HIV and HCV). Interestingly, a recent survey of 37 mother-to-child-transmission pairs found that the majority of new infections (∼75%) was initiated by the predominant maternal variant (Yang et al. 2017). If new infections are indeed usually initiated by those variants that have spent more time in the cccDNA state between rounds of replication, this implies that faster replicating variants usually are also evolutionary dead-ends within hosts. More research, for example, in the form of long-term longitudinal follow-up studies similar to those performed for hepatitis C virus (Raghwani et al. 2016), is needed to further examine whether the observed within-host dynamics match the evolutionary patterns that are predicted by this hypothesis.

More generally, this study demonstrates why evolutionary hypothesis testing should preferentially be based on probabilistic models that take the correlation structure into account that is induced by shared ancestry and that model sequence evolution as realistically as possible.

Supplementary data

Supplementary data are available at Virus Evolution online.

Conflict of interest: None declared.