Mechanical lifting energy consumption in work activities designed by means of the “revised NIOSH lifting equation”

Abstract

The aims of the present work were: to calculate lifting energy consumption (LEC) in work activities designed to have a growing lifting index (LI) by means of revised NIOSH lifting equation; to evaluate the relationship between LEC and forces at the L₅-S₁ joint. The kinematic and kinetic data of 20 workers were recorded during the execution of lifting tasks in three conditions. We computed kinetic, potential and mechanical energy and the corresponding LEC by considering three different centers of mass of: 1) the load (CoM_L); 2) the multi-segment upper body model and load together (CoM_Upp+L); 3) the whole body and load together (CoM_Tot). We also estimated compression and shear forces. Results shows that LEC calculated for CoM_Upp+L and CoM_Tot grew significantly with the LI and that all the lifting condition pairs are discriminated. The correlation analysis highlighted a relationship between LEC and forces that determine injuries at the L₅-S₁ joint.

Introduction

The manual lifting tasks that are found in almost every workplace¹⁾ can cause work-related low-back disorders (WLBDs)^{2, 3, 4, 5, 6, 7, 8, 9)}, which are the most common musculoskeletal problems^{5, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21)}.

An approach widely used for prevention of WLBDs is based on the revised NIOSH (National Institute for Occupational Safety and Health) lifting equation (RNLE), which provides an estimate of the physical stress level associated with the lifting task^{22, 23, 24)}. The RNLE defines a safe condition if the LI score is below 1.0, or as stressful and associated with a moderate or high risk of injury if the LI score is higher. The risk of WLBDs has been shown to increase as the LI increases from 1.0 to 3.0, with a significant odds ratio^{4, 11, 25, 26)}.

Unfortunately, approximately 35% of lifting tasks and 63% of workers cannot be assessed by means of the RNLE owing to its strict parameters and equation restrictions^{22, 27, 28, 29, 30, 31, 32, 33)}.

The development of methodologies based on new technologies for risk assessment may not only reduce the number of cases in which the RNLE cannot be applied, but also avoid job misidentification^{26, 34)}. Indeed, the huge technological advances, i.e. increased accuracy and miniaturization, have considerably enhanced the ability to identify the relationship between WLBDs and risk factors^{16, 35)}. Furthermore, the possibility to use these technologies connected to electronic smart devices (smartphones, phablets, tablets and smartwatches) via wireless protocols such as Wi-Fi and Bluetooth, would allow a simplified analysis in the worker-centered environments and distributed computing environments.

One such tool could be based on kinematic measurements designed to calculate the mechanical lifting energy consumption (LEC) in relation to the center of mass (CoM) of the system involved in the lifting task. Mechanical energy consumption, previously used in both normal^{36, 37)} and abnormal gait patterns^{38, 39)}, provides information on the mechanical energy consumed by the whole skeletal muscle system during the movement task. Higher values are indicative of greater energy expenditure. We hypothesize that this parameter may be used as an index that is sensitive to the LI and is closely related to the compression and shear forces at the L5–S1 joint.

It may be possible to study this approach in the laboratory by means of optoelectronic systems^{40, 41, 42, 43)} and apply it to indoor and outdoor work environments by means of wearable sensors⁴⁴⁾. Indeed, the recent development of microelectromechanical systems, such as inertial measurement units (IMUs) (i.e. combined accelerometers and gyroscopes), has paved the way for some noteworthy scientific breakthroughs that may be applied to a range of research areas^{45, 46)}.

The aims of the present work were: i) to calculate lifting energy consumption (LEC) during the execution of controlled lifting tasks designed on the basis of the RNLE and with an increasing lifting index (LI=l, LI=2 and LI=3); ii) to verify the sensitivity of LEC to the risk level and to evaluate its relationship with forces at the L5–S1 joint.

Subjects and Methods

Subjects

Twenty male subjects (mean age 33.30 ± 7.39 yr, height 1.80 ± 0.07 m, body mass index (BMI) 24.37 ± 2.67 kg/m2) were enrolled in the study. The workers had no history of musculoskeletal disorders, upper limb, lower limb and trunk surgery, or orthopedic and neurological diseases. All the participants gave their informed consent to the study, which complied with the Helsinki Declaration and was approved by the local ethics committee.

Kinematic and kinetic recordings

An eight infrared cameras (sampling frequency 340 Hz) optoelectronic motion analysis system (SMART-DX 6000 System, BTS, Milan, Italy) was used to detect the movements of 33 spherical markers (15 mm in diameter) covered with aluminum powder reflective material placed over the cutaneous projections of the spinous processes of the seventh and tenth cervical vertebrae, suprasternal notch (between the clavicular notches), sternum, sacrum and, bilaterally, over the temple, posterior-superior parietal bone, acromion, olecranon, ulnar styloid and radial processes, head of the third metacarpal bone, anterior superior iliac spine, great trochanter, lateral femoral condyle, fibula head, lateral malleoli, metatarsal head and heel^{47, 48, 49, 50, 51)}. Four markers were also placed over the 4 vertexes of a load consisting of a plastic crate.

Ground reaction forces were acquired by using four dynamometric platforms at a sampling rate of 680 Hz (P 6000, BTS, Milan, Italy) embedded in the floor.

Data acquisition from the infrared cameras and force platforms was integrated and synchronized.

Experimental procedures

The environmental data in the laboratory were collected using a portable multi-channel (sampling frequency 0.033 Hz) data logger (Lsi – Lastem, Babuc A, Permenugo, Italy). Air temperature and relative humidity were 23.30 ± 0.95°C and 40.60 ± 5.03% respectively.

Spatial accuracy after the calibration procedure was 0.2 mm in the x, y and z dimensions. A global reference system (GRS) in the laboratory was adopted in accordance with the International Society of Biomechanics^{47, 48)}.

The subjects were asked to perform the manual material lifting task standing in a neutral body position and lifting a plastic crate with handles using both hands in three different lifting conditions, according to the RNLE²²⁾. The six lifting conditions were chosen in order to obtain LI values of 1, 2 and 3. The task factors were arbitrarily chosen among a large number of combinations to have these three fixed LI values. Table 1 shows, for each lifting condition, the values of the load weight (L), horizontal (H) and vertical (V) locations, vertical travel distance (D), asymmetry angle (A) and lifting frequency (F), as well as the corresponding values of the multipliers. The hand-to-object coupling was defined as “good” for all three lifting conditions. Each participant was required to perform a total of 30 trials (5 repetitions X 6 lifting tasks). The order of each condition was randomly assigned.

Table 1. For each task (A, B, C, D, E and F), the values of the load weight (L), the horizontal (H) and vertical (V) locations, the vertical travel distance (D), the asymmetry angle (A), the lifting frequency (F) and the hand-to-object coupling (C) and the corresponding values of the multipliers and recommended weight limit (RWL).

Task	LC	H (cm)	HM	V (cm)	VM	D (cm)	DM	A (°)	AM	F (lift/min)	FM	C	CM	L (kg)	RWL	LI
A	23 kg	25	1	75	1	25	1	30	0.9	≤0.2	1	good	1	23	23	1
B	23 kg	25	1	75	1	25	1	0	1	≤0.2	1	good	1	20.7	20.7
C	23 kg	50	0.5	75	1	25	1	30	0.9	≤0.2	1	good	1	23	11.5	2
D	23 kg	50	0.5	75	1	25	1	0	1	≤0.2	1	good	1	20.7	10.35
E	23 kg	60	0.42	30	0.87	45	0.92	30	0.9	≤0.2	1	good	1	22.09	7.36	3
F	23 kg	63	0.4	30	0.87	45	0.92	0	1	≤0.2	1	Good	1	20.88	6.96

Data analysis

Lifting cycle detection

Acquisitions were performed using Smart Capture software (BTS, Milan, Italy), while the tracking procedure and data computing were performed by Smart Tracker (BTS, Milan, Italy), Smart Analyzer (BTS, Milan, Italy) and Matlab (version 8.0.0.783, MathWorks, Natick, MA, USA) software. The vertical displacement and velocity of one of the four markers placed over the vertexes of the crate were evaluated. Velocities were obtained by applying finite difference derivatives and a Butterworth filtered 4-Hz cut-off low-pass frequency. The onset of the lifting task was defined as the time point at which the crate marker velocity exceeded the velocity threshold by 0.025 m/s on the vertical axis. Termination of the lifting task was defined as the point on the graph at which the crate marker velocity fell below the velocity threshold in the opposite direction. Kinematic and kinetic data were time normalized to the duration of the lifting tasks and reduced to 101 samples using a polynomial procedure.

CoM calculation

We calculated three different CoM values referring respectively to the load (CoM_L), the multi-segment upper body model (head, trunk, upper arms, forearms and hands) and load together (CoM_Upp+L) as well as to the whole body (multi-segment upper body model, pelvis, thighs, shanks and feet) and load together (CoM_Tot). In all the three cases, the CoM was computed as the centroid of a set of elements composed by n body segments and the load. The computation was carried on by considering kinematic and anthropometric data together with the body segment parameters^{51, 52, 53)}, according to the weighted average of the individual body segments’ center of mass^{49, 54)}.

$$Co{M}_x=\frac{1}{m}\sum _{i=1}^n{x}_i*m_i$$ (1)

$$Co{M}_y=\frac{1}{m}\sum _{i=1}^n{y}_i*m_i$$ (2)

$$Co{M}_z=\frac{1}{m}\sum _{i=1}^n{z}_i*m_i$$ (3)

where CoM_x, CoM_y and CoM_z are, respectively, the instantaneous x, y and z components of the CoM position, m is the mass of the system being considered (load, upper body+load and whole body+load, respectively), n is the number of parts being considered (n=1, n=9 and n=16, respectively), x_i, y_i and z_i are the components of the CoM position of the i_th part, and m_i is the mass of the i_th segment or load.

Lifting energy consumption (LEC)

For each of the CoMs calculated, the kinetic energy (E_k) during the lifting tasks was calculated as the sum of the kinetic energy on the x (E_kx), y (E_ky) and z (E_kz) axes as follows:

$$E_k=E_{kx}+E_{ky}+E_{kx}=\frac{1}{2}m\left(v_x^2+v_y^2+v_z^2\right)$$ (4)

where m and v_x, v_y and v_z are, respectively, the mass and velocity components on x, y and z of the CoM being considered. Furthermore, the potential energy (E_p) was calculated using the following equation:

$$E_p=mgh$$ (5)

where h is the vertical (y) component of the CoM of the system being considered and g is the acceleration of gravity.

Lastly, the mechanical energy (E_M) was calculated as the sum of E_k and E_p. For each CoM, the difference between maximum and minimum values of each E_k, E_p and E_M within the lifting cycle were considered as LEC (LEC_k, LEC_p and LEC_M, respectively). In particular, we calculated LEC_{k_L}, LEC_{p_L}, and LEC_{M_L} for CoM_L, LEC_{k_Upp+L}, LEC_{p_Upp+L} and LEC_{M_Upp+L} for CoM_Upp+L, and LEC_{k_Tot}, LEC_{p_Tot} and LEC_{M_Tot} for CoM_Tot.

Force calculation

According to the multi-segment upper body model, the net forces (F_L5−S1) at the L₅−S₁ joint were calculated, in the local reference system (LRS) placed on the trunk in which the y′ axis is oriented as the vector C7-sacrum and x′−z′ represents the orthogonal plane to y, by using the following formula⁵⁵⁾:

$$F_{L5-S1}=-\sum _{j=1}^q{F}_j-\sum _{i=1}^p{m}_{i}g+\sum _{i=1}^p{m}_i{a}_i$$ (6)

where q is the number of external forces, F_j is the j_th external force, p is the number of body segments being considered, m_i and a_i are respectively the mass^{50, 51)} and the acceleration of the i_th segment.

In this LRS, the components of F_L5−S1 on the y′ axis and the x′−z′ plane were called compression (Fcompr_L5−S1) and shear (Fshear_L5−S1) forces, respectively.

Statistical analysis

All the analyses were performed using SPSS 17.0 software (SPSS Inc. Chicago, IL, USA). The Shapiro-Wilk and Kolmogorov-Smirnov test were used to analyze the normal distribution of the data. For each LEC_k, LEC_p and LEC_M, we performed a one-way repeated-measures ANOVA to determine whether there were any significant differences between the three risk levels. Post-hoc analyses were performed using a paired t test with Bonferroni’s corrections when significant differences were observed in the ANOVA. The Pearson test was used to investigate any correlations between LEC_k, LEC_p and LEC_M and the forces. A p value of less than 0.05 was considered statistically significant.

Results

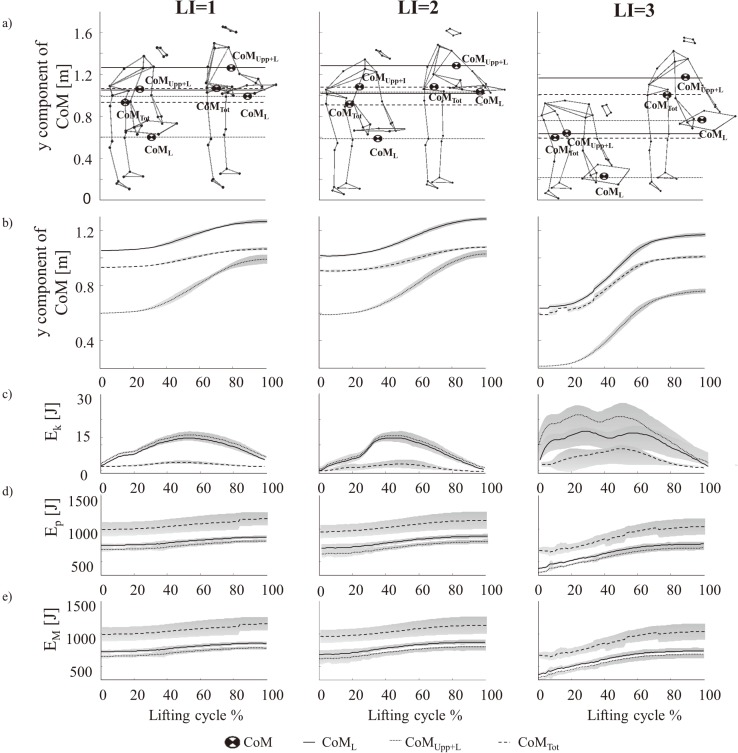
A description of the vertical displacements of the three CoMs considered, E_k, E_p and E_M during the execution of the lifting tasks in the three conditions is provided in Fig. 1: the qualitative analysis of energy expenditure revealed differences in both the E_p and E_M curves among the three lifting conditions (Fig. 1 (c) and Fig. 1 (d)) for each CoM considered.

Fig. 1.

A qualitative description in a representative subject of vertical displacements of CoM_L, CoM_Upp+L and CoM_Tot (a) (in meters), E_k (b), E_p (c) and E_M (d) (in Joule) for each CoM investigated during the execution of the three lifting conditions (LI=1, LI=2 and LI=3). Black curves represent the mean values, with the SDs of the means shown in grey. Data are normalized to the lifting cycle duration and reduced to 101 samples over the cycle.

Figure 2 shows the means and standard deviation values of LEC.

Fig. 2.

Means and standard deviations of the LEC_k (a), LEC_p (b) and LEC_M (c) calculated while performing manual material lifting tasks in the three different conditions (LI=1, LI=2 and LI=3) for the three CoMs (CoM_L, CoM_Upp+L, CoM_Tot). * and ** Significant differences at the post hoc analysis with p<0.05 and p<0.001 respectively.

As reported in Table 2, the repeated measures ANOVA revealed a significant effect of the lifting condition on LEC_p and LEC_M for all the CoMs considered. Statistically significant effects were also detected for LEC_{k_Upp+L} and LEC_{k_Tot}. Particularly, post hoc analysis showed significant differences (all p<0.001) between each pair of lifting conditions for LEC_p and LEC_M for all the CoMs considered and also for LEC_{k_Upp+L}. Furthermore, as regard LEC_{k_Tot} significant differences were found between each pair of lifting conditions (LI=1 vs LI=2: p=0.001; LI=1 vs LI=3: p= 0.005; LI=2 vs LI=3: p=0.021).

Table 2. The F, df and p-values of the repeated-measures ANOVA considering the L_k, L_p, and L_M in the three lifting conditions for the CoM_L, CoM_Upp+L and CoM_Tot. Bold type indicates statistical significance.

		CoML	CoMUpp+L	CoMTot
LECk	F	3.847	73.469	16.043
	df	1.118	1.081	1.047
	p	0.075	<0.001	0.003
LECp	F	150.992	173.479	65.755
	df	1.349	1.027	1.049
	p	<0.001	<0.001	<0.001
LECM	F	126.454	146.276	67.219
	df	1.154	1.012	1.050
	p	<0.001	<0.001	<0.001

The results of the correlation analysis between each LEC with Fcompr_L5−S1, Fshear_L5−S1 (scatter plots, regression line, correlation coefficients and p values) are reported in Fig. 3. Particularly, the correlation analysis highlighted i) a strong correlation (r>0.7) between each LEC relating to CoM_Upp+L and Fshear_L5−S1, ii) a moderate correlation (0.3<r<0.7) between each LEC relating to CoM_Upp+L and Fcompr_L5−S1, iii) a moderate correlation (0.3<r<0.7) between each LEC relating to CoM_Tot and only Fshear_L5−S1, iv) a strong correlation (r>0.7) between LEC_{p_L} and LEC_{M_L} and Fshear_L5−S1, v) a moderate correlation (0.3<r<0.7) between LEC_{p_L} and LEC_{M_L} and Fcompr_L5−S1.

Fig. 3.

Correlation between the LEC_{k_L}, LEC_{p_L}, LEC_{M_L}, LEC_{k_Upp+L}, LEC_{p_Upp+L}, LEC_{M_Upp+L}, LEC_{k_Tot}, LEC_{p_Tot} and LEC_{M_Tot} and the maximum values of Fcomp_L5−S1 (a) and Fshear_L5−S1 (b). Each plot contains 60 points, which correspond to the 20 subjects performing the three different lifting conditions (LI=1, LI=2 and LI=3). Triangles represent the mean of the twenty points for each lifting condition. Each plot shows the r and p values. Bold type indicates statistical significance.

Discussion

In this study, we investigated energy consumption, the forces at the L₅−S₁ joint and the relationship among these parameters during the execution of lifting tasks designed in such a way as to exert a growing biomechanical load using the RNLE. The rationale behind this investigation is that an instrumental tool based on energy consumption may be used as risk assessment method to combine with the NIOSH protocol.

Qualitative analysis of our results revealed differences in both the E_p and E_M curves among the three lifting conditions for each CoM considered and in E_k curves for the CoMs referred to the upper-body and whole body multi-segments systems (Fig. 1). Furthermore, a significant effect of the lifting condition was found on each lifting energy consumption for the CoM_Upp+L and CoM_Tot and also on LEC_P and LEC_M in relation to the CoM referring to the load (Fig. 2).

This is likely to be due to the fact that CoM_Upp+L and CoM_Tot take into account the dynamic body geometry during the execution of the lifting tasks and are, consequently, more sensitive to the RNLE factors that influence the risk level. By contrast, CoM_L is influenced above all by the motor strategy at the end effectors (hands), and does not take into account the dynamic body geometry during the execution of the lifting tasks. Indeed, for a given L, an equal D and different LI, CoM_L might not yield any differences in lifting energy consumption because the total movement dynamic would not be considered in the same way as for CoM_Upp+L and CoM_Tot, nor would the relevance of the other RNLE factors be considered, i.e. H and A.

Our results also highlighted that lifting energy consumption grew significantly with the LI and that all the lifting condition pairs are discriminated (Table 2 and Fig. 2): these trends indicate that lifting energy consumption correctly represents the greater energetic requirements due to the increased level of physical stress, and thus suggest that lifting energy consumption may be used as a risk assessment biomechanical index. In particular, it may be possible to use each lifting energy consumption related to CoM_Upp+L and COM_Tot to correctly interpret low-, medium- and high-risk jobs.

Certainly, the validity of lifting energy consumption method depends on the lifting conditions we set so depending on the multipliers of RNLE equation. On the other hand, findings of our study show the presence of a significant effect of LI on lifting energy consumption calculated by considering CoM_Upp+L and CoM_Tot, even if obtained within the boundaries of our experimental setup. These results allow us to comprehend that lifting energy consumption, although calculated by a different equation with respect to LI, is sensitive to the RNLE factors and to the risk level because centers of mass are linked to the dynamic body geometry during the execution of the lifting tasks.

The above considerations are supported by the correlation analysis (Fig. 3), which highlights a close relationship i) between each lifting energy consumption and Fshear_L5−S1 and Fcompr_L5−S1 when we considered the CoM_Upp+L, ii) between each lifting energy consumption and only Fshear_L5−S1 when we considered CoM_Tot and iii) between LEC_{p_L} and LEC_{M_L} and both the forces Fshear_L5−S1 and Fcompr_L5−S1. In particular, these findings point to the need to calculate the CoM_Upp+L for the lifting energy consumption analysis. For against a low correlation between LEC_k and forces was detected when we considered CoM_L. From a global point of view, mechanical energy expenditure during the execution of lifting tasks is always closely related to the shear forces because spinal loads are affected by lifting dynamics, i.e. flexed lifting⁵⁶⁾.

Our experimental data allowed us to identify the lifting energy consumption indices that are sensitive to an increasing LI (LI=l, LI=2 and LI=3) designed on the basis of the RNLE. These indices would be particularly useful as an instrumental risk assessment method if referred to the set of conditions studied to support the NIOSH protocol or to evaluate a varied range of conditions in which the NIOSH protocol cannot be used (lifting with one hand, for over eight hours, while seated or kneeling, in a restricted work space, unstable objects, while carrying, pushing or pulling, with wheelbarrows or shovels, in high speed motion, with unreasonable foot-floor coupling, in an unfavourable environment).

In literature, there are many studies considering the mechanical energy consumption and/or the body energy consumption^{57, 58)} during lifting tasks. Furthermore, a linear relationship between mechanical work and body energy consumption was found in different activities^{59, 60, 61)}. Particularly, in lifting tasks, for the same increase in absolute mechanical work there is a higher increase in body energy consumption for positive compared with negative work⁶¹⁾.

This relationship strengthens the choice of our index to risk assessment during lifting task. Certainly, the mechanical energy consumption method is easier to apply in work environments than the body energy consumption. In fact, measurements of oxygen consumption (VO₂) are generally carried out by using a portable system for pulmonary gas exchange measurement. In this kind of measurement, the subject needs to wear a mask that can interfere with the working activities and can introduce psychological stress in the works⁶²⁾.

Indeed, once these indices have been identified in the laboratory in controlled lifting conditions by means of the optoelectronic system, they could be applied in indoor and outdoor work environments by means of IMUs. In addition to being able to measure single- or multi-point motion trajectories of single or multiple body segments of the subject during the movement task, IMUs have become widely used in all activities that address complex motion analysis because of their interconnectivity, light weight, small size, low power consumption, portability and low cost. Moreover, since IMUs are included in smart devices (i.e. smartphones and tablets), which are now used in every walk of life, inertial sensor-based movement recognition has attracted increasing interest in a number of research fields, including biomechanics^{63, 64, 65, 66, 67, 68, 69)}. Such research might lead to an IMU-based lifting recognition tool built on data acquired in controlled lifting conditions that would increase the likelihood of detecting the risks associated with WLBDs.

For instance, a LEC-based lifting recognition tool could be designed by considering one criterion of risk classification based on LEC_M, as shown in Fig. 4.

Fig. 4.

An IMU-based lifting recognition tool designed by considering one criterion of risk classification (LEC_{M_L} (a) or LEC_{M_Upp+L} (b) or LEC_{M_Tot} (c)). The error bars represent the mean ± SD values.

Our LEC-based lifting recognition tool was built considering: low risk jobs as the interval between 0 and [mean+SD of LI=1] (all values under [mean-SD of LI=1] were associated with low risk jobs); medium risk jobs as the interval between [mean-SD of LI=2] and [mean+SD of LI=2]; high risk jobs as the interval between [mean-SD of LI=3] and [mean+SD of LI=3]. The values included in two different intervals or in any interval (Fig. 4), represent ranges for which it is not possible to make a choice because they should be associated with two different type of risk jobs. Whereas values above the high risk zone indicate very high-risk jobs (Fig. 4). In particular, LEC_{M_L} values within the range 0-[mean+SD of LI=1], [mean-SD of LI=2]-[mean+SD of LI=2] and [mean-SD of LI=3]-[mean+SD of LI=3] indicate low-, medium- and high- risk jobs, respectively (Fig. 4 (a)). Instead, as regards LEC_{M_Upp+L} and LEC_{M_Tot} values within the range 0-[mean-SD of LI=2], [mean+SD of LI=1]-[mean+SD of LI=2] and [mean-SD of LI=3]-[mean+SD of LI=3] indicate low-, medium- and high- risk jobs, respectively (Fig. 4 (b and c)). Others ranges for which it is not possible to make a choice are indicated as LI=?. Finally, values above the LI=3 zone indicate very high-risk jobs.

Limitations and future developments

One limitation of this method may be its suitability for the assessment of composite or sequential^{22, 70)} manual lifting jobs in which the lifting tasks are significantly different. Another limitation of this study is the use of only male workers; indeed, gender aspects are important and they may lead to different results.

This study may be developed further by: i) widening the range of lifting task types with the same LI but changing the multiplier values; ii) testing also lifting conditions with LI values lower than 1, between 1 and 2, and between 2 and 3; iii) analyzing changes in the criteria selected due to temperature and humidity, sex, age, work experience, etc. The study could also be extended by using, in addition to the optoelectronic motion analysis system, wearable inertial sensors during manual material lifting tasks in the laboratory in different lifting conditions.

This would allow us to compare the LEC calculated using the optoelectronic system with that calculated by means of inertial sensors, thereby validating and strengthening the applicability of this method in indoor and outdoor work environments, and further supporting the findings of previous noteworthy studies in this field^{45, 46, 47)}. An instrumental lifting recognition tool could be further implemented by using surface electromyography-based indices that would provide additional criteria of classification and enhance the power of the test.

Conclusion

Results of our study show that LEC significantly change in relation to the risk levels. In the light of these considerations, we believe that an IMU/Inertial sensor-based lifting recognition tool using LEC indices and designed according to the revised RNLE lends itself to the estimation of risk. It should be noted that the proposed IMU/Inertial sensor-based lifting recognition tool was based on 6 lifting conditions corresponding to three LI levels at 1, 2 and 3. Future research is recommended for validating the risk assessment tool for additional lifting conditions.