Corrigendum

In the article by D. C. Kadam, S. M. Potts, M. O. Bohn, A. F. Lipka and A. J. Lorenz (G3 Genes|Genomes|Genetics 6: 3443–3453) entitled “Genomic Prediction of Single Crosses in the Early Stages of a Maize Hybrid Breeding Pipeline,” genomic relationship matrices (GRMs) were inadvertently calculated as simple matching coefficient instead of method 1 of VanRaden (2008) as stated in the manuscript. We performed reanalysis using the GRMs calculated according to method 1 of VanRaden (2008). Only the results pertaining to comparisons of methods were different.

In summary, the sentence on page 3446 of the article that read:

“The random effect vectors $\mathit{f},\mathit{m},\text{and}\hspace{0.17em}\mathit{s}$ were assumed to have the following multivariate normal (MVN) distributions: $\mathit{f}\sim \mathit{MVN}\left(0\mathit{,}{\mathit{G}}_{\mathit{f}}{\sigma }_{\mathit{GCA}\_\mathit{F}}^2\right),m\mathrm{\sim }\mathit{MVN}\left(0,{\mathit{G}}_{\mathit{m}}{\sigma }_{\mathit{GCA}\_\mathit{M}}^2\right),\hspace{0.17em}\text{and}\hspace{0.17em}\mathit{s}\sim \mathit{MVN}\left(0,\mathit{S}{\sigma }_{\mathit{SCA}}^2\right),$ where ${\mathit{G}}_{\mathit{f}}$ and ${\mathit{G}}_{\mathit{m}}$ were additive genomic relationship matrices of females and males, respectively, calculated according to method 1 of VanRaden (2008).”

Has been rewritten to read:

“The random effect vectors $\mathit{f},\mathit{m},\hspace{0.17em}\text{and}\hspace{0.17em}\mathit{s}$ were assumed to have the following multivariate normal (MVN) distributions: $\mathit{f}\mathrm{\sim }\mathit{MVN}\left(0\mathit{,}{\mathit{G}}_{\mathit{f}}{\sigma }_{\mathit{GCA}\_\mathit{F}}^2\right),m\mathrm{\sim }\mathit{MVN}\left(0,{\mathit{G}}_{\mathit{m}}{\sigma }_{\mathit{GCA}\_\mathit{M}}^2\right),\hspace{0.17em}\text{and}\hspace{0.17em}\mathit{s}\mathrm{\sim }\mathit{MVN}\left(0,\mathit{S}{\sigma }_{\mathit{SCA}}^2\right),$ where ${\mathit{G}}_{\mathit{f}}$ and ${\mathit{G}}_{\mathit{m}}$ were additive genomic relationship matrices of females and males, respectively, calculated as simple marker similarity coefficients.”

Figure 3 and Table 3 have been modified as discussed below.

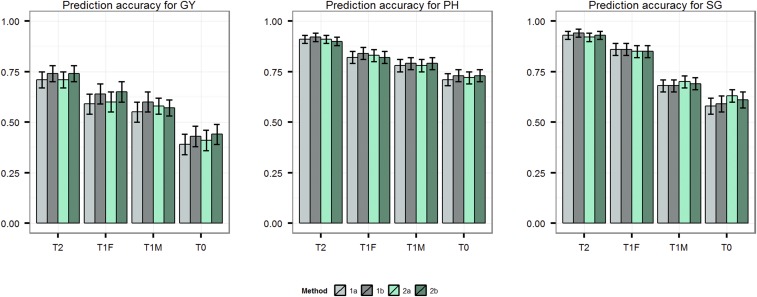
Figure 3 .

Prediction accuracy for T2, T1F, T1M and T0 cross-validation scenarios for traits grain yield (GY), plant height (PH), and staygreen (SG) obtained using the four methods 1a (Parent GCA), 1b (Parent GCA plus single-cross SCA), 2a (Additive genetic covariance among single crosses), and 2b (Additive plus dominance covariance among single crosses) as evaluated with training set of 250 and leave-one-individual-out cross-validation.

Table 3 .

General combining ability variance of stiff stalk synthetic (${\mathit{\sigma }}_{\mathit{GCA}\_\mathit{F}}^2$), and nonstiff stalk (${\mathit{\sigma }}_{\mathit{GCA}\_\mathit{M}}^2$) inbred progenies, and specific combining ability variance (${\mathit{\sigma }}_{\mathit{SCA}}^2$) of single crosses between them

Variance Components	Grain Yield	Plant Height	Staygreen
${\mathit{\sigma }}_{\mathit{GCA}\_\mathit{F}}^2$	0.22a	28.66a	0.12a
${\mathit{\sigma }}_{\mathit{GCA}\_\mathit{M}}^2$	0.20a	34.48a	0.23a
${\mathit{\sigma }}_{\mathit{SCA}}^2$	0.05a	2.6a	0.01a
${\mathit{\sigma }}_{\mathit{SCA}}^2/({\mathit{\sigma }}_{\mathit{GCA}\_\mathit{F}}^2+{\mathit{\sigma }}_{\mathit{GCA}\_\mathit{M}}^2)$	0.12	0.04	0.02

^aSignificant at α = 0.001.

Below we explain results that changed with use of a different GRM including the corresponding figure and table.

1. Methods based on the covariances among single crosses (i.e., methods 2a and 2b) provided similar prediction accuracies as the combining ability-based methods (i.e., methods 1a and 1b) with GRMs calculated as per method 1 of VanRaden (2008). Previously, when the GRMs were calculated as the simple matching coefficient, methods 2a and 2b resulted in lower prediction accuracies compared to methods 1a and 1b.

We explained in the paper that lower prediction accuracies of methods 2a and 2b were due to the confounding of genetic relationship and variance in deriving covariances among single-crosses. Specifically, we pointed out that different variances of male and female populations weigh their genomic relationships unequally in estimating covariances among single crosses. Knowing that the GRMs were previously calculated as a simple matching coefficient, the differences in allele frequencies between the two populations can also deteriorate the correlation between true (unknown) and estimated covariances among single-crosses. In method 1 of VanRaden (2008), the male and female genomic relationships are weighted by the frequency of the common reference allele, specifically the minor allele, in the corresponding populations. This helped to overcome the confounding effect of allele frequency differences in estimating covariances among single crosses.

To investigate this further, we estimated covariances among single crosses by directly using single-cross genotypes inferred using the parent genotypes. These served as an estimate of covariances among single crosses with reference to a single population. These covariances were correlated with estimates of single-cross covariances calculated in method 2a (i.e., single-cross covariance inferred from covariance among males and females parents belonging to two different populations). Both method 1 of VanRaden (2008) and a simple matching coefficient were used to calculate GRMs for purposes of comparison. The correlations obtained were as follow:

1. VanRaden method 1: 0.87.

2. Simple matching: 0.73.

The higher correlations for method 1 of VanRaden suggest low confounding due to allele frequency and variance component differences between the populations, and vice versa, for simple matching coefficient.

1. General combining ability (GCA)-based method (i.e., method 1a) provided similar prediction accuracy as the method including both GCA and specific combining ability (SCA) (i.e., method 1b) with GRM calculated as per method 1 of VanRaden. Previously, when the GRM was calculated using the simple matching coefficient, method 1b resulted in higher prediction accuracies compared to method 1a.

This difference in results could be attributed to a decrease in the proportion of SCA variance in using GRMs calculated as per method 1 of VanRaden compared to the proportion of SCA variance obtained in using GRMs calculated as simple matching coefficient. The decrease in the proportion of SCA variance in the former case is also due to weighing of genomic relationships with respect to reference allele frequency. This suggests that SCA may not provide additional benefit over GCA when the proportion of SCA variance is low. Our results are in accordance with a simulation study reporting that a high proportion of nonadditive variance and close genetic relationship are required to exploit nonadditive genetic effects in genomic prediction (Denis and Bouvet 2013).

A previous genomic selection study in maize reported that the choice of GRM did not affect prediction accuracies (Albrecht et al. 2011). This study involved a single reference population. Simple matching coefficient-based GRMs have also been used in previous genomic single-cross prediction studies (e.g., Massman et al. 2013). In that view, the new results obtained in this study suggest that choice of GRM for hybrid prediction applications is an important consideration.