Abstract
A synthetic approach to biology is a promising technique for various applications. Recent advancements have demonstrated the feasibility of constructing synthetic two-input logic gates in Escherichia coli cells with long-term memory based on DNA inversion induced by recombinases. Moreover, recent evidences indicate that DNA inversion mediated by genome editing tools is possible. Powerful genome editing technologies, such as CRISPR-Cas9 systems, have great potential to be exploited to implement large-scale recombinase-based circuits. What remains unclear is how to construct arbitrary Boolean functions based on these emerging technologies. In this paper, we lay the theoretical foundation formalizing the connection between recombinase-based genetic circuits and Boolean functions. It enables systematic construction of any given Boolean function using recombinase-based logic gates. We further develop a methodology leveraging existing electronic design automation (EDA) tools to automate the synthesis of complex recombinase-based genetic circuits with respect to area and delay optimization. In silico experimental results demonstrate the applicability of our proposed methods as a useful tool for recombinase-based genetic circuit synthesis and optimization.
Introduction
The development of synthetic biology shows the feasibility to implement computing devices with DNA genetic circuits in living cells. Synthetic cellular designs often intended to implement certain functions that make cells respond to specific environmental stimuli or even change their growth and cellular development. For instance, synthetic toggle switches1 and genetic oscillators2–5 can be used to control cell metabolism, synthetic counters6 can be potentially applied to the regulation of telomere length and cell aggregation, and genetic logic gates7–10 can achieve digital computation in response to stimulus input signals. In addition to these transcription-based DNA circuits, new emerging translational mRNA circuits11 are likely to have impact on mammalian regenerative medicine and gene therapy. Through the genetic engineering, synthetic cellular circuits are potentially useful to perform therapeutic and diagnostic functions.
For some situations where noxious chemical stimuli exist for many cell generations, the computational results from the synthetic circuits in parent cells are required to be propagated to their daughter cells so that the daughter cells can save time to respond to the environmental stimuli. To achieve this transgenerational memory, one possible method is to store the computational results in separate synthetic memory devices which can be duplicated in cell divisions. In the recent work of Siuti et al.12, a more efficient scheme for constructing synthetic cellular circuits with integrated logic and memory was proposed, where the computational result was automatically stored in the computing circuit configuration and the changes of configuration can be propagated to its descendant cells. The so-implemented circuits were built based on recombinases and tested in Escherichia coli cells and they showed a long-term memory for at least 90 cell generations. More recently, recombinase-based logic circuits has been applied in clinical uses. For instance, in recent work13 the authors demonstrate that biosensor made of recombinase-based logic gates can be used to detect pathological glycosuria in urine from diabetic patients. The ability to build complex recombinase-based logic circuits is an important step to enable widespread biomedical applications.
Specifically, the synthetic cellular circuits proposed by Siuti et al.12 used serine recombinases Bxb1 and phiC31 to implement various two-input logic gates. A serine recombinase targeting a pair of non-identical recognition sites known as attB (attachment site bacteria) and attP (attachment site phage) is able to induce irreversible DNA inversion. As illustrated in Fig. 1(a), since the inversion makes the recognition sites become hybrid sites called attR and attL which cannot be targeted by the recombinase, no further inversion is allowed afterwards.
Figure 1.
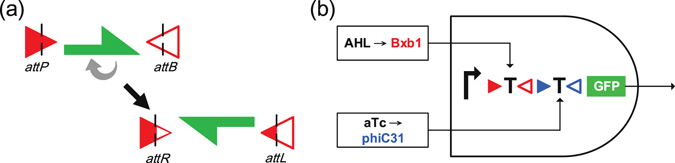
Recombinase-mediated DNA inversion and its application to the implementation of a logic gate. (a) Schematic illustration of the irreversible inversion of DNA sequences using serine recombinases. (b) Implementation of an AND gate using recombinases. The right-turn arrow represents a promoter; the red and blue triangles are the targeting sites of recombinases Bxb1 and phiC31, respectively; the letter T’s flanked by the targeting sites are transcription terminators; the green box represents the gene encoding the green fluorescent protein.
We illustrate how recombinases take part in the implementation of two-input logic gates with the two-input AND gate example shown in Fig. 1(b). (As a convention, in this paper we read a DNA sequence from left to right assuming the 5′-to-3′ direction of the coding strand). Let molecules AHL and aTc be the stimulus inputs to a cell and act as inducers activating the expressions of recombinases Bxb1 and phiC31, respectively. These recombinases when activated will irreversibly invert (flip) the DNA sequences flanked by their recognition sites (denoted by the colored triangle pairs). The DNA sequences being flanked can be a promoter, a transcription terminator, or a reporter, e.g., a green fluorescent protein (GFP). Inverting these DNA sequences will alter the output gene expression. In Fig. 1(b), two terminators were flanked by the recognition sites of recombinases Bxb1 and phiC31, and the output green fluorescent reporter is highly expressed only when both inducers AHL and aTc are in high concentration to activate BxB1 and phiC31 which together further flip and disable both terminators (denoted by letter “T”). Therefore, the circuit of Fig. 1(b) effectively implements a two-input AND gate. Note that such DNA sequence changes will survive through cell divisions and can be inherited to descendant cells in different generations. Hence the so-implemented logic function can achieve a long-term transgeneration memory.
Motivated by the viability and applicability of recombinase-based circuits, in this paper we formalize the construction of a general multi-input logic gate with its DNA sequence composed of series of promoters and transcription terminators targeted by multiple recombinases. We further characterize the set of Boolean functions realizable under such logic gates. In addition, we show a design flow for arbitrary Boolean function construction with cascaded recombinase-based logic gates. This automated design methodology is demonstrated by leveraging synthesis tool ABC14, an electronic design automation (EDA) tool developed at UC Berkeley, to synthesize cascaded multi-level recombinase-based circuits.
Methods and Results
To formalize the general multi-input gate construction, we use the three-input logic gates in Fig. 2(a–h) as examples to illustrate. Figure 2(a) shows a realization of a 3-input AND gate using three recombinases R 1, R 2, and R 3, where molecule I i is a stimulus input that activates the expression of recombinase R i, for i = 1, 2, 3. Then R i’s induce the inversions of their corresponding DNA sequence fragments. In order to express GFP in this gate, first we require R 1 to invert the inverted promoter so that the RNA polymerase can bind to it and begin the transcription of the downstream DNA sequence in which the GFP gene resides. Second, R 2 is needed to flip the terminator to avoid the termination of transcription before reaching the GFP gene. Third, R 3 is demanded to upright the GFP gene for the RNA polymerase to initiate GFP production. Collectively, to have GFP highly expressed all R i’s must exist, and thus this circuit implements a 3-input AND gate. Note that this 3-input AND gate, where the promoter and the reporter gene GFP can be flipped by recombinases, is designed in a different fashion from the 2-input AND gate in Fig. 1(b), where only transcription terminators are inverted by recombinases. The additional choice of flipping the DNA fragments of promoter and GFP gives more flexibility for logic gate construction.
Figure 2.
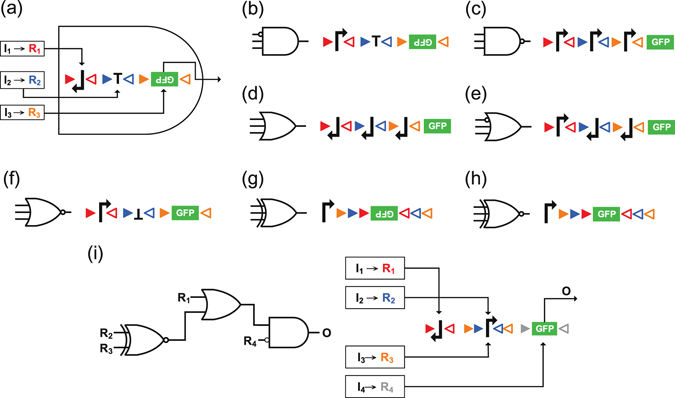
Examples of generalized multi-input recombinase-based logic gates. (a–h) Implementation of basic 3-input logic gates using recombinases. The inputs of each gate from top to down are recombinases R 1, R 2, and R 3, respectively; inducer I i monitored by the cell activates the expression of R i; the red, blue, and orange triangles denote the targeting sites of R i, i = 1, 2, 3, respectively. (i) Schematic illustration of a 4-bit non-basic logic function and corresponding implementation using recombinases.
In Fig. 2(b–h) we present seven other basic 3-input gates implemented with recombinases. Special implementations with nested targeting sites are applied on the XOR gate in (g) and the XNOR gate in (h). In the XOR gate in (g), the existence of one or three recombinases results in one or three times of GFP gene flipping and thus making the upside-down gene become upright, while the existence of two recombinases makes the GFP gene flip twice and remain upside down. Similar situations happen in the XNOR gate in (h).
Since the implementations of multi-input gates are possible, we are not constrained to using only 3-input gates and basic gate types, such as AND, OR, NAND, NOR, XOR, and XNOR gates. Rather, we can construct complex logic gates with more inputs. Figure 2(i) shows an example of a 4-input logic circuit
which can be directly realized by a single 4-input complex logic gate, instead of cascading multiple two-input gates.
Formalism of Recombinase-Based Logic Gates
Syntax of well-formed sequences
We define the following syntax to formalize the DNA sequences of logic gates constructed with recombinases. Here the basic elements composing a legal DNA sequence of a recombinase-based logic gate are “atomic terms”, including (inverted/non-inverted) transcription factors, (inverted/non-inverted) promoters, (inverted/non-inverted) genes, and targeting sites of recombinases. The syntax of DNA sequence forming a legal recombinase-based logic gate can be defined as follows.
Definition 1
An atomic term in a DNA sequence is a transcription terminator T, a promoter P, a gene G, an inverted transcription terminator
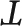 , an inverted promoter
, an inverted promoter
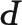 , or an inverted gene
, or an inverted gene
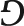 . The syntax of an atomic term can be expressed in Backus-Naur Form as
. The syntax of an atomic term can be expressed in Backus-Naur Form as
| 1 |
Let the targeting sites attP and attB of recombinase r in a DNA sequence be denoted as “{r” and “}r”, respectively. In the sequel, the subscripts of {r and }r may be omitted for brevity when they are clear from the context or immaterial to the discussion. Note that targeting sites “{” and “}” of a recombinase must appear in a pair.
Definition 2 The syntax of a well-formed sequence (wfs) is recursively defined as follows.
| 2 |
In this paper we concentrate on the special case of one-gene wfs (1g-wfs), where only one gene G, which is neither inverted nor sandwiched by targeting sites, appears at the end of the wfs and serves as the output. For example, 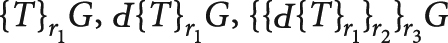 , and
, and 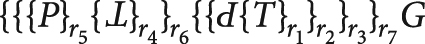 are 1g-wfs’s. Notice that under the 1g-wfs setting, the logic gate has a single output and the gene can only be transcribed in one direction from left to right.
are 1g-wfs’s. Notice that under the 1g-wfs setting, the logic gate has a single output and the gene can only be transcribed in one direction from left to right.
A pair of targeting sites of a recombinase is called basic if it only flanks an atomic term. Otherwise, it is called non-basic. We call a 1g-wfs basic if it contains only basic pairs of targeting sites, and non-basic if it contains some non-basic pair of targeting sites. For example, 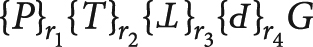 is a basic 1g-wfs. In contrast,
is a basic 1g-wfs. In contrast, 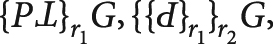 and
and 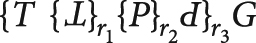 are non-basic 1g-wfs’s.
are non-basic 1g-wfs’s.
Furthermore, a non-basic pair of targeting sites can be nested. That is, a non-basic pair of targeting sites can be flanked by another pair of targeting sites. For instance, 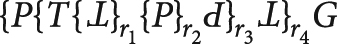 has nested two pairs of targeting sites targeted by the recombinases r
3 and r
4.
has nested two pairs of targeting sites targeted by the recombinases r
3 and r
4.
We discuss the logic functions induced by basic and non-basic 1g-wfs’s in the following.
Semantics of well-formed sequences – Basic well-formed sequences
We first study some reduction rules of basic 1g-wfs’s. Let σ be the DNA sequence of a basic 1g-wfs excluding the output gene, that is, σ is a basic wfs without any gene. We denote a wfs without any gene as 0g-wfs. Because σ is made of components 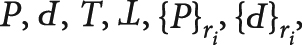 , and
, and 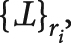 for any component C in σ the sequence σ can be decomposed into
for any component C in σ the sequence σ can be decomposed into
where σ 1 and σ 2 are two 0g-wfs’s, if non-empty. We show that the logic gate induced by the 1g-wfs σG can be further reduced to an equivalent form according to the type of the component C.
When C is a transcription terminator T, then σ equals
| 3 |
This equivalence holds because any transcription that starts from σ 1 to gene G is always blocked by the transcription terminator T in the middle, making σ 1 T a don’t-care and thus removable.
When C is an inverted terminator 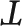 , then σ equals
, then σ equals
| 4 |
This equivalence holds because the inverted terminator 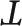 never blocks the transcription and is thus removable.
never blocks the transcription and is thus removable.
When C is a promoter P, then σ equals
| 5 |
This equivalence holds because no matter whether there is a transcription that starts from σ 1 to G or not, a transcription can always start from the promoter P. Therefore, σ 1 is a don’t-care and thus removable.
When C is an inverted promoter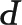 , then σ equals
, then σ equals
| 6 |
This equivalence holds because the transcription that begins at 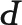 proceeds across σ
1 in the direction from right to left, it does not pass through G. As a result, the expression of G can not be initiated by
proceeds across σ
1 in the direction from right to left, it does not pass through G. As a result, the expression of G can not be initiated by 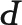 and thus
and thus 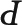 can be removed from the sequence.
can be removed from the sequence.
When C is 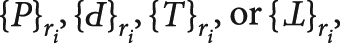 since an atomic term A is equivalent to {A}r for recombinase r being in low concentration (denoted R = 0 by treating r as a Boolean variable R of value 0) or
since an atomic term A is equivalent to {A}r for recombinase r being in low concentration (denoted R = 0 by treating r as a Boolean variable R of value 0) or 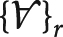 for recombinase r being in high concentration (denoted R = 1 by treating r as a Boolean variable R of value 1), the reduction rules for C can be easily extended from the previous rules as summarized below.
for recombinase r being in high concentration (denoted R = 1 by treating r as a Boolean variable R of value 1), the reduction rules for C can be easily extended from the previous rules as summarized below.
| 7 |
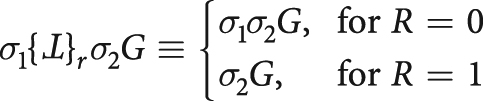 |
8 |
| 9 |
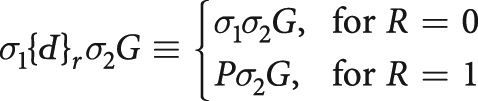 |
10 |
with the above analysis, we can derive the corresponding Boolean function of a given 1g-wfs. Consider the 1g-wfs σG with the sequence σ targeted by recombinases r
i, . Activating the expression of gene G requires the recombinases r
i’s have adequate (high or low) concentrations so that the 1g-wfs σG effectively reduces to PG. The Boolean function induced by σG is determined through a series of decisions made by r
i’s. In essence, it corresponds to a decision list15. To illustrate, consider the example 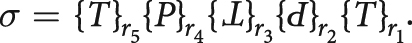 The decision list induced by the 1g-wfs σG is shown in Fig. 3. Note that given a sequence without non-basic targeting sites, the decisions always start from the rightmost to the leftmost components because a component closer to the gene may overwrite the effects imposed by the components on its left and thus it is of higher priority. Therefore, the Boolean function of σG is determined starting from R
1 to R
5. In order to reduce σ to P to express gene G, first we must require R
1 to be 1. Otherwise if R
1 = 0, σ becomes equivalent to a null sequence no matter what other R
i’s are. Next, if we let R
2 be 1, we can have an equivalent sequence equal to P as wished. Otherwise we can let R
2 be 0 and look for other possibilities for the reduction to P. If R
2 = 0, we can easily tell that the only possibility occurs when R
3 and R
4 are both 0 and that the logic of R
5 never affects the reduction. Collectively, the logic function of the gate σG is derived as , where symbol “+” denotes Boolean disjunction, symbol “·” denotes Boolean conjunction, and symbol “−” or “!” denotes Boolean negation. In the sequel, we sometimes omit the conjunction symbol “·” in a Boolean expression.
The decision list induced by the 1g-wfs σG is shown in Fig. 3. Note that given a sequence without non-basic targeting sites, the decisions always start from the rightmost to the leftmost components because a component closer to the gene may overwrite the effects imposed by the components on its left and thus it is of higher priority. Therefore, the Boolean function of σG is determined starting from R
1 to R
5. In order to reduce σ to P to express gene G, first we must require R
1 to be 1. Otherwise if R
1 = 0, σ becomes equivalent to a null sequence no matter what other R
i’s are. Next, if we let R
2 be 1, we can have an equivalent sequence equal to P as wished. Otherwise we can let R
2 be 0 and look for other possibilities for the reduction to P. If R
2 = 0, we can easily tell that the only possibility occurs when R
3 and R
4 are both 0 and that the logic of R
5 never affects the reduction. Collectively, the logic function of the gate σG is derived as , where symbol “+” denotes Boolean disjunction, symbol “·” denotes Boolean conjunction, and symbol “−” or “!” denotes Boolean negation. In the sequel, we sometimes omit the conjunction symbol “·” in a Boolean expression.
Figure 3.
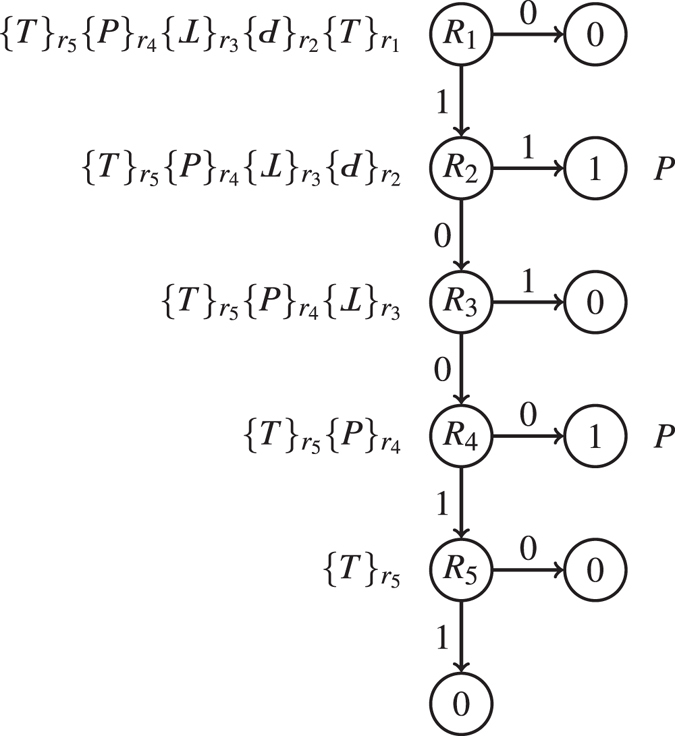
Decision list corresponding to 1g-wfs 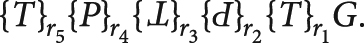 Node labelled R
i is the decision for the logic value of R
i. Nodes labelled 0 (resp. 1) stand for gene G cannot (resp. can) be expressed. The sequences beside nodes are the equivalent sequences after the corresponding (partial) decisions.
Node labelled R
i is the decision for the logic value of R
i. Nodes labelled 0 (resp. 1) stand for gene G cannot (resp. can) be expressed. The sequences beside nodes are the equivalent sequences after the corresponding (partial) decisions.
In general, we can systematically convert any basic 1g-wfs to its corresponding logic function. To achieve this conversion, the operator Ω over a 1g-wfs is defined in Table 1. For an empty sequence ⊥, we define Ω[⊥] = 0. For example, the Boolean function of the 1g-wfs 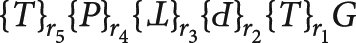 is derived by
is derived by
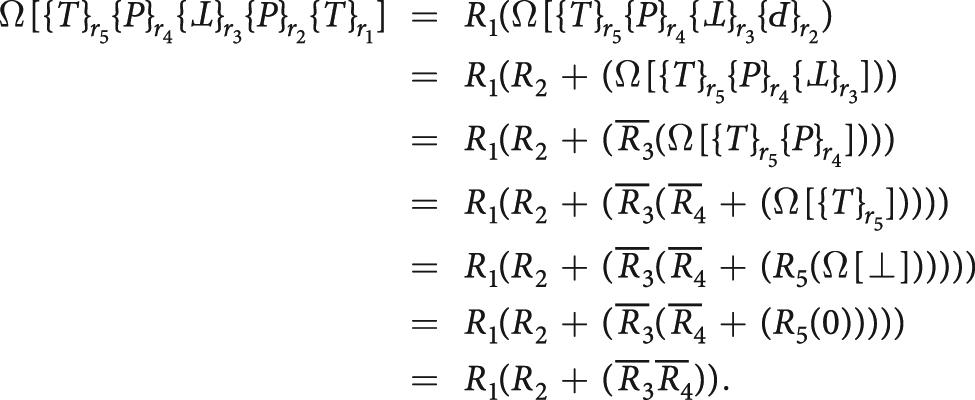 |
Table 1.
Operators for parsing basic 1g-wfs σCG, with (non-empty) 0g-wfs σ, component C, and gene G, to logic function.
| component C | operator Ω[σC] |
|---|---|
| T | 0 · (Ω[σ]) |
| P | 1 + (Ω[σ]) |
| {T}r | R · (Ω[σ]) |
| {P}r | |
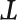
|
1 · (Ω[σ]) |
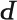
|
0 + (Ω[σ]) |
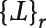
|
|
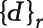
|
R + (Ω[σ]) |
Semantics of well-formed sequences – Non-basic well-formed sequences
We extend the above derivation of Boolean function to non-basic 1g-wfs’s by having the operator Ω over a 0g-wfs {σ}r (which can be basic or non-basic) defined as
| 11 |
where 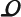 is the inverted sequence of σ. To understand equation (11), consider a 1g-wfs σG with only one pair of non-basic targeting sites. Suppose σ = {σ
1}r, where σ
1 is a basic 0g-wfs. Then σ is equal to σ
1 when R = 0 and to
is the inverted sequence of σ. To understand equation (11), consider a 1g-wfs σG with only one pair of non-basic targeting sites. Suppose σ = {σ
1}r, where σ
1 is a basic 0g-wfs. Then σ is equal to σ
1 when R = 0 and to 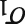 , the inverted sequence of σ
1, when R = 1. For example, the logic function for
, the inverted sequence of σ
1, when R = 1. For example, the logic function for  can be obtained by
can be obtained by
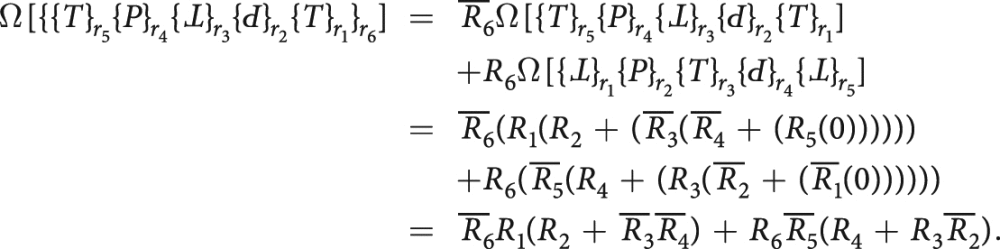 |
For a 1g-wfs with multiple (possibly nested) non-basic pairs of targeting sites, its logic function can also be directly derived by the Ω operator. For example, the logic function for 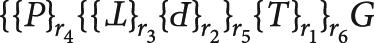 can be obtained by
can be obtained by
 |
Non-basic pairs of targeting sites can be exploited to efficiently construct special Boolean functions. One of such special functions is the parity function. An n-input odd parity function can be realized by the 1g-wfs
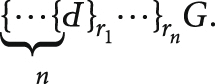 |
When there is an odd number of R i’s equal to 1, the 1g-wfs reduces to sequence PG and gene G can be expressed. Otherwise it reduces to sequence G and gene G cannot be expressed. On the other hand, the n-input even parity function can be realized by the 1g-wfs
Construction of Multi-level Recombinase-Based Logic Circuits
With the recombinase-based logic gates built from 1g-wfs’s, we can cascade them to implement arbitrary complex multi-level circuits. For example, the logic function Z = (A + B)(A ⊕ B) can be implemented with the two-level circuit shown in Fig. 4(a), which is composed of an OR-gate, an XOR-gate, and an AND-gate. One possible DNA implementation of Z with cascade can be derived by converting each gate to their 1g-wfs realizations as shown in Fig. 4(b). The 1g-wfs’s that encode the genes R 1, R 2, and Z correspond to the OR, XOR and AND gates, respectively. The recombinases r 1 and r 2 as the inputs to the AND gate are the intermediate signals.
Figure 4.
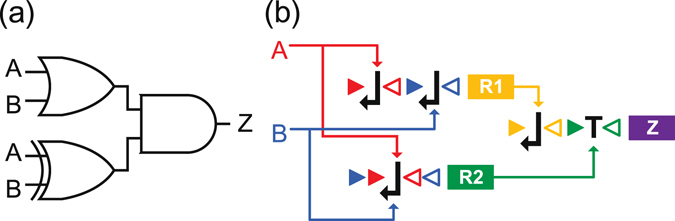
Example of a cascaded recombinase-based logic circuit. (a) Logic circuit of Boolean function Z = (A + B)(A ⊕ B). (b) The corresponding DNA implementation of the circuit in (a) with gate cascade. A and B denote the recombinase inputs of the overall circuit. The genes R1 and R2 encode the recombinases r 1 and r 2, respectively, which are the inputs to the downstream AND gate. The protein encoded by the gene Z is the output of the circuit.
Because the basic 1g-wfs gates can implement decision list functions, they form a functionally complete set of primitive logic gates that can be composed to implement any Boolean function. Therefore the 1g-wfs gates can be collected as a library for the synthesis of complex logic circuits. By leveraging conventional logic synthesis tools in electronic design automation (EDA), recombinase-based logic circuits can be synthesized with the flow shown in Fig. 5(a). Given a Boolean function or circuit netlist as the input, it is first optimized by technology-independent techniques for circuit simplification. The simplified circuit is further optimized by technology-dependent techniques for technology mapping using the primitive gates in the given standard cell library. To achieve recombinase-based logic circuit synthesis, the main task is to provide the library while all other optimization tasks can be done using existing logic synthesis tools.
Figure 5.
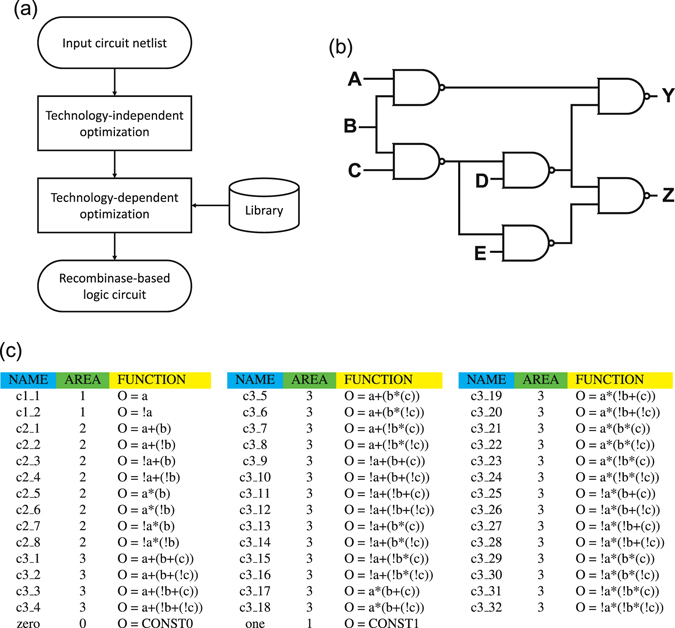
Illustration of the synthesis flow with an input circuit and a library of primitive gates. (a) Logic synthesis flow for the implementation of recombinase-based logic circuit. (b) Circuit diagram of an input circuit netlist example, ISCAS benchmark c17. Circuit c17 consists of six NAND gates with five inputs {A, B, C, D, E} and two outputs {Y, Z}. (c) Example of a library of DNA gates with area cost specified. The library contains 44 different cells and each cell corresponds to a DNA logic gate defined by a 1g-wfs with up to three inputs. The variables a, b, and c in a function specification represents the recombinase inputs to a gate, and the variable O denotes the gate output.
In this work, we adopt ABC14, an industrial-strength logic synthesis tool developed at UC Berkeley, for circuit synthesis and optimization. Given a circuit netlist, we first apply ABC to perform technology-independent optimization on the netlist, e.g., Boolean minimization to minimize the number of product terms and literals. We then use ABC to perform technology mapping to implement the area or performance optimized netlist using the 1g-wfs gates in the library.
To illustrate the synthesis flow, we consider implementing ISCAS benchmark circuit c17 shown in Fig. 5(b) with recombinase-based genetic circuit realization. The circuit consists of five inputs A, B, C, D, and E, and two outputs Y and Z with functions
| 12 |
For area-driven synthesis of benchmark c17, there are 44 DNA gates defined by their 1g-wfs’s with up to three recombinase inputs. They are collected as the library as shown in Fig. 5(c). According to the experiment in the previous work12, where the promoters and transcription terminators used are roughly of the same length, we treat the area cost of both promoter and transcription terminator as unity. Therefore, the area cost of a DNA gate is defined as the number of atomic terms, excluding the output gene, that appear in the 1g-wfs of the gate. For example, the gate c3_1 corresponding to a 3-input OR gate has three inverted promoters as shown in Fig. 2(d). Hence, the area cost of c3_1 is counted as 3 units. By providing the c17 netlist and the library to ABC, the tool can perform optimization and technology mapping to find an area-optimized circuit composed of DNA gates of the library. Note that area minimization of a recombinase-based circuit effectively reduces the number of used promoters and terminators on the DNA strand implementation. Therefore, less effort is required to synthesize the intended DNA strand via DNA assembly methods, e.g., Gibson assembly16. More importantly, a shorter DNA sequence is more likely to succeed in vector insertion to deploy the genetic circuit into the host cell to conduct the intended computation.
Figure 6(a) shows the result described in Verilog language of the synthesized c17 recombinase-based circuit using library gates listed in Fig. 5(c). The synthesized circuit comprises gates c2_4, c2_5, c3_14, and c3_25, and the total area cost is 10 units. Note that the naive DNA circuit implementation of c17 circuit by converting the digital logic gates in Fig. 5(b) to the corresponding DNA gates results in a total area cost of 12 units. Compared to the naive implementation, the area cost of the circuit synthesized by ABC technology mapping decreases. The logic functions of Y and Z in the synthesized circuit can be easily verified to be consistent with equation (12), implying the correctness of the synthesis result. The DNA circuit of module c17 in Fig. 6(a) is plotted in Fig. 6(c), where the symbols A, B, C, D, E, n7, and n8 represent some serine recombinases. In practice, to have recombinases achieve site-specific recombination in a synthetic genetic circuit, recombinases that have been reported to function outside their native hosts may be used. For example, well-reported recombinases17–29, such as ϕC31, ϕBT1, R4, BxB1, TP901-1, RV, SPBc, TG1, ϕFC1, MR11, ϕ370, ϕK38, A118, W β, and BL3 integrase, can be plausible molecular parts for realization of the recombinase signals in Fig. 6(c).
Figure 6.
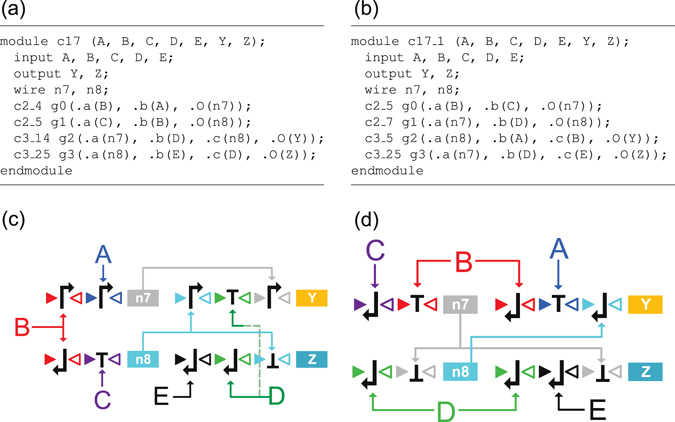
Synthesis results of circuit c17 in Verilog descriptions and in DNA circuit implementations. (a) Tool ABC synthesized c17 circuit in Verilog description. (b) Manually designed c17 circuit in Verilog description. (c) DNA circuit implementation of the ABC synthesized circuit in (a). (d) DNA circuit implementation of the manually designed circuit in (b). In both (c) and (d), symbols A, B, C, D, and E indicate the recombinase inputs, the proteins encoded by the genes Y and Z are the outputs of the circuit, and the DNA gates encoding recombinases n 7 and n 8 and proteins Y and Z are the gates g0, g1, g2, and g3, respectively, in the modules c17 and c17_1.
Note that there can be more than one area-optimized circuit of a logic function. For comparison, in Fig. 6(b) we show another manually designed DNA implementation of c17 circuit whose area cost is 10 units as well. The corresponding DNA circuit is plotted in Fig. 6(d). Notice that the two circuits in Fig. 6 differ not only in their constituent logic gates, but also in their logic depths. The circuit of Fig. 6(c) is of two logic levels, whereas that of Fig. 6(d) is of three logic levels. There are six longest paths in the former circuit:
They involve a cascade of two logic gates. On the other hand, there are two longest paths in the latter circuit:
They involve a cascade of three logic gates. In digital electronic circuits, a longer circuit path often corresponds to a longer propagation delay between circuit input and output signals. Similarly in biological circuits, a longer circuit path involves more transcription and translation cascades, resulting in a longer response time of output gene expression to input stimuli. Here, the former and latter circuits involve two (n7 and Y) and three (n7, n8, and Y) gene expression cascades, respectively. Therefore, although these two circuits have the same area cost, the circuit of Fig. 6(c) is preferred due to its better performance, i.e., shorter input-to-output response time. In addition, we will detail in Section Discussion that the delay optimization may present fewer foreign genes and thus impose less metabolic burden on the host cell. In the in silico experiments, we will synthesize circuits with area or performance optimized.
To demonstrate the feasibility of the proposed synthesis flow, we conduct in silico experiment on other 67 ISCAS benchmark circuits using recombinase-based DNA gates. We expanded the library such that it includes all 684 DNA gates with decision list functions up to five inputs. In the library, the area cost of a gate is determined by the number of atomic terms, excluding the output gene, appearing in its corresponding 1g-wfs. To reduce the number of gene expression cascades, we simply assume each logic gate is of the same unit delay. By specifying a unit delay for each gate in the library, the delay of a synthesized circuit equals the logic level, which equals the number of gene expression cascades in the longest path in the circuit. Consequently, under the unit delay model the performance-driven logic synthesis minimizes the delay time between input stimuli and output response in the synthesized recombinase-based circuit. Note that this simple unit delay model is not meant to reflect the timing behavior of actual biological systems, but to facilitate the logic synthesis algorithm to perform circuit logic level minimization.
The experimental results of 54 (out of the 67) circuits are shown in Table 2. The numbers of primary inputs/outputs, the number of inverters, and the number of logic gates (with the number of included buffers, if non-zero, reported in parentheses) are listed Columns 2, 3, and 4, respectively. The circuits were synthesized under two optimization settings: one for area optimization and the other for delay optimization. The results of area optimization are reported in Columns 5–7 and those of delay optimization are reported in Columns 8–10. For each synthesized circuit, its number of DNA gates, total area, and gate level are shown. In the naive implementations of benchmark circuits by simply converting the digital logic gates to the corresponding DNA gates, the total area of a DNA circuit can be roughly calculated as “#inverter” + 2 × “#gate”. Compared to the naive implementation, the circuits synthesized by ABC have much less area cost. Taking circuit b18 for example, we observe that the total area of the naive implementation is about 202110 which is much larger compared to the area 101870 of the area-optimized implementation and 105328 of the delay-optimized implementation. On the other hand, comparing area and delay optimized b18 circuits, delay optimization reduces the number of gate levels from 137 to 51 at cost of increasing area by 3500 units.
Table 2.
Results of technology mapping of ISCAS benchmark circuits.
| circuit name | benchmark profile | area optimization | delay optimization | ||||||
|---|---|---|---|---|---|---|---|---|---|
| #PI/#PO | #inverter | #gate (#buffer) | #DNA gate | area | #level | #DNA gate | area | #level | |
| b03 | 34/34 | 16 | 106 | 91 | 217 | 7 | 79 | 228 | 4 |
| b04 | 77/74 | 105 | 547 | 373 | 852 | 22 | 358 | 881 | 8 |
| b06 | 11/15 | 7 | 32 | 25 | 56 | 6 | 24 | 62 | 3 |
| b07 | 50/57 | 61 | 322 | 257 | 583 | 23 | 235 | 615 | 8 |
| b08 | 30/25 | 26 | 123 | 90 | 224 | 12 | 85 | 233 | 5 |
| b09 | 29/29 | 24 | 116 | 106 | 228 | 10 | 96 | 240 | 5 |
| b10 | 28/23 | 32 | 140 | 100 | 260 | 11 | 96 | 298 | 4 |
| b11 | 38/37 | 148 | 578 | 333 | 788 | 25 | 301 | 829 | 8 |
| b12 | 126/127 | 113 | 831 | 707 | 1648 | 15 | 673 | 1786 | 6 |
| b13 | 63/63 | 52 | 237 | 172 | 381 | 12 | 153 | 401 | 4 |
| b14 | 277/299 | 1531 | 8236 | 2851 | 6947 | 124 | 2791 | 7749 | 18 |
| b17 | 1452/1512 | 4474 | 26303 | 15344 | 37726 | 104 | 14802 | 39178 | 28 |
| b18 | 3357/3343 | 20372 | 90869 | 43018 | 101870 | 137 | 40277 | 105328 | 51 |
| b20 | 522/512 | 3068 | 16614 | 6119 | 14497 | 128 | 6111 | 16545 | 21 |
| b21 | 522/512 | 3089 | 16938 | 6173 | 14724 | 121 | 6147 | 16631 | 21 |
| b22 | 767/757 | 4491 | 24671 | 9302 | 22107 | 124 | 9286 | 24908 | 21 |
| c432 | 36/7 | 40 | 120 | 79 | 200 | 25 | 91 | 276 | 11 |
| c499 | 41/32 | 40 | 162 | 407 | 794 | 21 | 335 | 833 | 11 |
| c880 | 60/26 | 63 | 320 (26) | 234 | 530 | 26 | 208 | 553 | 8 |
| c1355 | 41/32 | 40 | 506 (32) | 394 | 781 | 19 | 328 | 878 | 10 |
| c1908 | 33/25 | 277 | 603 (162) | 336 | 690 | 28 | 271 | 736 | 13 |
| c2670 | 233/140 | 321 | 872 (196) | 409 | 956 | 19 | 400 | 1002 | 9 |
| c3540 | 50/22 | 490 | 1179 (223) | 566 | 1473 | 36 | 553 | 1649 | 14 |
| c5315 | 178/123 | 581 | 1726 (313) | 942 | 2202 | 25 | 908 | 2333 | 12 |
| c6288 | 32/32 | 32 | 2384 | 1825 | 3709 | 89 | 1502 | 3995 | 38 |
| c7552 | 207/108 | 876 | 2636 (534) | 1149 | 2496 | 59 | 1084 | 2754 | 11 |
| s208 | 19/10 | 35 | 61 | 39 | 100 | 8 | 39 | 105 | 3 |
| s298 | 17/20 | 44 | 75 | 55 | 125 | 7 | 52 | 138 | 3 |
| s344 | 24/26 | 59 | 101 | 82 | 178 | 11 | 67 | 175 | 4 |
| s349 | 24/26 | 57 | 104 | 84 | 179 | 11 | 67 | 175 | 4 |
| s382 | 24/27 | 59 | 99 | 78 | 172 | 8 | 70 | 191 | 3 |
| s386 | 13/13 | 41 | 118 | 71 | 186 | 7 | 61 | 195 | 3 |
| s400 | 24/27 | 56 | 106 | 80 | 173 | 9 | 76 | 220 | 3 |
| s420 | 35/18 | 74 | 122 | 79 | 202 | 11 | 72 | 196 | 4 |
| s444 | 24/27 | 62 | 119 | 75 | 169 | 9 | 74 | 210 | 3 |
| s510 | 25/13 | 32 | 179 | 116 | 311 | 8 | 102 | 324 | 4 |
| s526 | 24/27 | 52 | 141 | 88 | 202 | 11 | 79 | 223 | 3 |
| s641 | 54/43 | 272 | 107 | 94 | 217 | 17 | 82 | 232 | 6 |
| s713 | 54/42 | 254 | 139 | 90 | 212 | 16 | 85 | 237 | 6 |
| s820 | 23/24 | 33 | 256 | 130 | 353 | 8 | 129 | 394 | 4 |
| s832 | 23/24 | 25 | 262 | 132 | 358 | 9 | 135 | 406 | 4 |
| s838 | 67/34 | 149 | 241 | 163 | 415 | 12 | 142 | 398 | 5 |
| s1196 | 32/32 | 141 | 388 | 243 | 647 | 17 | 236 | 734 | 6 |
| s1238 | 32/32 | 80 | 428 | 278 | 734 | 17 | 259 | 790 | 7 |
| s1423 | 91/79 | 167 | 490 | 341 | 775 | 50 | 313 | 815 | 13 |
| s1488 | 14/25 | 103 | 550 | 299 | 820 | 12 | 272 | 910 | 4 |
| s1494 | 14/25 | 89 | 558 | 303 | 829 | 11 | 279 | 920 | 4 |
| s5378 | 214/228 | 1775 | 1004 | 844 | 1843 | 14 | 780 | 1849 | 7 |
| s9234 | 247/250 | 3570 | 2027 | 1065 | 2379 | 20 | 986 | 2442 | 9 |
| s13207 | 700/790 | 5378 | 2573 | 2006 | 4075 | 26 | 1818 | 4153 | 9 |
| s15850 | 611/684 | 6324 | 3448 | 2224 | 4946 | 35 | 2131 | 5018 | 16 |
| s35932 | 1763/2048 | 3861 | 12204 | 6776 | 14953 | 9 | 5565 | 14718 | 5 |
| s38417 | 1664/1742 | 13470 | 8709 | 6147 | 14319 | 23 | 5858 | 14551 | 10 |
| s38584 | 1464/1730 | 7805 | 11448 | 7066 | 16905 | 37 | 6243 | 16433 | 11 |
| avg ratio | 1.00 | 1.00 | 1.00 | 0.92 | 1.07 | 0.38 | |||
Discussion
Area vs. Delay Optimization
To pursue area or delay optimization in genetic circuit synthesis is a matter of tradeoff, and may depend on the intended application and/or biological feasibility. Nevertheless, Table 2 reveals that when the library of recombinase-based logic gates is used in ABC for logic synthesis, delay optimization often achieves effective reduction (62% on average) in logic level, or circuit depth, with a slight increase (7% on average) in circuit area compared to area optimization. Taking the largest circuit b18 benchmark for example, from area to delay optimization, the area cost increases by 3.39% while the logic level decreases by 62.77%. Particularly, in practice since we are limited by the biotechnology and the metabolic burden, circuits to be synthesized cannot be as large as b18 benchmark, which only serves as a proof of concept. Instead, small circuits, such as b06, are more likely to be implemented. For benchmark b06, the area cost increases by 10.71% (56 to 62) and the logic level decreases by 50% (6 to 3) from area to delay optimization. Moreover, the delay optimization helps reduce metabolic burden (to be discussed below). These facts imply that delay-driven optimization may often be a proper objective for logic synthesis of recombinase-based genetic circuits.
Metabolic Burden
One of the advantages of recombinase-based genetic circuits is its low metabolic burden imposed on the host cell30. Unlike a classic genetic circuit requiring continuous production of and action by activators or repressors to maintain the output gene expression, the output gene expression in a recombinase-based genetic circuit is determined by its DNA configuration, which is changed by DNA inversion or excision by recombinases; no further continuous recombinase supply and action is needed afterwards. This permanent configuration change is understood as a long-term (nonvolatile) memory, leading to the advantage of a lower metabolic burden on the host cell. This advantage may allow more complex genetic circuit implementation using recombinases. For example, recombinase-based finite state machines have been implemented in E. coli cells31. Moreover, a 6-input AND gate, a 2-data-input 4-select-input Boolean logic look-up table, a full adder, a full subtractor, and a half adder-subtractor were implemented in human embryonic kidney and Jurkat T cells32. Furthermore, we have shown recombinase-based logic gates can be adopted in the conventional logic synthesis flow for efficient circuit optimization. Because an efficient design can reduce metabolic burden and outperform an inferior counterpart even with the same functionality33, complex circuit implementation may benefit from the automation and optimization method proposed in this report.
Even with recombinase based construction, implementing a large circuit in a living cell may still be challenging due to the increase of metabolic burden34 caused by two major effects. First, a larger synthetic circuit requires more cellular energy to maintain its presence in the host cell35. Second, a large number of introduced genes will compete for the transcriptional and translational resources, resulting in resource redistribution36 and unexpected coupling among seemingly unconnected modules37, and thus leading to cell growth defects and poorly predictable circuit behavior. One approach to address these issues is to separate the target circuit into sub-circuits and implement the circuit across a consortium of host cells7,38–40. In particular, the consortium is divided into colonies of the same number of the sub-circuits. Each colony is composed of a strain implementing one of the sub-circuits. The sub-circuits are connected through cell-cell communication by wiring molecules (for example, quorum-sensing molecules and yeast pheromones) or metabolites like benzoic acid. Collectively, the whole cell population implements the target circuit. This distributed strategy may also apply to a large recombinase-based circuit implementation. For instance, the c17 circuit in Fig. 6(a) may be implemented by distributing the gates g0, g1, g2, and g3 into four strains of cells.
We note from Table 2 that when using recombinase-based logic gates as the library for a target circuit synthesis, the option of delay optimization introduces fewer DNA gates, each of which contains a gene, than the option of area optimization. Hence, delay optimization is preferred over area optimization due to a lower metabolic burden imposed by fewer foreign genes in the delay-optimized circuit.
Experimental Steps for Circuit Realization
Given a target Boolean function to be implemented as a genetic circuit, our method can be applied as the first step to build the blueprint for the wet-lab construction by using the logic synthesis tool ABC to derive the area or delay-optimized circuit. The next task is to associate the abstract signals of the synthesized netlist with concrete biochemical parts, including promoters, recombinases, and genes, for wet-lab implementation. After this association step, the DNA molecule of the genetic circuit is readily to be constructed by Gibson assembly16, Unique Nucleotide Sequence (UNS) Guided assembly41, or other assembly methods. Note that the promoters used here should have the ability to strongly promote transcription. After the assembly, the DNA constructs are transformed/transfected into cells using a standard protocol, such as the polyethylenimine (PEI) protocol. The cells should be kept and maintained in custom or standard media, such as Luria-Bertani (LB) medium and Dulbecco’s Modified Eagle’s medium (DMEM), and grown for one to two days in a stimuli-free medium. To test the synthetic circuit, cells have to be exposed to stimuli and grown for several hours, and then the fluorescence response from cells is measured by a flow cytometer. For each sample of the measurement, the same number of cells should be used for consistency. After creating a gate using forward scatter (FSC) and side scatter (SSC) and applying a proper fluorescence threshold on each fluorescent protein channel, the percentage of cells in an ON state is determined by flow cytometry analysis.
Alternative Genetic Circuit Construction with CRISPR/Cas9 Systems
Cas9 nucleases42 may possibly be exploited to achieve gene expression effects equivalent to what recombinases can achieve. For example, Cas9 nucleases are able to induce DNA deletion43,44, defective Cas9 nucleases (dCas9) can repress transcription by blocking transcriptional initiation or elongation45, and dCas9 fused with a transcriptional activator is capable of activating gene expression46. Specifically, DNA deletion of P and T may achieve an effect equivalent to inverting P and T, respectivley; transcription repression may achieve an effect equivalent to inverting P and 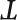 ; transcription activation may achieve an effect equivalent to inverting
; transcription activation may achieve an effect equivalent to inverting 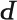 and T. These mechanisms allow CRISPR/Cas9 systems to be utilized as recombinase replacements for the implementation of decision list logic functions.
and T. These mechanisms allow CRISPR/Cas9 systems to be utilized as recombinase replacements for the implementation of decision list logic functions.
Conclusion
In this paper, we generalized the two-input recombinase-based DNA logic gates to multi-input cases. We formalized the syntax of recombinase-based logic gate construction, and obtained the Boolean function semantics of well-defined DNA sequences of recombinase-based logic gates. We also showed how to synthesize multi-level recombinase-based logic circuits using existing logic synthesis tools. In silico experimental results demonstrate the feasibility and efficiency of our proposed methods as a tool for recombinase-based genetic circuit minimization. As recombinase-based logic circuits have been used in clinical biomarker detection and tested in human cells, our tool can be useful to automate complex recombinase-based circuit construction for biologists to implement advanced biomedical applications.
Acknowledgements
This work was supported in part by the Ministry of Science and Technology of Taiwan under grant MOST 106-2923-E-002-002-MY3.
Author Contributions
T.Y.C. and J.H.J. conceived and designed the experiments. T.Y.C. performed the experiments. T.Y.C. and J.H.J. analyzed the data. T.Y.C. and J.H.J. contributed reagents/materials/analysis tools. T.Y.C. and J.H.J. wrote the paper.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 2.Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 3.Hasty J, Dolnik M, Rottschäfer V, Collins JJ. Synthetic gene network for entraining and amplifying cellular oscillations. Physical Review Letters. 2002;88:148101. doi: 10.1103/PhysRevLett.88.148101. [DOI] [PubMed] [Google Scholar]
- 4.Fung E, et al. A synthetic gene–metabolic oscillator. Nature. 2005;435:118–122. doi: 10.1038/nature03508. [DOI] [PubMed] [Google Scholar]
- 5.Stricker J, et al. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Friedland AE, et al. Synthetic gene networks that count. Science. 2009;324:1199–1202. doi: 10.1126/science.1172005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tamsir A, Tabor JJ, Voigt CA. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’. Nature. 2011;469:212–215. doi: 10.1038/nature09565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang B, Kitney RI, Joly N, Buck M. Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology. Nature communications. 2011;2:508. doi: 10.1038/ncomms1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moon TS, Lou C, Tamsir A, Stanton BC, Voigt CA. Genetic programs constructed from layered logic gates in single cells. Nature. 2012;491:249–253. doi: 10.1038/nature11516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bonnet J, Yin P, Ortiz ME, Subsoontorn P, Endy D. Amplifying genetic logic gates. Science. 2013;340:599–603. doi: 10.1126/science.1232758. [DOI] [PubMed] [Google Scholar]
- 11.Kopniczky MB, Moore SJ, Freemont PS. Multilevel regulation and translational switches in synthetic biology. IEEE transactions on biomedical circuits and systems. 2015;9:485–496. doi: 10.1109/TBCAS.2015.2451707. [DOI] [PubMed] [Google Scholar]
- 12.Siuti P, Yazbek J, Lu TK. Synthetic circuits integrating logic and memory in living cells. Nature biotechnology. 2013;31:448–452. doi: 10.1038/nbt.2510. [DOI] [PubMed] [Google Scholar]
- 13.Courbet, A., Endy, D., Renard, E., Molina, F. & Bonnet, J. Detection of pathological biomarkers in human clinical samples via amplifying genetic switches and logic gates. Science Translational Medicine7, 289ra83 (2015). [DOI] [PubMed]
- 14.Brayton, R. & Mishchenko, A. ABC: An academic industrial-strength verification tool. In Proceedings of International Conference on Computer Aided Verification, 24–40 (Springer, 2010).
- 15.Rivest RR. Learning decision lists. Machine Learning. 1987;2:229–246. [Google Scholar]
- 16.Gibson DG, et al. Enzymatic assembly of DNA molecules up to several hundred kilobases. Nature methods. 2009;6:343–345. doi: 10.1038/nmeth.1318. [DOI] [PubMed] [Google Scholar]
- 17.Brown WR, Lee NC, Xu Z, Smith MC. Serine recombinases as tools for genome engineering. Methods. 2011;53:372–379. doi: 10.1016/j.ymeth.2010.12.031. [DOI] [PubMed] [Google Scholar]
- 18.Thorpe HM, Smith MC. In vitro site-specific integration of bacteriophage DNA catalyzed by a recombinase of the resolvase/invertase family. Proceedings of the National Academy of Sciences. 1998;95:5505–5510. doi: 10.1073/pnas.95.10.5505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bibb LA, Hancox MI, Hatfull GF. Integration and excision by the large serine recombinase φ Rv1 integrase. Molecular microbiology. 2005;55:1896–1910. doi: 10.1111/j.1365-2958.2005.04517.x. [DOI] [PubMed] [Google Scholar]
- 20.Ghosh P, Kim AI, Hatfull GF. The orientation of mycobacteriophage Bxb1 integration is solely dependent on the central dinucleotide of attP and attB. Molecular cell. 2003;12:1101–1111. doi: 10.1016/S1097-2765(03)00444-1. [DOI] [PubMed] [Google Scholar]
- 21.Xu, Z. et al. Site-specific recombination in Schizosaccharomyces pombe and systematic assembly of a 400 kb transgene array in mammalian cells using the integrase of Streptomyces phage ϕBT1. Nucleic acids research36, e9–e9 (2008). [DOI] [PMC free article] [PubMed]
- 22.Keravala A, et al. A diversity of serine phage integrases mediate site-specific recombination in mammalian cells. Molecular Genetics and Genomics. 2006;276:135. doi: 10.1007/s00438-006-0129-5. [DOI] [PubMed] [Google Scholar]
- 23.Olivares EC, Hollis RP, Calos MP. Phage R4 integrase mediates site-specific integration in human cells. Gene. 2001;278:167–176. doi: 10.1016/S0378-1119(01)00711-9. [DOI] [PubMed] [Google Scholar]
- 24.Breüner A, Brøndsted L, Hammer K. Resolvase-like recombination performed by the TP901-1 integrase. Microbiology. 2001;147:2051–2063. doi: 10.1099/00221287-147-8-2051. [DOI] [PubMed] [Google Scholar]
- 25.Lazarevic V, et al. Nucleotide sequence of the Bacillus subtilis temperate bacteriophage SP β c2. Microbiology. 1999;145:1055–1067. doi: 10.1099/13500872-145-5-1055. [DOI] [PubMed] [Google Scholar]
- 26.Morita K, et al. In vitro characterization of the site-specific recombination system based on actinophage TG1 integrase. Molecular Genetics and Genomics. 2009;282:607–616. doi: 10.1007/s00438-009-0490-2. [DOI] [PubMed] [Google Scholar]
- 27.Yang H-Y, Kim Y-W, Chang H-I. Construction of an integration-proficient vector based on the site-specific recombination mechanism of Enterococcal temperate phage φ FC1. Journal of bacteriology. 2002;184:1859–1864. doi: 10.1128/JB.184.7.1859-1864.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rashel M, et al. A novel site-specific recombination system derived from bacteriophage ϕ MR11. Biochemical and biophysical research communications. 2008;368:192–198. doi: 10.1016/j.bbrc.2008.01.045. [DOI] [PubMed] [Google Scholar]
- 29.Canchaya C, et al. Genome analysis of an inducible prophage and prophage remnants integrated in the Streptococcus pyogenes strain SF370. Virology. 2002;302:245–258. doi: 10.1006/viro.2002.1570. [DOI] [PubMed] [Google Scholar]
- 30.Jusiak, B. et al. Synthetic gene circuits. Reviews in Cell Biology and Molecular Medicine (2014).
- 31.Roquet, N., Soleimany, A. P., Ferris, A. C., Aaronson, S. & Lu, T. K. Synthetic recombinase-based state machines in living cells. Science353, aad8559 (2016). [DOI] [PubMed]
- 32.Weinberg, B. H. et al. Large-scale design of robust genetic circuits with multiple inputs and outputs for mammalian cells. Nature Biotechnology (2017). [DOI] [PMC free article] [PubMed]
- 33.Ceroni F, Algar R, Stan G-B, Ellis T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nature methods. 2015;12:415–418. doi: 10.1038/nmeth.3339. [DOI] [PubMed] [Google Scholar]
- 34.Gorochowski TE, Van Den Berg E, Kerkman R, Roubos JA, Bovenberg RA. Using synthetic biological parts and microbioreactors to explore the protein expression characteristics of Escherichia coli. ACS synthetic biology. 2013;3:129–139. doi: 10.1021/sb4001245. [DOI] [PubMed] [Google Scholar]
- 35.Glick BR. Metabolic load and heterologous gene expression. Biotechnology advances. 1995;13:247–261. doi: 10.1016/0734-9750(95)00004-A. [DOI] [PubMed] [Google Scholar]
- 36.Gorochowski TE, Avcilar-Kucukgoze I, Bovenberg RA, Roubos JA, Ignatova Z. A minimal model of ribosome allocation dynamics captures trade-offs in expression between endogenous and synthetic genes. ACS synthetic biology. 2016;5:710–720. doi: 10.1021/acssynbio.6b00040. [DOI] [PubMed] [Google Scholar]
- 37.Gyorgy A, et al. Isocost lines describe the cellular economy of genetic circuits. Biophysical journal. 2015;109:639–646. doi: 10.1016/j.bpj.2015.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Regot S, et al. Distributed biological computation with multicellular engineered networks. Nature. 2011;469:207–211. doi: 10.1038/nature09679. [DOI] [PubMed] [Google Scholar]
- 39.Chen Y, Kim JK, Hirning AJ, Josić K, Bennett MR. Emergent genetic oscillations in a synthetic microbial consortium. Science. 2015;349:986–989. doi: 10.1126/science.aaa3794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Silva-Rocha R, de Lorenzo V. Engineering multicellular logic in bacteria with metabolic wires. ACS synthetic biology. 2013;3:204–209. doi: 10.1021/sb400064y. [DOI] [PubMed] [Google Scholar]
- 41.Torella JP, et al. Unique nucleotide sequence–guided assembly of repetitive DNA parts for synthetic biology applications. Nature protocols. 2014;9:2075–2089. doi: 10.1038/nprot.2014.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Doudna JA, Charpentier E. The new frontier of genome engineering with CRISPR-Cas9. Science. 2014;346:1258096. doi: 10.1126/science.1258096. [DOI] [PubMed] [Google Scholar]
- 43.Cong L, et al. Multiplex genome engineering using CRISPR/Cas systems. Science. 2013;339:819–823. doi: 10.1126/science.1231143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ran FA, et al. Double nicking by RNA-guided CRISPR Cas9 for enhanced genome editing specificity. Cell. 2013;154:1380–1389. doi: 10.1016/j.cell.2013.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Qi LS, et al. Repurposing CRISPR as an RNA-guided platform for sequence-specific control of gene expression. Cell. 2013;152:1173–1183. doi: 10.1016/j.cell.2013.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gilbert LA, et al. CRISPR-mediated modular RNA-guided regulation of transcription in eukaryotes. Cell. 2013;154:442–451. doi: 10.1016/j.cell.2013.06.044. [DOI] [PMC free article] [PubMed] [Google Scholar]


